Determining Regional-Scale Groundwater Recharge with GRACE and GLDAS
Abstract
1. Introduction
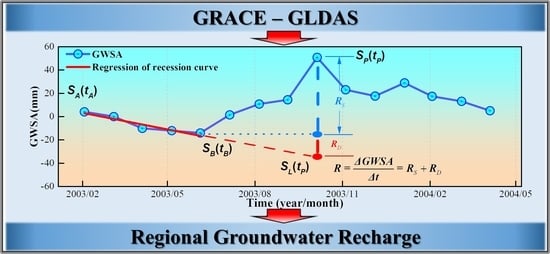
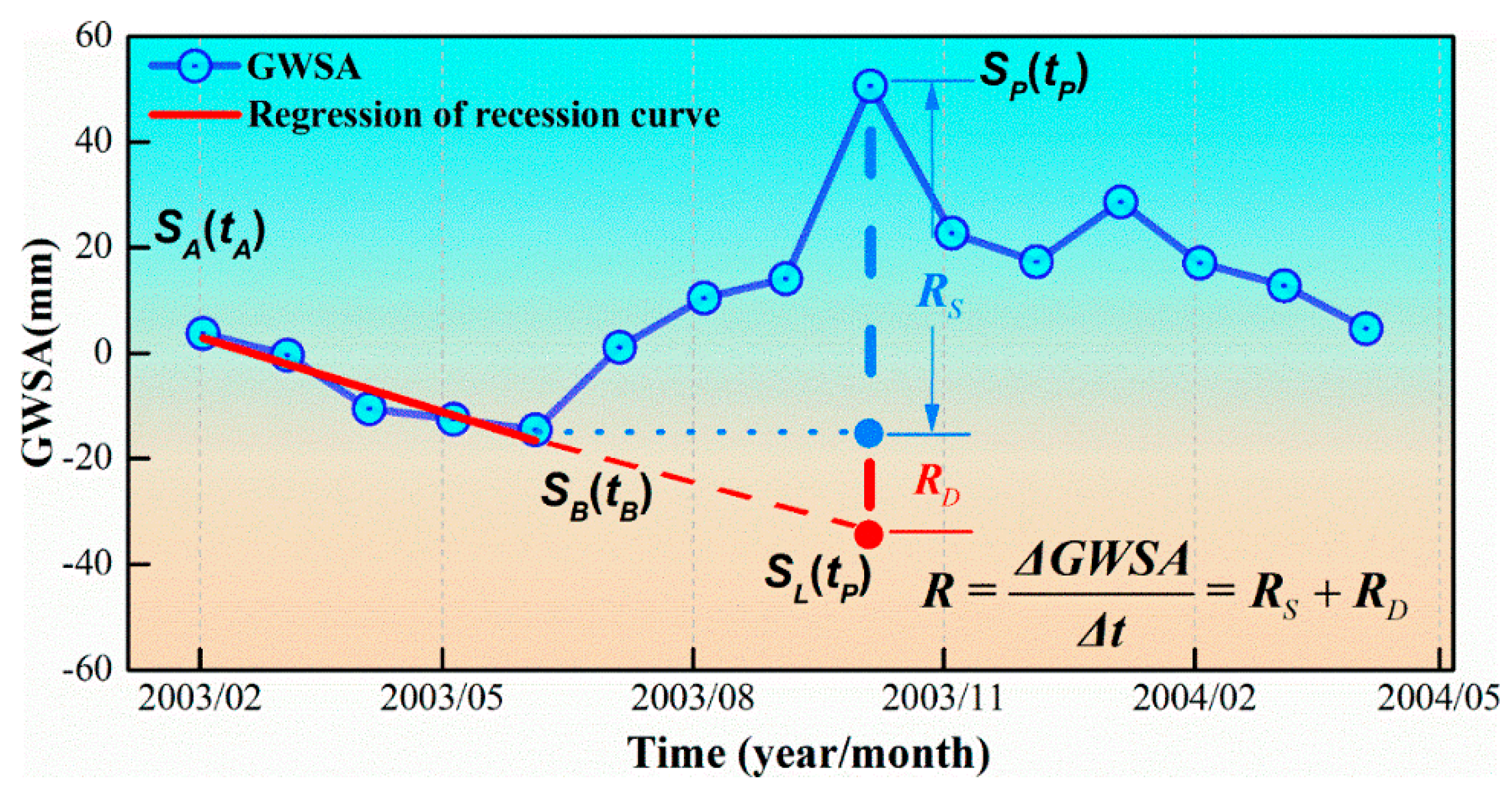
- The average recharge within a time period equals to the sum of change of groundwater storage and groundwater discharge [44,45]; the average change of groundwater storage can be evaluated by the slope of the best-fitted linear equation to the measured GWSA as a function of time; and the groundwater discharge is the sum of natural discharge and total water withdrawn by pumping wells, which need to be estimated from other methods or information.
- The water storage fluctuation method [43] is used to estimate recharge from the change of groundwater storage, which is analogous to the well-known water table fluctuation (WTF). More specifically, the change in GWSA between the peak and trough over the time interval of interest gives net recharge [43].
2. Materials and Methods
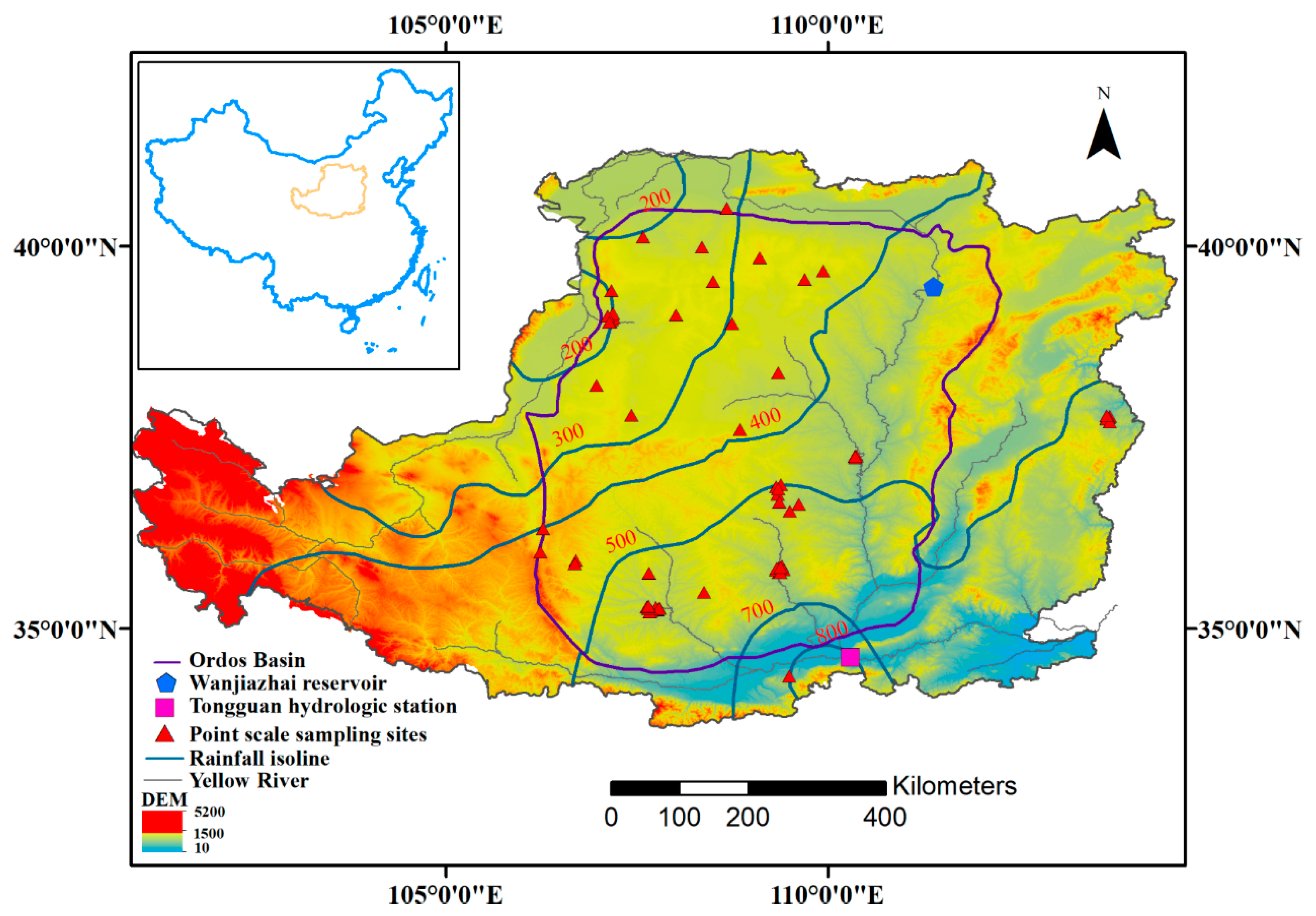
2.1. Study Area
2.2. Isolation of GWSA from TWSA
2.3. Estimation of Groundwater Recharge
2.4. Uncertainty in Estimated Recharge Rates
3. Results
3.1. GRACE-Derived Groundwater Storage Anomaly (GWSA) Variations
3.2. Comparison of GRACE-Derived Groundwater Recharge with Estimates from Other Methods
3.3. Evaluation of the Uncertainty of the Estimated Total Groundwater Recharge Rates at Regional Scale
4. Discussion
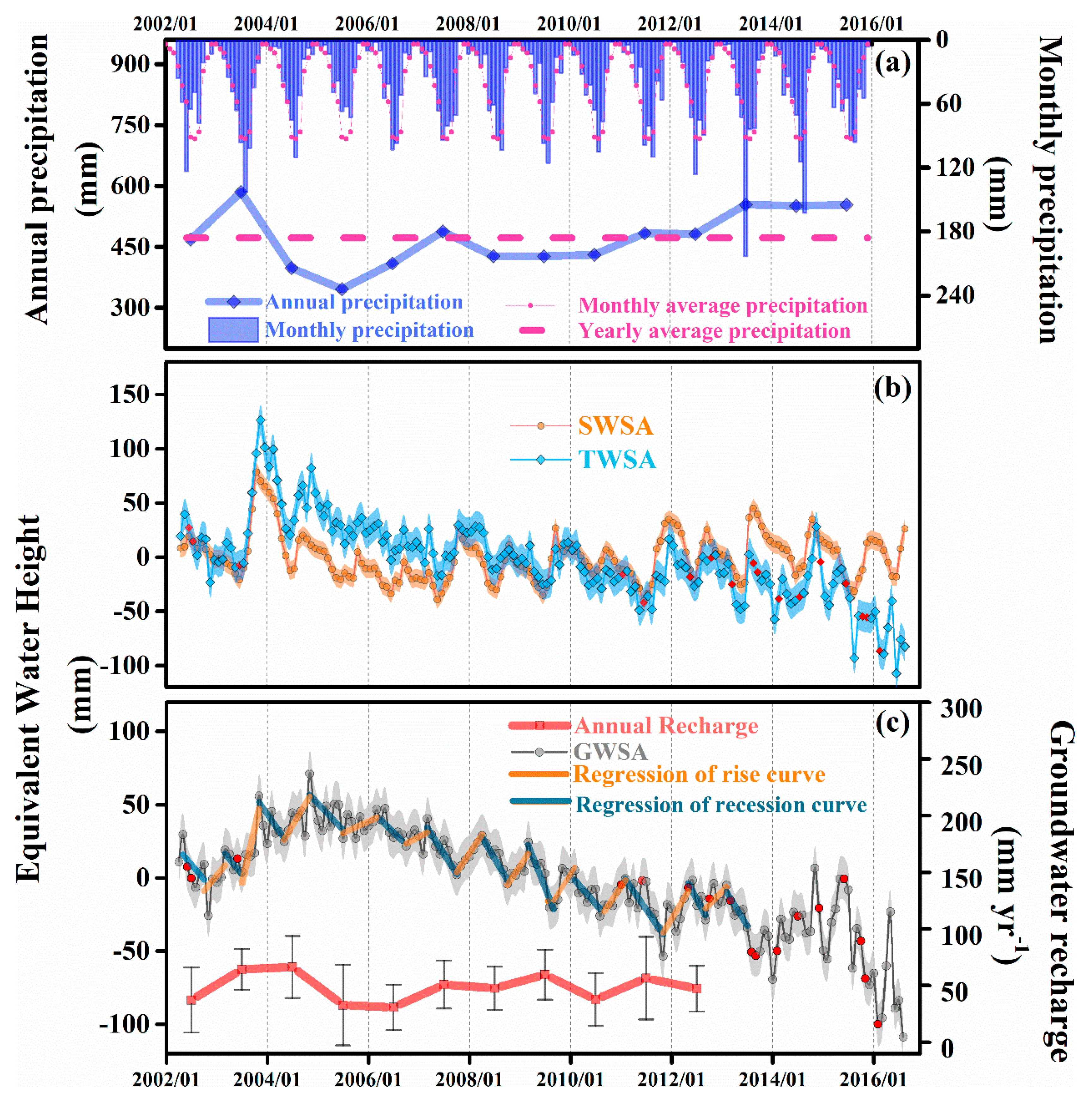
4.1. GWSA Seasonality, Long-Term Change and Delay in Response to Precipitation
4.2. What Is the Difference between Estimates from Our Method and Other Methods?
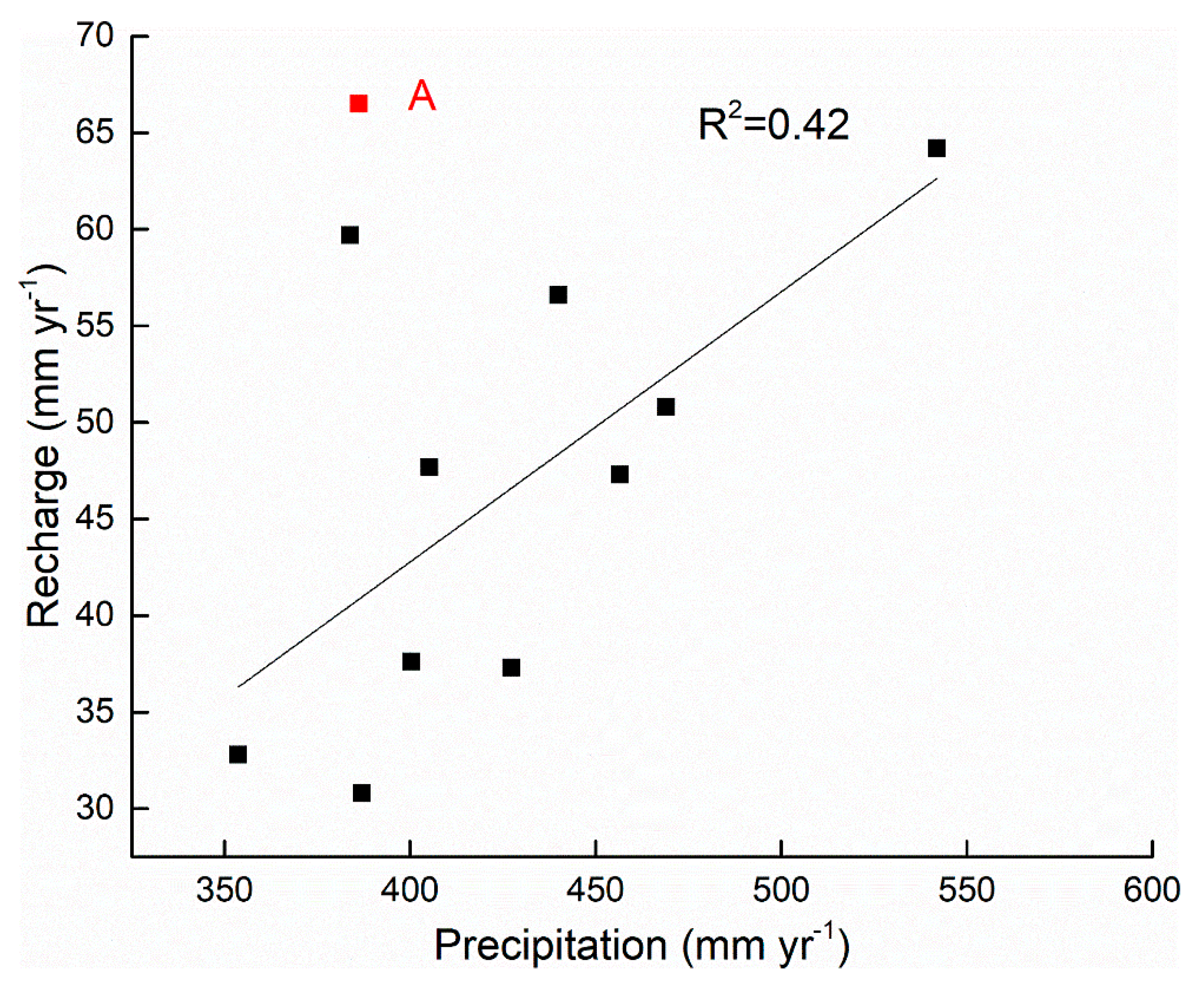
4.3. Precipitation Dominated the Interannual Variability in Groundwater Recharge between 2002 and 2012
4.4. Uncertainty of the Groundwater Recharge Estimate Based on GRACE Data Compared with Other Methods
4.5. Limitation
5. Conclusions
- Annual recharge varies from 30.8 to 66.5 mm year−1 between 2002 and 2012, 42% of which can be explained by annual precipitation variation. There was no obvious long-term trend in GR in the period. This suggests that precipitation dominates the interannual variability of GR in the Ordos Basin.
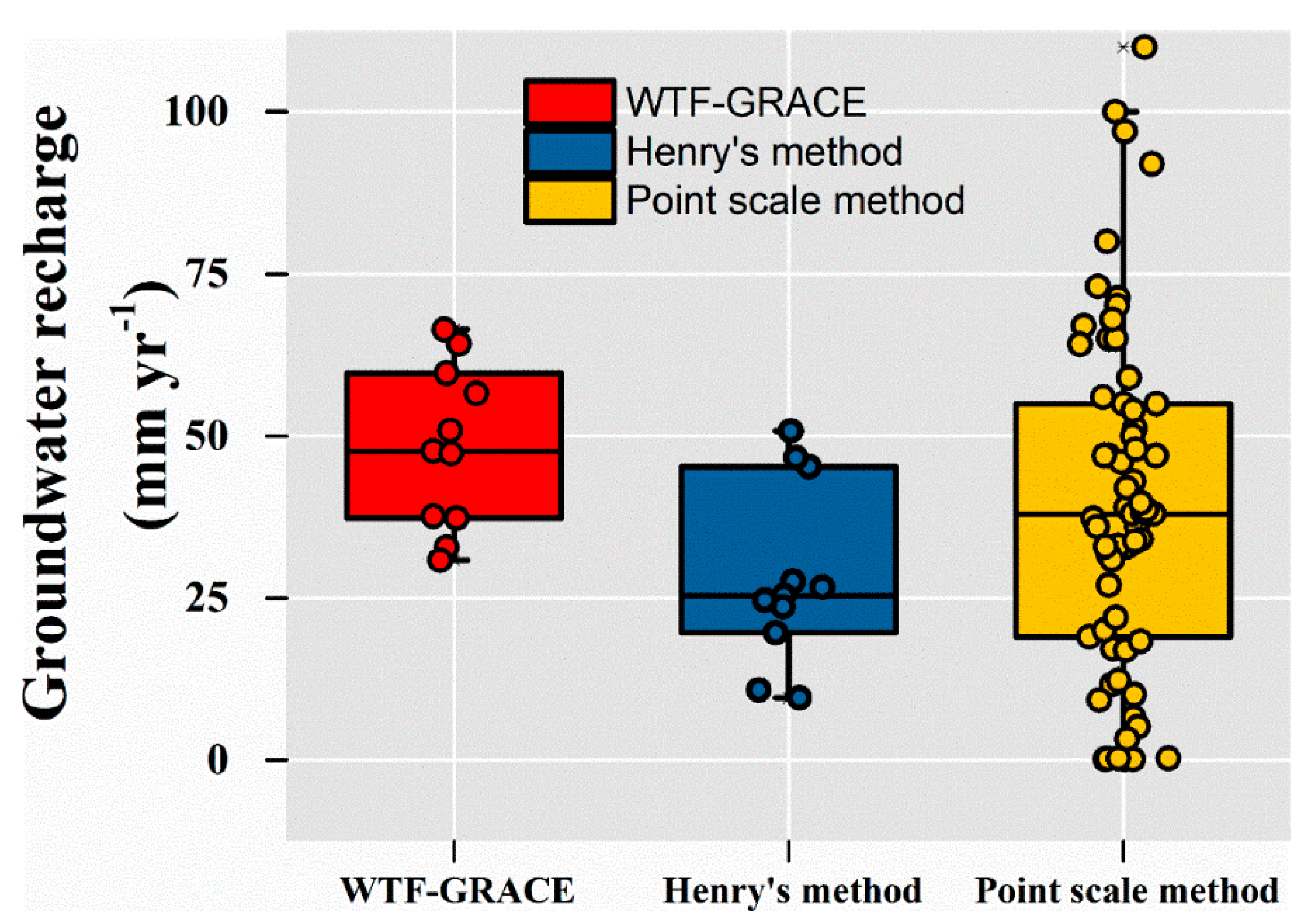
- The estimated mean recharge (48.3 mm year−1) was 20.0 mm year−1 greater than the mean net recharge obtained from the method of Henry et al. [43] and had no significant difference from the reported point-scale estimates.
- The estimated long-term recharge had a standard deviation of 16.0 mm year−1 and a CV of 33.1%, which was, in most cases, comparable to or smaller than that of other methods.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Cl | Chloride |
| CLM | Community Land Model |
| CMB | Chloride Mass Balance method |
| CSR | Center for Space Research |
| GLDAS | Global Land Data Assimilation System |
| GRACE | Gravity Recovery and Climate Experiment |
| GR | groundwater recharge |
| GWSA | Groundwater Storage Anomaly |
| 3H | Tritium |
| Mascon | Mass concentration |
| NASA | National Aeronautics and Space Administration |
| NOAH | National Centers for Environmental Prediction/Oregon State University/Air Force/Hydrologic Research Lab model |
| Slepian solutions | the Slepian localization of spherical harmonics solutions |
| SWSA | Soil Water Storage Anomaly |
| TWSA | Total Water Storage Anomaly |
| VIC | Variable Infiltration Capacity |
| WTF | Groundwater Table Fluctuation |
References
- Scanlon, B.R.; Faunt, C.C.; Longuevergne, L.; Reedy, R.C.; Alley, W.M.; McGuire, V.L.; McMahon, P.B. Groundwater depletion and sustainability of irrigation in the US High Plains and Central Valley. Proc. Natl. Acad. Sci. USA 2012, 109, 9320–9325. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground water and climate change. Nat. Clim. Chang. 2013, 3, 322–329. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing appropriate technique for quantifying groundwater recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Keese, K.E.; Flint, A.L.; Flint, L.E.; Gaye, C.B.; Edmunds, W.M.; Simmers, I. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Process. 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
- Petheram, C.; Walker, G.; Grayson, R.; Thierfelder, T.; Zhang, L. Towards a framework for predicting impacts of land-use on recharge: 1. A review of recharge studies in Australia. Soil Res. 2002, 40, 397. [Google Scholar] [CrossRef]
- Allison, G.B.; Gee, G.W.; Tyler, S.W. Vadose-Zone Techniques for Estimating Groundwater Recharge in Arid and Semiarid Regions. Soil Sci. Soc. Am. J. 1994, 58, 6. [Google Scholar] [CrossRef]
- Kim, J.H.; Jackson, R.B. A Global Analysis of Groundwater Recharge for Vegetation, Climate, and Soils. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Butler, M.J.; Verhagen, B.T. Isotope Studies of a Thick Unsaturated Zone in a Semi-Arid Area of Southern Africa. Available online: https://inis.iaea.org/search/search.aspx?orig_q=RN:33003268 (accessed on 30 November 2018).
- Gaye, C.B.; Edmunds, W.M. Groundwater recharge estimation using chloride, stable isotopes and tritium profiles in the sands of northwestern Senegal. Environ. Geol. 1996, 27, 246–251. [Google Scholar] [CrossRef]
- Rangarajan, R.; Athavale, R.N. Annual replenishable ground water potential of India—An estimate based on injected tritium studies. J. Hydrol. 2000, 234, 38–53. [Google Scholar] [CrossRef]
- Koeniger, P.; Gaj, M.; Beyer, M.; Himmelsbach, T. Review on soil water isotope-based groundwater recharge estimations. Hydrol. Process. 2016, 30, 2817–2834. [Google Scholar] [CrossRef]
- Gee, G.W.; Hillel, D. Groundwater Recharge In Arid Regions—Review And Critique Of Estimation Methods. Hydrol. Process. 1988, 2, 255–266. [Google Scholar] [CrossRef]
- Healy, R.W.; Cook, P.G. Using groundwater levels to estimate recharge. Hydrogeol. J. 2002, 10, 91–109. [Google Scholar] [CrossRef]
- Sophocleous, M.A. Combining the soilwater balance and water-level fluctuation methods to estimate natural groundwater recharge: Practical aspects. J. Hydrol. 1991. [Google Scholar] [CrossRef]
- Wine, M.L.; Hendrickx, J.M.H.; Cadol, D.; Zou, C.B.; Ochsner, T.E. Deep drainage sensitivity to climate, edaphic factors, and woody encroachment, Oklahoma, USA. Hydrol. Process. 2015, 29, 3779–3789. [Google Scholar] [CrossRef]
- Custodio, E.; Jódar, J. Simple solutions for steady–state diffuse recharge evaluation in sloping homogeneous unconfined aquifers by means of atmospheric tracers. J. Hydrol. 2016, 540, 287–305. [Google Scholar] [CrossRef]
- Li, Z.; Chen, X.; Liu, W.; Si, B. Determination of groundwater recharge mechanism in the deep loessial unsaturated zone by environmental tracers. Sci. Total Environ. 2017, 586, 827–835. [Google Scholar] [CrossRef] [PubMed]
- Wood, W.W.; Sanford, W.E. Chemical and Isotopic Methods for Quantifying Ground-Water Recharge in a Regional, Semiarid Environment. Ground Water 1995, 33, 458–468. [Google Scholar] [CrossRef]
- Dyck, M.F.; Kachanoski, R.G.; de Jong, E. Long-term Movement of a Chloride Tracer under Transient, Semi-Arid Conditions. Soil Sci. Soc. Am. J. 2003, 67, 471. [Google Scholar] [CrossRef]
- Chemingui, A.; Sulis, M.; Paniconi, C. An assessment of recharge estimates from stream and well data and from a coupled surface-water/groundwater model for the des Anglais catchment, Quebec (Canada). Hydrogeol. J. 2015, 23, 1731–1743. [Google Scholar] [CrossRef]
- Andreasen, M.; Andreasen, L.A.; Jensen, K.H.; Sonnenborg, T.O.; Bircher, S. Estimation of Regional Groundwater Recharge Using Data from a Distributed Soil Moisture Network. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Assefa, K.A.; Woodbury, A.D. Transient, spatially varied groundwater recharge modeling. Water Resour. Res. 2013, 49, 4593–4606. [Google Scholar] [CrossRef]
- Cao, G.; Zheng, C.; Scanlon, B.R.; Liu, J.; Li, W. Use of flow modeling to assess sustainability of groundwater resources in the North China Plain. Water Resour. Res. 2013, 49, 159–175. [Google Scholar] [CrossRef]
- Carrera-Hernández, J.J.; Smerdon, B.D.; Mendoza, C.A. Estimating groundwater recharge through unsaturated flow modelling: Sensitivity to boundary conditions and vertical discretization. J. Hydrol. 2012, 452–453, 90–101. [Google Scholar] [CrossRef]
- Qi, W.; Zhang, C.; Fu, G.T.; Zhou, H.C. Global Land Data Assimilation System data assessment using a distributed biosphere hydrological model. J. Hydrol. 2015, 528, 652–667. [Google Scholar] [CrossRef]
- Robock, A.; Luo, L.F.; Wood, E.F.; Wen, F.H.; Mitchell, K.E.; Houser, P.R.; Schaake, J.C.; Lohmann, D.; Cosgrove, B.; Sheffield, J.; et al. Evaluation of the North American Land Data Assimilation System over the southern Great Plains during the warm season. J. Geophys. Res. 2003, 108, 8846. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S. The potential for satellite-based monitoring of groundwater storage changes using GRACE: The High Plains aquifer, Central US. J. Hydrol. 2002, 263, 245–256. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Methods for inferring regional surface-mass anomalies from Gravity Recovery and Climate Experiment (GRACE) measurements of time-variable gravity. J. Geophys. Res. Solid Earth 2002, 107, 2193. [Google Scholar] [CrossRef]
- Molina, J.L.; García Aróstegui, J.L.; Benavente, J.; Varela, C.; de la Hera, A.; López Geta, J.A. Aquifers overexploitation in SE Spain: A proposal for the integrated analysis of water management. Water Resour. Manag. 2009. [Google Scholar] [CrossRef]
- Bhanja, S.N.; Mukherjee, A.; Saha, D.; Velicogna, I.; Famiglietti, J.S. Validation of GRACE based groundwater storage anomaly using in-situ groundwater level measurements in India. J. Hydrol. 2016, 543, 729–738. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Lo, M.; Ho, S.L.; Bethune, J.; Anderson, K.J.; Syed, T.H.; Swenson, S.C.; de Linage, C.R.; Rodell, M. Satellites measure recent rates of groundwater depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38, L03403. [Google Scholar] [CrossRef]
- Frappart, F.; Papa, F.; Güntner, A.; Werth, S.; Santos da Silva, J.; Tomasella, J.; Seyler, F.; Prigent, C.; Rossow, W.B.; Calmant, S.; et al. Satellite-based estimates of groundwater storage variations in large drainage basins with extensive floodplains. Remote Sens. Environ. 2011, 115, 1588–1594. [Google Scholar] [CrossRef]
- Feng, W.; Zhong, M.; Lemoine, J.M.; Biancale, R.; Hsu, H.T.; Xia, J. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
- Ramillien, G.; Frappart, F.; Cazenave, A.; Güntner, A. Time variations of land water storage from an inversion of 2 years of GRACE geoids. Earth Planet. Sci. Lett. 2005, 235, 283–301. [Google Scholar] [CrossRef]
- Huang, T.; Pang, Z.; Edmunds, W.M. Soil profile evolution following land-use change: Implications for groundwater quantity and quality. Hydrol. Process. 2013, 27, 1238–1252. [Google Scholar] [CrossRef]
- Huang, Z.; Pan, Y.; Gong, H.; Yeh, P.J.F.; Li, X.; Zhou, D.; Zhao, W. Subregional-scale groundwater depletion detected by GRACE for both shallow and deep aquifers in North China Plain. Geophys. Res. Lett. 2015, 42, 1791–1799. [Google Scholar] [CrossRef]
- Shamsudduha, M.; Taylor, R.G.; Longuevergne, L. Monitoring groundwater storage changes in the highly seasonal humid tropics: Validation of GRACE measurements in the Bengal Basin. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Shen, H.; Leblanc, M.; Tweed, S.; Liu, W. Groundwater depletion in the Hai River Basin, China, from in situ and GRACE observations. Hydrol. Sci. J. 2015, 60, 671–687. [Google Scholar] [CrossRef]
- Strassberg, G.; Scanlon, B.R.; Rodell, M. Comparison of seasonal terrestrial water storage variations from GRACE with groundwater-level measurements from the High Plains Aquifer (USA). Geophys. Res. Lett. 2007, 34, L14402. [Google Scholar] [CrossRef]
- Xie, X.; Xu, C.; Wen, Y.; Li, W. Monitoring Groundwater Storage Changes in the Loess Plateau Using GRACE Satellite Gravity Data, Hydrological Models and Coal Mining Data. Remote Sens. 2018, 10, 605. [Google Scholar] [CrossRef]
- Liesch, T.; Ohmer, M. Comparison of GRACE data and groundwater levels for the assessment of groundwater depletion in Jordan. Hydrogeol. J. 2016, 24, 1547–1563. [Google Scholar] [CrossRef]
- Yin, W.; Hu, L.; Jiao, J.J. Evaluation of Groundwater Storage Variations in Northern China Using GRACE Data. Geofluids 2017, 2017, 1–13. [Google Scholar] [CrossRef]
- Henry, C.M.; Allen, D.M.; Huang, J. Groundwater storage variability and annual recharge using well-hydrograph and GRACE satellite data. Hydrogeol. J. 2011, 19, 741–755. [Google Scholar] [CrossRef]
- Gonçalvès, J.; Petersen, J.; Deschamps, P.; Hamelin, B.; Baba-Sy, O. Quantifying the modern recharge of the “fossil” Sahara aquifers. Geophys. Res. Lett. 2013, 40, 2673–2678. [Google Scholar] [CrossRef]
- Ahmed, M.; Abdelmohsen, K. Quantifying Modern Recharge and Depletion Rates of the Nubian Aquifer in Egypt. Surv. Geophys. 2018, 39, 729–751. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, M.; Zhu, Y.; Liu, Z. Impacts of land use and plant characteristics on dried soil layers in different climatic regions on the Loess Plateau of China. Agric. For. Meteorol. 2011, 151, 437–448. [Google Scholar] [CrossRef]
- Huang, T.; Yang, S.; Liu, J.; Li, Z. How much information can soil solute profiles reveal about groundwater recharge? Geosci. J. 2016, 20, 495–502. [Google Scholar] [CrossRef]
- Liang, W.; Bai, D.; Wang, F.; Fu, B.; Yan, J.; Wang, S.; Yang, Y.; Long, D.; Feng, M. Quantifying the impacts of climate change and ecological restoration on streamflow changes based on a Budyko hydrological model in China’s Loess Plateau. Water Resour. Res. 2015, 51, 6500–6519. [Google Scholar] [CrossRef]
- Shi, H.; Shao, M. Soil and water loss from the Loess Plateau in China. J. Arid Environ. 2000, 45, 9–20. [Google Scholar] [CrossRef]
- Chen, J.S.; Liu, X.Y.; Wang, C.Y.; Rao, W.B.; Tan, H.B.; Dong, H.Z.; Sun, X.X.; Wang, Y.S.; Su, Z.G. Isotopic constraints on the origin of groundwater in the Ordos Basin of northern China. Environ. Earth Sci. 2012, 66, 505–517. [Google Scholar] [CrossRef]
- Gates, J.B.; Scanlon, B.R.; Mu, X.; Zhang, L. Impacts of soil conservation on groundwater recharge in the semi-arid Loess Plateau, China. Hydrogeol. J. 2011, 19, 865–875. [Google Scholar] [CrossRef]
- Huang, T.; Pang, Z. Estimating groundwater recharge following land-use change using chloride mass balance of soil profiles: A case study at Guyuan and Xifeng in the Loess Plateau of China. Hydrogeol. J. 2011, 19, 177–186. [Google Scholar] [CrossRef]
- Huang, T.; Pang, Z.; Liu, J.; Ma, J.; Gates, J. Groundwater recharge mechanism in an integrated tableland of the Loess Plateau, northern China: Insights from environmental tracers. Hydrogeol. J. 2017, 25, 2049–2065. [Google Scholar] [CrossRef]
- Huang, T.M.; Pang, Z.H.; Liu, J.L.; Yin, L.H.; Edmunds, W.M. Groundwater recharge in an arid grassland as indicated by soil chloride profile and multiple tracers. Hydrol. Process. 2017, 31, 1047–1057. [Google Scholar] [CrossRef]
- Yin, L.H.; Hu, G.C.; Huang, J.T.; Wen, D.G.; Dong, J.Q.; Wang, X.Y.; Li, H.B. Groundwater-recharge estimation in the Ordos Plateau, China: Comparison of methods. Hydrogeol. J. 2011, 19, 1563–1575. [Google Scholar] [CrossRef]
- Turkeltaub, T.; Jia, X.; Zhu, Y.; Shao, M.-A.; Binley, A. Recharge and Nitrate Transport Through the Deep Vadose Zone of the Loess Plateau: A Regional-Scale Model Investigation. Water Resour. Res. 2018, 54, 4332–4346. [Google Scholar] [CrossRef]
- Li, H.; Si, B.; Jin, J.; Zhang, Z.; Wu, Q.; Wang, H. Estimating of Deep Drainage Rates on the Slope Land of Loess Plateau Based on the Use of Environment Tritium (In Chinese). J. Soil Water Conserv. 2013, 30, 91–95. [Google Scholar]
- Hou, G.C.; Liang, Y.P.; Su, X.S.; Zhao, Z.H.; Tao, Z.P.; Yin, L.H.; Yang, Y.C.; Wang, X.Y. Groundwater Systems and Resources in the Ordos Basin, China. Acta Geol. Sin. Ed. 2008, 82, 1061–1069. [Google Scholar]
- Simunek, J.; Van Genuchten, M.T.; Sejna, M. The HYDRUS-1D software package for simulating the one-dimensional movement of water, heat, and multiple solutes in variably-saturated media. Univ. Calif. Riverside Res. Rep. 2005, 3, 1–240. [Google Scholar]
- Rodell, M.; Chao, B.F.; Au, A.Y.; Kimball, J.S.; McDonald, K.C. Global biomass variation and its geodynamic effects: 1982-98. Earth Interact. 2005, 9. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Wiese, D.N.; Landerer, F.W.; Long, D.; Longuevergne, L.; Chen, J. Global evaluation of new GRACE mascon products for hydrologic applications. Water Resour. Res. 2016, 52, 9412–9429. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating groundwater storage changes in the Mississippi River basin (USA) using GRACE. Hydrogeol. J. 2007, 15, 159–166. [Google Scholar] [CrossRef]
- Leblanc, M.J.; Tregoning, P.; Ramillien, G.; Tweed, S.O.; Fakes, A. Basin-scale, integrated observations of the early 21st century multiyear drought in Southeast Australia. Water Resour. Res. 2009, 45, 1–10. [Google Scholar] [CrossRef]
- Andersen, O.B.; Seneviratne, S.I.; Hinderer, J.; Viterbo, P. GRACE-derived terrestrial water storage depletion associated with the 2003 European heat wave. Geophys. Res. Lett. 2005, 32, L18405. [Google Scholar] [CrossRef]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, V.M.; Wahr, J.; Swenson, S. Dwindling groundwater resources in northern India, from satellite gravity observations. Geophys. Res. Lett. 2009, 36, 1–5. [Google Scholar] [CrossRef]
- Schenk, H.J.; Jackson, R.B. The Global Biogeography of Roots. Ecol. Monogr. 2002, 72, 311. [Google Scholar] [CrossRef]
- Schenk, H.J.; Jackson, R.B. Rooting depths, lateral root spreads and below-ground/above-ground allometries of plants in water-limited ecosystems. J. Ecol. 2002, 90, 480–494. [Google Scholar] [CrossRef]
- Schenk, H.J.; Jackson, R.B. Mapping the global distribution of deep roots in relation to climate and soil characteristics. Geoderma 2005, 126, 129–140. [Google Scholar] [CrossRef]
- Kang, S.; Zhang, L.; Liang, Y.; Hu, X.; Cai, H.; Gu, B. Effects of limited irrigation on yield and water use efficiency of winter wheat in the Loess Plateau of China. Agric. Water Manag. 2002, 55, 203–216. [Google Scholar] [CrossRef]
- Yang, L.; Wei, W.; Chen, L.; Chen, W.; Wang, J. Response of temporal variation of soil moisture to vegetation restoration in semi-arid Loess Plateau, China. CATENA 2014, 115, 123–133. [Google Scholar] [CrossRef]
- Zhou, L.-M.; Li, F.-M.; Jin, S.-L.; Song, Y. How two ridges and the furrow mulched with plastic film affect soil water, soil temperature and yield of maize on the semiarid Loess Plateau of China. Field Crop. Res. 2009, 113, 41–47. [Google Scholar] [CrossRef]
- Ma, L.H.; Wu, P.t.; Wang, Y.k. Spatial distribution of roots in a dense jujube plantation in the semiarid hilly region of the Chinese Loess Plateau. Plant Soil 2012, 354, 57–68. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, M.; Liu, Z.; Zhang, C. Characteristics of Dried Soil Layers Under Apple Orchards of Different Ages and Their Applications in Soil Water Managements on the Loess Plateau of China. Pedosphere 2015, 25, 546–554. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, B.; Zhang, Y. Soil moisture of different vegetation types on the loess Plateau. J. Geogr. Sci. 2009, 19, 707–718. [Google Scholar] [CrossRef]
- Zhou, Z.; Shangguan, Z. Vertical distribution of fine roots in relation to soil factors in Pinus tabulaeformis Carr. forest of the Loess Plateau of China. Plant Soil 2007, 291, 119–129. [Google Scholar] [CrossRef]
- Rui, H.; Beaudoing, H. Readme document for global land data assimilation system version 2 (GLDAS-2) products. GES DISC 2011, 2011. [Google Scholar]
- Freeze, R.A. The Mechanism of Natural Ground-Water Recharge and Discharge: 1. One-dimensional, Vertical, Unsteady, Unsaturated Flow above a Recharging or Discharging Ground-Water Flow System. Water Resour. Res. 1969, 5, 153–171. [Google Scholar] [CrossRef]
- Gerhart, J.M. Ground-Water Recharge and Its Effects on Nitrate Concentration Beneath a Manured Field Site in Pennsylvania. Groundwater 1986, 24, 483–489. [Google Scholar] [CrossRef]
- Calder, I.R.; Hall, R.L.; Prasanna, K.T. Hydrological impact of Eucalyptus plantation in India. J. Hydrol. 1993, 150, 635–648. [Google Scholar] [CrossRef]
- Heppner, C.S.; Nimmo, J.R. A Computer Program for Predicting Recharge with a Master Recession Curve. Available online: https://wwwrcamnl.wr.usgs.gov/uzf/abs_pubs/papers/SIR5172.pdf (accessed on 30 November 2018).
- Maréchal, J.C.; Dewandel, B.; Ahmed, S.; Galeazzi, L.; Zaidi, F.K. Combined estimation of specific yield and natural recharge in a semi-arid groundwater basin with irrigated agriculture. J. Hydrol. 2006, 329, 281–293. [Google Scholar] [CrossRef]
- Moon, S.K.; Woo, N.C.; Lee, K.S. Statistical analysis of hydrographs and water-table fluctuation to estimate groundwater recharge. J. Hydrol. 2004, 292, 198–209. [Google Scholar] [CrossRef]
- Nimmo, J.R.; Horowitz, C.; Mitchell, L. Discrete-Storm Water-Table Fluctuation Method to Estimate Episodic Recharge. Groundwater 2015, 53, 282–292. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, W.C.; Andreasen, G.E. Hydrologic Budget of the Beaverdam Creek Basin, Maryland; US Geol Surv Water Suppl Paper; USGS: Lawrence, KS, USA, 1959; Volume 1472, p. 106.
- Zhong, Y.; Zhong, M.; Feng, W.; Wu, D. Groundwater Depletion in the West Liaohe River Basin, China and Its Implications Revealed by GRACE and In Situ Measurements. Remote Sens. 2018, 10, 493. [Google Scholar] [CrossRef]
- Arras, K.O. An Introduction To Error Propagation: Derivation, Meaning and Examples of Equation Cy= Fx Cx FxT. EPFL-ASL-TR-98-01 R3 2014. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48, W04531. [Google Scholar] [CrossRef]
- Hozo, S.P.; Djulbegovic, B.; Hozo, I. Estimating the mean and variance from the median, range, and the size of a sample. BMC Med. Res. Methodol. 2005, 5, 13. [Google Scholar] [CrossRef]
- Vasquez, V.R.; Whiting, W.B. Accounting for Both Random Errors and Systematic Errors in Uncertainty Propagation Analysis of Computer Models Involving Experimental Measurements with Monte Carlo Methods. Risk Anal. 2005, 25, 1669–1681. [Google Scholar] [CrossRef]
- Feng, X.; Fu, B.; Piao, S.; Wang, S.; Ciais, P.; Zeng, Z.; Lü, Y.; Zeng, Y.; Li, Y.; Jiang, X.; et al. Revegetation in China’s Loess Plateau is approaching sustainable water resource limits. Nat. Clim. Chang. 2016, 6, 1019–1022. [Google Scholar] [CrossRef]
- He, J.; Yang, K. China Meteorological Forcing Dataset. Cold Arid Reg. Sci. Data Cent. Lanzhou 2011 2011. [Google Scholar] [CrossRef]
- Tang, X.; Miao, C.; Xi, Y.; Duan, Q.; Lei, X.; Li, H. Analysis of precipitation characteristics on the loess plateau between 1965 and 2014, based on high-density gauge observations. Atmos. Res. 2018, 213, 264–274. [Google Scholar] [CrossRef]
- Dripps, W.R.; Bradbury, K.R. The spatial and temporal variability of groundwater recharge in a forested basin in northern Wisconsin. Hydrol. Process. 2009, 24, 383–392. [Google Scholar] [CrossRef]
- Vogel, J.C.; Van Urk, H. Isotopic composition of groundwater in semi-arid regions of southern Africa. J. Hydrol. 1975, 25, 23–36. [Google Scholar] [CrossRef]
- Lettenmaier, D.P.; Famiglietti, J.S. Hydrology: Water from on high. Nature 2006, 444, 562–563. [Google Scholar] [CrossRef] [PubMed]
- Rodell, M.; Famiglietti, J.S. An analysis of terrestrial water storage variations in Illinois with implications for the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2001, 37, 1327–1339. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Estimating Large-Scale Precipitation Minus Evapotranspiration from GRACE Satellite Gravity Measurements. J. Hydrometeorol. 2006, 7, 252–270. [Google Scholar] [CrossRef]
- Velicogna, I. Short term mass variability in Greenland, from GRACE. Geophys. Res. Lett. 2005, 32, L05501. [Google Scholar] [CrossRef]
- Asoka, A.; Gleeson, T.; Wada, Y.; Mishra, V. Relative contribution of monsoon precipitation and pumping to changes in groundwater storage in India. Nat. Geosci. 2017, 10, 109–117. [Google Scholar] [CrossRef]
- Gurdak, J.J. Groundwater: Climate-induced pumping. Nat. Geosci. 2017, 10, 71. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, X.C.; Dang, T.; Ouyang, Z.; Li, Z.; Wang, J.; Wang, R.; Gao, C. Soil water dynamics and deep soil recharge in a record wet year in the southern Loess Plateau of China. Agric. Water Manag. 2010, 97, 1133–1138. [Google Scholar] [CrossRef]
- Lin, R.F.; Wei, K.Q. Tritium profiles of pore water in the Chinese loess unsaturated zone: Implications for estimation of groundwater recharge. J. Hydrol. 2006, 328, 192–199. [Google Scholar] [CrossRef]
- Kapetas, L.; Dror, I.; Berkowitz, B. Evidence of preferential path formation and path memory effect during successive infiltration and drainage cycles in uniform sand columns. J. Contam. Hydrol. 2014, 165, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Xiang, W.; Si, B.C.; Biswas, A.; Li, Z. Quantifying dual recharge mechanisms in deep unsaturated zone of Chinese Loess Plateau using stable isotopes. Geoderma 2019, 337, 773–781. [Google Scholar] [CrossRef]
- Turkeltaub, T.; Kurtzman, D.; Bel, G.; Dahan, O. Examination of groundwater recharge with a calibrated/validated flow model of the deep vadose zone. J. Hydrol. 2015, 522, 618–627. [Google Scholar] [CrossRef]
- Min, L.; Shen, Y.; Pei, H. Estimating groundwater recharge using deep vadose zone data under typical irrigated cropland in the piedmont region of the North China Plain. J. Hydrol. 2015, 527, 305–315. [Google Scholar] [CrossRef]
- Sheffer, N.A.; Dafny, E.; Gvirtzman, H.; Navon, S.; Frumkin, A.; Morin, E. Hydrometeorological daily recharge assessment model (DREAM) for the Western Mountain Aquifer, Israel: Model application and effects of temporal patterns. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; García-Aróstegui, J.L.; Molina, J.L.; Pulido-Velazquez, M. Assessment of future groundwater recharge in semi-arid regions under climate change scenarios (Serral-Salinas aquifer, SE Spain). Could increased rainfall variability increase the recharge rate? Hydrol. Process. 2015. [Google Scholar] [CrossRef]
- Wohling, D.L.; Leaney, F.W.; Crosbie, R.S. Deep drainage estimates using multiple linear regression with percent clay content and rainfall. Hydrol. Earth Syst. Sci. 2012, 16, 563–572. [Google Scholar] [CrossRef]
- Dyck, M.F.; Kachanoski, R.G.; de Jong, E. Spatial Variability of Long-Term Chloride Transport under Semiarid Conditions. Vadose Zone J. 2005. [Google Scholar] [CrossRef]
- Li, H.; Si, B.; Li, M. Rooting depth controls potential groundwater recharge on hillslopes. J. Hydrol. 2018, 564, 164–174. [Google Scholar] [CrossRef]
- Martos-Rosillo, S.; Marín-Lechado, C.; Pedrera, A.; Vadillo, I.; Motyka, J.; Molina, J.L.; Ortiz, P.; Ramírez, J.M.M. Methodology to evaluate the renewal period of carbonate aquifers: A key tool for their management in arid and semiarid regions, with the example of Becerrero aquifer, Spain. Hydrogeol. J. 2014. [Google Scholar] [CrossRef]
- Scanlon, B.R. Uncertainties in estimating water fluxes and residence times using environmental tracers in an arid unsaturated zone. Water Resour. Res. 2000, 36, 395–409. [Google Scholar] [CrossRef]
- Cook, P.G.; Jolly, I.D.; Leaney, F.W.; Walker, G.R.; Allan, G.L.; Fifield, L.K.; Allison, G.B. Unsaturated zone tritium and chlorine 36 profiles from southern Australia: Their use as tracers of soil water movement. Water Resour. Res. 1994, 30, 1709–1719. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, K.; Qin, J.; Zhao, L.; Tang, W.; Han, M. Evaluation of AMSR-E retrievals and GLDAS simulations against observations of a soil moisture network on the central Tibetan Plateau. J. Geophys. Res. Atmos. 2013, 118, 4466–4475. [Google Scholar] [CrossRef]
- Grippa, M.; Kergoat, L.; Frappart, F.; Araud, Q.; Boone, A.; De Rosnay, P.; Lemoine, J.M.; Gascoin, S.; Balsamo, G.; Ottlé, C.; et al. Land water storage variability over West Africa estimated by Gravity Recovery and Climate Experiment (GRACE) and land surface models. Water Resour. Res. 2011, 47, 1–18. [Google Scholar] [CrossRef]
- Poméon, T.; Diekkrüger, B.; Kumar, R. Computationally Efficient Multivariate Calibration and Validation of a Grid-Based Hydrologic Model in Sparsely Gauged West African River Basins. Water 2018, 10, 1418. [Google Scholar] [CrossRef]
- Ndehedehe, C.; Awange, J.; Agutu, N.; Kuhn, M.; Heck, B. Understanding changes in terrestrial water storage over West Africa between 2002 and 2014. Adv. Water Resour. 2016. [Google Scholar] [CrossRef]
- Zeng, J.; Li, Z.; Chen, Q.; Bi, H.; Qiu, J.; Zou, P. Evaluation of remotely sensed and reanalysis soil moisture products over the Tibetan Plateau using in-situ observations. Remote Sens. Environ. 2015, 163, 91–110. [Google Scholar] [CrossRef]
- Jackson, T.J.; Cosh, M.H.; Bindlish, R.; Starks, P.J.; Bosch, D.D.; Seyfried, M.; Goodrich, D.C.; Moran, M.S.; Du, J. Validation of Advanced Microwave Scanning Radiometer Soil Moisture Products. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4256–4272. [Google Scholar] [CrossRef]
- Brocca, L.; Massari, C.; Ciabatta, L.; Moramarco, T.; Penna, D.; Zuecco, G.; Pianezzola, L.; Borga, M.; Matgen, P.; Martínez-Fernández, J. Rainfall estimation from in situ soil moisture observations at several sites in Europe: An evaluation of the SM2RAIN algorithm. J. Hydrol. Hydromech. 2015. [Google Scholar] [CrossRef]
- Zhang, S.; Simelton, E.; Lövdahl, L.; Grip, H.; Chen, D. Simulated long-term effects of different soil management regimes on the water balance in the Loess Plateau, China. Field Crop. Res. 2007, 100, 311–319. [Google Scholar] [CrossRef]
- Huang, M.; Gallichand, J. Use of the SHAW model to assess soil water recovery after apple trees in the gully region of the Loess Plateau, China. Agric. Water Manag. 2006, 85, 67–76. [Google Scholar] [CrossRef]
| Year | GRi (mm year−1) | N | R2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 2002 | 19.1 | 14.9 | −18.2 | 23.7 | 37.3 | 28.7 | 5 | 0.52 | |
| 2003 | 56.2 | 14.9 | −8.1 | 8.0 | 64.3 | 18.1 | 4 | 0.66 | |
| 2004 | 71.3 | 14.9 | 4.9 | 22.2 | 66.4 | 27.5 | 6 | 0.50 | |
| 2005 | 46.9 | 14.9 | 14.1 | 31.7 | 32.8 | 35.6 | 8 | 0.36 | |
| 2006 | 40.7 | 14.9 | 9.8 | 11.9 | 30.9 | 20.1 | 6 | 0.46 | |
| 2007 | 29.1 | 14.9 | −21.8 | 13.5 | 50.9 | 21.1 | 6 | 0.81 | |
| 2008 | 24.5 | 14.9 | −23.1 | 10.0 | 47.6 | 19.0 | 5 | 0.89 | |
| 2009 | 5.4 | 14.9 | −54.3 | 15.0 | 59.7 | 22.1 | 5 | 0.88 | |
| 2010 | −0.4 | 14.9 | −38.0 | 16.7 | 37.6 | 23.3 | 6 | 0.53 | |
| 2011 | −6.5 | 14.9 | −63.2 | 32.8 | 56.7 | 36.6 | 6 | 0.63 | |
| 2012 | −4.9 | 14.9 | −52.2 | 12.0 | 47.3 | 20.2 | 5 | 0.68 | |
| Mean | 48.3 | 5.6 | 0.63 |
| Uncertainty | Equation | |
|---|---|---|
| 8.3 mm month−1 | (5) to (8) | |
| 14.9 mm month−1 | ||
| 7.7 mm year−1 | ||
| 0 mm year−1 | (9) | |
| 8.5 mm year−1 | ||
| 2.1 mm year−1 | ||
| 16.0 mm year−1 | (10) | |
| CV | 33.1% | (11) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Si, B.; He, H.; Wu, P. Determining Regional-Scale Groundwater Recharge with GRACE and GLDAS. Remote Sens. 2019, 11, 154. https://doi.org/10.3390/rs11020154
Wu Q, Si B, He H, Wu P. Determining Regional-Scale Groundwater Recharge with GRACE and GLDAS. Remote Sensing. 2019; 11(2):154. https://doi.org/10.3390/rs11020154
Chicago/Turabian StyleWu, Qifan, Bingcheng Si, Hailong He, and Pute Wu. 2019. "Determining Regional-Scale Groundwater Recharge with GRACE and GLDAS" Remote Sensing 11, no. 2: 154. https://doi.org/10.3390/rs11020154
APA StyleWu, Q., Si, B., He, H., & Wu, P. (2019). Determining Regional-Scale Groundwater Recharge with GRACE and GLDAS. Remote Sensing, 11(2), 154. https://doi.org/10.3390/rs11020154