Retrieval of Snow Properties from the Sentinel-3 Ocean and Land Colour Instrument
Abstract
1. Introduction
2. Materials and Methods
2.1. Theory
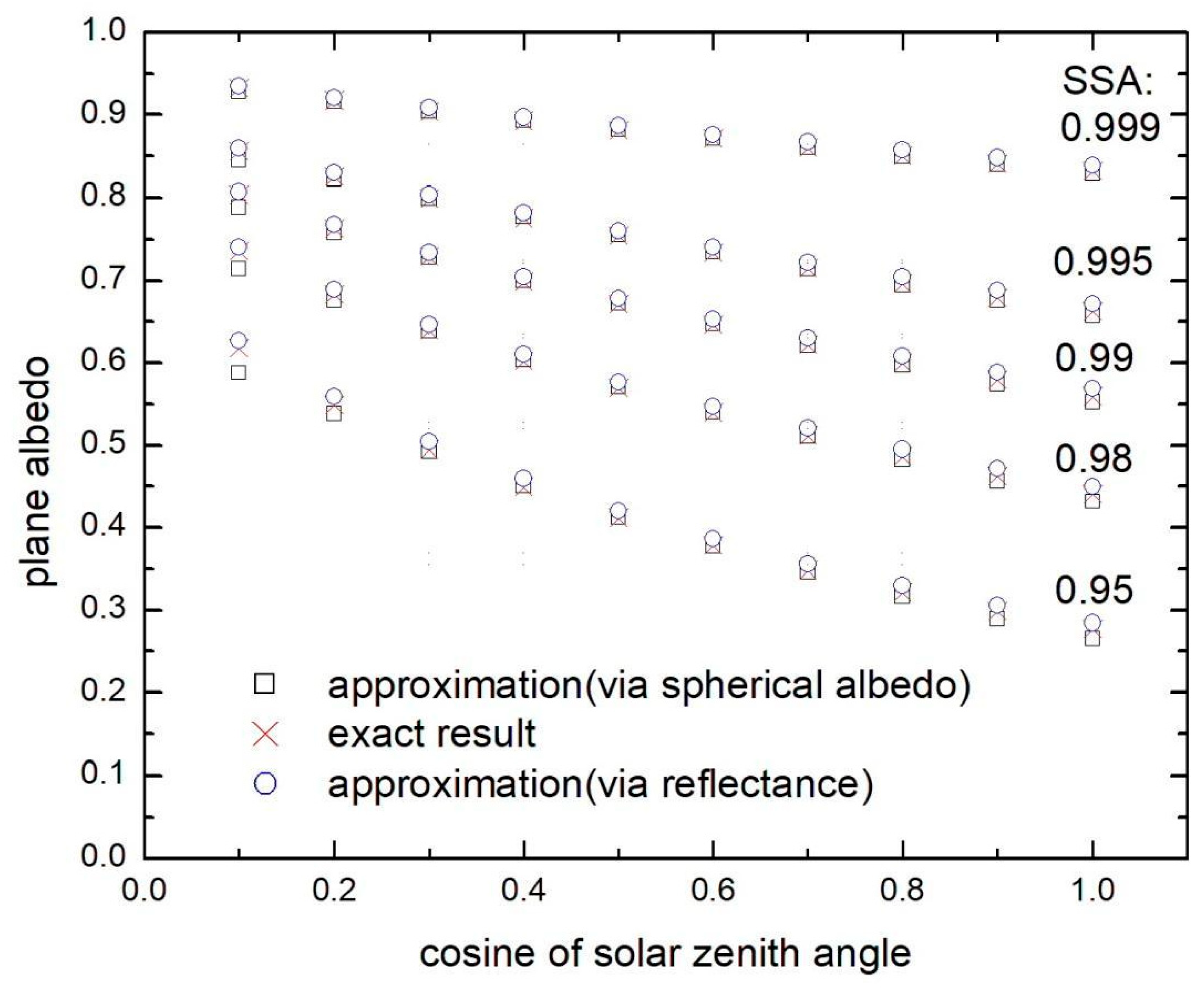
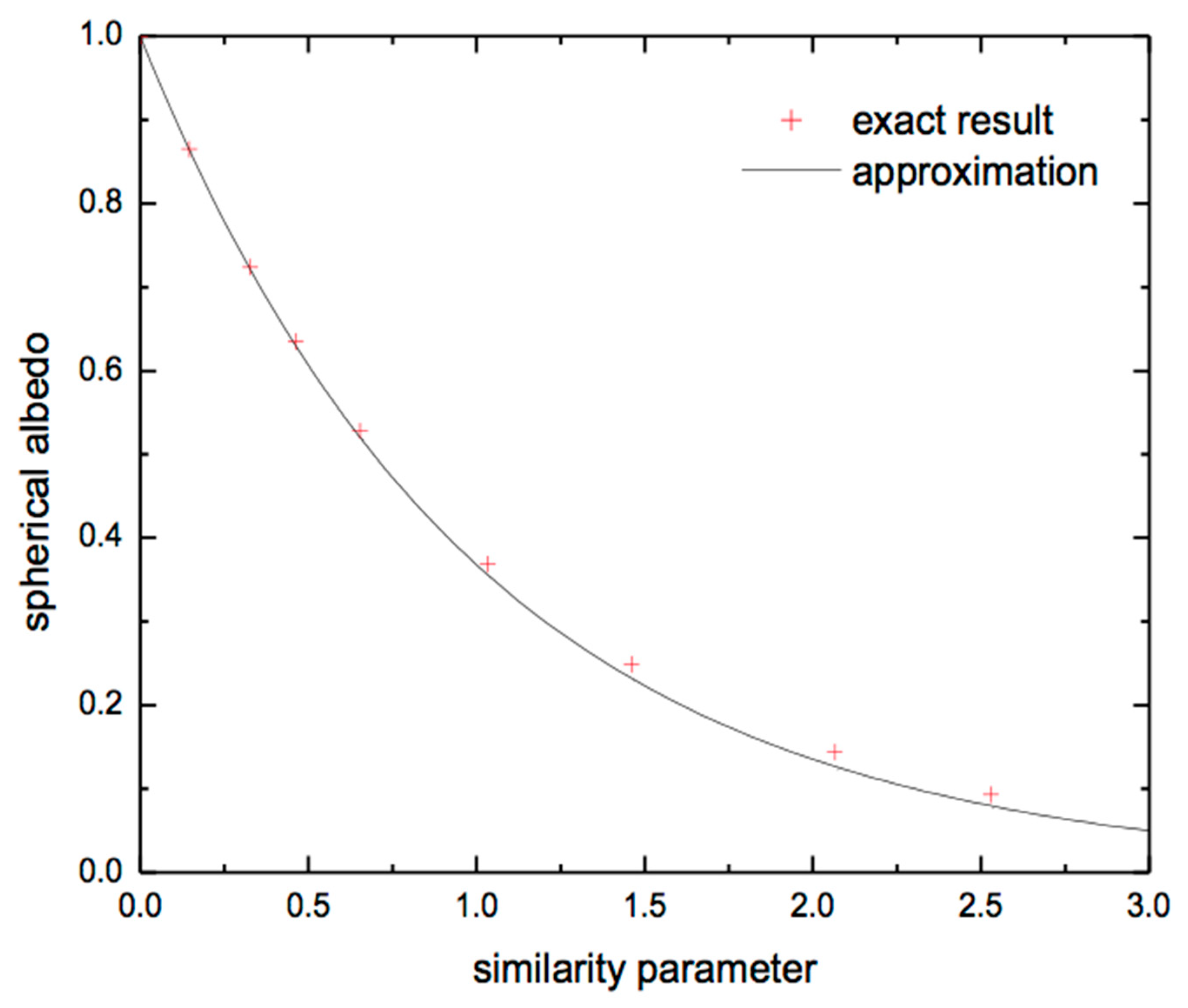
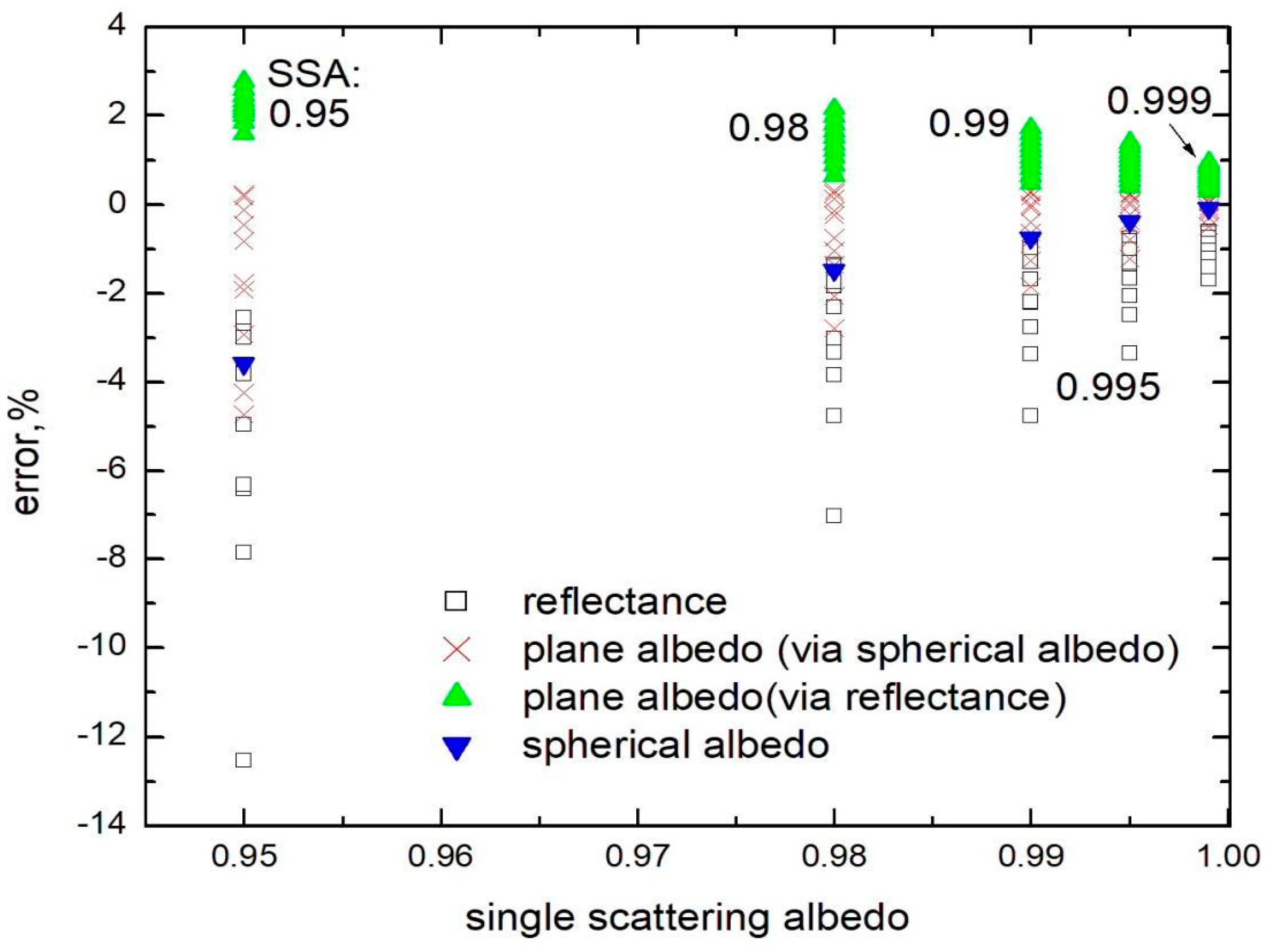
2.2. The Accuracy of Exponential Approximation
3. Results
3.1. The Approximate Solution of the Inverse Problem: Clean Snow
- the water vapor column: 2.085 g/m;
- the ozone column: 0.35 atm-cm;
- the tropospheric ozone: 0.0346 atm-cm;
- the aerosol model: rural;
- the vertical optical depth of boundary layer at 550 nm: 0.1;
- the altitude: 825 m;
- and the surface set to snow, calculated in SBDART using the Mie/δ-Edington model [44] with a snow grain diameter of 0.25 mm.
- BBAvisible (300–700 nm),
- near IR BBAnear IR (700–2400 nm),
- BBAshortwave (300–2400 nm).
3.2. The Determination of Polluted Snow Properties
3.2.1. Albedo
3.2.2. Snow Grain Size and Absorption Coefficient of Pollutants
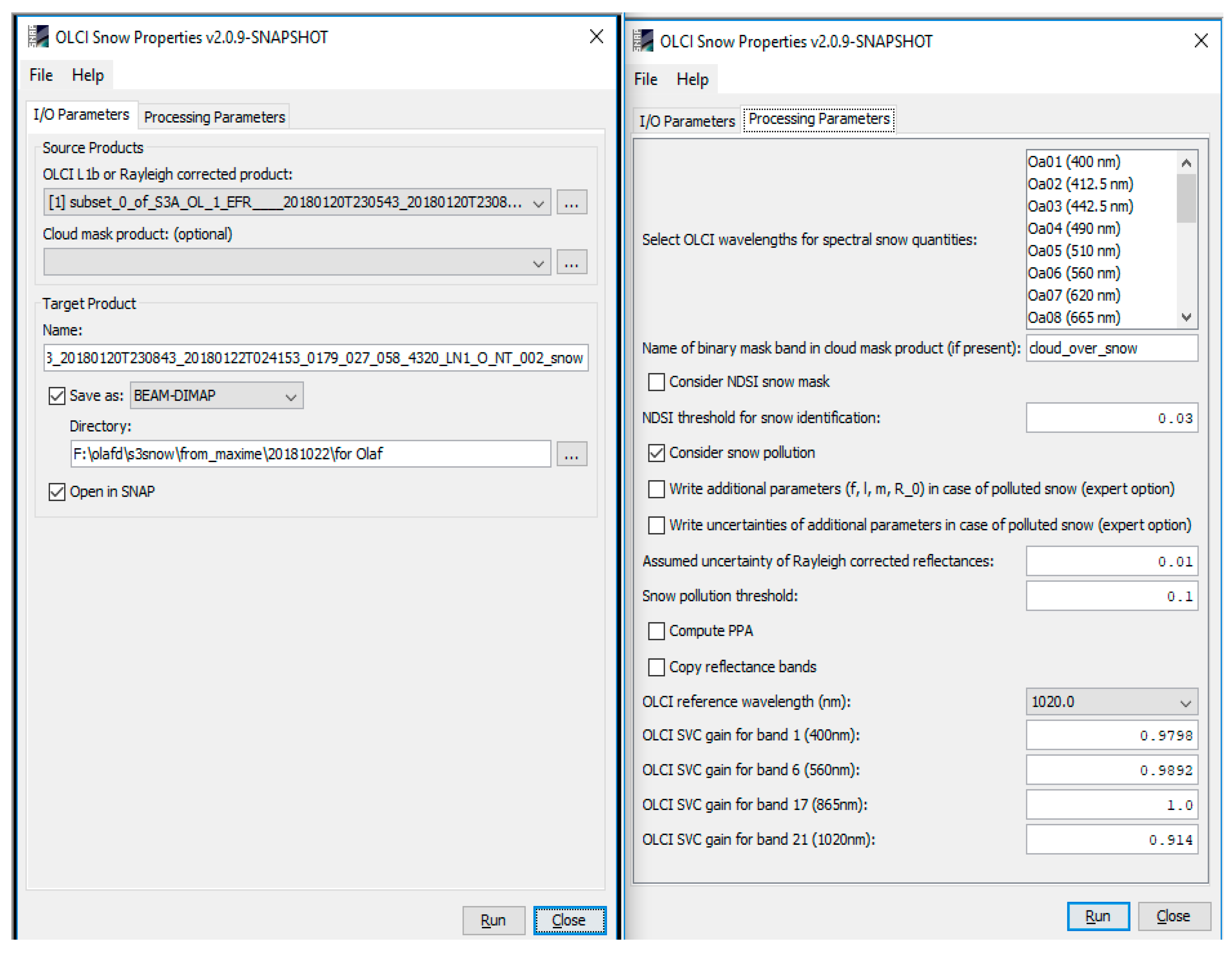
3.3. Snow Properties Processor for SNAP
- Select OLCI wavelengths for spectral snow quantities: for the selected wavelengths, the computed spectral snow quantities (i.e., spectral snow albedo) were written as the corresponding band into the target product.
- Name of binary mask band in cloud classification product (if present): see details in the software user manual at https://readthedocs.org/projects/s3tbx-snow/.
- Consider snow mask based on the OLCI Normalized-Difference Snow Index (NDSI): if selected, an NDSI value will be computed from atmospherically corrected reflectances at wavelengths 865 nm and 1020 nm (NDSI = (R(865 nm) − R(1020 nm))/(R(865 nm) + R(1020 nm)). If this value exceeded 0.03 (and reflectance at 410 nm > 0.5), the given pixel was regarded as a snow pixel. The normalized bare ice index (NDBI) was also provided in the output. It was defined as NDBI = (R(410 nm) − R(1020 nm))/(R(410 nm) + R(1020 nm)). It was assumed that the values of NDBI below 1/3 corresponded to snow and the ice was assumed for values of NDBI above 1/3. The dark bare areas correspond to values of NDBI above 2/3. OLCI snow mask is given in output (snow mask was equal to 1 for 100% snow pixels. Otherwise, the snow mask was zero).
- Consider snow pollution: if selected, a retrieval for polluted snow was applied for the considered snow pixel.
- Compute PPA: if selected, the spectral probability of photon absorption (PPA) was written to the target product for each selected OLCI wavelength.
- OLCI reference wavelength: reference wavelength used in the snow property algorithms.
- OLCI gain for band n: OLCI system vicarious calibration (SVC) gain for the relevant bands (n = 1, 6, 17, 21 (400, 560, 865, 1020 nm)) used in the retrieval algorithms outlined above.
3.4. Cloud Identification
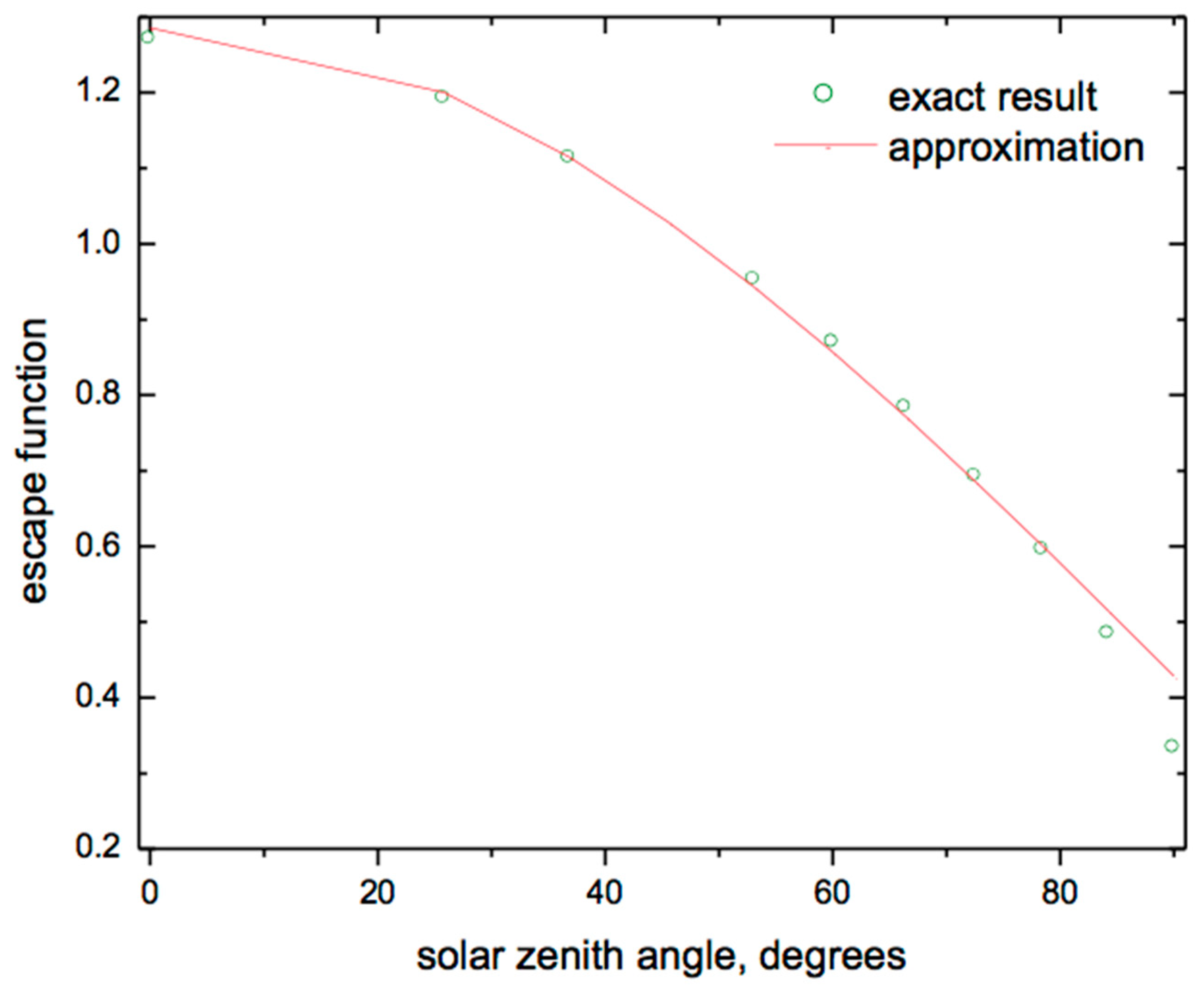
3.5. Validation of Snow OLCI Products
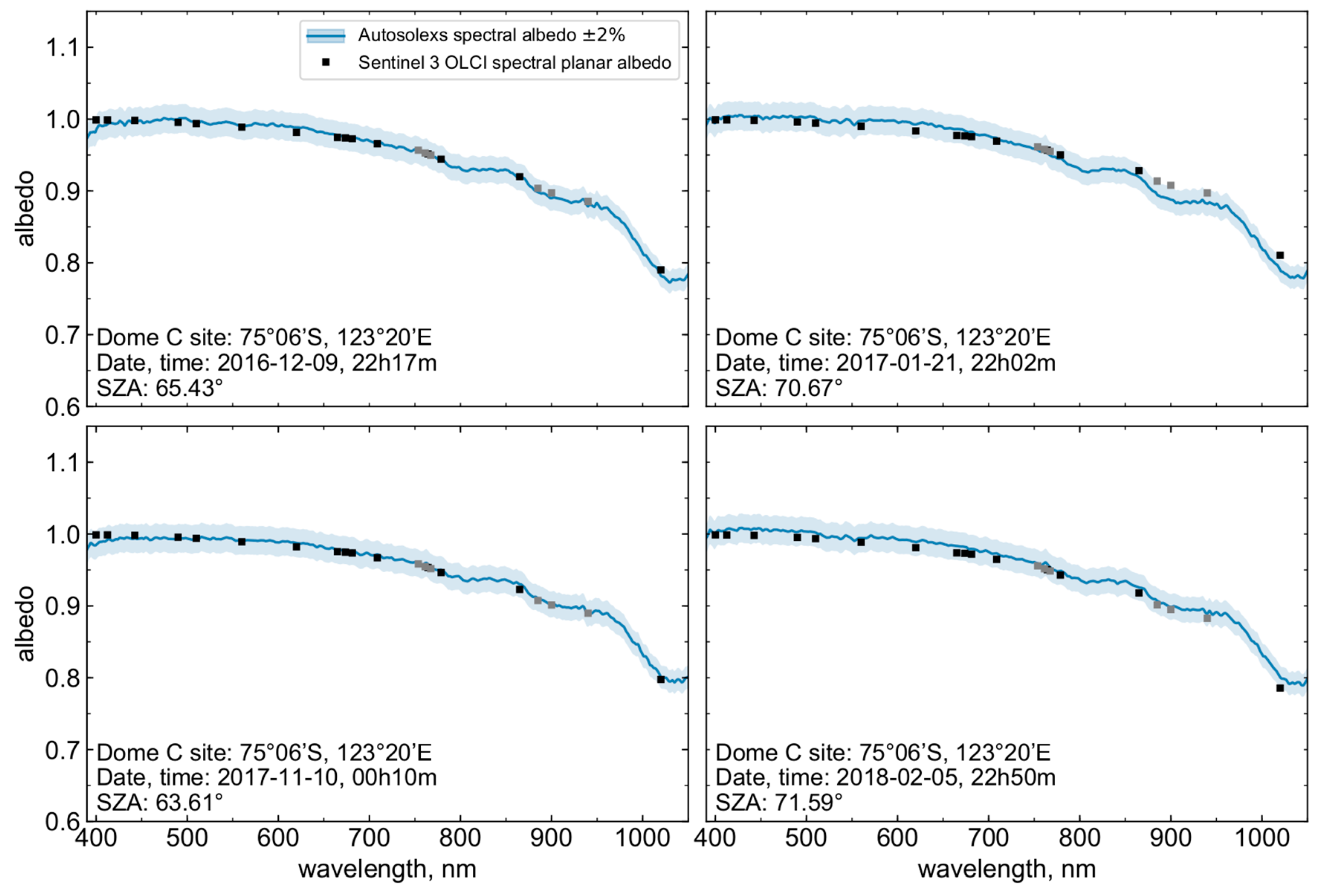
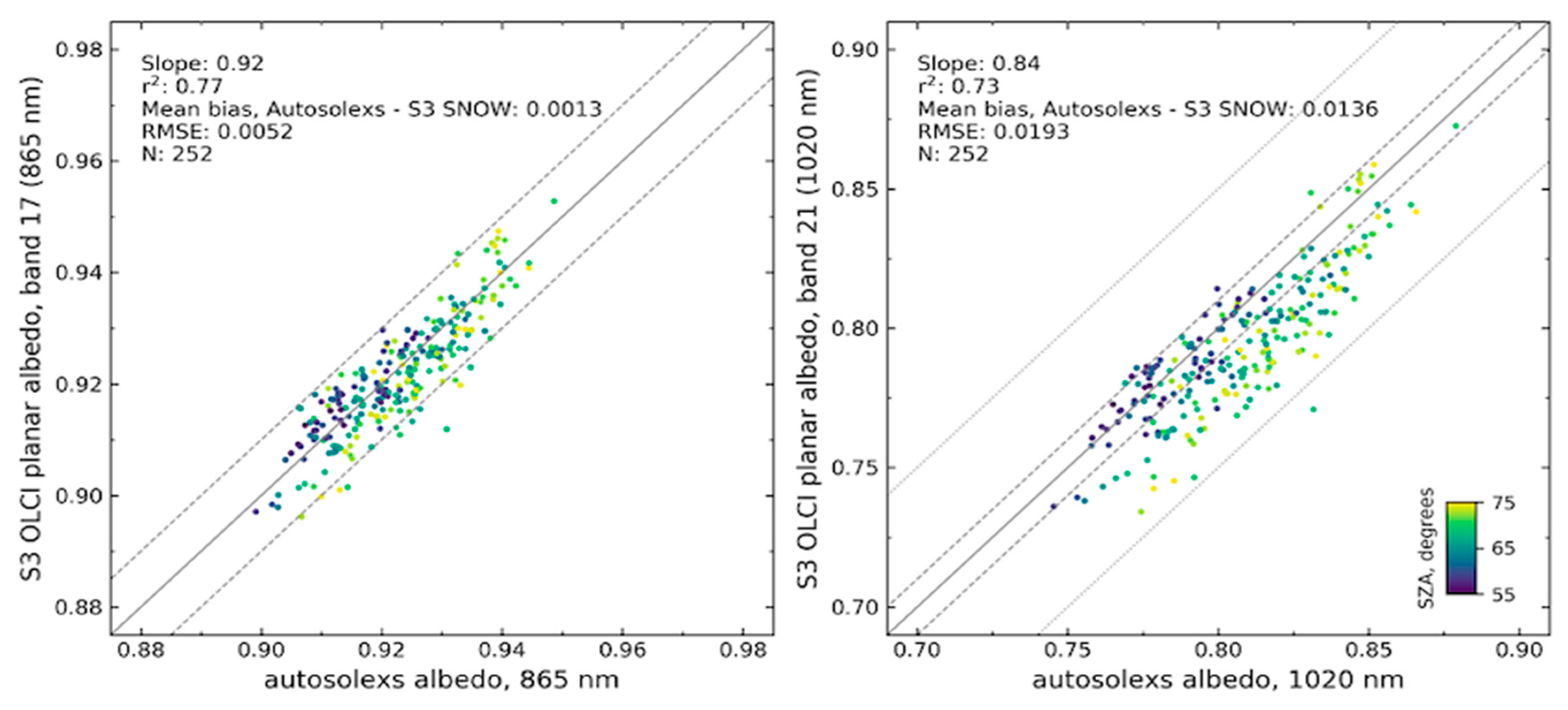
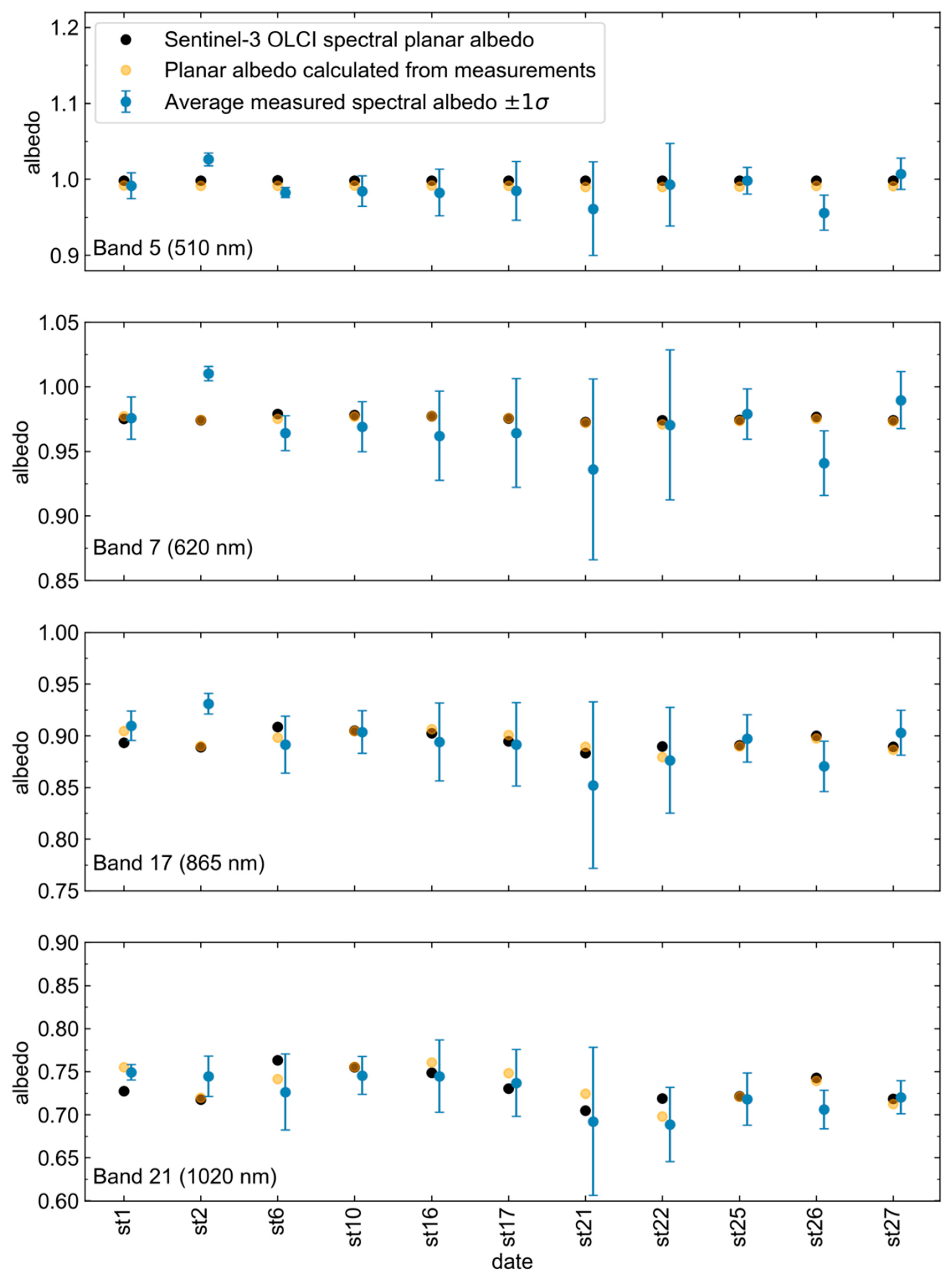
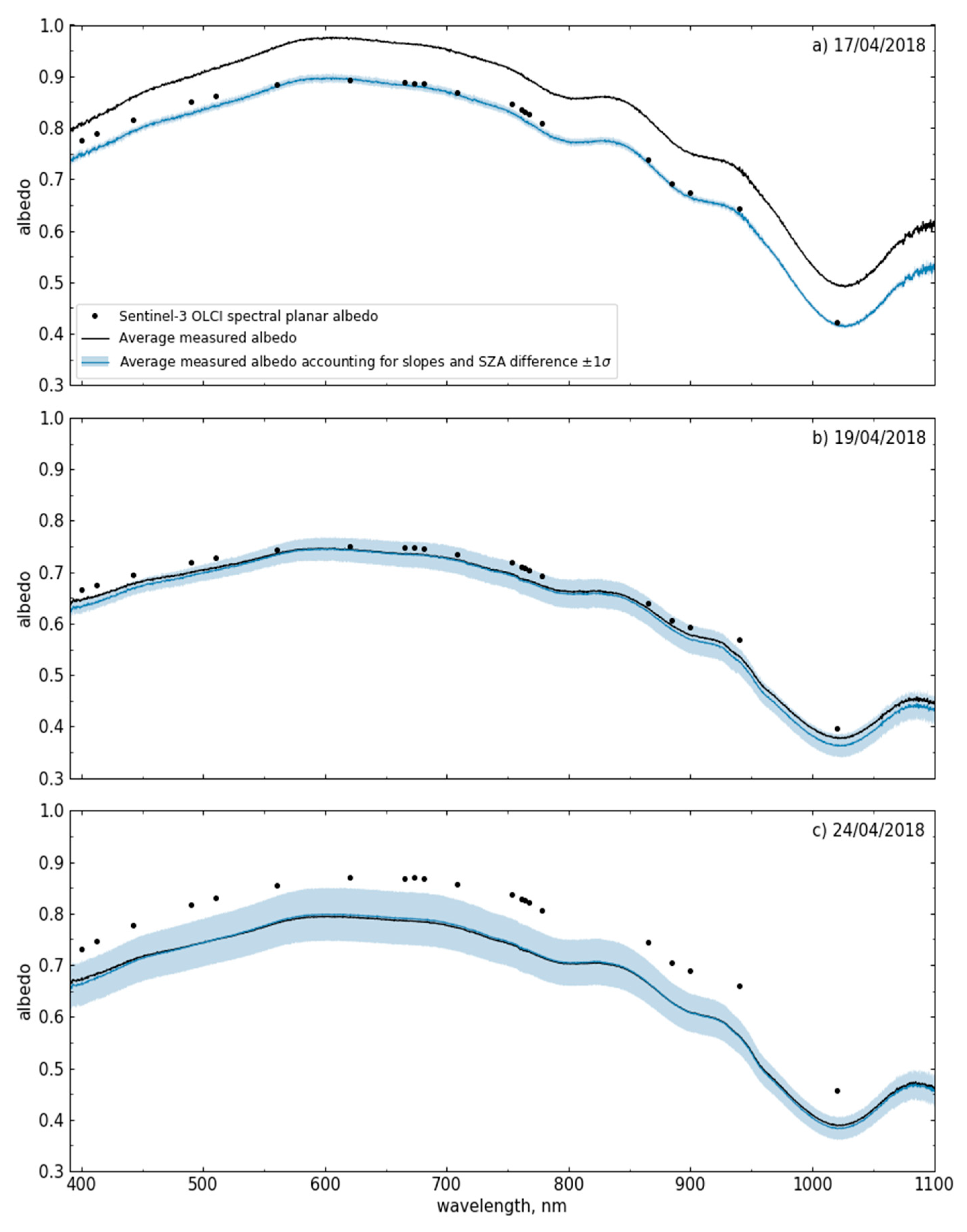
3.5.1. Snow Spectral Albedo
Data Processing and Instrumentation
Clean Snow
Polluted Snow
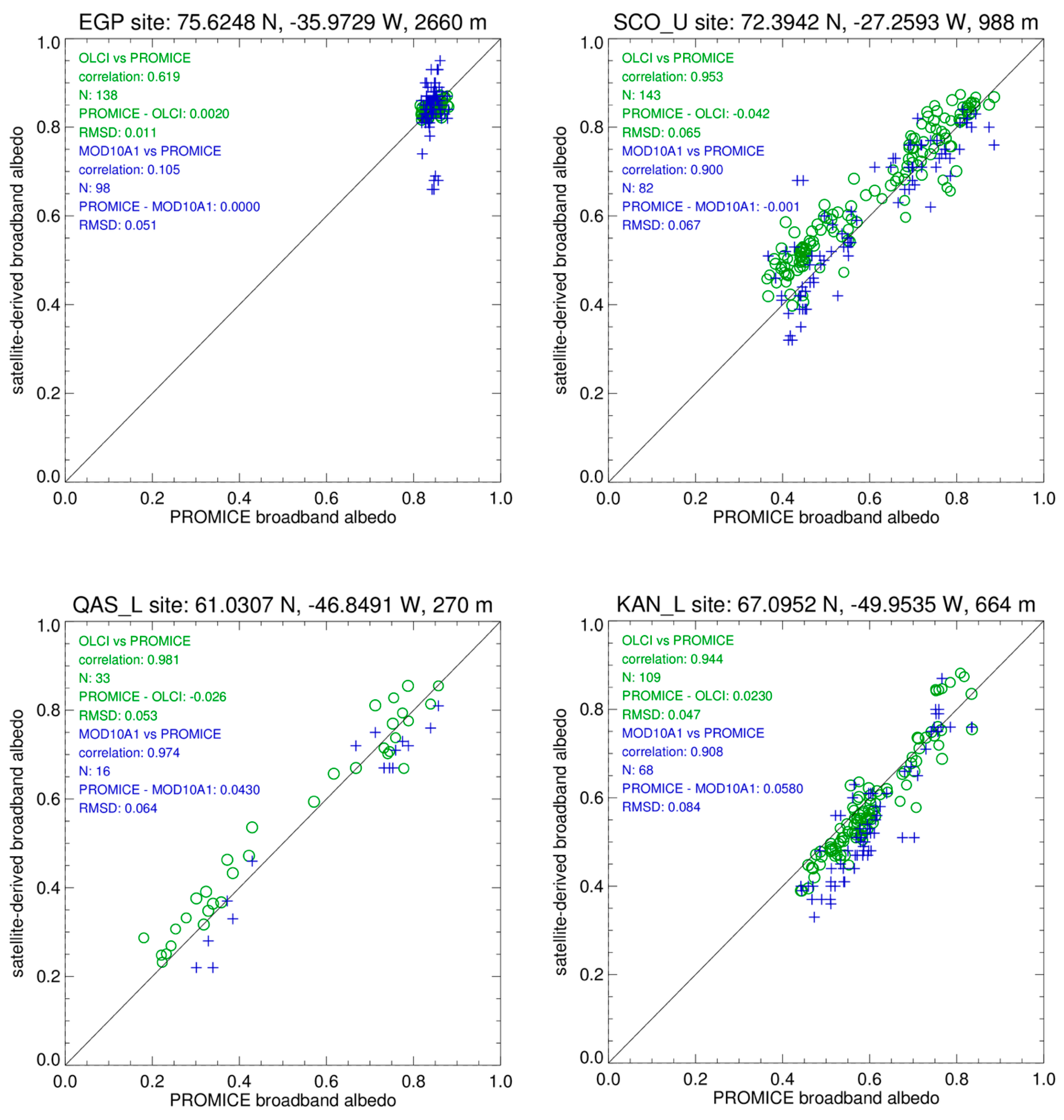
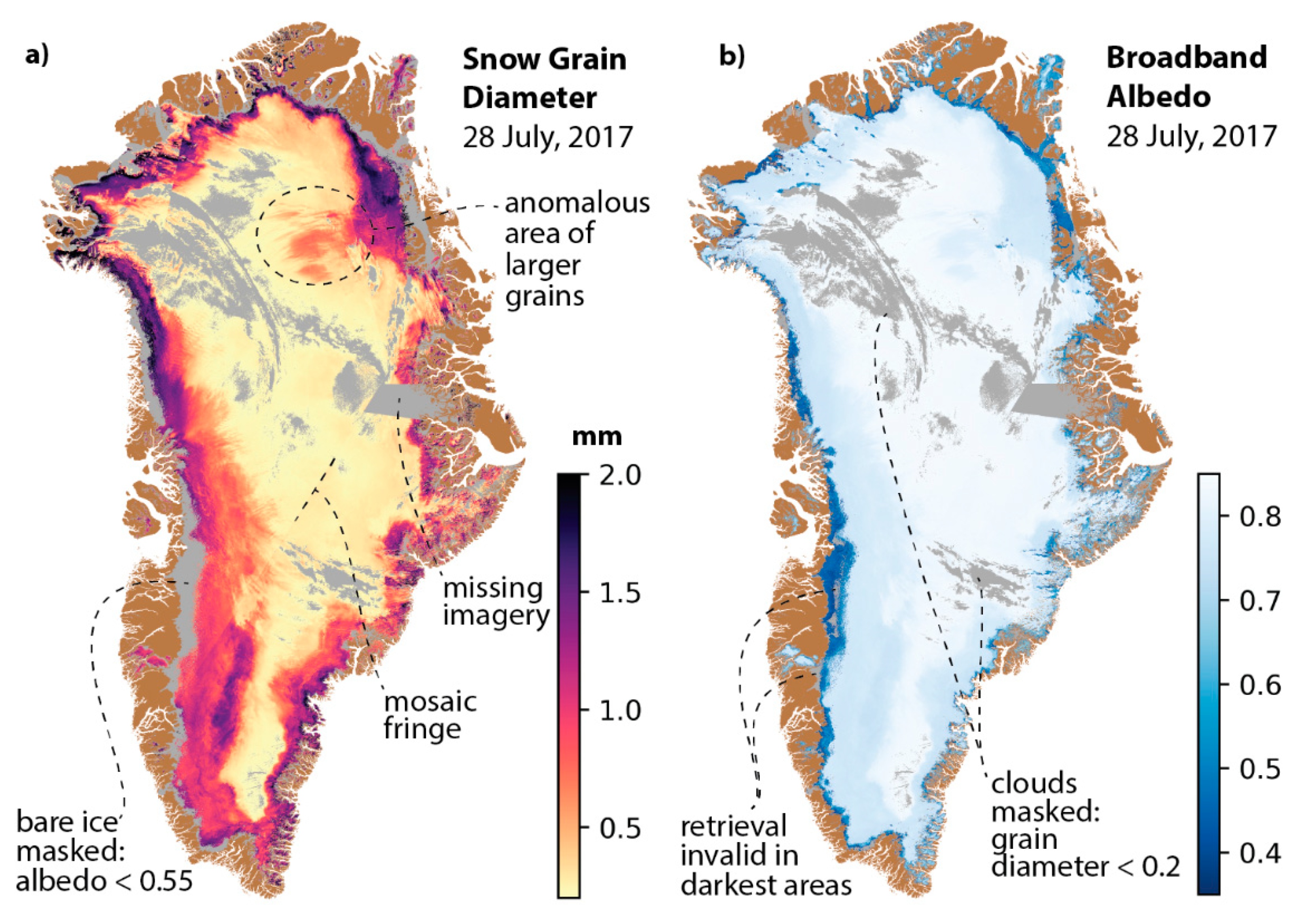
3.5.2. Broadband Albedo
Data Processing and Instrumentation
Broadband Albedo Validation
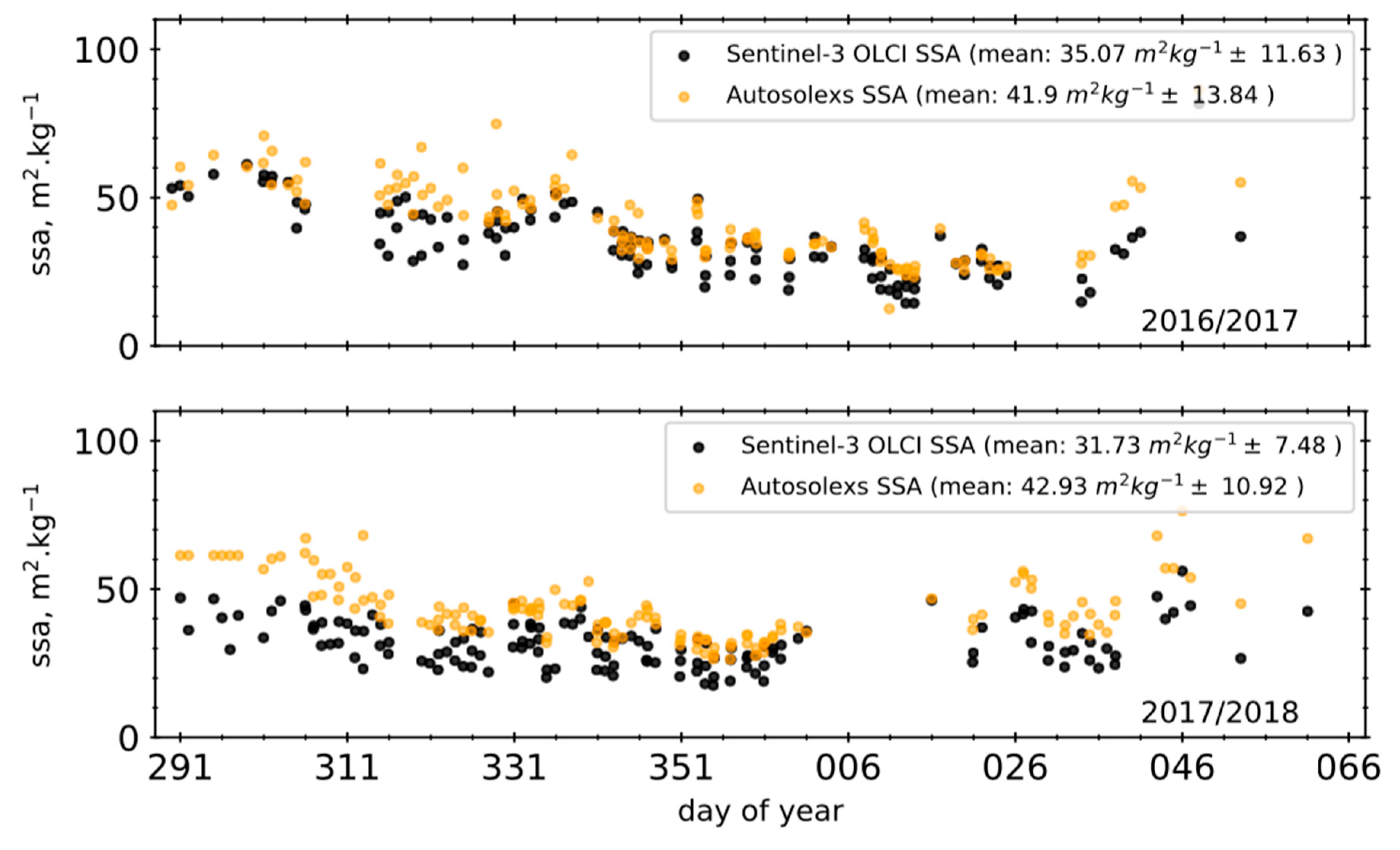
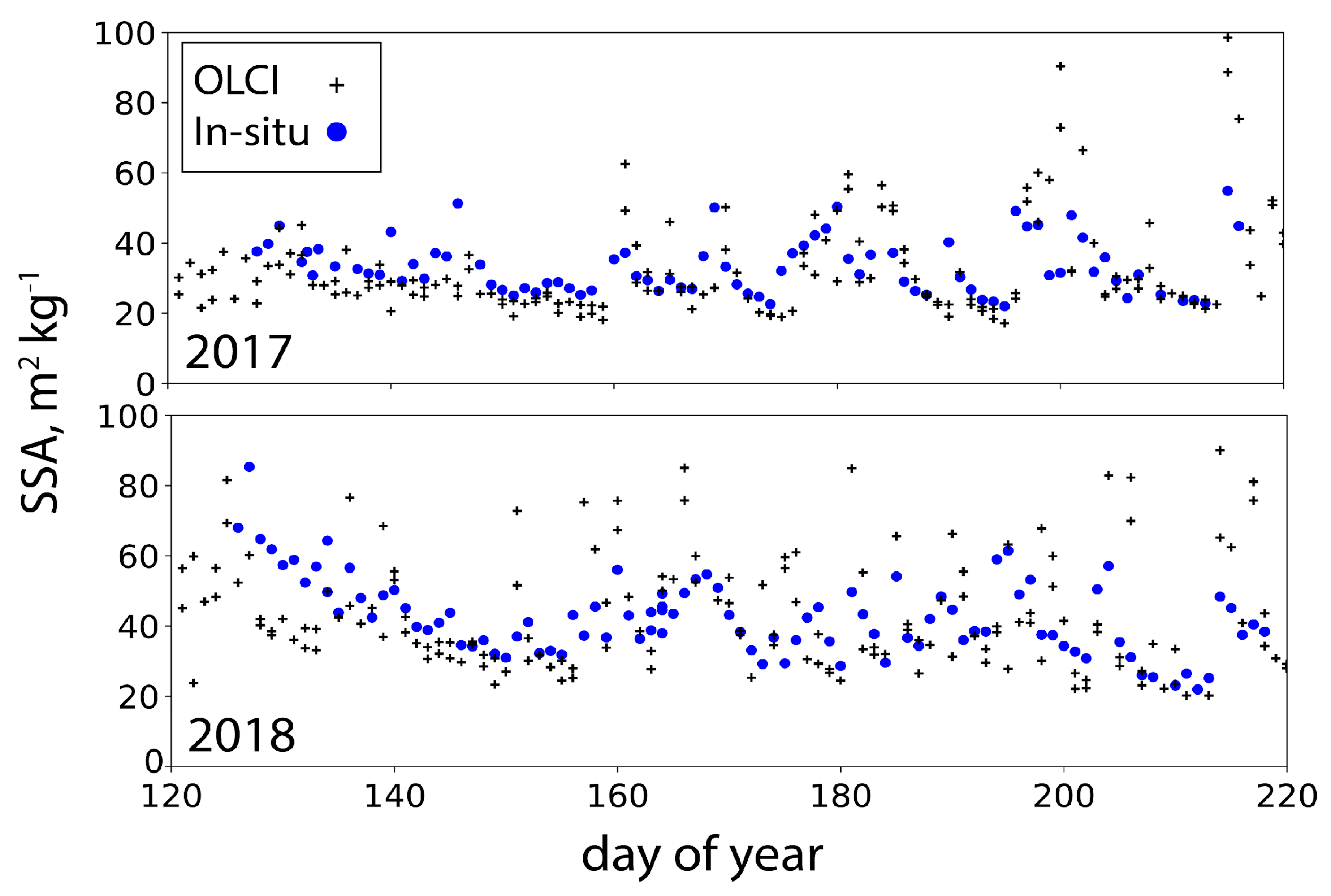
3.5.3. Specific Surface Area
Measurements in Antarctica
Measurements in Greenland
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Derivation of Main Equations
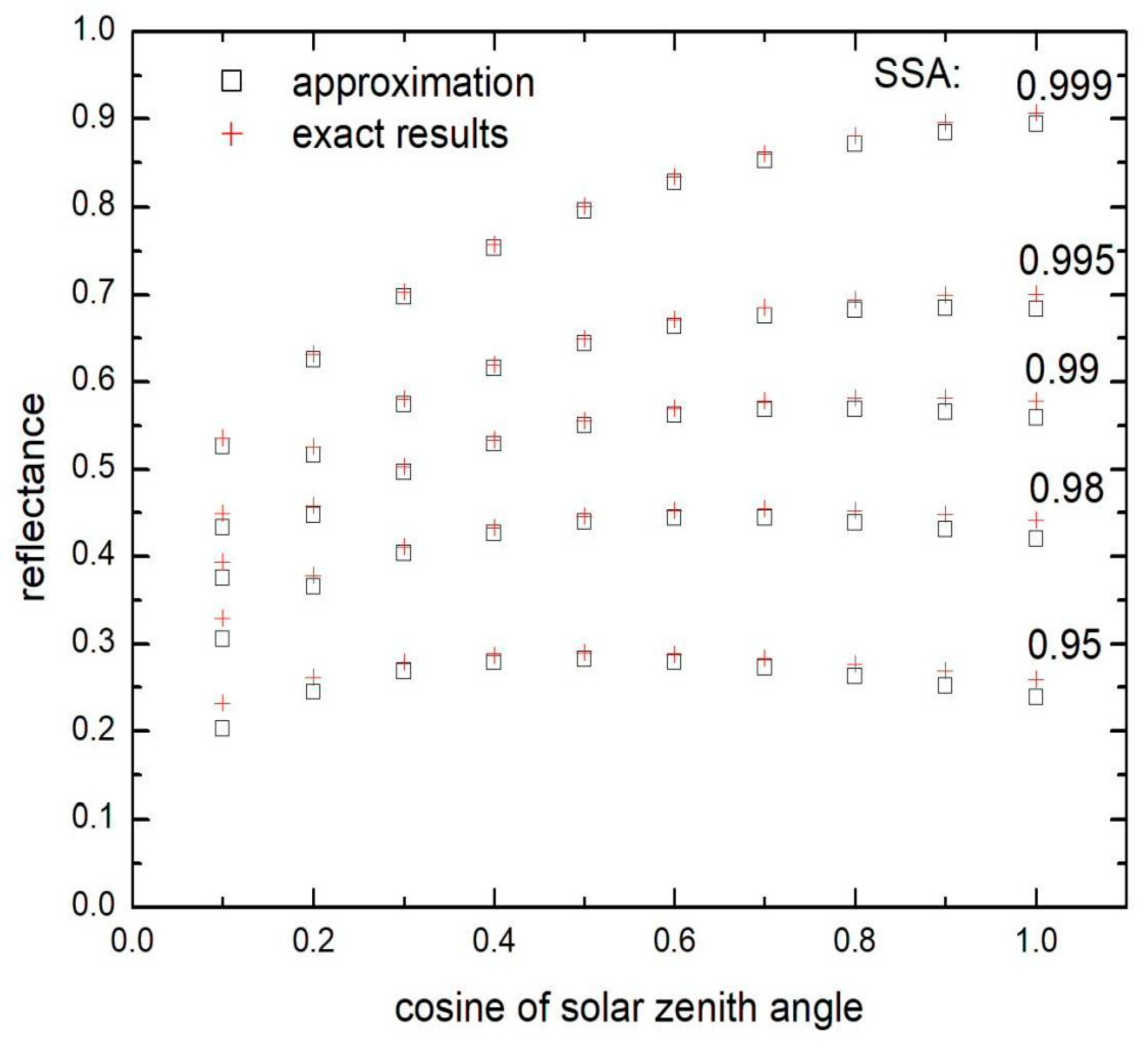
Appendix B. The Retrieval Errors and Uncertainties
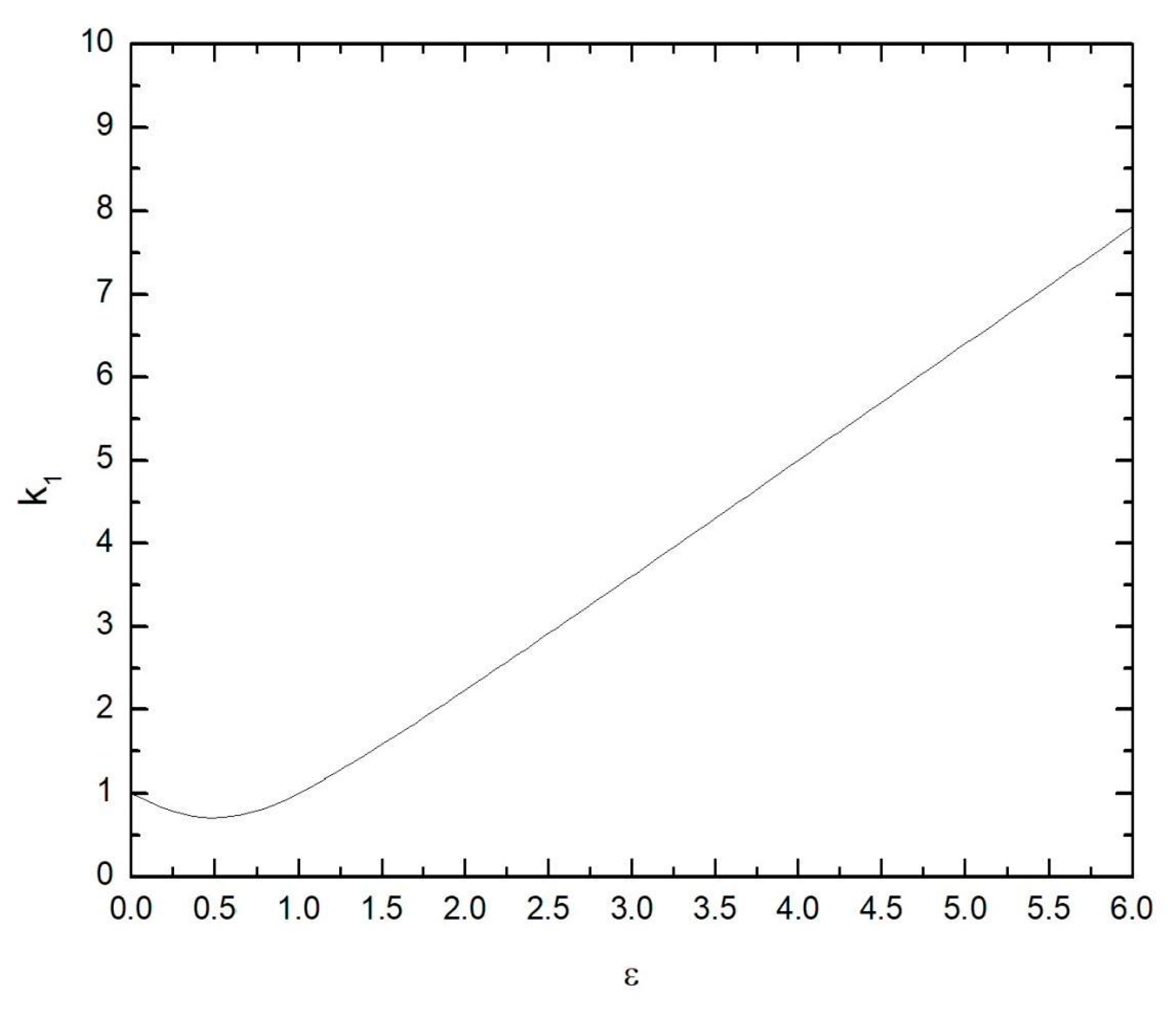
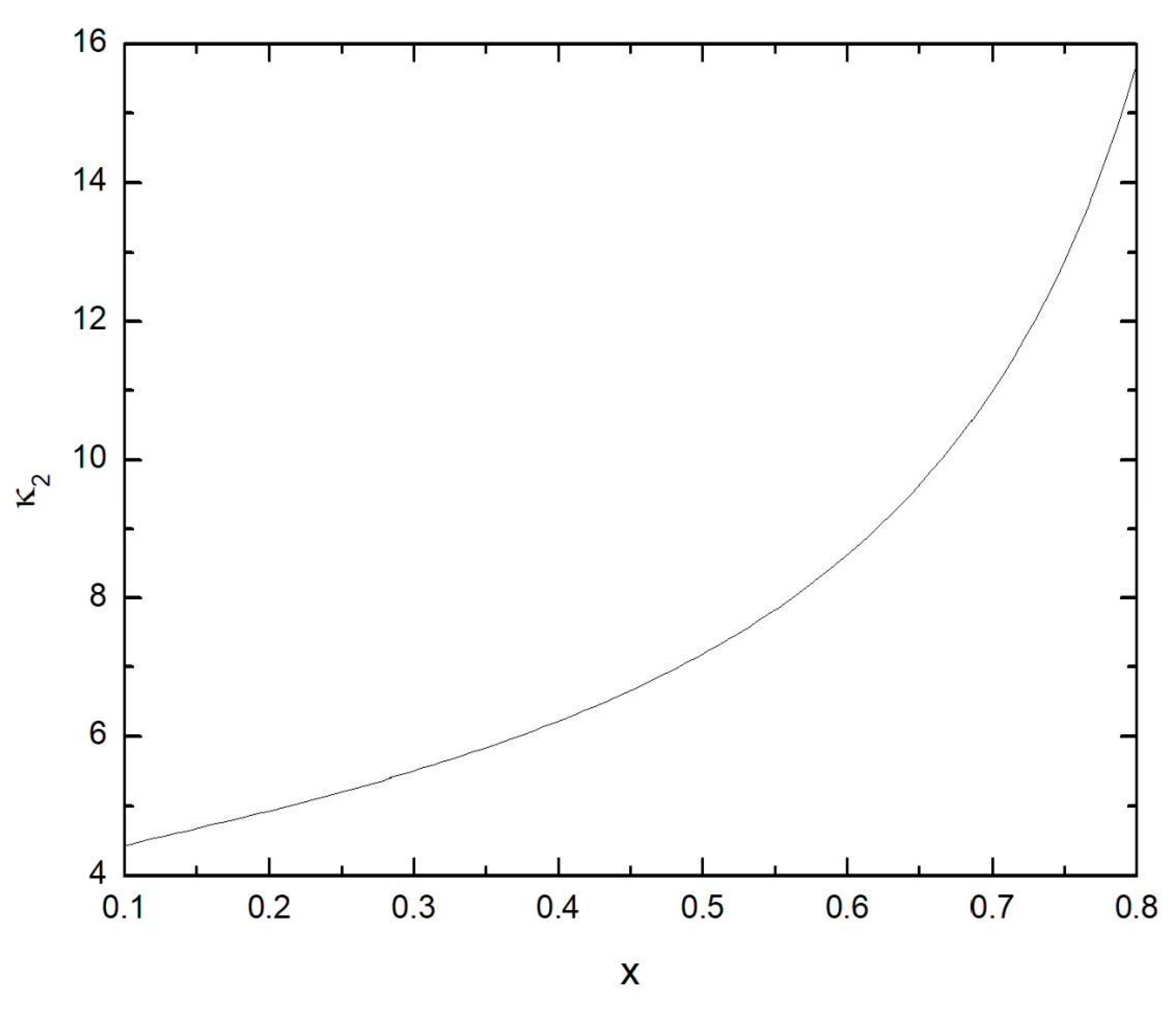
Appendix C. The Reflection Function of a Semi-Infinite Non-Absorbing Snow
Appendix D. The Error Budget in the Case of Polluted Snow
| N | Parameter | Equation | Comments | Physical Meaning |
|---|---|---|---|---|
| 1 | reflectance of nonabsorbing snow layer | |||
| 2 | effective absorption length | |||
| 3 | absorption Angström parameter | |||
| 4 | the snow impurity absorption coefficient at the wavelength (normalized to the snow grain concentration and also to the value of the absorption enhancement factor B) |
- The parameters (, l) can be found from the measurements at two wavelengths in the near-infrared. Therefore, the accuracy of their determination is determined by the accuracy of reflectance measurements at two wavelengths in near-infrared. In particular, the wavelengths 865 and 1020 nm can be used. The error enhancement coefficients depend on the ratio of the bulk ice absorption coefficients at the corresponding wavelengths. Both coefficients increase, if the wavelengths selected are to close one to another (see Appendix C).
- The accuracy of the pair (, m) determination depends on the accuracy of measurements at all four channels (two-in the visible, two- in the near infrared) used in the retrieval process.
Appendix E. Converting Measured Spectral Albedo Over Sloping Terrain to Spectral Planar Albedo in a Flat Terrain Configuration
References
- Hansen, J.; Nazarenko, L. Soot climate forcing via snow and ice albedos. Proc. Natl. Acad. Sci. USA 2004, 101, 423–428. [Google Scholar] [CrossRef] [PubMed]
- Warren, S.G. Optical properties of ice and snow. Philos. Trans. R. Soc. A 2019, 377, 20180161. [Google Scholar] [CrossRef] [PubMed]
- Frei, A.; Tedesco, M.; Lee, S.; Foster, J.; Hall, D.K.; Kelly, R.; Robinson, D.J. A review of global satellite—derived snow products. Adv. Space Res. 2012, 50, 1007–1029. [Google Scholar] [CrossRef]
- Tedesco, M. (Ed.) Remote Sensing of the Cryosphere; Wiley: New York, NY, USA, 2015. [Google Scholar]
- Sirguey, P.; Mathieu, R.; Arnaud, Y. Subpixel monitoring of the seasonal snow cover with MODIS at 250 m spatial resolution in the Southern Alps of New Zealand: Methodology and accuracy assessment. Remote Sens. Environ. 2009, 113, 160–181. [Google Scholar] [CrossRef]
- Klein, A.; Stroeve, J. Development and a validation of a snow albedo algorithm for the MODIS instrument. Ann. Glaciol. 2001, 34, 45–52. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V. Development of methods for mapping global snow cover using moderate resolution imaging spectroradiometer data. Remote Sens. Environ. 1995, 54, 127–140. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Solomonson, V.V.; De Girolamo, N.E.; Bayr, K.J. MODIS snow cover products. Remote Sens. Environ. 2002, 83, 181–194. [Google Scholar] [CrossRef]
- Lyasputin, A.; Tedesco, M.; Wang, Y.; Aoki, T.; Hori, M.; Kokhanovsky, A.A. Retrieval of snow grain size over Greenland from MODIS. Remote Sens. Environ. 2009, 113, 1976–1987. [Google Scholar] [CrossRef]
- Painter, T.H.; Rittger, K.; McKenzie, S.; Slaughter, P.; Davis, R.E.; Dozier, J. Retrieval of subpixel snow covered area, grain size, and albedo from MODIS. Remote Sens. Environ. 2009, 113, 868–879. [Google Scholar] [CrossRef]
- Zege, E.P.; Katsev, I.L.; Prikhach, A.; Heygster, G.; Wiebe, H. Algorithm for retrieval of the effective snow grain size and pollution amount from satellite measurements. Remote Sens. Environ. 2011, 115, 2674–2685. [Google Scholar] [CrossRef]
- Riggs, G.A.; Hall, D.K. MODIS Snow Products Collection 6, User Guide, 2015. Available online: https://nsidc.org/sites/nsidc.org/files/files/MODIS-snow-user-guide-C6.pdf (accessed on 23 September 2019).
- Stamnes, K.; Li, W.; Eide, H.; Aoki, T.; Hori, M.; Storvold, R. ADEOS-II/GLI Snow/ice Products—Part I: Scientific Basis. Remote Sens. Environ. 2007, 111, 258–273. [Google Scholar] [CrossRef]
- Li, W.; Stamnes, K.; Chen, B.; Xiong, X. Snow grain size retrieved from near-infrared radiances at multiple wavelengths. Geophys. Res. Lett. 2011, 28, 1699–1702. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; Rozanov, V.V.; Aoki, T.; Odermatt, D.; Brockmann, C.; Krüger, O.; Bouvet, M.; Drusch, M.; Hori, M. Sizing snow grains using backscattered solar light. Int. J. Remote Sens. 2011, 32, 6975–7008. [Google Scholar] [CrossRef]
- Appel, I. Retrieval and Validation of VIIRS Snow Cover Information for Terrestrial Water Cycle Applications. In Remote Sensing of Terrestrial Water Cycle; Laksmi, V., Alsdorf, D., Anderson, M., Biancamaria, S., Cosh, M., Entin, J., Huffman, G., Kustas, W., van Oevelen, P., Painter, T., et al., Eds.; AGU: Washington, DC, USA, 2014; pp. 175–197. [Google Scholar] [CrossRef]
- Gascoin, S.; Grizzonet, M.; Bouchet, M.; Salgues, G.; Hagolle, O. Theia snow collection: High resolution operational snow cover maps from Sentinel-2 and Lansat-8 data. Earth Syst. Sci. Data 2019, 11, 493–514. [Google Scholar] [CrossRef]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.-H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The Global Monitoring for Environment and Security (GMES) Sentinel-3 mission. Remote Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; Zege, E.P. Scattering optics of snow. Appl. Opt. 2004, 43, 1589–1602. [Google Scholar] [CrossRef]
- Kokhanovsky, A.; Lamare, M.; Di Mauro, B.; Picard, G.; Arnaud, L.; Dumont, M.; Tuzet, F.; Brockmann, C.; Box, J.E. On the reflectance spectroscopy of snow. Cryosphere 2018, 12, 2371–2382. [Google Scholar] [CrossRef]
- Warren, S.G.; Brandt, R.E. Optical constants of ice from the ultraviolet to the microwave: A revised compilation. J. Geophys. Res. 2008, 113, 3681–3691. [Google Scholar] [CrossRef]
- Picard, G.; Libois, Q.; Arnaud, L. Refinement of the ice absorption spectrum in the visible using radiance profile measurements in Antarctic snow. Cryosphere 2016, 10, 2655–2672. [Google Scholar] [CrossRef]
- Grenfell, T.C.; Warren, S.G.; Mullen, P.C. Reflection of solar radiation by the Antarctic snow surface at ultraviolet, visible, and near-infrared wavelengths. J. Geophys. Res. 1994, 99, 18669–18684. [Google Scholar] [CrossRef]
- Dumont, M.; Brissaud, O.; Picard, G.; Schmitt, B.; Gallet, J.-C.; Arnaud, Y. High-accuracy measurements of snow Bidirectional Reflectance Distribution Function at visible and NIR wavelengths—Comparison with modelling results. Atmos. Chem. Phys. 2010, 10, 2507–2520. [Google Scholar] [CrossRef]
- Di Mauro, B.; Fava, F.; Ferrero, L.; Garzonio, R.; Baccolo, G.; Delmonte, B.; Colombo, R. Mineral dust impact on snow radiative properties in the European Alps combining ground, UAV, and satellite observations. J. Geophys. Res. Atmos. 2015, 120, 6080–6097. [Google Scholar] [CrossRef]
- He, C.; Liou, K.-N.; Takano, Y.; Yang, P.; Qi, L.; Chen, F. Impact of grain shape and multiple black carbon internal mixing on snow albedo: Parameterization and radiative effect analysis. J. Geophys. Res. 2018, 123, 1253–1268. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; Aoki, T.; Hachikubo, A.; Hori, M.; Zege, E.P. Reflective properties of natural snow: Approximate asymptotic theory versus in situ measurements. IEEE Trans. Geosci. Rem. Sens. 2005, 43, 1529–1535. [Google Scholar] [CrossRef]
- Ding, A.; Jiao, Z.; Dong, Y.; Qu, Y.; Zhang, X.; Xiong, C.; He, D.; Yin, S.; Cui, L.; Chang, Y. An assessment of the performance of two snow kernels in characterizing snow scattering properties. Int. J. Remote Sens. 2019, 40, 6315–6335. [Google Scholar] [CrossRef]
- Jiao, Z.; Ding, A.; Kokhanovsky, A.; Schaaf, C.; Bréon, F.; Dong, Y.; Wang, Z.; Liu, Y.; Zhang, X.; Yin, S.; et al. Development of a snow kernel to better model the anisotropic reflectance of pure snow in a kernel-driven BRDF model framework. Remote Sens. Environ. 2019, 221, 198–209. [Google Scholar] [CrossRef]
- Rosenberg, G.V. Optical characteristics of thick weakly absorbing scattering layers. Dokl. Akad. Nauk 1962, 6, 775–777. [Google Scholar]
- Zege, E.P.; Katsev, I.L.; Ivanov, A.P. Image Transfer Through Scattering Media; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Kokhanovsky, A. Statistical properties of photon gas in random media. Phys. Rev. 2002, E66, 037601. [Google Scholar] [CrossRef]
- Sobolev, V.V. Light scattering in planetary atmospheres: International series of monographs in natural philosophy; M.: Nauka; Elsevier: Pergamon, Turkey, 1975. [Google Scholar]
- Korkin, S.; Lyapustin, A. Matrix exponential in C/C++ version of vector radiative transfer code IPOL. J. Quant. Spectrosc. Radiat. Transf. 2019, 227, 106–110. [Google Scholar] [CrossRef]
- Emde, C.; Barlakas, V.; Cornet, C.; Evans, F.; Korkin, S.; Ota, Y.; Labonnote, L.C.; Lyapustin, A.; Macke, A.; Mayer, B.; et al. IPRT polarized radiative transfer model intercomparison project—Phase A. J. Quant. Spectrosc. Radiat. Transf. 2015, 164, 8–36. [Google Scholar] [CrossRef]
- Picard, G.; Arnaud, L.; Dominé, F.; Fily, M. Determining snow specific surface area from near-infrared reflectance measurements: Numerical study of the influence of grain shape. Cold Reg. Sci. Technol. 2009, 56, 10–17. [Google Scholar] [CrossRef]
- Gallet, J.-C.; Domine, F.; Zender, C.; Picard, G. Measurement of the specific surface area of snow using infrared reflectance in an integrating sphere at 1310 and 1550 nm. Crysophere 2009, 3, 167–182. [Google Scholar] [CrossRef]
- Van de Hulst, H.C. Light Scattering by Small Particles; Dover: New York, NY, USA, 1981. [Google Scholar]
- Kokhanovsky, A.A. Scaling constant and its determination from simultaneous measurements of light reflection and methane adsorption by snow samples. Opt. Lett. 2006, 31, 3282–3284. [Google Scholar] [CrossRef] [PubMed]
- Libois, Q.; Picard, G.; Dumont, M.; Arnaud, L.; Sergent, C.; Pougatch, E.; Sudul, M.; Vial, D. Experimental determination of the absorption enhancement parameter of snow. J. Glaciol. 2014, 7, 714–724. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; Zege, E.P. Local optical parameters of spherical polydispersions: Simple approximations. Appl. Opt. 1995, 34, 5513–5519. [Google Scholar] [CrossRef] [PubMed]
- Dombrovsky, L.A.; Kokhanovsky, A.A. The influence of pollution on solar heating and melting of a snowpack. J. Quant. Spectrosc. Radiat. Transf. 2019, 233, 42–51. [Google Scholar] [CrossRef]
- Ricchiazzi, P.; Yang, S.; Gautier, C.; Sowle, D. SBDART, A research and teaching tool for plane-parellel radiative transfer in the Earth’s atmosphere. Bull. Am. Meteorol. Soc. 1998, 79, 2101–2114. [Google Scholar] [CrossRef]
- Wiscombe, W.J.; Warren, S.G. A Model for the Spectral Albedo of Snow. I: Pure Snow. J. Atmos. Sci. 1980, 37, 2712–2733. [Google Scholar] [CrossRef]
- Domine, F.; Salvatori, R.; Legagneux, L.; Salzano, R.; Fily, M.; Cassacchia, R. Correlation between the specific surface area and the short wave infrared (SWIR) reflectance of snow. Cold Reg. Sci. Technol. 2006, 46, 60–68. [Google Scholar] [CrossRef]
- Räisänen, P.; Kokhanovsky, A.; Guyot, G.; Jourdan, O.; Nousiainen, T. Parameterization of single-scattering properties of snow. Cryosphere 2015, 9, 1277–1301. [Google Scholar] [CrossRef]
- Hori, M.; Aoki, T.; Stamnes, K.; Chen, B.; Li, C. Preliminary validation of the GLI cryosphere algorithms with MODIS daytime data. Polar Meteorol. Glaciol. 2001, 15, 1–20. [Google Scholar]
- Garrett, T.J. Observational quantification of the optical properties of cirrus cloud. In Light Scattering Reviews; Kokhanovsky, A., Ed.; Praxis-Springer: Berlin/Heidelberg, Germany, 2008; Volume 3, pp. 1–26. [Google Scholar]
- Linow, S.; Horhold, M.W.; Freitag, J. Grain-size evolution of polar firn: A new empirical grain growth parameterization based on X-ray microcomputer tomography measurements. J. Glaciol. 2012, 58, 1245–1252. [Google Scholar] [CrossRef]
- Dozier, J.; Frew, J. Atmospheric corrections to satellite radiometric data over rugged terrain. Remote Sens. Environ. 1981, 11, 191–205. [Google Scholar] [CrossRef]
- Van As, D. Warming, glacier melt and surface energy budget from weather station observations in the Melville Bay region of northwest Greenland. J. Glaciol. 2011, 57, 208–220. [Google Scholar] [CrossRef]
- Van As, D.; van den Broeke, M.R.; Reijmer, C.; van de Wal, R. The summer surface energy balance of the high Antarctic plateau. Bound. Layer Meteorol. 2005, 115, 289–317. [Google Scholar]
- Tomasi, C.; Kokhanovsky, A.; Lupi, A.; Ritter, C.; Smirnov, A.; O’Neill, N.T.; Stone, R.S.; Holben, B.N.; Nyeki, S.; Wehrli, C.; et al. Aerosol remote sensing in polar regions. Earth Sci. Rev. 2015, 140, 108–157. [Google Scholar] [CrossRef]
- Dumont, M.; Arnaud, L.; Picard, G.; Libois, Q.; Lejeune, Y.; Nabat, P.; Voisin, D.; Morin, S. In situ continuous visible and near-infrared spectroscopy of an alpine snowpack. Cryosphere 2017, 11, 1091–1110. [Google Scholar] [CrossRef]
- Libois, Q.; Picard, G.; Arnaud, L.; Dumont, M.; Lafaysse, M.; Morin, S.; Lefebvre, E. Summertime evolution of snow specific surface area close to the surface on the Antarctic Plateau. Cryosphere 2015, 9, 2383–2398. [Google Scholar] [CrossRef]
- Arnaud, L.; Picard, G.; Champollion, N.; Domine, F.; Gallet, J.C.; Lefebvre, E.; MFily; Barnola, J.M. Measurement of vertical profiles of snow specific surface area with a 1cm resolution using infrared reflectance: Instrument description and validation. J. Glaciol. 2011, 57, 17–29. [Google Scholar] [CrossRef]
- Aoki, T.; Kuchiki, K.; Niwano, M.; Kodama, Y.; Hosaka, M.; Tanaka, T. Physically based snow albedo model for calculating broadband albedos and the solar heating profile in snowpack for general circulation models. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Stibal, M.; Box, J.E.; Cameron, K.A.; Langen, P.L.; Yallop, M.L.; Mottram, R.H.; Khan, A.L.; Molotch, N.P.; Chrismas, N.A.M.; Quaglia, F.C.; et al. Algae drive enhanced darkening of bare ice on the Greenland ice sheet. Geophys. Res. Lett. 2017, 44, 11463–11471. [Google Scholar] [CrossRef]
- Wientjes, I.G.M.; Van de Wal, R.S.W.; Reichart, G.J.; Sluijs, A.; Oerlemans, J. Dust from the dark region in the western ablation zone of the Greenland ice sheet. Cryosphere 2011, 5, 589–601. [Google Scholar] [CrossRef]
- Van Angelen, J.H.; Lenaerts, J.T.M.; Lhermitte, S.; Fettweis, X.; Kuipers Munneke, P.; van den Broeke, M.R.; van Meijgaard, E.; Smeets, C.J.P.P. Sensitivity of Greenland Ice Sheet surface mass balance to surface albedo parameterization: A study with a regional climate model. Cryosphere 2012, 6, 1175–1186. [Google Scholar] [CrossRef]
- Langen, P.L.; Fausto, R.S.; Vandecrux, B.; Mottram, R.H.; Box, J.E. Liquid water flow and retention on the Greenland ice sheet in the regional climate model HIRHAM5: Local and large-scale impacts. Front. Earth Sci. 2017, 4, 110. [Google Scholar] [CrossRef]
- Shao, D.; Xu, W.; Li, H.; Wang, J.; Hao, X. Reconstruction of remotely sensed snow albedo for quality improvements based on a combination of forward and retrieval models. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6969–6985. [Google Scholar] [CrossRef]
- Lv, Y.; Wu, D.; Sub, Z. Effect of black carbon concentration on the reflection property of snow: A comparison with model results. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6823–6839. [Google Scholar] [CrossRef]
- Saito, M.; Yang, P.; Loeb, N.G.; Kato, S. A novel parameterization of snow albedo based on a two-layer snow model with a mixture of habits. J. Atmos. Sci. 2019, 76, 1419–1436. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Stochastic problems in physics and astronomy. Rev. Mod. Phys. 1943, 1, 1–89. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A. Reflection of light from particulate media with irregularly shaped particles. J. Quant. Spectrosc. Radiat. Transf. 2005, 96, 1–10. [Google Scholar] [CrossRef]


| Name in Product | Units, When Not Dimensionless | Description |
|---|---|---|
| albedo_bb_spherical_vis | Spherical albedo in the broadband visible range from 300 nm to 700 nm | |
| albedo_bb_spherical_nir | Spherical albedo in the broadband near infrared range from 700 nm to 2400 nm | |
| albedo_bb_spherical_sw | Spherical albedo in the broadband shortwave range from 300 nm to 2400 nm | |
| albedo_bb_planar_vis | Planar albedo in the broadband visible range from 300 nm to 700 nm | |
| albedo_bb_planar_nir | Planar albedo in the broadband near infrared range from 700 nm to 2400 nm | |
| albedo_bb_planar_sw | Planar albedo in the broadband shortwave range from 300 nm to 2400 nm | |
| albedo_spectral_spherical | Spectral spherical albedo in 21 OLCI bands | |
| albedo_spectral_planar | Spectral planar albedo in 21 OLCI bands | |
| rBRR | Estimated bottom of atmosphere OLCI reflectance in 21 OLCI bands | |
| ppa_spectral | PPA in 21 OLCI bands | |
| grain_diameter | mm | Snow grain diameter |
| snow_specific_area | m2 kg−1 | Snow specific surface area |
| ndbi | Bare ice indicator | |
| pollution_mask | Pollution mask | |
| mm−1 | Normalized snow impurity absorption coefficient at 1 µm | |
| l | mm | Effective absorption length |
| m | Absorption Angstrom parameter | |
| r_0 | Reflectance of non-absorbing snow layer | |
| f_rel_err | Relative error of normalized snow impurity absorption coefficient at 1 µm | |
| l_rel_err | Relative error of parameter l | |
| m_rel_err | Relative error of parameter m | |
| r_0_rel_err | Relative error of parameter r_0 | |
| ndsi | Normalised differential snow index | |
| ndsi_mask | NDSI mask for snow identification | |
| quality_flags | L1b quality flags | |
| pixel_classif_flags | Pixel classification flags |
| Site Name | Sentinel-3 OLCI Acquisition Date/Time (UTC) | SZA/° | Average Latitude/Longitude of the Field Measurements | |
|---|---|---|---|---|
| S3 Overpass | Measurement | |||
| st1 | 2016/12/01, 22h21 | 59.14 | 64.1 | −66.881150, 139.280006 |
| st2 | 2016/12/02, 23h36 | 52.81 | 47.2 | −67.167791, 138.968926 |
| st6 | 2016/12/06, 21h51 | 63.25 | 68.5 | −68.872819, 135.303749 |
| st10 | 2016/12/10, 23h28 | 55.23 | 67.6 | −69.636122, 135.279596 |
| st16 | 2016/12/16, 22h32 | 58.60 | 70.8 | −69.953844, 138.551435 |
| st17 | 2016/12/17, 22h06 | 60.74 | 70.8 | −69.953799, 138.553538 |
| st21 | 2016/12/21, 22h02 | 60.01 | 75.6 | −69.786595, 141.972969 |
| st22 | 2016/12/22, 23h17 | 54.20 | 64.9 | −69.786595, 141.972969 |
| st25 | 2016/12/25, 23h40 | 53.39 | 64.7 | −69.376932, 139.016187 |
| st26 | 2016/12/26, 23h13 | 55.53 | 67.4 | −69.060033, 138.225079 |
| st27 | 2016/12/27, 22h47 | 57.90 | 55.3 | −68.747273, 137.443734 |
| Sentinel-3 OLCI Band | Sentinel-3 OLCI Spectral Planar Albedo Retrievals | Autosolexs Spectral Albedo Measurements | Mean Albedo Bias (Absolute): | Mean Albedo Bias (%): | ||
|---|---|---|---|---|---|---|
| Average | Std | Average | Std | |||
| 01 (400 nm) | 0.9988 | 0.0002 | 0.9899 | 0.0210 | 0.0089 | 0.9446 |
| 02 (421.5 nm) | 0.9987 | 0.0002 | 0.9941 | 0.018 | 0.0046 | 0.4991 |
| 03 (442.5 nm) | 0.9981 | 0.0003 | 0.9962 | 0.0136 | 0.0019 | 0.2099 |
| 04 (490 nm) | 0.9955 | 0.0006 | 0.9971 | 0.0086 | 0.0016 | 0.1572 |
| 05 (510 nm) | 0.9938 | 0.0008 | 0.9965 | 0.0061 | 0.0027 | 0.2651 |
| 06 (560 nm) | 0.9889 | 0.0015 | 0.9929 | 0.0044 | 0.0039 | 0.3951 |
| 07 (620 nm) | 0.9819 | 0.0024 | 0.9893 | 0.0040 | 0.0075 | 0.7550 |
| 08 (665 nm) | 0.9749 | 0.0034 | 0.9812 | 0.0052 | 0.0062 | 0.6345 |
| 09 (673.75 nm) | 0.9742 | 0.0034 | 0.9793 | 0.0052 | 0.0050 | 0.5133 |
| 10 (681.25 nm) | 0.9731 | 0.0037 | 0.9776 | 0.0052 | 0.0045 | 0.4581 |
| 11 (708.75 nm) | 0.9663 | 0.0046 | 0.9706 | 0.0057 | 0.0043 | 0.4466 |
| 12 (753.75 nm) | 0.9575 | 0.0057 | 0.9574 | 0.0063 | 0.0001 | 0.0112 |
| 13 (761.25 nm) | 0.9536 | 0.0062 | 0.9584 | 0.0072 | 0.0047 | 0.4905 |
| 14 (764.375 nm) | 0.9524 | 0.0064 | 0.9544 | 0.0072 | 0.0020 | 0.2072 |
| 15 (767.5 nm) | 0.9508 | 0.0066 | 0.9510 | 0.0073 | 0.0003 | 0.0270 |
| 16 (778.75 nm) | 0.9452 | 0.0073 | 0.9455 | 0.0078 | 0.0002 | 0.0248 |
| 17 (865 nm) | 0.9213 | 0.0104 | 0.9226 | 0.0099 | 0.0013 | 0.1444 |
| 18 (885 nm) | 0.9055 | 0.0124 | 0.9056 | 0.0118 | 0.0001 | 0.0050 |
| 19 (900 nm) | 0.8992 | 0.0132 | 0.8975 | 0.0127 | 0.0017 | 0.1906 |
| 20 (940 nm) | 0.8875 | 0.0146 | 0.8908 | 0.0147 | 0.0032 | 0.3576 |
| 21 (1020 nm) | 0.7939 | 0.0254 | 0.8075 | 0.0258 | 0.0136 | 1.6661 |
| Site Name | Latitude, Degrees N | Longitude, Degrees W | Elevation, m | Regression Slope | Regression Constant | Correlation | Average Difference, OLCI-PROMICE | RMSD | N obs |
|---|---|---|---|---|---|---|---|---|---|
| KPC_L | 79.908 | 24.080 | 366 | 0.734 | 0.217 | 0.936 | 0.053 | 0.082 | 221 |
| SCO_U | 72.394 | 27.259 | 988 | 0.890 | 0.094 | 0.921 | 0.024 | 0.046 | 22 |
| QAS_L | 61.031 | 46.849 | 270 | 0.900 | 0.046 | 0.979 | −0.008 | 0.055 | 23 |
| KAN_M | 67.067 | 48.838 | 1268 | 0.861 | 0.081 | 0.868 | −0.017 | 0.072 | 66 |
| KAN_U | 67.000 | 47.027 | 1842 | 0.571 | 0.347 | 0.707 | −0.003 | 0.022 | 100 |
| UPE_U | 72.887 | 53.585 | 929 | 1.106 | −0.033 | 0.918 | 0.030 | 0.066 | 62 |
| EGP | 75.625 | 35.973 | 2660 | 0.842 | 0.134 | 0.760 | 0.001 | 0.007 | 74 |
| mean | 70.8 | −40.5 | 1189 | 0.843 | 0.127 | 0.870 | 0.011 | 0.050 | 81 |
| std. | 6.3 | 11.5 | 839 | 0.164 | 0.124 | 0.100 | 0.025 | 0.027 | 67 |
| Satellite | Date | Overpass Time, UTC | Observation Time, UTC | OLCI-Retrieved Dimeter of Grains, mm | In-Situ Derived Diameter of Grains, mm | Difference in Diameters (OLCI-In-Situ), μm | % Bias |
|---|---|---|---|---|---|---|---|
| S3A | 8 July 2018 | 1414 | 1416 | 0.138 | 0.145 | −6.8 | 0.95% |
| 9 July 2018 | 1529 | 1528 | 0.209 | 0.206 | 3.5 | 1.02% | |
| 13 July 2018 | 1525 | 1523 | 0.164 | 0.124 | 40.1 | 1.32% | |
| average | 0.171 | 0.158 | 12.3 | 1.08% | |||
| S3B | 8 July 2018 | 1414 | 1416 | 0.135 | 0.145 | −10.1 | 0.93% |
| 9 July 2018 | 1528 | 1528 | 0.176 | 0.206 | −30.1 | 0.85% | |
| 13 July 2018 | 1525 | 1523 | 0.173 | 0.124 | 47.6 | 1.38% | |
| average | 0.161 | 0.158 | 2.5 | 1.02% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kokhanovsky, A.; Lamare, M.; Danne, O.; Brockmann, C.; Dumont, M.; Picard, G.; Arnaud, L.; Favier, V.; Jourdain, B.; Le Meur, E.; et al. Retrieval of Snow Properties from the Sentinel-3 Ocean and Land Colour Instrument. Remote Sens. 2019, 11, 2280. https://doi.org/10.3390/rs11192280
Kokhanovsky A, Lamare M, Danne O, Brockmann C, Dumont M, Picard G, Arnaud L, Favier V, Jourdain B, Le Meur E, et al. Retrieval of Snow Properties from the Sentinel-3 Ocean and Land Colour Instrument. Remote Sensing. 2019; 11(19):2280. https://doi.org/10.3390/rs11192280
Chicago/Turabian StyleKokhanovsky, Alexander, Maxim Lamare, Olaf Danne, Carsten Brockmann, Marie Dumont, Ghislain Picard, Laurent Arnaud, Vincent Favier, Bruno Jourdain, Emmanuel Le Meur, and et al. 2019. "Retrieval of Snow Properties from the Sentinel-3 Ocean and Land Colour Instrument" Remote Sensing 11, no. 19: 2280. https://doi.org/10.3390/rs11192280
APA StyleKokhanovsky, A., Lamare, M., Danne, O., Brockmann, C., Dumont, M., Picard, G., Arnaud, L., Favier, V., Jourdain, B., Le Meur, E., Di Mauro, B., Aoki, T., Niwano, M., Rozanov, V., Korkin, S., Kipfstuhl, S., Freitag, J., Hoerhold, M., Zuhr, A., ... Box, J. E. (2019). Retrieval of Snow Properties from the Sentinel-3 Ocean and Land Colour Instrument. Remote Sensing, 11(19), 2280. https://doi.org/10.3390/rs11192280







