Abstract
Sentinel-3A/3B (S3A/B) satellites are equipped with a number of precise instruments dedicated to the measurement of surface topography, sea and land surface temperatures and ocean and land surface color. The high-precision orbit is guaranteed by three instruments: Global Positioning System (GPS) receiver, laser retroreflector dedicated to Satellite Laser Ranging (SLR) and Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS) antenna. In this article, we check the possibility of using SLR observations and GPS-based reduced-dynamic orbits of active S3A/B satellites for the determination of global geodetic parameters, such as geocenter motion, Earth rotation parameters (ERPs) and the realization of the terrestrial reference frame, based on data from 2016-2018. The calculation process was preceded with the estimation of SLR site range biases, different network constraining tests and a different number of orbital arcs in the analyzed solutions. The repeatability of SLR station coordinates based solely on SLR observations to S3A/B is at the level of 8-16 mm by means of interquartile ranges even without network constraining in 7-day solutions. The combined S3A/B and LAGEOS solutions show a consistency of estimated station coordinates better than 13 mm, geocenter coordinates with a RMS of 6 mm, pole coordinates with a RMS of 0.19 mas and Length-of-day with a RMS of 0.07 ms/day when referred to the IERS-14-C04 series. The altimetry observations have to be corrected by the geocenter motion to obtain unbiased estimates of the mean sea level rise. The geocenter motion is typically derived from SLR measurements to passive LAGEOS cannonball-like satellites. We found, however, that SLR observations to active Sentinel satellites are well suited for the determination of global geodetic parameters, such as Earth rotation parameters and geocenter motion, which even further increases the potential applications of Sentinel missions for deriving geophysical parameters.
1. Introduction
1.1. Satellite Laser Ranging to Low Earth Orbiters
Satellite Laser Ranging (SLR) is an optical space-geodetic technique, which typically employs measurements to active satellites, such as Global Navigation Satellite Systems (GNSS) satellites or Low Earth Orbiters (LEOs) and passive geodetic satellites, for example, the cannonball LAGEOS-1/2 in medium Earth orbits (MEO) or Starlette, Stella, Ajisai, LARES in low Earth orbits. The geodetic satellites are used for the determination of the geocenter motion, global scale, Earth rotation parameters, the standard gravity parameter GM, low-degree Earth’s gravity field coefficients and for the verification of relativistic effects [1]. In the case of measurements to active LEOs, SLR is a state-of-art technique for the validation of orbits, based on tracking data of GNSS or Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS). The co-location of SLR and GNSS can be found on satellites, such as GOCE [2], GRACE-A/B [3], CHAMP [4], SWARM-A/B/C [5], TerraSAR-X [6] and TanDEM-X [7]. Moreover, DORIS technique is also used onboard satellites, including Jason-2 [8], Sentinel-3A/3B (S3A/B, [9]), HY-2A/2B [10] and Sentinel-6 (planned, [11]). The increasing amount of high-quality SLR data and microwave-based orbit data of LEO satellites enable us to use these observations for the co-location in space.
Arnold et al. [12] validated Global Positioning System (GPS) based orbits and the network of the International Laser Ranging Service (ILRS, [13]) stations using data from eight active LEO satellites, which resulted in residual repeatability of 5–10 mm. Hackel et al. [14] used SLR for the validation of long-term series of enhanced GPS-based orbits of TerraSAR-X and TanDEM-X and obtained mean biases of 1.6 mm and 1.2 mm with standard deviations of 11.4 mm and 12.5 mm, respectively. Montenbruck et al. [15] used undifferenced GPS carrier phase ambiguity fixing and non-gravitational force modeling for precise orbit determination of the SWARM satellites and obtained SLR residuals of the GPS-based orbits in the range of 5–10 mm. Guo et al. [16] used SLR observations to GPS-based kinematic orbits of GRACE-A covering the year 2012 for the determination of SLR station coordinates and achieved a consistency at the level of 20–30 mm with SLRF2014. Zelensky et al. [17] used SLR and DORIS observations to Jason-1/2 for the validation of GPS, DORIS/SLR and DORIS based orbits which resulted in a consistency of 10 mm.
Considering geocenter coordinates, Couhert et al. [18] used DORIS-only and also SLR-only observations to Jason-2. For SLR-only solutions, estimation of 10-day geocenter was used with unconstrained adjustment of station height and range bias values, resulting in amplitudes of 1.5, 3.1 and 5.6 mm for the geocenter X, Y, Z components, respectively. The SLR observations to active LEO satellites have never been used so far for the determination of other geodetic parameters, such as Earth rotation parameters (ERPs) using, for example, a different number of accumulated 1-day solutions. Moreover, it is unclear how and whether at all, the SLR network should be constrained when using SLR observations to GPS-based LEO orbits for this purpose.
For the LEO Precise Orbit Determination (POD) based on GPS, typically two methods are employed: a kinematic POD [19], where three-dimensional positions are determined at the measurement epochs by purely geometrical means; a dynamic POD [20], where satellite orbits have to fulfill an equation of motion. The most accurate methods for LEO POD employ so-called reduced-dynamic POD [21] or model all perturbing forces by using satellite macro-models (e.g., [22]). For the reduced-dynamic method, additional empirical or stochastic accelerations may be estimated thanks to the geometrical strength of the GNSS data to efficiently compensate force model deficiencies [23]. The arrangement of both SLR and GNSS techniques onboard active LEO satellites offers a possibility of exploring new geodetic applications, not only for POD but also for deriving geodetic parameters. This study focuses on the analysis of SLR observations to GPS-based precise reduced-dynamic orbits of S3A/B and on the combination of SLR solutions based on observations to the S3A/B and the LAGEOS-1/2 satellites.
S3A/B are the Earth observation satellites specifically designed to ensure the long-term collection and operational delivery of high-quality measurements to the ocean, land and atmospheric services while contributing to the European Copernicus (https://www.copernicus.eu/) program (former GMES), emergency and security services [9]. S3A/B are the only satellites in the Sentinel constellation which integrate three independent tracking techniques for POD onboard: GNSS, SLR and DORIS. So far, SLR to Sentinels was used only as an orbit validation tool and not for deriving global geodetic parameters. However, precise observables from the independent techniques integrated onboard S3A/B might be useful for the determination of global geodetic parameters and to be compared or even combined with LAGEOS-1/2 observations.
1.2. Goal and Objectives of This Study
The goal of this study is to investigate the quality of global geodetic parameters and the reference frame realization based solely on SLR observations to LEO satellites whose orbits are determined using GPS data. We check whether the SLR solutions based on external orbits have any remaining singularities when Earth rotation parameters, geocenter and station coordinates are simultaneously estimated or how and whether such a network should be constrained. In this study, we assume that the GNSS-based orbits are accurate as provided by the GPS-based reduced-dynamic orbits computed at the Astronomical Institute of the University of Bern (AIUB). We examine whether SLR observations to active LEOs can be used to determine SLR station coordinates, geocenter and pole coordinates and the UT1-UTC values by testing different types of SLR network constraining and a different number of accumulated 1-day orbit solutions. We compare our results to standard LAGEOS-based solutions and perform determination of combined solution based on S3A/B and LAGEOS-1/2 observations.
The manuscript is organized as follows: Section 2 starts with S3A/B satellite characteristics, paying particular attention to POD. Then, describes the methodology of the processing, using SLR to S3A/B solutions and the LAGEOS-1/2+Sentinel-3A/B combined solution with a residual analysis of SLR observations to S3A/B. Section 3 shows the results of different solution scenarios based on S3A/B for the datum realization. This section provides results of using different numbers of 1-day normal equations in the solution used to recover the parameters of interest and contains the results from the combined LAGEOS+S3A/B solution with regard to the ERP, geocenter and station coordinate determination. Finally, a discussion of results is provided in the Section 4 and conclusions are drawn in the last section.
2. Materials and Methods
2.1. Sentinel-3A/3B Mission Overview
The first Sentinel-3 satellite, Sentinel-3A was launched on February 16, 2016 and its twin Sentinel-3B was launched on April 25, 2018. The required S3A/B orbit accuracies are 20–30 mm after postprocessing [24] with special attention on the orbit quality in the radial direction, which is crucial for all altimetry missions. An independent orbit determination can be provided by the DORIS tracking system with a multichannel and digital receiver, similar to those mounted on Jason-2 and CryoSat-2 satellites. For SLR measurements, the Laser Retroreflectors (LRR) were mounted onboard S3A/B for GPS and DORIS-based POD validation. The LRR consists of seven corner cubes prisms made by the Russian Institute for Precision Instruments Engineering and is the same as used for Cryosat or PROBA-2 missions [12]. For Sentinels’ attitude determination, three-head star trackers were employed as a core device with additional coarse Sun sensors in eight satellite corners for the Sun direction estimation [25]. The first SLR station, Herstmonceux, started collecting observations on April 1, 2016 for Sentinel-3A, whereas for Sentinel-3B satellite the first SLR station with data acquisition was Potsdam on May 03, 2018.
2.2. Sentinel-3A/3B Orbits
S3A/B are orbiting the Earth at an altitude of about 814.5 km in sun-synchronous orbits with an inclination of 98.7°. This implies two passes above the same area per day: one descending pass at about 10 am and one ascending pass at about 10 pm of local time. Apart from the beginning of the mission, S3A/B are on the similar orbit with a separation of 140°, where Sentinel-3B orbits with ± 140° out of phase with regard to Sentinel-3A [26].
The Copernicus POD Service (CPOD), led by the GMV Innovating Solutions consortium is responsible for generating precise orbital products as operational service. The AIUB is one of the contributors to the CPOD which provide precise reduced-dynamic 1-day orbits of S3A/B (for details see [27]), generated using the Bernese GNSS Software [28]. The AIUB S3A/B orbits, which we used in our study, are based on GPS phase observations with constrained piecewise constant empirical accelerations, estimated every 6 minutes in the radial, along-track and cross-track direction [23]. The fixed GPS orbit and clock final products from the Center for Orbit Determination in Europe [29] were used in the orbit determination process. These orbits have also the GPS antenna phase-center variations applied, empirically derived by using the residual stacking approach, which relies on given center-of-mass (CoM) and antenna phase center information [30]. The Sentinel center of mass relative to the satellite-based origin varies during fuel depletion. Correction of this offset due to the center of mass change is provided by the International DORIS Service (ftp://ftp.ids-doris.org/pub/ids/satellites/s3amass.txt;ftp://ftp.ids-doris.org/pub/ids/satellites/s3bmass.txt). The LRR offset relative to the satellite center of mass has also been considered as a time-variable quantity (https://ilrs.cddis.eosdis.nasa.gov/docs/2015/SE3LR100E10A_MONTAGE_LRR_ON_PF.pdf). Due to the construction of the LRR, it is necessary to include systematic range measurement corrections due to the zenith angle as well as azimuth angle variability. The zenith angle culmination corrections vary between 23.13 and 16.25 mm (https://ilrs.cddis.eosdis.nasa.gov/docs/2015/User_manual_S3-LRR.pdf), whereas the azimuth angle corrections vary between 14.21 and 25.29 mm (https://ilrs.cddis.eosdis.nasa.gov/docs/TN_1101_IPIE_LRA_v1.0.pdf).
2.3. Methodology
First, we combined 1-day normal equations based on SLR range observations, a priori station coordinates from SLRF2014 [31], 1-day precise satellite orbits provided by the AIUB, satellite attitude data, ERP from IERS-14-C04 series [32] with near-zero constraints for station coordinates, the X, Y pole coordinates and the UT1-UTC. For S3A/B, the 1-day normal equations were accumulated in order to estimate the annual range bias values and one set of station coordinates for each year, without estimation of other parameters. Then again, the same normal equations, with re-substituted station-specific annual range biases were used and tested with different network and parameter constraints. In calculations, we used a modified version of the Bernese GNSS Software [28].
Having 1-day normal equations, we studied different solution scenarios for the determination of SLR station coordinates and global geodetic parameters, based solely on SLR observations to S3A/B. Specifically, we tested three different scenarios by changing the network constraints and the number of estimated parameters with stacking normal equations for the standard 7-day solution. In the next step, solutions with different numbers of 1-day normal equations: 1-, 3-, 5-, 7- and 15-day solutions, were tested for the estimation of station and geocenter coordinates, pole coordinates and UT1-UTC. In all tested solutions we stacked 1-day normal equations, where ERPs were always estimated with a 1-day resolution, parameterized as piece-wise linear [33]. Other parameters, such as station and geocenter coordinates were estimated as one set per one solution, for example, one set of coordinates for 7 days in the solution. The obtained results were compared with respect to SLRF2014 station coordinates, LAGEOS-based geocenter coordinates and the IERS-14-C04 series for ERPs. For comparison purposes and investigate how combining data influence the results, we calculated LAGEOS-based solution and performed combination of 1-day normal equations of LAGEOS and S3A/B satellites in standard 7-day solution.
2.4. Solution Constraining Scenarios
For S3A/B, we generated three main solution scenarios (Table 1). In solution 1, the No-Net-Rotation (NNR) and the No-Net-Translation (NNT) constraints were applied on the list of verified SLR core stations, for which discontinuity and performance analysis are provided by the ILRS Analysis Standing Committee (https://ilrs.dgfi.tum.de/fileadmin/data_handling/ILRS_Discontinuities_File.snx). All other SLR station coordinates were estimated as free parameters.

Table 1.
Constraints in tests of different network realization scenarios and different sets of estimated global parameters for S3A/B and LAG.
In solution 1, we also estimated geocenter coordinates, UT1-UTC with one parameter strongly constrained to the IERS-14-C04 series and pole coordinates. The constraints of 1 m imposed on remaining ERPs are similar to those used by the ILRS Analysis Standing Committee in the operational LAGEOS/Etalon solutions.
In solution 2, we used the same NNT/NNR constraints, but the global geodetic parameters, that is, ERPs and geocenter, were strongly constrained to zero, thus only station coordinates were derived.
In solution 3, we estimated only SLR station coordinates as free parameters. Thus, in solution 3 no network constraints are imposed. The global geodetic parameters, ERPs and geocenter, are not estimated, but strongly constrained to the a priori values. In solution 3, the datum definition for SLR station coordinates is transferred through the GPS-based Sentinel-3 orbits. Therefore, solution 3 can be considered as SLR Precise Point Positioning (PPP) solution in analogy to the static GNSS-PPP solutions, in which the GNSS orbits and clocks are fixed and the station coordinates of individual GNSS stations are estimated without any network constraints. In GNSS-PPP only station coordinates, station clock parameters and troposphere delays are typically estimated for individual GNSS stations. In SLR, the latter two parameters do not have to be estimated, because of the two-way SLR measurement principle employing only one clock (the station clock) and the troposphere delay taken from the well-performing model for optical measurements [34], which does not require estimating additional troposphere delay parameters for SLR. As a result, we name solution 3 as the “SLR-PPP”.
In the LAGEOS (LAG) solution, 1-day normal equations were combined based on SLR data, a priori station coordinates from SLRF2014 and the ERP from IERS-14-C04 series. The annual range bias values were calculated with the same processing as in the case of S3A/B satellites. Next, we used NNT and NNR constraining for the determination of station coordinates, geocenter coordinates, 1-day ERPs, 1-day orbital parameters and range bias parameters to generate the standard 7-day solution (Table 1). Here station and geocenter coordinates, range biases are estimated as one set of parameters for each 7-day solution.
After generating each solution, the Helmert transformation was performed between obtained coordinates of core stations and the SLRF2014 coordinates. For the station outlier rejection, a criterion of 20 mm for each component was imposed. When a particular station did not pass the threshold, it was excluded from the list of core stations and thus was not used for the reference frame realization. Eventually, the final solution was generated by considering the list of accepted and verified stations from the Helmert transformation, for the inversion of the final normal equations.
2.5. The Issue of Reference Frame Differences
The integration of observations from SLR and GPS, as well as different constraining of the solutions, imply differences in the frame realization, hence possible frame inconsistencies. The GPS orbits are realized in IGS14 [35], that is, integrated around the Earth’s Center of Mass (CoM), but results are provided in the Center of Figure (CoF). SLR sites are represented in SLRF2014 and in CoF when imposing NNT/NNR in solutions 1 and 2. The S3A/B reduced-dynamic orbits are estimated in IGS14, but with the determination of pseudo-stochastic orbit parameters, which may refer to a close representation of the CoM, due to a large number of estimated stochastic orbit parameters. The estimated stochastic orbit parameters are used to compensate unmodelled forces (e.g., non-gravitational forces) and to absorb further force mismodellings, including gravitational forces or tides. Thus, in the case of NNT/NNR constraining, the CoM vector w.r.t the CoF may represent geocenter motion. However, the CoM is given in IGS14, whereas the CoF is in SLRF2014, which may introduce some inconsistencies.
In solution 2, the geocenter signal is artificially suppressed by imposing NNT and without estimating geocenter as an additional parameter. However, solution 2 should be more stable than solution 1, because we reduce the number of estimated parameters and we rely on the IERS-14-C04 values for ERPs.
In solution 3, without network constraints and no estimation of additional parameters, the GPS constellation and the S3A/B orbits are in the same frame as in the previous solutions, but SLR sites are realized in the IGS14 (transferred through S3A/B orbits in IGS14). Hence, “SLR-PPP”-based station coordinates are estimated in IGS14 and in CoM. This is a unique case when the SLR stations achieve station coordinates not in the SLR-dedicated reference frame - SLRF2014 - but in the GPS-dedicated frame - IGS14.
3. Results
3.1. Solution Statistics
Figure 1 shows the number of SLR observations (normal points, NPs) to LAG, S3A/B and the combination of both in 7-day batches used in the analysis. A total of 345,692 NPs are used for LAG, 157,213 NPs for S3A/B and 502,905 NPs in the combination. The number of LAG observations is thus more than double of that of S3A/B NPs. The largest number of observations was collected during 2017 and after April 2018 when the SLR stations started providing data to Sentinel-3B. The characteristic observation minima are occurring in winters and in the middle of 2016, which is caused by the fact that a few of the most productive sites, such as Herstmonceux, Zimmerwald and Matera did not provide data.
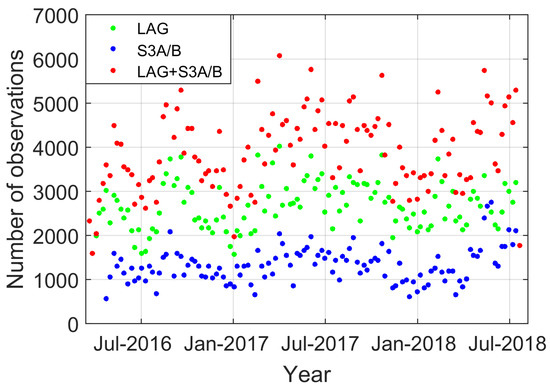
Figure 1.
Satellite Laser Ranging (SLR) observations to S3A/B and LAG in 7-day batches.
3.2. Significance of Proper Handling of Station Biases
The estimation of SLR site-specific annual range biases is one of the first steps in the calculation because it reduces detector-specific satellite signature effects, as well as various uncalibrated biases, occurring in timer circuits at SLR stations. The estimated annual range biases are re-introduced as known quantities following the approach described by [12]. Figure 2, Figure 3 and Figure 4 show a comparison of solutions when neglecting (left) and including (right) estimated annual bias corrections without estimating other parameters for Sentinel-3A (S3A) measurements. All SLR stations providing observations in 2016 are used for this analysis. We present residual histograms (Figure 2) and characterize them with the mean and RMS values. It can be seen that applying the annual range bias corrections improved both the mean residuals and the RMS of residuals from −0.86 to −0.21 mm and from 12.41 to 8.85 mm, respectively. The distribution of residuals becomes more symmetrical.
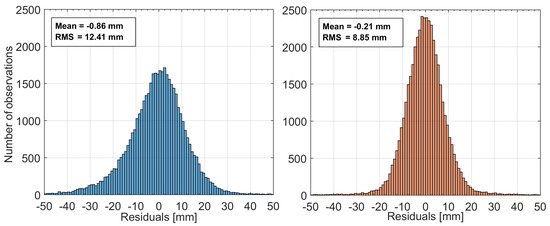
Figure 2.
Residual histograms for solutions with uncorrected (left) and corrected (right) range biases for all sites.
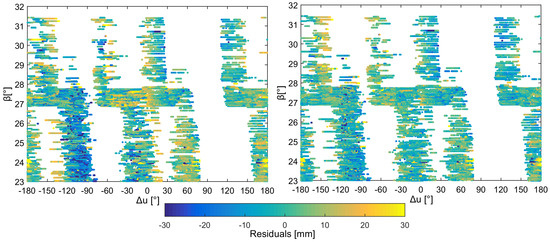
Figure 3.
Dependency of residuals on S3A as a function of and u angles for solutions with uncorrected (left) and corrected (right) range biases.
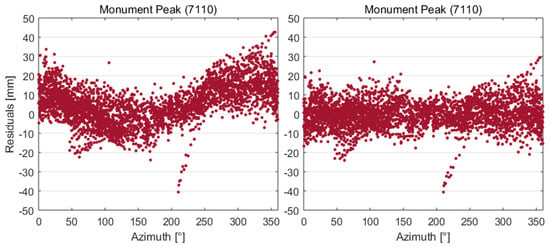
Figure 4.
Residual dependency on Monument Peak station azimuth angles for solutions with uncorrected (left) and corrected (right) range biases.
Figure 3 illustrates the dependency of the SLR residuals on , the Sun elevation angle above the S3A orbital plane and u, the satellites’ argument of latitude with respect to the Sun’s argument of latitude. The -angles for S3A oscillates between 23° and 32°, due to the S3A sun-synchronous orbits. Figure 3 shows that there are no observations for 75° < u < 120°, which manifests an uneven observation distribution caused by the lack of SLR stations in polar regions. Most of the large negative biases for −120° < u < −90° were caused by lower quality stations, which, may be erroneously assigned to GPS-based S3A orbit errors if not properly corrected. It should be noted that the range bias corrections significantly reduced discrepancies in the residuals, especially for 23° < < 28° and −120° < u < −90°.
When analyzing the dependency of residuals on the station azimuth angle, we observe a reduction of the residual dependency after considering annual range biases. Station biases may also map on residuals as a function of station azimuth angles (Figure 4) as found by [36] for the analysis of SLR residuals to GOCE orbits from certain stations, for example, Monument Peak. Figure 4 also shows a significant reduction of the dependency of S3A SLR residuals for Monument Peak from the range of −20 to 40 mm to about −20 to 20 mm. The large systematic dependency of the residuals from the station azimuth angle can be removed by applying an annual range bias.
3.3. Sentinel-3 Solution Scenario Tests
3.3.1. Station Coordinates
In total 27 SLR sites delivered observations to S3A and S3B satellites in the period 2016.3–2018.5. Figure 5 illustrates the SLR station coordinate repeatabilities based on SLR observations to the Sentinel satellites with stacking normal equations for standard 7-day solutions as a difference to SLRF2014-based coordinates. The results considering three test solutions are presented in Table 2.
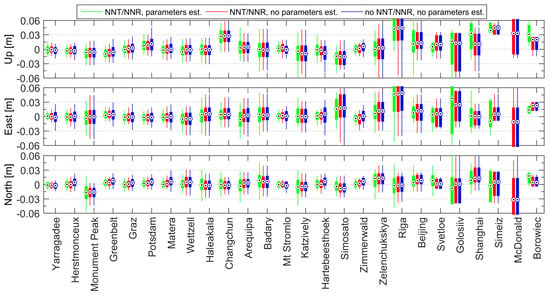
Figure 5.
SLR site coordinate repeatabilities in SLRF2014 based on SLR-to-S3A/B data for scenario 1 (green), scenario 2 (red), scenario 3 (blue). Minimum, maximum, 1st and 3rd quartiles and the median value are shown as elements of box-plots. Stations are sorted starting from that with the highest number of 7-day solutions (left) to the lowest number of solutions (right).

Table 2.
SLR station coordinate repeatability for the North, East, and Up components for tested S3A/B solutions for all and top SLR sites (in mm).
For stations with a large number of observations, the median values of differences w.r.t SLRF2014 are oscillating near zero, with the majority of differences at less than ±15 mm in case of all tested solutions. An increased repeatability of 20 mm occurs, for example, for Changchun and Potsdam site for the Up component, and in case of Monument Peak, for the North component. Offsets indicate wrong station coordinates in SLRF2014 for those sites. The ITRF2014 [37], as well as SLRF2014, are based on SLR observations, up to the end of 2014. Here, we analyze data after April 2016, which means that the SLRF2014 coordinates may not be perfectly valid for some stations, as in case of Monument Peak and Changchun due to the non-linear post-seismic deformations of this sites. The low performing sites show coordinate repeatabilities of more than 30 mm in all components, and large offsets w.r.t. SLRF2014, for example, Riga, Simosato or Golosiiv. Summarized data for Figure 5 are presented in Table 2. All station statistics show repeatability of coordinates at the level of 11, 13 and 16 mm for the North, East, and Up components, respectively (by means of the interquartile range, IQR) for solution 1. Similar results are obtained for solution 2, whereas for solution 3 a worse statistics by about 3 mm are obtained. Median values are in the range of ±1.5 mm for most of tested solutions and components. Statistics for the top performing sites, ranked according to the number of 7-day solutions and observations, IQR values, including Yarragadee, Herstmonceux, Greenbelt, Graz, Potsdam, Matera, Wettzell, Haleakala, Mt Stromlo, Hartebeesthoek and Zimmerwald, show lower IQR values by about 3 mm for all scenarios and components, and in most of the cases the median value less than 1 mm.
All three scenarios show similar repeatabilities of station coordinates, despite the different reference frames underlying in which the station coordinates are determined: SLRF2014 for scenario 1 and 2, IGS14 for scenario 3. This implies no need of network constraining for station coordinate determination by “SLR-PPP” solutions. Therefore solutions that fully rely on GPS-based orbits are fully plausible with coordinate repeatabilities at the level of 8–16 mm for high-performing stations.
Coordinates from scenario 3 “SLR-PPP” include the geocenter motion because they are determined in the CoM frame, whereas scenarios 1 and 2 are in CoF because the NNT constraint is imposed. Despite differences in the reference frames, that is IGS/SLRF, and the frame origin, that is CoM and CoF, all three solutions show a high level of consistency (Figure 5), implying remarkable robustness of the coordinate determination based on SLR observations to active LEOs.
Figure 6 shows the time series of station coordinate components for two sites: Potsdam (7841, left) and Yarragadee (7090, right) from 7-day solutions based on the three tested scenarios. The Yarragadee site is the station in the SLR network with the best performance in terms of data volume, providing about 310 observations to Sentinels-3 per week. Consequently, the quality of the station coordinate estimation is among the best within the ILRS network. The Potsdam site typically provides about 120 observations to Sentinels-3 per week. Figure 6 shows that the coordinates show a high consistency for both sites and all test scenarios, with deviations of X, Y, Z coordinates smaller than 20 mm with respect to the SLRF2014. For Potsdam, there are some data gaps at the end of 2017 and differences in the Up component between solutions 3 and 1, which may be caused by the misalignment of the frame origin to CoM and CoF, respectively. Station coordinate repeatability for Yarragadee falls between 5 and 9 mm, and for Potsdam falls between 7 and 14 mm for individual components and for all solution scenarios. Therefore, even the “SLR-PPP” solution without any network constraining (scenario 3, blue) provides station coordinates with IQR values at the level of 20 mm referring to SLR2014. The horizontal components show similar qualities as for the Up component in scenarios 1 and 2. In scenario 3, the East component is the weakest with some outliers, which can be explained by the fact that the Sentinel-3 satellites are in near-polar orbits, and thus dominate the north-south passes. Hence, sometimes the observation geometry in east-west directions is insufficient to properly determine the East station coordinate component. We conclude that for all constraining tests, it is possible to determinate SLR station coordinates based on S3A/B data with RMS better than 15 mm for the best performing sites.
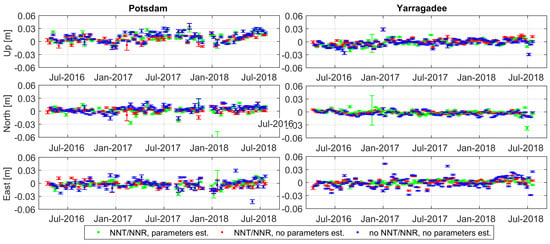
Figure 6.
Time series (with error bars) of estimated station coordinates for Potsdam (left) and Yarragadee (right) using SLR observations to S3A/B w.r.t a priori SLRF2014 coordinates for scenario 1 (green), 2 (red), 3 (blue).
3.3.2. Influence of the Number of NPs on Coordinate Residual Values
In a further test we analyze how the number of SLR NPs impacts the quality of derived station coordinates. Figure 7 shows the absolute value of coordinate residuals for all stations as the function of the number of NPs, delivered in the particular weekly solutions, for three tested scenarios. All tested scenarios obtained similar results for all components. Moreover, the increasing number of NPs reduces residual values. For all components, more than 50 NPs may deliver residuals of coordinates worse than 10 mm when compared to SLRF2014. For the North component about 100 NPs give residual values at the level of 5 mm for all scenarios, whereas for the East component at least 150 NPs are required and for the Up component over 200 NPs are required to obtain coordinates better than 5 mm. Exceeding the value of 250–300 NPs reduces residuals towards the level of 2–4 mm for all components.
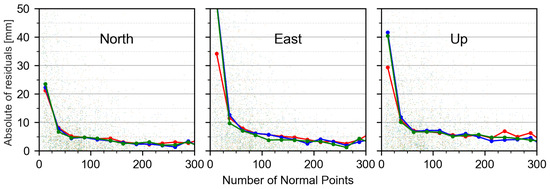
Figure 7.
Absolute of residuals of estimated SLR station coordinates based on S3A/B data referred to the a priori values from SLRF2014 as the function of the number of observations collected by all SLR stations for scenario 1 (green), 2 (red), 3 (blue).
3.4. Different Numbers of Stacked 1-day Solutions
In the next step, we analyze the station coordinate repeatability, geocenter coordinates, and ERPs as a function of the number of 1-day orbits used in solutions. In 1-, 3-, 5-, 7-, and 15-day solutions with the parameterization from scenario 1, that is, employing NNT/NNR constraints together, with estimated 1-day ERPs, and with geocenter and station coordinates estimated as one set per solution.
3.4.1. Station Coordinates
Figure 8 shows station coordinate repeatability for 1-, 3-, 7-, and 15-day solutions w.r.t SLRF2014. For all tests, the median values oscillate near zero for the majority of the best performing sites, such as Yarragadee, Herstmonceux, Greenbelt, and Graz. In case of 1-day orbits for all sites, the IQR exceeds 15, 24 and 30 mm for the North, East and Up component, respectively, or even more for stations with fewer data, where for the 3-day test there is a slight improvement of the results. The best results occur for both 7-day and 15-day solutions with IQR of less than ±13 mm for the North and East components, and less than 16 mm for the Up component for the best performing sites with just minor differences. We conclude that 1-day and 3-day S3A/B solutions are possible, but result in station coordinate repeatabilities at the level of 20–30 mm. Only the highest performing SLR stations provide a sufficient number of SLR observations to S3A/B to obtain stable 3-day solutions. To achieve station coordinate repeatabilities at the level of 10–15 mm for all components, the generation of 7-day solutions is indispensable.
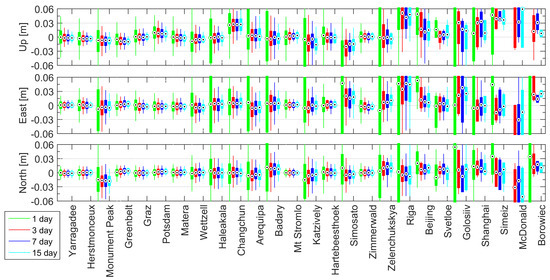
Figure 8.
Coordinate comparison to SLR2014 results from S3A/B when using different numbers of 1-day normal equations: 1-day (green), 3-day (red), 7-day (blue), 15-day (cyan). Minimum, maximum, 1st and 3rd quartiles and the median value are shown as elements of box-plots. Stations are sorted according to the number of 7-day solutions, starting with the highest number (left) to the lowest number of solutions (right).
3.4.2. Geocenter Coordinates
Figure 9 shows the geocenter coordinates from 3-, 5-, 7-day solutions. For all components, the 3-day solutions show the highest RMS value of 20 mm, 25 mm and 20 mm for the X, Y, and Z component, respectively and highest signal variations exceeding ±30 mm. For the 5-day orbit solutions, results improve to the RMS of 17 mm, 12 mm, 14 mm for the X, Y, and Z component. The best resulting 7-day orbit solutions are characterized by the mean RMS value of less than 2 mm and variations of less than ±10 mm (minima and maxima at ±20 mm). The poor geocenter estimates from 3-day and 5-day solutions are related to the number and distribution of SLR stations taken to the NNT constraint. Despite that the high-performing stations obtain reasonable 3-day station coordinate solutions (see Figure 8), the worldwide distribution and the number of these sites is insufficient to provide a stable geocenter. In 7-day solutions the number of SLR sites from different continents increases which stabilizes the geocenter estimates.
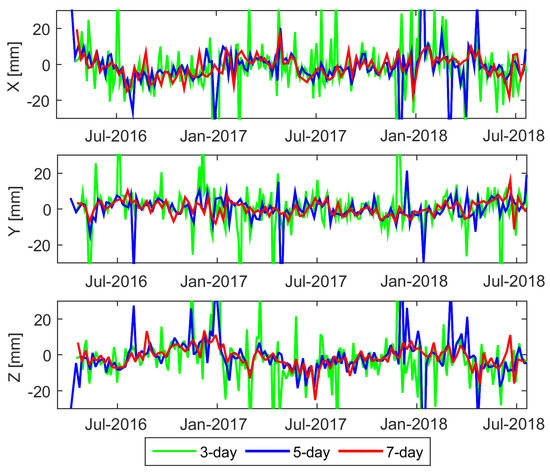
Figure 9.
Geocenter coordinates based on SLR observations to S3A/B from 3-day (green), 5-day (blue), 7-day (red) solutions all of which are based on stacking a different number of 1-day orbit solutions.
3.4.3. Earth Rotation Parameters
Figure 10 shows differences between estimated pole coordinates and UT1-UTC in 3-, 5-, 7-day solutions (values are referred to 0h UTC) compared to the a priori IERS-14-C04 (Bizouard et al. 2018) series. For the pole X, Y coordinates, 3-day solutions show the highest mean RMS value of 0.80 mas and 1.14 mas and the mean offsets of 0.06 and 0.20 mas for the X and Y components, respectively, where for 5-day solutions, results show slight improvement. The best results originate from the 7-day solutions and are characterized by the RMS of 0.29 mas for both components with the mean offsets of 0.17 and 0.07 mas for the X and Y components, respectively. RMS values for the UT1-UTC parameter are 0.10, 0.06, 0.02 ms for 3-day, 5-day, 7-day solutions, respectively, with a mean value at the level of ±0.002 ms for all three tested solutions.
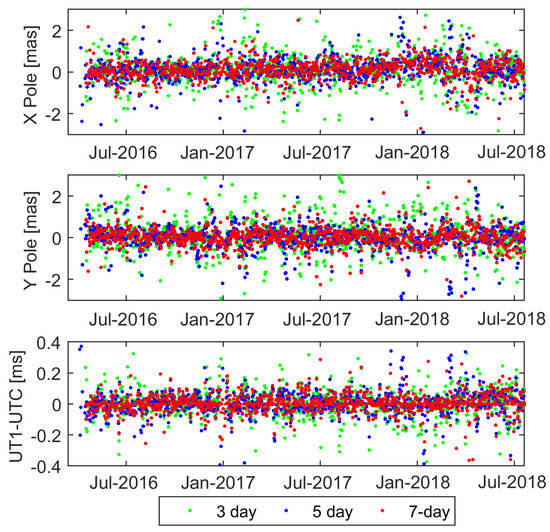
Figure 10.
Pole coordinates and the UT1-UTC from S3A/B w.r.t the IERS-14-C04 series for the tests using 3-day (green), 5-day (blue), and 7-day (red) solutions.
3.5. Combined Sentinel+LAGEOS Solutions
For the final combined solutions (LAG+Sent) we combine the normal equations of SLR observations to the Sentinel-3A/B and the LAGEOS-1/2 satellites by generating 7-day solutions, based on results from Section 4 and Section 5. We imposed NNT/NNR constraints together with the estimation of 1-day ERP, 7-day orbits (for LAGEOS), geocenter and station coordinates, range biases (for LAGEOS) as one set per one 7-day solutions. For the combined LAG+Sent solutions, a total of 39 SLR sites were used for the parameter determination. We compared LAG+Sent solutions with the result based on S3A/B only (Sent) with the same processing as for scenario 1 and with the LAG only solutions, both described in the Section 2.4 and Table 1.
3.5.1. Geocenter from the Combined LAGEOS+Sentinel Solutions
Figure 11 and Table 3 show the results from the geocenter determination comparison for 7-day solutions. The Sent, as well as the LAG+Sent results, show a good consistency with the LAG results. In all cases, the characteristic annual signal is reconstructed. Mean values for all components are at the level of ±1 mm for all solutions except for the Z component of the LAG+Sent solutions. The RMS values of X and Y are at the level of 4 mm, with an exception for the X component in Sent with RMS of 6 mm. For the Z component, the RMS is 6 mm for Sent and LAG+Sent solutions and 7 mm for LAG solutions. The combined LAG+Sent solutions show a dominating impact of LAGEOS satellites for the X and Y components, whereas the Z component is more influenced by Sentinel observations. The GPS-based Sentinel-3 orbits are fixed, whereas LAGEOS orbits are estimated which entails correlations of estimated LAGEOS empirical orbit parameters and the X, Y, Z geocenter components with the highest correlation for the Z geocenter coordinate.
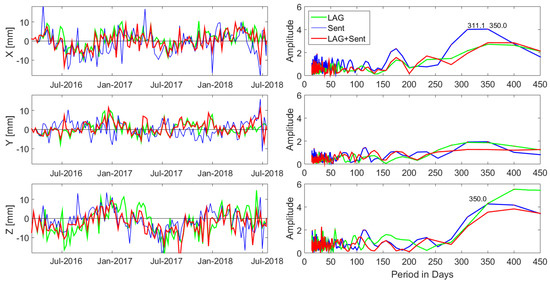
Figure 11.
Comparison of geocenter coordinates (left) and the spectral analysis (right) for LAG (green), Sent (blue), and LAG+Sent (red) solutions.

Table 3.
Mean offsets and RMS values of the estimated X, Y, Z geocenter coordinates (in mm). The mean values are calculated with respect to the ITRF2014/SLRF2014.
The spectral analysis shows a dominating 350-day signal which is close to the annual signal, especially for the X and Z components in all solutions. A positive aspect is that the geocenter coordinates seem to have no affection by any GPS draconitic-like signals [38,39], which means that the GPS orbital errors are not transferred to Sentinel orbits. Moreover, the geocenter coordinates do not show any Sentinel-related orbit signals, such as draconitic year of 182 days or S2 tide alias of 91 days, which strongly affects the GRACE results [40]. The determination of Sentinel orbits and Sentinel-based geocenter coordinates seems to be robust with no prominent orbit modeling issues. This aspect should be taken under further investigation by using a longer observation period.
We can conclude that SLR observations to Sentinel satellites can be used for the geocenter determination despite that the satellite orbits are given in a different reference frame (IGS14) than SLR station coordinates (SLRF2014) and despite that the GPS-based reduced-dynamic orbit of LEOs is employed. Typically, only kinematic LEO orbits are recommended for the gravity field determination (e.g., [41]) because the estimated pseudo-stochastic orbit parameters in reduced-dynamic LEO orbits do not fully absorb gravity field, which biases the gravity field recovery parameters. Figure 11 shows that the reduced-dynamic orbit carries information on geocenter motion and the reduced-dynamic orbit may represent the CoM frame, that is, the Sentinel satellites may orbit around actual Earth’s instantaneous center of mass.
3.5.2. ERP from the Combined LAGEOS+Sentinel Solutions
Figure 12 and Table 4 show a comparison of ERP results w.r.t the a priori IERS-14-C04 pole coordinates and UT1-UTC. The Sent solutions show larger deviations with RMS values of 0.32 mas for the pole X, Y coordinate components, which is nearly twice as large than for LAG. The LAG+Sent solutions show slightly worse statistics than LAG with RMS values of 0.14 and 0.19 mas, for X and Y, respectively. In 2018, there was an offset of nearly 0.2 mas for the X component that occurred for all solutions. In the whole analyzed period, depending on the solution, the mean offset of the X pole differs from the mean offset for the Y pole at the level of 0.07 mas. The spectral analysis of pole coordinates shows numerous signals, including those occurring with a 121-day period that may be related to Sentinel-3A/3B perigee revolution of 122 days. The result of UT1-UTC shows the best statistics for the Sent solutions, with mean and RMS values of -0.002 and 0.063 ms, respectively, which is better than the mean offset and RMS of 0.09 and 0.40 ms, respectively for LAG solutions. The LAG+Sent solutions are characterized by the mean offset of -0.011 and the RMS of 0.067 ms with no significant signals. Therefore, adding Sentinels-3 observations improves the determination of UT1-UTC. The UT1-UTC estimates based on LAGEOS data are strongly affected by correlations of the UT1-UTC and drifts of satellite ascending nodes. Adding Sentinel-3 satellites with fixed orbits stabilizes the relative orientation between terrestrial and celestial frames in a similar way as adding SLR observations to GNSS [42].
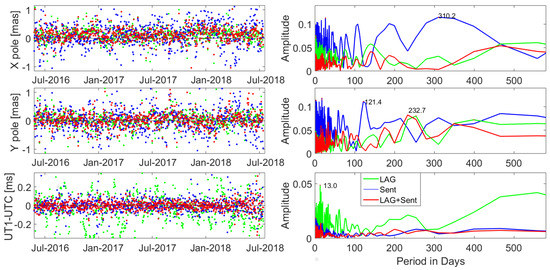
Figure 12.
Differences of pole coordinates and UT1-UTC w.r.t. IERS-14-C04 series and the spectral analysis of differences for LAG (green), Sent (blue), and LAG+Sent (red) solutions.

Table 4.
Mean offsets and RMS values of the estimated X, Y pole coordinates (in mas) and UT1-UTC (in ms) in reference to the a priori IERS-CO4-14 series.
3.5.3. Station Coordinates from the Combined LAGEOS+Sentinel Solutions
Figure 13 shows statistics of the station coordinate determination for particular SLR sites from LAG, Sent, and LAG+Sent solutions w.r.t. SLRF2014. In each solution, almost all stations have a median value close to zero. For the top performing sites, the Sent and the LAG+Sent solutions show similar results when compared to LAG with a consistency at the level of less than 20 mm. In the LAG solutions, the Up component for Changchun and the North component for Monument Peak have similar offsets as in the case of the previously tested Sent solutions, which means that the coordinates from SLRF2014 are not anymore fully valid for these stations in the period 2016-2018. Despite that the Sent solutions are mostly based on just one satellite and the number of SLR observations to Sentinels-3 is much lower than to LAGEOS-1/2 (see Figure 1), the quality of Sent-based station coordinates is similar to the LAG-based coordinates for most of the SLR stations. Moreover, using SLR observations to LEOs alone or combining these data with LAGEOS observations for the determination of SLR station coordinates does not introduce any prominent systematic offsets or errors when compared to only LAGEOS-based solutions (see Figure 13).
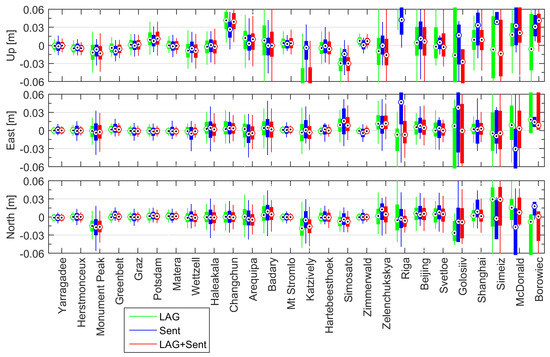
Figure 13.
Differences of estimated SLR station coordinates w.r.t. SLR2014 for LAG (green), Sent (blue), and LAG+Sent (red) solutions represented as box-plots with max., min., 1st, 3rd quartiles, and median values.
Table 5 shows the summarized statistics for SLR station coordinate determination from Figure 13. All sites can be characterized by the repeatability of coordinates at the level of 12 mm for the North and East components, and between 25 mm for the Up component by the means of IQR values for all solutions. The exception occurred for the Up component from the Sent solutions, for which IQR is 16 mm. Statistics for the top performing sites manifest with two times lower IQR values than for all sites in LAG and LAG+Sent solutions for all components. The Sent solutions for the top sites show IQR of nearly 8, 9, and 12 mm for the North, East, and Up components, respectively. The median values in all tested solutions are less than ±1 mm for all components. One has to keep in mind that the LAG+Sent solutions contain more epochs with successful solutions because for some weeks there are solutions based on LAGEOS only or Sentinel-3 only data. To conclude, the Sent solutions provide station coordinates for all sites at the comparable level to LAG solutions. In the case of top performing SLR sites, the horizontal components of station coordinates are better determined from LAG solutions or combined LAG+Sent, whereas the Up component of station coordinates can be determined with a superior quality from Sent solutions with properly calibrated annual range biases.

Table 5.
Statistics of summarized station coordinate repeatability for 7-day LAG, Sent, and LAG+Sent solutions with all SLR sites and top performing SLR sites decomposed into the North, East, and Up components (in mm).
Figure 14 shows the time series of SLR station coordinates for two representative stations: Arequipa (7403) and Potsdam (7841) for LAG, Sent, LAG+Sent solutions. The estimated station coordinates for the Potsdam site show a consistency at the level of 15-mm for the horizontal components, whereas the Up component shows a consistency above 20-mm for the Sent and LAG+Sent solutions. In the LAG solutions, the Up component is noisier because of the correlations between estimated LAGEOS range biases and the vertical station coordinate component. Some Sent solutions show up as single outliers due to the insufficient number of observations for high-quality station coordinate estimates. However, the combination of LAG+Sent data removes both error sources related to correlations with range biases for the Up component and the insufficient number of observations.
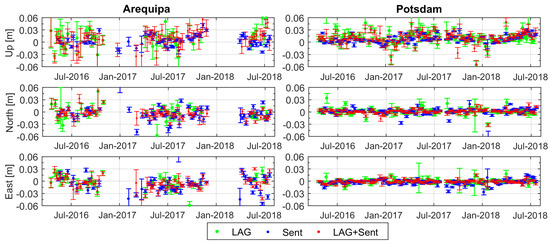
Figure 14.
Time series (error bars) for Arequipa (left) and Potsdam (right) site coordinates w.r.t SLRF2014 for LAG (green), Sent (blue), LAG+Sent (red) solutions.
For the Arequipa site, the Sent and LAG+Sent solutions show coordinate variations above 20 mm and 30 mm for the horizontal and Up components, respectively. The LAG solutions are affected by larger variabilities. Adding SLR observations to Sentinels-3 can thus increase the quality of the determination of station coordinates. Moreover, considering another source of data can increase the spatial distribution of observed satellites, in particular for the SLR stations providing few observations per week. The station coordinates of the Arequipa site can be determined using solely S3A/B observations in periods, when no LAGEOS data are available, for example, at the beginning of 2017, or 2018, or at the end of 2017 (Figure 14 left). Therefore, the SLR observations to LEO can be used not only to stabilize the LAGEOS solutions, but also to provide station coordinates based on LEO observations for stations with the limited capability of tracking high and MEO satellites.
4. Discussion
SLR observations to active LEOs constitute 81% of all SLR normal points registered in 2016–2018 (https://ilrs.cddis.eosdis.nasa.gov/network/system_performance/global_report_cards/index.html), and are typically employed only for the validation of LEO orbits. This paper shows that SLR is a valuable tool for the recovery of global geodetic parameters, such as Earth rotation parameters and geocenter motion, which is needed to correct altimetry data. Sentinel satellites can thus provide not only observations on sea surface topography, but also geocenter coordinates needed for removing biases from altimeter solutions. However, SLR observation require a proper handling of the SLR range biases, whereas the global network of SLR stations requires a proper network constraints to remove singularities from the normal equation systems.
We found that SLR range bias calibration through introducing the annual biases to Sentinel-3 observations improves the mean offset of residuals by more than 0.6 mm and the RMS by 3.5 mm for all stations. Correcting range biases reduces residual dependency with respect to the satellite orbital plane orientation and the Sun direction angles, as well as with respect to the local observation azimuth angle such as in the case of the Monument Peak site.
All tested constraining scenarios show a consistency of estimated station coordinates with median offsets w.r.t. SLRF2014 of 1-2 mm and of IQR values from 11.5 to 19.8 mm, whereas the top performing SLR sites disclose better results by about 4 mm. The tests with the different numbers of 1-day normal equations in SLR solutions show that it is possible to obtain station coordinates from 7- and 15-day orbit solutions with the consistency of 15 mm, even without network constraining, that is, from the so-called Sentinel-3A/B “SLR-PPP” solutions. To obtain station coordinate residual values at the level of less than 5 mm, 100, 150 and 200 normal points for the North, East and Up components, respectively, are required on average in 7-day Sentinel-3 only solutions.
Testing the influence of the number of 1-day normal equations on the geocenter coordinates and ERP determination from Sentinel-3 data results with the lowest RMS for 7-day solutions. The comparison of geocenter coordinates shows RMS of 6.2, 4.0, and 6.0 mm for the X, Y, and Z components, respectively, with the reconstruction of a characteristic annual signal for the X and Z components. In the 5-, and 3-day solutions show worse results due to inhomogeneous distribution of stations. These results correspond to DORIS-based geocenter coordinates from Jason-2 satellite orbits, providing amplitudes of the annual signal of 1.5, 3.1, and 5.6 mm for the X, Y, and Z components, respectively [18].
The RMS values of the X, Y pole coordinates and UT1-UTC, derived from SLR observations to Sentinel are equal to 0.32, 0.31 mas and 0.06 ms when compared to the IERS-14-C04 products. The obtained pole coordinates are better than those presented by [43] with 0.52–2.05 and 0.49–0.9 mas of standard deviation values for the X pole and Y pole, respectively, which were based on DORIS observations to SPOT-4, SPOT-5, Envisat, Cryosat-2 and Jason-2 satellites in 2011. However, our results are slightly worse than those shown in [44], who obtained 0.25 mas level of standard deviation with respect to the IERS-08-C04 products, when based on DORIS observations to Envisat, SPOT4/5, Jason-2, Cryosat-2, HY-2A, SARAL satellites in the period 2008.5-2015.0. The obtained UT1-UTC statistics are better than those presented by [45] with the standard deviation of 0.12 ms with respect to IERS-14-C04, which were based on DORIS observations to active LEOs, such as Jason-2, Envisat, CryoSat, HY2A, SARAL, SPOT satellites in the period 2012-2015. Moreover, those studies are based on a larger set of data and a longer period of observations.
The estimated station coordinates based on the combined LAG+Sent solutions are characterized by the IQR values at the level of 12 mm for the North and East components and 25 mm for the Up component w.r.t SLRF2014, which are comparable to the LAG solutions. For the top performing sites, the IQR values are reduced to 5 mm for the North and East components and to 12 mm for the Up component. The station horizontal components have the best statistics in LAG and LAG+Sent solutions, whereas the Up component has the lowest IQR values in the Sent solutions. For stations with a limited capability of tracking high and MEO satellites, such as Arequipa, the SLR observations to Sentinels-3 can be used for the proper determination of station coordinates and global geodetic parameters. The geocenter coordinates from the LAG+Sent solutions are characterized by RMS of 4.5, 3.4, 5.9 mm for the X, Y, Z components, respectively. The LAGEOS-based observations have a dominating impact on the geocenter X and Y components, whereas the Sentinels-3-based observations affect more to the Z component. The ERPs from the LAG+Sent solutions are characterized by the RMS of less than 0.19 mas and 0.07 ms for the pole components and the UT1-UTC, respectively. The Sentinels-3-based observations insignificantly deteriorate the pole coordinate statistics but increase the UT1-UTC precision in the combined LAG+Sent solutions.
5. Conclusions
In this paper, SLR observations and reduced-dynamic GPS orbits of Sentinel-3A/3B satellites are used for the determination of SLR station coordinates and global geodetic parameters. The solutions were preceded with estimation of SLR station annual range biases and the study of their impact on SLR observation residuals. We tested different constraining scenarios and a different number of daily orbits in the Sentinel-3 solutions. Finally, the combined Sentinel-3 and LAGEOS solutions were provided with the characteristics of the quality of global geodetic parameters.
The SLR observations in the process of the precise parameter determination require a correction of SLR site-specific and target-specific range biases. Correcting annual range bias values of Sentinel-3A/B and LAGEOS-1/2 observations reduces the systematic offset of coordinates. The annual range bias values may depend on the station measurement conditions, as well as the characteristics of the satellite orbit and the type of laser retroreflector array. The GPS-based reduced-dynamic orbits and SLR data to Sentinel-3A/3B, despite the reference frame differences, can be used for the precise determination of station coordinates, global geodetic parameters, such as geocenter, pole coordinates or UT1-UTC as they do not introduce any prominent systematic offsets or errors. Active LEO satellites provide data for the identification and calibration of SLR range biases and the satellite signature effects. The combined solutions with LAGEOS-1/2 satellites, besides the obvious increase of the number of solutions and the number of observations involved, may improve the spatial distribution of observations, provide high-quality station and geocenter coordinates and enhance especially the quality of the UT1-UTC parameter. Moreover, increasing the number of active LEOs and extending the observation period may improve the realization of the SLR reference frame and therefore should be taken into consideration in the further realizations of terrestrial reference frames. The presented article shows that SLR observations to active LEOs may be used not only for orbit validation but also as another source of data for the datum realization or the determination of global geodetic parameters while considering proper solution scenarios.
Author Contributions
D.S. performed the data analysis and wrote the paper, K.S. performed data analysis, edited the manuscript, and provided valuable insights, D.A. and A.J. provided GPS-based Sentinel orbits and edited the manuscript, R.Z. helped with visualization of results, G.B. and M.D. provided valuable insights.
Funding
This research received no external funding.
Acknowledgments
The authors gratefully acknowledge the International Satellite Laser Ranging Service (ILRS) for their effort to collect and provide SLR observations of LEO and LAGEOS satellites. D. Strugarek, K. Sośnica, R. Zajdel, G. Bury, are supported by the Polish National Science Centre (NCN), Grant No. UMO-2018/29/B/ST10/003802.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| S3A/B | Sentinel-3A/3B |
| SLR | Satellite Laser Ranging |
| GPS | Global Positioning System |
| ERPs | Earth Rotation Parameters |
| GNSS | Global Navigational Satellite Systems |
| LEOs | Low Earth Orbiters |
| MEO | Medium Earth Orbiters |
| DORIS | Doppler Orbitography and Radiopositioning Integrated by Satellite |
| ILRS | International Laser Ranging Service |
| POD | Precise Orbit Determination |
| AIUB | Astronomical Institute of the University of Bern |
| LRR | Laser Retroreflectors |
| CPOD | Copernicus POD Service |
| IGS | International GNSS Service |
| SLRF | Satellite Laser Ranging Frame |
| ITRF | International Terrestrial Reference Frame |
| NPs | Normal Points |
| CoM | Center of Mass |
| CoF | Center of Figure |
| NNR | No Net Rotation |
| NNT | No Net Translation |
| PPP | Precise Point Positioning |
| LAG | LAGEOS |
| IQR | Interquartile Range |
| RMS | Root Mean Square Error |
References
- Pearlman, M.; Arnold, D.; Davis, M.; Barlier, F.; Biancale, R.; Vasiliev, V.; Ciufolini, I.; Paolozzi, A.; Pavlis, E.; Sośnica, K.; et al. Laser geodetic satellites: A high accuracy scientific tool. J. Geod. 2019, 1–14. [Google Scholar] [CrossRef]
- Drinkwater, M.R.; Haagmans, R.; Muzi, D.; Popescu, A.; Floberghagen, R.; Kern, M.; Fehringer, M. The GOCE gravity mission: ESA’s first core explorer. In Proceedings of the 3rd International GOCE User Workshop, Frascati, Italy, 6–8 November 2006; pp. 1–3, ISBN 92-9092-938-3. [Google Scholar]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Reigber, C.; Lühr, H.; Schwintzer, P. Status of the CHAMP Mission. In Towards an Integrated Global Geodetic Observing System (IGGOS), (International Association of Geodesy Symposia, 120); Rummel, R., Drewes, H., Bosch, W., Hornik, H., Eds.; Springer: Berlin, Germany, 1998; pp. 63–65. [Google Scholar]
- Friis-Christensen, E.; Lühr, H.; Knudsen, D.; Haagmans, R. Swarm—An Earth Observation Mission investigating Geospace. Adv. Space Res. 2008, 41, 210–216. [Google Scholar] [CrossRef]
- Buckreuss, S.; Balzer, W.; Muhlbauer, P.; Werninghaus, R.; Pitz, W. The terraSAR-X satellite project. In Proceedings of the IGARSS 2003. 2003 IEEE International Geoscience and Remote Sensing Symposium. Proceedings (IEEE Cat. No.03CH37477), Toulouse, France, 21–25 July 2003; Volume 5, pp. 3096–3098. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A Satellite Formation for High-Resolution SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef]
- Lambin, J.; Morrow, R.; Fu, L.L.; Willis, J.K.; Bonekamp, H.; Lillibridge, J.; Perbos, J.; Zaouche, G.; Vaze, P.; Bannoura, W.; et al. The OSTM/Jason-2 Mission. Mar. Geod. 2010, 33 (Suppl. 1), 4–25. [Google Scholar] [CrossRef]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The Global Monitoring for Environment and Security (GMES) Sentinel-3 mission. Remote Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- Bao, L.; Gao, P.; Peng, H.; Jia, Y.; Shum, C.K.; Lin, M.; Guo, Q. First accuracy assessment of the HY-2A altimeter sea surface height observations: Cross-calibration results. Adv. Space Res. 2015, 55, 90–105. [Google Scholar] [CrossRef]
- Scharroo, R.; Bonekamp, H.; Ponsard, C.; Parisot, F.; Von Engeln, A.; Tahtadjiev, M.; De Vriendt, K.; Montagner, F. Jason continuity of services: Continuing the Jason altimeter data records as Copernicus Sentinel-6. Ocean Sci. 2016, 12, 471–479. [Google Scholar] [CrossRef]
- Arnold, D.; Montenbruck, O.; Hackel, S.; Sośnica, K. Satellite laser ranging to low Earth orbiters: Orbit and network validation. J. Geod. 2018. [Google Scholar] [CrossRef]
- Pearlman, M.; Degnan, J.; Bosworth, J. The International Laser Ranging Service. Adv. Space Res. 2002, 30, 135–143. [Google Scholar] [CrossRef]
- Hackel, S.; Gisinger, C.; Balss, U.; Wermuth, M.; Montenbruck, O. Long-Term Validation of TerraSAR-X and TanDEM-X Orbit Solutions with Laser and Radar Measurements. Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hackel, S.; van den Ijssel, J.; Arnold, D. Reduced dynamic and kinematic precise orbit determination for the Swarm mission from 4 years of GPS tracking. GPS Solut. 2018, 22, 79. [Google Scholar] [CrossRef]
- Guo, J.; Wang, Y.; Shen, Y.; Liu, X.; Sun, Y.; Kong, Q. Estimation of SLR station coordinates by means of SLR measurements to kinematic orbit of LEO satellites. Earth Planets Space 2018, 70, 201. [Google Scholar] [CrossRef]
- Zelensky, N.P.; Lemoine, F.G.; Ziebart, M.; Sibthorpe, A.; Beckley, B.D.; Klosko, S.M.; Chinn, D.S.; Rowlands, D.D.; Luthcke, S.B.; Pavlis, D.E.; et al. DORIS/SLR POD modeling improvements for Jason-1 and Jason-2. Adv. Space Res. 2010, 46, 1541–1558. [Google Scholar] [CrossRef]
- Couhert, A.; Mercier, F.; Moyard, J.; Biancale, R. Systematic Error Mitigation in DORIS-Derived Geocenter Motion. J. Geophys. Res. Solid Earth 2018, 123, 10142–10161. [Google Scholar] [CrossRef]
- Švehla, D.; Rothacher, M. Kinematic Orbit Determination of LEOs Based on Zero or Double-difference Algorithms Using Simulated and Real SST GPS Data. In Vistas for Geodesy in the New Millennium; Ádám, J., Schwarz, K.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 322–328. [Google Scholar]
- Schutz, B.E.; Tapley, B.D.; Abusali, P.A.M.; Rim, H.J. Dynamic orbit determination using GPS measurements from TOPEX/POSEIDON. Geophys. Res. Lett. 1994, 21, 2179–2182. [Google Scholar] [CrossRef]
- Wu, S.C.; Yunck, T.P.; Thorton, C.L. Reduced-dynamic technique for precise orbit determination of low earth satellites. J. Guidance Control Dyn. 1991, 14, 24–30. [Google Scholar] [CrossRef]
- Hackel, S.; Montenbruck, O.; Steigenberger, P.; Balss, U.; Gisinger, C.; Eineder, M. Model improvements and validation of TerraSAR-X precise orbit determination. J. Geod. 2017, 91, 547–562. [Google Scholar] [CrossRef]
- Jäggi, A.; Hugentobler, U.; Beutler, G. Pseudo-Stochastic Orbit Modeling Techniques for Low-Earth Orbiters. J. Geod. 2006, 80, 47–60. [Google Scholar] [CrossRef]
- Fernández, J.; Peter, H.; Calero, E.J.; Berzosa, J.; Gallardo, L.J.; Féménias, P. Sentinel-3A: Validation of Orbit Products at the Copernicus POD Service. In International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–8. [Google Scholar]
- Fletcher, K. Sentinel 3: ESA’s Global Land and Ocean Mission for GMES Operational Services, ESA SP-1322/3; ESA Communications: Noordwijk, The Netherlands, 2012. [Google Scholar]
- Fernández, J.; Fernández, C.; Féménias, P.; Peter, H. The Copernicus Sentinel-3 mission. In Proceedings of the ILRS Workshop 2016. pp. 1–4. Available online: https://cddis.nasa.gov/lw20/docs/2016/papers/P32-Fernandez{_}paper.pdf (accessed on 10 October 2018).
- GMV Consortium. Copernicus POD Regular Service Review Jun-Sep 2018. Tech. Rep.. 2018. Available online: https://sentinels.copernicus.eu/documents/247904/3372484/Copernicus-POD-Regular-Service-Review-Jun-Sep-2018.pdf (accessed on 10 October 2018).
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software Version 5.2. User Manual; University of Bern, Bern Open Publishing: Bern, Switzerland, 2015. [Google Scholar] [CrossRef]
- Dach, R.; Schaer, S.; Arnold, D.; Prange, L.; Sidorov, D.; Stebler, P.; Villiger, A.; Jaeggi, A. CODE ultra-rapid product series for the IGS; Tech. Rep.; Astronomical Institute, University of Bern: Bern, Switzerland, 2018. [Google Scholar] [CrossRef]
- Jäggi, A.; Dach, R.; Montenbruck, O.; Hugentobler, U.; Bock, H.; Beutler, G. Phase center modeling for LEO GPS receiver antennas and its impact on precise orbit determination. J. Geod. 2009, 83, 1145. [Google Scholar] [CrossRef]
- Luceri, V.; Pavlis, E.C.; Pace, B.; Kuźmicz-Cieślak, M.; König, M.; Bianco, G.; Evans, K. The ILRS Contribution to the Development of the ITRF2014. In Proceedings of the 26th IUGG General Assembly, Prague, Czech Republic, 22 June–2 July 2015. [Google Scholar]
- Bizouard, C.; Lambert, S.; Gattano, C.; Becker, O.; Richard, J.Y. The IERS EOP 14C04 solution for Earth orientation parameters consistent with ITRF 2014. J. Geod. 2018. [Google Scholar] [CrossRef]
- Sośnica, K.; Bury, G.; Zajdel, R.; Strugarek, D.; Drożdżewski, M.; Kazmierski, K. Estimating global geodetic parameters using SLR observations to Galileo, GLONASS, BeiDou, GPS, and QZSS. Earth Planets Space 2019, 71, 20. [Google Scholar] [CrossRef]
- Mendes, V.B.; Pavlis, E.C. High-accuracy zenith delay prediction at optical wavelengths. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Rebischung, P.; Schmid, R. IGS14/igs14.atx: A new Framework for the IGS Products. In AGU Fall Meeting Abstracts; American Geophysical Union: San Francisco, CA, USA, 2016. [Google Scholar]
- Strugarek, D.; Sośnica, K.; Jäggi, A. Characteristics of GOCE orbits based on Satellite Laser Ranging. Adv. Space Res. 2019, 63, 417–431. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
- Rodriguez-Solano, C.J.; Hugentobler, U.; Steigenberger, P.; Bloßfeld, M.; Fritsche, M. Reducing the draconitic errors in GNSS geodetic products. J. Geod. 2014, 88, 559–574. [Google Scholar] [CrossRef]
- Lutz, S.; Meindl, M.; Steigenberger, P.; Beutler, G.; Sośnica, K.; Schaer, S.; Dach, R.; Arnold, D.; Thaller, D.; Jäggi, A. Impact of the arc length on GNSS analysis results. J. Geod. 2016, 90, 365–378. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J. The unexpected signal in GRACE estimates of C20. J. Geod. 2017, 91, 897–914. [Google Scholar] [CrossRef]
- Jäggi, A.; Bock, H.; Prange, L.; Meyer, U.; Beutler, G. GPS-only gravity field recovery with GOCE, CHAMP, and GRACE. Adv. Space Res. 2011, 47, 1020–1028. [Google Scholar] [CrossRef]
- Sośnica, K.; Bury, G.; Zajdel, R. Contribution of Multi-GNSS Constellation to SLR-Derived Terrestrial Reference Frame. Geophys. Res. Lett. 2018, 45, 2339–2348. [Google Scholar] [CrossRef]
- Štěpánek, P.; Rodriguez-Solano, C.J.; Hugentobler, U.; Filler, V. Impact of orbit modeling on DORIS station position and Earth rotation estimates. Adv. Space Res. 2014, 53, 1058–1070. [Google Scholar] [CrossRef]
- Moreaux, G.; Capdeville, H.; Kuzin, S.; Otten, M.; Štěpánek, P.; Willis, P.; Ferrage, P. The International DORIS Service contribution to the 2014 realization of the International Terrestrial Reference Frame. Adv. Space Res. 2016, 58, 2479–2504. [Google Scholar] [CrossRef]
- Štěpánek, P.; Hugentobler, U.; Buday, M.; Filler, V. Estimation of the Length of Day (LOD) from DORIS observations. Adv. Space Res. 2018, 62, 370–382. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).