Cotton Yield Estimate Using Sentinel-2 Data and an Ecosystem Model over the Southern US
Abstract
1. Introduction
2. Materials and Methods
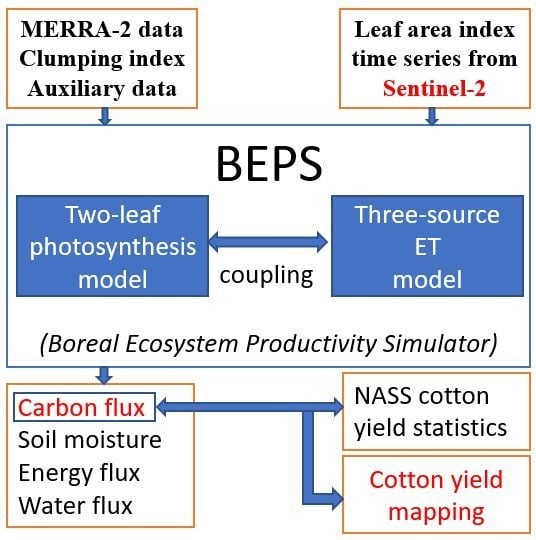
2.1. Ecosystem Model for GPP Simulation
2.2. Cotton-Specific Photosynthetic Parameters
2.3. Yield Estimation and Prediction
2.4. Sources of Model Input
3. Results
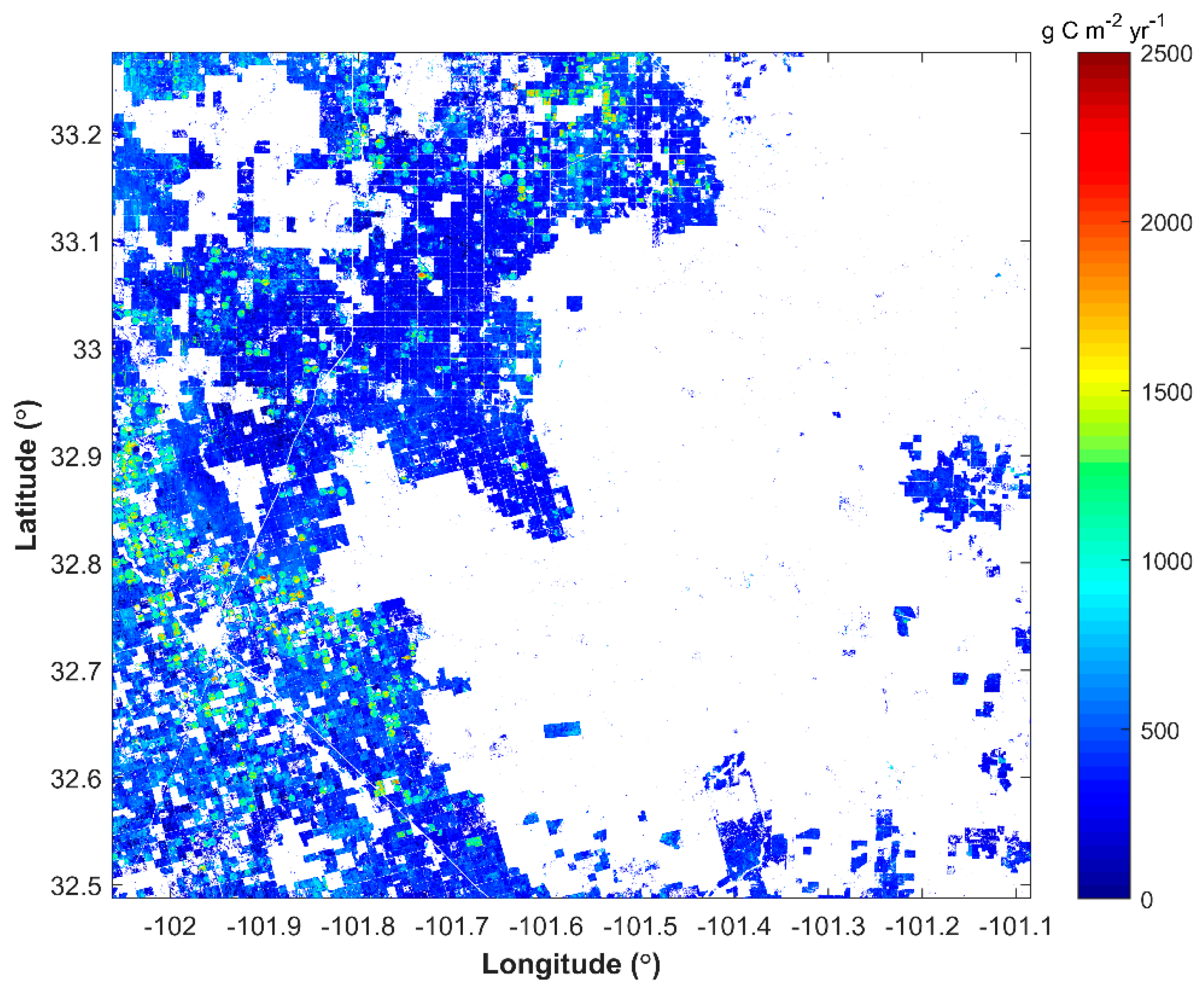
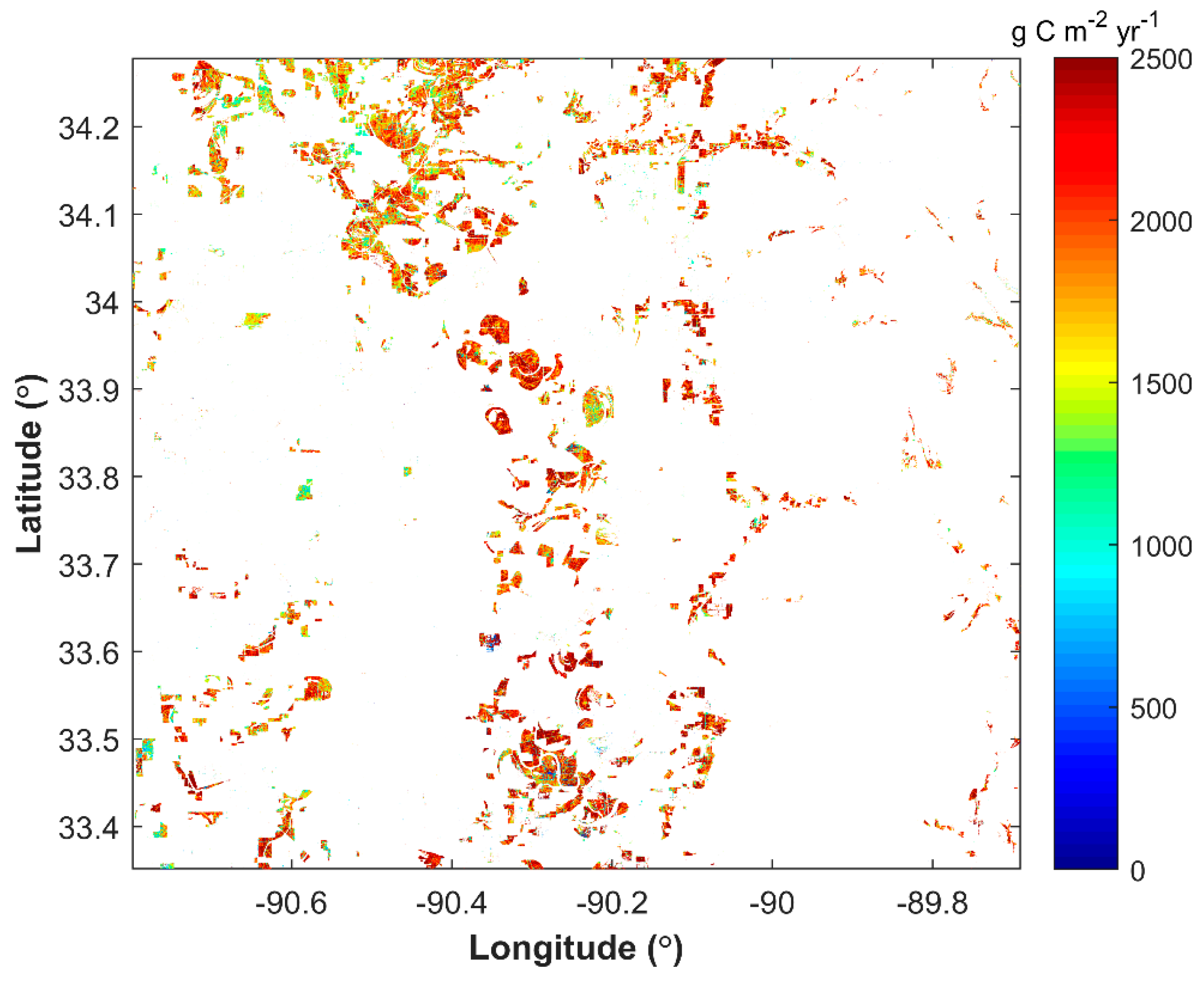
3.1. Spatial Distribution of Cotton GPP in Three Sentinel-2 Tiles
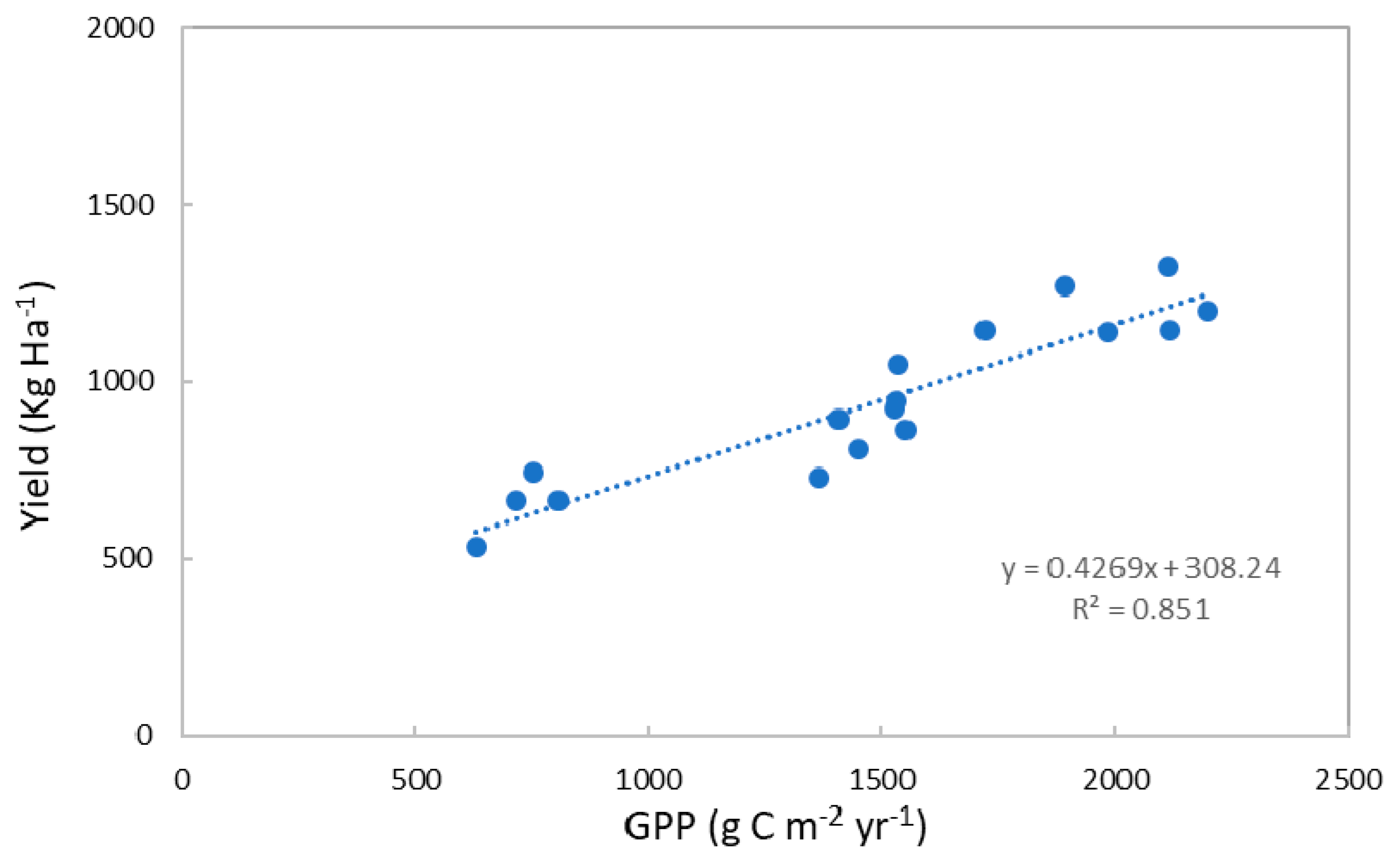
3.2. The GPP–Lint Yield Relationship for Upland Cotton
4. Discussions
4.1. Crop Growth Modeling
4.2. Yield Variations in Southern US Tiles
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Singh, P.; Boote, K.J.; Kadiyala, M.D.M.; Nedumaran, S.; Gupta, S.K.; Srinivas, K.; Bantilan, M.C.S. An assessment of yield gains under climate change due to genetic modification of pearl millet. Sci. Total Environ. 2017, 601–602, 1226–1237. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.; Mishra, S.K.; Singh, H.P.; Singh, A.; Chaudhary, O.P. Improved soil physical properties and cotton root parameters under sub-soiling enhance yield of Cotton-Wheat cropping system. Data Brief 2019, 24. [Google Scholar] [CrossRef]
- Raphael, J.P.A.; Echer, F.R.; Rosolem, C.A. Shading and nitrogen effects on cotton earliness assessed by boll yield distribution. Crop Sci. 2019, 59, 697–707. [Google Scholar] [CrossRef]
- Peng, Y.; Zhu, T.; Li, Y.; Dai, C.; Fang, S.; Gong, Y.; Wu, X.; Zhu, R.; Liu, K. Remote prediction of yield based on LAI estimation in oilseed rape under different planting methods and nitrogen fertilizer applications. Agric. For. Meteorol. 2019, 271, 116–125. [Google Scholar] [CrossRef]
- Gutierrez, A.P.; Ponti, L.; Herren, H.R.; Baumgärtner, J.; Kenmore, P.E. Deconstructing Indian cotton: Weather, yields, and suicides. Environ. Sci. Eur. 2015, 27, 12. [Google Scholar] [CrossRef]
- Masasi, B.; Taghvaeian, S.; Boman, R.; Datta, S. Impacts of irrigation termination date on cotton yield and irrigation requirement. Agriculture (Switzerland) 2019, 9, 39. [Google Scholar] [CrossRef]
- Li, P.; Ren, L. Evaluating the effects of limited irrigation on crop water productivity and reducing deep groundwater exploitation in the North China Plain using an agro-hydrological model: I. Parameter sensitivity analysis, calibration and model validation. J. Hydrol. 2019, 574, 497–516. [Google Scholar] [CrossRef]
- Du, X.; Chen, B.; Meng, Y.; Zhao, W.; Zhang, Y.; Shen, T.; Wang, Y.; Zhou, Z. Effect of cropping system on cotton biomass accumulation and yield formation in double-cropped wheat-cotton. Int. J. Plant Prod. 2015, 10, 29–44. [Google Scholar]
- Feng, L.; Wang, G.; Han, Y.; Li, Y.; Zhu, Y.; Zhou, Z.; Cao, W. Effects of planting pattern on growth and yield and economic benefits of cotton in a wheat-cotton double cropping system versus monoculture cotton. Field Crop. Res. 2017, 213, 100–108. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Battude, M.; Al Bitar, A.; Morin, D.; Cros, J.; Huc, M.; Marais Sicre, C.; Le Dantec, V.; Demarez, V. Estimating maize biomass and yield over large areas using high spatial and temporal resolution Sentinel-2 like remote sensing data. Remote Sens. Environ. 2016, 184, 668–681. [Google Scholar] [CrossRef]
- Gao, F.; Anderson, M.; Daughtry, C.; Johnson, D. Assessing the Variability of Corn and Soybean Yields in Central Iowa Using High Spatiotemporal Resolution Multi-Satellite Imagery. Remote Sens. 2018, 10, 1489. [Google Scholar] [CrossRef]
- Habyarimana, E.; Piccard, I.; Catellani, M.; De Franceschi, P.; Dall’Agata, M. Towards Predictive Modeling of Sorghum Biomass Yields Using Fraction of Absorbed Photosynthetically Active Radiation Derived from Sentinel-2 Satellite Imagery and Supervised Machine Learning Techniques. Agronomy 2019, 9, 203. [Google Scholar] [CrossRef]
- Jin, Z.; Azzari, G.; Burke, M.; Aston, S.; Lobell, D.B. Mapping smallholder yield heterogeneity at multiple scales in eastern Africa. Remote Sens. 2017, 9, 931. [Google Scholar] [CrossRef]
- Jin, Z.; Azzari, G.; You, C.; Di Tommaso, S.; Aston, S.; Burke, M.; Lobell, D.B. Smallholder maize area and yield mapping at national scales with Google Earth Engine. Remote Sens. Environ. 2019, 228, 115–128. [Google Scholar] [CrossRef]
- Liao, C.; Wang, J.; Dong, T.; Shang, J.; Liu, J.; Song, Y. Using spatio-temporal fusion of Landsat-8 and MODIS data to derive phenology, biomass and yield estimates for corn and soybean. Sci. Total Environ. 2019, 650, 1707–1721. [Google Scholar] [CrossRef]
- Meshesha, D.T.; Abeje, M. Developing crop yield forecasting models for four major Ethiopian agricultural commodities. Remote Sens. Appl. Soc. Environ. 2018, 11, 83–93. [Google Scholar] [CrossRef]
- Wang, P.; Sun, R.; Zhang, J.; Zhou, Y.; Xie, D.; Zhu, Q. Yield estimation of winter wheat in the North China Plain using the remote-sensing-photosynthesis-yield estimation for crops (RS-P-YEC) model. Int. J. Remote Sens. 2011, 32, 6335–6348. [Google Scholar] [CrossRef]
- Huang, J.; Gómez-Dans, J.L.; Huang, H.; Ma, H.; Wu, Q.; Lewis, P.E.; Liang, S.; Chen, Z.; Xue, J.-H.; Wu, Y.; et al. Assimilation of remote sensing into crop growth models: Current status and perspectives. Agric. For. Meteorol. 2019. [Google Scholar] [CrossRef]
- Huang, J.; Ma, H.; Sedano, F.; Lewis, P.; Liang, S.; Wu, Q.; Su, W.; Zhang, X.; Zhu, D. Evaluation of regional estimates of winter wheat yield by assimilating three remotely sensed reflectance datasets into the coupled WOFOST–PROSAIL model. Eur. J. Agron. 2019, 102, 1–13. [Google Scholar] [CrossRef]
- Huang, J.; Sedano, F.; Huang, Y.; Ma, H.; Li, X.; Liang, S.; Tian, L.; Zhang, X.; Fan, J.; Wu, W. Assimilating a synthetic Kalman filter leaf area index series into the WOFOST model to improve regional winter wheat yield estimation. Agric. For. Meteorol. 2016, 216, 188–202. [Google Scholar] [CrossRef]
- Chao, Z.; Liu, N.; Zhang, P.; Ying, T.; Song, K. Estimation methods developing with remote sensing information for energy crop biomass: A comparative review. Biomass Bioenergy 2019, 414–425. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Ustin, S.L.; Whiting, M.L. Temporal and spatial relationships between within-field yield variability in cotton and high-spatial hyperspectral remote sensing imagery. Agron. J. 2005, 97, 641–653. [Google Scholar] [CrossRef]
- Huang, Y.; Sui, R.; Thomson, S.J.; Fisher, D.K. Estimation of cotton yield with varied irrigation and nitrogen treatments using aerial multispectral imagery. Int. J. Agric. Biol. Eng. 2013, 6, 37–41. [Google Scholar]
- Zhao, D.; Reddy, K.R.; Kakani, V.G.; Read, J.J.; Koti, S. Canopy reflectance in cotton for growth assessment and lint yield prediction. Eur. J. Agron. 2007, 26, 335–344. [Google Scholar] [CrossRef]
- Yang, C.; Everitt, J.H.; Bradford, J.M.; Murden, D. Airborne hyperspectral imagery and yield monitor data for mapping cotton yield variability. Precis. Agric. 2004, 5, 445–461. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, X.L.; Liu, H.; Guo, D.; Yan, Y.; Qin, L.; Pan, Y. Estimation of Cotton Yield Using the Reconstructed Time-Series Vegetation Index of Landsat Data. Can. J. Remote Sens. 2017, 43, 244–255. [Google Scholar] [CrossRef]
- Haghverdi, A.; Washington-Allen, R.A.; Leib, B.G. Prediction of cotton lint yield from phenology of crop indices using artificial neural networks. Comput. Electron. Agric. 2018, 152, 186–197. [Google Scholar] [CrossRef]
- Maestrini, B.; Basso, B. Predicting spatial patterns of within-field crop yield variability. Field Crop. Res. 2018, 219, 106–112. [Google Scholar] [CrossRef]
- Shi, Z.; Ruecker, G.R.; Mueller, M.; Conrad, C.; Ibragimov, N.; Lamers, J.P.A.; Martius, C.; Strunz, G.; Dech, S.; Vlek, P.L.G. Modeling of cotton yields in the Amu Darya river floodplains of Uzbekistan integrating multitemporal remote sensing and minimum field data. Agron. J. 2007, 99, 1317–1326. [Google Scholar] [CrossRef]
- Guo, C.; Tang, Y.; Lu, J.; Zhu, Y.; Cao, W.; Cheng, T.; Zhang, L.; Tian, Y. Predicting wheat productivity: Integrating time series of vegetation indices into crop modeling via sequential assimilation. Agric. For. Meteorol. 2019, 272–273, 69–80. [Google Scholar] [CrossRef]
- Kang, Y.; Özdoğan, M. Field-level crop yield mapping with Landsat using a hierarchical data assimilation approach. Remote Sens. Environ. 2019, 228, 144–163. [Google Scholar] [CrossRef]
- Meng, L.; Liu, H.; Zhang, X.; Ren, C.; Ustin, S.; Qiu, Z.; Xu, M.; Guo, D. Assessment of the effectiveness of spatiotemporal fusion of multi-source satellite images for cotton yield estimation. Comput. Electron. Agric. 2019, 162, 44–52. [Google Scholar] [CrossRef]
- Ryu, Y.; Berry, J.A.; Baldocchi, D.D. What is global photosynthesis? History, uncertainties and opportunities. Remote Sens. Environ. 2019, 223, 95–114. [Google Scholar] [CrossRef]
- Hebbar, K.B.; Venugopalan, M.V.; Seshasai, M.V.R.; Rao, K.V.; Patil, B.C.; Prakash, A.H.; Kumar, V.; Hebbar, K.R.; Jeyakumar, P.; Bandhopadhyay, K.K.; et al. Predicting cotton production using Infocrop-cotton simulation model, remote sensing and spatial agro-climatic data. Curr. Sci. 2008, 95, 1570–1579. [Google Scholar]
- Thorp, K.R.; Hunsaker, D.J.; French, A.N.; Bautista, E.; Bronson, K.F. Integrating geospatial data and cropping system simulation within a geographic information system to analyze spatial seed cotton yield, water use, and irrigation requirements. Precis. Agric. 2015, 16, 532–557. [Google Scholar] [CrossRef]
- Alganci, U.; Ozdogan, M.; Sertel, E.; Ormeci, C. Estimating maize and cotton yield in southeastern Turkey with integrated use of satellite images, meteorological data and digital photographs. Field Crop. Res. 2014, 157, 8–19. [Google Scholar] [CrossRef]
- Kirschbaum, M.U.F. Does Enhanced Photosynthesis Enhance Growth? Lessons Learned from CO2 Enrichment Studies. Plant. Physiol. 2011, 155, 117–124. [Google Scholar] [CrossRef]
- Domenikiotis, C.; Spiliotopoulos, M.; Tsiros, E.; Dalezios, N.R. Early cotton yield assessment by the use of the NOAA/AVHRR derived Vegetation Condition Index (VCI) in Greece. Int. J. Remote Sens. 2004, 25, 2807–2819. [Google Scholar] [CrossRef]
- Palacios-Orueta, A.; Huesca, M.; Whiting, M.L.; Litago, J.; Khanna, S.; Garcia, M.; Ustin, S.L. Derivation of phenological metrics by function fitting to time-series of Spectral Shape Indexes AS1 and AS2: Mapping cotton phenological stages using MODIS time series. Remote Sens. Environ. 2012, 126, 148–159. [Google Scholar] [CrossRef]
- Guo, W.; Maas, S.J.; Bronson, K.F. Relationship between cotton yield and soil electrical conductivity, topography, and Landsat imagery. Precis. Agric. 2012, 13, 678–692. [Google Scholar] [CrossRef]
- Lambert, M.J.; Traoré, P.C.S.; Blaes, X.; Baret, P.; Defourny, P. Estimating smallholder crops production at village level from Sentinel-2 time series in Mali’s cotton belt. Remote Sens. Environ. 2018, 216, 647–657. [Google Scholar] [CrossRef]
- Gao, F.; Anderson, M.C.; Zhang, X.; Yang, Z.; Alfieri, J.G.; Kustas, W.P.; Mueller, R.; Johnson, D.M.; Prueger, J.H. Toward mapping crop progress at field scales through fusion of Landsat and MODIS imagery. Remote Sens. Environ. 2017, 188, 9–25. [Google Scholar] [CrossRef]
- Feng, G.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- Wu, M.; Yang, C.; Song, X.; Hoffmann, W.C.; Huang, W.; Niu, Z.; Wang, C.; Li, W.; Yu, B. Monitoring cotton root rot by synthetic Sentinel-2 NDVI time series using improved spatial and temporal data fusion. Sci. Rep. UK 2018, 8, 2016. [Google Scholar] [CrossRef]
- Falagas, A.; Karantzalos, K. A cotton yield estimation model based on agrometeorological and high resolution remote sensing data. Precis. Agric. 2019, 469–475. [Google Scholar] [CrossRef]
- Chen, B.Z.; Chen, J.M.; Ju, W.M. Remote sensing-based ecosystem-atmosphere simulation scheme (EASS)—Model formulation and test with multiple-year data. Ecol. Model. 2007, 209, 277–300. [Google Scholar] [CrossRef]
- Chen, J.M.; Mo, G.; Pisek, J.; Liu, J.; Deng, F.; Ishizawa, M.; Chan, D. Effects of foliage clumping on the estimation of global terrestrial gross primary productivity. Glob. Biogeochem. Cycles 2012, 26. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J.; Cihlar, J.; Goulden, M.L. Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecol. Model. 1999, 124, 99–119. [Google Scholar] [CrossRef]
- He, L.; Chen, J.M.; Liu, J.; Mo, G.; Bélair, S.; Zheng, T.; Wang, R.; Chen, B.; Croft, H.; Arain, M.A.; et al. Optimization of water uptake and photosynthetic parameters in an ecosystem model using tower flux data. Ecol. Model. 2014, 294, 94–104. [Google Scholar] [CrossRef]
- He, L.; Chen, J.M.; Liu, J.; Bélair, S.; Luo, X. Assessment of SMAP soil moisture for global simulation of gross primary production. J. Geophys. Res. Biogeosci. 2017, 122. [Google Scholar] [CrossRef]
- He, L.; Chen, J.M.; Gonsamo, A.; Luo, X.Z.; Wang, R.; Liu, Y.; Liu, R.G. Changes in the Shadow: The Shifting Role of Shaded Leaves in Global Carbon and Water Cycles Under Climate Change. Geophys. Res. Lett. 2018, 45, 5052–5061. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.M.; Cihlar, J.; Park, W.M. A process-based boreal ecosystem productivity simulator using remote sensing inputs. Remote Sens. Environ. 1997, 62, 158–175. [Google Scholar] [CrossRef]
- Matsushita, B.; Tamura, M. Integrating remotely sensed data with an ecosystem model to estimate net primary productivity in East Asia. Remote Sens. Environ. 2002, 81, 58–66. [Google Scholar] [CrossRef]
- Matsushita, B.; Xu, M.; Chen, J.; Kameyama, S.; Tamura, M. Estimation of regional net primary productivity (NPP) using a process-based ecosystem model: How important is the accuracy of climate data? Ecol. Model. 2004, 178, 371–388. [Google Scholar] [CrossRef]
- Feng, X.; Liu, G.; Chen, J.M.; Chen, M.; Liu, J.; Ju, W.M.; Sun, R.; Zhou, W. Net primary productivity of China’s terrestrial ecosystems from a process model driven by remote sensing. J. Environ. Manag. 2007, 85, 563–573. [Google Scholar] [CrossRef]
- Wang, Q.; Tenhunen, J.; Falge, E.; Bernhofer, C.; Granier, A.; Vesala, T. Simulation and scaling of temporal variation in gross primary production for coniferous and deciduous temperate forests. Glob. Chang. Biol 2004, 10, 37–51. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, J.M.; Zhang, S.; Zheng, X.; Ju, W.; Mo, G.; Lu, X. Optimization of terrestrial ecosystem model parameters using atmospheric CO2 concentration data with the Global Carbon Assimilation System (GCAS). J. Geophys. Res. Biogeosci. 2017. [Google Scholar] [CrossRef]
- Luo, X.Z.; Chen, J.M.; Liu, J.E.; Black, T.A.; Croft, H.; Staebler, R.; He, L.M.; Arain, M.A.; Chen, B.; Mo, G.; et al. Comparison of Big-Leaf, Two-Big-Leaf, and Two-Leaf Upscaling Schemes for Evapotranspiration Estimation Using Coupled Carbon-Water Modeling. J. Geophys. Res. Biogeosci. 2018, 123, 207–225. [Google Scholar] [CrossRef]
- Farquhar, G.D.; Caemmerer, S.V.; Berry, J.A. A Biochemical-Model of Photosynthetic CO2 Assimilation in Leaves of C-3 Species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef]
- Norman, J.M. Simulation of Microclimates. In Biometeorology in Integrated Pest Management; Jerry, H., Ed.; Academic Press: Cambridge, MA, USA, 1982; pp. 65–99. [Google Scholar]
- Zhang, Y.-L.; Hu, Y.-Y.; Luo, H.-H.; Chow, W.S.; Zhang, W.-F. Two distinct strategies of cotton and soybean differing in leaf movement to perform photosynthesis under drought in the field. Funct. Plant. Biol. 2011, 38, 567–575. [Google Scholar] [CrossRef]
- Harley, P.C.; Thomas, R.B.; Reynolds, J.F.; Strain, B.R. Modelling photosynthesis of cotton grown in elevated CO2. Plant Cell Environ. 1992, 15, 271–282. [Google Scholar] [CrossRef]
- Leuning, R. Temperature dependence of two parameters in a photosynthesis model. Plant Cell Environ. 2002, 25, 1205–1210. [Google Scholar] [CrossRef]
- Archontoulis, S.V.; Yin, X.; Vos, J.; Danalatos, N.G.; Struik, P.C. Leaf photosynthesis and respiration of three bioenergy crops in relation to temperature and leaf nitrogen: How conserved are biochemical model parameters among crop species? J. Exp. Bot. 2011, 63, 895–911. [Google Scholar] [CrossRef]
- Singh, S.K.; Badgujar, G.B.; Reddy, V.R.; Fleisher, D.H.; Timlin, D.J. Effect of Phosphorus Nutrition on Growth and Physiology of Cotton Under Ambient and Elevated Carbon Dioxide. J. Agron. Crop Sci. 2013, 199, 436–448. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, M.; Chen, H.; Adams, J. Global pattern of NPP to GPP ratio derived from MODIS data: Effects of ecosystem type, geographical location and climate. Glob. Ecol. Biogeogr. 2009, 18, 280–290. [Google Scholar] [CrossRef]
- Tang, X.; Carvalhais, N.; Moura, C.; Ahrens, B.; Koirala, S.; Fan, S.; Guan, F.; Zhang, W.; Gao, S.; Magliulo, V.; et al. Global variability of carbon use efficiency in terrestrial ecosystems. Biogeosci. Discuss. 2019, 2019, 1–19. [Google Scholar] [CrossRef]
- Schlesinger, W.H. Biogeochemistry: An Analysis of Global Change; Academic Press: San Diego, CA, USA, 1991. [Google Scholar]
- Hussein, F.; Janat, M.; Yakoub, A. Assessment of yield and water use effi ciency of drip-irrigated cotton (Gossypium hirsutum L.) as aff ected by defi cit irrigation. Turk. J. Agric. For. 2011, 35, 611–621. [Google Scholar]
- Maheswarappa, H.P.; Srinivasan, V.; Lal, R. Carbon Footprint and Sustainability of Agricultural Production Systems in India. J. Crop Improv. 2011, 25, 303–322. [Google Scholar] [CrossRef]
- Pettigrew, W.T.; Bruns, H.A.; Reddy, K.N. Agronomy and Soils: Growth and Agronomic Performance of Cotton When Grown in Rotation with Soybean. J. Cotton Sic. 2016, 20, 299–308. [Google Scholar]
- Huang, J. Effects of Meteorological Parameters Created by Different Sowing Dates on Drip Irrigated Cotton Yield and Yield Components in Arid Regions in China. J. Hortic. 2015, 2, 63–83. [Google Scholar] [CrossRef]
- Dowd, M.K.; Pelitire, S.M.; Delhom, C.D. Seed-Fiber Ratio, Seed Index, and Seed Tissue and Compositional Properties of Current Cotton Cultivars. J. Cotton Sci. 2018, 22, 60–74. [Google Scholar]
- Richter, R.; Louis, J.; Müller-Wilm, U. Sentinel-2 MSI—Level 2A Products Algorithm Theoretical Basis Document. S2PAD-ATBD-0001. Eur. Space Agency (Spec. Publ.) ESA SP 2012, 49, 1–72. [Google Scholar]
- CHEN, J.M.; BLACK, T.A. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Verrelst, J.; Muñoz, J.; Alonso, L.; Delegido, J.; Rivera, J.P.; Camps-Valls, G.; Moreno, J. Machine learning regression algorithms for biophysical parameter retrieval: Opportunities for Sentinel-2 and -3. Remote Sens. Environ. 2012, 118, 127–139. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Chen, J.M.; Deng, F.; Chen, M.Z. Locally adjusted cubic-spline capping for reconstructing seasonal trajectories of a satellite-derived surface parameter. IEEE Trans. Geosci. Remote 2006, 44, 2230–2238. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.K.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Hengl, T.; de Jesus, M.J.; Heuvelink, G.B.M.; Ruiperez Gonzalez, M.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. Plos ONE 2017, 12, e0169748. [Google Scholar] [CrossRef]
- USDA National Agricultural Statistics Service. Cropland Data Layer; USDA-NASS: Washington, DC, USA, 2017.
- Lark, T.J.; Mueller, R.M.; Johnson, D.M.; Gibbs, H.K. Measuring land-use and land-cover change using the U.S. department of agriculture’s cropland data layer: Cautions and recommendations. Int J. Appl. Earth Obs. 2017, 62, 224–235. [Google Scholar] [CrossRef]
- Saxton, K.E.; Rawls, W.J. Soil Water Characteristic Estimates by Texture and Organic Matter for Hydrologic Solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef]
- Dodds, D.M.; Dixon, T.H.; Catchot, A.L.; Golden, B.R.; Larson, E.; Varco, J.J.; Samples, C.A. Evaluation of Wheat Stubble Management and Seeding Rates for Cotton Grown Following Wheat Production. J. Cotton Sci. 2017, 21, 104–112. [Google Scholar]
- Holzworth, D.P.; Huth, N.I.; deVoil, P.G.; Zurcher, E.J.; Herrmann, N.I.; McLean, G.; Chenu, K.; van Oosterom, E.J.; Snow, V.; Murphy, C.; et al. APSIM—Evolution towards a new generation of agricultural systems simulation. Environ. Model. Softw. 2014, 62, 327–350. [Google Scholar] [CrossRef]
- Hearn, A.B. OZCOT: A simulation model for cotton crop management. Agric. Syst. 1994, 44, 257–299. [Google Scholar] [CrossRef]
- Singh, A.K.; Tripathy, R.; Chopra, U.K. Evaluation of CERES-Wheat and CropSyst models for water–nitrogen interactions in wheat crop. Agric. Water Manag. 2008, 95, 776–786. [Google Scholar] [CrossRef]
- de Wit, A.; Boogaard, H.; Fumagalli, D.; Janssen, S.; Knapen, R.; van Kraalingen, D.; Supit, I.; van der Wijngaart, R.; van Diepen, K. 25 years of the WOFOST cropping systems model. Agric. Syst. 2019, 168, 154–167. [Google Scholar] [CrossRef]
- Duchemin, B.; Maisongrande, P.; Boulet, G.; Benhadj, I. A simple algorithm for yield estimates: Evaluation for semi-arid irrigated winter wheat monitored with green leaf area index. Environ. Model. Softw. 2008, 23, 876–892. [Google Scholar] [CrossRef]
- Wang, P.; Xie, D.; Zhang, J.; Sun, R.; Chen, S.; Zhu, Q. Application of BEPS model in estimating winter wheat yield in North China Plain. Nongye Gongcheng Xuebao/Trans. Chin. Soc. Agric. Eng. 2009, 25, 148–153. [Google Scholar] [CrossRef]
- Ji, C.; Zhang, J.; Yao, F. The yield estimation of rapeseed in hubei province by BEPS process-based model and MODIS satellite data. Commun. Comput. Inf. Sci. 2015, 482, 643–652. [Google Scholar]
- Yao, F.; Tang, Y.; Wang, P.; Zhang, J. Estimation of maize yield by using a process-based model and remote sensing data in the Northeast China Plain. Phys. Chem. Earth 2015, 87–88, 142–152. [Google Scholar] [CrossRef]
- Yao, F.; Liu, D.; Zhang, J.; Wang, P. Estimation of Rice Yield with a Process-Based Model and Remote Sensing Data in the Middle and Lower Reaches of Yangtze River of China. J. Indian Soc. Remote Sens. 2017, 45, 477–484. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, J.; Bai, Y.; Koju, U.A.; Igbawua, T.; Chang, Q.; Zhang, D.; Yao, F. Evaluation and improvement of the daily boreal ecosystem productivity simulator in simulating gross primary productivity at 41 flux sites across Europe. Ecol. Model. 2018, 368, 205–232. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, J.; Zhang, S.; Yao, F.; Magliulo, V. A remote sensing-based two-leaf canopy conductance model: Global optimization and applications in modeling gross primary productivity and evapotranspiration of crops. Remote Sens. Environ. 2018, 215, 411–437. [Google Scholar] [CrossRef]
- Punalekar, S.M.; Verhoef, A.; Quaife, T.L.; Humphries, D.; Bermingham, L.; Reynolds, C.K. Application of Sentinel-2A data for pasture biomass monitoring using a physically based radiative transfer model. Remote Sens. Environ. 2018, 218, 207–220. [Google Scholar] [CrossRef]
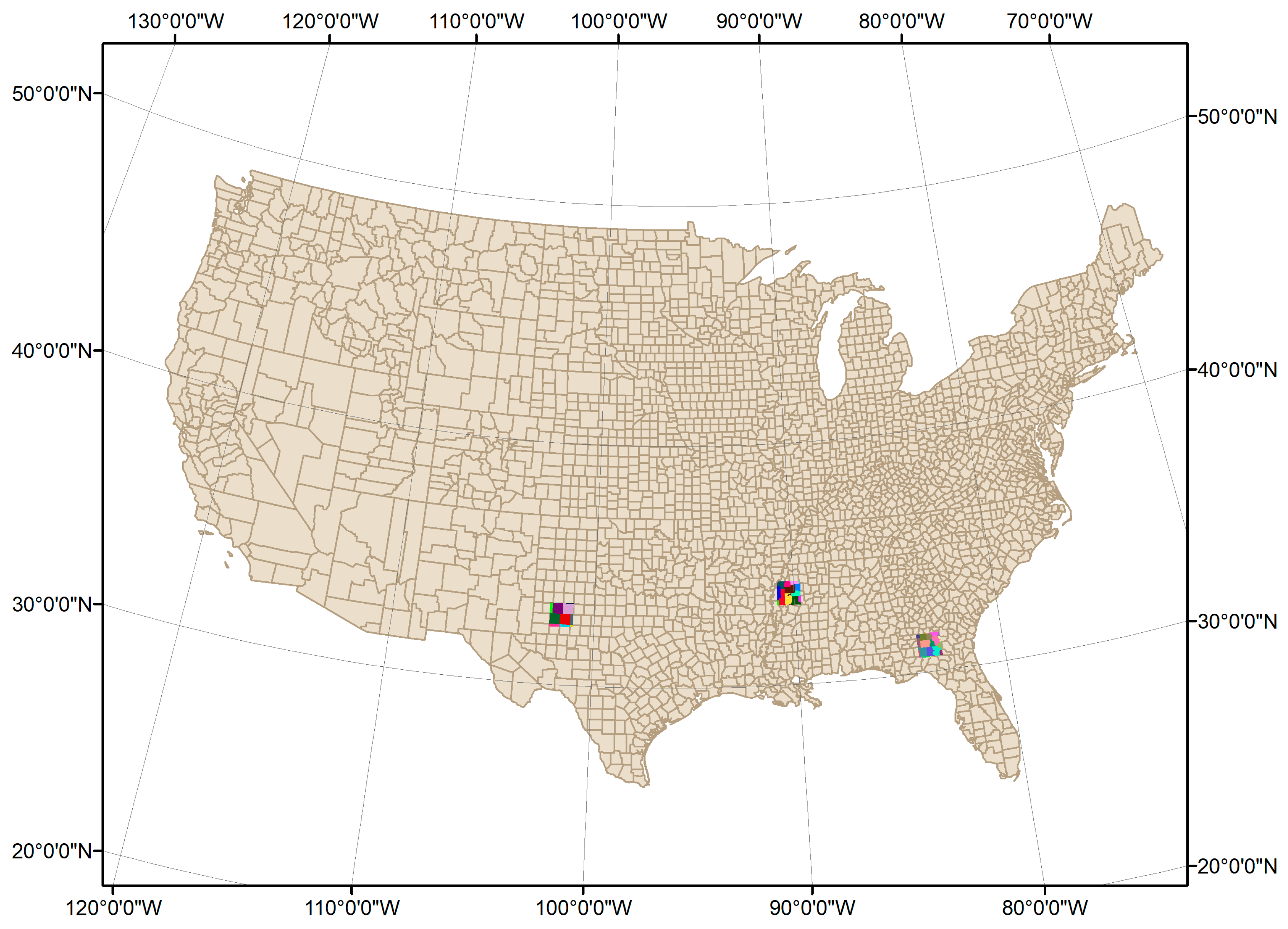

| Tile ID | Number of Images | Summary |
|---|---|---|
| 14SKB | 25 | TX, mainly rainfed |
| 15SYT | 16 | MS, largely irrigated |
| 17RKQ | 20 | GA, mainly rainfed |
| County | FIPS | Area | Production | Lint Yield | GPP (BEPS) |
|---|---|---|---|---|---|
| (ha) | (kg) | (kg/ha) | (g∙C∙m−2∙year−1) | ||
| TX (14SKB) | |||||
| Lynn | 48,305 | 120,522 | 79,922,356 | 663 | 715 |
| Garza | 48,169 | 16,593 | 12,322,983 | 743 | 752 |
| Dawson | 48,115 | 105,198 | 69,978,487 | 665 | 805 |
| Borden | 48,033 | 23,329 | 12,449,007 | 534 | 630 |
| MS (15SYT) | |||||
| Coahoma | 28,027 | 36,881 | 42,187,930 | 1144 | 1722 |
| Quitman | 28,119 | 10,192 | 11,590,623 | 1137 | 1985 |
| Tallahatchie | 28,135 | 17,839 | 23,602,659 | 1323 | 2116 |
| Sunflower | 28,133 | 8379 | 10,650,446 | 1271 | 1891 |
| Leflore | 28,083 | 17,748 | 21,326,898 | 1202 | 2200 |
| Carroll | 28,015 | 8859 | 10,161,688 | 1147 | 2118 |
| GA (17RKQ) | |||||
| Worth | 13,321 | 22,541 | 21,292,891 | 945 | 1532 |
| Tift | 13,277 | 9227 | 8,268,221 | 896 | 1409 |
| Colquitt | 13,071 | 19,223 | 20,181,571 | 1050 | 1536 |
| Cook | 13,075 | 7244 | 5,267,657 | 727 | 1364 |
| Berrien | 13,019 | 11,088 | 9,001,692 | 812 | 1451 |
| Thomas | 13,275 | 12,505 | 10,779,804 | 862 | 1552 |
| Brooks | 13,027 | 15,459 | 14,291,575 | 924 | 1529 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Mostovoy, G. Cotton Yield Estimate Using Sentinel-2 Data and an Ecosystem Model over the Southern US. Remote Sens. 2019, 11, 2000. https://doi.org/10.3390/rs11172000
He L, Mostovoy G. Cotton Yield Estimate Using Sentinel-2 Data and an Ecosystem Model over the Southern US. Remote Sensing. 2019; 11(17):2000. https://doi.org/10.3390/rs11172000
Chicago/Turabian StyleHe, Liming, and Georgy Mostovoy. 2019. "Cotton Yield Estimate Using Sentinel-2 Data and an Ecosystem Model over the Southern US" Remote Sensing 11, no. 17: 2000. https://doi.org/10.3390/rs11172000
APA StyleHe, L., & Mostovoy, G. (2019). Cotton Yield Estimate Using Sentinel-2 Data and an Ecosystem Model over the Southern US. Remote Sensing, 11(17), 2000. https://doi.org/10.3390/rs11172000