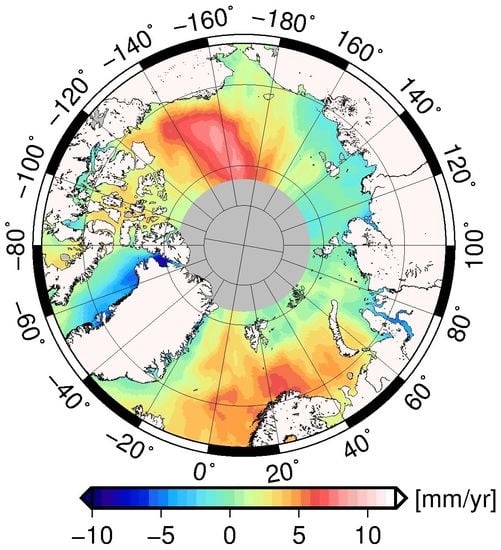
Arctic Ocean Sea Level Record from the Complete Radar Altimetry Era: 1991–2018
Abstract
1. Introduction
2. Data
2.1. Altimetry Data
2.2. Ice Concentration Data
2.3. Tide Gauge Data
3. Generation of the Sea Level Product
- Pre-processing
- Adding/removing geophysical corrections
- Sea-ice concentration data are used to discriminate between the sea-ice cover and the open ocean
- Threshold criterias are used to separate the leads/open ocean from the sea-ice
- Inter-satellite biases are determined and corrected
- Removing outliers
- Resampling and gridding the data to compute the final Arctic SLA
- Uncertainty analysis
3.1. Pre-Processing
3.2. Geophysical Corrections
3.3. Lead and Ocean Discrimination
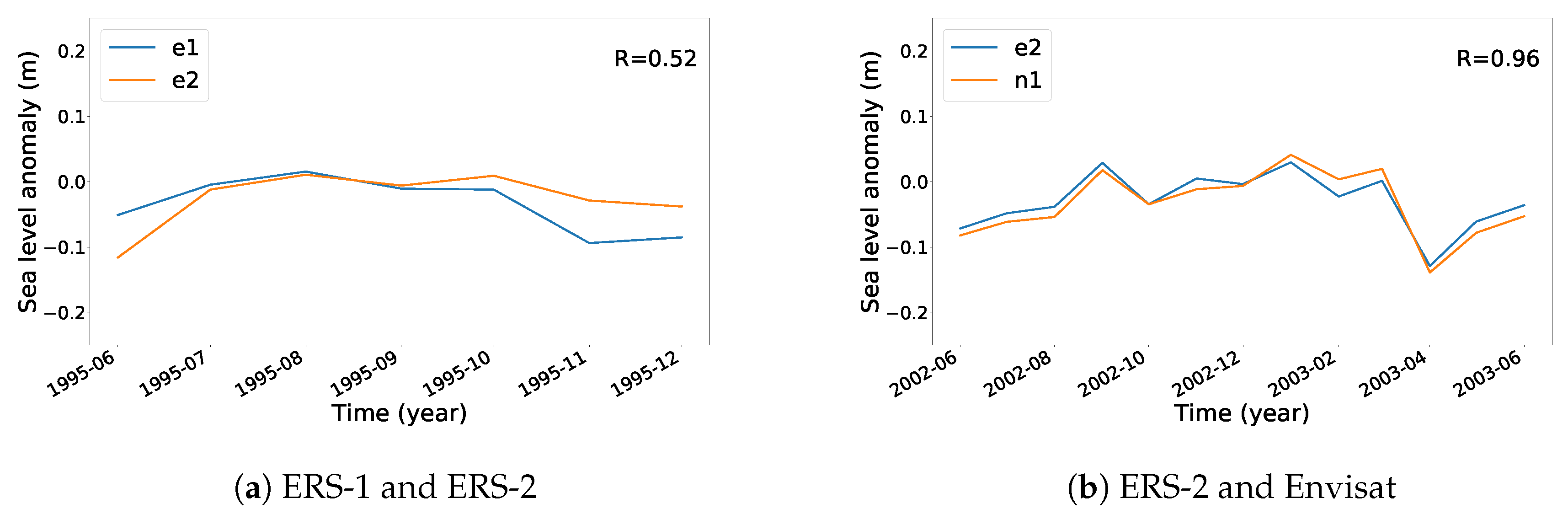
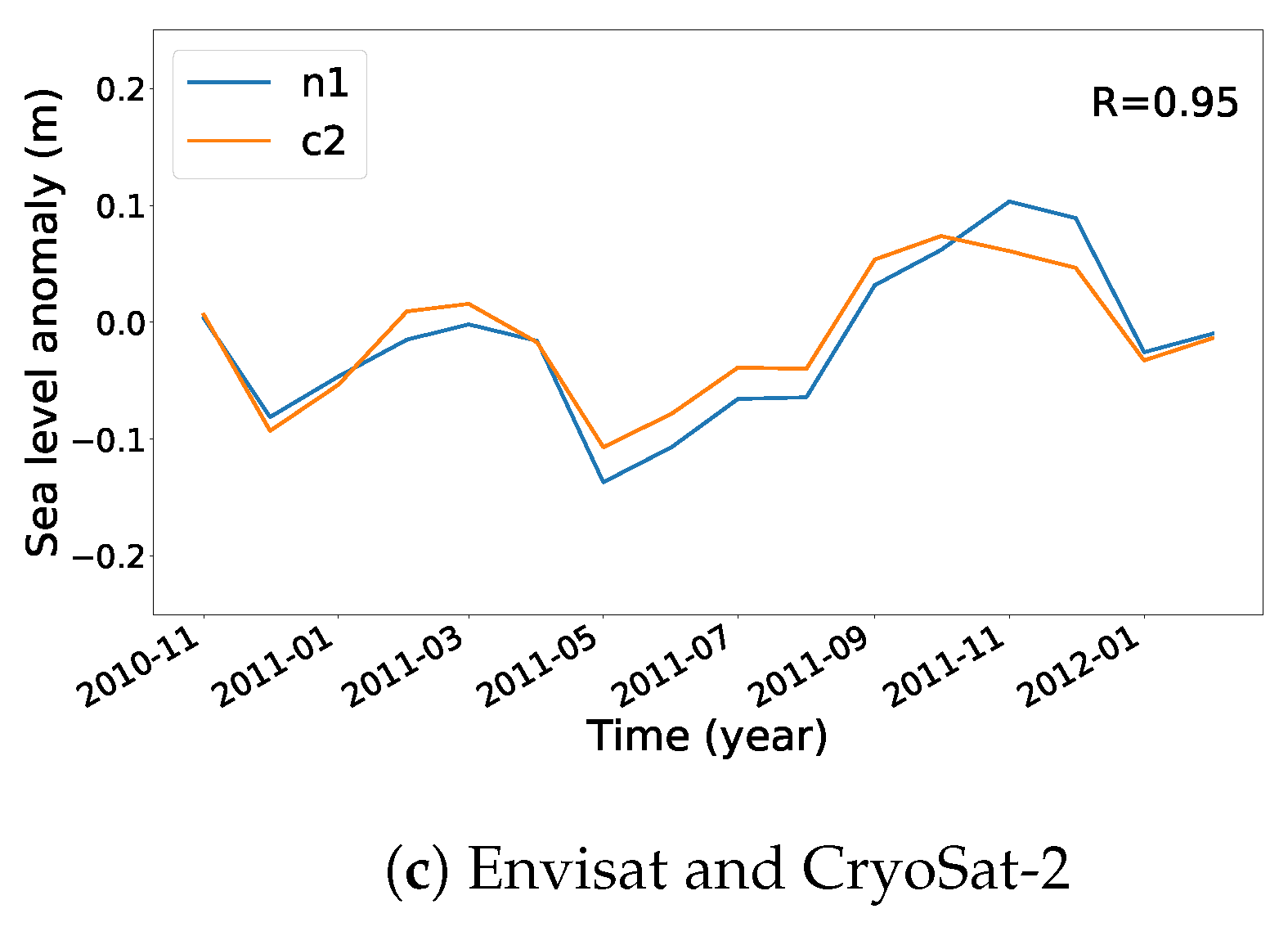
3.4. Intermission Bias
- Monthly medians were calculated for each mission, over the entire Arctic Ocean, covered by the data sets
- For overlapping mission pairs (either ERS-1 and ERS-2, ERS-2 and Envisat, or Envisat and CryoSat-2) coinciding months (only full months considered) were detected and extracted
- For each overlapping pair, the median difference was calculated and the data sets were aligned
- The biases between the satellites are: ERS-1/ERS-2 ∼0.67 m, ERS-2/Envisat ∼0.53 m and Envisat/CryoSat-2 ∼0.03 m
3.5. Removing Outliers
3.6. The Arctic Sea Level Anomaly Product
3.7. Uncertainty Estimates
4. The Arctic Sea Level Anomaly Record
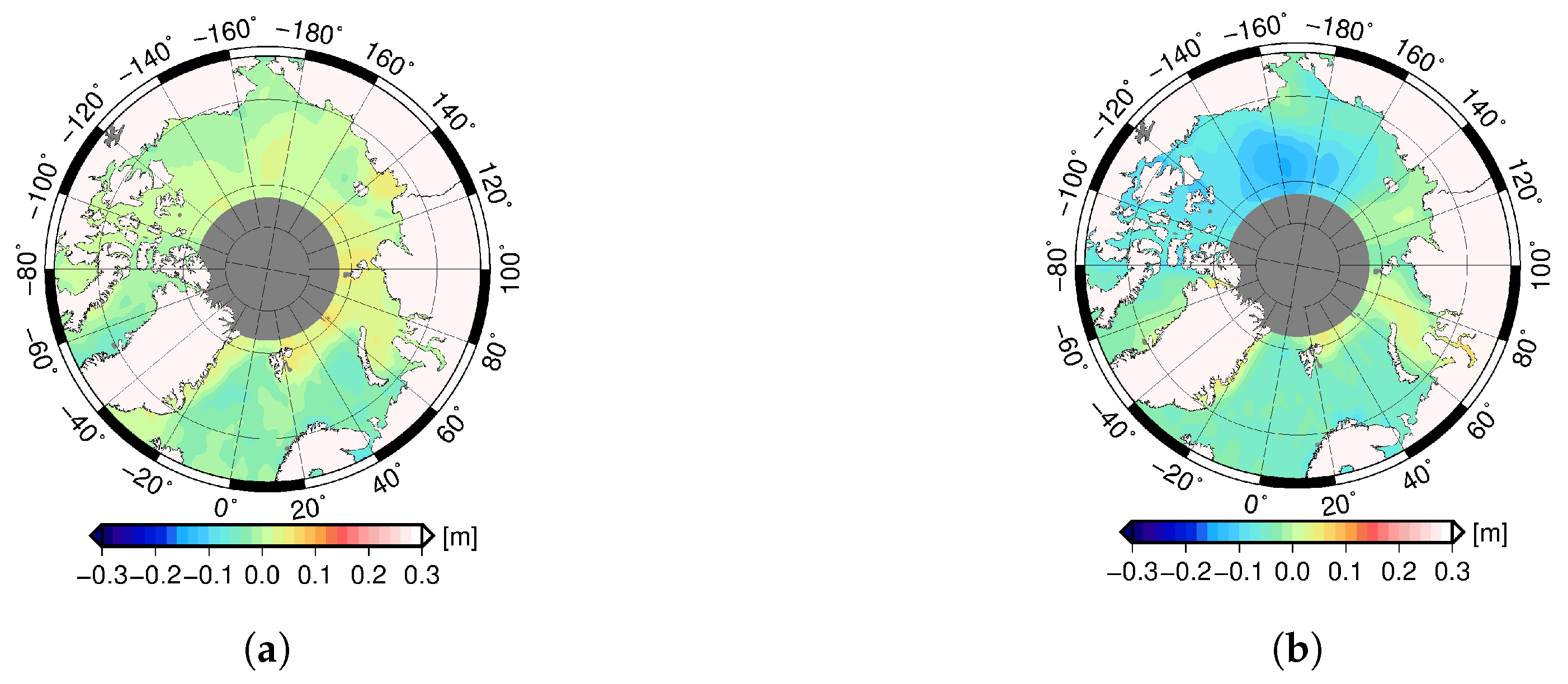
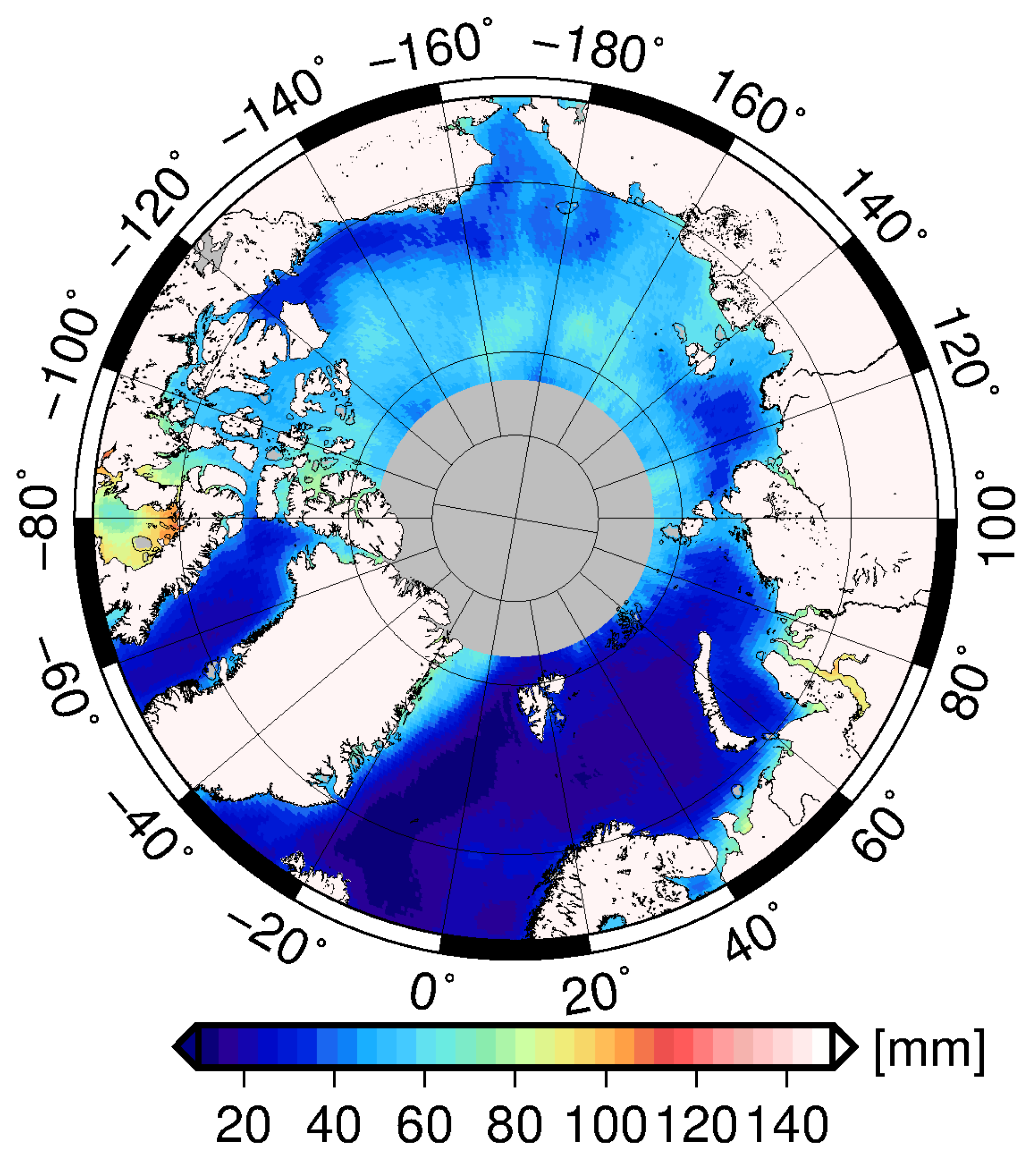
4.1. Uncertainty of the Arctic Sea Level Product
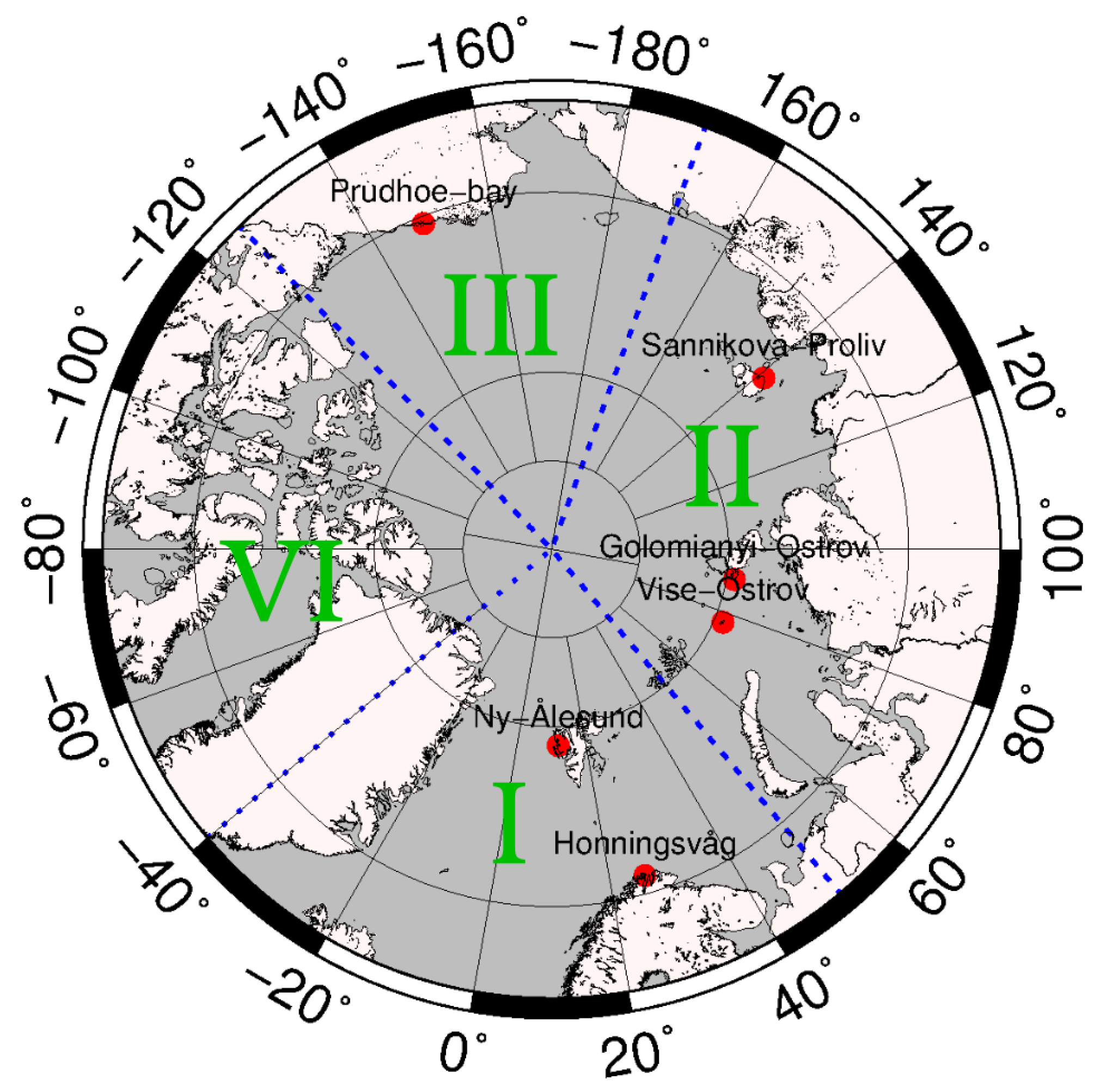
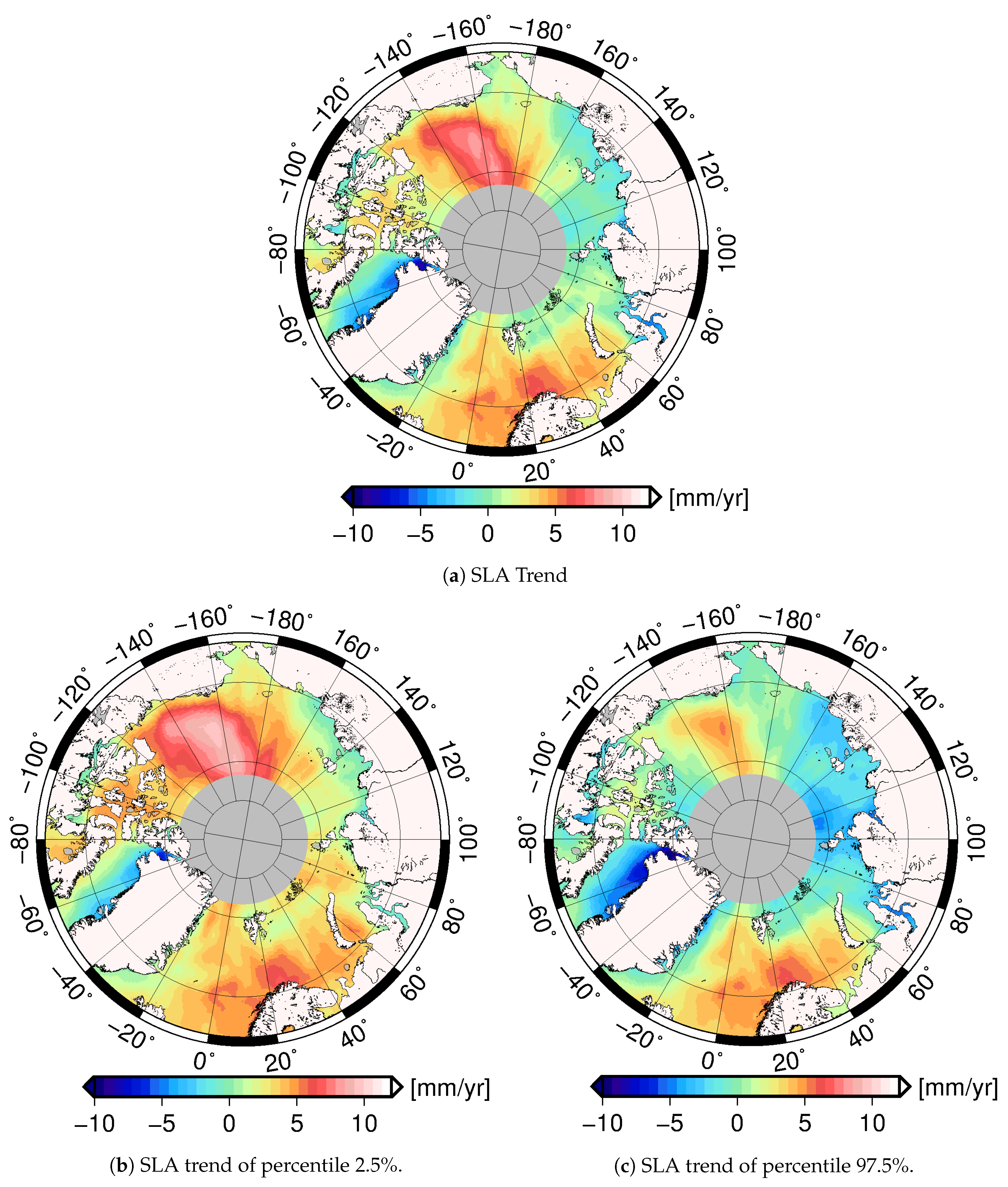
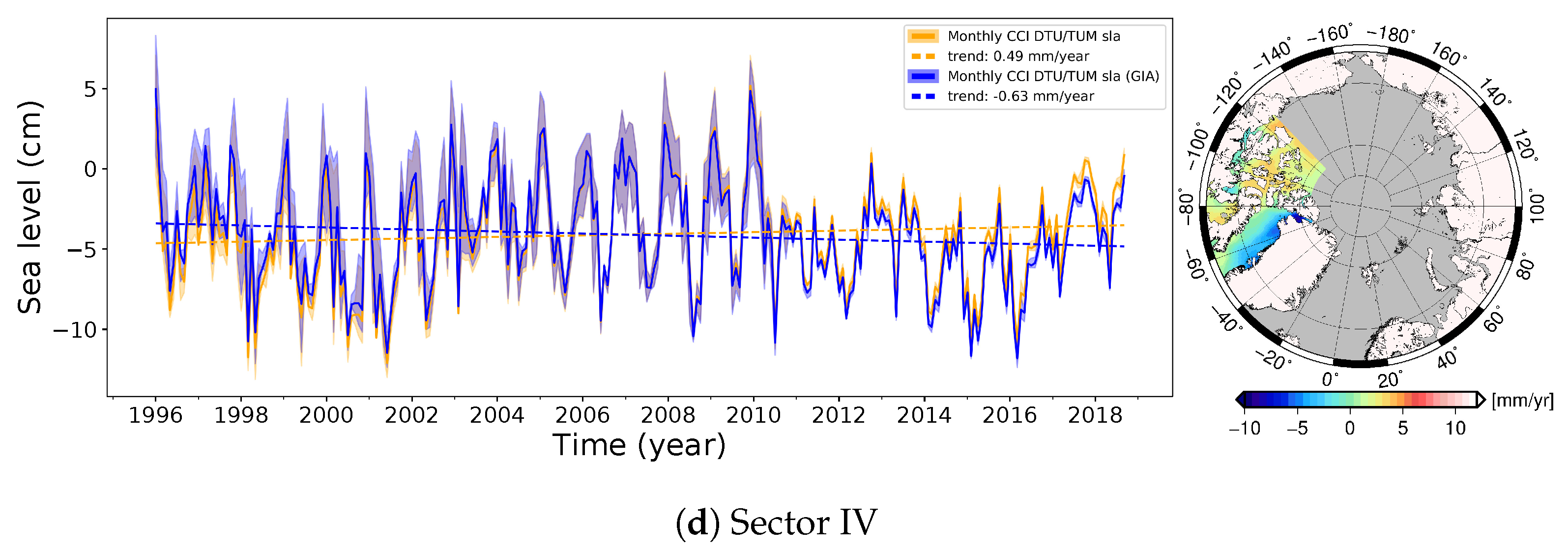
4.2. Regional Trends in the ERS-2 to CryoSat-2 Era
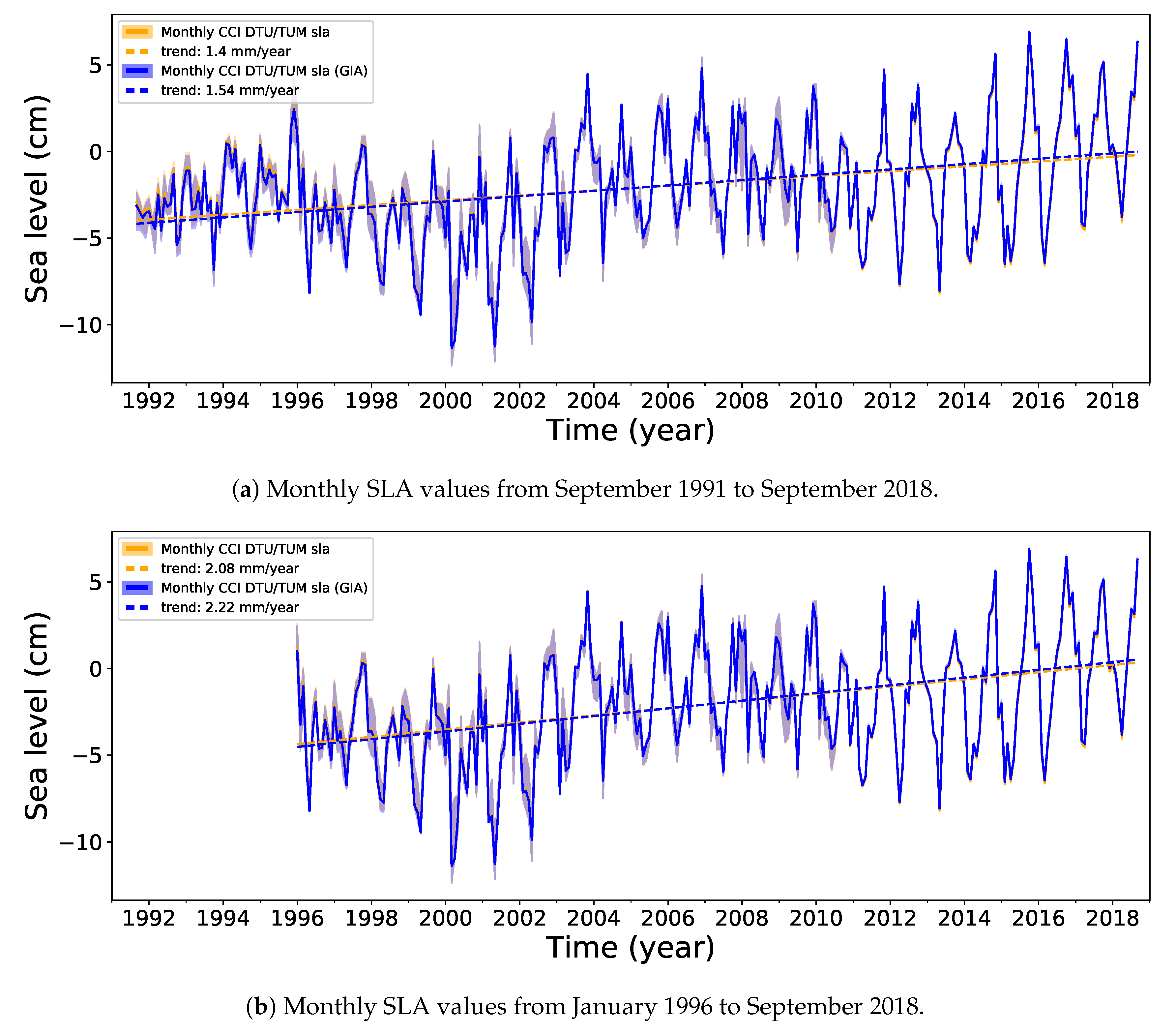
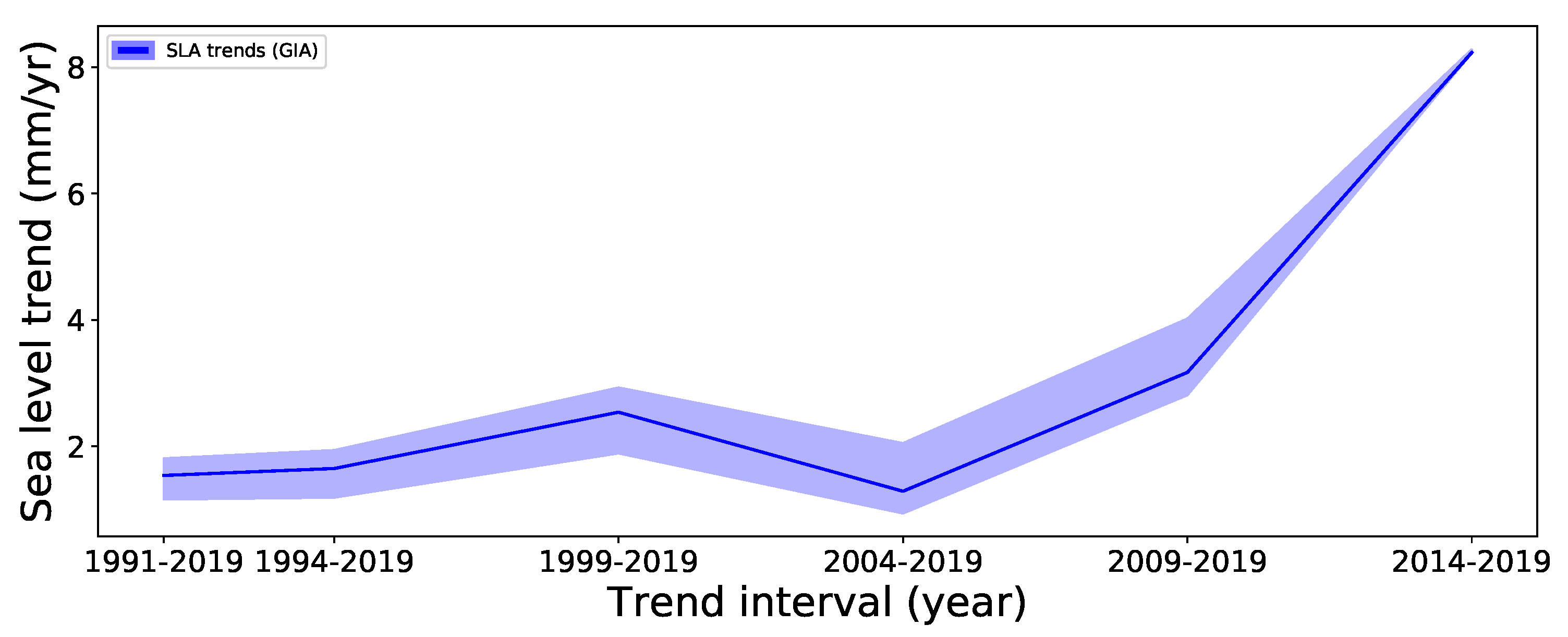
4.3. Inter-Annual Variability
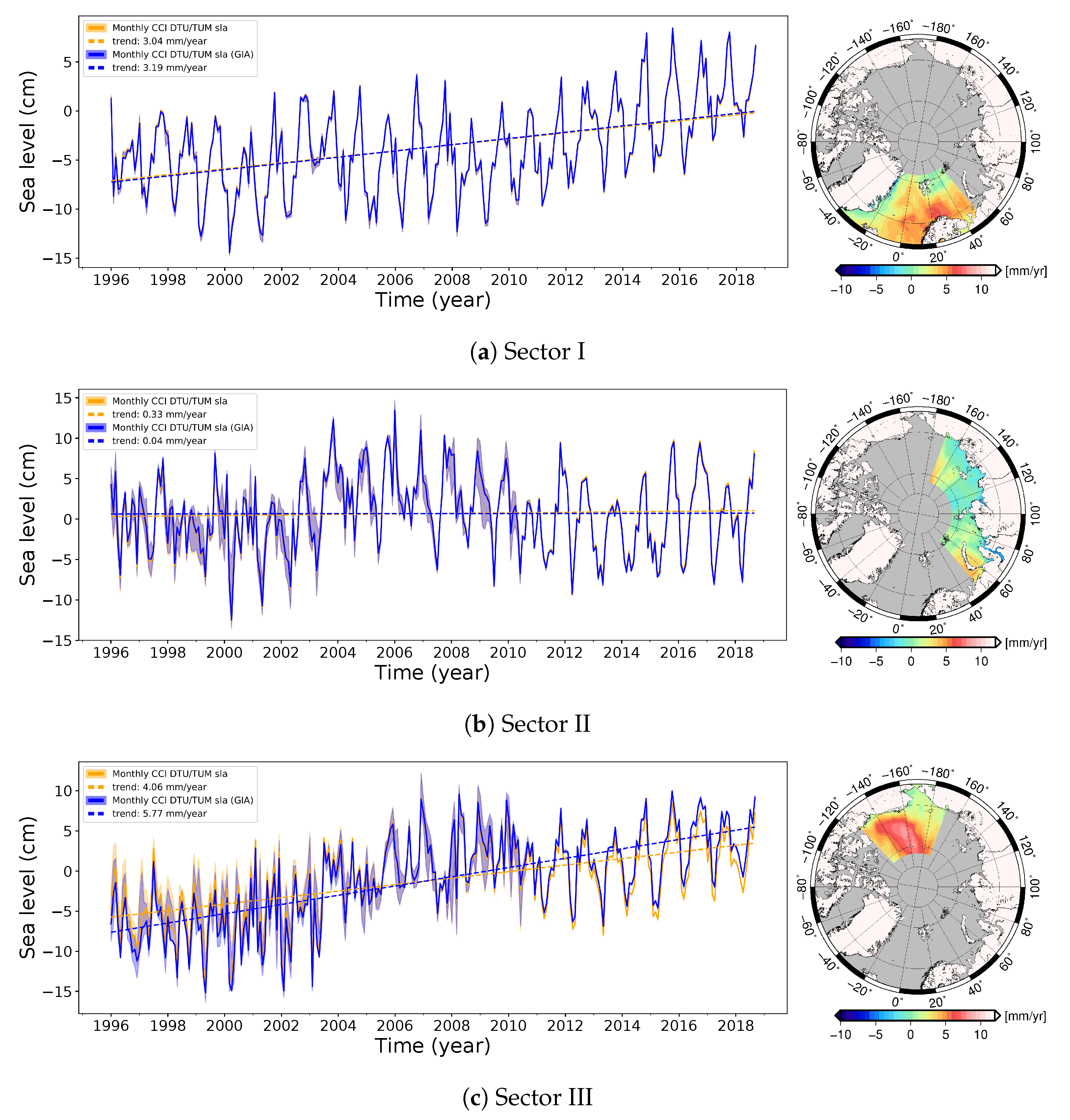
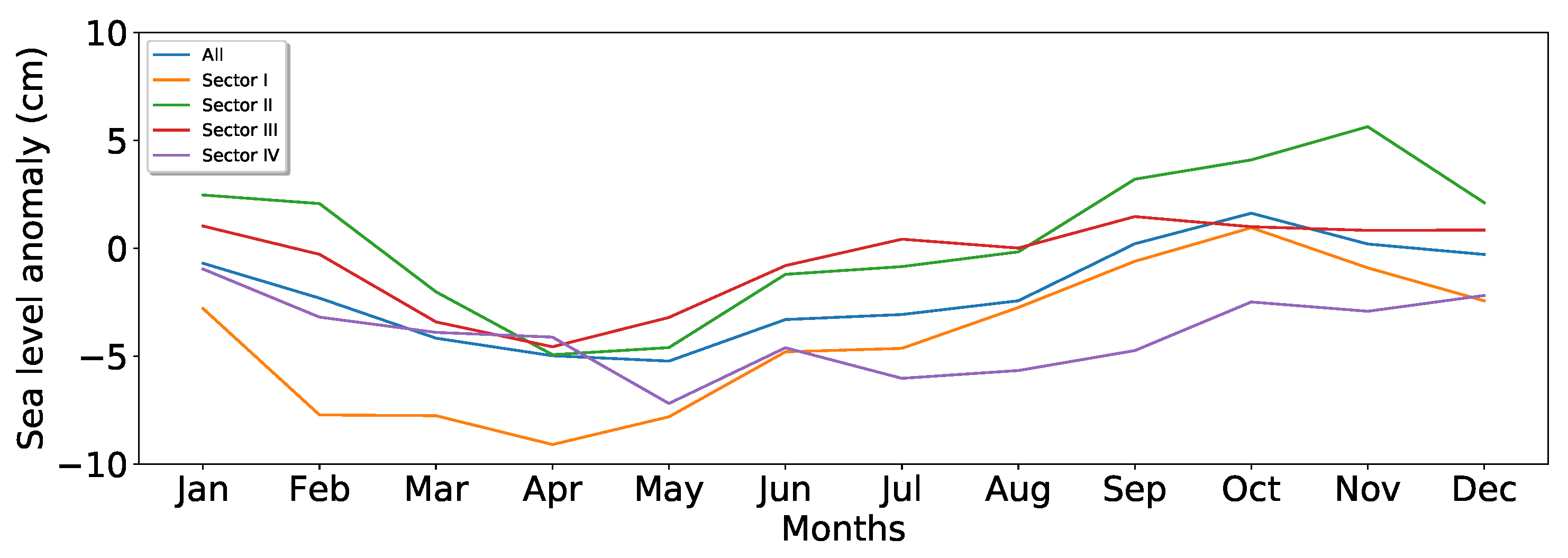
4.4. Regional Sea Level Variability
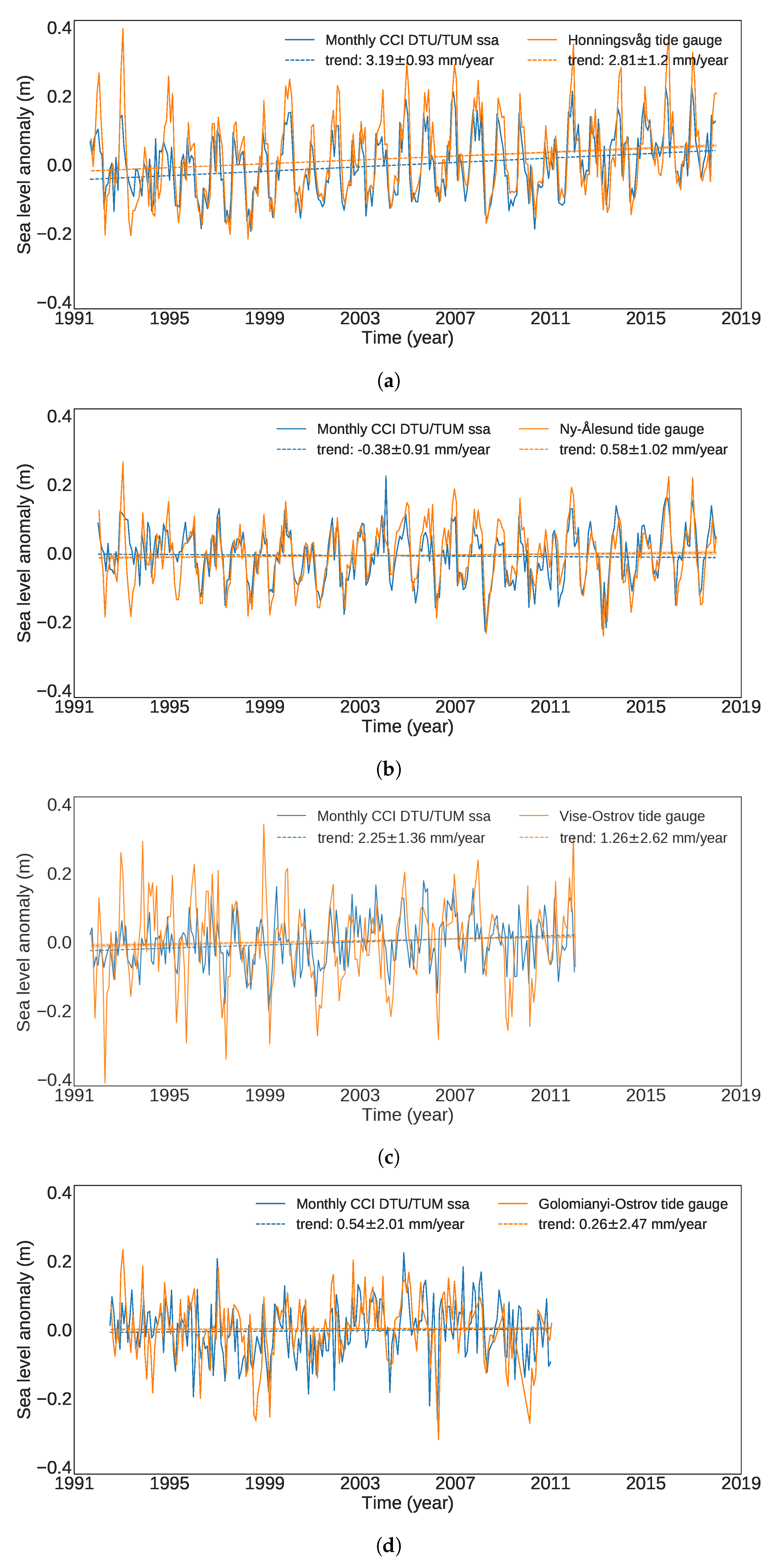
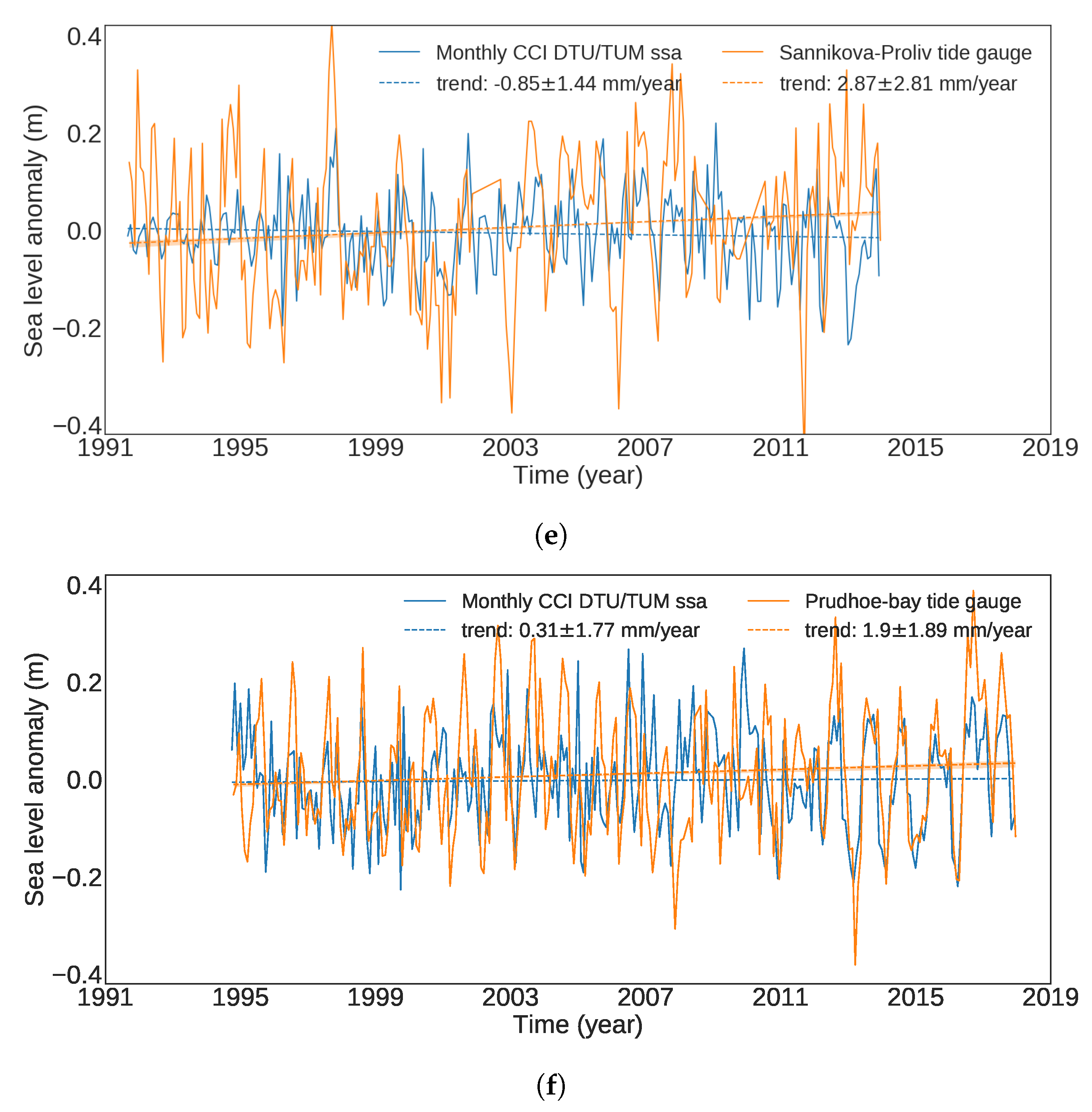
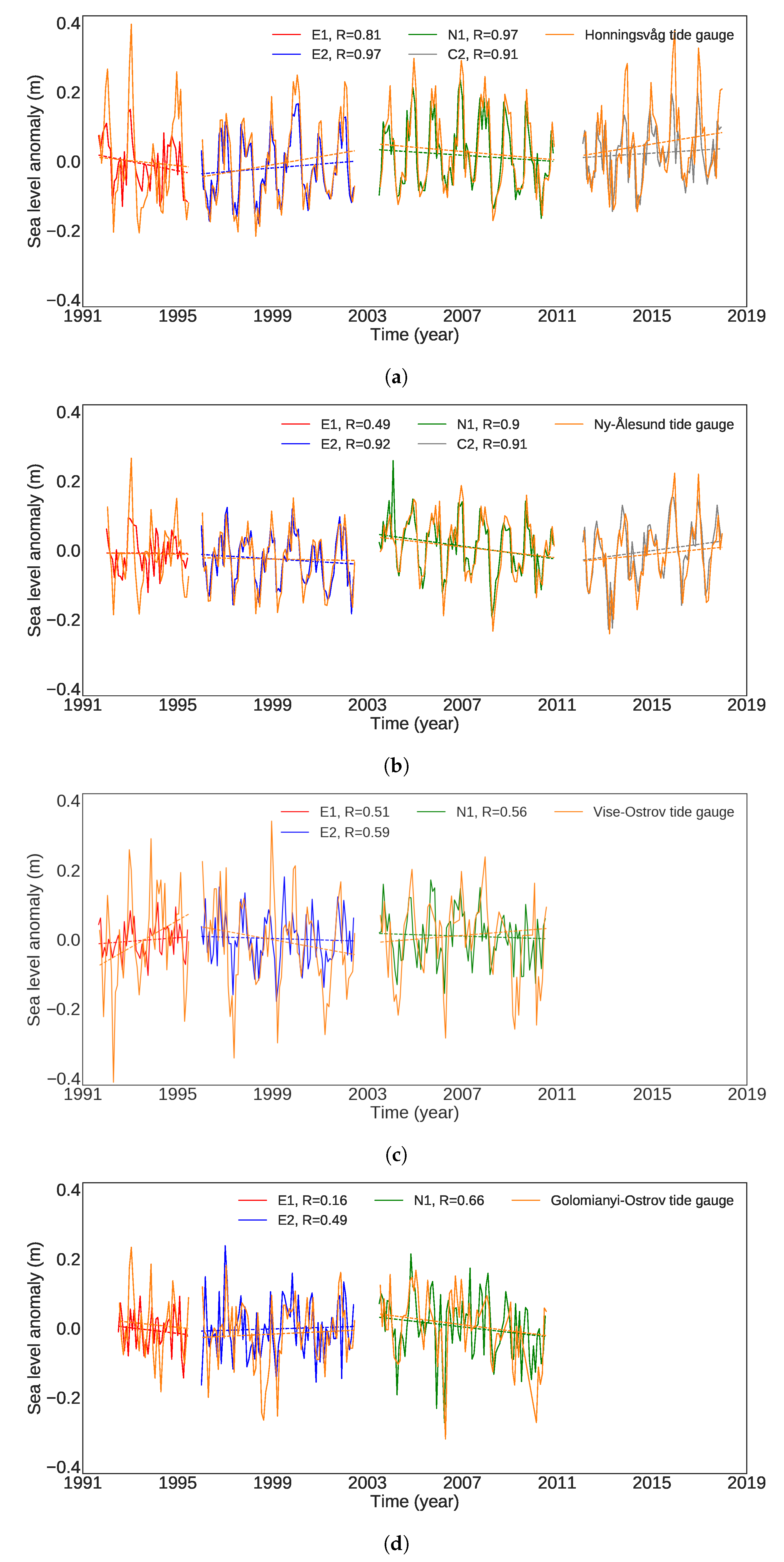
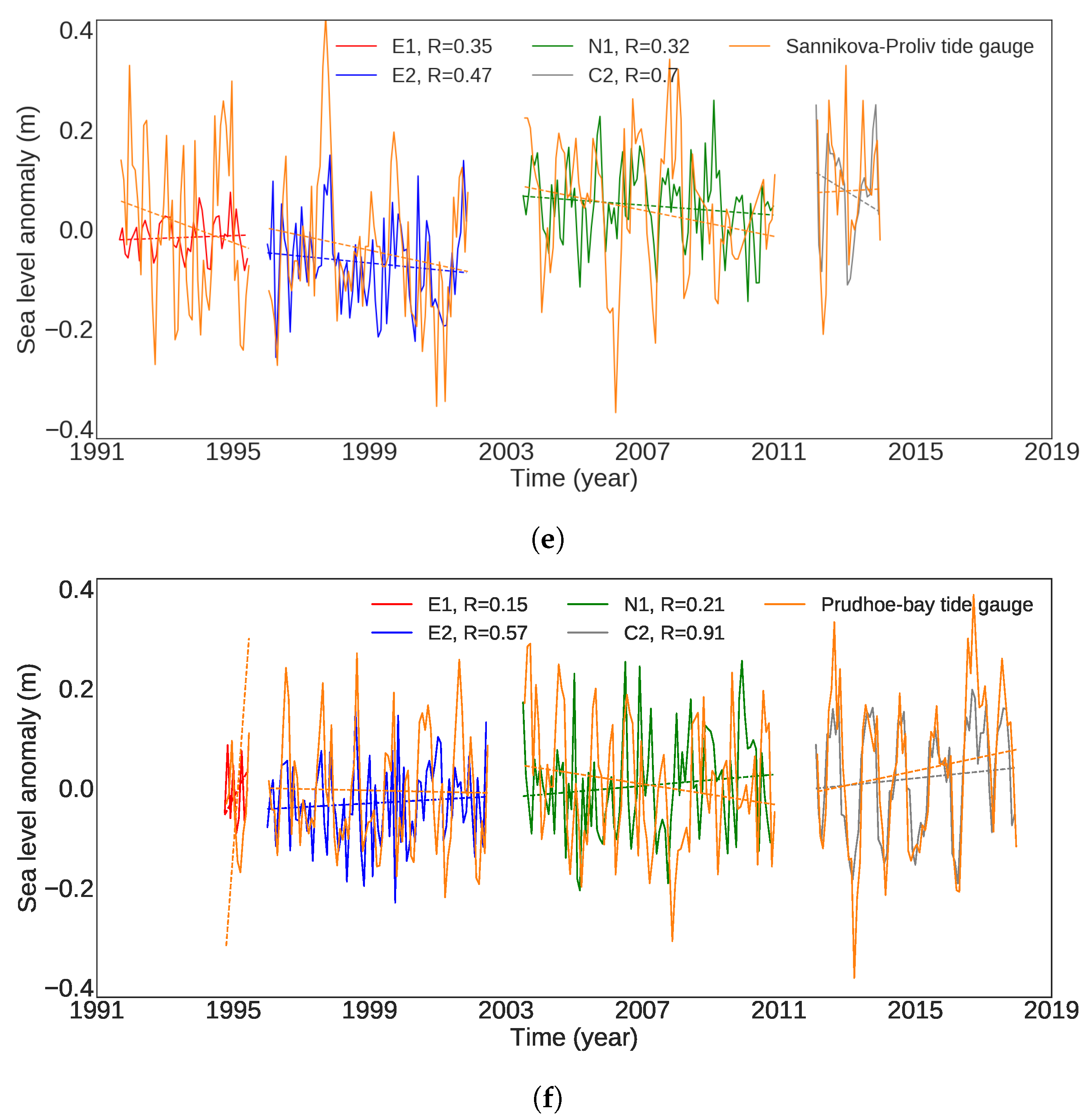
4.5. Validation
5. Discussion
5.1. The SLA Record
5.2. Error Analysis Evaluation
5.3. Regional and Seasonal Variability
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ALES | Adaptive Leading Edge Subwaveform |
| AO | Arctic Oscillation |
| DAC | Dynamic Atmosphere Correction |
| DTU | Technical University of Denmark |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| ESA | European Space Agency |
| ERS | European Remote Senesing satellite |
| GIA | Glacial Isostatic Ajustment |
| IBE | Inverse Barometer Effect |
| IPCC | Intergovernmental Panel on Climate Change |
| LRM | Low Resolution Mode |
| MAD | MediAn Deviation |
| MSS | Mean Sea Surface |
| PP | Pulse Peakiness |
| PSMSL | Permanent Service for Mean Sea Level |
| RADS | Radar Altimetry Database System |
| REAPER | Reprocessing of Altimeter Product for ERS |
| SSH | Sea Surface Height |
| SAR | Synthetic Aperture Radar |
| SARIn | SAR Interferometry |
| SGDR | Sensor Geophysical Data |
| SLA | Sea Level Anomaly |
| SLBC_CCI | Sea Level Budget Closure Climate Change Initiative |
| SL_CCI | Sea Level Climate Change Initiative |
| TUM | Technical University of Munich |
Appendix A. Satellite Specific Processing Details
Appendix A.1. ERS-1
Appendix A.2. ERS-2
Appendix A.3. Envisat
Appendix A.4. CryoSat-2
Appendix B. The Ice Concentration Grid
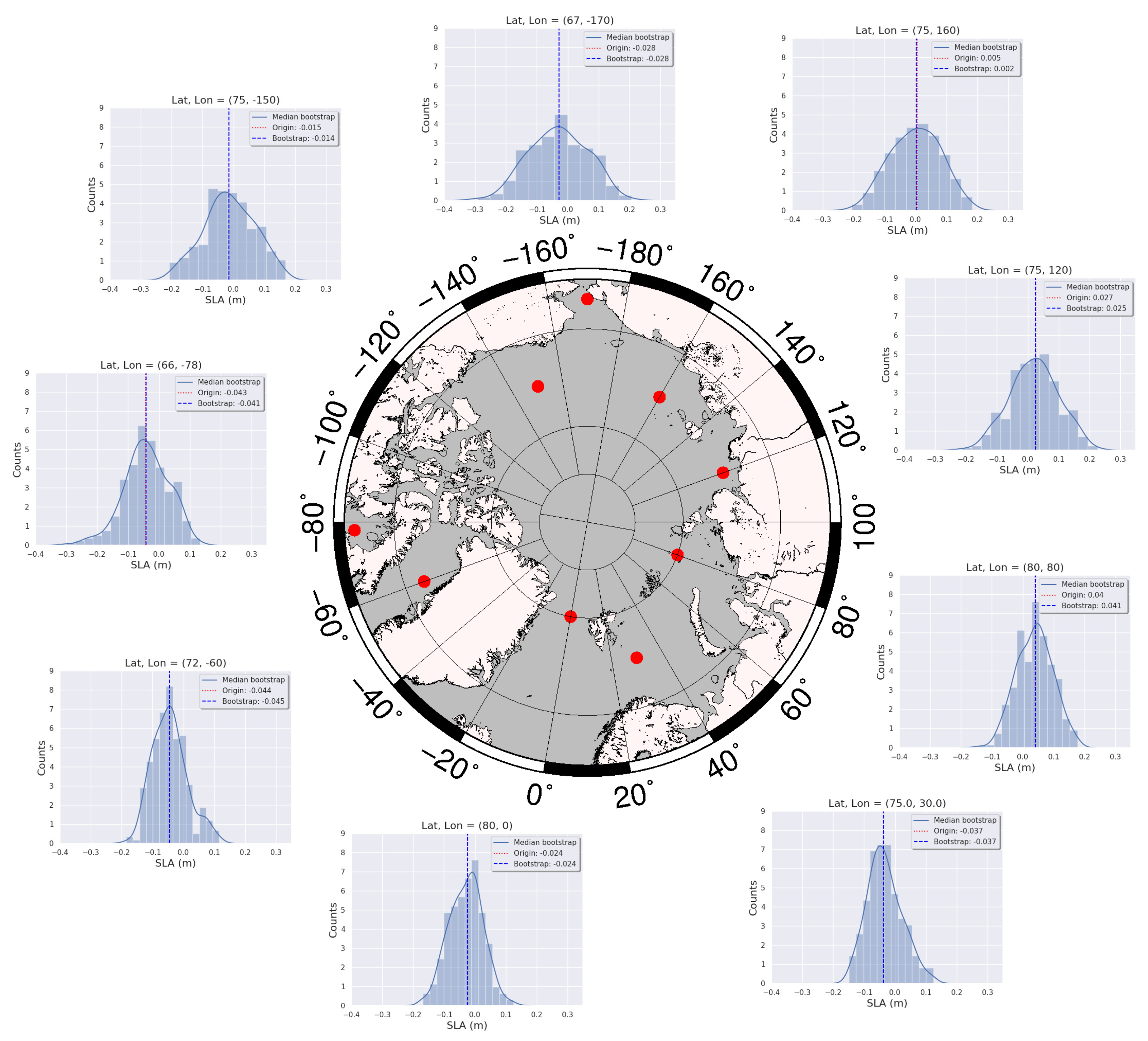
Appendix C. SLA Distributions and Uncertainty Estimates
Appendix D. Tide Gauge Comparison
References
- Serreze, M.C.; Stroeve, J.C. Arctic sea ice trends, variability and implications for seasonal ice forecasting. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140159. [Google Scholar] [CrossRef] [PubMed]
- Church, J.; Clark, P.; Cazenave, A.; Gregory, J.; Jevrejeva, S.; Levermann, A.; Merrifield, M.; Milne, G.; Nerem, R.; Nunn, P.; et al. Sea level change. In Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; PM Cambridge University Press: Cambridge, UK, 2013; pp. 1137–1216. [Google Scholar] [CrossRef]
- Wigley, T.M.L.; Raper, S.C.B. Thermal expansion of sea water associated with global warming. Nature 1987, 330, 127–131. [Google Scholar] [CrossRef]
- Cheng, L.; Abraham, J.; Hausfather, Z.; Trenberth, K.E. How fast are the oceans warming? Science 2019, 363, 128–129. [Google Scholar] [CrossRef] [PubMed]
- Lettenmaier, D.; Milly, P. Land waters and sea level. Nat. Geosci. 2009, 2, 452–454. [Google Scholar] [CrossRef]
- Rignot, E.; Velicogna, I.; Van Den Broeke, M.R.; Monaghan, A.; Lenaerts, J. Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise. Geophys. Res. Lett. 2011, 38, 1–5. [Google Scholar] [CrossRef]
- Moon, T.; Joughin, I.; Smith, B.; Howat, I. 21st-century evolution of Greenland outlet glacier velocities. Science 2012, 336, 576–578. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Dixon, T.H.; Myers, P.G.; Bonin, J.; Chambers, D.; van den Broeke, M.R. Recent increases in Arctic freshwater flux affects Labrador Sea convection and Atlantic overturning circulation. Nat. Commun. 2016, 7, 10525. [Google Scholar] [CrossRef]
- Ricker, R.; Hendricks, S.; Beckers, J.F. The impact of geophysical corrections on sea-ice freeboard retrieved from satellite altimetry. Remote Sens. 2016, 8, 317. [Google Scholar] [CrossRef]
- Fetterer, F.M.; Drinkwater, M.R.; Jezek, K.C.; Laxon, S.W.; Onstott, R.G. Sea ice altimetry. In Microwave Remote Sensing of Sea Ice; Carsey, F.D., Ed.; DTIC Document; American Geophysical Union: Washington, DC, USA, 1992. [Google Scholar]
- Connor, L.N.; Laxon, S.W.; Ridout, A.L.; Krabill, W.B.; McAdoo, D.C. Comparison of Envisat radar and airborne laser altimeter measurements over Arctic sea ice. Remote Sens. Environ. 2009, 113, 563–570. [Google Scholar] [CrossRef]
- Chelton, D.B.; McCabe, P.J. A review of satellite altimeter measurement of sea surface wind speed: With a proposed new algorithm. J. Geophys. Res. 1985, 90, 4707. [Google Scholar] [CrossRef]
- Armitage, T.; Davidson, M. Using the Interferometric Capabilities of the ESA CryoSat-2 Mission to Improve the Accuracy of Sea Ice Freeboard Retrievals. IEEE Trans. Geosci. Remote Sens. 2013, 52, 529–536. [Google Scholar] [CrossRef]
- Stammer, D.; Ray, R.D.; Andersen, O.B.; Arbic, B.K.; Bosch, W.; Carrère, L.; Cheng, Y.; Chinn, D.S.; Dushaw, B.D.; Egbert, G.D.; et al. Reviews of Geophysics Accuracy assessment of global barotropic ocean tide models. Rev. Geophys. 2014, 52, 243–282. [Google Scholar] [CrossRef]
- Scharroo, R.; Visser, P. Precise orbit determination and gravity field improvement for the ERS satellites. J. Geophys. Res. Oceans 1998, 103, 8113–8127. [Google Scholar] [CrossRef]
- Perovich, D.K.; Tucker, W.B.; Eicken, H.; Tucker, W.B.; Perovich, D.K. Indirect measurements of the mass balance of summer Arctic sea ice with an electromagnetic induction technique. Ann. Glaciol. 2001, 33, 194–200. [Google Scholar]
- Henry, O.; Prandi, P.; Llovel, W.; Cazenave, A.; Jevrejeva, S.; Stammer, D.; Meyssignac, B.; Koldunov, N. Tide gauge-based sea level variations since 1950 along the Norwegian and Russian coasts of the Arctic Ocean: Contribution of the steric and mass components. J. Geophys. Res. Oceans 2012, 117, 1–23. [Google Scholar] [CrossRef]
- Rose, S.; Skourup, H.; Forsberg, R. Arctic tides from GPS on sea-ice. J. Geodyn. 2013, 63. [Google Scholar] [CrossRef]
- Cazenave, A.; Lombard, A.; Llovel, W. Present-day sea level rise: A synthesis. C. R. Geosci. 2008, 340, 761–770. [Google Scholar] [CrossRef]
- Laxon, S.; Peacock, N.; Smith, D. High interannual variability of sea ice thickness in the Arctic region. Nature 2003, 425, 947–950. [Google Scholar] [CrossRef] [PubMed]
- Laxon, S.W.; MacAdoo, D. Arctic ocean gravity field derived from ERS-1 Satellite Altimetry. Science 1994, 265, 621–624. [Google Scholar] [CrossRef]
- Peacock, N.R.; Laxon, S.W. Sea surface height determination in the Arctic Ocean from ERS altimetry. J. Geophys. Res. 2004, 109, C07001. [Google Scholar] [CrossRef]
- Prandi, P.; Ablain, M.; Cazenave, A.; Picot, N. A New Estimation of Mean Sea Level in the Arctic Ocean from Satellite Altimetry. Mar. Geod. 2012, 35, 61–81. [Google Scholar] [CrossRef]
- Cheng, Y.; Andersen, O.B.; Knudsen, P. An Improved 20-Year Arctic Ocean Altimetric Sea Level Data Record. Mar. Geod. 2015, 38, 146–162. [Google Scholar] [CrossRef]
- Armitage, T.W.K.; Bacon, S.; Ridout, A.L.; Thomas, S.F.; Aksenov, Y.; Wingham, D.J. Arctic sea surface height variability and change from satellite radar altimetry and GRACE, 2003–2014. J. Geophys. Res. Oceans 2016, 121, 4303–4322. [Google Scholar] [CrossRef]
- Andersen, O.B.; Piccioni, G. Recent Arctic Sea Level Variations from Satellites. Front. Mar. Sci. 2016, 3, 76. [Google Scholar] [CrossRef]
- Schaeffer, P.; Faugére, Y.; Legeais, J.F.; Ollivier, A.; Guinle, T.; Picot, N. The CNES_CLS11 Global Mean Sea Surface Computed from 16 Years of Satellite Altimeter Data. Mar. Geod. 2012, 35, 3–19. [Google Scholar] [CrossRef]
- Andersen, O.B.; Knudsen, P. DNSC08 mean sea surface and mean dynamic topography models. J. Geophys. Res. Oceans 2009, 114, 1–12. [Google Scholar] [CrossRef]
- EUMETSAT. EUMETSAT Ocean and Sea Ice Satelitte Application Facility. Global Sea Ice Concentration Continuous Reprocessing Online Product; Norwegian and Danish Meteorological: Darmstadt, Germany, 2018. [Google Scholar]
- EUMETSAT. EUMETSAT Ocean and Sea Ice Satellite Application Facility. Global Sea Ice Concentration Climate Data Record 1979–2015 (v2.0, 2017); Norwegian and Danish Meteorological Institutes: Darmstadt, Germany, 2017. [Google Scholar]
- Holgate, S.J.; Matthews, A.; Woodworth, P.L.; Rickards, L.J.; Tamisiea, M.E.; Bradshaw, E.; Foden, P.R.; Gordon, K.M.; Jevrejeva, S.; Pugh, J. New Data Systems and Products at the Permanent Service for Mean Sea Level. J. Coast. Res. 2013, 288, 493–504. [Google Scholar] [CrossRef]
- PSML. Permanent Service for Mean Sea Level, Tide Gauge Data. Available online: http://www.psmsl.org/data/obtain (accessed on 20 December 2018).
- European Space Agency (ESA); University College London (UCL). CryoSat Product Handbook; Technical Report; ESRIN-ESA and Mullard Space Science Laboratory—University College London: London, UK, 2013. [Google Scholar]
- Gilbert, L.; Baker, S.; Dolding, C.; Vernier, A.; Brockley, D.; Martinez, B.; Gaudelli, J. REAPER Product Handbook for ERS Altimetry Reprocessed Products. Available online: https://earth.esa.int/web/guest/document-library/browse-document-library/-/article/reaper-product-handbook-for-ers-altimetry-reprocessed-products (accessed on 20 December 2018).
- Passaro, M.; Rose, S.; Andersen, O.; Boergens, E.; Calafat, F.; Dettmering, D.; Benveniste, J. ALES+: Adapting a homogenous ocean retracker for satellite altimetry to sea ice leads, coastal and inland waters. Remote Sens. Environ. 2018, 211, 456–471. [Google Scholar] [CrossRef]
- European Space Agency (ESA). ENVISAT RA2/MWR Product Handbook; European Space Agency: Paris, France, 2007. [Google Scholar]
- Stenseng, L.; Andersen, O.B. Preliminary gravity recovery from CryoSat-2 data in the Baffin Bay. Adv. Space Res. 2012, 50, 1158–1163. [Google Scholar] [CrossRef]
- Scharroo, R.; Leuliette, E.; Lillibridge, J.; Byrne, D.; Naeije, M.; Mitchum, G. RADS: Consistent multi-mission products. In Proceedings of the Symposium on 20 Years of Progress in Radar Altimetry (ESA SP-710), Venice, Italy, 24–29 September 2012; pp. 5–8. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Scharroo, R.; Smith, W. A GPS-based climatology for the total electron content in the ionosphere. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Jee, G.; Lee, H.B.; Kim, Y.H.; Chung, J.K.; Cho, J. Assessment of GPS global ionosphere maps (GIM) by comparison between CODE GIM and TOPEX/Jason TEC data: Ionospheric perspective. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Llewellyn, T.S.; Bent, R.B. Documentation and Description of the Bent Ionospheric Model; Atlantic Science Corp Indian Harbour Beach: Brevard, FL, USA, 1973. [Google Scholar]
- Carrere, L.; Faugère, Y.; Ablain, M. Major improvement of altimetry sea level estimations using pressure-derived corrections based on ERA-Interim atmospheric reanalysis. Ocean Sci. 2016, 12, 825–842. [Google Scholar] [CrossRef]
- Carrère, L.; Lyard, F. Modeling the barotropic response of the global ocean to atmospheric wind and pressure forcing Comparisons with observations. Geophy. Res. Lett. 2003, 30, 4. [Google Scholar] [CrossRef]
- Carrere, L.; Lyard, F.; Cancet, M.; Guillot, A. FES 2014, a new tidal model on the global ocean with enhanced accuracy in shallow seas and in the Arctic region. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 12–17 April 2015; Volume 17, p. 5481. [Google Scholar]
- Cartwright, D.E.; Edden, A.C. Corrected tables of tidal harmonics. Geophys. J. Int. 1973, 33, 253–264. [Google Scholar] [CrossRef]
- Wahr, J.M. Deformation induced by polar motion. J. Geophys. Res. 1985, 90, 9363–9368. [Google Scholar] [CrossRef]
- Passaro, M.; Nadzir, Z.A.; Quartly, G.D. Improving the precision of sea level data from satellite altimetry with high-frequency and regional sea state bias corrections. Remote Sens. Environ. 2018, 218, 245–254. [Google Scholar] [CrossRef]
- Andersen, O.B.; Stenseng, L.; Piccioni, G.; Knudsen, P. The DTU15 MSS (Mean Sea Surface) and DTU15LAT (Lowest Astronomical Tide) reference surface. In Proceedings of the ESA Living Planet Symposium 2016 (SP-740), Prague, Czech Republik, 9–13 May 2016. [Google Scholar]
- Fernandes, M.J.; Lázaro, C.; Ablain, M.; Pires, N. Improved wet path delays for all ESA and reference altimetric missions. Remote Sens. Environ. 2015, 169, 50–74. [Google Scholar] [CrossRef]
- Laxon, S.; Rapley, C. Radar altimeter data quality flagging. Adv. Space Res. 1987, 7, 315–318. [Google Scholar] [CrossRef]
- Ricker, R.; Hendricks, S.; Helm, V.; Skourup, H.; Davidson, M. Sensitivity of CryoSat-2 Arctic sea-ice freeboard and thickness on radar-waveform interpretation. Cryosphere 2014, 8, 1607–1622. [Google Scholar] [CrossRef]
- Knudsen, P.; Andersen, O.B.; Tscherning, C.C. Altimetric gravity anomalies in the Norwegian-Greenland Sea-Preliminary results from the ERS-1 35 days repeat mission. Geophys. Res. Lett. 1992, 19, 1795–1798. [Google Scholar] [CrossRef]
- Laxon, S. Sea ice extent mapping using the ERS-1 radar altimeter. EARSeL Adv. Remote Sens. 1994, 3, 112–116. [Google Scholar]
- Andersen, O.B. Shallow water tides in the northwest European shelf region from TOPEX/POSEIDON altimetry. J. Geophys. Res. 1999, 104, 7729–7741. [Google Scholar] [CrossRef]
- Ablain, M.; Cazenave, A.; Valladeau, G.; Guinehut, S. A new assessment of the error budget of global Mean Sea Level rate estimated by satellite altimetry over 1993–2008. Ocean Sci. 2009, 5, 193–201. [Google Scholar] [CrossRef]
- Lahiri, S. Resampling Methods for Dependent Data; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; p. 374. [Google Scholar]
- Caron, L.; Ivins, E.R.; Larour, E.; Adhikari, S.; Nilsson, J.; Blewitt, G. GIA Model Statistics fro GRACE Hydrology, Cryosphere, and Ocen Science. Geophy. Res. Lett. 2018, 45, 2203–2212. [Google Scholar] [CrossRef]
- Barletta, V.R.; Sabadini, R.; Bordoni, A. Isolating the PGR signal in the GRACE data: Impact on mass balance estimates in Antarctica and Greenland. Geophys. J. Int. 2008, 172, 18–30. [Google Scholar] [CrossRef]
- Barletta, V.R.; Sørensen, L.S.; Forsberg, R. Scatter of mass changes estimates at basin scale for Greenland and Antarctica. Cryosphere 2013, 7, 1411–1432. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Gravelle, M.; Collilieux, X.; Guichard, M.; Míguez, B.M.; Tiphaneau, P.; Wöppelmann, G. Mitigating the effects of vertical land motion in tide gauge records using a state-of-the-art GPS velocity field. Glob. Planet. Chang. 2012, 98–99, 6–17. [Google Scholar] [CrossRef]
- Sato, T.; Okuno, J.; Hinderer, J.; MacMillan, D.S.; Plag, H.P.; Francis, O.; Falk, R.; Fukuda, Y. A geophysical interpretation of the secular displacement and gravity rates observed at Ny-Ålesund, Svalbard in the Arctic—Effects of post-glacial rebound and present-day ice melting. Geophys. J. Int. 2006, 165, 729–743. [Google Scholar] [CrossRef]
- Lee, S.; Im, J.; Kim, J.; Kim, M.; Shin, M.; Cheol Kim, H.; Quackenbush, L.J. Arctic Sea Ice Thickness Estimation from CryoSat-2 Satellite Data Using Machine Learning-Based Lead Detection. Remote Sens. 2016, 8, 698. [Google Scholar] [CrossRef]
- Paul, S.; Hendricks, S.; Ricker, R.; Kern, S.; Rinne, E. Empirical parametrization of envisat freeboard retrieval of arctic and antarctic sea ice based on CryoSat-2: Progress in the ESA climate change initiative. Cryosphere 2018, 12, 2437–2460. [Google Scholar] [CrossRef]
- Poisson, J.C.; Quartly, G.D.; Kurekin, A.A.; Thibaut, P.; Hoang, D.; Nencioli, F. Development of an ENVISAT altimetry processor providing sea level continuity between open ocean and arctic leads. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5299–5319. [Google Scholar] [CrossRef]
- Maslanik, J.; Stroeve, J.; Fowler, C.; Emery, W. Distribution and trends in Arctic sea ice age through spring 2011. Geophys. Res. Lett. 2011, 38, 2–7. [Google Scholar] [CrossRef]
- Velicogna, I.; Wahr, J. Acceleration of Greenland ice mass loss in spring 2004. Nature 2006, 443, 329–331. [Google Scholar] [CrossRef] [PubMed]
- Volkov, D.L.; Landerer, F.W.; Kirillov, S.A. The genesis of sea level variability in the Barents Sea. Cont. Shelf Res. 2013, 66, 92–104. [Google Scholar] [CrossRef]
- Proshutinsky, A.; Ashik, I.M.; Dvorkin, E.N.; Häkkinen, S.; Krishfield, R.A.; Peltier, W.R. Secular sea level change in the Russian sector of the Arctic Ocean. J. Geophys. Res. Oceans 2004, 109, 1–19. [Google Scholar] [CrossRef]
- Proshutinsky, A.; Krishfield, R.; Timmermans, M.L.; Toole, J.; Carmack, E.; McLaughlin, F.; Williams, W.J.; Zimmermann, S.; Itoh, M.; Shimada, K. Beaufort Gyre freshwater reservoir: State and variability from observations. J. Geophys. Res. 2009, 114, 1–25. [Google Scholar] [CrossRef]
- Giles, K.A.; Laxon, S.W.; Ridout, A.L.; Wingham, D.J.; Bacon, S. Western Arctic Ocean freshwater storage increased by wind-driven spin-up of the Beaufort Gyre. Nat. Geosci. 2012, 5, 194–197. [Google Scholar] [CrossRef]
- Carret, A.; Johannessen, J.A.; Andersen, O.B.; Ablain, M.; Prandi, P.; Blazquez, A.; Cazenave, A. Arctic Sea Level During the Satellite Altimetry Era. Surv. Geophys. 2017, 38, 251–275. [Google Scholar] [CrossRef]
- European Space Agency (ESA). ESA Earth Observation Missions; ESA: Paris, France, 2018. [Google Scholar]
- Knudsen, P.; Brovelli, M. Collinear and cross-over adjustment of Geosat ERM and Seasat altimeter data in the Mediterranean Sea. Surv. Geophys. 1993, 14, 449–459. [Google Scholar] [CrossRef]
- Passaro, M.; Cipollini, P.; Vignudelli, S.; Quartly, G.D.; Snaith, H.M. ALES: A multi-mission adaptive subwaveform retracker for coastal and open ocean altimetry. Remote Sens. Environ. 2014, 145, 173–189. [Google Scholar] [CrossRef]

| ERS-1 | ERS-2 | Envisat | CryoSat-2 [33] | |
|---|---|---|---|---|
| Data origin | REAPER L2 [34] | ALES+ [34,35] | ALES+ [35,36] | LARS/RADS [33,37,38] |
| Wet troposphere | ECMWF [39] | ECMWF [39] | ECMWF [39] | ECMWF [39] |
| Dry troposphere | Radiometer/ECMWF [39] | Radiometer/ECMWF [39] | ECMWF [39] | ECMWF [39] |
| Ionosphere | NICO [40]/GIM [41] | NICO [40]/GIM [41] | Doris [36] | GIM [41]/Bent [42] |
| DAC | ERA-Interim [43] | ERA-Interim [43] | ERA-Interim [43] | DAC-ECMWF [44] |
| O, L, LP tides | FES2014 [45] | FES2014 [45] | FES2014 [45] | FES2014 [45] |
| LP otide + setide | Cartwright [46] | Cartwright [46] | Cartwright [46] | Cartwright [46] |
| Pole tide | Wahr [47] | Wahr [47] | Wahr [47] | Wahr [47] |
| Sea state bias | Altimetrics [34] | ALES+ [48] | ALES+ [48] | None/RADS [38] |
| Mean sea surface | DTU18 [49] | DTU18 [49] | DTU18 [49] | DTU18 [49] |
| Lead | Ocean | ||||
|---|---|---|---|---|---|
| PP > | St. Std | Width < | PP < | σ0 < | |
| ERS-1 | 0.60 (19) | - | 3 | 0.048 (1.5) | 15 |
| ERS-2 | 0.65 (20.5) | - | 3 | 0.048 (1.5) | 15 |
| Envisat | 0.71 (22.5) | - | 3 | 0.048 (1.5) | 15 |
| CryoSat-2 | 0.35/0.25 (11/7.9) | 4 | 0.9 | - | - |
| SLA Trend (No GIA) | 95% Conf. Level (No GIA) | SLA (GIA) | 95% Conf. Level (GIA) | |
|---|---|---|---|---|
| mm/year | mm/year | mm/year | mm/year | |
| Sector I | 3.04 | 2.96–3.23 | 3.19 | 3.10–3.37 |
| Sector II | 0.33 | −0.58–1.28 | 0.04 | −0.86–1.00 |
| Sector III | 4.06 | 2.41–4.71 | 5.77 | 4.12–6.42 |
| Sector IV | 0.49 | −0.72–1.15 | −0.63 | −1.84–0.03 |
| Tide Gauge | Vert. Disp. | GIA |
|---|---|---|
| mm/year | mm/year | |
| Ny Ålesund | 7.98 ± 0.49 1 | 0.47 ± 0.67 |
| Honningsvåg | 1.9 ± 0.3 2 | 1.344 ± 0.42 |
| Prudhoe bay | - | −1.51 ± 0.095 |
| Vise Ostrov | - | 1.96 ± 0.38 |
| Golomianyi Ostrov | - | 1.99 ± 0.33 |
| Sannikova Proliv | - | −0.48 ± 0.21 |
| Tide Gauges | No. of Month | RMSE (R) | ||||||
|---|---|---|---|---|---|---|---|---|
| E1 | E2 | N1 | C2 | Pre GIA | 1996– | Total | ||
| Ny Ålesund | 312 | 0.080 (0.49) | 0.031 (0.92) | 0.034 (0.90) | 0.038 (0.91) | 0.072 (0.70) | 0.042 (0.88) | 0.050 (0.81) |
| Honningsvåg | 316 | 0.089 (0.81) | 0.037 (0.97) | 0.032 (0.97) | 0.060 (0.91) | 0.057 (0.91) | 0.047 (0.94) | 0.055 (0.92) |
| Prudhoe bay | 273 | 0.11 (0.15) | 0.099 (0.57) | 0.15 (0.20) | 0.072 (0.91) | 0.12 (0.53) | 0.11 (0.57) | 0.12 (0.53) |
| Vise Ostrov | 221 | 0.12 (0.51) | 0.10 (0.59) | 0.097 (0.55) | - | 0.11 (0.52) | 0.098 (0.57) | 0.10 (0.53) |
| Golomianyi Ostrov | 202 | 0.099 (0.16 ) | 0.086 (0.49) | 0.077 (0.66) | - | 0.085 (0.53) | 0.081 (0.59) | 0.081 (0.53) |
| Sannikova Proliv | 244 | 0.16 (0.35) | 0.13 (0.47) | 0.13 (0.32) | 0.092 (0.70) | 0.14 (0.36) | 0.14 (0.37) | 0.14 (0.36) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rose, S.K.; Andersen, O.B.; Passaro, M.; Ludwigsen, C.A.; Schwatke, C. Arctic Ocean Sea Level Record from the Complete Radar Altimetry Era: 1991–2018. Remote Sens. 2019, 11, 1672. https://doi.org/10.3390/rs11141672
Rose SK, Andersen OB, Passaro M, Ludwigsen CA, Schwatke C. Arctic Ocean Sea Level Record from the Complete Radar Altimetry Era: 1991–2018. Remote Sensing. 2019; 11(14):1672. https://doi.org/10.3390/rs11141672
Chicago/Turabian StyleRose, Stine Kildegaard, Ole Baltazar Andersen, Marcello Passaro, Carsten Ankjær Ludwigsen, and Christian Schwatke. 2019. "Arctic Ocean Sea Level Record from the Complete Radar Altimetry Era: 1991–2018" Remote Sensing 11, no. 14: 1672. https://doi.org/10.3390/rs11141672
APA StyleRose, S. K., Andersen, O. B., Passaro, M., Ludwigsen, C. A., & Schwatke, C. (2019). Arctic Ocean Sea Level Record from the Complete Radar Altimetry Era: 1991–2018. Remote Sensing, 11(14), 1672. https://doi.org/10.3390/rs11141672