Evaluating the Effectiveness of Using Vegetation Indices Based on Red-Edge Reflectance from Sentinel-2 to Estimate Gross Primary Productivity
Abstract
1. Introduction
2. Materials and Methods
2.1. Field Sites
2.2. Data
2.2.1. Tower-Based Carbon Flux Data
2.2.2. Sentinel-2 Remote-Sensing Products
2.2.3. MODIS GPP Product
2.3. Methods
2.3.1. Remote-Sensing-Based Indices
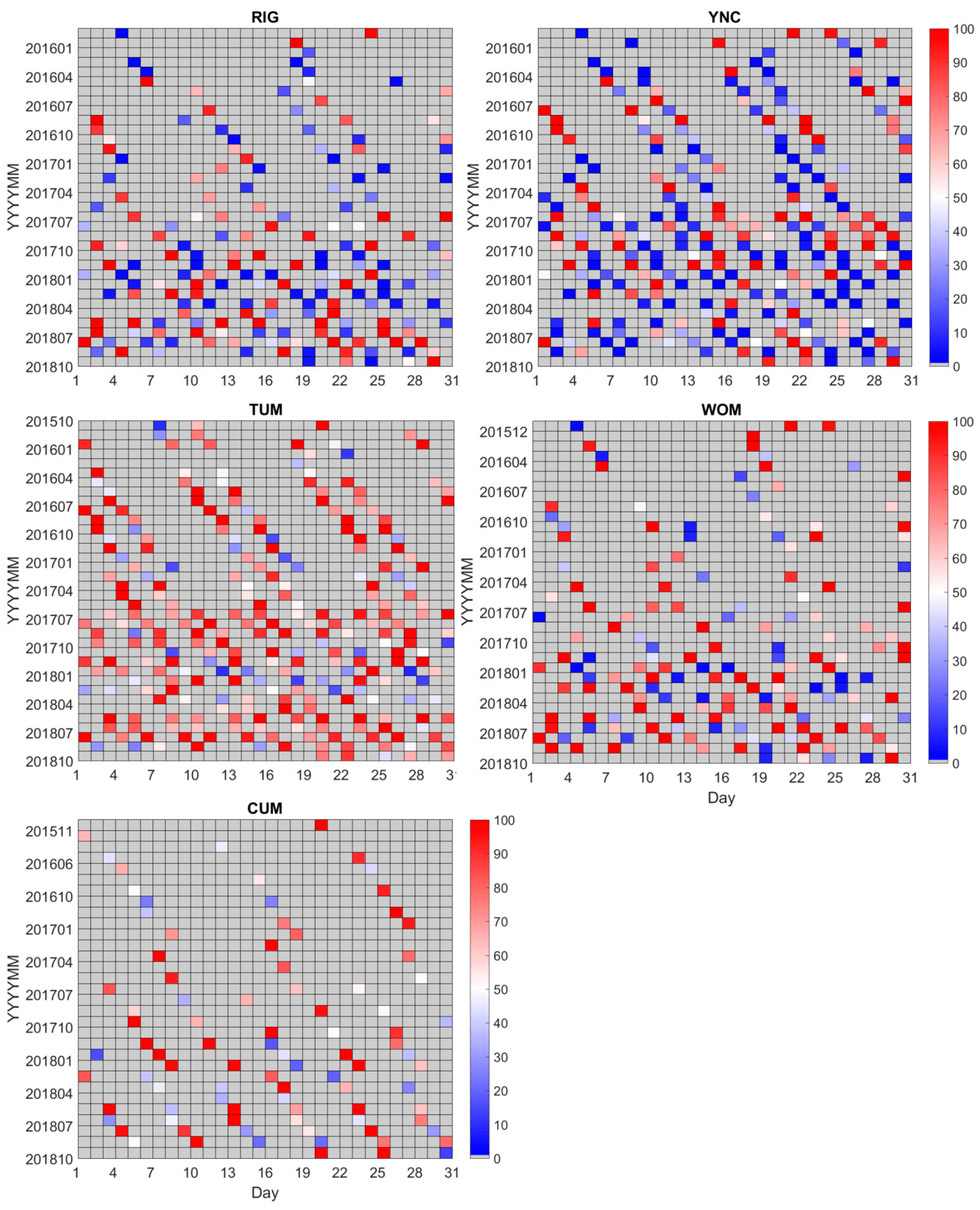
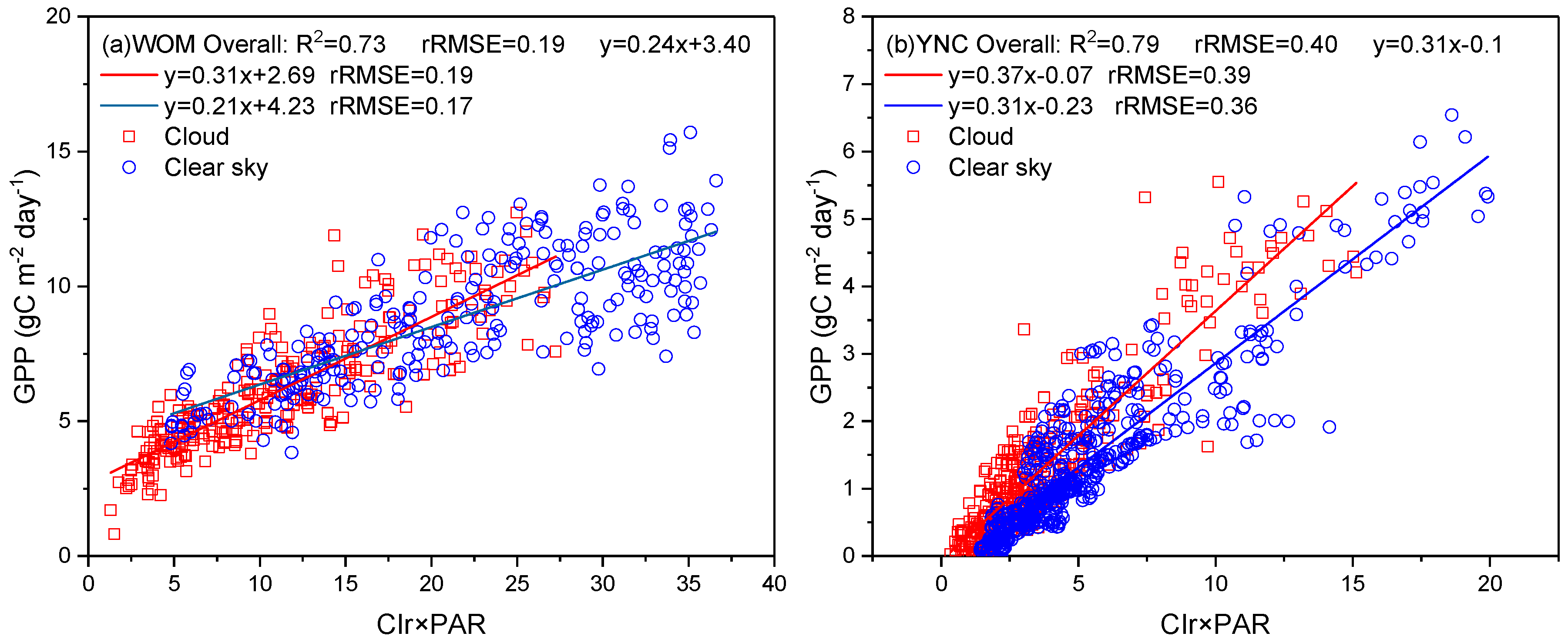
2.3.2. Evaluation of the Cloud Effect
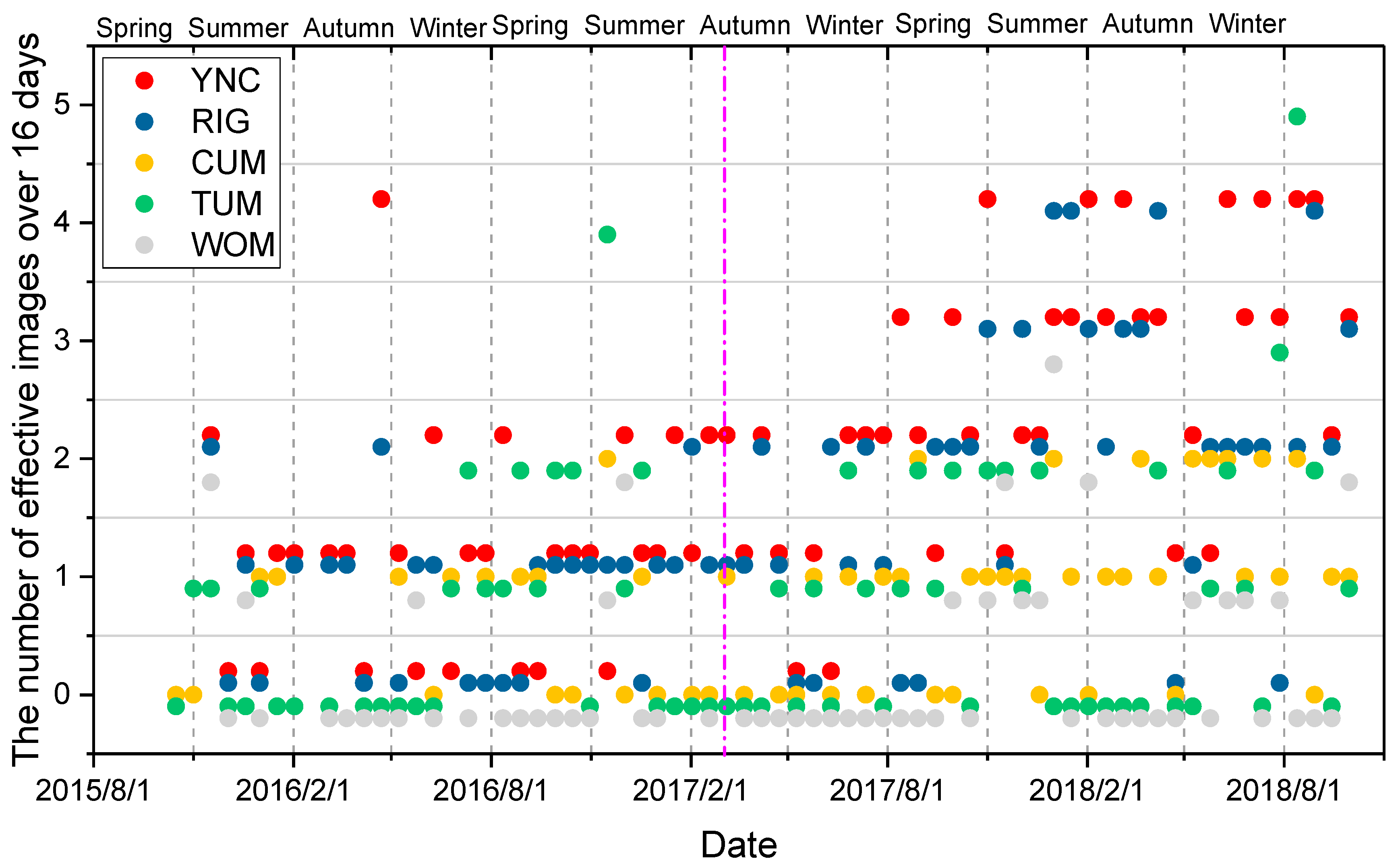
2.3.3. Rebuilding the Time Series of Vegetation Indices at the Sites
- (1)
- The reflectance was selected in each image from the Sentinel reflectance product in the 450 × 450-m spatial window.
- (2)
- The reflectance values were removed from the pixels where there were cloud and shadow masks.
- (3)
- The was calculated in the spatial window.
- (4)
- The VI was calculated from the reflectance in each pixel where there were no cloud and shadow masks.
- (5)
- The maximal VI was chosen with Pclear > 0.8 during the standard interval in each pixel (here, we defined it as a 16-day interval from the first day of the year) as the true VI value [80].
- (6)
- A continuous VI time series in each pixel was rebuilt by a Savitzky–Golay filter [81].
2.3.4. Estimating GPP by VI and Statistical Analysis
3. Results
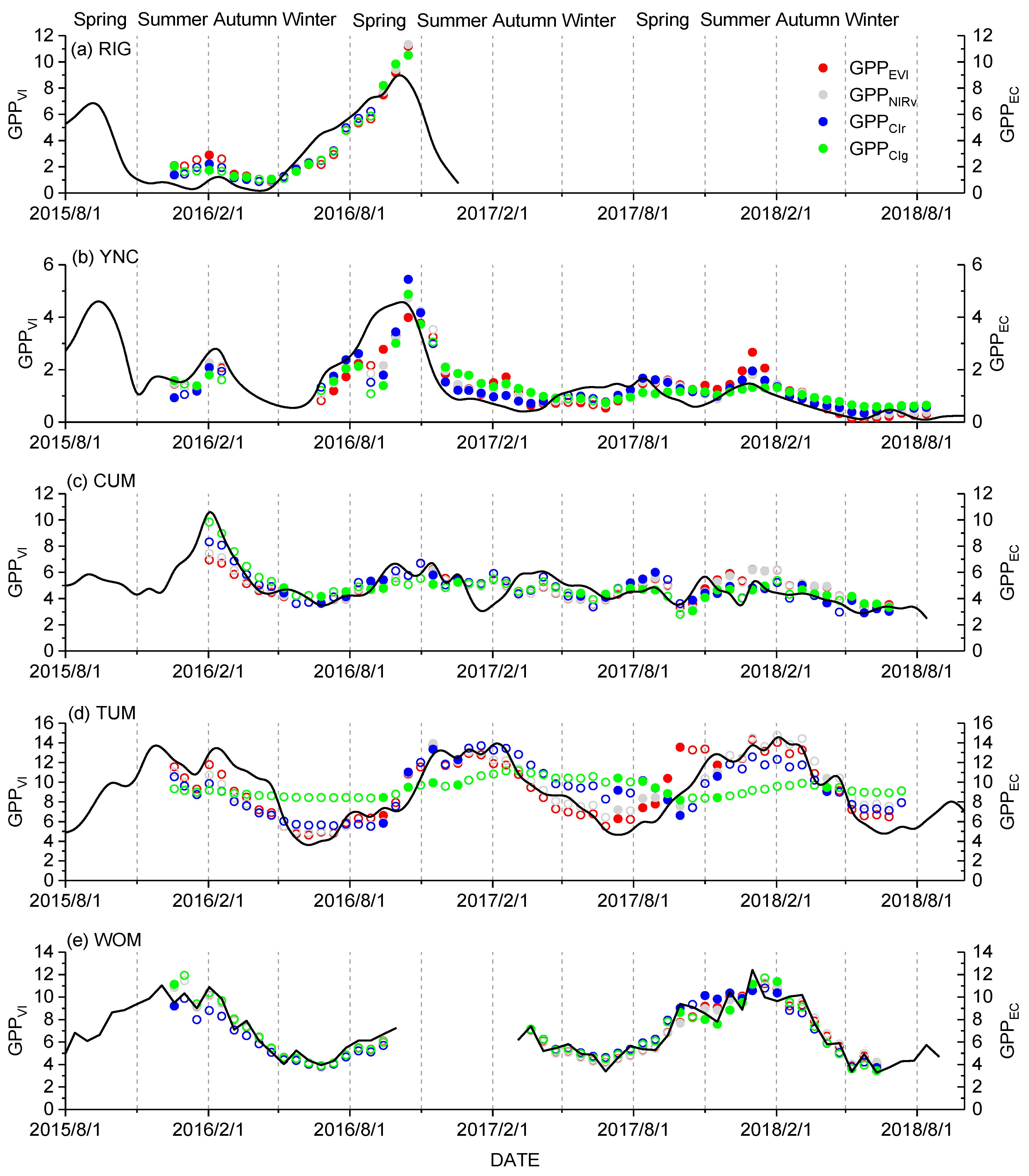
3.1. Temporal Relationship between GPPVI and GPPEC
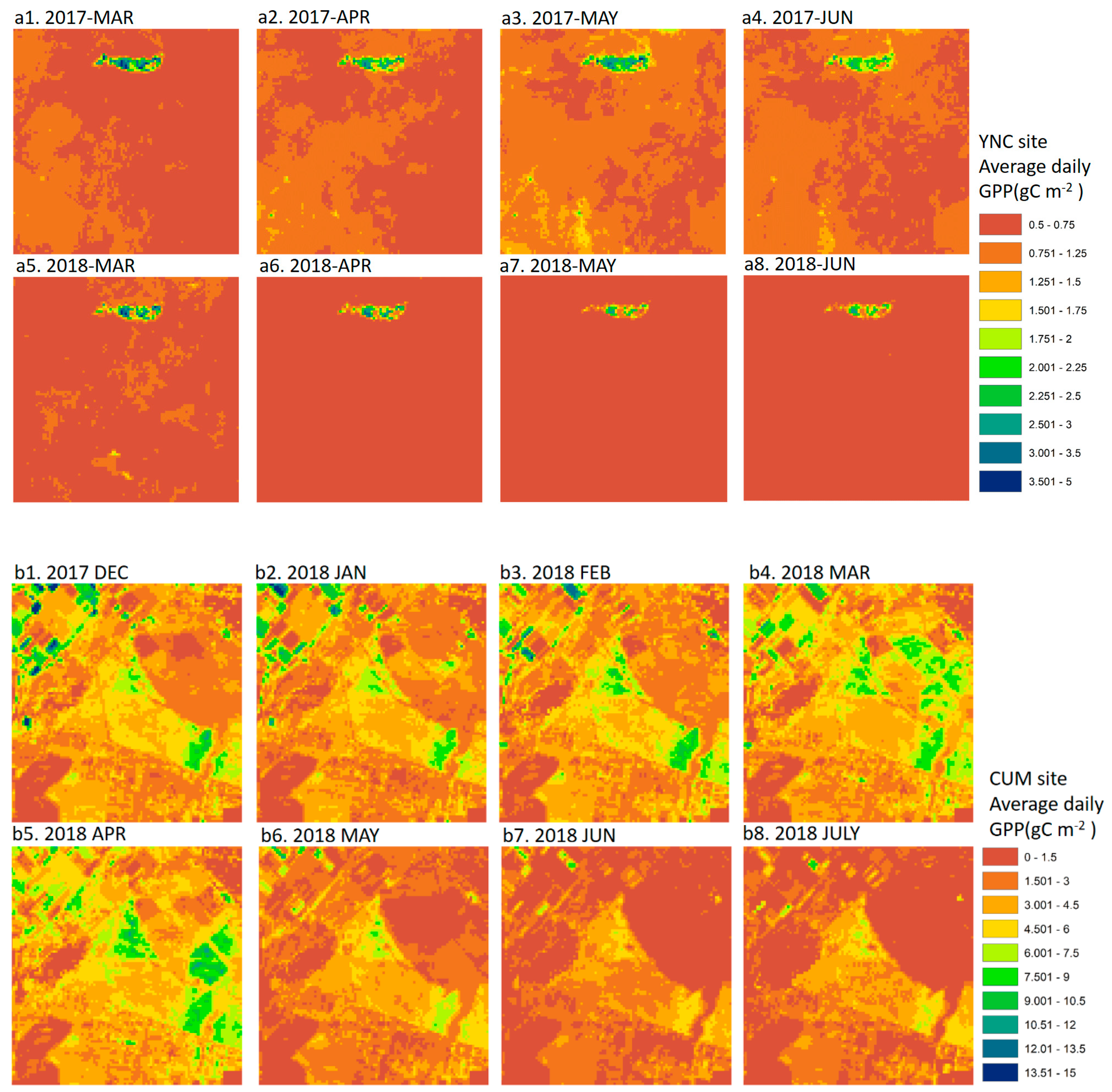
3.2. Spatial Distribution of GPPCIr
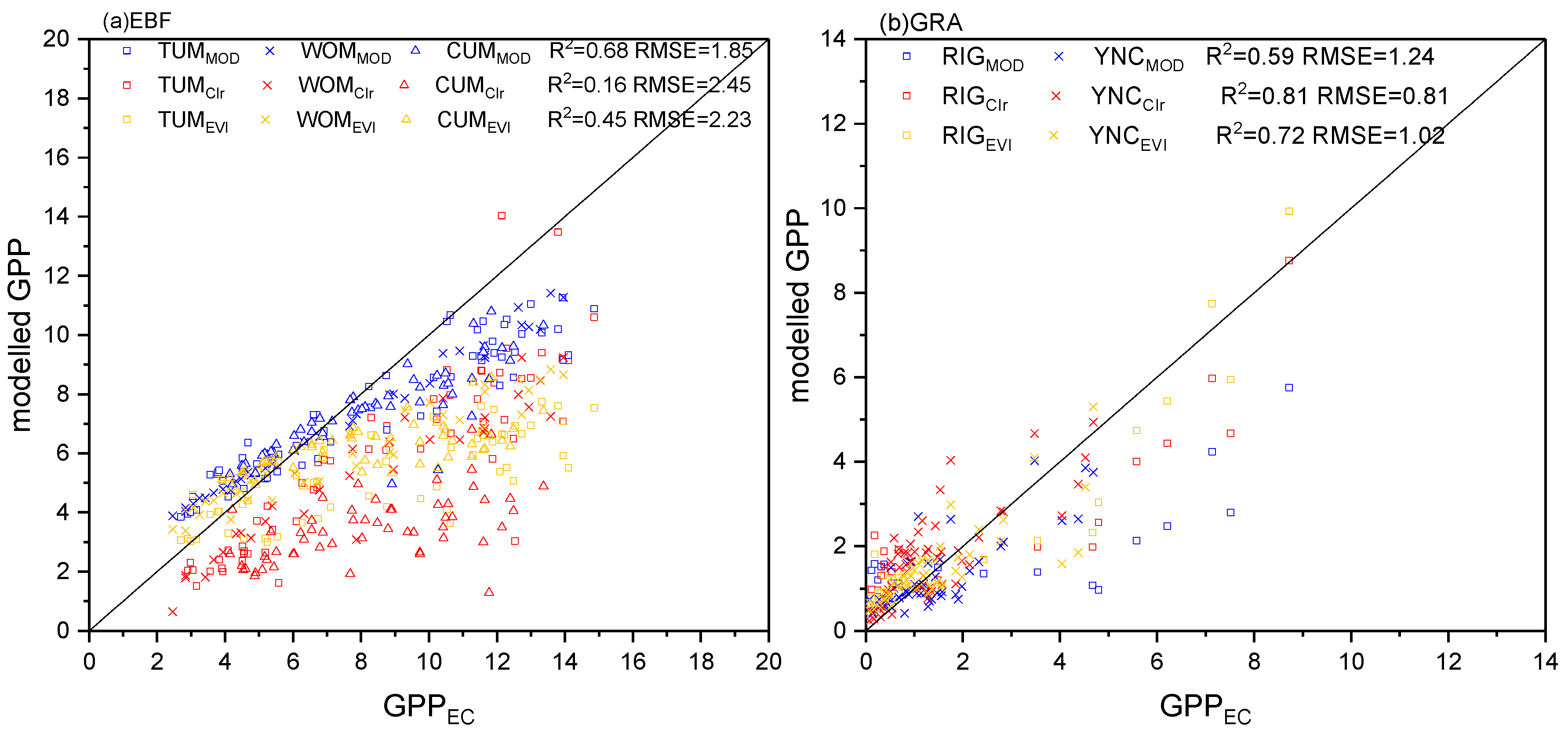
3.3. Comparison of GPP Modeling Results based on Sentinel-2 Data and MODIS Products
4. Discussion
4.1. Improvements to GPP Modeling with Vegetation Red-Edge Information
4.2. Advantages of Sentinel-2 High-Spatial-Resolution Data for GPP Modeling
4.3. Outlook for High-Spatial-Resolution Satellite GPP Mapping
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed]
- Running, S.; Mu, Q.; Zhao, M. Mod17a2h modis/terra gross primary productivity 8-day l4 global 500m sin grid v006. Available online: https://lpdaac.usgs.gov/products/mod17a2hv006/ (accessed on 29 May 2019).
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.S.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Jiang, C.; Ryu, Y. Multi-scale evaluation of global gross primary productivity and evapotranspiration products derived from breathing earth system simulator (bess). Remote Sens. Environ. 2016, 186, 528–547. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, Q.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Iii, B.M.; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, X.; Wu, X.; Zhou, S.; Zhang, G.; Qin, Y.; Dong, J. A global moderate resolution dataset of gross primary production of vegetation for 2000–2016. Sci. Data 2017, 4, 170165. [Google Scholar] [CrossRef] [PubMed]
- Yuan, W.; Liu, S.; Yu, G.; Bonnefond, J.; Chen, J.; Davis, K.J.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F. Global estimates of evapotranspiration and gross primary production based on modis and global meteorology data. Remote Sens. Environ. 2010, 114, 1416–1431. [Google Scholar] [CrossRef]
- Baldocchi, D. Breathing of the terrestrial biosphere: Lessons learned from a global network of carbon dioxide flux measurement systems. Aust. J. Bot. 2008, 56, 1–26. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, J.; Liu, S.; Rentch, J.S.; Sun, P.; Lu, C. Global gross primary productivity and water use efficiency changes under drought stress. Environ. Res. Lett. 2017, 12, 014016. [Google Scholar] [CrossRef]
- Huang, L.; He, B.; Han, L.; Liu, J.; Wang, H.; Chen, Z. A global examination of the response of ecosystem water-use efficiency to drought based on modis data. Sci. Total Environ. 2017, 601, 1097–1107. [Google Scholar] [CrossRef]
- Ahmadi, B.; Ahmadalipour, A.; Tootle, G.; Moradkhani, H. Remote sensing of water use efficiency and terrestrial drought recovery across the contiguous united states. Remote Sens. 2019, 11, 731. [Google Scholar] [CrossRef]
- Ryu, Y.; Berry, J.A.; Baldocchi, D.D. What is global photosynthesis? History, uncertainties and opportunities. Remote Sens. Environ. 2019, 223, 95–114. [Google Scholar] [CrossRef]
- Cai, W.; Yuan, W.; Liang, S.; Zhang, X.; Dong, W.; Xia, J.; Fu, Y.; Chen, Y.; Liu, D.; Zhang, Q. Improved estimations of gross primary production using satellite-derived photosynthetically active radiation. J. Geophys. Res. Biogeosci. 2014, 119, 110–123. [Google Scholar] [CrossRef]
- Chen, J.M. Canopy architecture and remote sensing of the fraction of photosynthetically active radiation absorbed by boreal conifer forests. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1353–1368. [Google Scholar] [CrossRef]
- Farquhar, G.D.; Von, C.S.; Berry, J.A. A biochemical model of photosynthetic CO2 assimilation in leaves of c 3 species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef] [PubMed]
- Ainsworth, E.A.; Long, S.P. What have we learned from 15 years of free-air CO2 enrichment (face)? A meta-analytic review of the responses of photosynthesis, canopy properties and plant production to rising CO2. New Phytol. 2005, 165, 351–372. [Google Scholar] [CrossRef] [PubMed]
- Yuan, W.; Liu, S.; Zhou, G.; Zhou, G.; Tieszen, L.L.; Baldocchi, D.D.; Bernhofer, C.; Gholz, H.L.; Goldstein, A.H.; Goulden, M.L. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef]
- Joiner, J.; Yoshida, Y.; Zhang, Y.; Duveiller, G.; Jung, M.; Lyapustin, A.; Wang, Y.; Tucker, C. Estimation of terrestrial global gross primary production (gpp) with satellite data-driven models and eddy covariance flux data. Remote Sens. 2018, 10, 1346. [Google Scholar] [CrossRef]
- Inoue, Y.; Peñuelas, J.; Miyata, A.; Mano, M. Normalized difference spectral indices for estimating photosynthetic efficiency and capacity at a canopy scale derived from hyperspectral and CO2 flux measurements in rice. Remote Sens. Environ. 2008, 112, 156–172. [Google Scholar] [CrossRef]
- Tucker, C.; Fung, I.; Keeling, C.; Gammon, R. Relationship between atmospheric CO2 variations and a satellite-derived vegetation index. Nature 1986, 319, 195. [Google Scholar] [CrossRef]
- Rahman, A.; Sims, D.; Cordova, V.; El-Masri, B. Potential of modis evi and surface temperature for directly estimating per-pixel ecosystem C fluxes. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Sims, D.A.; Rahman, A.F.; Cordova, V.D.; El-Masri, B.Z.; Baldocchi, D.D.; Flanagan, L.B.; Goldstein, A.H.; Hollinger, D.Y.; Misson, L.; Monson, R.K. On the use of modis evi to assess gross primary productivity of north american ecosystems. J. Geophys. Res. Biogeosci. 2006, 111. [Google Scholar] [CrossRef]
- Shi, H.; Li, L.; Eamus, D.; Huete, A.; Cleverly, J.; Tian, X.; Yu, Q.; Wang, S.; Montagnani, L.; Magliulo, V. Assessing the ability of modis evi to estimate terrestrial ecosystem gross primary production of multiple land cover types. Ecol. Indic. 2017, 72, 153–164. [Google Scholar] [CrossRef]
- Los, S.O.; Justice, C.; Tucker, C. A global 1 by 1 ndvi data set for climate studies derived from the gimms continental ndvi data. Int. J. Remote Sens. 1994, 15, 3493–3518. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, C.; Peng, D.; Wang, S.; Gonsamo, A.; Fang, B.; Yuan, W. Improved modeling of gross primary production from a better representation of photosynthetic components in vegetation canopy. Agric. For. Meteorol. 2017, 233, 222–234. [Google Scholar] [CrossRef]
- Drolet, G.G.; Huemmrich, K.F.; Hall, F.G.; Middleton, E.M.; Black, T.A.; Barr, A.G.; Margolis, H.A. A MODIS-derived photochemical reflectance index to detect inter-annual variations in the photosynthetic light-use efficiency of a boreal deciduous forest. Remote Sens. Environ. 2005, 98, 212–224. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Peñuelas, J.; Papale, D.; Filella, I. Remote estimation of carbon dioxide uptake by a mediterranean forest. Glob. Chang. Biol. 2008, 14, 2860–2867. [Google Scholar] [CrossRef]
- Hall, F.G.; Hilker, T.; Coops, N.C. Photosynsat, photosynthesis from space: Theoretical foundations of a satellite concept and validation from tower and spaceborne data. Remote Sens. Environ. 2011, 115, 1918–1925. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Peñuelas, J.; Gamon, J.; Inoue, Y.; Filella, I. The photochemical reflectance index (pri) and the remote sensing of leaf, canopy and ecosystem radiation use efficiencies: A review and meta-analysis. Remote Sens. Environ. 2011, 115, 281–297. [Google Scholar] [CrossRef]
- Gates, D.M.; Keegan, H.J.; Schleter, J.C.; Weidner, V.R. Spectral properties of plants. Appl. Opt. 1965, 4, 11–20. [Google Scholar] [CrossRef]
- Horler, D.; Dockray, M.; Barber, J. The red edge of plant leaf reflectance. Int. J. Remote Sens. 1983, 4, 273–288. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Signature analysis of leaf reflectance spectra: Algorithm development for remote sensing of chlorophyll. J. Plant Physiol. 1996, 148, 494–500. [Google Scholar] [CrossRef]
- Blackburn, G.A. Hyperspectral remote sensing of plant pigments. J. Ep. Bot. 2006, 58, 855–867. [Google Scholar] [CrossRef] [PubMed]
- Richardson, A.D.; Duigan, S.P.; Berlyn, G.P. An evaluation of noninvasive methods to estimate foliar chlorophyll content. New Phytol. 2002, 153, 185–194. [Google Scholar] [CrossRef]
- Clevers, J.G.; Kooistra, L. Using hyperspectral remote sensing data for retrieving canopy chlorophyll and nitrogen content. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 574–583. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Croft, H.; Chen, J.M.; Luo, X.; Bartlett, P.; Chen, B.; Staebler, R.M. Leaf chlorophyll content as a proxy for leaf photosynthetic capacity. Glob. Chang. Biol. 2017, 23, 3513–3524. [Google Scholar] [CrossRef] [PubMed]
- Gamon, J.A.; Huemmrich, K.F.; Wong, C.Y.; Ensminger, I.; Garrity, S.; Hollinger, D.Y.; Noormets, A.; Peñuelas, J. A remotely sensed pigment index reveals photosynthetic phenology in evergreen conifers. Proc. Natl. Acad. Sci. USA 2016, 113, 13087–13092. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Vina, A.; Verma, S.B.; Rundquist, D.C.; Arkebauer, T.J.; Keydan, G.P.; Leavitt, B.; Ciganda, V.; Burba, G.; Suyker, A.E. Relationship between gross primary production and chlorophyll content in crops: Implications for the synoptic monitoring of vegetation productivity. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.F.; Cescatti, A.; Gitelson, A.A. Leaf chlorophyll constraint on model simulated gross primary productivity in agricultural systems. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 160–176. [Google Scholar] [CrossRef]
- Main, R.; Cho, M.A.; Mathieu, R.; O’Kennedy, M.M.; Ramoelo, A.; Koch, S. An investigation into robust spectral indices for leaf chlorophyll estimation. ISPRS J. Photogramm. Remote Sens. 2011, 66, 751–761. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Verma, S.B.; Vina, A.; Rundquist, D.C.; Keydan, G.P.; Leavitt, B.; Arkebauer, T.J.; Burba, G.; Suyker, A.E. Novel technique for remote estimation of CO2 flux in maize. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Peng, Y.; Arkebauer, T.J.; Schepers, J.S. Relationships between gross primary production, green lai, and canopy chlorophyll content in maize: Implications for remote sensing of primary production. Remote Sens. Environ. 2014, 144, 65–72. [Google Scholar] [CrossRef]
- Peng, Y.; Gitelson, A.A.; Keydan, G.; Rundquist, D.C.; Moses, W. Remote estimation of gross primary production in maize and support for a new paradigm based on total crop chlorophyll content. Remote Sens. Environ. 2011, 115, 978–989. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W.; Rivard, B.; Feng, J. Remote estimation of gross primary production in wheat using chlorophyll-related vegetation indices. Agric. For. Meteorol. 2009, 149, 1015–1021. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Harris, A.; Dash, J. The potential of the meris terrestrial chlorophyll index for carbon flux estimation. Remote Sens. Environ. 2010, 114, 1856–1862. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P. Sentinel-2: Esa’s optical high-resolution mission for gmes operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Chen, B.; Coops, N.C.; Fu, D.; Margolis, H.A.; Amiro, B.D.; Barr, A.G.; Black, T.A.; Arain, M.A.; Bourque, C.P.A.; Flanagan, L.B. Assessing eddy-covariance flux tower location bias across the fluxnet-canada research network based on remote sensing and footprint modelling. Agric. For. Meteorol. 2011, 151, 87–100. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Zhao, M.; Running, S.W.; Wofsy, S.C.; Urbanski, S.; Dunn, A.L.; Munger, J. Scaling gross primary production (GPP) over boreal and deciduous forest landscapes in support of modis gpp product validation. Remote Sens. Environ. 2003, 88, 256–270. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Peng, Y.; Vina, A.; Arkebauer, T.J.; Schepers, J.S. Efficiency of chlorophyll in gross primary productivity: A proof of concept and application in crops. J. Plant Physiol. 2016, 201, 101–110. [Google Scholar] [CrossRef] [PubMed]
- Clevers, J.G.; Gitelson, A.A. Remote estimation of crop and grass chlorophyll and nitrogen content using red-edge bands on sentinel-2 and-3. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the köppen-geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 259–263. [Google Scholar] [CrossRef]
- Reed, D.E.; Ewers, B.E.; Pendall, E.; Naithani, K.J.; Kwon, H.; Kelly, R.D. Biophysical factors and canopy coupling control ecosystem water and carbon fluxes of semiarid sagebrush ecosystems. Rangel. Ecol. Manag. 2018, 71, 309–317. [Google Scholar] [CrossRef]
- van Gorsel, E. Tumbarumba Ozflux Tower Site Ozflux: Australian and New Zealand Flux Research and Monitoring. 2013. Available online: http://data.ozflux.org.au/portal/pub/viewColDetails.jspx?collection.id=1882717&collection.owner.id=2022264&viewType=anonymous (accessed on 30 May 2019).
- Arndt, S. Wombat State Forest Ozflux-Tower Site Ozflux: Australian and New Zealand Flux Research and Monitoring. 2013. Available online: http://data.ozflux.org.au/portal/pub/viewColDetails.jspx?collection.id=1882713&collection.owner.id=2021351&viewType=anonymous (accessed on 30 May 2019).
- Beringer, J. Riggs Creek OzFlux tower site OzFlux: Australian and New Zealand Flux Research and Monitoring hdl: 102.100.100/14246. 2014. Available online: http://data.ozflux.org.au/portal/pub/viewColDetails.jspx?collection.id=1882722&collection.owner.id=304&viewType=anonymous (accessed on 30 May 2019).
- Beringer, J. Yanco Jaxa Ozflux Tower Site. Ozflux: Australian and New Zealand Flux Research and Monitoring. 2013. Available online: http://data.ozflux.org.au/portal/pub/viewColDetails.jspx?collection.id=1882711&collection.owner.id=304&viewType=anonymous (accessed on 30 May 2019).
- Beringer, J.; Hutley, L.B.; Mchugh, I.; Arndt, S.K.; Campbell, D.I.; Cleugh, H.A.; Cleverly, J.; De Dios, V.R.; Eamus, D.; Evans, B. An introduction to the australian and new zealand flux tower network—ozflux. Biogeosciences 2016, 13, 5895–5916. [Google Scholar] [CrossRef]
- Beringer, J.; Hutley, L.B.; Hacker, J.M.; Neininger, B.; Paw U, K.T. Patterns and processes of carbon, water and energy cycles across northern australian landscapes: From point to region. Agric. For. Meteorol. 2011, 151, 1409–1416. [Google Scholar] [CrossRef]
- Beringer, J.; McHugh, I.; Hutley, L.B.; Isaac, P.; Kljun, N. Dynamic integrated gap-filling and partitioning for ozflux (dingo). Biogeosciences 2017, 14, 1457–1460. [Google Scholar] [CrossRef]
- Cleverly, J.; Eamus, D.; Coupe, N.R.; Chen, C.; Maes, W.; Li, L.; Faux, R.; Santini, N.S.; Rumman, R.; Yu, Q. Soil moisture controls on phenology and productivity in a semi-arid critical zone. Sci. Total Environ. 2016, 568, 1227–1237. [Google Scholar] [CrossRef]
- Cleverly, J.; Eamus, D.; Van Gorsel, E.; Chen, C.; Rumman, R.; Luo, Q.; Coupe, N.R.; Li, L.; Kljun, N.; Faux, R. Productivity and evapotranspiration of two contrasting semiarid ecosystems following the 2011 global carbon land sink anomaly. Agric. For. Meteorol. 2016, 220, 151–159. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y.P.; Beringer, J.; Shi, H.; Cleverly, J.; Cheng, L.; Eamus, D.; Huete, A.; Hutley, L.; Lu, X. Responses of lai to rainfall explain contrasting sensitivities to carbon uptake between forest and non-forest ecosystems in australia. Sci. Rep. 2017, 7, 11720. [Google Scholar] [CrossRef]
- Wutzler, T.; Lucas-Moffat, A.; Migliavacca, M.; Knauer, J.; Sickel, K.; Šigut, L.; Menzer, O.; Reichstein, M. Basic and extensible post-processing of eddy covariance flux data with reddyproc. Biogeosciences 2018, 15, 5015–5030. [Google Scholar] [CrossRef]
- Sun, X.; Zou, C.B.; Wilcox, B.; Stebler, E. Effect of vegetation on the energy balance and evapotranspiration in tallgrass prairie: A paired study using the eddy-covariance method. Boundary Layer Meteorol. 2019, 170, 127–160. [Google Scholar] [CrossRef]
- Luo, Y.; El-Madany, T.; Filippa, G.; Ma, X.; Ahrens, B.; Carrara, A.; Gonzalez-Cascon, R.; Cremonese, E.; Galvagno, M.; Hammer, T. Using near-infrared-enabled digital repeat photography to track structural and physiological phenology in mediterranean tree–grass ecosystems. Remote Sens. 2018, 10, 1293. [Google Scholar] [CrossRef]
- Lasslop, G.; Reichstein, M.; Papale, D.; Richardson, A.D.; Arneth, A.; Barr, A.; Stoy, P.; Wohlfahrt, G. Separation of net ecosystem exchange into assimilation and respiration using a light response curve approach: Critical issues and global evaluation. Glob Change Biol. 2010, 16, 187–208. [Google Scholar] [CrossRef]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.C.; Skakun, S.V.; Justice, C. The harmonized landsat and sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Kimerling, A.J.; Buckley, A.R.; Muehrcke, P.C.; Muehrcke, J.O. Map Use: Reading and Analysis; Esri Press: Redlands, CA, USA, 2009. [Google Scholar]
- Chen, B.; Coops, N.C.; Fu, D.; Margolis, H.A.; Amiro, B.D.; Black, T.A.; Arain, M.A.; Barr, A.G.; Bourque, C.P.A.; Flanagan, L.B. Characterizing spatial representativeness of flux tower eddy-covariance measurements across the canadian carbon program network using remote sensing and footprint analysis. Remote Sens. Environ. 2012, 124, 742–755. [Google Scholar] [CrossRef]
- Chen, B.; Black, T.A.; Coops, N.C.; Hilker, T.; Trofymow, J.T.; Morgenstern, K. Assessing tower flux footprint climatology and scaling between remotely sensed and eddy covariance measurements. Boundary Layer Meteorol. 2009, 130, 137–167. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the modis vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Rouse Jr, J.W.; Haas, R.; Schell, J.; Deering, D. Monitoring vegetation systems in the great plains with ERTS. Available online: https://ntrs.nasa.gov/search.jsp?R=19740022614 (accessed on 29 May 2019).
- Badgley, G.; Field, C.B.; Berry, J.A. Canopy near-infrared reflectance and terrestrial photosynthesis. Sci. Adv. 2017, 3, e1602244. [Google Scholar] [CrossRef]
- Barnes, E.; Clarke, T.; Richards, S.; Colaizzi, P.; Haberland, J.; Kostrzewski, M.; Waller, P.; Choi, C.; Riley, E.; Thompson, T. Coincident Detection of Crop Water Stress, Nitrogen Status and Canopy Density using Ground Based Multispectral Data. In Proceedings of the Fifth International Conference on Precision Agriculture, Bloomington, MN, USA, 16–19 July 2000. [Google Scholar]
- Chen, J.M.; Liu, J.; Cihlar, J.; Goulden, M.L. Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecol. Modell. 1999, 124, 99–119. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Peng, Y.; Masek, J.G.; Rundquist, D.C.; Verma, S.; Suyker, A.; Baker, J.M.; Hatfield, J.L.; Meyers, T. Remote estimation of crop gross primary production with landsat data. Remote Sens. Environ. 2012, 121, 404–414. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of maximum-value composite images from temporal avhrr data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality ndvi time-series data set based on the savitzky–golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Croft, H.; Chen, J.; Froelich, N.; Chen, B.; Staebler, R. Seasonal controls of canopy chlorophyll content on forest carbon uptake: Implications for gpp modeling. J. Geophys. Res. Biogeosci. 2015, 120, 1576–1586. [Google Scholar] [CrossRef]
- Hill, M.J. Vegetation index suites as indicators of vegetation state in grassland and savanna: An analysis with simulated sentinel 2 data for a north american transect. Remote Sens. Environ. 2013, 137, 94–111. [Google Scholar] [CrossRef]
- Bourdeau, P.F. Seasonal variations of the photosynthetic efficiency of evergreen conifers. Ecology 1959, 40, 63–67. [Google Scholar] [CrossRef]
- Soudani, K.; Hmimina, G.; Dufrêne, E.; Berveiller, D.; Delpierre, N.; Ourcival, J.M.; Rambal, S.; Joffre, R. Relationships between photochemical reflectance index and light-use efficiency in deciduous and evergreen broadleaf forests. Remote Sens. Environ. 2014, 144, 73–84. [Google Scholar] [CrossRef]
- Goerner, A.; Reichstein, M.; Rambal, S. Tracking seasonal drought effects on ecosystem light use efficiency with satellite-based pri in a mediterranean forest. Remote Sens. Environ. 2009, 113, 1101–1111. [Google Scholar] [CrossRef]
- Woodgate, W.; Suarez, L.; van Gorsel, E.; Cernusak, L.; Dempsey, R.; Devilla, R.; Held, A.; Hill, M.; Norton, A. Tri-PRI: A three band reflectance index tracking dynamic photoprotective mechanisms in a mature eucalypt forest. Agric. For. Meteorol. 2019, 272, 187–201. [Google Scholar] [CrossRef]
- Gebremichael, M.; Barros, A.P. Evaluation of modis gross primary productivity (gpp) in tropical monsoon regions. Remote Sens. Environ. 2006, 100, 150–166. [Google Scholar] [CrossRef]
- Hutyra, L.R.; Munger, J.W.; Saleska, S.R.; Gottlieb, E.; Daube, B.C.; Dunn, A.L.; Amaral, D.F.; De Camargo, P.B.; Wofsy, S.C. Seasonal controls on the exchange of carbon and water in an amazonian rain forest. J. Geophys. Res. Biogeosci. 2015, 112, 488–497. [Google Scholar] [CrossRef]
- He, L.; Chen, J.M.; Gonsamo, A.; Luo, X.; Wang, R.; Liu, Y.; Liu, R. Changes in the shadow: The shifting role of shaded leaves in global carbon and water cycles under climate change. Geophys. Res. Lett. 2018. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Hall, F.G.; Black, T.A.; Wulder, M.A.; Nesic, Z.; Krishnan, P. Separating physiologically and directionally induced changes in pri using brdf models. Remote Sens. Environ. 2008, 112, 2777–2788. [Google Scholar] [CrossRef]
- Hilker, T.; Nesic, Z.; Coops, N.C.; Lessard, D. A new, automated, multiangular radiometer instrument for tower-based observations of canopy reflectance (AMSPEC II). Instrum. Sci. Technol. 2010, 38, 319–340. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, J.; Liu, Q.; Huete, A.R.; Xu, B.; Yin, G.; Zhao, J.; Yang, L.; Fan, W.; Wu, S. An iterative brdf/ndvi inversion algorithm based ona posteriorivariance estimation of observation errors. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6481–6496. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, B.; Yin, G.; Wu, S.; Hu, G.; Yan, K.; Yang, B.; Song, W.; Li, J. Spectral invariant provides a practical modeling approach for future biophysical variable estimations. Remote Sens. 2018, 10, 1508. [Google Scholar] [CrossRef]
- Zhang, J. Multi-source remote sensing data fusion: Status and trends. Int. J. Image Data Fusion 2010, 1, 5–24. [Google Scholar] [CrossRef]
- Zhao, J.; Li, J.; Liu, Q.; Fan, W.; Zhong, B.; Wu, S.; Yang, L.; Zeng, Y.; Xu, B.; Yin, G. Leaf area index retrieval combining hj1/ccd and landsat8/oli data in the heihe river basin, china. Remote Sens. 2015, 7, 6862–6885. [Google Scholar] [CrossRef]
- Verma, M.; Friedl, M.A.; Law, B.E.; Bonal, D.; Kiely, G.; Black, T.A.; Wohlfahrt, G.; Moors, E.J.; Montagnani, L.; Marcolla, B. Improving the performance of remote sensing models for capturing intra- and inter-annual variations in daily gpp: An analysis using global fluxnet tower data. Agric. For. Meteorol. 2015, 214, 416–429. [Google Scholar] [CrossRef]
- Zhang, Y.; Guanter, L.; Berry, J.A.; Joiner, J.; Van, d.T.C.; Huete, A.; Gitelson, A.; Voigt, M.; Köhler, P. Estimation of vegetation photosynthetic capacity from space-based measurements of chlorophyll fluorescence for terrestrial biosphere models. Glob Chang. Biol. 2015, 20, 3727–3742. [Google Scholar] [CrossRef]
- Miyazawa, S.I.; Terashima, I. Slow development of leaf photosynthesis in an evergreen broad-leaved tree, castanopsis sieboldii: Relationships between leaf anatomical characteristics and photosynthetic rate. Plant Cell Environ. 2001, 24, 279–291. [Google Scholar] [CrossRef]
- Wu, J.; Guan, K.; Hayek, M.; Restrepocoupe, N.; Wiedemann, K.T.; Xu, X.; Wehr, R.; Christoffersen, B.O.; Miao, G.; Da, S.R. Partitioning controls on amazon forest photosynthesis between environmental and biotic factors at hourly to inter-annual time scales. Glob. Chang. Biol. 2017, 23, 1240. [Google Scholar] [CrossRef]
- Radeloff, V.; Dubinin, M.; Coops, N.; Allen, A.; Brooks, T.; Clayton, M.; Costa, G.; Graham, C.; Helmers, D.; Ives, A. The dynamic habitat indices (dhis) from modis and global biodiversity. Remote Sens. Environ. 2019, 222, 204–214. [Google Scholar] [CrossRef]

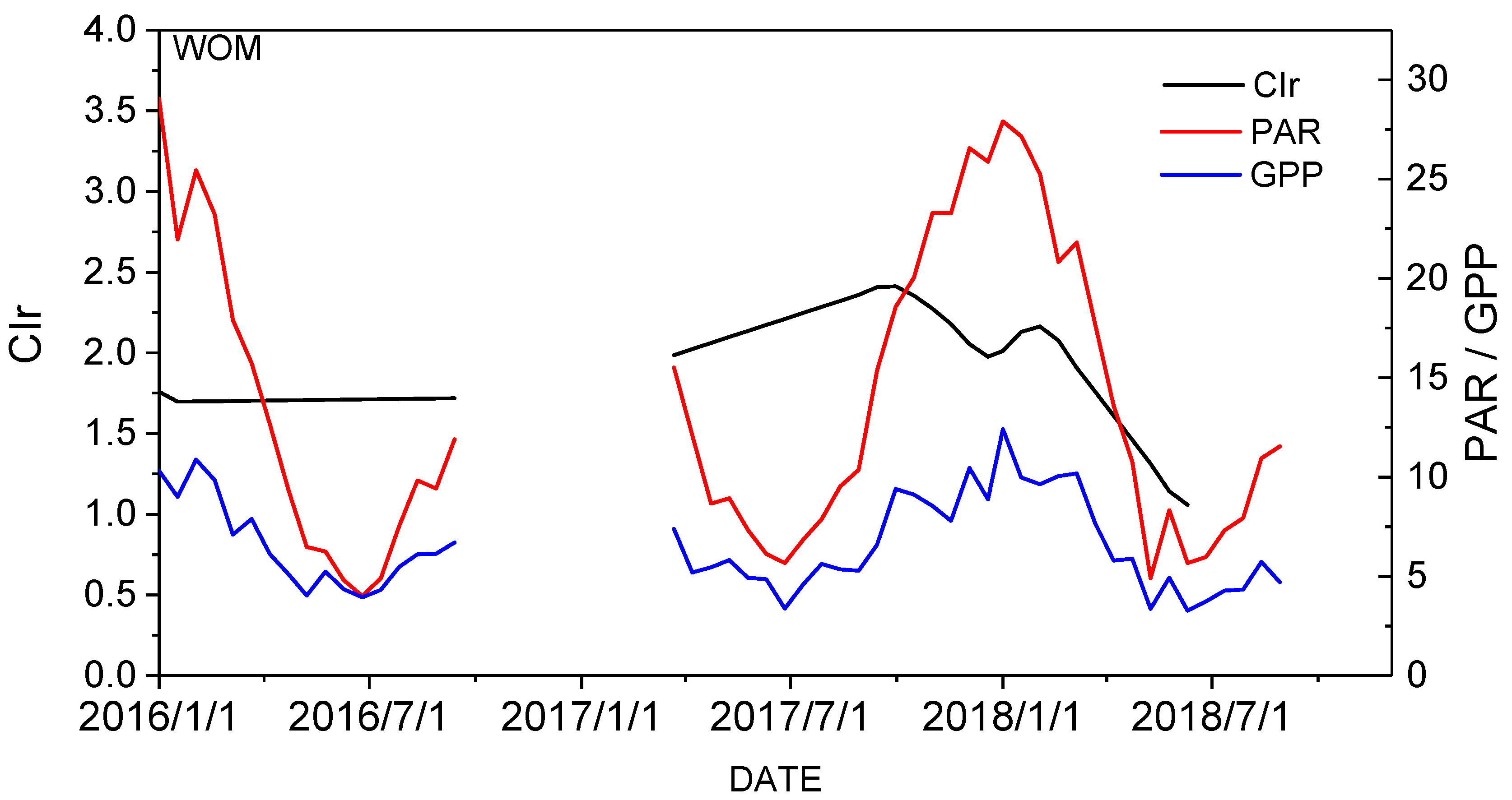
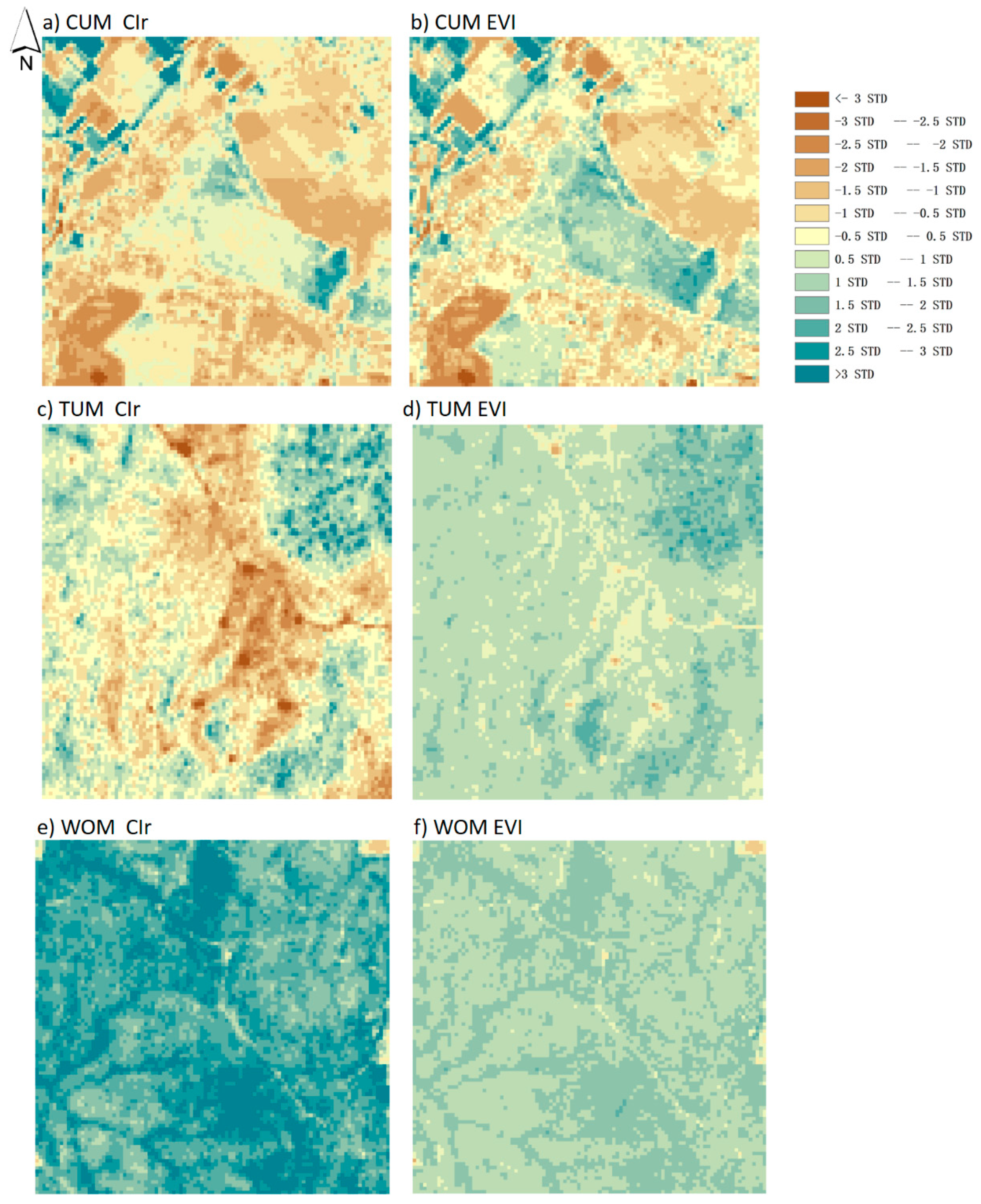
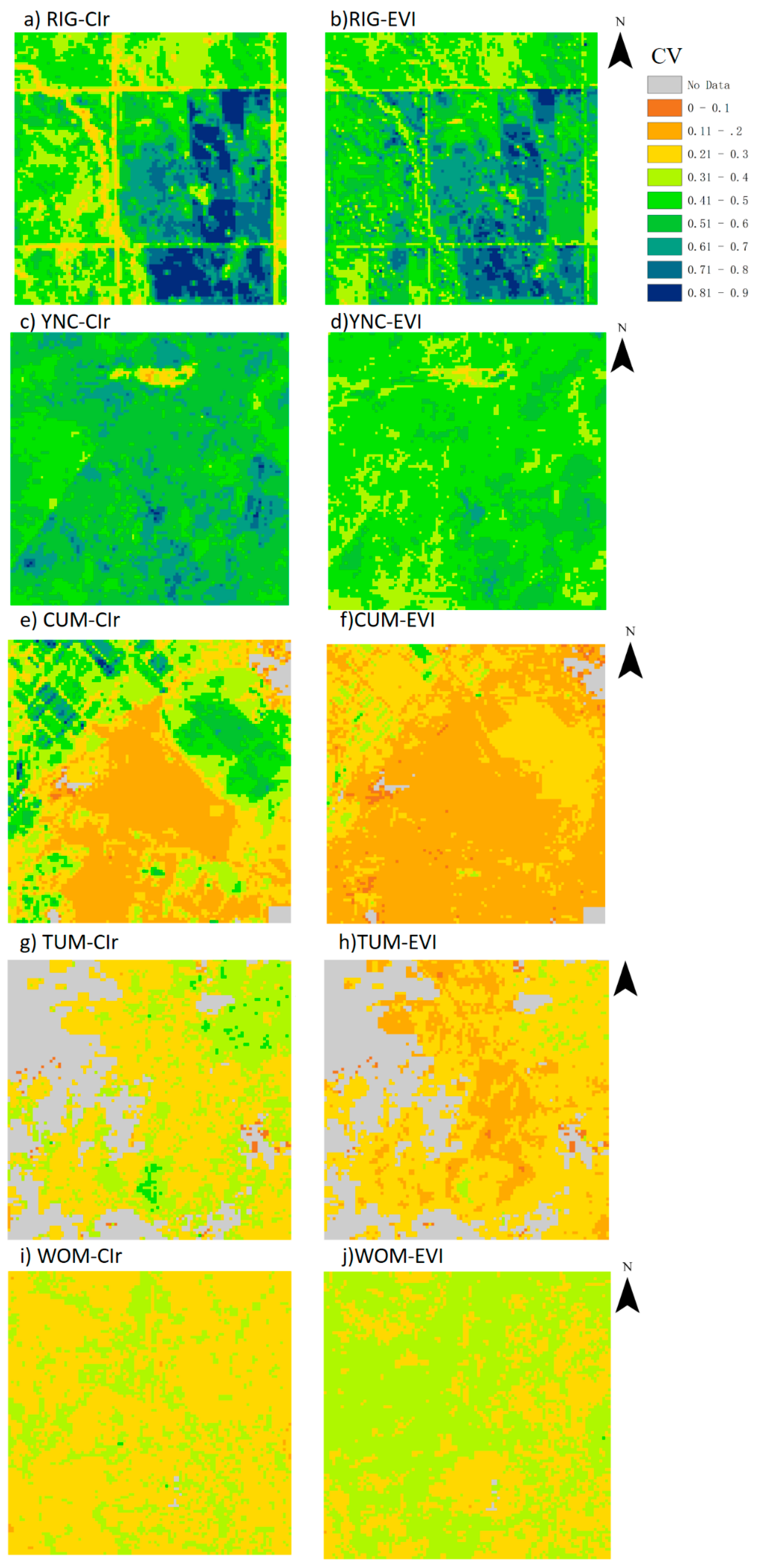
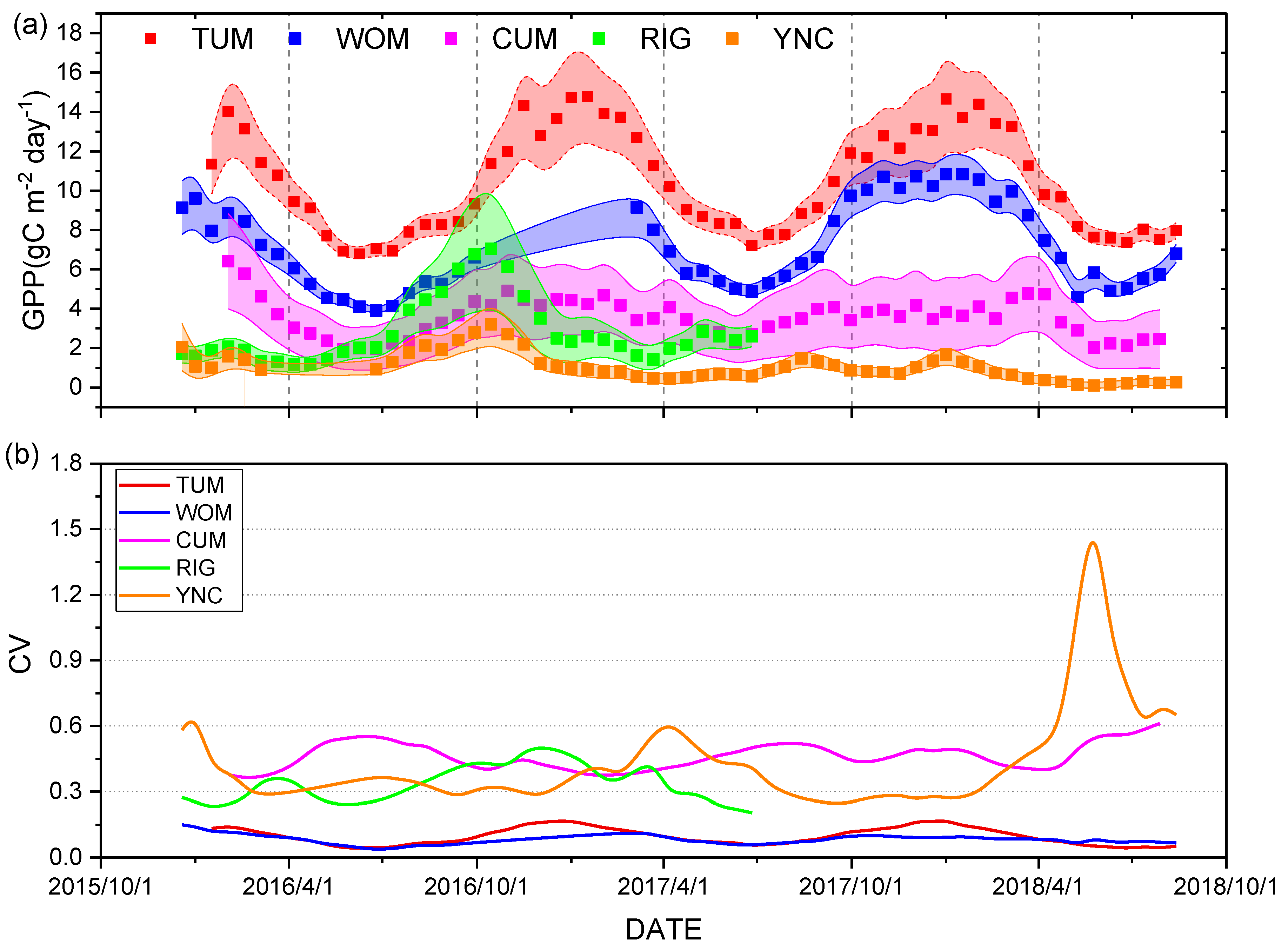
| Site ID | Full Name | CO2 Flux Years | Location (Lat, Lon) | Vegetation Type | Military Grid Reference System (HLS-Sentinel Tile) | Annual Precipitation (mm) | Climate Type | Reference |
|---|---|---|---|---|---|---|---|---|
| CUM | Cumberland Plain | Jan 2015–Oct 2018 | −33.6152, 150.724 | EBF | 56HKH | 800 | Cfa | [55] |
| TUM | Tumbarumba | Jan 2015–Oct 2018 | −35.6566, 148,152 | EBF | 55HFA | 1000 | Cfb | [56] |
| WOM | Wombat Forest | Jan 2015–Oct 2018 | −37.4222, 144.094 | EBF | 55HBU | 600 | Cfb | [57] |
| RIG | Riggs Creek | Jan 2015–Jan 2017 | −36.6499, 145.576 | GRA | 55HCV | 650 | Cfb | [58] |
| YNC | Yanco | Jan 2015–Oct 2018 | −34.9893, 146.291 | GRA | 55HDB | 465 | BSk | [59] |
| Index | Formulation | Reference |
|---|---|---|
| EVI | [74] | |
| NDVI | [75] | |
| NIRv | [76] | |
| CI red edge (CIr) | [39,43] | |
| CI green (CIg) | [39,43] | |
| MTCI | [47] | |
| NDRE1 | [36] | |
| NDRE2 | [77] |
| TUM (N = 60) | WOM (N = 36) | CUM (N = 56) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | rRMSE | a | b | R2 | RMSE | rRMSE | a | b | R2 | RMSE | rRMSE | a | b | |
| CIr | 0.53 | 2.35 | 0.25 | 0.36 | 5.01 | 0.87 | 0.96 | 0.14 | 0.30 | 2.88 | 0.53 | 1.05 | 0.21 | 0.31 | −0.13 |
| CIg | 0.08 | 3.33 | 0.35 | 0.01 | 8.32 | 0.90 | 0.78 | 0.11 | 0.04 | 2.75 | 0.53 | 1.01 | 0.21 | 0.04 | 1.90 |
| MTCI | 0.75 | 1.70 | 0.18 | 0.32 | 2.89 | 0.83 | 0.98 | 0.14 | 0.21 | 2.47 | 0.36 | 1.25 | 0.25 | 0.18 | 0.47 |
| NDRE1 | 0.73 | 1.77 | 0.19 | 0.36 | 3.28 | 0.89 | 0.82 | 0.12 | 0.24 | 2.58 | 0.45 | 1.15 | 0.23 | 0.21 | 0.60 |
| NDRE2 | 0.70 | 1.86 | 0.20 | 0.29 | 3.52 | 0.87 | 0.86 | 0.12 | 0.19 | 2.65 | 0.46 | 1.14 | 0.23 | 0.18 | 0.42 |
| EVI | 0.76 | 1.67 | 0.18 | 2.48 | 2.83 | 0.91 | 0.74 | 0.11 | 1.85 | 2.54 | 0.38 | 1.23 | 0.25 | 1.15 | 1.85 |
| NIRv | 0.70 | 1.89 | 0.20 | 5.40 | 3.67 | 0.91 | 0.75 | 0.11 | 4.17 | 2.52 | 0.43 | 1.17 | 0.24 | 2.92 | 1.59 |
| NDVI | 0.69 | 1.92 | 0.20 | 1.06 | 4.26 | 0.90 | 0.78 | 0.11 | 0.81 | 2.60 | 0.38 | 1.23 | 0.25 | 0.58 | 1.46 |
| MOD17A2H | 0.66 | 1.76 | 0.30 | - | - | 0.85 | 0.93 | 0.18 | - | - | 0.28 | 0.97 | 0.28 | - | - |
| RIG (N = 17) | YNC (N = 54) | YNC (N = 109) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | rRMSE | a | b | R2 | RMSE | rRMSE | a | b | R2 | RMSE | rRMSE | a | b | |
| CIr | 0.87 | 1.02 | 0.37 | 0.32 | 0.14 | 0.69 | 0.63 | 0.46 | 0.31 | −0.05 | 0.89 | 0.34 | 0.33 | 0.31 | −0.29 |
| CIg | 0.84 | 1.13 | 0.42 | 0.04 | 0.37 | 0.48 | 0.80 | 0.59 | 0.03 | 0.32 | 0.73 | 0.53 | 0.51 | 0.03 | 0.00 |
| MTCI | 0.54 | 2.05 | 0.76 | 0.32 | −1.23 | 0.08 | 1.10 | 0.81 | 0.02 | 1.04 | 0.12 | 0.95 | 0.93 | 0.11 | 1.80 |
| NDRE1 | 0.51 | 2.08 | 0.79 | 0.27 | −0.79 | 0.23 | 0.99 | 0.73 | 0.10 | 0.03 | 0.37 | 0.80 | 0.78 | 0.12 | −0.60 |
| NDRE2 | 0.55 | 1.99 | 0.76 | 0.23 | −0.73 | 0.25 | 0.98 | 0.72 | 0.10 | −0.01 | 0.41 | 0.78 | 0.76 | 0.11 | −0.66 |
| EVI | 0.77 | 1.36 | 0.52 | 1.60 | −0.87 | 0.61 | 0.69 | 0.51 | 0.97 | −0.32 | 0.76 | 0.50 | 0.49 | 0.99 | −0.53 |
| NIRv | 0.86 | 1.07 | 0.39 | 2.77 | −0.25 | 0.66 | 0.64 | 0.47 | 2.30 | −0.13 | 0.83 | 0.42 | 0.41 | 2.32 | −0.34 |
| NDVI | 0.66 | 1.67 | 0.65 | 1.31 | −1.47 | 0.49 | 0.80 | 0.59 | 0.49 | −0.10 | 0.76 | 0.50 | 0.49 | 0.52 | −0.48 |
| MOD17A2H | 0.66 | 1.76 | 0.30 | - | - | 0.81 | 0.91 | 0.17 | - | - | 0.85 | 0.93 | 0.18 | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.; Li, J.; Liu, Q.; Li, L.; Zhao, J.; Yu, W. Evaluating the Effectiveness of Using Vegetation Indices Based on Red-Edge Reflectance from Sentinel-2 to Estimate Gross Primary Productivity. Remote Sens. 2019, 11, 1303. https://doi.org/10.3390/rs11111303
Lin S, Li J, Liu Q, Li L, Zhao J, Yu W. Evaluating the Effectiveness of Using Vegetation Indices Based on Red-Edge Reflectance from Sentinel-2 to Estimate Gross Primary Productivity. Remote Sensing. 2019; 11(11):1303. https://doi.org/10.3390/rs11111303
Chicago/Turabian StyleLin, Shangrong, Jing Li, Qinhuo Liu, Longhui Li, Jing Zhao, and Wentao Yu. 2019. "Evaluating the Effectiveness of Using Vegetation Indices Based on Red-Edge Reflectance from Sentinel-2 to Estimate Gross Primary Productivity" Remote Sensing 11, no. 11: 1303. https://doi.org/10.3390/rs11111303
APA StyleLin, S., Li, J., Liu, Q., Li, L., Zhao, J., & Yu, W. (2019). Evaluating the Effectiveness of Using Vegetation Indices Based on Red-Edge Reflectance from Sentinel-2 to Estimate Gross Primary Productivity. Remote Sensing, 11(11), 1303. https://doi.org/10.3390/rs11111303







