Improved Modeling of Gross Primary Productivity of Alpine Grasslands on the Tibetan Plateau Using the Biome-BGC Model
Abstract
:1. Introduction
2. Study Area and Dataset
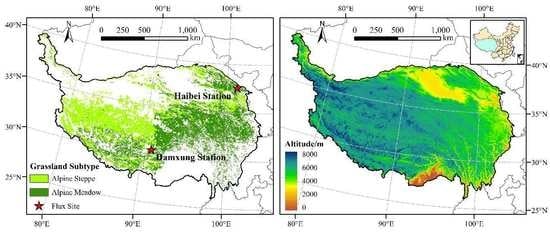
2.1. Study Area
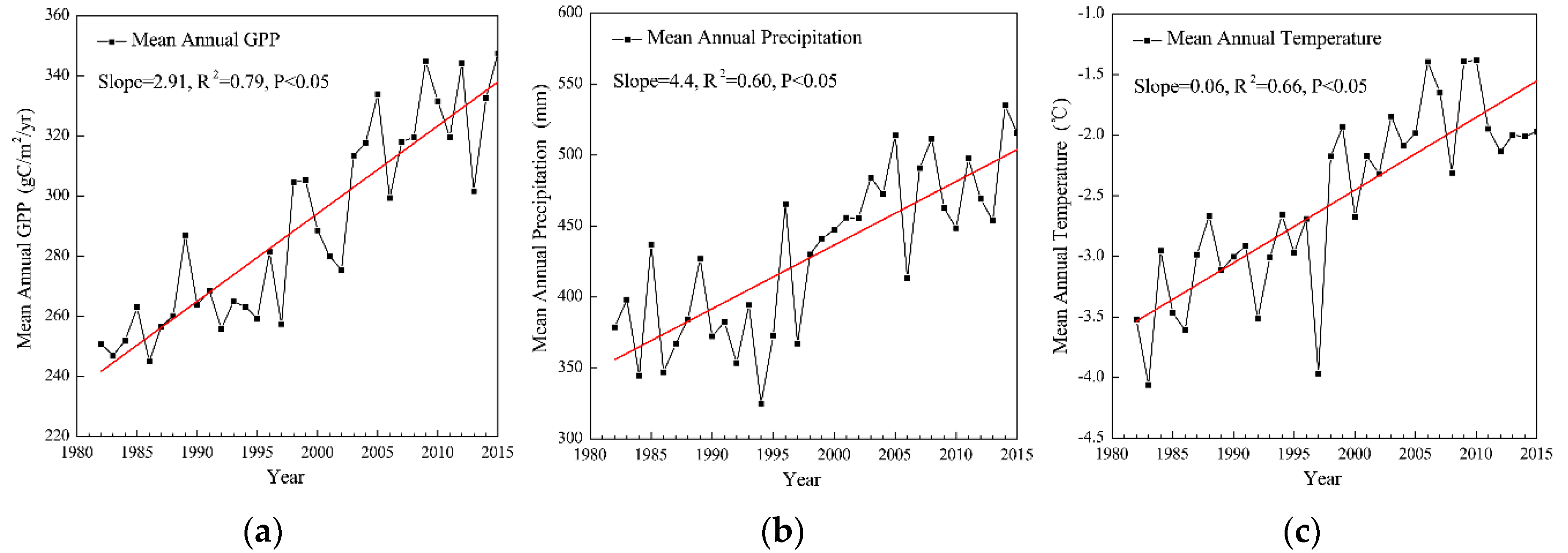
2.2. Dataset
2.2.1. Meteorological Forcing and Land Surface Initial Conditions for the Biome-BGC Model
2.2.2. GIMMS NDVI Dataset and Preprocessing
3. Methodology
3.1. The Biome-BGC Model
3.2. Phenology Module Modification
3.3. Model Parameterization
3.3.1. Sensitivity Analysis
3.3.2. Parameter Calibration
3.4. Biome-BGC Model Simulation
4. Results and Analysis
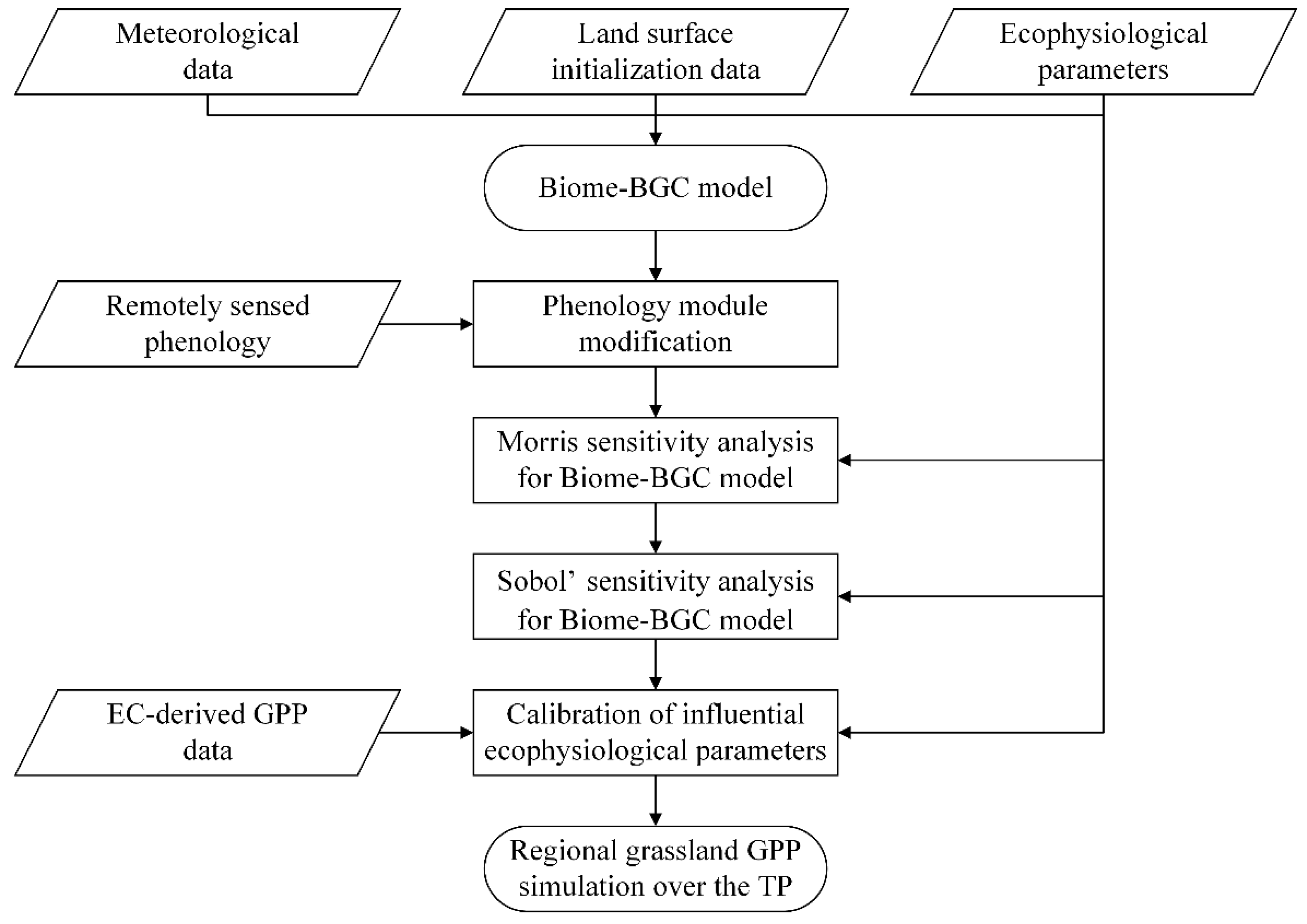
4.1. Remotely Sensed Phenology
4.2. Parameter Sensitivity Analysis and Calibration
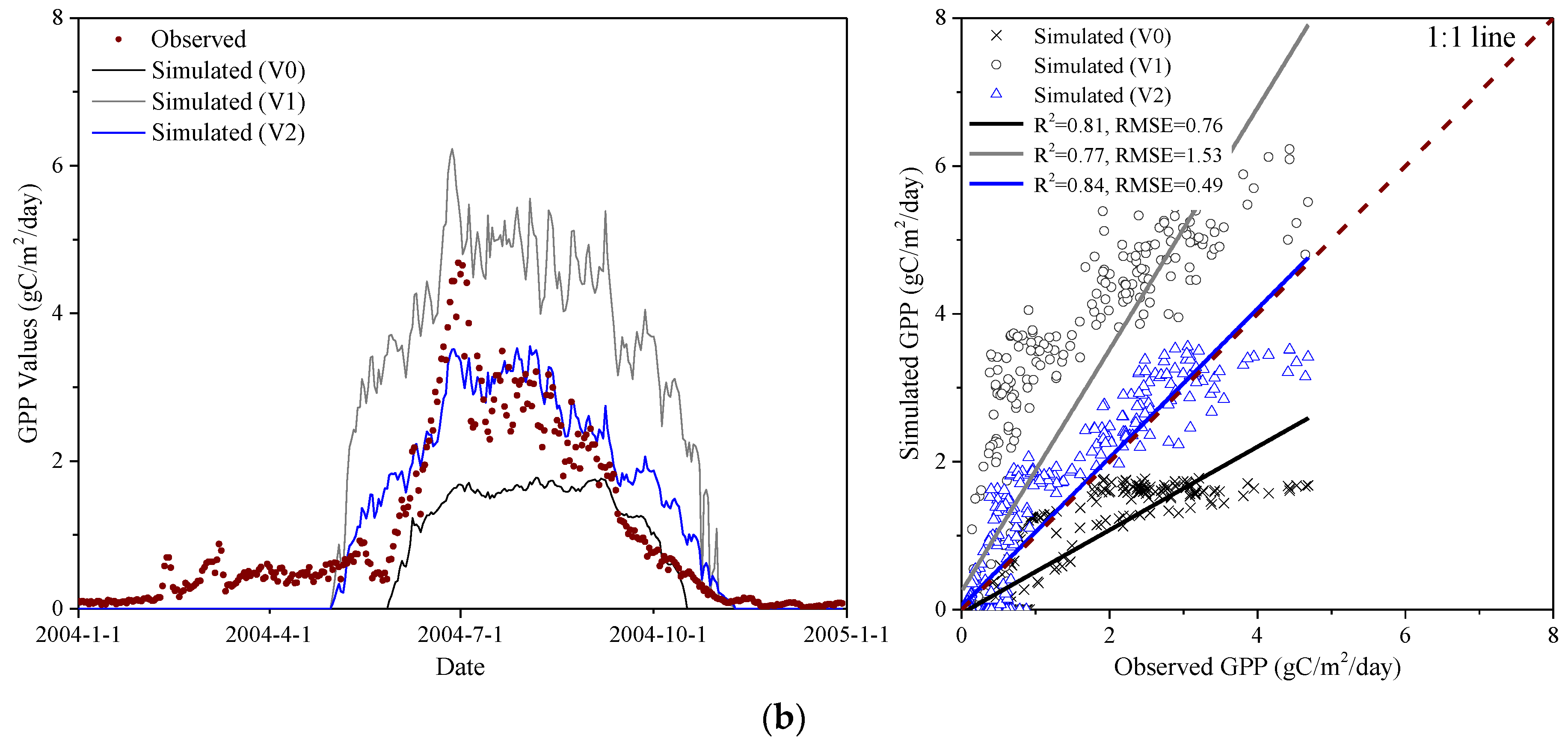
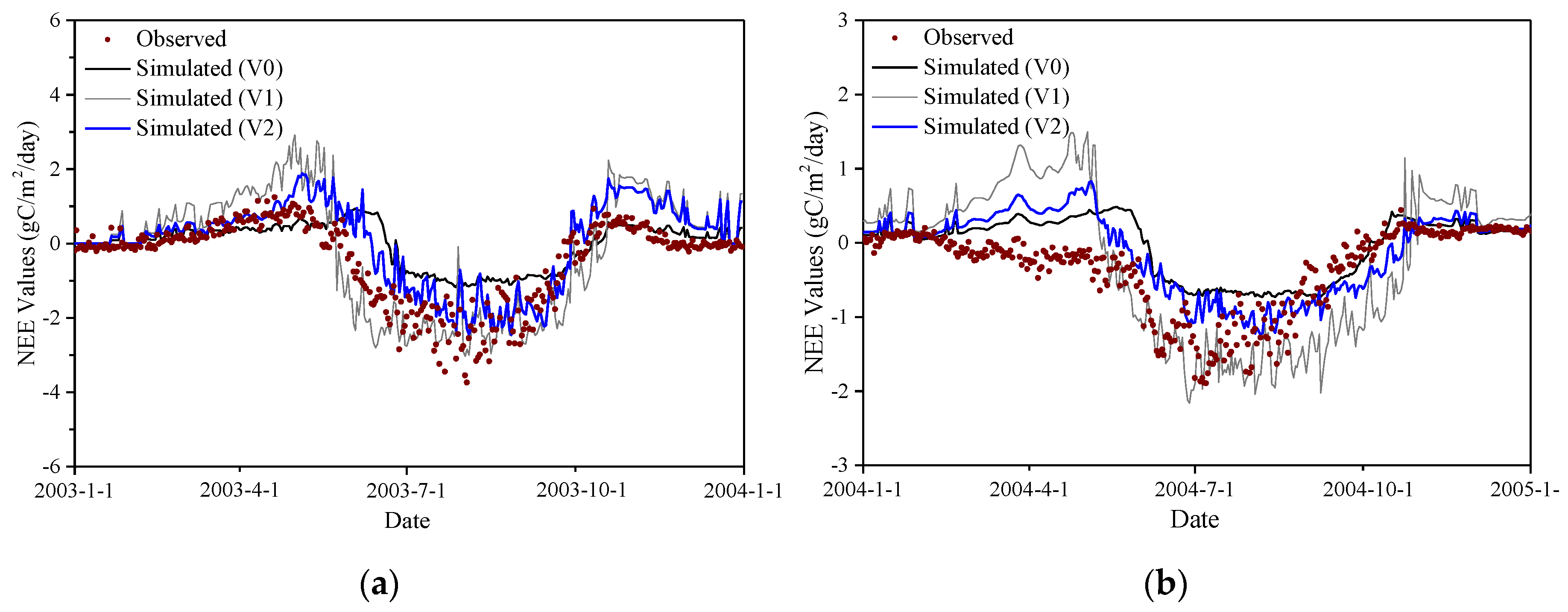
4.3. Site-Level Evaluation
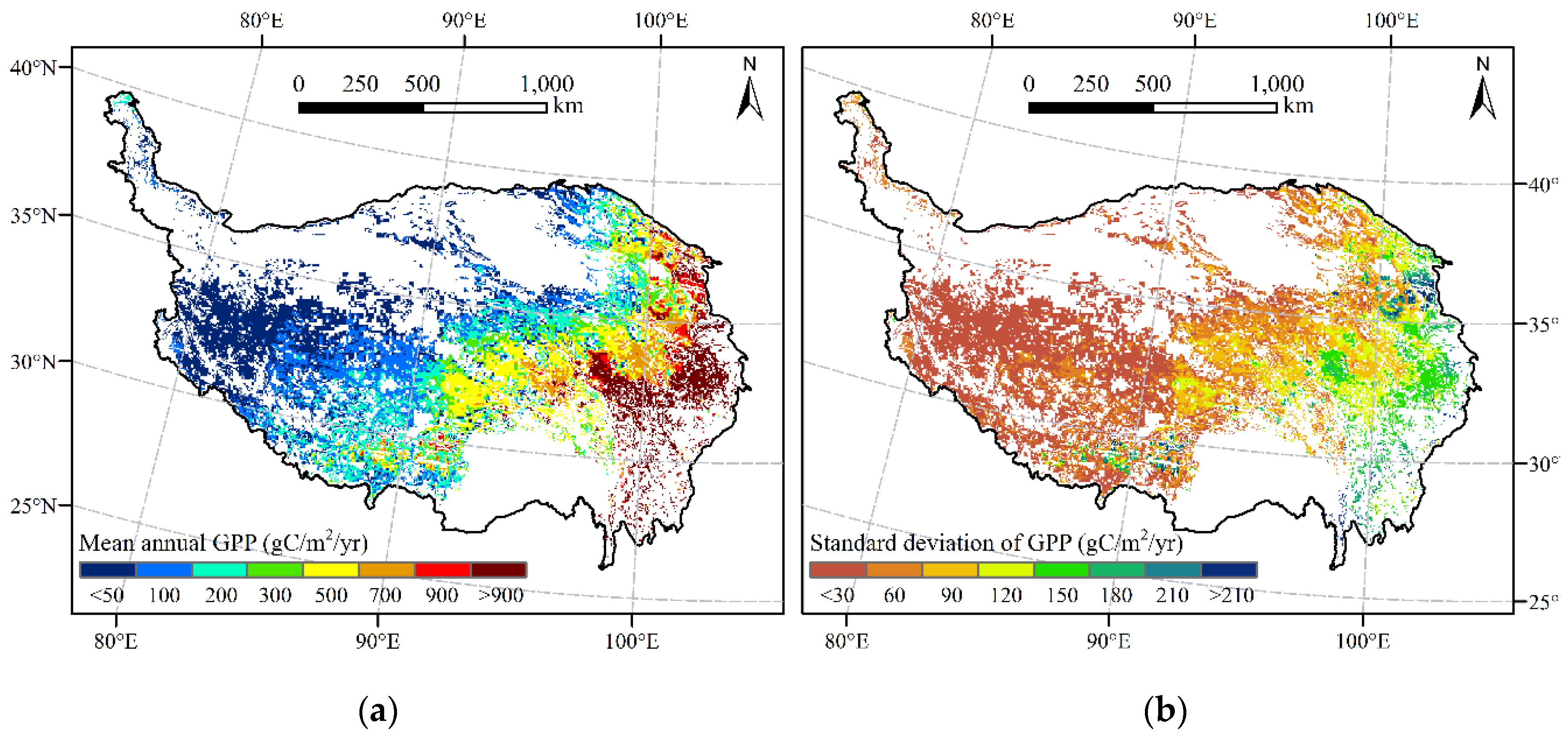
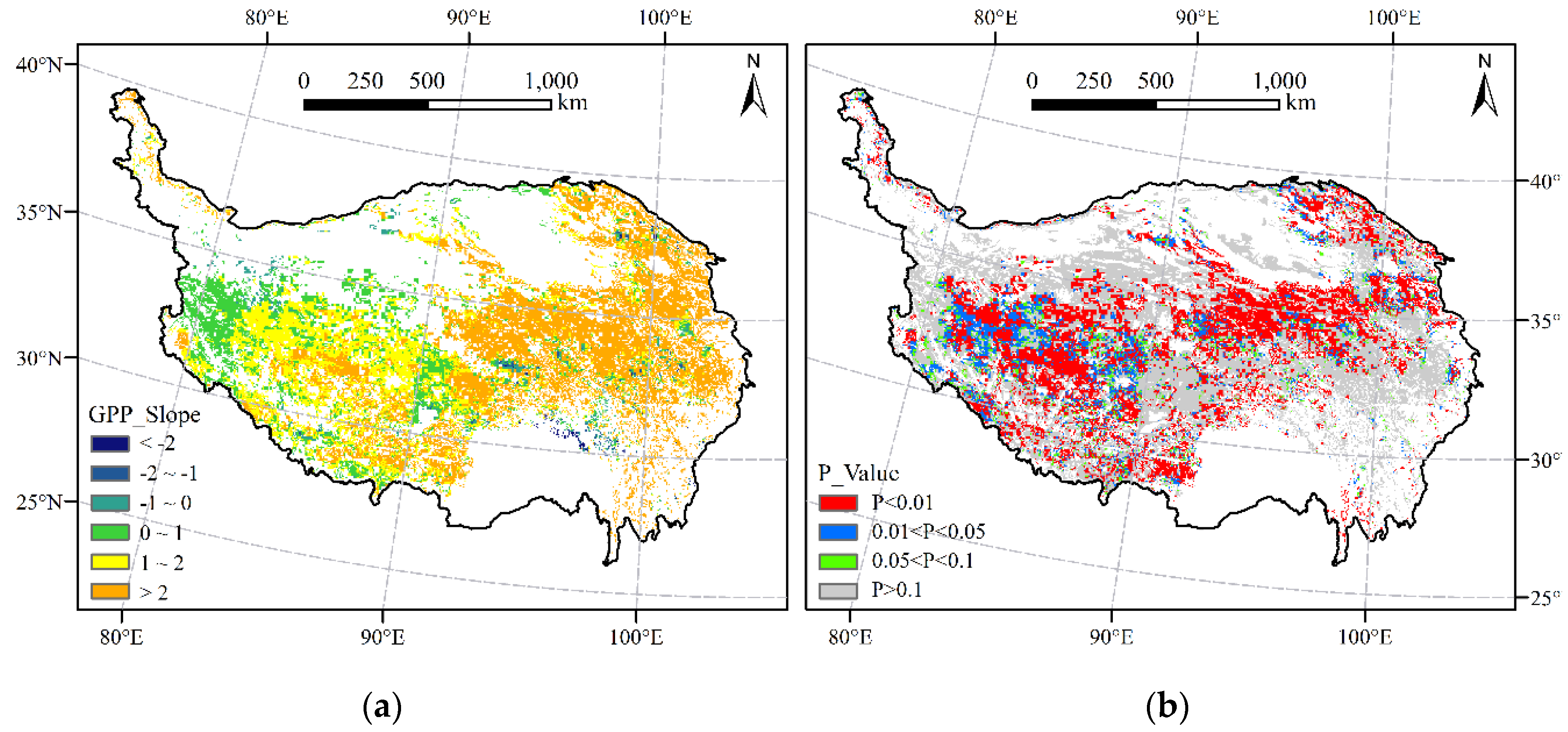
4.4. Spatial Patterns and Trends of GPP
5. Discussion
5.1. The Role of Remotely Sensed Phenology in the Biome-BGC Model
5.2. Performance of the Calibrated Biome-BGC Model
5.3. Uncertainties and Limitations
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.S.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Vina, A.; Verma, S.B.; Rundquist, D.C.; Arkebauer, T.J.; Keydan, G.; Leavitt, B.; Ciganda, V.; Burba, G.G.; Suyker, A.E. Relationship between gross primary production and chlorophyll content in crops: Implications for the synoptic monitoring of vegetation productivity. J. Geophys. Res. Atmos. 2006, 111, D08S11. [Google Scholar] [CrossRef]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rodenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial Gross Carbon Dioxide Uptake: Global Distribution and Covariation with Climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tan, K.; Ciais, P.; Piao, S.L.; Wu, X.P.; Tang, Y.H.; Vuichard, N.; Liang, S.; Fang, J.Y. Application of the ORCHIDEE global vegetation model to evaluate biomass and soil carbon stocks of Qinghai-Tibetan grasslands. Glob. Biogeochem. Cycles 2010, 24, GB1013. [Google Scholar] [CrossRef]
- Piao, S.L.; Ciais, P.; Huang, Y.; Shen, Z.H.; Peng, S.S.; Li, J.S.; Zhou, L.P.; Liu, H.Y.; Ma, Y.C.; Ding, Y.H.; et al. The impacts of climate change on water resources and agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef]
- Piao, S.L.; Tan, K.; Nan, H.J.; Ciais, P.; Fang, J.Y.; Wang, T.; Vuichard, N.; Zhu, B.A. Impacts of climate and CO2 changes on the vegetation growth and carbon balance of Qinghai-Tibetan grasslands over the past five decades. Glob. Planet. Chang. 2012, 98, 73–80. [Google Scholar] [CrossRef]
- Wylie, B.K.; Fosnight, E.A.; Gilmanov, T.G.; Frank, A.B.; Morgan, J.A.; Haferkamp, M.R.; Meyers, T.P. Adaptive data-driven models for estimating carbon fluxes in the Northern Great Plains. Remote Sens. Environ. 2007, 106, 399–413. [Google Scholar] [CrossRef] [Green Version]
- Veroustraete, F.; Sabbe, H.; Eerens, H. Estimation of carbon mass fluxes over Europe using the C-Fix model and Euroflux data. Remote Sens. Environ. 2002, 83, 376–399. [Google Scholar] [CrossRef]
- Xiao, X.M.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.Y.; Moore, B. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Melillo, J.M.; McGuire, A.D.; Kicklighter, D.W.; Moore, B.; Vorosmarty, C.J.; Schloss, A.L. Global climate-change and terrestrial net primary production. Nature 1993, 363, 234–240. [Google Scholar] [CrossRef]
- Running, S.W.; Hunt, E.R. Generalization of a Forest Ecosystem Process Model for Other Biomes, BIOME-BGC, and an Application for Global-Scale Models. In Scaling Physiological Processes; Ehleringer, J.R., Field, C.B., Eds.; Academic Press: San Diego, CA, USA, 1993; pp. 141–158. [Google Scholar]
- Krinner, G.; Viovy, N.; de Noblet-Ducoudre, N.; Ogee, J.; Polcher, J.; Friedlingstein, P.; Ciais, P.; Sitch, S.; Prentice, I.C. A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system. Glob. Biogeochem. Cycles 2005, 19, GB1015. [Google Scholar] [CrossRef]
- Zhuang, Q.; He, J.; Lu, Y.; Ji, L.; Xiao, J.; Luo, T. Carbon dynamics of terrestrial ecosystems on the Tibetan Plateau during the 20th century: An analysis with a process-based biogeochemical model. Glob. Ecol. Biogeogr. 2010, 19, 649–662. [Google Scholar] [CrossRef]
- He, H.L.; Liu, M.; Xiao, X.M.; Ren, X.L.; Zhang, L.; Sun, X.M.; Yang, Y.H.; Li, Y.N.; Zhao, L.; Shi, P.L.; et al. Large-scale estimation and uncertainty analysis of gross primary production in Tibetan alpine grasslands. J. Geophys. Res. Biogeosci. 2014, 119, 466–486. [Google Scholar] [CrossRef] [Green Version]
- Ma, M.N.; Yuan, W.P.; Dong, J.; Zhang, F.W.; Cai, W.W.; Li, H.Q. Large-scale estimates of gross primary production on the Qinghai-Tibet plateau based on remote sensing data. Int. J. Digit Earth 2018, 11, 1166–1183. [Google Scholar] [CrossRef]
- Chen, S.; Huang, Y.; Gao, S.; Wang, G. Impact of physiological and phenological change on carbon uptake on the Tibetan Plateau revealed through GPP estimation based on spaceborne solar-induced fluorescence. Sci. Total Environ. 2019, 663, 45–59. [Google Scholar] [CrossRef] [PubMed]
- Thornton, P.E.; Law, B.E.; Gholz, H.L.; Clark, K.L.; Falge, E.; Ellsworth, D.S.; Golstein, A.H.; Monson, R.K.; Hollinger, D.; Falk, M.; et al. Modeling and measuring the effects of disturbance history and climate on carbon and water budgets in evergreen needleleaf forests. Agric. For. Meteorol. 2002, 113, 185–222. [Google Scholar] [CrossRef]
- Chiesi, M.; Maselli, F.; Moriondo, M.; Fibbi, L.; Bindi, M.; Running, S.W. Application of BIOME-BGC to simulate Mediterranean forest processes. Ecol. Model. 2007, 206, 179–190. [Google Scholar] [CrossRef]
- Mao, F.J.; Li, P.H.; Zhou, G.M.; Du, H.Q.; Xu, X.J.; Shi, Y.J.; Mo, L.F.; Zhou, Y.F.; Tu, G.Q. Development of the BIOME-BGC model for the simulation of managed Moso bamboo forest ecosystems. J. Environ. Manag. 2016, 172, 29–39. [Google Scholar] [CrossRef]
- Hidy, D.; Barcza, Z.; Haszpra, L.; Churkina, G.; Pinter, K.; Nagy, Z. Development of the Biome-BGC model for simulation of managed herbaceous ecosystems. Ecol. Model. 2012, 226, 99–119. [Google Scholar] [CrossRef]
- Sun, Q.; Li, B.; Zhang, T.; Yuan, Y.; Gao, X.; Ge, J.; Li, F.; Zhang, Z. An improved Biome-BGC model for estimating net primary productivity of alpine meadow on the Qinghai-Tibet Plateau. Ecol. Model. 2017, 350, 55–68. [Google Scholar] [CrossRef]
- White, M.A.; Thornton, P.E.; Running, S.W. A continental phenology model for monitoring vegetation responses to interannual climatic variability. Glob. Biogeochem. Cycles 1997, 11, 217–234. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Chen, G.; Yang, Q.; Wang, B.; Ma, Y.; Shen, M. Complex responses of spring alpine vegetation phenology to snow cover dynamics over the Tibetan Plateau, China. Sci. Total Environ. 2017, 593, 449–461. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.L.; Zhang, Y.J.; Dong, J.W.; Xiao, X.M. Green-up dates in the Tibetan Plateau have continuously advanced from 1982 to 2011. Proc. Natl. Acad. Sci. USA 2013, 110, 4309–4314. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Zhang, B.; Yang, Q.; Chen, G.; Yang, B.; Lu, L.; Shen, M.; Peng, Y. Responses of net primary productivity to phenological dynamics in the Tibetan Plateau, China. Agric. For. Meteorol. 2017, 232, 235–246. [Google Scholar] [CrossRef]
- Wang, X.; Wu, C.; Peng, D.; Gonsamo, A.; Liu, Z. Snow cover phenology affects alpine vegetation growth dynamics on the Tibetan Plateau: Satellite observed evidence, impacts of different biomes, and climate drivers. Agric. For. Meteorol. 2018, 256, 61–74. [Google Scholar] [CrossRef]
- Arora, V.K.; Boer, G.J. A parameterization of leaf phenology for the terrestrial ecosystem component of climate models. Glob. Chang. Biol. 2005, 11, 39–59. [Google Scholar] [CrossRef]
- Gonsamo, A.; Chen, J.M.; Price, D.T.; Kurz, W.A.; Liu, J.; Boisvenue, C.; Hember, R.A.; Wu, C.Y.; Chang, K.H. Improved assessment of gross and net primary productivity of Canada’s landmass. J. Geophys. Res. Biogeosci. 2013, 118, 1546–1560. [Google Scholar] [CrossRef]
- Wang, J.; Wu, C.Y.; Zhang, C.H.; Ju, W.M.; Wang, X.Y.; Chen, Z.; Fang, B. Improved modeling of gross primary productivity (GPP) by better representation of plant phenological indicators from remote sensing using a process model. Ecol. Indic. 2018, 88, 332–340. [Google Scholar] [CrossRef]
- Zheng, D.; Lin, Z.Y.; Zhang, X.Q. Progress in studies of Tibetan Plateau and global environmental change. Earth Sci. Front. 2002, 9, 95–102. [Google Scholar]
- Chen, X.Q.; An, S.; Inouye, D.W.; Schwartz, M.D. Temperature and snowfall trigger alpine vegetation green-up on the world’s roof. Glob. Chang. Biol. 2015, 21, 3635–3646. [Google Scholar] [CrossRef]
- Ni, J. Carbon storage in grasslands of China. J. Arid Environ. 2002, 50, 205–218. [Google Scholar] [CrossRef]
- Hungerford, D.R.; Nemani, R.; Running, W.S.; Coughlan, C.J. MT-CLIM: A Mountain Microclimate Simulation Model; US Department of Agriculture, Forest Service, Intermountain Research Station: Ogden, UT, USA, 1989.
- Yu, G.R.; Wen, X.F.; Sun, X.M.; Tanner, B.D.; Lee, X.H.; Chen, J.Y. Overview of ChinaFLUX and evaluation of its eddy covariance measurement. Agric. For. Meteorol. 2006, 137, 125–137. [Google Scholar] [CrossRef]
- Li, C.; He, H.L.; Liu, M.; Su, W.; Fu, Y.L.; Zhang, L.M.; Wen, X.F.; Yu, G.R. The design and application of CO2 flux data processing system at ChinaFLUX. Geo-Inf. Sci. 2008, 10, 557–565. (In Chinese) [Google Scholar]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, G.; Clement, R.; Dolman, H.; et al. Gap filling strategies for long term energy flux data sets. Agric. For. Meteorol. 2001, 107, 71–77. [Google Scholar] [CrossRef] [Green Version]
- Lloyd, J.; Taylor, J.A. On the temperature-dependence of soil respiration. Funct. Ecol. 1994, 8, 315–323. [Google Scholar] [CrossRef]
- Wang, B. Study on Carbon Flux and Its Controlling Mechanisms in a Degraded Alpine Meadow and an Artificial Pasture in the Three-River Source Region of the Qinghai-Tibetan Plateau; Nankai University: Tianjin, China, 2014. [Google Scholar]
- White, M.A.; Thornton, P.E.; Running, S.W.; Nemani, R.R. Parameterization and sensitivity analysis of the BIOME–BGC terrestrial ecosystem model: Net primary production controls. Earth Interact. 2000, 4, 1–85. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Chang, Q.; Zhang, J.H.; Jiao, W.Z.; Yao, F.M. A comparative analysis of the NDVIg and NDVI3g in monitoring vegetation phenology changes in the Northern Hemisphere. Geocarto Int. 2016, 33, 1–20. [Google Scholar] [CrossRef]
- Zhu, Z.C.; Bi, J.; Pan, Y.Z.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.L.; Nemani, R.R.; Myneni, R.B. Global Data Sets of Vegetation Leaf Area Index (LAI)3g and Fraction of Photosynthetically Active Radiation (FPAR)3g Derived from Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) for the Period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar] [CrossRef] [Green Version]
- Holben, B.N. Characteristics of maximum-value composite images from temporal avhrr data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Chen, J.; Jonsson, P.; Tamura, M.; Gu, Z.H.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky-Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Running, S.W.; Coughlan, J.C. A general-model of forest ecosystem processes for regional applications I. hydrologic balance, canopy gas-exchange and primary production processes. Ecol. Model. 1988, 42, 125–154. [Google Scholar] [CrossRef]
- Yan, M.; Tian, X.; Li, Z.Y.; Chen, E.X.; Wang, X.F.; Han, Z.T.; Sun, H. Simulation of Forest Carbon Fluxes Using Model Incorporation and Data Assimilation. Remote Sens. 2016, 8, 567. [Google Scholar] [CrossRef]
- Farquhar, G.D.; von Caemmerer, S.; Berry, J.A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta. 1980, 149, 78–90. [Google Scholar] [CrossRef]
- dePury, D.G.G.; Farquhar, G.D. Simple scaling of photosynthesis from leaves to canopies without the errors of big-leaf models. Plant Cell Environ. 1997, 20, 537–557. [Google Scholar] [CrossRef]
- Richardson, A.D.; Anderson, R.S.; Arain, M.A.; Barr, A.G.; Bohrer, G.; Chen, G.S.; Chen, J.M.; Ciais, P.; Davis, K.J.; Desai, A.R.; et al. Terrestrial biosphere models need better representation of vegetation phenology: Results from the North American Carbon Program Site Synthesis. Glob. Chang. Biol. 2012, 18, 566–584. [Google Scholar] [CrossRef]
- Burgan, R.E.; Hartford, R.A. Monitoring Vegetation Greenness with Satellite Data; Gen. Tech. Rep. INT-GTR-297; US Department of Agriculture, Forest Service, Intermountain Research Station: Ogden, UT, USA, 1993; Volume 297, p. 13.
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Kaduk, J.; Heimann, M. A prognostic phenology scheme for global terrestrial carbon cycle models. Clim. Res. 1996, 6, 1–19. [Google Scholar] [CrossRef]
- Reed, B.C.; Brown, J.F.; Vanderzee, D.; Loveland, T.R.; Merchant, J.W.; Ohlen, D.O. Measuring phenological variability from satellite imagery. J. Veg. Sci. 1994, 5, 703–714. [Google Scholar] [CrossRef]
- Richardson, A.D.; Black, T.A.; Ciais, P.; Delbart, N.; Friedl, M.A.; Gobron, N.; Hollinger, D.Y.; Kutsch, W.L.; Longdoz, B.; Luyssaert, S.; et al. Influence of spring and autumn phenological transitions on forest ecosystem productivity. Philos. Trans. R. Soc. B-Biol. Sci. 2010, 365, 3227–3246. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hufkens, K.; Friedl, M.; Sonnentag, O.; Braswell, B.H.; Milliman, T.; Richardson, A.D. Linking near-surface and satellite remote sensing measurements of deciduous broadleaf forest phenology. Remote Sens. Environ. 2012, 117, 307–321. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; John Wiley & Sons: Chichester, England, 2004. [Google Scholar]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Metropolis, N.; Ulam, S. The monte carlo method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. OPTIMIZATION BY SIMULATED ANNEALING. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Wang, W.; Ichii, K.; Hashimoto, H.; Michaelis, A.R.; Thornton, P.E.; Law, B.E.; Nemani, R.R. A hierarchical analysis of terrestrial ecosystem model Biome-BGC: Equilibrium analysis and model calibration. Ecol. Model. 2009, 220, 2009–2023. [Google Scholar] [CrossRef]
- Churkina, G.; Brovkin, V.; von Bloh, W.; Trusilova, K.; Jung, M.; Dentener, F. Synergy of rising nitrogen depositions and atmospheric CO2 on land carbon uptake moderately offsets global warming. Glob. Biogeochem. Cycles 2009, 23. [Google Scholar] [CrossRef]
- Sun, Q.L.; Li, B.L.; Yuan, Y.C.; Jiang, Y.H.; Zhang, T.; Gao, X.Z.; Ge, J.S.; Li, F.; Zhang, Z.J. A prognostic phenology model for alpine meadows on the Qinghai-Tibetan Plateau. Ecol. Indic. 2018, 93, 1089–1100. [Google Scholar] [CrossRef]
- Aguilos, M.; Takagi, K.; Liang, N.; Ueyama, M.; Fukuzawa, K.; Nomura, M.; Kishida, O.; Fukazawa, T.; Takahashi, H.; Kotsuka, C.; et al. Dynamics of ecosystem carbon balance recovering from a clear-cutting in a cool-temperate forest. Agric. For. Meteorol. 2014, 197, 26–39. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.H.; Liu, H.Y.; Chung, H.; Yu, L.F.; Mi, Z.R.; Geng, Y.; Jing, X.; Wang, S.P.; Zeng, H.; Cao, G.M.; et al. Non-growing-season soil respiration is controlled by freezing and thawing processes in the summer monsoon-dominated Tibetan alpine grassland. Glob. Biogeochem. Cycles 2014, 28, 1081–1095. [Google Scholar] [CrossRef]
- Makela, A.; Valentine, H.T. The ratio of NPP to GPP: Evidence of change over the course of stand development. Tree Physiol. 2001, 21, 1015–1030. [Google Scholar] [CrossRef]
- Fontana, F.; Rixen, C.; Jonas, T.; Aberegg, G.; Wunderle, S. Alpine grassland phenology as seen in AVHRR, VEGETATION, and MODIS NDVI time series—A comparison with in situ measurements. Sensors 2008, 8, 2833–2853. [Google Scholar] [CrossRef] [PubMed]
- Zeng, H.Q.; Jia, G.S.; Epstein, H. Recent changes in phenology over the northern high latitudes detected from multi-satellite data. Environ. Res. Lett. 2011, 6, 045508. [Google Scholar] [CrossRef] [Green Version]
- Kern, A.; Marjanovic, H.; Barcza, Z. Evaluation of the Quality of NDVI3g Dataset against Collection 6 MODIS NDVI in Central Europe between 2000 and 2013. Remote Sens. 2016, 8, 955. [Google Scholar] [CrossRef]
- Li, W.; Wu, J.; Bai, E.; Jin, C.; Wang, A.; Yuan, F.; Guan, D. Response of terrestrial carbon dynamics to snow cover change: A meta-analysis of experimental manipulation (II). Soil Biol. Biochem. 2016, 103, 388–393. [Google Scholar] [CrossRef]
- Hidy, D.; Barcza, Z.; Marjanovic, H.; Sever, M.Z.O.; Dobor, L.; Gelybo, G.; Fodor, N.; Pinter, K.; Churkina, G.; Running, S.; et al. Terrestrial ecosystem process model Biome-BGCMuSo v4.0: Summary of improvements and new modeling possibilities. Geosci. Model. Dev. 2016, 9, 4405–4437. [Google Scholar] [CrossRef]


| No. | Ecophysiological Parameters | Symbol | Units 1 | PDF 2 | Source |
|---|---|---|---|---|---|
| 1 | Transfer growth period as fraction of growing season | TGGS | proportion | Wang [38] | |
| 2 | Litterfall as fraction of growing season | LGS | proportion | Sun et al. [21] | |
| 3 | Annual whole plant mortality fraction | WPM | 1/year | White et al. [39] | |
| 4 | Annual fire mortality fraction | FM | 1/year | / | / |
| 5 | New fine root C: new leaf C | FRC:LC | ratio | White et al. [39] | |
| 6 | Current growth proportion | CGP | proportion | White et al. [39] | |
| 7 | C:N ratio of leaves | C:Nleaf | kgC/kgN | White et al. [39] | |
| 8 | C:N ratio of leaf litter | C:Nlit | kgC/kgN | White et al. [39] | |
| 9 | C:N ratio of fine roots | C:Nfr | kgC/kgN | White et al. [39] | |
| 10 | Leaf litter labile proportion | Llab | DIM | 1-Lcel-Llig | / |
| 11 | Leaf litter cellulose proportion | Lcel | DIM | White et al. [39] | |
| 12 | Leaf litter lignin proportion | Llig | DIM | White et al. [39] | |
| 13 | Fine root labile proportion | FRlab | DIM | 1-FRcel-FRlig | / |
| 14 | Fine root cellulose proportion | FRcel | DIM | White et al. [39] | |
| 15 | Fine root lignin proportion | FRlig | DIM | White et al. [39] | |
| 16 | Canopy water interception coefficient | Wint | 1/LAI/day | White et al. [39] | |
| 17 | Canopy light extinction coefficient | LEC | DIM | White et al. [39] | |
| 18 | All-sided to projected leaf area ratio | LAIall:prj | DIM | White et al. [39] | |
| 19 | Canopy average specific leaf area | SLA | m2/kgC | White et al. [39] | |
| 20 | Ratio of shaded SLA: sunlit SLA | SLAsha:sun | DIM | White et al. [39] | |
| 21 | Percent of leaf N in Rubisco | PLNR | DIM | White et al. [39] | |
| 22 | Maximum stomatal conductance | Gsmax | m/s | White et al. [39] | |
| 23 | Cuticular conductance | Gcut | m/s | 0.01*Gsmax | / |
| 24 | Boundary layer conductance | Gbl | m/s | White et al. [39] | |
| 25 | Leaf water potential: start of conductance reduction | LWPi | MPa | White et al. [39] | |
| 26 | Leaf water potential: complete conductance reduction | LWPf | MPa | White et al. [39] | |
| 27 | Vapor pressure deficit: start of conductance reduction | VPDi | Pa | White et al. [39] | |
| 28 | Vapor pressure deficit: complete conductance reduction | VPDf | Pa | White et al. [39] |
| Site | Grassland Subtype | Coordinate | Elevation | Canopy Height | Period |
|---|---|---|---|---|---|
| Haibei Station | Alpine Meadow | 37°37′N, 101°19′E | 3190 m | 0.2–0.3 m | 2003–2004 |
| Damxung Station | Alpine Steppe | 30°29′N, 91°04′E | 4330 m | <0.2 m | 2004–2005 |
| Influential Parameters 1 | Default Value | Calibrated Value | |
|---|---|---|---|
| Haibei Station | Damxung Station | ||
| FRC:LC | 2.0 | 2.07 | 1.94 |
| C:Nleaf | 24.0 | 32.93 | 35.04 |
| C:Nlit | 49.0 | 45.12 | 44.23 |
| C:Nfr | 42.0 | 43.66 | 35.42 |
| SLA | 45.0 | 44.39 | 44.61 |
| PLNR | 0.15 | 0.124 | 0.137 |
| Gsmax | 0.005 | 0.0025 | 0.0059 |
| LWPi | −0.6 | / 2 | −0.84 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, Y.; Wang, S.; Ma, Y.; Wang, X.; Liu, W. Improved Modeling of Gross Primary Productivity of Alpine Grasslands on the Tibetan Plateau Using the Biome-BGC Model. Remote Sens. 2019, 11, 1287. https://doi.org/10.3390/rs11111287
You Y, Wang S, Ma Y, Wang X, Liu W. Improved Modeling of Gross Primary Productivity of Alpine Grasslands on the Tibetan Plateau Using the Biome-BGC Model. Remote Sensing. 2019; 11(11):1287. https://doi.org/10.3390/rs11111287
Chicago/Turabian StyleYou, Yongfa, Siyuan Wang, Yuanxu Ma, Xiaoyue Wang, and Weihua Liu. 2019. "Improved Modeling of Gross Primary Productivity of Alpine Grasslands on the Tibetan Plateau Using the Biome-BGC Model" Remote Sensing 11, no. 11: 1287. https://doi.org/10.3390/rs11111287
APA StyleYou, Y., Wang, S., Ma, Y., Wang, X., & Liu, W. (2019). Improved Modeling of Gross Primary Productivity of Alpine Grasslands on the Tibetan Plateau Using the Biome-BGC Model. Remote Sensing, 11(11), 1287. https://doi.org/10.3390/rs11111287