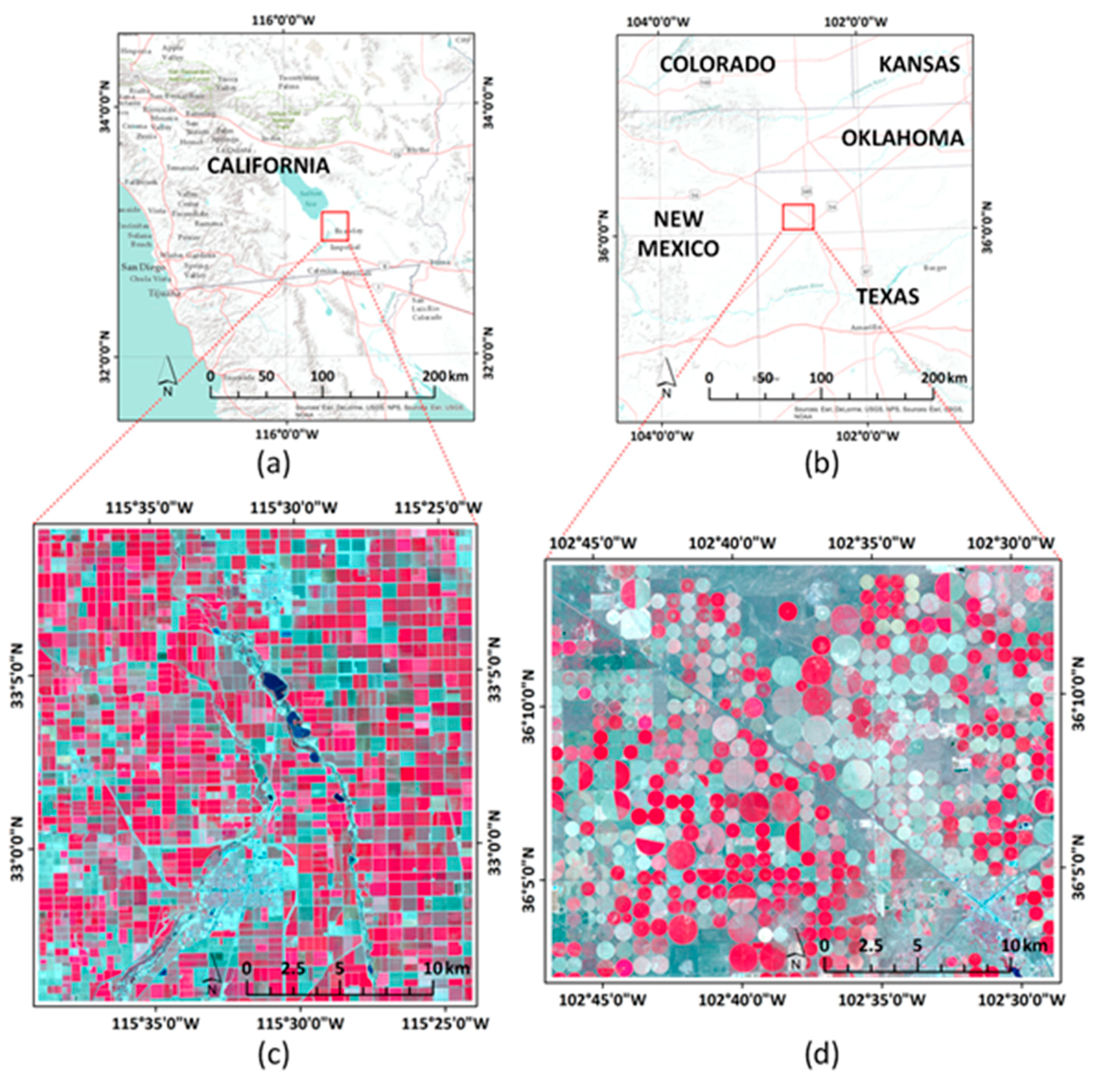
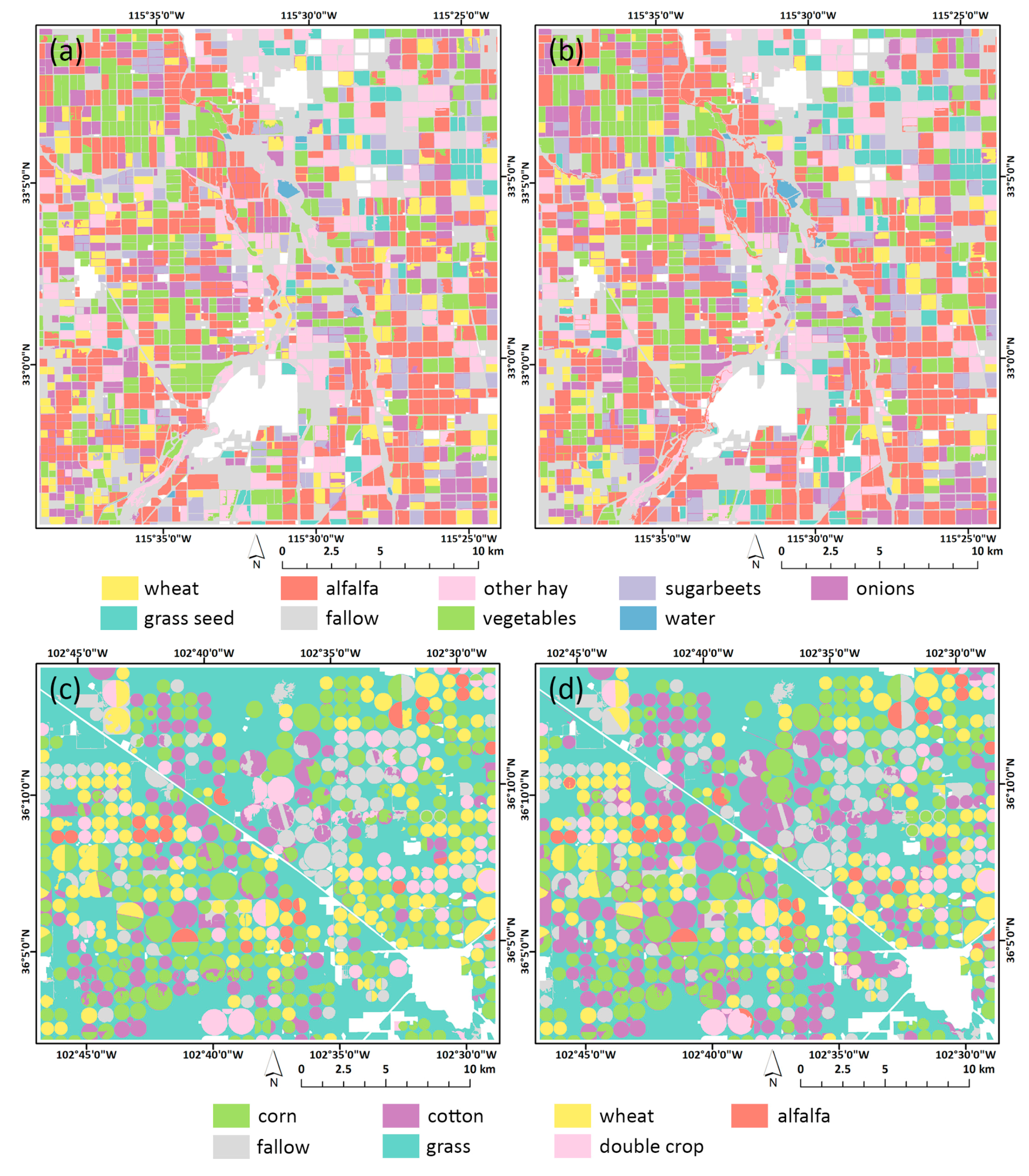
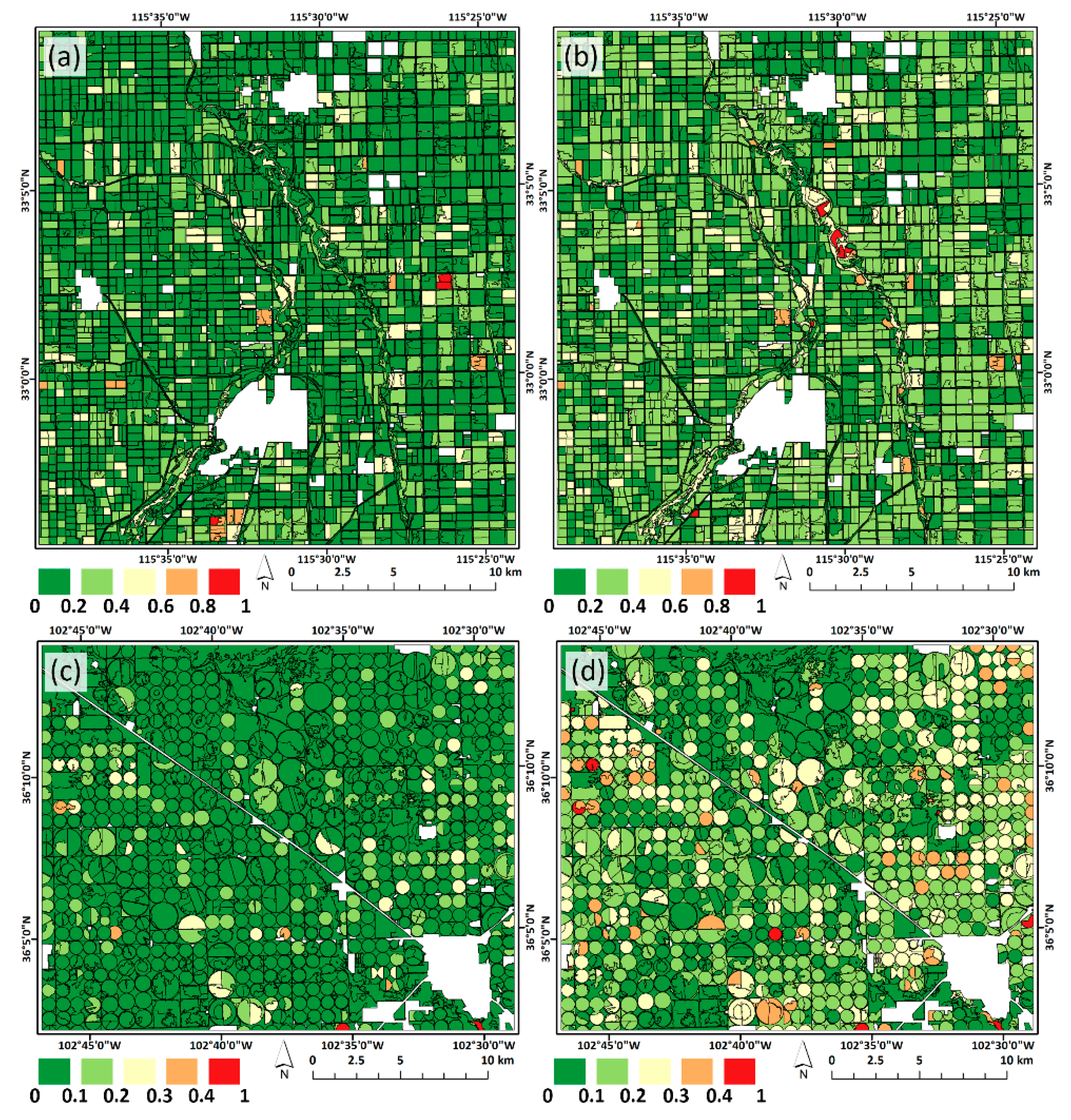
Figure 1.
Test area locations in California (first test area (TA1)) (a) and Texas (second test area (TA2)) (b). The false color composites for TA1 (1 May 2017) and TA2 (20 July 2017) are depicted in (c) and (d), respectively.
Figure 1.
Test area locations in California (first test area (TA1)) (a) and Texas (second test area (TA2)) (b). The false color composites for TA1 (1 May 2017) and TA2 (20 July 2017) are depicted in (c) and (d), respectively.
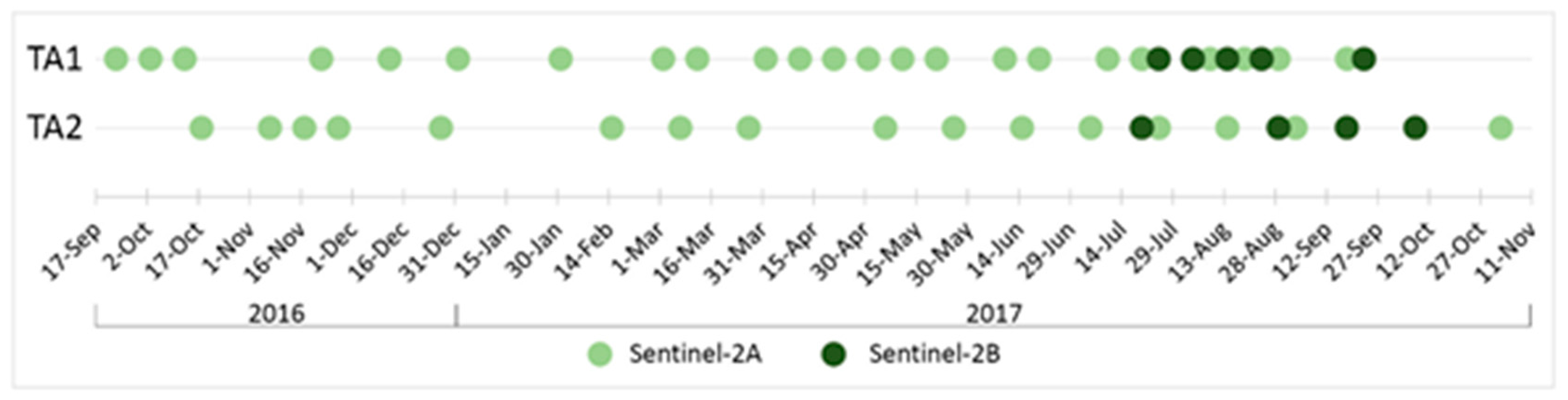
Figure 2.
Timeline of the two satellite image time series (SITS) used, composed of Sentinel-2A and 2B images with an irregular temporal distribution.
Figure 2.
Timeline of the two satellite image time series (SITS) used, composed of Sentinel-2A and 2B images with an irregular temporal distribution.
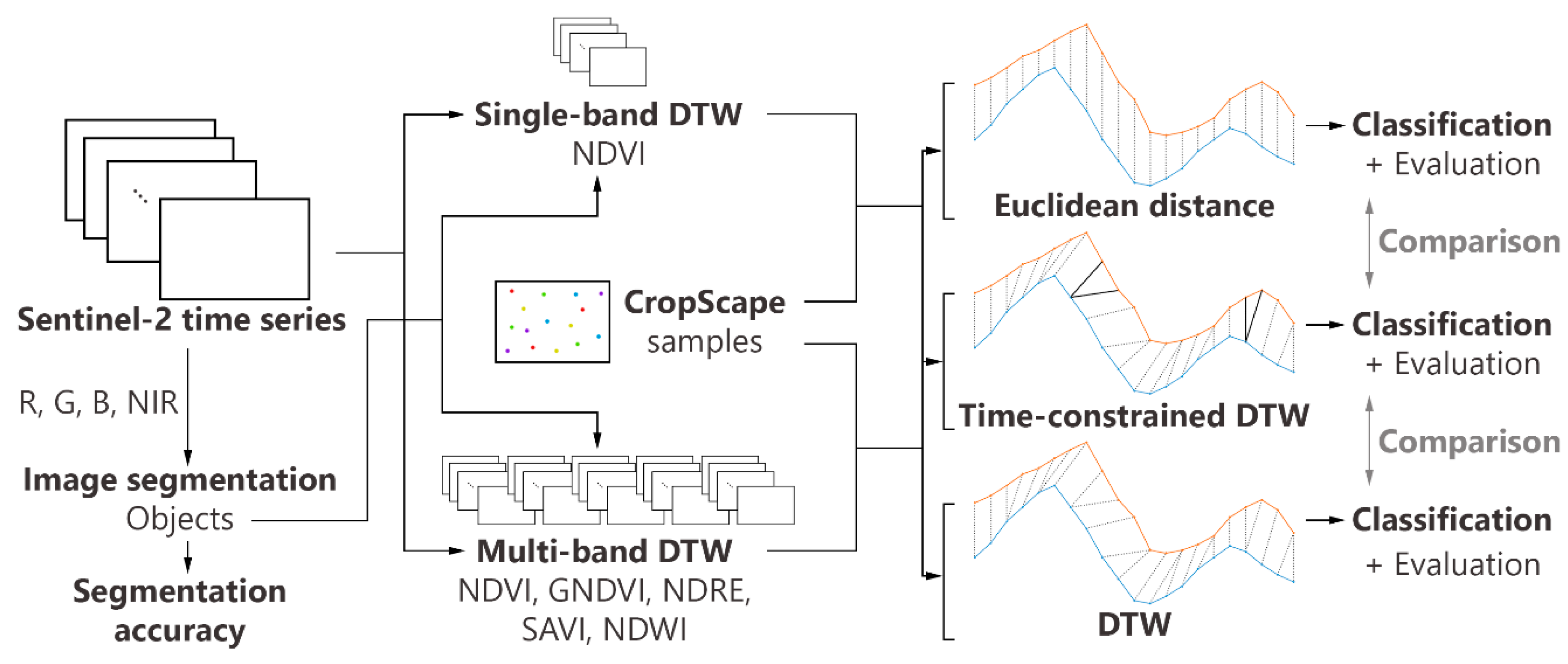
Figure 3.
Workflow of our object-based dynamic time warping (DTW) classifications using multiple vegetation indices extracted from Sentinel-2 SITS, as shown in
Table 1.
Figure 3.
Workflow of our object-based dynamic time warping (DTW) classifications using multiple vegetation indices extracted from Sentinel-2 SITS, as shown in
Table 1.
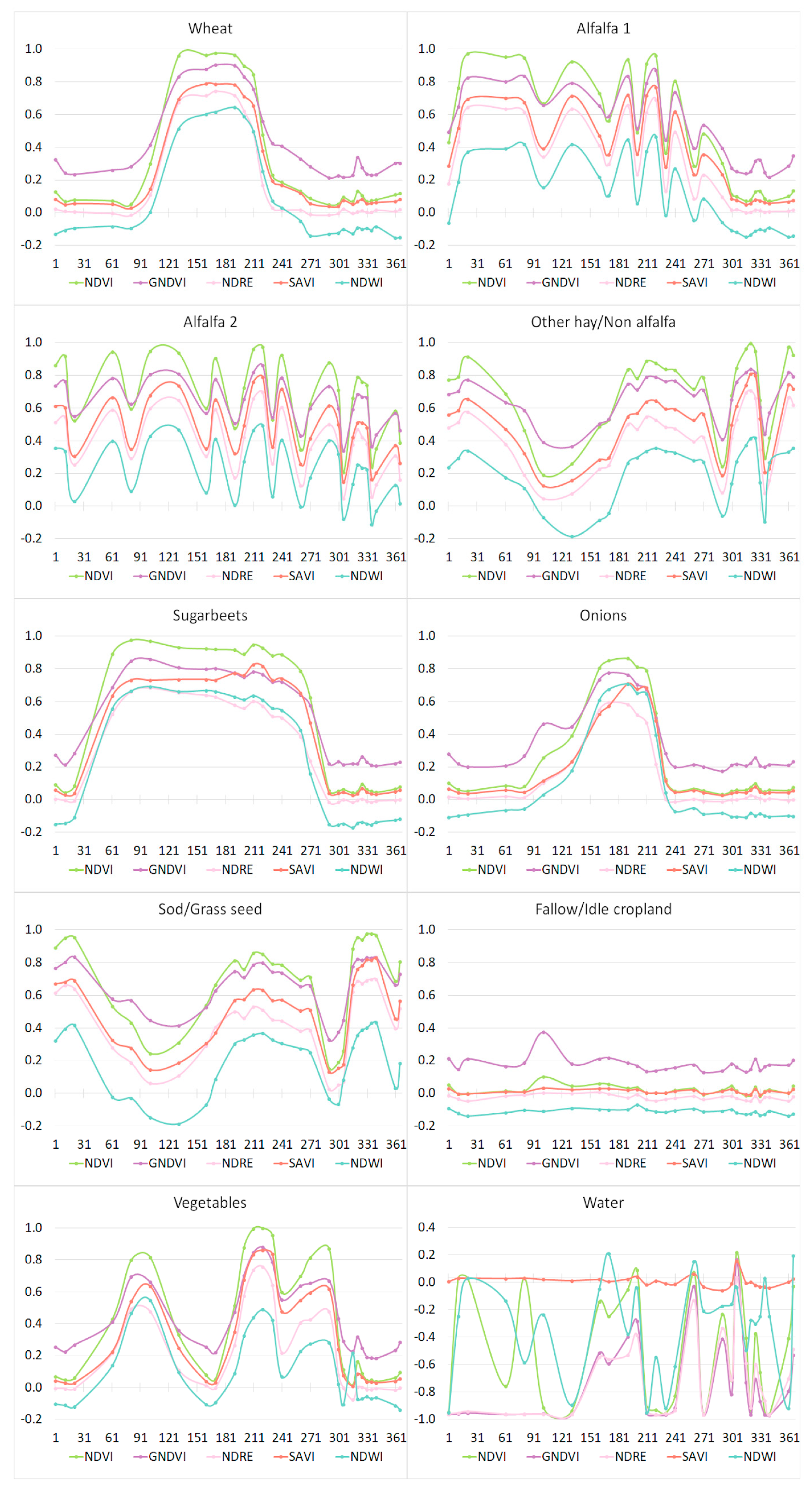
Figure 4.
The temporal patterns of the classes analyzed for TA1, with values of five vegetation indices shown on the vertical axis. We analyzed a single agricultural year, the horizontal axis shows the day-of-the-time-series, namely from 23 September 2016 to 23 September 2017 (365 days). Two temporal patterns were identified for alfalfa (1 and 2). The vegetation indices are the Normalized Difference Vegetation Index (NDVI), Green Normalized Difference Vegetation Index (GNDVI), Normalized Difference Red-Edge (NDRE), Soil Adjusted Vegetation Index (SAVI), and Normalized Difference Water Index (NDWI), derived as shown in
Table 1.
Figure 4.
The temporal patterns of the classes analyzed for TA1, with values of five vegetation indices shown on the vertical axis. We analyzed a single agricultural year, the horizontal axis shows the day-of-the-time-series, namely from 23 September 2016 to 23 September 2017 (365 days). Two temporal patterns were identified for alfalfa (1 and 2). The vegetation indices are the Normalized Difference Vegetation Index (NDVI), Green Normalized Difference Vegetation Index (GNDVI), Normalized Difference Red-Edge (NDRE), Soil Adjusted Vegetation Index (SAVI), and Normalized Difference Water Index (NDWI), derived as shown in
Table 1.
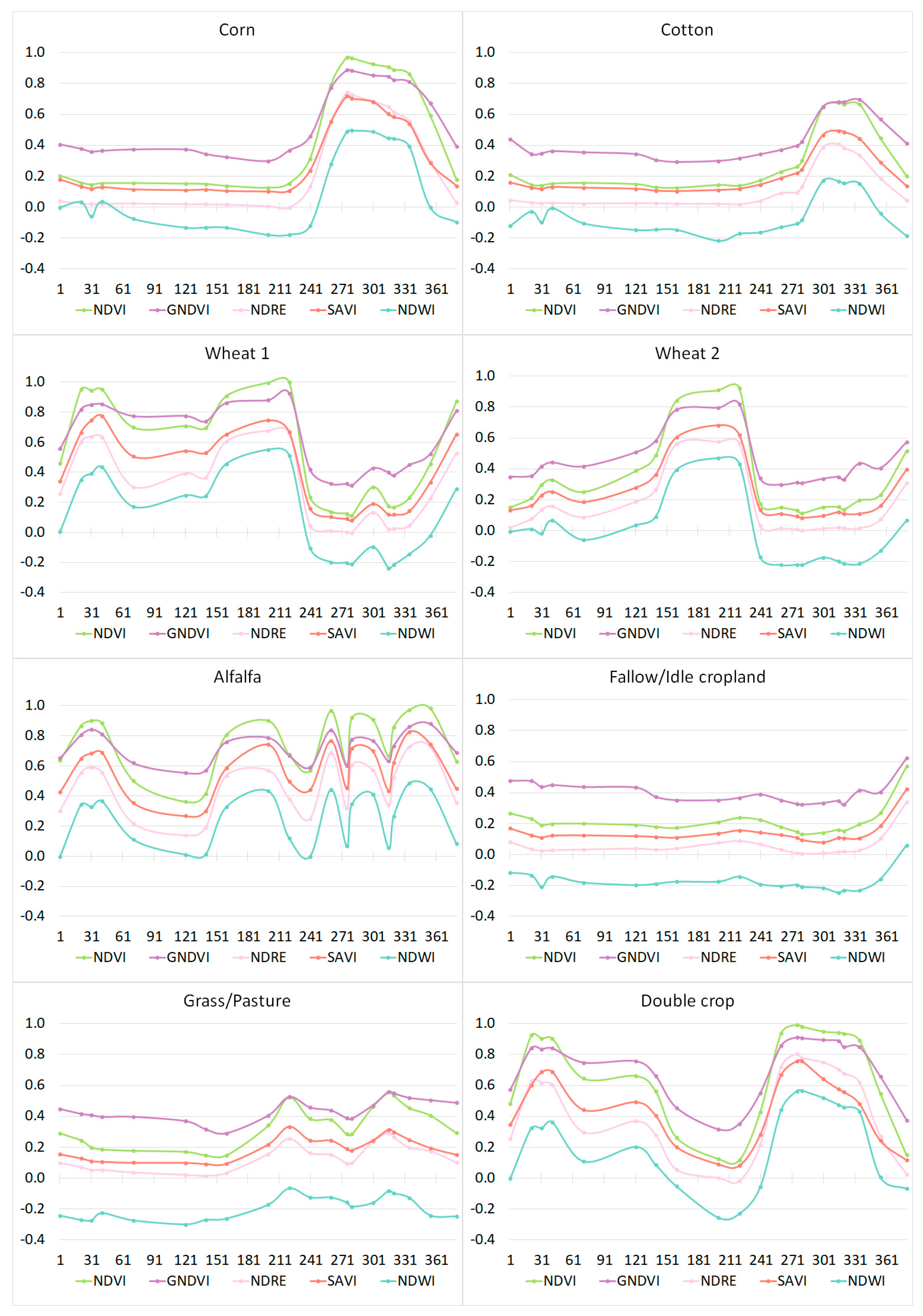
Figure 5.
The temporal patterns of the classes analyzed for TA2, with values of five vegetation indices shown on the vertical axis (NDVI, GNDVI, NDRE, SAVI, and NDWI). We analyzed a single agricultural year, the horizontal axis shows the day-of-the-time-series, namely from 18 October 2016 to 2 November 2017 (380 days). Two temporal patterns were identified for winter wheat (wheat 1 and 2).
Figure 5.
The temporal patterns of the classes analyzed for TA2, with values of five vegetation indices shown on the vertical axis (NDVI, GNDVI, NDRE, SAVI, and NDWI). We analyzed a single agricultural year, the horizontal axis shows the day-of-the-time-series, namely from 18 October 2016 to 2 November 2017 (380 days). Two temporal patterns were identified for winter wheat (wheat 1 and 2).
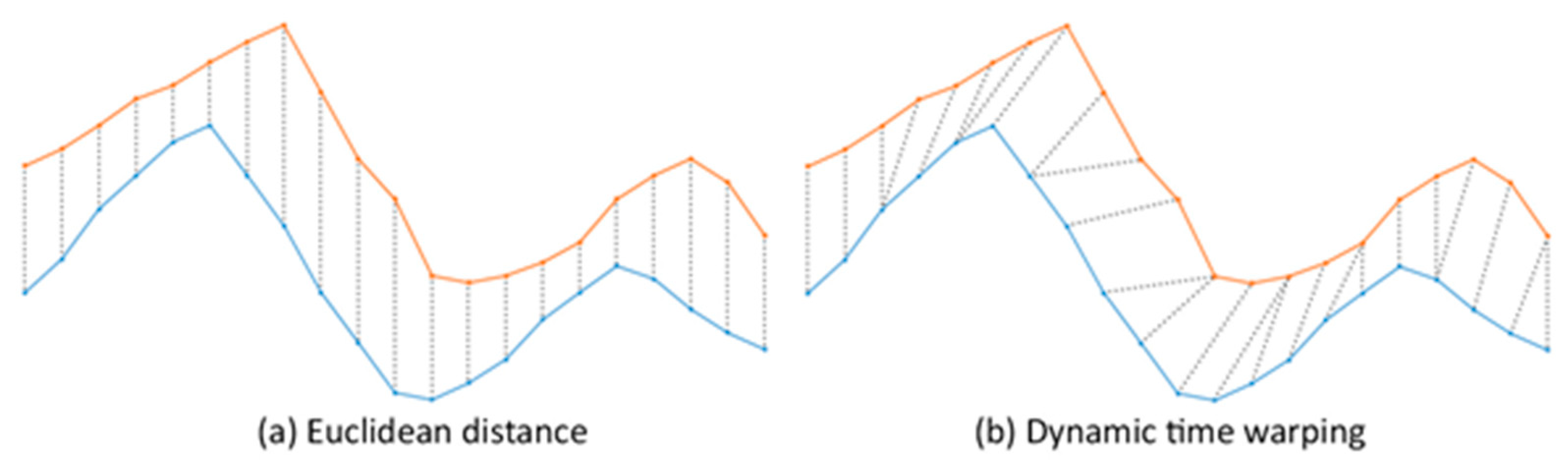
Figure 6.
Comparison between two sequences: (a) while Euclidean distance is time-rigid, (b) the dynamic time warping (DTW) is time-flexible in dealing with possible time distortion between the sequences. This flexibility is desirable for crop mapping, to deal with the intra-class phenological discrepancies caused by different environmental conditions.
Figure 6.
Comparison between two sequences: (a) while Euclidean distance is time-rigid, (b) the dynamic time warping (DTW) is time-flexible in dealing with possible time distortion between the sequences. This flexibility is desirable for crop mapping, to deal with the intra-class phenological discrepancies caused by different environmental conditions.
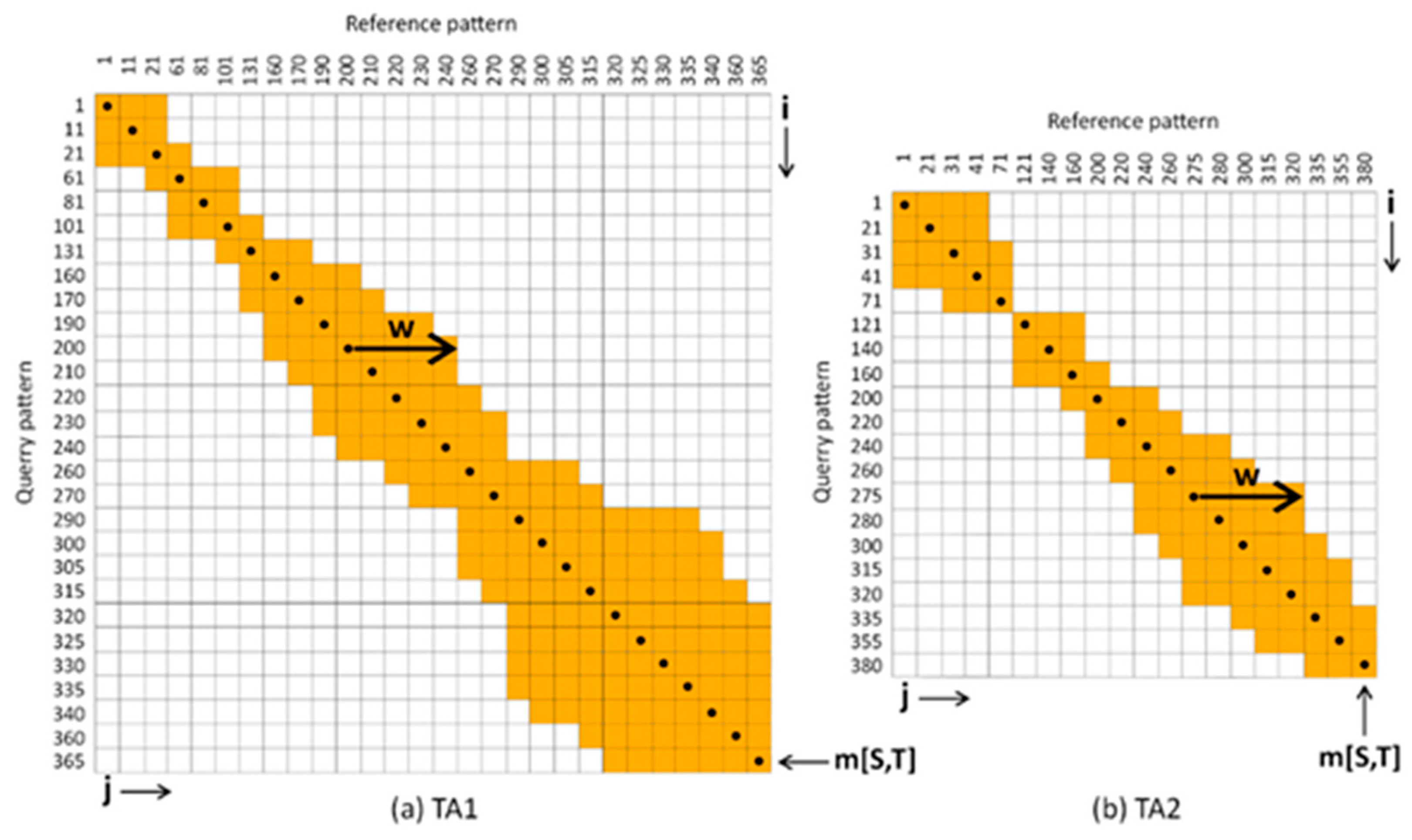
Figure 7.
Computing the alignment between two sequences of TA1 (a) and TA2 (b). The vertical and horizontal values represent the date of an image from SITS, starting from 1 to 365 for TA1 and from 1 to 380 for TA2. Indices i and j are used to parse the matrix by line and by column, respectively. In these two examples, a maximum time delay, w, of 45 days is depicted, meaning that only the elements of the matrix who fall within this condition (orange) are computed. With black dots is represented the main diagonal of the DTW matrix (resembling Euclidean distance). After computing the matrix from upper left to lower right, the last element of the matrix, m[S,T], is returned, as a measure of DTW dissimilarity between the two compared sequences.
Figure 7.
Computing the alignment between two sequences of TA1 (a) and TA2 (b). The vertical and horizontal values represent the date of an image from SITS, starting from 1 to 365 for TA1 and from 1 to 380 for TA2. Indices i and j are used to parse the matrix by line and by column, respectively. In these two examples, a maximum time delay, w, of 45 days is depicted, meaning that only the elements of the matrix who fall within this condition (orange) are computed. With black dots is represented the main diagonal of the DTW matrix (resembling Euclidean distance). After computing the matrix from upper left to lower right, the last element of the matrix, m[S,T], is returned, as a measure of DTW dissimilarity between the two compared sequences.
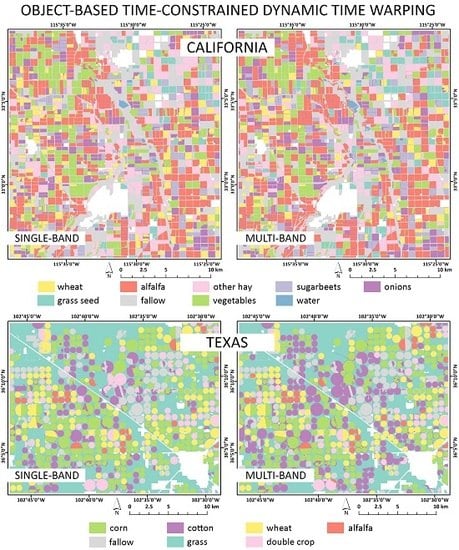
Figure 8.
Best classification results for single-band (a) and multi-band DTW (b) for TA1 using in both cases a time constraint of 30 days (DTW30). Best classification results for single-band (c) and multi-band DTW (d) for TA2 using 45- and 30-day time constraints, respectively (DTW45 and DTW 30). For clarity, the developed/low to medium intensity areas are masked with white.
Figure 8.
Best classification results for single-band (a) and multi-band DTW (b) for TA1 using in both cases a time constraint of 30 days (DTW30). Best classification results for single-band (c) and multi-band DTW (d) for TA2 using 45- and 30-day time constraints, respectively (DTW45 and DTW 30). For clarity, the developed/low to medium intensity areas are masked with white.
Figure 9.
DTW dissimilarity values for single-band (a) and multi-band DTW (b) for TA1 using in both cases a time constraint of 30 days (DTW30). DTW dissimilarity values for single-band DTW45 (c) and multi-band DTW30 (d) for TA2 using 45- and 30-day time constraints, respectively. For clarity, the developed/low to medium intensity areas are masked with white.
Figure 9.
DTW dissimilarity values for single-band (a) and multi-band DTW (b) for TA1 using in both cases a time constraint of 30 days (DTW30). DTW dissimilarity values for single-band DTW45 (c) and multi-band DTW30 (d) for TA2 using 45- and 30-day time constraints, respectively. For clarity, the developed/low to medium intensity areas are masked with white.
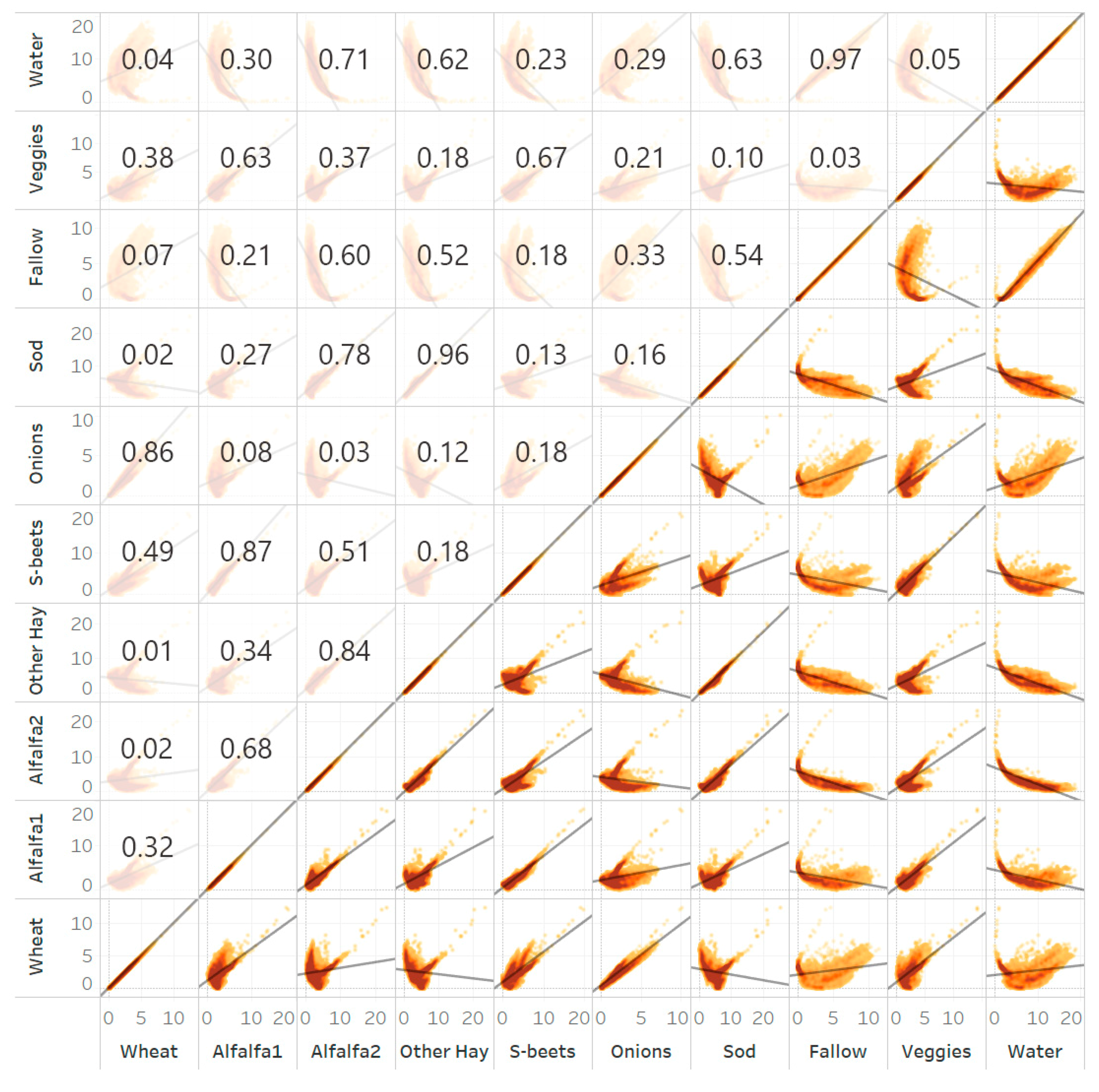
Figure 10.
DTW dissimilarity values scatter plots computed for each class for the single-band DTW30 of California, with R2 values in the upper left of the diagonal. Classes analyzed are wheat, alfalfa1, alfalfa2, other hay/non-alfalfa, sugarbeets, onions, sod/grass seed, fallow/idle cropland, vegetables, and water.
Figure 10.
DTW dissimilarity values scatter plots computed for each class for the single-band DTW30 of California, with R2 values in the upper left of the diagonal. Classes analyzed are wheat, alfalfa1, alfalfa2, other hay/non-alfalfa, sugarbeets, onions, sod/grass seed, fallow/idle cropland, vegetables, and water.
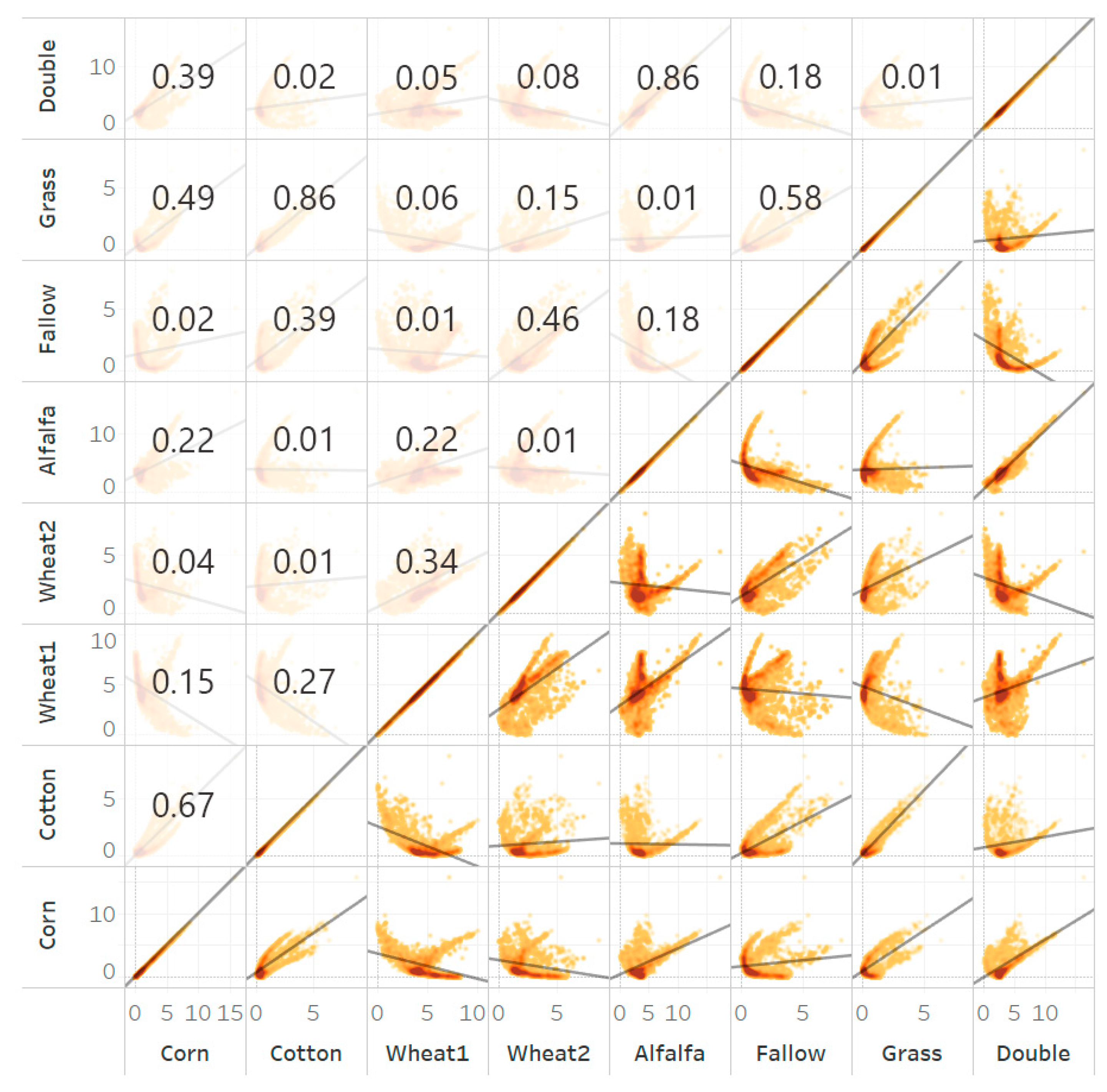
Figure 11.
DTW dissimilarity values scatter plots computed for each class for the single-band DTW45 of Texas, with R2 values in the upper left of the diagonal. Classes analyzed are corn, cotton, winter wheat1, winter wheat2, alfalfa, fallow/idle cropland, grass/pasture, and double crop.
Figure 11.
DTW dissimilarity values scatter plots computed for each class for the single-band DTW45 of Texas, with R2 values in the upper left of the diagonal. Classes analyzed are corn, cotton, winter wheat1, winter wheat2, alfalfa, fallow/idle cropland, grass/pasture, and double crop.
Table 1.
Vegetation indices we used for crop mapping, their equation and range of values. Sentinel-2 bands used are the green (B3, 0.560 μm), red (B4, 0.665 μm), red-edge 1 (B5, 0.705 μm), red-edge 2 (B6, 0.740 μm), near-infrared (B8, 0.842 μm), narrow near-infrared (B8A, 0.865 μm), and SWIR (B11, 1.610 μm).
Table 1.
Vegetation indices we used for crop mapping, their equation and range of values. Sentinel-2 bands used are the green (B3, 0.560 μm), red (B4, 0.665 μm), red-edge 1 (B5, 0.705 μm), red-edge 2 (B6, 0.740 μm), near-infrared (B8, 0.842 μm), narrow near-infrared (B8A, 0.865 μm), and SWIR (B11, 1.610 μm).
| Name | Description | Equation | Range |
|---|
| NDVI | Normalized Difference Vegetation Index | (B8 − B4) / (B8 + B4) | [−1, 1] |
| GNDVI | Green Normalized Difference Vegetation Index | (B8 − B3) / (B8 + B3) | [−1, 1] |
| NDRE | Normalized Difference Red-Edge | (B6 − B5) / (B6 + B5) | [−1, 1] |
| SAVI | Soil Adjusted Vegetation Index | ((B8 − B4) / (B8 + B4 + 0.5)) × (1 + 0.5) | [−1, 1] |
| NDWI | Normalized Difference Water Index | (B8A − B11) / (B8A + B11) | [−1, 1] |
Table 2.
The number of reference (ref.) and validation (valid.) samples for TA1 and TA2, respectively. For alfalfa in TA1 and winter wheat in TA2, two distinct temporal patterns were identified, as detailed in
Section 2.1.5.
Table 2.
The number of reference (ref.) and validation (valid.) samples for TA1 and TA2, respectively. For alfalfa in TA1 and winter wheat in TA2, two distinct temporal patterns were identified, as detailed in
Section 2.1.5.
| California (TA1) | Texas (TA2) |
|---|
| Class | Ref. | Valid. | Class | Ref. | Valid. |
|---|
| Wheat | 3 | 48 | Corn | 3 | 287 |
| Alfalfa | 3, 3 | 569 | Cotton | 3 | 122 |
| Other hay/non-alfalfa | 3 | 116 | Winter wheat | 3, 3 | 171 |
| Sugarbeets | 3 | 70 | Alfalfa | 3 | 34 |
| Onions | 3 | 98 | Fallow/idle cropland | 3 | 41 |
| Sod/grass seed | 3 | 82 | Grass/pasture | 3 | 129 |
| Fallow/idle cropland | 3 | 76 | Double crop | 3 | 60 |
| Vegetables | 3 | 47 | | | |
| Water | 3 | 30 | | | |
| Total | 30 | 1136 | Total | 24 | 844 |
Table 3.
Segmentation accuracy measures, their equations, ideal values and their range (C represents the total area of evaluated objects; R denotes the total area of reference objects). Area fit index (AFI), over-segmentation (OS), under-segmentation (US), root mean square (D), quality rate (QR).
Table 3.
Segmentation accuracy measures, their equations, ideal values and their range (C represents the total area of evaluated objects; R denotes the total area of reference objects). Area fit index (AFI), over-segmentation (OS), under-segmentation (US), root mean square (D), quality rate (QR).
| Measure | Equation | Ideal Value | Range |
|---|
| Over-segmentation | | 0 | [0, 1] |
| Under-segmentation | | 0 | [0, 1] |
| Area fit index | | 0 | OS: AFI > 0; US: AFI < 0 |
| Root mean square | | 0 | [0, 1] |
| Quality rate | | 1 | [0, 1] |
Table 4.
Segmentation accuracy results depicting the scale parameter (SP), number of objects, over-segmentation (OS), under-segmentation (US), area fit index (AFI), root mean square (D), and quality rate (QR) metrics, as detailed in
Table 3.
Table 4.
Segmentation accuracy results depicting the scale parameter (SP), number of objects, over-segmentation (OS), under-segmentation (US), area fit index (AFI), root mean square (D), and quality rate (QR) metrics, as detailed in
Table 3.
| Test Area | SP | Objects | OS | US | AFI | D | QR |
|---|
| TA1 | 241 | 3492 | 0.05 | 0.04 | 0.01 | 0.05 | 0.91 |
| TA2 | 307 | 1585 | 0.16 | 0.02 | 0.14 | 0.11 | 0.82 |
Table 5.
Classification accuracies for single-band and multi-band object-based time-constrained dynamic time warping (DTW) using 15, 30, 45, and 60 days. For comparison, the accuracies obtained using no time constraint (DTWFull) and using Euclidean distance (DTW0) are shown. With bold fonts are shown the DTW classifications with the highest overall accuracies.
Table 5.
Classification accuracies for single-band and multi-band object-based time-constrained dynamic time warping (DTW) using 15, 30, 45, and 60 days. For comparison, the accuracies obtained using no time constraint (DTWFull) and using Euclidean distance (DTW0) are shown. With bold fonts are shown the DTW classifications with the highest overall accuracies.
| Test Area | DTW Type | DTW0 (%) | DTW15 (%) | DTW30 (%) | DTW45 (%) | DTW60 (%) | DTWFull (%) |
|---|
| TA1 | single-band | 75.2 | 77.7 | 79.5 | 79.5 | 76.6 | 72.3 |
| | multi-band | 76.1 | 80.3 | 85.6 | 85.6 | 84.3 | 82.3 |
| TA2 | single-band | 86.8 | 86.7 | 87.8 | 89.1 | 88.6 | 82.3 |
| | multi-band | 86.1 | 86.1 | 87.6 | 86.0 | 85.5 | 83.3 |
Table 6.
User’s (UA) and producer’s accuracy (PA) for most accurate single-band (DTW30) and multi-band (DTW30) object-based time-constrained DTWs for TA1, in California.
Table 6.
User’s (UA) and producer’s accuracy (PA) for most accurate single-band (DTW30) and multi-band (DTW30) object-based time-constrained DTWs for TA1, in California.
| Crop | Single-Band DTW30 | Multi-Band DTW30 |
|---|
| UA | PA | UA | PA |
|---|
| Wheat | 56.5 | 81.3 | 82.0 | 85.4 |
| Alfalfa | 98.2 | 77.7 | 98.8 | 85.4 |
| Other hay/non-alfalfa | 65.9 | 78.4 | 74.4 | 75.0 |
| Sugarbeets | 69.6 | 91.4 | 77.3 | 97.1 |
| Onions | 88.4 | 85.7 | 91.8 | 90.8 |
| Sod/grass seed | 82.4 | 51.2 | 77.9 | 64.6 |
| Fallow/idle cropland | 86.4 | 100 | 92.7 | 100 |
| Vegetables | 33.8 | 97.8 | 39.1 | 97.8 |
| Water | 100 | 63.3 | 100 | 86.7 |
Table 7.
User’s (UA) and producer’s accuracy (PA) for most accurate single-band (DTW45) and multi-band (DTW30) object-based time-constrained DTWs for TA2, in Texas.
Table 7.
User’s (UA) and producer’s accuracy (PA) for most accurate single-band (DTW45) and multi-band (DTW30) object-based time-constrained DTWs for TA2, in Texas.
| Crop | Single-Band DTW45 | Multi-Band DTW30 |
|---|
| UA | PA | UA | PA |
|---|
| Corn | 96.0 | 92.3 | 96.5 | 86.8 |
| Cotton | 88.6 | 82.8 | 72.4 | 92.6 |
| Wheat | 98.1 | 90.6 | 98.0 | 87.1 |
| Alfalfa | 87.2 | 100 | 85.0 | 100 |
| Fallow/idle cropland | 66.7 | 48.8 | 55.8 | 58.5 |
| Grass/pasture | 77.3 | 97.7 | 84.0 | 97.7 |
| Double crop | 79.7 | 85.0 | 97.8 | 73.3 |
Table 8.
Errors for UAs and PAs for single-band DTW30 and multi-band DTW30 for California, compared with those from CropScape. With * are shown the CropScape errors at the scale of California and UA+ and PA+ represent the combined errors, shown in bold.
Table 8.
Errors for UAs and PAs for single-band DTW30 and multi-band DTW30 for California, compared with those from CropScape. With * are shown the CropScape errors at the scale of California and UA+ and PA+ represent the combined errors, shown in bold.
| | CropScape | Single-band DTW30 | Multi-band DTW30 |
|---|
| Crop | UA* | PA* | UA | UA+ | PA | PA+ | UA | UA+ | PA | PA+ |
|---|
| Wheat | 27.6 | 31.9 | 43.5 | 51.5 | 18.7 | 37.0 | 18.0 | 33.0 | 14.6 | 35.1 |
| Alfalfa | 12.5 | 8.4 | 1.8 | 12.6 | 22.3 | 23.8 | 1.2 | 12.6 | 14.6 | 16.8 |
| Other hay | 34.5 | 46.4 | 34.1 | 48.5 | 21.6 | 51.2 | 25.6 | 43.0 | 25.0 | 52.7 |
| Sugarbeets | 14.0 | 53.3 | 30.4 | 33.5 | 8.6 | 54.0 | 22.7 | 26.7 | 2.9 | 53.4 |
| Onions | 28.6 | 21.4 | 11.6 | 30.9 | 14.3 | 25.7 | 8.2 | 29.8 | 9.2 | 23.3 |
| Sod | 34.7 | 52.8 | 17.6 | 38.9 | 48.8 | 71.9 | 22.1 | 41.1 | 35.4 | 63.6 |
| Fallow | 19.5 | 19.2 | 13.6 | 23.8 | 0 | 19.2 | 7.3 | 20.8 | 0 | 19.2 |
| Vegetables | 79.9 | 54.9 | 66.2 | 103.8 | 2.2 | 54.9 | 60.9 | 100.5 | 2.2 | 54.9 |
| Water | 7 | 7.8 | 0 | 7.0 | 36.7 | 37.5 | 0 | 7.0 | 13.3 | 15.4 |
Table 9.
Errors for UAs and PAs for single-band DTW45 and multi-band DTW30 for Texas (TA2), compared with those from CropScape. With * are shown the CropScape errors at the scale of Texas and UA+ and PA+ represent the combined errors, shown in bold.
Table 9.
Errors for UAs and PAs for single-band DTW45 and multi-band DTW30 for Texas (TA2), compared with those from CropScape. With * are shown the CropScape errors at the scale of Texas and UA+ and PA+ represent the combined errors, shown in bold.
| | CropScape | Single-band DTW45 | Multi-band DTW30 |
|---|
| Crop | UA* | PA* | UA | UA+ | PA | PA+ | UA | UA+ | PA | PA+ |
|---|
| Corn | 9.7 | 16.2 | 4.0 | 10.5 | 7.7 | 17.9 | 3.5 | 10.3 | 13.2 | 20.9 |
| Cotton | 16.6 | 10.7 | 13.4 | 21.3 | 17.2 | 20.3 | 27.6 | 32.2 | 7.4 | 13.0 |
| Wheat | 16.9 | 13.5 | 1.9 | 17.0 | 9.4 | 16.5 | 2.0 | 17.0 | 12.9 | 18.7 |
| Alfalfa | 13.0 | 26.1 | 12.8 | 18.2 | 0 | 26.1 | 15.0 | 19.8 | 0 | 26.1 |
| Fallow | 30.5 | 57.0 | 33.3 | 45.2 | 51.2 | 76.6 | 44.2 | 53.7 | 41.5 | 70.5 |
| Grass | 30.7 | 17.1 | 22.7 | 38.2 | 2.3 | 17.3 | 16.0 | 34.6 | 2.3 | 17.3 |
| Double | 75.2 | 83.9 | 20.3 | 77.9 | 15 | 85.2 | 2.2 | 75.2 | 26.7 | 88.0 |