Estimation of Winter Wheat Residue Coverage Using Optical and SAR Remote Sensing Images
Abstract
1. Introduction
2. Materials and Methods
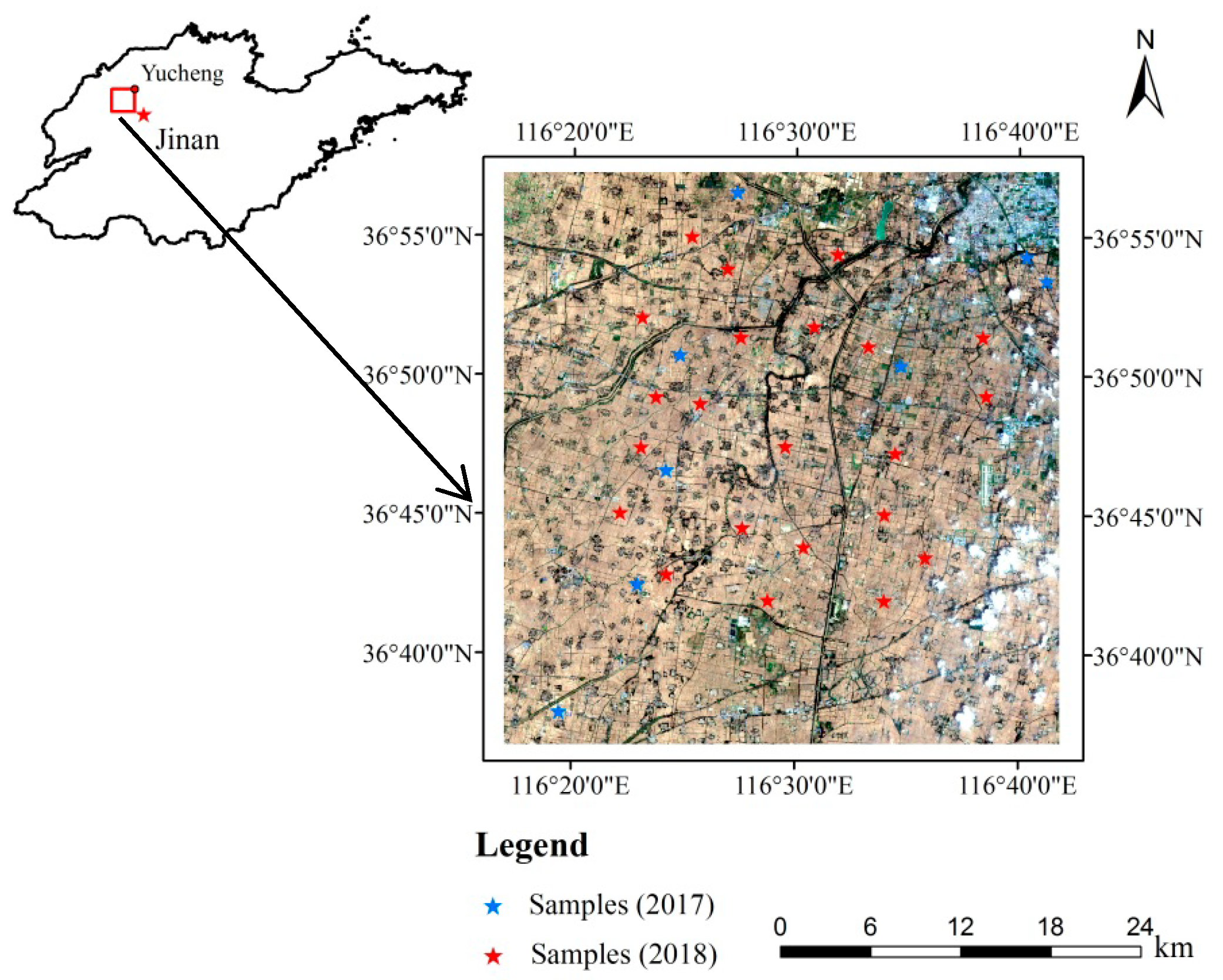
2.1. Study Area
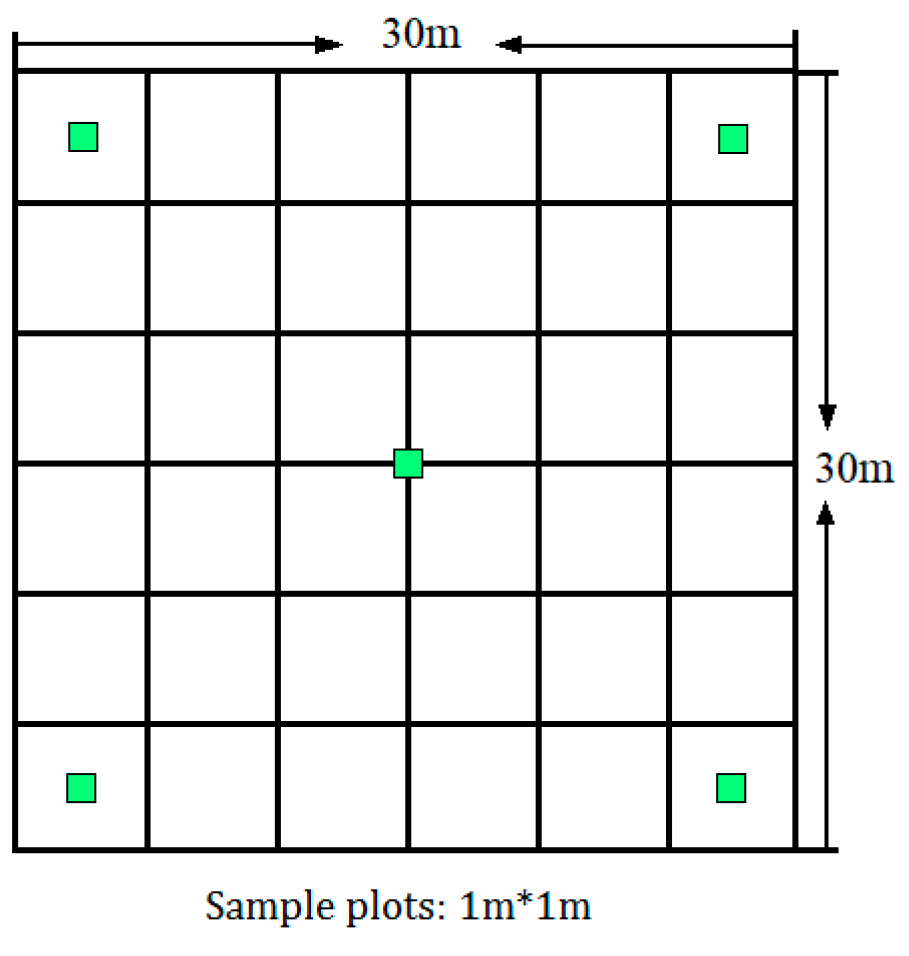
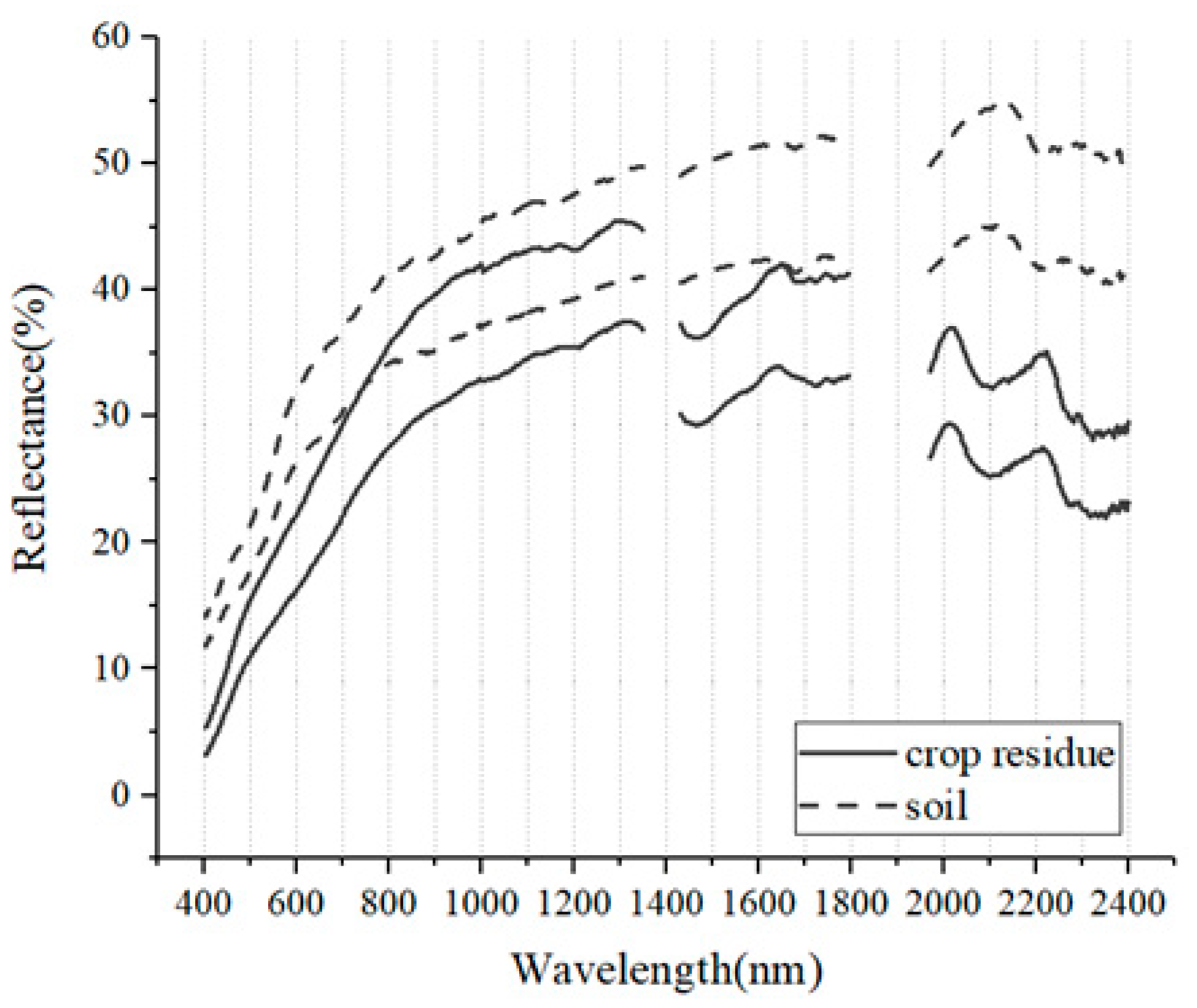
2.2. Field Measurement Data
2.3. Satellite Data and Pre-Processing
2.3.1. Sentinel-1 Imagery
2.3.2. Sentinel-2 Imagery
2.4. Methods
2.4.1. Calculations of Satellite Derived Variables
2.4.2. Optimal Subset Regression Method
2.4.3. Statistical Analysis
2.4.4. Extraction of Winter Wheat Cultivation Area
3. Results
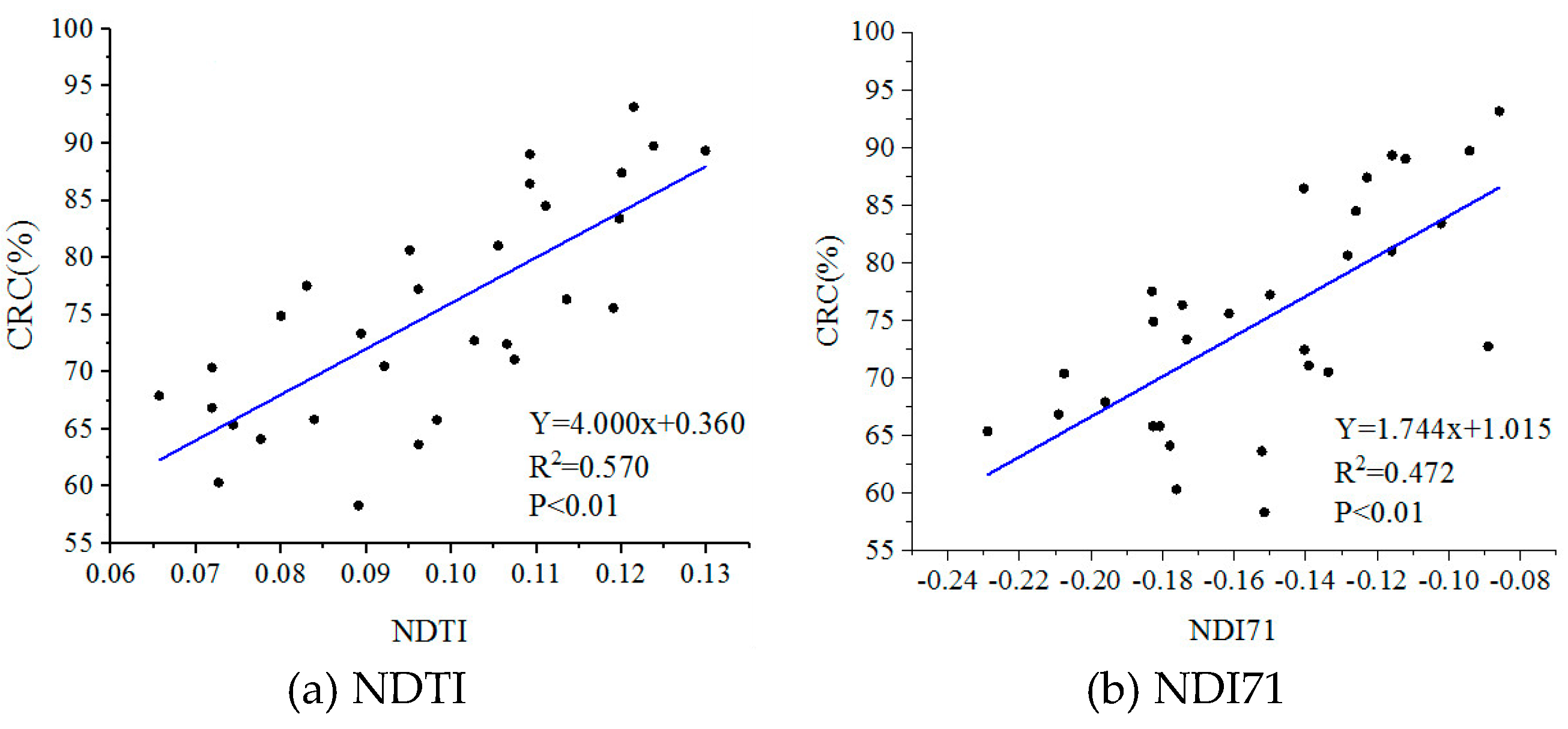
3.1. Correlation between Optical Crop Residue Indices and Field Measured CRC
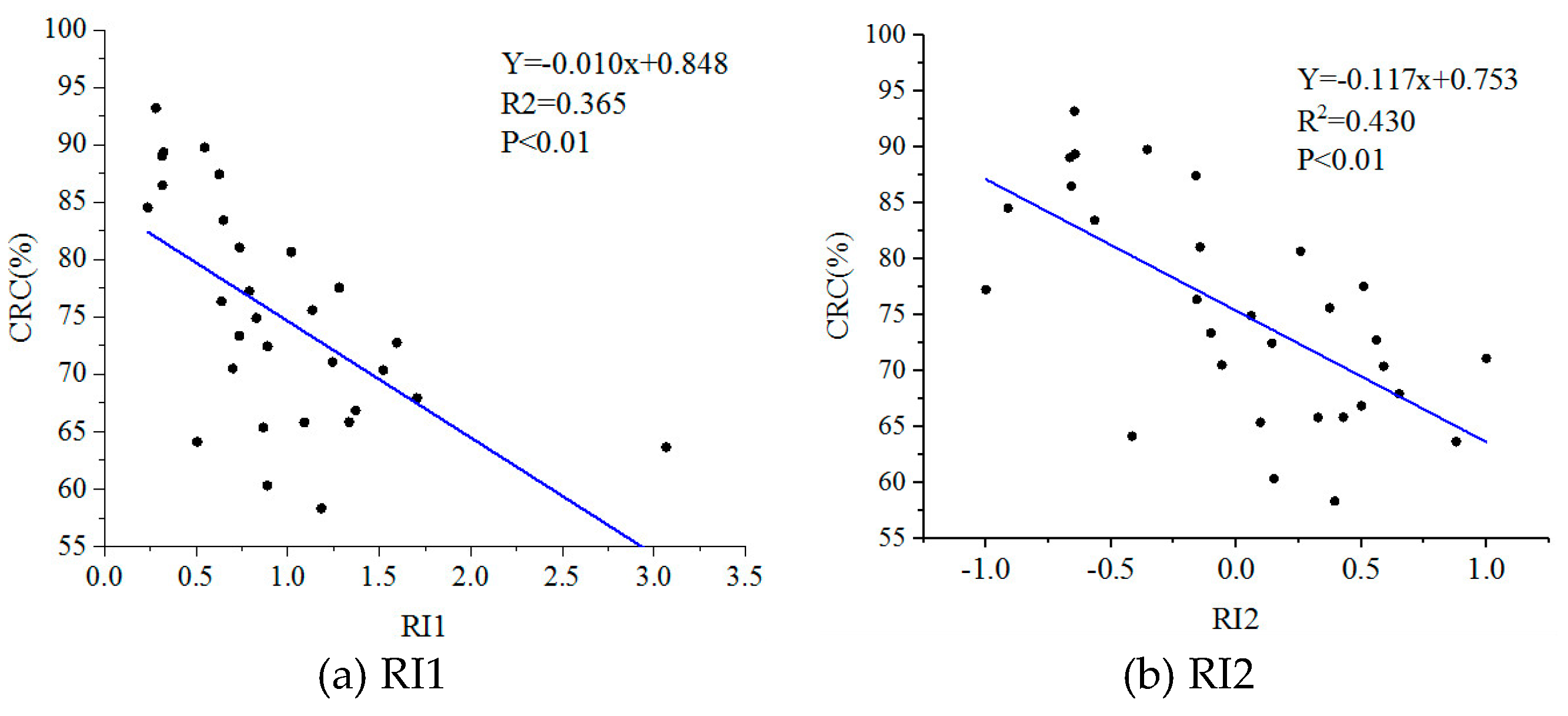
3.2. Correlation between Radar Parameters and Field Measured CRC
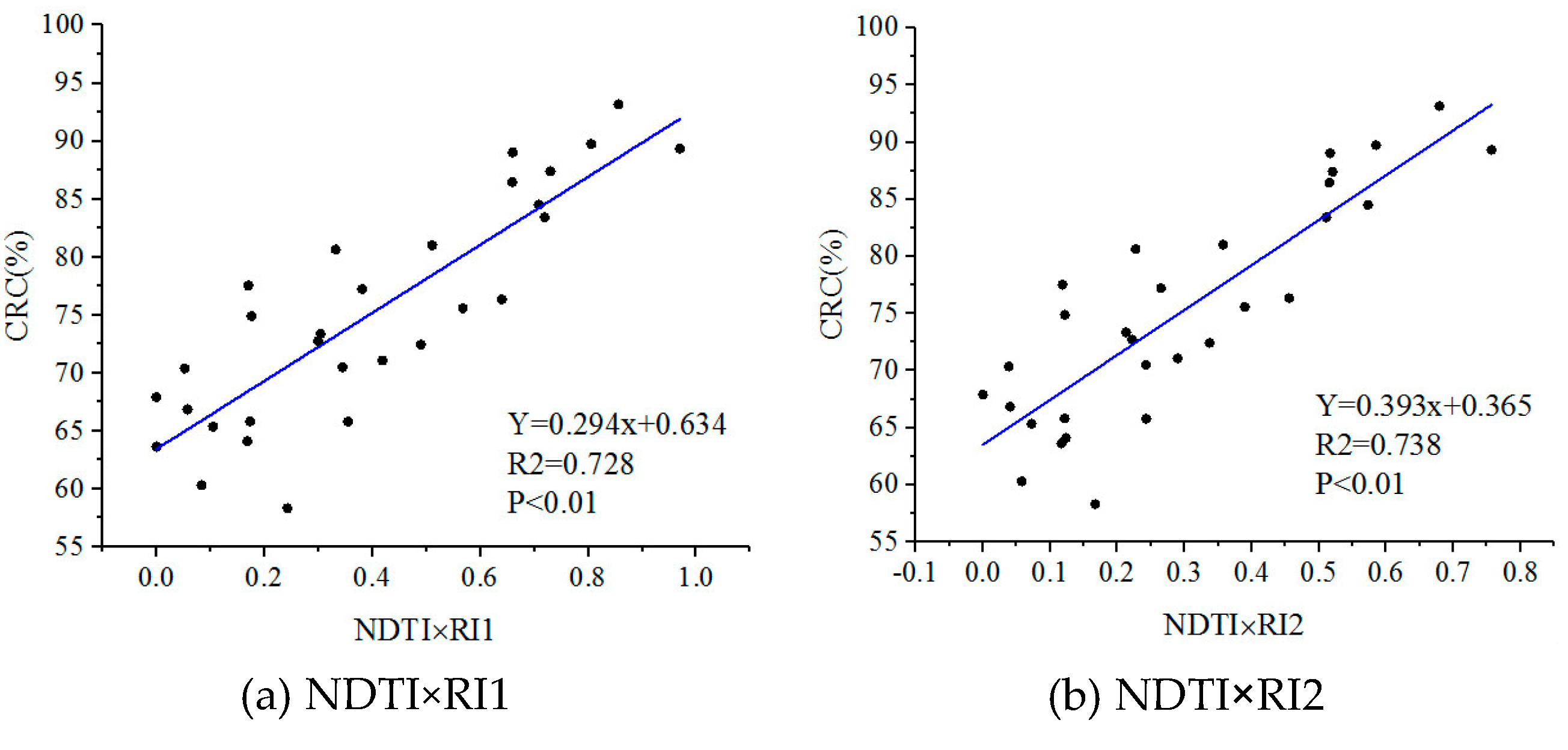
3.3. Correlation of Combined Optical Crop Residue Indices and Radar Parameters with CRC
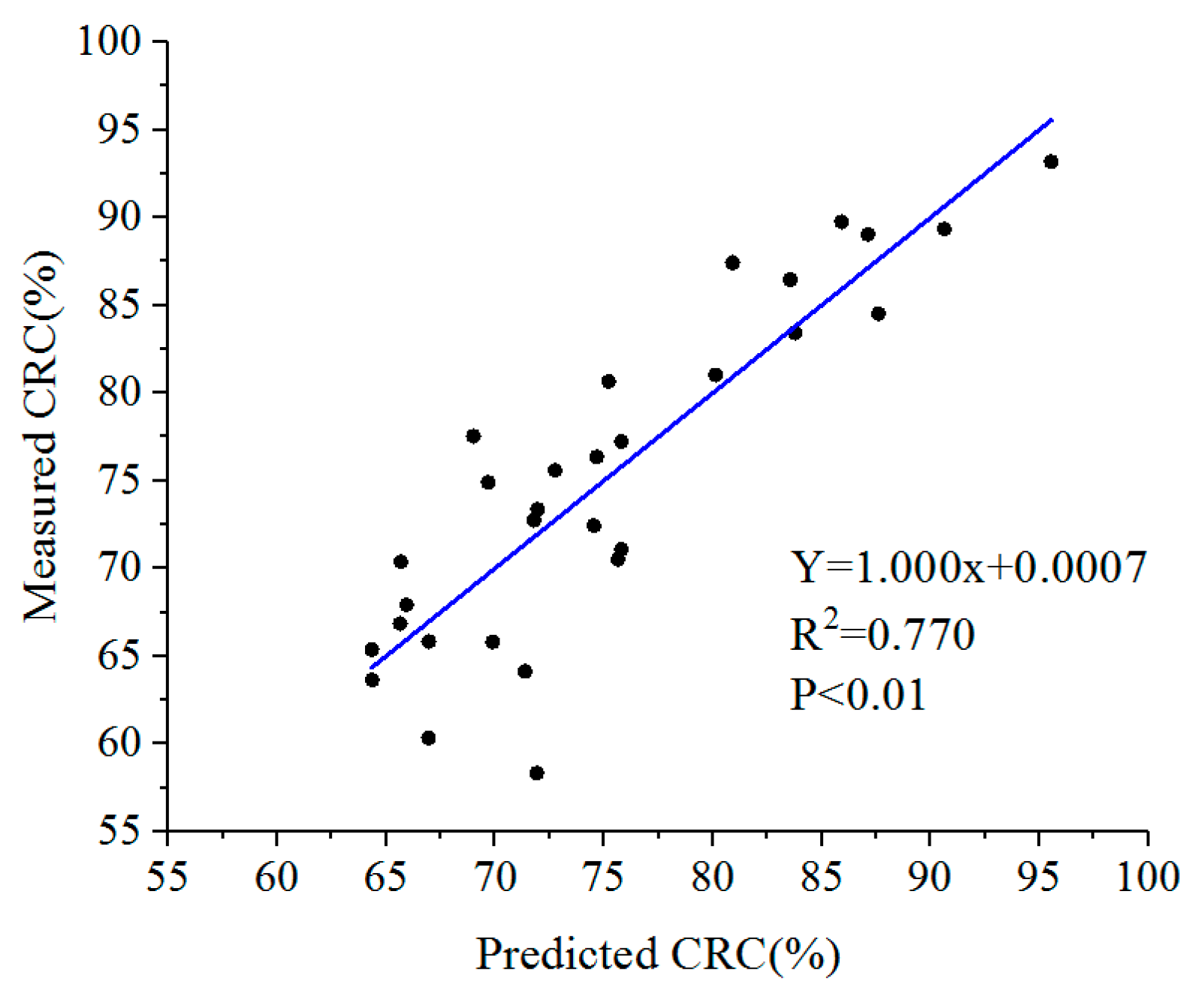
3.4. CRC Estimation Based on Optimal Subset Regression
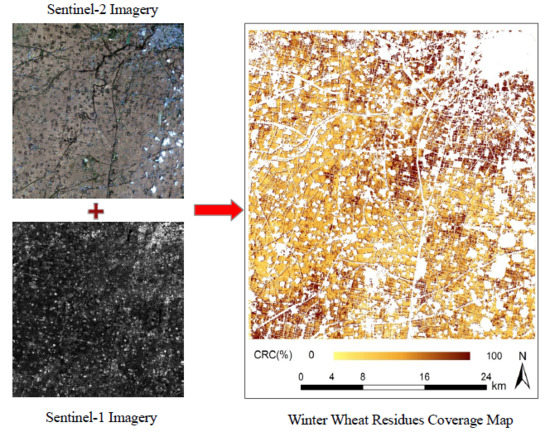
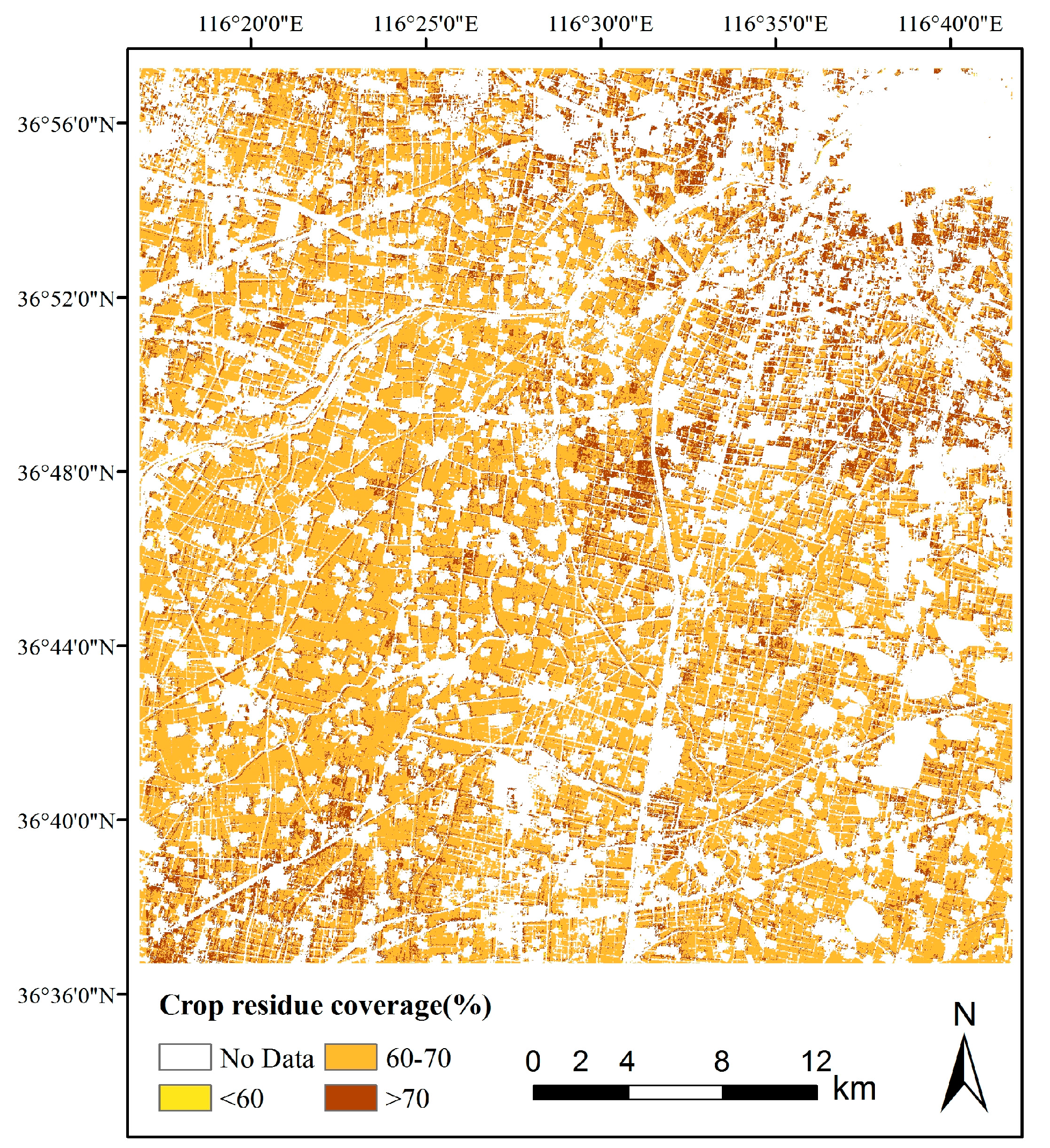
3.5. CRC Mapping in Study Area
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Daughtry, C.S.T.; Hunt, E.R.; Mcmurtrey, J.E. Assessing crop residue cover using shortwave infrared reflectance. Remote Sens. Environ. 2004, 90, 126–134. [Google Scholar] [CrossRef]
- Zhuang, Y.; Chen, D.; Li, R.; Chen, Z.; Cai, J.; He, B.; Gao, B.; Cheng, N.; Huang, Y. Understanding the Influence of Crop Residue Burning on PM2.5 and PM10 Concentrations in China from 2013 to 2017 Using MODIS Data. Remote Sens. 2018, 15, 1504. [Google Scholar] [CrossRef]
- Chen, S.; Xu, C.; Yan, J.; Zhang, X.; Zhang, X.; Wang, D. The influence of the type of crop residue on soil organic carbon fractions: An 11-year field study of rice-based cropping systems in southeast China. Agric. Ecosyst. Environ. 2016, 223, 261–269. [Google Scholar] [CrossRef]
- Lemke, R.L.; Vandenbygaart, A.J.; Campbell, C.A.; Lafond, G.P.; Grant, B. Crop residue removal and fertilizer N: Effects on soil organic carbon in a long-term crop rotation experiment on a Udic Boroll. Agric. Ecosyst. Environ. 2010, 135, 42–51. [Google Scholar] [CrossRef]
- Turmel, M.S.; Speratti, A.; Baudron, F.; Verhulst, N.; Govaerts, B. Crop residue management and soil health: A systems analysis. Agric. Syst. 2015, 134, 6–16. [Google Scholar] [CrossRef]
- Liu, D.L.; Zeleke, K.T.; Wang, B.; Macadam, L.; Scott, F.; Martin, R.J. Crop residue incoRPsoration can mitigate negative climate change impacts on crop yield and improve water use efficiency in a semiarid environment. Eur. J. Agron. 2017, 85, 51–68. [Google Scholar] [CrossRef]
- Abderrazak, B.; Karl, S.; Catherine, C.K.; Shahid, K. Spatial variability mapping of crop residue using Hyperion (EO-1) hyperspectral data. Remote Sens. 2015, 7, 8107–8127. [Google Scholar]
- Radicetti, E.; Mancinelli, R.; Moscetti, R.; Campiglia, E. Management of winter cover crop residues under different tillage conditions affects nitrogen utilization efficiency and yield of eggplant (Solanum melanogena L.) in Mediterranean environment. Soil Tillage Res. 2016, 155, 329–338. [Google Scholar] [CrossRef]
- Lampurlanés, J.; Plaza-Bonilla, D.; Álvaro-Fuentes, J.; Cantero-Martinez, C. Long-term analysis of soil water conservation and crop yield under different tillage systems in Mediterranean rainfed conditions. Field Crop. Res. 2016, 189, 59–67. [Google Scholar] [CrossRef]
- Huang, S.; Zeng, Y.; Wu, J.; Shi, Q.; Pan, X. Effect of crop residue retention on rice yield in China: A meta-analysis. Field Crop. Res. 2013, 154, 188–194. [Google Scholar] [CrossRef]
- Cao, G.L.; Zhang, X.Y.; Gong, S.L.; Zheng, F.C. Investigation on emission variables of particulate matter and gaseous pollutants from crop residue burning. J. Environ. Sci. 2008, 20, 50–55. [Google Scholar] [CrossRef]
- Yin, S.; Wang, X.; Xiao, Y.; Tani, H.; Zhong, G.; Sun, Z. Study on spatial distribution of crop residue burning and PM 2.5, change in China. Environ. Pollut. 2016, 220, 204–221. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.; Campbell, J.B.; Beurs, K.M.D. Remote sensing of crop residue cover using multi-temporal Landsat imagery. Remote Sens. Environ. 2012, 117, 117–183. [Google Scholar] [CrossRef]
- Pacheco, A.; McNairn, H. Evaluating multispectral remote sensing and spectral unmixing analysis for crop residue mapping. Remote Sens. Environ. 2010, 114, 2219–2228. [Google Scholar] [CrossRef]
- Bannari, A.; Pacheco, A.; Staenz, K.; McNairn, H.; Omari, K. Estimating and mapping crop residues cover on agricultural lands using hyperspectral and IKONOS data. Remote Sens. Environ. 2006, 104, 447–459. [Google Scholar] [CrossRef]
- Hively, W.D.; Lamb, B.T.; Daughtry, C.S.T.; Shermeyer, J.; McCarty, G.W.; Quemada, M. Mapping crop residue and tillage intensity usingWorldView-3 satellite shortwave infrared residue indices. Remote Sens. 2018, 10, 1657. [Google Scholar] [CrossRef]
- VanDeventer, A.P.; Ward, A.D.; Gowda, P.H.; Lyon, J.G. Using Thematic Mapper data to identify contrasting soil plains and tillage practices. ISPRS J. Photogramm. Eng. Remote Sens. 1997, 63, 87–93. [Google Scholar]
- Qi, J.; Marsett, R.; Heilman, P.; Bieden-Bender, S.; Moran, S.; Goodrich, D.; Weltz, M. RANGES improves satellite-based information and land cover assessments in southwest United States. Eos Trans. Am. Geophys. Union 2002, 83, 601–606. [Google Scholar] [CrossRef]
- Gelder, B.K.; Kaleita, A.L.; Cruse, R.M. Estimating Mean Field Residue Cover on Midwestern Soils Using Satellite Imagery. Agron. J. 2009, 101, 635–643. [Google Scholar] [CrossRef]
- McNairn, H.; Protz, R. Mapping Corn Residue Cover on Agricultural Fields in Oxford County, Ontario, Using Thematic Mapper. Can. J. Remote Sens. 1993, 19, 8. [Google Scholar] [CrossRef]
- Cai, W.; Zhao, S.; Zhang, Z.; Peng, F.; Xu, J. Comparison of different crop residue indices for estimating crop residue cover using field observation data. In Proceedings of the IEEE 2018 7th International Conference on Agro-geoinformatics, Hangzhou, China, 6–9 August 2018. [Google Scholar]
- Galloza, M.S.; Crawford, M.M.; Heathman, G.C. Crop residue modeling and mapping using Landsat, ALI, Hyperion and airborne remote sensing data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2013, 6, 446–456. [Google Scholar] [CrossRef]
- Narayanan, R.M.; Mielke, L.N.; Dalton, J.P. Crop residue cover estimation using radar techniques. Appl. Eng. Agric. 1992, 8, 863–869. [Google Scholar] [CrossRef]
- McNairn, H.; Duguay, C.; Boisvert, J.; Huffman, E.; Brisco, B. Defining the Sensitivity of Multi-Frequency and Multi-Polarized Radar Backscatter to Post-Harvest Crop Residue. Can. J. Remote Sens. 2001, 27, 17. [Google Scholar] [CrossRef]
- McNairn, H.; Duguay, C.; Brisco, B.; Pultz, T.J. The Effect of Soil and Crop Residue Characteristics on Polarimetric Radar Response. Remote Sens. Environ. 2002, 80, 308–320. [Google Scholar] [CrossRef]
- McNairn, H.; Boisvert, J.B.; Major, D.J.; Gwyn, Q.H.J.; Brown, R.J.; Smith, A.M. Identification of Agricultural Tillage Practices from C-Band Radar Backscatter. Can. J. Remote Sens. 1996, 22, 154–162. [Google Scholar] [CrossRef]
- Adams, J.R.; Berg, A.A.; Mcnairn, H.; Merzouki, A. Sensitivity of C-band SAR polarimetric variables to unvegetated agricultural fields. Can. J. Remote Sens. 2013, 39, 1–16. [Google Scholar] [CrossRef]
- Zheng, B.; Campbell, J.B.; Serbin, G.; Galbraith, J.M. Remote sensing of crop residue and tillage practices: Present capabilities and future prospects. Soil Tillage Res. 2014, 138, 26–34. [Google Scholar] [CrossRef]
- Jin, X.; Yang, G.; Xu, X.; Yang, H.; Feng, H.; Li, Z.; Shen, J.; Zhao, C.; Lan, Y. Combined Multi-Temporal Optical and Radar Parameters for Estimating LAI and Biomass in Winter Wheat Using HJ and RADARSAR-2 Data. Remote Sens. 2015, 7, 13251–13272. [Google Scholar] [CrossRef]
- Huang, C.; Ye, X.; Deng, C.; Zhang, Z.; Wan, Z. Mapping Above-Ground Biomass by Integrating Optical and SAR Imagery: A Case Study of Xixi National Wetland Park, China. Remote Sens. 2016, 8, 647. [Google Scholar] [CrossRef]
- Cutler, M.E.J.; Boyd, D.S.; Foody, G.M.; Vetrivel, A. Estimating tropical forest biomass with a combination of SAR image texture and Landsat TM data: An assessment of predictions between regions. Isprs J. Photogramm. Remote Sens. 2012, 70, 66–77. [Google Scholar] [CrossRef]
- Yang, Z.; Shao, Y.; Li, K.; Liu, Q.; Liu, L.; Brian, B. An improved scheme for rice phenology estimation based on time-series multispectral HJ-1A/B and polarimetric RADARSAT-2 data. Remote Sens. Environ. 2017, 195, 184–201. [Google Scholar] [CrossRef]
- Laurin, G.V.; Pirotti, F.; Callegari, M.; Chen, Q.; Cuozzo, G.; Lingua, E.; Notarnicola, C.; Papale, D. Potential of ALOS2 and NDVI to Estimate Forest Above-Ground Biomass, and Comparison with Lidar-Derived Estimates. Remote Sens. 2017, 9, 18. [Google Scholar] [CrossRef]
- Fieuzal, R.; Baup, F. Estimation of leaf area index and crop height of sunflowers using multi-temporal optical and SAR satellite data. Int. J. Remote Sens. 2016, 37, 2780–2809. [Google Scholar] [CrossRef]
- Betbeder, J.; Fieuzal, R.; Philippetsa, Y.; Ferro-Fimil, L.; Baup, F. Estimation of crop parameters using multi-temporal optical and radar polarimetric satellite data. SPIE Remote Sens. 2015, 9637, 02. [Google Scholar]
- Najafi, P.; Navid, H.; Feizizadeh, B.; Eskandari, I. Object-based satellite image analysis applied for crop residue estimating using Landsat OLI imagery. Int. J. Remote Sens. 2018, 39, 6117–6136. [Google Scholar] [CrossRef]
- Jin, X.L.; Ma, J.H.; Wen, Z.D.; Song, K.S. Estimation of Maize Residue Cover Using Landsat-8 OLI Image Spectral Information and Textural Features. Remote Sens. 2015, 7, 14559–14575. [Google Scholar] [CrossRef]
- Theil, H. Principles of Econometrics; Wiley: New York, NY, USA, 1971. [Google Scholar]
- Esquerdo, J.C.D.M.; Zullo Júnior, J.; Antunes, J.F.G. Use of NDVI/AVHRR time-series profiles for soybean crop monitoring in Brazil. International Int. J. Remote Sens. 2011, 32, 3711–3727. [Google Scholar] [CrossRef]
- Ren, J.; Chen, Z.; Zhou, Q.; Tang, H. Regional yield estimation for winter wheat with MODIS-NDVI data in Shandong, China. Int. J Appl. Earth Observ. Geoinf. 2008, 10, 403–413. [Google Scholar] [CrossRef]
- Zhao, Q.; Jiang, L.; Li, W.; Feng, Z. Spatial-temporal pattern change of winter wheat area in northwest Shandong Province during 2000–2014. Remote Sens. Land Resour. 2017, 29, 173–180. [Google Scholar]
- Papendick, R.I.; Parr, J.F.; Meyer, R.E. Managing Crop Residues to Optimize Crop/Livestock Production Systems for Dryland Agriculture. In Dryland Agriculture Strategies for Sustainability; Springer: New York, NY, USA, 1990. [Google Scholar]
- Godwin, R.J. Agricultural Engineering in Development: Tillage for Crop Production in Areas of Low Rainfall; Food and Agriculture Organisation of the United Nations (FAO): Rome, Italy, 1990. [Google Scholar]
- Guy, S.; Raymond, H.E.; Daughtry, C.S.; Mccarty, G.W.; Doraiswamy, P.C. An improved ASTER index for remote sensing of crop residue. Remote Sens. 2009, 1, 971–991. [Google Scholar]
- Wanjura, D.F.; Bilbro, J.D. Ground Cover and Weathering Effects on Reflectances of Three Crop Residues. Agron. J. 1986, 78, 694–698. [Google Scholar] [CrossRef]
- Kim, Y.; Jackson, T.; Bindlish, R.; Hong, S.; Jung, G.; Lee, K. Retrieval of wheat growth parameters with radar vegetation indices. IEEE Geosci. Remote Sens. Lett. 2013, 11, 808–812. [Google Scholar]
- Cosh, M.; O’Neill, P.; Joseph, A.; Lang, R.; Srivastava, P. Evaluation of Radar Vegetation Indices for Vegetation Water Content Estimation Using Data from a Ground-Based SMAP Simulator. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar]

| Vegetation Index | Abbreviation | Formula | Reference |
|---|---|---|---|
| Normalized Difference Residue Index | NDRI | (b4 − b12)/(b4 + b12) | [19] |
| Normalized Difference Index 7 | NDI7 | (b8 − b12)/(b8 + b12) | [20] |
| Normalized Difference Tillage Index | NDTI | (b11 − b12)/(b11 + b12) | [17] |
| Normalized Difference Index 71 | NDI71 | (b5 − b12)/(b5 + b12) | This paper |
| Normalized Difference Index 72 | NDI72 | (b6 − b12)/(b6 + b12) | This paper |
| Normalized Difference Index 73 | NDI73 | (b7 − b12)/(b7 + b12) | This paper |
| Normalized Difference Index 74 | NDI74 | (b8A − b12)/(b8A + b12) | This paper |
| Crop Residue Indices | Regression Equations | R2 | RMSE (%) |
|---|---|---|---|
| NDRI | Y = 1.391x + 1.064 | 0.462 ** | 7.430 |
| NDI7 | Y = 1.299x + 0.820 | 0.425 ** | 7.597 |
| NDTI | Y = 4.000x + 0.360 | 0.570 ** | 6.560 |
| NDI71 | Y = 1.744x + 1.015 | 0.472 ** | 7.317 |
| NDI72 | Y = 1.10x + 0.864 | 0.285 ** | 8.498 |
| NDI73 | Y = 0.769x + 0.796 | 0.157 * | 9.155 |
| NDI74 | Y = 0.935x + 0.770 | 0.238 ** | 8.714 |
| Radar Parameters | Regression Equations | R2 | RMSE (%) |
|---|---|---|---|
| Y = −1.576x + 0.903 | 0.341 ** | 8.086 | |
| Y = 9.177x + 0.638 | 0.319 ** | 8.241 | |
| RI1 | Y = −0.010x + 0.848 | 0.365 ** | 8.515 |
| RI2 | Y = −0.117x + 0.753 | 0.430 ** | 7.052 |
| VV_ME | Y = −0.001x + 0.875 | 0.123 n.s. | 9.327 |
| VH_ME | Y = 0.001x + 0.628 | 0.359 ** | 7.955 |
| Variables | Regression Equations | R2 | RMSE (%) |
|---|---|---|---|
| NDRI × | Y = 0.300x + 0.647 | 0.625 ** | 6.296 |
| NDI7 × | Y = 0.303x + 0.662 | 0.552 ** | 6.846 |
| NDTI × | Y = 0.298x + 0.643 | 0.671 ** | 5.741 |
| NDI71 × | Y = 0.308x + 0.634 | 0.667 ** | 5.763 |
| NDRI × | Y = 0.366x + 0.685 | 0.567 ** | 6.528 |
| NDI7 × | Y = 0.451x + 0.685 | 0.576 ** | 6.599 |
| NDTI × | Y = 0.324x + 0.690 | 0.585 ** | 6.435 |
| NDI71 × | Y = 298x + 0.691 | 0.507 ** | 7.097 |
| NDRI × RI1 | Y = 0.306x + 0.633 | 0.672 ** | 5.789 |
| NDI7 × RI1 | Y = 0.309x + 0.651 | 0.595 ** | 6.423 |
| NDTI × RI1 | Y = 0.294x + 0.634 | 0.728 ** | 5.221 |
| NDI71 × RI1 | Y = 0.300x + 0.624 | 0.683 ** | 5.578 |
| NDRI × RI2 | Y = 0.419x + 0.631 | 0.690 ** | 5.630 |
| NDI7 × RI2 | Y = 0.433x + 0.647 | 0.623 ** | 6.198 |
| NDTI × RI2 | Y = 0.393x + 0.635 | 0.738 ** | 5.140 |
| NDI71 × RI2 | Y = 0.403x + 0.625 | 0.696 ** | 5.473 |
| NDRI × VH_ME | Y = 0.395x + 0.685 | 0.568 ** | 6.606 |
| NDI7 × VH_ME | Y = 0.443x + 0.689 | 0.525 ** | 6.936 |
| NDTI × VH_ME | Y = 0.334x + 0.692 | 0.551 ** | 6.755 |
| NDI71 × VH_ME | Y = 0.326x + 0.692 | 0.515 ** | 7.522 |
| Model | Adj R2 | AIC | BIC | RMSE | Composite Index | Selected Independent Variables in Model |
|---|---|---|---|---|---|---|
| 1 | 0.73 | −3.04 | −33.34 | 5.14 | 2.34 | NDTI × RVI2 |
| 2 | 0.75 | −3.86 | −33.89 | 4.85 | 3.26 | NDI71 × , NDTI × |
| 3 | 0.76 | −3.33 | −32.76 | 4.83 | 3.17 | NDI71 × , NDTI × , NDI71 × |
| 4 | 0.77 | −2.52 | −31.33 | 4.78 | 2.99 | NDI7 × RVI1, NDRI × , NDI7 × , NDTI × |
| 5 | 0.77 | −1.10 | −28.94 | 5.08 | 2.01 | NDRI × RVI1, NDI71 × RVI1, NDRI × , NDI71 × , NDI71 × |
| 6 | 0.77 | −0.05 | −27.28 | 5.42 | 1.17 | NDRI × VH_ME, NDRI × , NDI71 × , NDI71 × VH_ME, NDRI × RVI1, NDI71 × RVI1 |
| 7 | 0.79 | −0.17 | −28.15 | 5.73 | 1.31 | NDRI_RVI1, NDI71_, NDI71_RVI1, NDRI_VH_ME, NDI71_, NDRI_ NDI7_VH_ME |
| 8 | 0.79 | 1.31 | −25.89 | 5.31 | 1.09 | NDRI_RVI1, NDRI_, NDRI_, NDI71_, NDTI_, NDI71_RVI1, NDTI_VH_ME, NDI71_VH_ME, |
| Satellite Derived Variables | 0–60% | 60–70% | 70–100% |
|---|---|---|---|
| NDTI | 0.03 | 0.08 | 0.12 |
| NDI71 | −0.18 | −0.17 | −0.15 |
| RI1 | 0.37 | 0.60 | 0.44 |
| RI2 | 0.19 | 0.19 | −0.13 |
| NDI71 × | 0.02 | 0.05 | 0.30 |
| NDTI × | −0.52 | 0.04 | 0.43 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, W.; Zhao, S.; Wang, Y.; Peng, F.; Heo, J.; Duan, Z. Estimation of Winter Wheat Residue Coverage Using Optical and SAR Remote Sensing Images. Remote Sens. 2019, 11, 1163. https://doi.org/10.3390/rs11101163
Cai W, Zhao S, Wang Y, Peng F, Heo J, Duan Z. Estimation of Winter Wheat Residue Coverage Using Optical and SAR Remote Sensing Images. Remote Sensing. 2019; 11(10):1163. https://doi.org/10.3390/rs11101163
Chicago/Turabian StyleCai, Wenting, Shuhe Zhao, Yamei Wang, Fanchen Peng, Joon Heo, and Zheng Duan. 2019. "Estimation of Winter Wheat Residue Coverage Using Optical and SAR Remote Sensing Images" Remote Sensing 11, no. 10: 1163. https://doi.org/10.3390/rs11101163
APA StyleCai, W., Zhao, S., Wang, Y., Peng, F., Heo, J., & Duan, Z. (2019). Estimation of Winter Wheat Residue Coverage Using Optical and SAR Remote Sensing Images. Remote Sensing, 11(10), 1163. https://doi.org/10.3390/rs11101163