Coherence Difference Analysis of Sentinel-1 SAR Interferogram to Identify Earthquake-Induced Disasters in Urban Areas
Abstract
1. Introduction
2. Materials and Methods
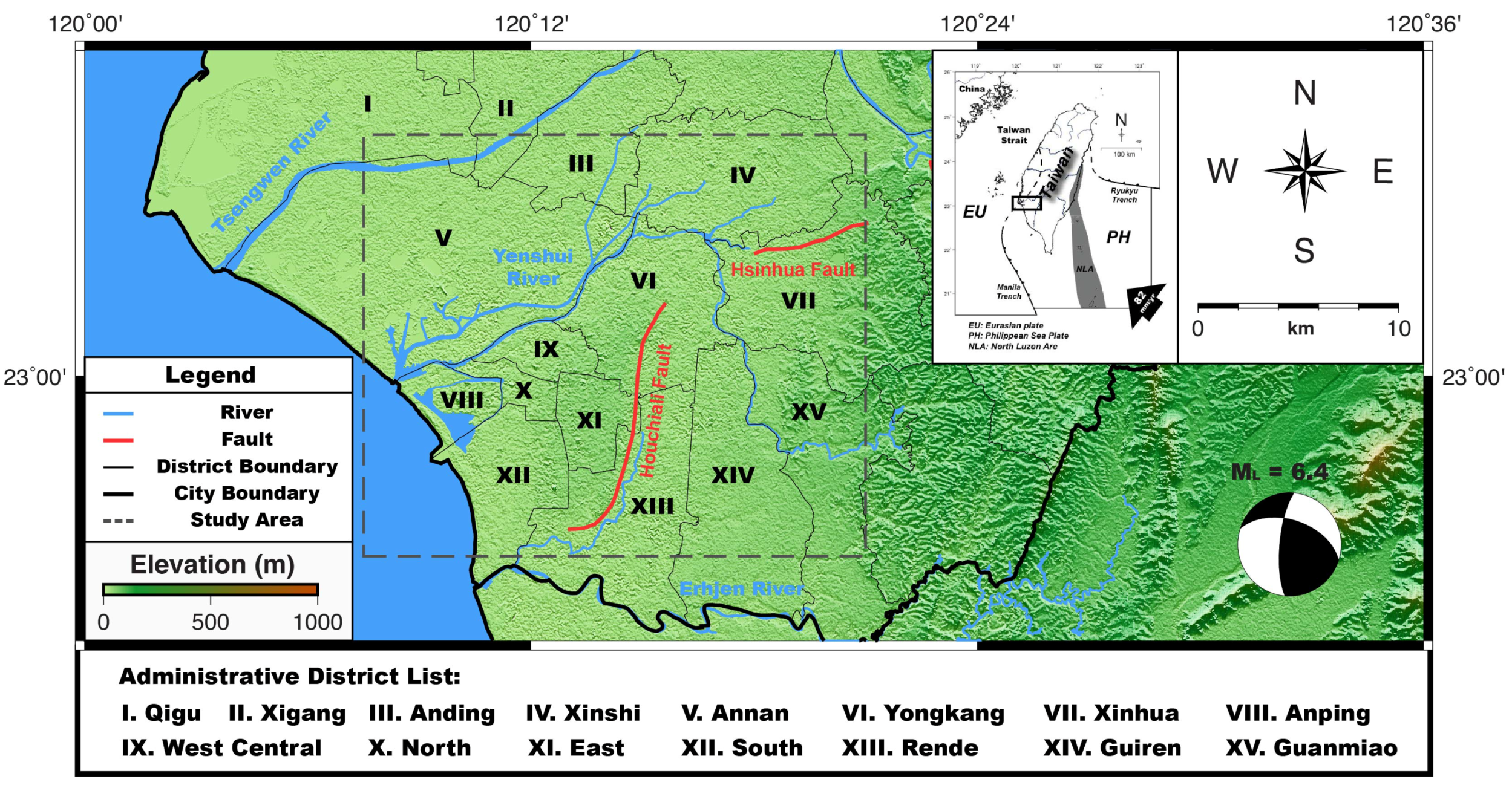
2.1. Study Area
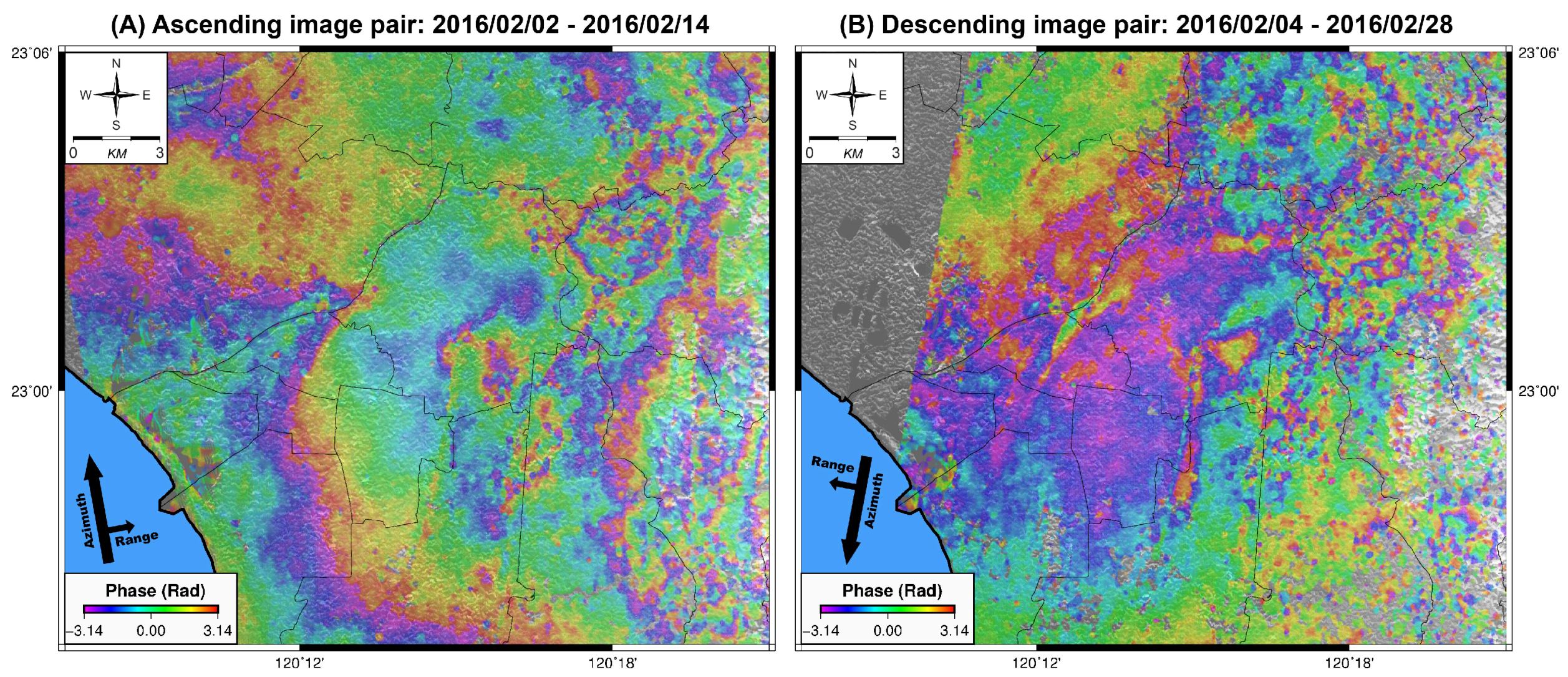
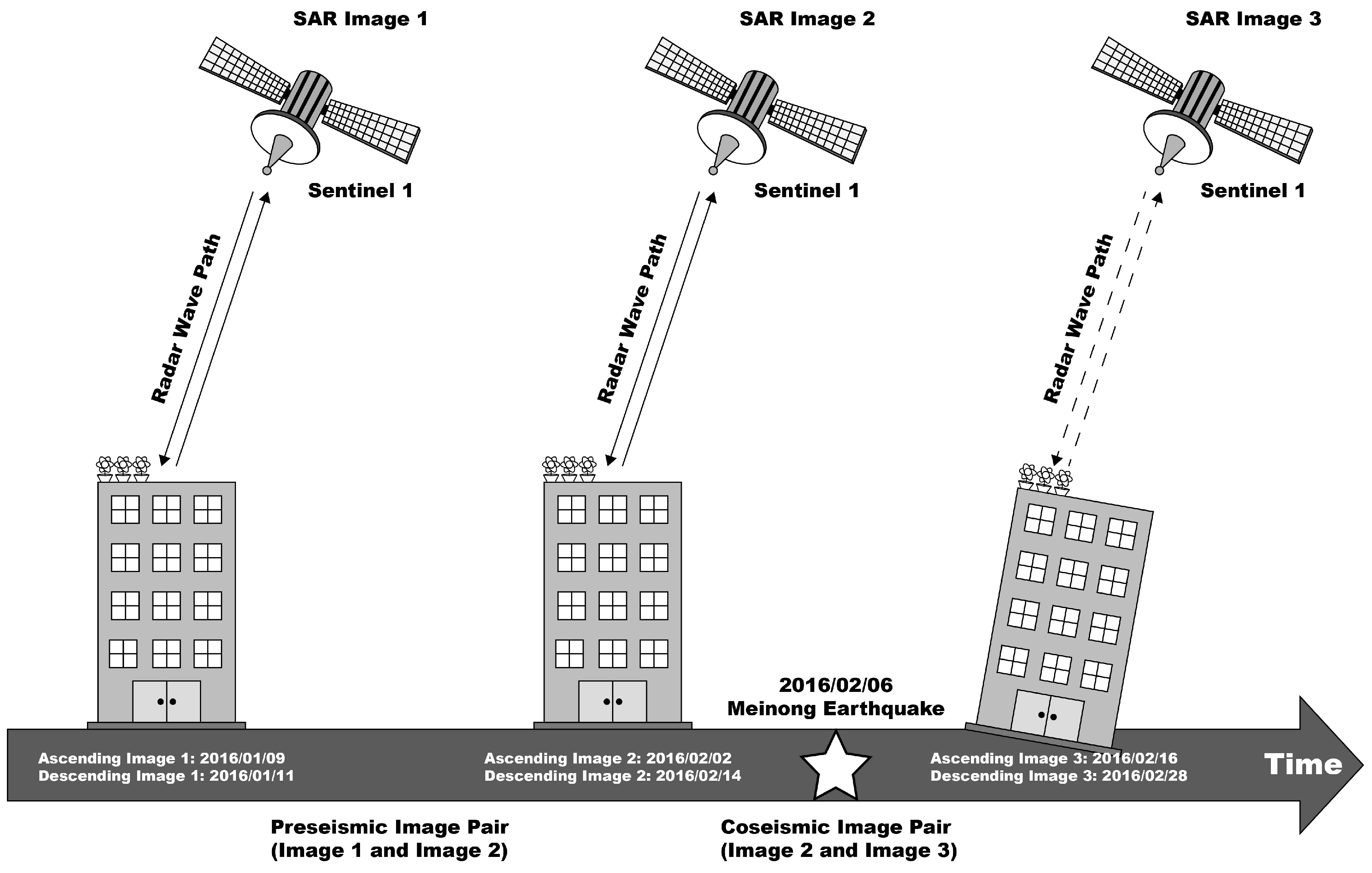
2.2. Interferogram Process
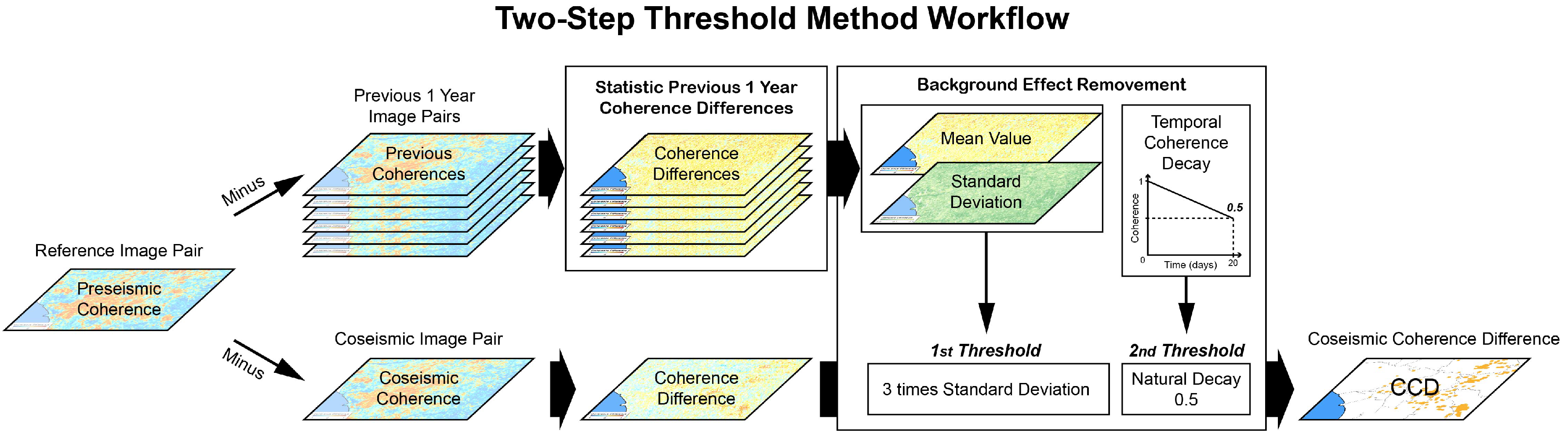
2.3. Coherence Difference Induced by the Earthquake
3. Results
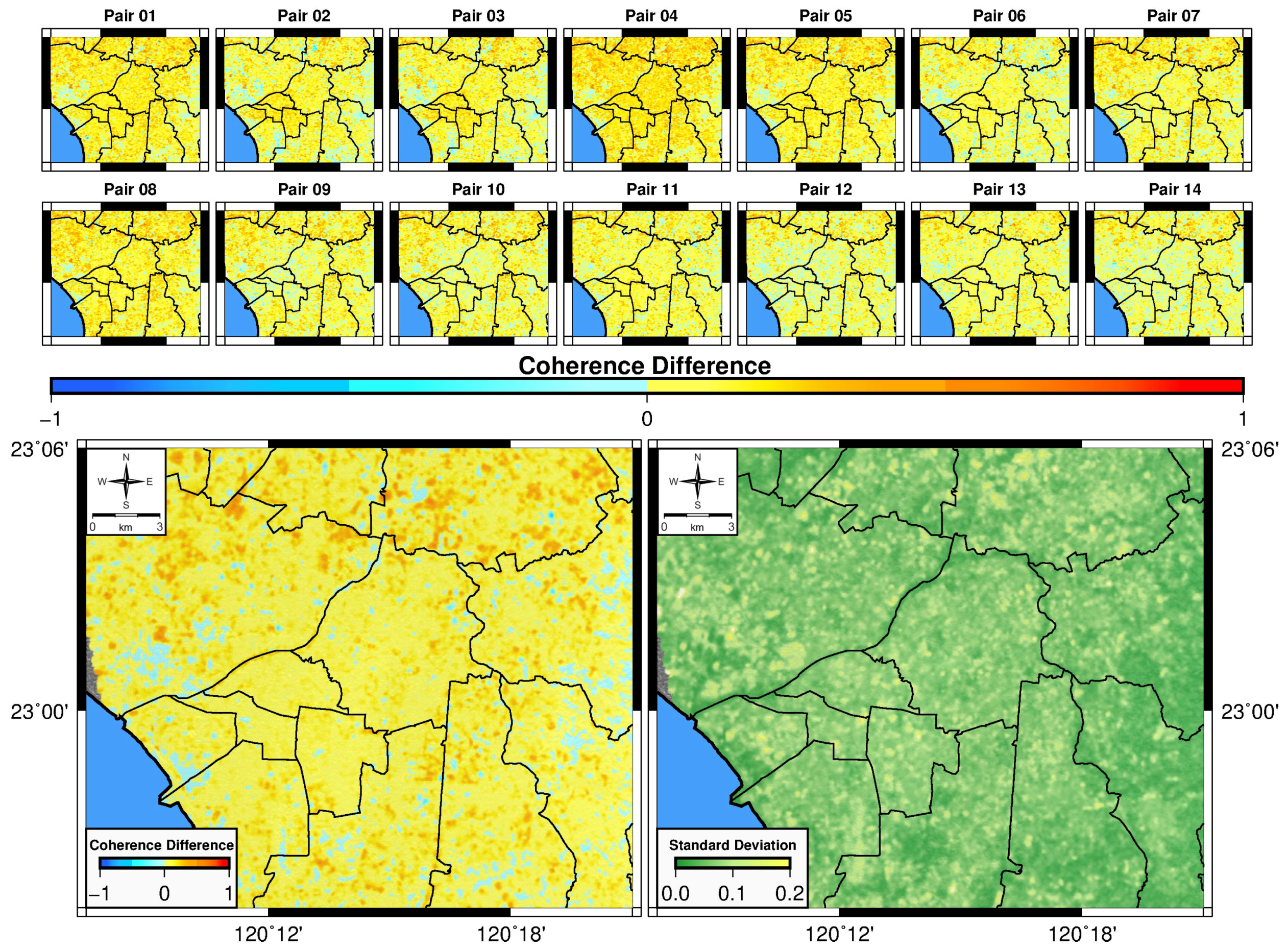
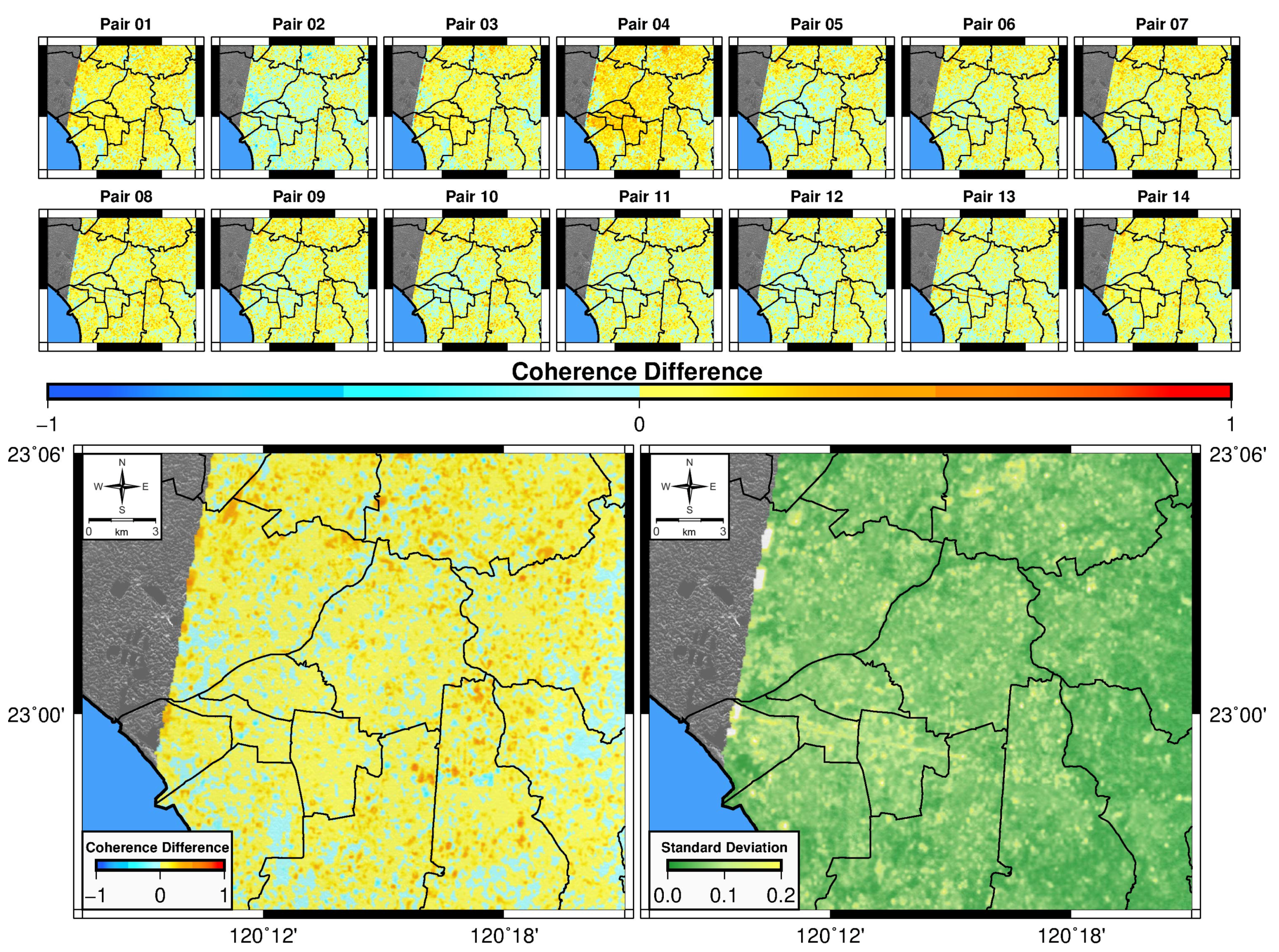
3.1. Background Effects
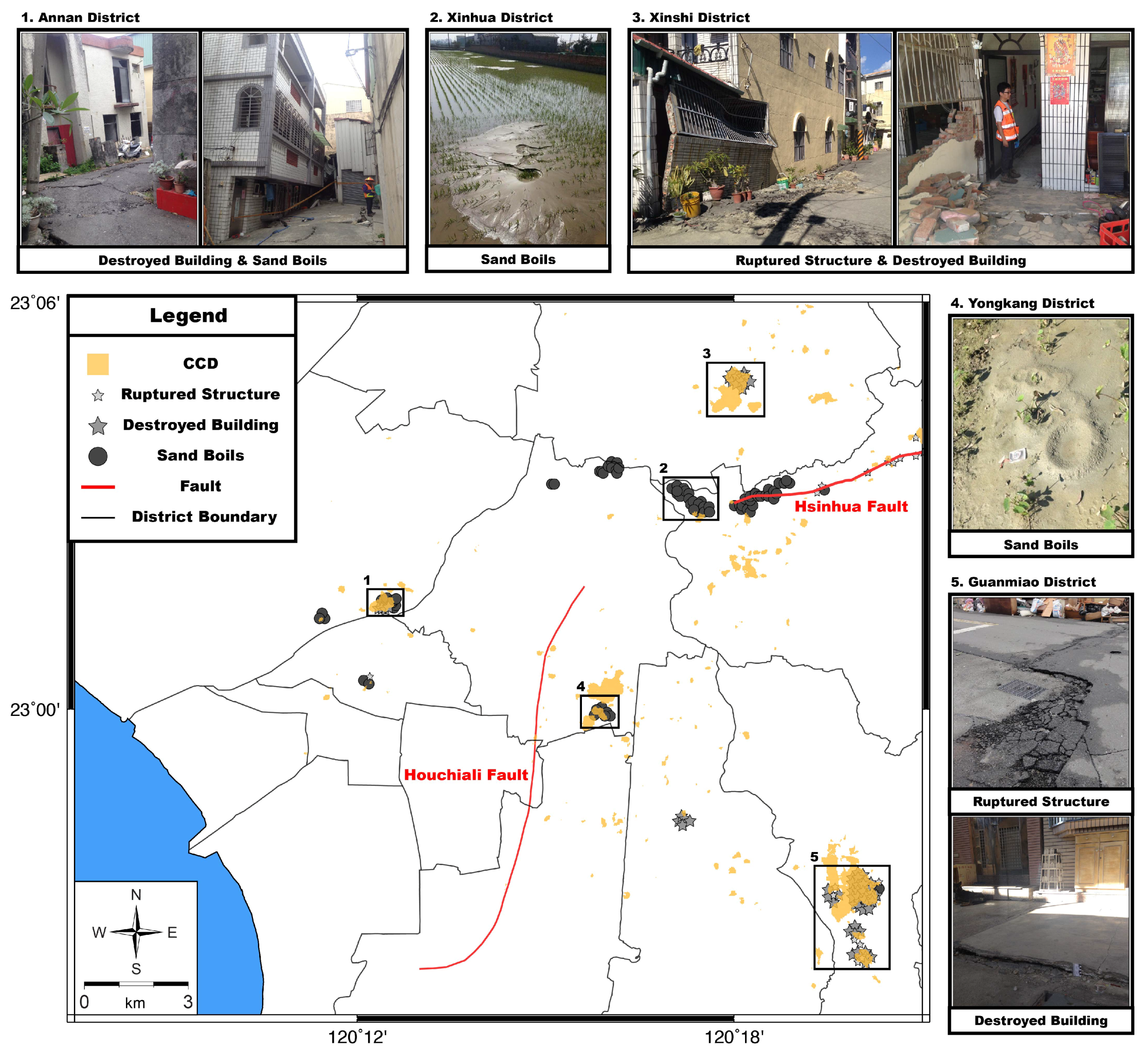
3.2. Validation of the CCD Map
3.2.1. CCD Map
3.2.2. Comparison with Field Surveys
3.2.3. Comparison with the Land Use Investigation Map
4. Discussion
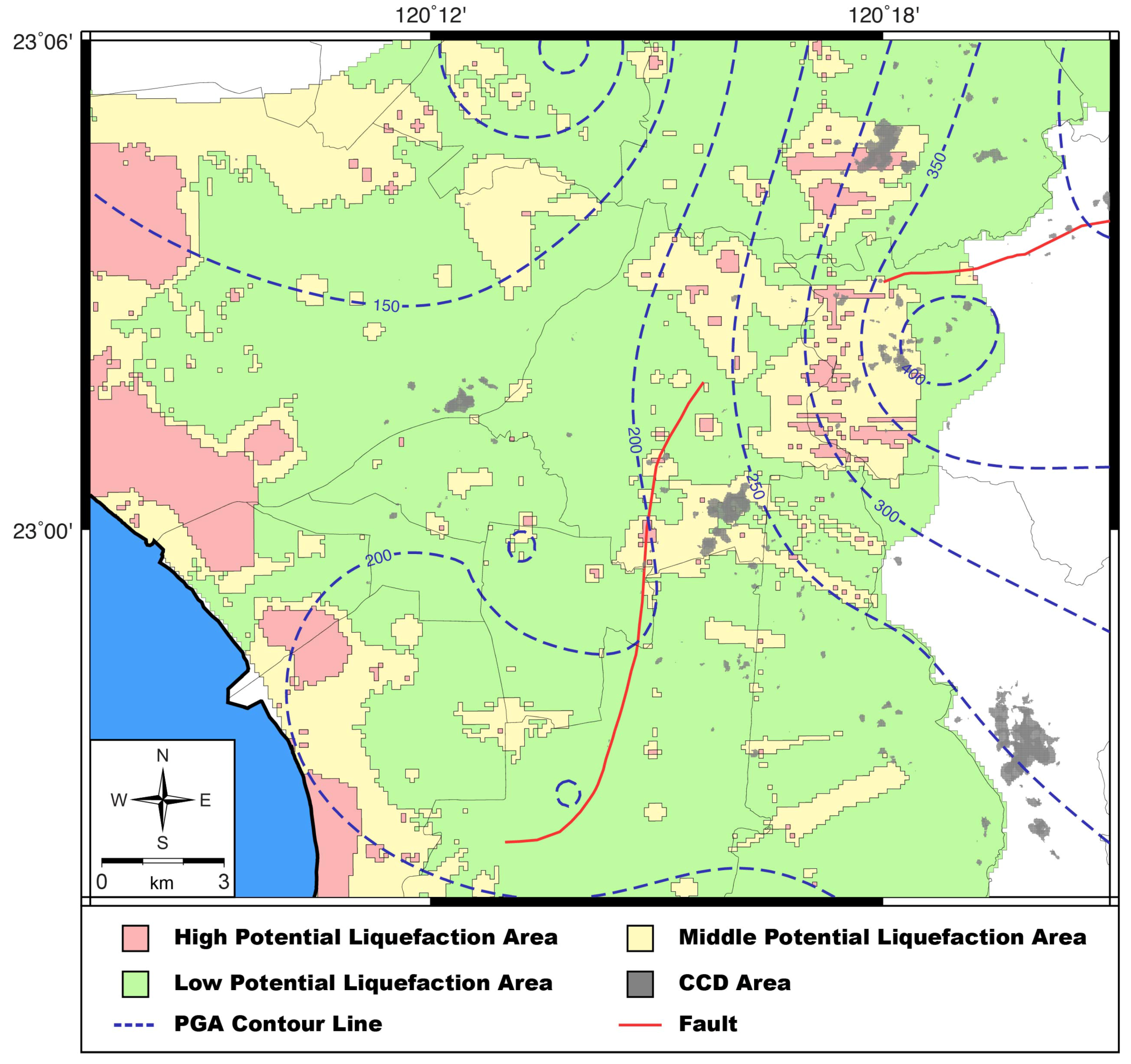
4.1. Comparison of CCD and Liquefaction Potential and PGA Maps
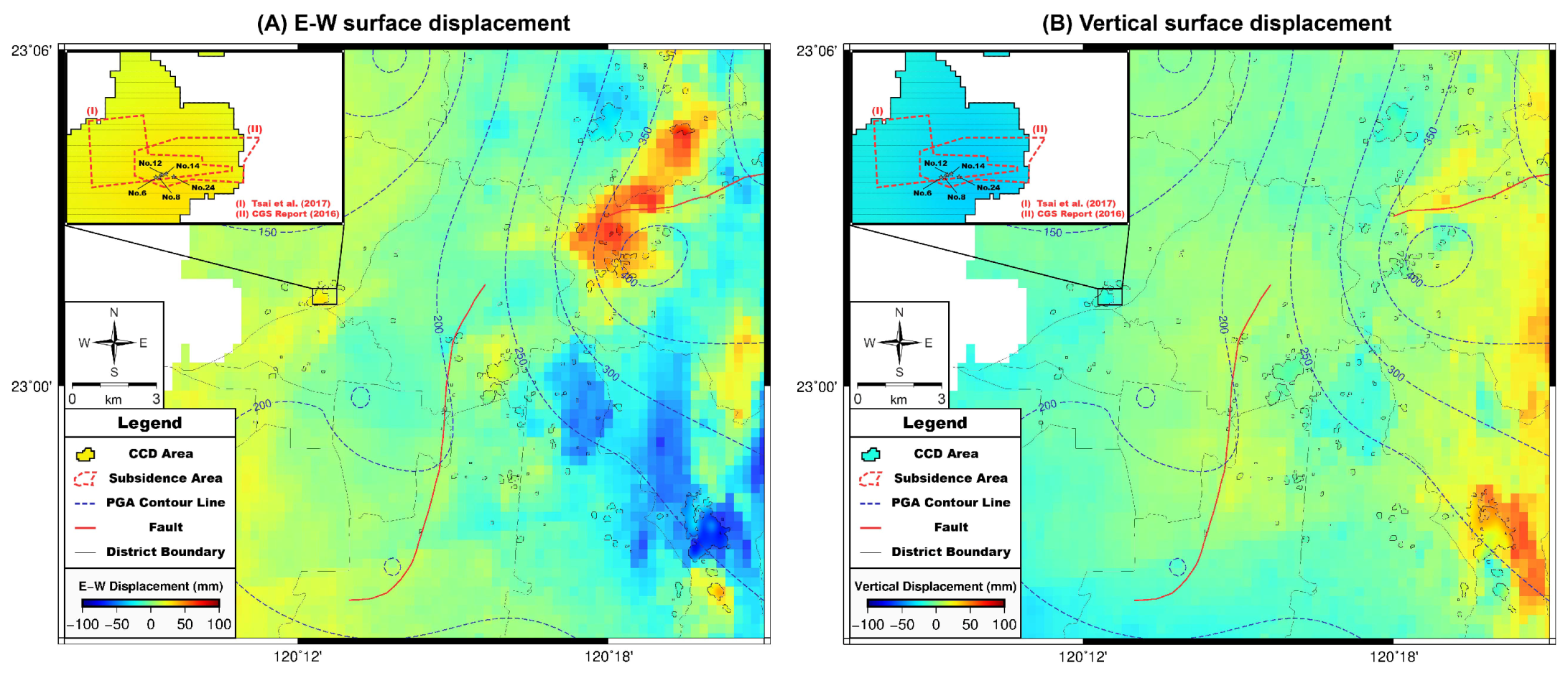
4.2. Inversion of 2D Surface Displacements
4.2.1. Overview of Surface Deformation
4.2.2. Land Subsidence in Annan District
4.2.3. Surface Deformation in Guanmiao District
5. Conclusions
- (1)
- The CCD could accurately map the disaster locations in numerous districts, including Xinshi, Annan, Xinhua, Yongkang and Guanmiao. More specifically, the land subsidence induced by the soil liquefaction was clearly distinguished by the CCD results. Obvious land surface changes such as the change from sand and rocks to mud with water can result in significant drops of coherence and were also identified by the developed CCD map.
- (2)
- Except for Annan district, most high CCD values were located in middle and high potential liquefaction areas and were distributed in areas of PGA between 200 and 400 gal. Special conditions of the disasters in Annan district may result from the previous land use types and human activities. The disasters were mainly located in the so-called old pond area, where the lowlands had poor quality of backfill materials. Moreover, the low resolution of engineering boreholes in the areas might also have led to uncertainties in quantifying the index of liquefaction potential.
- (3)
- The study found that Guanmiao district encountered severe liquefaction in many locations. We examined the sedimentary environment and groundwater levels in Guanmiao district and found that the sand and mud deposits associated with shallow groundwater levels could be the key factors for soil liquefaction, even if the district is in the foothill area and is not included in the LPM released by Taiwan CGS.
- (4)
- The conversion of 2D surface displacement can be used to estimate the surface displacements in east-west and vertical directions. Summarizing the estimated displacements in Tainan City, Guanmiao district had high variations of east-west and vertical displacements. In other districts, such as Annan, Xinshin, Xinhua and Yongkang, the displacements could be east-west or the opposite way, depending on the location.
- (5)
- Our results showed that most differences between the estimated vertical displacements and field surveys were on the order of a few centimeters in Annan district. The inaccuracy may be influenced by neglecting surface movements in the north-south direction, the coarse spatial resolution or ionosphere effects.
- (6)
- The surface displacements in Guanmiao district behaved differently in the urban areas. The main factor could be inferred from the axis activities of the Kuanmiao syncline on the northern side. Additionally, tectonic movements and tilted buildings might also contribute to the calculation of displacements.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Huang, H.H.; Wu, Y.M.; Lin, T.L.; Chao, W.A.; Shyu, J.B.H.; Chan, C.H.; Chang, C.H. The Preliminary Study of the 4 March 2010 Mw 6.3 Jiasian, Taiwan Earthquake Sequence. Terr. Atmos. Ocean. Sci. 2011, 22, 283–290. [Google Scholar] [CrossRef]
- Hsu, T.Y.; Wang, H.H.; Lin, P.Y.; Lin, C.M.; Kuo, C.H.; Wen, K.L. Performance of the NCREE’s on-site warning system during the 5 February 2016 Mw 6.53 Meinong earthquake. Geophys. Res. Lett. 2016, 43, 8954–8959. [Google Scholar] [CrossRef]
- Lee, S.J.; Yeh, T.Y.; Lin, Y.Y. Anomalously Large Ground Motion in the 2016 ML 6.6 Meinong, Taiwan, Earthquake: A Synergy Effect of Source Rupture and Site Amplification. Seismol. Res. Lett. 2016, 87, 1319–1326. [Google Scholar] [CrossRef]
- Wu, Y.M.; Liang, W.T.; Mittal, H.; Chao, W.A.; Lin, C.H.; Huang, B.S.; Lin, C.M. Performance of a Low-Cost Earthquake Early Warning System (P-Alert) during the 2016 ML 6.4 Meinong (Taiwan) Earthquake. Seismol. Res. Lett. 2016, 87, 1050–1059. [Google Scholar] [CrossRef]
- Rau, R.J.; Liang, W.T. Introduction to the special issue on the 2016 Meinong, Taiwan, earthquake. Terr. Atmos. Ocean. Sci. 2017, 28, I–III. [Google Scholar] [CrossRef]
- Lee, Y.T.; Wang, Y.J.; Chan, C.H.; Ma, K.F. The 2016 Meinong earthquake to TEM PSHA2015. Terr. Atmos. Ocean. Sci. 2017, 28, 703–713. [Google Scholar] [CrossRef]
- Central Geological Survey (CGS). Report on the 2016/02/06 Earthquake; Central Geological Survey, Ministry of Economic Affairs: New Taipei City, Taiwan, 2016; p. 103. (In Chinese)
- Le Béon, M.; Huang, M.H.; Suppe, J.; Huang, S.T.; Pathier, E.; Huang, W.J.; Chen, C.L.; Fruneau, B.; Baize, S.; Ching, K.E.; et al. Shallow geological structures triggered during the Mw 6.4 Meining earthquake, southwestern Taiwan. Terr. Atmos. Ocean. Sci. 2017, 28, 663–681. [Google Scholar] [CrossRef]
- Tsai, C.C.; Hsu, S.Y.; Wang, K.L.; Yang, H.C.; Chang, W.K.; Chen, C.H.; Hwang, Y.W. Geotechnical Reconnaissance of the 2016 ML6.6 Meinong Earthquake in Taiwan. J. Earthq. Eng. 2017. [Google Scholar] [CrossRef]
- Chang, C.P.; Wang, C.T.; Chang, T.Y.; Chen, K.S.; Liang, L.S.; Pathier, E.; Angelier, J. Application of SAR interferometry to a large thrust deformation: the 1999 Mw = 7.6 Chichi earthquake in central Taiwan. Geophys. J. Int. 2004, 159, 9–16. [Google Scholar] [CrossRef]
- Chang, C.P.; Chen, K.S.; Wang, C.T.; Yen, J.Y.; Chang, T.Y.; Lin, C.W. Application of Space-borne Radar Interferometry on Crustal Deformations in Taiwan: A Perspective from the Nature of Events. Terr. Atmos. Ocean. Sci. 2004, 15, 523–543. [Google Scholar] [CrossRef]
- Chang, C.P.; Chang, T.Y.; Wang, C.T.; Kuo, C.H.; Chen, K.S. Land-surface deformation corresponding to seasonal ground-water fluctuation, determining by SAR interferometry in the SW Taiwan. Math. Comput. Simulat. 2004, 67, 351–359. [Google Scholar] [CrossRef]
- Yen, J.Y.; Chen, K.S.; Chang, C.P.; Ng, S.M. Deformation and “deformation quiescence” prior to the Chi-Chi earthquake evidenced by DInSAR and groundwater records during 1995-2002 in Central Taiwan. Earth Planets Space 2006, 58, 805–813. [Google Scholar] [CrossRef]
- Yen, J.Y.; Chen, K.S.; Chang, C.P.; Boerner, W.M. Evaluation of earthquake potential and surface deformation by Differential Interferometry. Remote Sens. Environ. 2008, 112, 782–795. [Google Scholar] [CrossRef]
- Chang, C.P.; Yen, J.Y.; Hooper, A.; Chou, F.M.; Chen, Y.A.; Hou, C.S.; Hung, W.C.; Lin, M.S. Monitoring of Surface Deformation in Northern Taiwan Using DInSAR and PSInSAR Techniques. Terr. Atmos. Ocean. Sci. 2010, 21, 447–461. [Google Scholar] [CrossRef]
- Hung, W.C.; Hwang, C.; Chang, C.P.; Yen, J.Y.; Liu, C.H.; Yang, W.H. Monitoring severe aquifer-system compaction and land subsidence in Taiwan using multiple sensors: Yunlin, the southern Choushui River Alluvial Fan. Environ. Earth Sci. 2010, 59, 1535–1548. [Google Scholar] [CrossRef]
- Yen, J.Y.; Lu, C.H.; Chang, C.P.; Hooper, A.J.; Chang, Y.H.; Liang, W.T.; Chang, T.Y.; Lin, M.S.; Chen, K.S. Investigating Active Deformation in the Northern Longitudinal Valley and City of Hualien in Eastern Taiwan Using Persistent Scatterer and Small-Baseline SAR Interferometry. Terr. Atmos. Ocean. Sci. 2011, 22, 291–304. [Google Scholar] [CrossRef]
- Hung, W.C.; Hwang, C.; Chen, Y.A.; Chang, C.P.; Yen, J.Y.; Hooper, A.; Yang, C.Y. Surface deformation from persistent scatterers SAR interferometry and fusion with leveling data: A case study over the Choushui River Alluvial Fan, Taiwan. Remote Sens. Environ. 2011, 115, 957–967. [Google Scholar] [CrossRef]
- Wu, Y.Y.; Hu, J.C.; Lin, G.P.; Chang, C.P.; Tung, H.; Lu, C.H. Transient active deformation in Tainan tableland using persistent scatterers SAR interferometry. Bull. Soc. Géol. Fr. 2013, 184, 441–450. [Google Scholar] [CrossRef]
- Kang, C.C.; Chang, C.P.; Siame, L.; Lee, J.C. Present-day surface deformation and tectonic insights of the extensional Ilan Plain, NE Taiwan. J. Asian Earth Sci. 2015, 105, 408–417. [Google Scholar] [CrossRef]
- Lu, C.H.; Ni, C.F.; Chang, C.P.; Chen, Y.A.; Yen, J.Y. Geostatistical Data Fusion of Multiple Type Observations to Improve Land Subsidence Monitoring Resolution in the Choushui River Fluvial Plain, Taiwan. Terr. Atmos. Ocean. Sci. 2016, 27, 505–520. [Google Scholar] [CrossRef]
- Hunag, M.H.; Tung, H.; Fieldong, E.J.; Huang, H.H.; Liang, C.; Huang, C.; Hu, J.C. Multiple fault slip triggered above the 2016 Mw 6.4 MeiNong earthquake in Taiwan. Geophys. Res. Lett. 2016, 43, 7459–7467. [Google Scholar] [CrossRef]
- Zebker, H.A.; Villasenor, J. Decorrelation in Interferometric Radar Echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res. 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar Interferometry and Its application to Changes in the Earth’s Surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Bürgmann, R.; Rosen, P.A.; Fielding, E.J. Synthetic Aperture Radar Interferometry to Measure Earth’s Surface Topography and Its Deformation. Annu. Rev. Earth Planet. Sci. 2000, 28, 169–209. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Zebker, H.A.; Webb, F.H.; Fielding, E.J. Surface deformation and coherence measurements of Kilauea Volcano, Hawaii, from SIR-C radar interferometry. J. Geophys. Res. 1996, 101, 23109–23125. [Google Scholar] [CrossRef]
- Simons, M.; Fialko, Y.; Rivera, L. Coseismic deformation from the 1999 Mw 7.1 Hector Mine, California, Earthquake as Inferred from InSAR and GPS Observations. Bull. Seismol. Soc. Am. 2002, 92, 1390–1402. [Google Scholar] [CrossRef]
- Fielding, E.J.; Talebian, M.; Rosen, P.A.; Nazari, H.; Jackson, J.A.; Ghorashi, M.; Walker, R. Surface ruptures and building damage of the 2003 Bam, Iran, earthquake mapped by satellite synthetic aperture radar interferometric correlation. J. Geophys. Res. 2005, 110, B03302. [Google Scholar] [CrossRef]
- Atzori, S.; Tolomei, C.; Antonioli, A.; Merryman Boncori, J.P.; Bannister, S.; Trasatti, E.; Pasquali, P.; Salvi, S. The 2010–2011 Canterbury, New Zealand, seismic sequence: Multiple source analysis from InSAR data and modeling. J. Geophys. Res. 2012, 117, B08305. [Google Scholar] [CrossRef]
- Ishitsuka, K.; Tsuji, T.; Matsuoka, T. Detection and mapping of soil liquefaction in the 2011 Tohoku earthquake using SAR interferometry. Earth Planets Space 2012, 64, 1267–1276. [Google Scholar] [CrossRef]
- Tantianuparp, P.; Shi, X.; Zhang, L.; Balz, T.; Liao, M. Characterization of Landslide Deformations in Three Gorges Area Using Multiple InSAR Data Stacks. Remote Sens. 2013, 5, 2704–2719. [Google Scholar] [CrossRef]
- ElGharbawi, T.; Tamura, M. Coseismic and postseismic deformation estimation of the 2011 Tohoku earthquake in Kanto Region, Japan, using InSAR time series analysis and GPS. Remote Sens. Environ. 2015, 168, 374–387. [Google Scholar] [CrossRef]
- ElGharbawi, T.; Tamura, M. Estimating deformation due to soil liquefaction in Urayasu city, Japan using permanent scatterers. ISPRS J. Photogramm. 2015, 109, 152–164. [Google Scholar] [CrossRef]
- Takeuchi, S.; Suga, Y.; Yonezawa, C.; Chen, A.J. Detection of Urban Disaster Using InSAR. A Case Study for the 1999 Great Taiwan Earthquake. In Proceedings of the IEEE IGARSS, Honolulu, HI, USA, 24–28 July 2000; pp. 339–341. [Google Scholar]
- Wen, S.; Yeh, Y.L.; Chang, Y.Z.; Chen, C.H. The seismogenic process of the 2016 Meinong earthquake, southwest Taiwan. Terr. Atmos. Ocean. Sci. 2017, 28, 651–662. [Google Scholar] [CrossRef]
- Tsai, M.C.; Shin, T.C.; Kuo, K.W. Pre-seismic strain anomalies and coseismic deformation of Meinong earthquake from continuous GPS. Terr. Atmos. Ocean. Sci. 2017, 28, 763–785. [Google Scholar] [CrossRef]
- Kuo-Chen, H.; Chen, K.X.; Sun, W.F.; Ho, C.W.; Lee, Y.H.; Guan, Z.K.; Kang, C.C.; Chang, W.Y. 3D Vs ambient noise tomography of the 2016 Mw 6.4 Meinong Earthquake source region in Taiwan. Terr. Atmos. Ocean. Sci. 2017, 28, 693–701. [Google Scholar] [CrossRef]
- Sandwell, D.; Mellors, R.; Tong, X.; Wei, M.; Wessel, P. GMTSAR: An InSAR Processing System Based on Generic Mapping Tools. UC San Diego 2011. Available online: http://escholarship.org/uc/item/8zq2c02m (accessed on 5 May 2016).
- Wessel, P.; Smith, W.H.F. New, improved version of Generic Mapping Tools released. Eos Trans. AGU 1998, 79, 579. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Phase unwrapping for large SAR interferograms: Statistical segmentation and generalized network models. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1709–1719. [Google Scholar] [CrossRef]
- Sandwell, D.; Mellors, R.; Tong, X.; Wei, M.; Wessel, P. Open radar interferometry software for mapping surface deformation. Eos Trans. AGU 2011, 92. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Price, E.J. Phase gradient approach to stacking interferograms. J. Geophys. Res. 1998, 103, 30183–30204. [Google Scholar] [CrossRef]
- Lee, C.W.; Lu, Z.; Jung, H.S. Simulation of time series surface deformation to validate a multi-interferogram InSAR processing technique. Int. J. Remote Sens. 2012, 33, 7075–7087. [Google Scholar] [CrossRef]
- Chang, L.S.; Chow, M.C.; Chen, P.Y. The Taiwan earthquake of December 5, 1946. Taiwan Geol. Surv. Bull. 1947, 1, 17–20. [Google Scholar]
- Hsu, M.T. Seismicity of Taiwan and some related problems. Bull. Int. Inst. Seismol. Earthq. Eng. Jpn. 1971, 8, 41–160. [Google Scholar]
- Bonilla, M.G. A review of recently active faults in Taiwan. In U.S. Geological Survey Open-File Report 75-41; version 1.1; USGS: Reston, VA, USA, 1975; p. 43. [Google Scholar]
- Santoro, M.; Wegmuller, U.; Askne, J.I. Signatures of ERS?Envisat interferometric SAR coherence and phase of short vegetation: An analysis in the case of maize fields. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1702–1713. [Google Scholar] [CrossRef]
- National Land Surveying and Mapping Center (NLSC). Land Use Investigation Maps; National Land Surveying and Mapping Center, Ministry of the Interior: Taichung, Taiwan, 2015. Available online: http://tma.geospatial.org.tw (accessed on 15 July 2018). (In Chinese)
- Central Geological Survey (CGS). Integration and Analysis of Geological Information for Hazard Mitigation in Urbane Area (2/4), Tainan, Project No. 104-5926901000-05; Central Geological Survey, Ministry of Economic Affairs: New Taipei City, Taiwan, 2015. (In Chinese)
- Iwasaki, T.; Arakawa, T.; Tokida, K.I. Simplified procedures for assessing soil liquefaction during earthquakes. Soil Dyn. Earthq. Eng. 1984, 3, 49–58. [Google Scholar] [CrossRef]
- Lin, C.W. Geological map of Taiwan scale 1:50,000—Qishan Sheet; Central Geological Survey, Ministry of Economic Affairs: New Taipei City, Taiwan, 2013; Volume 56, p. 93. ISBN 978-986-03-7077-5. (In Chinese)
- Gomba, G.; González, R.F.; Zan, F.D. Ionospheric Phase Screen Compensation for the Sentinel-1 TOPS and ALOS-2 ScanSAR Modes. IEEE Trans. Geosci. Remote Sens. 2017, 55, 223–235. [Google Scholar] [CrossRef]
| Orbit Direction | Pair Type | Master | Slave | Days | Bperp (m) |
|---|---|---|---|---|---|
| Ascending | Preseismic | 2016/01/09 | 2016/02/02 | 24 | −35.93 |
| Ascending | Coseismic | 2016/02/02 | 2016/02/14 | 12 | −24.07 |
| Descending | Preseismic | 2016/01/11 | 2016/02/04 | 24 | −12.00 |
| Descending | Coseismic | 2016/02/04 | 2016/02/28 | 24 | −29.86 |
| Pair No. | Master | Slave | Days | Bperp (m) |
|---|---|---|---|---|
| Pair 01 | 2015/01/14 | 2015/03/15 | 60 | −92.95 |
| Pair 02 | 2015/03/15 | 2015/04/08 | 24 | 198.12 |
| Pair 03 | 2015/04/08 | 2015/05/02 | 24 | −224.76 |
| Pair 04 | 2015/05/02 | 2015/05/26 | 24 | −5.00 |
| Pair 05 | 2015/05/26 | 2015/06/19 | 24 | 99.51 |
| Pair 06 | 2015/06/19 | 2015/07/01 | 12 | −98.63 |
| Pair 07 | 2015/07/01 | 2015/07/25 | 24 | −29.31 |
| Pair 08 | 2015/07/25 | 2015/08/18 | 24 | 104.17 |
| Pair 09 | 2015/08/18 | 2015/09/11 | 24 | 6.02 |
| Pair 10 | 2015/09/11 | 2015/10/05 | 24 | −69.95 |
| Pair 11 | 2015/10/05 | 2015/10/29 | 24 | 132.65 |
| Pair 12 | 2015/10/29 | 2015/11/22 | 24 | −54.36 |
| Pair 13 | 2015/11/22 | 2015/12/16 | 24 | 2.19 |
| Pair 14 | 2015/12/16 | 2016/01/09 | 24 | 38.65 |
| Pair No. | Master | Slave | Days | Bperp (m) |
|---|---|---|---|---|
| Pair 01 | 2015/01/16 | 2015/03/05 | 48 | 95.39 |
| Pair 02 | 2015/03/05 | 2015/03/29 | 24 | −69.94 |
| Pair 03 | 2015/03/29 | 2015/04/22 | 24 | −194.22 |
| Pair 04 | 2015/04/22 | 2015/05/16 | 24 | 228.95 |
| Pair 05 | 2015/05/16 | 2015/06/09 | 24 | 5.58 |
| Pair 06 | 2015/06/09 | 2015/07/03 | 24 | 40.93 |
| Pair 07 | 2015/07/03 | 2015/07/27 | 24 | −22.22 |
| Pair 08 | 2015/07/27 | 2015/08/20 | 24 | −13.72 |
| Pair 09 | 2015/08/20 | 2015/09/13 | 24 | −40.72 |
| Pair 10 | 2015/09/13 | 2015/10/07 | 24 | −17.18 |
| Pair 11 | 2015/10/07 | 2015/10/31 | 24 | 75.81 |
| Pair 12 | 2015/10/31 | 2015/11/24 | 24 | −20.92 |
| Pair 13 | 2015/11/24 | 2015/12/18 | 24 | −44.30 |
| Pair 14 | 2015/12/18 | 2016/01/11 | 24 | 71.07 |
| Area No. | Total CCD Points | Non-Vegetation | Vegetation | Water |
|---|---|---|---|---|
| 1. Annan | 969 | 86.2% | 10.8% | 3% |
| (836/969) | (104/969) | (29/969) | ||
| 2. Xinhua | 222 | 74.3% | 25.7% | N/A |
| (165/222) | (57/222) | |||
| 3. Xinshi | 3277 | 88.2% | 11.8% | N/A |
| (2890/3277) | (387/3277) | |||
| 4. Yongkang | 1107 | 91.8% | 8.2% | N/A |
| (1017/1107) | (90/1107) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, C.-H.; Ni, C.-F.; Chang, C.-P.; Yen, J.-Y.; Chuang, R.Y. Coherence Difference Analysis of Sentinel-1 SAR Interferogram to Identify Earthquake-Induced Disasters in Urban Areas. Remote Sens. 2018, 10, 1318. https://doi.org/10.3390/rs10081318
Lu C-H, Ni C-F, Chang C-P, Yen J-Y, Chuang RY. Coherence Difference Analysis of Sentinel-1 SAR Interferogram to Identify Earthquake-Induced Disasters in Urban Areas. Remote Sensing. 2018; 10(8):1318. https://doi.org/10.3390/rs10081318
Chicago/Turabian StyleLu, Chih-Heng, Chuen-Fa Ni, Chung-Pai Chang, Jiun-Yee Yen, and Ray Y. Chuang. 2018. "Coherence Difference Analysis of Sentinel-1 SAR Interferogram to Identify Earthquake-Induced Disasters in Urban Areas" Remote Sensing 10, no. 8: 1318. https://doi.org/10.3390/rs10081318
APA StyleLu, C.-H., Ni, C.-F., Chang, C.-P., Yen, J.-Y., & Chuang, R. Y. (2018). Coherence Difference Analysis of Sentinel-1 SAR Interferogram to Identify Earthquake-Induced Disasters in Urban Areas. Remote Sensing, 10(8), 1318. https://doi.org/10.3390/rs10081318






