A Spatial-Temporal Adaptive Neighborhood-Based Ratio Approach for Change Detection in SAR Images

Abstract

The neighborhood-based method was proposed and widely used in the change detection of synthetic aperture radar (SAR) images because the neighborhood information of SAR images is effective to reduce the negative effect of speckle noise. Nevertheless, for the neighborhood-based method, it is unreasonable to use a fixed window size for the entire image because the optimal window size of different pixels in an image is different. Hence, if you let the neighborhood-based method use a large window to significantly suppress noise, it cannot preserve the detail information such as the edge of a changed area. To overcome this drawback, we propose a spatial-temporal adaptive neighborhood-based ratio (STANR) approach for change detection in SAR images. STANR employs heterogeneity to adaptively select the spatial homogeneity neighborhood and uses the temporal adaptive strategy to determine multi-temporal neighborhood windows. Experimental results on two data sets show that STANR can both suppress the negative influence of noise and preserve edge details, and can obtain a better difference image than other state-of-the-art methods.

1. Introduction

Change detection techniques can be applied to detect changes that occurred in the study area, which usually uses remote sensing images acquired in the same geographical area on two different dates [1]. In the last few decades, this technique has been widely used in environmental monitoring, forest monitoring, disaster assessment, etc. [1,2,3]. Moreover, it has significant potential in dynamic monitoring for the national geographical state of China [4].

Compared with the optical remote sensing satellites, synthetic aperture radar (SAR) satellites are insensitive to atmospheric and sunlight conditions, which increases the significance of extracting information from SAR images [5]. Hence, in recent years, with the development of SAR images processing methods and the launch of more SAR satellites, SAR images have been widely used in environmental remote sensing [6], ground subsidence monitoring [7], topographic mapping [8], resource exploration [9], change detection [10,11,12,13], etc.

Generating the difference image is a key step for change detection in SAR images [5,13]. In this context, subtraction and ratio (R) operators are two classic methods. Because of the multiplicative nature of speckle noise [14,15] in SAR images, compared with the subtraction operator, the R operator can decrease the influence of calibration and radiometric errors, and is suitable for obtaining the difference image from SAR images [16,17]. To highlight different radiometries (e.g., with increasing and decreasing radiometries) changing simultaneously, an improved ratio (IR) operator was proposed for the change detection in SAR images [18]. In addition, a log ratio (LR) operator was widely used in the change detection of SAR images [19,20] because it can not only transform multiplicative noise into additive noise but also compresses the value range of the R operator. To restrain the influence of noise with local mean information, a mean ratio (MR) operator was reported for change detection in SAR images [21]. Recently, inspired by the heterogeneity of the local neighborhood used in filter algorithms [14,22], the neighborhood-based ratio (NR) [5] and improved neighborhood-based ratio (INR) [13] methods were proposed to improve the performance of MR. For MR, NR, and INR, a window with a certain size will be applied to the entire image. However, good change detection results are obtained with them when the optimal window is used. The optimal window size of the entire image is the compromised window size of the optimal window sizes of all pixels. The optimal window size of the pixels in a homogeneous area is larger than that in a heterogeneous area and the number of the pixels in homogeneous areas of an image is usually larger than that in heterogeneous areas [22,23]. Therefore, the optimal window size of the most pixels (i.e., the pixels in homogeneous areas of an image) is the same as (or approximately equal to) the optimal window size of the entire image, while the optimal window size of the other pixels (i.e., the pixels in heterogeneous areas of an image) is significantly different from the optimal window size of the entire image. For a given image, the optimal window size for the entire image is generally artificially determined by comparing multiple experimental results at different window sizes. Actually, there is an implicit assumption for such an artificial method to determine the optimal window size that the experimenter has a desired experimental result (the reference map), which is compared with the experimental results at different window sizes to determine the optimal window size. Nevertheless, in the practical application of change detection, we do not have the reference map and do not know which areas have changed, thus we do not know what kind of result is good. Therefore, in the practical application of change detection, it is hard to determine the optimal window artificially, which affects the reliability of change detection results generated with MR, NR, and INR [5,13,21], thereby reducing their value in practical applications. Moreover, it is unreasonable to extract neighborhood information with the same window size for all the pixels of an image because the optimal window size of different pixels in an image is different. On one hand, the optimal window is a large window for a homogeneous area because it is beneficial to significantly restrain the negative influence of speckle noise, thereby accurately describing the change occurred in multi-temporal SAR images. On the other hand, the optimal window is a small window for a heterogeneous area because it is beneficial to preserve the detail information, such as edges, thereby obtaining the change map with accurate edges of changed areas. Hence, it would be better to extract the neighborhood information of all the pixels from their optimal windows rather than a fixed window; that is, different window sizes are used for different pixels rather than the same window size for the entire image. The neighborhood information extracted from the homogeneous region is valuable and meaningful, thus the optimal neighborhood window of a pixel should be a homogeneous region. Therefore, we employ the heterogeneity of a neighborhood to describe its homogeneity degree and select the optimal window size that satisfies the setting condition adaptively. On this basis, the spatial-temporal adaptive neighborhood-based ratio (STANR) method is proposed for change detection in SAR images.

This paper is organized into five sections. Section 2 describes the INR and proposed method. Section 3 presents experimental data sets and results. Discussion on the experimental results and the proposed method is shown in Section 4. Finally, conclusions are drawn in Section 5. The general scheme of the proposed approach is shown in Figure 1.

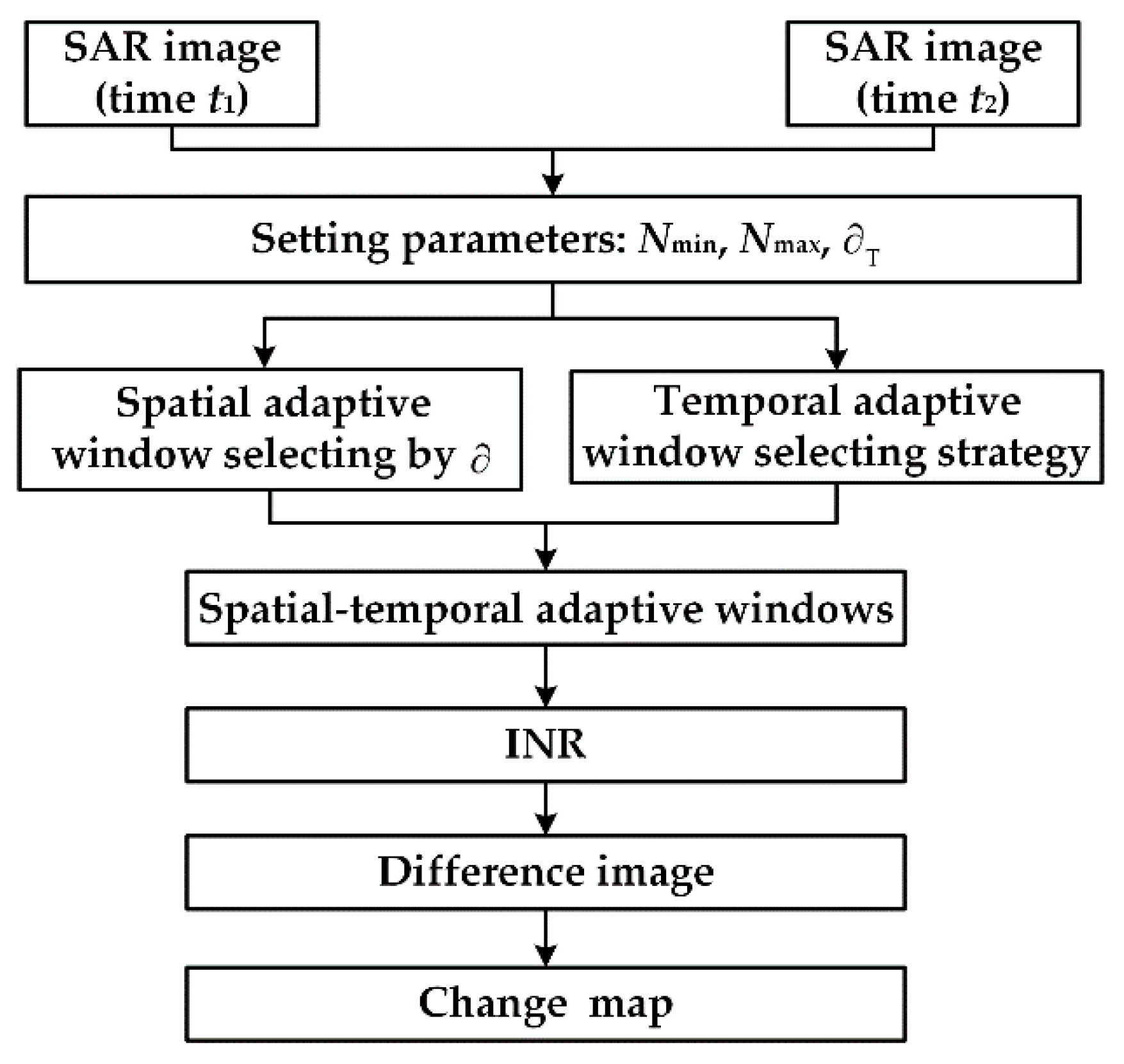
2. Methods

2.1. INR

Different from MR, INR utilizes the heterogeneity $\partial$ to combine the center pixel information and its neighborhood information, where $\partial$ is used to balance between restraining noise and preserving the detail information [5].

$$\partial =\frac{\sigma (x)}{u(x)},$$

(1)

where $\sigma (x)$ is the standard deviation of a neighborhood area, and $u(x)$ is the mean of a neighborhood area. A large $\partial$ corresponds to the small homogeneity, thus the homogeneous region has small heterogeneity $\partial$.

INR, as shown in Equation (2), was proposed to overcome three drawbacks of NR [13].

$$DINR\left(x\right)=1-\frac{\min \left\{\left({\partial }_{\mathrm{n}1}{I}_1\left(x\right)+\left(1-{\partial }_{\mathrm{n}1}\right)\times u_1^{\prime }\right),\left({\partial }_{\mathrm{n}2}{I}_2\left(x\right)+\left(1-{\partial }_{\mathrm{n}2}\right)\times u_2^{\prime }\right)\right\}}{\max \left\{\left({\partial }_{\mathrm{n}1}{I}_1\left(x\right)+\left(1-{\partial }_{\mathrm{n}1}\right)\times u_1^{\prime }\right),\left({\partial }_{\mathrm{n}2}{I}_2\left(x\right)+\left(1-{\partial }_{\mathrm{n}2}\right)\times u_2^{\prime }\right)\right\}},$$

(2)

where $DINR\left(x\right)$ is the gray value of the pixel at position $x$ on difference image $DINR$; the changed pixel has large intensity while the unchanged pixel has small intensity. $I_1(x)$ and $I_2(x)$ are the intensities of the pixels at position $x$ in multi-temporal images $I_1$ and $I_2$; $u_1^{\prime }$ and $u_2^{\prime }$ are the means of the neighborhood areas ${\Omega }_x^1$ and ${\Omega }_x^2$ which have removed the center pixels; and ${\partial }_{\mathrm{n}1}$ and ${\partial }_{\mathrm{n}2}$ are normalized heterogeneity measurements, which can be computed using Equation (3)

$${\partial }_{\mathrm{n}1}=\frac{{\partial }_1}{{\partial }_{\max }},{\partial }_{\mathrm{n}2}\frac{{\partial }_2}{{\partial }_{\max }},$$

(3)

where ${\partial }_1$ and ${\partial }_2$ are heterogeneity measurements of the neighborhood areas ${\Omega }_x^1$ and ${\Omega }_x^2$, and ${\partial }_{\max }$ is the maximum value of all the heterogeneity measurements of multi-temporal SAR images.

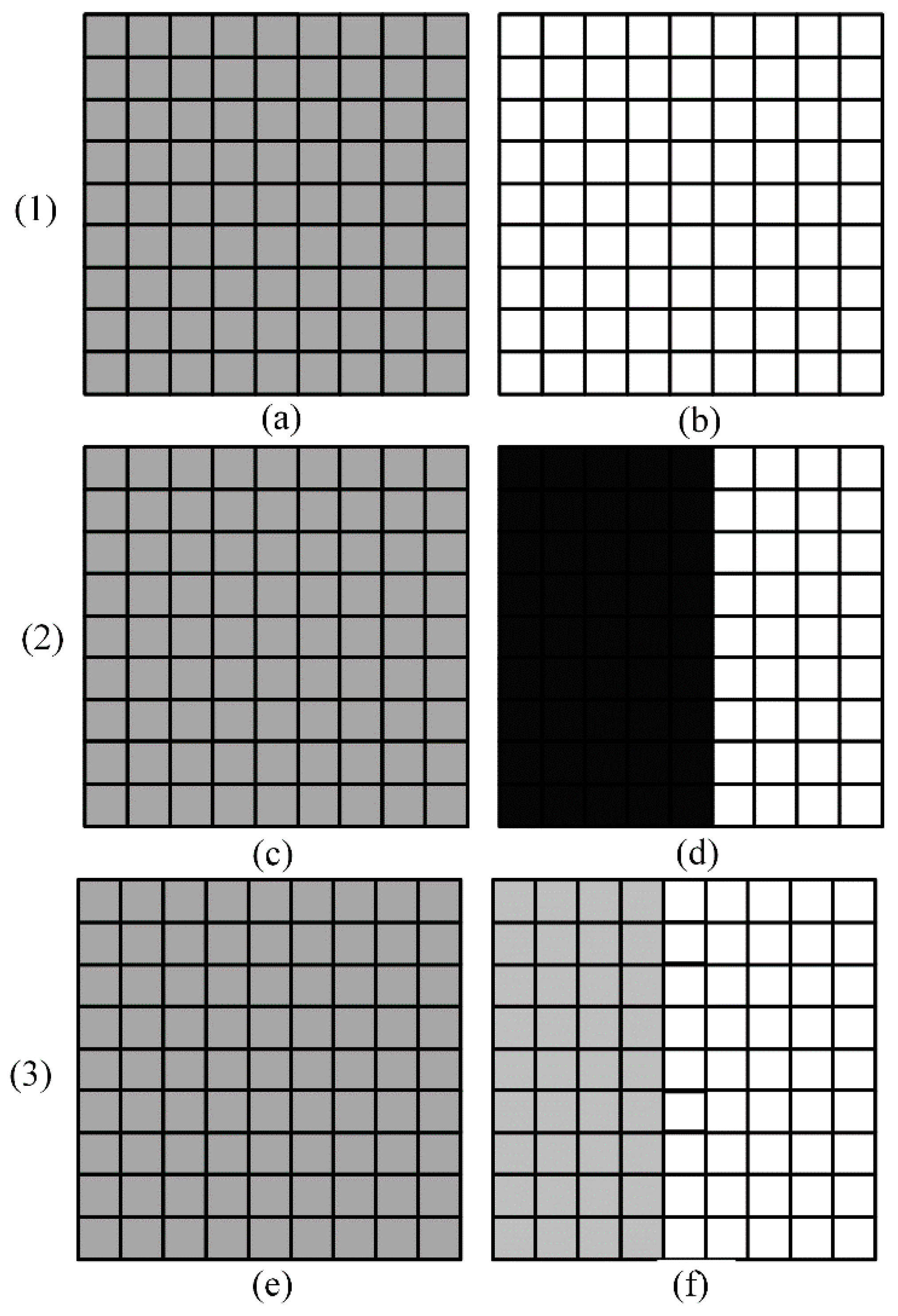
2.2. Spatial Adaptive Window

Given a pixel, its optimal window size is unknown; however, we can confirm its dynamic range $[N_{\min },N_{\max }]$. If the heterogeneity $\partial$ of a window is smaller than a threshold, the window can be treated as a homogeneous window. The balance between noise suppression and detail preservation is the key to suppress the influence of speckle noise by using the neighborhood information. For a homogeneous region, a larger window is useful to suppress the influence of speckle noise, and for a heterogeneous region, a smaller window is useful to keep details such as edges. However, there is significant bias when estimating neighborhood information with smaller sample sizes [24]. The heterogeneity test with a large window is more reliable than a small window. Therefore, we adopted the window search strategy from large window to small window. The spatial adaptive window algorithm is described as Algorithm 1.

Algorithm 1: Spatial adaptive window

Begin

(1) Set the minimum window $N_{\min }$ and the maximum window $N_{\max }$. There are $N_{\mathrm{w}}$ = ($N_{\max }$ − $N_{\min }$)/2 + 1 different sizes of windows.

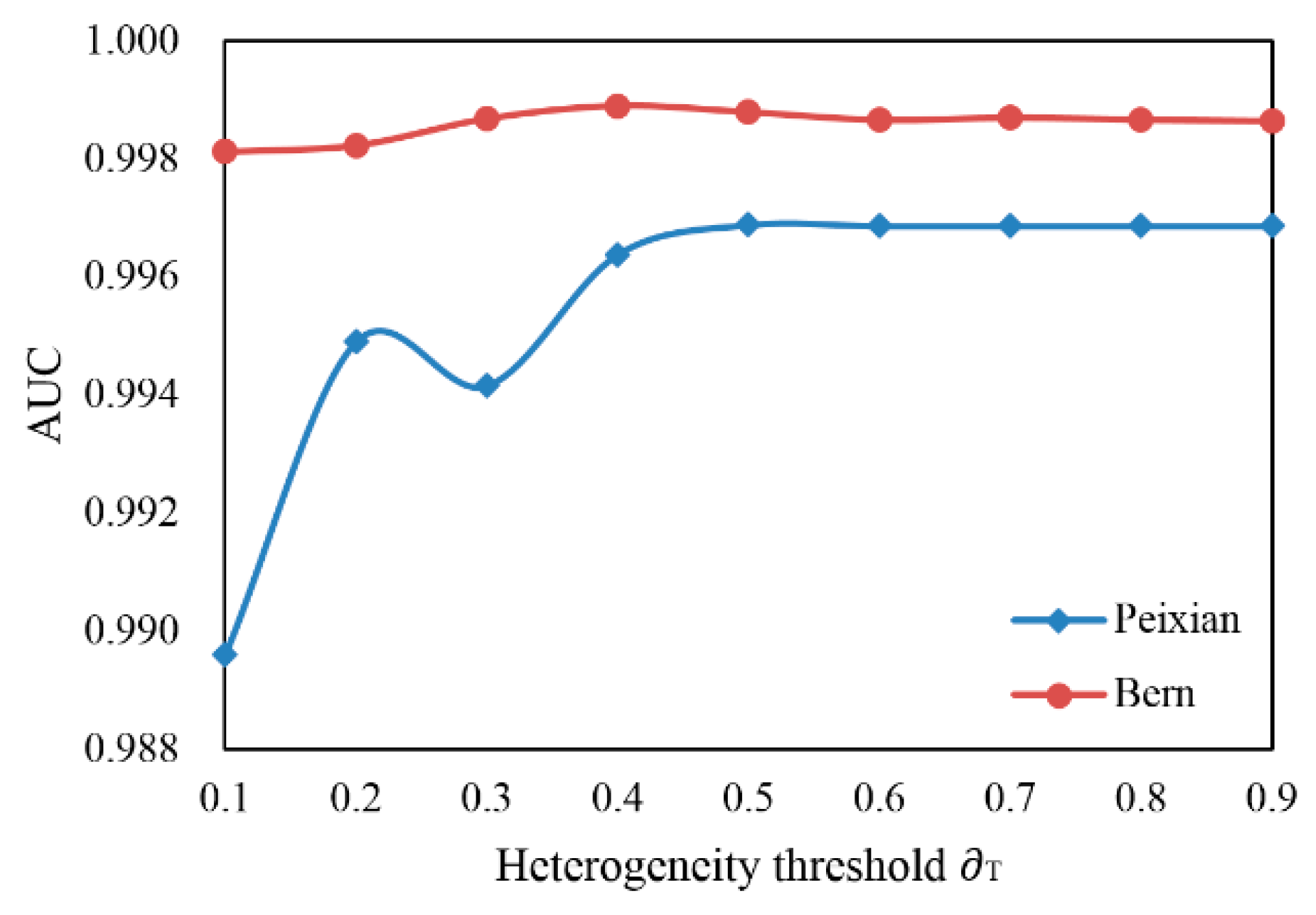
(2) Set the heterogeneity threshold ${\partial }_{\mathrm{T}}$. If the heterogeneity $\partial$ of a window is smaller than ${\partial }_{\mathrm{T}}$, then this window is treated as a homogeneous window.

(3) Set current window $N=N_{\max }$.

(4) Compute the heterogeneity ${\partial }_N$ of the current window. If ${\partial }_N$ < ${\partial }_{\mathrm{T}}$, go to Step (6); otherwise, go to Step (5).

(5) If $N=N_{\min }$, go to Step (6); otherwise, $N=N-2$, go to Step (4).

(6) Save the optimal window $N$ of the current center pixel. If the current pixel is not the last pixel, move to the next pixel, and continue from Step (3); otherwise, the adaptive window of the entire image has been calculated, therefore, go to End.

End

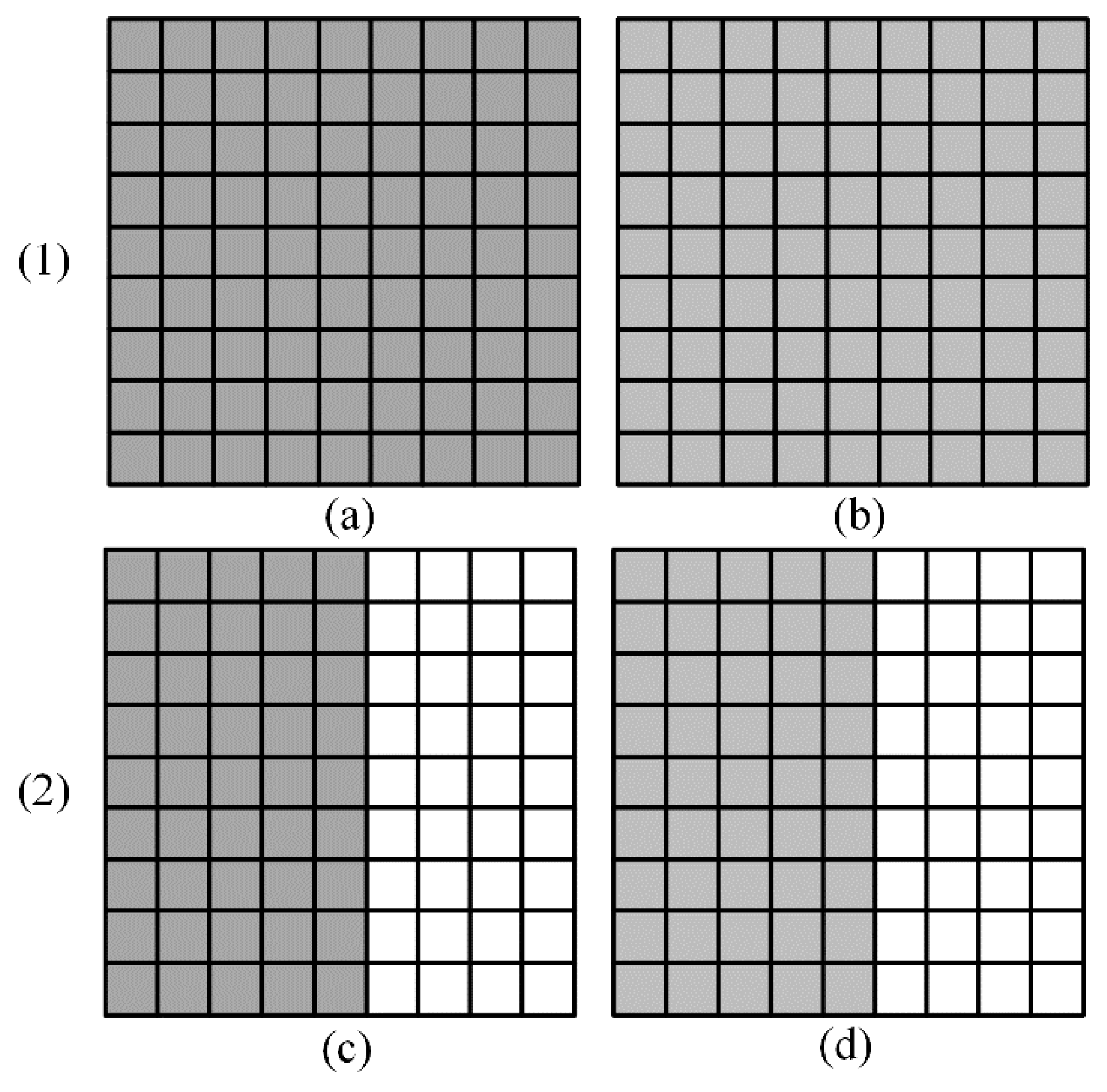
2.3. Temporal Adaptive Window

For change detection, multiple images are needed for processing. For the pixels in the same location in multi-temporal images, how to select the window size adaptively is a problem that needs to be considered. In this context, we originally proposed three main strategies to select the multi-temporal window sizes: (1) Computing the spatial adaptive window of the image acquired in ${\mathrm{T}}_1$ (${\mathrm{T}}_2$), then the window size is used in both the images acquired in ${\mathrm{T}}_1$ and ${\mathrm{T}}_2$. (2) Computing the spatial adaptive window of the new multi-channel image (similar to multispectral image) combined with the images acquired in ${\mathrm{T}}_1$ and ${\mathrm{T}}_2$, where the number of the channels is equal to the number of the multi-temporal images and the neighborhood area of the combined new image includes all the pixels in the two neighborhood areas in the same location in multi-temporal images and is used to compute the heterogeneity in Algorithm 1 (for example, if the neighborhood size is 7 × 7, the combined new neighborhood area includes all the pixels (i.e., 2 × 7 × 7 pixels) in the two neighborhood areas of the same location in multi-temporal images. The mean and standard deviation of the 2 × 7 × 7 pixels is used to compute the heterogeneity of the combined new neighborhood). Then, the window size is used in both the images acquired in ${\mathrm{T}}_1$ and ${\mathrm{T}}_2$. (3) Temporal adaptive window selecting strategy: compute the spatial adaptive windows of the images acquired in ${\mathrm{T}}_1$ and ${\mathrm{T}}_2$, respectively, then the window sizes are respectively used in the images acquired in ${\mathrm{T}}_1$ and ${\mathrm{T}}_2$, and two different window sizes may be applied to the pixels in the same location in multi-temporal images (this special case (for example the following Figure 2c,d) is caused by the changes that occurred in the study area, where the center pixel of Figure 2c is located in a homogeneous area, and thus a larger window is selected by the third strategy to specifically restrain the negative influence of speckle noise; however, the center pixel of Figure 2d is located in a heterogeneous area, and thus a small window is selected by the third strategy to preserve detailed information such as edges).

Taking into account the special change detection problem, multi-temporal images can be divided into the changed and unchanged areas. For the windows acquired with the aforementioned three multi-temporal window selecting strategies, there is a small difference for the unchanged areas, while there is a large difference for the changed areas and the boundary areas of the changed and unchanged areas.

Figure 2 presents three examples of multi-temporal neighborhood areas whose center pixels are changed. The first type of changed multi-temporal neighborhood areas is shown in Figure 2a,b, the gray area shown in Figure 2a becomes the white area shown in Figure 2b. In this case, the window selected with the first strategy is similar to the third strategy because ${\partial }_1\approx {\partial }_2$. The large window could be selected by using the first and third strategies. However, a small window was selected by the second strategy because the heterogeneity ${\partial }_{12}$ is significantly larger than ${\partial }_1$ and ${\partial }_2$. The first and third strategies were better than the second strategy for the first type of changed multi-temporal neighborhood areas because they were homogeneous areas and the large window should be selected for them. The second type of changed multi-temporal neighborhood areas is shown in Figure 2c,d, where the gray area shown in Figure 2c became the black and white areas shown in Figure 2d. The center pixel of Figure 2d is located in the boundary area of two changed areas. For the third strategy, the large window could be selected for Figure 2c, and the small window could be selected for Figure 2d. However, for the first and second strategies, a single window was applied to Figure 2c,d, which was significantly unreasonable because the large window should be selected for Figure 2c (a homogeneous area) and the small window should be selected for Figure 2d (a heterogeneous area). The third type of changed multi-temporal neighborhood areas is shown in Figure 2e,f, where no changes occurred in the left part of Figure 2e, and the right part of Figure 2e became the white area in Figure 2f. The center pixel of Figure 2f is located in the boundary area of the unchanged and changed areas. Similar to the second type, the third strategy was better than the first and second strategies because the large window should be selected for Figure 2e (a homogeneous area) and the small window should be selected for Figure 2 (a heterogeneous area).

Two examples of multi-temporal neighborhood areas whose center pixels located in the unchanged areas of multi-temporal images are shown in Figure 3. The first type of unchanged multi-temporal neighborhood areas is shown as Figure 3a,b, whose center pixels are located in the homogeneous areas. The second type of unchanged multi-temporal neighborhood areas is shown as Figure 3c,d, whose center pixels are located in the boundary areas of two unchanged areas. For the multi-temporal neighborhood areas shown in Figure 3, the windows acquired with the aforementioned three strategies are similar because there no changes occurred in the multi-temporal images such that the heterogeneity of the neighborhood area in image acquired in ${\mathrm{T}}_1$ or ${\mathrm{T}}_2$ is similar to the combined new neighborhood area. The large spatial adaptive window will be selected for most unchanged pixels (such as the center pixels of Figure 3a,b) to suppress the negative influence of speckle noise, while the small spatial adaptive window will be selected for a few unchanged pixels (such as the center pixels of Figure 3c,d) to preserve edge details.

In summary, compared with the first and second strategies, it was more reasonable to use the third strategy (temporal adaptive window selecting strategy) for multi-temporal neighborhood areas in change detection.

2.4. STANR

STANR was proposed on the basis of the aforementioned spatial adaptive window algorithm and temporal adaptive window selecting strategy. First, a spatial adaptive window algorithm was used for multi-temporal SAR images to compute the optimal windows. The temporal adaptive window selecting strategy made it that the different window sizes may be used for a pixel pair in multi-temporal SAR images. Second, the heterogeneity maps of multi-temporal SAR images were computed by using the optimal windows, and normalizing them to [0, 1]. Finally, the neighborhood-based ratio difference image was computed with Equation (2). The algorithm of STANR is described as Algorithm 2.

Algorithm 2: STANR

Begin

(1) Set the minimum window $N_{\min }$ and the maximum window $N_{\max }$. There are $N_{\mathrm{w}}$ = ($N_{\max }$ − $N_{\min }$)/2 + 1 different sizes of windows.

(2) Set the heterogeneity threshold ${\partial }_{\mathrm{T}}$. If the heterogeneity $\partial$ of a window is smaller than ${\partial }_{\mathrm{T}}$, then this window is treated as a homogeneous window.

(3) On the basis of spatial-temporal adaptive window selecting strategy, compute the adaptive windows $N({\mathrm{T}}_1)$ and $N({\mathrm{T}}_2)$ of multi-temporal SAR images with Algorithm 1.

(4) On the basis of the adaptive windows $N({\mathrm{T}}_1)$ and $N({\mathrm{T}}_2)$, compute the heterogeneity maps $\partial ({\mathrm{T}}_1)$ and $\partial ({\mathrm{T}}_2)$ of multi-temporal SAR images, and normalize them to [0, 1] by using Equation (3) to get the normalizing heterogeneity maps ${\partial }_{\mathrm{n}}({\mathrm{T}}_1)$ and ${\partial }_{\mathrm{n}}({\mathrm{T}}_2)$.

(5) Compute the neighborhood-based ratio difference with Equation (2) for each pixel pair of multi-temporal SAR images.

End

The proposed STANR method has three input parameters: the minimum window $N_{\min }$, the maximum window $N_{\max }$, and the heterogeneity threshold ${\partial }_{\mathrm{T}}$. If the minimum window is set as 3 × 3, the detail information, such as the edge, will be well preserved; however, the neighborhood information, such as heterogeneity, affected by speckle noise, is unreliable, which will limit the performance of the proposed approach [24]. Equation (2) can well preserve detailed information, such as the edge, because it uses heterogeneity to achieve balance between noise suppression and detail preservation, thus the minimum window 5 × 5 is used in this paper. The large window can restrain the impact of speckle noise well in homogeneous areas; however, the computation time of a spatial-temporal adaptive window will increase with the increase of the maximum window. An appropriate range for the maximum window is 7 × 7 to 15 × 15. Typically, an 11 × 11 window is enough for most images [23]. The tiny change of ${\partial }_{\mathrm{T}}$ has a small impact on the experimental results obtained with STANR because ${\partial }_{\mathrm{T}}$ is also used as a weight to control the influence of the neighborhood information to the center pixel in Equation (2). The appropriate range of the heterogeneity parameter ${\partial }_{\mathrm{T}}$ is 0.4–0.6. Typically, ${\partial }_{\mathrm{T}}=0.5$ is enough for most images. To confirm the heterogeneity settings, STANR with ${\partial }_{\mathrm{T}}$ from 0.1 to 0.9 was tested on Peixian and Bern data sets (shown in Section 3.1). The area under curve (AUC) [25] of the difference images obtained with STANR is shown in Figure 4. The larger the AUC, the better the performance of the method. In the experiment on the Peixian data set, the AUC had the maximum value when ${\partial }_{\mathrm{T}}=0.5$; when ${\partial }_{\mathrm{T}}>0.5$, the AUC was approximately equal to that with ${\partial }_{\mathrm{T}}=0.5$. In the experiment on Bern data set, the AUC corresponding to ${\partial }_{\mathrm{T}}=0.5$ was approximately equal to the maximum value corresponding to ${\partial }_{\mathrm{T}}=0.4$. For two difference images with the same AUC, the difference image with the smaller ${\partial }_{\mathrm{T}}$ had an advantage in preserving the detailed information, such as the edge, because the smaller ${\partial }_{\mathrm{T}}$ made the spatial adaptive window algorithm select a smaller window for heterogeneous areas such as edges. Therefore, ${\partial }_{\mathrm{T}}=0.5$ was enough for the data sets used in this study.

3. Experiments and Results

3.1. Description of Data Sets

The first data set has two images with resolution 10 m (i.e., Figure 5a,b) acquired in the same area through the ALOS-1 satellite. The area shown in the two images is a section of a scene acquired in Peixian, China, in July 2008 and August 2009. The second data set (i.e., Figure 6a,b) is composed of two images with resolution 30 m acquired by ERS-2 over an area in Bern, Switzerland, in April 1999 and May 1999. Figure 5c and Figure 6c, defined manually according to an accurate and time-consuming visual inspection of the considered SAR images, are reference maps used to facilitate the quantitative evaluation of change maps.

3.2. Experimental Design

We first used IR [18], LR [19], MR [21], NR [5], INR [13], generalized likelihood ratio test (GLRT) [26], non-local mean ratio (NLMR) [27], and STANR to generate 20 difference images. The windows 3 × 3, 5 × 5, 7 × 7, and 9 × 9 were applied to MR, NR, INR, and GLRT. The similarity window 5 × 5 and the search window 11 × 11 were used for NLMR. The minimum window $N_{\min }$ = 5, the maximum window $N_{\max }$ = 11, and the heterogeneity threshold ${\partial }_{\mathrm{T}}$ = 0.5 were used for STANR. Then, the change maps were acquired from these difference images with the reasonable thresholds for further comparing the performance of different methods. The optimal threshold of the existing automatic threshold selection approaches [1,28,29,30,31,32,33,34] was calculated under a certain assumption and was unreasonable when the assumption was inappropriate [1,13]. To avoid the negative impact of the unreasonable threshold on the experiments, a manual trial-and-error procedure (MTEP) was employed to obtain the threshold, which has been widely used in the literature focusing on change detection [32,35,36,37].

3.3. Experimental Results on Peixian Data Set

The difference images generated from the Peixian data set by using different methods are shown in Figure 7. The section in rectangle A is an unchanged area, while two changed areas are included in rectangle B. The changed pixel had a large intensity, while the unchanged pixel had a small intensity. In the difference image acquired with IR, it can be seen that many pixels in the rectangle A had large intensities, and many pixels in the changed areas of the rectangle B had small intensities. In the difference image acquired with LR, the pixels in the unchanged area of the rectangle B had small intensities; however, some pixels in the changed areas of the rectangle B also had small intensities. In the difference image generated with NLMR, the pixel intensity in the rectangle A was smooth, and there was a small intensity difference between the changed and unchanged pixels in rectangle B. For the difference images acquired by using MR, with the increase of the window size, the pixel intensity in the rectangle A became very smooth because MR exploits the neighborhood information of SAR image; the intensity of the unchanged pixel in the rectangle B became larger, and it was hard to distinguish the changed and unchanged areas in rectangle B when the window was 9 × 9, which also reflected the drawback of using the same window size for the entire image. As the window size increased, in the difference images obtained with NR and INR, the pixel intensity in the rectangle A became very smooth, while the number of the unchanged pixels with small intensities in the unchanged area between two changed areas in the rectangle B became smaller. In the difference images obtained by GLRT, the unchanged pixel in rectangle A had a small intensity, and the boundaries between the changed and unchanged areas in rectangle B were a bit fuzzy. In the difference image acquired with STANR, the pixel intensity in rectangle A was very smooth, and there were clear boundaries between the changed and unchanged areas in rectangle B, which was a benefit from the spatial-temporal adaptive window selection strategy adopted by the proposed method.

For the difference images acquired by using MR, NR, INR, and GLRT with different window sizes on the Peixian data set, the quantitative comparison of them will be carried out in Section 4.1 to select the best difference image of each method so that we can adequately compare them with STANR. The change maps generated from the difference images obtained with IR, LR, NLMR, and STANR, and the change maps generated from the best difference images obtained with MR, NR, INR, and GLRT by using the MTEP threshold are presented in Figure 8. Compared with the change maps generated with the methods using the neighborhood information of SAR image, there were some false alarm pixels in rectangle A of the change maps obtained with IR and LR, which shows that the neighborhood information of the SAR image was useful to suppress the adverse effects of the false alarm pixels. A further quantitative comparison of the change maps generated from the Peixian data set will be presented in Section 4.1.

3.4. Experimental Results on Bern Data Set

Figure 9 presents the difference images obtained from the Bern data set by using different methods. The section in rectangle A was an unchanged area, two changed areas included in rectangle B were separated by an unchanged area. Experimental results were similar to that in the Peixian data set. For the difference images obtained with IR and LR, some pixels in the unchanged area of the rectangle A had large intensities. The difference image acquired with STANR performed better than the other methods using the neighborhood information of SAR images, the pixel intensity in rectangle A was very smooth, and there were clear boundaries between the changed and unchanged areas in rectangle B.

The quantitative comparison of the difference images obtained with different methods on the Bern data set will be carried out in Section 4.2. For the difference images obtained with IR, LR, NLMR, and STANR, and the best difference images obtained with MR, NR, INR, and GLRT in the Bern data set, the change maps acquired by using MTEP threshold are shown in Figure 10. The experimental results were similar to that in the Peixian data set. Compared with the change maps obtained with the methods using neighborhood information, there were many false alarm pixels in rectangle A of the change maps acquired with IR and LR. Visually, the other change maps were similar to the reference map shown in Figure 6c. The further quantitative comparison of the change maps generated from the Bern data set will be presented in Section 4.2.

4. Discussion

The experimental results acquired from the two data sets have been given in Section 3, which also presented the qualitative description of the performance of different methods. This section will focus on the quantitative discussion of the experimental results and the discussion on the proposed method. The receiver operating characteristic (ROC) curve and AUC [25] were employed to compare the difference images obtained with different methods. The discussion of change maps is based on the following quantitative evaluation parameters: missed alarms, overall error, detected changes, Kappa coefficient [38], and F1 score [39]. Let $P_{\mathrm{cc}}$ represent the number of the pixels that were detected as changed and actually changed. Let $P_{\mathrm{cu}}$ represent the number of the pixels that were detected as changed but were actually unchanged. Let $P_{\mathrm{uc}}$ represent the number of the pixels that were detected as unchanged but were actually changed. Let $P_{\mathrm{uu}}$ represent the number of the pixels that were detected as unchanged and actually unchanged. Then, missed alarms is equal to $P_{\mathrm{uc}}$, detected changes is equal to $P_{\mathrm{cc}}$, and overall error is equal to the sum of $P_{\mathrm{cu}}$ and $P_{\mathrm{uc}}$. Let $P_{\mathrm{n}}$ represent the number of the pixels in the SAR image, which is equal to the sum of $P_{\mathrm{cc}}$, $P_{\mathrm{cu}}$, $P_{\mathrm{uc}}$, and $P_{\mathrm{uu}}$. Then, the Kappa coefficient can be computed with Equation (4) [38]

$$\mathrm{Kappa}=(k_1-k_2)/(1-k_2),$$

(4)

where $k_1$ and $k_2$ are computed with Equations (5) and (6)

$$k_1=(P_{\mathrm{cc}}+P_{\mathrm{uu}})/P_{\mathrm{n}},$$

(5)

$$k_2=\frac{(P_{\mathrm{cc}}+P_{\mathrm{cu}})(P_{\mathrm{cc}}+P_{\mathrm{uc}})+(P_{\mathrm{uc}}+P_{\mathrm{uu}})(P_{\mathrm{cu}}+P_{\mathrm{uu}})}{P_{\mathrm{n}}\times P_{\mathrm{n}}},$$

(6)

The F1 score is computed with Equation (7) [39]

$$\mathrm{F}1=2F_{\mathrm{p}}{F}_{\mathrm{r}}/(F_{\mathrm{p}}+F_{\mathrm{r}}),$$

(7)

where $F_{\mathrm{p}}$ and $F_{\mathrm{r}}$ are computed with Equations (8) and (9)

$$F_{\mathrm{p}}=P_{\mathrm{cc}}/(P_{\mathrm{cc}}+P_{\mathrm{cu}}),$$

(8)

$$F_{\mathrm{r}}=P_{\mathrm{cc}}/(P_{\mathrm{cc}}+P_{\mathrm{uc}}),$$

(9)

Substituting Equations (8) and (9) into Equation (7), we can get the simplified form of Equation (7)

$$\mathrm{F}1=2P_{\mathrm{cc}}/(2P_{\mathrm{cc}}+P_{\mathrm{cu}}+P_{\mathrm{uc}}),$$

(10)

4.1. Discussion on Experimental Results of Peixian Data Set

The ROC curves of the difference images obtained from the Peixian data set with different methods are shown in Figure 11. To clearly compare the difference images obtained by using MR, NR, INR, and GLRT with different window sizes and the proposed method, the ROC curves of MR, NR, INR, and GLRT are plotted separately with STANR, which are shown as Figure 11a–d. The performance of the method is better when the ROC curve is closer to the upper left corner. It is clear that STANR performed better than MR, NR, INR, and GLRT. For MR, the difference images acquired with the window sizes 7 × 7 and 9 × 9 were obviously better than those with the window sizes 3 × 3 and 5 × 5; and the difference image obtained with the 7 × 7 window was slight better than that with the 9 × 9 window. For NR, INR, and GLRT, the ROC curve of the difference image obtained with the 7 × 7 window was the closest to the upper left corner and performed better than that of the other window sizes. Figure 11e presents the ROC curves of the difference images obtained by using IR, LR, NLMR, and STANR, and the ROC curves of the best difference images obtained by using MR, NR, INR, and GLRT, and

Table 1. AUC from using R, LR, NLMR, MR, NR, INR, GLRT, and STANR on the Peixian data set.

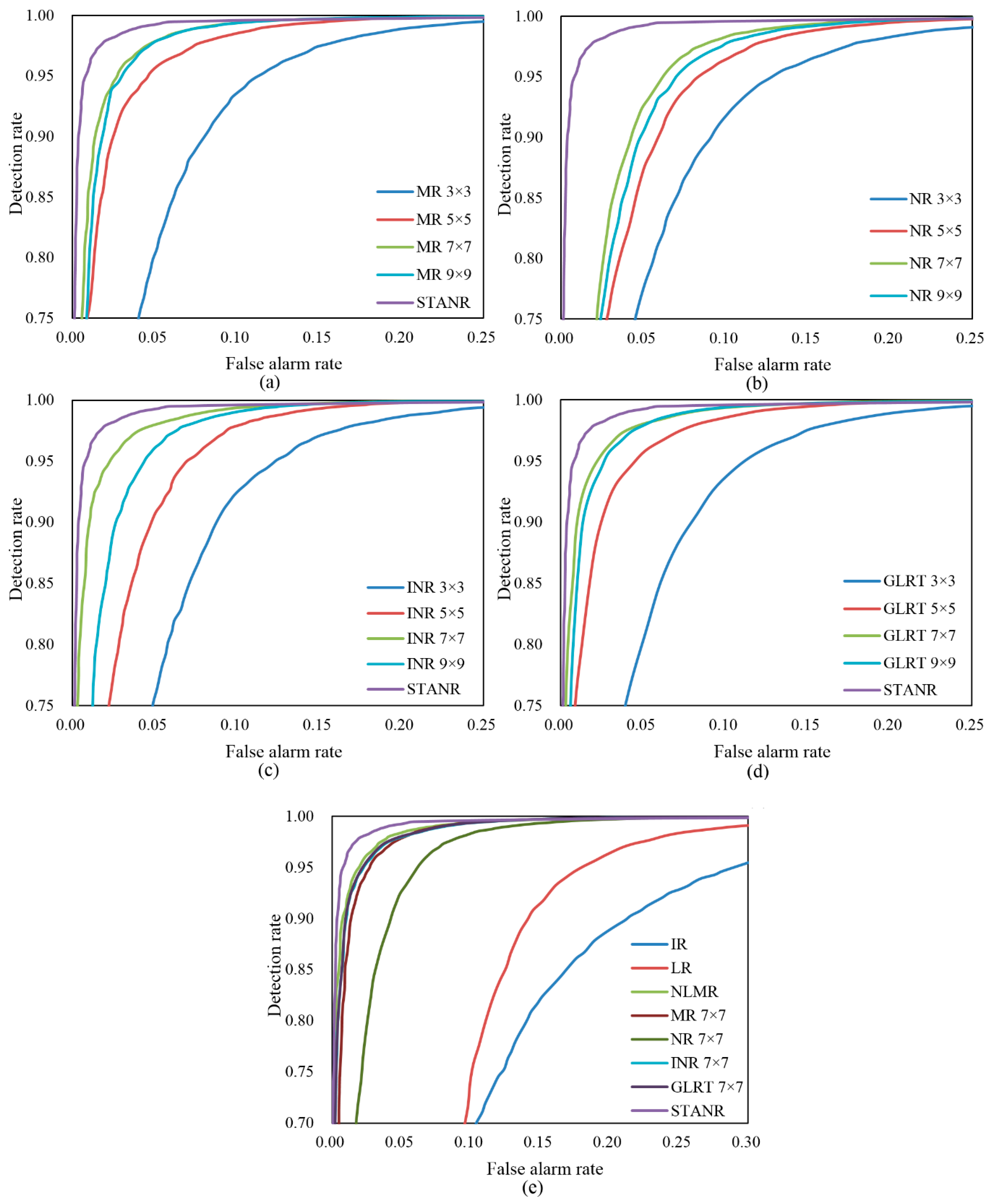
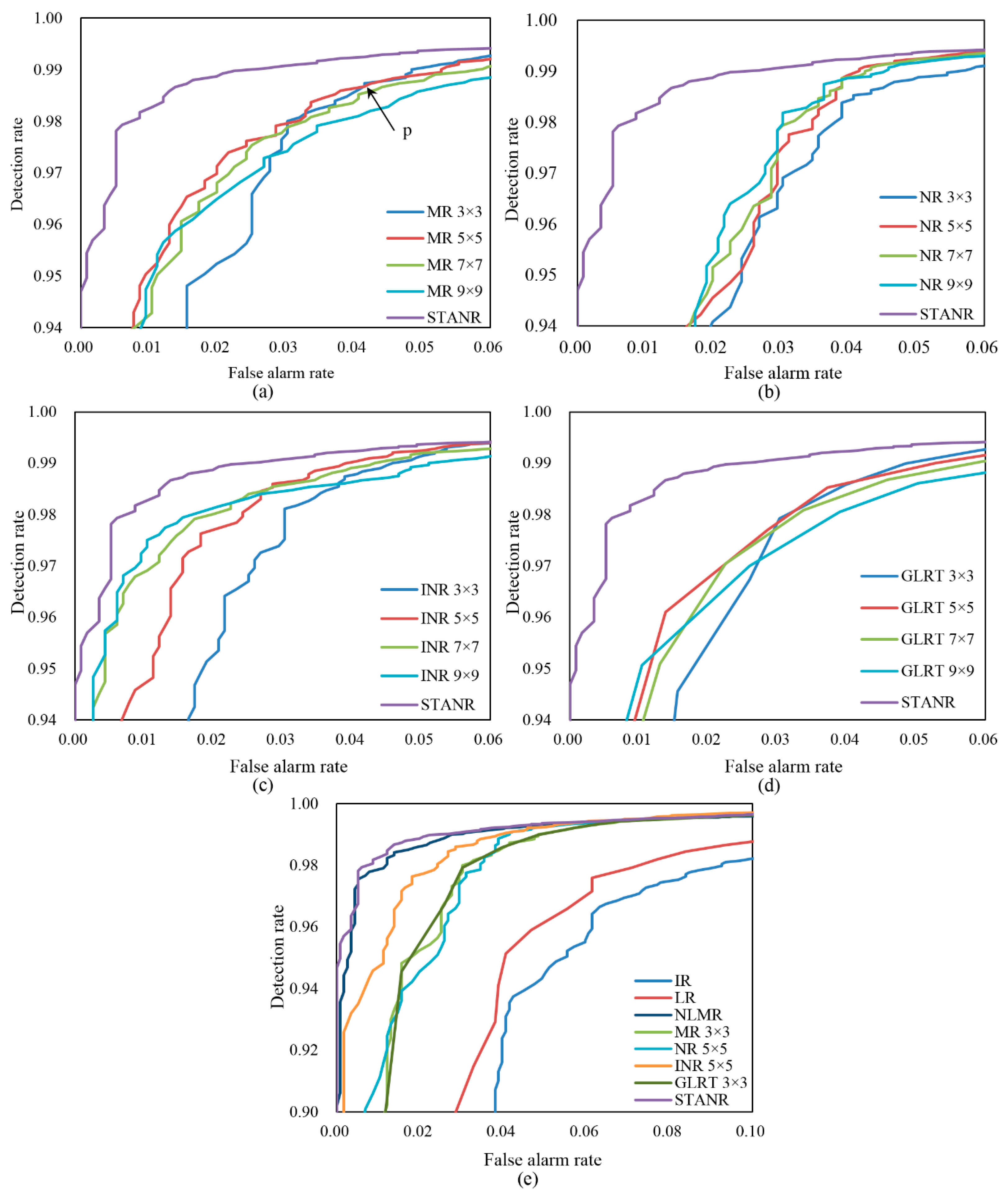
Method	IR	LR	NLMR	MR-7 × 7	NR-7 × 7	INR-7 × 7	GLRT-7 × 7	STANR
AUC	0.908	0.906	0.995	0.992	0.981	0.994	0.994	0.997

shows their AUC. The larger the AUC, the better the performance of the method. The performance of IR and LR was worse than NLMR, MR, NR, INR, GLRT, and STANR because they ignore the spatial neighborhood information of SAR images. The performance of the difference image acquired with STANR was the best, whose ROC curve was closest to the upper left corner and the AUC was the largest, which shows the superiority of the spatial-temporal adaptive window selection strategy adopted by the proposed method and its applicability in the change detection of SAR images.

Table 2. Missed alarms, overall error, detected changes (in number of pixels), Kappa, and F1 score resulting from different approaches on the Peixian data set.

Method	Missed Alarms	Overall Error	Detected Changes	Kappa	F1 Score
IR	3635	4134	2586	0.544	0.556
LR	2321	2871	3900	0.722	0.731
NLMR	1119	1360	5102	0.878	0.882
MR-7 × 7	1134	1431	5087	0.872	0.877
NR-7 × 7	1332	1720	4889	0.845	0.850
INR-7 × 7	1047	1302	5174	0.884	0.888
GLRT-7 × 7	1051	1333	5170	0.882	0.886
STANR	855	1217	5366	0.894	0.898

presents the five quantitative evaluation parameters of the change maps shown in Figure 8. A better change map characterizes the smaller missed alarms and overall error, more detected changes, and larger Kappa and F1 score. The following is the analysis of Table 2: (1) the change map acquired with IR possessed the highest missed alarms (3635) and overall error (4134), the lowest detected changes (2586), Kappa (0.544), and F1 score (0.556), which was affected by the speckle noise of the SAR image; (2) the change map generated with LR was better than IR because the former could transform multiplicative noise into additive noise; (3) NLMR, MR, NR, INR, GLRT, and STANR performed better than IR and LR from the perspective of the five quantitative evaluation parameters because the neighborhood information was used to restrain the negative impact of speckle noise; (4) the change map generated with STANR outperformed the other methods, which had the lowest missed alarms and overall error, and the highest detected changes, Kappa, and F1 score because STANR selects the window with spatial-temporal adaptive strategy which makes STANR can well suppress the negative impact of speckle noise and preserve detailed information such as an edge.

4.2. Discussion of Experimental Results of Bern Data Set

Figure 12 shows the ROC curves of the difference images obtained from the Bern data set with different methods. Similar to Peixian data set, to clearly compare the difference images acquired by using MR, NR, INR, and GLRT with different window sizes and the proposed method, the ROC curves of MR, NR, INR, and GLRT are plotted separately with STANR, shown as Figure 12a–d. Obviously, the performance of STANR was better than MR, NR, INR, and GLRT. The ROC curves related to the Peixian data set were smooth, thus it was easy to compare their performances. However, there were a lot of cross-points (such as $P$ in Figure 12a) among the ROC curves related to the Bern data set. In this situation, the right part of $P$ should be used to compare their performances [13]. MR and GLRT had the best difference image when the window was 3 × 3. NR and INR had the best difference image when the window was 5 × 5. The ROC curves of the difference images obtained by using IR, LR, NLMR, and STANR, and the ROC curves of the best difference images obtained by using MR, NR, INR, and GLRT are presented in Figure 12e, and

Table 3. AUC from using R, LR, NLMR, MR, NR, INR, GLRT, and STANR on the Bern data set.

Method	IR	LR	NLMR	MR-3 × 3	NR-5 × 5	INR-5 × 5	GLRT-3 × 3	STANR
AUC	0.977	0.985	0.998	0.995	0.996	0.997	0.993	0.999

shows their AUC. NLMR, MR, NR, INR, GLRT, and STANR outperformed IR and LR because they exploited the neighborhood information of SAR images. STANR performed better than the other methods, which was benefit from the spatial-temporal adaptive window selecting strategy adopted by the proposed method.

Table 4. Missed alarms, overall error, detected changes (in number of pixels), Kappa, and F1 score resulting from different approaches on the Bern data set.

Method	Missed Alarms	Overall Error	Detected Changes	Kappa	F1 Score
IR	368	665	787	0.699	0.703
LR	357	546	798	0.742	0.745
NLMR	267	395	888	0.816	0.818
MR-3 × 3	230	318	925	0.851	0.853
NR-5 × 5	234	347	921	0.839	0.841
INR-5 × 5	218	303	937	0.859	0.861
GLRT-3 × 3	222	317	933	0.853	0.855
STANR	214	302	941	0.860	0.862

presents the five quantitative evaluation parameters of the change maps generated from the difference images obtained with IR, LR, NLMR, and STANR, and the best difference images obtained with MR, NR, INR, and GLRT on the Bern data set. Considering all five measurements, the change map acquired with IR was the worst, while the best one was generated with STANR. LR outperformed IR because the LR could transform multiplicative noise into additive noise. IR and LR performed worse than NLMR, MR, NR, INR, GLRT, and STANR because the neighborhood information was ignored by them. STANR performed better than NLMR, MR, NR, INR, and GLRT, which had the lowest missed alarms (214) and overall error (302), and the highest detected changes (941), Kappa (0.860), and F1 score (0.862) because the spatial-temporal adaptive window selecting strategy adopted by STANR could exploit the neighborhood information more reasonably.

4.3. Discussion of the Study

This study reports a STANR method for change detection in SAR images, which aimed to not only reduce the negative influence of noise but also obtain the change result with an accurate edge of the changed area. In order to achieve this purpose, we needed to extract the valuable neighborhood information from a homogeneous window. First, the spatial and temporal adaptive window selecting strategies were presented and compared in Section 2.2 and Section 2.3 respectively. Then, the method selecting the adaptive window in space and time simultaneously was used for the proposed STANR. The experiments were conducted on two SAR data sets with spatial resolutions of 10 m and 30 m, respectively, and the experimental results showed the efficiency of STANR. Compared with seven famous methods for change detection of SAR images, Table 1 and Table 3 showed that STANR could acquire a better difference image with a larger AUC, and Table 2 and Table 4 showed that STANR could obtain a more accurate change map with smaller missed alarms and overall error, and larger detected changes, Kappa, and F1 score. The performance of STANR was benefited from the adaptive window in space and time simultaneously, which made STANR use a larger window in homogeneous areas to reduce the negative influence of noise and use a small window in heterogeneous areas to preserve the edge information of the changed area.

STANR had several input parameters, whose settings have been discussed in Section 2.4. The settings recommended and used in this study were effective in the experiments; however, one could also try to change them in the applications. For most images, an 11 × 11 maximum window was enough for restraining the influence of noise, and a larger window will increase the computational cost [23]. The change of heterogeneity threshold in the recommended range 0.4–0.6 had a small influence on the change detection result because it was also used as a weight to determine the influence of neighborhood information to the center pixel in STANR (i.e., compared with heterogeneous areas, the neighborhood information played a more important role in homogeneous areas).

5. Conclusions

STANR for change detection in multi-temporal SAR images was proposed in this paper. Unlike classical methods using the neighborhood information of SAR images with a single window size for the entire image, this approach exploited the window sizes selected adaptively, not only in space, but also in time. Experiments were conducted on two data sets to confirm the performance of the proposed method, and the Kappa and F1 score of STANR were larger than that of the other seven methods. For example, for the Peixian data set, the Kappa and F1 score of STANR were 0.894 and 0.898, respectively, while the highest values of other methods were 0.884 and 0.888, respectively. Experimental results showed that STANR could exploit the neighborhood information of multi-temporal SAR images more reasonably and could both suppress the negative influence of noise and preserve edge details. This work contributes to (1) proposing and comparing the applicability of three multi-temporal neighborhood windows selecting strategies in change detection, and draw the conclusion that the temporal adaptive window selecting strategy is the best; and (2) proposing STANR based on a spatial-temporal adaptive neighborhood for change detection in SAR images, which can reduce the uncertainty of the change detection results brought by the fixed window determined on the experience of user and improve the usability and accuracy in practical applications.