Single-Polarized SAR Classification Based on a Multi-Temporal Image Stack
Abstract
1. Introduction
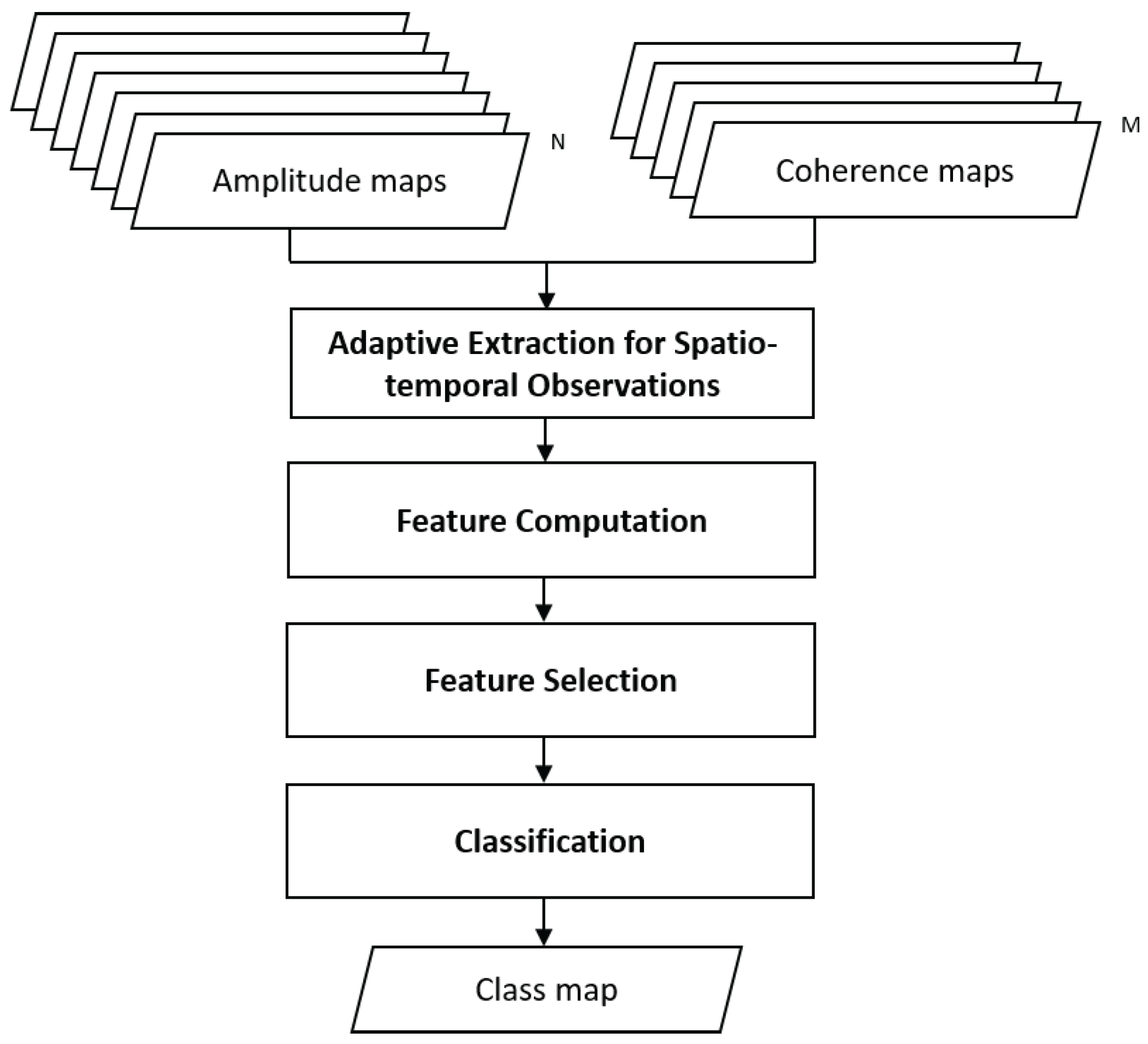
2. Methodology
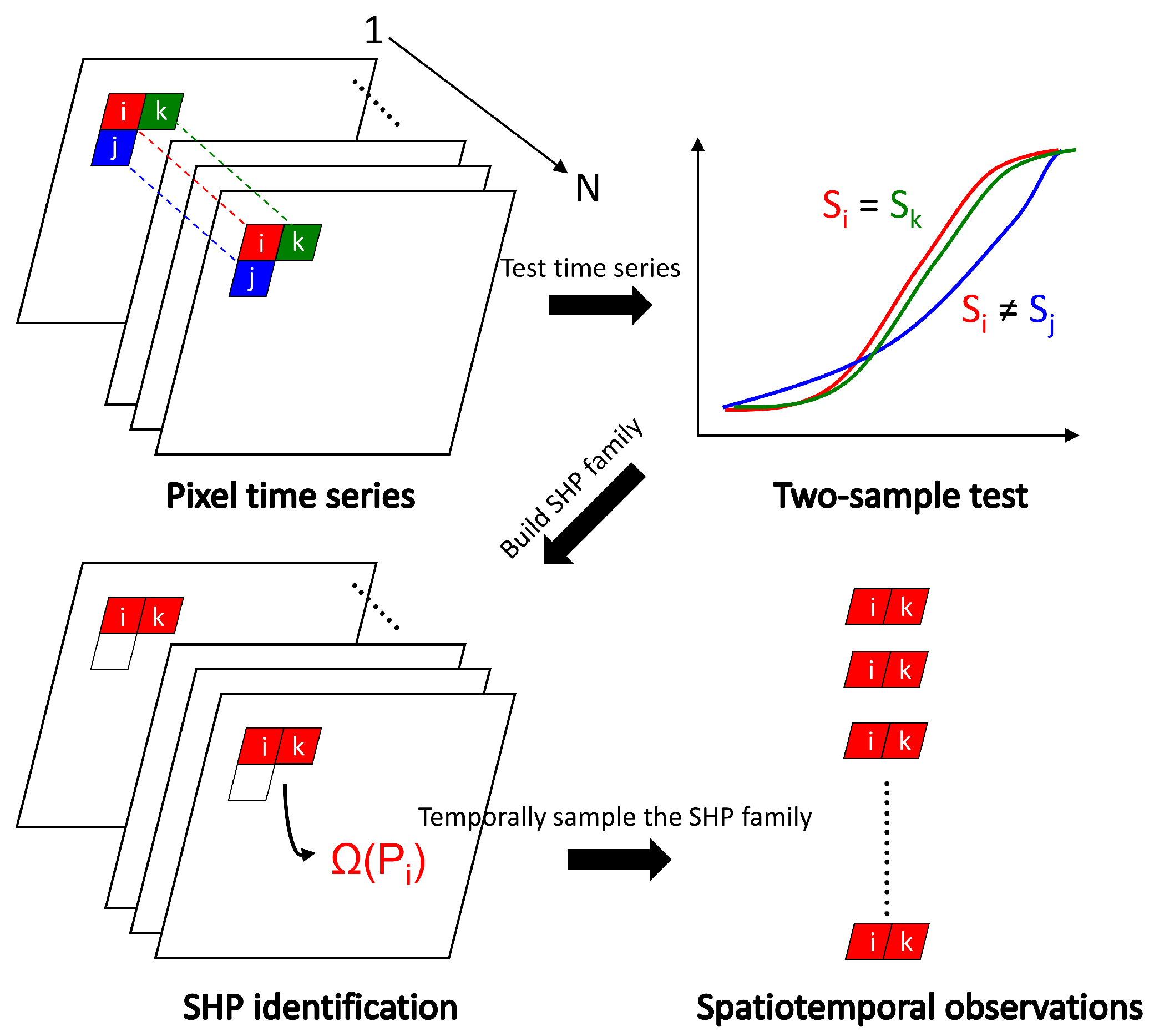
2.1. Adaptive Extraction of Spatio-Temporal Observations
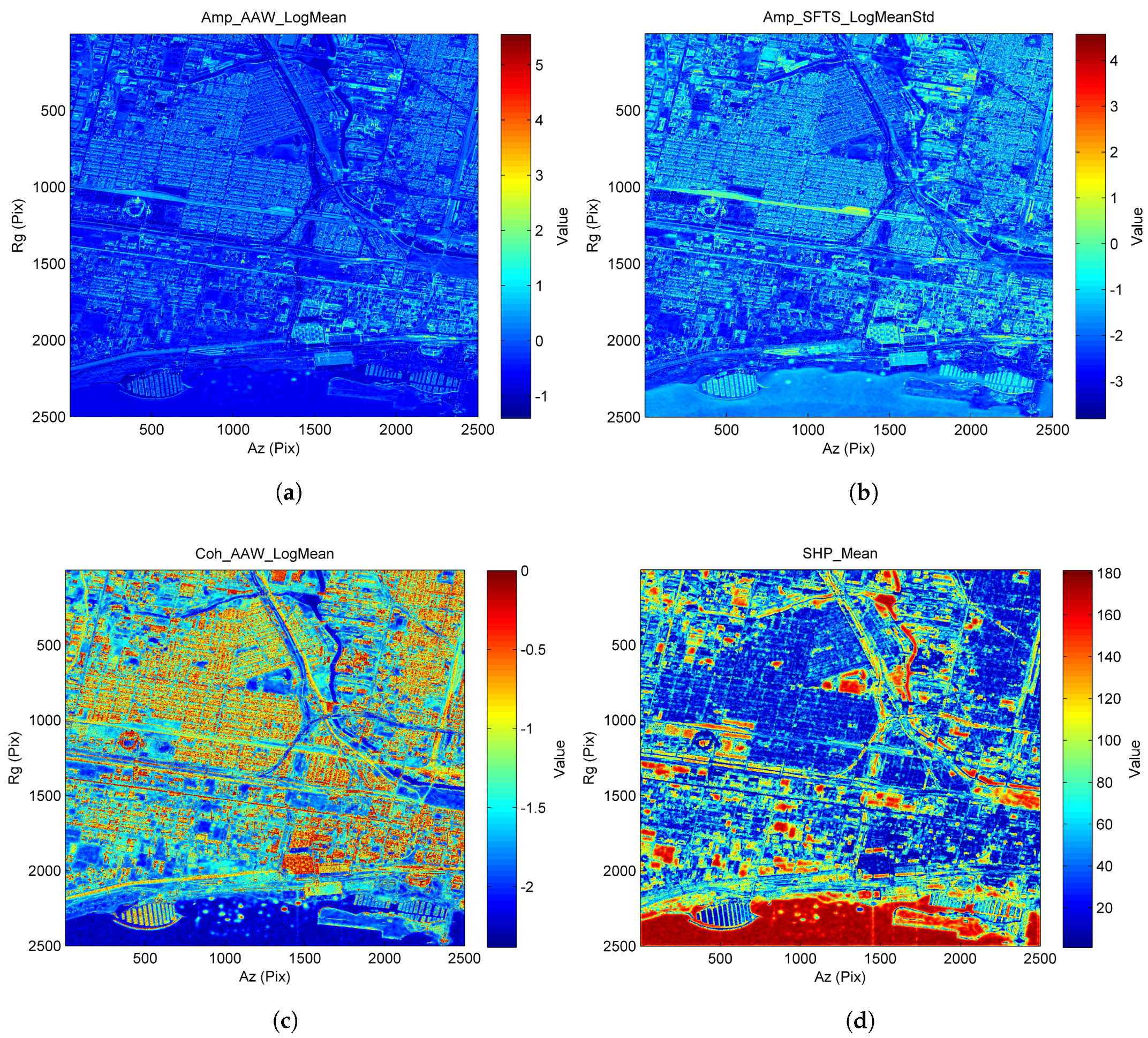
2.2. Feature Computation for Information Extraction
- Time series features: These features are related to the group statistics of and . We design these features by adjusting the processing order of logarithm (log), mean, standard deviation (std), saturation, etc. With different combinations, various statistics can be calculated. For example, one can first compute the spatial average of to obtain a time series vector and then calculate the standard deviation of this vector, and vice versa. One can also compute a single mean or a single std of or .
- SHP features: These features represent the statistics specifically regarding the SHP. For example, one can first compute the SHP size at each pixel (i.e., area of ), obtaining an SHP size map. Then, the mean or std of can be calculated based on the SHP size map to acquire different SHP features.
- Textural features: These features analyze the statistics of spatial relations among neighboring pixels (e.g., smoothness, roughness, periodicity). Different types of textural features have been developed (see [20]). As we have obtained the spatial contents through , we can compute each of these features accordingly. We implement several textural features (e.g., energy and entropy) based on the gray level co-occurrence matrix (GLCM) (GLCM utilizes the second-order statistics of the grayscale image histograms to calculate the textures) [21]. We acquire these features using the reflectivity map (temporal average of the incoherent data stack) and the long-term coherence map (temporal average of the coherent data stack).
- Geometric features: These features measure the geometric characteristics of . Many intuitive features can be computed, such as the border length, shape index, compactness, asymmetry, etc. These features have been extensively used in OBIA as they provide spatial information that is not well depicted in PBIA.
2.3. Feature Selection for Dimensionality Reduction
2.4. Pixel Labeling
3. Study Areas and Data Description
3.1. TanDEM-X Data Stack in Los Angeles
3.2. COSMO-SkyMed Data Stack in Chicago
4. Experiments and Discussions
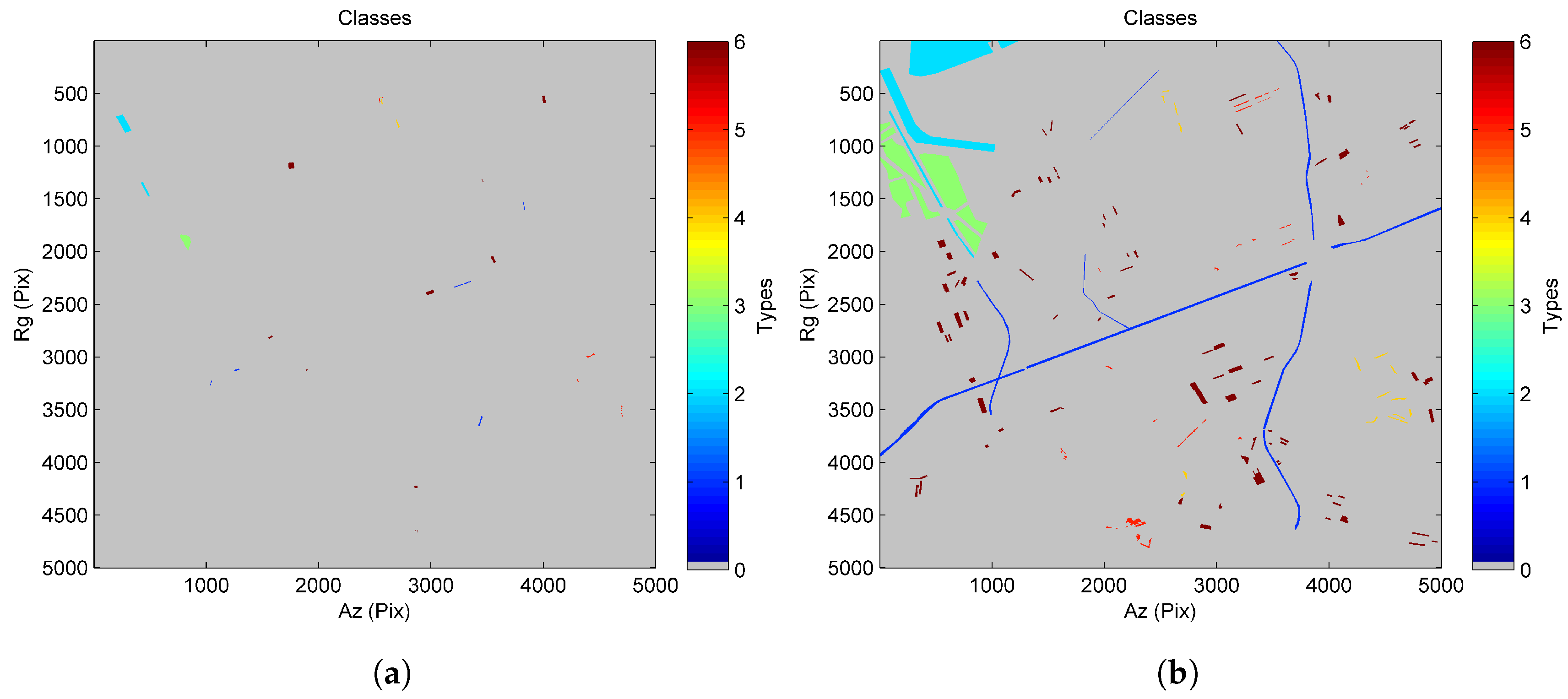
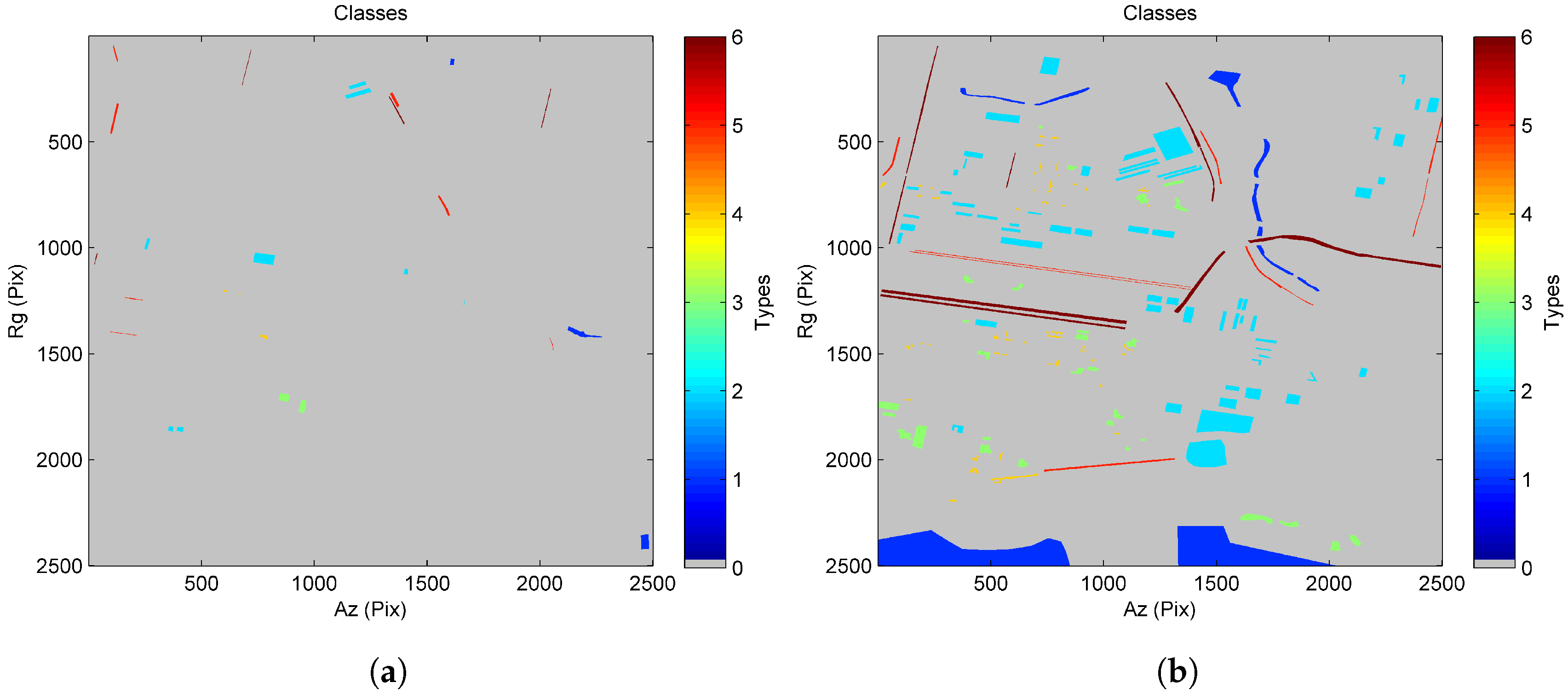
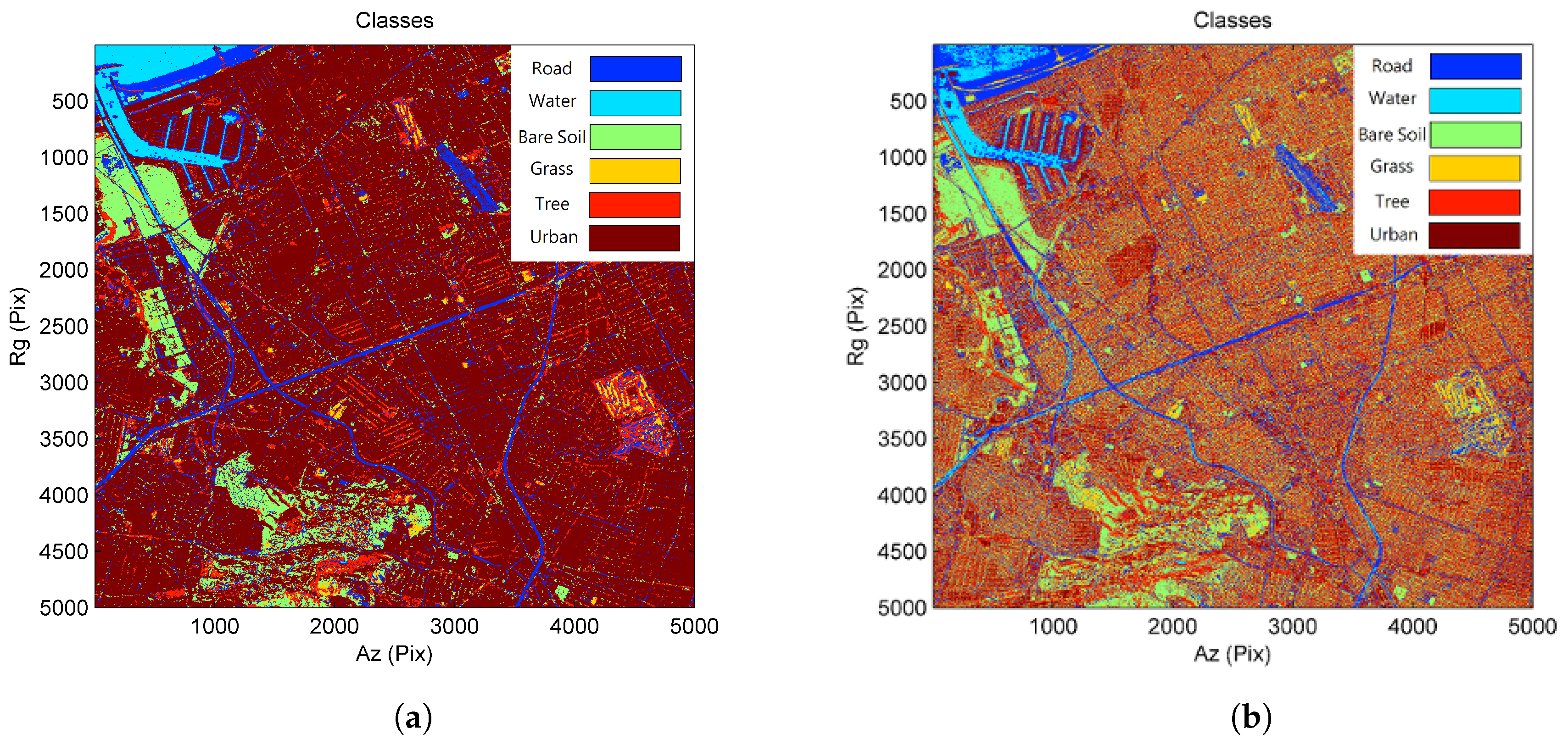
4.1. Results for the TanDEM-X Data Stack
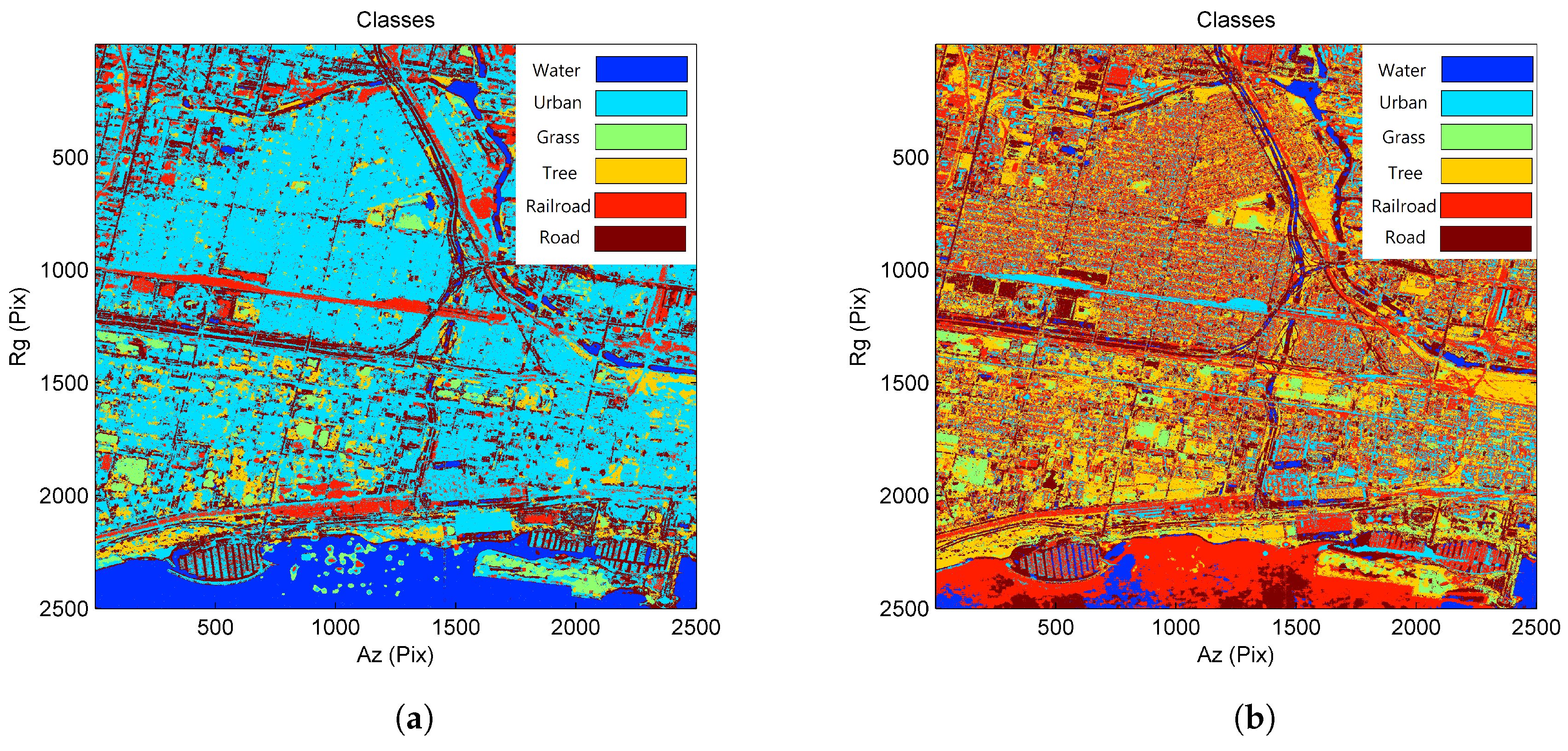
4.2. Results for the COSMO-SkyMed Data Stack
5. Conclusions
- Considering spatial/temporal and coherent/incoherent observations significantly increases the information content of single-polarized datasets. On the one hand, the spatial/temporal observations help reduce the speckle effect and improve the local statistics. On the other hand, the coherent/incoherent observations provide different information aspects to the observed regions. As these observations are complementary with each other, the concurrent utilization of this information significantly augments the potential of classifying single-polarized datasets.
- A highly automatic classification scheme is attained. With a sufficient number of images, the proposed approach can address the multi-class problem with only a few user-defined parameters (e.g., window size for SHP identification). No prior knowledge of the characteristics of the land cover is required either. The entire classification scheme can be carried out once the training set is created.
- Full resolution can be used under the proposed framework. No filtering procedures are required during the analysis. This effect results in the preservation of details while enriching the information content for each pixel.
- The proposed system is equipped with favorable generalization. Once SAR data stacks are provided, various analyses can be conducted. Furthermore, different processing techniques (e.g., feature selection methods or classifiers) can be incorporated into the same framework. This generalization supplies a large amount of potential for SAR applications.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gómez, C.; White, J.C.; Wulder, M.A. Optical remotely sensed time series data for land cover classification: A review. ISPRS J. Photogramm. Remote Sens. 2016, 116, 55–72. [Google Scholar] [CrossRef]
- Bruzzone, L.; Marconcini, M.; Wegmüller, U.; Wiesmann, A. An advanced system for the automatic classification of multitemporal SAR images. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1321–1334. [Google Scholar] [CrossRef]
- Raj, B.; Sharma, A.; Kapoor, K.; Jyoti, D. Noise Reduction: A Review. Int. J. Adv. Res. Innov. Technol. 2016, 2, 19–23. [Google Scholar]
- Zhou, Y.; Wang, H.; Xu, F.; Jin, Y.Q. Polarimetric SAR image classification using deep convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1935–1939. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, Z.; Turnbull, J.; Song, Q.; Qi, F. Pol-SAR Classification Based on Generalized Polar Decomposition of Mueller Matrix. IEEE Geosci. Remote Sens. Lett. 2016, 13, 565–569. [Google Scholar] [CrossRef]
- Hütt, C.; Koppe, W.; Miao, Y.; Bareth, G. Best Accuracy Land Use/Land Cover (LULC) Classification to Derive Crop Types Using Multitemporal, Multisensor, and Multi-Polarization SAR Satellite Images. Remote Sens. 2016, 8, 684. [Google Scholar] [CrossRef]
- Waske, B.; Braun, M. Classifier ensembles for land cover mapping using multitemporal SAR imagery. ISPRS J. Photogramm. Remote Sens. 2009, 64, 450–457. [Google Scholar] [CrossRef]
- Chen, K.S.; Huang, W.; Tsay, D.; Amar, F. Classification of multifrequency polarimetric SAR imagery using a dynamic learning neural network. IEEE Trans. Geosci. Remote Sens. 1996, 34, 814–820. [Google Scholar] [CrossRef]
- Liu, C.; Yin, J.; Yang, J.; Gao, W. Classification of multi-frequency polarimetric SAR Images Based on Multi-Linear Subspace Learning of Tensor Objects. Remote Sens. 2015, 7, 9253–9268. [Google Scholar] [CrossRef]
- Yang, F.; Gao, W.; Xu, B.; Yang, J. Multi-frequency polarimetric SAR classification based on Riemannian manifold and simultaneous sparse representation. Remote Sens. 2015, 7, 8469–8488. [Google Scholar] [CrossRef]
- Ban, Y.; Howarth, P. Multitemporal ERS-1 SAR data for crop classification: A sequential-masking approach. Can. J. Remote Sens. 1999, 25, 438–447. [Google Scholar] [CrossRef]
- Quegan, S.; Le Toan, T.; Yu, J.J.; Ribbes, F.; Floury, N. Multitemporal ERS SAR analysis applied to forest mapping. IEEE Trans. Geosci. Remote Sens. 2000, 38, 741–753. [Google Scholar] [CrossRef]
- Skriver, H.; Mattia, F.; Satalino, G.; Balenzano, A.; Pauwels, V.R.; Verhoest, N.E.; Davidson, M. Crop classification using short-revisit multitemporal SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 423–431. [Google Scholar] [CrossRef]
- Lu, J.; Li, J.; Chen, G.; Zhao, L.; Xiong, B.; Kuang, G. Improving pixel-based change detection accuracy using an object-based approach in multitemporal SAR flood Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3486–3496. [Google Scholar] [CrossRef]
- Wang, L.; Sousa, W.; Gong, P. Integration of object-based and pixel-based classification for mapping mangroves with IKONOS imagery. Int. J. Remote Sens. 2004, 25, 5655–5668. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Parizzi, A.; Brcic, R. Adaptive InSAR stack multilooking exploiting amplitude statistics: A comparison between different techniques and practical results. IEEE Geosci. Remote Sens. Lett. 2011, 8, 441–445. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, X.; Li, Z. Hybrid approach for unbiased coherence estimation for multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2459–2473. [Google Scholar] [CrossRef]
- Lin, K.F.; Perissin, D. Identification of Statistically Homogeneous Pixels Based on One-Sample Test. Remote Sens. 2017, 9, 37. [Google Scholar] [CrossRef]
- Bharati, M.H.; Liu, J.J.; MacGregor, J.F. Image texture analysis: methods and comparisons. Chemom. Intell. Lab. Syst. 2004, 72, 57–71. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Richards, J.A. Remote Sensing Digital Image Analysis: An Introduction, 5th ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Li, J.; Plaza, A. Hyperspectral Image Processing: Methods and Approaches. In Remotely Sensed Data Characterization, Classification, and Accuracies; CRC Press: Boca Raton, FL, USA, 2015; pp. 247–258. [Google Scholar]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Dopico, J.R.R.; de la Calle, J.D.; Sierra, A.P. Feature Selection. In Encyclopedia of artificial intelligence; IGI Publishing: Hershey, PA, USA, 2009; pp. 632–638. [Google Scholar]
- Tang, J.; Alelyani, S.; Liu, H. Feature selection for classification: A review. In Data Classification: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2014; pp. 37–64. [Google Scholar]
- Whitney, A.W. A direct method of nonparametric measurement selection. IEEE Trans. Comput. 1971, 100, 1100–1103. [Google Scholar] [CrossRef]
- Pohjalainen, J.; Räsänen, O.; Kadioglu, S. Feature selection methods and their combinations in high-dimensional classification of speaker likability, intelligibility and personality traits. Comput. Speech Lang. 2015, 29, 145–171. [Google Scholar] [CrossRef]
- McLachlan, G. Discriminant Analysis and Statistical Pattern Recognition; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-validation. In Encyclopedia of Database Systems; Springer: New York, NY, USA, 2009; pp. 532–538. [Google Scholar]
- Google. Google Earth Pro V 7.3.1.4507. (February 6, 2018). Area of interest, Los Angeles, United States. 34°00′01.17″ N, 118°24′39.46″ W, Eye Altitude 22.06 km. 2018. Available online: http://www.earth.google.com (accessed on 20 February 2017).
- Google. Google Earth Pro V 7.3.1.4507. (February 6, 2018). Area of Interest, Chicago, United States. 41°51′52.54″ N, 87°39′17.74″ W, Eye Altitude 13.15 km. DigitalGlobe. 2018. Available online: http://www.earth.google.com (accessed on 1 March 2017).

| Class | Training Set | Testing Set |
|---|---|---|
| Road | 3959 | 215,243 |
| Water | 13,580 | 336,003 |
| Bare Soil | 8177 | 327,836 |
| Grass | 1654 | 18,650 |
| Tree | 2130 | 24,761 |
| Urban | 9821 | 171658 |
| Total | 39,321 | 1,094,151 |
| Class | Training Set | Testing Set |
|---|---|---|
| Water | 5168 | 189,506 |
| Urban | 9970 | 163,348 |
| Grass | 3009 | 39,018 |
| Tree | 619 | 11,270 |
| Railroad | 4228 | 19,788 |
| Road | 2029 | 55,139 |
| Total | 25,023 | 478,069 |
| Classified | Producer’s Accuracy | |||||||
|---|---|---|---|---|---|---|---|---|
| Road | Water | Bare Soil | Grass | Tree | Urban | |||
| Reference | Road | 155,157 | 45 | 5086 | 1353 | 8572 | 45,030 | 72.08% |
| Water | 27,584 | 306,994 | 117 | 489 | 187 | 632 | 91.37% | |
| Bare Soil | 16,126 | 0 | 287,988 | 6237 | 4998 | 12,487 | 87.85% | |
| Grass | 7307 | 27 | 1368 | 6405 | 2885 | 658 | 34.34% | |
| Tree | 644 | 0 | 563 | 0 | 12,241 | 11,313 | 49.44% | |
| Urban | 6638 | 1 | 9311 | 373 | 1757 | 153,578 | 89.47% | |
| User’s accuracy | 72.69% | 99.98% | 94.60% | 43.11% | 39.95% | 68.65% | Overall accuracy: 84.30% Kappa coefficient: 79.32% | |
| Classified | Producer’s Accuracy | |||||||
|---|---|---|---|---|---|---|---|---|
| Road | Water | Bare Soil | Grass | Tree | Urban | |||
| Reference | Road | 139,688 | 23,325 | 13,571 | 7376 | 21,561 | 9722 | 64.90% |
| Water | 132,640 | 198,371 | 107 | 60 | 878 | 3947 | 59.04% | |
| Bare Soil | 16,843 | 17 | 271,925 | 6243 | 31,775 | 1033 | 82.95% | |
| Grass | 7019 | 147 | 2217 | 8408 | 810 | 49 | 45.08% | |
| Tree | 780 | 30 | 5857 | 969 | 14,884 | 2244 | 60.11% | |
| Urban | 20,939 | 512 | 32,095 | 10,266 | 61,536 | 46,310 | 35.85% | |
| User’s accuracy | 43.94% | 89.19% | 83.47% | 25.23% | 11.32% | 73.15% | Overall accuracy: 62.11% Kappa coefficient: 51.36% | |
| Overall Accuracy (%) | Kappa (%) | |
|---|---|---|
| QDA | 89.25 ± 0.15 | 85.82 ± 0.20 |
| QDA | 84.30 | 79.32 |
| QDA | 77.14 | 70.02 |
| Skriver’s Approach | 62.11 | 51.36 |
| LDA | 82.70 | 77.17 |
| Naive QDA | 84.02 | 78.94 |
| Naive LDA | 82.65 | 76.93 |
| Decision Tree | 82.31 | 76.98 |
| Classified | Producer’s Accuracy | |||||||
|---|---|---|---|---|---|---|---|---|
| Water | Urban | Grass | Tree | Railroad | Road | |||
| Reference | Water | 176,643 | 1312 | 600 | 812 | 853 | 9286 | 93.21% |
| Urban | 1628 | 145,611 | 0 | 396 | 5461 | 10,252 | 89.14% | |
| Grass | 304 | 4469 | 28,522 | 1661 | 389 | 3673 | 73.10% | |
| Tree | 0 | 4610 | 0 | 5871 | 90 | 699 | 52.09% | |
| Railroad | 0 | 5291 | 0 | 70 | 14,390 | 37 | 72.72% | |
| Road | 1617 | 9530 | 0 | 110 | 2374 | 41,508 | 75.28% | |
| User’s Accuracy | 98.03% | 85.24% | 97.94% | 65.82% | 61.09% | 63.41% | Overall Accuracy: 86.29% Kappa Coefficient: 80.57% | |
| Classified | Producer’s Accuracy | |||||||
|---|---|---|---|---|---|---|---|---|
| Water | Urban | Grass | Tree | Railroad | Road | |||
| Reference | Water | 35,336 | 709 | 226 | 813 | 79,473 | 72949 | 18.65% |
| Urban | 2882 | 41,610 | 3580 | 24,959 | 73,276 | 17,041 | 25.47% | |
| Grass | 2 | 87 | 22,542 | 10,032 | 1323 | 5032 | 57.77% | |
| Tree | 0 | 378 | 373 | 6781 | 3122 | 616 | 60.17% | |
| Railroad | 0 | 6498 | 10 | 1590 | 11,625 | 65 | 58.75% | |
| Road | 4914 | 3109 | 820 | 2787 | 9280 | 34,229 | 62.08% | |
| User’s Accuracy | 81.92% | 79.42% | 81.82% | 14.44% | 6.53% | 26.34% | Overall Accuracy: 31.82% Kappa Coefficient: 21.90% | |
| Overall Accuracy (%) | Kappa (%) | |
|---|---|---|
| QDA | 89.64 ± 0.05 | 85.35 ± 0.07 |
| QDA | 86.29 | 80.57 |
| QDA | 77.41 | 67.11 |
| Skriver’s Approach | 31.82 | 21.90 |
| LDA | 85.76 | 80.12 |
| Naive QDA | 84.96 | 78.80 |
| Naive LDA | 84.59 | 78.18 |
| Decision Tree | 79.19 | 71.10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, K.-F.; Perissin, D. Single-Polarized SAR Classification Based on a Multi-Temporal Image Stack. Remote Sens. 2018, 10, 1087. https://doi.org/10.3390/rs10071087
Lin K-F, Perissin D. Single-Polarized SAR Classification Based on a Multi-Temporal Image Stack. Remote Sensing. 2018; 10(7):1087. https://doi.org/10.3390/rs10071087
Chicago/Turabian StyleLin, Keng-Fan, and Daniele Perissin. 2018. "Single-Polarized SAR Classification Based on a Multi-Temporal Image Stack" Remote Sensing 10, no. 7: 1087. https://doi.org/10.3390/rs10071087
APA StyleLin, K.-F., & Perissin, D. (2018). Single-Polarized SAR Classification Based on a Multi-Temporal Image Stack. Remote Sensing, 10(7), 1087. https://doi.org/10.3390/rs10071087





