Three-Dimensional Reconstruction of Soybean Canopies Using Multisource Imaging for Phenotyping Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Overall Process Flow for 3D Reconstruction
2.2. Experimental Treatments and Measurement of Phenotypic Traits
2.3. Multisource Imaging System
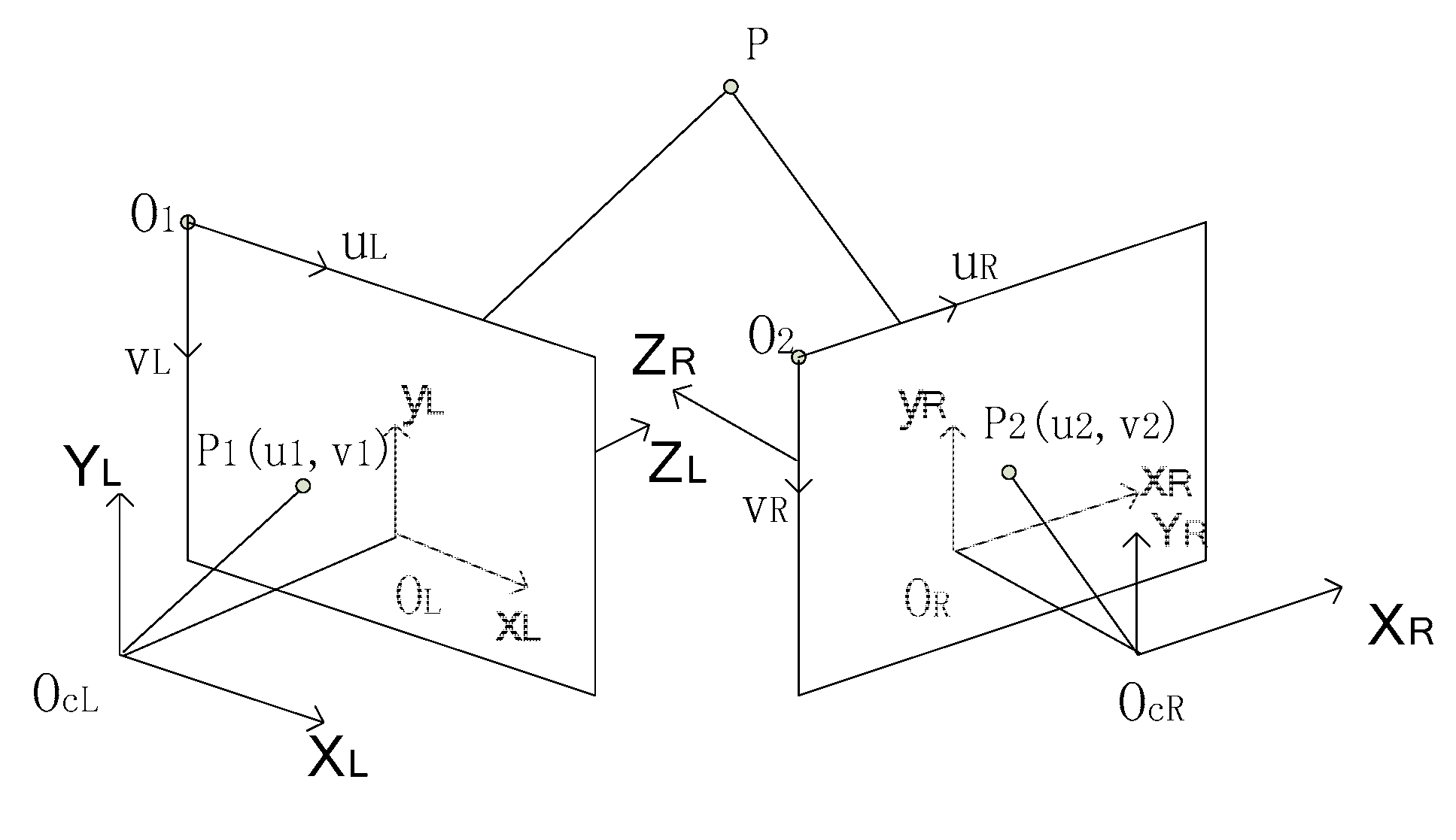
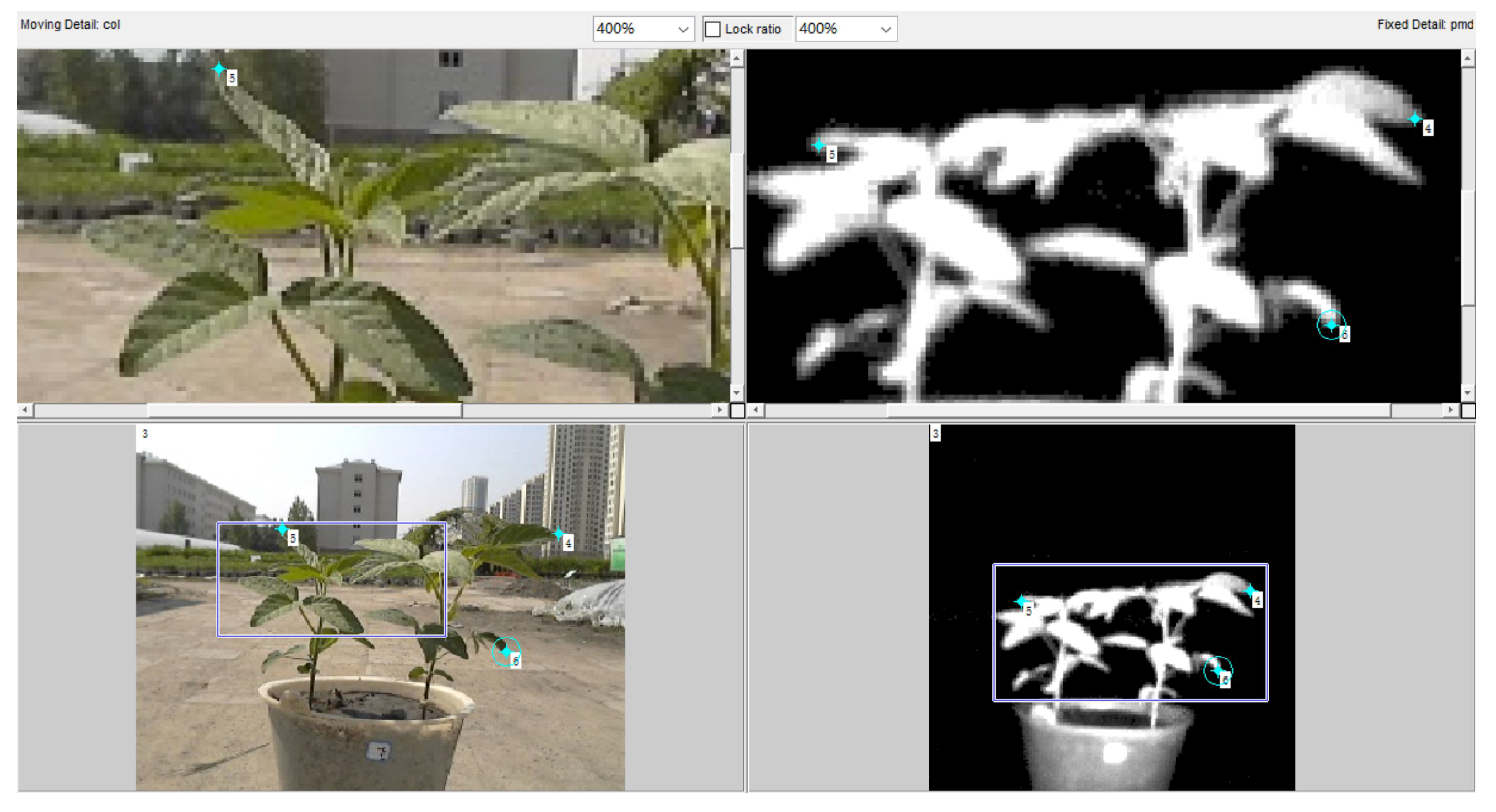
2.4. Calibration of Multisource Imaging System
2.5. Data Collection and RGB Image Preprocessing
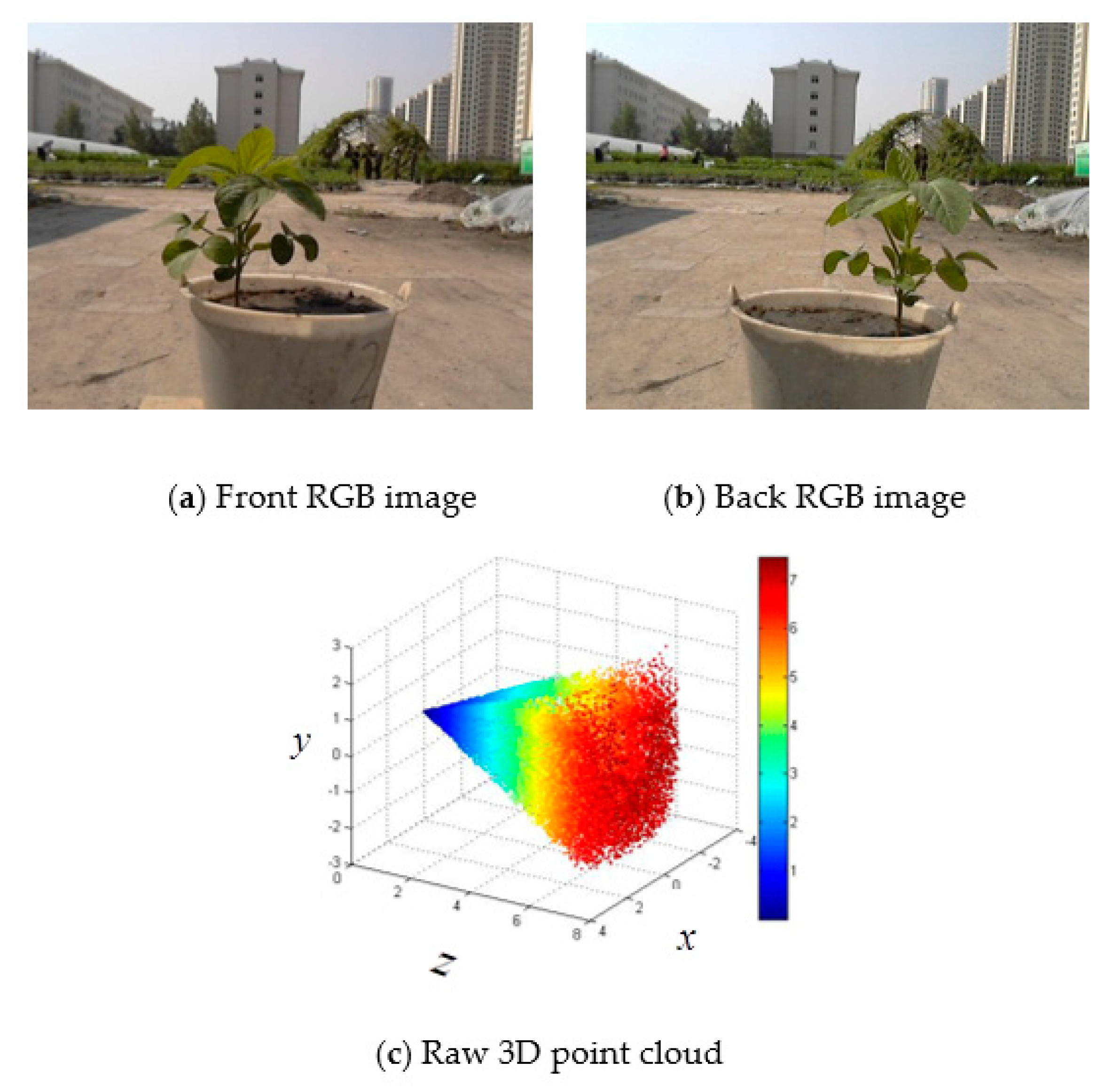
2.6. 3D Reconstruction
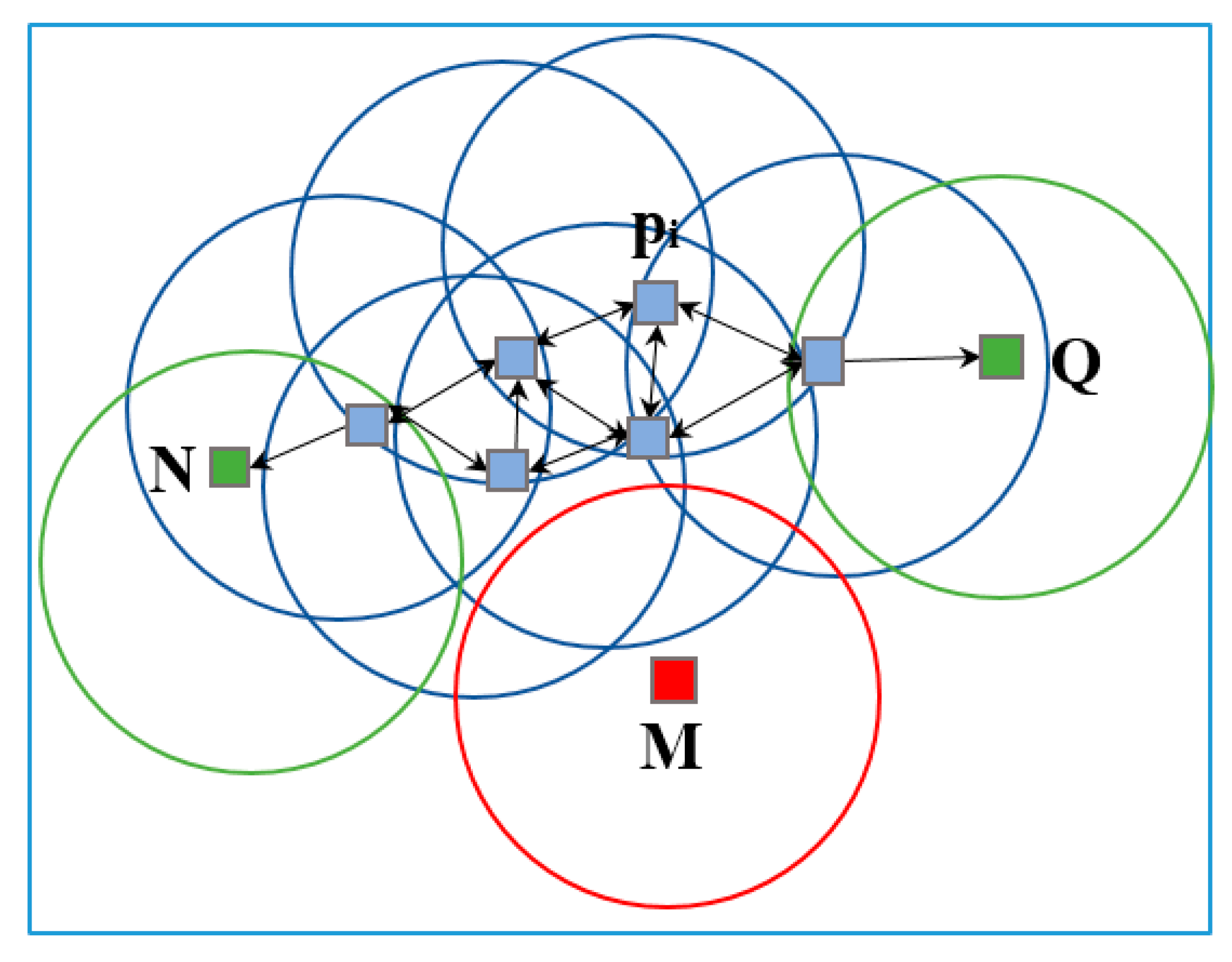
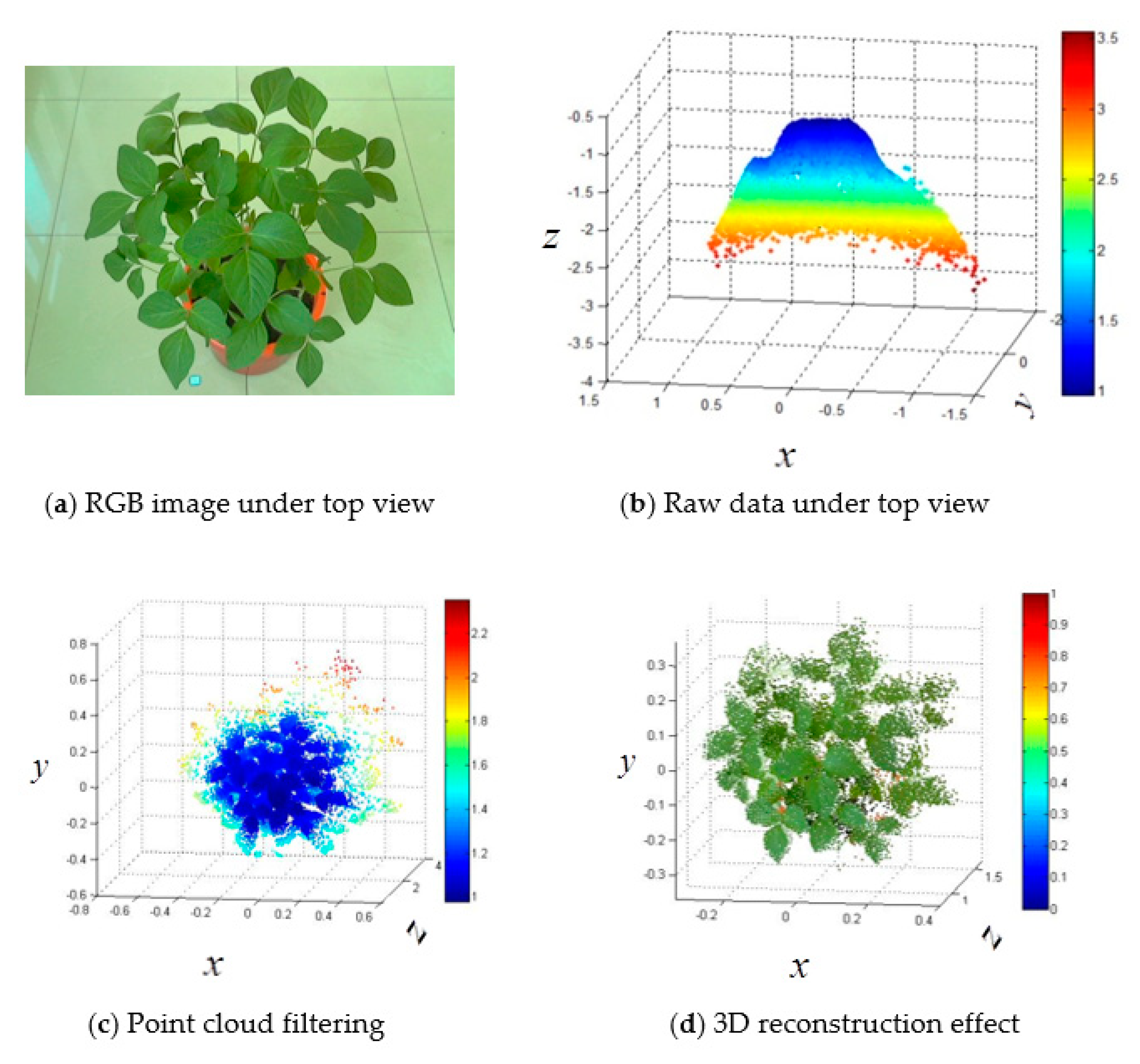
2.6.1. DBSCAN Algorithm for Point Cloud Filtering
2.6.2. Fusion of Multisource Images
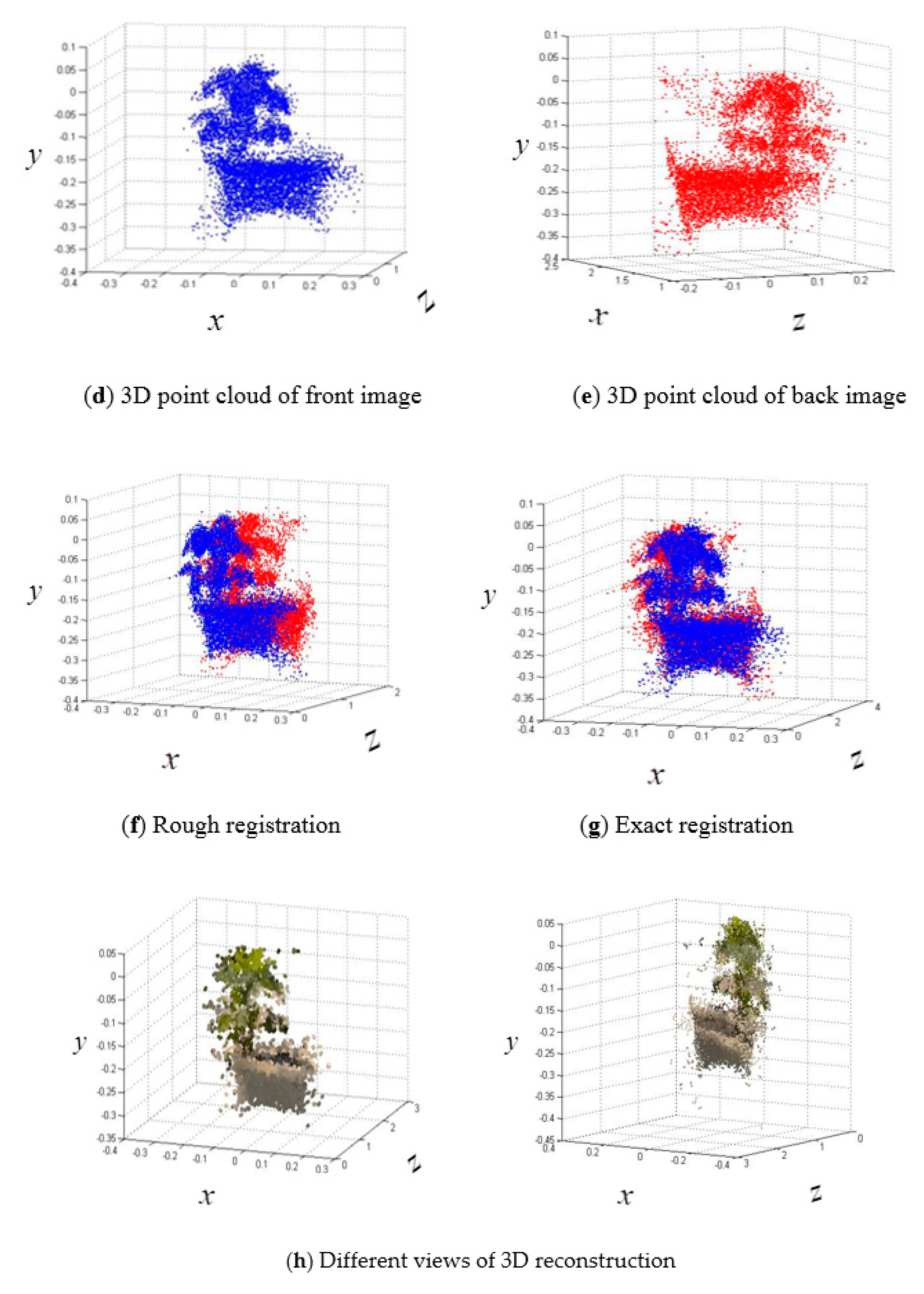
2.6.3. Registration of 3D Point Clouds between Front and Back Sides
2.7. Methods of Calculating 3D Phenotypic Traits
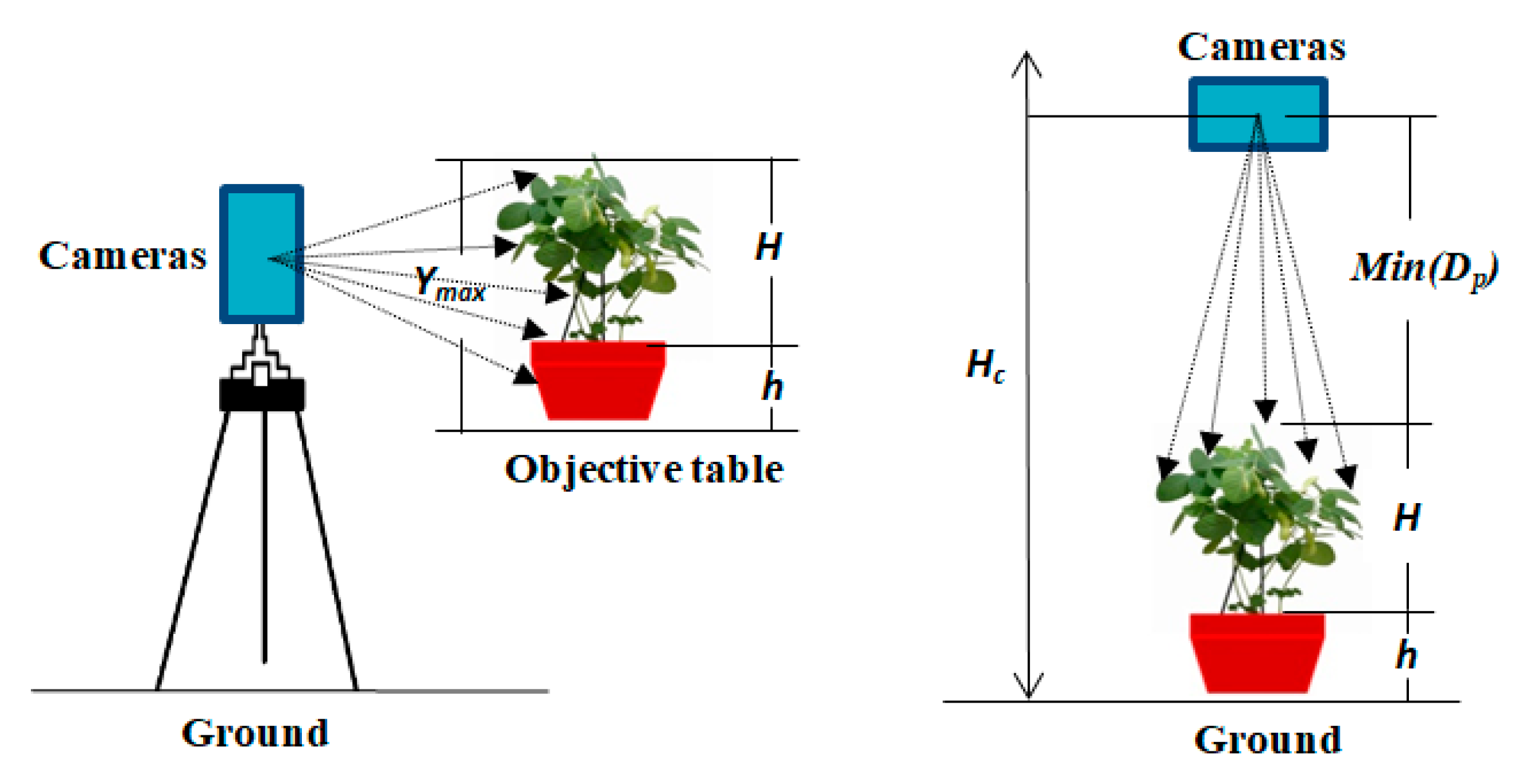
2.7.1. Method of Calculating Plant Height
2.7.2. Method of Calculating Greenness Index
3. Results
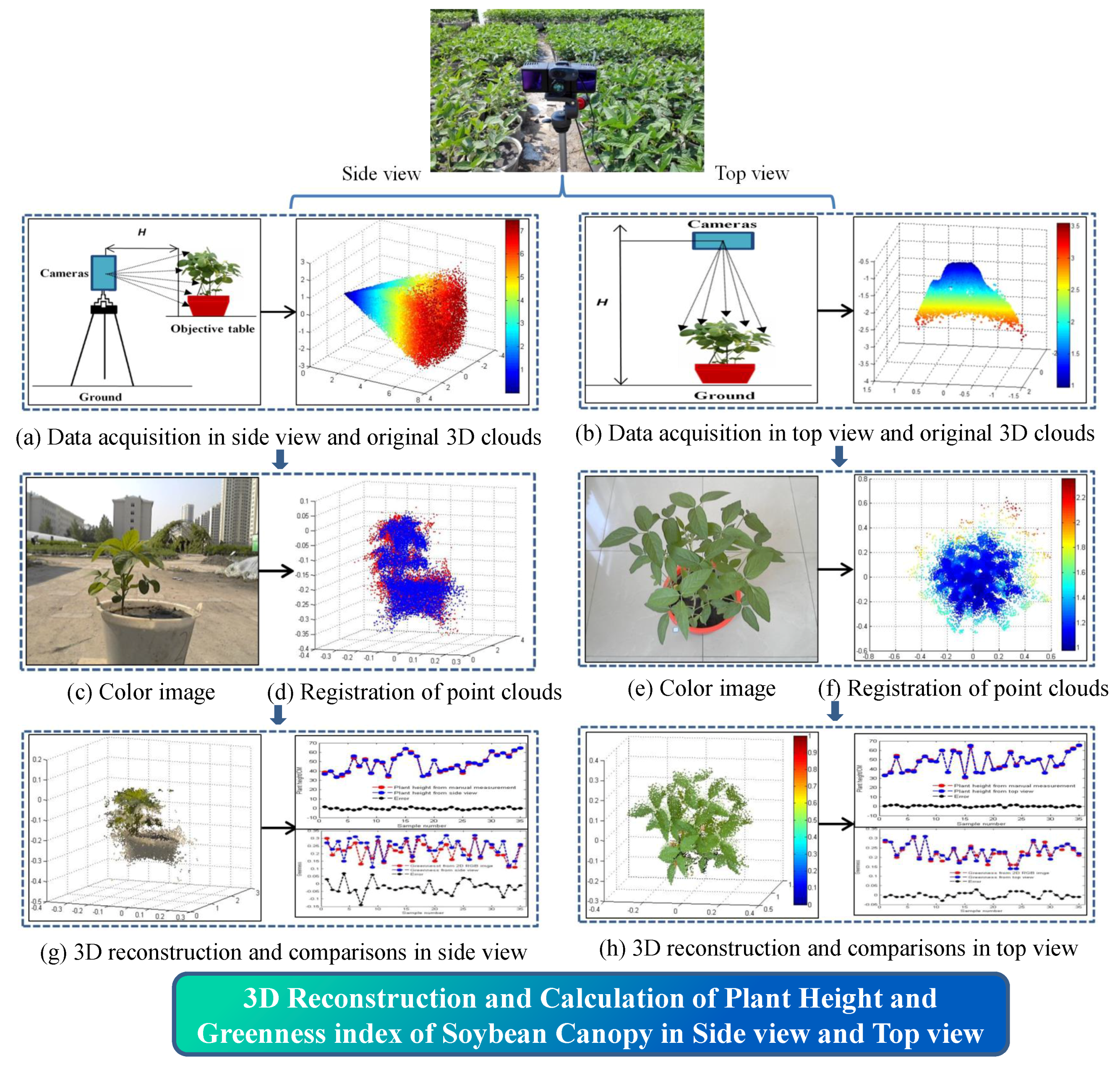
3.1. 3D Reconstruction
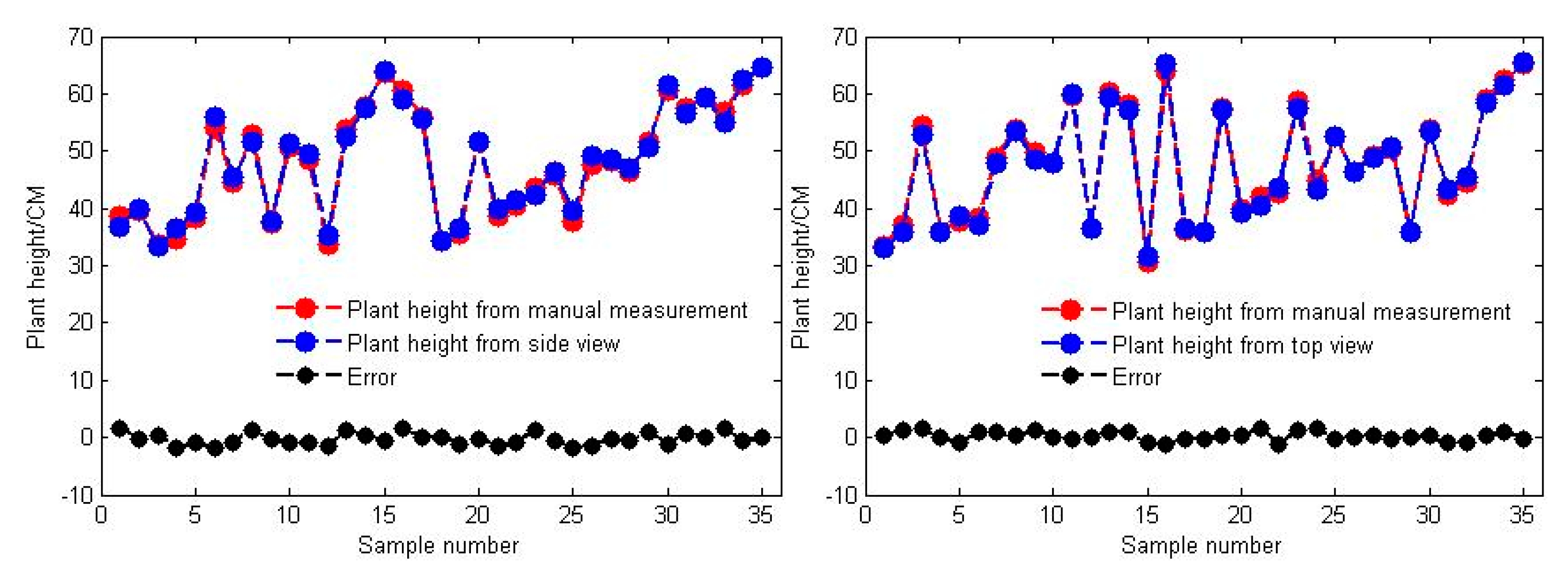
3.2. Accuracy of Plant Height Measurements in the Side and Top Views
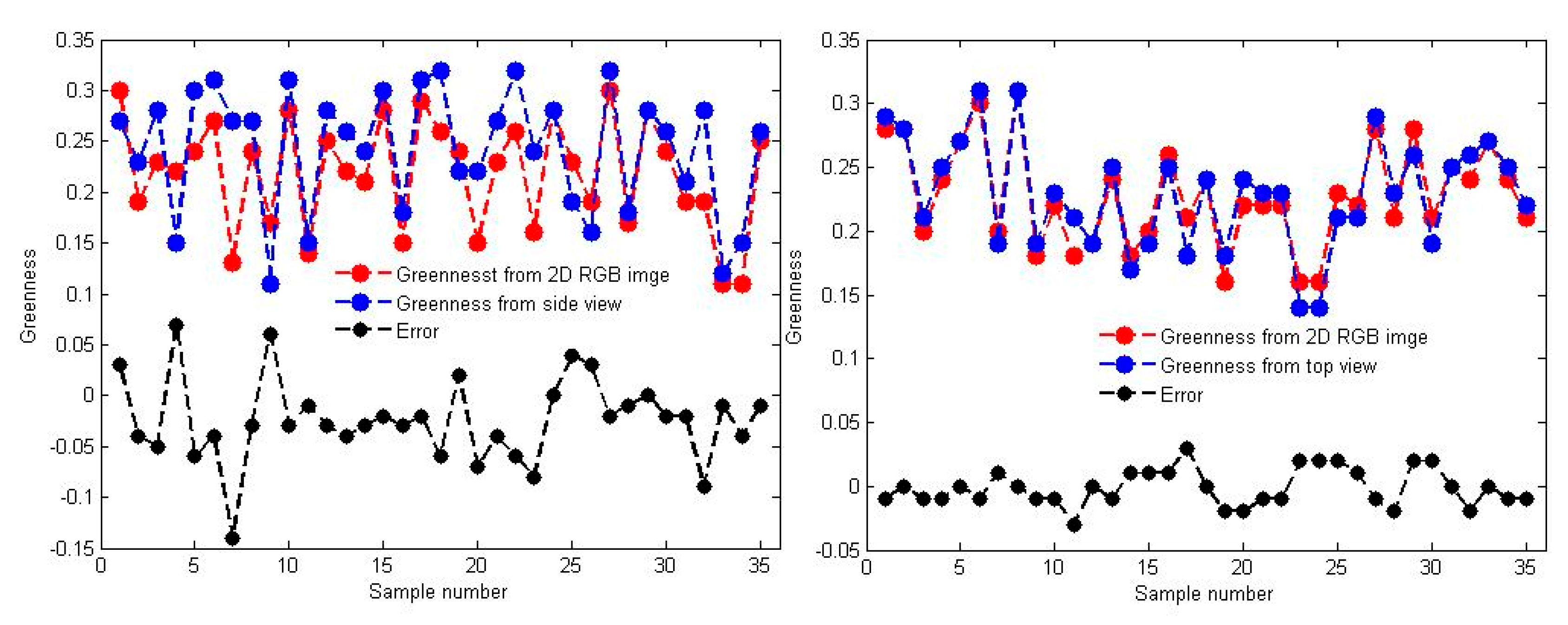
3.3. Accuracy of Greenness in the Side and Top Views
4. Discussion
4.1. Analysis of Experimental Results
4.2. Evaluation of Algorithm Robustness
4.3. Advantages of Multisource Imaging Systems
4.4. Future Work
5. Conclusions
- (1)
- An active imaging system consisting of a PMD camera and an RGB camera was used to collect multi-images of soybean plants. First, the DBSCAN algorithm was used to extract soybean plant information from the complex raw dataset. Next, the multisource images were fused together for the purpose of constructing 3D images that contain color information. Last, 3D points from the front and back sides were registered using the ICP algorithm. The proposed methodology can be used to reconstruct a 3D soybean plant for a phenotyping analysis that includes measurements of plant height and greenness.
- (2)
- By combining this multisource imaging system and the proposed algorithms, we can accurately measure soybean plant height. Correlation analysis between the estimated and manual measurements yielded R2 values of 0.9890 and 0.9936 for the side view and top view, respectively, and their average errors were 0.6713 cm and 0.2600 cm, respectively. From a plant breeding perspective, this finding could be especially useful for rapidly predetecting a subset of soybean genotypes that are of suitable height for expected yields and machine harvesting.
- (3)
- Compared with the side view-based greenness, the top view-based greenness was much more accurate. The greenness index estimated from the top view-based data was highly correlated with the manually assessed greenness index: the R2 value was 0.8864, and the average error was 0.0117. However, the R2 value decreased to 0.6059 (average error of 0.0386) for the side view-based results. This result was primarily due to the impact of the natural environment, such as wind and sunlight, which led to some fusion and registration deviations between the 3D points and their corresponding RGB images. The algorithm itself needs to be improved.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, L.; Zhang, Q.; Huang, D. A review of imaging techniques for plant phenotyping. Sensors 2014, 14, 20078–20111. [Google Scholar] [CrossRef] [PubMed]
- Phillips, R.L. Mobilizing science to break yield barriers. Crop Sci. 2010, 50 (Suppl. 1), S-99–S-108. [Google Scholar] [CrossRef]
- Houle, D.; Govindaraju, D.R.; Omholt, S. Phenomics: The next challenge. Nat. Rev. Genet. 2010, 11, 855. [Google Scholar] [CrossRef] [PubMed]
- Dhondt, S.; Wuyts, N.; Inzé, D. Cell to whole-plant phenotyping: The best is yet to come. Trends Plant Sci. 2013, 18, 428–439. [Google Scholar] [CrossRef] [PubMed]
- Fiorani, F.; Schurr, U. Future scenarios for plant phenotyping. Annu. Rev. Plant Biol. 2013, 64, 267–291. [Google Scholar] [CrossRef] [PubMed]
- Minervini, M.; Scharr, H.; Tsaftaris, S.A. Image analysis: The new bottleneck in plant phenotyping. IEEE Signal Process. Mag. 2015, 32, 126–131. [Google Scholar] [CrossRef]
- Furbank, R.T.; Tester, M. Phenomics–technologies to relieve the phenotyping bottleneck. Trends Plant Sci. 2011, 166, 35–644. [Google Scholar] [CrossRef] [PubMed]
- Golbach, F.; Kootstra, G.; Damjanovic, S.; Otten, G.; van de Zedde, R. Validation of plant part measurements using a 3D reconstruction method suitable for high-throughput seedling phenotyping. Mach. Vis. Appl. 2016, 27, 663–680. [Google Scholar] [CrossRef]
- Haughton, A.J.; Bohan, D.A.; Clark, S.J.; Mallott, M.D.; Mallott, V.; Sage, R.; Karp, A. Dedicated biomass crops can enhance biodiversity in the arable landscape. GCB Bioenergy 2016, 8, 1071–1081. [Google Scholar] [CrossRef] [PubMed]
- Chaudhury, A.; Ward, C.; Talasaz, A.; Ivanov, A.G.; Brophy, M.; Grodzinski, B.; Huner, N.P.A.; Patel, R.V.; Barron, J.L. Machine Vision System for 3D Plant Phenotyping. arXiv 2017, arXiv:1705.00540. [Google Scholar]
- Chéné, Y.; Rousseau, D.; Lucidarme, P.; Bertheloot, J.; Caffier, V.; Morel, P.; Belin, É.; Chapeau-Blondeau, F. On the use of depth camera for 3D phenotyping of entire plants. Comput. Electron. Agric. 2012, 82, 122–127. [Google Scholar] [CrossRef]
- Ruiz-Altisent, M.; Ruiz-Garcia, L.; Moreda, G.P.; Lu, R.; Hernandez-Sanchez, N.; Correa, E.C.; Diezma, B.; Nicolaï, B.; García-Ramos, J. Sensors for product characterization and quality of specialty crops—A review. Comput. Electron. Agric. 2010, 74, 176–194. [Google Scholar] [CrossRef]
- Paulus, S.; Behmann, J.; Mahlein, A.K.; Plümer, L.; Kuhlmann, H. Low-cost 3D systems: Suitable tools for plant phenotyping. Sensors 2014, 14, 3001–3018. [Google Scholar] [CrossRef] [PubMed]
- Pound, M.P.; French, A.P.; Murchie, E.H.; Pridmore, T.P. Automated recovery of three-dimensional models of plant shoots from multiple color images. Plant Physiol. 2014, 166, 1688–1698. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, D.; Shi, P.; Omasa, K. Estimating rice chlorophyll content and leaf nitrogen concentration with a digital still color camera under natural light. Plant Methods 2014, 10, 36. [Google Scholar] [CrossRef] [PubMed]
- Guan, H.; Li, J.; Ma, X. Recognition of soybean nutrient deficiency based on color characteristics of canopy. J. Northwest A F Univ. 2016, 44, 136–142. [Google Scholar]
- Cheng, H.; Shi, Z.X.; Li, J.T.; Pang, L.X.; Feng, J. A color correction method based on standard white board. J. Agric. Univ. Heibei 2007, 30, 105–109. [Google Scholar]
- Pan, B.; Liang, S. Estimation of chlorophyll content in apple tree canopy based on hyperspectral parameters. Spectrosc. Spectr. Anal. 2013, 33, 2203–2206. [Google Scholar]
- Baresel, J.P.; Rischbeck, P.; Hu, Y.; Kipp, S.; Barmeier, G.; Mistele, B.; Schmidhalter, U. Use of a digital camera as alternative method for non-destructive detection of the leaf chlorophyll content and the nitrogen nutrition status in wheat. Comput. Electron. Agric. 2017, 140, 25–33. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, L.; Xiang, L.; Wu, Q.; Jiang, H. Automatic non-destructive growth measurement of leafy vegetables based on kinect. Sensors 2018, 18, 806. [Google Scholar] [CrossRef] [PubMed]
- Bai, G.; Ge, Y.; Hussain, W.; Baenziger, P.S.; Graef, G. A multi-sensor system for high throughput field phenotyping in soybean and wheat breeding. Comput. Electron. Agric. 2016, 128, 181–192. [Google Scholar] [CrossRef]
- Araus, J.L.; Cairns, J.E. Field high-throughput phenotyping: The new crop breeding frontier. Trends Plant Sci. 2014, 19, 52–61. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Liu, G.; Ma, X.; Feng, J. Study on multi-image registration of apple tree at different growth stages. Acta Opt. Sin. 2014, 34, 0215001. [Google Scholar] [CrossRef]
- Naik, H.S.; Zhang, J.; Lofquist, A.; Assefa, T.; Sarkar, S.; Ackerman, D.; Singh, A.; Singh, A.K.; Ganapathysubramanian, B. A real-time phenotyping framework using machine learning for plant stress severity rating in soybean. Plant Methods 2017, 13, 23. [Google Scholar] [CrossRef] [PubMed]
- Parimala, M.; Lopez, D.; Senthilkumar, N.C. A survey on density based clustering algorithms for mining large spatial databases. Int. J. Adv. Sci. Technol. 2011, 31, 59–66. [Google Scholar]
- Li, S.; Kang, X.; Fang, L.; Hu, J.; Yin, H. Pixel-level image fusion: A survey of the state of the art. Inf. Fusion 2017, 33, 100–112. [Google Scholar] [CrossRef]
- Glira, P.; Pfeifer, N.; Briese, C.; Ressl, C. Rigorous strip adjustment of airborne laserscanning data based on the ICP algorithm. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 73–80. [Google Scholar] [CrossRef]
- Deshpande, N.T.; Ravishankar, S. Face Detection and recognition using Viola-Jones algorithm and fusion of PCA and ANN. Adv. Comput. Sci. Technol. 2017, 10, 1173–1189. [Google Scholar]
- Chen, B.; Deng, L.; Duan, Y.; Chen, A.; Zhou, J. Multiple model fusion in 3D reconstruction: Illumination and scale invariance. J. Tsinghua Univ. 2016, 56, 969–973. [Google Scholar]
- Paulus, S.; Schumann, H.; Kuhlmann, H.; Léon, J. High-precision laser scanning system for capturing 3D plant architecture and analysing growth of cereal plants. Biosyst. Eng. 2014, 121, 1–11. [Google Scholar] [CrossRef]
- Peìrez-Harguindeguy, N.; Díaz, S.; Garnier, E.; Lavorel, S.; Poorter, H.; Jaureguiberry, P. New handbook for standardised measurement of plant functional traits worldwide. Aust. J. Bot. 2013, 61, 167–234. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, C.; Paterson, A.H. High throughput phenotyping of cotton plant height using depth images under field conditions. Comput. Electron. Agric. 2016, 130, 57–68. [Google Scholar] [CrossRef]
- Demir, N.; Sönmez, N.K.; Akar, T.; Ünal, S. Automated measurement of plant height of wheat genotypes using a DSM derived from UAV imagery. Multidiscip. Digit. Publ. Inst. Proc. 2018, 2, 350. [Google Scholar] [CrossRef]
- Zotz, G.; Hietz, P.; Schmidt, G. Small plants, large plants: The importance of plant size for the physiological ecology of vascular epiphytes. J. Exp. Bot. 2001, 52, 2051–2056. [Google Scholar] [CrossRef] [PubMed]
- De Ocampoa, A.L.P.; Albob, J.B.; de Ocampoc, K.J. Image analysis of foliar greenness for quantifying relative plant health. Ed. Board 2015, 1, 27–31. [Google Scholar]
- Kurc, S.A.; Benton, L.M. Digital image-derived greenness links deep soil moisture to carbon uptake in a creosotebush-dominated shrubland. J. Arid Environ. 2010, 74, 585–594. [Google Scholar] [CrossRef]
- Ienco, D.; Bordogna, G. Fuzzy extensions of the DBScan clustering algorithm. Soft Comput. 2018, 22, 1719–1730. [Google Scholar] [CrossRef]
- Cheng, S.; Marras, I.; Zafeiriou, S.; Pantic, M. Statistical non-rigid ICP algorithm and its application to 3D face alignment. Image Vis. Comput. 2017, 58, 3–12. [Google Scholar] [CrossRef]
- Guo, C.; Zong, Z.; Zhang, X.; Liu, G. Apple tree canopy geometric parameters acquirement based on 3D point clouds. Trans. Chin. Soc. Agric. Eng. 2017, 33, 175–181. [Google Scholar]
- Ma, X.; Feng, J.; Guan, H.; Liu, G. Prediction of chlorophyll content in different light areas of apple tree canopies based on the color characteristics of 3D reconstruction. Remote Sens. 2018, 10, 429. [Google Scholar] [CrossRef]
- Baloch, M.J.; Khan, N.U.; Rajput, M.A.; Jatoi, W.A.; Gul, S.; Rind, I.H.; Veesar, N.F. Yield related morphological measures of short duration cotton genotypes. J. Anim. Plant Sci. 2014, 24, 1198–1211. [Google Scholar]
- Sun, S.; Li, C.; Paterson, A. In-field high-throughput phenotyping of cotton plant height using LIDAR. Remote Sens. 2017, 9, 377. [Google Scholar] [CrossRef]
- Zhang, L.; Grift, T.E. A Lidar-based crop height measurement system for Miscanthus giganteus. Comput. Electron. Agric. 2012, 85, 70–76. [Google Scholar] [CrossRef]
- Sass, L.; Majer, P.; Hideg, É. Leaf hue measurements: A high-throughput screening of chlorophyll content. In High-Throughput Phenotyping in Plants; Humana Press: Totowa, NJ, USA, 2012; pp. 61–69. [Google Scholar]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, H.; Liu, M.; Ma, X.; Yu, S. Three-Dimensional Reconstruction of Soybean Canopies Using Multisource Imaging for Phenotyping Analysis. Remote Sens. 2018, 10, 1206. https://doi.org/10.3390/rs10081206
Guan H, Liu M, Ma X, Yu S. Three-Dimensional Reconstruction of Soybean Canopies Using Multisource Imaging for Phenotyping Analysis. Remote Sensing. 2018; 10(8):1206. https://doi.org/10.3390/rs10081206
Chicago/Turabian StyleGuan, Haiou, Meng Liu, Xiaodan Ma, and Song Yu. 2018. "Three-Dimensional Reconstruction of Soybean Canopies Using Multisource Imaging for Phenotyping Analysis" Remote Sensing 10, no. 8: 1206. https://doi.org/10.3390/rs10081206
APA StyleGuan, H., Liu, M., Ma, X., & Yu, S. (2018). Three-Dimensional Reconstruction of Soybean Canopies Using Multisource Imaging for Phenotyping Analysis. Remote Sensing, 10(8), 1206. https://doi.org/10.3390/rs10081206




