Extraction of Photosynthesis Parameters from Time Series Measurements of In Situ Production: Bermuda Atlantic Time-Series Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Model of the Production Profile
2.2. Bermuda Atlantic Time-Series Study Data Set
3. Results
3.1. Determining the Attenuation Coefficient
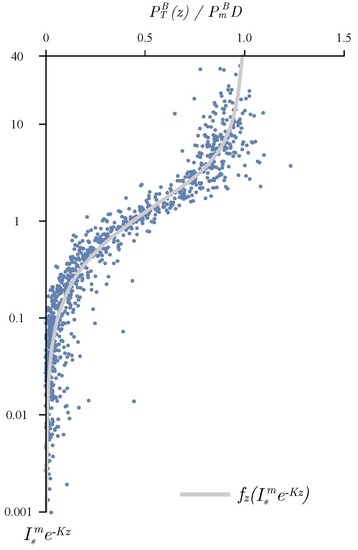
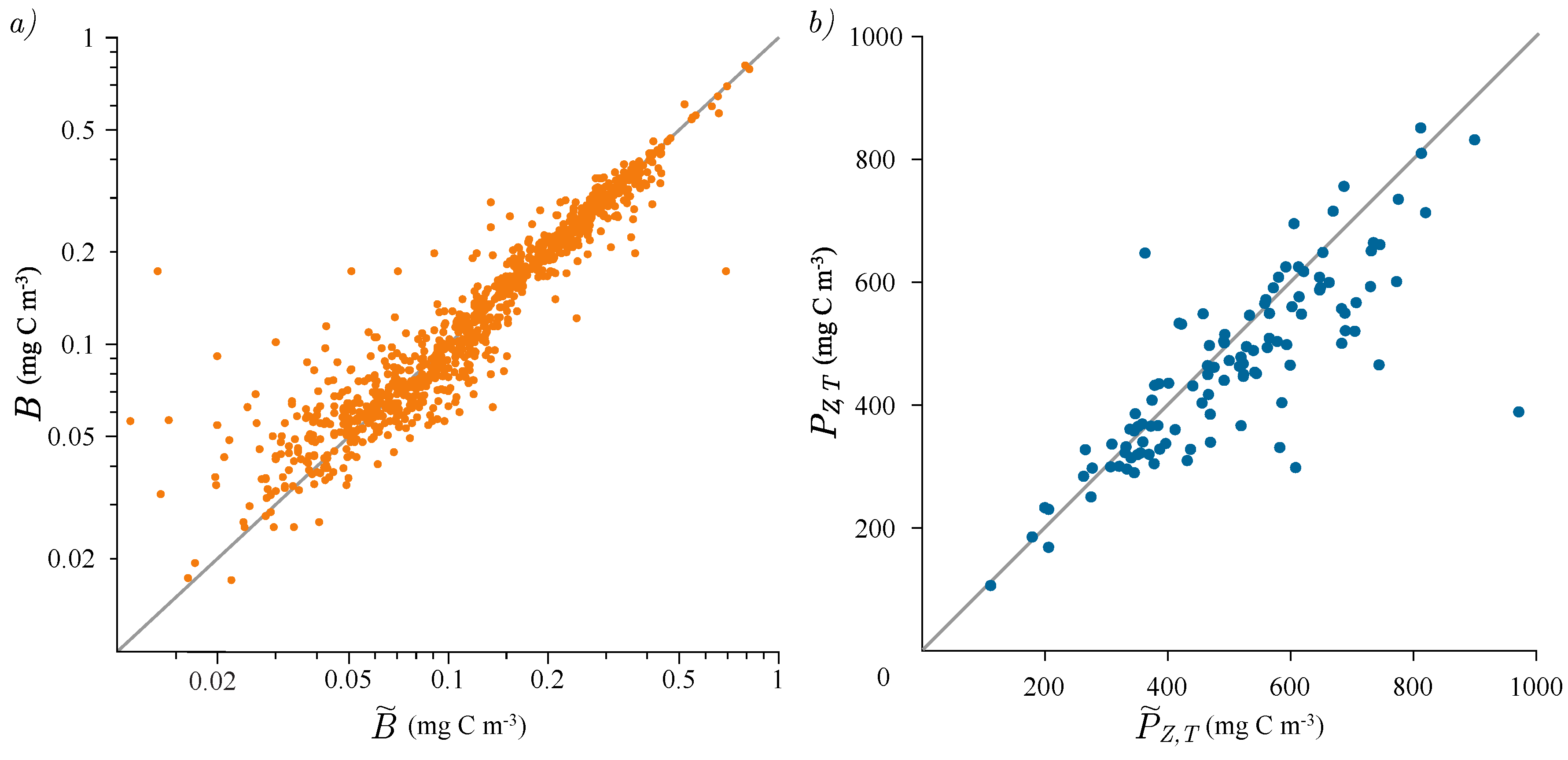
3.2. Photosynthesis Parameters Extraction
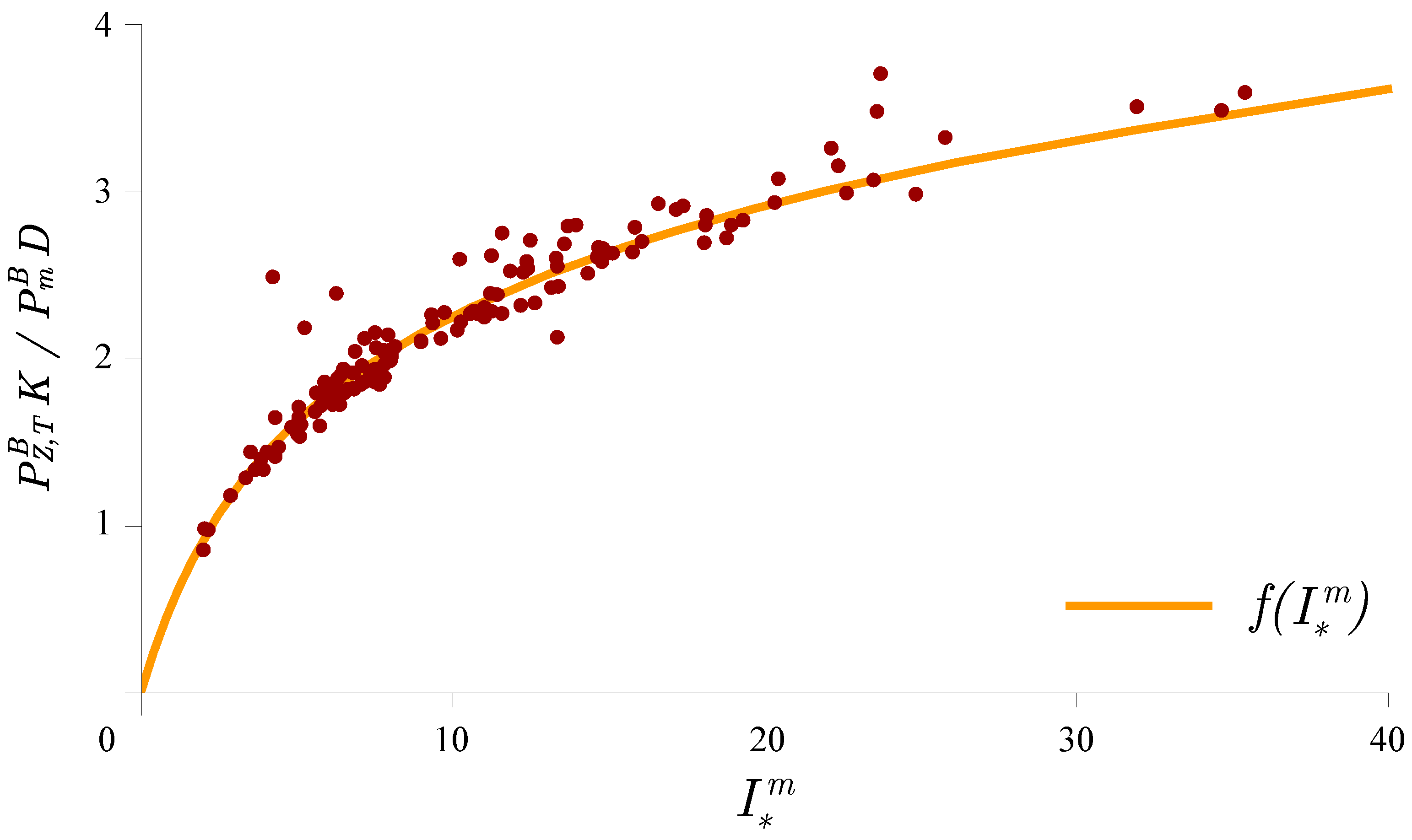
3.3. Estimation of Watercolumn Production
3.4. Estimation of Growth Rates
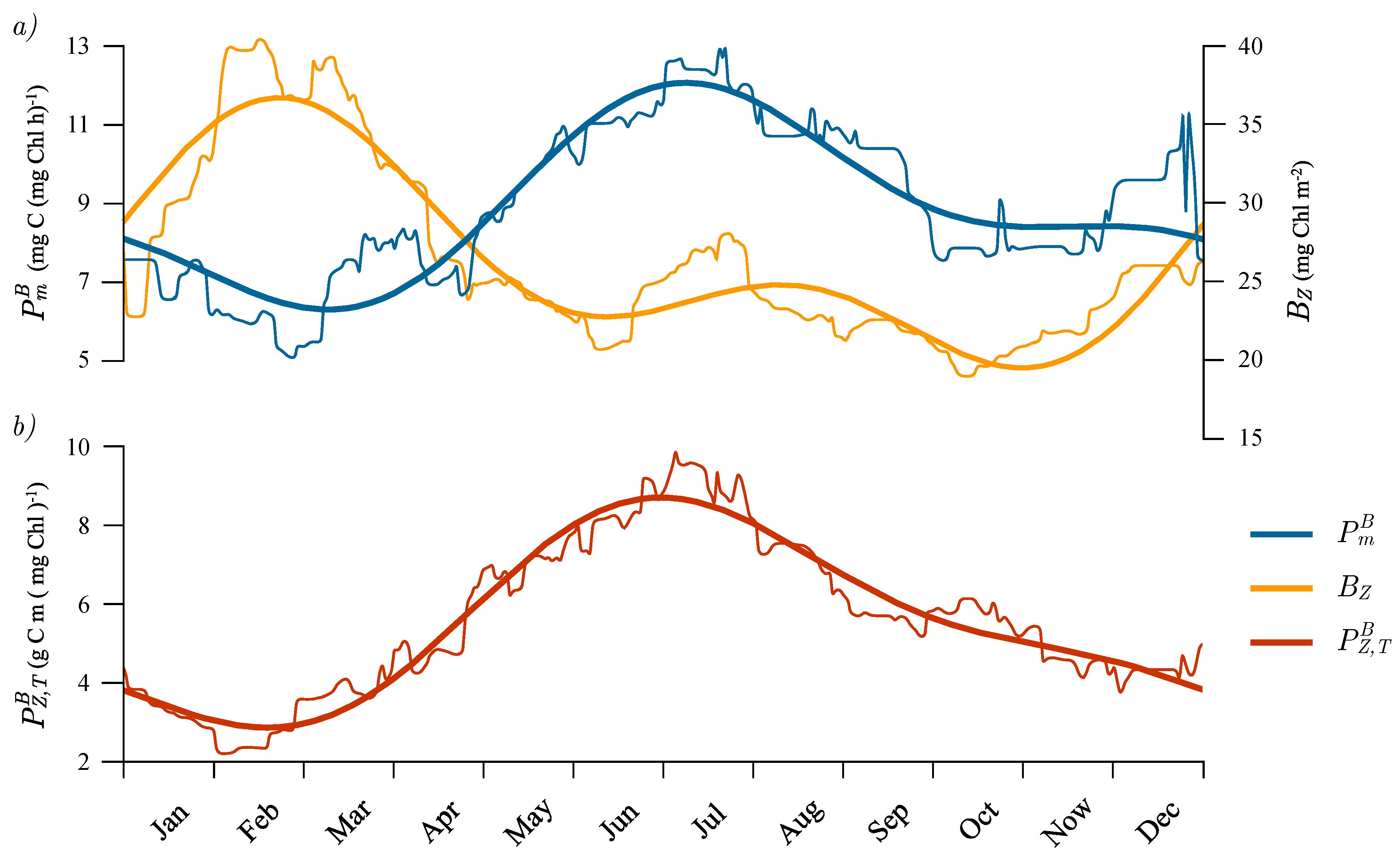
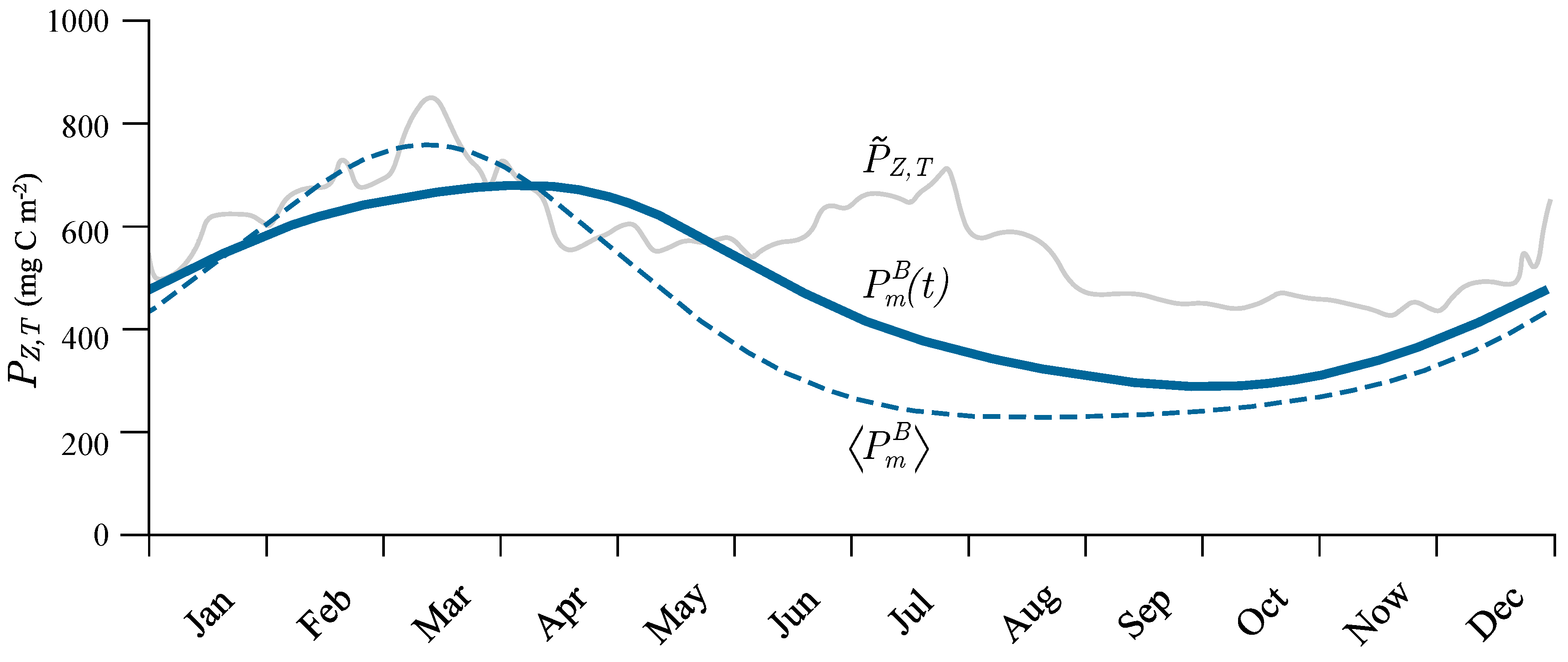
3.5. Seasonal Cycle
3.6. Application to Remote Sensing
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Steemann Nielsen, E. The use of radioactive carbon (C14) for measuring organic production in the sea. ICES J. Mar. Sci. 1952, 18, 117–140. [Google Scholar] [CrossRef]
- Platt, T.; Denman, K.L.; Jassby, A.D. Modelling the productivity of phytoplankton. In The Sea: Ideas and Observations on Progress in the Study of the Seas; Wiley: New York, NY, USA, 1977; pp. 807–856. [Google Scholar]
- Platt, T.; Gallegos, C.L. Modelling primary production. In Environmental Science Research; Plenum Publishing Corporation: New York, NY, USA, 1980; pp. 339–362. [Google Scholar]
- Longhurst, A.; Sathyendranath, S.; Platt, T. An estimate of global primary production in the ocean from satellite radiometer data. J. Plankton Res. 1995, 17, 1245–1271. [Google Scholar] [CrossRef]
- Antoine, D.; Andre, J.M.; Morel, A. Oceanic primary production 2. Estimation at global scale from satellite (coastal zone color scanner) chlorophyll. Glob. Biogeochem. Cycles 1996, 10, 57–69. [Google Scholar] [CrossRef]
- Westberry, T.; Behrenfeld, M.J.; Siegel, D.A.; Boss, E. Carbon-based primary productivity modeling with vertically resolved photoacclimation. Glob. Biogeochem. Cycles 2008, 22, GB2024. [Google Scholar] [CrossRef]
- Buitenhuis, E.T.; Hashioka, T.; Quéré, L. Combined constraints on global ocean primary production using observations and models. Glob. Biogeochem. Cycles 2013, 27, 847–858. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Platt, T. Remote sensing of water-column primary production. ICES Mar. Sci. Symp. 1993, 197, 236–243. [Google Scholar]
- Tin, H.; Lomas, M.; Ishizaka, J. Satellite-derived estimates of primary production during the Sargasso Sea winter/spring bloom: Integration of in-situ time-series data and ocean color remote sensing observations. Reg. Stud. Mar. Sci. 2016, 3, 131–143. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Boss, E.; Siegel, D.A.; Shea, D.M. Carbon-based ocean productivity and phytoplankton physiology from space. Glob. Biogeochem. Cycles 2005, 19, GB1006. [Google Scholar] [CrossRef]
- Platt, T.; Jassby, A. The relationship between photosynthesis and light for natural assemblages of coastal marine phytoplankton. J. Phycol. 1976, 12, 421–430. [Google Scholar] [CrossRef]
- Jassby, A.D.; Platt, T. Mathematical formulation of the relationship between photosynthesis and light for phytoplankton. Limnol. Oceanogr. 1976, 21, 540–547. [Google Scholar] [CrossRef]
- Jones, C.T.; Craig, S.E.; Barnett, A.B.; MacIntyre, H.L.; Cullen, J.J. Curvature in models of the photosynthesis-irradiance response. J. Phycol. 2014, 50, 341–355. [Google Scholar] [CrossRef] [PubMed]
- Platt, T.; Sathyendranath, S. Fundamental issues in measurement of primary production. ICES Mar. Sci. Symp. 1993, 197, 3–8. [Google Scholar]
- Sakshaug, E.; Bricaud, A.; Dandonneau, Y.; Falkowski, P.; Kiefer, D.A.; Legendre, L.; Morel, A.; Parslow, J.; Takahashi, M. Parameters of photosynthesis: Definitions, theory and interpretation of results. J. Plankton Res. 1997, 19, 1637–1670. [Google Scholar] [CrossRef]
- Kovač, Ž.; Platt, T.; Sathyendranath, S.; Morović, M.; Jackson, T. Recovery of photosynthesis parameters from in situ profiles of phytoplankton production. ICES J. Mar. Sci. 2016, 73, 275–285. [Google Scholar] [CrossRef]
- Peterson, B.J. Aquatic primary production and the 14C-CO2 method: A history of the productivity problem. Annu. Rev. Ecol. Evol. Syst. 1980, 11, 359–385. [Google Scholar] [CrossRef]
- Barber, R.T.; Hilting, A.K. History of the study of plankton productivity. In Phytoplankton Productivity–Carbon Assimilation in Marine and Freshwater Ecosystems; Blackwell Science: Hoboken, NJ, USA, 2002; pp. 16–43. [Google Scholar] [CrossRef]
- Kovač, Ž.; Platt, T.; Sathyendranath, S.; Antunović, S. Models for estimating photosynthesis parameters from in situ production profiles. Prog. Oceanogr. 2017, 159, 255–266. [Google Scholar] [CrossRef]
- Kovač, Ž.; Platt, T.; Sathyendranath, S.; Morović, M. Analytical solution for the vertical profile of daily production in the ocean. J. Geophys. Res. Oceans 2016, 121. [Google Scholar] [CrossRef]
- Bouman, H.; Platt, T.; Doblin, M.; Figueiras, F.G.; Gudmundsson, K.; Gudfinnsson, H.; Huang, B.; Hickman, A.; Hiscock, M.; Jackson, T.; et al. Photosynthesis-irradiance parameters of marine phytoplankton: Synthesis of a global data set. Earth Syst. Sci. Data 2017, 10, 251–266. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S. Biological production models as elements of coupled, atmosphere-ocean models for climate research. J. Geophys. Res. 1991, 96, 2585–2592. [Google Scholar] [CrossRef]
- Franks, P.J.S. NPZ Models of plankton dynamics: Their construction, coupling to physics, and application. J. Oceanogr. 2002, 58, 379–387. [Google Scholar] [CrossRef]
- Sathyedranath, S.; Longhurst, A.; Caverhill, C.M.; Platt, T. Regionally and seasonally differentiated primary production in the North Atlantic. Deep Sea Res. Part I 1995, 42, 1773–1802. [Google Scholar] [CrossRef]
- Karl, D.M.; Lukas, R. The Hawaii Ocean Time-series (HOT) program: Background, rationale and field implementation. Deep Sea Res. Part II 1996, 43, 129–156. [Google Scholar] [CrossRef]
- Steinberg, D.K.; Carlson, C.A.; Bates, N.R.; Johnson, R.J.; Michaels, A.F.; Knap, A.H. Overview of the US JGOFS Bermuda Atlantic Time-series Study (BATS): a decade-scale look at ocean biology and biogeochemistry. Deep Sea Res. Part II 2001, 48, 1405–1447. [Google Scholar] [CrossRef]
- Muller-Karger, F.; Varela, R.; Thunell, R.; Scranton, M.; Bohrer, R.; Taylor, G.; Capelo, J.; Astor, Y.; Tappa, E.; Ho, T.Y.; et al. Annual cycle of primary production in the Cariaco Basin: Response to upwelling and implications for vertical export. J. Geophys. Res. 2001, 106, 4527–4542. [Google Scholar] [CrossRef]
- Pennington, J.T.; Chavez, F.P. Seasonal fuctuations of temperature, salinity, nitrate, chlorophyll and primary production at station H3/M1 over 1989-1996 in Monterey Bay, California. Deep Sea Res. Part II 2000, 47, 947–973. [Google Scholar] [CrossRef]
- Chavez, F.P.; Messié, M.; Pennington, J.T. Marine Primary Production in Relation to Climate Variability and Change. Ann. Rev. Mar. Sci. 2011, 3, 227–260. [Google Scholar] [CrossRef] [PubMed]
- Church, M.J.; Lomas, M.W.; Muller-Karger, F. Sea change: Charting the course for biogeochemical ocean time-series research in a new millennium. Deep Sea Res. Part II 2013, 93, 2–14. [Google Scholar] [CrossRef]
- Kovač, Ž.; Platt, T.; Antunović, S.; Sathyendranath, S.; Morović, M.; Gallegos, C. Extended Formulations and Analytic Solutions for Watercolumn Production Integrals. Front. Mar. Sci. 2017, 4, 163. [Google Scholar] [CrossRef]
- Longhurst, A.R. Ecological Geography of the Sea, 2nd ed.; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Mignot, A.; Claustre, H.; Uitz, J.; Poteau, A.; D’Ortenzio, F.; Xing, X. Understanding the seasonal dynamics of phytoplankton biomass and the deep chlorophyll maximum in oligotrophic environments: A Bio-Argo float investigation. Glob. Biogeochem. Cycles 2014, 28, 856–876. [Google Scholar] [CrossRef]
- Kirk, J.T.O. Light and Photosynthesis in Quatic Ecosystems, 3rd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Platt, T. The spectral irradiance field at the surface and in the interior of the ocean: A model for applications in oceanography and remote sensing. J. Geophys. Res. 1988, 93, 9270–9280. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S.; White, G.N.; Ravindran, P. Attenuation of visible light by phytoplankton in a vertically structured ocean: solutions and applications. J. Plankton Res. 1994, 16, 1461–1487. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S. Estimators of Primary Production for Interpretation of Remotely Sensed Data on Ocean Color. J. Geophys. Res. 1993, 98, 14561–14576. [Google Scholar] [CrossRef]
- Frenette, J.; Demers, S.; Legendre, L. Lack of agreement among models for estimating the photosynthetic parameters. Limnol. Oceanogr. 1993, 38, 679–687. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S.; Ravindran, P. Primary Production by Phytoplankton: Analytic Solutions for Daily Rates per Unit Area of Water Surface. Proc. R. Soc. B 1990, 241, 101–111. [Google Scholar] [CrossRef]
- Platt, T.; Gallegos, C.L.; Harrison, W.G. Photoinhibition of photosynthesis in natural assemblages of marine phytoplahnkton. J. Mar. Res. 1980, 38, 687–701. [Google Scholar]
- Michaels, A.F.; Knap, A.H. Overview of the U.S. JGOFS Bermuda Atlantic Time-series Study and the Hydrostation S Program. Deep Sea Res. Part II Top. Stud. Oceanogr. 1996, 43, 157–198. [Google Scholar] [CrossRef]
- Morel, A.; Smith, R.C. Relation between total quanta and total energy for aquatic photosynthesis. Limnol. Oceanogr. 1974, 19, 591–600. [Google Scholar] [CrossRef]
- Allen, J.G.; Nelson, N.B.; Siegel, D.A. Seasonal to multi-decadal trends in apparent optical properties in the Sargasso Sea. Deep Sea Res. Part I Oceanogr. Res. Pap. 2017, 119, 58–67. [Google Scholar] [CrossRef]
- Lomas, M.W.; Bates, N.R.; Johnson, R.J.; Knap, A.H.; Steinberg, D.K.; Carlson, C.A. Two decades and counting: 24-years of sustained open ocean biogeochemical measurements. Deep Sea Res. II 2013, 93, 16–32. [Google Scholar] [CrossRef]
- Platt, T.; Caverhill, C.; Sathyendranath, S. Basin-scale estimates of oceanic primary production by remote sensing: The North Atlantic. J. Geophys. Res. 1991, 96, 15147–15159. [Google Scholar] [CrossRef]
- Baldick, R. Applied Optimization: Formulation and Algorithms for Engineering Systems, 1st ed.; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Knyazev, A.V.; Lashuk, I. Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning. SIAM J. Matrix Anal. Appl. 2008, 29, 1267–1281. [Google Scholar] [CrossRef]
- Kirchman, D.L. Calculating microbial growth rates from data on production and standing stocks. Mar. Ecol. Prog. Ser. 2002, 233, 303–306. [Google Scholar] [CrossRef]
- Marañon, E. Phytoplankton growth rates in the Atlantic subtropical gyres. Limnol. Oceanogr. 2005, 50, 299–310. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Stuart, V.; Nair, A.; Oka, K.; Nakane, T.; Bouman, H.; Forget, M.; Maass, H.; Platt, T. Carbon-to-chlorophyll ratio and growth rate of phytoplankton in the sea. Mar. Ecol. Prog. Ser. 2009, 383, 73–84. [Google Scholar] [CrossRef]
- Gasol, J.M.; del Giorgio, P.A.; Duarte, C.M. Biomass distribution in marine planktonic communities. Limnol. Oceanogr. 1997, 42, 1353–1363. [Google Scholar] [CrossRef]
- Harris, G.P. Phytoplankton productivity and growth measurements: past, present and future. J. Plankton Res. 1984, 6, 219–237. [Google Scholar] [CrossRef]
- Falkowski, P.G. Light-shade adaptation and assimilation numbers. J. Plankton Res. 1981, 3, 203–216. [Google Scholar] [CrossRef]
- Casey, J.R.; Lomas, M.W.; Mandecki, J.; Walker, D.E. Prochlorococcus contributes to new production in the Sargasso Sea deep chlorophyll maximum. Geophys. Res. Lett. 2007, 34, L10604. [Google Scholar] [CrossRef]
- Platt, T.; Bird, D.F.; Sathyendranath, S. Critical depth and marine primary production. Proc. R. Soc. B 1991, 246, 205–217. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Platt, T. New production and mixed-layer physics. Proc. Indian Acad. Sci. Earth Planet. 1994, 103, 177–188. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S. Latitude as a factor in the calculation of primary production. In Ecology of Fjords and Coastal Waters: Proceedings of the Mare Nor Symposium on the Ecology of Fjords and Coastal; Elsevier: New York, NY, USA, 1995; pp. 3–13. [Google Scholar]
- Evans, G.T.; Parslow, J.S. Model of Annual Plankton Cycles. Biol. Oceanogr. 1985, 3, 327–347. [Google Scholar] [CrossRef]
- Sarmiento, J.L.; Gruber, N. Ocean Biogeochem. Cycles, 1st ed.; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Chisholm, S.W. Phytoplankton Size. In Primary Productivity and Biogeochemical Cycles in the Sea; Plenum Press: New York, NY, USA, 1992; pp. 213–237. [Google Scholar]
- Casey, J.R.; Aucan, J.P.; Goldberg, S.R.; Lomas, M.W. Changes in partitioning of carbon amongst photosynthetic pico- and nano-plankton groups in the Sargasso Sea in response to changes in the North Atlantic Oscillation. Deep Sea Res. Part II Top. Stud. Oceanogr. 2013, 93, 58–70. [Google Scholar] [CrossRef]
- Wallhead, P.J. Long-term variability of phytoplankton carbon biomass in the Sargasso Sea. Glob. Biogeochem. Cycles 2014, 28, 1–17. [Google Scholar] [CrossRef]
- Armstrong, R.A. Grazing limitation and nutrient limitation in marine ecosystems: Steady state solutions of an ecosystem model with multiple food chains. Limnol. Oceanogr. 1994, 39, 597–608. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Brewin, R.J.W.; Jackson, T.; Mélin, F.; Platt, T. Ocean-colour products for climate-change studies: What are their ideal characteristics? Remote Sens. Environ. 2017, 203, 125–138. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Groom, S.; Grant, M.; Brewin, R.; Thompson, A.; Chuprin, A.; Horseman, A.; Jackson, T.; Martinez Vicente, V.; Platt, T.; et al. ESA Ocean Colour Climate Change Initiative: Version 3.1; Centre for Environmental Data Analysis: Didcot, UK, 1 June 2018. [Google Scholar]
- Geider, R.J.; Macintyre, H.L.; Kana, T.M. Dynamic model of phytoplankton growth and acclimation: responses of the balancedgrowth rate and chlorophyll a:carbon ratio to light, nutrient-limitation and termperature. Mar. Ecol. Prog. Ser. 1997, 148, 187–200. [Google Scholar] [CrossRef]
- Jackson, T.; Sathyendranath, S.; Platt, T. An Exact Solution For Modeling Photoacclimation of the Carbon-to-Chlorophyll Ratio in Phytoplankton. Front. Mar. Sci. 2017, 4, 283. [Google Scholar] [CrossRef]
- Cushman-Roisin, B.; Beckers, J.M. Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects, 2nd ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Izhikevich, E.M. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting, 1st ed.; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar] [CrossRef]
- Forget, M.H.; Sathyendranath, S.; Platt, T.; Pommier, J.; Vis, C.; Kyewalyanga, M.S.; Hudon, C. Extraction of photosynthesis-irradiance parameters from phytoplankton production data: Demonstration in various aquatic systems. J. Plankton Res. 2007, 29, 249–262. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S.; Ulloa, O.; Harrison, W.G.; Hoepffner, N.; Goes, J. Nutrient control of phytoplankton photosynthesis in the Western North Atlantic. Nature 1992, 356, 229–231. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S.; White, G.N.; Jackson, T.; Saux Picart, S.; Bouman, H. Primary Production: Sensitivity to Surface Irradiance and Implications for Archiving Data. Front. Mar. Sci. 2017, 4, 387. [Google Scholar] [CrossRef]
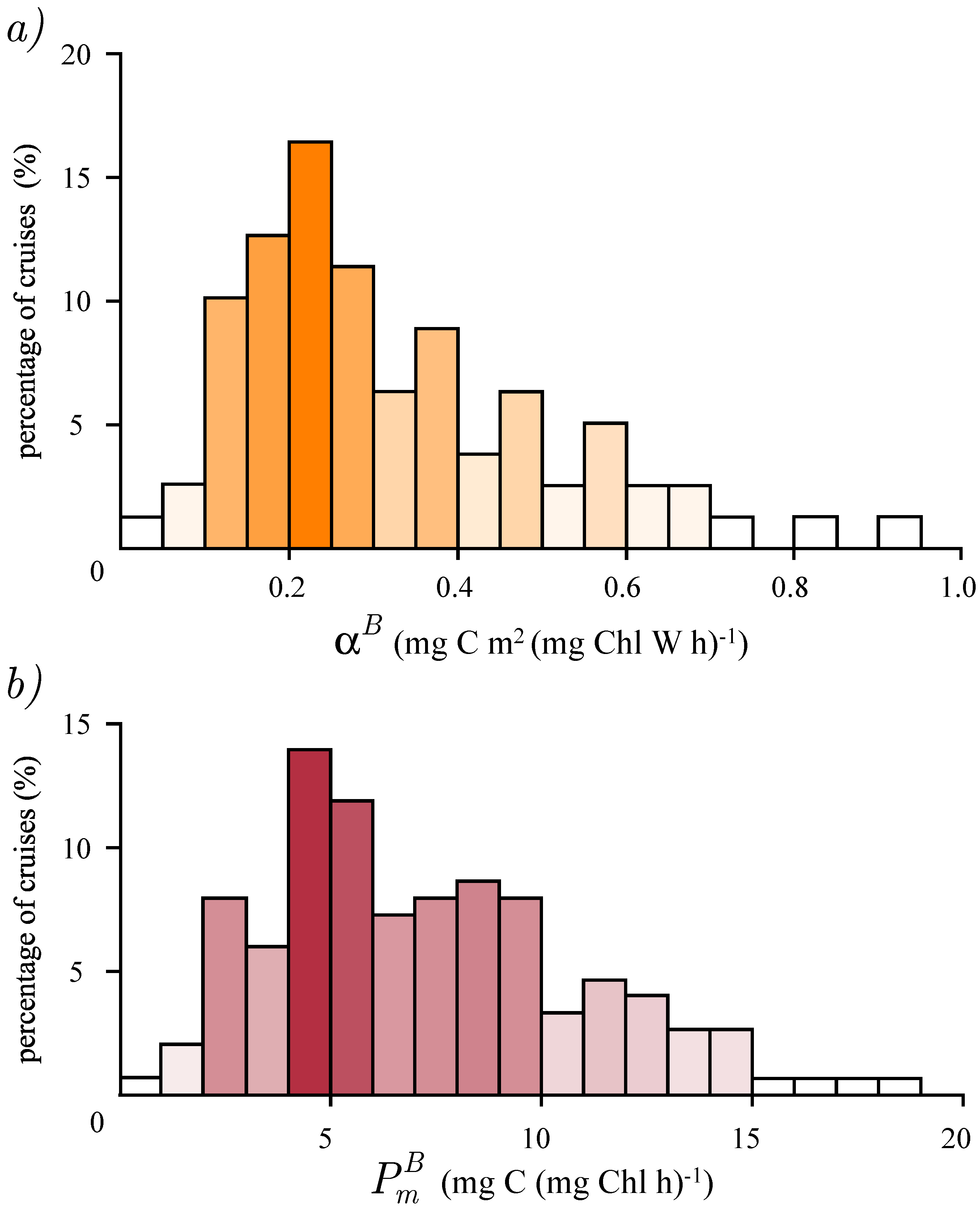
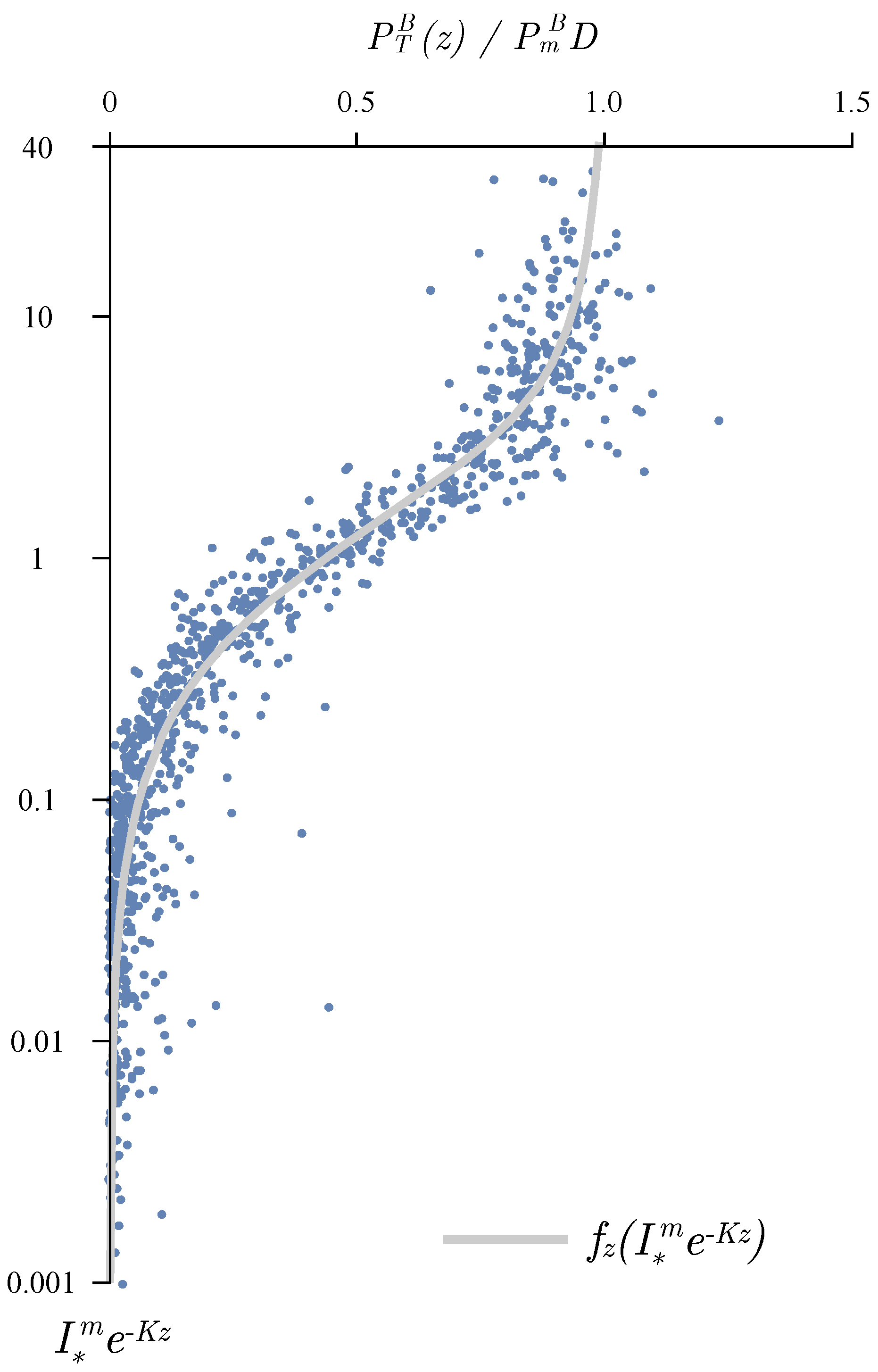
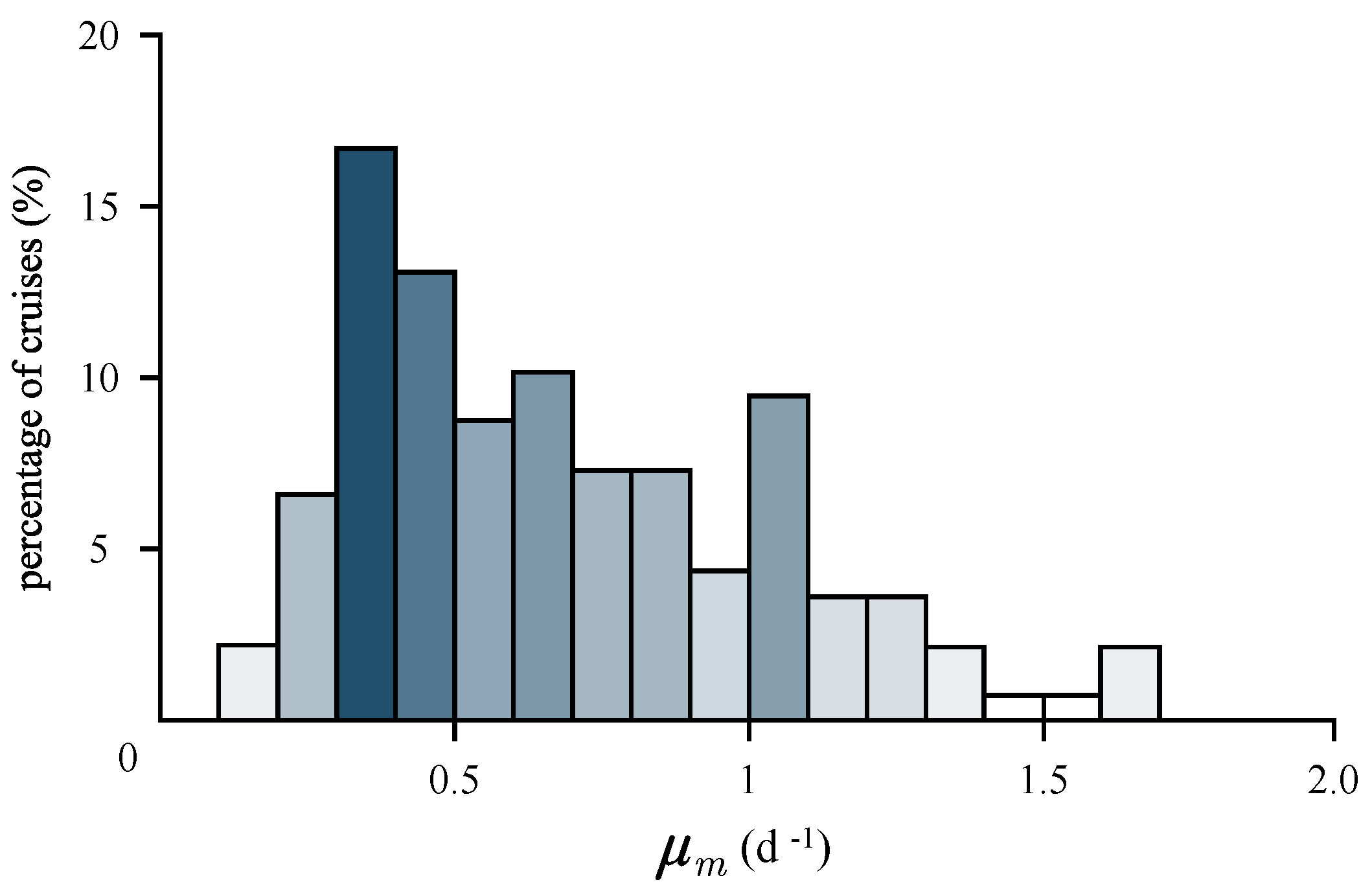
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovač, Ž.; Platt, T.; Sathyendranath, S.; Lomas, M.W. Extraction of Photosynthesis Parameters from Time Series Measurements of In Situ Production: Bermuda Atlantic Time-Series Study. Remote Sens. 2018, 10, 915. https://doi.org/10.3390/rs10060915
Kovač Ž, Platt T, Sathyendranath S, Lomas MW. Extraction of Photosynthesis Parameters from Time Series Measurements of In Situ Production: Bermuda Atlantic Time-Series Study. Remote Sensing. 2018; 10(6):915. https://doi.org/10.3390/rs10060915
Chicago/Turabian StyleKovač, Žarko, Trevor Platt, Shubha Sathyendranath, and Michael W. Lomas. 2018. "Extraction of Photosynthesis Parameters from Time Series Measurements of In Situ Production: Bermuda Atlantic Time-Series Study" Remote Sensing 10, no. 6: 915. https://doi.org/10.3390/rs10060915
APA StyleKovač, Ž., Platt, T., Sathyendranath, S., & Lomas, M. W. (2018). Extraction of Photosynthesis Parameters from Time Series Measurements of In Situ Production: Bermuda Atlantic Time-Series Study. Remote Sensing, 10(6), 915. https://doi.org/10.3390/rs10060915