Estimating Satellite-Derived Bathymetry (SDB) with the Google Earth Engine and Sentinel-2
Abstract
1. Introduction
2. Materials and Methods
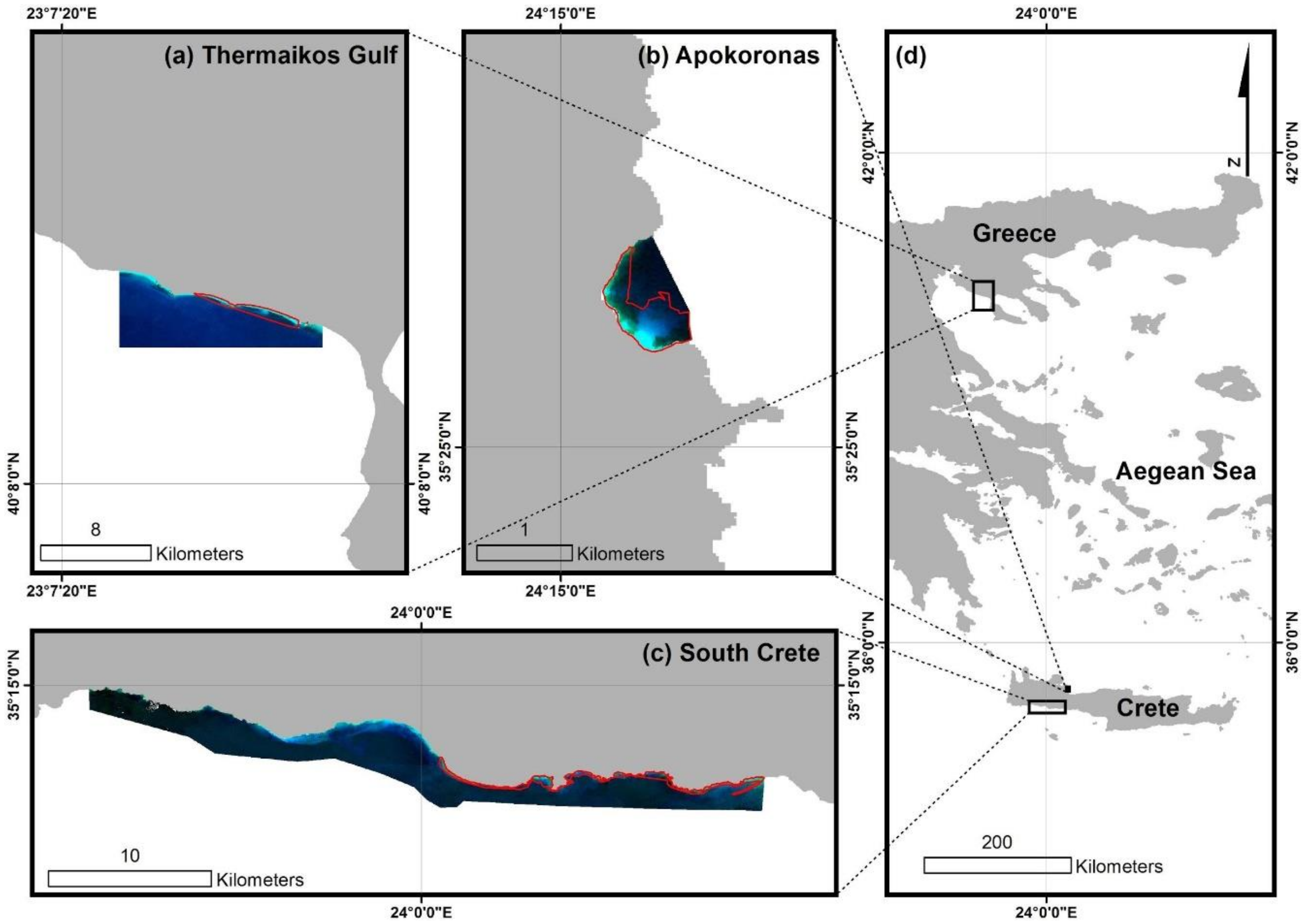
2.1. Study Sites and In Situ Data
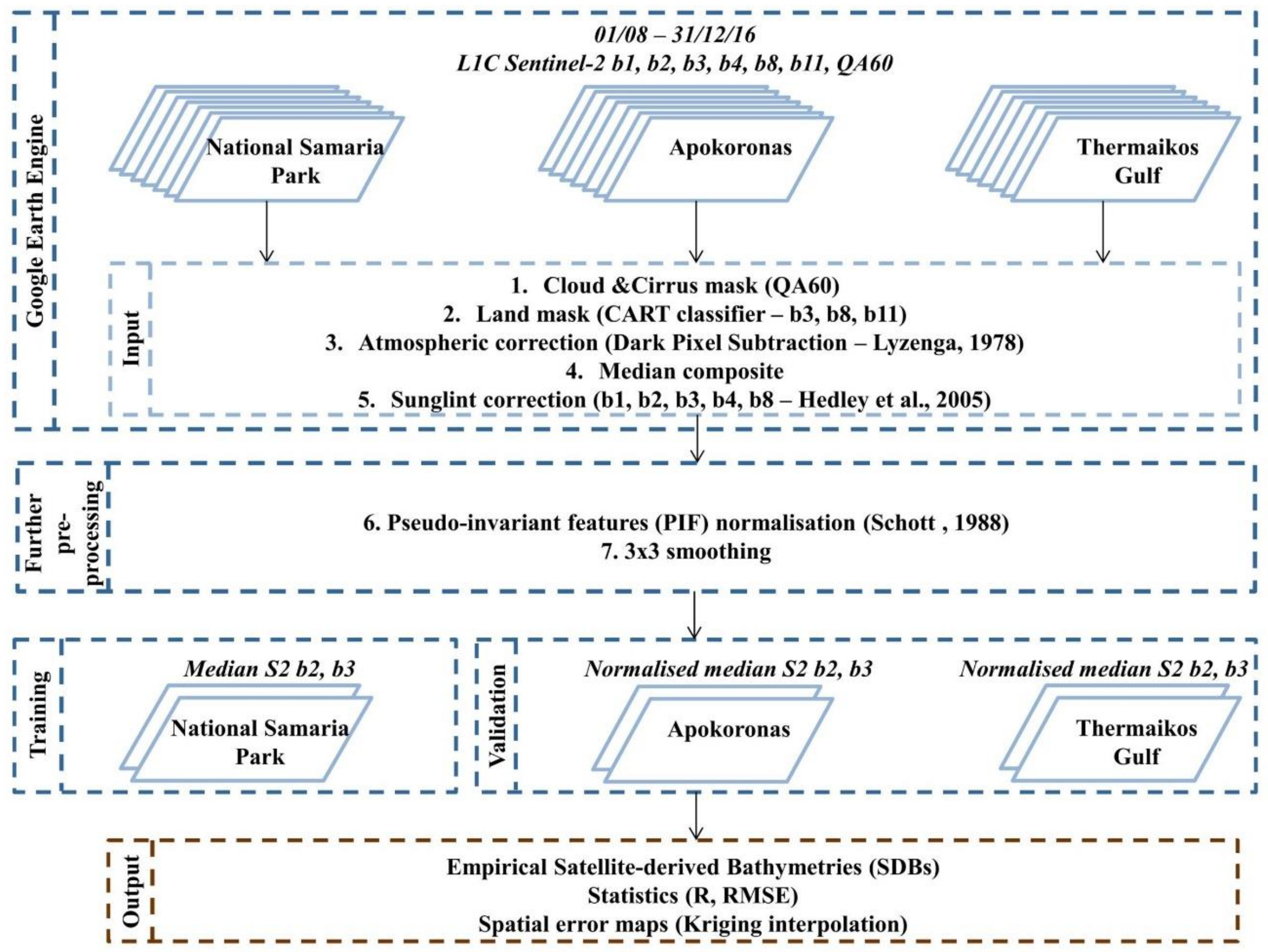
2.2. Sentinel-2 Data Preprocessing
- We employ the QA60 bitmask band which contains cloud information to mask out opaque and cirrus clouds and scale S2 L1C TOA data by 10,000 (S2 quantification value).
- We use a classification and regression tree (CART) classifier [24] on a b3-b8-b11 composite to mask the terrestrial environment. It is noteworthy that although the classifier is trained with selected aquatic and terrestrial points (35 and 32, respectively) around Crete Island only (Figure 1d), it is utilised in all three sites.
- To atmospherically correct the masked for clouds and land images, we implement a modified dark pixel subtraction (DPS) method after [25] which subtracts the mean radiance of optically deep-water pixels (>40 m) to address path radiance and two standard deviations to address sensor-related noise in all bands.
- We employ the so-called image composition where a new pseudo-image is created using—in our case—the median values of the already pre-processed images [16]. This approach aims to further reduce image artefacts which have not been corrected by the previous preprocessing steps. In fact, 79 tiles (34 SGE, 34 SGD, 35 SKV and 35 SKU; also called granules—100 × 100 km2 ortho images projected in Universal Transverse Mercator UTM/WGS84 [26]) form the Samaria National Park and Apokoronas pseudo-image, while 18 tiles (34 TFK) form the Thermaikos pseudo-image.
- We apply the sun glint correction algorithm from [27] to the median composite. Following a user-defined set of pixels that represents sun glint of variable intensity (two polygons in the south of tSamaria National Park site in South Crete), the algorithm equals the sun glint-corrected/sun glint-polluted median composite reduced by the product of the slope of the regression of NIR b8 against b1–b4 and the difference between b8 and its minimum value. We should state here that in [28], the preprocessing step included the mean and not the minimum NIR signal over optically deep water. The two last steps of our preprocessing chain are performed in a GIS environment (ArcMap 10.5) as we export the sun glint-corrected median composites from the previous step for all three areas of interest.
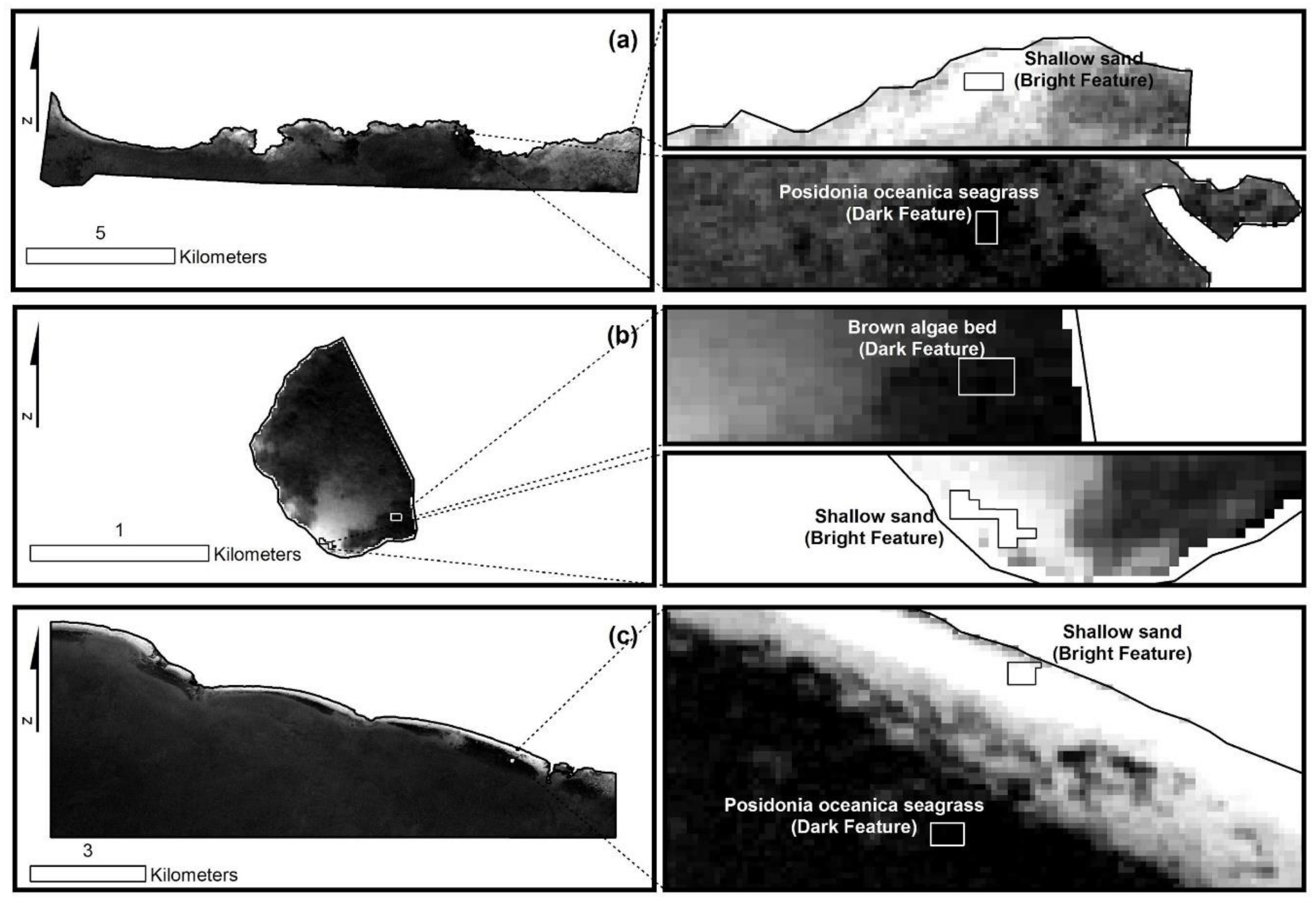
- We implement the pseudo-invariant features (PIF) [21] to radiometrically normalise b2 and b3 bands which are used in the validation of the SDB models (Apokoronas and Thermaikos composites; Figure 1a,b) to the b2 and b3 of the National Samaria Park composite (Figure 1c). This technique was developed to quantitatively transform a subject multispectral image to the reference multispectral image as if they were sensed under the same atmospheric conditions, and in the case of a coastal study, the same water surface and column conditions. The PIF-based composite normalisation is employed here to decrease the spectral differences which caused high RMSEs in our first SDB validation experiments (results are not shown here). Figure 3 displays the location of the selected PIF features (44 in total for each site), with shallow sands as the bright features and Posidonia oceanica seagrasses (National Samaria Park and Thermaikos) and brown algae (Apokoronas; mainly Cystoseira sp.) as the dark features. Figure S1 shows the linear equations which are utilised in the radiometric normalisations. We select these specific features because they occupy the extremes (high, low) of the observed reflectance range in all three sites following the recommendations that can be found in [29]; the underlying assumption here is that the PIF changes little between the same tiles (=same site) and different composites (=different site).
- We apply a 3 × 3 low pass filter to the normalised S2 b2 and b3 bands to further reduce noise before the training and validation of the empirical SDB models.
2.3. Empirical Satellite-Derived Bathymetries (SDB)
2.4. Spatial Distribution of Model Residuals
3. Results
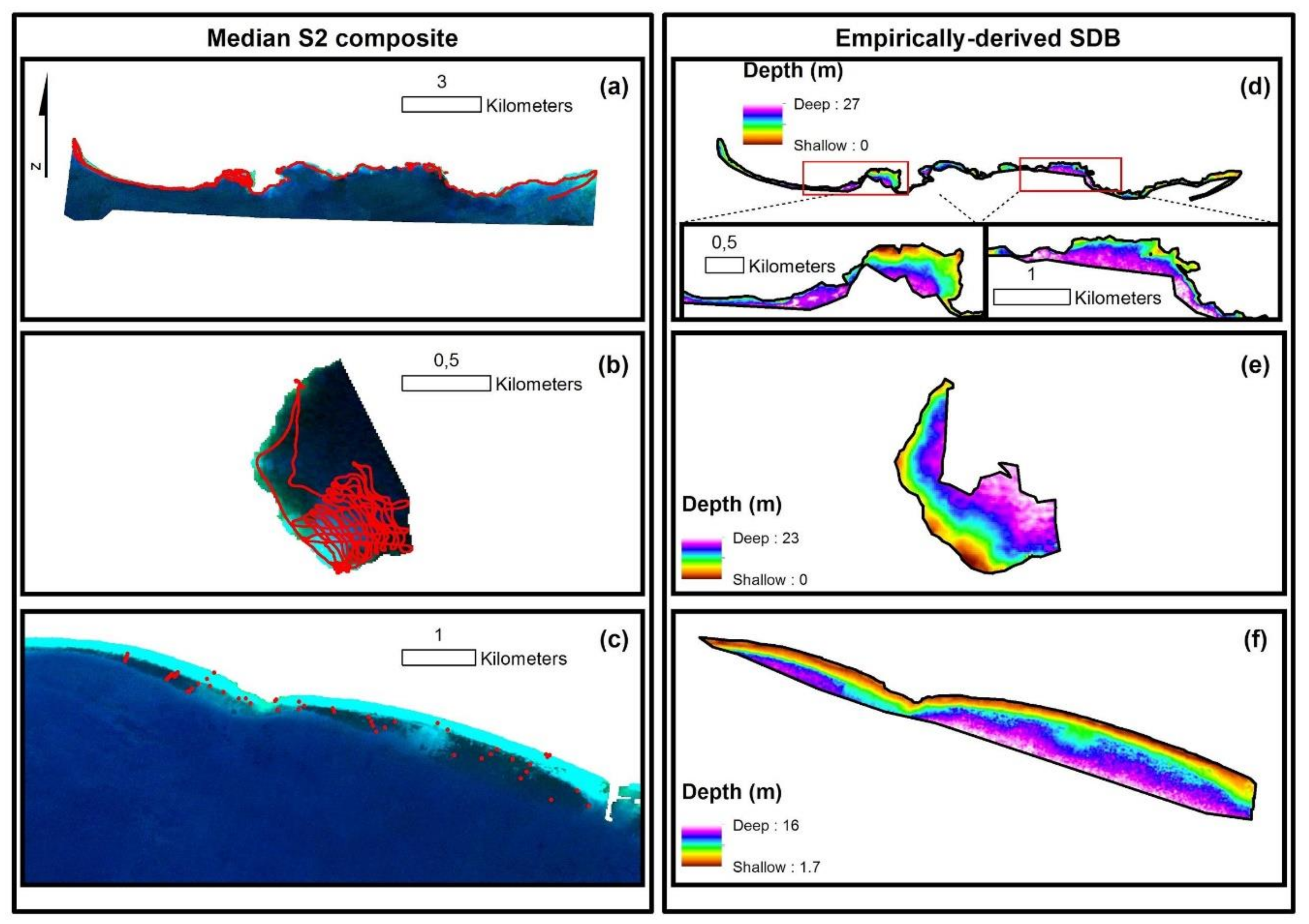
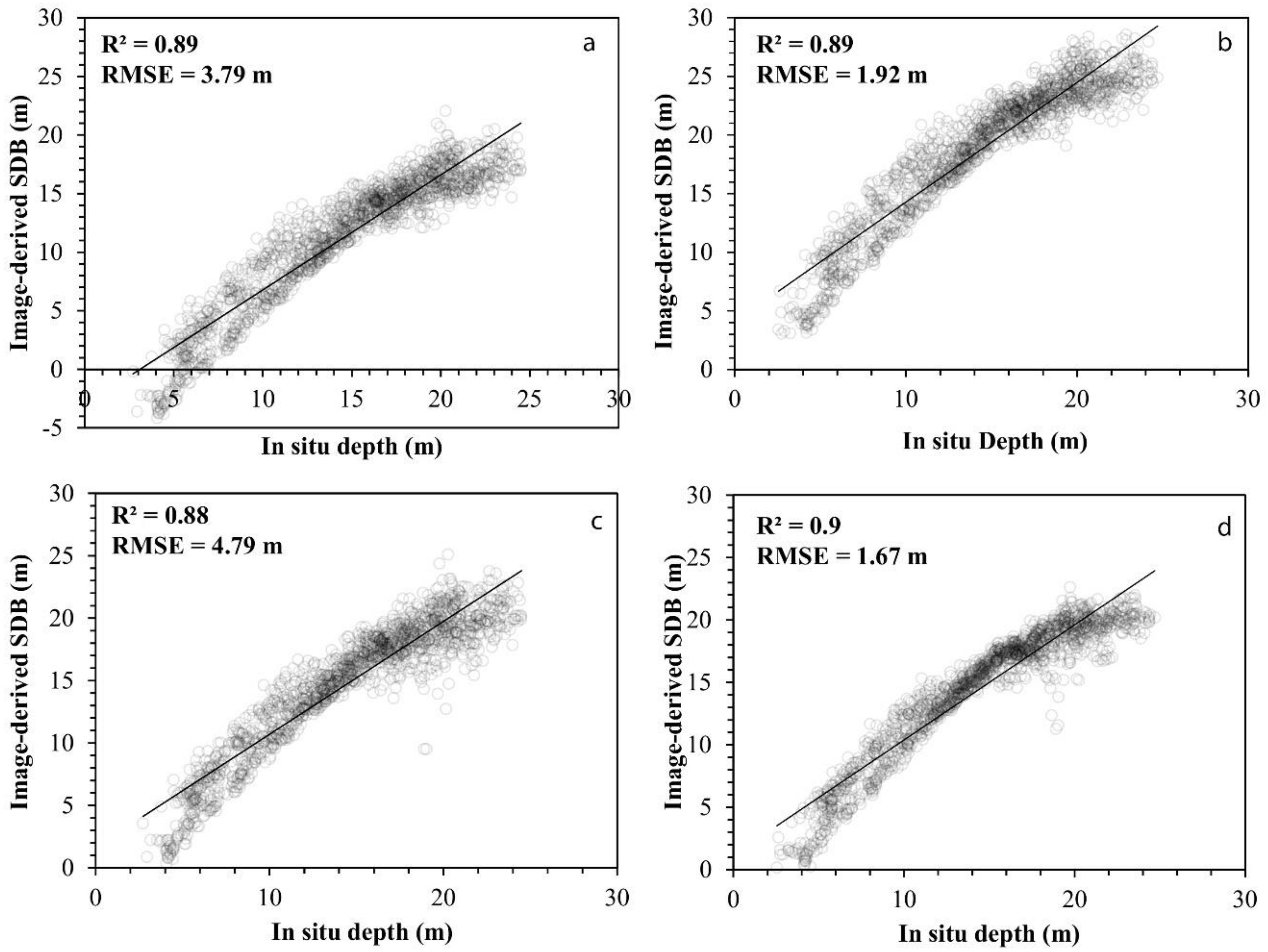
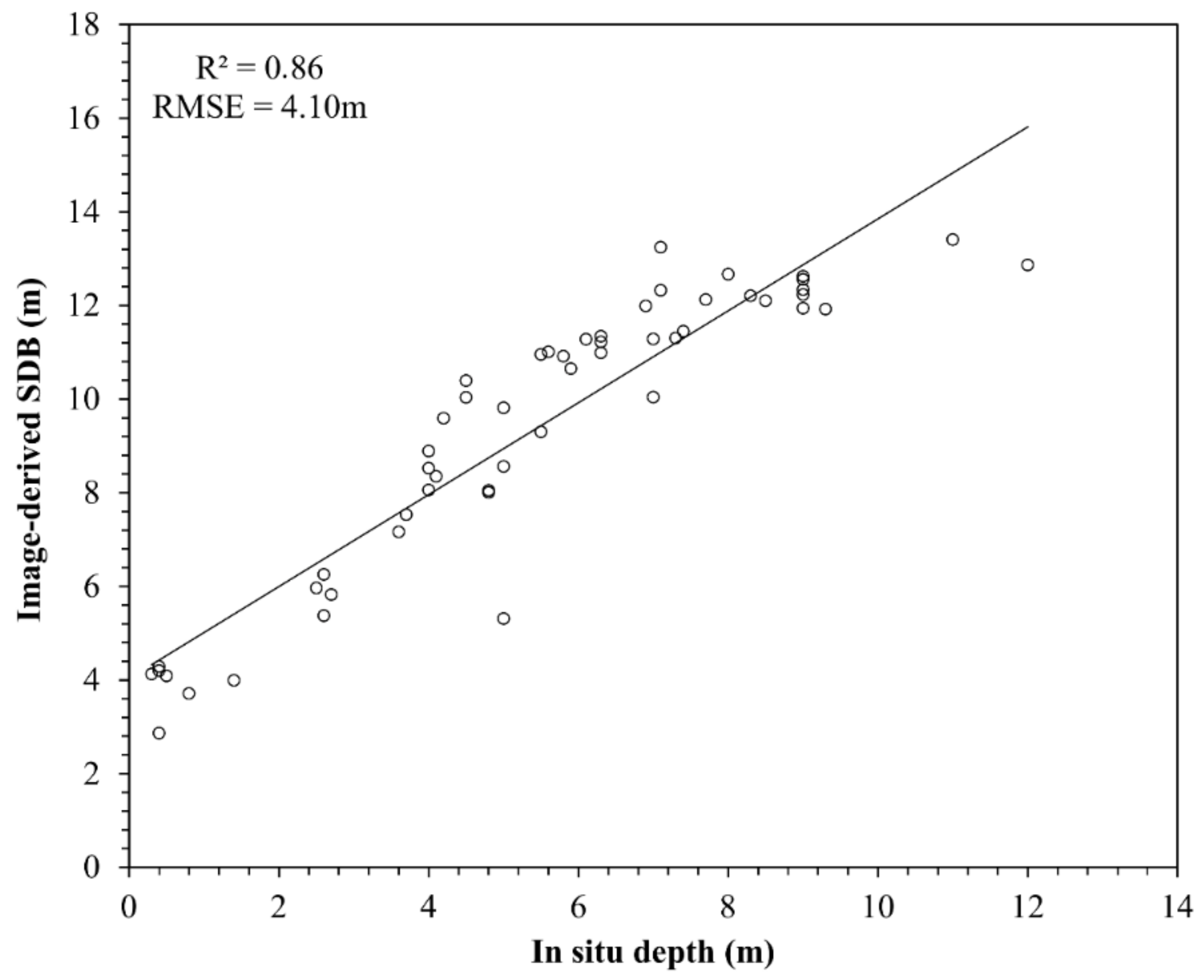
3.1. SDB Estimations
3.2. Methodological Gains Using a PIF Normalisation and 3 × 3 Smoothing
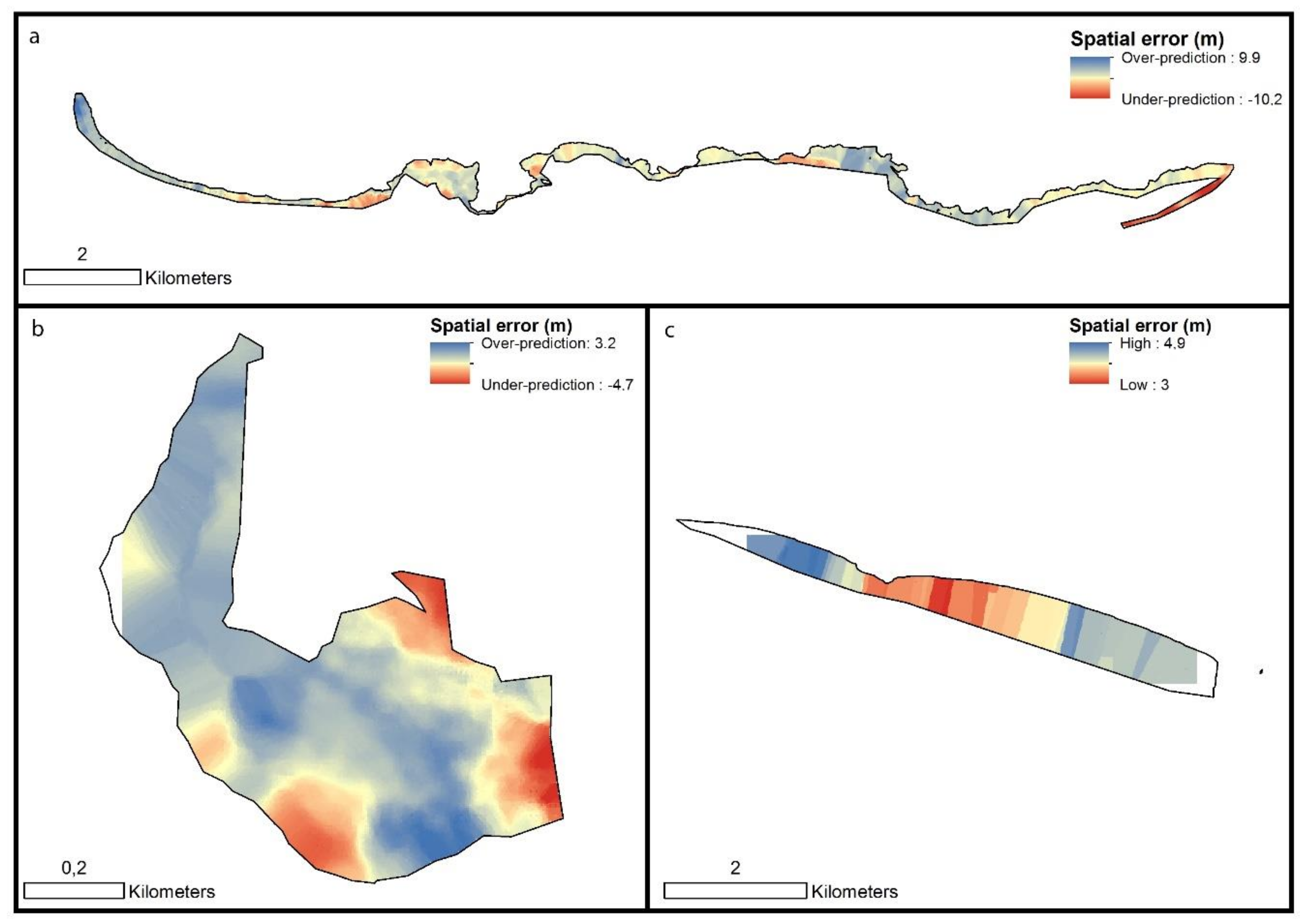
3.3. Spatial Distribution of Model Residuals
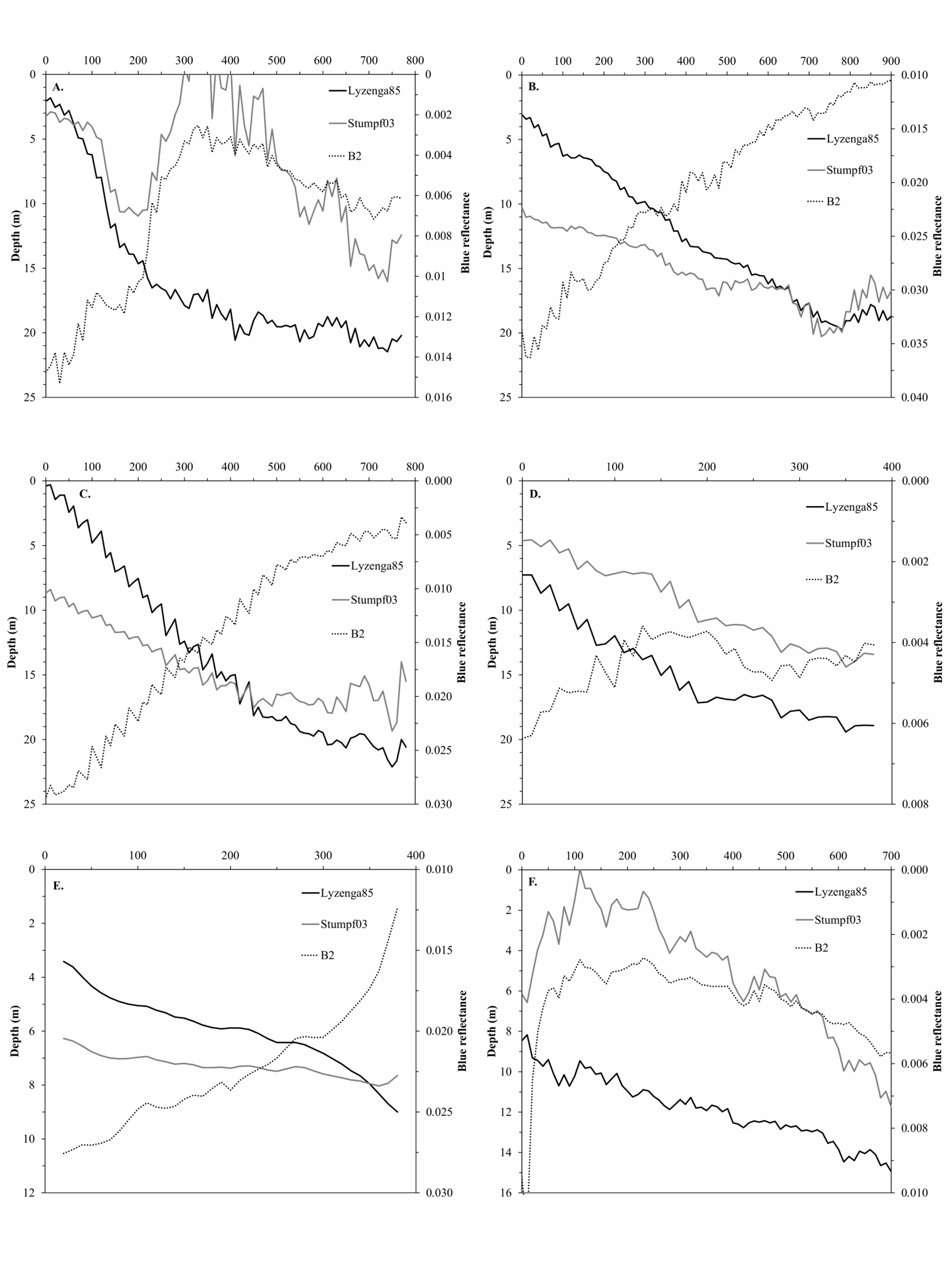
3.4. SDB Sensitivity to Variation in Seabed Habitat and Reflectance
4. Discussion
4.1. Cloud-Based SDB and Model Performance
4.2. On the Importance of Image Composition, PIF and the Spatial Distribution of Errors
4.3. In Situ Data Collection, Crowdsourced Information and an Outlook for SDB
- Τhe implementation of the estimated spatial error parameter as a postprocessing step to increase the statistical accuracy of the empirically derived SDB models following the work in [34].
- Τhe utilisation of best-available-pixel (BAP) composition, which employs a series of pixel-based scores related to distance to clouds and shadow masks, atmospheric opacity, day of the year etc., instead of image composition across a relevant time series to the user’s study region [42].
- Τhe use of the proposed preprocessing workflow to conduct sea- to basin-wide habitat mapping and monitoring.
- Τhe fusion of the Copernicus Sentinel-1 (also available in GEE) and the Sentinel-2 open and free image archive for the development of 10-m topobathymetric digital elevation models (DEMs)—seamless merged elevation products of terrestrial and underwater topography [45] useful for numerous Earth science applications including mapping and modelling of inundation, sediment transport, sea-level rise, and storm surge [46].
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Paterson, D.M.; Hanley, N.D.; Black, K.; Defew, E.C.; Solan, M. (Eds.) Biodiversity, ecosystems and coastal zone management: Linking science and policy. Theme Section. Mar. Ecol. Prog. Ser. 2011, 434, 201–301. [Google Scholar] [CrossRef]
- Robertson, E. Crowd-Sourced Bathymetry Data via Electronic Charting Systems. ESRI Ocean GIS Forum, 2016. Available online: http://proceedings.esri.com/library/userconf/oceans16/papers/oceans_12.pdf (accessed on 20 April 2018).
- Li, R.; Liu, J.-K.; Felus, Y. Spatial Modeling and Analysis for Shoreline Change Detection and Coastal Erosion Monitoring. Mar. Geod. 2010, 24, 1–12. [Google Scholar] [CrossRef]
- Omira, R.; Baptista, M.A.; Leone, F.; Matias, L.; Mellas, S.; Zourarah, B.; Miranda, J.M.; Carrilho, F.; Cherel, J.P. Performance of coastal sea-defense infrastructure at El Jadida (Morocco) against tsunami threat: Lessons learned from the Japanese 11 March 2011 tsunami. Nat. Hazards Earth Syst. Sci. 2013, 13, 1779–1794. [Google Scholar] [CrossRef]
- Roelfsema, C.; Kovacs, E.; Ortiz, J.C.; Wolff, N.H.; Callaghan, D.; Wettle, M.; Ronan, M.; Hamylton, S.M.; Mumby, P.J.; Phinn, S. Coral reef habitat mapping: A combination of object-based image analysis and ecological modelling. Remote Sens. Environ. 2018, 208, 27–41. [Google Scholar] [CrossRef]
- Wang, J.; Yi, S.; Li, M.; Wang, L.; Song, C. Effects of sea level rise, land subsidence, bathymetric change and typhoon tracks on storm flooding in the coastal areas of Shanghai. Sci. Total Environ. 2018, 621, 228–234. [Google Scholar] [CrossRef] [PubMed]
- Sandwell, D.T.; Smith, W.H. Marine gravity anomaly from Geosat and ERS 1 satellite altimetry. J. Geophys. Res. Solid Earth 1997, 102, 10039–10054. [Google Scholar] [CrossRef]
- Olson, C.J.; Becker, J.J.; Sandwell, D.T. A new global bathymetry map at 15 arcsecond resolution for resolving seafloor fabric: SRTM15_PLUS. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 15–19 December 2014. [Google Scholar]
- Pe’eri, S.; Madore, B.; Nyberg, J.; Snyder, L.; Parrish, C.; Smith, S. Identifying bathymetric differences over Alaska’s North Slope using a satellite-derived bathymetry multi-temporal approach. J. Coast. Res. 2016, 76, 56–63. [Google Scholar] [CrossRef]
- Misra, A.; Vojinovic, Z.; Ramakrishnan, B.; Luijendijk, A.; Ranasinghe, R. Shallow water bathymetry mapping using Support Vector Machine (SVM) technique and multispectral imagery. Int. J. Remote Sens. 2018. [Google Scholar] [CrossRef]
- Pacheco, A.; Horta, J.; Loureiro, C.; Ferreira, Ó. Retrieval of nearshore bathymetry from Landsat 8 images: A tool for coastal monitoring in shallow waters. Remote Sens. Environ. 2015, 159, 102–116. [Google Scholar] [CrossRef]
- Dörnhöfer, K.; Göritz, A.; Gege, P.; Pflug, B.; Oppelt, N. Water Constituents and Water Depth Retrieval from Sentinel-2A—A First Evaluation in an Oligotrophic Lake. Remote Sens. 2016, 8, 941. [Google Scholar] [CrossRef]
- Chybicki, A. Mapping South Baltic Near-Shore Bathymetry Using Sentinel-2 Observations. Pol. Mar. Res. 2017, 24, 15–25. [Google Scholar] [CrossRef]
- Chybicki, A. Three-Dimensional Geographically Weighted Inverse Regression (3GWR) Model for Satellite Derived Bathymetry Using Sentinel-2 Observations. Mar. Geod. 2017, 41, 1–23. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Robinson, N.P.; Allred, B.W.; Jones, M.O.; Moreno, A.; Kimball, J.S.; Naugle, D.E.; Erickson, T.A.; Richardson, A.D. A Dynamic Landsat Derived Normalized Difference Vegetation Index (NDVI) Product for the Conterminous United States. Remote Sens. 2017, 9, 863. [Google Scholar] [CrossRef]
- Xiong, J.; Thenkabail, P.S.; Tilton, J.C.; Gumma, M.K.; Teluguntla, P.; Oliphant, A.; Congalton, R.G.; Yadav, K.; Gorelick, N. Nominal 30-m Cropland Extent Map of Continental Africa by Integrating Pixel-Based and Object-Based Algorithms Using Sentinel-2 and Landsat-8 Data on Google Earth Engine. Remote Sens. 2017, 9, 1065. [Google Scholar] [CrossRef]
- Parastatidis, D.; Mitraka, Z.; Chrysoulakis, N.; Abrams, M. Online Global Land Surface Temperature Estimation from Landsat. Remote Sens. 2017, 9, 1208. [Google Scholar] [CrossRef]
- Chrysoulakis, N.; Mitraka, Z.; Gorelick, N. Exploiting satellite observations for global surface albedo trends monitoring. Theor. Appl. Climatol. 2018. accepted. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Schott, J.R.; Salvaggio, C.; Vochok, W.J. Radiometric scene normalization using pseudo-invariant features. Remote Sens. Environ. 1988, 26, 1–16. [Google Scholar] [CrossRef]
- Poursanidis, D.; Topouzelis, K.; Chrysoulakis, N. Mapping coastal marine habitats and delineating the deep limits of the Neptune’s seagrass meadows using Very High Resolution Earth Observation data. Int. J. Remote Sens. 2018. accepted. [Google Scholar]
- Tanhua, T.; Hainbucher, D.; Schroeder, K.; Cardin, V.; Álvarez, M.; Civitarese, G. The Mediterranean Sea system: A review and an introduction to the special issue. Ocean Sci. 2013, 9, 789–803. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman & Hall/CRC: Boca Raton, FL, USA, 1984. [Google Scholar]
- Armstrong, R.A. Remote sensing of submerged vegetation canopies for biomass estimation. Int. J. Remote Sens. 1993, 14, 621–627. [Google Scholar] [CrossRef]
- European Space Agency (ESA). SENTINEL-2 User Handbook; ESA: Paris, France, 2015; p. 64. [Google Scholar]
- Hedley, J.D.; Harborne, A.R.; Mumby, P.J. Technical note: Simple and robust removal of sun glint for mapping shallow-water benthos. Int. J. Remote Sens. 2005, 26, 2107–2112. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Shallow-water bathymetry using combined lidar and passive multispectral scanner data. Int. J. Remote Sens. 1985, 6, 115–125. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Dietz, J.B.; Berkelmans, R.; Andréfouët, S.; Skirving, W.; Strong, A.E.; Tuttle, B.T. Satellite observation of Keppel Islands (Great Barrier Reef) 2002 coral bleaching using IKONOS data. Coral Reefs 2004, 23, 461–462. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Traganos, D.; Reinartz, P. Mapping Mediterranean seagrasses with Sentinel-2. Mar. Pollut. Bull. 2017. [Google Scholar] [CrossRef] [PubMed]
- Dierssen, H.M.; Zimmerman, R.C.; Leathers, R.A.; Downes, T.V.; Davis, C.O. Ocean color remote sensing of seagrass and bathymetry in the Bahamas Banks by high- resolution airborne imagery. Limnol. Oceanogr. 2003, 48, 444–455. [Google Scholar] [CrossRef]
- Hamylton, S.M.; Hedley, J.D.; Beaman, R.J. Derivation of High-Resolution Bathymetry from Multispectral Satellite Imagery: A Comparison of Empirical and Optimisation Methods through Geographical Error Analysis. Remote Sens. 2015, 7, 16257–16273. [Google Scholar] [CrossRef]
- Traganos, D.; Reinartz, P. Interannual Change Detection of Mediterranean Seagrasses Using RapidEye Image Time Series. Front. Plant Sci. 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- TeamSurv, 2018. Available online: https://www.teamsurv.com/ (accessed on 28 Match 2018).
- Hedley, J.D.; Roelfsema, C.M.; Chollett, I.; Harborne, A.R.; Heron, S.F.; Weeks, S.; Skirving, W.J.; Strong, A.E.; Eakin, C.M.; Christensen, T.R.L.; et al. Remote Sensing of Coral Reefs for Monitoring and Management: A Review. Remote Sens. 2016, 8, 118. [Google Scholar] [CrossRef]
- Saylam, K.; Hupp, J.R.; Averett, A.R.; Gutelius, W.F.; Gelhar, B.W. Airborne lidar bathymetry: Assessing quality assurance and quality control methods with Leica Chiroptera examples. Int. J. Remote Sens. 2018, 39, 2518–2542. [Google Scholar] [CrossRef]
- Ierodiaconou, D.; Schimel, A.C.G.; Kennedy, D.; Rattray, A. Combining pixel and object based image analysis of ultra-high resolution multibeam bathymetry and backscatter for habitat mapping in shallow marine waters. Mar. Geophys. Res. 2018, 39, 271. [Google Scholar] [CrossRef]
- International Hydrographic Organization. Guidance on Crowdsourced Bathymetry; IHO, Monaco Cedex, 2018; p. 55. Available online: https://www.iho.int/iho_pubs/draft_pubs/CSB-Guidance_Document-Ed1.0.0.pdf (accessed on 20 April 2018).
- BioBase, 2018. Available online: https://www.cibiobase.com/ (accessed on 28 Match 2018).
- Nippon Foundation-GEBCO, 2018. Available online: https://seabed2030.gebco.net/ (accessed on 2 May 2018).
- White, J.C.; Wulder, M.A.; Hobart, G.W.; Luther, J.E.; Hermosilla, T.; Griffiths, P.; Coops, N.C.; Hall, R.J.; Hostert, P.; Dyk, A.; et al. Pixel-based image compositing for large-area dense time series applications and science. Can. J. Remote Sens. 2014, 40, 192–212. [Google Scholar] [CrossRef]
- Lee, Z.P.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters: 2. Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef] [PubMed]
- Danilo, C.; Melgani, F. Wave period and coastal bathymetry using wave propagation on optical images. IEEE Trans. Geosci. Remote Sens. 2016, 54. [Google Scholar] [CrossRef]
- Collin, A.; Hench, J.L.; Pastol, Y.; Planes, S.; Thiault, L.; Schmitt, R.J.; Holbrook, S.J.; Davies, N.; Troyer, M. High resolution topobathymetry using a Pleiades-1 triplet: Moorea Island in 3D. Remote Sens. Environ. 2018, 208, 109–119. [Google Scholar] [CrossRef]
- Poursanidis, D.; Chrysoulakis, N. Remote Sensing, natural hazards and the contribution of ESA Sentinels missions. Remote Sens. Appl. Soc. Environ. 2017, 6, 25–38. [Google Scholar] [CrossRef]
| Survey Site | National Samaria Park (Training) | Apokoronas (Validation) | Thermaikos Gulf (Validation) |
|---|---|---|---|
| Survey area (km2) | 46.3 | 1.3 | 20.6 |
| Number of in situ points | 4978 (25-m models) 3230 (12-m models) | 1557 | 53 |
| Depth range and intervals of in situ points (m) | 0–25: 0–5 (675), 5–10 (1998), 10–15 (1247), 15–20 (659), 20–25 (399) 0–12: 10–12 (556) | 0–25: 0–5 (57), 5–10 (301), 10–15 (428), 15–20 (517), 20–25 (254) | 0–12 0–5 (25), 5–10 (26), 10–15 (2) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Traganos, D.; Poursanidis, D.; Aggarwal, B.; Chrysoulakis, N.; Reinartz, P. Estimating Satellite-Derived Bathymetry (SDB) with the Google Earth Engine and Sentinel-2. Remote Sens. 2018, 10, 859. https://doi.org/10.3390/rs10060859
Traganos D, Poursanidis D, Aggarwal B, Chrysoulakis N, Reinartz P. Estimating Satellite-Derived Bathymetry (SDB) with the Google Earth Engine and Sentinel-2. Remote Sensing. 2018; 10(6):859. https://doi.org/10.3390/rs10060859
Chicago/Turabian StyleTraganos, Dimosthenis, Dimitris Poursanidis, Bharat Aggarwal, Nektarios Chrysoulakis, and Peter Reinartz. 2018. "Estimating Satellite-Derived Bathymetry (SDB) with the Google Earth Engine and Sentinel-2" Remote Sensing 10, no. 6: 859. https://doi.org/10.3390/rs10060859
APA StyleTraganos, D., Poursanidis, D., Aggarwal, B., Chrysoulakis, N., & Reinartz, P. (2018). Estimating Satellite-Derived Bathymetry (SDB) with the Google Earth Engine and Sentinel-2. Remote Sensing, 10(6), 859. https://doi.org/10.3390/rs10060859








