Vegetation Response to the 2012–2014 California Drought from GPS and Optical Measurements
Abstract
:1. Introduction
2. Materials and Methods
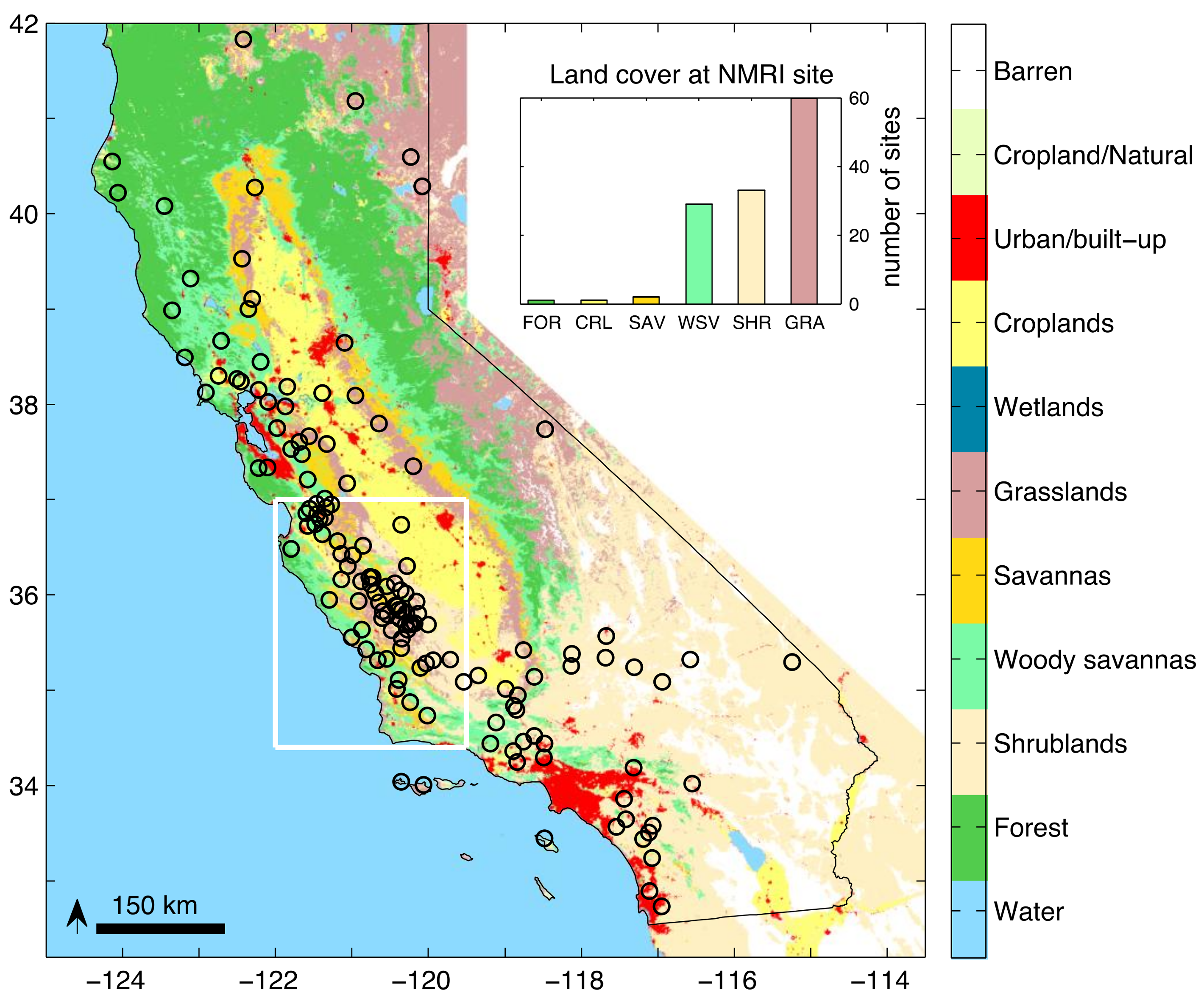
2.1. Study Area
2.2. NMRI
2.3. NDVI
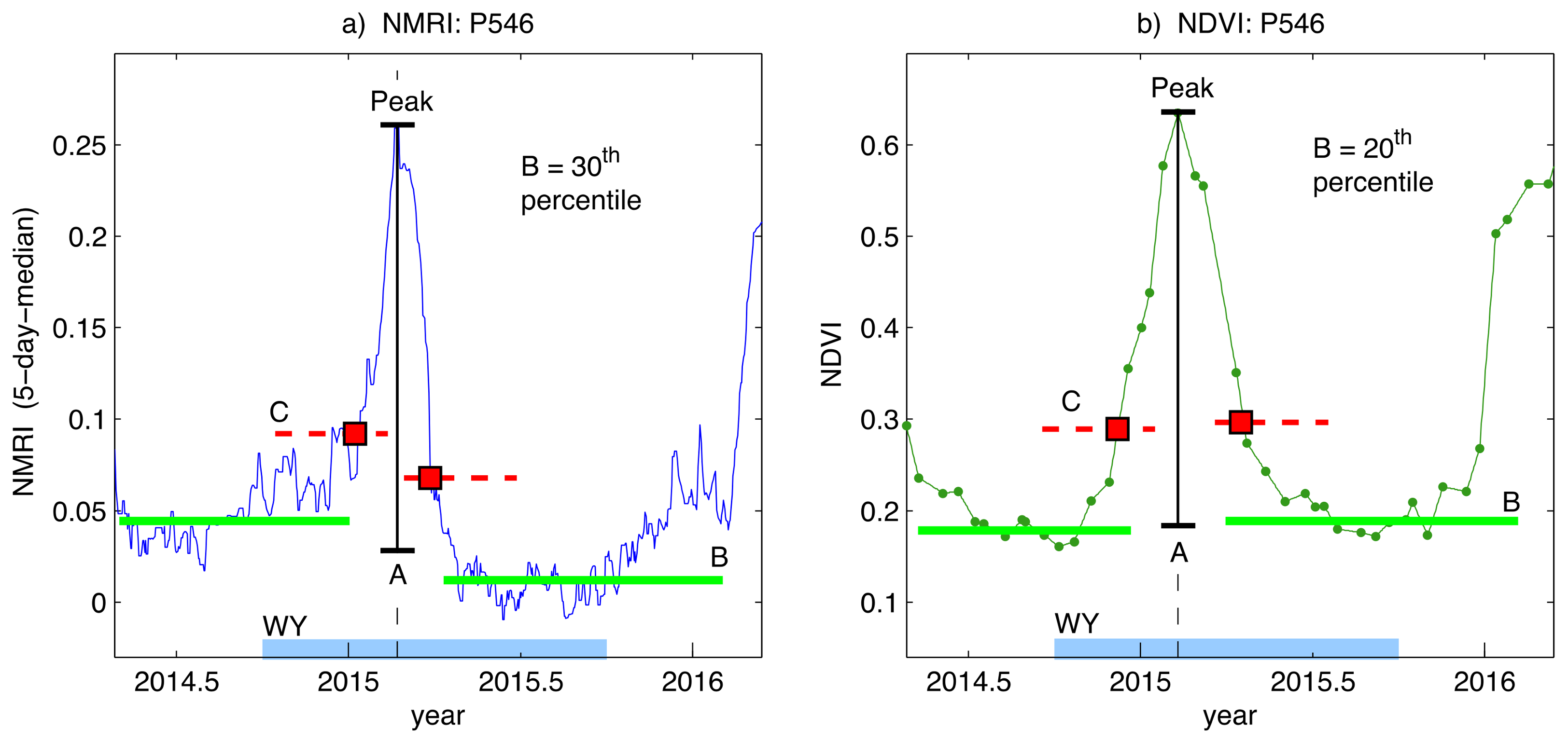
2.4. Phenology Analysis of NMRI and NDVI Data
3. Results
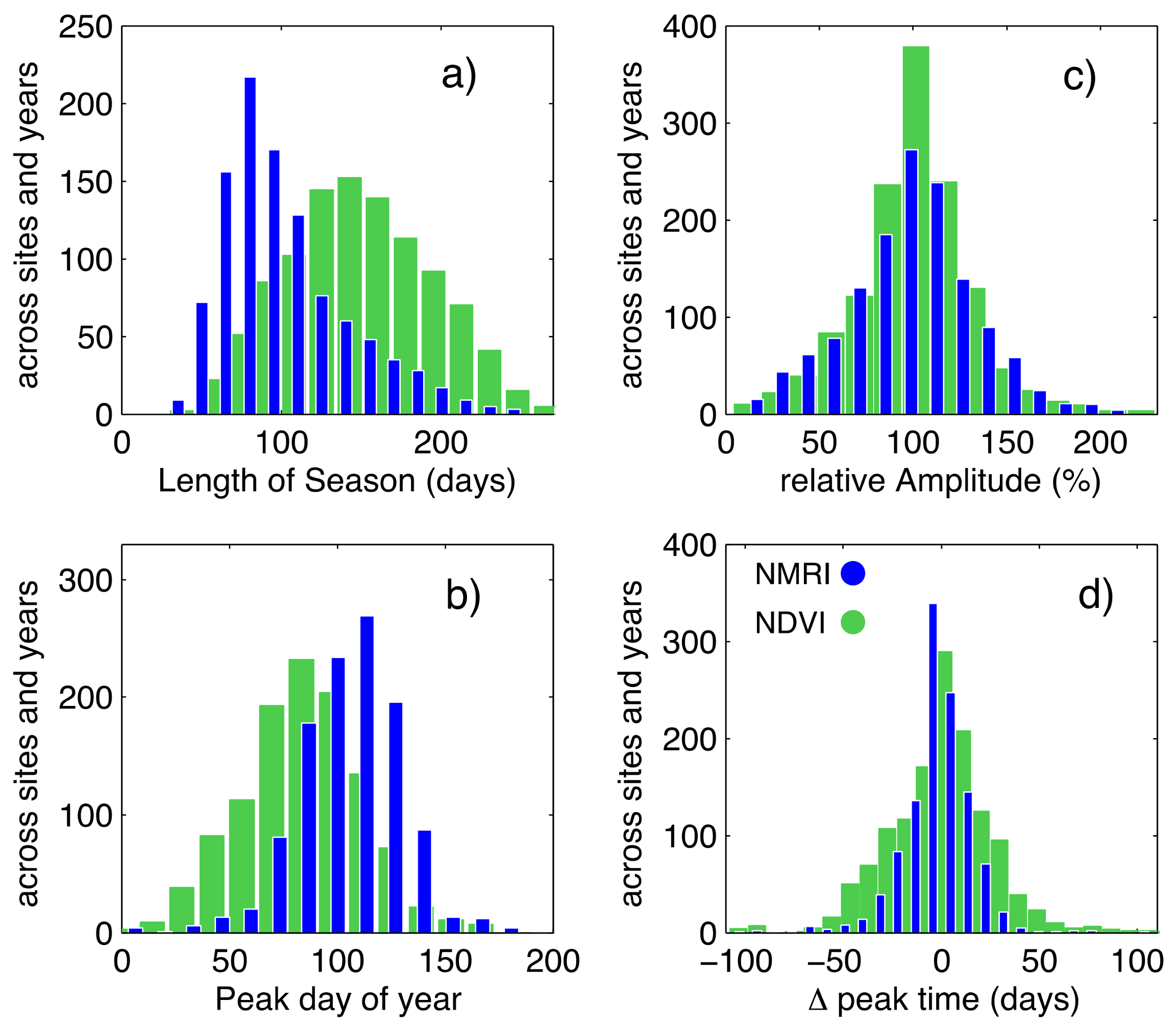
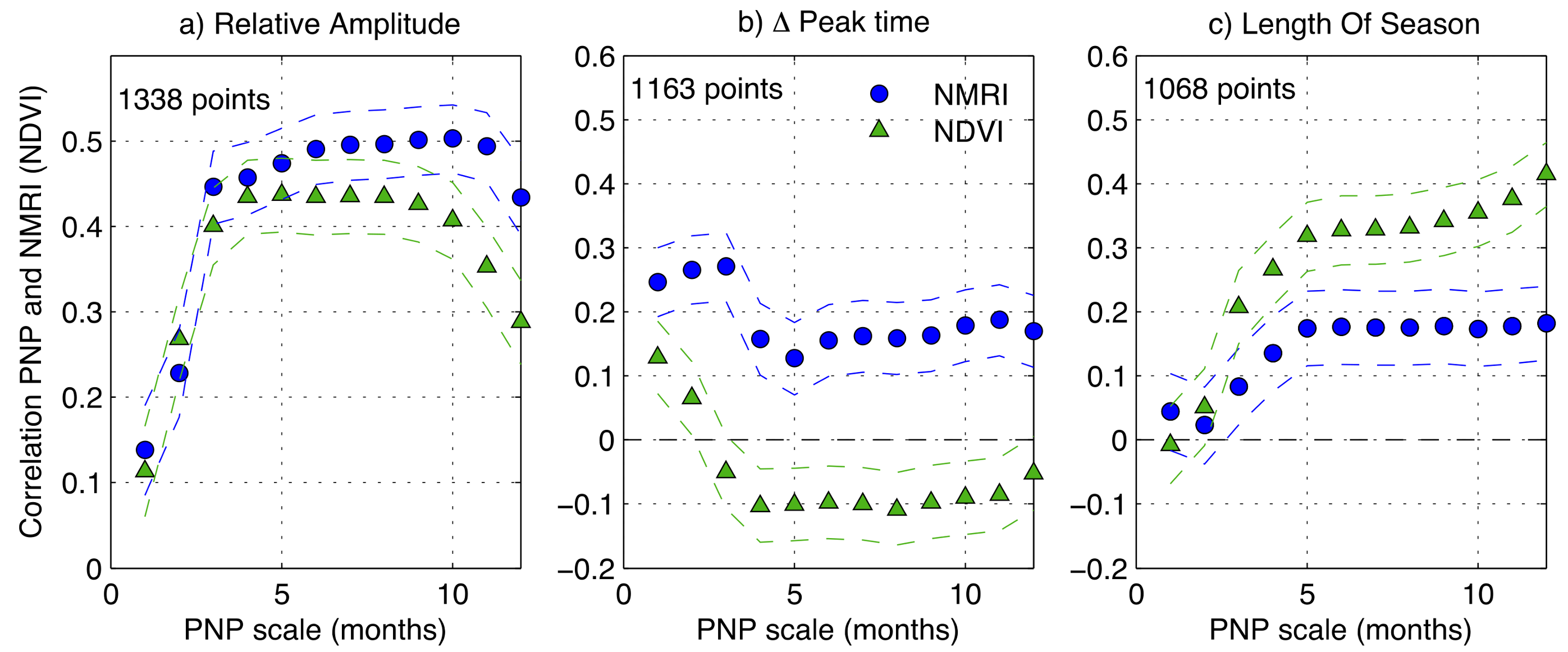
3.1. General Comparison of Phenology Analysis
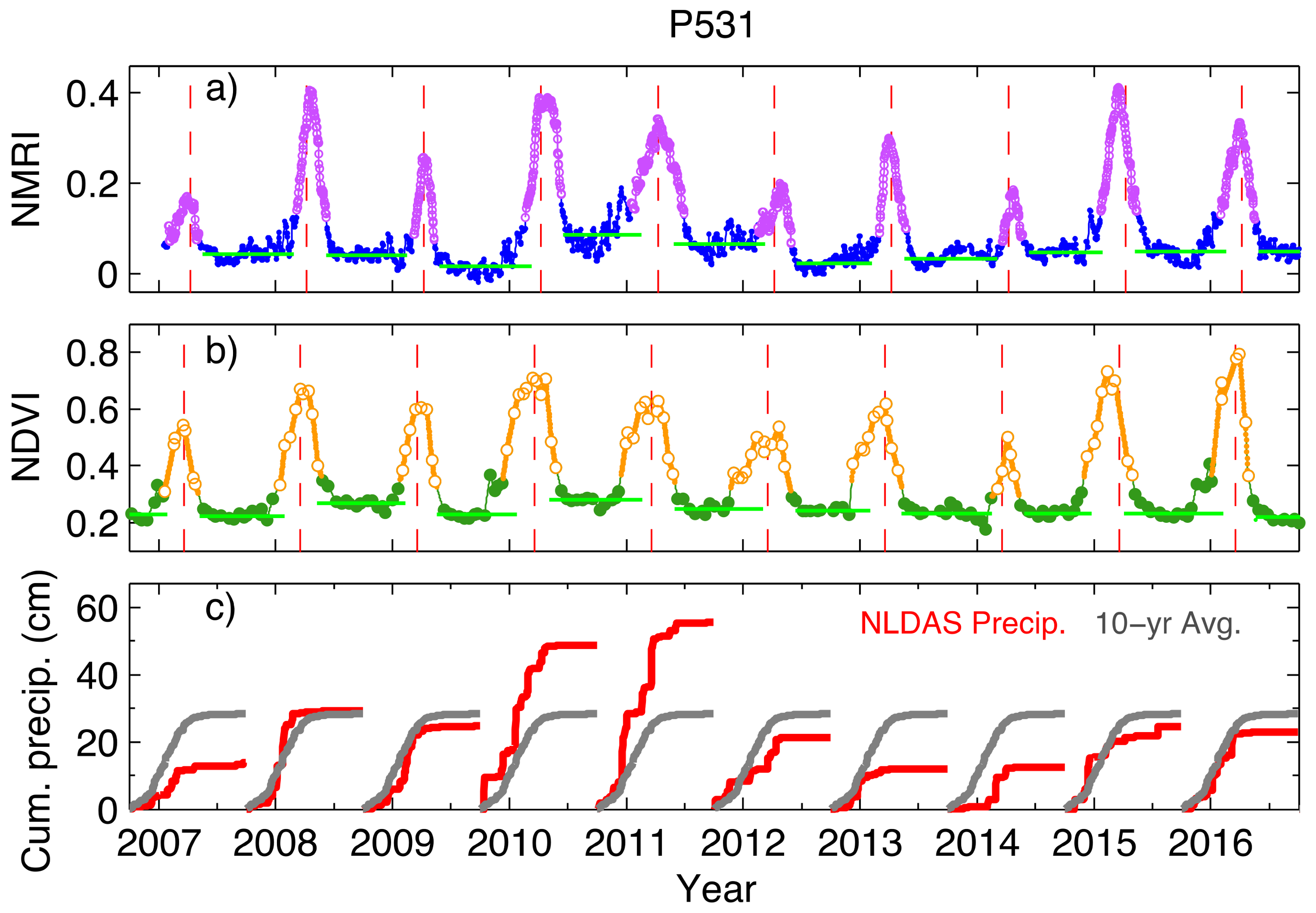
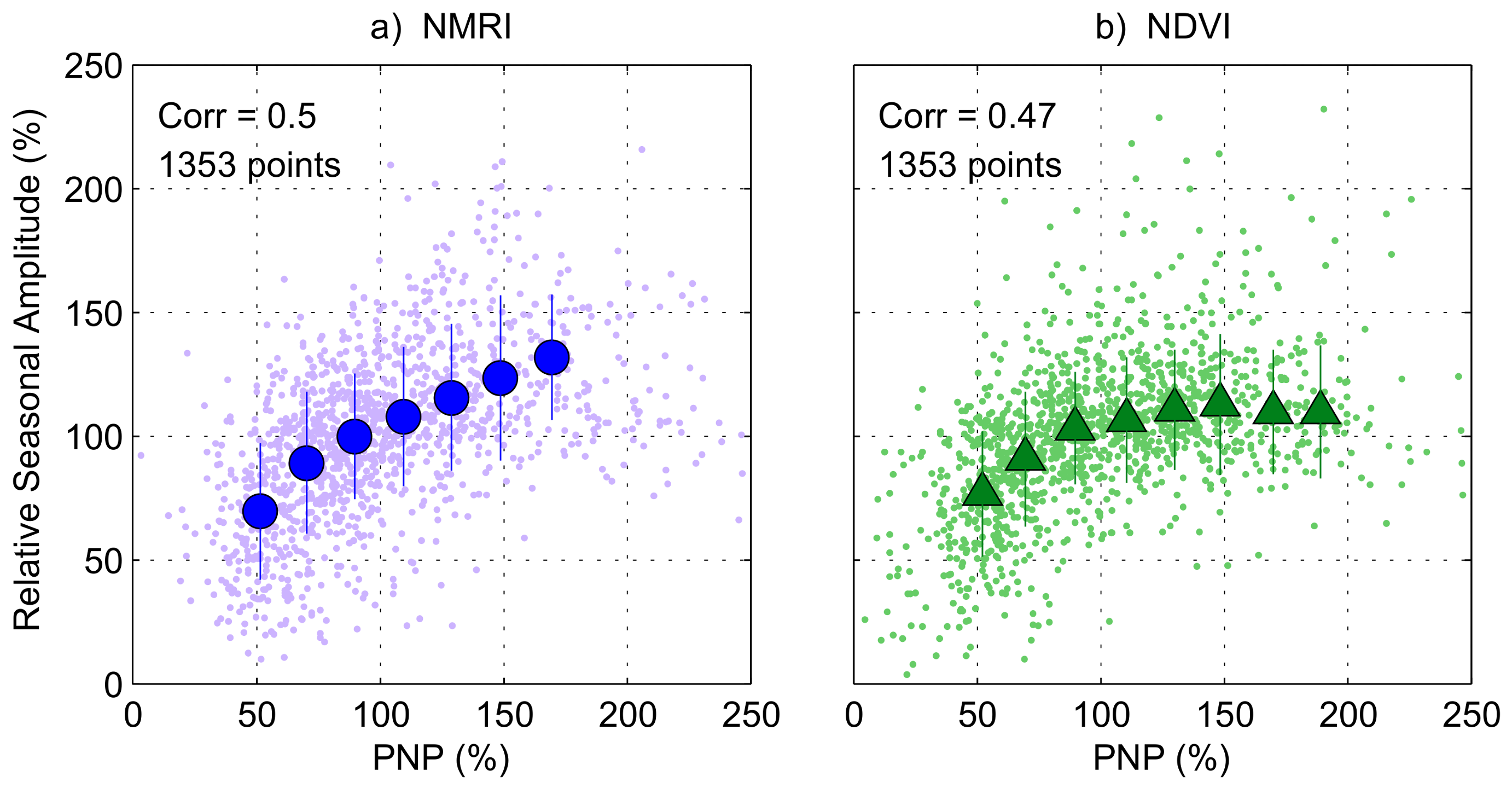
3.2. Link to Drought at the Site Level
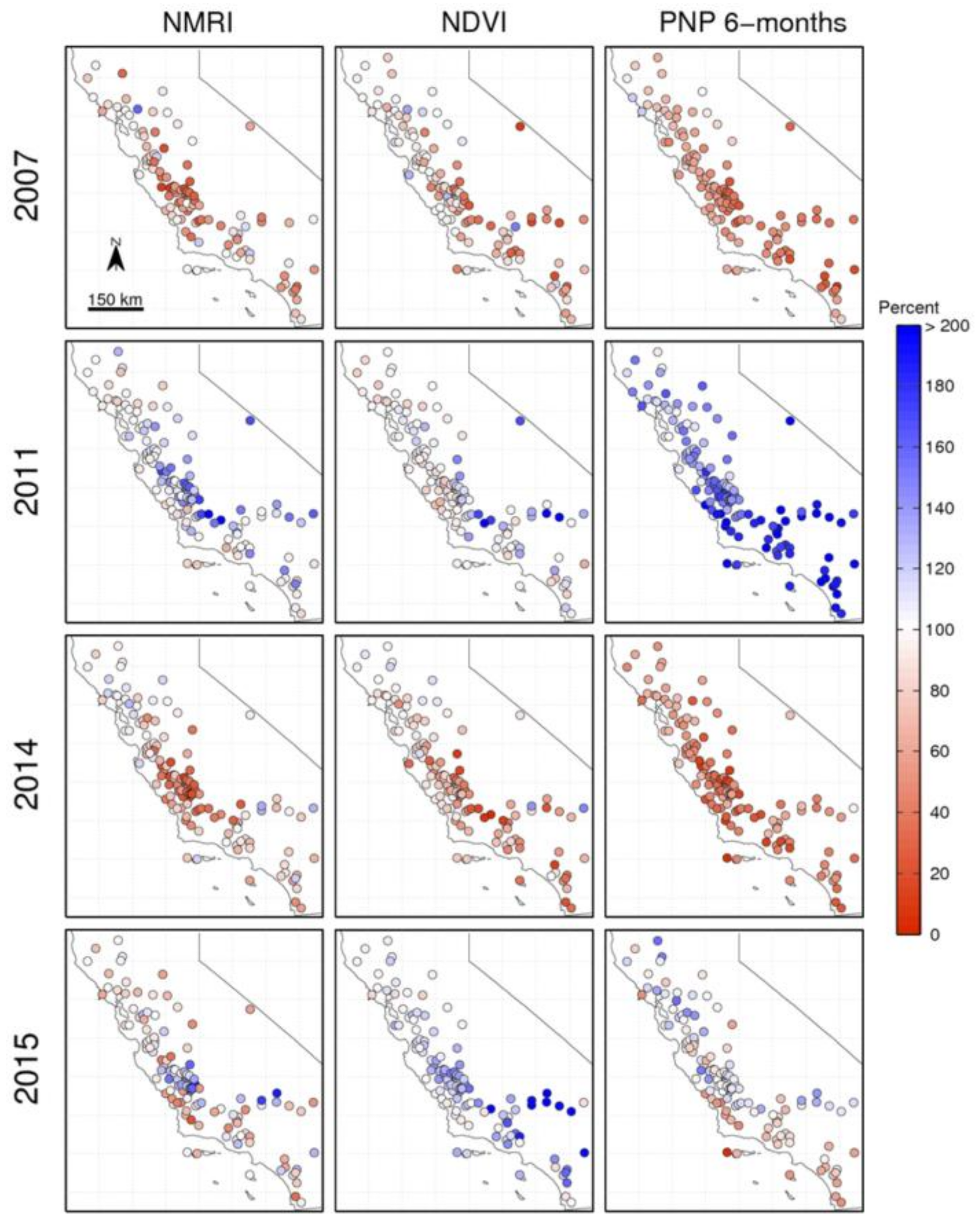
3.3. Spatial Patterns in Dry and Wet Years
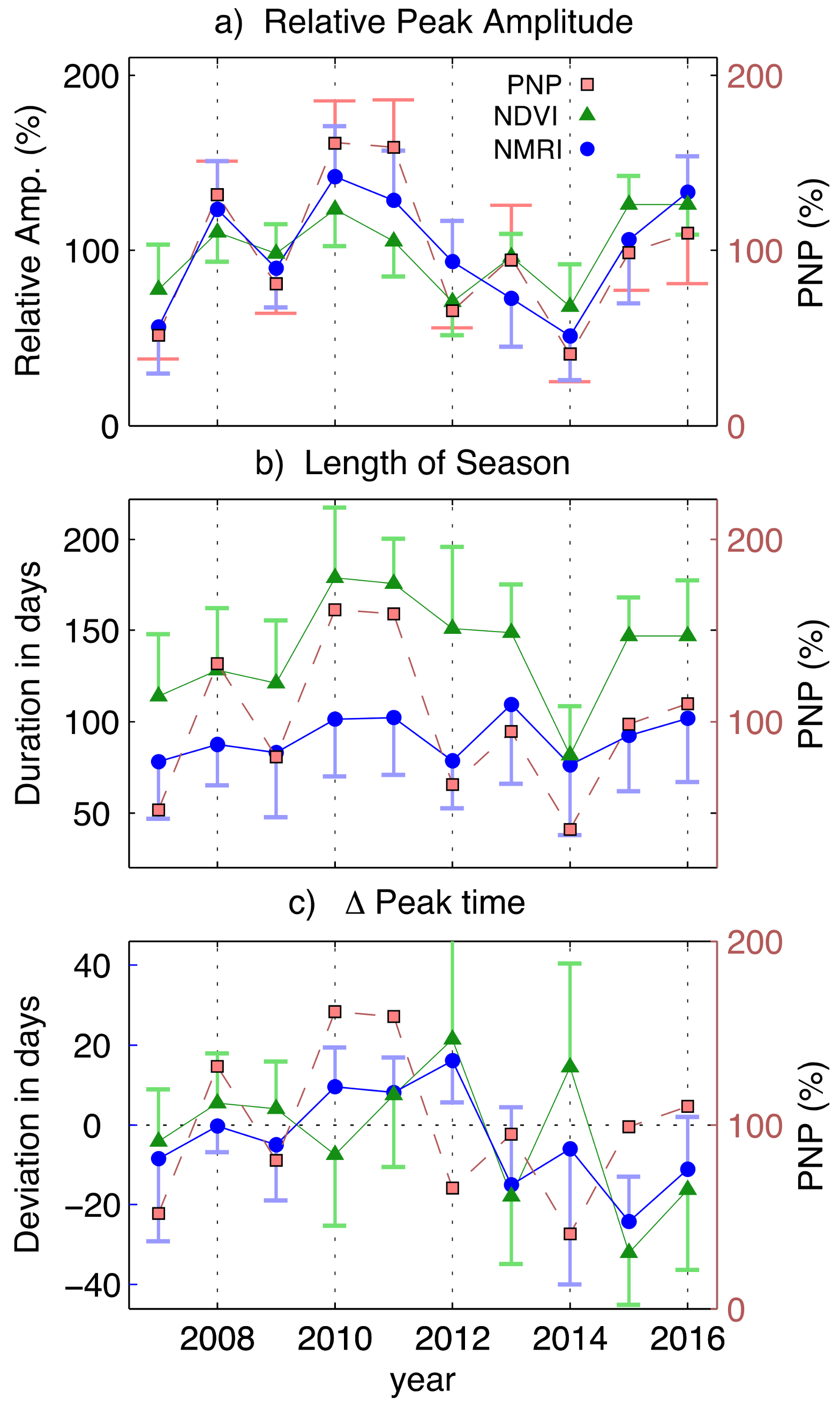
3.4. Regional-Scale Fluctuations in Precipitation and Vegetation
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Asner, G.P.; Brodrick, P.G.; Anderson, C.B.; Vaughn, N.; Knapp, D.R.; Martin, R.E. Progressive forest canopy water loss during the 2012-2015 California drought. Proc. Natl. Acad. Sci. USA 2016, 113, E249–E255. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.P.; Meng, X.H.; McCabe, M.F. Land surface albedo and vegetation feedbacks enhanced the millennium drought in South-East Australia. Hydrol. Earth Syst. Sci. 2017, 21, 409–422. [Google Scholar] [CrossRef]
- Ji, L.; Peters, A.J. Assessing vegetation response to drought in the northern Great Plains using vegetation and drought indices. Remote Sens. Environ. 2004, 87, 85–98. [Google Scholar] [CrossRef]
- Breshears, D.D.; Cobb, N.S.; Rich, P.M.; Price, K.P.; Allen, C.D.; Balice, R.G.; Romme, W.H.; Kastens, J.H.; Floyd, M.L.; Belnap, J.; et al. Regional vegetation die-off in response to global-change-type drought. Proc. Natl. Acad. Sci. USA 2005, 102, 15144–15148. [Google Scholar] [CrossRef] [PubMed]
- Malone, S.L.; Tulbure, M.G.; Perez-Luque, A.J.; Assal, T.J.; Bremer, L.L.; Drucker, D.P.; Hillis, V.; Varela, S.; Goulden, M.L. Drought resistance across California ecosystems: Evaluating changes in carbon dynamics using satellite imagery. Ecosphere 2016, 7, e01561. [Google Scholar] [CrossRef]
- Wang, J.; Rich, P.M.; Price, K.P. Temporal responses of NDVI to precipitation and temperature in the central Great Plains, USA. Int. J. Remote Sens. 2003, 24, 2345–2364. [Google Scholar] [CrossRef]
- Tucker, C.J.; Choudhury, B.J. Satellite remote sensing of drought conditions. Remote Sens. Environ. 1987, 23, 243–251. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Chen, D.Y.; Huang, J.F.; Jackson, T.J. Vegetation water content estimation for corn and soybeans using spectral indices derived from MODIS near- and short-wave infrared bands. Remote Sens. Environ. 2005, 98, 225–236. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Serrano, L.; Filella, I.; Penuelas, J. Remote sensing of biomass and yield of winter wheat under different nitrogen supplies. Crop Sci. 2000, 40, 723–731. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Wilson, E.A. Microwave attenuation properties of vegetation canopies. IEEE TGRS 1985, 23, 746–753. [Google Scholar] [CrossRef]
- Jones, M.O.; Jones, L.A.; Kimball, J.S.; McDonald, K.C. Satellite passive microwave remote sensing for monitoring global land surface phenology. Remote Sens. Environ. 2011, 115, 1102–1114. [Google Scholar] [CrossRef]
- Liu, Y.Y.; de Jeu, R.A.M.; McCabe, M.F.; Evans, J.P.; van Dijk, A. Global long-term passive microwave satellite-based retrievals of vegetation optical depth. Geophys. Res. Lett. 2011, 38, L18402. [Google Scholar] [CrossRef]
- Jones, M.; Kimball, J.; Small, E.E.; Larson, K.M. Comparing Land Surface Phenology Derived from Satellite and GPS Network Microwave Remote Sensing. Int. J. Biometeorol. 2014, 58, 1305–1315. [Google Scholar] [CrossRef] [PubMed]
- Konings, A.G.; Piles, M.; Das, N.; Entekhabi, D. L-band vegetation optical depth and effective scattering albedo estimation from SMAP. Remote Sens. Environ. 2017, 198, 460–470. [Google Scholar] [CrossRef]
- Tian, F.; Brandt, M.; Liu, Y.Y.; Verger, A.; Tagesson, T.; Diouf, A.A.; Rasmussedn, K.; Mbow, C.; Wang, Y.; Fensholt, R. Remote sensing of vegetation dynamics in drylands: Evaluating vegetation optical depth (VOD) using AVHRR NDVI and in situ green biomass data over West African Sahel. Remote Sens. Environ. 2016, 177, 265–276. [Google Scholar] [CrossRef]
- Hill, M.J.; Donald, G.E.; Vickery, P.J. Relating radar backscatter to biophysical properties of temperate perennial grassland. Remote Sens. Environ. 1999, 67, 15–31. [Google Scholar] [CrossRef]
- Paloscia, S.; Macelloni, G.; Pampaloni, P.; Santi, E. The contribution of multitemporal SAR data in assessing hydrological parameters. IEEE Geosci. Remote Sens. Lett. 2004, 1, 201–205. [Google Scholar] [CrossRef]
- Kim, Y.; Jackson, T.; Bindlish, R.; Lee, H.; Hong, S. Radar Vegetation Index for Estimating the Vegetation Water Content of Rice and Soybean. IEEE Geosci. Remote Sens. Lett. 2012, 9, 564–568. [Google Scholar] [CrossRef]
- Bousbih, S.; Zribi, M.; Lili-Chabaane, Z.; Baghdadi, N.; El Hajj, M.; Gao, Q.; Mougenot, B. Potential of Sentinel-1 Radar Data for the Assessment of Soil and Cereal Cover Parameters. Sensors 2017, 17, 2617. [Google Scholar] [CrossRef] [PubMed]
- Larson, K.M.; Small, E.E. Normalized Microwave Reflection Index, I: A Vegetation Measurement Derived from GPS Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1501–1511. [Google Scholar] [CrossRef]
- Small, E.E.; Larson, K.M.W.; Smith, W. Normalized Microwave Reflection Index, II: Validation of Vegetation Water Content Estimates at Montana Grasslands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1512–1521. [Google Scholar] [CrossRef]
- Larson, K.M. GPS Interferometric Reflectometry: Applications to Surface Soil Moisture, Snow Depth, and Vegetation Water Content in the Western United States. WIREs Water 2016, 3, 775–787. [Google Scholar] [CrossRef]
- He, X.; Wada, Y.; Wanders, N.; Sheffield, J. Human water management intensifies hydrological drought in California. Geophys. Res. Lett. 2017, 44, 1777–1785. [Google Scholar] [CrossRef]
- Thomas, B.F.; Famiglietti, J.S.; Landerer, F.W.; Wiese, D.N.; Molotch, N.P.; Argus, D.F. GRACE Groundwater Drought Index: Evaluation of California Central Valley groundwater drought. Remote Sens. Environ. 2017, 198, 384–392. [Google Scholar] [CrossRef]
- Berg, N.; Hall, A. Anthropogenic warming impacts on California snowpack during drought. Geophys. Res. Lett. 2017, 44, 2511–2518. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Cheng, L.; Mazdiyasni, O.; Farahmand, A. Global warming and changes in risk of concurrent climate extremes: Insights from the 2014 California drought. Geophys. Res. Lett. 2014, 41, 8847–8852. [Google Scholar] [CrossRef]
- Luo, L.F.; Apps, D.; Arcand, S.; Xu, H.T.; Pan, M.; Hoerling, M. Contribution of temperature and precipitation anomalies to the California drought during 2012–2015. Geophys. Res. Lett. 2017, 44, 3184–3192. [Google Scholar] [CrossRef]
- Potter, C. Assessment of the immediate impacts of the 2013–2014 drought on ecosystems of the California central coast. West. N. Am. Nat. 2015, 75, 129–145. [Google Scholar] [CrossRef]
- Coates, A.R.; Dennison, P.E.; Roberts, D.A.; Roth, K.L. Monitoring the Impacts of Severe Drought on Southern California Chaparral Species using Hyperspectral and Thermal Infrared Imagery. Remote Sens. 2015, 7, 14276–14291. [Google Scholar] [CrossRef]
- Rao, M.; Silber-Coats, Z.; Powers, S.; Fox, L.; Ghulam, A. Mapping drought-impacted vegetation stress in California using remote sensing. GIScience Remote Sens. 2017, 54, 185–201. [Google Scholar] [CrossRef]
- Evans, S.G.; Small, E.E.; Larson, K.M. Comparison of vegetation phenology in the western United States from reflected GPS microwave signals and NDVI. Int. J. Remote Sens. 2014, 35, 2996–3017. [Google Scholar] [CrossRef]
- Schwartz, M.D.; Ahas, R.; Aasa, A. Onset of spring starting earlier across the Northern Hemisphere. Glob. Chang. Biol. 2006, 12, 343–351. [Google Scholar] [CrossRef]
- Cleland, E.E.; Chuine, I.; Menzel, A.; Mooney, H.A.; Schwartz, M.D. Shifting plant phenology in response to global change. Trends Ecol. Evol. 2007, 22, 357–365. [Google Scholar] [CrossRef] [PubMed]
- Herring, T.A.; Melbourne, T.I.; Murray, M.H.; Floyd, M.A.; Szeliga, W.M.; King, R.W.; Phillips, D.A.; Puskas, C.M.; Santillan, M.; Wang, L. Plate Boundary Observatory and related networks: GPS data analysis methods and geodetic products. Rev. Geophys. 2016, 54, 759–808. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.; Bilich, A.; Braun, J.; Zavorotny, V. Use of GPS receivers as a soil moisture network for water cycle studies. Geophys. Res. Lett. 2008, 35, L24405. [Google Scholar] [CrossRef]
- Larson, K.M.; Gutmann, E.; Zavorotny, V.; Braun, J.; Williams, M.; Nievinski, F. Can We Measure Snow Depth with GPS Receivers? Geophys. Res. Lett. 2009, 36, L17502. [Google Scholar] [CrossRef]
- Small, E.E.; Larson, K.M.; Braun, J.J. Sensing Vegetation Growth with GPS Reflection. Geophys. Res. Lett. 2010, 37, L12401. [Google Scholar] [CrossRef]
- Swets, D.L.; Reed, B.C.; Rowland, J.R.; Marko, S.E. A weighted least-squares approach to temporal smoothing of NDVI. In Proceedings of the 1999 ASPRS Annual Conference, from Image to Information, Portland, OR, USA, 17–21 May 1999. [Google Scholar]
- Xia, Y.; Mitchell, K.; Ek, M.; Sheffield, J.; Cosgrove, B.; Wood, E.; Luo, L.; Alonge, C.; Wei, H.; Meng, J.; et al. (NLDAS-2): 1. Intercomparison and application of model products. J. Geophys. Res. 2012, 117, D03109. [Google Scholar] [CrossRef]
- Daly, C.; Neilson, R.P.; Phillips, D.L. A statistical-topographic model for mapping climatological precipitation over mountainous terrain. J. Appl. Meteorol. 1994, 33, 140–158. [Google Scholar] [CrossRef]
- McKee, T.B.; Doeskin, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology. American Meteorological Society, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Huxman, T.E.; Smith, M.D.; Fay, P.A.; Knapp, A.K.; Shaw, M.R.; Loik, M.E.; Smith, S.D.; Tissue, D.T.; Zak, J.C.; Weltzin, J.F.; et al. Convergence across biomes to a common rain-use efficiency. Nature 2004, 429, 651–654. [Google Scholar] [CrossRef] [PubMed]
- Huete, A.R.; Liu, H.Q.; van Leeuwen, W.J.D. The use of vegetation indices in forested regions: Issues of linearity and saturation. In Proceedings of the IGARSS ’97: 1997 International Geoscience and Remote Sensing Symposium: Remote Sensing—A Scientific Vision for Sustainable Development, Singapore, 3–8 August 1997; pp. 1966–1968. [Google Scholar]
- Chew, C.; Shah, R.; Zuffada, C.; Hajj, G.; Masters, D.; Mannucci, A.J. Demonstrating soil moisture remote sensing with observations from the UK TechDemoSat-1 satellite mission. Geophys. Res. Lett. 2016, 43, 3317–3324. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Small, E.E.; Roesler, C.J.; Larson, K.M. Vegetation Response to the 2012–2014 California Drought from GPS and Optical Measurements. Remote Sens. 2018, 10, 630. https://doi.org/10.3390/rs10040630
Small EE, Roesler CJ, Larson KM. Vegetation Response to the 2012–2014 California Drought from GPS and Optical Measurements. Remote Sensing. 2018; 10(4):630. https://doi.org/10.3390/rs10040630
Chicago/Turabian StyleSmall, Eric E., Carolyn J. Roesler, and Kristine M. Larson. 2018. "Vegetation Response to the 2012–2014 California Drought from GPS and Optical Measurements" Remote Sensing 10, no. 4: 630. https://doi.org/10.3390/rs10040630
APA StyleSmall, E. E., Roesler, C. J., & Larson, K. M. (2018). Vegetation Response to the 2012–2014 California Drought from GPS and Optical Measurements. Remote Sensing, 10(4), 630. https://doi.org/10.3390/rs10040630





