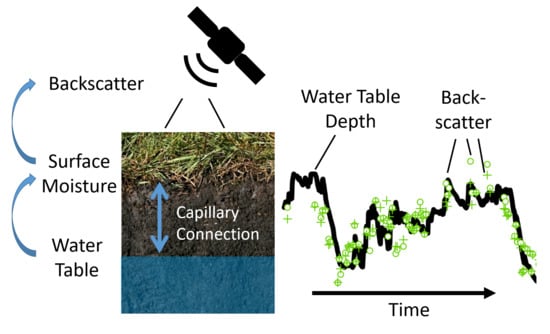
Inferring Water Table Depth Dynamics from ENVISAT-ASAR C-Band Backscatter over a Range of Peatlands from Deeply-Drained to Natural Conditions
Abstract
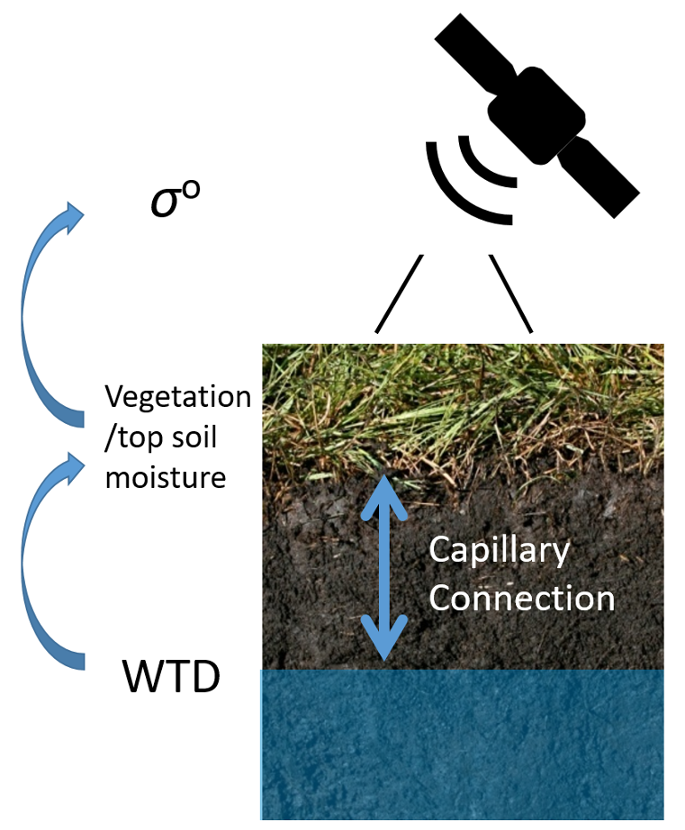
1. Introduction
2. Data
2.1. ENVISAT-ASAR Backscatter Intensity
2.1.1. Environmental Scene Filter
2.2. Ground-Based WTD Data in Peatlands
3. Methodology
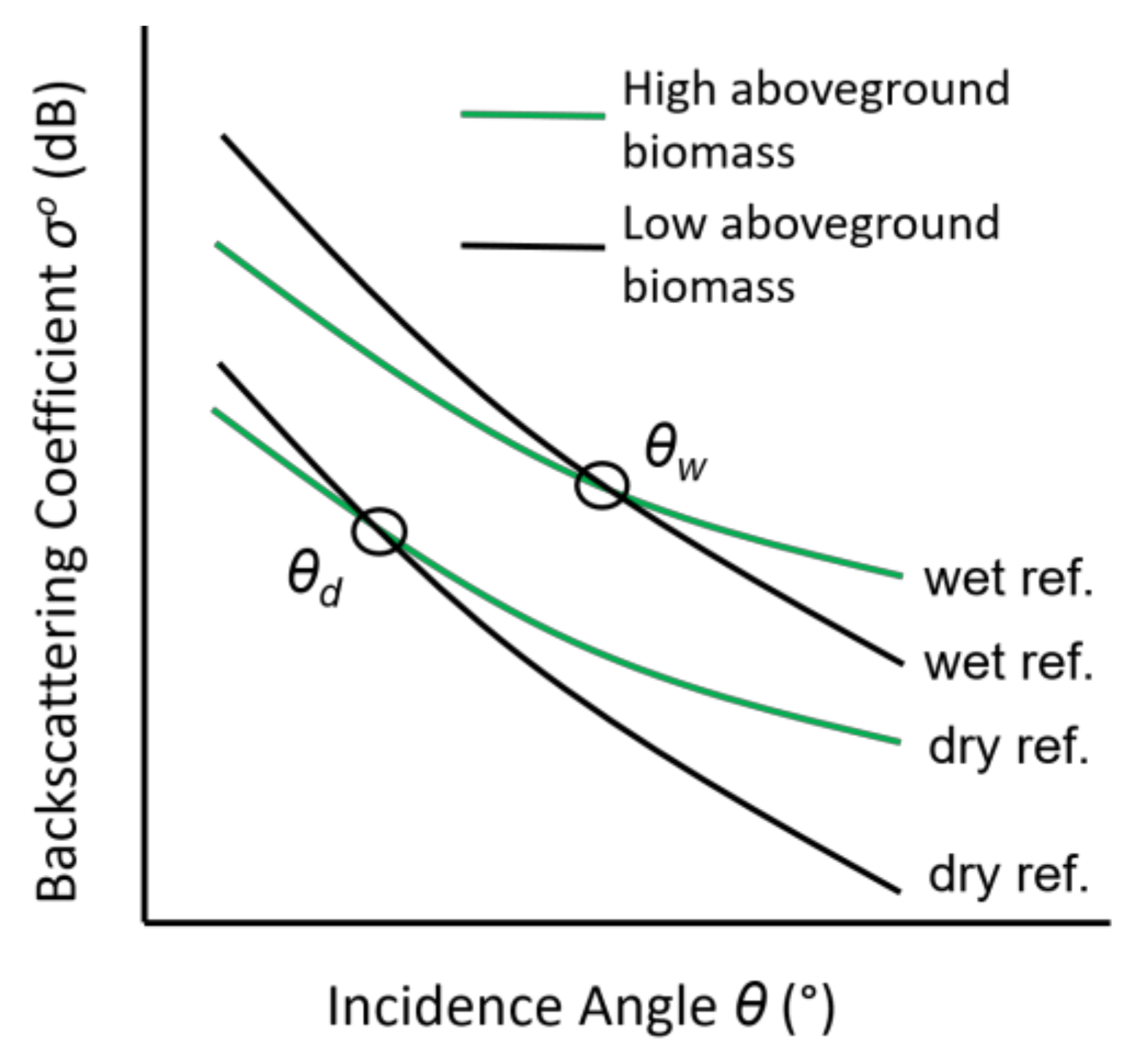
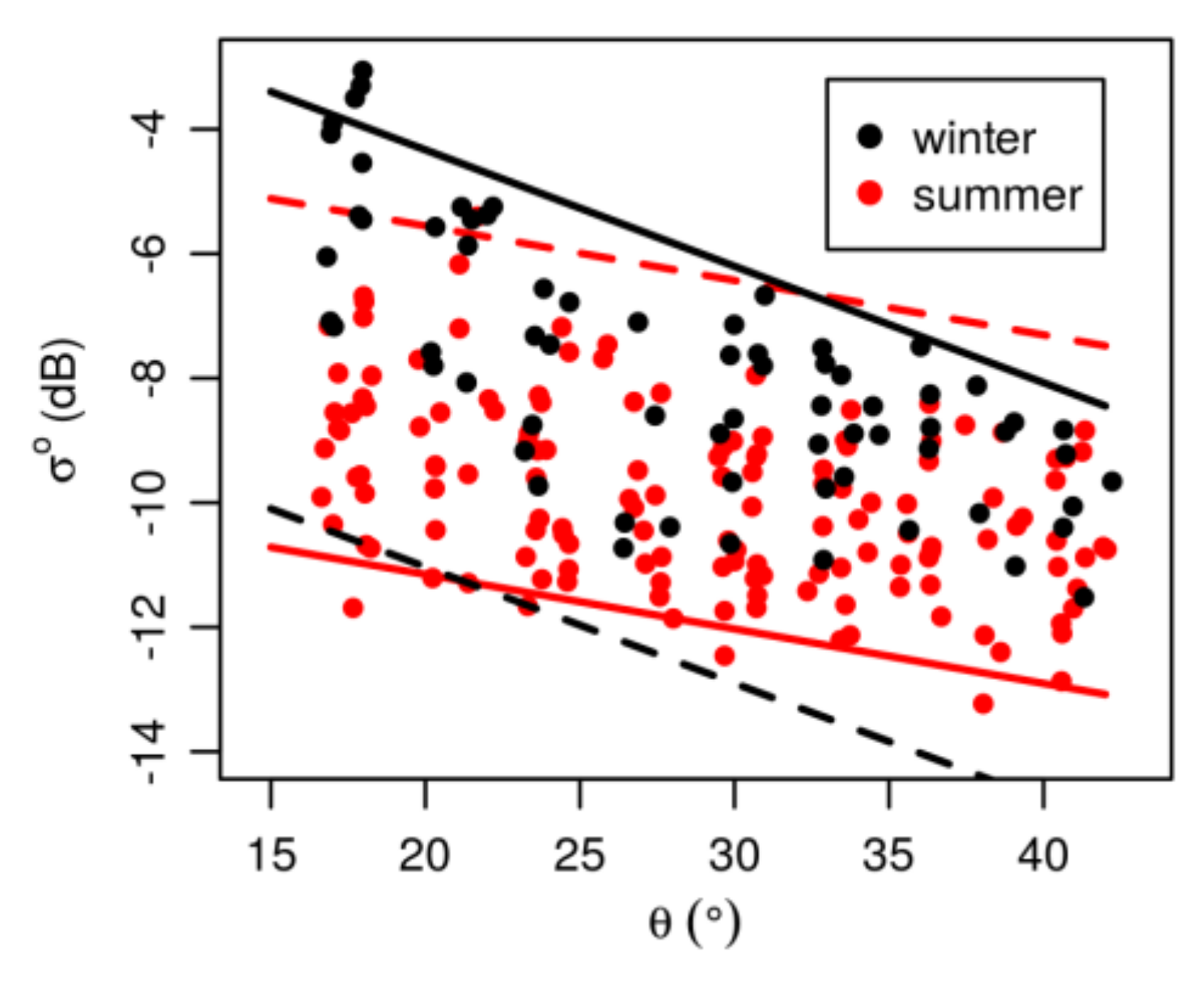
3.1. Incidence Angle Normalization and Cross-Over Angle Concept
3.1.1. Linear Normalization with Constant Site-Specific Slope Parameter (βconst)
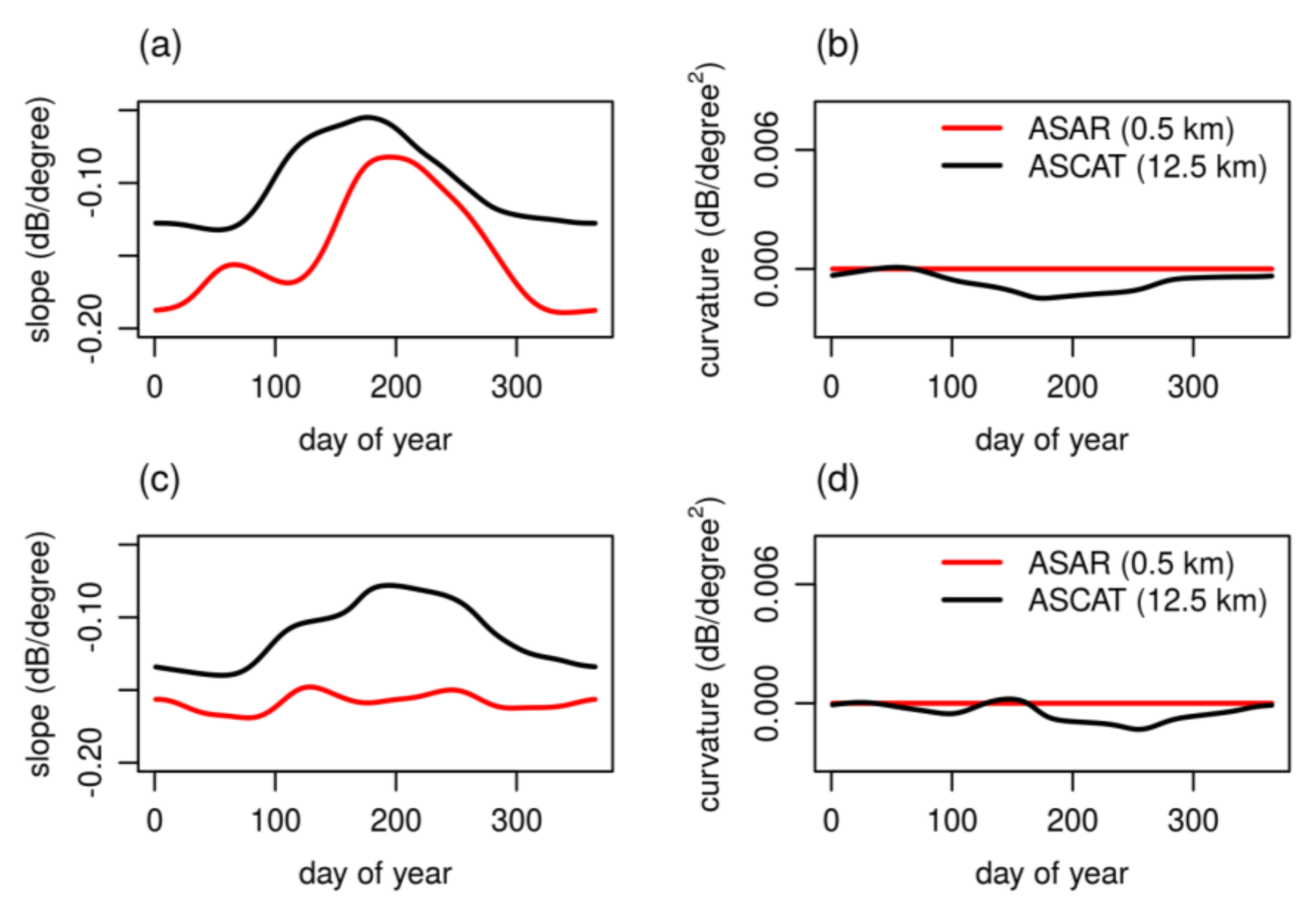
3.1.2. Dynamical Site-Specific Slope (βdoy)
Weighing
Ascending/Descending Incidence Angle Dependency
3.1.3. Cross-Over Angle Concept
3.2. Comparison of Backscatter with WTD Observations
3.2.1. Application of Different Processing Configurations
- UNCOR: Uncorrected backscatter time series neglecting the incidence angle dependency
- CONST: Constant slope normalization (Section 3.1.1) [32]
- COASCAT: Application of the cross-over concept using site-specific βdoy and curvature climatology from the corresponding ASCAT pixels at 12.5 km grid spacing (provided by TU Vienna). Approach as presented in Section 3.1.3, but additionally including curvature values for normalization (see Wagner et al. [18]).
- COASAR: Application of the cross-over concept using site-specific slope climatology βdoy derived from ASAR data (Section 3.1.2).
3.2.2. Skill Metrics
4. Results
4.1. Climatology of Site-Specific Slope Parameter Based on ASAR Data
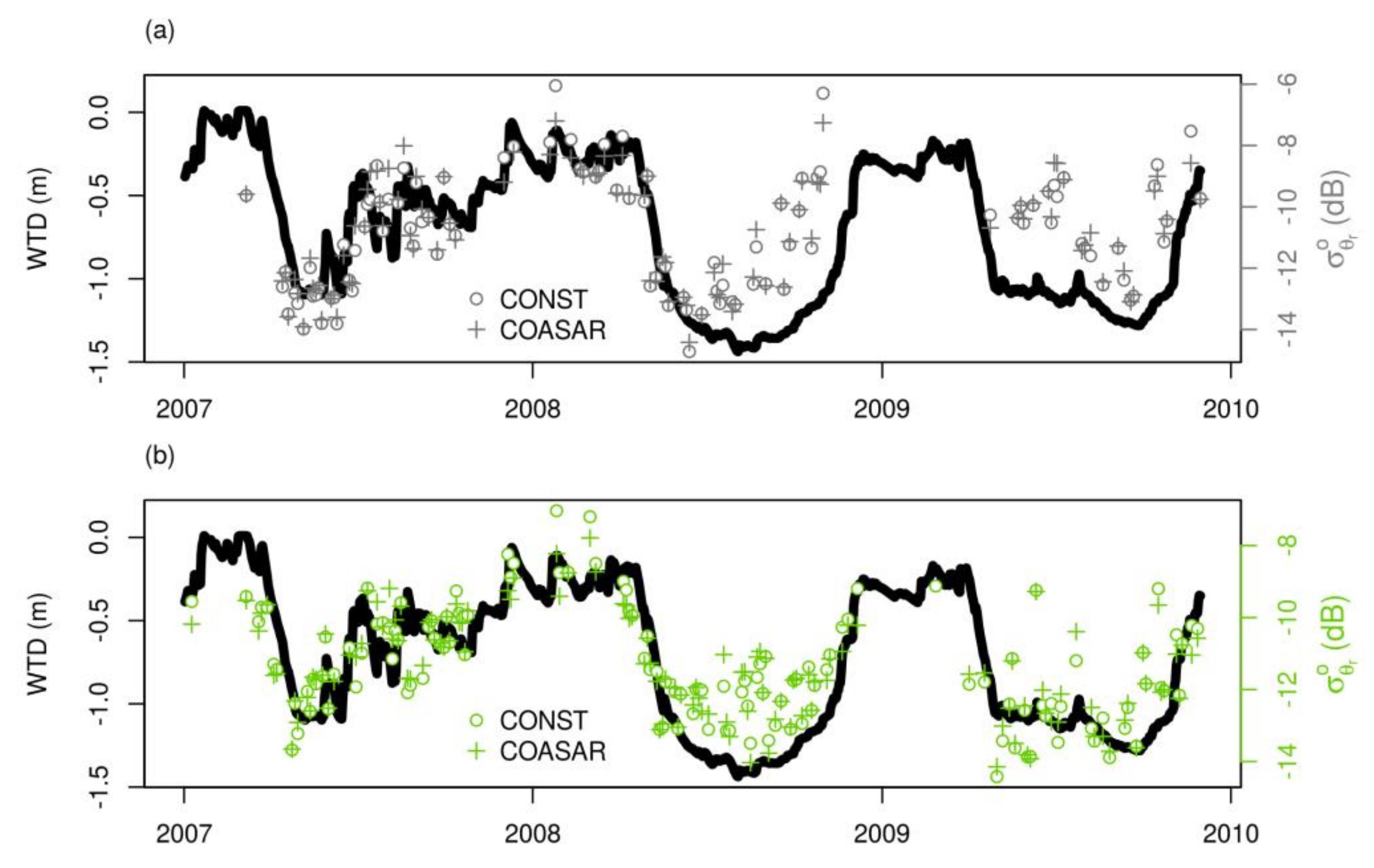
4.2. Comparison of Backscatter and Water Table Depth Time Series
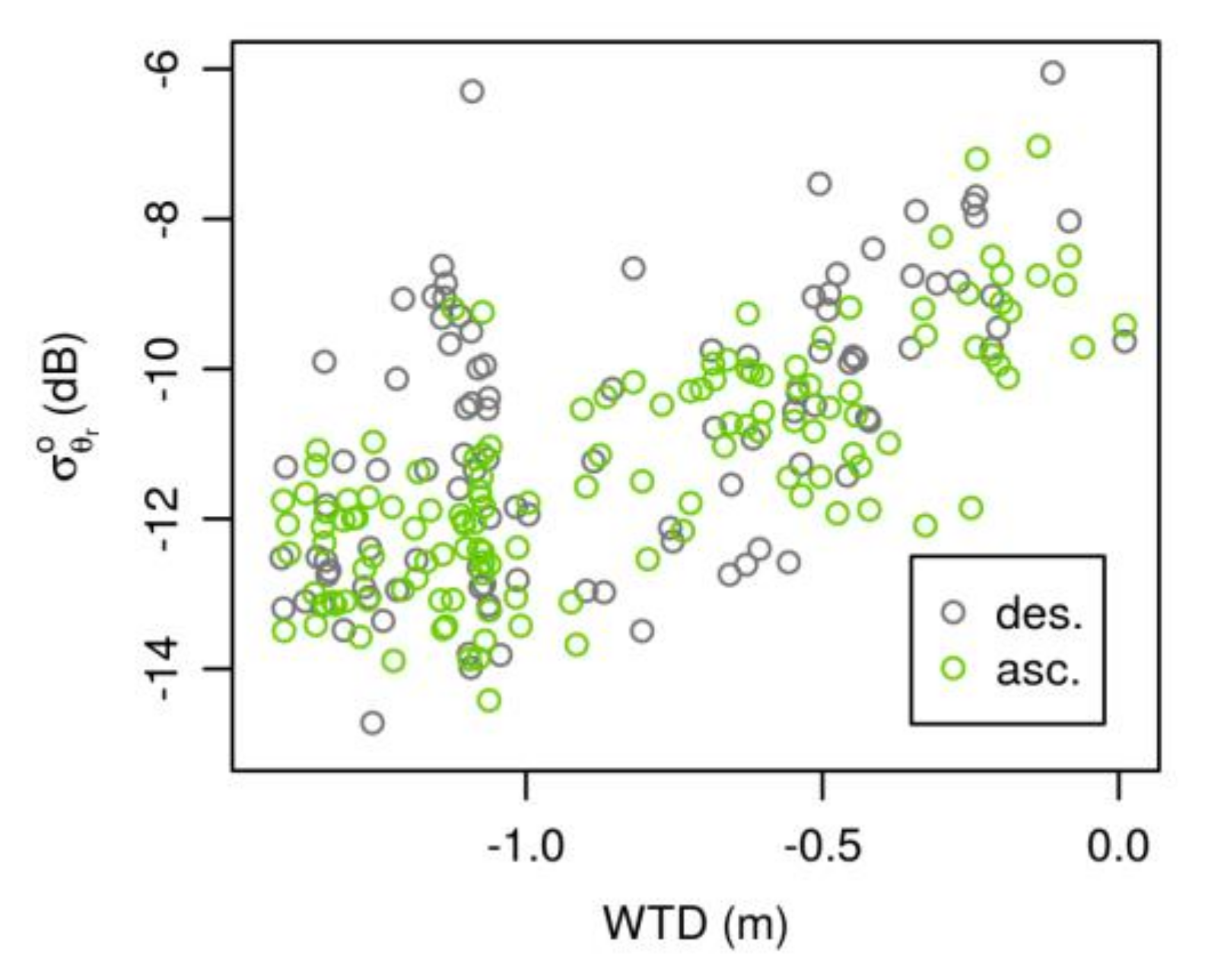
- There is a nearly linear increase of σ° with shallower water tables over most of the observed range of WTD, irrespective of the processing configuration (CONST, COASAR).
- The link between σ° and WTD becomes weaker towards the dry end of WTD. In Figure 6, the dependency seems to vanish at a WTD of approximately −1 m. We could not identify a systematic threshold WTD for all of our sites and, where present, it varied from about −0.5 to 1.5 m.
- The σ° time series enabled to monitor to some degree the interannual variability of WTD dynamics, i.e., anomalous dry or wet periods.
- The differences between descending and ascending σ° time series are remarkable during parts of the year, although not systematic over different sites.
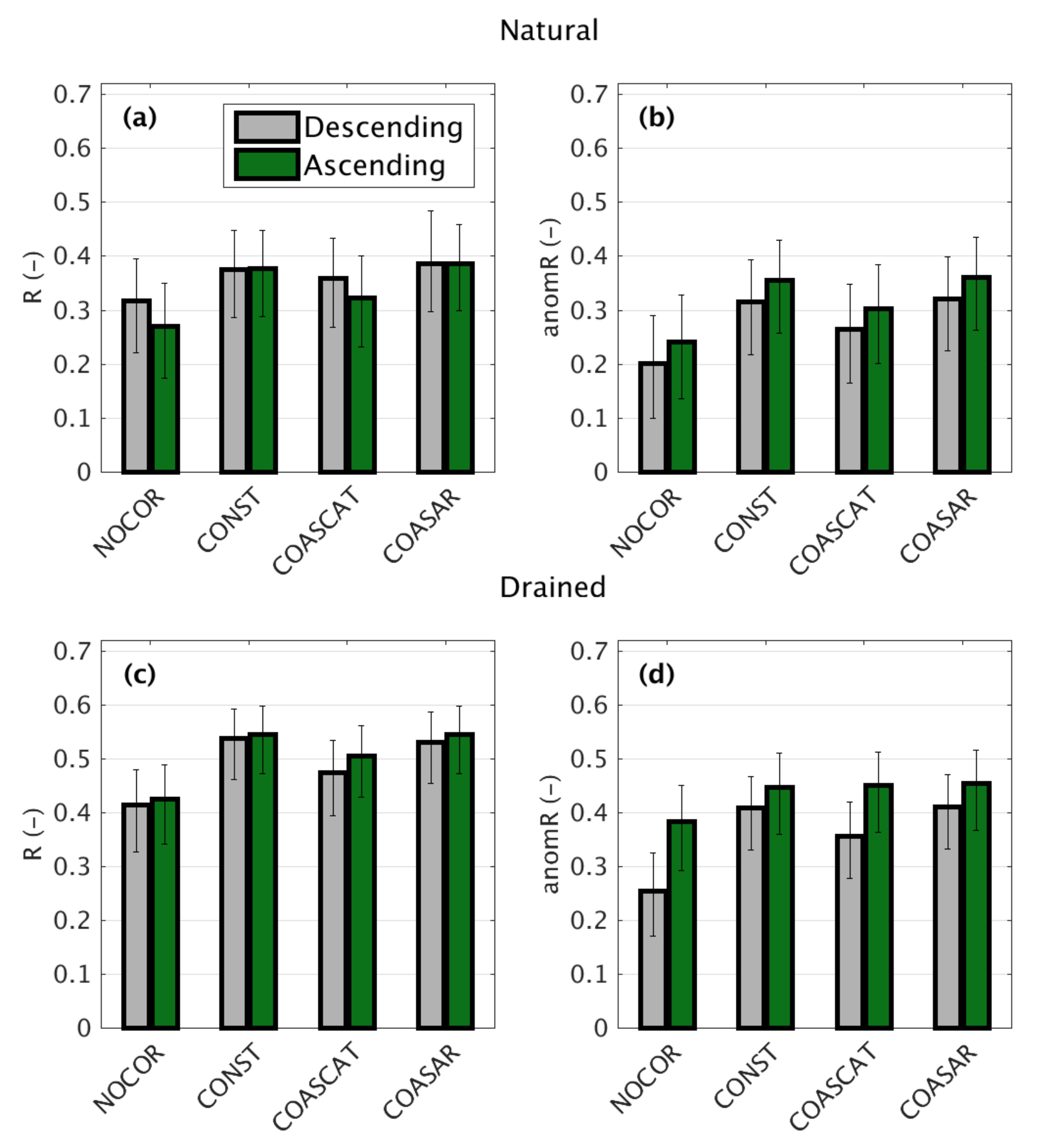
4.3. Skill Metrics for Different Backscatter Time Series
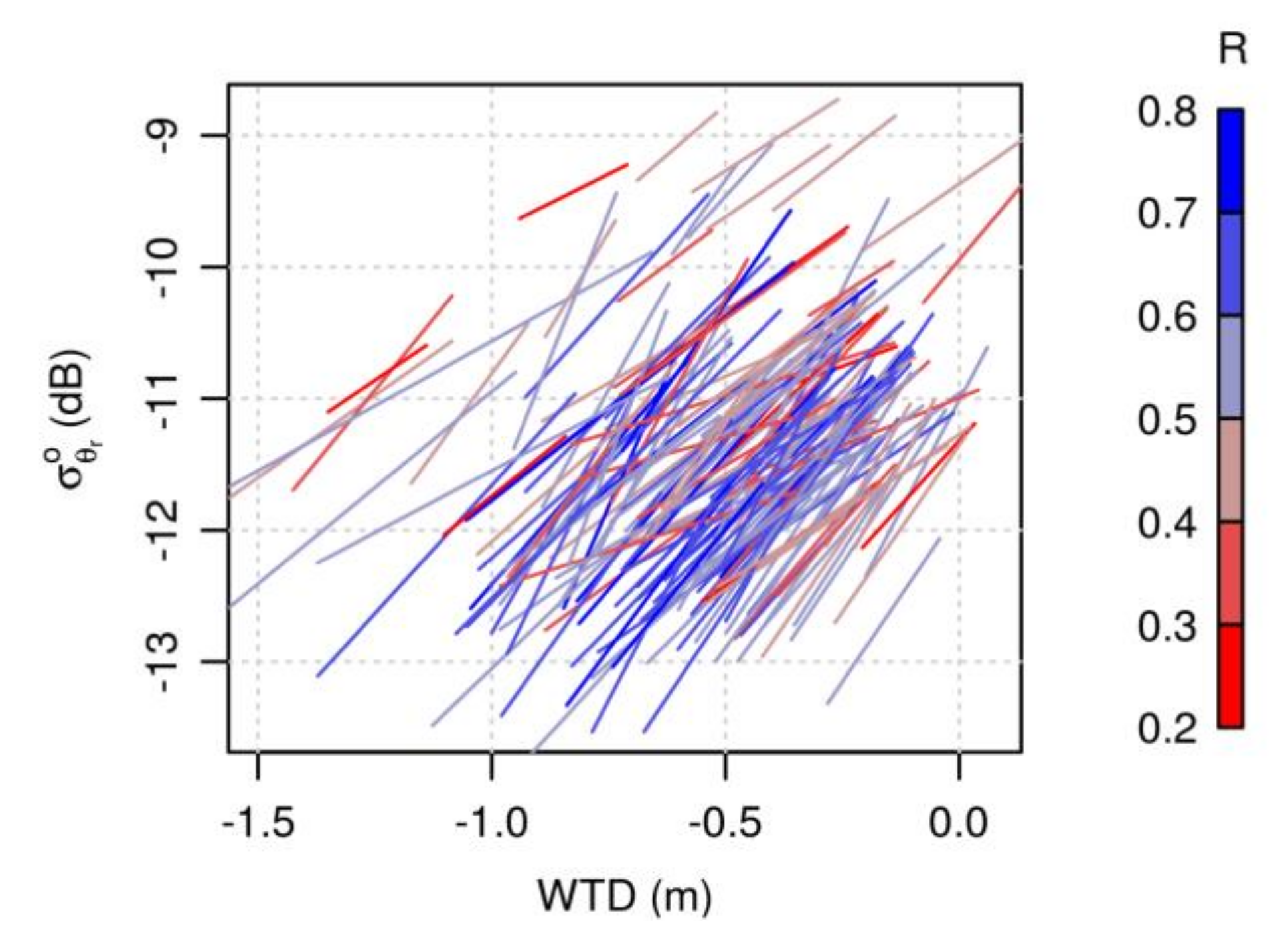
- The temporal correlation coefficient between σ° and WTD is rather independent of the mean WTD of a site. High R values of up to 0.8 can be observed for deeply-drained sites as well as for sites with shallow WTD (which comprise shallowly-drained, as well as natural sites).
- While at all sites a positive correlation can be observed, there is a strong variability of the absolute level of σ° across sites.
5. Discussion
5.1. Differences between Descending and Ascending Data
5.2. Impact of Different Processing Configurations
5.2.1. Possible Optimization of Cross-Over Angles over Peatlands
5.3. Potential and Limitations of C-Band Backscatter for Water Table Depth Monitoring
6. Conclusions
- backscatter is a good indicator for water table depth dynamics, but the interpretation seems to be more difficult for natural than for drained peatlands;
- the use of ENVISAT-ASAR (fine resolution) as opposed to ASCAT (coarse) has a high potential for future analysis over peatlands; and
- the use of various incidence angle correction techniques improved the correlation between backscatter and water table depth but differences between the various methods were small.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tubiello, F.N.; Biancalani, R.; Salvatore, M.; Rossi, S.; Conchedda, G. A worldwide assessment of greenhouse gas emissions from drained organic soils. Sustainability 2016, 8. [Google Scholar] [CrossRef]
- Kieckbusch, J.J.; Schrautzer, J. Nitrogen and phosphorus dynamics of a re-wetted shallow-flooded peatland. Sci. Total Environ. 2007, 380, 3–12. [Google Scholar] [CrossRef] [PubMed]
- Grayson, R.; Holden, J.; Rose, R. Long-term change in storm hydrographs in response to peatland vegetation change. J. Hydrol. 2010, 389, 336–343. [Google Scholar] [CrossRef]
- Chapman, S.; Buttler, A.; Francez, A.J.; Laggoun-Défarge, F.; Vasander, H.; Schloter, M.; Combe, J.; Grosvernier, P.; Harms, H.; Epron, D.; et al. Exploitation of northern peatlands and biodiversity maintenance: A conflict between economy and ecology. Front. Ecol. Environ. 2003, 1, 525–532. [Google Scholar] [CrossRef]
- Joosten, H. The Global Peatland CO2 Picture. Peatland Status and Drainage Related Emissions in All Countries of The World; Wetlands International: Wageningen, The Netherlands, 2010; p. 36. [Google Scholar]
- Tiemeyer, B.; Bechtold, M.; Belting, S.; Freibauer, A.; Förster, C.; Schubert, E.; Dettmann, U.; Frank, S.; Fuchs, D.; Gelbrecht, J.; et al. Moorschutz in Deutschland—Optimierung des Moormanagements in Hinblick auf den Schutz der Biodiversität und der Ökosystemleistungen. BfN Skripten 2017, 462, 320. [Google Scholar]
- Bircher, S.; Andreasen, M.; Vuollet, J.; Vehviläinen, J.; Rautiainen, K.; Jonard, F.; Weihermüller, L.; Zakharova, E.; Wigneron, J.P.; Kerr, H.Y. Soil moisture sensor calibration for organic soil surface layers. Geosci. Instrum. Methods Data Syst. 2016, 5, 109–125. [Google Scholar] [CrossRef]
- Kasischke, E.S.; Bourgeau-Chavez, L.L.; Rober, A.R.; Wyatt, K.H.; Waddington, J.M.; Turetsky, M.R. Effects of soil moisture and water depth on ERS SAR backscatter measurements from an Alaskan wetland complex. Remote Sens. Environ. 2009, 113, 1868–1873. [Google Scholar] [CrossRef]
- Harris, A.; Bryant, R.G. A multi-scale remote sensing approach for monitoring northern peatland hydrology: Present possibilities and future challenges. J. Environ. Manag. 2009, 90, 2178–2188. [Google Scholar] [CrossRef] [PubMed]
- Meingast, K.M.; Falkowski, M.J.; Kane, E.S.; Potvin, L.R.; Benscoter, B.W.; Smith, A.M.S.; Bourgeau-Chavez, L.L.; Miller, M.E. Spectral detection of near-surface moisture content and water-table position in northern peatland ecosystems. Remote Sens. Environ. 2014, 152, 536–546. [Google Scholar] [CrossRef]
- Kim, J.W.; Lu, Z.; Gutenberg, L.; Zhu, Z. Characterizing hydrologic changes of the Great Dismal Swamp using SAR/InSAR. Remote Sens. Environ. 2017, 198, 187–202. [Google Scholar] [CrossRef]
- Tiemeyer, B.; Albiac Borraz, E.; Augustin, J.; Bechtold, M.; Beetz, S.; Beyer, C.; Drösler, M.; Ebli, M.; Eickenscheidt, T.; Fiedler, S.; Förster, C.; Freibauer, A.; et al. High emissions of greenhouse gases from grasslands on peat and other organic soils. Glob. Chang. Biol. 2016, 22, 4134–4149. [Google Scholar] [CrossRef] [PubMed]
- Kasischke, E.S.; Smith, K.B.; Bourgeau-Chavez, L.L.; Romanowicz, E.A.; Brunzell, S.; Richardson, C.J. Effects of seasonal hydrologic patterns in south Florida wetlands on radar backscatter measured from ERS-2 SAR imagery. Remote Sens. Environ. 2003, 88, 423–441. [Google Scholar] [CrossRef]
- Kim, J.W.; Lu, Z.; Lee, H.; Shum, C.K.; Swarzenski, C.M.; Doyle, T.W.; Baek, S.H. Integrated analysis of PALSAR/Radarsat-1 InSAR and ENVISAT altimeter data for mapping of absolute water level changes in Louisiana wetlands. Remote Sens. Environ. 2009, 113, 2356–2365. [Google Scholar] [CrossRef]
- Bartsch, A.; Trofaier, A.M.; Hayman, G.; Sabel, D.; Schlaffer, S.; Clark, D.B.; Blyth, E. Detection of open water dynamics with ENVISAT ASAR in support of land surface modelling at high latitudes. Biogeosciences 2012, 9, 703–714. [Google Scholar] [CrossRef]
- Schlaffer, S.; Chini, M.; Dettmering, D.; Wagner, W. Mapping wetlands in Zambia using seasonal backscatter signatures derived from ENVISAT ASAR time series. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive. Volume 3—From Theory to Applications; Artech House, Inc.: Norwood, MA, USA, 1986; Volume 3, ISBN 0890061920. [Google Scholar]
- Wagner, W.; Lemoine, G.; Borgeaud, M.; Rott, H. A study of vegetation cover effects on ers scatterometer data. IEEE Trans. Geosci. Remote Sens. 1999, 37, 938–948. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Gruber, A.; De Jeu, R.A.M.; Wagner, W.; Stacke, T.; Loew, A.; Albergel, C.; Brocca, L.; Chung, D.; Parinussa, R.M.; et al. Evaluation of the ESA CCI soil moisture product using ground-based observations. Remote Sens. Environ. 2015, 162, 380–395. [Google Scholar] [CrossRef]
- Bechtold, M.; Tiemeyer, B.; Laggner, A.; Leppelt, T.; Frahm, E.; Belting, S. Large-scale regionalization of water table depth in peatlands optimized for greenhouse gas emission upscaling. Hydrol. Earth Syst. Sci. 2014, 18, 3319–3339. [Google Scholar] [CrossRef]
- Pathe, C.; Wagner, W.; Sabel, D.; Doubkova, M.; Basara, J.B. Using ENVISAT ASAR global mode data for surface soil moisture retrieval over Oklahoma, USA. IEEE Trans. Geosci. Remote Sens. 2009, 47, 468–480. [Google Scholar] [CrossRef]
- Ikonen, J.; Smolander, T.; Pratola, C. ESA Climate Change Initiative Phase II Soil Moisture. Comprehensive Error Characterisation Report Revision 1 (CECR) D2.2.1. Verion 1.0.; ESA: Paris, France, 2016. [Google Scholar]
- European Space Agency (ESA). ENVISAT-1 Products Specifications Volume 9: DORIS Product Specifications; Document reference: PO-RS-MDA-GS-2009; ESA: Paris, France, 2008. [Google Scholar]
- Gruber, A.; Wagner, W.; Hegyiova, A.; Greifeneder, F.; Schlaffer, S. Potential of Sentinel-1 for high-resolution soil moisture monitoring. In International Geoscience and Remote Sensing Symposium (IGARSS); ESA: Paris, France, 2013; pp. 4030–4033. [Google Scholar]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.Ö.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Small, D.; Schubert, A. Guide to ASAR Geocoding; ESA-ESRIN Technical Note RSL-ASAR-GC-AD, Iss. 1.01; University of Zurich: Zurich, Switzerland, 2008; p. 36. [Google Scholar]
- Jarvis, A.; Reuter, H.; Nelson, A.; Guevara, E. Hole-filled Seamless SRTM Data V4. International Centre for Tropical Agriculture (CIAT), 2008.
- Gevaert, A.I.; Parinussa, R.M.; Renzullo, L.J.; van Dijk, A.I.J.M.; de Jeu, R.A.M. Spatio-temporal evaluation of resolution enhancement for passive microwave soil moisture and vegetation optical depth. Int. J. Appl. Earth Obs. Geoinfom. 2015, 45, 235–244. [Google Scholar] [CrossRef]
- IPCC. IPCC Guidelines For National Greenhouse Gas Inventories; Eggleston, H.S., Buendia, L., Miwa, K., Ngara, T.K.T., Eds.; IGES: Yokohama, Japan, 2006. [Google Scholar]
- Von Asmuth, J.R.; Maas, K.; Bakker, M.; Petersen, J. Modeling time series of ground water head fluctuations subjected to multiple stresses. Ground Water 2008, 46, 30–40. [Google Scholar] [CrossRef] [PubMed]
- Loew, A.; Ludwig, R.; Mauser, W. Derivation of surface soil moisture from ENVISAT ASAR wide swath and image mode data in agricultural areas. IEEE Trans. Geosci. Remote Sens. 2006, 44, 889–898. [Google Scholar] [CrossRef]
- Hahn, S.; Reimer, C.; Vreugdenhil, M.; Melzer, T.; Wagner, W. Dynamic Characterization of the Incidence Angle Dependence of Backscatter Using Metop ASCAT. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2348–2359. [Google Scholar] [CrossRef]
- Van Doninck, J.; Wagner, W.; Melzer, T.; De Baets, B.; Verhoest, N.E.C. Seasonality in the angular dependence of ASAR wide swath backscatter. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1423–1427. [Google Scholar] [CrossRef]
- R Core Team. R Development Core Team. Available online: http://www.r-project.org/ (accessed on 11 November 2018).
- Bates, D.; Maechler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- De Lannoy, G.J.M.; Reichle, R.H. Global Assimilation of Multiangle and Multipolarization SMOS Brightness Temperature Observations into the GEOS-5 Catchment Land Surface Model for Soil Moisture Estimation. J. Hydrometeorol. 2016, 17, 669–691. [Google Scholar] [CrossRef]
- Wang, P.; Pozdniakov, S.P. A statistical approach to estimating evapotranspiration from diurnal groundwater level fluctuations. Water Resour. Res. 2014, 50, 2276–2292. [Google Scholar] [CrossRef]
- Bartalis, Z.; Scipal, K.; Wagner, W. Azimuthal anisotropy of scatterometer measurements over land. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2083–2092. [Google Scholar] [CrossRef]
- Wagner, W. Evaluation of the agreement between the first global remotely sensed soil moisture data with model and precipitation data. J. Geophys. Res. 2003, 108, 4611. [Google Scholar] [CrossRef]
- Dettmann, U.; Bechtold, M. Deriving Effective Soil Water Retention Characteristics from Shallow Water Table Fluctuations in Peatlands. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef]
- Querner, E.P.; Jansen, P.C.; van den Akker, J.J.H.; Kwakernaak, C. Analysing water level strategies to reduce soil subsidence in Dutch peat meadows. J. Hydrol. 2012, 446–447, 59–69. [Google Scholar] [CrossRef]
- Ali, I.; Schuster, C.; Zebisch, M.; Förster, M.; Kleinschmit, B.; Notarnicola, C. First results of monitoring nature conservation sites in alpine region by using very high resolution (VHR) X-band SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2265–2274. [Google Scholar] [CrossRef]

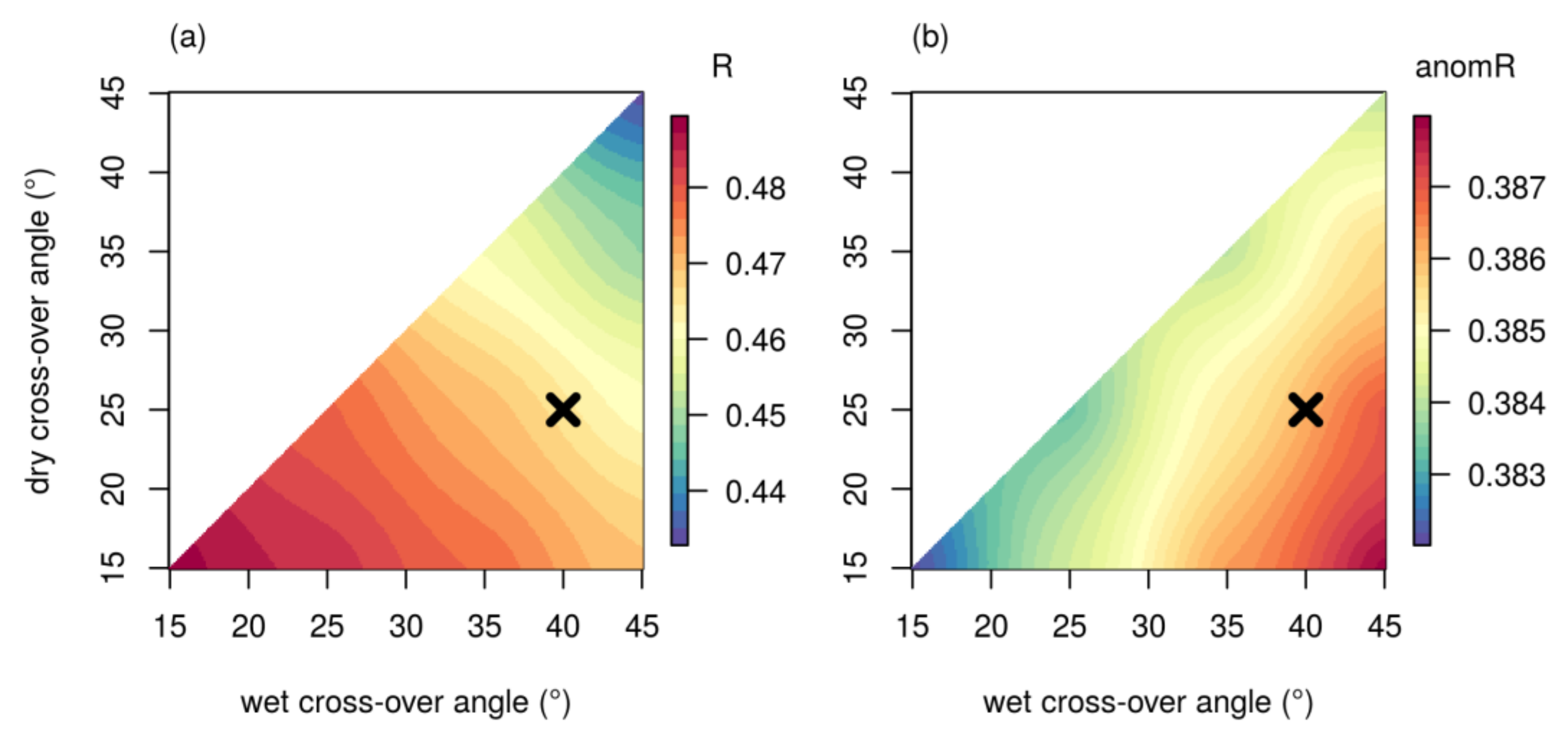
| Method | R ± ½ CI 1 | anomR ± ½ CI |
|---|---|---|
| NOCOR | 0.37 ± 0.04 | 0.27 ± 0.05 |
| CONST | 0.46 ± 0.04 | 0.38 ± 0.04 |
| COASCAT | 0.42 ± 0.04 | 0.34 ± 0.04 |
| COASAR | 0.47 ± 0.04 | 0.39 ± 0.04 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bechtold, M.; Schlaffer, S.; Tiemeyer, B.; De Lannoy, G. Inferring Water Table Depth Dynamics from ENVISAT-ASAR C-Band Backscatter over a Range of Peatlands from Deeply-Drained to Natural Conditions. Remote Sens. 2018, 10, 536. https://doi.org/10.3390/rs10040536
Bechtold M, Schlaffer S, Tiemeyer B, De Lannoy G. Inferring Water Table Depth Dynamics from ENVISAT-ASAR C-Band Backscatter over a Range of Peatlands from Deeply-Drained to Natural Conditions. Remote Sensing. 2018; 10(4):536. https://doi.org/10.3390/rs10040536
Chicago/Turabian StyleBechtold, Michel, Stefan Schlaffer, Bärbel Tiemeyer, and Gabrielle De Lannoy. 2018. "Inferring Water Table Depth Dynamics from ENVISAT-ASAR C-Band Backscatter over a Range of Peatlands from Deeply-Drained to Natural Conditions" Remote Sensing 10, no. 4: 536. https://doi.org/10.3390/rs10040536
APA StyleBechtold, M., Schlaffer, S., Tiemeyer, B., & De Lannoy, G. (2018). Inferring Water Table Depth Dynamics from ENVISAT-ASAR C-Band Backscatter over a Range of Peatlands from Deeply-Drained to Natural Conditions. Remote Sensing, 10(4), 536. https://doi.org/10.3390/rs10040536