HY-2A Altimeter Data Initial Assessment and Corresponding Two-Pass Waveform Retracker
Abstract
1. Introduction
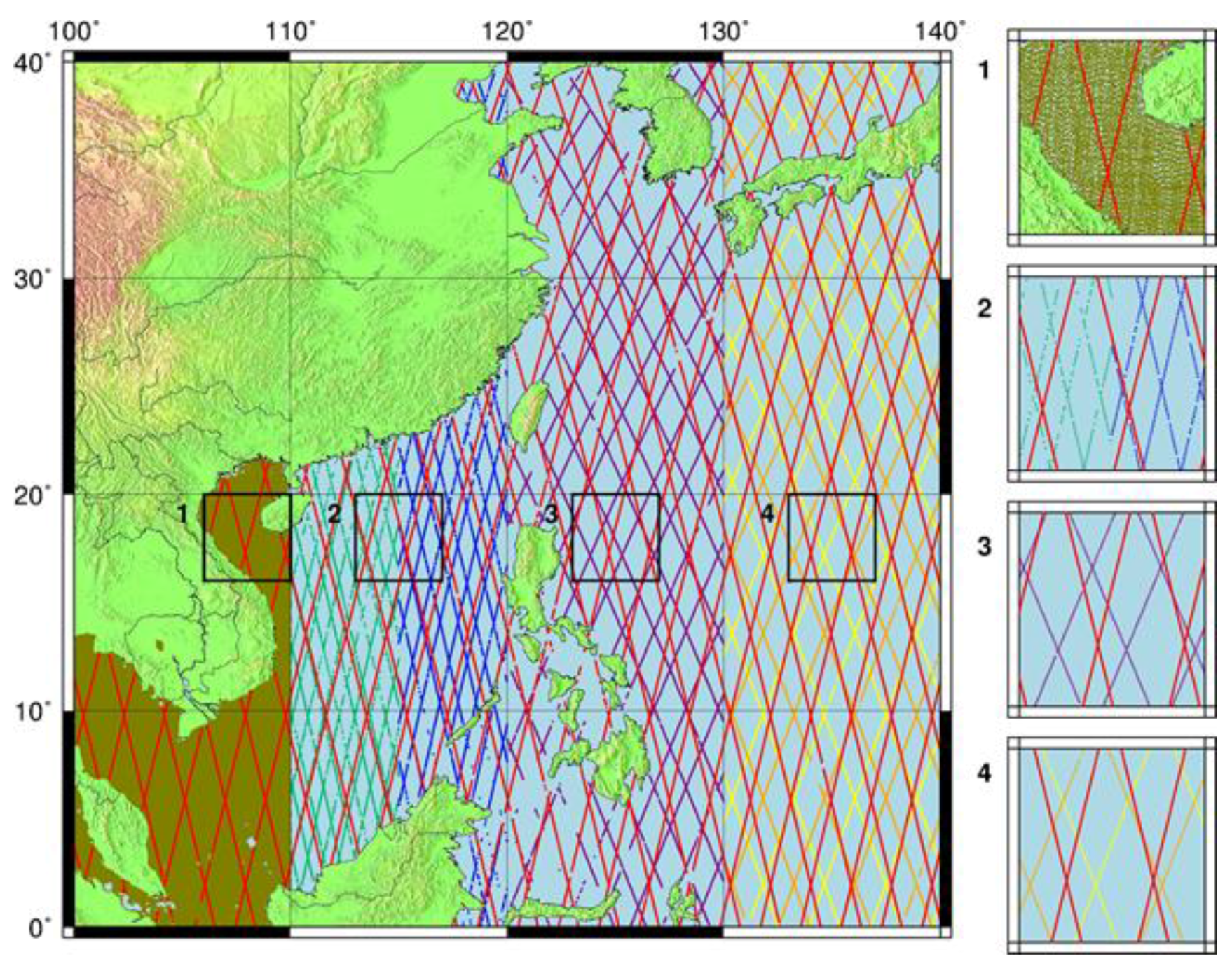
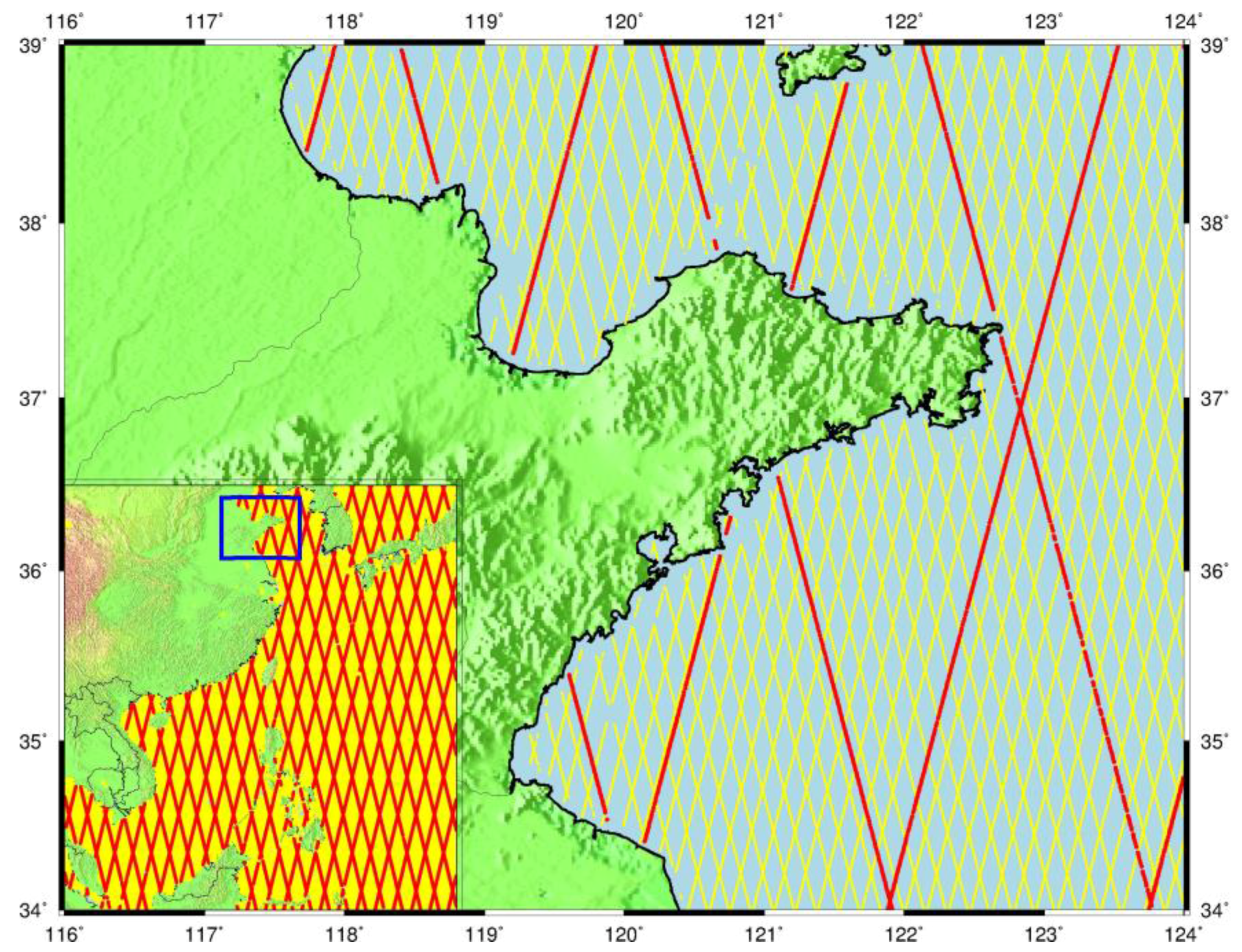
2. HY-2A Data Description
3. Initial Assessment of HY-2A Measurement
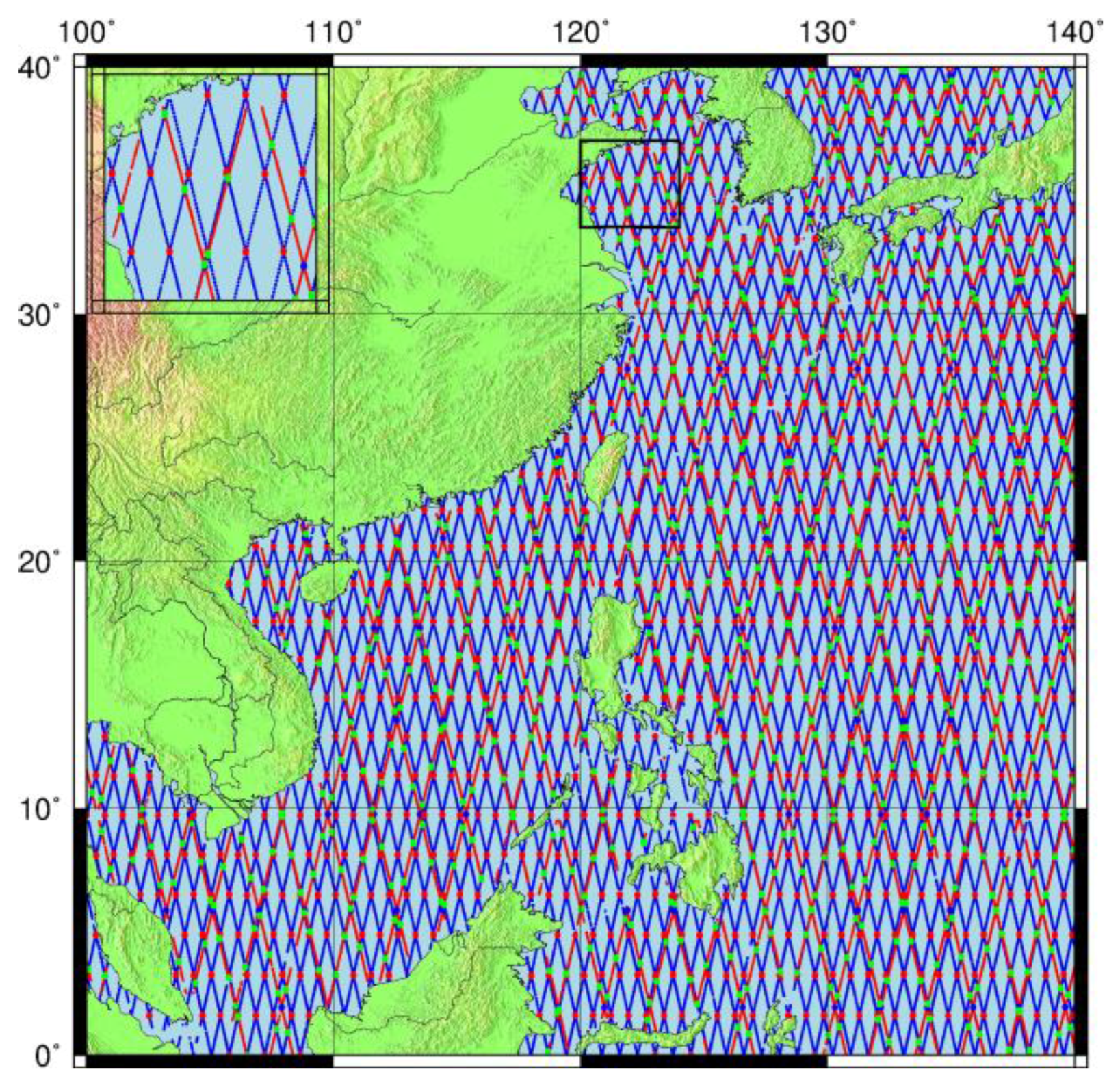
3.1. Multi-Mission Crossover Analysis
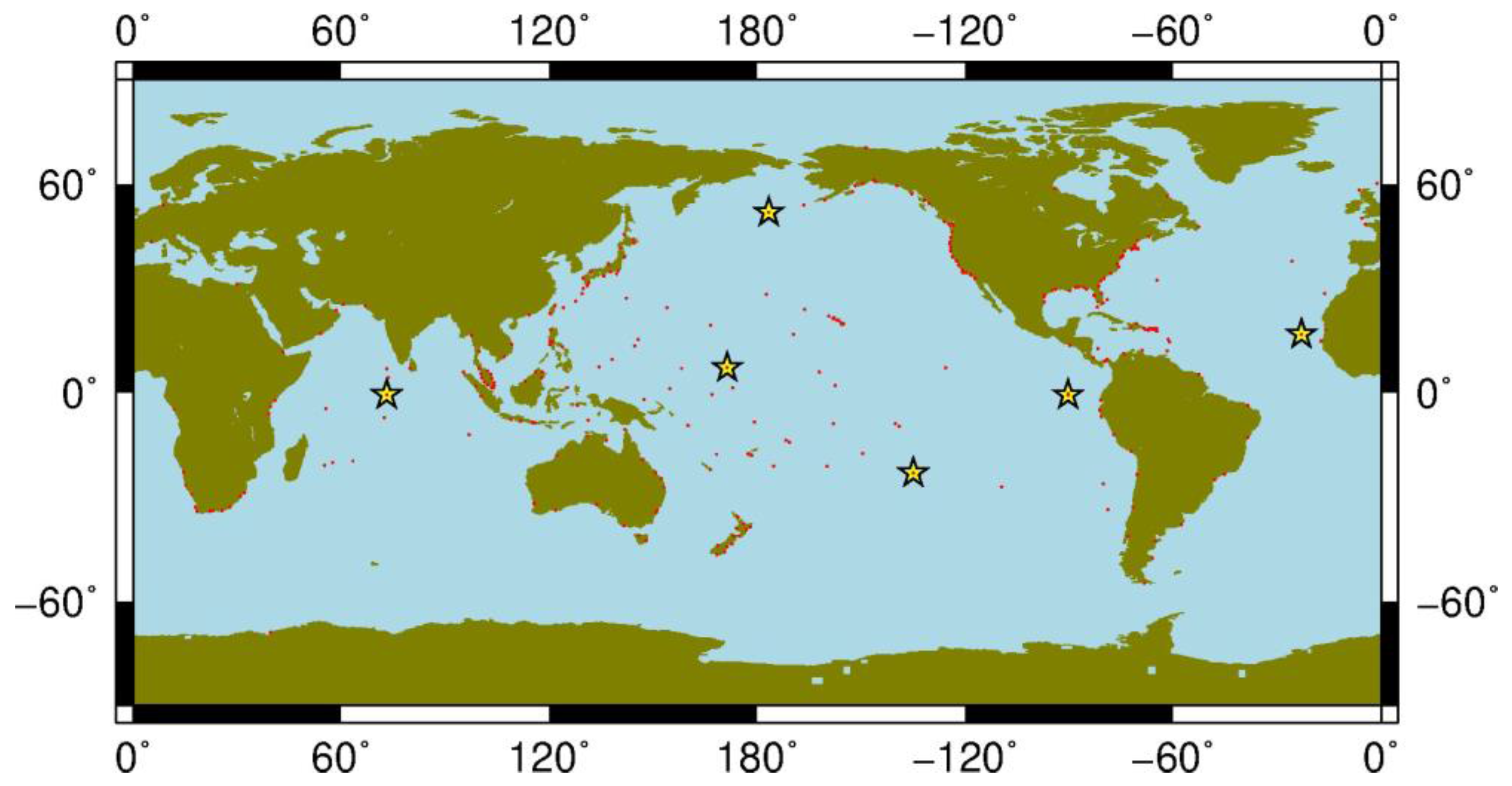
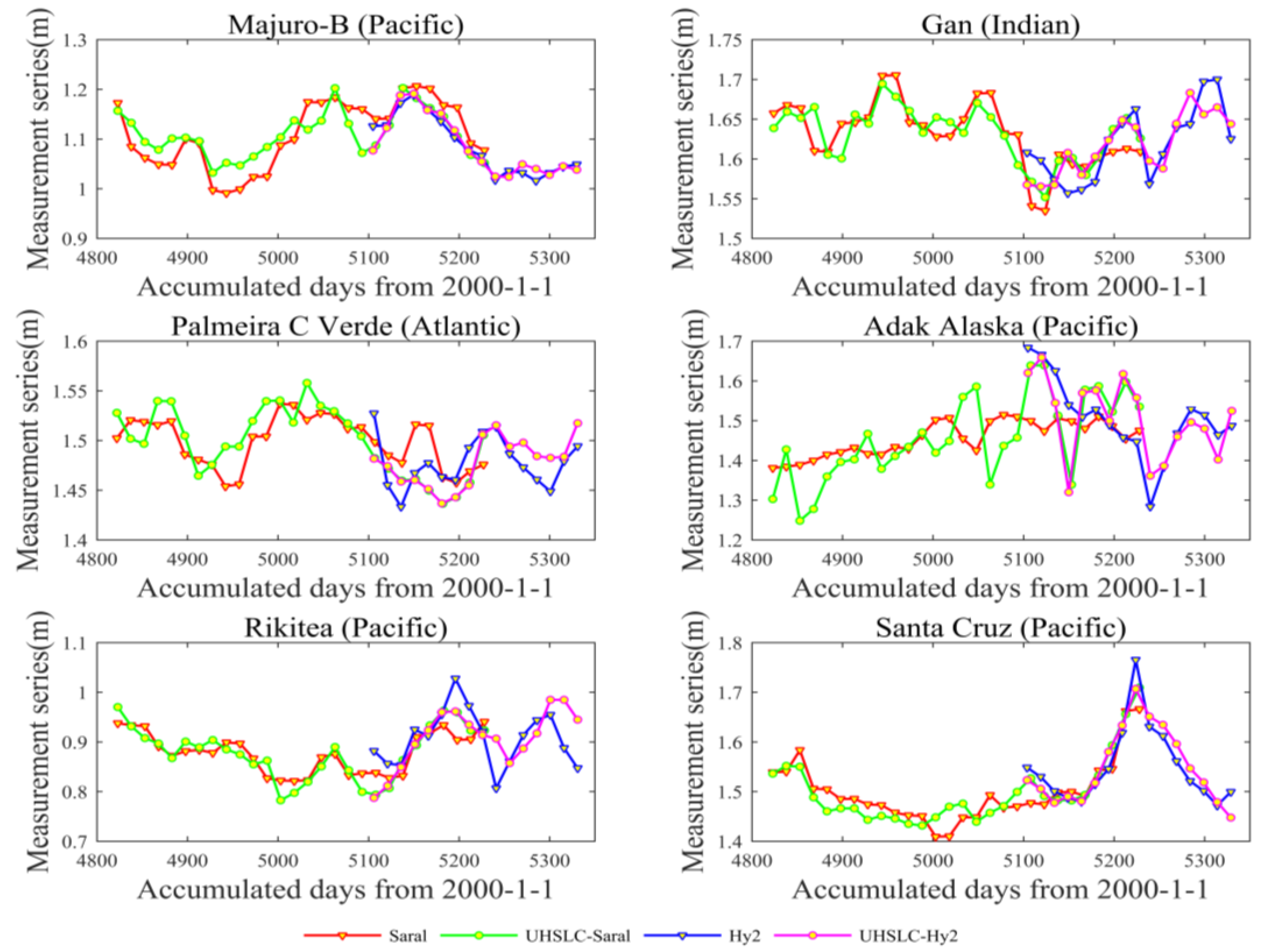
3.2. Validation with Tide Gauge Measurements
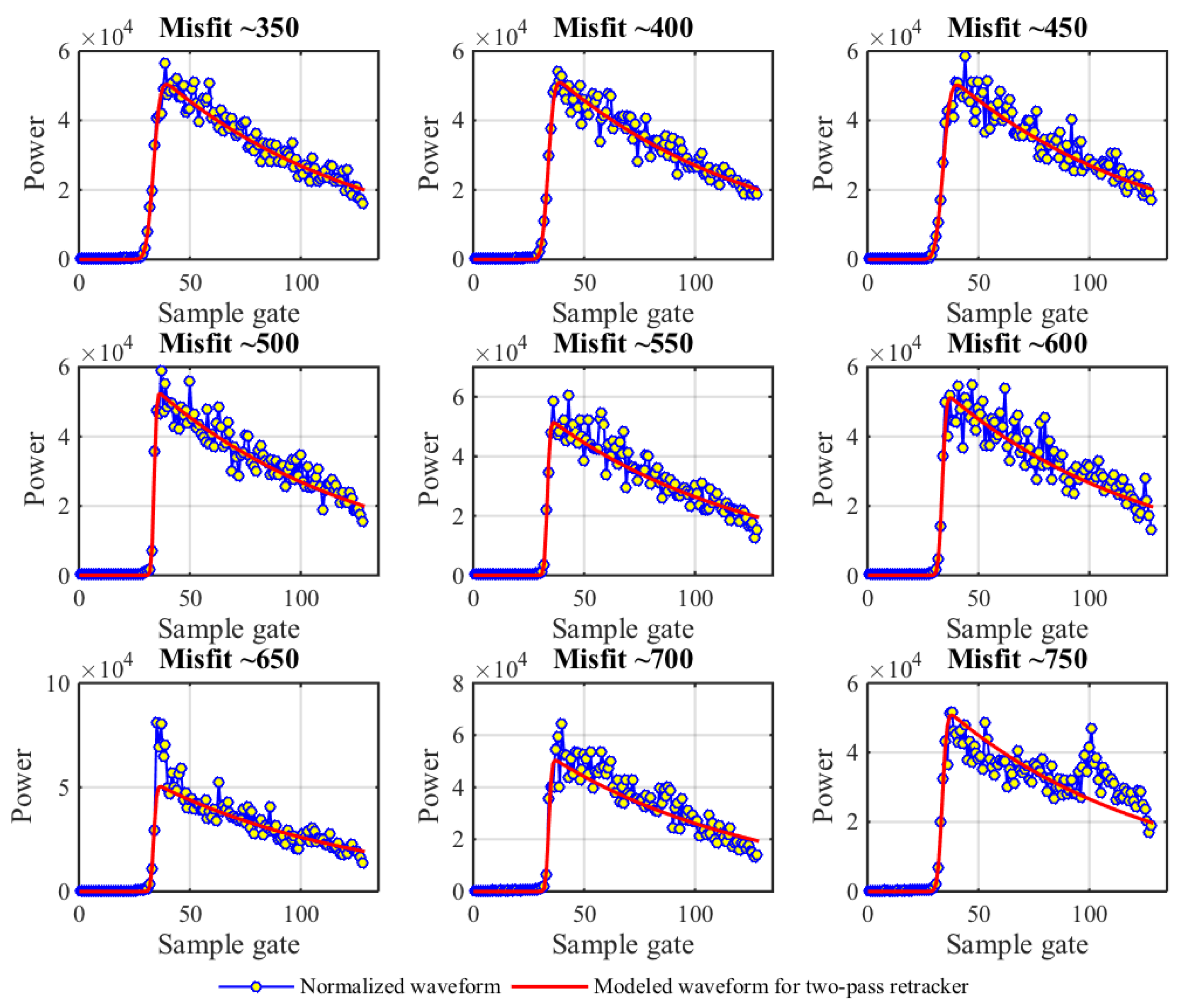
4. Two-Pass Retracker for HY-2A
4.1. Theory of Two-Pass Retracker
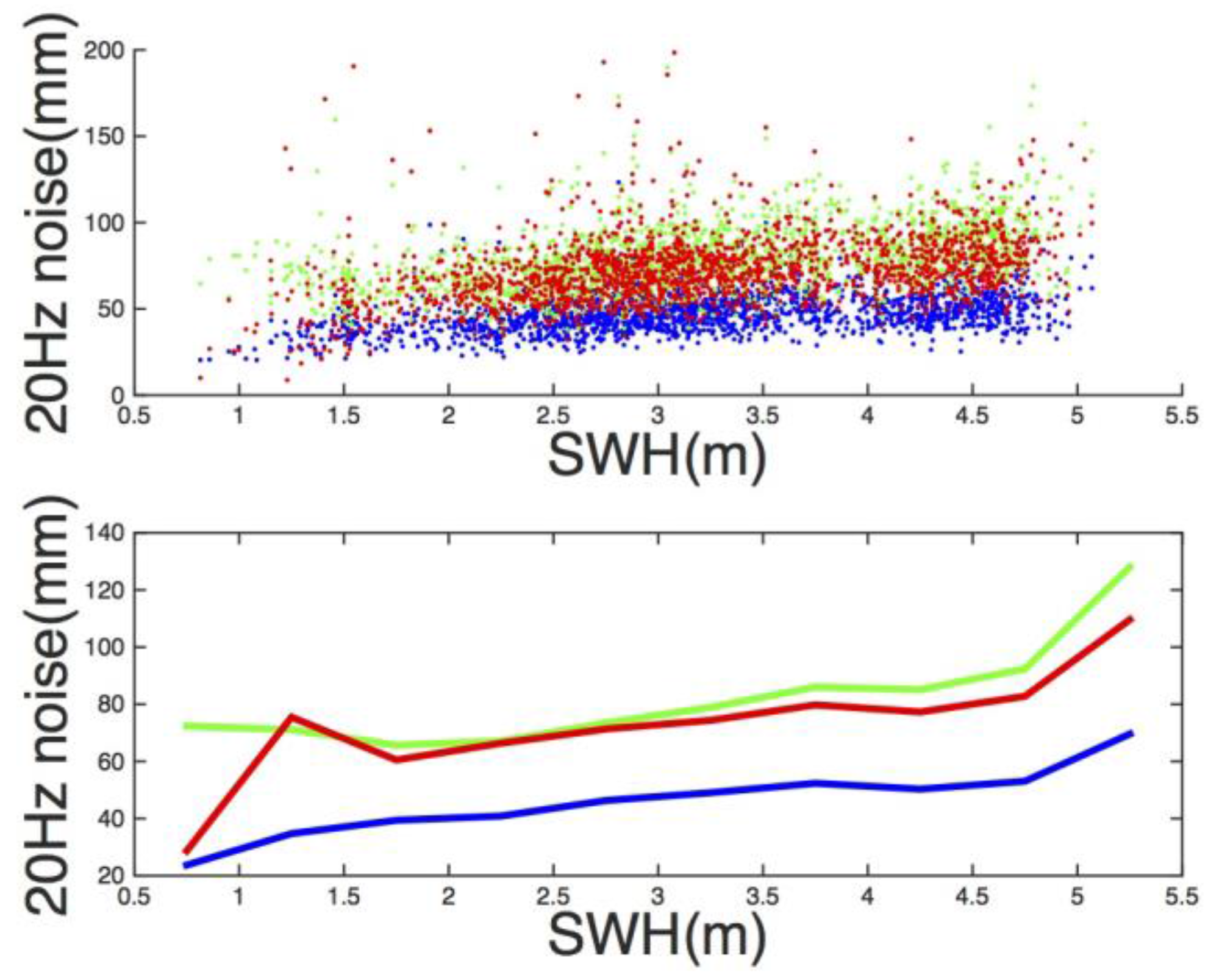
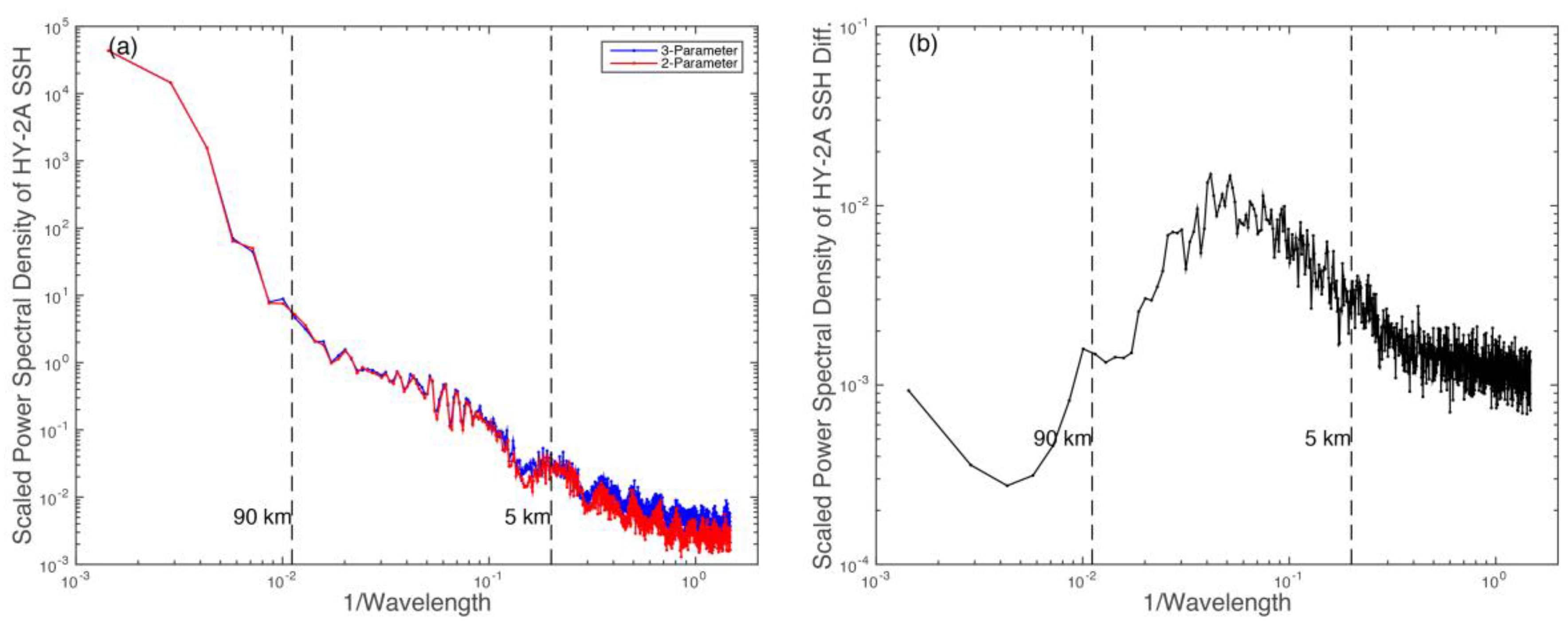
4.2. Parameter Determination
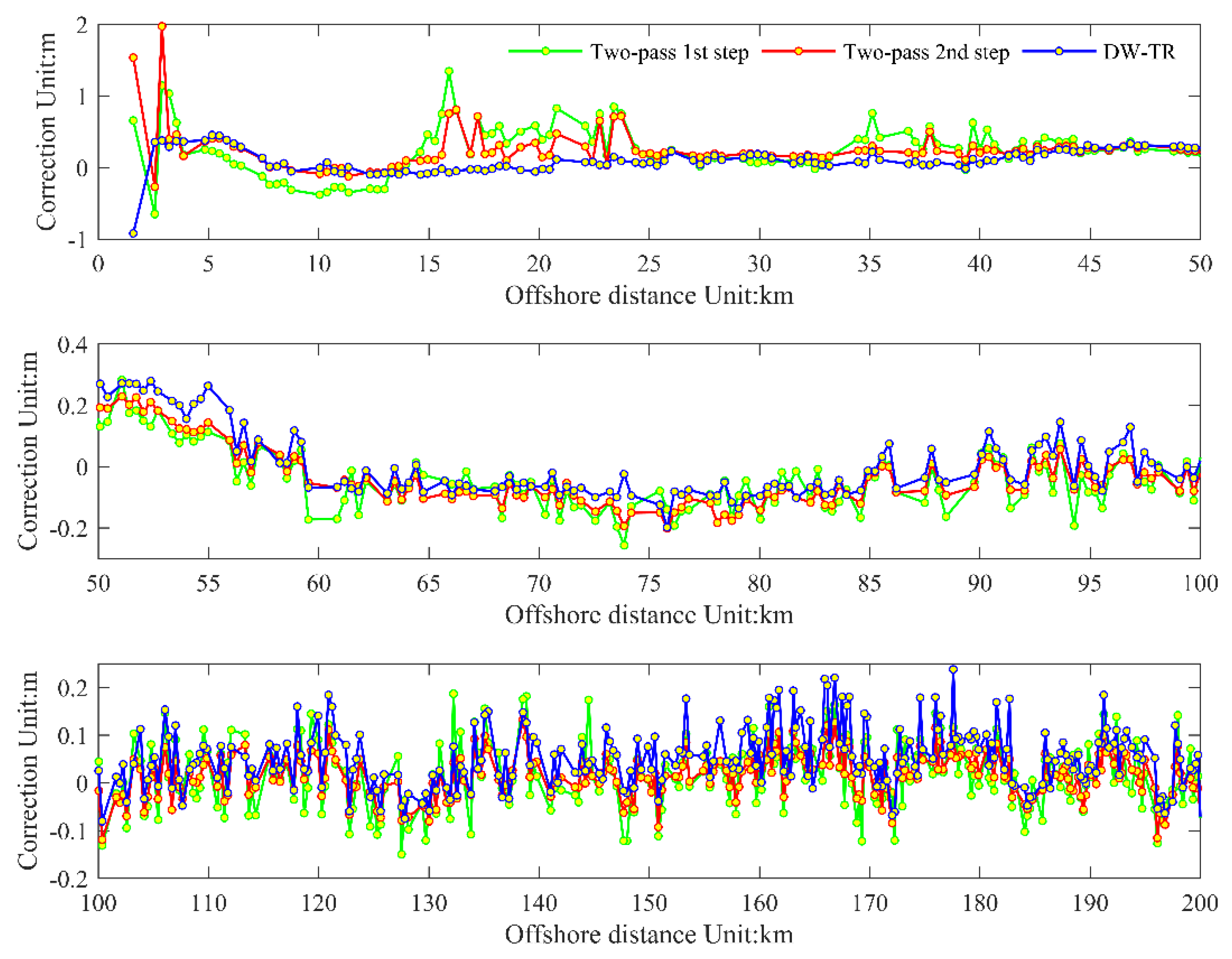
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rapp, R.H. Geos 3 data processing for the recovery of geoid undulations and gravity anomalies. J. Geophys. Res. 1979, 84, 3784–3792. [Google Scholar] [CrossRef]
- Haxby, W.F.; Karner, G.D.; Labrecque, J.L.; Weissel, J.K. Digital images of combined oceanic and continental data sets and their use in tectonic studies. EOS Trans. Am. Geophys. Union 1983, 64, 995–1004. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Smith, W.H.F. Marine gravity anomaly from Geosat and ERS1 satellite altimetry. J. Geophys. Res. 1997, 102, 10039–10054. [Google Scholar] [CrossRef]
- Andersen, O.B.; Knudsen, P. Global marine gravity field from the ERS-1 and Geosat geodetic mission altimetry. J. Geophys. Res. 1998, 103, 8129–8137. [Google Scholar] [CrossRef]
- Hwang, C. Inverse Vening Meinesz formula and deflection-geoid formula: Applications to the predictions of gravity and geoid over the South China Sea. J. Geodesy 1998, 72, 304–312. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Garcia, E.S.; Soofi, K.; Wessel, P.; Chandler, M.; Smith, W.H. Towards 1-mGal accuracy in global marine gravity from Cryosat-2, Envisat and Jason-1. Lead. Edge 2013, 32, 892–898. [Google Scholar] [CrossRef]
- Andersen, O.B.; Jain, M.; Knudsen, P. The Impact of Using Jason-1 and Cryosat-2 Geodetic Mission Altimetry for Gravity Field Modeling. IAG 150 Years Symp. 2016, 143, 205–210. [Google Scholar]
- Zhang, S.; Sandwell, D.T.; Jin, T.; Li, D. Inversion of marine gravity anomalies over southeastern China seas from multi-satellite altimeter vertical deflections. J. Appl. Geophys. 2017, 137, 128–137. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Smith, W.H.F. Retracking ERS-1 altimeter waveforms for optimal gravity field recovery. Geophys. J. Int. 2005, 163, 79–89. [Google Scholar] [CrossRef]
- Hwang, C.; Guo, J.; Deng, X.; Hsu, H.Y.; Liu, Y. Coastal gravity anomalies from retracked Geosat GM altimetry: Improvement, limitation and the role of airborne gravity data. J. Geodesy 2006, 80, 204–216. [Google Scholar] [CrossRef]
- Andersen, O.B.; Knudsen, P.; Berry, P. The DNSC08GRA global marine gravity field from double retracked satellite altimetry. J. Geodesy 2010, 84, 191–199. [Google Scholar] [CrossRef]
- Sandwell, D.T. Antarctic marine gravity field from high-density satellite altimetry. Geophys. J. Int. 1992, 109, 437–448. [Google Scholar] [CrossRef]
- Zhao, G.; Zhou, X. Precise orbit determination of Haiyang-2 using satellite laser ranging. Chin. Sci. Bull. 2013, 58, 589–597. [Google Scholar] [CrossRef]
- Legeais, J.-F.; Ablain, M.; Faugère, Y.; Mertz, F.; Soussi, B.; Vincent, P. HY-2A and DUACS (Data Unification and Altimeter Combination System) altimeter products. In Proceedings of the OSTST 2012 (Ocean Surface Topography Science Team) Meeting, Venice, Italy, 22–29 September 2012. [Google Scholar]
- Bao, L.; Gao, P.; Peng, H.; Jia, Y.; Shum, C.K.; Lin, M.; Guo, Q. First accuracy assessment of the HY-2A altimeter sea surface height observations: Cross-calibration results. Adv. Space Res. 2015, 55, 90–105. [Google Scholar] [CrossRef]
- Peng, H.; Lin, M.; Mu, B. Global statistical evaluation and performance analysis of HY-2A satellite radar altimeter data. Haiyang Xuebao 2015, 37, 54–66. (In Chinese) [Google Scholar]
- Yang, L.; Zhou, X.; Lin, M.; Lei, N.; Mu, B.; Zhu, L. Global statistical assessment of HY-2A altimeter IGDR data. Prog. Geophys. 2016, 31, 629–636. (In Chinese) [Google Scholar] [CrossRef]
- Sandwell, D.T.; Smith, W.H.F. Global marine gravity from retracked Geosat and ERS-1 altimetry: Ridge segmentation versus spreading rate. J. Geophys. Res. 2009, 114, B014411. [Google Scholar] [CrossRef]
- Garcia, E.S.; Sandwell, D.T.; Smith, W.H.F. Retracking CryoSat-2, Envisat, and Jason-1 radar altimetry waveforms for improved gravity field recovery. Geophys. J. Int. 2014, 196, 1402–1422. [Google Scholar] [CrossRef]
- Zhang, S.; Sandwell, D.T. Retracking of SARAL/AltiKa Radar Altimetry Waveforms for Optimal Gravity Field Recovery. Mar. Geodesy 2017, 40, 40–56. [Google Scholar] [CrossRef]
- Prandi, P.S.; Philipps, S.; Pignot, V.; Picot, N. SARAL/AltiKa global statistical assessment and cross-calibration with Jason-2. Mar. Geodesy 2015, 38, 297–312. [Google Scholar] [CrossRef]
- Vu, P.; Frappart, F.; Darrozes, L. Multi-Satellite Altimeter Validation along the French Atlantic Coast in the Southern Bay of Biscay from ERS-2 to SARAL. Remote Sens. 2018, 10, 93. [Google Scholar] [CrossRef]
- Salameh, E.; Frappart, F.; Marieu, V. Monitoring Sea Level and Topography of Coastal Lagoons Using Satellite Radar Altimetry: The Example of the Arcachon Bay in the Bay of Biscay. Remote Sens. 2018, 10, 297. [Google Scholar] [CrossRef]
- Wahr, L.W. Deformation of the earth induced by polar motion. J. Geophys. Res. (Solid Earth) 1985, 90, 9363–9368. [Google Scholar] [CrossRef]
- Valladeau, G.; Legeais, J.F.; Ablain, M.; Guinehut, S.; Picot, N. Comparing altimetry with tide gauges and Argo profiling floats for data quality assessment and mean sea level studies. Mar. Geodesy 2012, 35, 42–60. [Google Scholar] [CrossRef]
- CalVal In-Situ Altimetry/tide Gauges. Validation of Altimeter Data by Comparison with Tide Gauge Measurements; CLS: Ramonville St-Agne, France, 2014; CLS.DOS/NT/13-285, Issue 1.1, Nomenclature: SALP-RP-MA-EA-22294-CLS. [Google Scholar]
- Caldwell, P.C.; Merrifield, M.A.; Thompson, P.R. Sea Level Measured by Tide Gauges from Global Oceans—The Joint Archive for Sea Level Holdings (NCEI Accession 0019568); Version 5.5; NOAA National Centers for Environmental Information: Silver Spring, MD, USA, 2015.
- Huang, Z.; Wang, H.; Luo, Z.; Shum, C.K.; Tseng, K.-H.; Zhong, B. Improving Jason-2 Sea Surface Heights within 10 km Offshore by Retracking Decontaminated Waveforms. Remote Sens. 2017, 9, 1077. [Google Scholar] [CrossRef]
- Xu, X.; Birol, F.; Cazenave, A. Evaluation of Coastal Sea Level Offshore Hong Kong from Jason-2 Altimetry. Remote Sens. 2018, 10, 282. [Google Scholar] [CrossRef]
- Brown, G. The average impulse response of a rough surface and its applications. IEEE Trans. Antennas Propag. 1977, 25, 67–74. [Google Scholar] [CrossRef]
- Maus, S.; Green, C.M.; Fairhead, J.D. Improved ocean-geoid resolution from retracked ERS-1 satellite altimeter waveforms. Geophys. J. Int. 1998, 134, 243–253. [Google Scholar] [CrossRef][Green Version]
- Rodriguez, E. Altimetry for non-Gaussian oceans: Height biases and estimation of parameters. J. Geophys. Res. Oceans 1988, 93, 14107–14120. [Google Scholar] [CrossRef]
- Martin, T.V.; Zwally, H.J.; Brenner, A.C.; Bindschadler, R.A. Analysis and retracking of continental ice sheet radar altimeter waveforms. J. Geophys Res. 1983, 88, 1608–1616. [Google Scholar] [CrossRef]
- Davis, C.H. A surface and volume scattering retracking algorithm for ice sheet satellite altimetry. IEEE Trans. Geosci. Remote Sens. 1993, 31, 811–818. [Google Scholar] [CrossRef]
- Welch, P.D. The use of fast Fourier transforms for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Andersen, O.B.; Knudsen, P.; Kenyon, S.; Holmes, S. Global and arctic marine gravity field from recent satellite altimetry (DTU13). In Proceedings of the 76th EAGE Conference and Exhibition, Amsterdam, The Netherlands, 16–19 June 2014. [Google Scholar]
- Sandwell, D.T.; Müller, R.D.; Smith, W.H.F.; Garcia, E.; Francis, R. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure. Science 2014, 346, 65–67. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.L.; Ubelmann, C. On the transition from profile altimeter to swath altimeter for observing global ocean surface topography. J. Atmos. Ocean. Technol. 2013, 31, 560–568. [Google Scholar] [CrossRef]
| HY-2A | |
|---|---|
| Mission duration | 16 August 2011–present |
| Size | 8.56 m × 4.55 m × 3.185 m |
| Mass | ≤1575 kg |
| Orbit type | Sun-synchronous orbit |
| Altitude | 971~973 km |
| Inclination | 99.34° |
| Repeat period | ~14 days, ~168 days |
| Mode | Pulse-limited |
| Footprint size | 2~10 km |
| Frequency | 13.58 GHz. 5.2 GHz |
| Chirp bandwidth(Ku) | 320 MHz/80 MHz/20 MHz |
| Chirp bandwidth(C) | 160 MHz |
| Cycle | Time Scope | Data Quantity | Cycle | Time Scope | Data Quantity |
|---|---|---|---|---|---|
| E059 | 2013.12.21–2014.01.04 | 386 passes | E074 | 2014.07.19–2014.07.28 | 273 passes |
| E060 | 2014.01.04–2014.01.18 | 386 passes | E075 | 2014.08.03–2014.08.16 | 336 passes |
| E061 | 2014.01.18–2014.02.01 | 386 passes | E109 | 2015.11.21–2015.12.04 | 201 passes |
| E062 | 2014.02.01–2014.02.15 | 386 passes | E110 | 2015.12.07–2015.12.19 | 301 passes |
| E063 | 2014.02.15–2014.03.01 | 386 passes | E111 | 2015.12.19–2016.01.02 | 386 passes |
| E064 | 2014.03.01–2014.03.15 | 386 passes | E112 | 2016.01.02–2016.01.16 | 324 passes |
| E065 | 2014.03.15–2014.03.29 | 363 passes | E113 | 2016.01.16–2016.01.28 | 223 passes |
| E066 | 2014.03.29–2014.04.12 | 386 passes | E114 | 2016.01.30–2016.02.13 | 308 passes |
| E067 | 2014.04.12–2014.04.26 | 386 passes | E115 | 2016.02.13–2016.02.27 | 386 passes |
| E068 | 2014.04.26–2014.05.10 | 386 passes | E116 | 2016.02.27–2016.03.12 | 307 passes |
| E069 | 2014.05.10–2014.05.24 | 334 passes | E117 | 2016.03.12–2016.03.15 | 108 passes |
| E070 | 2014.05.24–2014.06.07 | 386 passes | Geodetic Mission | ||
| E071 | 2014.06.07–2014.06.21 | 386 passes | G001 | 2016.03.24–2016.09.08 | 4542 passes |
| E072 | 2014.06.21–2014.07.05 | 376 passes | G002 | 2016.09.08–2017.02.23 | 4630 passes |
| E073 | 2014.07.05–2014.07.19 | 386 passes | G003 | 2017.02.23–2017.05.10 | 2030 passes |
| Contrastive Parameters | HY-2A | SARAL |
|---|---|---|
| Cycle range | 59–68 | 1–12 |
| Time scope | 2013.12.21–2014.5.10 | 2013.3.14–2014.5.8 |
| Dry troposphere correction | ECMWF | ECMWF |
| Wet troposphere correction | Radiometer | Radiometer |
| Ionospheric correction | Dual-frequency | GIM |
| Sea state bias | NSOAS empirical solution | NOAA empirical solution |
| Ocean tide | GOT00.2 | GOT4.8 |
| Solid earth tide | Cartwright and Tayler tables | Cartwright and Tayler tables |
| Pole tide | Wahr [24] | Wahr [24] |
| Inverted barometer correction | ECMWF | ECMWF |
| High-frequency fluctuations | Mog2D model | Mog2D model |
| Mean sea surface | NSOAS gridding solution | MSS_CNES_CLS_2011 |
| Time Limit | HY-2A | SARAL | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Num | Min | Max | Mean | RMS | Num | Min | Max | Mean | RMS | |
| -- | 5136 | −0.995 | 0.998 | 0.083 | 0.232 | 32146 | −0.976 | 0.893 | 0.016 | 0.142 |
| ≤10 days | 816 | −0.979 | 0.841 | 0.096 | 0.182 | 2937 | −0.607 | 0.732 | 0.017 | 0.082 |
| ≤5 days | 442 | −0.931 | 0.841 | 0.090 | 0.177 | 1468 | −0.255 | 0.297 | 0.016 | 0.071 |
| ≤2 days | 242 | −0.899 | 0.841 | 0.086 | 0.170 | 557 | −0.232 | 0.279 | 0.014 | 0.062 |
| ≤1 day | 143 | −0.664 | 0.608 | 0.095 | 0.148 | 371 | −0.196 | 0.279 | 0.015 | 0.061 |
| Mission | Time Limit | OTC in GDR | Updated OTC with GOT-e | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Num | Min | Max | Mean | RMS | Num | Min | Max | Mean | RMS | ||
| HY_A & SA_D | -- | 13,784 | −0.998 | 0.958 | 0.191 | 0.250 | 13,216 | −0.999 | 0.980 | 0.070 | 0.199 |
| ≤1 day | 131 | −0.804 | 0.543 | 0.242 | 0.140 | 127 | −0.942 | 0.406 | 0.097 | 0.139 | |
| HY_D & SA_A | -- | 11,590 | −0.999 | 0.917 | 0.100 | 0.206 | 11,302 | −0.999 | 0.782 | −0.029 | 0.190 |
| ≤1 day | 100 | −0.868 | 0.641 | 0.092 | 0.151 | 99 | −0.999 | 0.321 | −0.046 | 0.155 | |
| HY_A & SA_A | -- | 418 | −0.993 | 0.650 | 0.209 | 0.226 | 396 | −0.993 | 0.515 | 0.081 | 0.181 |
| ≤1 day | 5 | 0.041 | 0.439 | 0.222 | 0.162 | 5 | −0.097 | 0.312 | 0.087 | 0.165 | |
| HY_D & SA_D | -- | 359 | −0.992 | 0.951 | 0.124 | 0.224 | 349 | −0.717 | 0.802 | −0.0002 | 0.201 |
| ≤1 day | 3 | 0.047 | 0.419 | 0.175 | 0.211 | 3 | −0.078 | 0.294 | 0.046 | 0.210 | |
| HY & SA | -- | 26,151 | −0.999 | 0.958 | 0.150 | 0.235 | 25,263 | −0.999 | 0.980 | 0.024 | 0.201 |
| ≤1 day | 239 | −0.868 | 0.641 | 0.178 | 0.184 | 234 | −0.999 | 0.406 | 0.035 | 0.175 | |
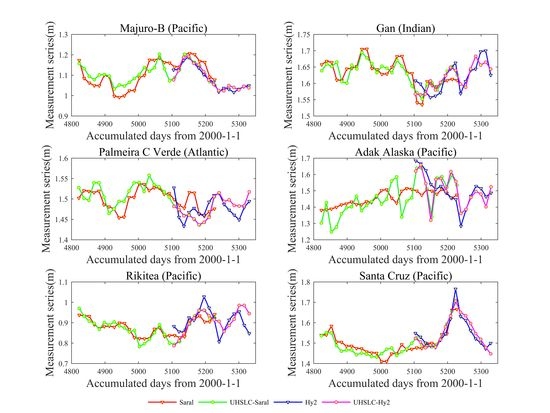
| Station | Latitude | Longitude | QC-YEARS | CI | Country | Contributor | Correlation Coefficient | |
|---|---|---|---|---|---|---|---|---|
| SARAL | HY-2A | |||||||
| Majuro-B | 07°–07°N | 171°–22°E | 1993–2016 | 98 | Rep. Marshall I. | Nat. Tidal Ctr., BOM | 0.8079 | 0.9572 |
| Gan | 00°–41°S | 073°–09°E | 1987–2015 | 93 | Rep. of Maldives | UH Sea Level Center | 0.8224 | 0.7606 |
| Palmeira C.Verde | 16°–45°N | 022°–59°W | 2000–2015 | 92 | Portugal | UH Sea Level Cente | 0.6278 | 0.5135 |
| Adak Alaska | 51°–52°N | 176°–38°W | 1950–2016 | 92 | USA | National Ocean Service | 0.4677 | 0.6054 |
| Rikitea | 23°–08°S | 134°–57°W | 1969–2015 | 93 | French Polynesia | UH Sea Level Center | 0.8859 | 0.4982 |
| Santa Cruz | 00°–45°S | 090°–19°W | 1978–2015 | 96 | Ecuador | UH Sea Level Center | 0.9016 | 0.9281 |
| Los Angeles, CA | 33°–43°N | 118°–16°W | 1923–2016 | 99 | USA | National Ocean Service | 0.6589 | 0.6276 |
| Cape May, NJ | 38°–58°N | 074°–58°W | 1965–2016 | 91 | USA | National Ocean Service | 0.8171 | 0.7386 |
| Ko Lak | 11°–48°N | 099°–49°E | 1985–2017 | 95 | Thailand | Naval Hydro. Dept. | 0.9157 | 0.9407 |
| Hong Kong-B | 22°–18°N | 114°–13°E | 1986–2016 | 99 | China | HK Observatory | 0.8045 | 0.1467 |
| Mission | Geosat | ERS-1 | Envisat | T/P Jason-1 | CryoSat-2 LRM | CryoSat-2 SAR/SIN | SARAL | HY-2A |
|---|---|---|---|---|---|---|---|---|
| α value | 0.006 | 0.022 | 0.09 | 0.0058 | 0.013 | 0.00744 | 0.0351 | 0.0105 |
| Mission | Retracker Description | Crossover Points | Min | Max | MEAN | RMS |
|---|---|---|---|---|---|---|
| HY-2A | No retracker | 125 | −0.984 | 0.958 | −0.287 | 0.412 |
| SDR—MLE4 | 125 | −0.985 | 0.833 | −0.280 | 0.391 | |
| 3-parameter | 125 | −0.975 | 0.916 | −0.290 | 0.389 | |
| 2-parameter | 125 | −0.918 | 0.630 | −0.272 | 0.377 | |
| Jason-1 GM | No retracker | 126 | −1.996 | 1.031 | 0.026 | 0.439 |
| SDR—MLE3 | 126 | −0.713 | 0.547 | 0.048 | 0.191 | |
| 3-parameter | 126 | −0.531 | 1.286 | 0.072 | 0.230 | |
| 2-parameter | 126 | −0.446 | 1.006 | 0.066 | 0.208 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Li, J.; Jin, T.; Che, D. HY-2A Altimeter Data Initial Assessment and Corresponding Two-Pass Waveform Retracker. Remote Sens. 2018, 10, 507. https://doi.org/10.3390/rs10040507
Zhang S, Li J, Jin T, Che D. HY-2A Altimeter Data Initial Assessment and Corresponding Two-Pass Waveform Retracker. Remote Sensing. 2018; 10(4):507. https://doi.org/10.3390/rs10040507
Chicago/Turabian StyleZhang, Shengjun, Jiancheng Li, Taoyong Jin, and Defu Che. 2018. "HY-2A Altimeter Data Initial Assessment and Corresponding Two-Pass Waveform Retracker" Remote Sensing 10, no. 4: 507. https://doi.org/10.3390/rs10040507
APA StyleZhang, S., Li, J., Jin, T., & Che, D. (2018). HY-2A Altimeter Data Initial Assessment and Corresponding Two-Pass Waveform Retracker. Remote Sensing, 10(4), 507. https://doi.org/10.3390/rs10040507