Estimation of Global Vegetation Productivity from Global LAnd Surface Satellite Data
Abstract
1. Introduction
2. Materials and Methods
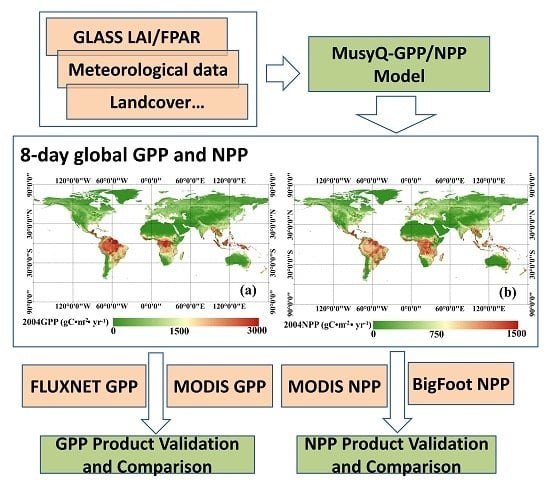
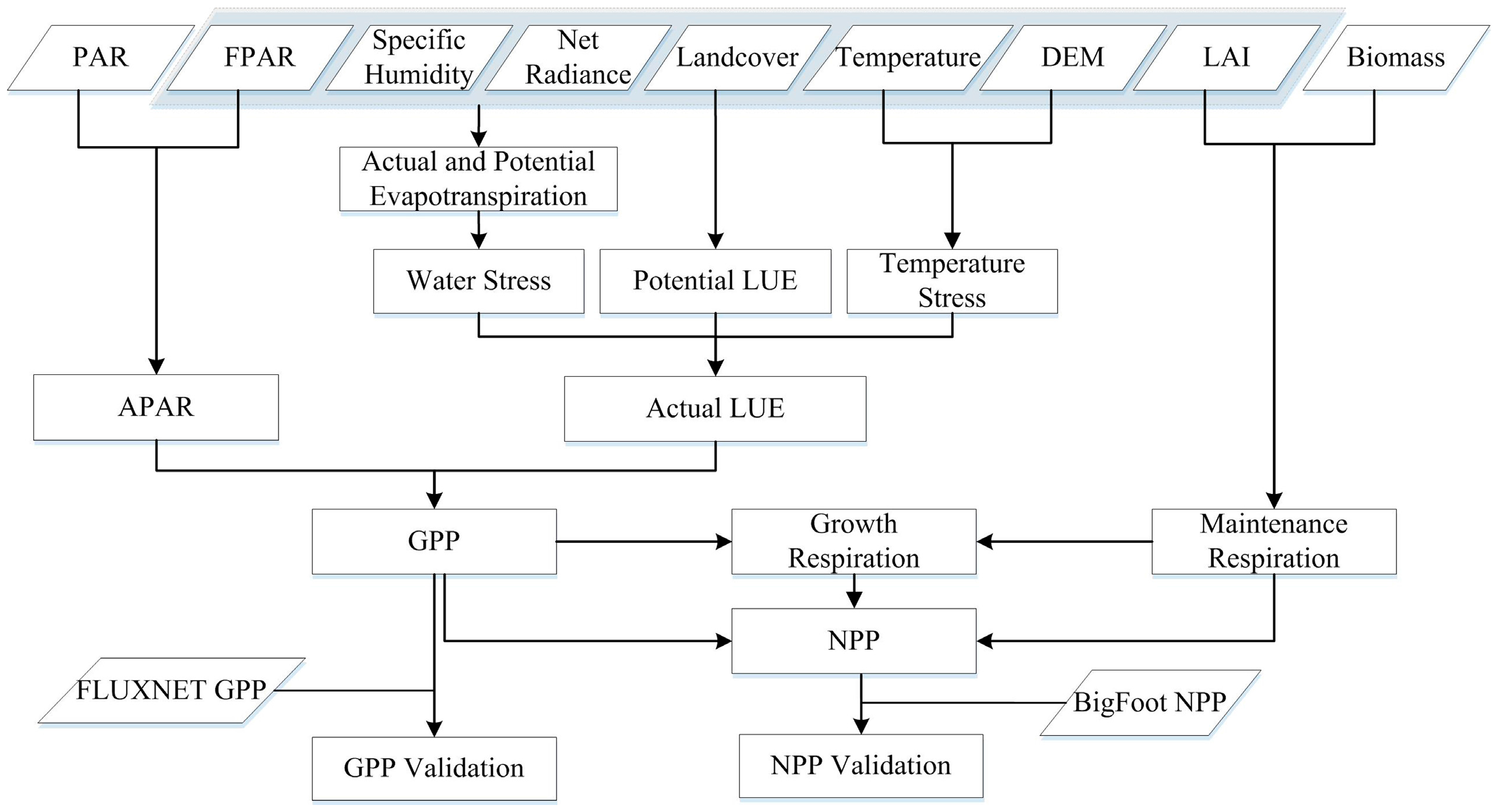
2.1. Method
2.1.1. Estimation of GPP and NPP
2.1.2. Validation of Estimated GLASS GPP and NPP
2.2. Data and Data Processing
2.2.1. Remote Sensing Data
2.2.2. Meteorological Data
2.2.3. Field Data
3. Results
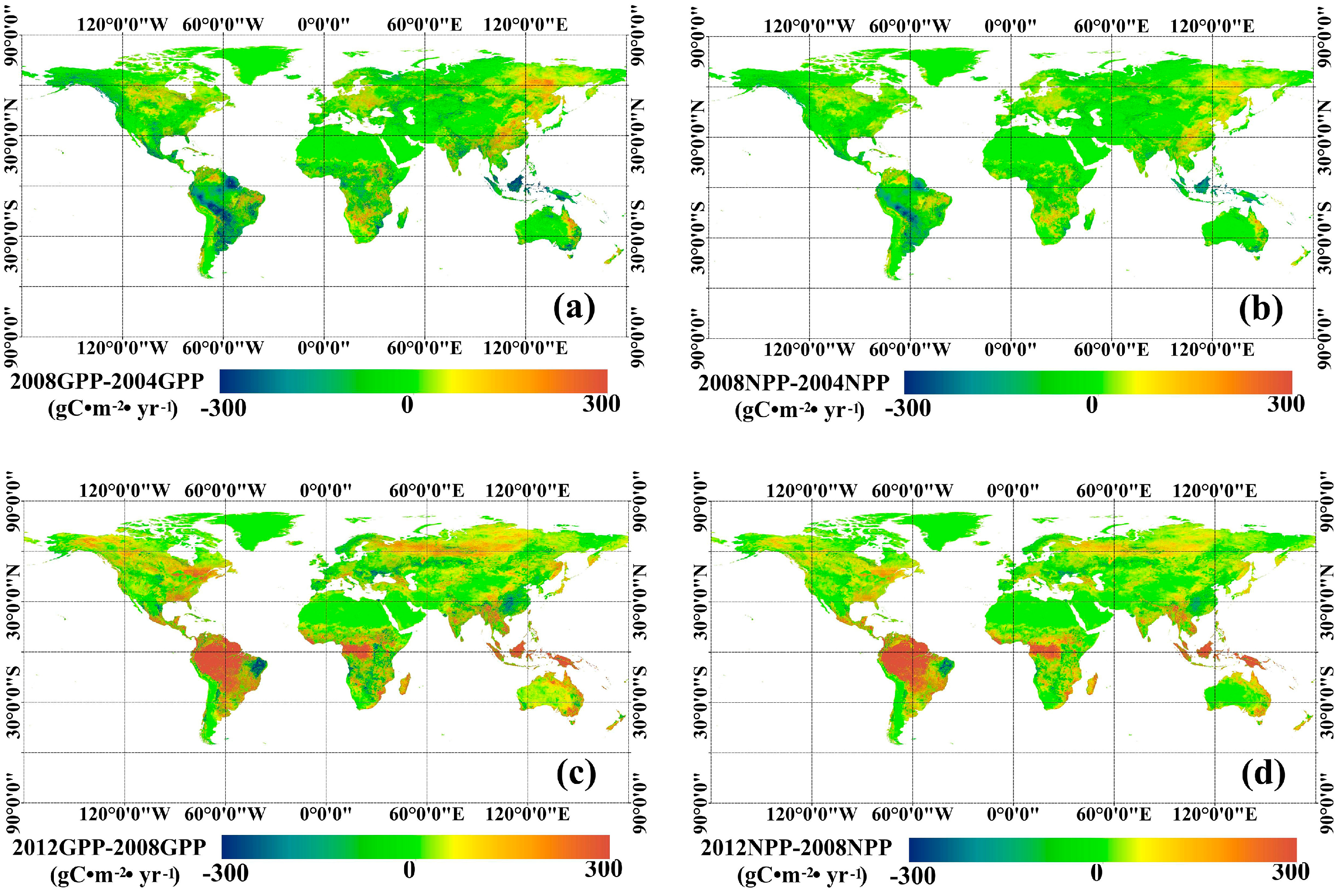
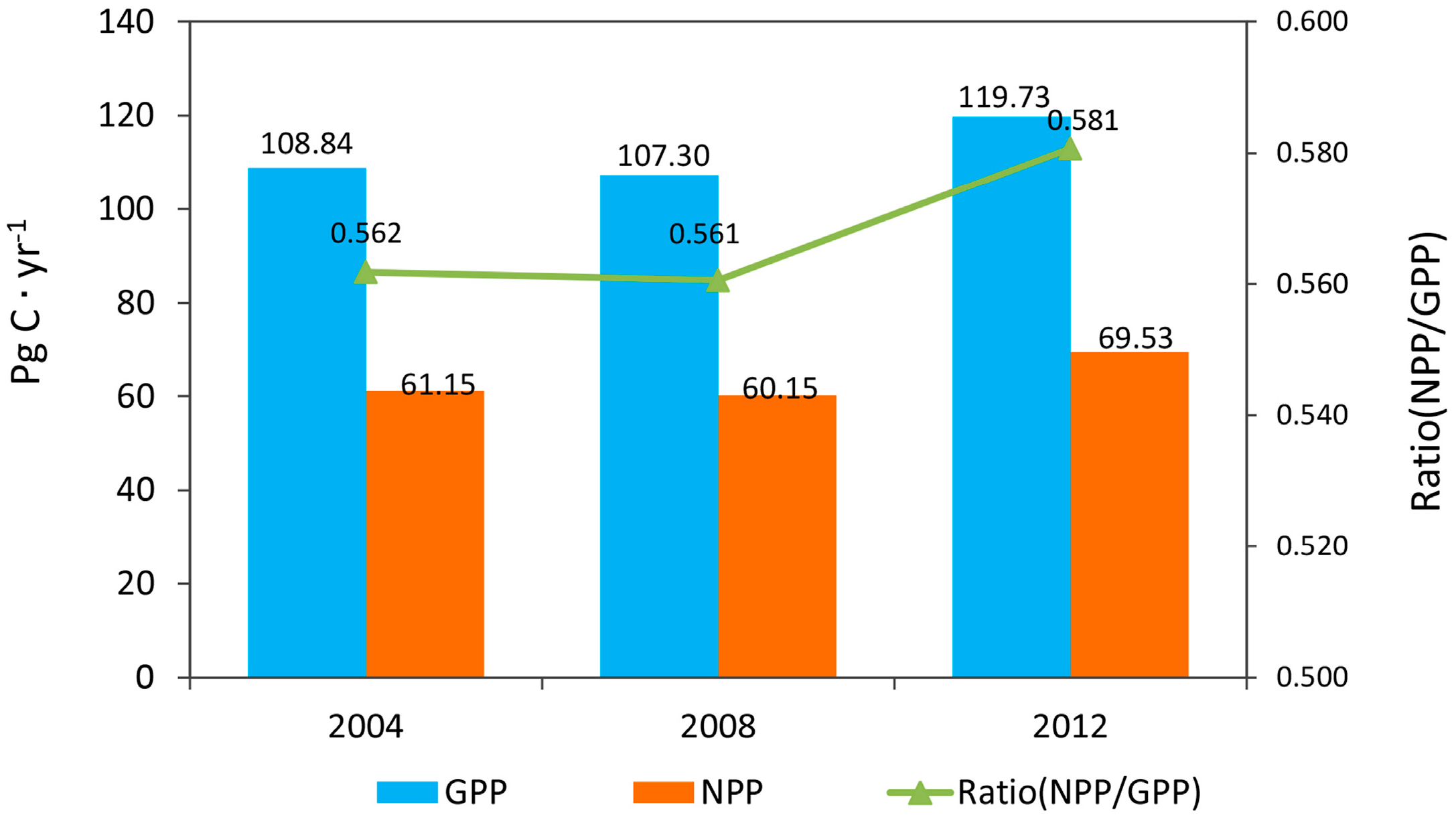
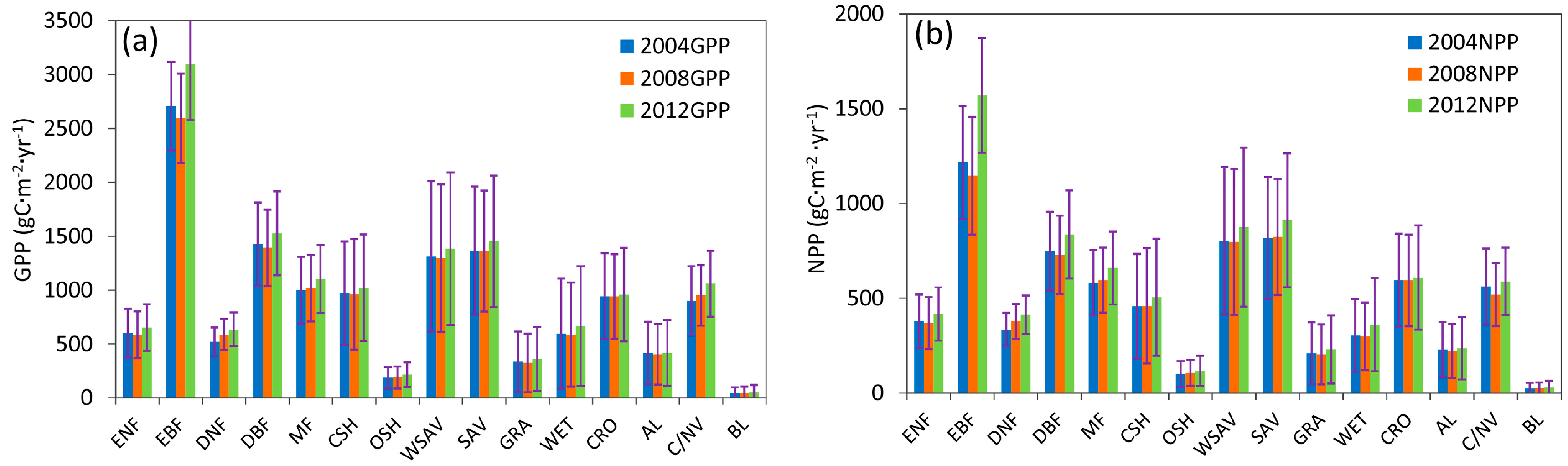
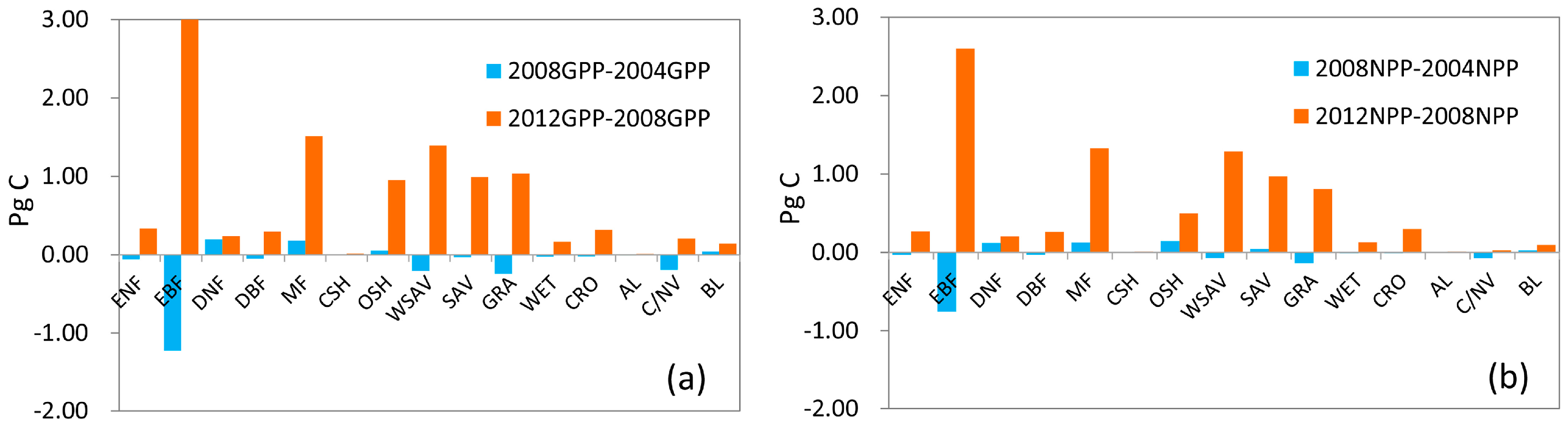
3.1. Temporal and Spatial Variation of Global GPP and NPP
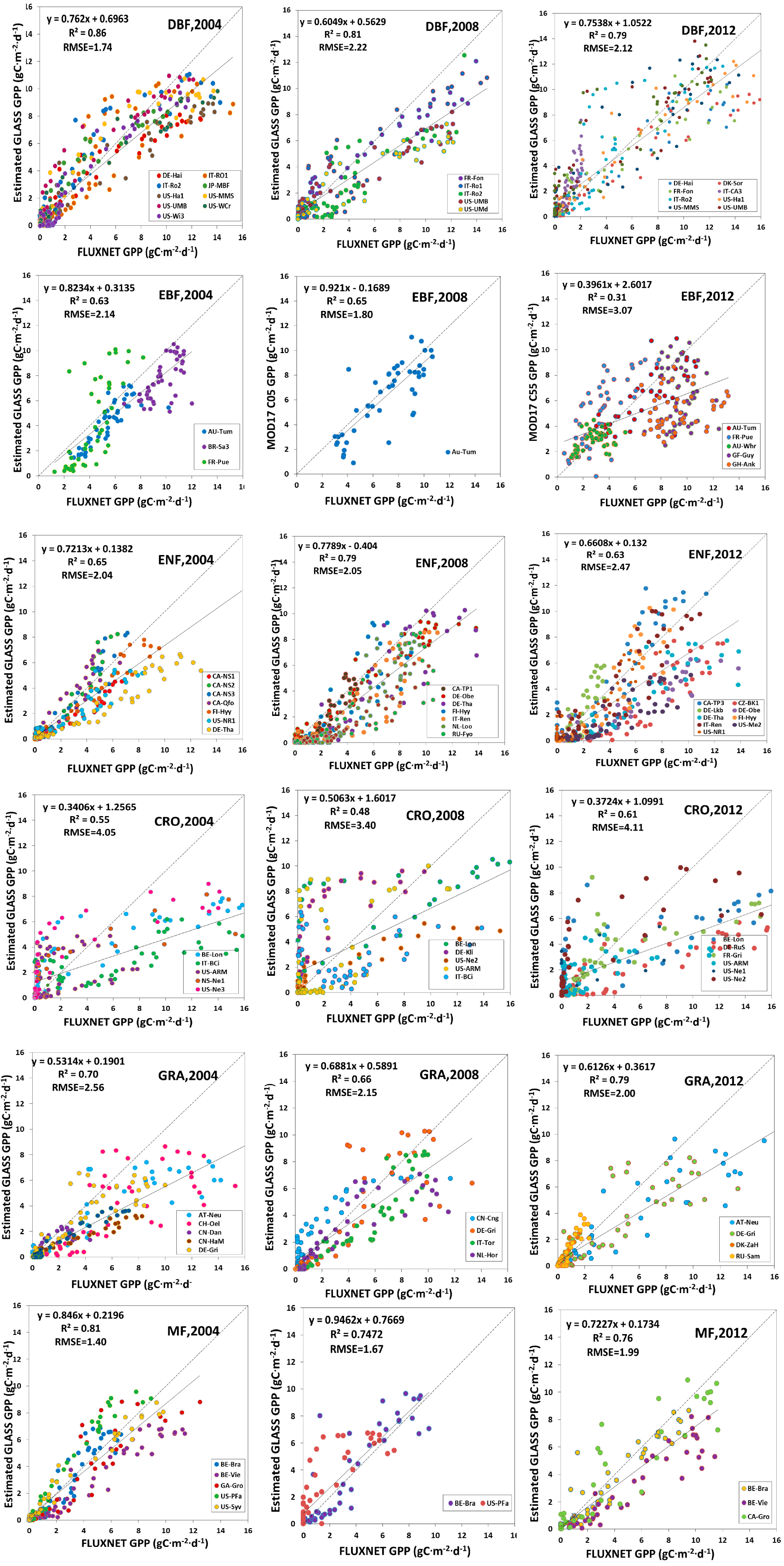
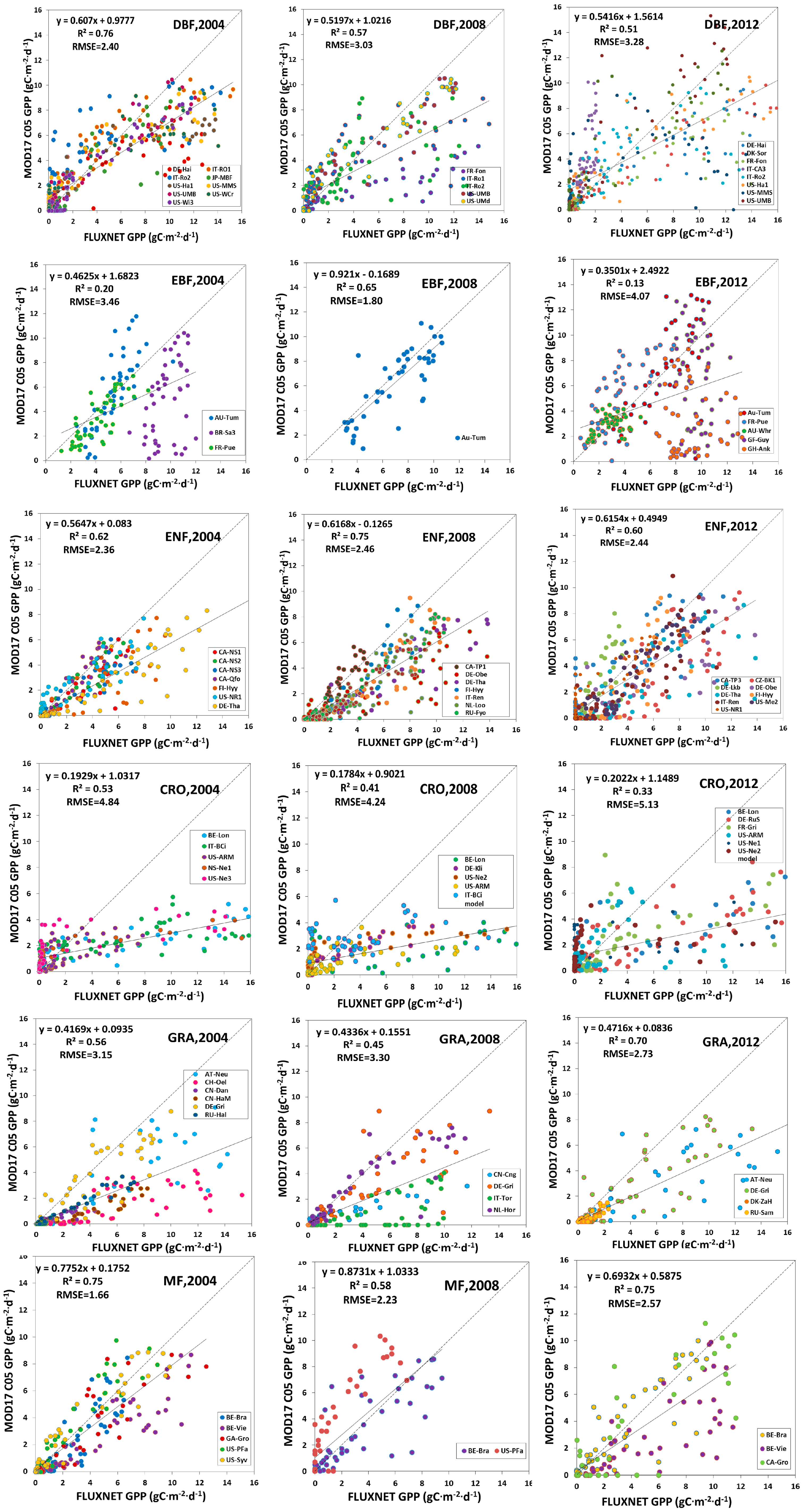
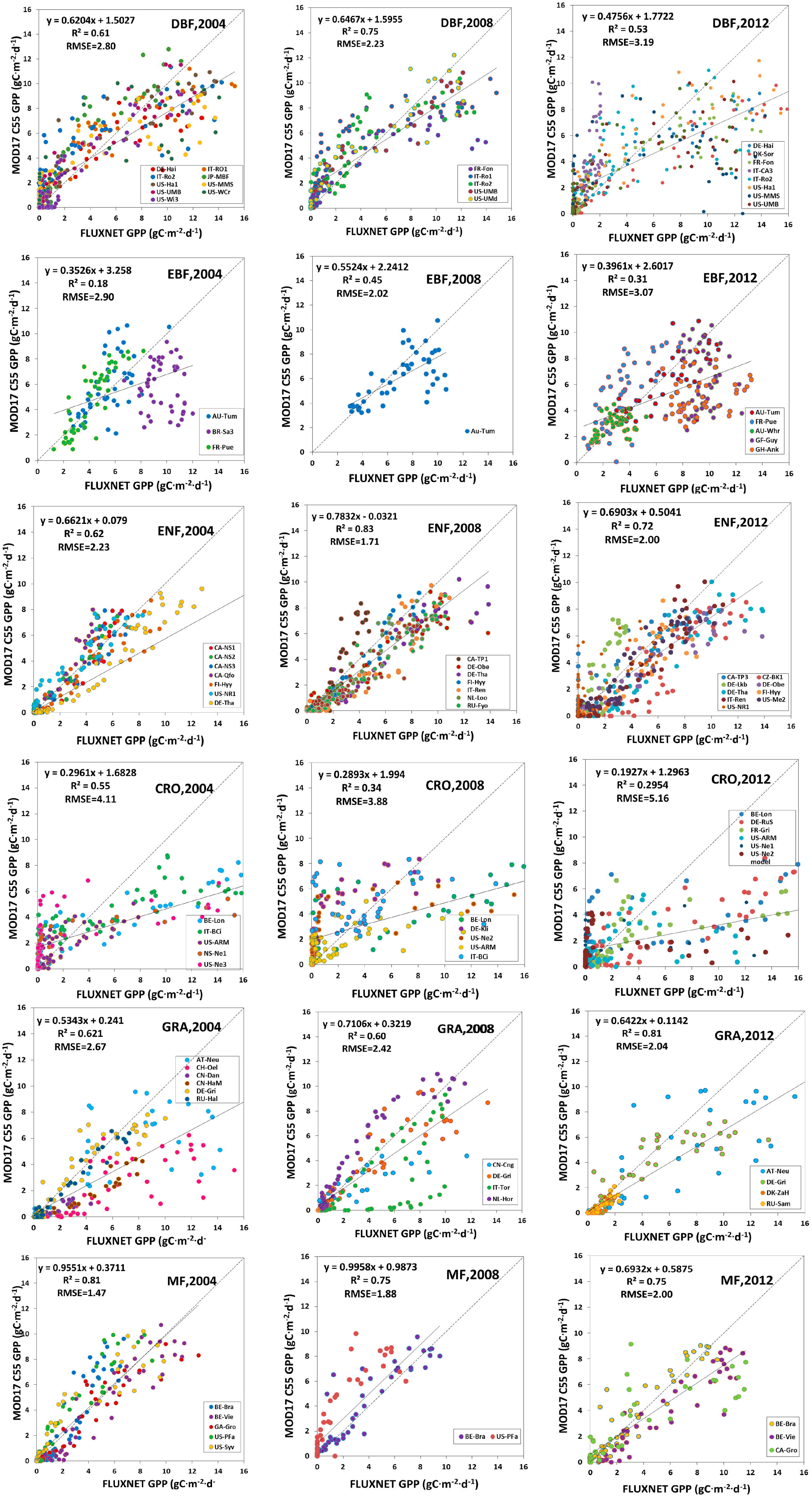
3.2. Validation of Estimated GLASS GPP
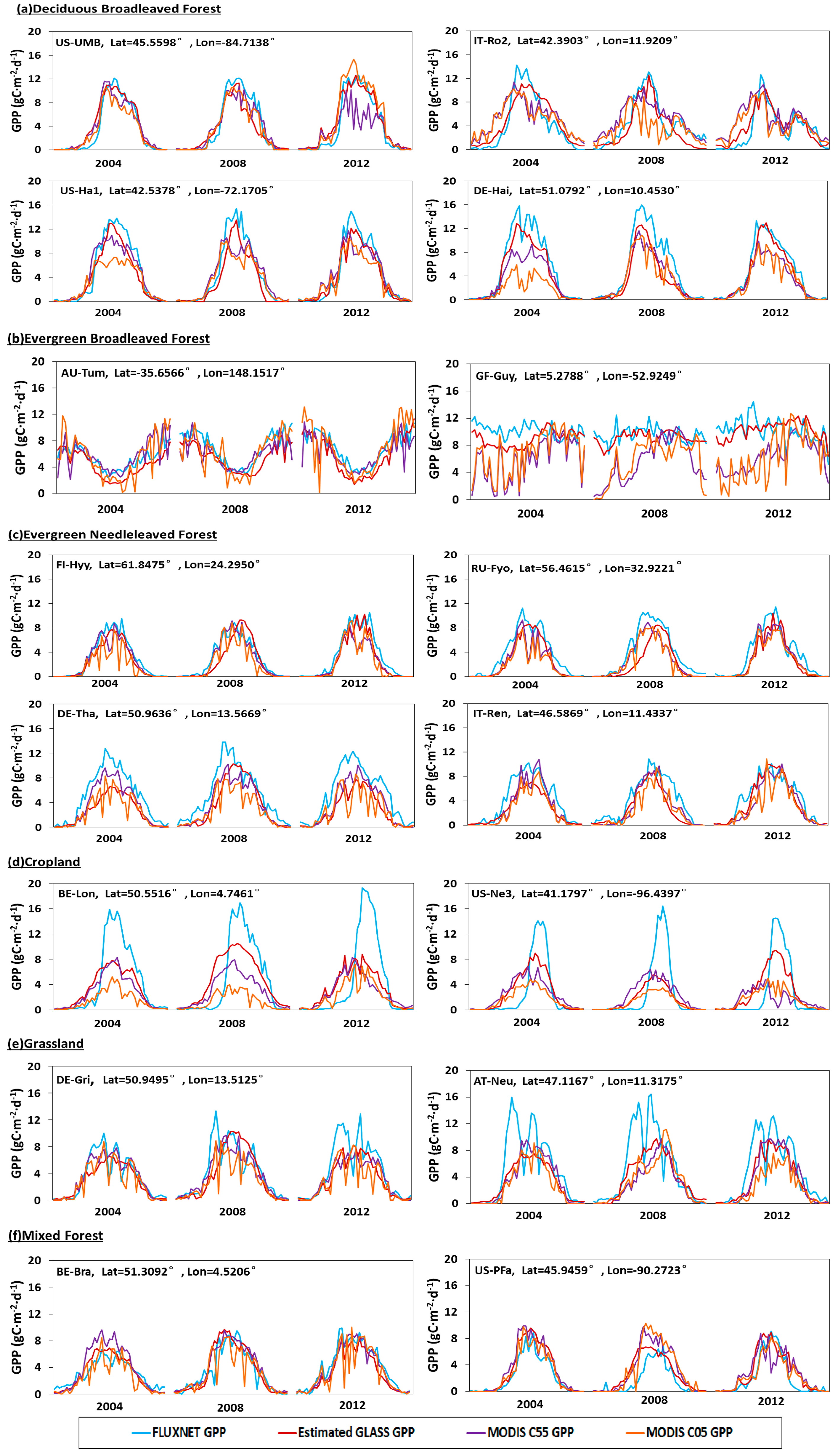
3.2.1. Seasonal Variation in GPP
3.2.2. Validation against FLUXNET GPP
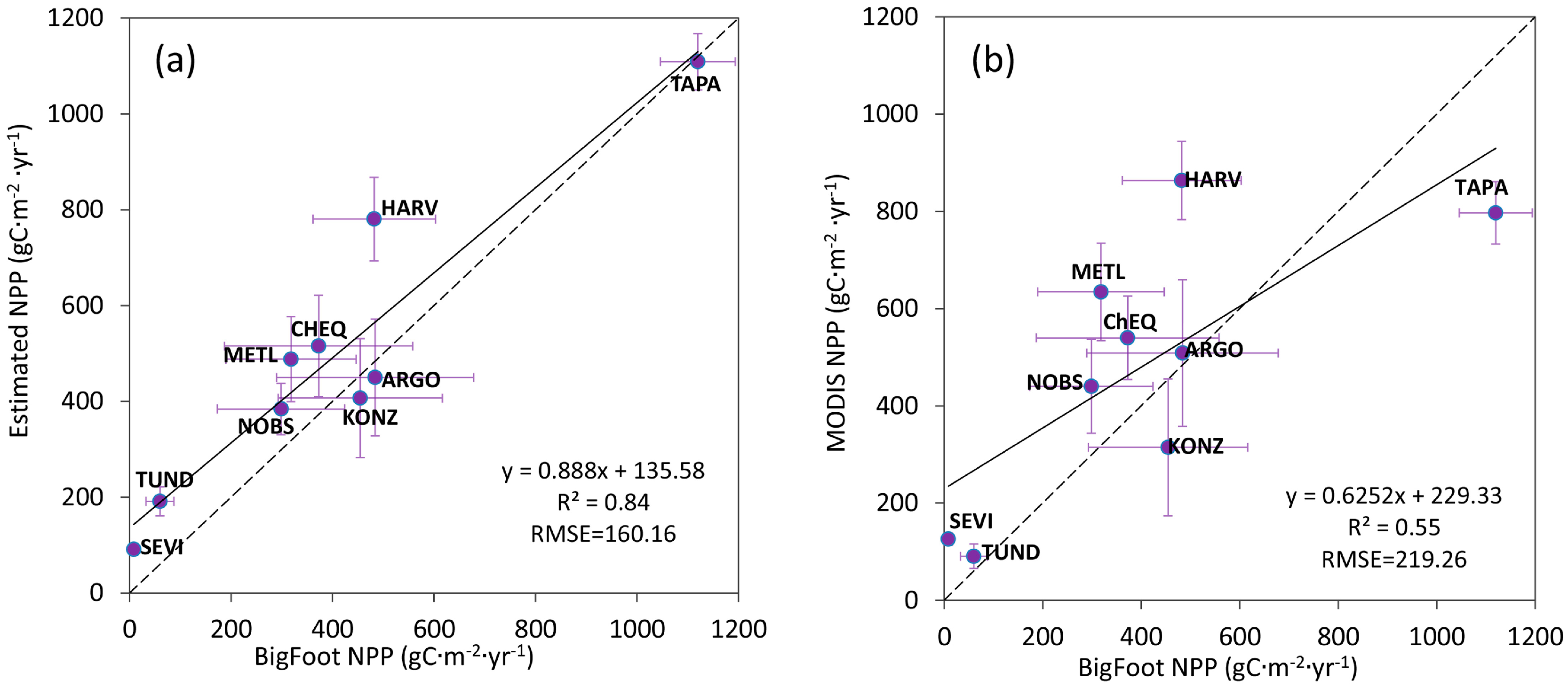
3.3. Validation of Estimated NPP
4. Discussion
4.1. Reasons for GPP Underestimation in Croplands
4.2. Limitations in NPP Validation
4.3. Future Work
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, J.M.; Mo, G.; Pisek, J.; Liu, J.; Deng, F.; Ishizawa, M.; Chan, D. Effects of foliage clumping on the estimation of global terrestrial gross primary productivity. Glob. Biogeochem. Cycles 2012, 26, GB1019. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. AIBS Bull. 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Heinsch, F.A.; Reeves, M.; Bowker, C.F. User’s Guide, GPP and NPP (MOD 17A2/A3) Products, NASA MODIS Land Algorithm. Available online: https://www.researchgate.net/publication/242118371_User’s_guide_GPP_and_NPP_MOD17A2A3_products_NASA_MODIS_land_algorithm (accessed on 5 December 2017).
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar] [CrossRef]
- Martínez, B.; Camacho, F.; Verger, A.; García-Haro, F.J.; Gilabert, M.A. Intercomparison and quality assessment of MERIS, MODIS and SEVIRI FAPAR products over the Iberian Peninsula. Int. J. Appl. Earth Obs. 2013, 21, 463–476. [Google Scholar] [CrossRef]
- McCallum, I.; Wagner, W.; Schmullius, C.; Shvidenko, A.; Obersteiner, M.; Fritz, S.; Nilsson, S. Comparison of four global FAPAR datasets over Northern Eurasia for the year 2000. Remote Sens. Environ. 2010, 114, 941–949. [Google Scholar] [CrossRef]
- Tao, X.; Liang, S.; Wang, D. Assessment of five global satellite products of fraction of absorbed photosynthetically active radiation: Intercomparison and direct validation against ground-based data. Remote Sens. Environ. 2015, 163, 270–285. [Google Scholar] [CrossRef]
- Ma, H.; Liu, Q.; Liang, S.; Xiao, Z. Simultaneous estimation of leaf area index, fraction of absorbed photosynthetically active radiation, and surface albedo from multiple-satellite data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4334–4354. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of general regression neural networks for generating the GLASS leaf area index product from time series MODIS surface reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Xiang, Y.; Zhao, X.; Song, J. Long-time-series global land surface satellite leaf area index product derived from MODIS and AVHRR surface reflectance. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5301–5318. [Google Scholar] [CrossRef]
- Liang, S.; Zhao, X.; Liu, S.; Yuan, W.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H.; et al. A long-term Global LAnd Surface Satellite (GLASS) data-set for environmental studies. Int. J. Digit. Earth 2013, 6 (Suppl. S1), 5–33. [Google Scholar] [CrossRef]
- Fang, H.; Jiang, C.; Li, W.; Wei, S.; Baret, F.; Chen, J.; Garcia-Haro, J.; Liang, S.; Liu, R.; Myneni, R.; et al. Characterization and intercomparison of global moderate resolution leaf area index (LAI) products: Analysis of climatologies and theoretical uncertainties. J. Geophys. Res. Biogeogr. 2013, 118, 529–548. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Sun, R.; Wang, J.; Jiang, B. Estimating the fraction of absorbed photosynthetically active radiation from the MODIS data based GLASS leaf area index product. Remote Sens. Environ. 2015, 171, 105–117. [Google Scholar] [CrossRef]
- Lieth, H. Modeling the primary productivity of the world. In Primary Productivity of the Biosphere; Springer: Berlin/ Heidelberg, Germany, 1975; pp. 237–263. [Google Scholar]
- Uchijima, Z.; Seino, H. Agroclimatic evaluation of net primary productivity of natural vegetations. J. Agric. Meteorol. 1985, 40, 343–352. [Google Scholar] [CrossRef]
- Running, S.W.; Thornton, P.E.; Nemani, R.; Glassy, J.M. Global terrestrial gross and net primary productivity from the Earth Observing System. In Methods in Ecosystem Science; Springer: Berlin/ Heidelberg, Germany, 2000; Volume 3, pp. 44–45. [Google Scholar]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Prince, S.D.; Goward, S.N. Global primary production: A remote sensing approach. J. Biogeogr. 1995, 22, 815–835. [Google Scholar] [CrossRef]
- Parton, W.J.; Scurlock, J.M.O.; Ojima, D.S.; Gilmanov, T.G.; Scholes, R.J.; Schimel, D.S.; Kirchner, T.; Menaut, J.-C.; Garcia, M.E.; Kamnalrut, A.; et al. Observations and modeling of biomass and soil organic matter dynamics for the grassland biome worldwide. Glob. Biogeochem. Cycles 1993, 7, 785–809. [Google Scholar] [CrossRef]
- McGuire, A.D.; Melillo, J.M.; Kicklighter, D.W.; Joyce, L.A. Equilibrium responses of soil carbon to climate change: Empirical and process-based estimates. J. Biogeogr. 1995, 22, 785–796. [Google Scholar] [CrossRef]
- Running, S.W.; Hunt, E.R., Jr. Generalization of a forest ecosystem process model for other biomes, BIOME-BCG, and an application for global-scale models. In Scaling Physiological Processes; Academic Press: San Diego, CA, USA, 1993; pp. 141–158. [Google Scholar]
- Cui, T.; Wang, Y.; Sun, R.; Qiao, C.; Fan, W.; Jiang, G.; Hao, L.; Zhang, L. Estimating vegetation primary production in the Heihe River Basin of China with multi-source and multi-scale data. PLoS ONE 2016, 11, e0153971. [Google Scholar] [CrossRef] [PubMed]
- Running, S.W.; Zhao, M.S. User’s Guide. Daily GPP and Annual NPP (MOD17A2/A3) Products NASA Earth Observing System MODIS Land Algorithm. Version 3.0 for Collection 6. 2015. Available online: https://lpdaac.usgs.gov/sites/default/files/public/product_documentation/mod17_user_guide.pdf (accessed on 5 December 2017).
- Qiao, C.; Sun, R.; Xu, Z.; Zhang, L.; Liu, L.; Hao, L.; Jiang, G. A study of shelterbelt transpiration and cropland evapotranspiration in an irrigated area in the middle reaches of the Heihe River in northwestern China. IEEE Geosci. Remote Sens. 2015, 12, 369–373. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Mu, Q.; Jones, L.A.; Goetz, S.J.; Running, S.W. Satellite based analysis of northern ET trends and associated changes in the regional water balance from 1983 to 2005. J. Hydrol. 2009, 379, 92–110. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.M.; Cihlar, J.; Park, W.M. A process-based boreal ecosystem productivity simulator using remote sensing inputs. Remote Sens. Environ. 1997, 62, 158–175. [Google Scholar] [CrossRef]
- The GLASS LAI Product at Beijing Normal University. Available online: http://www.bnu-datacenter.com/en (accessed on 5 December 2017).
- The GLASS LAI Product at the Global Land Cover Facility. Available online: http://glcf.umd.edu (accessed on 5 December 2017).
- MODIS Land Cover Type/Dynamics. Available online: https://modis.gsfc.nasa.gov/data/dataprod/mod12.php (accessed on 5 December 2017).
- Channan, S.; Collins, K.; Emanuel, W.R. Global Mosaics of The Standard MODIS Land Cover Type Data; University of Maryland and the Pacific Northwest National Laboratory: College Park, MD, USA, 2014.
- Xiao, Z.; Wang, T.; Liang, S.; Sun, R. Estimating the fractional vegetation cover from GLASS leaf area index product. Remote Sens. 2016, 8, 337. [Google Scholar] [CrossRef]
- Carbon Dioxide Information Analysis Center. Available online: http://cdiac.ornl.go (accessed on 5 December 2017).
- Ruesch, A.; Gibbs, H.K. New IPCC Tier1 Global Biomass Carbon Map for the Year 2000; Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2008.
- Eggleston, H.S.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K. IPCC Guidelines for National Greenhouse Gas Inventories; Institute for Global Environmental Strategies: Hayama, Japan, 2006. [Google Scholar]
- Global Land Data Assimilation System. Available online: http://ldas.gsfc.nasa.gov/gldas/GLDASgoals.php (accessed on 5 December 2017).
- Rodell, M.; Houser, P.R.; Jambor, U.E.A.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Fang, H.; Beaudoing, H.K.; Teng, W.L.; Vollmer, B.E. Global Land data assimilation system (GLDAS) products, services and application from NASA hydrology data and information services center (HDISC). In Proceedings of the ASPRS 2009 Annual Conference, Baltimore, MD, USA, 8–13 March 2009. [Google Scholar]
- Friend, A.D.; Arneth, A.; Kiang, N.Y.; Lomas, M.; Ogee, J.; RÖDENBECK, C.; Running, S.W.; Santaren, J.; Sitch, S.; Viovy, N.; et al. FLUXNET and modelling the global carbon cycle. Glob. Chang. Biol. 2007, 13, 610–633. [Google Scholar] [CrossRef]
- Knorr, W.; Kattge, J. Inversion of terrestrial ecosystem model parameter values against eddy covariance measurements by Monte Carlo sampling. Glob. Chang. Biol. 2005, 11, 1333–1351. [Google Scholar] [CrossRef]
- Fluxdata. Available online: http://fluxnet.fluxdata.org (accessed on 5 December 2017).
- Cohen, W.B.; Turner, D.P.; Gower, S.T.; Running, S.W. Linking In Situ Measurements, Remote Sensing, and Models to Validate MODIS Products Related to the Terrestrial Carbon Cycle. NASA Terrestrial Ecology Program. 2009. Available online: http://www.fsl.orst.edu/larse/bigfoot/index.html (accessed on 5 December 2017).
- Yuan, W.; Liu, S.; Yu, G.; Bonnefond, J.M.; Chen, J.; Davis, K.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F.; et al. Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data. Remote Sens. Environ. 2010, 114, 1416–1431. [Google Scholar] [CrossRef]
- Field, C.B.; Behrenfeld, M.J.; Randerson, J.T.; Falkowski, P. Primary production of the biosphere: Integrating terrestrial and oceanic components. Science 1998, 281, 237–240. [Google Scholar] [CrossRef] [PubMed]
- Cramer, W.; Kicklighter, D.W.; Bondeau, A.; Moore, B., III; Churkina, G.; Nemry, B.; Ruimy, A.; Schloss, A.L.; Model, P.O.T.P.N. Comparing global models of terrestrial net primary productivity (NPP): Overview and key results. Glob. Chang. Boil. 1999, 5, 1–15. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Maeirsperger, T.K.; Gower, S.T.; Kirschbaum, A.A.; Running, S.W.; Zhao, M.; Wofsy, S.C.; Dunn, A.L.; et al. Site-level evaluation of satellite-based global terrestrial gross primary production and net primary production monitoring. Glob. Chang. Biol. 2005, 11, 666–684. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M.; Saleska, S.R.; et al. Evaluation of MODIS NPP and GPP products across multiple biomes. Remote Sens. Environ. 2006, 102, 282–292. [Google Scholar] [CrossRef]
- Yuan, W.; Cai, W.; Nguy-Robertson, A.L.; Fang, H.; Suyker, A.E.; Chen, Y.; Dong, W.; Liu, S.; Zhang, H. Uncertainty in simulating gross primary production of cropland ecosystem from satellite-based models. Agric. For. Meteorol. 2015, 207, 48–57. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, Q.; Jiang, J.I.E.; Tang, Y. Calibration of Terra/MODIS gross primary production over an irrigated cropland on the North China Plain and an alpine meadow on the Tibetan Plateau. Glob. Chang. Biol. 2008, 14, 757–767. [Google Scholar] [CrossRef]
- Zhang, Q.; Cheng, Y.B.; Lyapustin, A.I.; Wang, Y.; Gao, F.; Suyker, A.; Verma, S.; Middleton, E.M. Estimation of crop gross primary production (GPP): FAPAR chl versus MOD15A2 FPAR. Remote Sens. Environ. 2014, 153, 1–6. [Google Scholar] [CrossRef]
- Turner, D.P.; Ollinger, S.; Smith, M.L.; Krankina, O.; Gregory, M. Scaling net primary production to a MODIS footprint in support of earth observing system product validation. Int. J. Remote Sens. 2004, 25, 1961–1979. [Google Scholar] [CrossRef]
- Olson, R.J.; Holladay, S.K.; Cook, R.B.; Falge, E.; Baldocchi, D.; Gu, L. FLUXNET. Database of Fluxes, Site Characteristics, and Flux-Community Information; Oak Ridge National Laboratory (ORNL): Oak Ridge, TN, USA, 2004.
- Schuepp, P.H.; Leclerc, M.Y.; Macpherson, J.I.; Desjardins, R.L. Footprint prediction of scalar fluxes from analytical solutions of the diffusion equation. Bound. Layer Meteorol. 1990, 50, 353–373. [Google Scholar] [CrossRef]
- Sogachev, A.; Menzhulin, G.V.; Heimann, M.; Lloyd, J. A simple three-dimensional canopy—Planetary boundary layer simulation model for scalar concentrations and fluxes. Tellus B 2002, 54, 784–819. [Google Scholar]
- Chen, B.; Ge, Q.; Fu, D.; Yu, G.; Sun, X.; Wang, S.; Wang, H. Data-model fusion approach for upscaling gross ecosystem productivity to the landscape scale based on remote sensing and flux footprint modeling. Biogeosciences 2010, 7, 2943–2958. [Google Scholar] [CrossRef]
- Green, D.S.; Erickson, J.E.; Kruger, E.L. Foliar morphology and canopy nitrogen as predictors of light-use efficiency in terrestrial vegetation. Agric. For. Meteorol. 2003, 115, 163–171. [Google Scholar] [CrossRef]
- Van Oijen, M.; Dreccer, M.F.; Firsching, K.H.; Schnieders, B.J. Simple equations for dynamic models of the effects of CO2 and O3 on light-use efficiency and growth of crops. Ecol. Model. 2004, 179, 39–60. [Google Scholar] [CrossRef]
- Turner, D.P.; Gower, S.T.; Cohen, W.B.; Gregory, M.; Maiersperger, T.K. Effects of spatial variability in light use efficiency on satellite-based NPP monitoring. Remote Sens. Environ. 2002, 80, 397–405. [Google Scholar] [CrossRef]
- Ito, A.; Oikawa, T. Global Mapping of Terrestrial Primary Productivity and Light-Use Efficiency with a Process-Based Model; Global Environmental Change in the Ocean and on Land, Terrapub: Tokyo, Japan, 2004; pp. 343–358. [Google Scholar]
- Still, C.J.; Randerson, J.T.; Fung, I.Y. Large-scale plant light-use efficiency inferred from the seasonal cycle of atmospheric CO2. Glob. Chang. Biol. 2004, 10, 1240–1252. [Google Scholar] [CrossRef]
- Xiao, X. Light absorption by leaf chlorophyll and maximum light use efficiency. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1933–1935. [Google Scholar] [CrossRef]

| Site Name | Latitude | Longitude | Biome Type | Year |
|---|---|---|---|---|
| NOBS | 55.8853 | −98.4773 | Boreal forest | 2001–2003 |
| AGRO | 40.0067 | −88.2915 | Crop | 2000 |
| HARV | 42.5285 | −72.1729 | Temperate mixed forest | 2003 |
| CHEQ | 45.9453 | −90.2731 | Temperate mixed forest | 2000–2002 |
| METL | 44.4508 | −121.5733 | Temperate needleleaf forest | 2002 |
| TAPA | −2.86957 | −54.9497 | Tropical broadleaf evergreen forest | 2004 |
| KONZ | 39.0890 | −96.5714 | Tallgrass prairie | 2000–2002 |
| SEVI | 34.3509 | −106.6900 | Desert | 2003 |
| TUND | 71.2719 | −156.6130 | Arctic tundra | 2002 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, T.; Sun, R.; Xiao, Z.; Zhang, Q.; Liu, G.; Cui, T.; Wang, J. Estimation of Global Vegetation Productivity from Global LAnd Surface Satellite Data. Remote Sens. 2018, 10, 327. https://doi.org/10.3390/rs10020327
Yu T, Sun R, Xiao Z, Zhang Q, Liu G, Cui T, Wang J. Estimation of Global Vegetation Productivity from Global LAnd Surface Satellite Data. Remote Sensing. 2018; 10(2):327. https://doi.org/10.3390/rs10020327
Chicago/Turabian StyleYu, Tao, Rui Sun, Zhiqiang Xiao, Qiang Zhang, Gang Liu, Tianxiang Cui, and Juanmin Wang. 2018. "Estimation of Global Vegetation Productivity from Global LAnd Surface Satellite Data" Remote Sensing 10, no. 2: 327. https://doi.org/10.3390/rs10020327
APA StyleYu, T., Sun, R., Xiao, Z., Zhang, Q., Liu, G., Cui, T., & Wang, J. (2018). Estimation of Global Vegetation Productivity from Global LAnd Surface Satellite Data. Remote Sensing, 10(2), 327. https://doi.org/10.3390/rs10020327