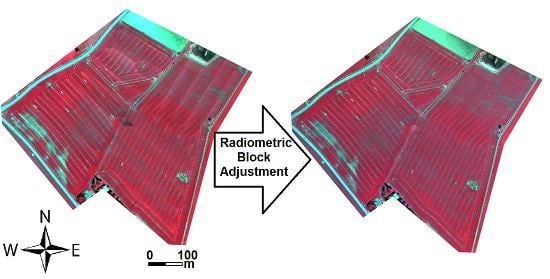
Radiometric Correction of Close-Range Spectral Image Blocks Captured Using an Unmanned Aerial Vehicle with a Radiometric Block Adjustment
Abstract
1. Introduction
2. Materials and Methods
2.1. Radiometric Block Adjustment of UAV Image Blocks
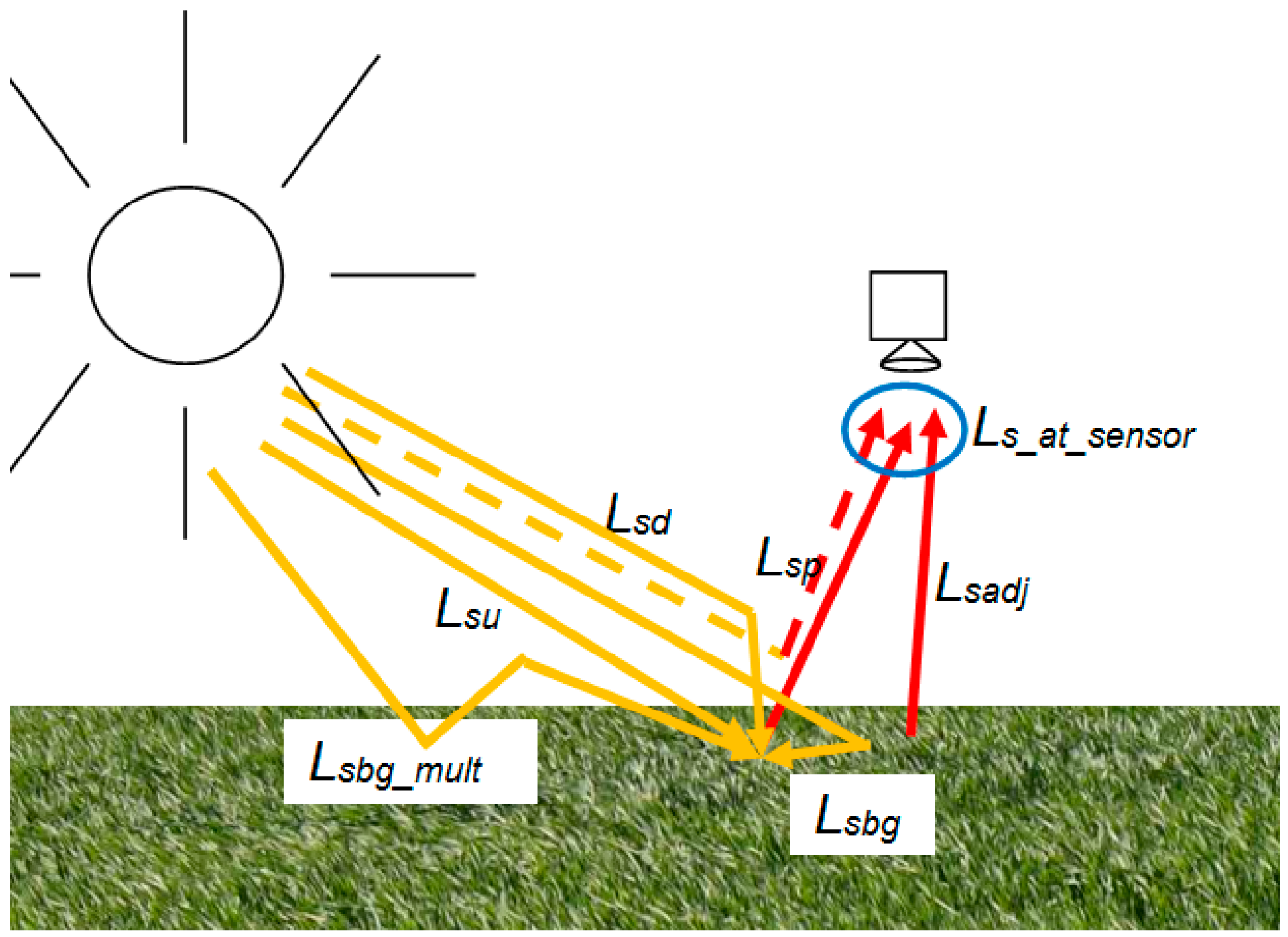
2.1.1. Radiometric Model
- Absolute reflectance transformation parameters for the entire block: ,
- image-wise relative correction parameters for number-of-images—1 images (one of the images is selected as the reference image): , ;
- BRDF model parameters: , m = 1, …, number-of-parameters;
- nadir reflectance for each radiometric tie point k: .
2.1.2. Weighting the Observations
2.1.3. Implementation
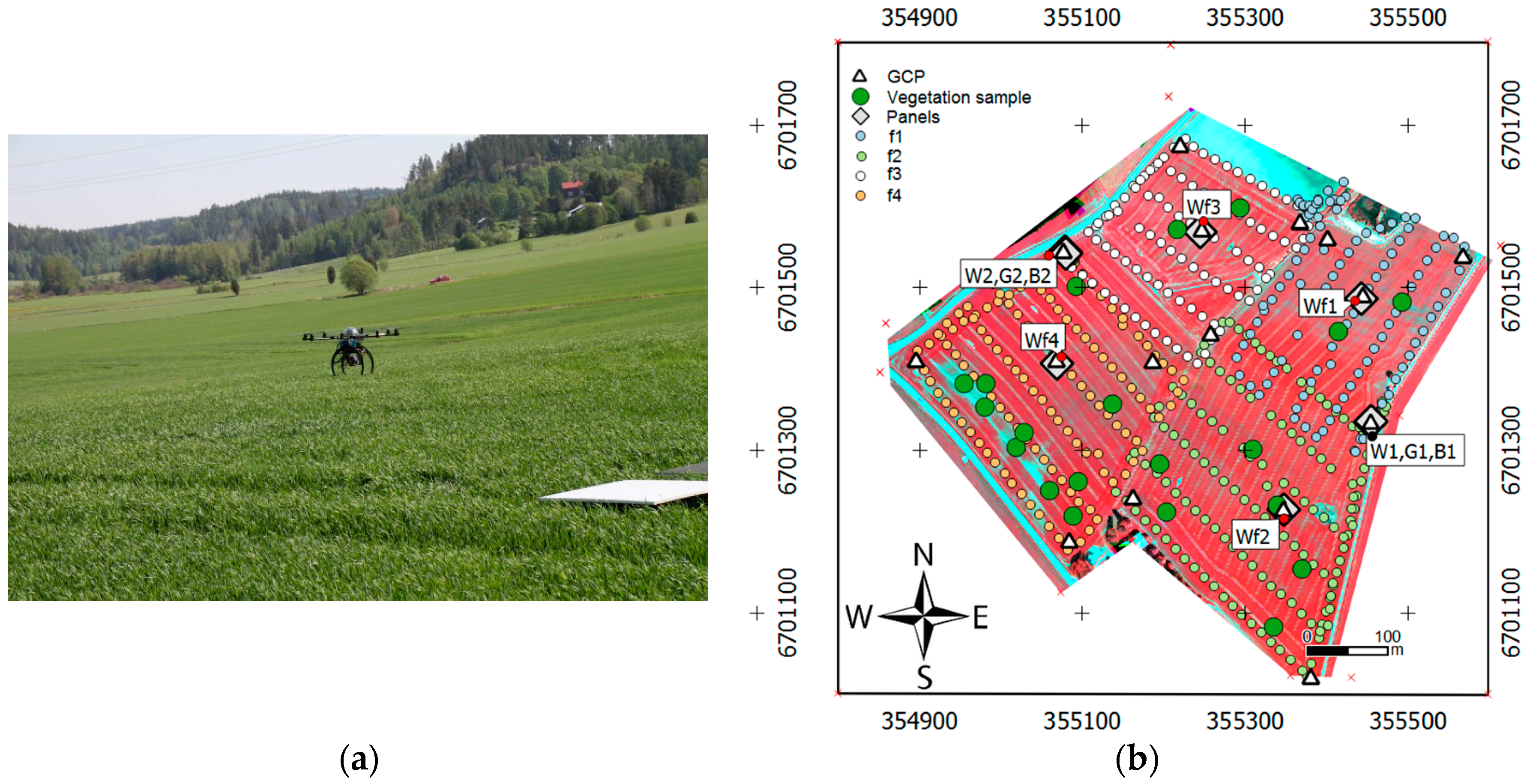
2.2. Agricultural Test Site
2.3. UAV Campaign
2.4. Data Processing Chain
- Applying radiometric laboratory calibration corrections to images;
- Determining the orientation parameters of the images;
- Using dense image matching to create a DSM;
- Determining a radiometric imaging model;
- Calculating the hyperspectral image mosaics.
2.4.1. Geometric Processing
2.4.2. Radiometric Processing
- Absolute calibration via the empirical line method for each of flights: f1, f2 and f34 (el3) and the combined flight f34 (el1); cases 1, 5;
- el3 or el1 and BRDF correction; cases 2, 6;
- or el1 and BRDF and relative image-wise corrections (); cases 3, 7;
- full model with absolute calibration and BRDF and corrections; cases 4, 8.
2.4.3. Mosaic and Point Cloud Calculations
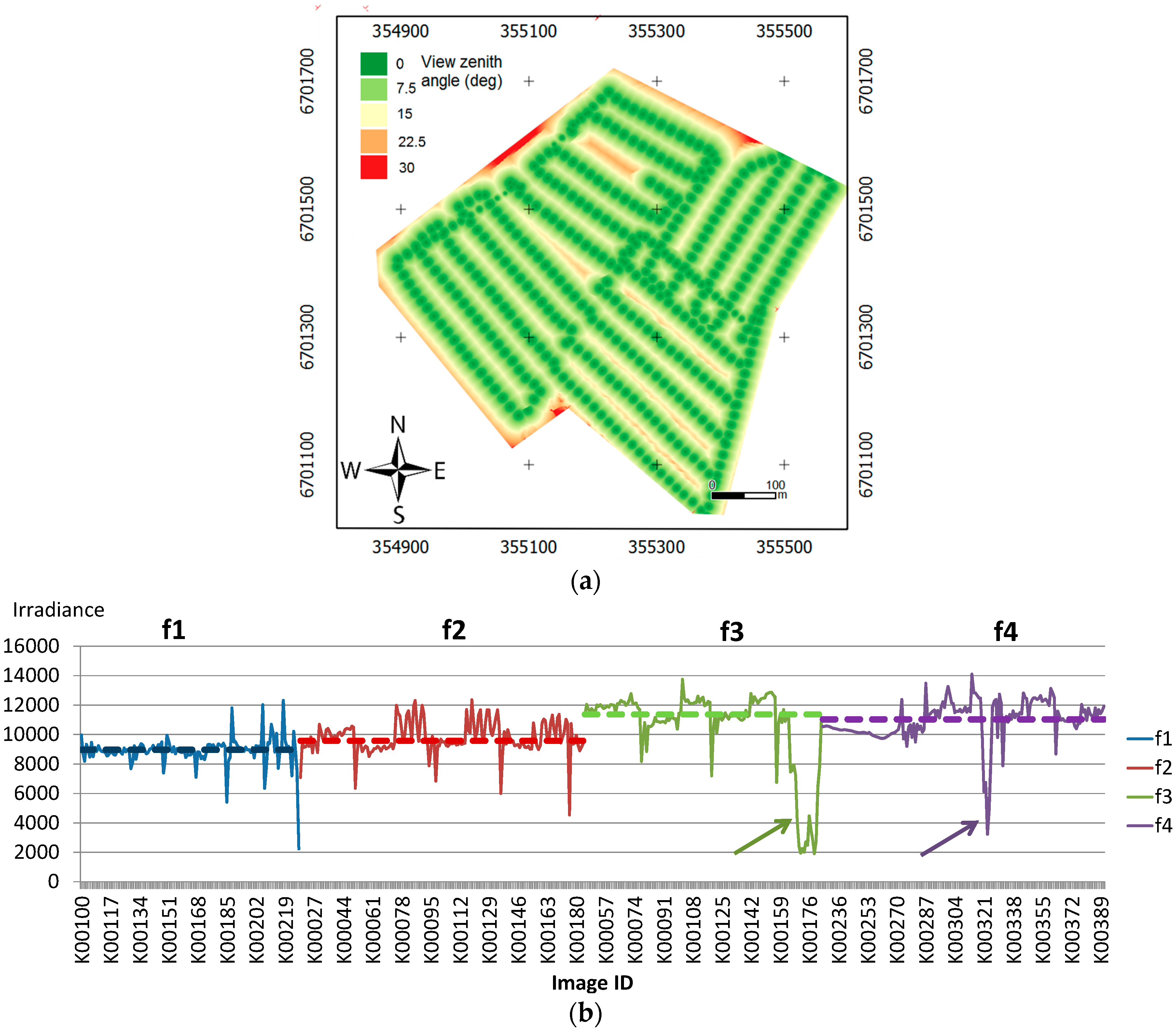
2.5. Performance Assessment
3. Results
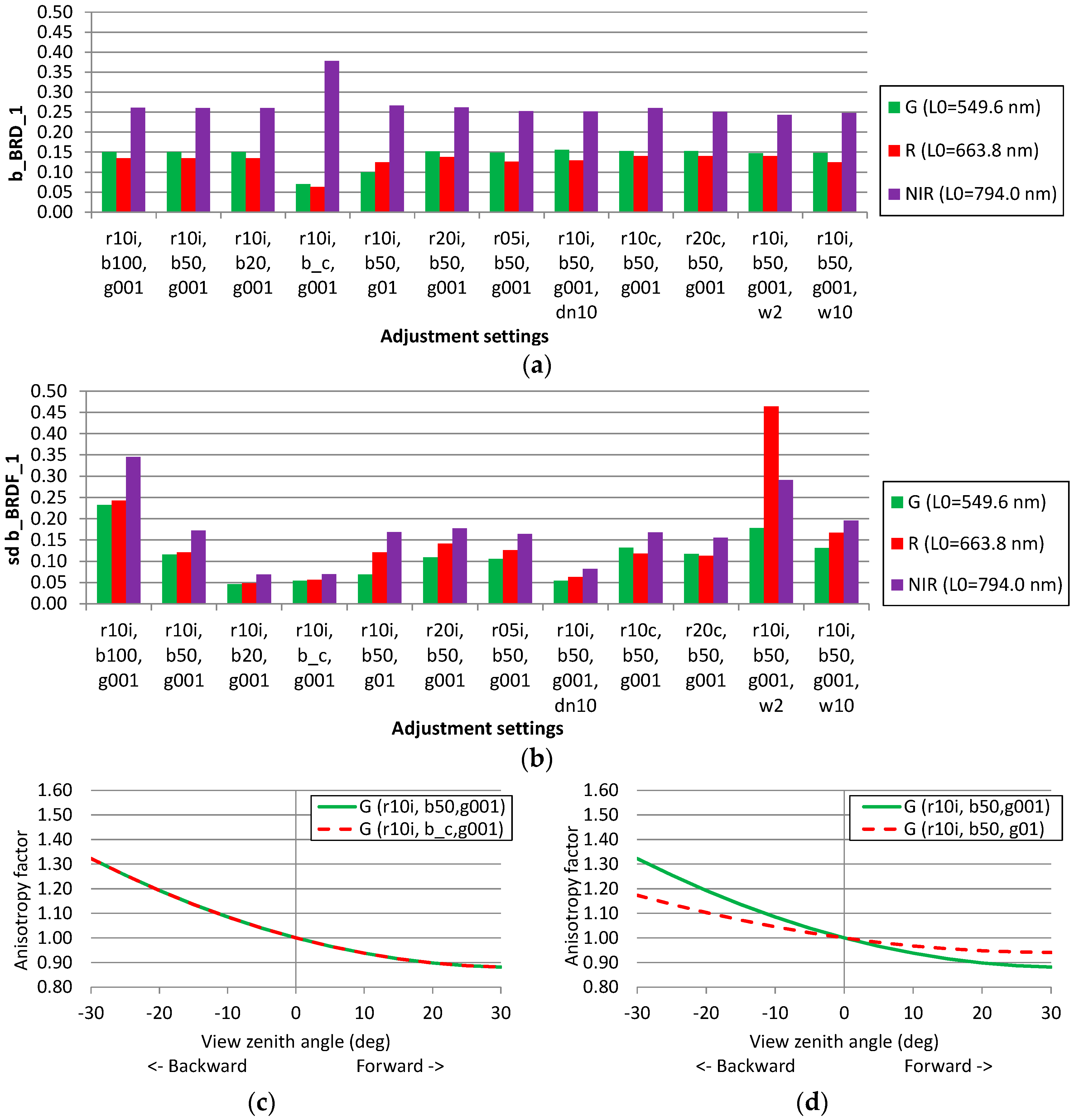
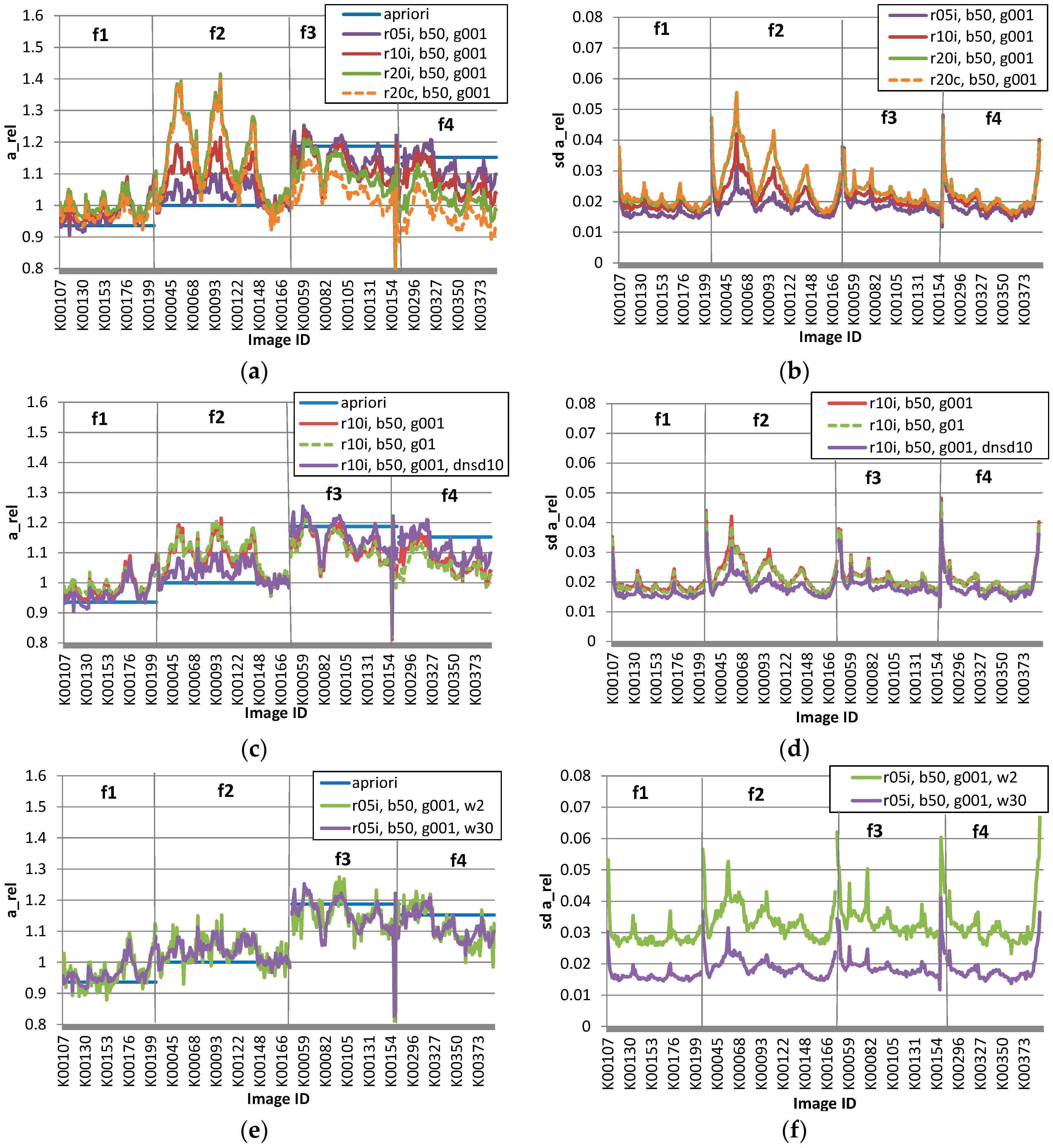
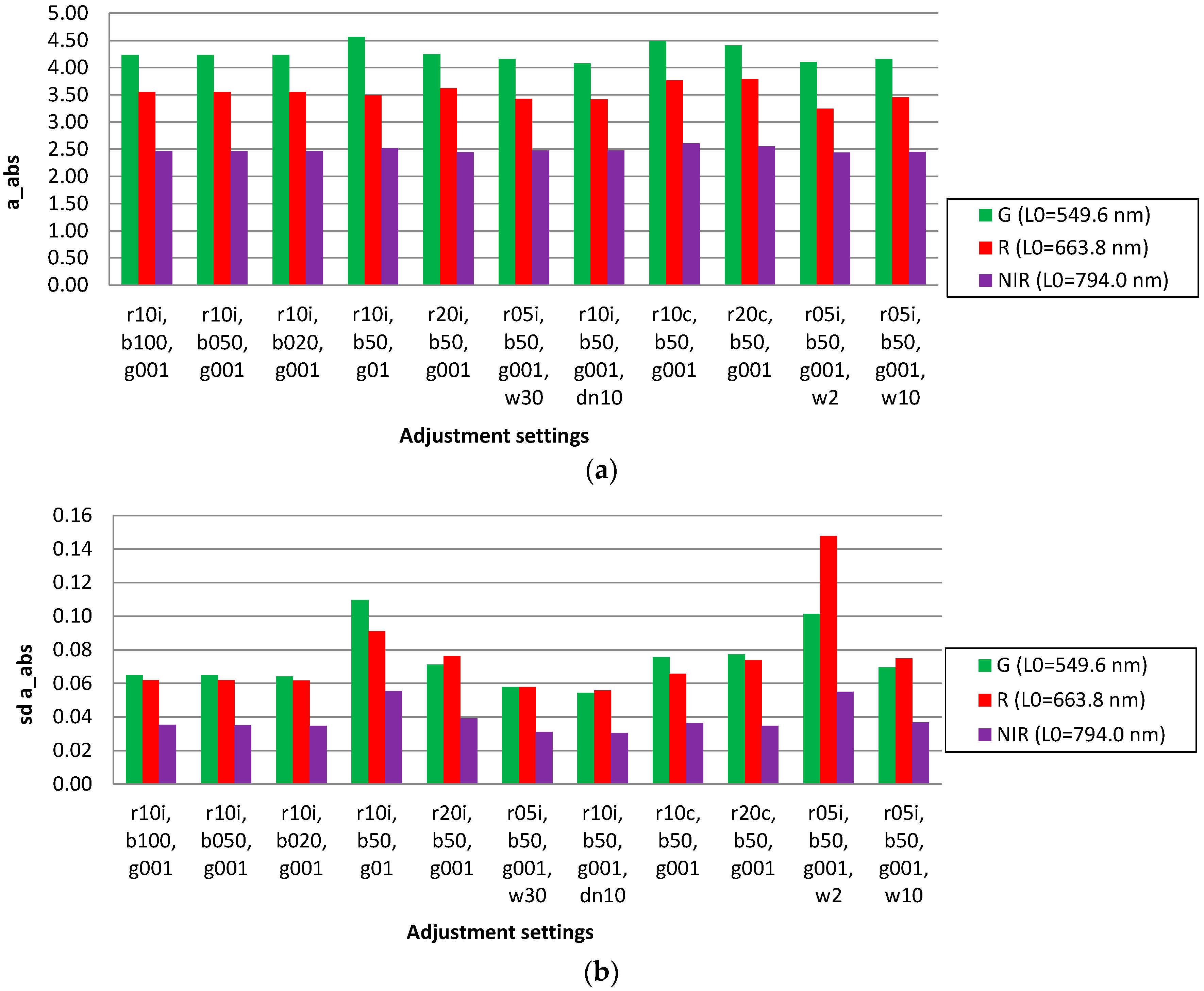
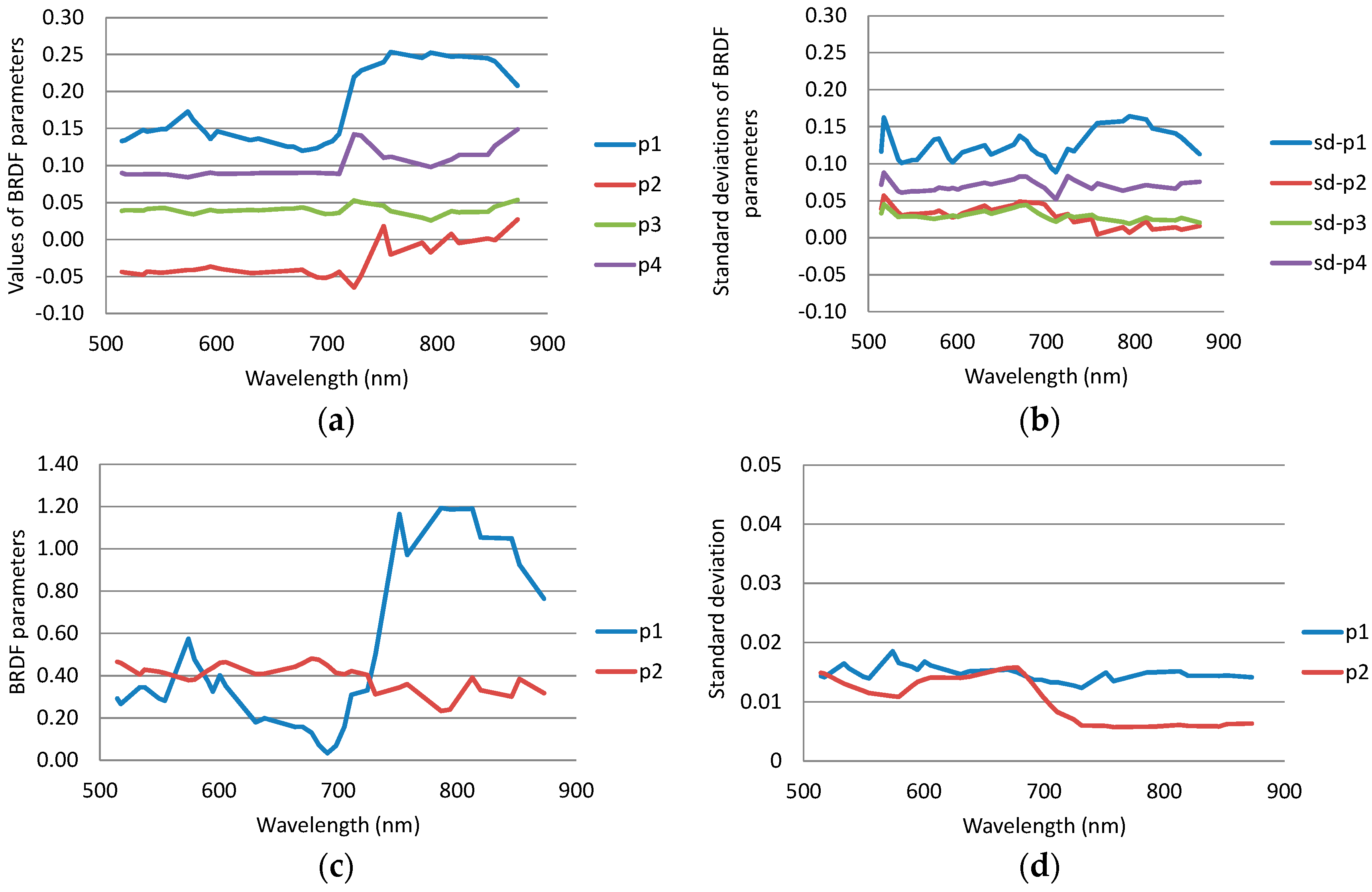
3.1. Studies of the Radiometric Model Parameters
3.1.1. Impact of Different Weighting, a Priori Values and Parameters
3.1.2. Impact of the Calibration Model
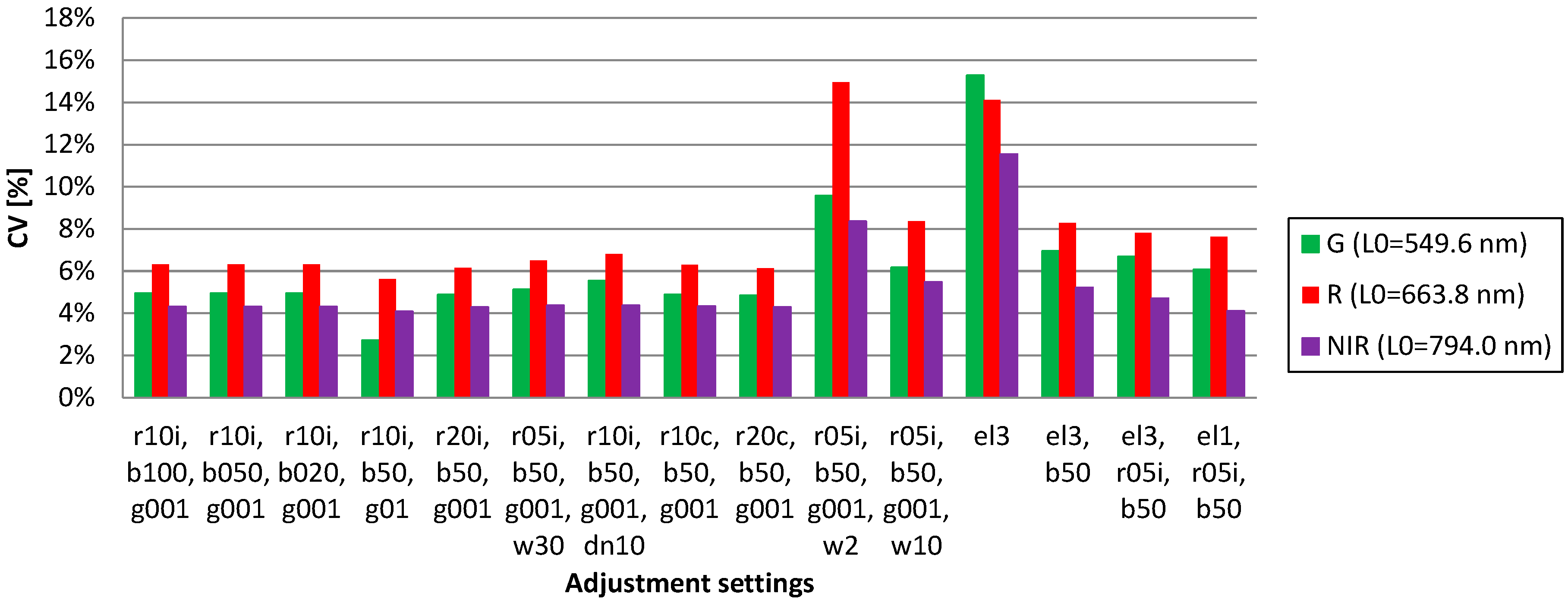
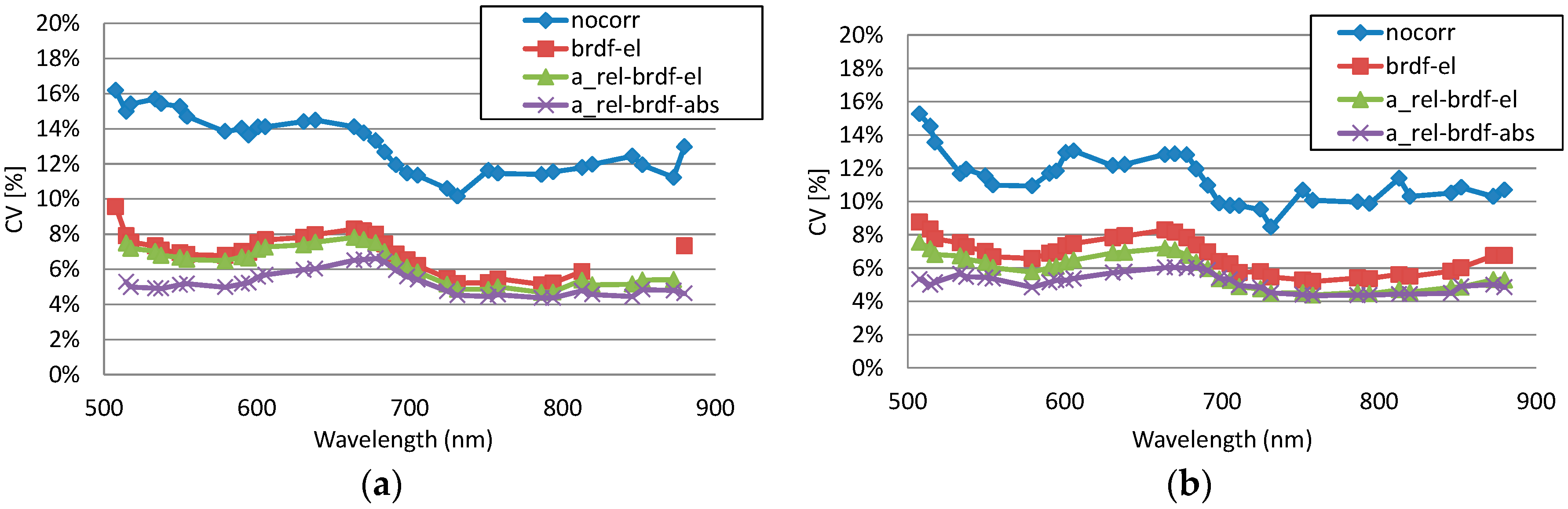
3.1.3. Coefficient of Variation Statistics
3.1.4. Selected Adjustment Model
3.2. Radiometric Adjustment of All Bands
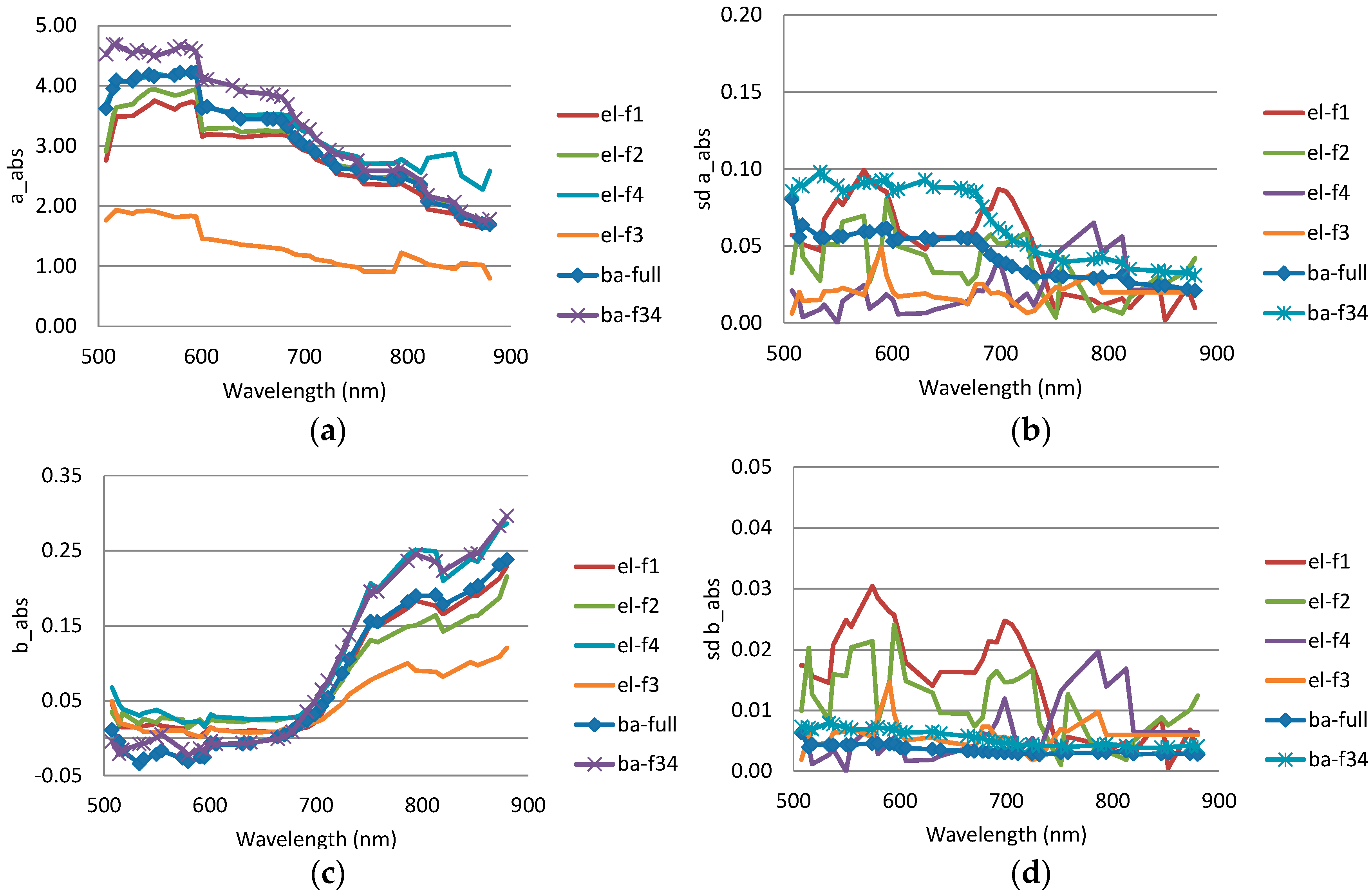
3.2.1. Reflectance Transformation Parameters
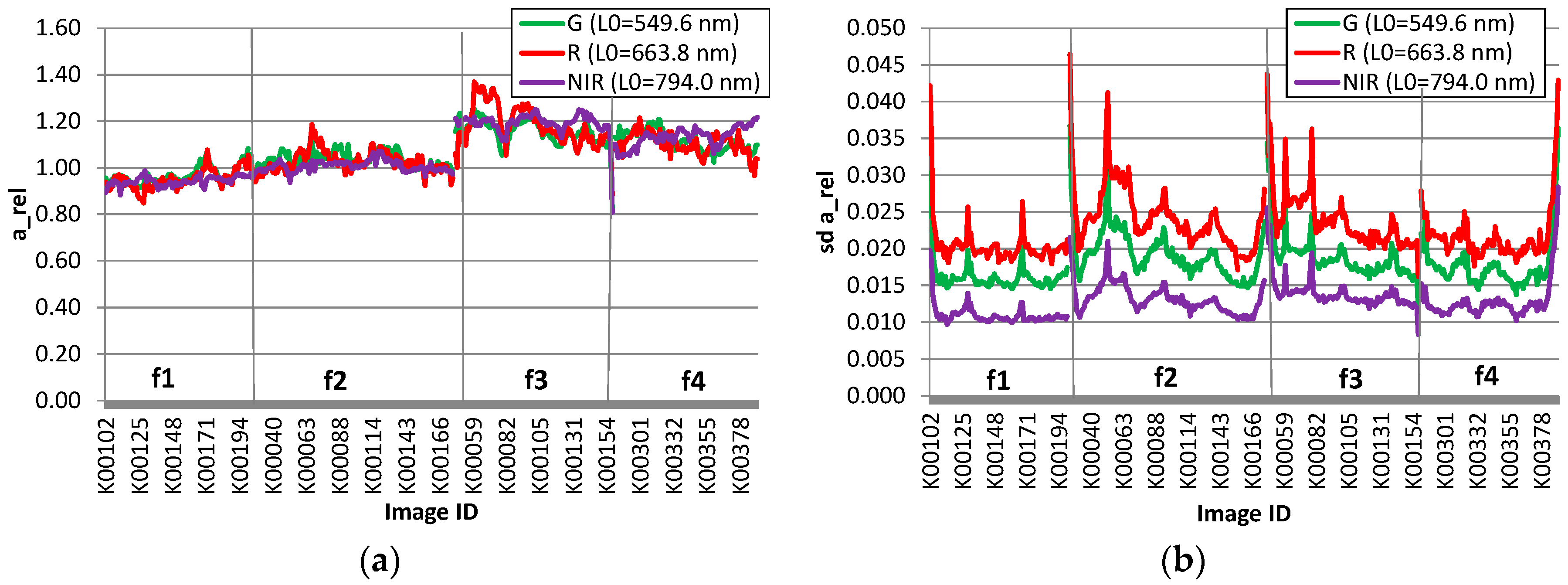
3.2.2. Relative Parameters
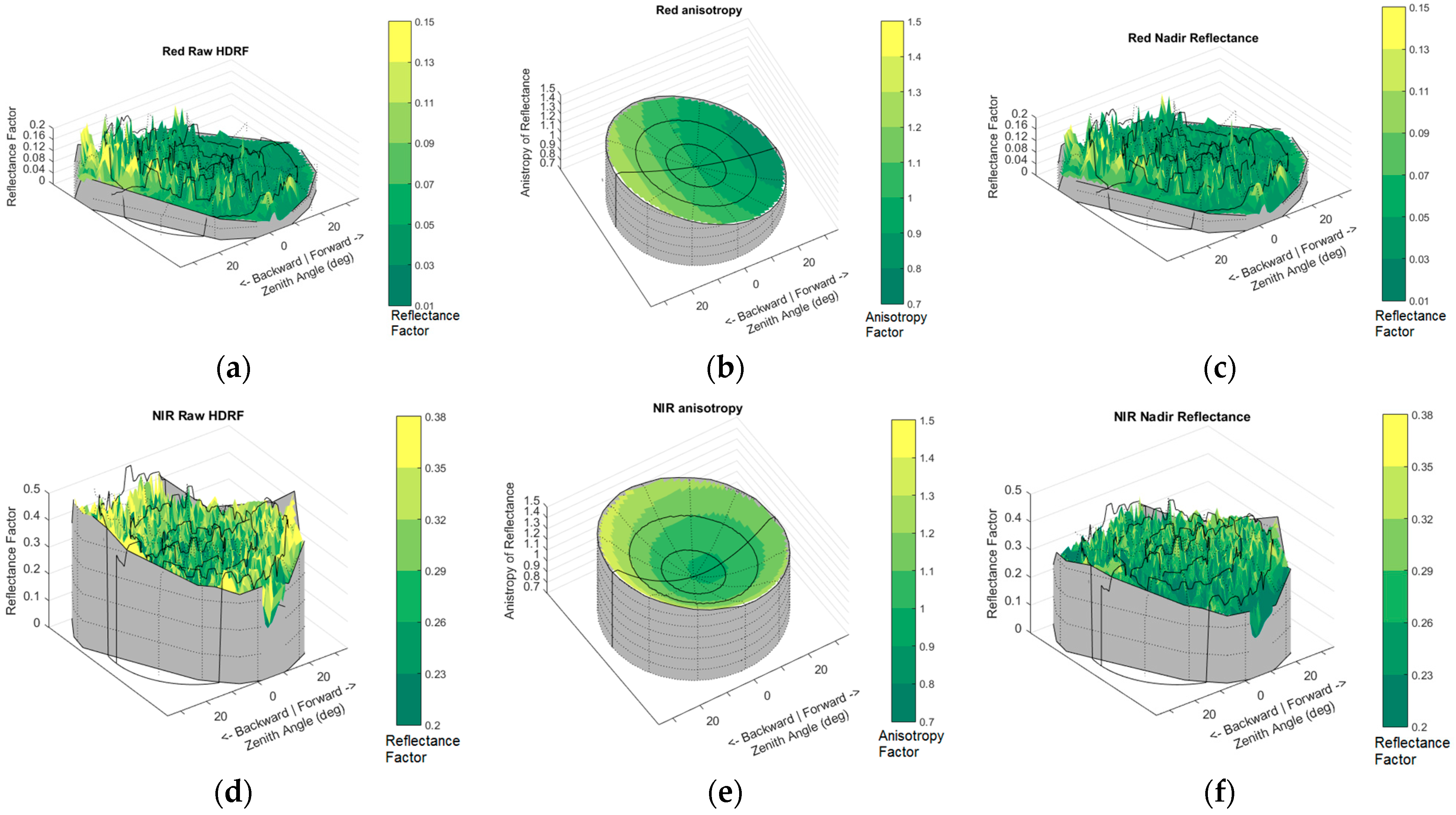
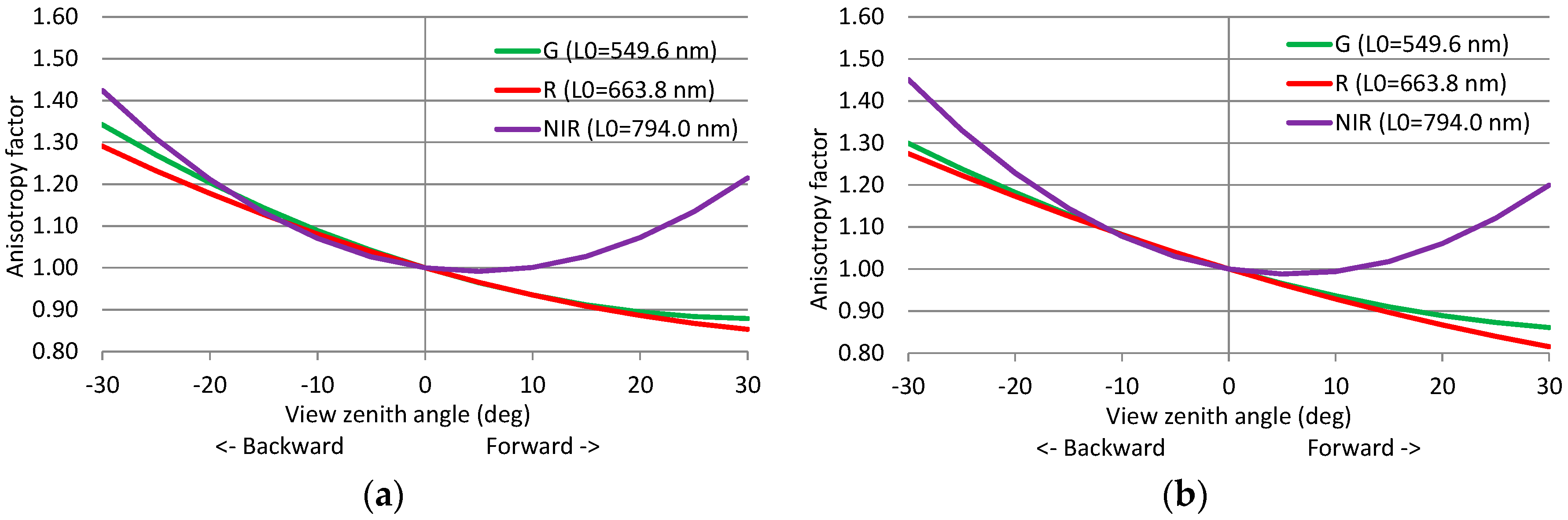
3.2.3. BRDF Correction
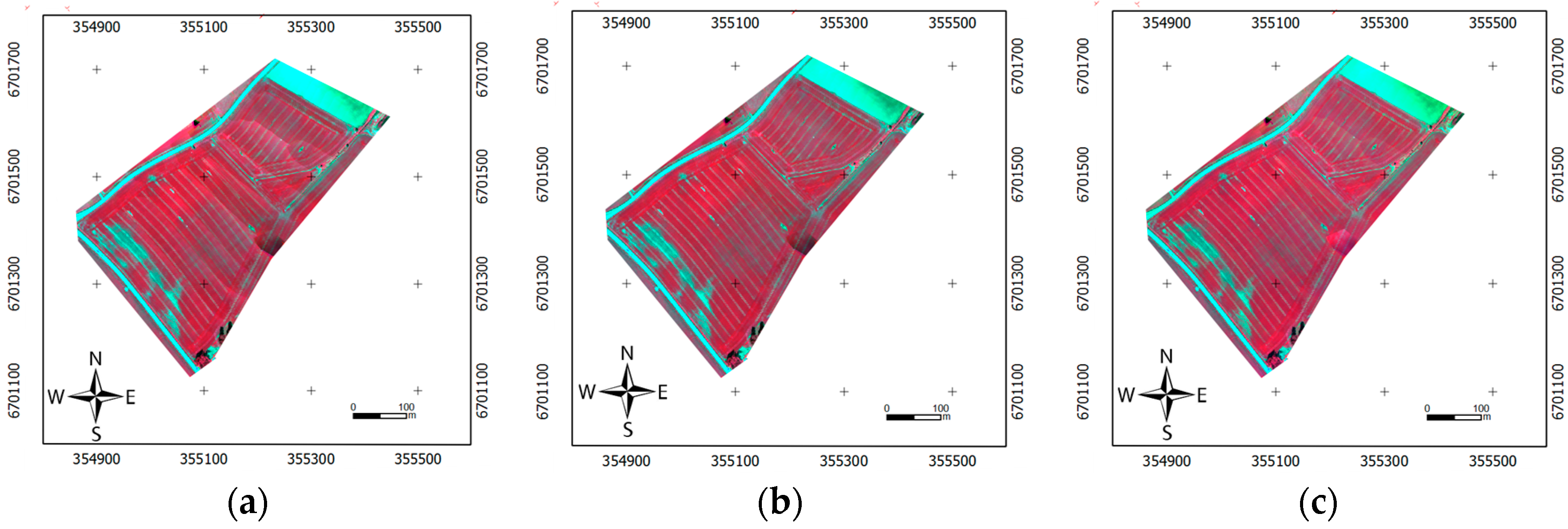
3.3. Performance Assessment
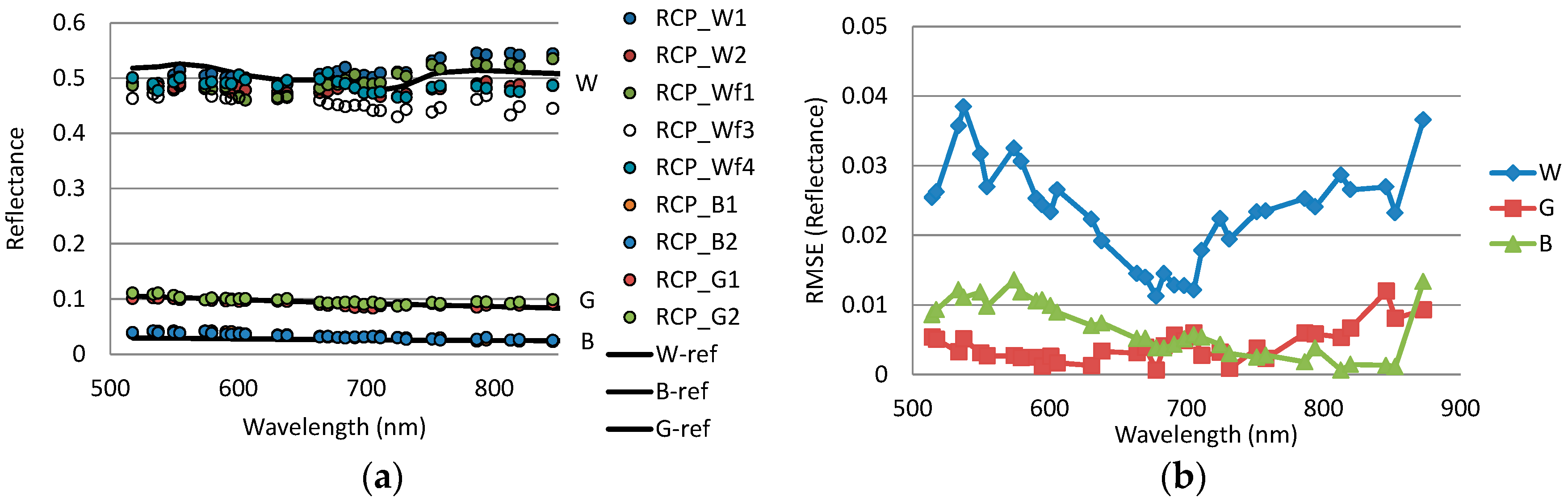
3.3.1. Uniformity of the Image Block
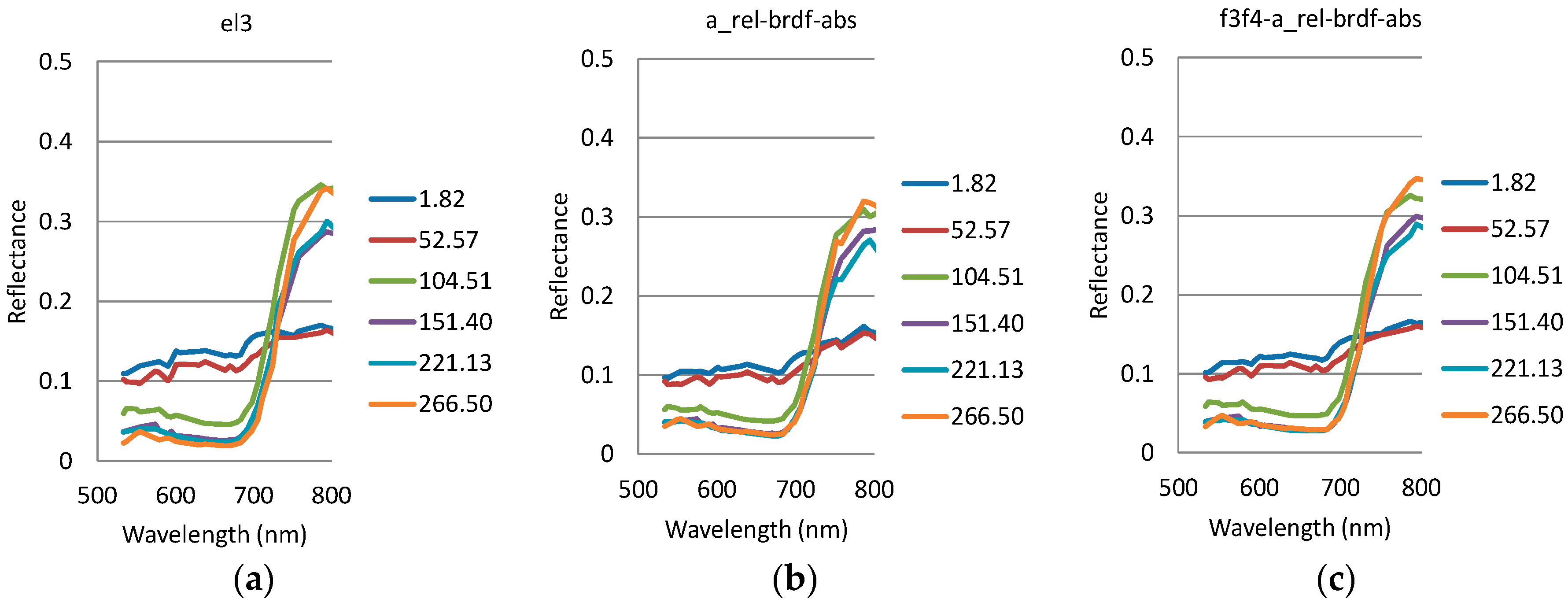
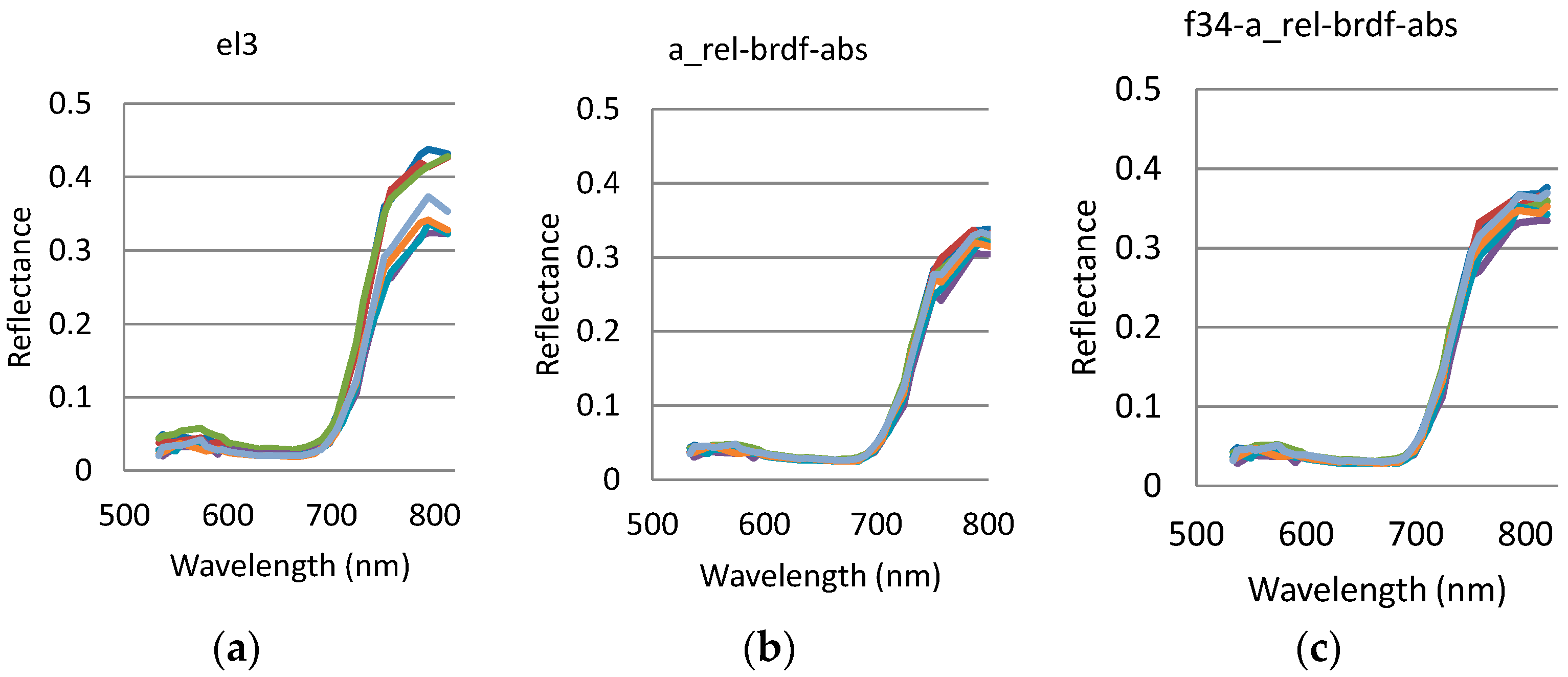
3.3.2. Vegetation Spectra
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| , | The empirical line parameters to transform reflectance to DN |
| The relative image-wise gain and offset parameters | |
| The reflectance factor for specific view/illumination geometry of image | |
| , | Incident illumination zenith and azimuth angles |
| , | Reflectance zenith and azimuth angles |
| Digital grey value of object k in image j | |
| The vertical reflectance of object k at the specific solar illumination angle of | |
| The modeled reflectance based on the 4-parameter BRDF-model | |
| The modeled reflectance based on the 3-parameter BRDF-model | |
| The anisotropy factor | |
| Parameter of the 3 or 4 parameter BRDF-model, m = 1, …, 3 or 4 | |
| , | Calculated and observed reflectance of a radiometric control point |
| Weight matrix used in the radiometric block adjustment | |
| A priori standard deviation of unit weight | |
| Standard deviation of the image observation | |
| Standard deviation and weight for the relative image-wise correction parameter | |
| , | Standard deviation and weight of the RCP |
| , | Standard deviations and weight of the BRDF parameters, m = 1, …, 3 or 4 |
| Coefficient of variation for radiometric tie point k | |
| f1, f2, f3, f4 | Independent flights 1, 2, 3 and 4 used in the study. f34 is combination of flights f3 and f4. |
| BRDF | Bidirectional Reflectance Distribution Function |
| CV | Coefficient of Variation |
| DN | Digital Number (Image grey value) |
| DSM | Digital Surface Model |
| EL | Empirical Line method |
| EOP | Exterior Orientation Parameter |
| FPI | Fabry-Pérot Interferometer |
| FWHM | Full Width of Half Maximum |
| G | Green |
| GCP | Ground Control Point |
| HDRF | Hemispherical Directional Reflectance Factor |
| IOP | Interior Orientation Parameter |
| NIR | Near-Infrared |
| R | Red |
| RCP | Radiometric control points |
| RMSE | Root-Mean-Square-Error |
| RTP | Radiometric Tie Point |
| UAV | Unmanned Aerial Vehicle |
| VRS-GPS | Virtual reference station real-time kinematic GPS method |
References
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Gonzalez-Dugo, V.; Berni, J.A.J. Fluorescence, temperature and narrow-band indices acquired from a UAV platform for water stress using a micro-hyperspectral images and a thermal camera. Remote Sens. Environ. 2012, 117, 322–337. [Google Scholar] [CrossRef]
- Hruska, R.; Mitchell, J.; Anderson, M.; Glenn, N.F. Radiometric and Geometric Analysis of Hyperspectral Imagery Acquired from an Unmanned Aerial Vehicle. Remote Sens. 2012, 4, 2736–2752. [Google Scholar] [CrossRef]
- Büttner, A.; Röser, H. Hyperspectral Remote Sensing with the UAS “Stuttgarter Adler”–System Setup, Calibration and First Results. Photogramm. Fernerkund. Geoinf. 2014, 4, 265–274. [Google Scholar] [CrossRef] [PubMed]
- Lucieer, A.; Malenovský, Z.; Veness, T.; Wallace, L. HyperUAS—Imaging spectroscopy from a multirotor unmanned aircraft system. J. Field Robot. 2014, 31, 571–590. [Google Scholar] [CrossRef]
- Suomalainen, J.; Anders, N.; Iqbal, S.; Roerink, G.; Franke, J.; Wenting, P.; Hünniger, D.; Bartholomeus, H.; Becker, R.; Kooistra, L. A lightweight hyperspectral mapping system and photogrammetric processing chain for unmanned aerial vehicles. Remote Sens. 2014, 6, 11013–11030. [Google Scholar] [CrossRef]
- Burkart, A.; Aasen, H.; Alonso, L.; Menz, G.; Bareth, G.; Rascher, U. Angular Dependency of Hyperspectral Measurements over Wheat Characterized by a Novel UAV Based Goniometer. Remote Sens. 2015, 7, 725–746. [Google Scholar] [CrossRef]
- Burkhart, J.F.; Kylling, A.; Schaaf, C.B.; Wang, Z.; Bogren, W.; Storvold, R.; Solbø, S.; Pedersen, C.A.; Gerland, S. Unmanned aerial system nadir reflectance and MODIS nadir BRDF-adjusted surface reflectances intercompared over Greenland. Cryosphere 2017, 11, 1575–1589. [Google Scholar] [CrossRef]
- Mäkynen, J.; Holmlund, C.; Saari, H.; Ojala, K.; Antila, T. Unmanned aerial vehicle (UAV) operated megapixel spectral camera. Proc. SPIE 2011. [Google Scholar] [CrossRef]
- Saari, H.; Pellikka, I.; Pesonen, L.; Tuominen, S.; Heikkilä, J.; Holmlund, C.; Mäkynen, J.; Ojala, K.; Antila, T. Unmanned Aerial Vehicle (UAV) operated spectral camera system for forest and agriculture applications. Proc. SPIE 2011. [Google Scholar] [CrossRef]
- Saari, H.; Pölönen, I.; Salo, H.; Honkavaara, E.; Hakala, T.; Holmlund, C.; Mäkynen, J.; Mannila, R.; Antila, T.; Akujärvi, A. Miniaturized hyperspectral imager calibration and UAV flight campaigns. Proc. SPIE 2013. [Google Scholar] [CrossRef]
- Honkavaara, E.; Saari, H.; Kaivosoja, J.; Pölönen, I.; Hakala, T.; Litkey, P.; Mäkynen, J.; Pesonen, L. Processing and Assessment of Spectrometric, Stereoscopic Imagery Collected Using a Lightweight UAV Spectral Camera for Precision Agriculture. Remote Sens. 2013, 5, 5006–5039. [Google Scholar] [CrossRef]
- Aasen, H.; Burkart, A.; Bolten, A.; Bareth, G. Generating 3D hyperspectral information with lightweight UAV snapshot cameras for vegetation monitoring: From camera calibration to quality assurance. ISPRS J. Photogramm. Remote Sens. 2015, 108, 245–259. [Google Scholar] [CrossRef]
- Jakob, S.; Zimmermann, R.; Gloaguen, R. The Need for Accurate Geometric and Radiometric Corrections of Drone-Borne Hyperspectral Data for Mineral Exploration: MEPHySTo—A Toolbox for Pre-Processing Drone-Borne Hyperspectral Data. Remote Sens. 2017, 9, 88. [Google Scholar] [CrossRef]
- Yang, G.; Li, C.; Wang, Y.; Yuan, H.; Feng, H.; Xu, B.; Yang, X. The DOM Generation and Precise Radiometric Calibration of a UAV-Mounted Miniature Snapshot Hyperspectral Imager. Remote Sens. 2017, 9, 642. [Google Scholar] [CrossRef]
- Rikola Hyperspectral Camera Web Site. Available online: http://senop.fi/optronics-hyperspectral#hyperspectralCamera (accessed on 23 November 2017).
- Cubert Hyperspectral Camera Web Site. Available online: http://cubert-gmbh.de/ (accessed on 23 November 2017).
- Sequioa Multispectral Camera Web Site. Available online: https://www.parrot.com/us/business-solutions/parrot-sequoia#parrot-sequoia- (accessed on 23 November 2017).
- Mikhail, E.M.; Bethel, J.S.; McGlone, J.C. Introduction to Modern Photogrammetry; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Hirshmüller, H. Semi-Global matching: Motivation, development and applications. In Photogrammetric Week 2011; Fritsch, D., Ed.; Wichmann Verlag: Heidelberg, Germany, 2011; pp. 173–184. [Google Scholar]
- Honkavaara, E.; Arbiol, R.; Markelin, L.; Martinez, L.; Cramer, M.; Bovet, S.; Chandelier, L.; Ilves, R.; Klonus, S.; Marshal, P.; et al. Digital Airborne Photogrammetry—A New Tool for Quantitative Remote Sensing?—A State-of-the-Art Review On Radiometric Aspects of Digital Photogrammetric Images. Remote Sens. 2009, 1, 577–605. [Google Scholar] [CrossRef]
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance quantities in optical remote sensing—Definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Schott, J.R. Remote Sensing: The Image Chain Approach, 2nd ed.; Oxford University Press: New York, NY, USA, 2007. [Google Scholar]
- Schowengerdt, R.A. Remote Sensing–Models and Methods for Image Processing, 3rd ed.; Academic Press: San Diego, CA, USA, 2007. [Google Scholar]
- Richter, R.; Schläpfer, D. Geo-atmospheric processing of airborne imaging spectrometry data. Part 2: Atmospheric/topographic correction. Int. J. Remote Sens. 2002, 23, 2631–2649. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lee, J.; Fox, M.J.; Adler-Golden, S.M.; Chetwynd, J.H.; Hoke, M.L.; et al. MODTRAN5: A reformulated atmospheric band model with auxiliary species and practical multiple scattering options. Proc. SPIE 2004. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanré, D.; Deuzé, J.L.; Herman, M.; Morcrette, J.-J. Second simulation of the satellite signal in the solar spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Von Schönermark, M.; Geiger, B.; Röser, H. Reflection Properties of Vegetation and Soil with a BRDF Data Base; Wissenschaft und Technik Verlag: Berlin, Germany, 2004. [Google Scholar]
- Dare, P.M. Shadow analysis in high resolution satellite imagery of urban areas. Photogramm. Eng. Remote Sens. 2005, 71, 169–177. [Google Scholar] [CrossRef]
- Hakala, T.; Honkavaara, E.; Saari, H.; Mäkynen, J.; Kaivosoja, J.; Pesonen, L.; Pölönen, I. Spectral imaging from UAVs under varying illumination conditions. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Rostock, Germany, 4–6 September 2013; pp. 189–194. [Google Scholar] [CrossRef]
- Honkavara, E.; Hakala, T.; Saari, H.; Markelin, L.; Mäkynen, J.; Rosnell, T. A process for radiometric correction of UAV image blocks. Photogramm. Fernerkund. Geoinf. 2012, 2012, 115–127. [Google Scholar] [CrossRef]
- Honkavaara, E.; Eskelinen, M.A.; Pölönen, I.; Saari, H.; Ojanen, H.; Mannila, R.; Holmlund, C.; Hakala, T.; Litkey, P.; Rosnell, T.; et al. Remote sensing of 3-D geometry and surface moisture of a peat production area using hyperspectral frame cameras in visible to short-wave infrared spectral ranges onboard a small unmanned airborne vehicle (UAV). IEEE Trans. Geosci. Remote Sens. 2016, 54, 5440–5454. [Google Scholar] [CrossRef]
- Näsi, R.; Honkavaara, E.; Lyytikäinen-Saarenmaa, P.; Blomqvist, M.; Litkey, P.; Hakala, T.; Viljanen, N.; Kantola, T.; Tanhuanpää, T.; Holopainen, M. Using UAV-based photogrammetry and hyperspectral imaging for mapping bark beetle damage at tree-level. Remote Sens. 2015, 7, 15467–15493. [Google Scholar] [CrossRef]
- Nevalainen, O.; Honkavaara, E.; Tuominen, S.; Viljanen, N.; Hakala, T.; Yu, X.; Hyyppä, J.; Saari, H.; Pölönen, I.; Imai, N.N.; Tommaselli, A.M.G. Individual Tree Detection and Classification with UAV-Based Photogrammetric Point Clouds and Hyperspectral Imaging. Remote Sens. 2017, 9, 185. [Google Scholar] [CrossRef]
- Tuominen, S.; Balazs, A.; Honkavaara, E.; Pölönen, I.; Saari, H.; Hakala, T.; Viljanen, N. Hyperspectral UAV-imagery and photogrammetric canopy height model in estimating forest stand variables. Silva Fenn. 2017, 51, 5. [Google Scholar] [CrossRef]
- Laliberte, A.S.; Goforth, M.A.; Steele, C.M.; Rango, A. Multispectral Remote Sensing from Unmanned Aircraft: Image Processing Workflows and Applications for Rangeland Environments. Remote Sens. 2011, 3, 2529–2551. [Google Scholar] [CrossRef]
- Lelong, C.C.D.; Burger, P.; Jubelin, G.; Roux, B.; Labbé, S.; Baret, F. Assessment of Unmanned Aerial Vehicles Imagery for Quantitative Monitoring of Wheat Crop in Small Plots. Sensors 2008, 8, 3557–3585. [Google Scholar] [CrossRef] [PubMed]
- Chandelier, L.; Martinoty, G. Radiometric aerial triangulation for the equalization of digital aerial images and orthoimages. Photogramm. Eng. Remote Sens. 2009, 75, 193–200. [Google Scholar] [CrossRef]
- Collings, S.; Cacetta, P.; Campbell, N.; Wu, X. Empirical models for radiometric calibration of digital aerial frame mosaics. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2573–2588. [Google Scholar] [CrossRef]
- López, D.H.; García, B.F.; Piqueras, J.G.; Aöcázar, G.V. An approach to the radiometric aerotriangulation of photogrammetric images. ISPRS J. Photogramm. Remote Sens. 2011, 66, 883–893. [Google Scholar] [CrossRef]
- Gehrke, S.; Beshah, B.T. Radiometric normalization of large airborne image data sets acquired by different sensor types. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016; pp. 317–326. [Google Scholar] [CrossRef]
- Beisl, U. Reflectance calibration scheme for airborne frame camera images. In Proceedings of the 2012 XXII ISPRS Congress International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Melbourne, Australia, 25 August–1 September 2012; pp. 1–5. [Google Scholar]
- Walthall, C.L.; Norman, J.M.; Welles, J.M.; Campbell, G.; Blad, B.L. Simple equation to approximate the bidirectional reflectance from vegetative canopies and bare soil surfaces. Appl. Opt. 1985, 24, 383–387. [Google Scholar] [CrossRef] [PubMed]
- Nilson, T.; Kuusk, A. A reflectance model for the homogeneous plant canopy and its inversion. Remote Sens. Environ. 1989, 27, 157–167. [Google Scholar] [CrossRef]
- Beisl, U.; Telaar, J.; von Schönemark, M. Atmospheric Correction, Reflectance Calibration and BRDF Correction for ADS40 Image Data. In Proceedings of the XXI ISPRS Congress Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Commission VII, Beijing, China, 3–11 July 2008. [Google Scholar]
- Mikhail, E.M. Observations and Least Squares; Thomas, Y., Ed.; Crowell Company, Inc.: New York, NY, USA, 1976. [Google Scholar]
- Häkli, P. Practical test on accuracy and usability of Virtual Reference Station method in Finland. In Proceedings of the FIG Working Week, The Olympic Spirit in Surveying, Athens, Greece, 22–27 May 2004. [Google Scholar]
- Honkavaara, E.; Markelin, L.; Hakala, T.; Peltoniemi, J. The metrology of directional, spectral reflectance factor measurements based on area format imaging by UAVs. Photogramm. Fernerkund. Geoinf. 2014, 2014, 175–188. [Google Scholar] [CrossRef]
- Honkavaara, E.; Rosnell, T.; Oliveira, R.; Tommaselli, A. Band registration of tuneable frame format hyperspectral UAV imagers in complex scenes. ISPRS J. Photogramm. Remote Sens. 2017, 134, 96–109. [Google Scholar] [CrossRef]
- Roosjen, P.P.J.; Suomalainen, J.M.; Bartholomeus, H.M.; Clevers, J.G.P.W. Hyperspectral Reflectance Anisotropy Measurements Using a Pushbroom Spectrometer on an Unmanned Aerial Vehicle—Results for Barley, Winter Wheat, and Potato. Remote Sens. 2016, 8, 909. [Google Scholar] [CrossRef]
- Markelin, L.; Honkavaara, E.; Schläpfer, D.; Bovet, S.; Korpela, I. Assessment of radiometric correction methods for ADS40 imagery. Photogramm. Fernerkund. Geoinf. 2012, 3, 251–266. [Google Scholar] [CrossRef] [PubMed]
- Roosjen, P.P.J.; Suomalainen, J.M.; Bartholomeus, H.M.; Kooistra, L.; Clevers, J.G.P.W. Mapping Reflectance Anisotropy of a Potato Canopy Using Aerial Images Acquired with an Unmanned Aerial Vehicle. Remote Sens. 2017, 9, 417. [Google Scholar] [CrossRef]
- Hakala, T.; Suomalainen, J.; Peltoniemi, J.I. Acquisition of Bidirectional Reflectance Factor Dataset Using a Micro Unmanned Aerial Vehicle and a Consumer Camera. Remote Sens. 2010, 2, 819–832. [Google Scholar] [CrossRef]

| Central wavelength L0 (nm) | 507.60, 514.50, 517.50, 533.60, 537.40, 549.60, 554.40, 574.20, 579.30, 590.40, 594.70, 600.80, 605.70, 630.70, 638.20, 663.80, 670.10, 677.80, 683.70, 691.10, 698.40, 705.30, 711.10, 724.60, 731.30, 751.50, 757.90, 786.40, 794.00, 812.80, 819.70, 845.80, 852.30, 872.80, 879.90 |
| FWHM (nm) | 24.00, 20.00, 22.00, 24.00, 24.00, 24.00, 24.00, 24.00, 20.00, 22.00, 22.00, 32.00, 28.00, 32.00, 30.00, 32.00, 30.00, 28.00, 32.00, 32.00, 30.00, 28.00, 28.00, 30.00, 30.00, 28.00, 30.00, 30.00, 28.00, 30.00, 32.00, 30.00, 34.00, 32.00, 30.00 |
| Date, Flight | Time (UTC + 3) | Exposure (ms) | SunZen (°) | SunAz (°) | FH (m) | GSD (cm) | Overlaps p, q (%) |
|---|---|---|---|---|---|---|---|
| Flight 1 (f1) | 10:39–10:47 | 4 | 48.2 | 128.2 | 97.9 | 9.4 | 74, 60 |
| Flight 2 (f2) | 11:17–11:26 | 4 | 45 | 139.2 | 83.5 | 7.97 | 68, 51 |
| Flight 3 (f3) | 13:03–13:11 | 4 | 39.9 | 175.9 | 94.4 | 9.12 | 72, 60 |
| Flight 4 (f4) | 13:17–13:23 | 4 | 39.8 | 187.3 | 99.2 | 9.65 | 74, 60 |
| Flight number | Number of Cubes | N adj ima | N GCPs | GSD (cm) | N pts/m2 | Reprojection Error (pix) |
|---|---|---|---|---|---|---|
| Flight 1 | 128 | 426/384 | 5 | 9.4 | 113.177 | 0.419 |
| Flight 2 | 166 | 498/498 | 6 | 7.97 | 157.322 | 0.377 |
| Flight 3 | 139 | 414/414 | 7 | 9.12 | 120.24 | 0.39 |
| Flight 4 | 204 | 612/611 | 7 | 9.65 | 107.389 | 0.435 |
| Case | BRDF | , | EL | RTP | RTP-obs | RCP | |
|---|---|---|---|---|---|---|---|
| (1) full, el3 | - | - | - | 3 × 2 | - | - | - |
| (2) full, brdf, el3 | - | 4 | - | 3 × 2 | 1426 | 10,303 | - |
| (3) full, , brdf, el3 | 451 | 4 | - | 3 × 2 | 1426 | 10,303 | - |
| (4) full, , brdf, abs | 451 | 4 | 2 | - | 1426 | 10,303 | 8 |
| (5) f34, el1 | - | - | - | 2 | - | - | - |
| (6) f34, brdf, el1 | - | 2 | - | 2 | 816 | 5252 | - |
| (7) f34, , brdf, el1 | 212 | 2 | - | 2 | 816 | 5252 | - |
| (8) f34, , brdf, abs | 212 | 2 | 2 | - | 816 | 5252 | 4 |
| Case | a Priori | m: 1; 2; 3; 4_1/4_2 | m: 1; 2; 3; 4_1/4_2 | |||
|---|---|---|---|---|---|---|
| r10i,b50,g001 | Irrad. | 0.10 | 0; 0; 0; 0.1/0.2 | 0.25; 0.25; 0.25; 0.05/0.1 | 0.001 | 0.05 |
| r10i,b20,g001 | Irrad. | 0.10 | 0; 0; 0; 0.1/0.2 | 0.10; 0.10; 0.10; 0.02/0.04 | 0.001 | 0.05 |
| r10i,b100,g001 | Irrad. | 0.10 | 0; 0; 0; 0.1/0.2 | 0.50; 0.50; 0.50; 0.1/0.2 | 0.001 | 0.05 |
| r05i,b50,g001 | Irrad. | 0.05 | 0; 0; 0; 0.1/0.2 | 0.25; 0.25; 0.25; 0.05/0.1 | 0.001 | 0.05 |
| r10i,b_c,g001 | Irrad. | 0.10 | 0; 0; 0; 0.05/0.4 | 0.10; 0.10; 0.10; 0.025/0.05 | 0.001 | 0.05 |
| r20i,b50,g001 | Irrad. | 0.20 | 0; 0; 0; 0.1/0.2 | 0.25; 0.25; 0.25; 0.05/0.1 | 0.001 | 0.05 |
| r10i,b50,g01 | Irrad. | 0.10 | 0; 0; 0; 0.1/0.2 | 0.25; 0.25; 0.25; 0.05/0.1 | 0.01 | 0.05 |
| r10i,b50,g001,dn10 | Irrad. | 0.10 | 0; 0; 0; 0.1/0.2 | 0.25; 0.25; 0.25; 0.05/0.1 | 0.001 | 0.10 |
| r10c,b50,g001 | 1.0 | 0.10 | 0; 0; 0; 0.1/0.2 | 0.25; 0.25; 0.25; 0.05/0.1 | 0.001 | 0.05 |
| r20c,b50,g001 | 1.0 | 0.20 | 0; 0; 0; 0.1/0.2 | 0.25; 0.25; 0.25; 0.05/0.1 | 0.001 | 0.05 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Honkavaara, E.; Khoramshahi, E. Radiometric Correction of Close-Range Spectral Image Blocks Captured Using an Unmanned Aerial Vehicle with a Radiometric Block Adjustment. Remote Sens. 2018, 10, 256. https://doi.org/10.3390/rs10020256
Honkavaara E, Khoramshahi E. Radiometric Correction of Close-Range Spectral Image Blocks Captured Using an Unmanned Aerial Vehicle with a Radiometric Block Adjustment. Remote Sensing. 2018; 10(2):256. https://doi.org/10.3390/rs10020256
Chicago/Turabian StyleHonkavaara, Eija, and Ehsan Khoramshahi. 2018. "Radiometric Correction of Close-Range Spectral Image Blocks Captured Using an Unmanned Aerial Vehicle with a Radiometric Block Adjustment" Remote Sensing 10, no. 2: 256. https://doi.org/10.3390/rs10020256
APA StyleHonkavaara, E., & Khoramshahi, E. (2018). Radiometric Correction of Close-Range Spectral Image Blocks Captured Using an Unmanned Aerial Vehicle with a Radiometric Block Adjustment. Remote Sensing, 10(2), 256. https://doi.org/10.3390/rs10020256