Towards Estimating Land Evaporation at Field Scales Using GLEAM
Abstract
:1. Introduction
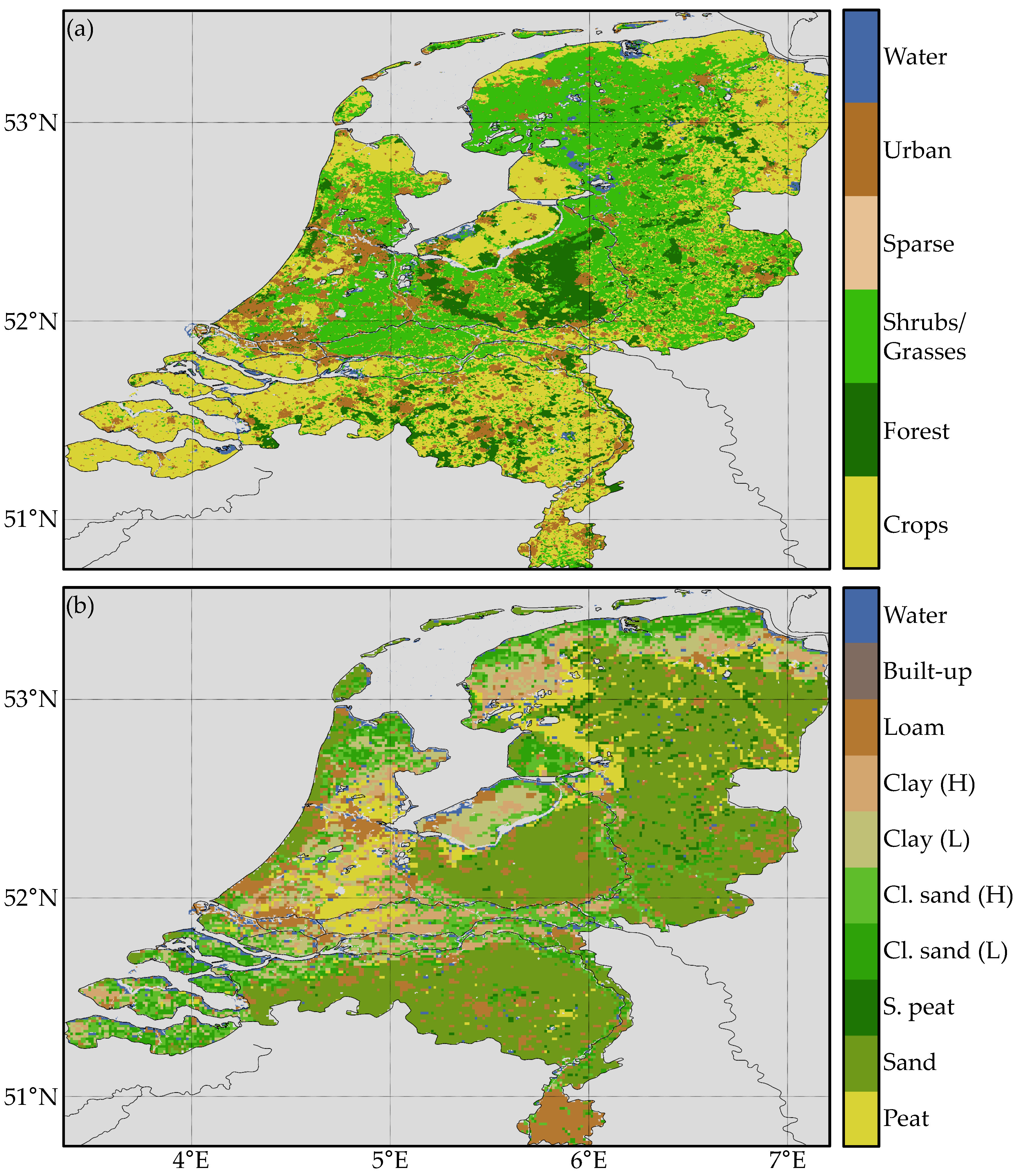
2. Materials and Methods
2.1. GLEAM
2.2. Forcing Data
2.3. Evaluation Data
2.3.1. In Situ Soil Moisture and Evaporation
2.3.2. Gridded Evaporation
3. Results and Discussion
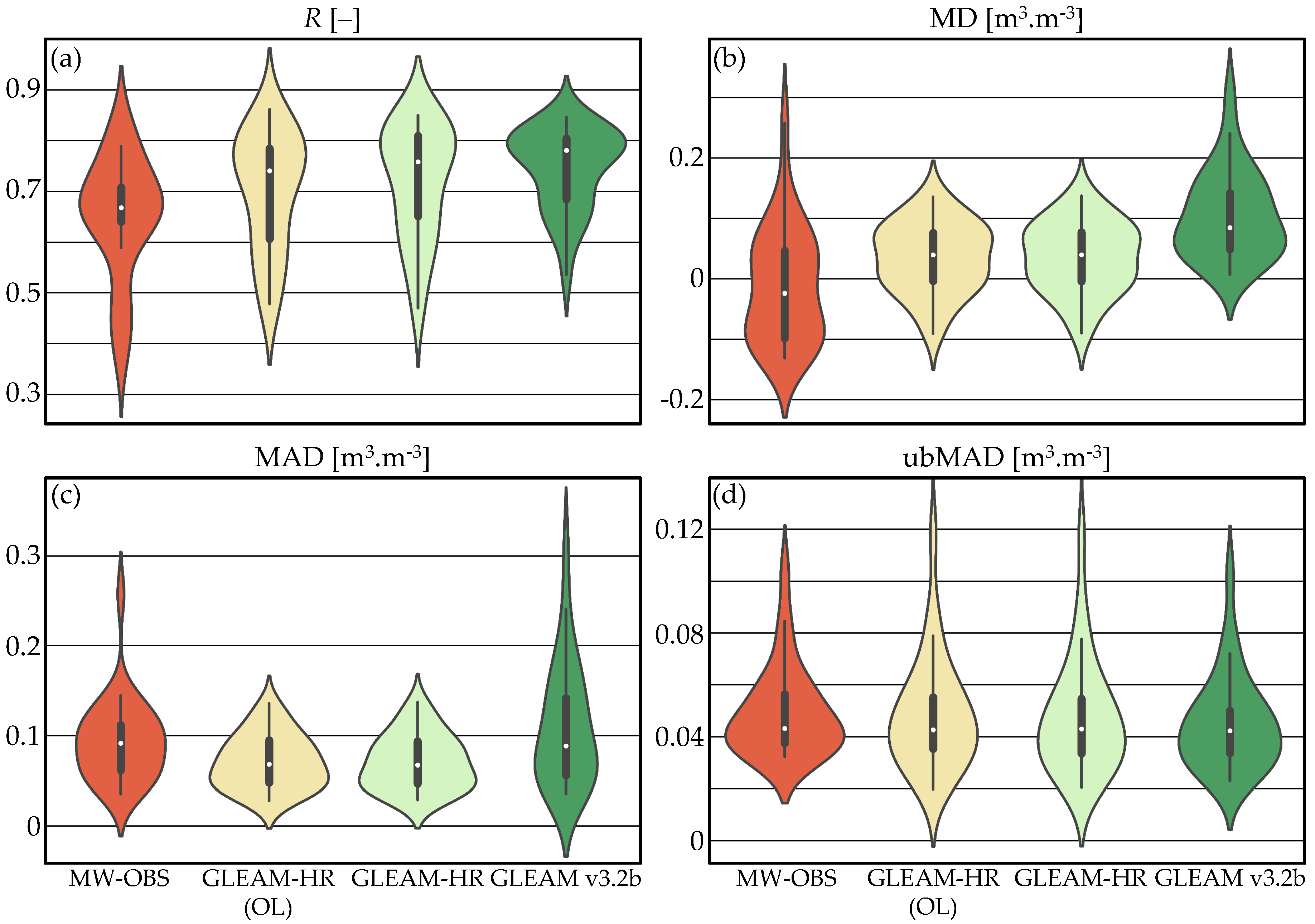
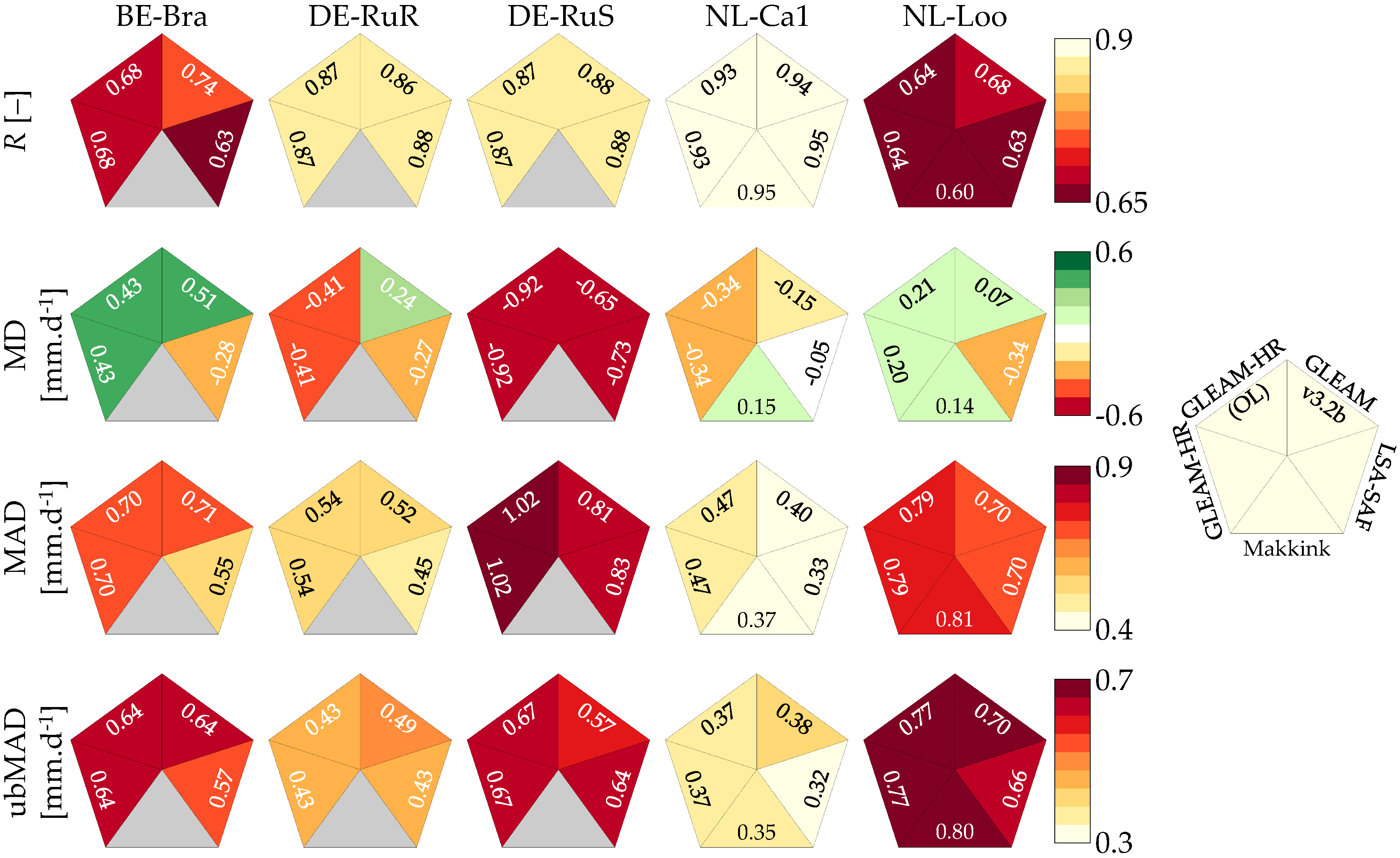
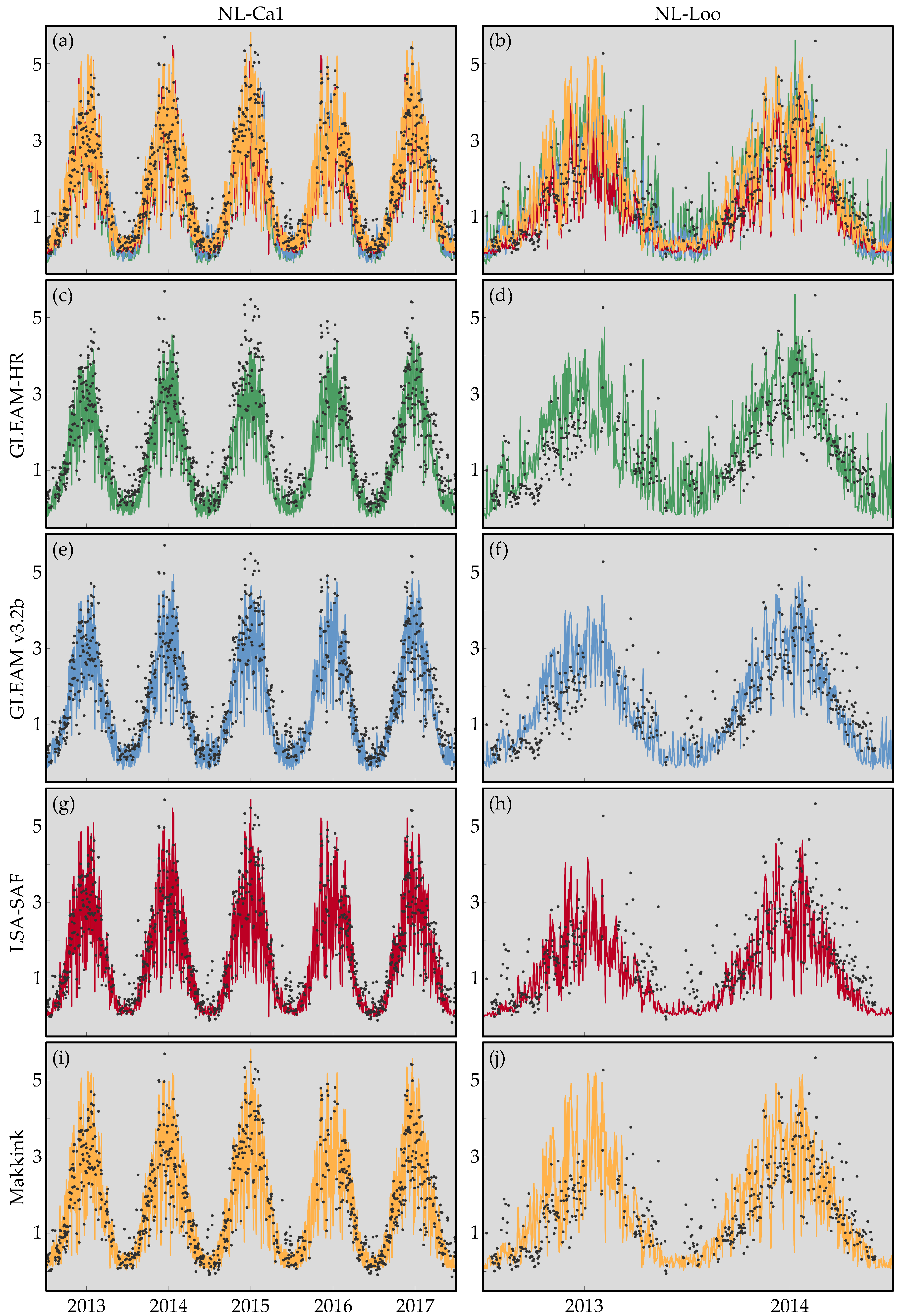
3.1. Temporal Evaluation of Surface Soil Moisture
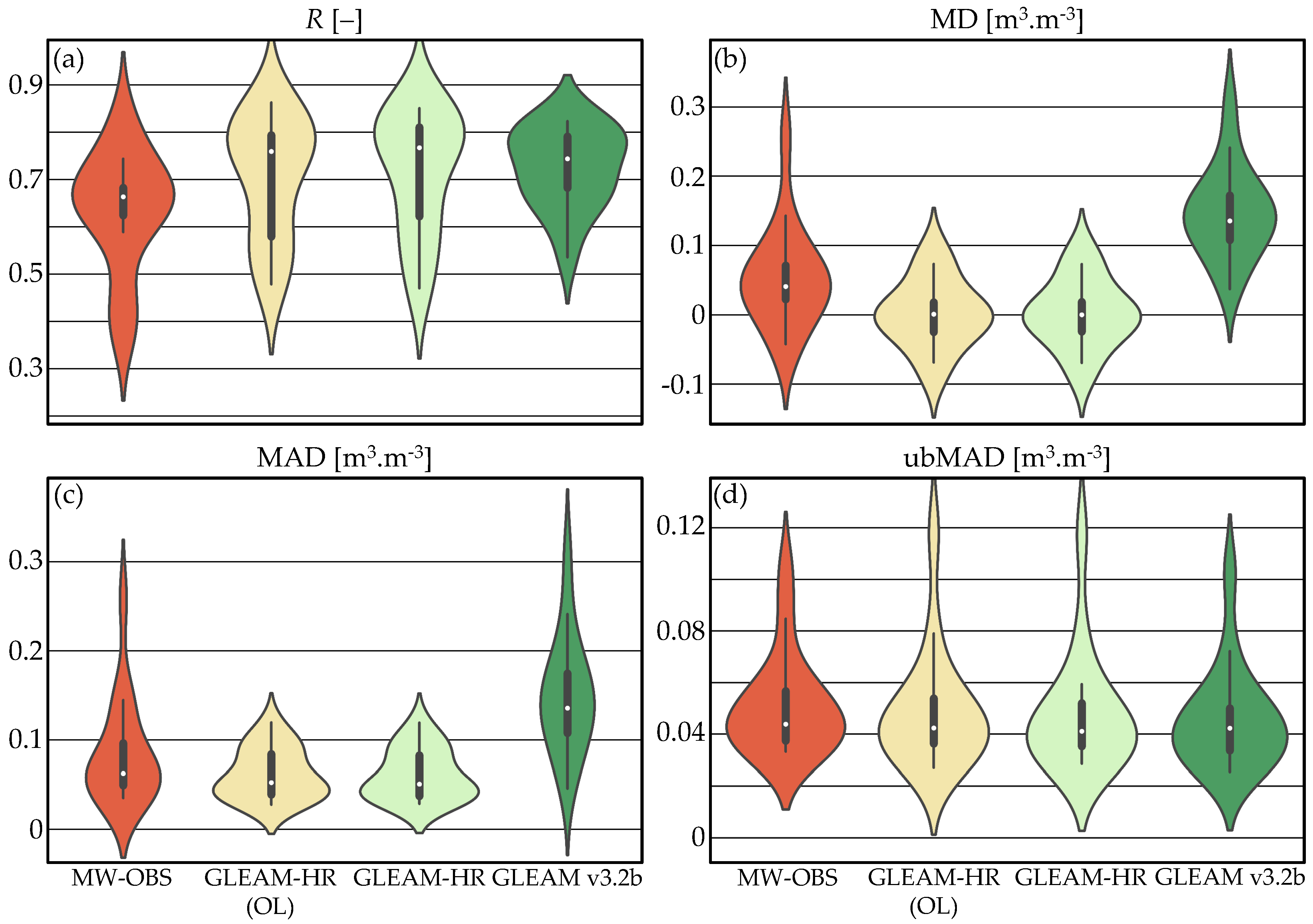
3.2. Evaluation of Evaporation
3.2.1. Temporal Evaluation
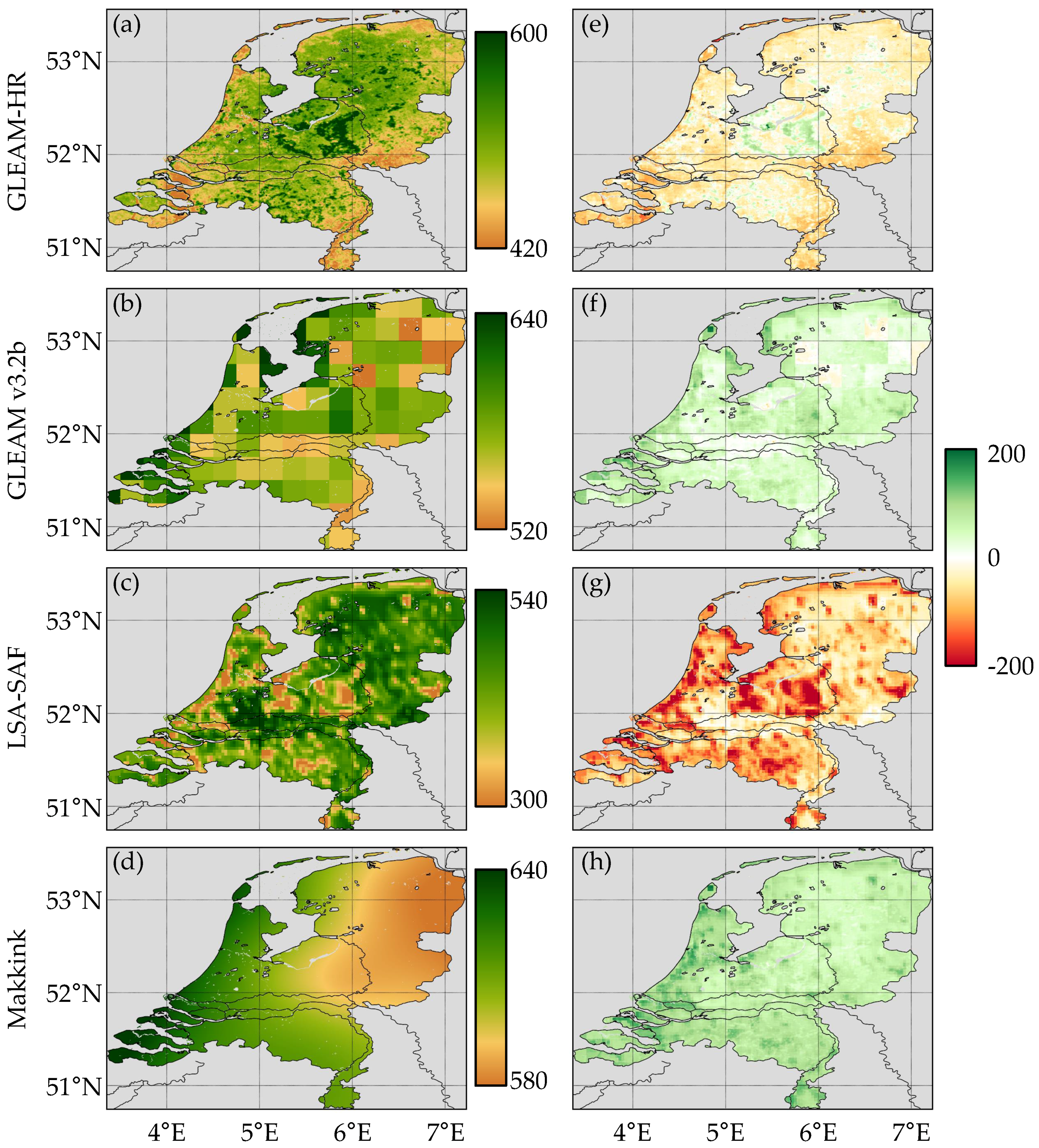
3.2.2. Spatial Evaluation
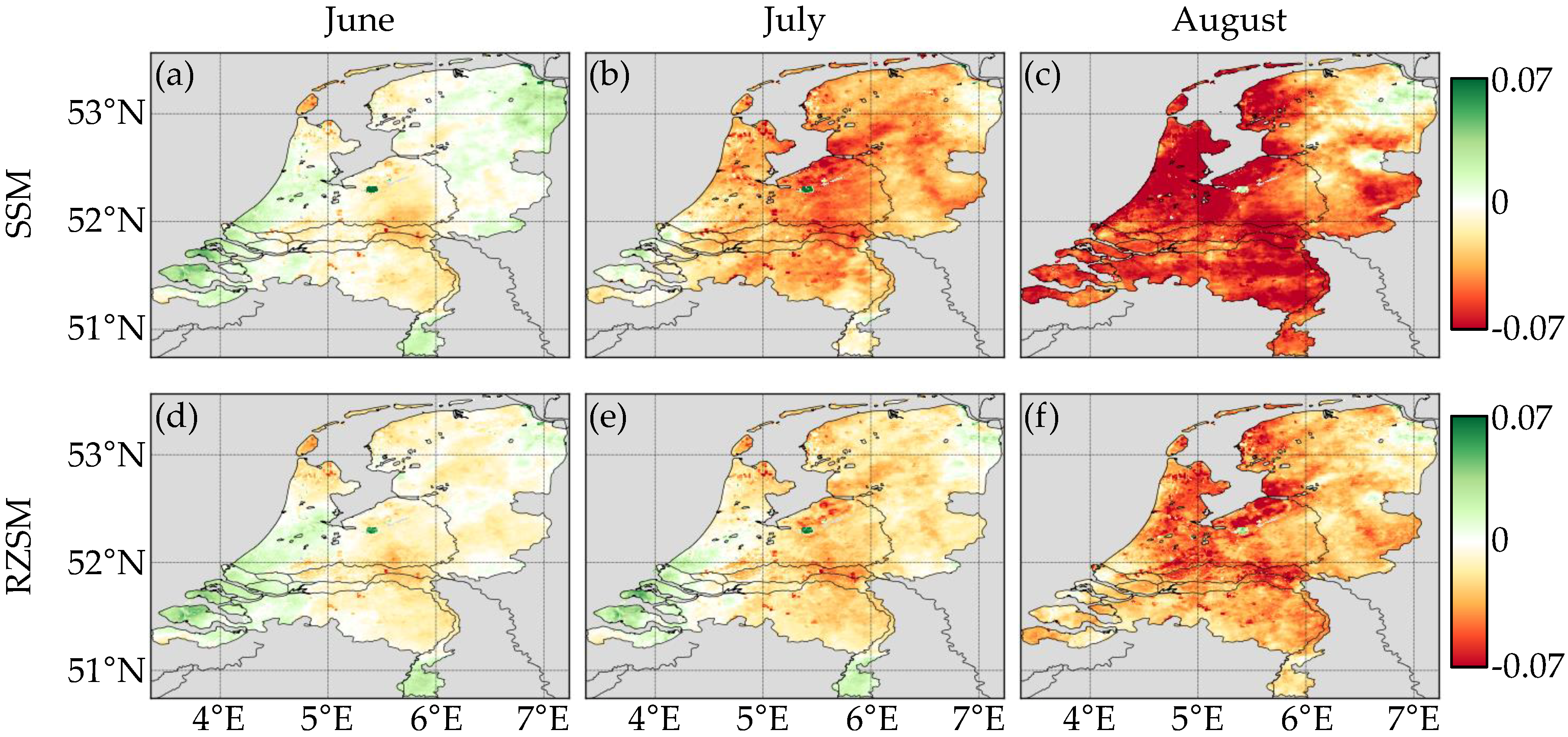
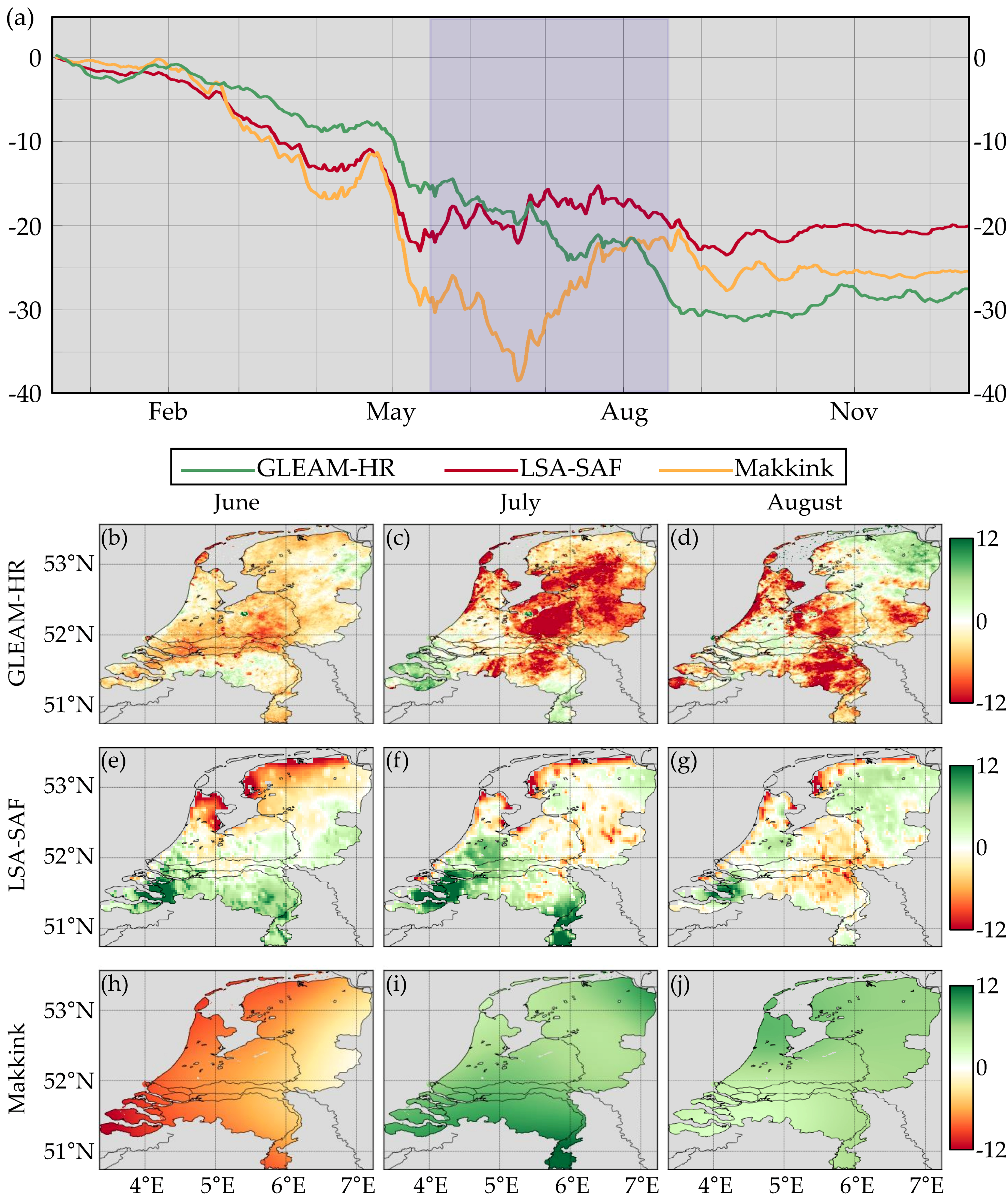
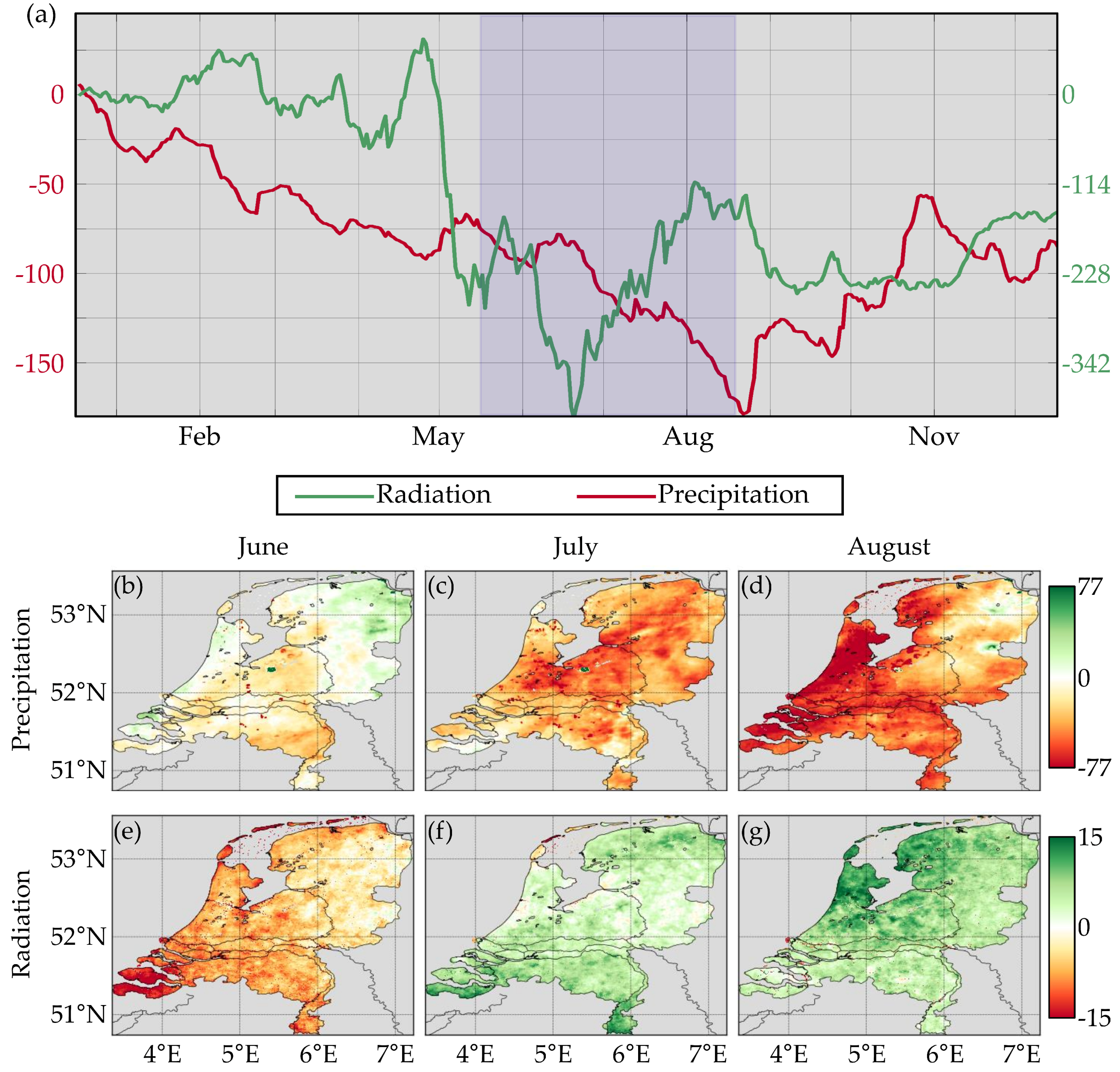
3.3. Summer Drought 2013
4. Conclusions
5. Data Availability
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Bias-Correction Radiation Components
Appendix B. Supplementary Figures
References
- Le Quéré, C.; Andrew, R.M.; Canadell, J.G.; Sitch, S.; Ivar Korsbakken, J.; Peters, G.P.; Manning, A.C.; Boden, T.A.; Tans, P.P.; Houghton, R.A.; et al. Global carbon budget 2016. Earth Syst. Sci. Data 2016, 8, 605–649. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, L.; Wang, Y.P.; Canadell, J.G.; Chiew, F.H.S.; Beringer, J.; Li, L.; Miralles, D.G.; Piao, S.; Zhang, Y. Recent increases in terrestrial carbon uptake at little cost to the water cycle. Nat. Commun. 2017, 8, 110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture-climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Taylor, C.M.; de Jeu, R.; Guichard, F.; Harris, P.P.; Dorigo, W.A. Afternoon rain more likely over drier soils. Nature 2012, 489, 423–426. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Teuling, A.J.; Taylor, C.M.; Meirink, J.F.; Melsen, L.A.; Miralles, D.G.; van Heerwaarden, C.C.; Vautard, R.; Stegehuis, A.I.; Nabuurs, G.J.; de Arellano, J.V.G. Observational evidence for cloud cover enhancement over western European forests. Nat. Commun. 2017, 8, 14065. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miralles, D.G.; Nieto, R.; McDowell, N.G.; Dorigo, W.A.; Verhoest, N.E.; Liu, Y.Y.; Teuling, A.J.; Dolman, A.J.; Good, S.P.; Gimeno, L. Contribution of water-limited ecoregions to their own supply of rainfall. Environ. Res. Lett. 2016, 11, 124007. [Google Scholar] [CrossRef]
- Roundy, J.K.; Ferguson, C.R.; Wood, E.F. Temporal variability of land—Atmosphere coupling and its implications for drought over the Southeast United States. J. Hydrometeorol. 2013, 14, 622–635. [Google Scholar] [CrossRef]
- Miralles, D.; Gentine, P.; Seneviratne, S.; Teuling, A. Land-atmospheric feedback during droughts and heatwaves: State of the science and current challenges. Ann. N. Y. Acad. Sci. 2018, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Chang. 2013, 3, 1449–1455. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; Van Der Schrier, G.; Jones, P.D.; Barichivich, J.; Briffa, K.R.; Sheffield, J. Global warming and changes in drought. Nat. Clim. Chang. 2014, 4, 17–22. [Google Scholar] [CrossRef]
- Otkin, J.A.; Anderson, M.C.; Hain, C.; Svoboda, M.; Johnson, D.; Mueller, R.; Tadesse, T.; Wardlow, B.; Brown, J. Assessing the evolution of soil moisture and vegetation conditions during the 2012 United States flash drought. Agric. For. Meteorol. 2016, 218–219, 230–242. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Miralles, D.G.; Domínguez-Castro, F.; Azorin-Molina, C.; El Kenawy, A.; McVicar, T.R.; Tomás-Burguera, M.; Beguería, S.; Maneta, M.; Peña-Gallardo, M.; et al. Global assessment of the Standardized Evapotranspiration Deficit Index (SEDI) for drought analysis and monitoring. J. Clim. 2018. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.H.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modelling, climatology and climatic variability. Rev. Geophys. 2012, 50, RG2005. [Google Scholar] [CrossRef]
- Michel, D.; Jiménez, C.; Miralles, D.G.; Jung, M.; Hirschi, M.; Ershadi, A.; Martens, B.; McCabe, M.; Fisher, J.B.; Senviratne, S.I.; et al. The WACMOS-ET project—Part 1: Tower-scale evaluation of four remote-sensing-based evapotranspiration algorithms. Hydrol. Earth Syst. Sci. 2016, 20, 803–822. [Google Scholar] [CrossRef] [Green Version]
- Miralles, D.G.; Jiménez, C.; Jung, M.; Michel, D.; Ershadi, A.; McCabe, M.F.; Hirschi, M.; Martens, B.; Dolman, A.J.; Fisher, J.B.; et al. The WACMOS-ET project—Part 2: Evaluation of global terrestrial evaporation datasets. Hydrol. Earth Syst. Sci. 2016, 20, 823–842. [Google Scholar] [CrossRef] [Green Version]
- Poyatos, R.; Granda, V.; Molowny-Horas, R.; Mencuccini, M.; Steppe, K.; Martínez-Vilalta, J. SAPFLUXNET: Towards a global database of sap flow measurements. Tree Physiol. 2016, 36, 1449–1455. [Google Scholar] [CrossRef] [PubMed]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; Mccabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The future of evapotranspiration: Global requirements for ecosystemfunctioning, carbon and climate feedback, agriculturalmanagement, and water resources. Water Resour. Res. 2017, 2618–2626. [Google Scholar] [CrossRef]
- McCabe, M.F.; Alsdorf, D.E.; Miralles, D.G.; Uijlenhoet, R.; Wagner, W.; Lucieer, A.; Houborg, R.; Verhoest, N.E.C.; Trenton, E.F.; Jiancheng, S.; et al. The future of earth observation in hydrology. Hydrology and Earth system sciences. Hydrol. Earth Syst. Sci. 2017, 21, 3879–3914. [Google Scholar] [CrossRef] [PubMed]
- Dolman, A.J.; Miralles, D.G.; de Jeu, R.A. Fifty years since Monteith’s 1965 seminal paper: The emergence of global ecohydrology. Ecohydrology 2014, 7, 897–902. [Google Scholar] [CrossRef]
- McCabe, M.F.; Ershadi, A.; Jimenez, C.; Miralles, D.G.; Michel, D.; Wood, E.F. The GEWEX LandFlux project: Evaluation of model evaporation using tower-based and globally gridded forcing data. Geosci. Model Dev. 2016, 9, 283–305. [Google Scholar] [CrossRef] [Green Version]
- Kustas, W. Estimates of evapotranspiration with a one- and two-layer model of heat transfer over partial canopy cover. J. Appl. Meteorol. Climatol. 1990, 29, 704–715. [Google Scholar] [CrossRef]
- Bastiaanssen, W.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.; Roerink, G.; van der Wal, T. A remote sensing surface energy balance algorithm for land (SEBAL). J. Hydrol. 1998, 212–213, 213–229. [Google Scholar] [CrossRef]
- Su, Z. The surface energy balance system (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Anderson, M.C.; Kustas, W.P.; Norman, J.M.; Hain, C.R.; Mecikalski, J.R.; Schultz, L.; González-Dugo, M.P.; Cammalleri, C.; D’Urso, G.; Pimstein, A.; et al. Mapping daily evapotranspiration at field to continental scales using geostationary and polar orbiting satellite imagery. Hydrol. Earth Syst. Sci. 2011, 15, 223–239. [Google Scholar] [CrossRef] [Green Version]
- Mccabe, M.F.; Aragon, B.; Houborg, R.; Mascaro, J. CubeSats in hydrology: Ultrahigh-resolution insights Into vegetation dynamics and terrestrial evaporation. Water Resour. Res. 2017, 17–24. [Google Scholar] [CrossRef]
- Hoffmann, H.; Nieto, H.; Jensen, R.; Guzinski, R.; Zarco-Tejada, P.; Friborg, T. Estimating evaporation with thermal UAV data and two-source energy balance models. Hydrol. Earth Syst. Sci. 2016, 20, 697–713. [Google Scholar] [CrossRef] [Green Version]
- Holmes, T.R.H.; Hain, C.R.; Anderson, M.C.; Crow, W.T. Cloud tolerance of remote-sensing technologies to measure land surface temperature. Hydrol. Earth Syst. Sci. 2016, 20, 3263–3275. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 1. Model formulation. J. Geophys. Res. Atmos. 2007, 112, 1–17. [Google Scholar] [CrossRef]
- Holmes, T.R.; Hain, C.R.; Crow, W.T.; Anderson, M.C.; Kustas, W.P. Microwave implementation of two-source energy balance approach for estimating evapotranspiration. Hydrol. Earth Syst. Sci. 2018, 22, 1351–1369. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land-atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W. A continuous satellite-derived global record of land surface evapotranspiration from 1983 to 2006. Water Resour. Res. 2010, 46, W09522. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Peña-Arancibia, J.L.; McVicar, T.R.; Chiew, F.H.S.; Vaze, J.; Liu, C.; Lu, X.; Zheng, H.; Wang, Y.; Liu, Y.Y.; et al. Multi-decadal trends in global terrestrial evapotranspiration and its components. Sci. Rep. 2016, 6, 19124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miralles, D.G.; van den Berg, M.J.; Gash, J.H.; Parinussa, R.M.; de Jeu, R.A.M.; Beck, H.E.; Holmes, T.R.H.; Jiménez, C.; Verhoest, N.E.C.; Dorigo, W.A.; et al. El Niño–La Niña cycle and recent trends in continental evaporation. Nat. Clim. Chang. 2014, 4, 1–5. [Google Scholar] [CrossRef]
- Martens, B.; Waegeman, W.; Dorigo, W.; Verhoest, N.; Miralles, D. Terrestrial evaporation response to modes of climate variability. Clim. Atmos. Sci. 2018. in review. [Google Scholar]
- Miralles, D.G.; Teuling, A.J.; Van Heerwaarden, C.C.; De Arellano, J.V.G. Mega-heatwave temperatures due to combined soil desiccation and atmospheric heat accumulation. Nat. Geosci. 2014, 7, 345–349. [Google Scholar] [CrossRef]
- Guillod, B.P.; Orlowsky, B.; Miralles, D.G.; Teuling, A.J.; Seneviratne, S.I. Reconciling spatial and temporal soil moisture effects on afternoon rainfall. Nat. Commun. 2015, 6, 6443. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Kauwe, M.G.; Kala, J.; Lin, Y.S.; Pitman, A.J.; Medlyn, B.E.; Duursma, R.A.; Abramowitz, G.; Wang, Y.P.; Miralles, D.G. A test of an optimal stomatal conductance scheme within the CABLE land surface model. Geosci. Model Dev. 2015, 8, 431–452. [Google Scholar] [CrossRef] [Green Version]
- Reichle, R.H.; Draper, C.S.; Liu, Q.; Girotto, M.; Mahanama, S.P.P.; Koster, R.D.; De Lannoy, G.J.M. Assessment of MERRA-2 land surface hydrology estimates. J. Clim. 2017. [Google Scholar] [CrossRef]
- Van der Schalie, R.; Parinussa, R.; Renzullo, L.J.; van Dijk, A.I.J.M.; Su, C.H.; de Jeu, R.A.M. SMOS soil moisture retrievals using the land parameter retrieval model: Evaluation over the murrumbidgee catchment, southeast Australia. Remote Sens. Environ. 2015, 163, 70–79. [Google Scholar] [CrossRef]
- Van der Schalie, R.; Kerr, Y.H.; Wigneron, J.P.; Rodríguez-Fernández, N.J.; Al-Yaari, A.; de Jeu, R.A.M. Global SMOS soil moisture retrievals from the land parameter retrieval model. Int. J. Appl. Earth Obs. 2016, 45, 125–134. [Google Scholar] [CrossRef]
- VanderSat, B.V. Method and System for Improving the Resolution of Sensor Data. Patent WO2017216186, 13 June 2016. [Google Scholar]
- Martens, B.; Miralles, D.G.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Gash, J.H.C. An analytical model of rainfall interception by forests. Q. J. R. Meteorol. Soc. 1979, 105, 43–55. [Google Scholar] [CrossRef]
- Valente, F.; David, J.S.; Gash, J.H.C. Modelling interception loss for two sparse eucalypt and pine forests in central Portugal using reformulated Rutter and Gash analytical models. J. Hydrol. 1997, 190, 141–162. [Google Scholar] [CrossRef]
- Miralles, D.G.; Gash, J.H.; Holmes, T.R.; De Jeu, R.A.; Dolman, A.J. Global canopy interception from satellite observations. J. Geophys. Res.-Atmos. 2010, 115, 1–8. [Google Scholar] [CrossRef]
- Priestley, C.; Taylor, R. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Liu, Y.Y.; van Dijk, A.I.J.M.; McCabe, M.F.; Evans, J.P.; de Jeu, R.A.M. Global vegetation biomass change (1988–2008) and attribution to environmental and human drivers. Glob. Ecol. Biogeogr. 2013, 22, 692–705. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.; Lievens, H.; Fernández-Prieto, D.; Verhoest, N. Improving terrestrial evaporation estimates over continental Australia through assimilation of SMOS soil moisture. Int. J. Appl. Earth Obs. 2016, 48, 146–162. [Google Scholar] [CrossRef]
- Murphy, D.M.; Koop, T. Review of the vapour pressures of ice and supercooled water for atmospheric applications. Q. J. R. Meteorol. Soc. 2005, 131, 1539–1565. [Google Scholar] [CrossRef] [Green Version]
- Trigo, I.F.; Dacamara, C.C.; Viterbo, P.; Roujean, J.L.; Olesen, F.; Barroso, C.; Camacho-De-Coca, F.; Carrer, D.; Freitas, S.C.; García-Haroj, J.; et al. The satellite application facility for land surface analysis. Int. J. Remote Sens. 2011, 32, 2725–2744. [Google Scholar] [CrossRef]
- Schaaf, C.; Wang, Z. MCD43A3 MODIS/Terra+Aqua BRDF/Albedo Daily L3 Global—500 m V006 [Data Set]; NASA EOSDIS Land Process; DAAC, USGS/Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA, 2015. [CrossRef]
- Wielicki, B.A. Clouds and the Earth’s radiant energy system (CERES): An earth observing system experiment. Bull. Am. Meteorol. Soc. 1996, 77, 853–868. [Google Scholar] [CrossRef]
- Royal Haskoning DHV. Nelen and Schuurmans. Nationale Regenradar: Toelichting Operationele Producten. Available online: https://nationaleregenradar.nl/pdfs/hoofdrapport_NRR_definitief.pdf (accessed on 30 October 2018).
- Owe, M.; de Jeu, R.; Holmes, T. Multisensor historical climatology of satellite-derived global land surface moisture. J. Geophys. Res. Earth 2008, 113, F01002. [Google Scholar] [CrossRef]
- Albergel, C.; Rüdiger, C.; Pellarin, T.; Calvet, J.C.; Fritz, N.; Froissard, F.; Suquia, D.; Petitpa, A.; Piguet, B.; Martin, E. From near-surface to root-zone soil moisture using an exponential filter: An assessment of the method based on in situ observations and model simulations. Hydrol. Earth Syst. Sci. 2008, 5, 1603–1640. [Google Scholar] [CrossRef]
- Stauffer, D.R.; Seaman, N.L. Use of four-dimensional data assimilation in a limited-area mesoscale model. Part I: Experiments with synoptic-scale data. Mon. Weather Rev. 1990, 118, 1250–1277. [Google Scholar] [CrossRef]
- Hengl, T.; De Jesus, J.M.; Heuvelink, G.B.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [PubMed]
- Dimiceli, C.; Carroll, M.; Sohlberg, R.; Kim, D.; Kelly, M.; Townshend, J. MOD44B MODIS/Terra Vegetation Continuous Fields Yearly L3 Global 250 m SIN Grid V006 [Data Set]; NASA EOSDIS Land Process; DAAC, USGS/Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA, 2015. [CrossRef]
- Mach, D.; Christian, H.; Blakeslee, R.; Boccippio, D.; Goodman, S.; Boeck, W. Performance assessment of the optical transient detector and lighning Imaging sensor. J. Geophys. Res. 2007, 112, D09210. [Google Scholar] [CrossRef]
- Jacobs, A.F.; Heusinkveld, B.G.; Kruit, R.J.; Berkowicz, S.M. Contribution of dew to the water budget of a grassland area in The Netherlands. Water Resour. Res. 2006, 42, 1–8. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; Van Oevelen, P.; et al. The international soil moisture network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef]
- Dorigo, W.; Xaver, A.; Vreugdenhil, M.; Gruber, A.; Hegyiová, A.; Sanchis-Dufau, A.; Zamojski, D.; Cordes, C.; Wagner, W.; Drusch, M. Global automated quality control of in situ soil moisture data from the international soil moisture network. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Benninga, H.J.F.; Carranza, C.D.; Pezij, M.; Van Santen, P.; Van Der Ploeg, M.J.; Augustijn, D.C.; Van Der Velde, R. The Raam regional soil moisture monitoring network in The Netherlands. Earth Syst. Sci. Data 2018, 10, 61–79. [Google Scholar] [CrossRef]
- Carrara, A.; Janssens, I.A.; Curiel Yuste, J.; Ceulemans, R. Seasonal changes in photosynthesis, respiration and NEE of a mixed temperate forest. Agric. For. Meteorol. 2004, 126, 15–31. [Google Scholar] [CrossRef]
- Borchard, N.; Schirrmann, M.; von Hebel, C.; Schmidt, M.; Baatz, R.; Firbank, L.; Vereecken, H.; Herbst, M. Spatio-temporal drivers of soil and ecosystem carbon fluxes at field scale in an upland grassland in Germany. Agric. Ecosyst. Environ. 2015, 211, 84–93. [Google Scholar] [CrossRef] [Green Version]
- Eder, F.; Schmidt, M.; Damian, T.; Träumer, K.; Mauder, M. Mesoscale eddies affect near-surface turbulent exchange: Evidence from lidar and tower measurements. J. Appl. Meteorol. Climatol. 2015, 54, 189–206. [Google Scholar] [CrossRef]
- Chen, T.H.; Henderson-Sellers, A.; Milly, P.C.; Pitman, A.J.; Beljaars, A.C.; Polcher, J.; Abramopoulos, F.; Boone, A.; Chang, S.; Chen, F.; et al. Cabauw experimental results from the project for intercomparison of land-surface parameterization schemes. J. Clim. 1997, 10, 1194–1215. [Google Scholar] [CrossRef]
- Ghilain, N.; Arboleda, A.; Gellens-Meulenberghs, F. Evapotranspiration modelling at large scale using near-real time MSG SEVIRI derived data. Hydrol. Earth Syst. Sci. 2011, 15, 771–786. [Google Scholar] [CrossRef] [Green Version]
- Masson, V.; Champeaux, J.L.; Chauvin, F.; Meriguet, C.; Lacaze, R. A global database of land surface parameters at 1-km resolution in meteorological and climate models. J. Clim. 2003, 16, 1261–1282. [Google Scholar] [CrossRef]
- Makkink, G. Testing the Penman formula by means of lysimeters. J. Inst. Water Eng. 1957, 11, 277–288. [Google Scholar]
- De Bruin, H. The determination of (reference crop) evapotranspiration from routine weather data. In Evaporation and Weather: Proceedings and Information; Hooghart, C., Ed.; TNO Committee on Hydrological Research: The Hague, The Netherlands, 1981; Volume 28, pp. 25–37. [Google Scholar]
- Jacobs, A.F.G.; De Bruin, H.A.R. Makkink’s equation for evapotranspiration applied to unstressed maize. Hydrol. Process. 1998, 12, 1063–1066. [Google Scholar] [CrossRef]
- Jacobs, A.F.; Heusinkveld, B.G.; Holtslag, A.A. Eighty years of meteorological observations at Wageningen, The Netherlands: Precipitation and evapotranspiration. Int. J. Climatol. 2010, 30, 1315–1321. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Bitar, A.A.; Cabot, F.; Gruhier, C.; Juglea, S.E.; et al. The SMOS soil moisture retrieval algorithm. IEEE Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Chan, S.K.; Bindlish, R.; Neill, P.O.; Jackson, T.; Njoku, E.; Dunbar, S.; Chaubell, J.; Piepmeier, J.; Yueh, S.; Entekhabi, D.; et al. Development and assessment of the SMAP enhanced passive soil moisture product. Remote Sens. Environ. 2018, 204, 931–941. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.; Gao, F.; Knipper, K.; Hain, C.; Dulaney, W.; Baldocchi, D.; Eichelmann, E.; Hemes, K.; Yang, Y.; Medellin-Azuara, J.; et al. Field-scale assessment of land and water use change over the california delta using remote sensing. Remote Sens. 2018, 10, 889. [Google Scholar] [CrossRef]
- Miralles, D.G.; De Jeu, R.A.; Gash, J.H.; Holmes, T.R.; Dolman, A.J. Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. Sci. 2011, 15, 967–981. [Google Scholar] [CrossRef] [Green Version]
- Ter Maat, H.W.; Moors, E.J.; Hutjes, R.W.A.; Holtslag, A.A.M.; Dolman, A.J. Exploring the impact of land cover and topography on rainfall maxima in The Netherlands. J. Hydrometeorol. 2013, 14, 524–542. [Google Scholar] [CrossRef]
- Jarvis, P.G. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. R. Soc. B 1976, 273, 593–610. [Google Scholar] [CrossRef]
- WUR-Alterra. Grondsoortenkaart van Nederland 2006 [Data Set]; Wageningen University and Research: Wageningen, The Netherlands, 2006. [Google Scholar]
| Variable | Dataset | Resolution | References | |
|---|---|---|---|---|
| Spatial | Temporal | |||
| , , , | CERES L3SYN1DEG | 100 km | 1 day | Wielicky et al. [56] |
| , | Meteosat LSA SAF DIDSSF/DIDSLF | 3.1 km | 1 day | Trigo et al. [54] |
| Emissivity | Meteosat LSA SAF EM | 3.1 km | 1 day | Trigo et al. [54] |
| Albedo | MODIS MCD43A3 | 500 m | 16 day | Schaaf and Wang [55] |
| LST | VanderSat LST-100 | 100 m | 1 day | VanderSat [45] |
| Precipitation | Nationale Regenradar | 1 km | 5 min | Royal Haskoning DHV and |
| Nelen and Schuurmans [57] | ||||
| VOD | VanderSat VOD-C1N-100 | 100 m | 1 day | VanderSat [45] |
| Soil Moisture | VanderSat SM-C1N-100-SWI-T10 | 100 m | 1 day | VanderSat [45] |
| ASCAT-SWI | 10 km | 1 day | Albergel et al. [59] | |
| Cover Fractions | MODIS MOD44B | 250 m | 1 year | Dimiceli et al. [62] |
| Soil Properties | SoilGrids250m | 250 m | — | Hengl et al. [61] |
| Lightning Frequency | LIS/OTD | 5 km | — | Mach et al. [63] |
| ID | Latitude | Longitude | LC | Data Coverage | Reference/PI |
|---|---|---|---|---|---|
| BE-Bra | 51.31 | 4.52 | MF | 2013–2014 (187) | Carrara et al. [68] |
| DE-RuR * | 50.62 | 6.30 | GRA | 2013–2016 (334/1253 *) | Borchard et al. [69] |
| DE-RuS * | 50.87 | 6.45 | CRO | 2013–2015 (193/573 *) | Eder et al. [70] |
| Nl-Ca1 | 51.97 | 4.93 | GRA | 2013–2017 (473) | Chen et al. [71] |
| Nl-Loo * | 52.17 | 5.74 | ENF | 2013–2014 (193/576 *) | Eddy Moors |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martens, B.; De Jeu, R.A.M.; Verhoest, N.E.C.; Schuurmans, H.; Kleijer, J.; Miralles, D.G. Towards Estimating Land Evaporation at Field Scales Using GLEAM. Remote Sens. 2018, 10, 1720. https://doi.org/10.3390/rs10111720
Martens B, De Jeu RAM, Verhoest NEC, Schuurmans H, Kleijer J, Miralles DG. Towards Estimating Land Evaporation at Field Scales Using GLEAM. Remote Sensing. 2018; 10(11):1720. https://doi.org/10.3390/rs10111720
Chicago/Turabian StyleMartens, Brecht, Richard A. M. De Jeu, Niko E. C. Verhoest, Hanneke Schuurmans, Jonne Kleijer, and Diego G. Miralles. 2018. "Towards Estimating Land Evaporation at Field Scales Using GLEAM" Remote Sensing 10, no. 11: 1720. https://doi.org/10.3390/rs10111720
APA StyleMartens, B., De Jeu, R. A. M., Verhoest, N. E. C., Schuurmans, H., Kleijer, J., & Miralles, D. G. (2018). Towards Estimating Land Evaporation at Field Scales Using GLEAM. Remote Sensing, 10(11), 1720. https://doi.org/10.3390/rs10111720






