An Extension of Phase Correlation-Based Image Registration to Estimate Similarity Transform Using Multiple Polar Fourier Transform
Abstract
1. Introduction
2. Background
2.1. Feature-Based Methods
2.2. Area-Based Methods
3. Methodology
3.1. Math Theory of Image Registration Based on Phase Correlation
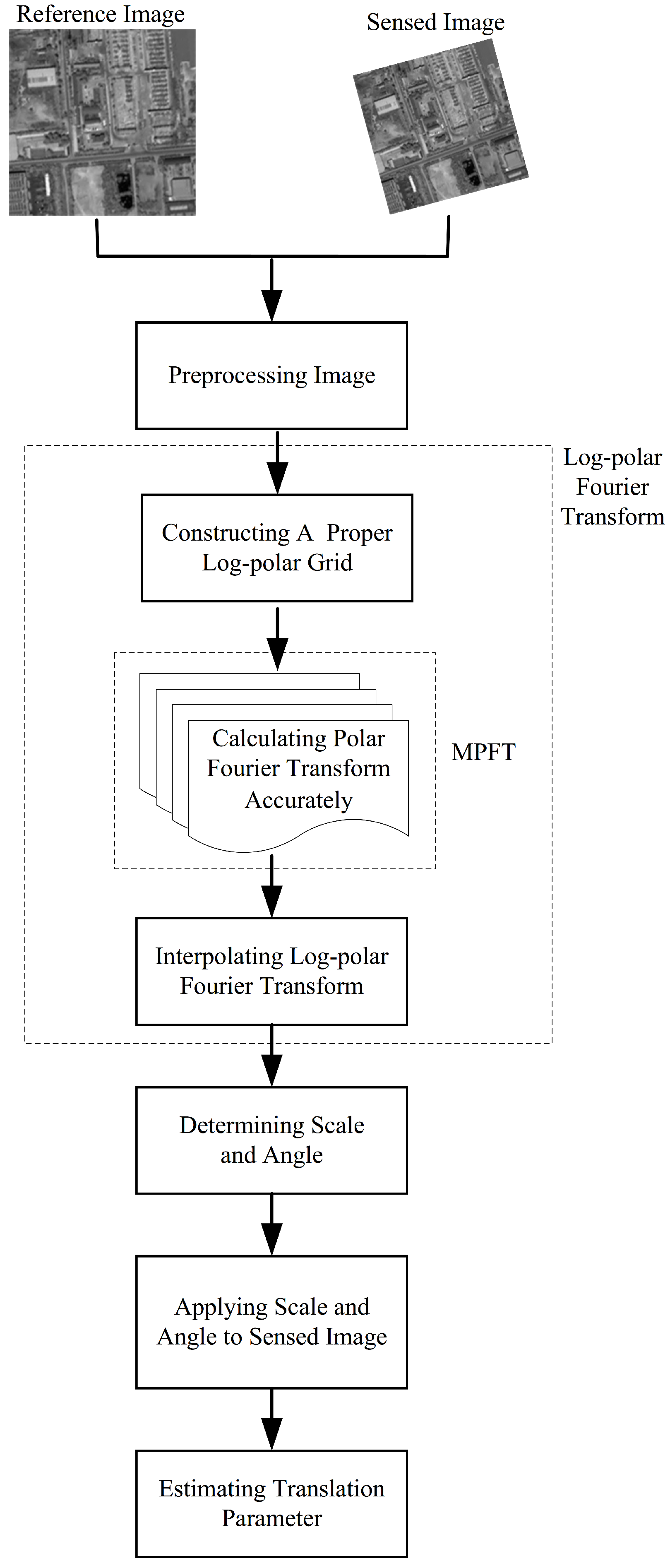
3.2. Overview of the Proposed Method
- (1)
- Image preprocessing: In general, for an image, its opposite borders (up and down or left and right frames) are not similar. so, the implicit periodic image presents strong discontinuities across the frame border. So, preprocessing of the image border is vital when directly estimating the linear phase difference in the frequency domain. In our method, during preprocessing, the original image is decomposed into two components, the ‘periodic component’ and the ‘smooth component’ by using the image decomposition method [42]. Then, the ‘smooth’ component is discarded and ‘periodic component’ is undergoes the log-polar Fourier transform [43].
- (2)
- Calculate the log-polar Fourier transform: There is no way to calculate the log-polar Fourier transform exactly except for the direct brute force computation whose complexity is . However, the accuracy of the estimation of the scale and angle heavily depends on the accuracy of the log-polar Fourier transform. In this paper, a novel calculation of the log-polar Fourier transform is proposed, which is described in detail in Section 3.3 and Section 3.4.
- (3)
- Determine the scale and angle parameters: According to the derivation expression 9, the magnitude spectra of the log-polar Fourier transform of one image and its scaled and rotational version have a translation relationship only. In our method, a phase correlation-based method is applied to estimate the displacements ( and ) in the radial direction and angular direction, respectively. According to the suggestion that aliasing and noise are also two of many factors that corrupt the sub-pixel accuracy of phase correlation-based image registration and that avoiding the inverse Fourier transform can alleviate the side effects of aliasing and noise [30], the displacements (, ) are estimated by calculating the linear phase difference directly in the frequency domain as well as identifying the location of the dominant peak of the inverse Fourier transform of the normalized cross-relation matrix. Then, , are converted to scale s and angle , respectively, with the following formula:where is the log-base and is the angular sampling interval.
- (4)
- Apply the scale and angle parameters to the original image: The sensed image is transformed by the scale and rotation factors, and then only the shift is left between the referenced image and the corrected sensed image.
- (5)
- Estimate the translation parameter: After scaling and rotating the sensed image, the phase correlation-based method is again applied to estimate the displacement between the reference and sensed images. At this point, all of the scale, rotation, and translation parameters have been determined.
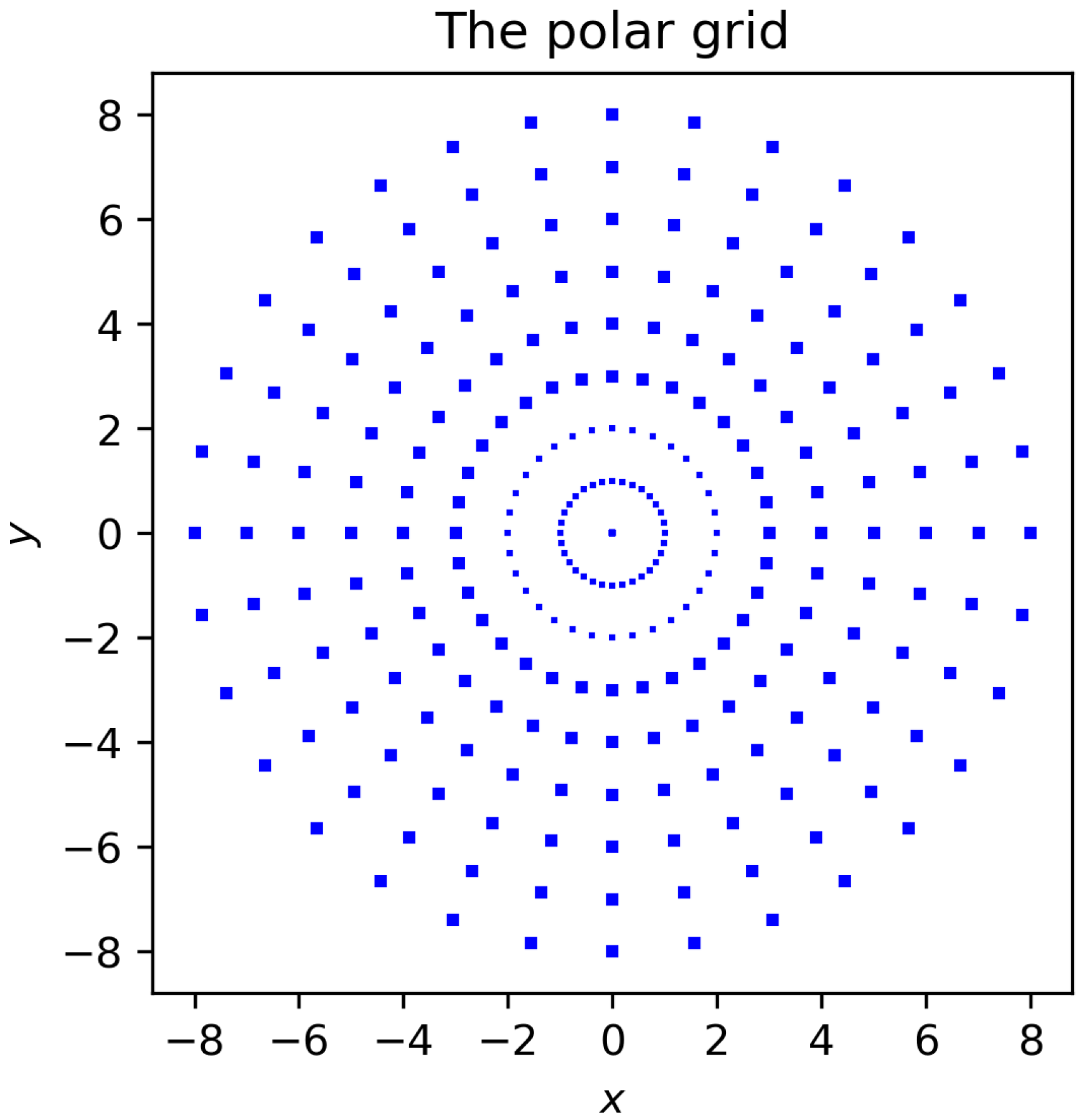
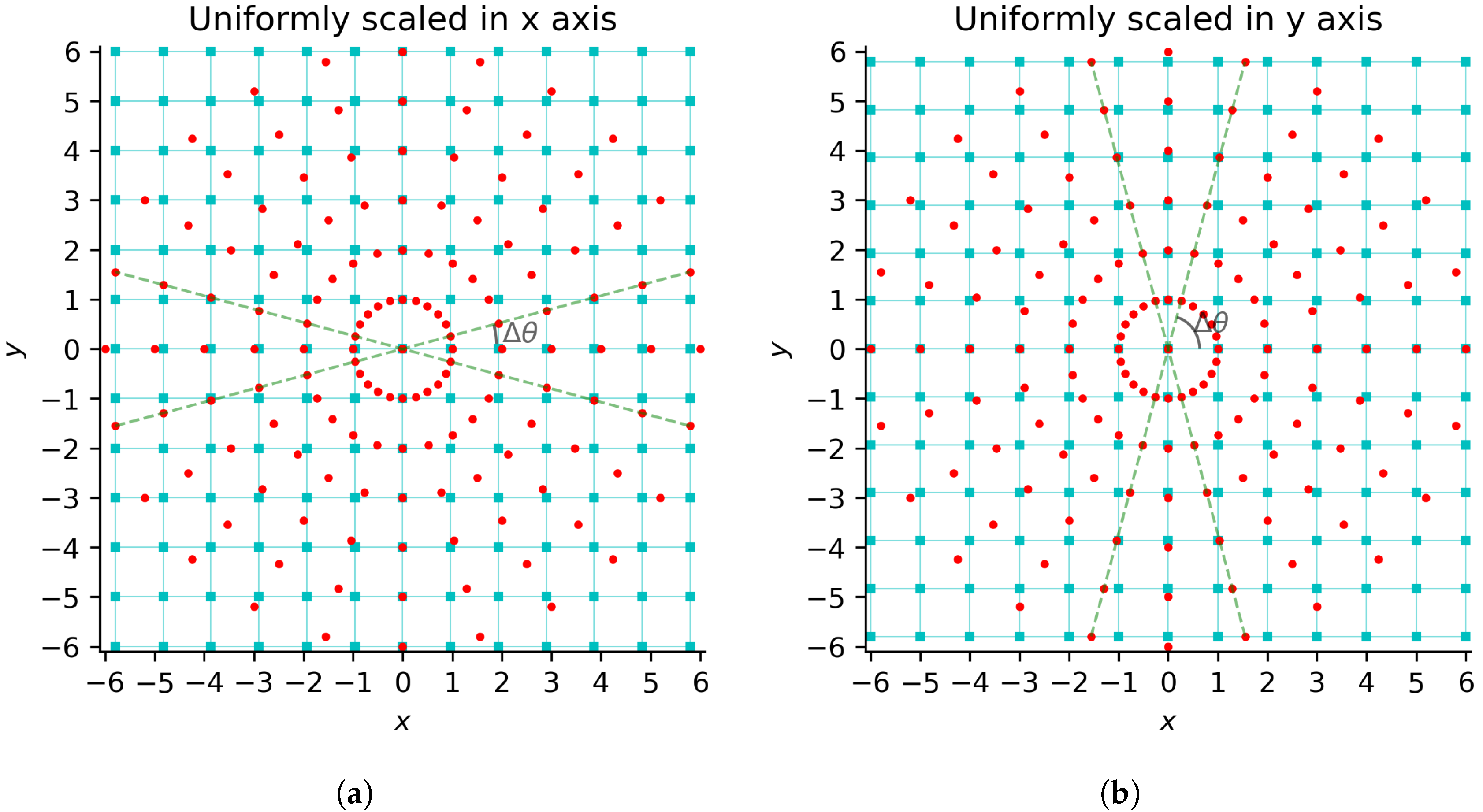
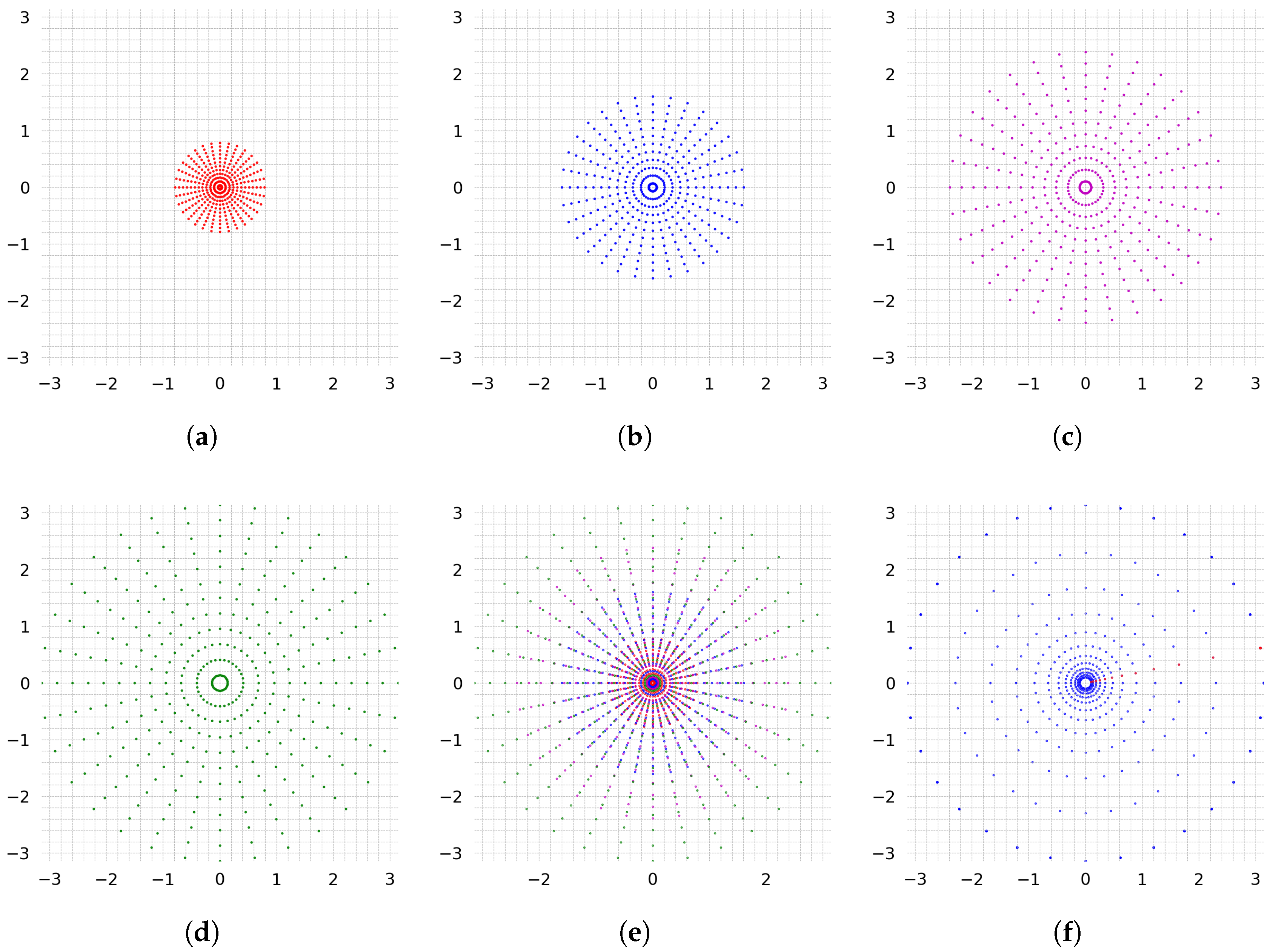
3.3. Construction of the Proper Destination Grid of the Log-Polar Grid
3.4. Calculation of the Log-Polar Fourier Transform
3.4.1. Preliminaries: 1D Fractional Fourier Transform
3.4.2. Fast and Exact Computation of the Discrete Fourier Transform for the Polar Grid
3.4.3. Interpolation of the Log-Polar Fourier Transform
4. Experiments and Analysis
4.1. Qualitative Experiment
4.2. Quantitative Experiment
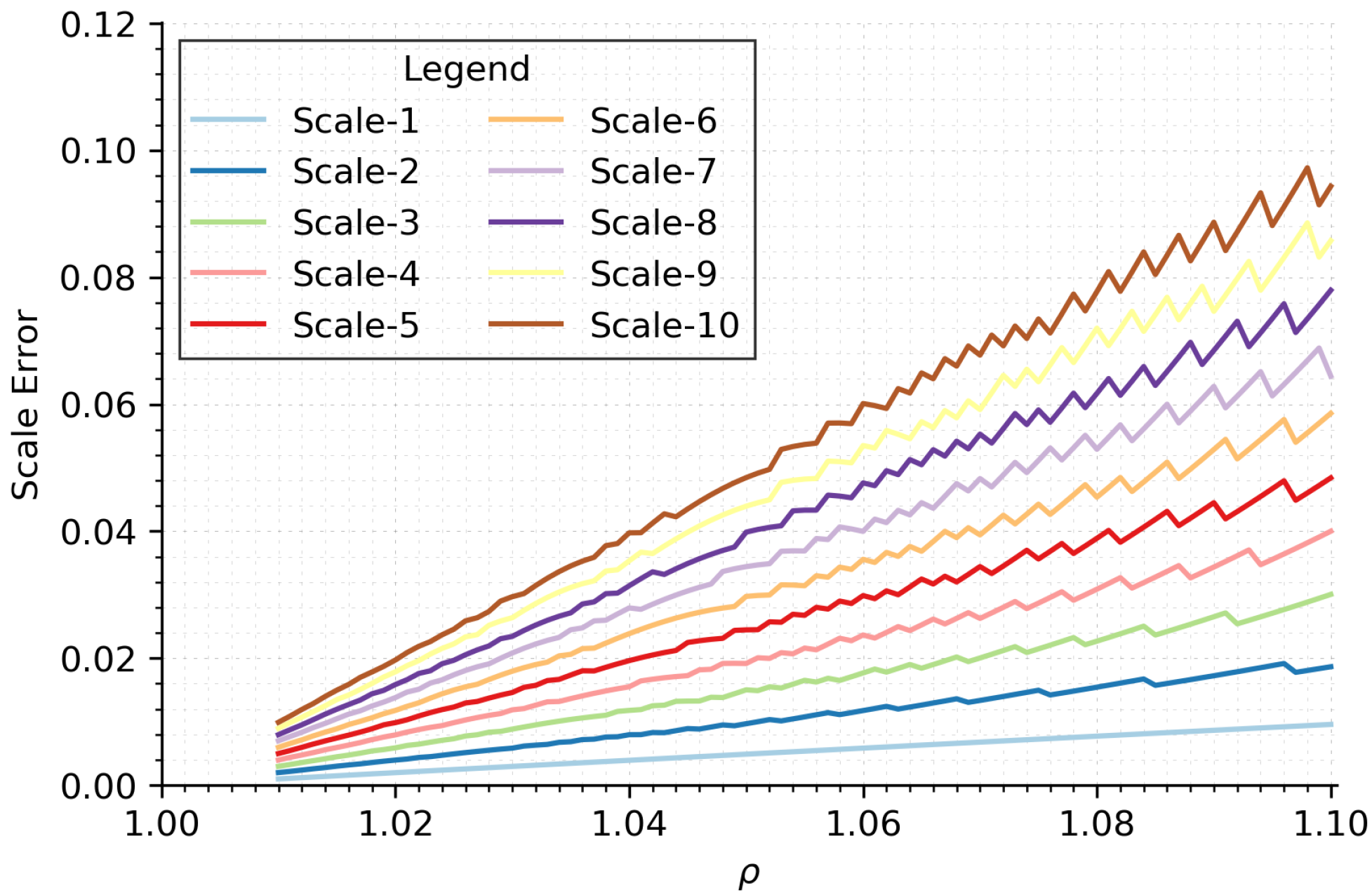
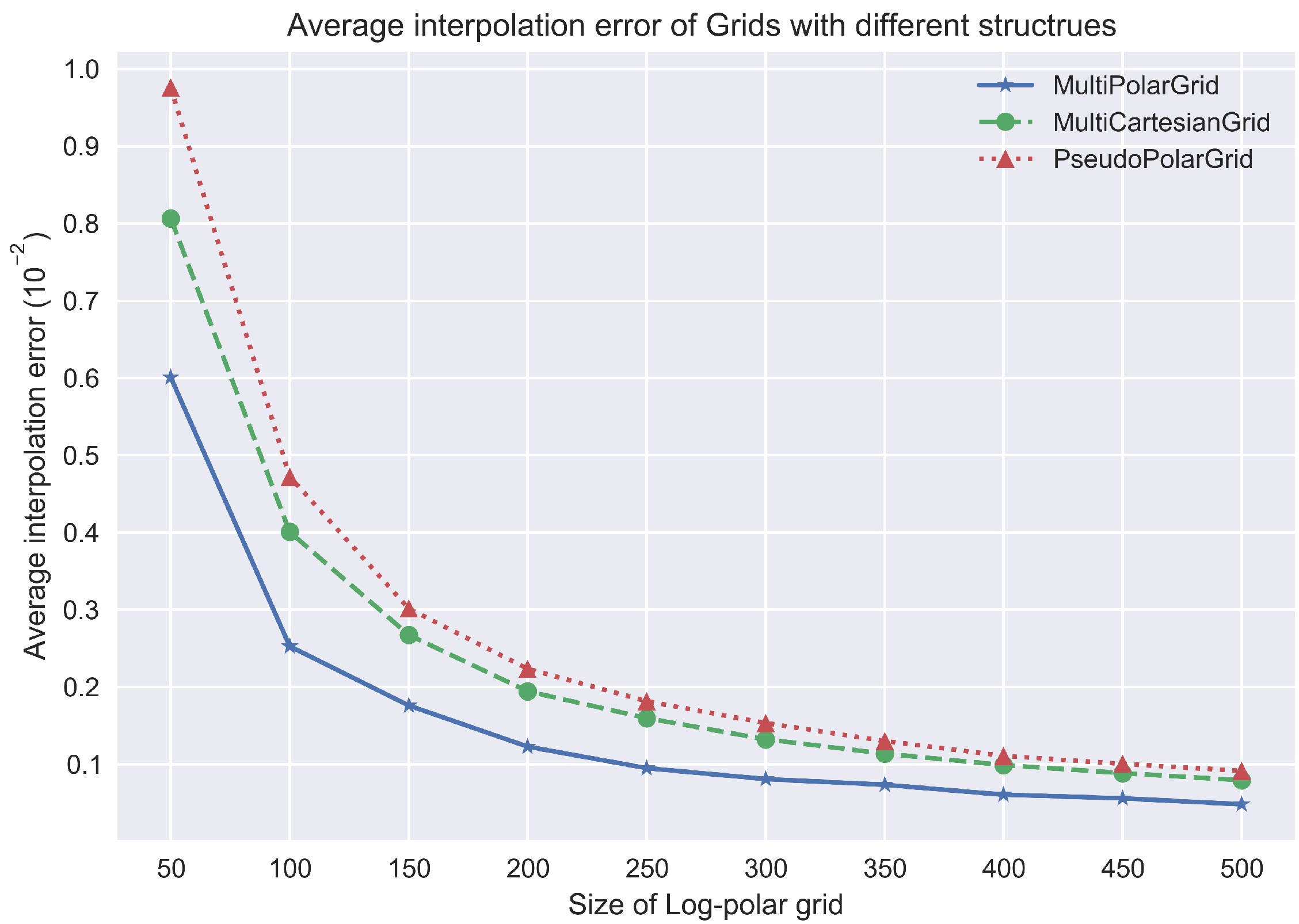
4.2.1. Numerical Simulation of the Interpolation Error
4.2.2. Synthetic Data Experiments
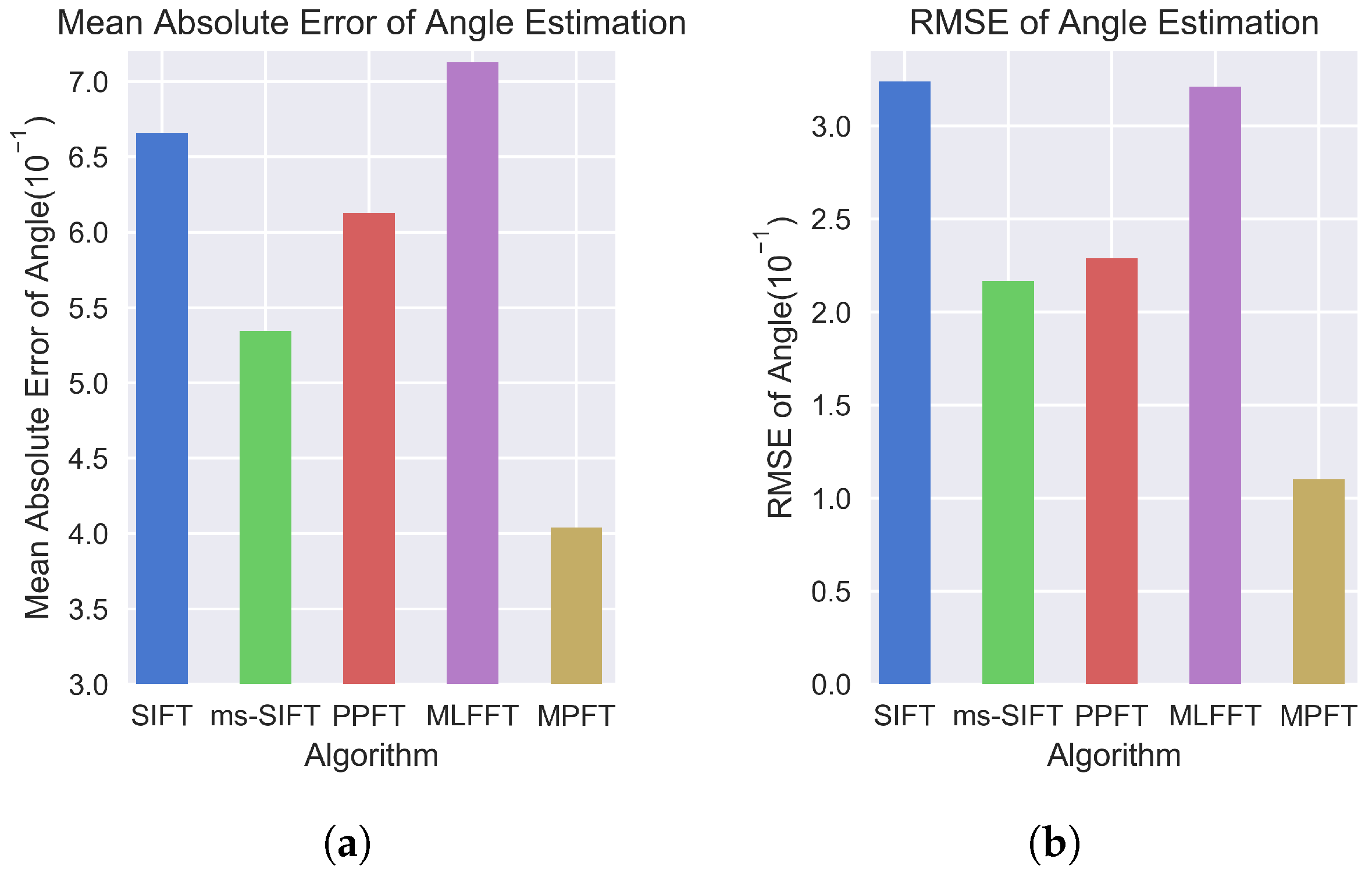
Angle Estimation
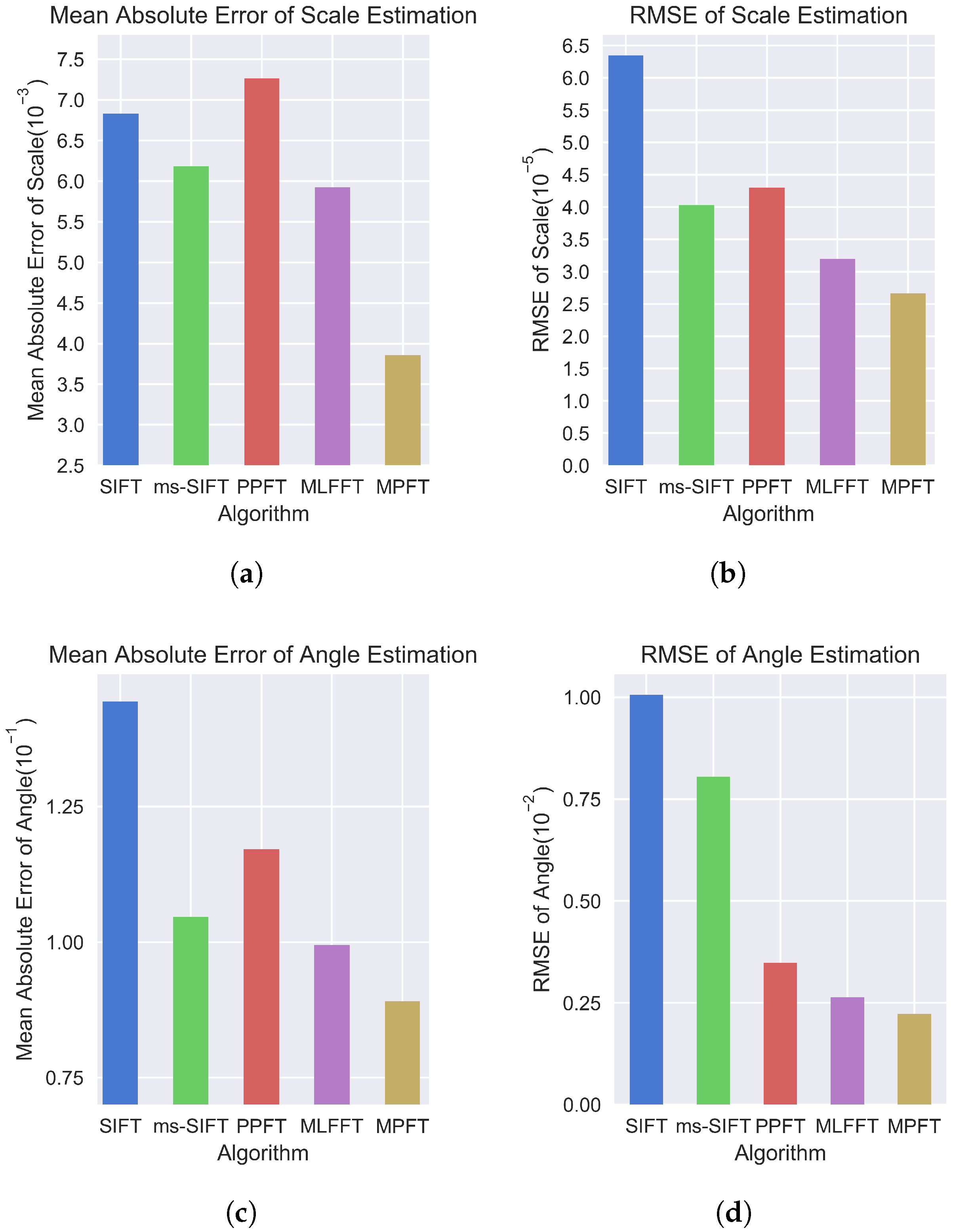
Similarity Transformation Estimation
4.2.3. Real Experiments and Analysis
4.2.3.1. Estimation of the Similarity Transform between Remote Sensing Images Directly
4.2.3.2. Register Scenes of Remote Sensing by Tiling
5. Discussion
5.1. Analysis of the Parameter Settings
5.2. Analysis of Performance
5.3. Analysis of Efficiency
5.4. Analysis of Applicability and Limitations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Brown, L.G. A survey of image registration techniques. ACM Comput. Surv. (CSUR) 1992, 24, 325–376. [Google Scholar] [CrossRef]
- Zitova, B.; Flusser, J. Image registration methods: A survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef]
- Behling, R.; Roessner, S.; Segl, K.; Kleinschmit, B.; Kaufmann, H. Robust automated image co-registration of optical multi-sensor time series data: Database generation for multi-temporal landslide detection. Remote Sens. 2014, 6, 2572–2600. [Google Scholar] [CrossRef]
- Modersitzki, J. Numerical Methods for Image Registration; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Sundaresan, A.; Varshney, P.K.; Arora, M.K. Robustness of change detection algorithms in the presence of registration errors. Photogramm. Eng. Remote Sens. 2007, 73, 375–383. [Google Scholar] [CrossRef]
- Yan, L.; Roy, D.P.; Zhang, H.; Li, J.; Huang, H. An automated approach for sub-pixel registration of Landsat-8 Operational Land Imager (OLI) and Sentinel-2 Multi Spectral Instrument (MSI) imagery. Remote Sens. 2016, 8, 520. [Google Scholar] [CrossRef]
- Dai, X.; Khorram, S. The effects of image misregistration on the accuracy of remotely sensed change detection. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1566–1577. [Google Scholar]
- Liu, Y.; Mo, F.; Tao, P. Matching Multi-Source Optical Satellite Imagery Exploiting a Multi-Stage Approach. Remote Sens. 2017, 9, 1249. [Google Scholar] [CrossRef]
- Stumpf, A.; Michéa, D.; Malet, J.P. Improved Co-Registration of Sentinel-2 and Landsat-8 Imagery for Earth Surface Motion Measurements. Remote Sens. 2018, 10, 160. [Google Scholar] [CrossRef]
- Long, T.; Jiao, W.; He, G.; Zhang, Z. A fast and reliable matching method for automated georeferencing of remotely-sensed imagery. Remote Sens. 2016, 8, 56. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Wang, S.; Quan, D.; Liang, X.; Ning, M.; Guo, Y.; Jiao, L. A deep learning framework for remote sensing image registration. ISPRS J. Photogramm. Remote Sens. 2018, 145, 148–164. [Google Scholar] [CrossRef]
- Tong, X.; Li, L.; Liu, S.; Xu, Y.; Ye, Z.; Jin, Y.; Wang, F.; Xie, H. Detection and estimation of ZY-3 three-line array image distortions caused by attitude oscillation. ISPRS J. Photogramm. Remote Sens. 2015, 101, 291–309. [Google Scholar] [CrossRef]
- Almonacid-Caballer, J.; Pardo-Pascual, J.E.; Ruiz, L.A. Evaluating fourier cross-correlation sub-pixel registration in landsat images. Remote Sens. 2017, 9, 1051. [Google Scholar] [CrossRef]
- Skakun, S.; Roger, J.C.; Vermote, E.F.; Masek, J.G.; Justice, C.O. Automatic sub-pixel co-registration of Landsat-8 Operational Land Imager and Sentinel-2A Multi-Spectral Instrument images using phase correlation and machine learning based mapping. Int. J. Dig. Earth 2017, 10, 1253–1269. [Google Scholar] [CrossRef]
- Scheffler, D.; Hollstein, A.; Diedrich, H.; Segl, K.; Hostert, P. AROSICS: An automated and robust open-source image co-registration software for multi-sensor satellite data. Remote Sens. 2017, 9, 676. [Google Scholar] [CrossRef]
- Reddy, B.S.; Chatterji, B.N. An FFT-based technique for translation, rotation, and scale-invariant image registration. IEEE Trans. Image Process. 1996, 5, 1266–1271. [Google Scholar] [CrossRef] [PubMed]
- Stone, H.S.; Tao, B.; McGuire, M. Analysis of image registration noise due to rotationally dependent aliasing. J. Vis. Commun. Image Represent. 2003, 14, 114–135. [Google Scholar] [CrossRef]
- Kupfer, B.; Netanyahu, N.S.; Shimshoni, I. An Efficient SIFT-Based Mode-Seeking Algorithm for Sub-Pixel Registration of Remotely Sensed Images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 379–383. [Google Scholar] [CrossRef]
- Sedaghat, A.; Ebadi, H. Accurate affine invariant image matching using oriented least square. Photogramm. Eng. Remote Sens. 2015, 81, 733–743. [Google Scholar] [CrossRef]
- Sedaghat, A.; Ebadi, H. Remote sensing image matching based on adaptive binning SIFT descriptor. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5283–5293. [Google Scholar] [CrossRef]
- Ye, Y.; Shan, J.; Bruzzone, L.; Shen, L. Robust registration of multimodal remote sensing images based on structural similarity. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2941–2958. [Google Scholar] [CrossRef]
- Sedaghat, A.; Mokhtarzade, M.; Ebadi, H. Uniform robust scale-invariant feature matching for optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4516–4527. [Google Scholar] [CrossRef]
- Sedaghat, A.; Mohammadi, N. Uniform competency-based local feature extraction for remote sensing images. ISPRS J. Photogramm. Remote Sens. 2018, 135, 142–157. [Google Scholar] [CrossRef]
- Ye, Y.; Shan, J.; Hao, S.; Bruzzone, L.; Qin, Y. A local phase based invariant feature for remote sensing image matching. ISPRS J. Photogramm. Remote Sens. 2018, 142, 205–221. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M.; Zhong, R. Robust feature matching via support-line voting and affine-invariant ratios. ISPRS J. Photogramm. Remote Sens. 2017, 132, 61–76. [Google Scholar] [CrossRef]
- Argyriou, V.; Vlachos, T. A Study of Sub-Pixel Motion Estimation Using Phase Correlation; BMVC: York, UK, 2006; pp. 387–396. [Google Scholar]
- Tian, Q.; Huhns, M.N. Algorithms for subpixel registration. Comput. Vis. Graph. Image Process. 1986, 35, 220–233. [Google Scholar] [CrossRef]
- Abdou, I.E. Practical approach to the registration of multiple frames of video images. In Proceedings of the International Society for Optics and Photonics, Visual Communications and Image Processing ’99, San Jose, CA, USA, 28 December 1998; Volume 3653, pp. 371–383. [Google Scholar]
- Stone, H.S.; Orchard, M.T.; Chang, E.C.; Martucci, S.A. A fast direct Fourier-based algorithm for subpixel registration of images. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2235–2243. [Google Scholar] [CrossRef]
- Liu, J.G.; Yan, H. Robust phase correlation methods for sub-pixel feature matching. In Proceedings of the 1st Annual Conference System Eng. Autonomous System Defence Technology Centre, Edinburgh, UK, 7–9 September 2006; p. A13. [Google Scholar]
- Liu, J.; Yan, H. Phase correlation pixel-to-pixel image co-registration based on optical flow and median shift propagation. Int. J. Remote Sens. 2008, 29, 5943–5956. [Google Scholar] [CrossRef]
- Tong, X.; Xu, Y.; Ye, Z.; Liu, S.; Li, L.; Xie, H.; Wang, F.; Gao, S.; Stilla, U. An improved phase correlation method based on 2-D plane fitting and the maximum kernel density estimator. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1953–1957. [Google Scholar] [CrossRef]
- Hoge, W.S. A subspace identification extension to the phase correlation method [MRI application]. IEEE Trans. Med. Imaging 2003, 22, 277–280. [Google Scholar] [CrossRef] [PubMed]
- Tong, X.; Ye, Z.; Xu, Y.; Liu, S.; Li, L.; Xie, H.; Li, T. A novel subpixel phase correlation method using singular value decomposition and unified random sample consensus. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4143–4156. [Google Scholar] [CrossRef]
- Leprince, S.; Barbot, S.; Ayoub, F.; Avouac, J. Automatic, precise, ortho-rectification and co-registration for satellite image correlation, application to seismotectonics. IEEE Trans. Geosci. Remote Sens 2007, 45, 1529–1558. [Google Scholar] [CrossRef]
- Dong, Y.; Long, T.; Jiao, W.; He, G.; Zhang, Z. A novel image registration method based on phase correlation using low-rank matrix factorization with mixture of Gaussian. IEEE Trans. Geosci. Remote Sens. 2018, 56, 446–460. [Google Scholar] [CrossRef]
- Chen, Q.; Defrise, M.; Deconinck, F. Symmetric phase-only matched filtering of Fourier-Mellin transforms for image registration and recognition. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 1156–1168. [Google Scholar] [CrossRef]
- Keller, Y.; Averbuch, A.; Israeli, M. Pseudopolar-based estimation of large translations, rotations, and scalings in images. IEEE Trans. Image Process. 2005, 14, 12–22. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Guo, B.; Feng, Z. Pseudo-log-polar Fourier transform for image registration. IEEE Signal Process. Lett. 2006, 13, 17–20. [Google Scholar]
- Pan, W.; Qin, K.; Chen, Y. An adaptable-multilayer fractional Fourier transform approach for image registration. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 400–414. [Google Scholar] [CrossRef] [PubMed]
- Moisan, L. Periodic plus smooth image decomposition. J. Math. Imaging Vis. 2011, 39, 161–179. [Google Scholar] [CrossRef]
- Dong, Y.; Long, T.; Jiao, W. Eliminating effect of image border with image decomposition for phase correlation based image registration. In Proceedings of the 2018 IEEE International, Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 23–27 July 2018. [Google Scholar]
- Abbas, S.A.; Sun, Q.; Foroosh, H. An Exact and Fast Computation of Discrete Fourier Transform for Polar and Spherical Grid. IEEE Trans. Signal Process. 2017, 65, 2033–2048. [Google Scholar] [CrossRef]
- Bailey, D.H.; Swarztrauber, P.N. The fractional Fourier transform and applications. SIAM Rev. 1991, 33, 389–404. [Google Scholar] [CrossRef]
- Averbuch, A.; Coifman, R.R.; Donoho, D.L.; Elad, M.; Israeli, M. Fast and accurate polar Fourier transform. Appl. Comput. Harmon. Anal. 2006, 21, 145–167. [Google Scholar] [CrossRef]
- Vedaldi, A.; Fulkerson, B. VLFeat: An open and portable library of computer vision algorithms. In Proceedings of the 18th ACM international conference on Multimedia, Firenze, Italy, 25–29 October 2010; pp. 1469–1472. [Google Scholar]
- Fraser, C.S.; Dial, G.; Grodecki, J. Sensor orientation via RPCs. ISPRS J. Photogramm. Remote Sens. 2006, 60, 182–194. [Google Scholar] [CrossRef]
- Long, T.; Jiao, W.; He, G. RPC Estimation via ℓ1-Norm-Regularized Least Squares (L1LS). IEEE Trans. Geosci. Remote Sens. 2015, 53, 4554–4567. [Google Scholar] [CrossRef]




| Experiment | Constuction of the Log-Polar Grid (or Polar Grid) | Number of Single Grids | ||||
|---|---|---|---|---|---|---|
| Size | Log-Base | MPFT | MLFFT | |||
| Number of Radial Lines | Number of Points in the Radial Line | |||||
| Numerical Experiment | … | … | 1.044 | 4 | 4 | |
| Synthetic Data Experiment | Similarity Transform Estimation Angle Estimation | 128 | 128 | 4 | 4 | |
| 250 | 250 | – | 1 | 4 | ||
| Real Data Experiment | 128 | 128 | 4 | 4 | ||
| Further Analysis | 128 | 128 | … | 4 | 4 | |
| Category | Sensed Image | Reference Image | Number of Image Pairs |
|---|---|---|---|
| I | Sensor: GF-2 Panchromatic Resolution: 0.81 m Size: 512 × 512 Acquisition Data: November 2017 | Sensor: GF-1 Panchromatic Resolution: 2.0 m Size: 207 × 207 Acquisition Data: June 2013 | 15 |
| II | Sensor: GF-1 Panchromatic Resolution: 2.0 m Size: 829 × 829 Acquisition Data: June 2013 | Sensor: GF-2 Multispectral Resolution: 3.24 m Size: 512 × 512 Acquisition Data: November 2017 | 15 |
| III | Sensor: GF-2 Multispectral Resolution: 3.24 m Size: 800 × 800 Acquisition Data: June 2013 | Sensor: GF-1 Multispectral Resolution: 16 m Size: 162 × 162 Acquisition Data: November 2017 | 15 |
| Algorithm | e | ||||
|---|---|---|---|---|---|
| SIFT | 0.8041 | 1.6291 | 0.7203 | 1.8937 | 1.1908 |
| ms-SIFT | 0.6291 | 1.5721 | 0.6715 | 1.6382 | 0.9925 |
| PPFT | 0.7052 | 1.4650 | 0.7133 | 1.5320 | 1.1201 |
| MLFFT | 0.6183 | 1.3952 | 0.6201 | 1.3905 | 0.9729 |
| MPFT | 0.5623 | 1.3815 | 0.5738 | 1.3902 | 0.9017 |
| Algorithm | e | ||||
|---|---|---|---|---|---|
| PC | 1.3671 | 3.1459 | 0.5196 | 1.5505 | 1.4625 |
| PPFT | 1.2539 | 2.3720 | 0.4912 | 1.2318 | 1.3466 |
| MLFFT | 1.1997 | 2.2225 | 0.5187 | 1.8221 | 1.3071 |
| MPFT | 1.0850 | 2.1370 | 0.4385 | 1.4062 | 1.1703 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Jiao, W.; Long, T.; He, G.; Gong, C. An Extension of Phase Correlation-Based Image Registration to Estimate Similarity Transform Using Multiple Polar Fourier Transform. Remote Sens. 2018, 10, 1719. https://doi.org/10.3390/rs10111719
Dong Y, Jiao W, Long T, He G, Gong C. An Extension of Phase Correlation-Based Image Registration to Estimate Similarity Transform Using Multiple Polar Fourier Transform. Remote Sensing. 2018; 10(11):1719. https://doi.org/10.3390/rs10111719
Chicago/Turabian StyleDong, Yunyun, Weili Jiao, Tengfei Long, Guojin He, and Chengjuan Gong. 2018. "An Extension of Phase Correlation-Based Image Registration to Estimate Similarity Transform Using Multiple Polar Fourier Transform" Remote Sensing 10, no. 11: 1719. https://doi.org/10.3390/rs10111719
APA StyleDong, Y., Jiao, W., Long, T., He, G., & Gong, C. (2018). An Extension of Phase Correlation-Based Image Registration to Estimate Similarity Transform Using Multiple Polar Fourier Transform. Remote Sensing, 10(11), 1719. https://doi.org/10.3390/rs10111719






