Deep Distillation Recursive Network for Remote Sensing Imagery Super-Resolution
Abstract
1. Introduction
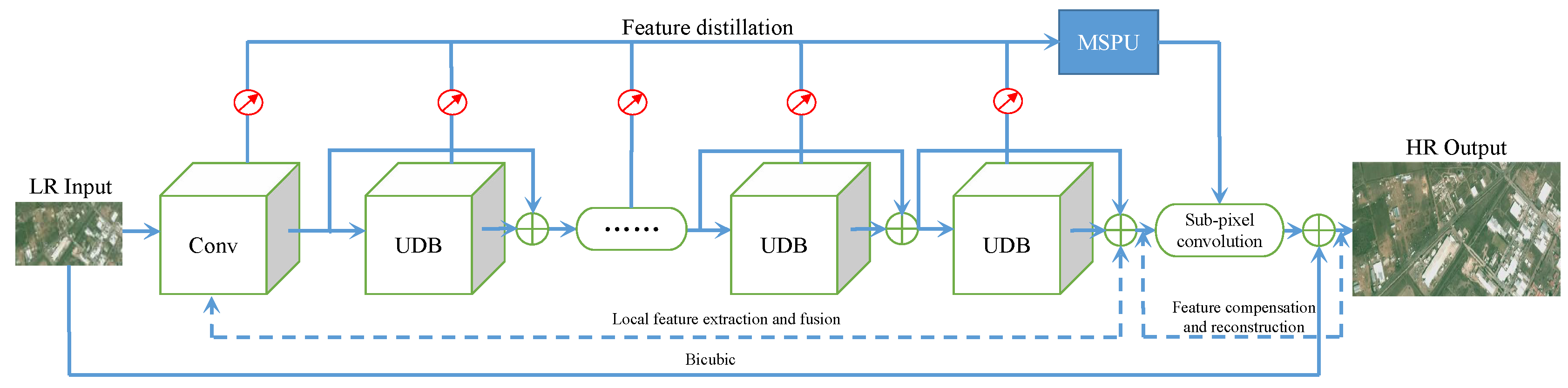
- We propose a novel deep distillation recursive network DDRN for remote sensing satellite image SR reconstruction in a convenient and effective end-to-end training manner.
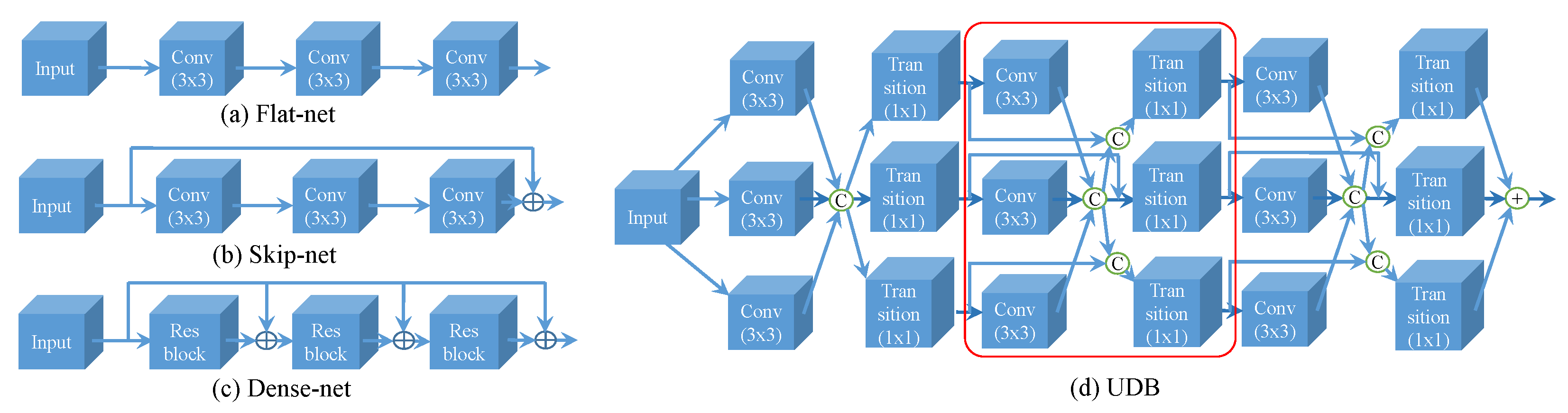
- We propose a novel multiple-path residual block UDB, which provides additional possibilities for feature extraction through ultra-dense connections, quite agreeing with the uneven complexity of image content.
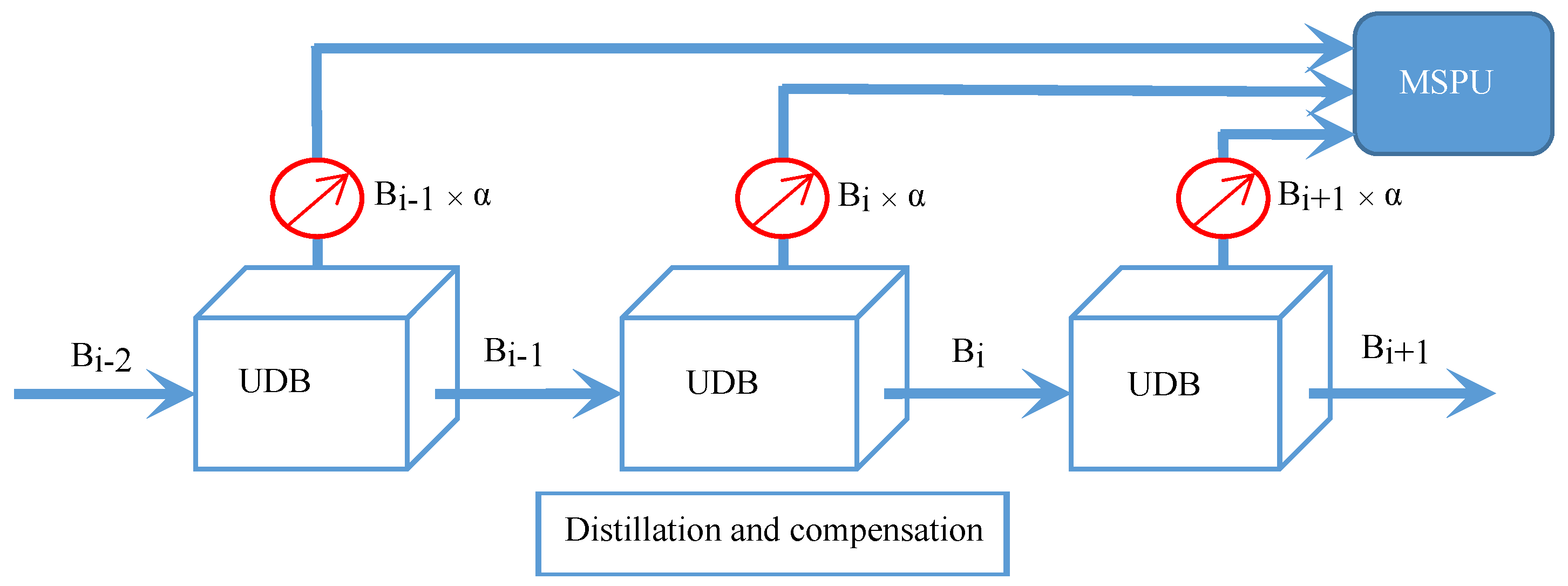
- We construct a distillation and compensation mechanism to compensate for the high-frequency details lost during information propagation through the network with a special distillation ratio.
2. Related Work
3. Network Architecture
4. Feature Extraction and Distillation
4.1. Ultra-Dense Residual Block (UDB)
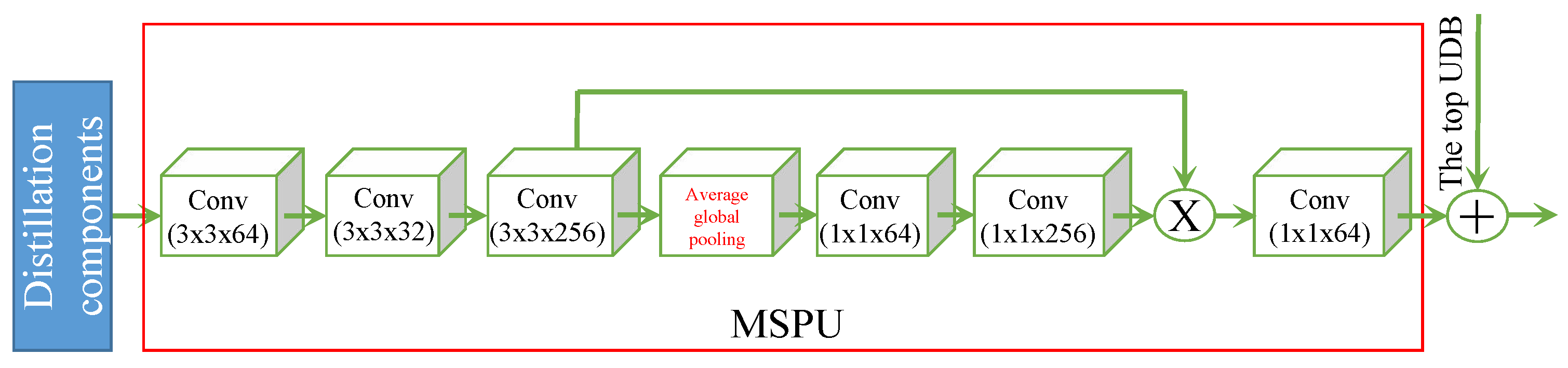
4.2. Multi-Scale Purification Unit (MSPU)
4.3. Resolution Lifting
4.4. Loss Function
5. Experimental Results and Analysis
5.1. Data Collection
- The first imagery dataset is the Kaggle Open Source Dataset (https://www.kaggle.com/c/draper-satellite-image-chronology/data), which contains more than 1000 HR images of aerial photographs captured in southern California. The photographs were taken from a plane and meant as a reasonable facsimile for satellite images. The images are grouped into five sets, each of which having the same setId. Each scenario in a set contains five images captured on different days (not necessarily at the same time each day). The images for each set cover approximately the same area but are not exactly aligned. Images are named according to the convention (setId-day). In this dataset, the scene has 3099 × 2329 pixels and 324 different scenarios. A total of 1720 satellite images cover agriculture, airplane, buildings, golf course, forest, freeway, parking lot, tennis court, storage tanks, and harbor. In this study, 30 different categories are selected for the test and 10 for the evaluation. Meanwhile, a total of 350 images are used for the training. Regarding the training dataset, the entire images are cropped into many batches with 720 × 720 pixels, but only the central area of the testing images with size of 720 × 720 pixels is cropped for testing and evaluation.
- The second satellite dataset is from Jilin-1 video satellite imagery. In 2015, the Changchun Institute of Optics, Fine Mechanics, and Physics successfully launched the Jilin-1 video satellite which had 1.12 m resolution. To cover the duration of video sequences, we select one for every five frames from each video and crop the central part with the size of 480 × 204 as test samples. We select several areas in different countries with certain typical surface coverage types, including vegetation, harbor, and a variety of buildings as the test images.
5.2. Model Parameters and Experiment Setup
5.3. Quantitative Indicators (QI)
5.4. Validation of the Ultra-Dense Residual Block
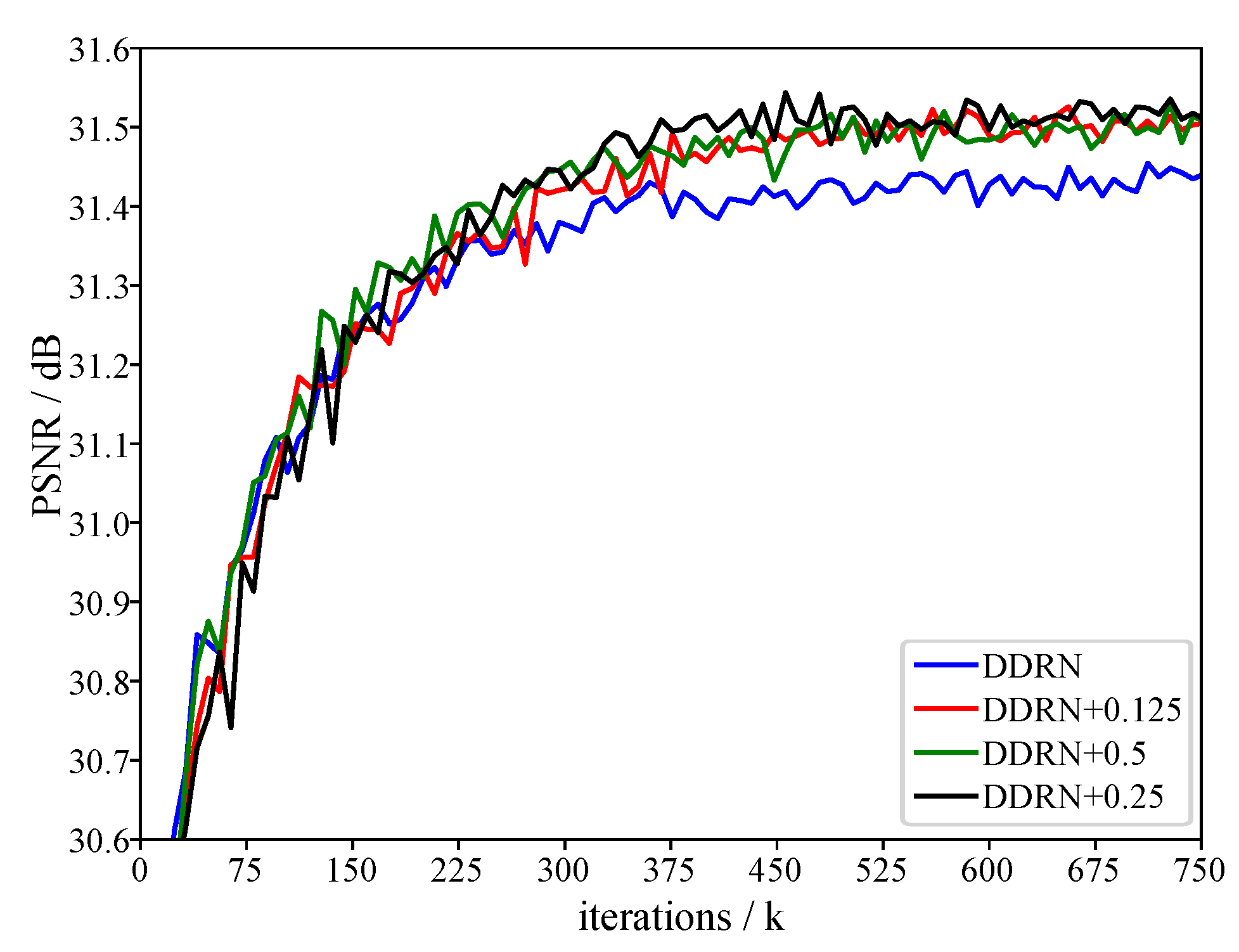
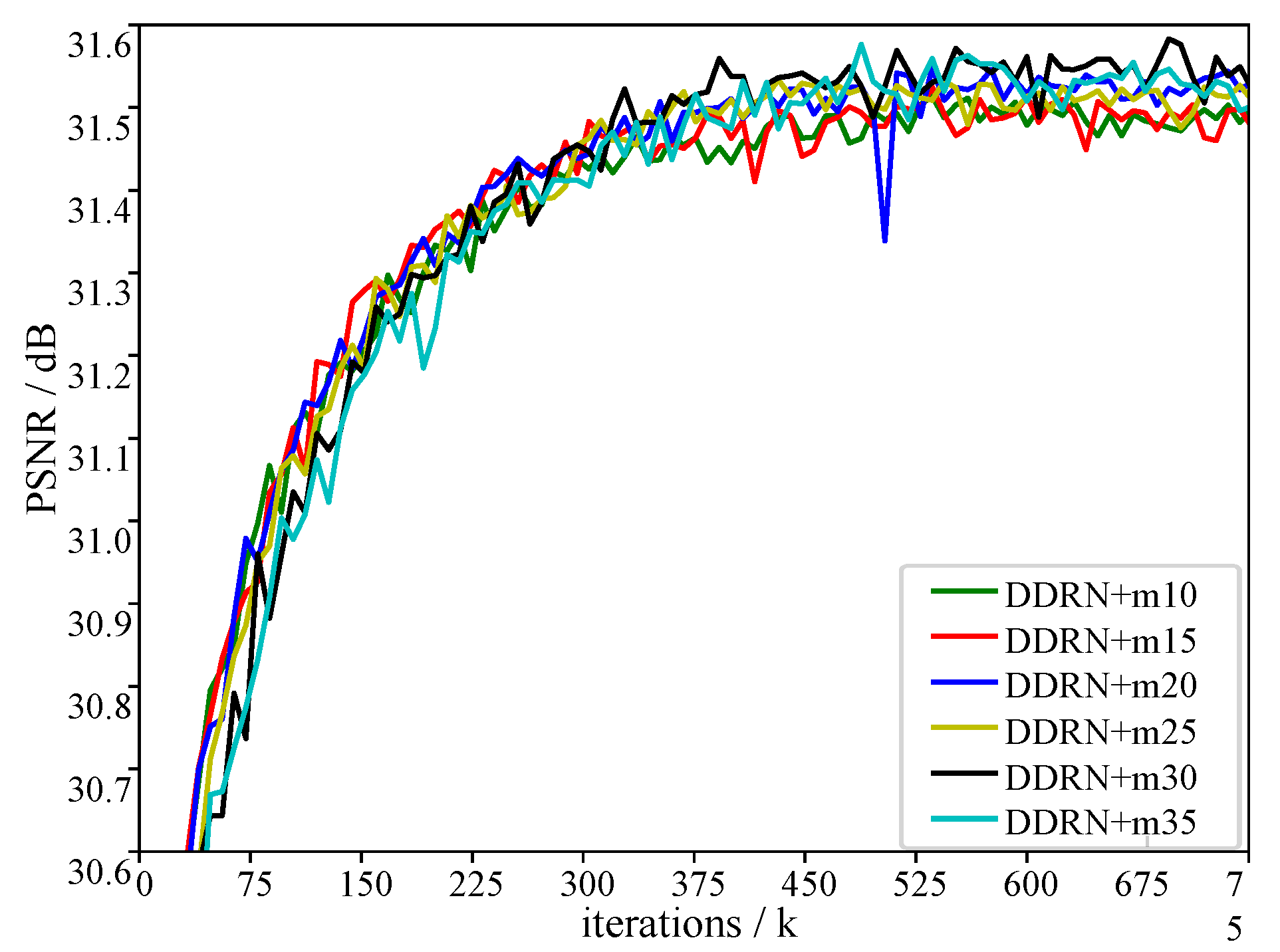
5.5. Influence of Parameters and m
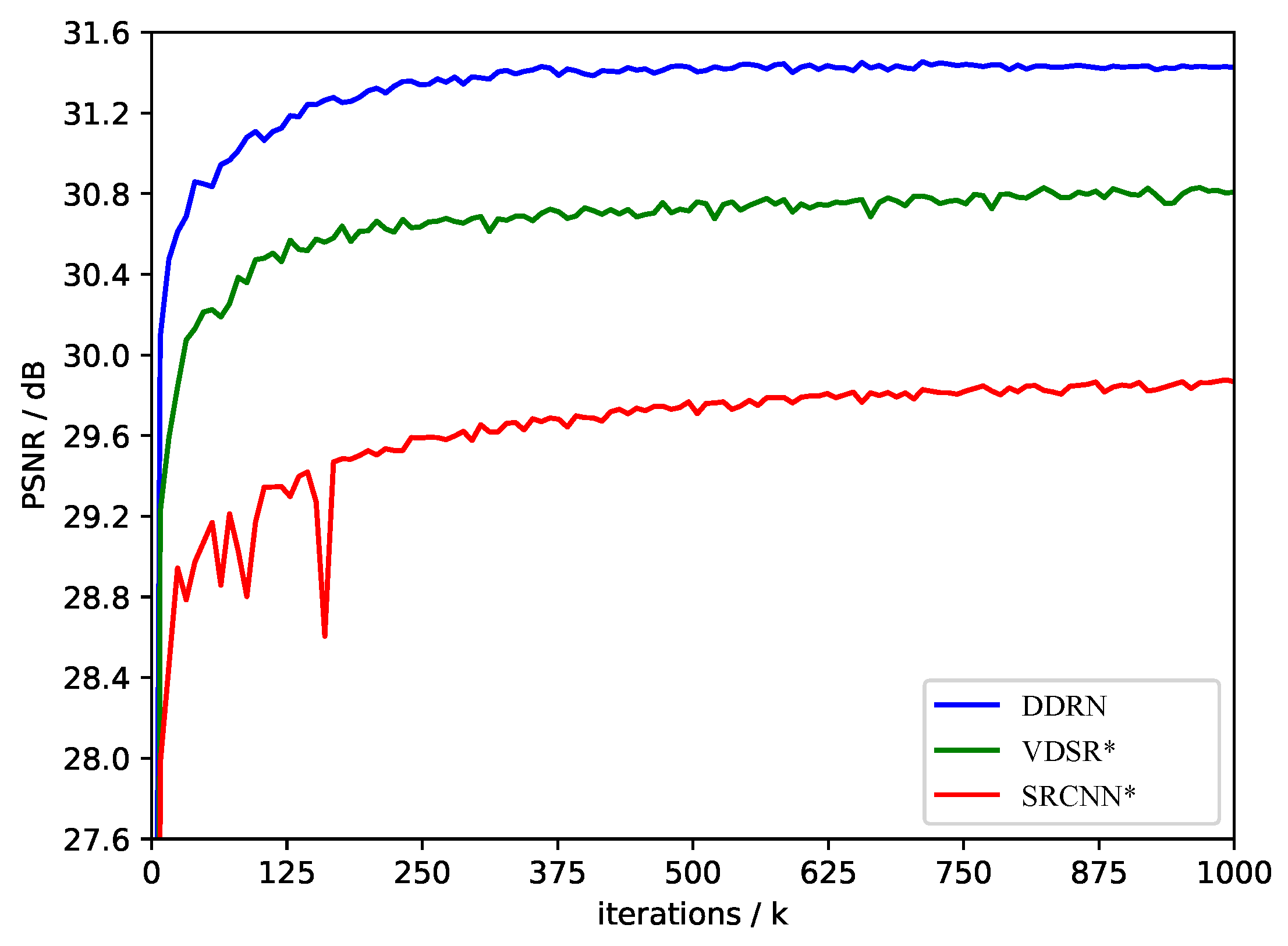
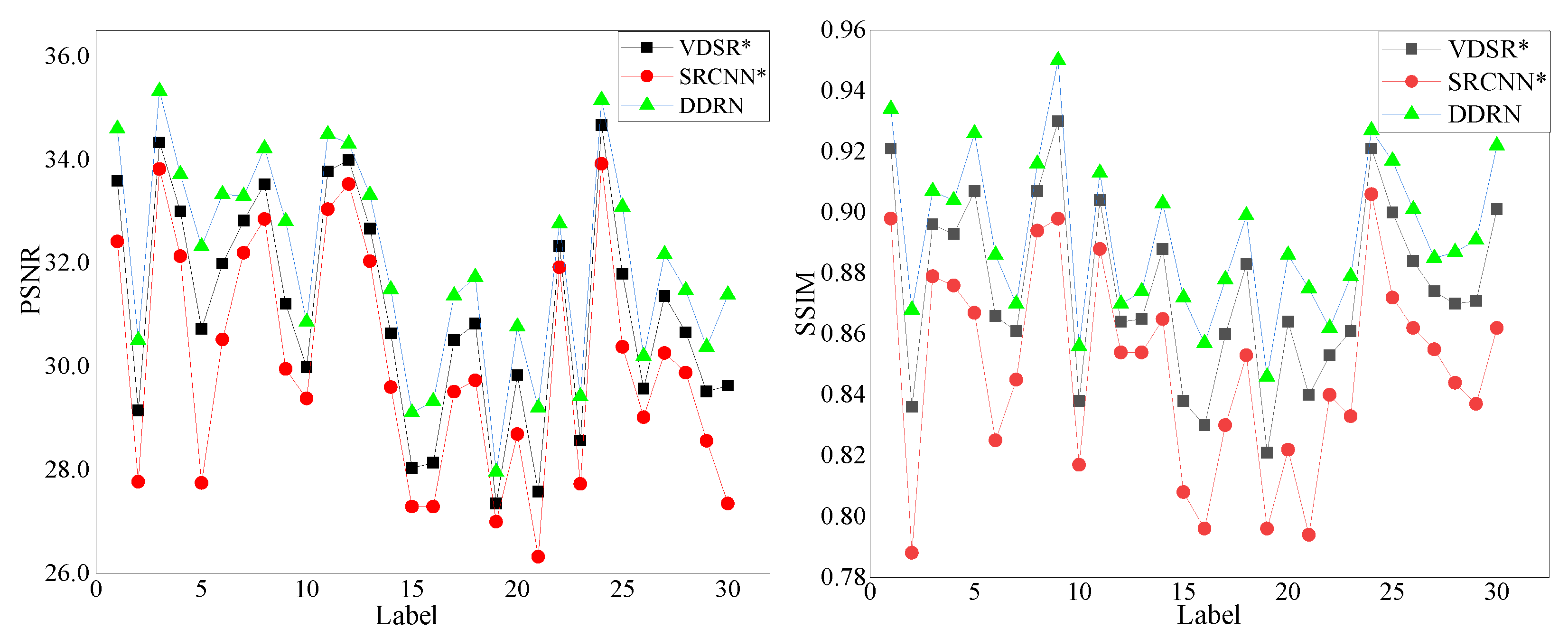
5.6. Comparison Results with the State-of-the-Art
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CNNs | Convolutional neural networks |
| SR | Super-resolution |
| SISR | Single image super-resolution |
| LR | Low resolution |
| HR | High resolution |
| DDRN | Deep distillation recursive network |
| UDB | Ultra-dense residual block |
| MSPU | Multi-scale purification unit |
References
- Xu, Y.; Zhu, M.; Li, S.; Feng, H.; Ma, S.; Che, J. End-to-end airport detection in remote sensing images combining cascade region proposal networks and multi-threshold detection networks. Remote Sens. 2018, 10, 1516. [Google Scholar] [CrossRef]
- Shao, Z.; Wu, W.; Wang, Z.; Du, W.; Li, C. SeaShips: A large-scale precisely annotated dataset for ship detection. IEEE Trans. Multimed. 2018, 20, 2593–2604. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, J.; Tian, J.; Yuille, A.L.; Tu, Z. Robust point matching via vector field consensus. IEEE Trans. Image Process. 2014, 23, 1706–1721. [Google Scholar]
- Ma, J.; Jiang, J.; Zhou, H.; Zhao, J.; Guo, X. Guided locality preserving feature matching for remote sensing image registration. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4435–4447. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, J.; Chen, C.; Wang, Z.; Cai, Z.; Wang, L. SuperPCA: A superpixelwise PCA approach for unsupervised feature extraction of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4581–4593. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, J.; Wang, Z.; Chen, C.; Liu, X. Hyperspectral image classification in the presence of noisy labels. IEEE Trans. Geosci. Remote Sens. 2018. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Mei, X.; Liu, C.; Ma, J. Hyperspectral unmixing with robust collaborative sparse regression. Remote Sens. 2016, 8, 588. [Google Scholar] [CrossRef]
- Ma, J.; Ma, Y.; Li, C. Infrared and visible image fusion methods and applications: A survey. Inf. Fus. 2019, 45, 153–178. [Google Scholar] [CrossRef]
- Ma, J.; Yu, W.; Liang, P.; Li, C.; Jiang, J. FusionGAN: A generative adversarial network for infrared and visible image fusion. Inf. Fus. 2019, 48, 11–26. [Google Scholar] [CrossRef]
- Dong, W.; Fu, F.; Shi, G.; Cao, X.; Wu, J.; Li, G.; Li, X. Hyperspectral image super-resolution via non-negative structured sparse representation. IEEE Trans. Image Process. 2016, 25, 2337–2352. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Sun, F.; Wang, M.; Liu, Z.; Jiao, L. Novel super resolution restoration of remote sensing images based on compressive sensing and example patches-aided dictionary learning. In Proceedings of the International Workshop on Multi-Platform/Multi-Sensor Remote Sensing and Mapping, Xiamen, China, 10–12 January 2011; pp. 1–6. [Google Scholar]
- Jiang, K.; Wang, Z.; Yi, P.; Jiang, J. A progressively enhanced network for video satellite imagery superresolution. IEEE Signal Process. Lett. 2018, 25, 1630–1634. [Google Scholar] [CrossRef]
- Luo, Y.; Zhou, L.; Wang, S.; Wang, Z. Video satellite imagery super resolution via convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2398–2402. [Google Scholar] [CrossRef]
- Xiao, A.; Wang, Z.; Wang, L.; Ren, Y. Super-resolution for “Jilin-1” satellite video imagery via a convolutional network. Sensors 2018, 18, 1194. [Google Scholar] [CrossRef] [PubMed]
- Merino, M.T.; Nunez, J. Super-resolution of remotely sensed images with variable-pixel linear reconstruction. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1446–1457. [Google Scholar] [CrossRef]
- Li, F.; Jia, X.; Fraser, D. Universal HMT based super resolution for remote sensing images. In Proceedings of the 15th IEEE Conference on ICIP, San Diego, CA, USA, 12–15 October 2008; pp. 333–336. [Google Scholar]
- Gou, S.; Liu, S.; Yang, S.; Jiao, L. Remote sensing image super-resolution reconstruction based on nonlocal pairwise dictionaries and double regularization. IEEE J. Sel. Top. Appl. Earth Observ. 2014, 7, 4784–4792. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Huang, X.; Zhu, H.; Ma, J. Large-scale remote sensing image retrieval by deep hashing neural networks. IEEE Trans. Geosci. Remote Sens. 2018, 56, 950–965. [Google Scholar] [CrossRef]
- Shao, Z.; Cai, J. Remote sensing image fusion with deep convolutional neural network. IEEE J. Sel. Top. Appl. Earth Observ. 2018, 11, 1656–1669. [Google Scholar] [CrossRef]
- Zhou, W.; Newsam, S.; Li, C.; Shao, Z. Learning low dimensional convolutional neural networks for high-resolution remote sensing image retrieval. Remote Sens. 2017, 9, 489. [Google Scholar] [CrossRef]
- Lu, T.; Ming, D.; Lin, X.; Hong, Z.; Bai, X.; Fang, J. Detecting building edges from high spatial resolution remote sensing imagery using richer convolution features network. Remote Sens. 2018, 10, 1496. [Google Scholar] [CrossRef]
- Zhang, W.; Witharana, C.; Liljedahl, A.K.; Kanevskiy, M. Deep convolutional neural networks for automated characterization of arctic ice-wedge polygons in very high spatial resolution aerial imagery. Remote Sens. 2018, 10, 1487. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on CVPR, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Lai, W.S.; Huang, J.B.; Ahuja, N.; Yang, M.H. Deep laplacian pyramid networks for fast and accurate super-resolution. In Proceedings of the IEEE Conference on CVPR, Honolulu, HI, USA, 21–26 July 2017; pp. 5835–5843. [Google Scholar]
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on CVPR, Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar]
- Tong, T.; Li, G.; Liu, X.; Gao, Q. Image super-resolution using dense skip connections. In Proceedings of the IEEE Conference on ICCV, Venice, Italy, 22–29 October 2017; pp. 4809–4817. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X.; Xu, C. MemNet: A persistent memory network for image restoration. In Proceedings of the IEEE Conference on ICCV, Venice, Italy, 22–29 October 2017; pp. 4549–4557. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-recursive convolutional network for image super-resolution. In Proceedings of the IEEE Conference on CVPR, Las Vegas, NV, USA, 27–30 June 2016; pp. 1637–1645. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X. Image super-resolution via deep recursive residual network. In Proceedings of the IEEE Conference on CVPR, Honolulu, HI, USA, 21–26 July 2017; pp. 2790–2798. [Google Scholar]
- Yang, W.; Feng, J.; Yang, J.; Zhao, F.; Liu, J.; Guo, Z.; Yan, S. Deep edge guided recurrent residual learning for image super-resolution. IEEE Trans. Image Process. 2017, 26, 5895–5907. [Google Scholar] [CrossRef] [PubMed]
- Yim, J.; Joo, D.; Bae, J.; Kim, J. A gift from knowledge distillation: Fast optimization, network minimization and transfer learning. In Proceedings of the IEEE Conference on CVPR, Honolulu, HI, USA, 21–26 July 2017; pp. 7130–7138. [Google Scholar]
- Gupta, S.; Hoffman, J.; Malik, J. Cross modal distillation for supervision transfer. In Proceedings of the IEEE Conference on CVPR, Las Vegas, NV, USA, 27–30 June 2016; pp. 2827–2836. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. Comput. Sci. 2015, 14, 38–39. [Google Scholar]
- Pintea, S.L.; Liu, Y.; van Gemert, J.C. Recurrent knowledge distillation. In Proceedings of the 25th IEEE Conference on ICIP, Athens, Greece, 7–10 October 2018; pp. 3393–3397. [Google Scholar]
- Zhao, P.; Liu, K.; Zou, H.; Zhen, X. Multi-stream convolutional neural network for SAR automatic target recognition. Remote Sens. 2018, 10, 1473. [Google Scholar] [CrossRef]
- Gu, S.; Zuo, W.; Xie, Q.; Meng, D.; Feng, X.; Zhang, L. Convolutional sparse coding for image super-resolution. In Proceedings of the IEEE Conference on ICCV, Santiago, Chile, 7–13 December 2015; pp. 1823–1831. [Google Scholar]
- Huang, G.; Chen, D.; Li, T.; Wu, F.; van der Maaten, L.; Weinberger, K.Q. Multi-scale dense networks for resource efficient image classification. arXiv, 2018; arXiv:1703.09844. [Google Scholar]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Timofte, R.; De, V.; Gool, L.V. Anchored neighborhood regression for fast example-based super-resolution. In Proceedings of the IEEE Conference on ICCV, Sydney, Australia, 8 April 2013; pp. 1920–1927. [Google Scholar]
- Yang, J.; Wright, J.; Huang, T.; Ma, Y. Image super-resolution as sparse representation of raw image patches. In Proceedings of the IEEE Conference on CVPR, Anchorage, Alaska, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Yang, C.Y.; Yang, M.H. Fast direct super-resolution by simple functions. In Proceedings of the IEEE Conference on ICCV, Sydney Australia, 8 April 2013; pp. 561–568. [Google Scholar]
- Dong, C.; Chen, C.L.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the IEEE Conference on ECCV, Amsterdam, The Netherlands, 8–16 October 2016; pp. 391–407. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. arXiv, 2018; arXiv:1709.0150. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Osendorfer, C.; Soyer, H.; Smagt, P.V.D. Image super-resolution with fast approximate convolutional sparse coding. In Proceedings of the International Conference on Neural Information Processing, Kuching, Malaysia, 3–6 November 2014; pp. 250–257. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on CVPR, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on CVPRW, Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar]
- Yang, C.Y.; Ma, C.; Yang, M.H. Single-image super-resolution: A nenchmark. Lect. Notes Comput. Sci. 2014, 8692, 372–386. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Lai, W.; Huang, J.; Ahuja, N.; Yang, M. Fast and accurate image super-resolution with deep laplacian pyramid networks. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 1. [Google Scholar] [CrossRef] [PubMed]
- Timofte, R.; Agustsson, E.; Gool, L.V.; Yang, M.H.; Zhang, L.; Limb, B.; Som, S.; Kim, H.; Nah, S.; Lee, K.M.; et al. NTIRE 2017 challenge on single image super-resolution: Methods and results. In Proceedings of the IEEE Conference on CVPRW, Honolulu, HI, USA, 21–26 July 2017; pp. 1110–1121. [Google Scholar]
- Huang, J.B.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on CVPR, Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar]
- Tao, X.; Gao, H.; Liao, R.; Wang, J.; Jia, J. Detail-revealing deep video super-resolution. In Proceedings of the International Conference on ICCV, Venice, Italy, 22–29 October 2017; pp. 4482–4490. [Google Scholar]
- Loncan, L.; de Almeida, L.B.; Bioucas-Dias, J.M.; Briottet, X.; Chanussot, J.; Dobigeon, N.; Fabre, S.; Liao, W.; Licciardi, G.A.; Simoes, M.; et al. Hyperspectral pansharpening: A review. IEEE Geosc. Remote Sens. Mag. 2015, 3, 27–46. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Mura, M.D.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Kwan, C.; Budavari, B.; Bovik, A.C.; Marchisio, G. Blind quality assessment of fused WorldView-3 images by using the combinations of pansharpening and hypersharpening paradigms. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1835–1839. [Google Scholar] [CrossRef]
- Chen, A.; Chen, B.; Chai, X.; Bian, R.; Li, H. A novel stochastic stratified average gradient method: Convergence rate and its complexity. arXiv, 2017; arXiv:1710.07783. [Google Scholar]



| Labels | Methods | Bicubic | SRCNN [23] | SRCNN * | VDSR [24] | VDSR * | LapSRN [25] | DDRN (Our) | DDRN+ (Our) |
|---|---|---|---|---|---|---|---|---|---|
| Scale | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | |
| (1) | 2 | 36.77/0.960/3.468 | 39.17/0.973/3.878 | 39.49/0.974/3.849 | 40.52/0.978/3.887 | 40.83/0.979/3.881 | 40.65/0.979/3.881 | 41.33/0.980/3.958 | 41.38/0.981/3.958 |
| (2) | 2 | 31.97/0.919/4.729 | 35.27/0.953/5.848 | 35.21/0.951/5.791 | 35.99/0.959/5.907 | 36.58/0.962/5.838 | 35.95/0.959/5.879 | 37.10/0.965/5.915 | 37.23/0.965/5.920 |
| (3) | 2 | 37.42/0.945/2.700 | 39.20/0.959/3.176 | 39.31/0.960/3.100 | 40.20/0.965/3.197 | 40.36/0.966/3.170 | 40.34/0.966/3.177 | 40.77/0.968/3.216 | 40.82/0.968/3.220 |
| (4) | 2 | 36.78/0.953/3.698 | 39.07/0.968/4.172 | 38.97/0.966/4.119 | 39.47/0.969/4.174 | 39.70/0.970/4.147 | 39.61/0.970/4.158 | 39.95/0.971/4.194 | 40.05/0.971/4.201 |
| (5) | 2 | 31.97/0.948/6.149 | 35.63/0.970/6.808 | 35.54/0.969/6.846 | 36.75/0.974/6.821 | 37.23/0.976/6.860 | 36.84/0.975/6.808 | 37.16/0.977/6.921 | 37.66/0.978/6.903 |
| (6) | 2 | 33.81/0.913/3.614 | 35.78/0.936/4.238 | 35.91/0.935/4.192 | 37.16/0.944/4.346 | 37.26/0.945/4.269 | 37.20/0.945/4.310 | 37.57/0.946/4.357 | 37.73/0.947/4.373 |
| (7) | 2 | 35.80/0.924/3.474 | 37.26/0.941/4.020 | 37.10/0.939/3.908 | 37.50/0.943/4.037 | 37.56/0.944/3.986 | 37.59/0.944/4.022 | 37.72/0.945/4.054 | 37.79/0.945/4.061 |
| (8) | 2 | 36.66/0.953/2.538 | 39.05/0.968/3.050 | 38.88/0.966/3.022 | 40.00/0.971/3.067 | 40.02/0.971/3.048 | 39.96/0.971/3.041 | 40.66/0.973/3.097 | 40.74/0.973/3.104 |
| (9) | 2 | 33.39/0.962/5.090 | 37.62/0.982/5.652 | 38.29/0.982/5.785 | 39.77/0.987/5.604 | 40.02/0.988/5.705 | 39.72/0.987/5.576 | 40.81/0.989/5.748 | 41.10/0.990/5.737 |
| (10) | 2 | 32.91/0.922/3.573 | 35.15/0.950/4.470 | 35.35/0.950/4.440 | 36.29/0.957/4.540 | 36.90/0.960/4.525 | 36.25/0.957/4.499 | 37.96/0.964/4.622 | 37.88/0.964/4.608 |
| (11) | 2 | 37.05/0.951/2.866 | 39.42/0.966/3.352 | 39.27/0.964/3.290 | 39.81/0.967/3.353 | 40.07/0.968/3.304 | 39.92/0.968/3.325 | 40.35/0.969/3.356 | 40.38/0.969/3.360 |
| (12) | 2 | 38.34/0.949/2.916 | 40.53/0.967/3.486 | 40.40/0.966/3.422 | 40.91/0.968/3.510 | 41.04/0.970/3.499 | 41.06/0.969/3.497 | 41.24/0.970/3.543 | 41.31/0.971/3.548 |
| (13) | 2 | 36.20/0.941/3.775 | 38.55/0.959/4.353 | 38.51/0.958/4.306 | 38.93/0.960/4.364 | 39.07/0.962/4.368 | 38.99/0.961/4.355 | 39.33/0.963/4.399 | 39.36/0.963/4.405 |
| (14) | 2 | 33.84/0.945/4.742 | 36.50/0.964/5.355 | 36.43/0.963/5.305 | 37.18/0.967/5.349 | 37.64/0.969/5.348 | 37.44/0.968/5.333 | 38.15/0.970/5.424 | 38.17/0.970/5.427 |
| (15) | 2 | 31.83/0.936/6.327 | 35.17/0.966/7.572 | 35.60/0.967/7.550 | 36.46/0.972/7.548 | 37.21/0.975/7.534 | 36.72/0.974/7.532 | 38.02/0.978/7.652 | 38.08/0.978/7.660 |
| (16) | 2 | 31.26/0.920/5.463 | 34.63/0.956/6.625 | 34.61/0.955/6.569 | 36.14/0.964/6.717 | 36.44/0.966/6.648 | 35.99/0.964/6.701 | 37.19/0.969/6.740 | 37.35/0.969/6.747 |
| (17) | 2 | 33.78/0.933/4.433 | 36.88/0.959/5.294 | 36.82/0.958/5.199 | 37.56/0.963/5.300 | 37.86/0.964/5.247 | 37.69/0.964/5.270 | 38.22/0.966/5.355 | 38.35/0.966/5.362 |
| (18) | 2 | 34.00/0.944/4.304 | 37.17/0.967/5.066 | 37.15/0.966/4.986 | 38.28/0.972/5.065 | 38.51/0.973/5.022 | 38.40/0.973/5.029 | 39.04/0.975/5.085 | 39.21/0.975/5.085 |
| (19) | 2 | 31.33/0.924/6.328 | 34.07/0.957/7.558 | 33.80/0.954/7.620 | 34.77/0.963/7.567 | 34.76/0.963/7.619 | 34.72/0.963/7.518 | 35.15/0.966/7.659 | 35.32/0.967/7.664 |
| (20) | 2 | 32.37/0.926/4.947 | 35.42/0.956/5.800 | 35.75/0.959/5.739 | 37.20/0.968/5.867 | 37.56/0.970/5.786 | 37.17/0.968/5.828 | 38.07/0.972/5.890 | 38.19/0.972/5.897 |
| (21) | 2 | 29.57/0.905/5.137 | 32.84/0.945/6.269 | 32.72/0.944/6.186 | 34.62/0.959/6.412 | 35.03/0.961/6.308 | 34.29/0.958/6.324 | 36.10/0.967/6.434 | 36.08/0.967/6.430 |
| (22) | 2 | 35.46/0.931/3.450 | 37.54/0.954/4.091 | 37.45/0.952/3.990 | 38.33/0.959/4.103 | 38.41/0.960/4.065 | 38.34/0.959/4.082 | 38.72/0.962/4.153 | 38.80/0.962/4.157 |
| (23) | 2 | 31.57/0.934/5.460 | 35.06/0.964/6.485 | 34.96/0.963/6.549 | 36.23/0.970/6.487 | 36.63/0.972/6.499 | 36.32/0.971/6.445 | 37.32/0.975/6.553 | 37.47/0.975/6.560 |
| (24) | 2 | 38.26/0.965/3.085 | 40.78/0.976/3.375 | 40.47/0.974/3.367 | 41.25/0.977/3.362 | 41.17/0.977/3.391 | 41.44/0.978/3.358 | 41.63/0.978/3.437 | 41.69/0.979/3.437 |
| (25) | 2 | 34.75/0.948/3.281 | 37.61/0.968/3.958 | 37.70/0.967/3.946 | 39.04/0.974/4.018 | 39.37/0.975/4.014 | 39.12/0.974/3.991 | 40.31/0.978/4.097 | 40.20/0.978/4.098 |
| (26) | 2 | 32.86/0.946/3.699 | 34.87/0.966/4.312 | 34.75/0.964/4.242 | 36.62/0.976/4.480 | 37.29/0.978/4.310 | 36.98/0.977/4.314 | 39.34/0.983/4.514 | 39.86/0.984/4.535 |
| (27) | 2 | 34.43/0.944/3.425 | 37.35/0.965/4.132 | 37.36/0.963/4.092 | 38.35/0.967/4.176 | 38.80/0.969/4.143 | 38.37/0.968/4.136 | 39.14/0.970/4.188 | 39.21/0.970/4.193 |
| (28) | 2 | 33.36/0.930/4.591 | 36.51/0.959/5.420 | 36.25/0.957/5.359 | 37.56/0.965/5.411 | 37.73/0.967/5.364 | 37.57/0.966/5.367 | 38.13/0.968/5.417 | 38.19/0.969/5.422 |
| (29) | 2 | 32.19/0.929/4.881 | 35.30/0.959/5.782 | 35.53/0.959/5.813 | 36.52/0.967/5.819 | 37.07/0.969/5.804 | 36.59/0.967/5.778 | 37.61/0.971/5.881 | 37.70/0.972/5.886 |
| (30) | 2 | 31.26/0.941/5.749 | 34.69/0.964/6.484 | 34.43/0.963/6.527 | 35.69/0.969/6.513 | 36.54/0.971/6.559 | 35.76/0.970/6.486 | 37.10/0.974/6.605 | 37.23/0.974/6.604 |
| Avg | 2 | 34.04/0.938/4.263 | 36.80/0.961/5.004 | 36.80/0.960/4.970 | 37.83/0.966/5.033 | 38.15/0.968/5.008 | 37.90/0.967/5.000 | 38.70/0.970/5.080 | 38.81/0.970/5.085 |
| Labels | Methods | Bicubic | SRCNN [23] | SRCNN * | VDSR [24] | VDSR * | DDRN (Our) | DDRN+ (Our) |
|---|---|---|---|---|---|---|---|---|
| Scale | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | |
| (1) | 3 | 33.06/0.915/3.021 | 34.58/0.935/3.579 | 35.07/0.940/3.586 | 36.22/0.953/3.616 | 36.65/0.955/3.599 | 37.63/0.961/3.653 | 37.70/0.962/3.663 |
| (2) | 3 | 28.25/0.821/3.717 | 30.10/0.871/4.911 | 30.12/0.870/4.941 | 31.68/0.903/5.274 | 31.86/0.903/5.047 | 32.97/0.919/5.333 | 33.12/0.920/5.346 |
| (3) | 3 | 34.30/0.897/2.256 | 35.38/0.913/2.796 | 35.76/0.918/2.737 | 36.56/0.930/2.812 | 36.57/0.930/2.798 | 37.51/0.938/2.868 | 37.68/0.939/2.864 |
| (4) | 3 | 32.88/0.901/3.197 | 34.68/0.926/3.825 | 34.89/0.925/3.780 | 35.58/0.934/3.796 | 35.71/0.935/3.766 | 36.40/0.940/3.881 | 36.49/0.941/3.884 |
| (5) | 3 | 27.86/0.885/5.309 | 30.35/0.921/6.439 | 30.87/0.923/6.403 | 32.11/0.940/6.345 | 33.31/0.945/6.531 | 34.68/0.953/6.502 | 34.43/0.953/6.452 |
| (6) | 3 | 31.17/0.852/3.031 | 32.44/0.880/3.686 | 32.38/0.879/3.728 | 33.72/0.901/3.803 | 34.03/0.902/3.731 | 35.13/0.912/3.843 | 35.27/0.914/3.870 |
| (7) | 3 | 32.92/0.870/2.979 | 34.18/0.893/3.548 | 34.15/0.891/3.474 | 34.83/0.902/3.546 | 34.67/0.900/3.519 | 35.11/0.905/3.589 | 35.25/0.906/3.609 |
| (8) | 3 | 33.32/0.907/2.070 | 34.90/0.930/2.593 | 34.93/0.929/2.566 | 35.89/0.939/2.611 | 35.74/0.938/2.573 | 36.48/0.943/2.668 | 36.70/0.944/2.680 |
| (9) | 3 | 29.16/0.897/4.537 | 32.80/0.945/5.666 | 32.79/0.943/5.643 | 34.18/0.964/5.508 | 34.90/0.966/5.432 | 36.07/0.974/5.563 | 36.29/0.974/5.578 |
| (10) | 3 | 29.89/0.843/2.766 | 31.04/0.878/3.594 | 31.04/0.877/3.579 | 31.79/0.894/3.743 | 32.21/0.897/3.710 | 33.06/0.906/3.803 | 33.05/0.907/3.793 |
| (11) | 3 | 33.43/0.903/2.384 | 35.52/0.930/2.971 | 35.44/0.928/2.961 | 36.16/0.937/2.988 | 36.23/0.937/2.927 | 36.87/0.942/3.050 | 37.01/0.943/3.062 |
| (12) | 3 | 34.62/0.888/2.311 | 35.95/0.913/2.991 | 35.97/0.912/2.937 | 36.47/0.919/3.007 | 36.50/0.919/2.972 | 36.86/0.923/3.070 | 36.93/0.923/3.078 |
| (13) | 3 | 32.70/0.881/3.189 | 34.14/0.908/3.837 | 34.22/0.908/3.804 | 35.17/0.916/3.871 | 35.35/0.917/3.860 | 35.81/0.920/3.927 | 35.88/0.921/3.940 |
| (14) | 3 | 30.20/0.888/4.099 | 32.03/0.919/4.961 | 32.24/0.919/4.888 | 33.07/0.931/4.898 | 33.50/0.933/4.900 | 34.37/0.940/4.947 | 34.58/0.942/4.966 |
| (15) | 3 | 27.84/0.844/5.081 | 29.70/0.893/7.098 | 30.40/0.907/6.934 | 31.27/0.924/7.059 | 31.69/0.927/7.010 | 32.46/0.942/7.138 | 33.49/0.948/7.104 |
| (16) | 3 | 27.70/0.822/4.472 | 29.21/0.872/5.548 | 29.29/0.872/5.605 | 30.99/0.902/5.901 | 31.20/0.904/5.744 | 32.33/0.916/5.947 | 32.60/0.918/5.969 |
| (17) | 3 | 29.95/0.854/3.684 | 31.87/0.896/4.683 | 32.18/0.897/4.620 | 33.26/0.916/4.722 | 33.22/0.915/4.644 | 33.98/0.924/4.793 | 34.13/0.925/4.807 |
| (18) | 3 | 30.15/0.875/3.615 | 32.14/0.913/4.622 | 32.36/0.913/4.540 | 33.61/0.933/4.625 | 33.66/0.931/4.550 | 34.52/0.940/4.699 | 34.68/0.941/4.703 |
| (19) | 3 | 27.82/0.829/5.063 | 29.49/0.886/6.717 | 29.46/0.884/6.934 | 30.36/0.907/6.705 | 30.07/0.901/6.727 | 30.79/0.915/6.951 | 30.97/0.918/6.957 |
| (20) | 3 | 28.97/0.842/4.186 | 30.99/0.891/5.177 | 31.20/0.895/5.132 | 32.50/0.921/5.324 | 32.68/0.923/5.276 | 33.62/0.934/5.392 | 33.85/0.936/5.397 |
| (21) | 3 | 26.45/0.808/4.169 | 28.29/0.865/5.253 | 28.30/0.863/5.204 | 29.87/0.900/5.555 | 30.04/0.901/5.449 | 31.57/0.920/5.623 | 31.59/0.921/5.637 |
| (22) | 3 | 32.43/0.866/2.898 | 33.84/0.895/3.522 | 33.77/0.893/3.453 | 34.45/0.905/3.524 | 34.38/0.904/3.488 | 34.81/0.909/3.572 | 34.91/0.911/3.586 |
| (23) | 3 | 27.88/0.852/4.529 | 30.12/0.900/5.799 | 30.11/0.898/5.763 | 31.24/0.919/5.785 | 31.40/0.920/5.731 | 32.41/0.932/5.829 | 32.53/0.932/5.833 |
| (24) | 3 | 34.58/0.927/2.702 | 36.80/0.948/3.215 | 36.72/0.947/3.185 | 37.82/0.956/3.164 | 37.66/0.955/3.191 | 38.46/0.960/3.199 | 38.64/0.961/3.210 |
| (25) | 3 | 31.05/0.891/2.640 | 32.75/0.921/3.440 | 33.19/0.923/3.448 | 34.36/0.938/3.549 | 34.60/0.938/3.467 | 35.75/0.947/3.575 | 35.97/0.949/3.592 |
| (26) | 3 | 29.70/0.884/3.075 | 30.66/0.912/3.843 | 30.90/0.913/3.724 | 31.01/0.923/3.967 | 31.55/0.928/3.747 | 32.31/0.940/3.991 | 33.16/0.948/4.009 |
| (27) | 3 | 30.89/0.880/2.747 | 32.44/0.909/3.499 | 32.70/0.909/3.452 | 33.80/0.922/3.584 | 34.07/0.923/3.538 | 34.83/0.929/3.623 | 34.92/0.929/3.632 |
| (28) | 3 | 30.14/0.862/3.958 | 32.37/0.905/4.850 | 32.09/0.900/4.838 | 33.41/0.923/4.877 | 33.21/0.920/4.801 | 34.02/0.930/4.731 | 34.18/0.932/4.747 |
| (29) | 3 | 28.67/0.851/4.072 | 30.74/0.899/5.104 | 30.92/0.900/5.130 | 32.09/0.924/5.207 | 32.33/0.926/5.162 | 33.23/0.936/5.277 | 33.41/0.938/5.294 |
| (30) | 3 | 27.62/0.876/4.913 | 29.80/0.916/5.971 | 29.86/0.915/5.927 | 31.03/0.933/5.969 | 31.91/0.937/6.018 | 33.74/0.949/6.097 | 33.49/0.948/6.065 |
| Avg | 3 | 30.52/0.870/3.555 | 32.31/0.906/4.457 | 32.44/0.906/4.430 | 33.48/0.923/4.511 | 33.69/0.924/4.463 | 34.59/0.933/4.571 | 34.76/0.935/4.577 |
| Labels | Methods | Bicubic | SRCNN [23] | SRCNN * | VDSR [24] | VDSR * | LapSRN [25] | DDRN (Our) | DDRN+ (Our) |
|---|---|---|---|---|---|---|---|---|---|
| Scale | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | PSNR/SSIM/AG | |
| (1) | 4 | 30.84/0.867/2.664 | 32.15/0.892/3.234 | 32.41/0.897/3.150 | 33.29/0.917/3.281 | 33.69/0.922/3.311 | 33.50/0.920/3.263 | 34.60/0.934/3.343 | 34.74/0.936/3.354 |
| (2) | 4 | 26.41/0.739/2.997 | 27.80/0.792/4.129 | 27.77/0.788/3.924 | 28.92/0.834/4.438 | 29.27/0.839/4.290 | 28.96/0.835/4.328 | 30.51/0.868/4.547 | 30.67/0.872/4.680 |
| (3) | 4 | 32.35/0.852/1.929 | 33.31/0.873/2.475 | 33.81/0.878/2.349 | 34.49/0.895/2.502 | 34.58/0.898/2.474 | 34.72/0.899/2.469 | 35.33/0.907/2.467 | 35.67/0.910/2.551 |
| (4) | 4 | 30.52/0.847/2.809 | 32.19/0.880/3.432 | 32.13/0.875/3.385 | 32.94/0.893/3.452 | 33.11/0.894/3.387 | 33.06/0.895/3.404 | 33.72/0.904/3.362 | 33.95/0.906/3.365 |
| (5) | 4 | 25.31/0.816/4.522 | 27.18/0.861/5.814 | 27.75/0.867/5.655 | 28.30/0.888/5.735 | 30.92/0.909/6.079 | 28.39/0.890/5.738 | 32.32/0.926/6.258 | 31.94/0.924/6.364 |
| (6) | 4 | 29.57/0.799/2.610 | 30.85/0.836/3.258 | 30.51/0.825/3.169 | 31.41/0.856/3.440 | 32.04/0.865/3.393 | 32.03/0.865/3.331 | 33.33/0.886/3.401 | 33.55/0.888/3.485 |
| (7) | 4 | 31.03/0.822/2.635 | 32.32/0.849/3.171 | 32.20/0.845/3.105 | 32.95/0.864/3.205 | 32.89/0.862/3.177 | 33.07/0.865/3.173 | 33.30/0.870/3.137 | 33.45/0.873/3.276 |
| (8) | 4 | 31.58/0.871/1.771 | 32.81/0.895/2.196 | 32.84/0.894/2.138 | 33.66/0.908/2.208 | 33.63/0.908/2.177 | 33.76/0.909/2.188 | 34.22/0.916/2.187 | 34.45/0.918/2.189 |
| (9) | 4 | 26.90/0.831/4.097 | 30.23/0.904/5.256 | 29.94/0.898/5.059 | 31.51/0.935/4.986 | 31.42/0.933/4.864 | 31.69/0.938/4.957 | 32.81/0.950/5.094 | 33.18/0.954/5.228 |
| (10) | 4 | 28.47/0.783/2.246 | 29.26/0.816/2.947 | 29.37/0.817/2.864 | 29.77/0.835/3.061 | 30.09/0.839/3.004 | 29.71/0.834/3.013 | 30.86/0.856/3.153 | 30.88/0.856/3.182 |
| (11) | 4 | 31.32/0.858/2.041 | 33.19/0.891/2.586 | 33.03/0.887/2.518 | 33.81/0.903/2.637 | 33.87/0.904/2.549 | 33.94/0.905/2.605 | 34.49/0.913/2.554 | 34.71/0.915/2.552 |
| (12) | 4 | 32.49/0.830/1.867 | 33.53/0.856/2.479 | 33.53/0.854/2.360 | 33.99/0.866/2.529 | 34.05/0.865/2.554 | 34.01/0.867/2.481 | 34.31/0.870/2.408 | 34.52/0.873/2.394 |
| (13) | 4 | 30.75/0.822/2.745 | 31.95/0.853/3.404 | 32.04/0.853/3.320 | 32.59/0.865/3.412 | 32.68/0.865/3.344 | 32.62/0.866/3.358 | 33.32/0.874/3.340 | 33.55/0.876/3.333 |
| (14) | 4 | 27.94/0.830/3.570 | 29.52/0.868/4.509 | 29.60/0.865/4.340 | 30.29/0.884/4.413 | 30.72/0.889/4.437 | 30.51/0.888/4.414 | 31.49/0.903/4.555 | 31.79/0.907/4.601 |
| (15) | 4 | 25.70/0.744/4.120 | 27.11/0.805/6.071 | 27.29/0.808/5.721 | 28.16/0.842/6.114 | 28.27/0.845/6.140 | 28.33/0.850/6.032 | 29.11/0.872/6.271 | 29.37/0.875/6.326 |
| (16) | 4 | 25.98/0.738/3.809 | 27.29/0.797/4.809 | 27.29/0.796/4.712 | 28.00/0.827/4.964 | 28.15/0.830/4.890 | 28.02/0.828/4.894 | 29.33/0.857/5.089 | 29.84/0.863/5.152 |
| (17) | 4 | 27.91/0.784/3.139 | 29.49/0.832/4.069 | 29.51/0.930/3.904 | 30.56/0.862/4.130 | 30.60/0.862/3.997 | 30.63/0.864/4.101 | 31.37/0.878/4.083 | 31.61/0.881/4.100 |
| (18) | 4 | 28.10/0.810/3.091 | 29.65/0.855/4.082 | 29.72/0.853/3.910 | 30.81/0.884/4.117 | 30.93/0.885/4.172 | 30.90/0.886/4.072 | 31.73/0.899/4.083 | 31.89/0.902/4.108 |
| (19) | 4 | 25.79/0.734/4.064 | 27.01/0.802/5.738 | 27.00/0.796/5.497 | 27.55/0.827/5.677 | 27.48/0.823/5.552 | 27.57/0.829/5.684 | 27.96/0.846/5.910 | 28.17/0.852/5.999 |
| (20) | 4 | 27.06/0.766/3.612 | 28.50/0.818/4.575 | 28.69/0.821/4.411 | 29.57/0.854/4.643 | 29.90/0.864/4.606 | 29.64/0.858/4.621 | 30.77/0.886/4.753 | 31.18/0.893/4.787 |
| (21) | 4 | 24.87/0.733/3.487 | 26.18/0.792/4.517 | 26.32/0.794/4.429 | 27.12/0.831/4.737 | 27.70/0.841/4.798 | 27.07/0.832/4.684 | 29.20/0.875/4.943 | 28.96/0.873/5.042 |
| (22) | 4 | 30.72/0.811/2.541 | 31.96/0.844/0.050 | 31.91/0.840/2.941 | 32.37/0.855/3.066 | 32.42/0.854/3.003 | 32.41/0.855/3.025 | 32.77/0.862/2.945 | 32.87/0.864/2.935 |
| (23) | 4 | 25.85/0.779/3.834 | 27.52/0.832/5.104 | 27.73/0.833/4.950 | 28.47/0.860/5.037 | 28.62/0.862/4.988 | 28.60/0.862/4.991 | 29.42/0.879/5.049 | 29.67/0.882/5.120 |
| (24) | 4 | 32.16/0.883/2.382 | 34.09/0.912/2.929 | 33.91/0.906/2.800 | 35.09/0.926/2.902 | 34.82/0.922/2.872 | 35.18/0.927/2.877 | 35.16/0.927/2.904 | 35.86/0.934/2.909 |
| (25) | 4 | 29.08/0.839/2.174 | 30.34/0.872/2.898 | 30.38/0.871/2.819 | 31.50/0.898/3.091 | 31.97/0.901/3.140 | 31.59/0.901/3.075 | 33.09/0.917/3.149 | 33.39/0.919/3.173 |
| (26) | 4 | 27.96/0.824/2.586 | 28.89/0.864/3.433 | 29.01/0.861/3.194 | 28.89/0.877/3.787 | 29.78/0.888/3.629 | 29.13/0.879/3.489 | 30.20/0.901/3.626 | 30.82/0.910/3.629 |
| (27) | 4 | 29.06/0.824/2.275 | 30.30/0.855/2.943 | 30.25/0.854/2.885 | 31.15/0.873/3.054 | 31.45/0.875/2.987 | 31.23/0.874/2.995 | 32.17/0.885/3.012 | 32.35/0.887/3.001 |
| (28) | 4 | 28.33/0.800/3.517 | 30.02/0.850/4.333 | 29.87/0.844/4.237 | 30.93/0.874/4.340 | 30.74/0.871/4.310 | 31.02/0.876/4.289 | 31.47/0.887/4.352 | 31.72/0.891/4.357 |
| (29) | 4 | 26.80/0.783/3.483 | 28.46/0.837/4.489 | 28.56/0.836/4.439 | 29.41/0.868/4.537 | 29.61/0.872/4.440 | 29.47/0.870/4.509 | 30.38/0.891/4.610 | 30.65/0.895/4.709 |
| (30) | 4 | 25.46/0.810/4.213 | 27.40/0.863/5.412 | 27.34/0.862/5.313 | 28.18/0.888/5.406 | 30.00/0.904/5.599 | 28.26/0.891/5.428 | 31.39/0.922/5.756 | 31.26/0.920/5.729 |
| Avg | 4 | 28.54/0.808/3.028 | 30.01/0.850/3.911 | 30.06/0.848/3.783 | 30.86/0.873/3.963 | 31.08/0.875/3.60 | 30.97/0.875/3.916 | 32.00/0.892/4.018 | 32.22/0.895/4.064 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, K.; Wang, Z.; Yi, P.; Jiang, J.; Xiao, J.; Yao, Y. Deep Distillation Recursive Network for Remote Sensing Imagery Super-Resolution. Remote Sens. 2018, 10, 1700. https://doi.org/10.3390/rs10111700
Jiang K, Wang Z, Yi P, Jiang J, Xiao J, Yao Y. Deep Distillation Recursive Network for Remote Sensing Imagery Super-Resolution. Remote Sensing. 2018; 10(11):1700. https://doi.org/10.3390/rs10111700
Chicago/Turabian StyleJiang, Kui, Zhongyuan Wang, Peng Yi, Junjun Jiang, Jing Xiao, and Yuan Yao. 2018. "Deep Distillation Recursive Network for Remote Sensing Imagery Super-Resolution" Remote Sensing 10, no. 11: 1700. https://doi.org/10.3390/rs10111700
APA StyleJiang, K., Wang, Z., Yi, P., Jiang, J., Xiao, J., & Yao, Y. (2018). Deep Distillation Recursive Network for Remote Sensing Imagery Super-Resolution. Remote Sensing, 10(11), 1700. https://doi.org/10.3390/rs10111700








