Sensitivity of Evapotranspiration Components in Remote Sensing-Based Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Models and Data
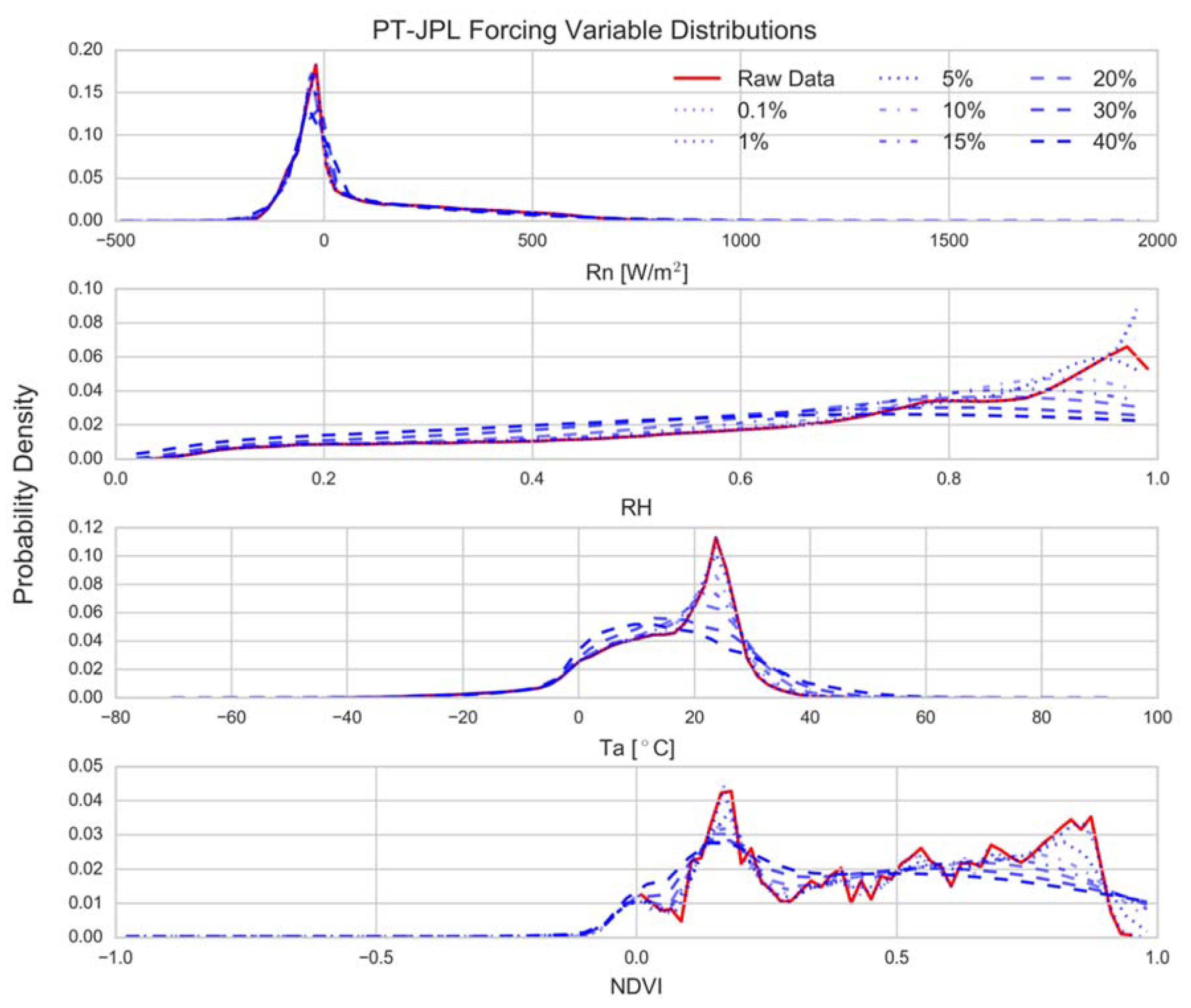
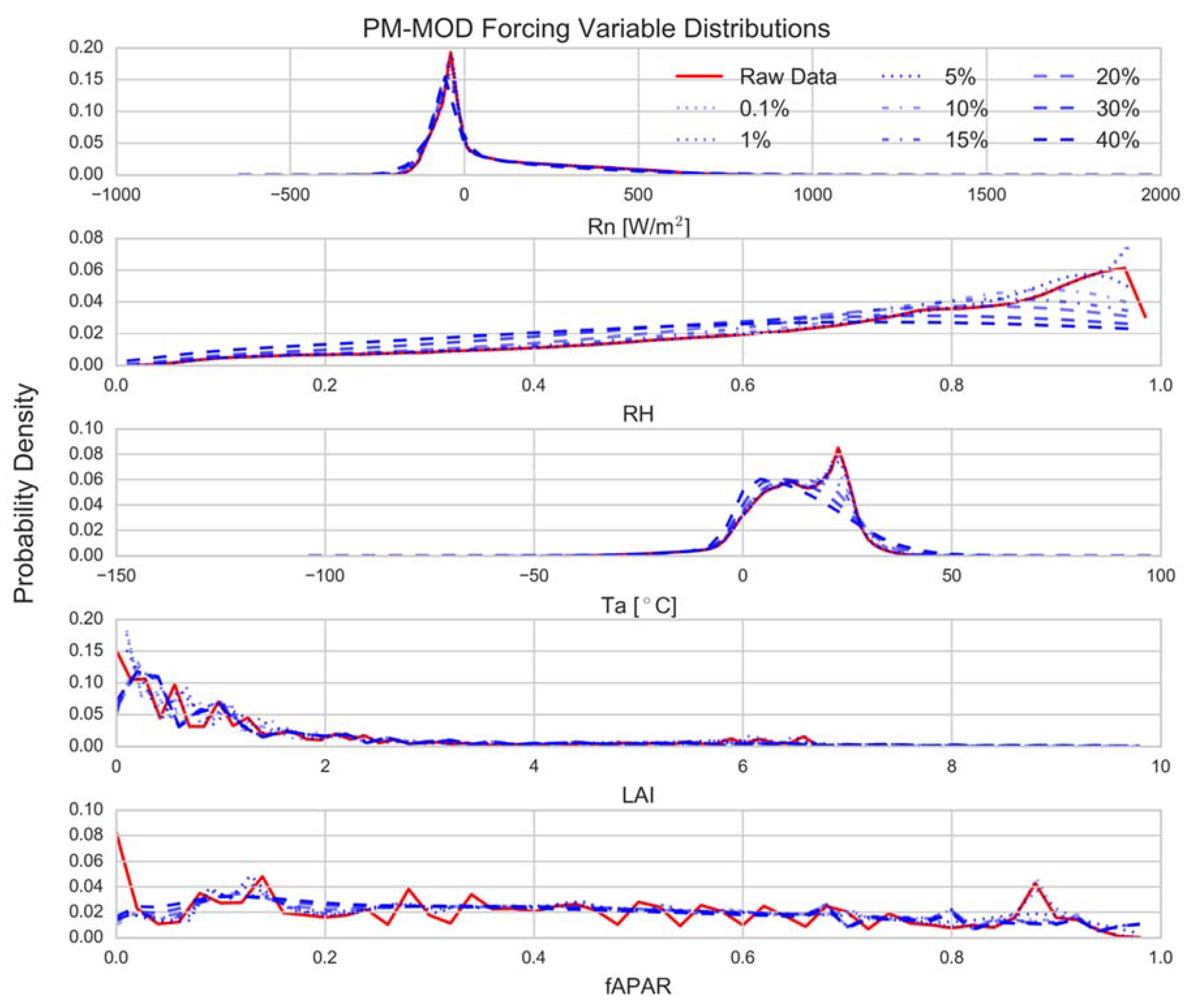
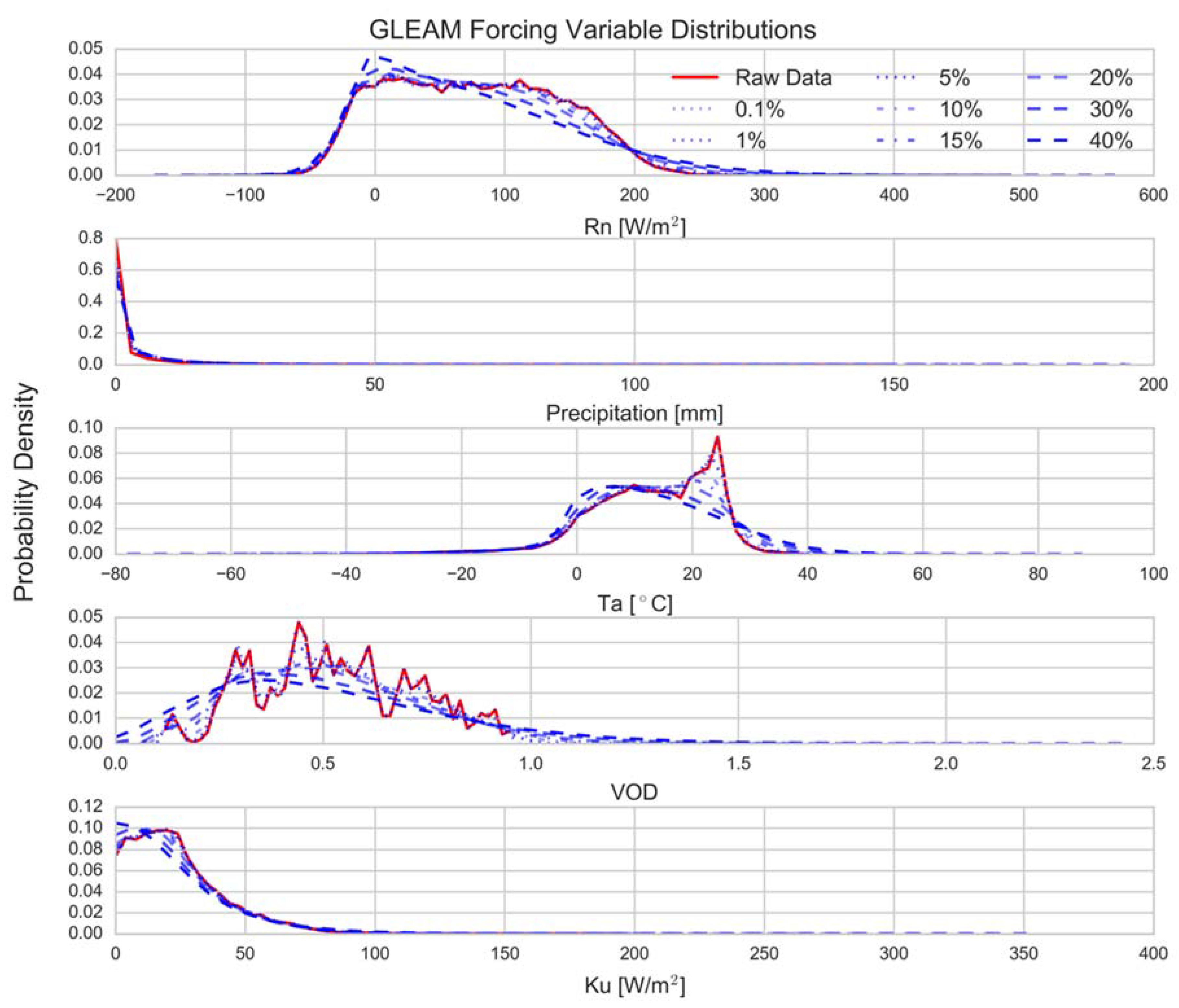
2.2. Monte Carlo Sensitivity Analysis
2.3. Error and Bias Assessment
3. Results
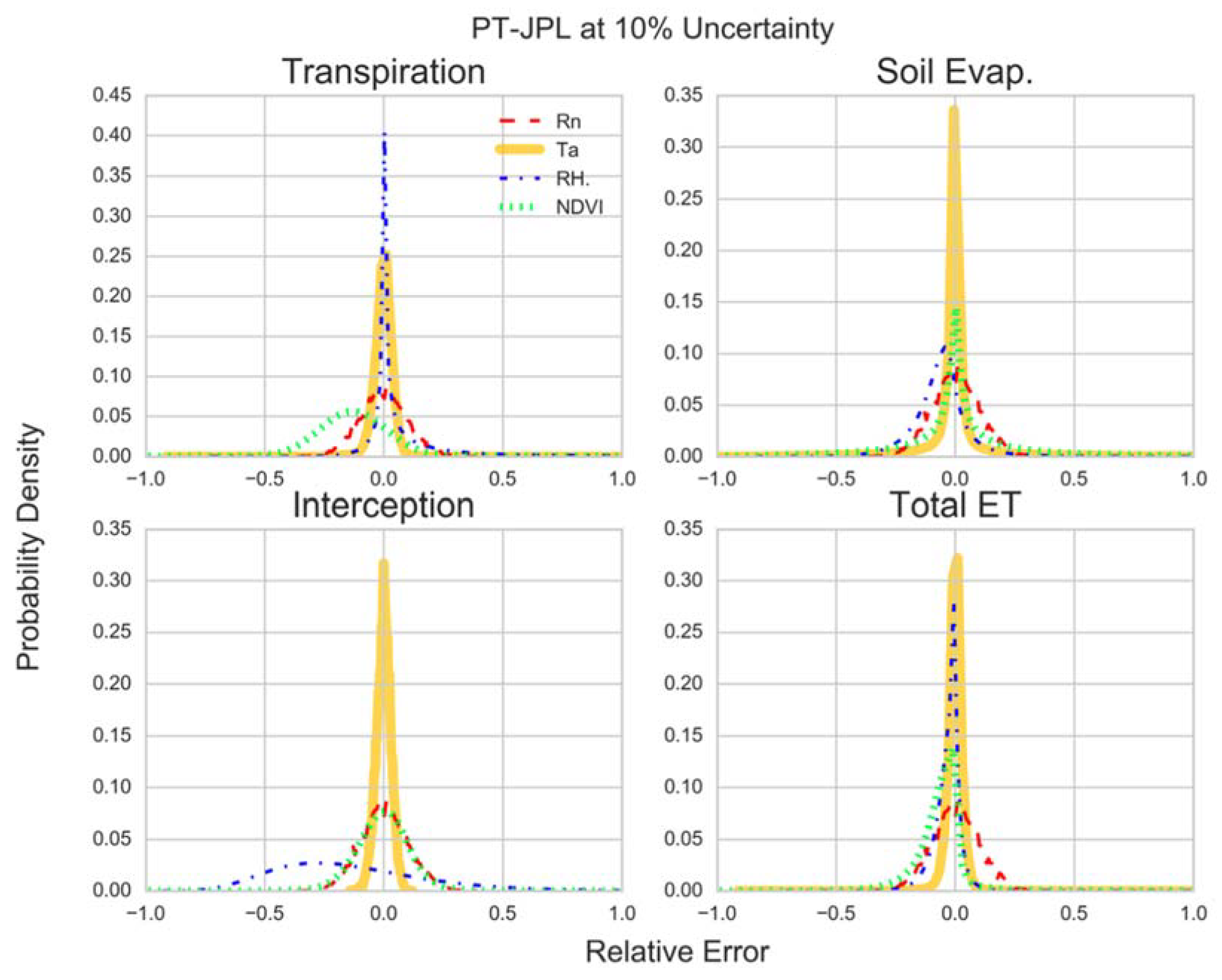
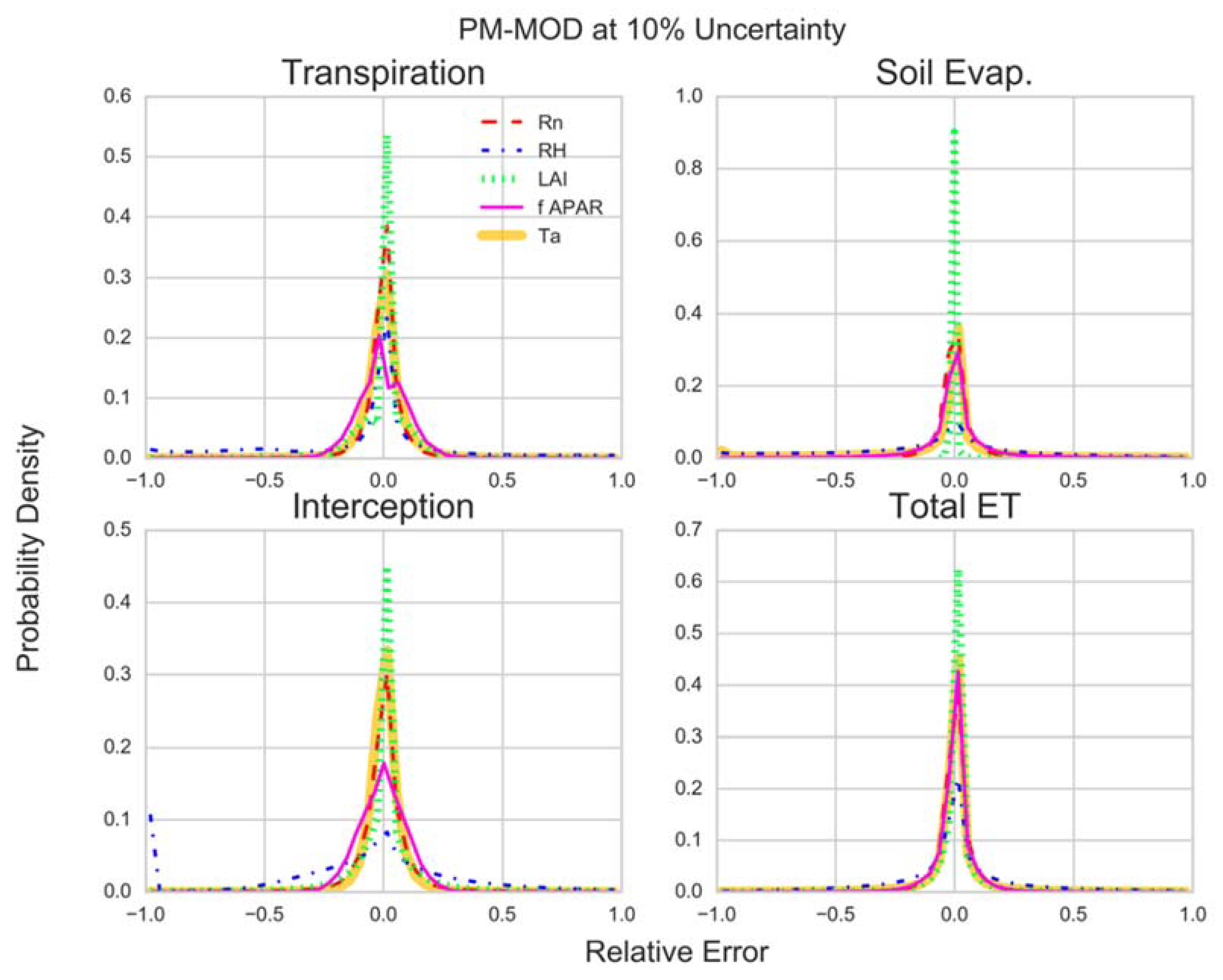
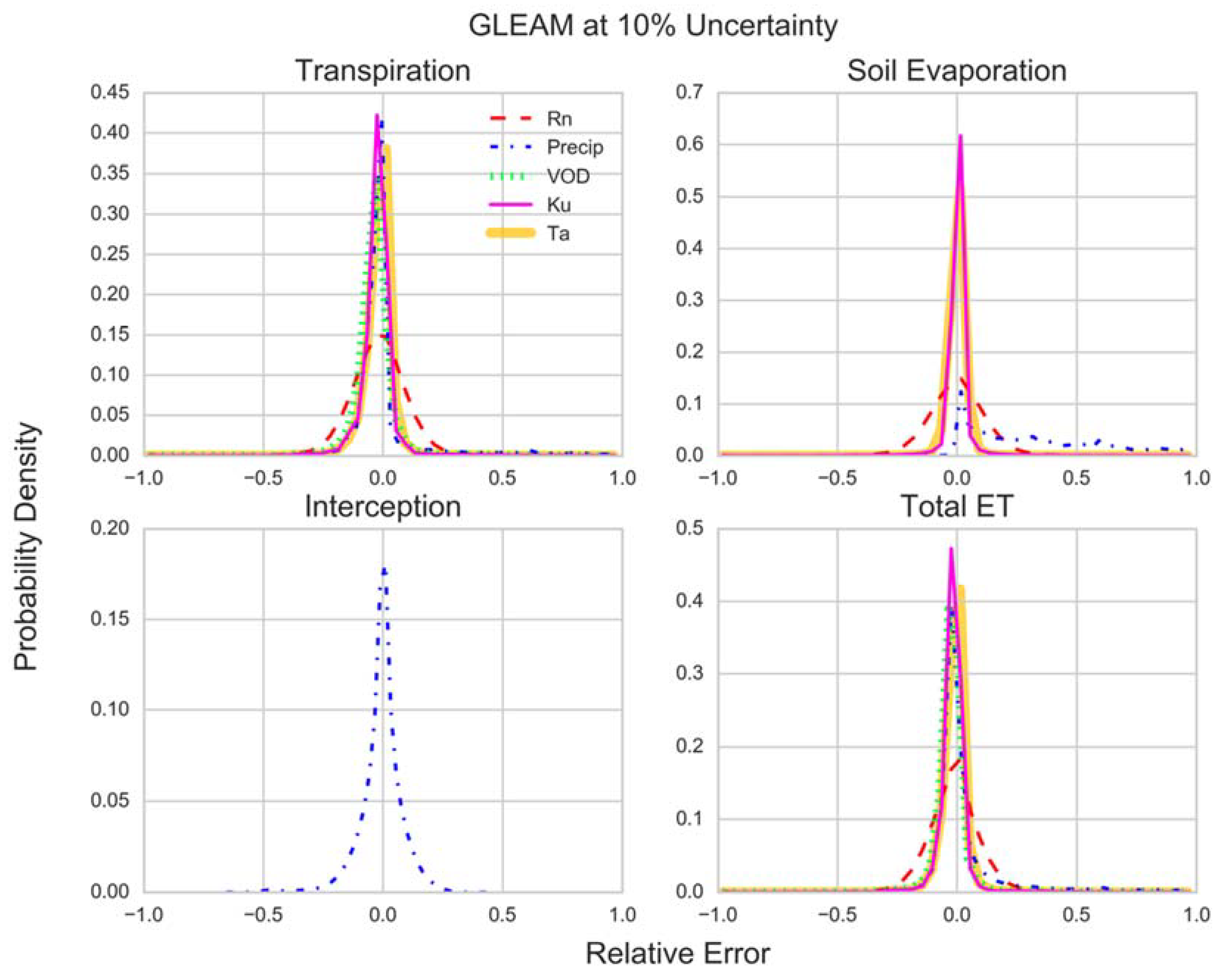
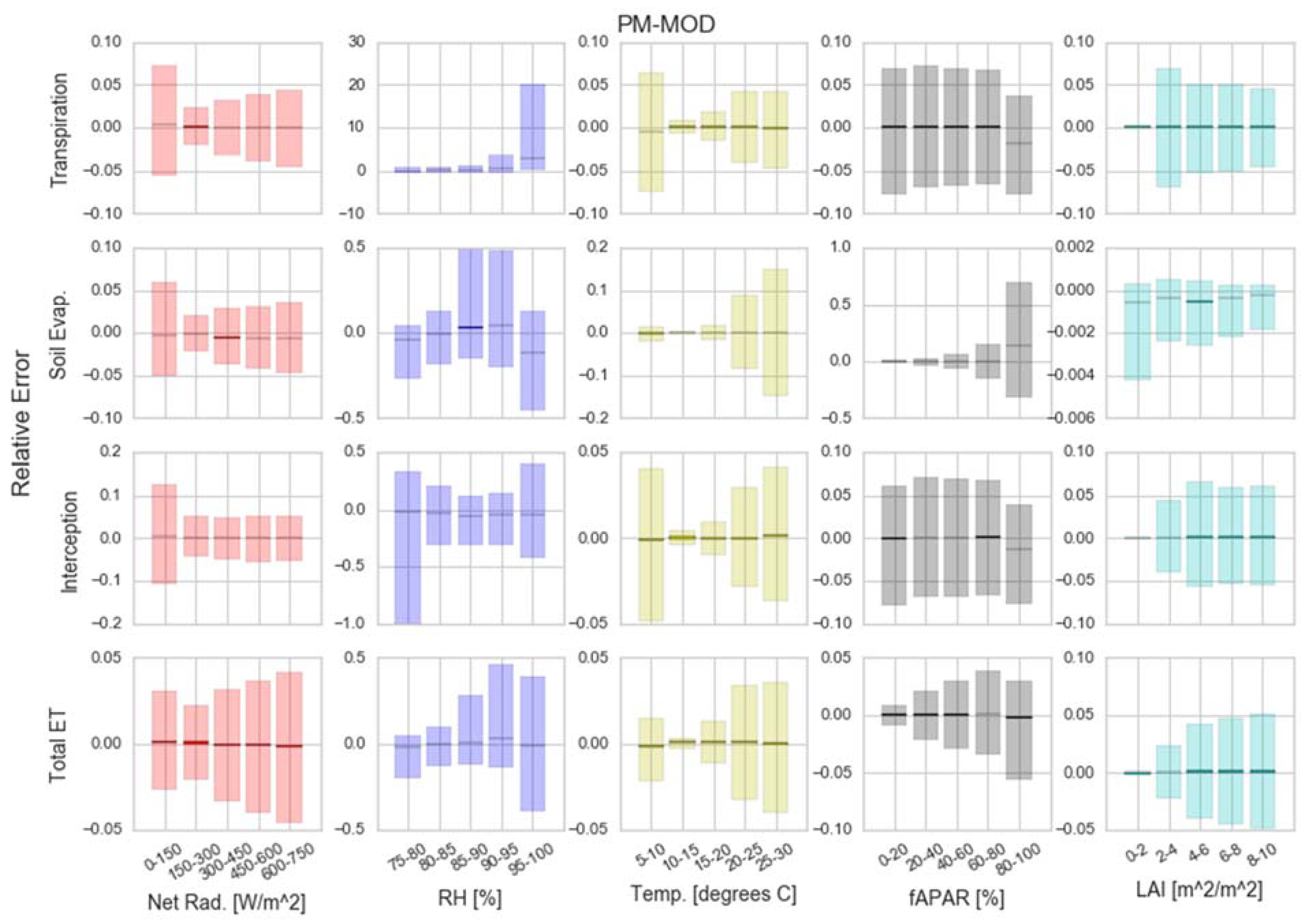
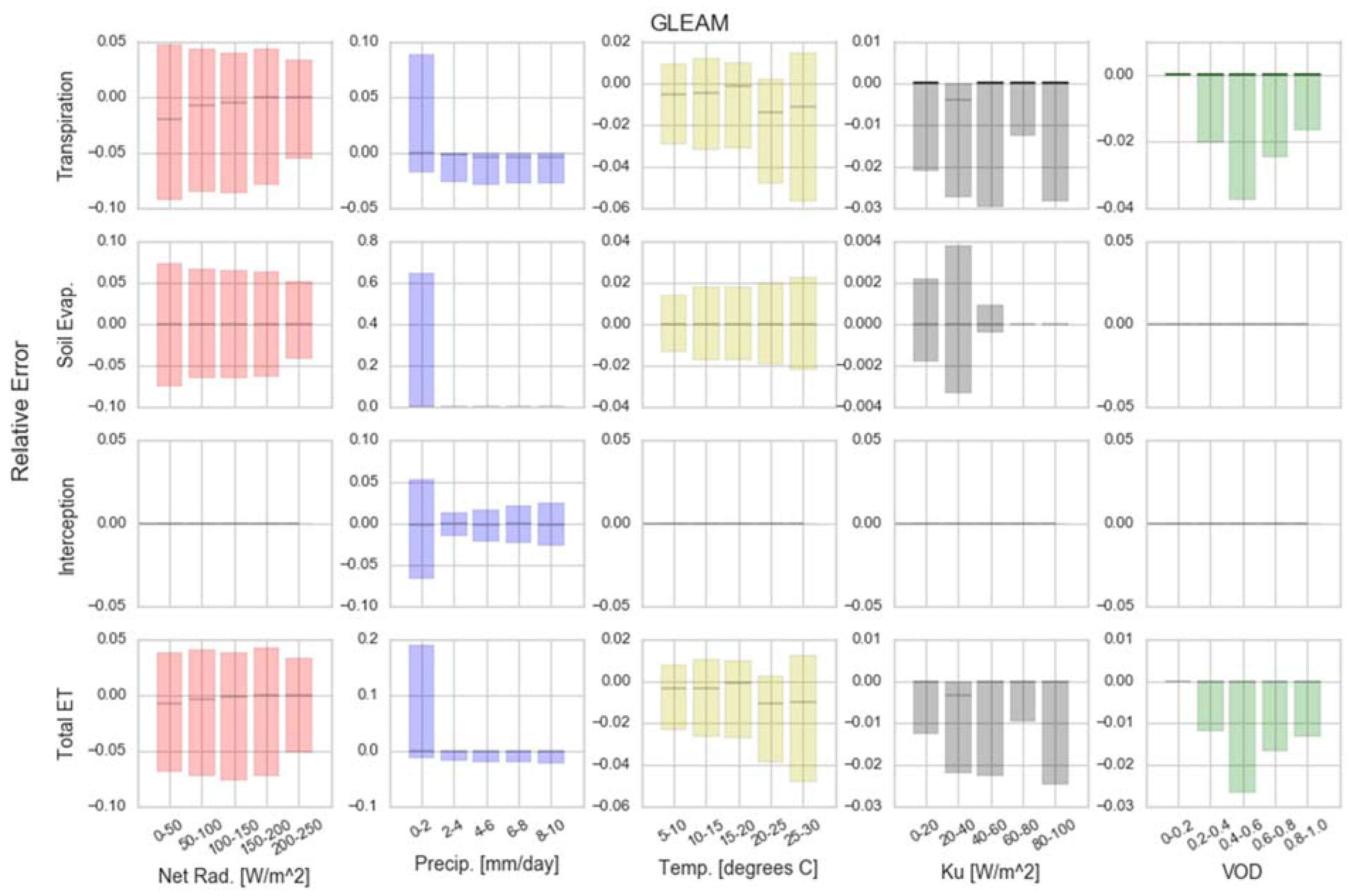
3.1. Model Sensitivity Distributions
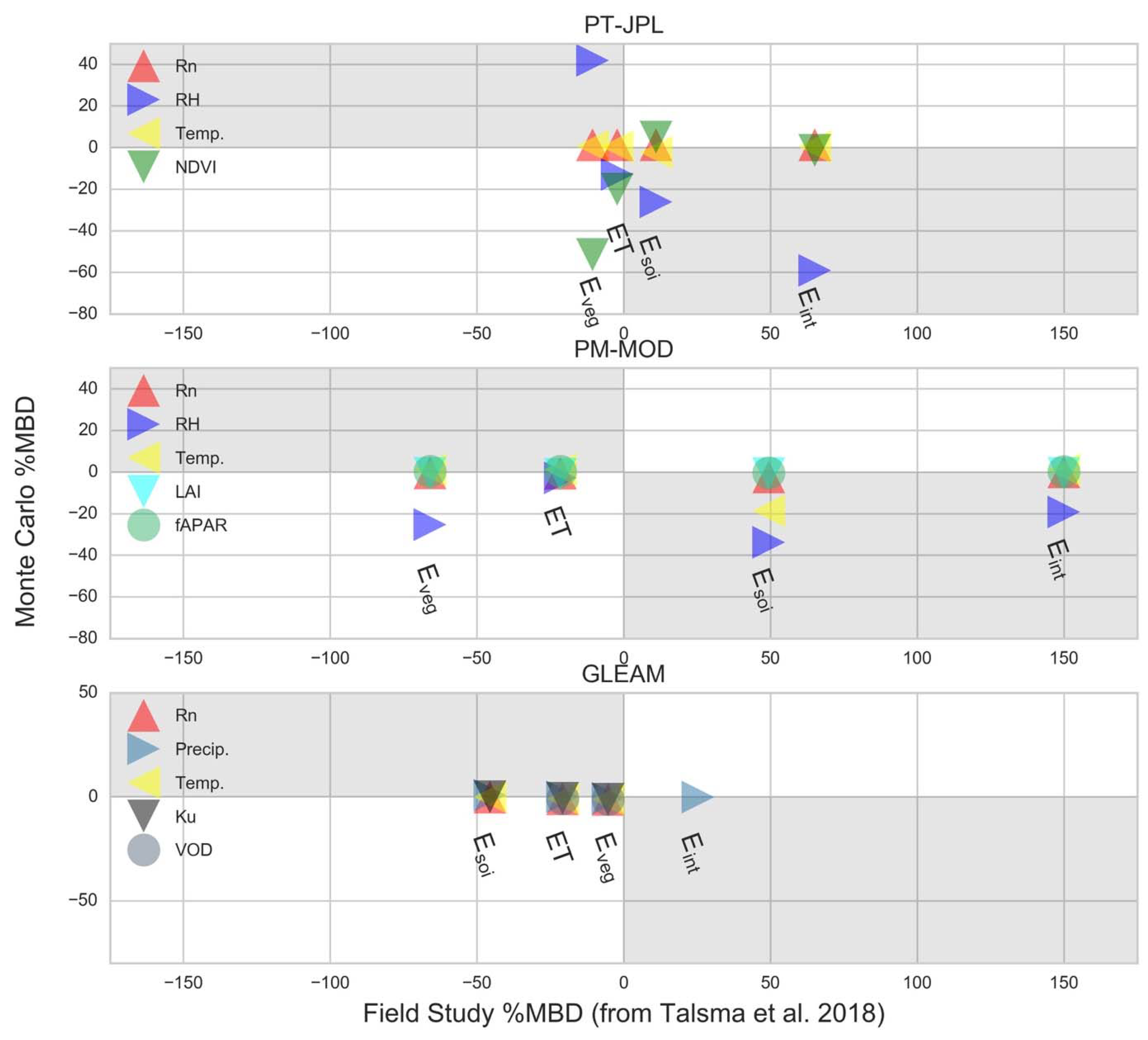
3.2. Model-Field Sensitivity Inter-Comparison
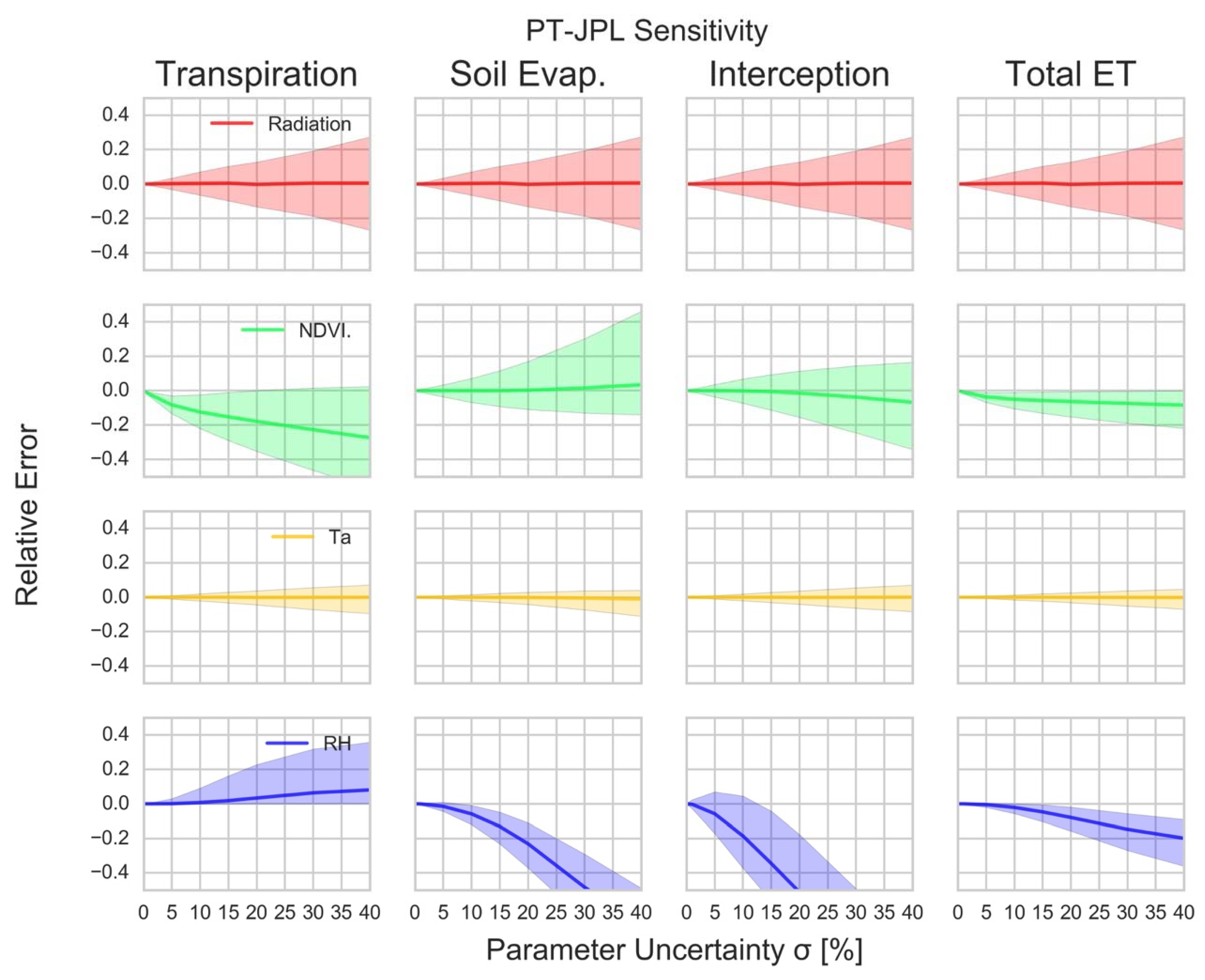
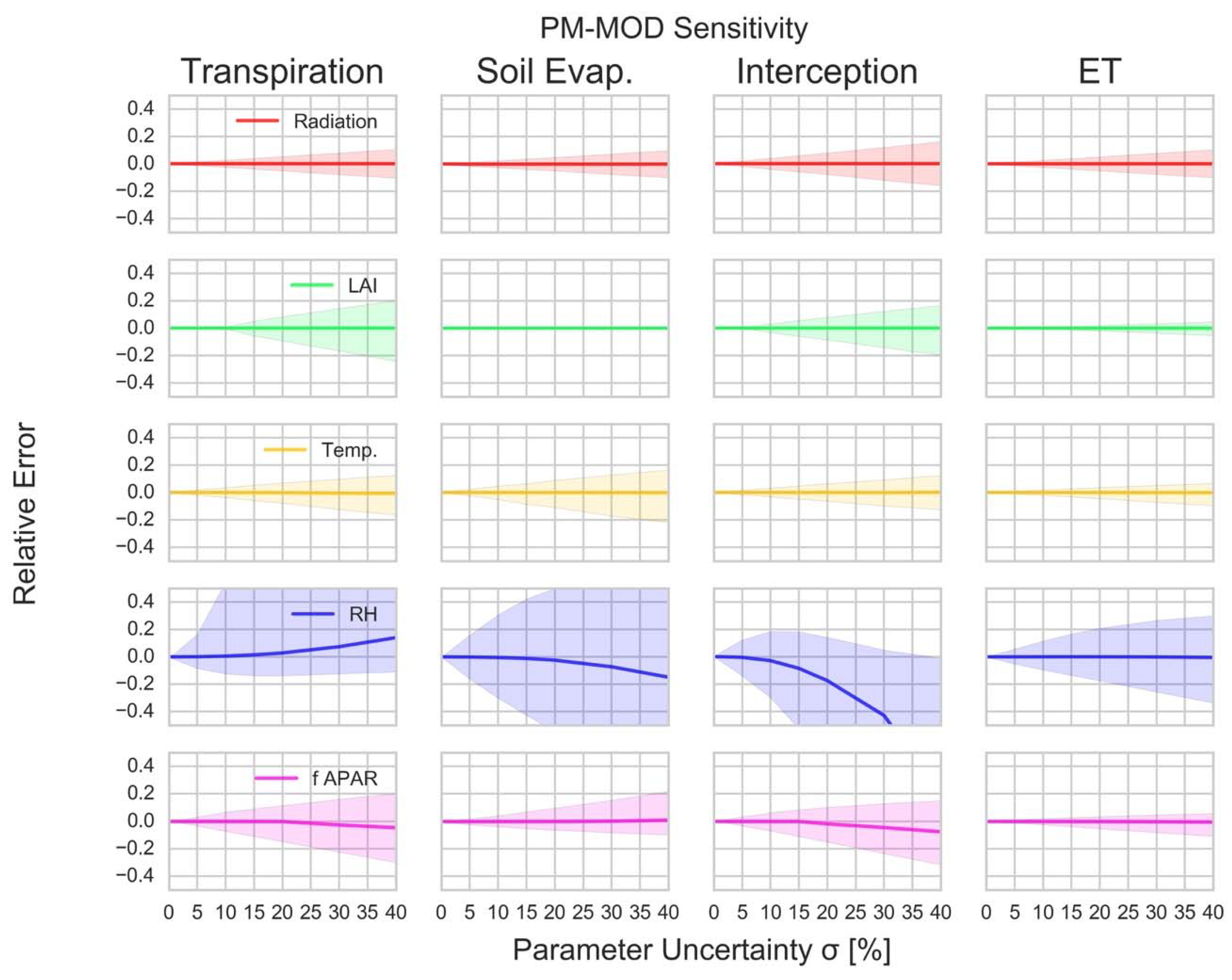
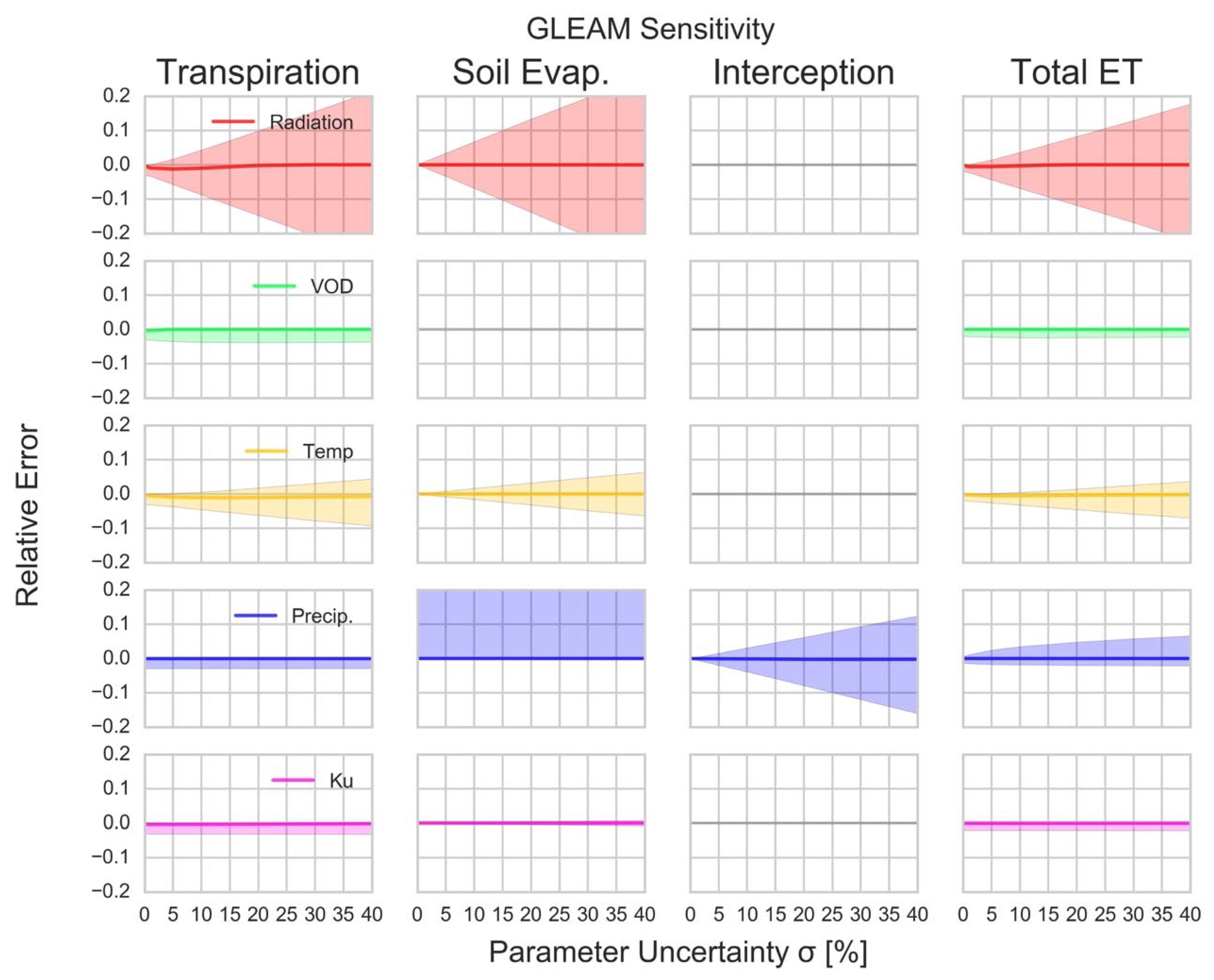
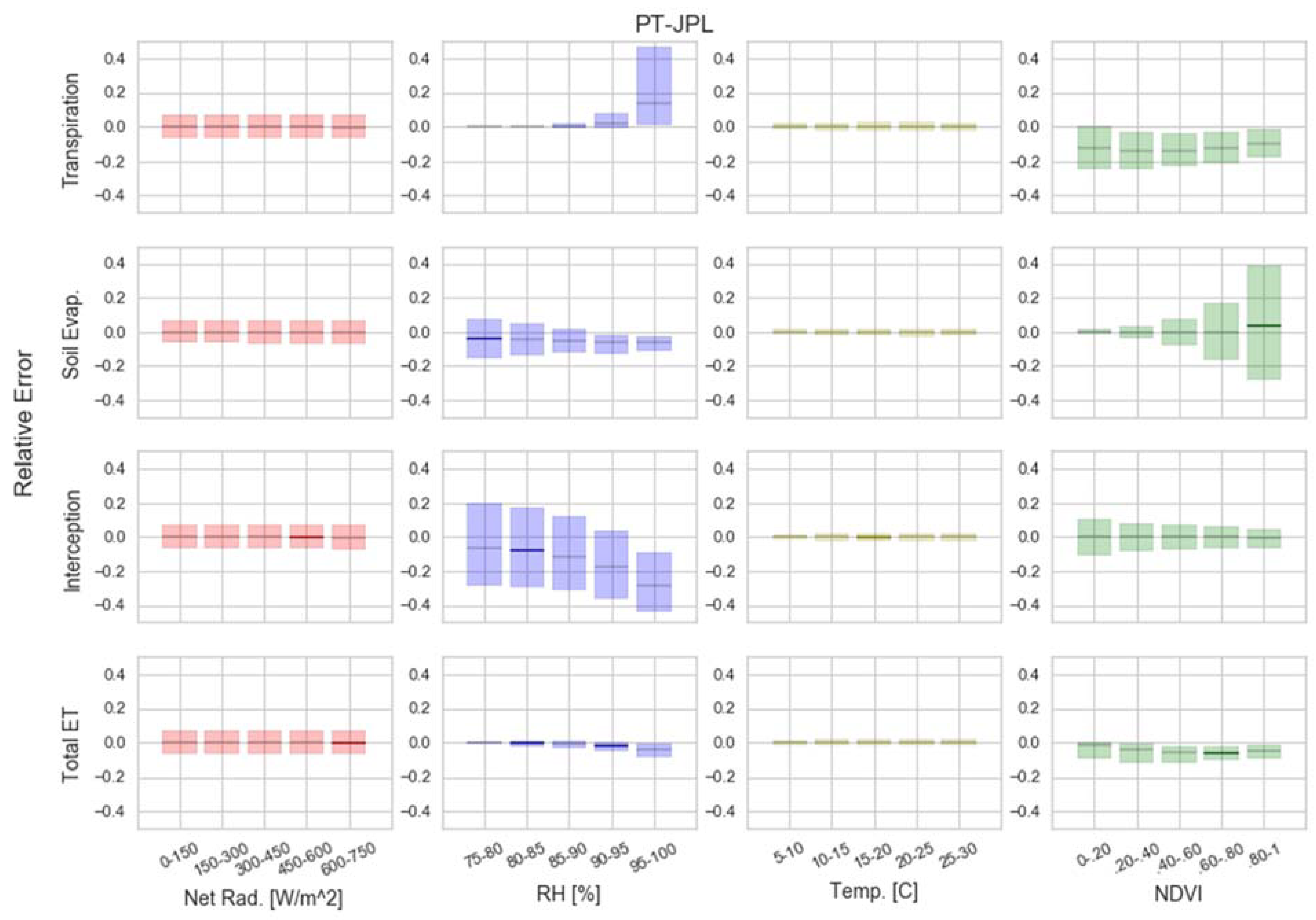
3.3. Model Sensitivity across Forcing Conditions
4. Discussion
4.1. Model Sensitivity
4.2. Non-Linearity and Model Bias
4.3. Model-Field Sensitivity Inter-Comparison
5. Conclusions
- GLEAM is primarily sensitive to net radiation (RMSD = 7.49–8.07%), except for the interception component, which is driven by precipitation (RMDS = 4.1%).
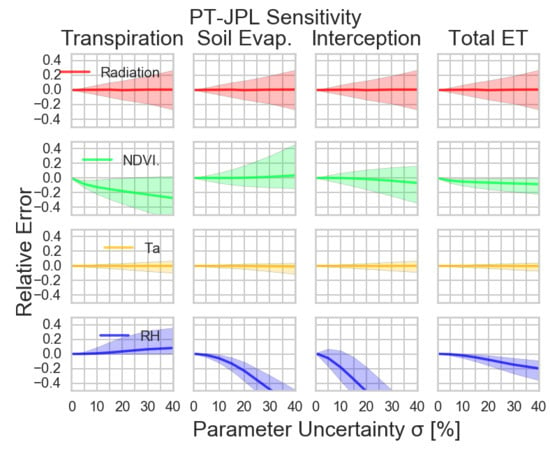
- PT-JPL components are generally sensitive to RH (RMSD = 60.6–151.4%) and NDVI (RMSD = 51.4–112%), while the total ET estimate is most sensitive to NDVI (RMSD = 100%).
- Both the components and the total ET estimate of PM-MOD are primarily sensitive to RH (RMSD = 122.3–174.2%).
- GLEAM is comparatively less sensitive to changes in its forcing variables than PM-MOD and PT-JPL. The higher complexity and daily resolution of GLEAM makes it more constrained but potentially more sensitive to the model parameterizations. Note that the soil moisture data assimilation of GLEAM was not evaluated here.
- Both PT-JPL and PM-MOD soil evaporation show large sensitivity to forcing inputs, creating greater overall uncertainty in the soil evaporation estimate for our study sites.
- Non-linear formulations of RH and vegetation indices in PT-JPL and PM-MOD often result in large biases (|MBD| > 50%) in component estimates due to variable uncertainty. However, bias in the component estimates often balance each other and limit the bias and uncertainty of the total ET estimate (|MBD| ≤ 20%). Changes to forcing could cause large changes to model partitioning with comparatively smaller changes to the overall ET estimate.
- Bias in PT-JPL due to uncertainties in NDVI are consistent with errors found when comparing model estimates to field estimates. This suggests that uncertainty in NDVI may be introducing significant error to the partitioning of PT-JPL.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Huntington, T.G. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Zhang, Y.; Peña-Arancibia, J.L.; McVicar, T.R.; Chiew, F.H.S.; Vaze, J.; Liu, C.; Lu, X.; Zheng, H.; Wang, Y.; Liu, Y.Y.; et al. Multi-decadal trends in global terrestrial evapotranspiration and its components. Sci. Rep. 2016, 6, 19124. [Google Scholar] [CrossRef] [PubMed]
- Zaitchik, B.F.; Santanello, J.A.; Kumar, S.V.; Peters-Lidard, C.D.; Zaitchik, B.F.; Santanello, J.A.; Kumar, S.V.; Peters-Lidard, C.D. Representation of Soil Moisture Feedbacks during Drought in NASA Unified WRF (NU-WRF). J. Hydrometeorol. 2013, 14, 360–367. [Google Scholar] [CrossRef]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.H.; et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Carrao, H.; Barbosa, P.; Vogt, J. World drought frequency, duration, and severity for 1951–2010. Int. J. Climatol. 2014, 34, 2792–2804. [Google Scholar] [CrossRef]
- Miralles, D.G.; Gentine, P.; Seneviratne, S.I.; Teuling, A.J. Land-atmospheric feedbacks during droughts and heatwaves: State of the science and current challenges. Ann. N. Y. Acad. Sci. 2018. [Google Scholar] [CrossRef] [PubMed]
- Friedlingstein, P.; Meinshausen, M.; Arora, V.K.; Jones, C.D.; Anav, A.; Liddicoat, S.K.; Knutti, R.; Friedlingstein, P.; Meinshausen, M.; Arora, V.K.; et al. Uncertainties in CMIP5 Climate Projections due to Carbon Cycle Feedbacks. J. Clim. 2014, 27, 511–526. [Google Scholar] [CrossRef]
- Mancosu, N.; Snyder, R.; Kyriakakis, G.; Spano, D. Water Scarcity and Future Challenges for Food Production. Water 2015, 7, 975–992. [Google Scholar] [CrossRef]
- Ciais, P.; Reichstein, M.; Viovy, N.; Granier, A.; Ogée, J.; Allard, V.; Aubinet, M.; Buchmann, N.; Bernhofer, C.; Carrara, A.; et al. Europe-wide reduction in primary productivity caused by the heat and drought in 2003. Nature 2005, 437, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.H.; Evans, J.P.; McCabe, M.F.; Meng, X.H.; Evans, J.P.; McCabe, M.F. The Impact of Observed Vegetation Changes on Land–Atmosphere Feedbacks During Drought. J. Hydrometeorol. 2014, 15, 759–776. [Google Scholar] [CrossRef]
- Goulden, M.L.; Bales, R.C. Mountain runoff vulnerability to increased evapotranspiration with vegetation expansion. Proc. Natl. Acad. Sci. USA 2014, 111, 14071–14075. [Google Scholar] [CrossRef] [PubMed]
- Porkka, M.; Gerten, D.; Schaphoff, S.; Siebert, S.; Kummu, M. Causes and trends of water scarcity in food production. Environ. Res. Lett. 2016, 11, 015001. [Google Scholar] [CrossRef]
- Dolman, A.J.; Miralles, D.G.; de Jeu, R.A.M. Fifty years since Monteith’s 1965 seminal paper: The emergence of global ecohydrology. Ecohydrology 2014, 7, 897–902. [Google Scholar] [CrossRef]
- McCabe, M.F.; Rodell, M.; Alsdorf, D.E.; Miralles, D.G.; Uijlenhoet, R.; Wagner, W.; Lucieer, A.; Houborg, R.; Verhoest, N.E.C.; Franz, T.E.; et al. The future of Earth observation in hydrology. Earth Syst. Sci. 2017, 21, 3879–3914. [Google Scholar] [CrossRef] [PubMed]
- Miralles, D.G.; Jiménez, C.; Jung, M.; Michel, D.; Ershadi, A.; McCabe, M.F.; Hirschi, M.; Martens, B.; Dolman, A.J.; Fisher, J.B.; et al. The WACMOS-ET project-Part 2: Evaluation of global terrestrial evaporation data sets. Hydrol. Earth Syst. Sci. Discuss. 2016, 12, 10651–10700. [Google Scholar] [CrossRef]
- Talsma, C.J.; Good, S.P.; Jimenez, C.; Martens, B.; Fisher, J.B.; Miralles, D.G.; McCabe, M.F.; Purdy, A.J. Partitioning of evapotranspiration in remote sensing-based models. Agric. For. Meteorol. 2018, 260, 131–143. [Google Scholar] [CrossRef]
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, D.M.; Thornton, P.E.; Oleson, K.W.; Bonan, G.B.; Lawrence, D.M.; Thornton, P.E.; Oleson, K.W.; Bonan, G.B. The Partitioning of Evapotranspiration into Transpiration, Soil Evaporation, and Canopy Evaporation in a GCM: Impacts on Land–Atmosphere Interaction. J. Hydrometeorol. 2007, 8, 862–880. [Google Scholar] [CrossRef]
- Wang, L.; Good, S.P.; Caylor, K.K. Global synthesis of vegetation control on evapotranspiration partitioning. Geophys. Res. Lett. 2014, 41, 6753–6757. [Google Scholar] [CrossRef]
- Good, S.P.; Moore, G.W.; Miralles, D.G. A mesic maximum in biological water use demarcates biome sensitivity to aridity shifts. Nat. Ecol. Evol. 2017, 1, 1883–1888. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chiew, F.H.S.; Peña-Arancibia, J.; Sun, F.; Li, H.; Leuning, R. Global variation of transpiration and soil evaporation and the role of their major climate drivers. J. Geophys. Res. Atmos. 2017, 122, 6868–6881. [Google Scholar] [CrossRef]
- McCabe, M.F.; Aragon, B.; Houborg, R.; Mascaro, J. CubeSats in Hydrology: Ultrahigh-Resolution Insights Into Vegetation Dynamics and Terrestrial Evaporation. Water Resour. Res. 2017, 53, 10017–10024. [Google Scholar] [CrossRef]
- Michel, D.; Jiménez, C.; Miralles, D.G.; Jung, M.; Hirschi, M.; Ershadi, A.; Martens, B.; McCabe, M.F.; Fisher, J.B.; Mu, Q.; et al. The WACMOS-ET project-Part 1: Tower-scale evaluation of four remote-sensing-based evapotranspiration algorithms. Hydrol. Earth Syst. Sci. 2016, 20, 803–822. [Google Scholar] [CrossRef]
- Badgley, G.; Fisher, J.B.; Jiménez, C.; Tu, K.P.; Vinukollu, R.; Badgley, G.; Fisher, J.B.; Jiménez, C.; Tu, K.P.; Vinukollu, R. On Uncertainty in Global Terrestrial Evapotranspiration Estimates from Choice of Input Forcing Datasets. J. Hydrometeorol. 2015, 16, 1449–1455. [Google Scholar] [CrossRef]
- Vinukollu, R.K.; Meynadier, R.; Sheffield, J.; Wood, E.F. Multi-model, multi-sensor estimates of global evapotranspiration: Climatology, uncertainties and trends. Hydrol. Process. 2011, 25, 3993–4010. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Wood, E.F. Impact of model structure and parameterization on Penman-Monteith type evaporation models. J. Hydrol. 2015, 525, 521–535. [Google Scholar] [CrossRef]
- McCabe, M.F.; Ershadi, A.; Jimenez, C.; Miralles, D.G.; Michel, D.; Wood, E.F. The GEWEX LandFlux project: Evaluation of model evaporation using tower-based and globally gridded forcing data. Geosci. Model Dev. 2016, 9, 283–305. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of sruface heat flux and evaporation using large scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Myneni, R.; Knyazikhin, Y.; Park, T. MOD15A2H MODIS/Terra Leaf Area Index/FPAR 8-Day L4 Global 500 m SIN Grid V006. Available online: https://lpdaac. usgs. gov/dataset_discovery/modis/modis_products_table/mod15a2h_v006 (accessed on 16 October 2016).
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2009, 114, 168–182. [Google Scholar] [CrossRef]
- Poole, D.K.; Roberts, S.W.; Miller, P.C. Water utilization. In Resources Use by Chaparral and Matorral; Miller, P.C., Ed.; Springer: New York, NY, USA, 1981; pp. 123–149. [Google Scholar]
- McJannet, D.; Fitch, P.; Disher, M.; Wallace, J. Measurements of transpiration in four tropical rainforest types of north Queensland, Australia. Hydrol. Process. 2007, 21, 3549–3564. [Google Scholar] [CrossRef]
- Calder, I.R.; Wright, I.R.; Murdiyarso, D. A study of evaporation from tropical rain forest—West Java. J. Hydrol. 1986, 89, 13–31. [Google Scholar] [CrossRef]
- Nizinski, J.J.; Galat, G.; Galat-Luong, A. Water balance and sustainability of eucalyptus plantations in the Kouilou basin (Congo-Brazzaville). Russ. J. Ecol. 2011, 42, 305–314. [Google Scholar] [CrossRef]
- Leopoldo, P.R.; Franken, W.K.; Villa Nova, N.A. Real evapotranspiration and transpiration through a tropical rain forest in central Amazonia as estimated by the water balance method. For. Ecol. Manag. 1995, 73, 185–195. [Google Scholar] [CrossRef]
- Salati, E.; Vose, P.B. Amazon Basin: A system in equilibrium. Science 1984, 225, 129–138. [Google Scholar] [CrossRef] [PubMed]
- Tani, M.; Rah Nik, A.I.; Yasuda, Y.; Shamsuddin, S.; Sahat, M.; Takanashi, S. Long-term estimation of évapotranspiration from a tropical rain forest in Peninsular Malaysia. In Proceedings of the International Symposium (Symposium HS02a) Held during IUGG 2003, the XXIII General Assembly of the International Union of Geodesy and Geophysics, Sapporo, Japan, 30 June–11 July 2003. [Google Scholar]
- Ataroff, M.; Rada, F. Deforestation Impact on Water Dynamics in a Venezuelan Andean Cloud Forest. AMBIO J. Hum. Environ. 2000, 29, 440–444. [Google Scholar] [CrossRef]
- Aparecido, L.M.T.; Miller, G.R.; Cahill, A.T.; Moore, G.W. Comparison of tree transpiration under wet and dry canopy conditions in a Costa Rican premontane tropical forest. Hydrol. Process. 2016, 30, 5000–5011. [Google Scholar] [CrossRef]
- Tanaka, N.; Kuraji, K.; Tantasirin, C.; Takizawa, H.; Tangtham, N.; Suzuki, M. Relationships between rainfall, fog and throughfall at a hill evergreen forest site in northern Thailand. Hydrol. Process. 2011, 25, 384–391. [Google Scholar] [CrossRef]
- Galloux, A.; Benecke, P.; Gietle, G.; Hager, H.; Kayser, C.; Kiese, O.; Knoerr, K.N.; Murphy, C.E.; Schnock, G.; Sinclair, T.R. Radiation, Heat, Water and Carbon Dioxide Balances; Dynamic Properties of Forest Ecosystems; Cambridge University Press: New York, NY, USA, 1981. [Google Scholar]
- Scott, R.L.; Huxman, T.E.; Cable, W.L.; Emmerich, W.E. Partitioning of evapotranspiration and its relation to carbon dioxide exchange in a Chihuahuan Desert shrubland. Hydrol. Process. 2006, 20, 3227–3243. [Google Scholar] [CrossRef]
- Cavanaugh, M.L.; Kurc, S.A.; Scott, R.L. Evapotranspiration partitioning in semiarid shrubland ecosystems: A two-site evaluation of soil moisture control on transpiration. Ecohydrology 2011, 4, 671–681. [Google Scholar] [CrossRef]
- Liu, B.; Phillips, F.; Hoines, S.; Campbell, A.R.; Sharma, P. Water movement in desert soil traced by hydrogen and oxygen isotopes, chloride, and chlorine-36, southern Arizona. J. Hydrol. 1995, 168, 91–110. [Google Scholar] [CrossRef]
- Schlesinger, W.H.; Fonteyn, P.J.; Marion, G.M. Soil moisture content and plant transpiration in the Chihuahuan Desert of New Mexico. J. Arid Environ. 1987, 12, 119–126. [Google Scholar] [CrossRef]
- Kumagai, T.; Saitoh, T.M.; Sato, Y.; Takahashi, H.; Manfroi, O.J.; Morooka, T.; Kuraji, K.; Suzuki, M.; Yasunari, T.; Komatsu, H. Annual water balance and seasonality of evapotranspiration in a Bornean tropical rainforest. Agric. For. Meteorol. 2005, 128, 81–92. [Google Scholar] [CrossRef]
- McNulty, S.G.; Vose, J.M.; Swank, W.T. Loblolly pine hydrology and productivity across the southern United States. For. Ecol. Manag. 1996, 86, 241–251. [Google Scholar] [CrossRef]
- Waring, R.H.; Rogers, J.J.; Swank, W.T. Water Relations and Hydrologic Cycles; Cambridge University Press: Cambridge, UK, 1981. [Google Scholar]
- Floret, C.; Pontanier, R.; Rambal, S. Measurement and modelling of primary production and water use in a south tunisian steppe. J. Arid Environ. 1982, 5, 77–90. [Google Scholar] [CrossRef]
- Wilson, K.B.; Hanson, P.J.; Mulholland, P.J.; Baldocchi, D.D.; Wullschleger, S.D. A comparison of methods for determining forest evapotranspiration and its components: Sap-flow, soil water budget, eddy covariance and catchment water balance. Agric. For. Meteorol. 2001, 106, 153–168. [Google Scholar] [CrossRef]
- Smith, S.D.; Herr, C.A.; Leary, K.L.; Piorkowski, J.M. Soil-plant water relations in a Mojave Desert mixed shrubcommunity: A comparison of three geomorphic surfaces. J. Arid Environ. 1995, 29, 339–351. [Google Scholar] [CrossRef]
- Paço, T.A.; David, T.S.; Henriques, M.O.; Pereira, J.S.; Valente, F.; Banza, J.; Pereira, F.L.; Pinto, C.; David, J.S. Evapotranspiration from a Mediterranean evergreen oak savannah: The role of trees and pasture. J. Hydrol. 2009, 369, 98–106. [Google Scholar] [CrossRef]
- Pereira, F.L.; Gash, J.H.C.; David, J.S.; David, T.S.; Monteiro, P.R.; Valente, F. Modelling interception loss from evergreen oak Mediterranean savannas: Application of a tree-based modelling approach. Agric. For. Meteorol. 2009, 149, 680–688. [Google Scholar] [CrossRef]
- Hu, Z.; Yu, G.; Zhou, Y.; Sun, X.; Li, Y.; Shi, P.; Wang, Y.; Song, X.; Zheng, Z.; Zhang, L.; et al. Partitioning of evapotranspiration and its controls in four grassland ecosystems: Application of a two-source model. Agric. For. Meteorol. 2009, 149, 1410–1420. [Google Scholar] [CrossRef]
- Liu, R.; Li, Y.; Wang, Q.-X. Variations in water and CO2 fluxes over a saline desert in western China. Hydrol. Process. 2012, 26, 513–522. [Google Scholar] [CrossRef]
- Telmer, K.; Veizer, J. Isotopic constraints on the transpiration, evaporation, energy, and gross primary production Budgets of a large boreal watershed: Ottawa River Basin, Canada. Glob. Biogeochem. Cycles 2000, 14, 149–165. [Google Scholar] [CrossRef]
- Tajchman, S.J. The Radiation and Energy Balances of Coniferous and Deciduous Forests. J. Appl. Ecol. 1972, 9, 359–375. [Google Scholar] [CrossRef]
- Granier, A.; Biron, P.; Lemoine, D. Water balance, transpiration and canopy conductance in two beech stands. Agric. For. Meteorol. 2000, 100, 291–308. [Google Scholar] [CrossRef]
- Pražák, J.; Šír, M.; Tesarř, M. Estimation of plant transpiration from meteorological data under conditions of sufficient soil moisture. J. Hydrol. 1994, 162, 409–427. [Google Scholar] [CrossRef]
- Delfs, J. Interception and stemflow in stands of Norway spruce and beech in West Germany. In Forest Hydrology; Sopper, W.E., Lull, H.W., Eds.; Pergamon Press: Univerity Park, PA, USA, 1967; pp. 179–185. [Google Scholar]
- Choudhury, B.J.; DiGirolamo, N.E. A biophysical process-based estimate of global land surface evaporation using satellite and ancillary data I. Model description and comparison with observations. J. Hydrol. 1998, 205, 164–185. [Google Scholar] [CrossRef]
- Hudson, J.A. The contribution of soil moisture storage to the water balances of upland forested and grassland catchments. Hydrol. Sci. J. 1988, 33, 289–309. [Google Scholar] [CrossRef]
- Valente, F.; David, J.S.; Gash, J.H.C. Modelling interception loss for two sparse eucalypt and pine forests in central Portugal using reformulated Rutter and Gash analytical models. J. Hydrol. 1997, 190, 141–162. [Google Scholar] [CrossRef]
- Ladekarl, U.L. Estimation of the components of soil water balance in a Danish oak stand from measurements of soil moisture using TDR. For. Ecol. Manag. 1998, 104, 227–238. [Google Scholar] [CrossRef]
- Gibson, J.J.; Edwards, T.W.D. Regional water balance trends and evaporation-transpiration partitioning from a stable isotope survey of lakes in northern Canada. Glob. Biogeochem. Cycles 2002, 16. [Google Scholar] [CrossRef]
- Stackhouse, P.; Gupts, S.; Cox, S.; Mikovits, J.; Zhang, T.; Chiachiio, M. 12-year surface radiation budget data set. GEWEX News 2004, 14, 10–12. [Google Scholar]
- Dee, D.; Uppala, M.S.; Simmons, J.A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, A.M.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.-P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The Version-2 Global Precipitation Climatology Project (GPCP) Monthly Precipitation Analysis (1979–Present). J. Hydrometeorol. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Didan, K. MOD13A2 MODIS/Terra Vegetation Indices 16-Day L3 Global 1km SIN GRID V006. Available online: https://data.world/us-nasa-gov/8ad39ef2-8617-4804-b004-fd82a0d2698b (accessed on 8 October 2018).
- Owe, M.; de Jeu, R.; Walker, J. A methodology for surface soil moisture and vegetation optical depth retrieval using the microwave polarization difference index. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1643–1654. [Google Scholar] [CrossRef]
- Hammersley, J.M.; Handscomb, D.C. General Principles of the Monte Carlo Method. In Monte Carlo Methods; Springer: Dordrecht, The Netherlands, 1964; pp. 50–75. [Google Scholar]
- Demaria, E.M.; Nijssen, B.; Wagener, T. Monte Carlo sensitivity analysis of land surface parameters using the Variable Infiltration Capacity model. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Robert, C.P. Simulation of truncated normal variables. Stat. Comput. 1995, 5, 121–125. [Google Scholar] [CrossRef]
- Miralles, D.G.; De Jeu, R.A.M.; Gash, J.H.; Holmes, T.R.H.; Dolman, A.J. Hydrology and Earth System Sciences Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. Sci. 2011, 15, 967–981. [Google Scholar] [CrossRef]
- Kumar, S.; Holmes, T.; Mocko, D.M.; Wang, S.; Peters-Lidard, C. Attribution of Flux Partitioning Variations between Land Surface Models over the Continental U.S. Remote Sens. 2018, 10, 751. [Google Scholar] [CrossRef]
- Stone, P.H.; Chow, S.; Quirr, W.J.; Stone, P.H.; Chow, S.; Quirr, W.J. The July Climate and a Comparison of the January and July Climates Simulated by the GISS General Circulation Model. Mon. Weather Rev. 1977, 105, 170–194. [Google Scholar] [CrossRef]
- Sun, L.; Anderson, M.C.; Gao, F.; Hain, C.; Alfieri, J.G.; Sharifi, A.; McCarty, G.W.; Yang, Y.; Yang, Y.; Kustas, W.P.; et al. Investigating water use over the Choptank River Watershed using a multisatellite data fusion approach. Water Resour. Res. 2017, 53, 5298–5319. [Google Scholar] [CrossRef]
- Marshall, M.; Thenkabail, P.; Biggs, T.; Post, K. Hyperspectral narrowband and multispectral broadband indices for remote sensing of crop evapotranspiration and its components (transpiration and soil evaporation). Agric. For. Meteorol. 2016, 218, 122–134. [Google Scholar] [CrossRef]
| Reference | Location | Lat. | Long. | Landcover Type | Methods | Precip. [mm/yr] | Aridity |
|---|---|---|---|---|---|---|---|
| Poole et al., 1981 [37] | Chile | −33.07 | −71.00 | Mediterranean Shrubland | Xylem pressure potential | 590 | 0.43 |
| McJannet et al., 2007 [38] | Queensland | −17.45 | 145.50 | LMCF | Sapflow | 2983.00 | 1.83 |
| McJannet et al., 2007 | Queensland | −17.36 | 145.66 | Broadleaf Evergreen Forest | Sapflow | 2702 | 1.83 |
| McJannet et al., 2007 | Queensland | −16.53 | 145.28 | LMCF | Sapflow | 3040 | 1.94 |
| Calder et al., 1986 [39] | Indonesia | −6.58 | 106.28 | Tropical Rainforest | Model (with met. data), Isotopes | 2851 | 1.79 |
| Nizinski et al., 2011 [40] | D.R. Congo | −4.69 | 12.08 | Tropical Rainforest | Radial flow meter | 1019 | 0.74 |
| Leopoldo et al., 1995 [41] | Amazon | −3.13 | −60.03 | Tropical Rainforest | Model (with met. Data) Water Balance | 2209 | 1.29 |
| Salati and Vose 1984 [42] | Brazil | −2.95 | −59.95 | Tropical Rainforest | Model (with met. Data) Water Balance | 2000 | 1.29 |
| Tani et al., 2003 [43] | Malaysia | 2.97 | 102.30 | Tropical lowland forest | Model(with met. data) Water Balance | 1571 | 0.93 |
| Ataroff 2000 [44] | Venezuela | 8.63 | −71.03 | TMCF | Micromet | 4450 | 4.40 |
| Aparecido 2016 [45] | Costa Rica | 10.39 | −84.63 | TMRF | Sapflow + other | 4200 | 2.72 |
| Tanaka 2011 [46] | Thailand | 18.80 | 98.90 | LMCF | Sapflow | 1768 | 1.01 |
| Banerjee in Galoux et al., 1981 [47] | India | 22.50 | 87.30 | Tropical Rainforest | - | 1623 | 1.00 |
| Scott et al., 2006 [48] | United States | 31.70 | −110.40 | Desert | Sap Flow | 322 | 0.21 |
| Cavanaugh et al., 2011 [49] | United States | 31.74 | −110.05 | Desert | Model (with met. data), Sap flow | 260 | 0.17 |
| Cavanaugh et al., 2011 | United States | 31.91 | −110.84 | Desert | Model (with met. data), Sap flow | 212 | 0.15 |
| Liu et al., 1995 [50] | United States | 31.95 | −112.94 | Desert | Model (with met. Data), Isotopes | 200 | 0.11 |
| Schlesinger et al., 1987 [51] | United States | 32.52 | −106.80 | Desert | Water-balance; control and bare plots | 210 | 0.14 |
| Poole et al., 1981 | United States | 32.83 | −116.43 | Mediterranean Shrubland | Xylem pressure potential | 475 | 0.33 |
| Kumagai et al., 2005 [52] | Japan | 33.13 | 130.72 | Temperate Forest | Model (with met. data), sap flow | 2128 | 2.24 |
| McNulty 1996 [53] | United States | 34.00 | −85.80 | Temperate Forest | Xylem pressure potential | 1225 | 0.92 |
| Waring et al., 1981 [54] | United States | 34.64 | −111.78 | Temperate Forest | Xylem pressure potential | 1085 | 0.80 |
| Floret et al., 1982 [55] | Tunisia | 35.80 | 9.20 | Steppe | Model (with met. data) | 144 | 0.11 |
| Wilson et al., 2001 [56] | United States | 35.96 | −84.29 | Temperate Deciduous Forests | Model (with met. data), sap flow | 1333 | 1.07 |
| Smith et al., 1995 [57] | United States | 36.93 | −116.56 | Desert | Xylem pressure potential | 150 | 0.10 |
| Paco et al., 2009 [58] | Portugal | 38.50 | −8.00 | Temperate Deciduous Forests | Sap flow | 669 | 0.57 |
| Pereira et al., 2009 [59] | Iberian Peninsula | 38.53 | −8.01 | Broadleaf Evergreen Forest | - | 669 | 0.57 |
| Hu et al., 2009 [60] | China | 43.55 | 116.67 | Temperate Grassland | Model (with met. data) | 580 | 0.53 |
| Waring et al., 1981 | United States | 44.20 | −122.30 | Temperate Forest | Xylem pressure potential | 2355 | 2.75 |
| Liu et al., 2012 [61] | China | 44.28 | 87.93 | Desert | Energy balance model | 150 | 0.15 |
| Telmer and Veizer 2000 [62] | Canada | 45.70 | −76.90 | Boreal Forest | Isotope-based (catchment) | 872 | 1.04 |
| Tajchman 1972 [63] | Germany | 48.04 | 11.56 | Temperate Forest | Energy balance model | 725 | 0.96 |
| Granier et al., 2000 [64] | France | 48.67 | 7.08 | Temperate Deciduous Forests | Sap flow | 763 | 0.99 |
| Prazak et al., 1994 [65] | Czech Republic | 49.06 | 13.66 | Temperate Forest | Model (with met. data) | 366 | 0.50 |
| Molchanov cited in Galoux et al., 1981 | Russia | 50.75 | 42.50 | Temperate Deciduous Forests | - | 513 | 0.64 |
| Two studies by Delfs (1967), cited by Choudhury et al., 1998 [66,67] | Germany | 51.76 | 10.51 | Boreal Forest | - | 1237 | 1.83 |
| Hudson 1988 [68] | United Kingdom | 52.00 | −3.50 | Temperate Forest | Model (with met. data) | 2620 | 4.63 |
| Valente et al., 1997 [69] | United Kingdom | 52.42 | 0.67 | Temperate Forest | Model (with met. data) | 595 | 0.91 |
| Ladekarl 1998 [70] | Denmark | 56.41 | 9.35 | Temperate Deciduous Forests | Model (with met. data) | 549 | 0.98 |
| Gibson and Edwards, 2002 [71] | Canada | 63.41 | −114.26 | Boreal Forest | Isotope-based (catchment) | 340 | 0.80 |
| Gibson and Edwards, 2002 | Canada | 64.50 | −112.70 | Tundra | Isotope-based (catchment) | 310 | 0.88 |
| Variable | Product | PT-JPL | PM-MOD | GLEAM |
|---|---|---|---|---|
| Surface Radiation | SRB [72] | ✓ | ✓ | ✓ |
| Temperature | ERA-Interim [73] | ✓ | ✓ | ✓ |
| Relative Humidity | ERA-Interim [73] | ✓ | ✓ | |
| Precipitation | SFR-GPCP [74] | ✓ | ||
| fAPAR | MODIS [75] | ✓ | ||
| LAI | MODIS [75] | ✓ | ||
| NDVI | MODIS [75] | ✓ | ||
| Vegetation Optical Depth | LRPM [76] | ✓ |
| PT-JPL | ||||||||
| %RMSD | %MBD | |||||||
| Eveg | Esoil | Eint | ET | Eveg | Esoil | Eint | ET | |
| Rn | 38.8 | 38.8 | 38.8 | 38.8 | 1.4 | 1.4 | 1.4 | 1.4 |
| RH | 122.6 | 60.6 | 151.4 | 33.1 | 41.9 | −26.1 | −59.0 | −12.9 |
| Ta | 32.3 | 71.3 | 13.6 | 35.9 | 0.9 | −2.3 | 0.5 | 0.5 |
| NDVI | 91.0 | 112.0 | 51.4 | 100.0 | −51.4 | 5.1 | −1.4 | −20.0 |
| PM-MOD | ||||||||
| %RMSD | %MBD | |||||||
| Eveg | Esoil | Eint | ET | Eveg | Esoil | Eint | ET | |
| Rn | 47.4 | 49.6 | 42.4 | 49.1 | −0.3 | −2.3 | 0.2 | −0.5 |
| RH | 144.5 | 174.2 | 129.3 | 122.3 | −25.3 | −33.7 | −19.2 | −2.7 |
| Ta | 48.3 | 125.7 | 28.0 | 68.1 | 1.0 | −18.6 | 1.3 | 1.2 |
| fAPAR | 44.2 | 83.3 | 30.8 | 44.0 | −0.6 | −0.8 | −0.6 | −1.1 |
| LAI | 37.7 | 8.7 | 45.5 | 38.6 | 0.4 | −0.4 | 0.3 | 0.4 |
| GLEAM | ||||||||
| %RMSD | %MBD | |||||||
| Eveg | Esoil | Eint | ET | Eveg | Esoil | Eint | ET | |
| Rn | 8.07 | 8.15 | NA | 7.49 | −1.16 | −0.03 | NA | −0.83 |
| P | 4.54 | 4.07 | 4.10 | 4.82 | −0.74 | 0.80 | −0.14 | 0.02 |
| Ta | 4.49 | 2.79 | NA | 3.88 | −1.14 | 0.00 | NA | −0.80 |
| Ku | 3.96 | 2.69 | NA | 3.28 | −1.13 | 0.02 | NA | −0.78 |
| VOD | 3.94 | NA | NA | 3.21 | −1.16 | NA | NA | −0.85 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Talsma, C.J.; Good, S.P.; Miralles, D.G.; Fisher, J.B.; Martens, B.; Jimenez, C.; Purdy, A.J. Sensitivity of Evapotranspiration Components in Remote Sensing-Based Models. Remote Sens. 2018, 10, 1601. https://doi.org/10.3390/rs10101601
Talsma CJ, Good SP, Miralles DG, Fisher JB, Martens B, Jimenez C, Purdy AJ. Sensitivity of Evapotranspiration Components in Remote Sensing-Based Models. Remote Sensing. 2018; 10(10):1601. https://doi.org/10.3390/rs10101601
Chicago/Turabian StyleTalsma, Carl J., Stephen P. Good, Diego G. Miralles, Joshua B. Fisher, Brecht Martens, Carlos Jimenez, and Adam J. Purdy. 2018. "Sensitivity of Evapotranspiration Components in Remote Sensing-Based Models" Remote Sensing 10, no. 10: 1601. https://doi.org/10.3390/rs10101601
APA StyleTalsma, C. J., Good, S. P., Miralles, D. G., Fisher, J. B., Martens, B., Jimenez, C., & Purdy, A. J. (2018). Sensitivity of Evapotranspiration Components in Remote Sensing-Based Models. Remote Sensing, 10(10), 1601. https://doi.org/10.3390/rs10101601