Abstract
The optimal water level prediction and control of the Great Lakes is critical for balancing ecological, economic, and societal demands. This study proposes a multi-objective planning model integrated with a fuzzy control algorithm to address the conflicting interests of stakeholders and dynamic hydrological complexities. First, a network flow model is established to capture the interconnected flow dynamics among the five Great Lakes, incorporating lake volume equations derived from paraboloid-shaped bed assumptions. Multi-objective optimization aims to maximize hydropower flow while minimizing water level fluctuations, solved via a hybrid Ford–Fulkerson and simulated annealing approach. A fuzzy controller is designed to regulate dam gate openings based on water level deviations and seasonal variations, ensuring stability within ±0.6096 m of target levels. Simulations demonstrate rapid convergence (T = 5 time units) and robustness under environmental disturbances, with sensitivity analysis confirming effectiveness in stable conditions (parameter ≥ 0.2). The results highlight the framework’s capability to harmonize stakeholder needs and ecological sustainability, offering a scalable solution for large-scale hydrological systems.
1. Introduction
The Great Lakes, spanning the United States and Canada, represent the world’s largest freshwater system, supporting critical ecological, economic, and societal functions. However, global climate change and anthropogenic activities led to unprecedented hydrological variability, posing significant challenges to sustainable water resource management. Therefore, it has become important to rationalize hydrologic modeling and achieve optimal prediction and control.
In past studies, scholars confirmed from several perspectives that the water level of the Great Lakes is critical for maintaining ecological balance, supporting economic activities, and ensuring community well-being [1,2,3,4,5]. Among these is the instability of the climate leading to erratic weather patterns that can directly affect Great Lakes water levels [6,7]. Unprecedented rainfall, extended droughts, and variable snowmelt contribute to unpredictable water volume fluctuations [8,9]. Meanwhile, the expansion of human activities, such as urbanization and agriculture, led to increased water consumption, further complicating water level management [10,11,12].
Past studies have also shown that the diverse stakeholders with interests in the Great Lakes have distinct priorities regarding water levels [13,14,15]. Shipping companies need high water levels for unhindered navigation of large-cargo vessels, while dockyard management companies and lakeside inhabitants worry about flooding risks associated with high water [16]. Fisherfolk, the entertainment industry, and shore owners generally prefer a moderate water level for fishing, recreational boating, and property stability [17,18]. Environmentalists emphasize the significance of seasonal water level variations for ecosystem health and biodiversity [19,20,21].
Despite extensive research on hydrological modeling, traditional single-objective approaches to water level management are insufficient as they focus on a single aspect, such as maximizing water level differences or flow rates to increase hydropower generation, optimize power output, or minimize flood risk, without considering the broader impacts on other stakeholders and the ecosystem [22,23,24,25]. Although recent studies advocate for integrated models that account for hydrological and socio-economic factors, there are still challenges in balancing real-time control with long-term predictive accuracy under non-stationary environmental conditions [26,27,28,29].
This study bridges these gaps by developing a multi-objective framework combining network flow modeling, simulated annealing optimization, and fuzzy logic control. The contributions are threefold: (1) a paraboloid-based lake volume model simplifies bed morphology while preserving hydrological realism; (2) a stakeholder-centric optimization model resolves conflicts between hydropower maximization and water level stability; and (3) a fuzzy controller adapts to seasonal variations and external disturbances, ensuring robust water level regulation. By addressing these challenges, the proposed framework advances sustainable water resource management in large, interconnected lake systems.
2. Data Sources and Descriptions
This study uses historical water level conditions in the Great Lakes basin for hydrologic model modeling, optimal water level prediction, and control. Among other things, the Great Lakes (including Lakes Superior, Michigan, Huron, Erie, and Ontario) are interconnected by a complex system of rivers and waterways such as the St. Mary’s, St. Clair, Detroit, Niagara, Ottawa, and St. Lawrence Rivers.
It is important to note that the Great Lakes form a hydraulically connected system with unidirectional flow dynamics. Water movement is driven by the natural elevation gradient of the lakes, with Lake Superior at its highest level and Lake Ontario at its lowest. This gradient ensures that flow through the connecting rivers is not reversible under natural conditions. Unlike man-made reservoir systems that allow for two-way flow regulation through gate control (gate making), one-way flow in the Great Lakes is limited by geology and topography. However, it is still possible to manage water levels by controlling outflow rates at downstream bottlenecks, which helps to balance storage and reduce fluctuations throughout the system.
For model reliability and credibility, water level data of the Great Lakes and river flow data were sourced from publicly available and authoritative databases. The water level data for each lake in the Great Lakes were calculated via a coordinated water level measurement network, with detailed monthly average data retrieved from the US Army Corps of Engineers’ Great Lakes Information website. River flow data, including those of the St. Mary’s, St. Clair, and Detroit rivers from the US Geological Survey’s Water Resources Data website, the Niagara River at Buffalo from the Great Lakes Coordinating Committee, the Ottawa River at Carillon from its official website, and the St. Lawrence River at Cornwall from the US Geological Survey, were also crucial. These data detailed the flow conditions of each river at different times. These water level data are based on the North American Vertical Datum of 1988 (NAVD88). By using such data, this study accurately constructed models and deeply analyzed the Great Lakes’ hydrological system, laying a solid data foundation for subsequent multi-objective planning and water level control research.
Fracture box line plots of the historical data obtained show the distribution of historical water levels as shown in Figure 1.
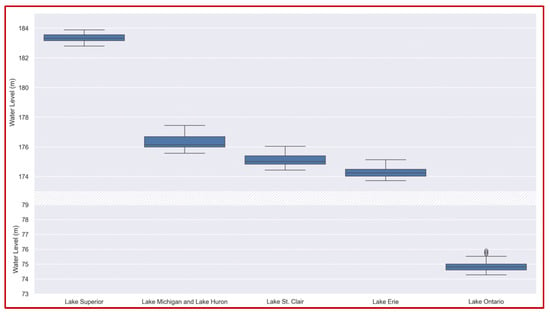
Figure 1.
Historical water level distribution.
3. Assumptions and Justifications
Assumption 1.
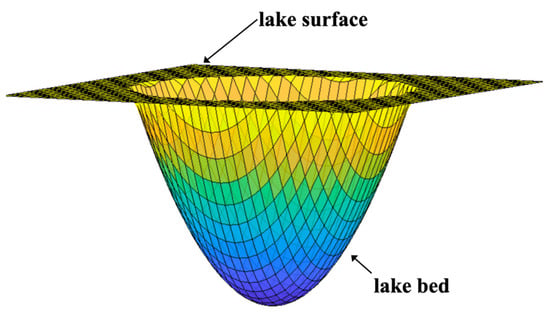
The lake bed is a smooth paraboloid, and the lake surface is a smooth plane, as shown in Figure 2.

Figure 2.
Mathematical model of lakes.
Justification.
Although the actual lake bed morphology can vary greatly, with various irregularities and complex geological structures, from a macroscopic scale and overall characteristics perspective, the assumption of a smooth paraboloid can reasonably reflect the basic features of the lake bed to a certain extent. During the formation and evolution of many natural lakes, under the combined effects of geological structures, water flow erosion, and other factors, the general shape of the lake bed often exhibits certain regularity and symmetry, which is somewhat similar to a paraboloid. This assumption is conducive to the establishment of algorithms and, at the same time, maximally reflects the real-world situation of the lake bed in the later stage. Through this assumption, the volume of the lake is simplified into the following formula:
where x and y represent the coordinates in the plane, a and b are the parameters of the paraboloid, and h is the maximum depth.
Assumption 2.
The water level change is a periodic change and is a stationary non-white noise sequence or becomes a stationary non-white noise sequence after first-order differencing.
Justification.
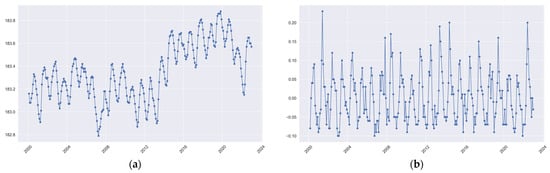
The assumption of a stationary non-white noise sequence means that the statistical characteristics of the water level change do not change significantly over time, and there is a certain correlation between the various observed values in the sequence, rather than there being completely random white noise. To verify this assumption, take Lake Superior as an example. The water level change from January 2000 to December 2022 is shown in Figure 3a, and it can be seen that it shows an annual cycle change. After first-order differencing, it is shown in Figure 3b.

Figure 3.
The water level data of Lake Superior: (a) is the original data, and (b) is the data after first-order differencing.
For the differenced data, the original hypothesis H0 is that there is a unit root in the time series, i.e., the time series is non-stationary, and the alternative hypothesis H1 is that there is no unit root in the time series, i.e., the time series is stationary, through the ADF test. The ADF test statistic is as follows:
where denotes the statistic, denotes the estimated value of , and denotes the standard error of .
After calculating, the ADF test statistic value is −3.56 with a p-value of 0.0066, i.e., the null hypothesis is rejected and the series does not have a unit root, and hence the data are considered to be weakly smooth.
For the differenced data, the original hypothesis H0 is that the time series is a white noise series and the alternative hypothesis H1 is that the time series is not a white noise series according to the LB white noise test. The LB white noise test statistic is as follows:
where n is the number of observed samples of the sequence, m is the specified maximum delay order, and is the sample autocorrelation coefficient for delay order k.
By calculation, the p-value of the LB white noise test for lags 1 to 12 is less than 0.05. Again, the null hypothesis is rejected and the data are considered to be a non-white noise series.
Assumption 3.
The water level change follows a normal distribution.
Justification.
The sample size is 276, which is considered a large sample. Therefore, we used the Kolmogorov–Smirnov test to calculate the level of significance to determine its normality. The original hypothesis is H0: the overall distribution from which the sample data comes is not significantly different from the specified normal distribution, i.e., the sample data obey a normal distribution, and the alternative hypothesis, H1, is that the overall distribution from which the sample data comes is significantly different from the specified normal distribution, i.e., the sample data do not obey a normal distribution. The KS test statistic is as follows:
where is the empirical distribution function of the sample and is the distribution function of the assumed normal distribution.
Through calculation, the KS test statistic is 0.06, and the p-value is 0.3003. That is, the null hypothesis is not rejected, and it is considered that there is no significant difference between the sample distribution and the normal distribution. Therefore, it can be considered that the water level change can be fitted to a normal distribution. The histogram and QQ plot are shown in Figure 4a,b.
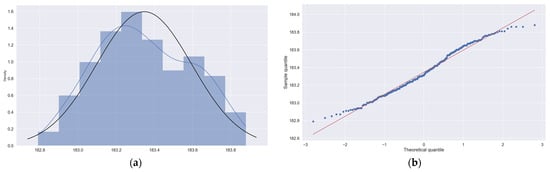
Figure 4.
Results of normality test: (a) is the histogram of the historical water levels of Lake Superior, blue curve is kernel density curve, black curve is normal distribution curve; (b) is the QQ plot.
4. Optimal Water Level Prediction
4.1. Great Lakes Network Flow Model
When determining the optimal water level of the Great Lakes, it is essential to recognize that treating the five lakes as an isolated, monolithic basin is insufficient. Instead, a comprehensive Great Lakes network flow model is necessary for in-depth analysis. The Great Lakes, including Lake Superior, Lake Michigan, Lake Huron, Lake Erie, and Lake Ontario, are interconnected through a complex system of rivers and channels, such as the St. Mary’s River, St. Clair River, Detroit River, Niagara River, Ottawa River, and St. Lawrence River. This intricate network allows water to flow between the lakes, and understanding these flow dynamics is crucial for predicting the optimal water levels. Therefore, based on the actual hydrological situation, the Great Lakes network flow model is established, as shown in Figure 5.
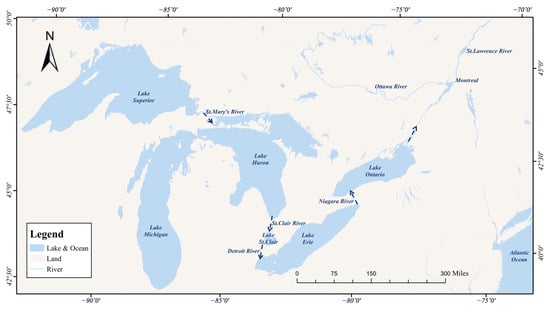
Figure 5.
Great Lakes network flow model.
In the Great Lakes network flow model, the river flow is defined as the derivative of the lake volume with respect to time. Mathematically, this relationship is expressed in the following equations:
where , , , , and represent the volumes of Lake Superior, Lake Michigan and Lake Huron, Lake St. Clair, Lake Erie, and Lake Ontario, respectively. W1, W2, W3, W4, W5, and W6 denote the river flows of the St. Mary’s River, St. Clair River, Detroit River, Niagara River, Ottawa River, and St. Lawrence River, respectively. The volume of each lake can be calculated using Equation (1) derived from Assumption 1 for the shape of the lake bed.
It should be noted that Equations (5)–(9) of this model mainly consider surface water inflows (W) and outflows (W), and do not include factors such as groundwater fluxes, evapotranspiration, and precipitation. This is because (1) Kayastha et al. noted that groundwater exchange is relatively slow and spatially heterogeneous in the Great Lakes system, making it difficult to accurately quantify at the macro-scale [24]. Therefore, groundwater exchange is usually ignored. (2) The study of evapotranspiration by Yang et al. shows that there is a correlation between evapotranspiration and precipitation changes, with a decrease in evapotranspiration occurring simultaneously with a decrease in precipitation [9]. Therefore, on an interannual scale, evapotranspiration has a compensatory effect with precipitation that can be ignored.
It is important to note that each river has a limited maximum flow per unit time. This limitation is not only a physical constraint, but also has a significant impact on the water volume changes of adjacent lakes. For example, if the flow capacity of the St. Mary’s River (W1) is restricted, it will directly affect the water volume change of Lake Superior () and Lake Michigan-Huron (). This interdependence among the lakes and rivers emphasizes the complexity of the Great Lakes’ hydrological system and the importance of an accurate network flow model in predicting optimal water levels.
4.2. Multi-Objective Planning
4.2.1. Analysis of Stakeholders and Their Claims
The water resources of the Great Lakes serve a wide range of purposes, and multiple stakeholders have diverse interests and claims regarding the water level. A comprehensive understanding of these stakeholders and their demands is the foundation for establishing an appropriate multi-objective planning model.
The major stakeholders in the Great Lakes region and their claims are presented in Table 1. The table details the water level claims and stability claims for each stakeholder.

Table 1.
Major stakeholders in the Great Lakes and their claims.
This study focuses on a few key stakeholders and does not consider the less impactful shipping company, dockyard management company, and inhabitants as shown in Table 2. By concentrating on these stakeholders, this study can simplify the analysis while still addressing the major concerns related to the optimal water level. The demands of these stakeholders can be broadly categorized into three types: moderate stability, high and low seasonal variability, and high flow in the Great Lakes. These categories form the basis for determining the objective function of the multi-objective programming model.

Table 2.
Stakeholders in the spotlight of this study.
4.2.2. Modeling
To formulate the multi-objective programming model, this study denotes the lake level as a decision variable , where represents the optimal water level for each lake (i = 1, 2, 3, 4, and 5) in the Great Lakes system.
Our first goal is to maximize the flow. Hydroelectric utilities rely on a sufficient flow of water to maximize their power generation. This problem is related to the maximum-flow problem in network flow theory. To solve this, this study integrates the Ford–Fulkerson algorithm and the simulated annealing algorithm. The Ford–Fulkerson algorithm is a well-known method for finding the maximum flow in a network. However, due to the complexity of the Great Lakes network and the large number of possible flow combinations, a brute-force application of the Ford–Fulkerson algorithm can be computationally expensive. Therefore, this study introduces the simulated annealing algorithm. The simulated annealing algorithm is a heuristic search method inspired by the annealing process in metallurgy. It can explore the solution space more efficiently and avoid becoming trapped in local optima, enabling us to find a near-optimal solution for the maximum flow problem through the Great Lakes basin.
The second goal is to minimize the change in water level. An in-depth analysis of the stakeholders’ claims reveals that most of them prefer stable water levels. This implies that the difference between the inflow and outflow of each lake should be minimized. Mathematically, this study expresses this as minimizing :
where represents the change in the volume of lake i. A stable water level not only satisfies the needs of stakeholders such as fisherfolk, the entertainment industry, and shore owners, but also helps to maintain the ecological balance of the Great Lakes.
In addition to the objective functions, this study needs to set up constraints. First, considering the natural flow direction in the Great Lakes system, the water level in the upstream lake must be higher than that in the downstream lake. This is expressed as for and i, j = 1, 2, 3, 4, and 5. Second, to prevent any disproportionate negative impact on the interests of stakeholders, this study limits the water level to be within 2 feet (approximately 0.6096 m) above the normal level. The normal level is defined as the arithmetic average of the water levels at the same time point in each year, denoted as EHi. So, the constraint is as follows:
When dealing with the maximum flow problem in a model, it is computationally difficult to directly enumerate all possible flows. Therefore, based on the above equation and Assumptions 1–3 on the one hand, and simulated annealing algorithm on the other hand, the solution is optimized.
The simulated annealing algorithm starts with an initial solution. To ensure algorithmic soundness, faster convergence of the algorithm, as well as trapping in local optimal solutions, the initial water levels of the Superior, M&H, St. Clair, Erie, and Ontario lakes were set to the long term historical monthly averages of each lake, i.e., (183.35, 176.33, 175.10, 174.28, and 74.83). The algorithm also requires the specification of several parameters: the initial temperature T0, the cooling rate , the maximum number of iterations N, and the number of iterations at each temperature M. It is important to emphasize that these parameters are key parameters for the iterative solution of the simulated annealing algorithm and are not the water temperature or cooling rate of the Great Lakes. Here, this study set is T0 = 1000, = 0.95, N = 1000, and M = 300.
The algorithm iteratively explores the solution space. At each step, it generates a new solution by making a small perturbation to the current solution. It then calculates the objective function value for the new solution. If the new solution is better (in terms of maximizing the flow and minimizing the water level change), it is always accepted. If the new solution is worse, it is accepted with a certain probability pt. The probability pt is calculated based on the difference in objective function values and the current temperature T using the Boltzmann distribution formula:
where is the difference in the objective function values between the new and current solutions. As the algorithm progresses, the temperature T is gradually decreased according to the cooling rate (), reducing the probability of accepting worse solutions over time.
After running the simulated annealing algorithm, the optimal solution obtained represents the maximum flow through the Great Lakes basin. Based on the relationship between flow and water level (derived from the network flow model), this study can then calculate the optimal water level for each lake. The optimal water levels for each lake in the Great Lakes basin throughout the year are presented in Table 3.

Table 3.
Optimal water levels for the Great Lakes.
This study can also visualize these optimal water levels in a line graph, as shown in the Figure 6. These graphs clearly illustrate the seasonal variations in the optimal water levels for each lake. For example, Lake Superior shows a relatively stable trend with a slight increase from winter to summer and then a decrease in the fall.
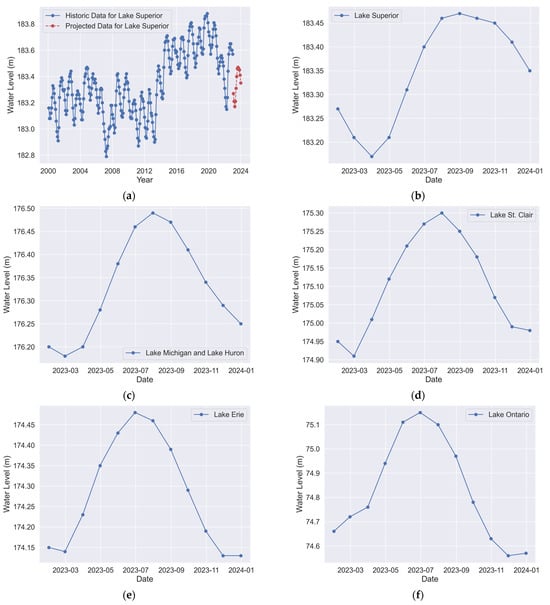
Figure 6.
Predicted results: (a) Lake Superior raw data and best water level predictions; (b–f) best water level predictions for Lake Superior, Lake Michigan and Lake Huron, Lake St. Clair, Lake Erie, and Lake Ontario in that order.
5. Optimal Water Level Control
The water levels in the Great Lakes are intricately determined by the volume of water flowing in and out of the lakes. This inflow and outflow are, in turn, significantly influenced by the dams that regulate the water discharge, particularly from Lake Superior and Lake Ontario. Although the Great Lakes water levels show a pattern of annual cyclical changes, a relatively small change of two to three feet compared to the normal level can have far-reaching consequences for various stakeholders. For instance, a sudden rise in water levels may lead to flooding, affecting the safety and property of lakeside inhabitants and dockyard operations. Conversely, a significant drop can impact shipping, fishing, and the recreational activities on the lakes. Therefore, it is crucial to develop an effective solution to maintain the Great Lakes at their optimal water levels by precisely controlling the dam gate openings and regulating the dam outflows.
In response to these challenges, this study introduces the water level fuzzy controller. Leveraging the principles of fuzzy logic, this controller can handle the imprecision and complexity inherent in the water level control problem. Based on the water level fuzzy controller algorithm, this study establishes a Simulink model for water level fuzzy control, which provides a powerful tool for simulating and analyzing the control process.
5.1. Structural Design of Water Level Fuzzy Controller
5.1.1. Variable Analysis
The design of a fuzzy controller begins with the identification of its input and output variables. The input variables are selected as water level deviation E and rate of change in water level deviation EC. The water level deviation E is calculated as the difference between the target water level r and the actual water level y. To obtain a more representative value for E, this study takes the monthly optimal water level ri and subtracts the monthly actual water level yi for each month. Then, this study averages these monthly differences to obtain the input E. This averaging process helps to smooth out the short-term fluctuations and provides a more stable measure of the overall water level deviation.
The rate of change in the water level deviation EC is also a crucial input. Seasonal variations play a significant role in the water level dynamics of the Great Lakes. To account for this, this study fits a sinusoidal function. This study calculates the differences between the maximum difference, the minimum difference, and the expected difference. Considering that a water level change of two to three feet (equivalent to 0.6096 m) can have a substantial impact on stakeholders, this study takes the absolute minimum of these three differences as the coefficients of the sine function to obtain the input EC. Mathematically, the relationships are expressed as follows:
The output variable of the fuzzy controller is the control gate opening U, which directly affects the amount of water flowing out of the dams. By adjusting U, this study regulates the water levels in the Great Lakes to meet the desired targets.
5.1.2. The Spatial Partitioning of Linguistic Variables
Linguistic variables are used to represent the input and output variables in a more human-understandable and fuzzy logic-compatible way. For the water level deviation E, it corresponds to the linguistic variable “level”. The domain of “level” is defined as X = {−1, −0.6667, −0.3333, 0, 0.3333, 0.6667, 1}, and the corresponding linguistic values are {PB, PM, PS, ZO, NS, NM, NB}. Here, positive big (PB) indicates that the current water level is significantly high, and positive medium (PM) and positive small (PS) represent moderately high and slightly high water levels, respectively. Zero (ZO) means the water level is just right, while negative small (NS), negative medium (NM), and negative big (NB) represent slightly low, moderately low, and significantly low water levels.
The rate of change in the water level deviation EC corresponds to the linguistic variable “rate”. Its domain is Y= {−0.1, −0.03333, 0, 0.03333, 0.1}, and the linguistic values are {NB, NS, ZO, PS, PB}. NB indicates that the water level is rapidly decreasing, NS represents a decreasing water level, ZO means the water level change is unchanged, PS indicates an increasing water level, and PB represents a rapidly rising water level.
The output variable, the control gate opening U, corresponds to the linguistic variable “value”. Its domain is {−3, −2, −1, 0, 1, 2, 3}, and the linguistic values are {NB, NM, NS, ZO, PS, PM, PB}. These values represent different degrees of gate-opening actions, such as “fast gate” (rapidly close or open the gate), “medium gate” (moderate closing or opening), “slow gate” (gradual closing or opening), and “constant gate opening” (maintaining the current gate position).
5.1.3. The Affiliation Function for Language Values
Affiliation functions are used to define the degree to which a particular value belongs to a linguistic variable. For the “level” and “rate” linguistic variables, this study uses Gaussian-type affiliation membership functions. Gaussian functions are suitable for representing the fuzziness around a central value. They have a bell-shaped curve, which can effectively model the uncertainty associated with the water level deviation and its rate of change. For example, a Gaussian function for the positive small (“PS”) level of water level deviation would have a peak at the value corresponding to a slightly high water level deviation, and the membership degree would gradually decrease as the deviation moves away from this central value.
For the “valve” (control gate opening) linguistic variable, this study uses a triangular affiliation membership function. Triangular functions are simple and intuitive, making them suitable for representing the discrete-like nature of the gate-opening control. A triangular function for the positive medium (“PM”) level of gate opening would have a linear increase to a peak at the value corresponding to a medium gate opening and a linear decrease on either side.
5.1.4. The Structure of the Water Level Fuzzy Controller
The structure of the water level fuzzy controller is depicted in Figure 7. The fuzzy controller is enclosed in a dotted-line box. It takes the target water level r(t) and the original signal of water level deviation e(k) as inputs. The actuator, in this case, is the gate that controls the water outflow from the dams. The controlled object is the water level of the lake. The fuzzy controller processes the input information, which includes the water level deviation E and the rate of change in the water level deviation EC and generates an output signal U that is used to adjust the gate opening. This structure provides a systematic way to transform the imprecise input information into a control action that can regulate the water levels in the Great Lakes.
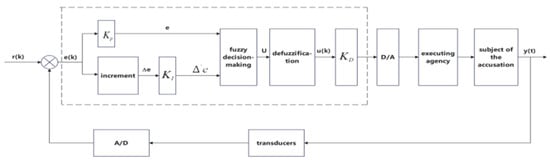
Figure 7.
Structure of water level fuzzy controller.
5.2. Simulink Modeling for Water Level Fuzzy Control
5.2.1. Fuzzy Controller Design
In the Simulink model for water level fuzzy control, the fuzzy controller is designed as a two-dimensional fuzzy controller. The input variables are the error level (equivalent to the water level deviation E) and the error rate of change (equivalent to the rate of change in the water level deviation EC), and the output variable is the gate-opening degree “valve”. This study employs Mamdani’s relational matrix method as the fuzzy control algorithm. This method is widely used in fuzzy logic control systems due to its simplicity and effectiveness.
A crucial part of the fuzzy controller design is the creation of the fuzzy control rule table. The table presented shows the relationship between the input linguistic variables “level” and “rate” and the output linguistic variable “valve”. For example, the rule “NB-NB-NB” in Table 4 indicates that when the current water level is low (NB for “level”) and the water level is dropping rapidly (NB for “rate”), the fuzzy controller calculates that the appropriate measure is to close the gate quickly (NB for “valve”).

Table 4.
Fuzzy control rules for water level.
To better understand the operation of the fuzzy controller, consider an example where for level = 0.4 and rate = 0.02, the fuzzy controller calculates a value of 0.366. The surface observation window, shown in Figure 8, provides a visual representation of the relationship between “level”, “rate”, and “valve”. This window allows us to observe how changes in the input variables affect the output, which is essential for tuning and analyzing the performance of the fuzzy control system.
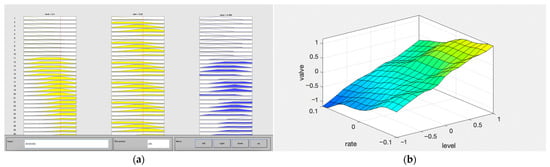
Figure 8.
Fuzzy controller visualization diagram: (a) shows the input–output correspondence of each rule in the fuzzy system, and (b) shows the 3D surface of the mapping relationship.
5.2.2. Building Simulink Models
The overall block diagram of the Simulink model for water level fuzzy control is shown in Figure 9.
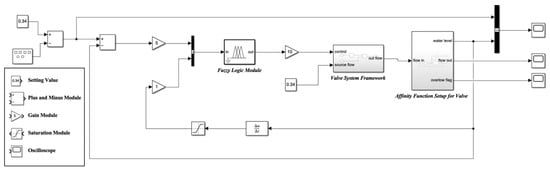
Figure 9.
Simulink overall block diagram.
The “0.34” on the left side is the normalized optimal water level-setting value, and the square input module is used for manual intervention to adjust the target water level. The first plus and minus module is responsible for calculating the deviation of the actual water level from the set value; the water level deviation signal is processed by the second plus and minus module, amplified by the gain “5” and fed into the fuzzy logic module. The water level feedback value is calculated by the “Δu/Δt” module to calculate the rate of change and then processed by the limiting (saturation module) and gain “1” as another input to the fuzzy controller. The fuzzy logic module converts the deviation and the rate of change into control quantities based on preset fuzzy rules (affiliation function, control rules) and the output is amplified by gain “10”. The amplified fuzzy control quantities are fed into the “control” module, which calculates the actual inflow flow (flow in) in combination with the “source flow” (fixed flow characterized by external natural factors). The “water level” module on the right-hand side is used as a water level object model to calculate the real-time water level based on the inflow (flow in) and outflow (flow out) flows, and to output the status of the water level and the overflow flag. Eventually, the water level output is fed back to the deviation calculation module to form a closed-loop control: water level change → deviation and rate of change calculation → fuzzy decision-making → flow adjustment → water level impact, which realizes the stable control of water level through cyclic iteration. The right oscilloscope is used to observe the results.
The coefficients in this model are not arbitrarily chosen; they are obtained through multiple rounds of debugging. This iterative process ensures that the model accurately represents the real-world water level control scenario in the Great Lakes.
The valve subsystem block diagram shown in Figure 10a and the water box system block diagram shown in Figure 10b are integral components of the overall Simulink model.
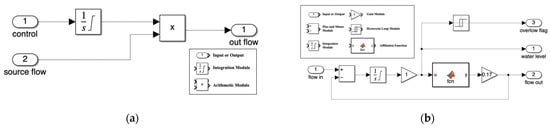
Figure 10.
Subsystem framework: (a) for valve system framework; (b) for affinity function setup for valve.
For the former, the subsystem focuses on valve flow control. Input “control” for the control signal, through the integration module on the control amount of accumulation, reflecting the dynamic adjustment process; “source flow” represents the external base flow input and the integration of the control amount through the arithmetic module processing, the final output of the actual valve outflow flow (out flow), to realize the comprehensive control of the valve flow. The final output of the actual outflow flow of the valve realizes the comprehensive control of the valve flow.
For the latter, the subsystem is used to simulate the dynamic operation of the tank. The difference between the inflow flow rate and the outflow flow rate is accumulated by the integration module to calculate the water level change, and then the real-time water level is output through the gain 1. At the same time, the water level signal is input to the hysteresis loop module to determine whether it is overflowed or not, and the overflow flag is output if it exceeds the threshold. In addition, the relationship between water level and flow is processed through the affiliation function to calculate the outflow flow, and finally the outflow flow is output through the gain 0.17 to form a dynamic equilibrium simulation of inflow, outflow, and water level.
6. Simulation Results
In order to evaluate the performance of the developed water level control model, Simulink simulations are performed in this paper. Without loss of generality, we simulated the control of the two lakes at the optimal water level using Lake Superior and Lake Michigan and Lake Huron as examples, as shown in Figure 11, with time on the horizontal axis and water level change on the vertical axis.
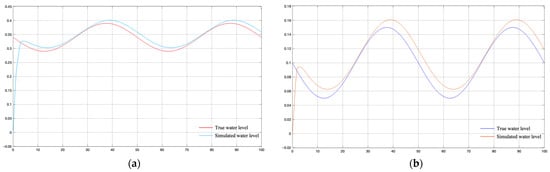
Figure 11.
Simulation results: (a) with Lake Superior as an example; (b) with Lake Michigan and Lake Huron as examples.
The performance of the control algorithm can be derived by observing the curves. Between the two curves at the initial time when the system gradually fits with the real water level takes about T = 5, then the two curves are highly fitted without hysteresis and the difference is basically 0, which indicates that the control algorithm is able to effectively regulate the actual water level to the target water level and keep it stable for a longer period of time.
7. Sensitivity Analysis
In addition to human-made factors such as dam operations, lake levels are also significantly influenced by natural factors. In the spring, as snow and ice melt, water levels rise. In early summer, with increased precipitation, water levels typically reach their peak. However, as surface water temperatures increase, evapotranspiration also rises, causing water levels to drop in the fall. In winter, snow and ice cover parts of the lakes and rivers, and the extent of this coverage and the occurrence of ice jams can further impact water levels.
Since the optimal water level prediction model assumes the effects of non-surface runoff, terms such as groundwater fluxes, evapotranspiration, and precipitation are not considered. Therefore, the external environmental parameters are fixed in the optimal water level control model. In order to account for variations in these natural factors in the water level control model, the effects of natural factors can be reflected by adjusting the natural factor coefficients in the control model. This allows us to analyze the sensitivity of the control algorithm to changes in environmental conditions.
To visualize the sensitivity of the control algorithm, we vary the debugged optimal parameters successively to the values (0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0).
Here, the parameter value represents the harshness of the environment. A smaller value (e.g., 0) indicates a harsher environment, while a larger value (e.g., 1) represents a more stable environment. Keeping other parameters unchanged, we perform Simulink simulations, and the results are shown in Figure 12.
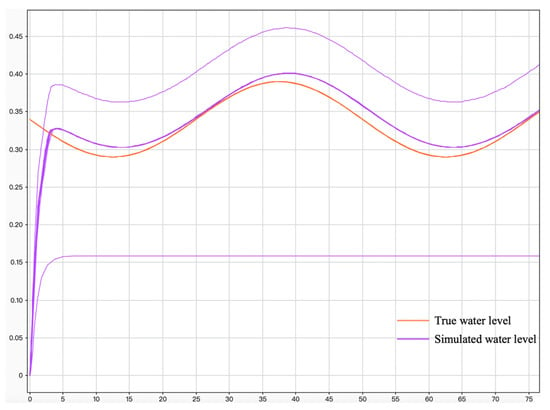
Figure 12.
Sensitivity analysis under external influence.
According to the sensitivity analysis simulation results, the orange color indicates the target optimal water level change, and the purple line indicates the water level change adjusted by the algorithm under parameters 0 to 1, and the horizontal axis is the time. From the analysis of these curves, it can be seen that in the case of extreme external environment (parameters 0, 0.1), the curves have low fit and high sensitivity, and there are two cases of control failure and over-control, i.e., two cases of the graphs are obviously lower than the target optimal water level curve and obviously higher than the target optimal water level curve, which indicates that the algorithm fails to adjust the water level to the optimal water level under the extremely poor environmental conditions The algorithm fails to regulate the water level to the optimal water level under extreme environmental conditions. When the environmental changes are relatively stable (parameter greater than or equal to 0.2), the curve fitting effect is good, hysteresis is low, and the target optimal water level curve and the simulated water level curve are basically coincident, which indicates that the regulation is fast, the sensitivity to environmental changes is low, and the water level can be quickly adjusted to the optimal water level.
8. Conclusions
This study presents a holistic approach to predicting and controlling water levels in the Great Lakes, integrating multi-objective optimization with fuzzy control. Key findings include the following:
- Network flow model: The paraboloid-based lake volume equations and interconnected flow dynamics effectively capture seasonal and spatial variations, validated by stationarity and normality tests. The model successfully quantified the interdependencies between lakes and rivers, enabling accurate predictions of water volume changes (e.g., Lake Superior’s volume fluctuated within ±0.6096 m of the target levels), which aligns with the objectives of balancing ecological and economic needs.
- Stakeholder balancing: The hybrid Ford–Fulkerson and simulated annealing algorithm resolves conflicting objectives, achieving near-optimal flow rates (e.g., 75.15 m for Lake Ontario in June) while limiting fluctuations to ±0.6096 m. This approach outperforms traditional single-objective models by simultaneously maximizing hydropower generation (hydroelectric companies’ demand) and minimizing water level volatility (stakeholders’ stability needs), as demonstrated by rapid convergence (T = five time units) in simulations.
- Fuzzy control: The Mamdani-based controller adapts to deviations and environmental factors, demonstrating rapid convergence (T = 5) and resilience under moderate disturbances (parameter ≥ 0.2). Compared to previous studies relying on static control strategies, this dynamic fuzzy system adjusts gate openings in real time, ensuring stability even during seasonal variations (e.g., ice melt in spring and evapotranspiration in summer).
To enhance the applicability and transparency of the framework, Table 5 summarizes the key parameters, optimization results, and stakeholder priorities for each lake. The table highlights the interdependencies between hydrological characteristics, operational constraints, and stakeholder demands, demonstrating the model’s adaptability to diverse conditions within the Great Lakes system.

Table 5.
Summary of lake-specific parameters, optimization results, and stakeholder interactions.
In contrast to past studies, which focused on hydrologic modeling (e.g., seasonal water supply prediction) or stakeholder preferences (e.g., navigational demand), there is a lack of integrated optimal water level solutions as well as optimal water level control solutions. This study bridges these gaps by combining multi-objective optimization to balance hydropower maximization, ecological stability, and stakeholder needs, and by introducing a fuzzy control algorithm to adaptively regulate dam operations. This integrated approach addresses the limitations of previous work that emphasized predictive modeling or static control strategies rather than dynamic stakeholder-centric solutions.
Although this study enhances adaptability through parameter tuning and fuzzy control, limitations remain: (1) The model assumes stable environmental conditions and therefore ignores the effects of groundwater flux, evapotranspiration, and precipitation. Even though the parameter effects of natural factors were included in the sensitivity analysis, these factors were only as a whole, and the effects of these factors were not quantitatively studied. Future studies can incorporate the effects of these factors. (2) The sensitivity analysis shows that the control effect decreases in extreme environments (parameter < 0.2), and future studies can incorporate machine learning, such as hybrid CNN-LSTM models, to optimize real-time parameter tuning. (3) The coverage of stakeholders is not yet comprehensive enough, and to simplify the model, this study appropriately reduces the stakeholder analysis. The study only focuses on the main stakeholders, and future research can incorporate the needs of aboriginal communities and local industries.
In conclusion, this research offers a scalable and adaptable template for managing complex hydrological systems. The integration of computational algorithms with ecological sustainability considerations is a step forward in addressing the challenges faced by the Great Lakes and other similar large-scale water bodies. By building on the results of this study and exploring the proposed future directions, we can move towards more effective and sustainable water level management practices.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/su17083690/s1.
Author Contributions
Conceptualization, R.O., Y.W. and K.G.; methodology, R.O.; software, R.O. and Q.L.; validation, Q.G.; formal analysis, R.O.; investigation, X.L.; resources, Y.W. and K.G.; data curation, X.L.; writing—original draft preparation, R.O.; writing—review and editing, X.L.; visualization, X.L.; supervision, K.G.; project administration, K.G.; funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
The Fundamental Research Funds for the Central Universities under Grant No. GK122401320.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article and Supplementary Materials.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Watras, C.J.; Heald, E.; Teng, H.Y.; Rubsam, J.; Asplund, T. Extreme water level rise across the upper Laurentian Great Lakes region: Citizen science documentation 2010–2020. J. Great Lakes Res. 2022, 48, 1135–1139. [Google Scholar] [CrossRef]
- Houser, C.; Arbex, M.; Trudeau, C. Short communication: Economic impact of drowning in the Great Lakes Region of North America. Ocean Coast. Manag. 2021, 212, 105847. [Google Scholar] [CrossRef]
- Carlson, A.K.; Leonard, N.J.; Munawar, M.; Taylor, W.W. Assessing and implementing the concept of Blue Economy in Laurentian Great Lakes fisheries: Lessons from coupled human and natural systems. Aquat. Ecosyst. Health Manag. 2024, 27, 74–84. [Google Scholar] [CrossRef]
- Ives, J.T.; McMeans, B.C.; McCann, K.S.; Fisk, A.T.; Johnson, T.B.; Bunnell, D.B.; Frank, K.T.; Muir, A.M. Food-web structure and ecosystem function in the Laurentian Great Lakes—Toward a conceptual model. Freshw. Biol. 2018, 64, 1–23. [Google Scholar] [CrossRef]
- Deting, Y.; Qian, Y.; Yi, S. Spatial Aggregation Within the Population and the Upgrading of Traditional Industries in the Great Lakes Megalopolis. J. Beijing Adm. Inst. 2022, 2, 89–99. [Google Scholar] [CrossRef]
- Notaro, M.; Zhong, Y.F.; Xue, P.F.; Peters-Lidard, C.; Cruz, C.; Kemp, E.; Kristovich, D.; Kulie, M.; Wang, J.M.; Huang, C.F.; et al. Cold Season Performance of the NU-WRF Regional Climate Model in the Great Lakes Region. J. Hydrometeorol. 2021, 22, 2423–2454. [Google Scholar] [CrossRef]
- Bergstrom, R.D.; Johnson, L.B.; Sterner, R.W.; Bullerjahn, G.S.; Fergen, J.T.; Lenters, J.D.; Norris, P.E.; Steinman, A.D. Building a research network to better understand climate governance in the Great Lakes. J. Great Lakes Res. 2022, 48, 1329–1336. [Google Scholar] [CrossRef]
- Hameed, M.M.; Razali, S.F.M.; Mohtar, W.H.M.W.; Rahman, N.A.; Yaseen, Z.M. Machine learning models development for accurate multi-months ahead drought forecasting: Case study of the Great Lakes, North America. PLoS ONE 2023, 18, e0290891. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, J.L.; Qian, Y.; Chakraborty, T.C.; Xue, P.F.; Pringle, W.J.; Huang, C.F.; Kayastha, M.B.; Huang, H.L.; Li, J.F.; et al. Summer Convective Precipitation Changes Over the Great Lakes Region Under a Warming Scenario. J. Geophys. Res. Atmos. 2024, 129, e2024JD041011. [Google Scholar] [CrossRef]
- Philip, E.; Rudra, R.P.; Goel, P.K.; Ahmed, S.I. Investigation of the Long-Term Trends in the Streamflow Due to Climate Change and Urbanization for a Great Lakes Watershed. Atmosphere 2022, 13, 225. [Google Scholar] [CrossRef]
- Shen, Z. Review on the Impact of Climate Change on Great Lakes Region’s Agriculture and Water Resources. J. Geosci. Environ. Prot. 2024, 12, 165–176. [Google Scholar]
- Soonthornrangsan, J.T.; Lowry, C.S. Vulnerability of water resources under a changing climate and human activity in the lower Great Lakes region. Hydrol. Process. 2021, 35, e14440. [Google Scholar] [CrossRef]
- Yang, H.; Du, Z.; Zheng, Q. Optimal Water Level Study Based on Great Lakes Water Issues. Environ. Resour. Ecol. J. 2024, 8, 35–44. [Google Scholar]
- Qi, W.; Tang, Z. Dynamic Regulation of Great Lakes Water Levels Using Multiple Model Algorithms. Acad. J. Comput. Inf. Sci. 2024, 7, 140–146. [Google Scholar]
- Zhang, X.; Li, Y.; Shi, K. A New Optimal Water Level Evaluation Strategy of the Great Lakes. World Sci. Res. J. 2024, 10, 23–31. [Google Scholar]
- Fry, L.M.; Apps, D.; Gronewold, A.D. Operational Seasonal Water Supply and Water Level Forecasting for the Laurentian Great Lakes. J. Water Resour. Plan. Manag. 2020, 146, 04020072. [Google Scholar] [CrossRef]
- Bergmann-Baker, U.; Brotton, J.; Wall, G. Socio-Economic Impacts of Fluctuating Water Levels on Recreational Boating in the Great Lakes. Can. Water Resour. J. 1995, 20, 185–194. [Google Scholar] [CrossRef][Green Version]
- Wright, D.A.; Mitchelmore, C.L.; Place, A.; Williams, E.; Orano-Dawson, C. Genomic and Microscopic Analysis of Ballast Water in the Great Lakes Region. Appl. Sci. 2019, 9, 2441. [Google Scholar] [CrossRef]
- Tang, A.C.I.; Bohrer, G.; Malhotra, A.; Missik, J.; Machado-Silva, F.; Forbrich, I. Rising Water Levels and Vegetation Shifts Drive Substantial Reductions in Methane Emissions and Carbon Dioxide Uptake in a Great Lakes Coastal Freshwater Wetland. Glob. Change Biol. 2025, 31, e70053. [Google Scholar] [CrossRef]
- Anderson, O.; Harrison, A.; Heumann, B.; Godwin, C.; Uzarski, D. The influence of extreme water levels on coastal wetland extent across the Laurentian Great Lakes. Sci. Total Environ. 2023, 885, 163755. [Google Scholar] [CrossRef]
- Hohman, T.R.; Howe, R.W.; Tozer, D.C.; Giese, E.E.G.; Wolf, A.T.; Niemi, G.J.; Gehring, T.M.; Grabas, G.P.; Norment, C.J. Influence of lake levels on water extent, interspersion, and marsh birds in Great Lakes coastal wetlands. J. Great Lakes Res. 2021, 47, 534–545. [Google Scholar] [CrossRef]
- Herath, M.; Jayathilaka, T.; Hoshino, Y.; Rathnayake, U. Deep Machine Learning-Based Water Level Prediction Model for Colombo Flood Detention Area. Appl. Sci. 2023, 13, 2194. [Google Scholar] [CrossRef]
- Fijani, E.; Khosravi, K. Hybrid Iterative and Tree-Based Machine Learning Algorithms for Lake Water Level Forecasting. Water Resour. Manag. 2023, 37, 5431–5457. [Google Scholar] [CrossRef]
- Kayastha, M.B.; Ye, X.Y.; Huang, C.F.; Xue, P.F. Future rise of the Great Lakes water levels under climate change. J. Hydrol. 2022, 612, 128205. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Coupling a hybrid CNN-LSTM deep learning model with a Boundary Corrected Maximal Overlap Discrete Wavelet Transform for multiscale Lake water level forecasting. J. Hydrol. 2021, 598, 126196. [Google Scholar] [CrossRef]
- Chen, W.; Shum, C.K.; Forootan, E.; Feng, W.; Zhong, M.; Jia, Y.; Li, W.; Guo, J.; Wang, C.; Li, Q.; et al. Understanding Water Level Changes in the Great Lakes by an ICA-Based Merging of Multi-Mission Altimetry Measurements. Remote Sens. 2022, 14, 5194. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, S.; Liu, A. Great lakes basin model based on physical flow and Data-Driven. J. Phys. Conf. Ser. 2024, 2865, 012019. [Google Scholar] [CrossRef]
- Lin, H. Simulation of lake system based on multi-objective optimization algorithm and system dynamics model. Acad. J. Comput. Inf. Sci. 2024, 7, 21–26. [Google Scholar]
- Kurt, O. Model-based prediction of water levels for the Great Lakes: A comparative analysis. Earth Sci. Inform. 2024, 17, 3333–3349. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).