Analysis of Factors Affecting Electric Vehicle Range Estimation: A Case Study of the Eskisehir Osmangazi University Campus
Abstract
1. Introduction
- It focuses on the energy consumption and remaining range estimation for a small three-wheeled electric vehicle designed for use in last-mile delivery logistics. In this context, it aims to determine the critical role of such vehicles in energy management and to increase the sustainability of logistics operations.
- In order to systematically observe the effects of slope, speed, load, and acceleration factors on energy consumption, an experimental design is established. The effects of particular factors that cause energy consumption are examined.
- Experiments are carried out with an electric vehicle used in real-life cargo delivery. This implementation increases the validity of the research by verifying the designed experiment in real-life conditions and helping to observe the effects of driving dynamics and environmental factors.
- The effects of slope, speed, load, and acceleration factors on energy consumption are statistically analyzed. The separate effects of each factor are explained, and ideas about the vehicle’s energy consumption and the estimation of the remaining range are presented.
- As one of the rare studies in the literature investigating the effect of the characteristics of small-scale regions on energy consumption, it emphasizes the effect of local factors on electric vehicle performance.
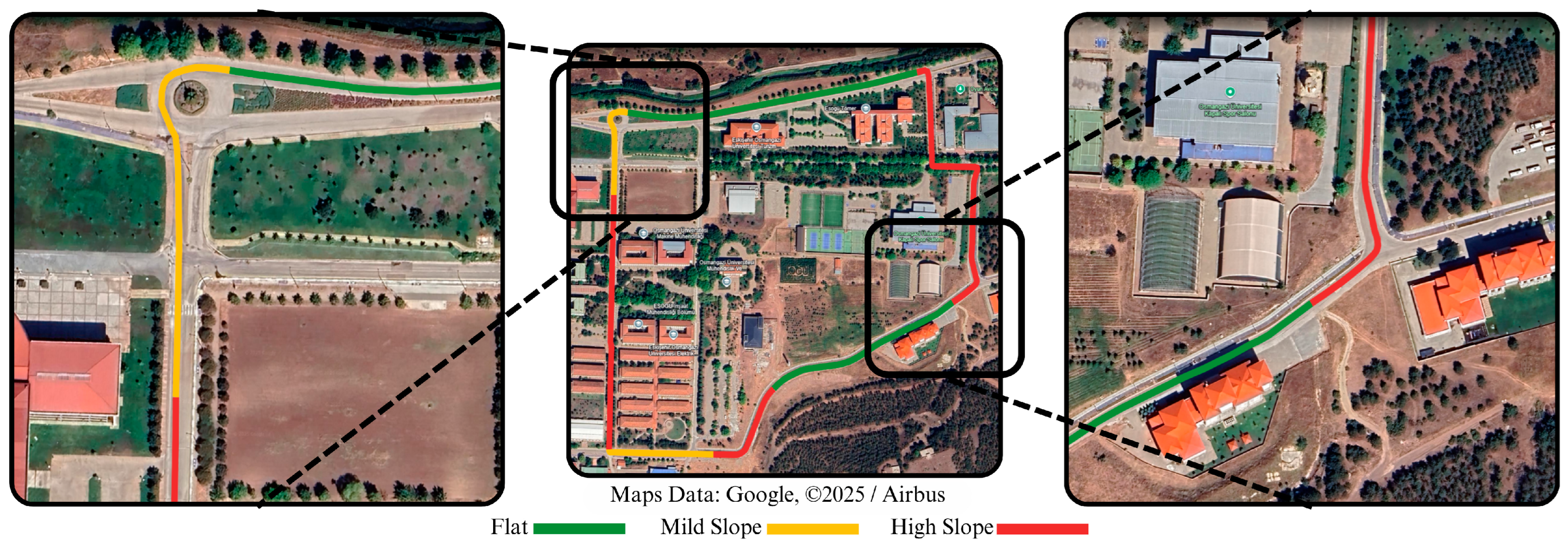
- In this context, the energy consumption analysis is carried out by focusing on shorter road segments with an average length of 150 m. This approach allows the dynamic changes in driving conditions and their immediate effects on energy consumption to be realized more precisely. For each road segment, the energy consumption is calculated using the State of Charge (SoC) value of the battery at the starting and ending points of the road segment. The relationship of energy consumption with specific factors in each segment provides valuable information about how these factors affect energy consumption and range. The remainder of the paper is organized as follows: Section 2 presents the related works, focusing on factors and algorithms used in the prediction of energy consumption and range estimation of electric vehicles. The dataset and the methodology used in the study are given in Section 3. Section 4 presents the experimental results and identifies the factors affecting the prediction of range. Finally, the discussions, conclusions, and suggestions for future work are presented in Section 5.
2. Related Studies
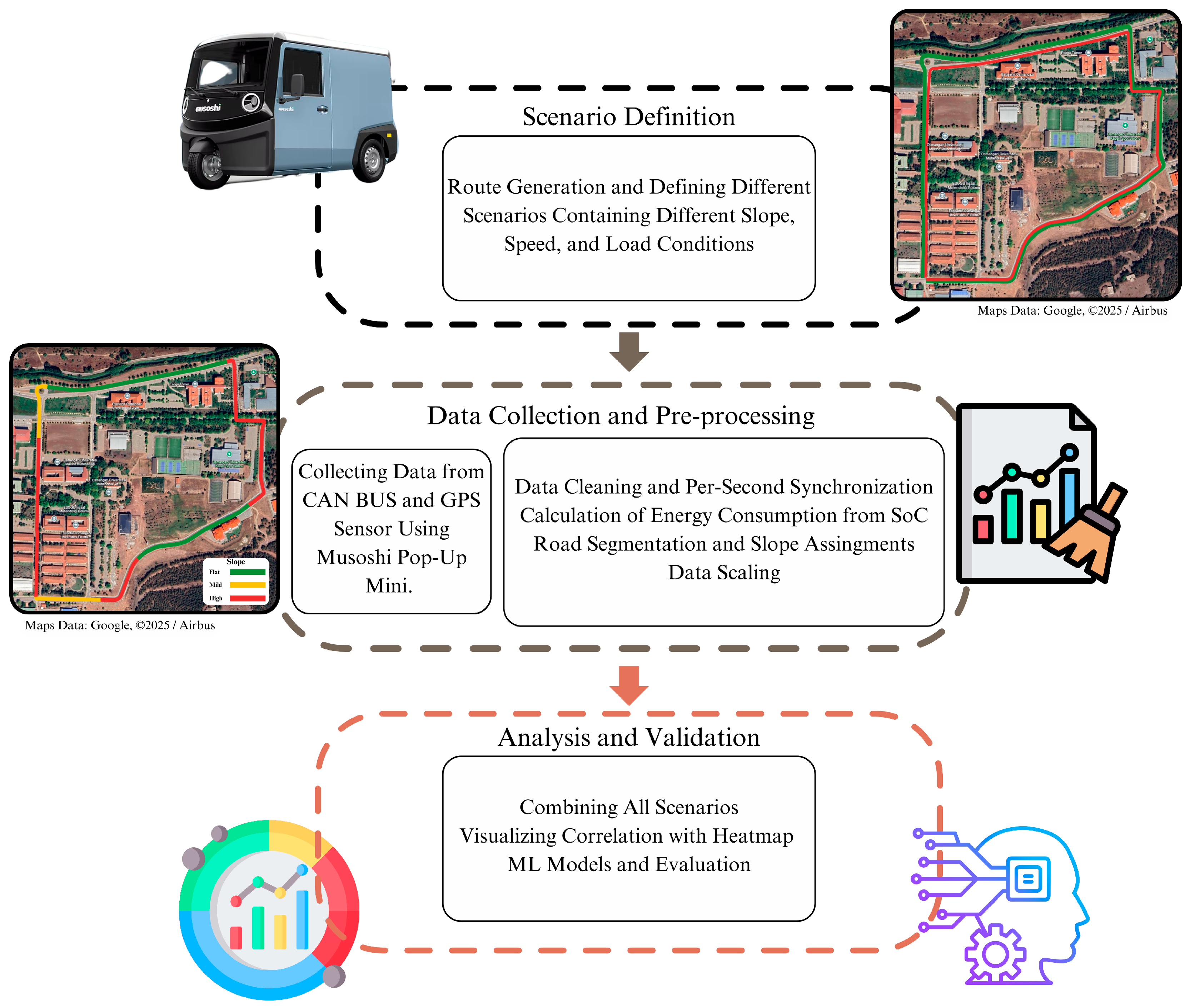
3. Materials and Methods
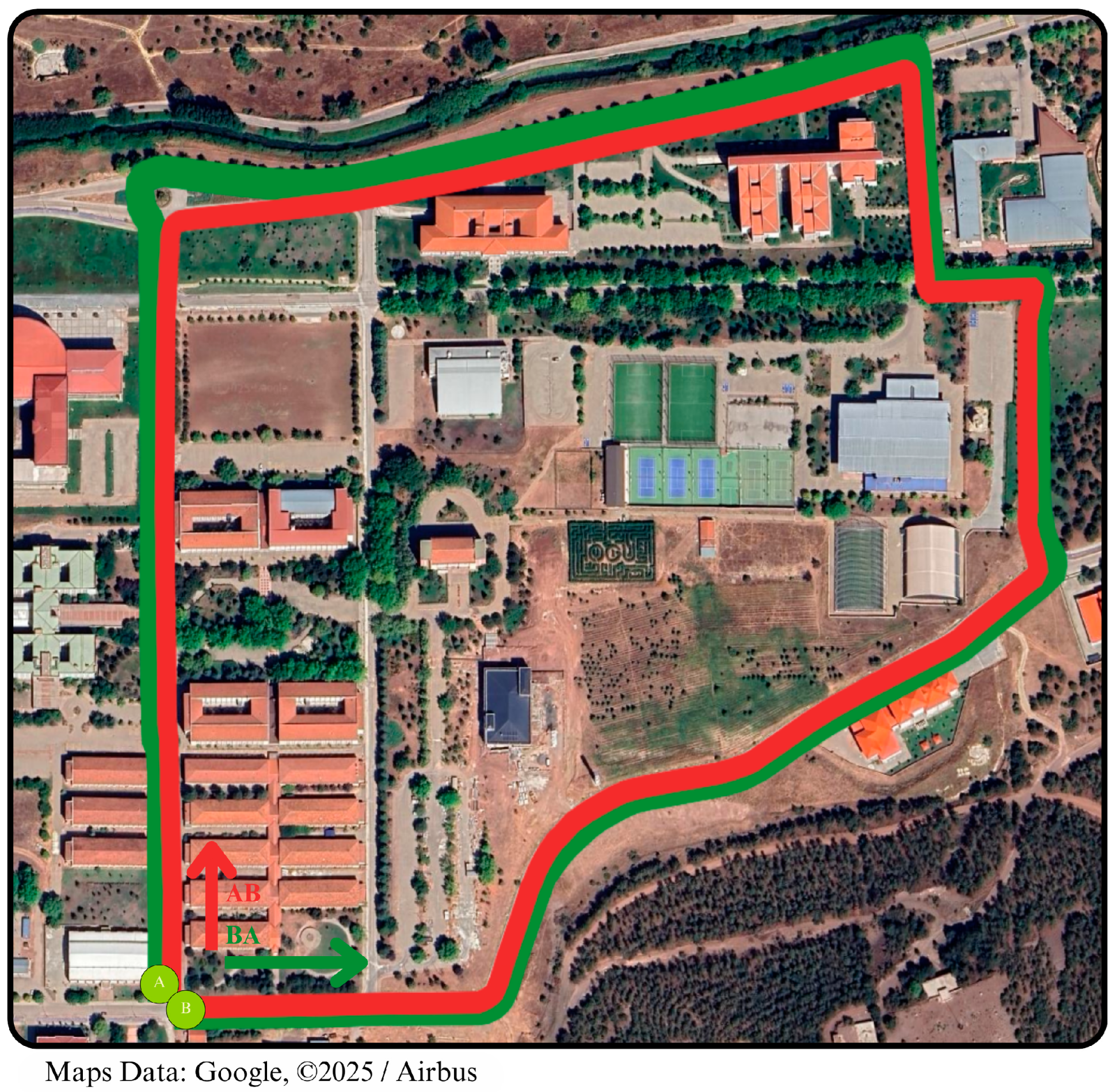
3.1. Scenario Definition
3.2. Data Collection and Pre-Processing
3.3. Analysis and Validation
3.3.1. Analysis of Factors for Energy Consumption
3.3.2. Validation of Range Estimation
4. Experimental Results
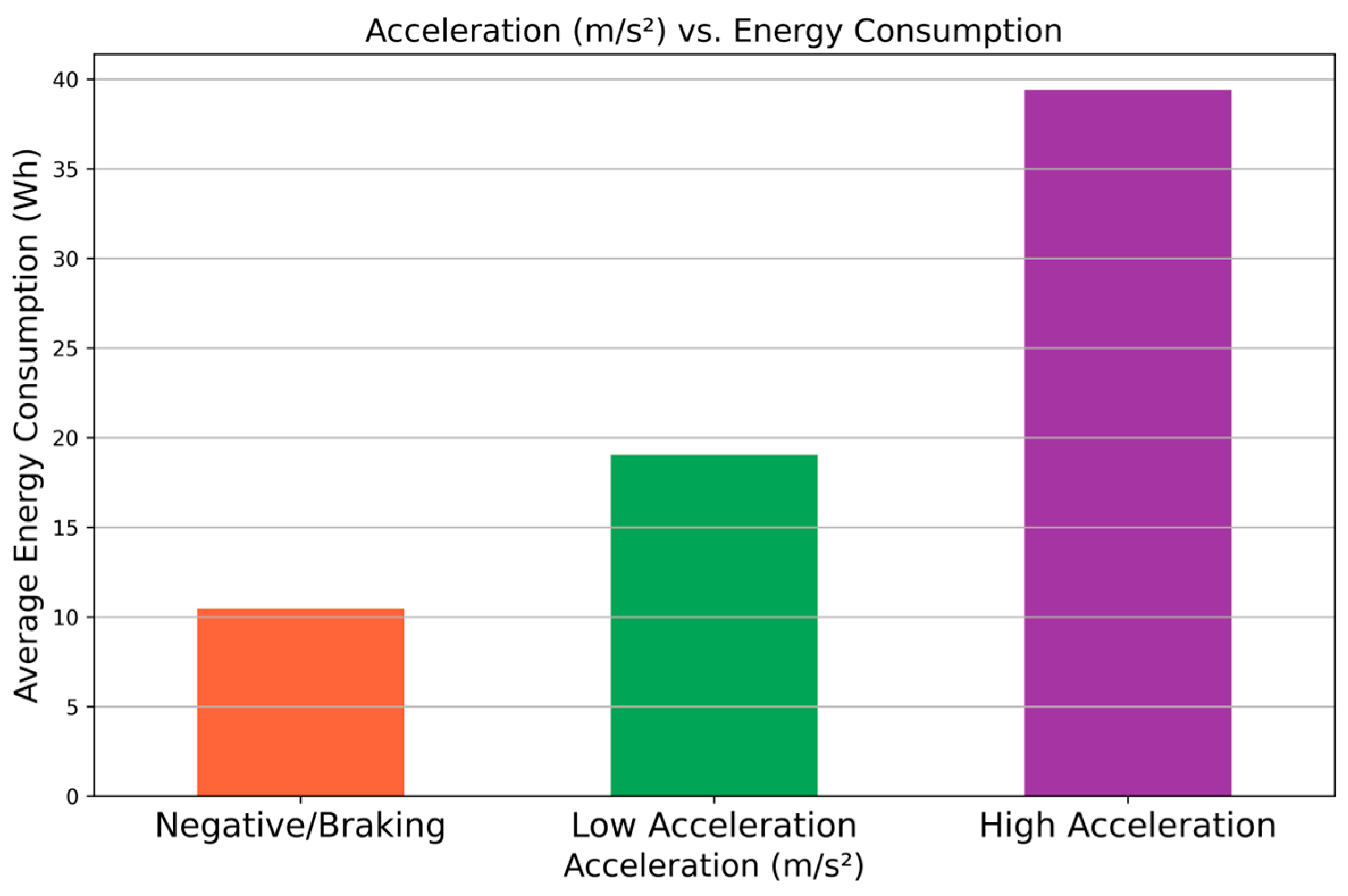
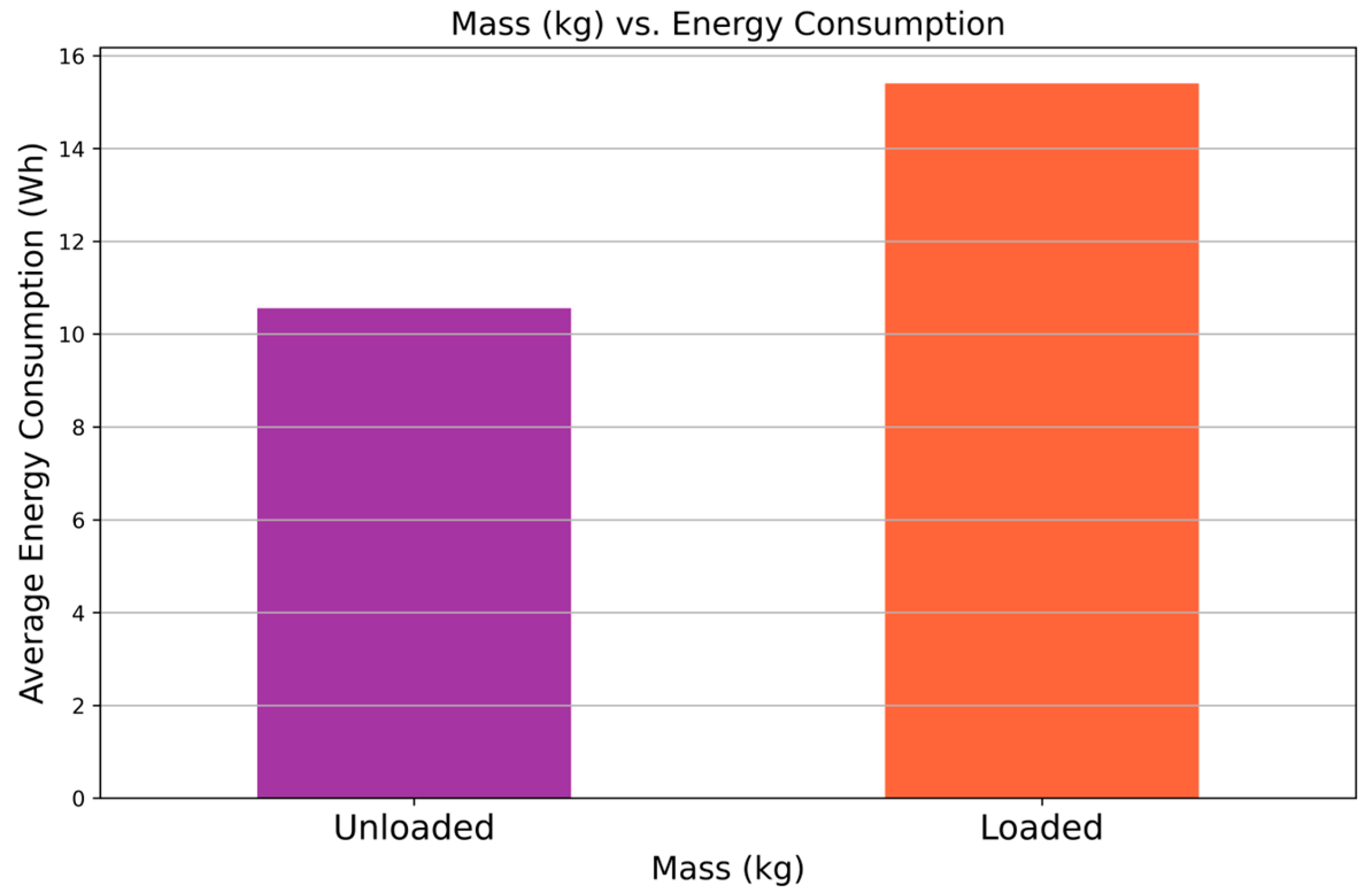
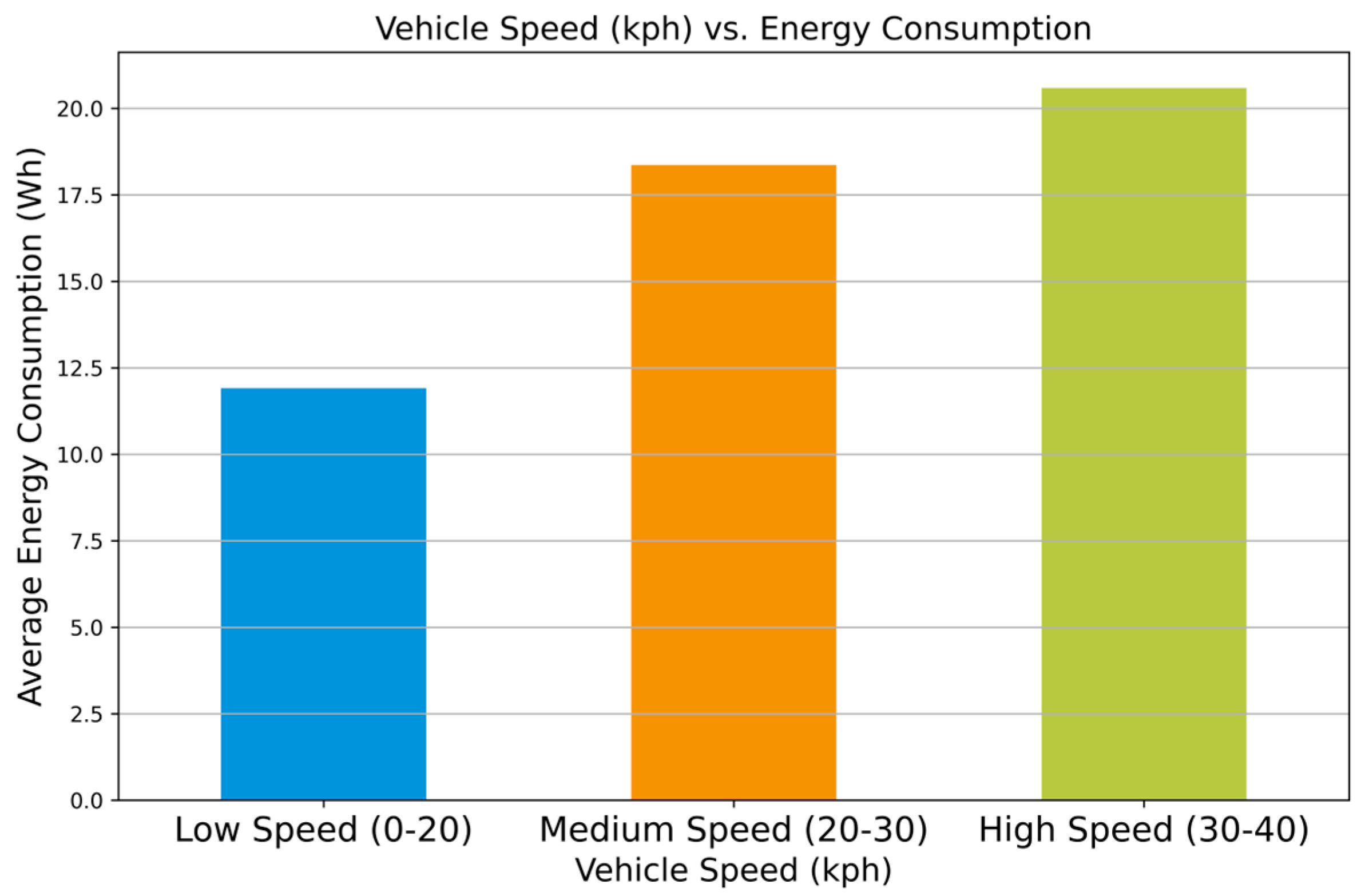
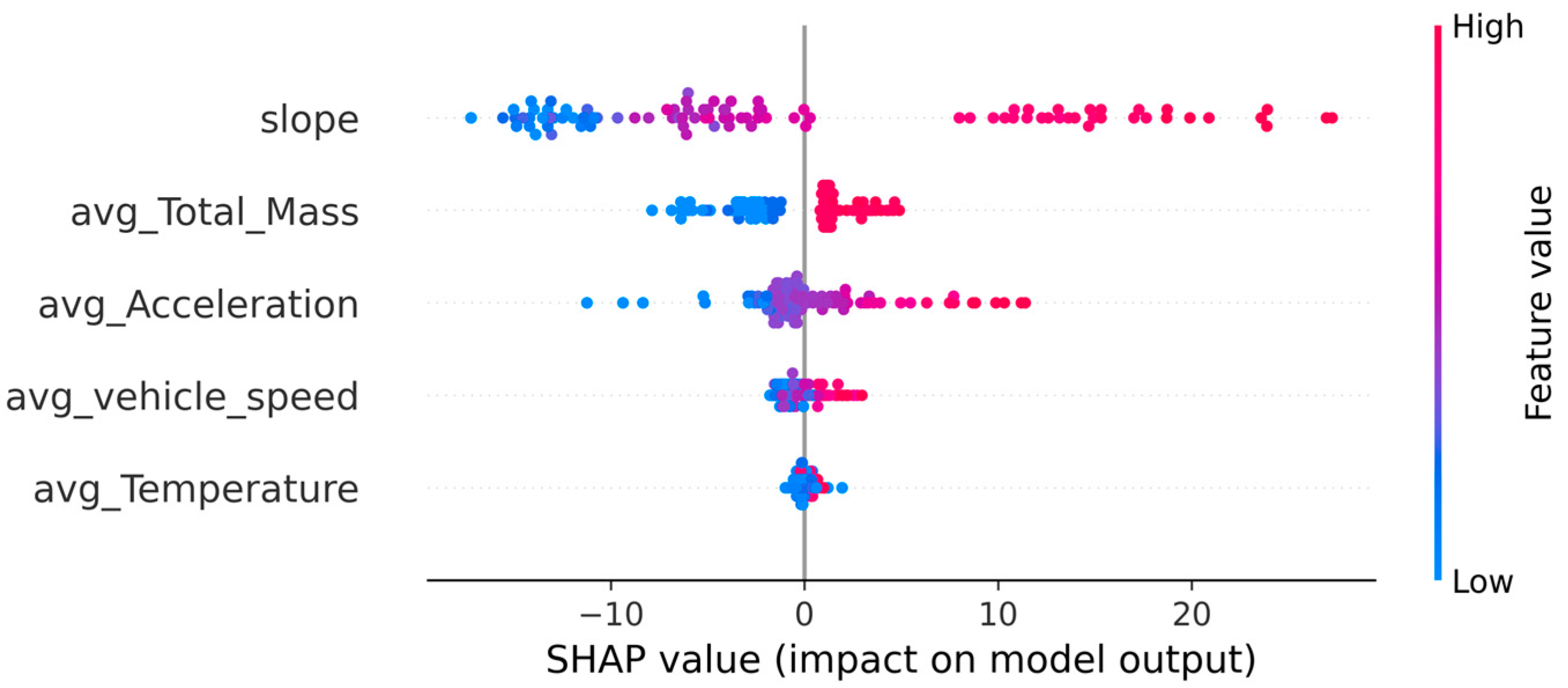
4.1. Analysis of Factors
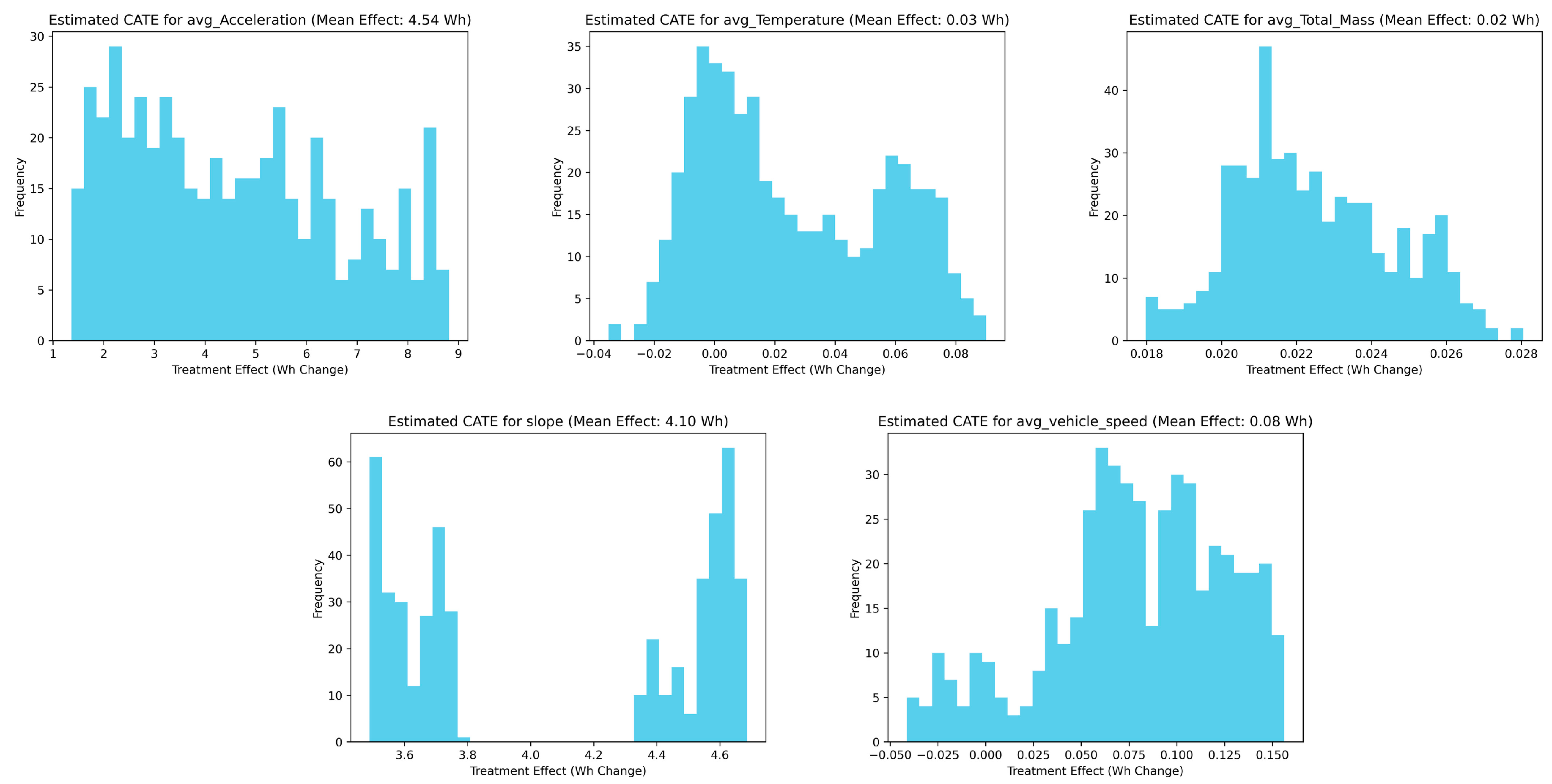
4.2. Estimation of Energy Consumption and Range
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Coignard, J.; MacDougall, P.; Stadtmueller, F.; Vrettos, E. Will Electric Vehicles Drive Distribution Grid Upgrades?: The Case of California. IEEE Electrif. Mag. 2019, 7, 46–56. [Google Scholar]
- Qadir, S.A.; Ahmad, F.; Al-Wahedi, A.M.A.B.; Iqbal, A.; Ali, A. Navigating the complex realities of electric vehicle adoption: A comprehensive study of government strategies, policies, and incentives. Energy Strat. Rev. 2024, 53, 101379. [Google Scholar]
- Ghosh, A. Possibilities and Challenges for the Inclusion of the Electric Vehicle (EV) to Reduce the Carbon Footprint in the Transport Sector: A Review. Energies 2020, 13, 2602. [Google Scholar] [CrossRef]
- Richardson, D.B. Electric vehicles and the electric grid: A review of modeling approaches, Impacts, and renewable energy integration. Renew. Sustain. Energy Rev. 2013, 19, 247–254. [Google Scholar]
- Weldon, P.; Morrissey, P.; O’mahony, M. Long-term cost of ownership comparative analysis between electric vehicles and internal combustion engine vehicles. Sustain. Cities Soc. 2018, 39, 578–591. [Google Scholar]
- Rauh, N.; Franke, T.; Krems, J.F. Understanding the Impact of Electric Vehicle Driving Experience on Range Anxiety. Hum. Factors J. Hum. Factors Ergon. Soc. 2015, 57, 177–187. [Google Scholar]
- Liu, Q.; Zhang, Z.; Zhang, J. Research on the interaction between energy consumption and power battery life during electric vehicle acceleration. Sci. Rep. 2024, 14, 157. [Google Scholar]
- Liu, K.; Yamamoto, T.; Morikawa, T. Impact of road gradient on energy consumption of electric vehicles. Transp. Res. Part D Transp. Environ. 2017, 54, 74–81. [Google Scholar]
- Abousleiman, R.; Rawashdeh, O. Energy Consumption Model of an Electric Vehicle. In Proceedings of the 2015 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 14–17 June 2015; pp. 1–5. [Google Scholar]
- Brady, J.; O’Mahony, M. Travel to Work in Dublin. The Potential Impacts of Electric Vehicles on Climate Change and Urban Air Quality. Transp. Res. D Transp. Environ. 2011, 16, 188–193. [Google Scholar]
- Neubauer, J.; Wood, E. The impact of range anxiety and home, workplace, and public charging infrastructure on simulated battery electric vehicle lifetime utility. J. Power Sources 2014, 257, 12–20. [Google Scholar]
- Vaz, W.; Nandi, A.K.; Landers, R.G.; Koylu, U.O. Electric vehicle range prediction for constant speed trip using multi-objective optimization. J. Power Sources 2015, 275, 435–446. [Google Scholar] [CrossRef]
- Hong, J.; Park, S.; Chang, N. Accurate Remaining Range Estimation for Electric Vehicles. In Proceedings of the 2016 21st Asia and South Pacific Design Automation Conference (ASP-DAC), Macao, China, 25–28 January 2016; pp. 781–786. [Google Scholar]
- Sarrafan, K.; Sutanto, D.; Muttaqi, K.M.; Town, G. Accurate range estimation for an electric vehicle including changing environmental conditions and traction system efficiency. IET Electr. Syst. Transp. 2017, 7, 117–124. [Google Scholar] [CrossRef]
- Helmbrecht, M.; Olaverri-Monreal, C.; Bengler, K.; Vilimek, R.; Keinath, A. How Electric Vehicles Affect Driving Behavioral Patterns. IEEE Intell. Transp. Syst. Mag. 2014, 6, 22–32. [Google Scholar]
- Kurczveil, T.; López, P.Á.; Schnieder, E. Implementation of an Energy Model and a Charging Infrastructure in SUMO. In Proceedings of the Simulation of Urban Mobility: First International Conference, SUMO 2013, Berlin, Germany, 15–17 May 2013; Revised Selected Papers 1. Springer: Berlin/Heidelberg, Germany, 2014; pp. 33–43. [Google Scholar]
- Pan, Y.; Fang, W.; Zhang, W. Development of an energy consumption prediction model for battery electric vehicles in real-world driving: A combined approach of short-trip segment division and deep learning. J. Clean. Prod. 2023, 400, 136742. [Google Scholar] [CrossRef]
- Yao, E.; Yang, Z.; Song, Y.; Zuo, T. Comparison of Electric Vehicle’s Energy Consumption Factors for Different Road Types. Discret. Dyn. Nat. Soc. 2013, 2013, 328757. [Google Scholar] [CrossRef]
- Zhang, R.; Yao, E. Electric vehicles’ energy consumption estimation with real driving condition data. Transp. Res. Part D Transp. Environ. 2015, 41, 177–187. [Google Scholar] [CrossRef]
- Amirkhani, A.; Haghanifar, A.; Mosavi, M.R. Electric Vehicles Driving Range and Energy Consumption Investigation: A Comparative Study of Machine Learning Techniques. In Proceedings of the 2019 5th Iranian Conference on Signal Processing and Intelligent Systems (ICSPIS), Shahrood, Iran, 18–19 December 2019; pp. 1–6. [Google Scholar]
- Fetene, G.M.; Kaplan, S.; Mabit, S.L.; Jensen, A.F.; Prato, C.G. Harnessing big data for estimating the energy consumption and driving range of electric vehicles. Transp. Res. Part D Transp. Environ. 2017, 54, 1–11. [Google Scholar]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Tiwary, A.; Mishra, S.; Kumar, U. Electric Vehicle Range Estimation Based on Driving Behaviour Employing Long Short-Term Memory Neural Network. In Proceedings of the 2024 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Ischia, Italy, 19–21 June 2024; pp. 551–555. [Google Scholar]
- Huang, H.; Li, B.; Wang, Y.; Zhang, Z.; He, H. Analysis of Factors Influencing Energy Consumption of Electric Vehicles: Statistical, Predictive, and Causal Perspectives. Appl. Energy 2024, 375, 124110. [Google Scholar]
- Gurusamy, A.; Bokdia, A.; Kumar, H.; Ashok, B.; Gunavathi, C. Appositeness of automated machine learning libraries on prediction of energy consumption for electric two-wheelers based on micro-trip approach. Energy 2025, 320, 135199. [Google Scholar] [CrossRef]
- Yılmaz, M.; Çinar, E.; Yazıcı, A. A Transformer-Based Model for State of Charge Estimation of Electrical Vehicle Batteries. IEEE Access 2025, 13, 33035–33048. [Google Scholar]
- Lee, C.-H.; Wu, C.-H. A Novel Big Data Modeling Method for Improving Driving Range Estimation of EVs. IEEE Access 2015, 3, 1980–1993. [Google Scholar] [CrossRef]
- Sarrafan, K.; Muttaqi, K.M.; Sutanto, D.; Town, G.E. A Real-Time Range Indicator for EVs Using Web-Based Environmental Data and Sensorless Estimation of Regenerative Braking Power. IEEE Trans. Veh. Technol. 2018, 67, 4743–4756. [Google Scholar]
- Çeven, S.; Albayrak, A.; Bayır, R. Real-time range estimation in electric vehicles using fuzzy logic classifier. Comput. Electr. Eng. 2020, 83, 106577. [Google Scholar]
- Rhode, S.; Van Vaerenbergh, S.; Pfriem, M. Power prediction for electric vehicles using online machine learning. Eng. Appl. Artif. Intell. 2020, 87, 103278. [Google Scholar]
- Zhao, L.; Yao, W.; Wang, Y.; Hu, J. Machine Learning-Based Method for Remaining Range Prediction of Electric Vehicles. IEEE Access 2020, 8, 212423–212441. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Zamee, M.A.; Han, D.; Cha, H.; Won, D. Self-supervised online learning algorithm for electric vehicle charging station demand and event prediction. J. Energy Storage 2023, 71, 108189. [Google Scholar]
- Dong, Z.; Ji, X.; Wang, J.; Gu, Y.; Wang, J.; Qi, D. ICNCS: Internal Cascaded Neuromorphic Computing System for Fast Electric Vehicle State-of-Charge Estimation. IEEE Trans. Consum. Electron. 2023, 70, 4311–4320. [Google Scholar]
- Selvaraj, V.; Vairavasundaram, I. A Bayesian optimized machine learning approach for accurate state of charge estimation of lithium ion batteries used for electric vehicle application. J. Energy Storage 2024, 86, 111321. [Google Scholar] [CrossRef]
- Mishra, D.P.; Kumar, P.; Rai, P.; Kumar, A.; Salkuti, S.R. Exploratory data analysis for electric vehicle driving range prediction: Insights and evaluation. Int. J. Appl. Power Eng. 2024, 13, 474–482. [Google Scholar] [CrossRef]
- Topić, J.; Škugor, B.; Deur, J. Neural Network-Based Modeling of Electric Vehicle Energy Demand and All Electric Range. Energies 2019, 12, 1396. [Google Scholar] [CrossRef]
- Varga, B.O.; Sagoian, A.; Mariasiu, F. Prediction of Electric Vehicle Range: A Comprehensive Review of Current Issues and Challenges. Energies 2019, 12, 946. [Google Scholar] [CrossRef]
- López, F.C.; Fernández, R.Á. Predictive model for energy consumption of battery electric vehicle with consideration of self-uncertainty route factors. J. Clean. Prod. 2020, 276, 124188. [Google Scholar]
- Miri, I.; Fotouhi, A.; Ewin, N. Electric vehicle energy consumption modelling and estimation—A case study. Int. J. Energy Res. 2021, 45, 501–520. [Google Scholar]
- Ullah, I.; Liu, K.; Yamamoto, T.; Zahid, M.; Jamal, A. Electric vehicle energy consumption prediction using stacked generalization: An ensemble learning approach. Int. J. Green Energy 2021, 18, 896–909. [Google Scholar]
- Kocaarslan, I.; Zehir, M.A.; Uzun, E.; Uzun, E.C.; Korkmaz, M.E.; Cakiroglu, Y. High-Fidelity Electric Vehicle Energy Consumption Modelling and Investigation of Factors in Driving on Energy Consumption. In Proceedings of the 2022 4th Global Power, Energy and Communication Conference (GPECOM), Cappadocia, Turkey, 14–17 June 2022; pp. 227–231. [Google Scholar]
- Sun, L.; An, X.; Geng, P.; Geng, Y. Energy Consumption Evaluation of an Electric Vehicle Under Different Driving Conditions. In Proceedings of the 2023 7th International Conference on Power and Energy Engineering (ICPEE), Chengdu, China, 22–24 December 2023; pp. 229–234. [Google Scholar]
- Achariyaviriya, W.; Wongsapai, W.; Janpoom, K.; Katongtung, T.; Mona, Y.; Tippayawong, N.; Suttakul, P. Estimating Energy Consumption of Battery Electric Vehicles Using Vehicle Sensor Data and Machine Learning Approaches. Energies 2023, 16, 6351. [Google Scholar] [CrossRef]
- Yılmaz, H.; Yagmahan, B. Electric vehicle energy consumption prediction for unknown route types using deep neural networks by combining static and dynamic data. Appl. Soft Comput. 2024, 167, 112336. [Google Scholar]
- Wang, L.; Yang, Y.; Zhang, K.; Liu, Y.; Zhu, J.; Dang, D. Enhancing Electric Vehicle Energy Consumption Prediction: Integrating Elevation into Machine Learning Model. In Proceedings of the 2024 IEEE Intelligent Vehicles Symposium (IV), Jeju Island, Republic of Korea, 2–5 June 2024; pp. 2936–2941. [Google Scholar]
- Gioldasis, C.; Christoforou, Z.; Katsiadrami, A. Usage factors influencing e-scooter energy consumption: An empirical investigation. J. Clean. Prod. 2024, 452, 142165. [Google Scholar]
- Kozłowski, E.; Wiśniowski, P.; Gis, M.; Zimakowska-Laskowska, M.; Borucka, A. Vehicle Acceleration and Speed as Factors Determining Energy Consumption in Electric Vehicles. Energies 2024, 17, 4051. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely Randomized Trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. arXiv 2017, arXiv:1706.09516. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- ESOGU-ML5EV Dataset (v1.0.0). Zenodo. Available online: https://doi.org/10.5281/zenodo.14912892 (accessed on 10 January 2025).



| RW | Slope | Acceleration | Speed | Load | Model |
|---|---|---|---|---|---|
| Topić, Škugor, and Deur, 2019 [37] | √ | √ | DD | ||
| Varga, Sagoian, and Mariasiu 2019 [38] | √ | √ | √ | √ | DD |
| López and Fernández, 2020 [39] | √ | PM | |||
| Miri, Fotouhi, and Ewin, 2021 [40] | √ | √ | √ | √ | PM, DD |
| Ullah, Liu, Yamamoto, Zahid, and Jamal, 2021 [41] | √ | √ | √ | DD | |
| Kocaarslan et al., 2022 [42] | √ | √ | √ | √ | PM |
| Sun, An, Geng, and Geng, 2023 [43] | √ | √ | PM | ||
| Achariyaviriya et al., 2023 [44] | √ | √ | √ | DD | |
| Yılmaz and Yagmahan, 2024 [45] | √ | √ | √ | DD | |
| Wang et al., 2024 [46] | √ | √ | DD | ||
| Gioldasis, Christoforou, and Katsiadrami, 2024 [47] | √ | √ | DD | ||
| Kozłowski, Wiśniowski, Gis, Zimakowska-Laskowska, and Borucka, 2024 [48] | √ | √ | PM | ||
| Our work | √ | √ | √ | √ | PM, DD |
| Description | Value |
|---|---|
| Vehicle Mass | 700 kg |
| Payload Capacity | 400 kg |
| Top Speed | 50 km/h |
| Acceleration | 1 m/s2 |
| Range | 120 km |
| Battery Capacity | 15.6 kW/h |
| Front Surface Area | 2.55 m2 |
| Segment Length | Best Model | R2 | MAE | RMSE |
|---|---|---|---|---|
| 50 m | CatBoost | 0.88 | 1.59 | 2.23 |
| 75 m | Extra Trees | 0.92 | 1.70 | 2.44 |
| 100 m | CatBoost | 0.93 | 1.95 | 2.74 |
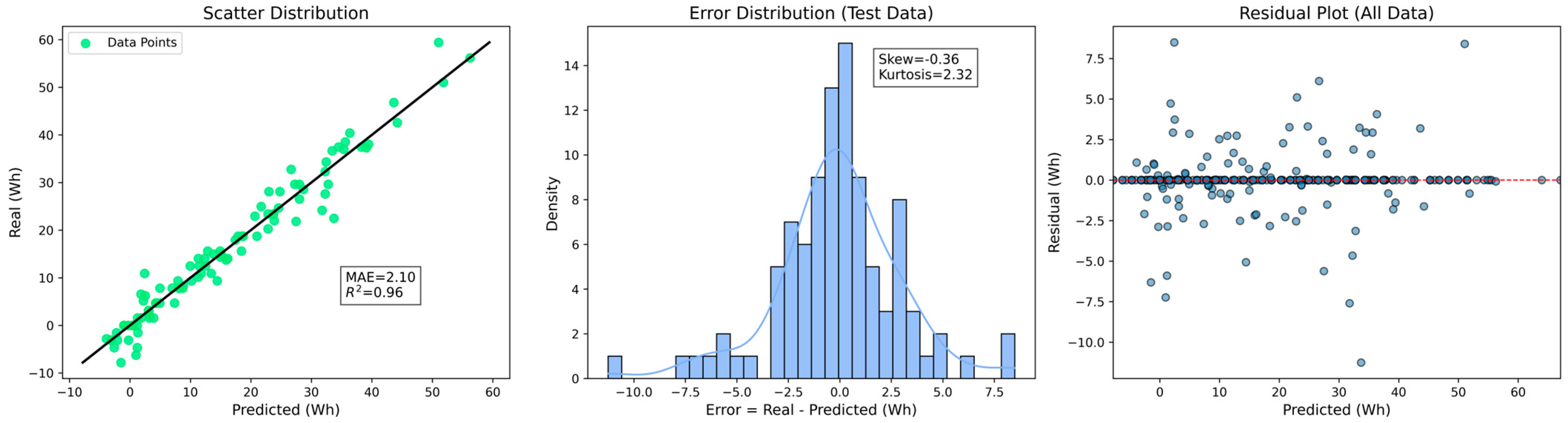
| 150 m | Extra Trees | 0.96 | 2.10 | 3.02 |
| 200 m | Extra Trees | 0.93 | 3.81 | 5.01 |
| 250 m | Extra Trees | 0.92 | 3.32 | 5.02 |
| Variable | PR (>F) |
|---|---|
| segment_length | 0.3404 |
| slope | 0.0 |
| avg_vehicle_speed | 0.1169 |
| avg_Acceleration | 0.0 |
| avg_Total_Mass | 0.0 |
| avg_Temperature | 0.0002 |
| Model | R2 Score | MAE | RMSE | Training Time (s) | Prediction Time (s) |
|---|---|---|---|---|---|
| Extra Trees | 0.96 | 2.1 | 3.02 | 0.28 | 0.03 |
| CatBoost | 0.96 | 2.32 | 3.17 | 2.37 | 0.0 |
| LightGBM | 0.95 | 2.63 | 3.4 | 0.06 | 0.0 |
| Voting Regressor | 0.95 | 2.58 | 3.46 | 0.66 | 0.04 |
| Random Forest | 0.94 | 2.68 | 3.56 | 0.52 | 0.02 |
| Stacking Regressor | 0.94 | 2.74 | 3.59 | 3.39 | 0.02 |
| Gradient Boosting | 0.93 | 2.92 | 3.81 | 0.2 | 0.0 |
| XGBoost | 0.92 | 2.95 | 4.1 | 0.22 | 0.01 |
| Polynomial Regression (Degree 3) | 0.89 | 3.36 | 4.9 | 0.01 | 0.01 |
| Decision Tree | 0.87 | 3.97 | 5.32 | 0.01 | 0.0 |
| AdaBoost | 0.87 | 4.4 | 5.39 | 0.17 | 0.02 |
| Linear Regression | 0.81 | 4.91 | 6.46 | 0.01 | 0.0 |
| Ridge Regression | 0.81 | 4.91 | 6.46 | 0.0 | 0.0 |
| Bayesian Ridge | 0.81 | 4.94 | 6.47 | 0.0 | 0.0 |
| Lasso Regression | 0.81 | 4.94 | 6.47 | 0.0 | 0.0 |
| ElasticNet | 0.81 | 5.0 | 6.51 | 0.01 | 0.0 |
| Huber Regressor | 0.81 | 4.88 | 6.53 | 0.08 | 0.0 |
| Support Vector Regressor (SVR) | 0.8 | 4.6 | 6.68 | 0.01 | 0.01 |
| Theil-Sen Regressor | 0.74 | 4.88 | 7.59 | 0.75 | 0.0 |
| K-Nearest Neighbors (KNN) | 0.58 | 6.91 | 9.73 | 0.0 | 0.0 |
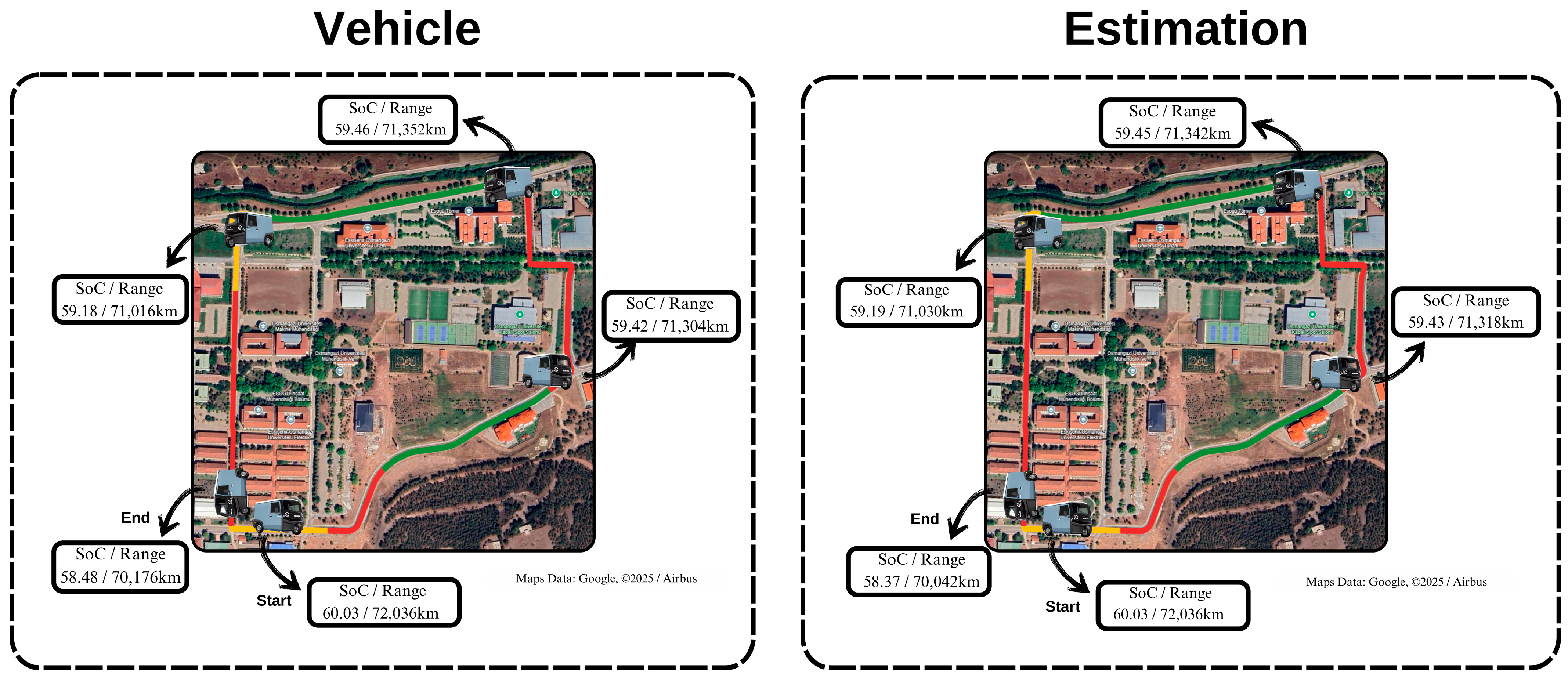
| Route | Mass (kg) | Actual Distance (m) | Average Velocity (kph) | Vehicle Range Difference (m) | Estimated Range Difference (m) | PM Range Difference (m) | Actual vs. Vehicle | Actual vs. Predicted | Actual vs. PM |
|---|---|---|---|---|---|---|---|---|---|
| 15LC | 1195 | 2047 | 14.01 | 1860 | 1994 | 1551 | 9.14% | 2.58% | 24.22% |
| 15LM | 1195 | 1970 | 14.32 | 1716 | 2019 | 1587 | 12.89% | 2.48% | 19.43% |
| 15UC | 870 | 2047 | 14.72 | 1260 | 1935 | 1166 | 38.45% | 5.49% | 43.06% |
| 15UM | 870 | 1970 | 14.4 | 1176 | 1691 | 1153 | 40.30% | 14.14% | 41.45% |
| 25LC | 1220 | 2047 | 23.26 | 2143 | 2176 | 2034 | 4.70% | 6.25% | 0.62% |
| 25LM | 1195 | 1970 | 22.39 | 1956 | 2033 | 2166 | 0.71% | 3.18% | 9.96% |
| 25UC | 870 | 2047 | 25.63 | 1524 | 1736 | 1671 | 25.55% | 15.19% | 18.37% |
| 25UM | 870 | 1970 | 25.05 | 1512 | 1727 | 1784 | 23.25% | 12.35% | 9.42% |
| 35LC | 1220 | 2047 | 32.02 | 2295 | 2224 | 2626 | 12.14% | 8.62% | 28.28% |
| 35LM | 1220 | 1970 | 30.65 | 2364 | 2178 | 2828 | 20.00% | 10.56% | 43.57% |
| 35UC | 870 | 2047 | 34.32 | 1882 | 1997 | 2014 | 8.02% | 2.45% | 1.63% |
| 35UM | 870 | 1970 | 33.73 | 2076 | 1928 | 2306 | 5.38% | 2.15% | 17.07% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polat, A.A.; Bozkurt Keser, S.; Sarıçiçek, İ.; Yazıcı, A. Analysis of Factors Affecting Electric Vehicle Range Estimation: A Case Study of the Eskisehir Osmangazi University Campus. Sustainability 2025, 17, 3488. https://doi.org/10.3390/su17083488
Polat AA, Bozkurt Keser S, Sarıçiçek İ, Yazıcı A. Analysis of Factors Affecting Electric Vehicle Range Estimation: A Case Study of the Eskisehir Osmangazi University Campus. Sustainability. 2025; 17(8):3488. https://doi.org/10.3390/su17083488
Chicago/Turabian StylePolat, Ahmet Alperen, Sinem Bozkurt Keser, İnci Sarıçiçek, and Ahmet Yazıcı. 2025. "Analysis of Factors Affecting Electric Vehicle Range Estimation: A Case Study of the Eskisehir Osmangazi University Campus" Sustainability 17, no. 8: 3488. https://doi.org/10.3390/su17083488
APA StylePolat, A. A., Bozkurt Keser, S., Sarıçiçek, İ., & Yazıcı, A. (2025). Analysis of Factors Affecting Electric Vehicle Range Estimation: A Case Study of the Eskisehir Osmangazi University Campus. Sustainability, 17(8), 3488. https://doi.org/10.3390/su17083488








