A Stochastic Multi-Objective Optimization Framework for Integrating Renewable Resources and Gravity Energy Storage in Distribution Networks, Incorporating an Enhanced Weighted Average Algorithm and Demand Response

Abstract

This paper introduces a novel stochastic multi-objective optimization framework for the integration of gravity energy storage (GES) with renewable resources—photovoltaic (PV) and wind turbine (WT)—in distribution networks incorporating demand response (DR), addressing key gaps in uncertainty handling and optimization efficiency. The GES plays a pivotal role in this framework by contributing to a techno-economic improvement in distribution networks through enhanced flexibility and a more effective utilization of intermittent renewable energy generation and economically viable storage capacity. The proposed multi-objective model aims to minimize energy losses, pollution costs, and investment and operational expenses. A new multi-objective enhanced weighted average algorithm integrated with an elite selection mechanism (MO-EWAA) is proposed to determine the optimal sizing and placement of PV, WT, and GES units. To address uncertainties in renewable generation and load demand, the two-point estimation method (2m + 1 PEM) is employed. Simulation results on a standard 33-bus test system demonstrate that the coordinated use of GES with renewables reduces energy losses and emission costs by 14.55% and 0.21%, respectively, compared to scenarios without storage, and incorporating the DR decreases the different costs. Moreover, incorporating the stochastic model increases the costs of energy losses, pollution, and investment and operation by 6.50%, 2.056%, and 3.94%, respectively, due to uncertainty. The MO-EWAA outperforms conventional MO-WAA and multi-objective particle swarm optimization (MO-PSO) in computational efficiency and solution quality, confirming its effectiveness for stochastic multi-objective optimization in distribution networks.

1. Introduction

1.1. Motivation

The integration of renewable energy sources, such as PV and WT systems, into distribution networks is indispensable towards a sustainable energy future. However, the intermittency and uncertainty inherent in solar and wind power generation pose serious challenges to grid stability, power quality, and operational planning [1,2,3]. This may bring about difficulties in balancing supply and demand and in increasing energy losses, and result in costly reserve capacity from conventional fossil-fuel plants, thus offsetting the environmental benefits that could come with the use of RES [4,5].

Among these, ESS is widely recognized as a vital solution to counteract these challenges by storing excess energy during high generation periods and releasing it during high demand or low generation periods [6]. Though BESS has been a widely studied topic, GES presents a promising alternative with a few distinctive advantages, including high reliability, long lifecycle, and low environmental degradation [7,8]. Simultaneously, DR programs work on the demand side by incentivizing consumers to adjust their load pattern to help flatten the demand curve [9].

However, the optimal integration of RES, advanced ESS such as GES, and DR into distribution networks is still a complex multi-objective problem. The complexity further becomes exacerbated by the requirement to handle renewable generation and load demand uncertainties. To attain techno-economic efficiency with an environmentally friendly distribution system, a sophisticated framework must be designed capable of determining, simultaneously, the optimal sizing and placement of these resources while negotiating their inherent uncertainties.

1.2. Related Works and Gaps

The integration of RES and ESS into radial distribution networks has been one of the broad research areas to improve the overall performance of the system, stabilize the grid, and address the challenges of intermittent generation. Research in this domain is evolving along several key trajectories: development of advanced metaheuristic optimizers, considering uncertainty, and exploring various storage technologies.

Various optimization algorithms represent, early and ongoing, the focus of efforts. As an example, studies have used adaptive grey wolf optimization (AGWO) for BESS allocation [10] and multi-objective particle swarm optimization (MOPSO) for operational cost and loss minimization [11], while an improved moth flame optimization (IMFO) was deployed for hybrid PV/battery scheduling [12]. More recently, researchers have proposed algorithms like the multi-objective modified artificial hummingbird algorithm (MOMAHA) [13] and parallel multi-objective method based on multi-verse optimizer (PMOMVO) [14] for tackling the complex, non-convex nature of optimal placement problems. Beyond the realm of algorithm development, new concepts such as Virtual Participation Theory have also been developed to enhance loss calculation accuracy in active networks [15].

A critical development in this field is the transition from deterministic to probabilistic models, able to cope with the inherent uncertainties of renewable generation and load. Methods vary between the exhaustive yet very time-consuming MCS for wind/PV/battery integration [16] and other probabilistic simulation techniques for DG placement [17], all within a persistent tradeoff between computational efficiency and modeling accuracy.

In addition, research has become diversified into the integration of different technologies. This ranges from the optimization of swapping stations for electric vehicles [18], the strategic siting of resources during unique scenarios like that of the COVID-19 pandemic [19], to the consideration of power quality metrics such as flicker emissions [20]. Despite all this progress, a synthesis of the literature reveals several consistent limitations, as outlined in detail in

Table 1. Synthesis of related works and identified research gaps.

Ref.	Focus/Method	Limitations/Gaps	Addressed in This Work
[10]	BESS allocation using AGWO for frequency/voltage stability.	Deterministic; focuses on BESS, not GES.	✓
[11]	MOPSO for wind uncertainty and storage dispatch.	Does not integrate GES or GES-based DR.	✓
[12]	IMFO for PV/battery scheduling to minimize loss.	Deterministic model; limited storage technology.	✓
[13]	MOMAHA for WT and BESS placement.	Deterministic; does not consider GES.	✓
[14]	PMOMVO for DG and BESS allocation.	Deterministic model.	✓
[15]	Virtual Participation Theory for loss reduction.	Focused on loss allocation, not integrated resource planning.	--
[16]	Probabilistic allocation (MCS) for Wind/PV/Battery.	Uses MCS, which is computationally heavy; focuses on BESS.	✓
[17]	Probabilistic framework for DG placement.	Does not incorporate energy storage or DR.	✓
[18]	Differential Evolution for solar-wind swapping stations.	System-level focus, not distribution network operation.	--
[19]	Turbulent Flow of Water-based Optimization for Wind/Solar.	Crisis-context planning; deterministic.	--
[20]	Gaussian Pied Kingfisher algorithm for PV/WT/Battery.	Focus on power quality; deterministic approach.	✓
[21]	Sand Cat Swarm Optimization for PV/Battery scheduling.	Considers randomness but with a single heuristic; uses BESS.	✓
[22]	AOA for DG placement with a new VSI.	Deterministic; no integrated storage or DR model.	✓

.

The following are the critical gaps in the literature based on the synthesis above:

• Most of the works focus only on BESS. The potential for GES as a storage solution with long duration and high cycle life for distribution networks remains unexploited, and most of the discussed applications are novel in a demand response framework [8].
• Though some studies [16,17,21] acknowledge uncertainty, most depend on deterministic models or computationally intensive methods, such as Monte Carlo Simulation. There is a lack of efficient modern probabilistic approaches, such as the two-point estimation method (2m + 1 PEM), applied to this problem.
• Most algorithms are applied to a narrow set of objectives. In this respect, it is necessary to develop an approach that simultaneously minimizes energy loss, pollution, and investment/operational costs within a unified stochastic framework.
• The potential synergy between demand response and gravity-based energy storage for enhancing voltage stability, reducing peak demand, and generally offering more flexibility to the grid has not been duly explored.

1.3. Contributions of the Paper

Building on the identified gaps in the state-of-the-art, this paper proposes an all-inclusive framework for optimum integration of renewable resources and gravity energy storage in distribution networks. The main contributions, which altogether advance the state-of-the-art in distribution system planning, are summed up as follows:

• This paper is among the first to formally model and integrate gravity energy storage within a demand response strategy. Unlike traditional incentive-based DR or battery-focused approaches, the proposed GES-based DR provides a physical, storage-backed mechanism for dynamic load management. This allows for a more robust peak shaving, increasing grid flexibility and contributing to voltage stability by active time-shifting of energy, hence offering a tangible alternative against pure financial load reduction.
• This paper proposes a new metaheuristic called MO-EWAA, standing for multi-objective enhanced weighted average algorithm with an elite selection mechanism. While elite mechanisms are well recognized in optimization, their incorporation into the WAA is novel. More importantly, the ESM is deliberately designed to overcome the difficulties of a highly nonconvex, multimodal search space inherent in the simultaneous allocation of PV, WT, and GES units. The systematic preservation of the most promising nondominated solutions across iterations by the MO-EWAA effectively avoids premature convergence and local optima entrapment, which are common drawbacks of the classical WAA. This ensures the derivation of a well-distributed, high-quality Pareto front that offers network planners an improved set of trade-off solutions.
• This work implements an efficient probabilistic model based on the 2m + 1 PEM to capture uncertainties associated with renewable generation and load demand effectively. This represents a computationally tractable but powerful alternative compared to other, more intensive methods such as Monte Carlo Simulation. It allows a detailed assessment of how input uncertainties propagate to affect those key system outputs, such as energy losses and costs, that are of vital interest, thus leading to resilient and reliable planning decisions under real-world variability.
• This paper formulates and then solves a holistic multi-objective optimization problem of minimizing three conflicting objectives—the total cost of energy losses, the total cost of pollutant emissions, and the total investment and operational costs of integrated PV, WT, and GES systems—simultaneously. The model encompasses the full set of operational constraints: power balance, bus voltage limits, and line thermal ratings. Application of the fuzzy-based mechanism facilitates a balanced optimization among these competing goals and, as a result, presents a practical and comprehensive decision-support tool towards techno-economic-environmental optimality of modern distribution networks.

1.4. Organization of the Paper

This research is segregated into the following sections. In Section 2 an overview of the methodology is presented. In this section, renewable resources and GES storage modeling, demand response strategy, problem objective function and constraints, proposed optimizer, and probabilistic approach for modeling uncertainties are discussed. In Section 3, simulation results in several scenarios are presented, and the discussions are presented. And finally, in the last section, i.e., Section 4, the conclusion of the findings of the paper is presented.

2. Methodology

Mathematical models and an optimization framework have been developed to achieve this optimal integration of resources. Note that each of the component models for PV, WT, GES, and DR is grounded in well-established formulations in the literature since the core contribution of the work is built around their novel integration and optimization under uncertainty. These standard models are outlined in the following sections for completeness and to set out the problem structure, before the proposed objective functions, constraints, and the novel MO-EWAA optimizer are presented.

2.1. Renewable Resources and GES Storage Modeling

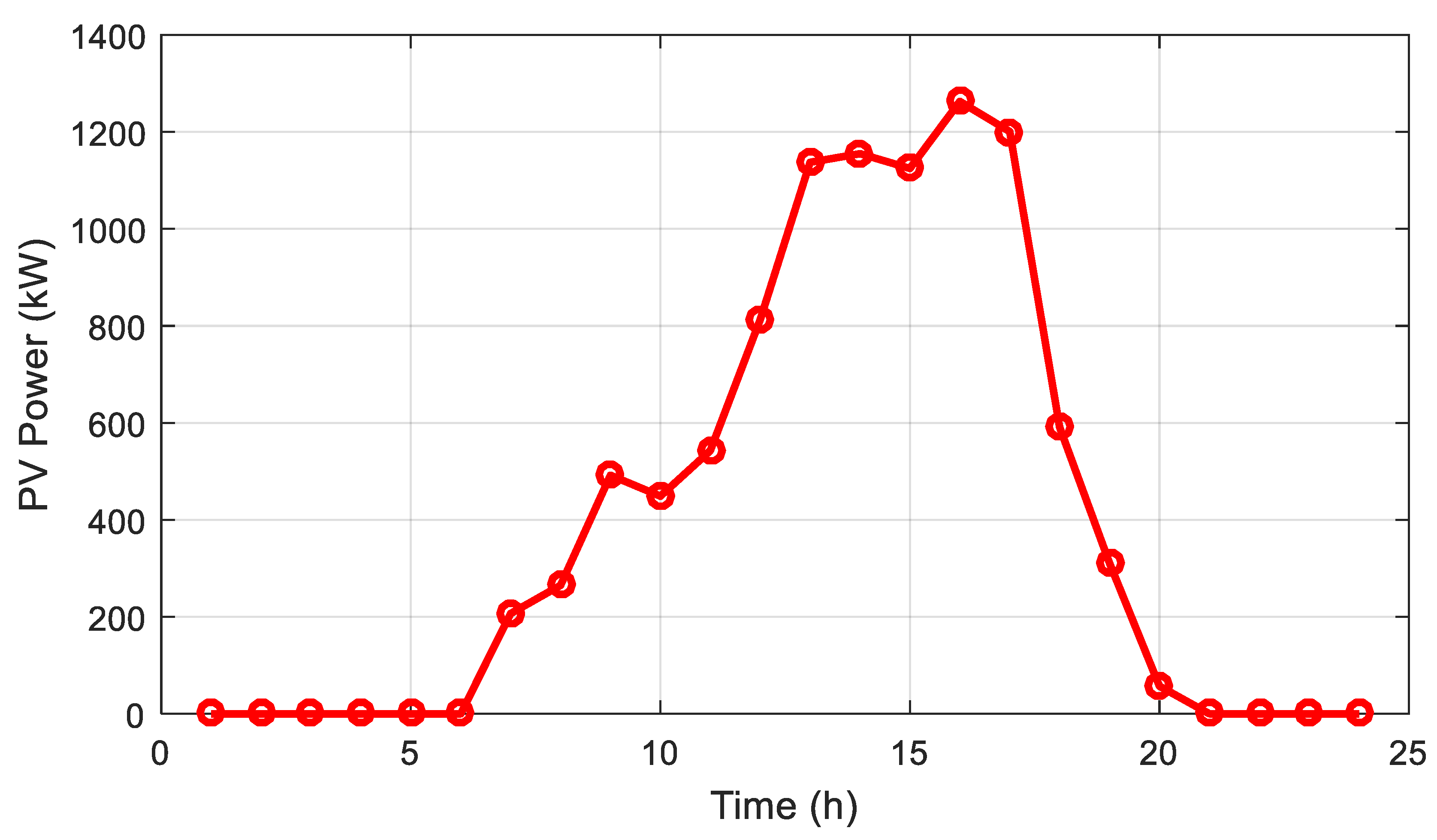
2.1.1. Photovoltaic Model

The output power of the PV system, $P_{PV}\left(t\right)$, is estimated with a standard model that takes into consideration solar irradiance and cell temperature, presented in detail in [2,4,5]. The equations governing these are represented in Equations (A1) and (A2) as represented in Appendix A.

2.1.2. Wind Turbine Model

In various studies, the power generated by a wind turbine, $P_{WT}$, is a function of the wind speed at hub height, modeled using a standard power curve with cut-in, rated, and cut-out speeds [2,4,5]. The wind speed at the turbine’s hub height is estimated using the logarithmic wind profile law, given in Equations (A3) and (A4) as defined in Appendix A.

2.1.3. Gravity Energy Storage (GES) Model

The basic energy and power dynamics of the GES system are used to model it [23,24,25]. The energy capacity E is dependent on the following: the piston mass m, height h, and system efficiency μ:

$$E=\mu \times m\times g\times h$$

(1)

The charging ($P_{ch}$) and discharging ($P_{disch}$) powers are linearly dependent on the piston’s mass and velocity, governed by the following:

$$P_{ch}={\displaystyle \frac{m\times g\times V}{{\eta }_{ch}}};P_{disch}={\eta }_{disch}\times m\times g\times V$$

(2)

Energy capacity in kWh and power rating in kW are the main decision variables in this optimization, with the physical design abstracted. However, there are distinct deployment challenges that GES faces compared to mature Battery Energy Storage Systems. BESS is commercially established at TRL 9–10, while GES is mostly at the demonstration stage at TRL 4–7, with its feasibility highly dependent on specific geographical features like disused mine shafts or suitable land for tall structures. Currently, such siting constraints—considering also the civil engineering complexities related to deep excavations or high-rise construction—affect the cost and flexibility of GES. Still, because GES has exceptional longevity, uses abundant materials, and is inherently safe, it is considered a promising candidate for long-duration storage, with further cost reductions expected in the future when this technology matures and such barriers are overcome.

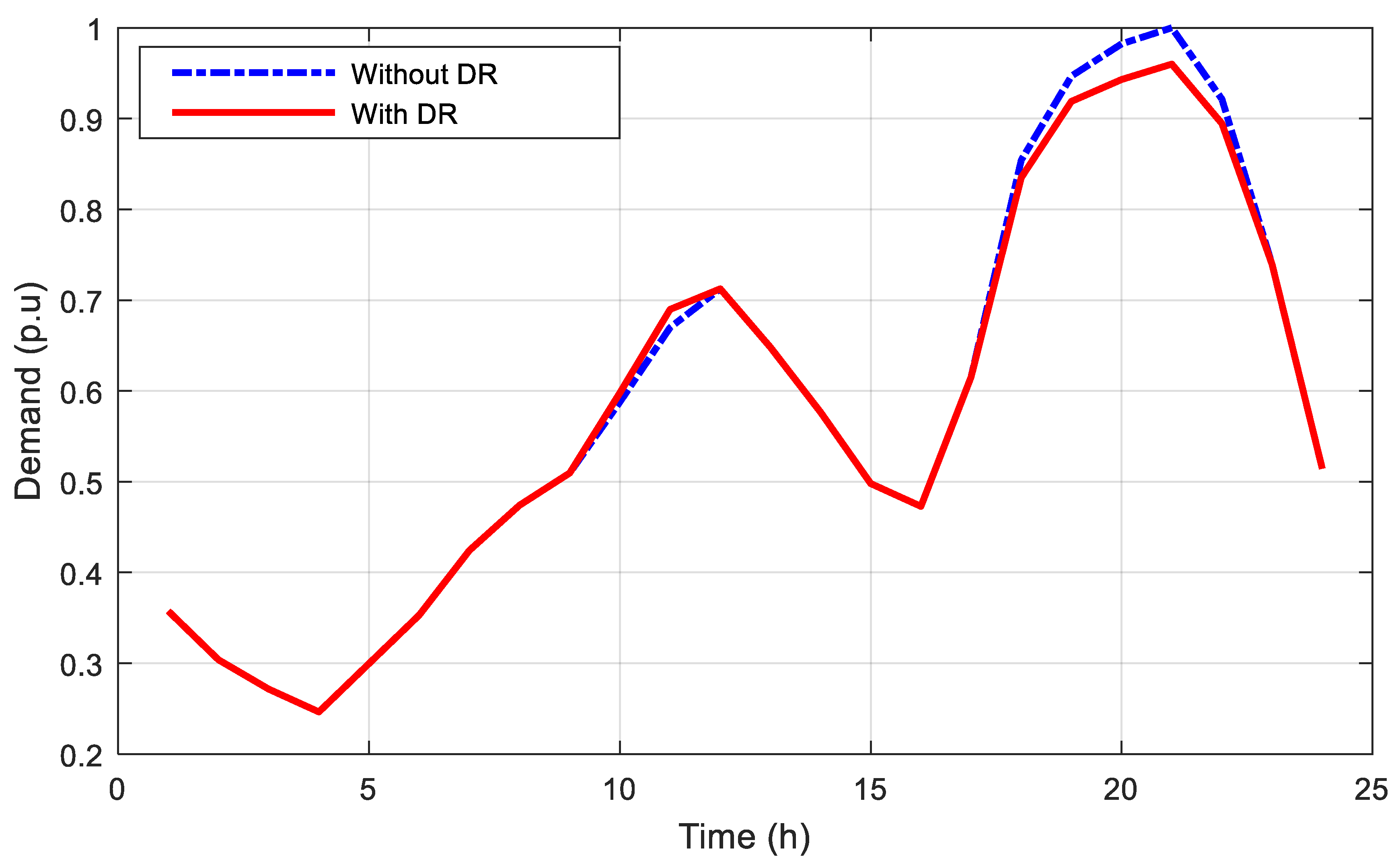
2.2. Demand Response Model

An incentive-based demand response program is incorporated, following the model presented in [26]. The model categorizes consumers into residential ($r$), commercial ($c$), and industrial ($i$) classes. The load reduction for each class at time $t$ is bounded by a maximum allowable limit ($R{C}_t^{\mathrm{m}\mathrm{a}\mathrm{x}}$, $C{C}_t^{\mathrm{m}\mathrm{a}\mathrm{x}}$, $I{C}_t^{\mathrm{m}\mathrm{a}\mathrm{x}}$), and the cost of this reduction is calculated based on specific incentive payments (${\pi }_{r,t},{\pi }_{c,t},{\pi }_{i,t}$), as defined in Equations (A5)–(A7).

2.3. Objective Function

Energy Loss Cost: The primary goal is to minimize the annual cost incurred by power loss in the network. To this end, this cost can be computed by (3). The losses of a certain period for a one-year time frame are multiplied by 365 days [27,28]:

$${Cost}_{Loss}=C_E\times 365\times {\sum }_{t=1}^T·P_{Loss}^t \left(USD\right),\forall t$$

(3)

where C_E indicates the cost associated with energy losses (kWh).

Pollution Costs: The second objective is to reduce the expense incurred due to environmental pollution. In this, each source of energy is analyzed considering three various classes of pollutant emissions. The cost of pollution annually is determined as follows [27,28]:

$${Cost}_{Emission}={CE}_T\times 365\times {\sum }_{t=1}^T\left(E_{Grid}^t\right) \left(USD\right),\forall t$$

(4)

$$E_{Grid}^t=\left({CO}_{2,Grid}^t+{SO}_{2,Grid}^t+{NO}_{x,Grid}^t\right)\times P_{Grid}^t$$

(5)

where Cost_Emission represents the annual cost related to pollutant emissions. The term $E_{Grid}^t$denotes the emission levels (measured in kg per kWh) from the grid at hour t, calculated based on the previously defined equations. ${CE}_T$ refers to the cost of emission. Factors of ${CO}_{2,Grid}^t$, ${SO}_{2,Grid}^t$, and ${NO}_{x,Grid}^t$ represent the emission quantities.

Investment and Operational Costs for Renewable Resources and Storage: The third objective function focuses on the expenses related to the investment in and operation of wind turbines (WTs), PV, and GES, as follows [6]:

$$ost\left(Renewable\&GES\right)={Cost}_{Inv}+{Cost}_{O\&M}$$

(6)

$${Cost}_{Inv}={CRF}_{Com}\times C_{Com}^{cap}\times {Cap}_{Com}$$

(7)

$${CRF}_{Com}={\displaystyle \frac{I{r\left(1+Ir\right)}^{{LT}_{Com}}}{{\left(1+Ir\right)}^{{LT}_{Com}}-1}}$$

(8)

$${Cost}_{O\&M}=C_{Com}^{O\&M}\times {\sum }_{t=1}^T{PorM}_{Com}^t$$

(9)

where ${Cost}_{Inv}$ and ${Cost}_{O\&M }$are the investment and operation, and maintenance costs of each component, ${CRF}_{Com}$ is the cost recovery factor of each component, $C_{Com}^{cap}$denotes the capital cost of each unit component, ${Cap}_{Com}$is the installed capacity of each component, $Ir$ and ${LT}_{Com}$are the interest rate and the lifetime of each component, and $C_{Com}^{O\&M}$and ${PorM}_{Com}^t$ refer to the O&M cost of each component and the total used or installed power or mass of each component, respectively.

In the fuzzy multi-objective optimization method, each objective function is transformed into a fuzzy membership function, ${\mu }_i$, which scales its value between 0 and 1. A value of 1 indicates full satisfaction of the objective, while 0 indicates it is not satisfied at all. For minimization objectives, this membership function is defined as [29] follows:

$${\mu }_i^k= \left\{\begin{array}{c}1 f_i\le f_i^{min}\\ {\displaystyle \frac{f_i^{max}-f_i}{f_i^{max}-f_i^{min}}} f_i^{max}<f_i<f_i^{min}\\ 0 f_i\ge f_i^{max} \end{array}\right.$$

(10)

Here, $f_i^{\mathrm{m}\mathrm{i}\mathrm{n}}$ and $f_i^{\mathrm{m}\mathrm{a}\mathrm{x}}$ represent the ideal (best) and anti-ideal (worst) values for the $i$-th objective, respectively, defining the range of acceptable solutions.

The overall goal is to find a solution that provides the best compromise, making all objectives as satisfied as possible simultaneously. This is achieved by maximizing the minimum membership value among all objectives (a max–min approach). The overall fuzzy satisfaction degree, ${\mu }_D$, and the final single objective function ($OF$) to be maximized are given by [29] the following:

$${\mu }_D=\mathit{min}\left\{\left(\mu \right(F_1),\mu (F_2),\mu (F_3)\right\}$$

(11)

$$OF=\mathit{max}({\mu }_D)$$

(12)

This approach effectively ensures that the optimization search is guided towards a balanced solution where no single objective is severely compromised.

2.4. Constraints

In this section, the constraints of the problem are presented [6,27,28].

2.4.1. Power Balance

The distribution system’s active and reactive power balances are given in Equations (13) and (14). The overall main grid active and reactive power and the renewable power, as well as the power balance constraint, require that the discharged power from the GES must meet the total system demand plus the active and reactive power losses and is expressed as follows:

$$P_{Grid}\left(t\right)+P_{PV}\left(t\right)+P_{WT}\left(t\right)+P_{GES}\left(t\right)=P_{Load}\left(t\right)+P_{Loss}\left(t\right)$$

(13)

where $P_{GES}\left(t\right)$ is the active power from the GES (positive when discharging, negative when charging).

$$Q_{Grid}\left(t\right)+Q_{PV}\left(t\right)+Q_{WT}\left(t\right)+Q_{GES}\left(t\right)=Q_{Load}\left(t\right)+Q_{Loss}\left(t\right)$$

(14)

where $P_{Grid}\left(t\right)/Q_{Grid}\left(t\right)$ is the active/reactive power from the main grid. $Q_{PV}\left(t\right)$ and $Q_{WT}\left(t\right)$ are the reactive power injections from the PV and wind systems, respectively. $P_{GES}\left(t\right)/Q_{GES}\left(t\right)$ is the active/reactive power injection from the gravity energy storage system. $Q_{Load}\left(t\right)$ and $Q_{Loss}\left(t\right)$ are the reactive power demand and losses, respectively. $P_{Loss\left(t\right) }$and $Q_{Loss\left(t\right) }$are the real and reactive losses at time t, and $P_{Load\left(t\right) }$and $Q_{Load\left(t\right) }$are the power demands of real and reactive at time t. These variables collectively determine the network’s load flow and loss characteristics.

2.4.2. Bus Voltage

The voltage at each bus must remain within specified operational limits to ensure network stability:

$${\vartheta }_{L bus}\le {\vartheta }_{bus\left(t\right) }\le {\vartheta }_{U bus}$$

(15)

where ${\vartheta }_{bus\left(t\right) }$ is the bus voltage at time t. The lower and upper voltage limits, ${\vartheta }_{L bus}$ and ${\vartheta }_{U bus}$, are set to 0.90 p.u. and 1.05 p.u., respectively.

2.4.3. Capacity of Line

The current in any line must not exceed its thermal rating to prevent overheating and damage:

$$I_{i\left(t\right)}\le I_{U line}$$

(16)

where $I_{i\left(t\right)}$ is the current flowing through line i at time t, and $I_{U line}$ is its maximum permissible thermal current-carrying capacity.

2.4.4. Renewable and GES Capacity

• PV size

$$P_{L PV}\le P_{PV\left(t\right)}\le P_{U PV}$$

(17)

where $P_{PV\left(t\right)}$denotes the PV capacity at time t, and $P_{L PV}$and $P_{U PV}$ are lower and upper PV capacity, respectively.

• Wind turbine size

$$P_{L WT}\le P_{WT\left(t\right)}\le P_{U WT}$$

(18)

where $P_{WT\left(t\right) }$ is the power of WT at time t, and $P_{L WT}$and $P_{U WT}$ are lower and upper wind turbine power, respectively.

• GES size

$$P_{L GES}\le P_{GES\left(t\right)}\le P_{U GES}$$

(19)

where,$P_{GES\left(t\right)}$is the GES charge and discharge capacities (kW) at time t, and $P_{L GES}$and $P_{U GES}$ are lower and upper GES power, respectively.

2.4.5. Reactive Power Capability of Inverter-Based Resources

The reactive power output of the inverter-based resources (PV, WT, GES) is constrained by the apparent power rating of their respective power converters. For each resource $j$ (where $j$ can be PV, WT, or GES), the following constraint must hold:

$$Q_{j,min}\le Q_j\left(t\right)\le Q_{j,max}$$

(20)

Furthermore, the reactive power limits are coupled with the active power output through the converter’s apparent power rating $S_j^{rated}$:

$$\sqrt{P_j(t{)}^2+Q_j(t{)}^2}\le S_j^{rated}$$

(21)

For the GES system, the apparent power rating $S_{GES}^{rated}$ is a key design parameter that determines its ability to provide simultaneous active and reactive power services to the grid.

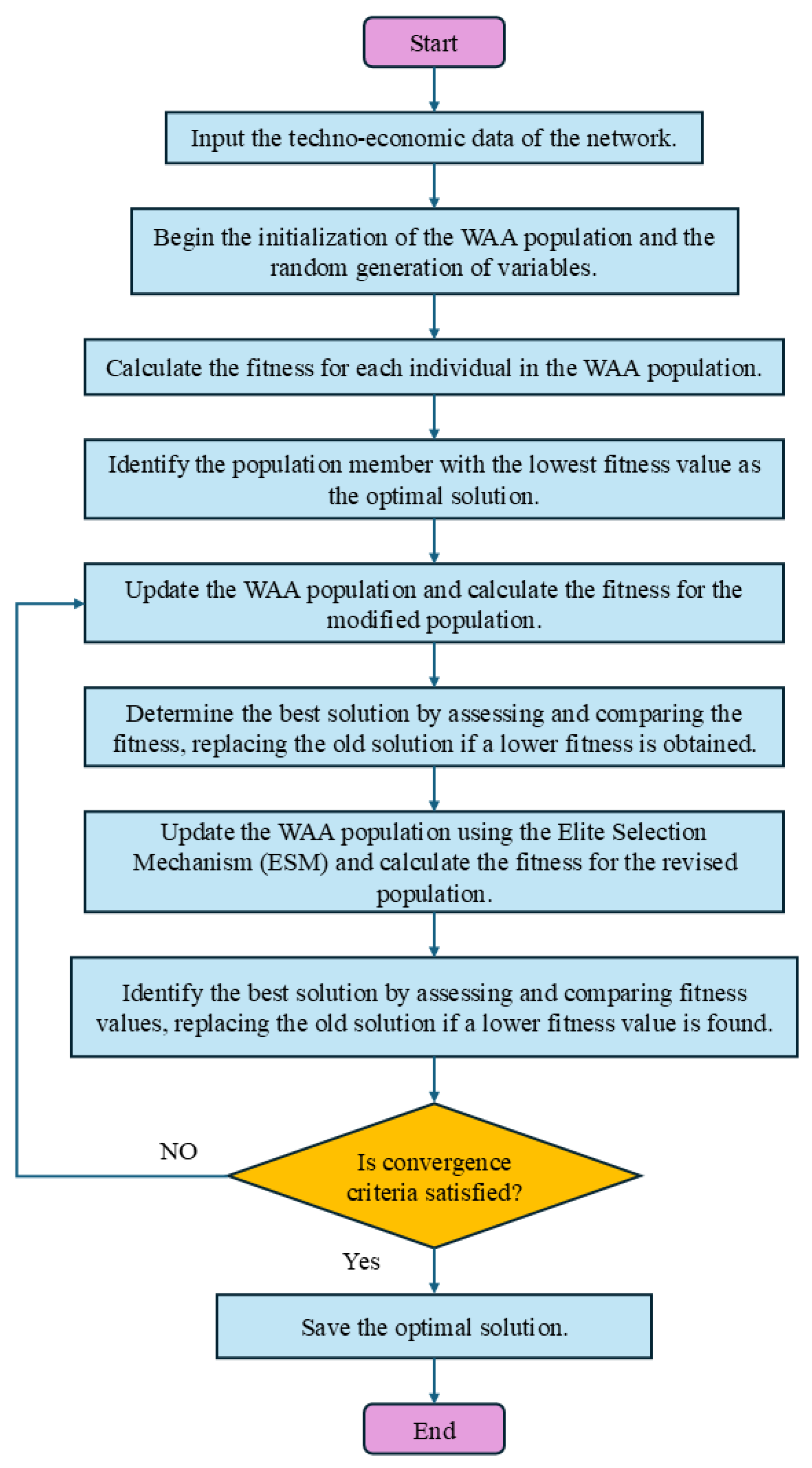
2.5. Proposed Optimizer (MO-EWAA)

This section describes the proposed MO-EWAA. First, the fundamental mechanism of classical WAA is introduced. Then, the newly developed ESM, incorporated into the WAA in order to create an improved EWAA, is described.

2.5.1. Foundation: The Weighted Average Algorithm (WAA)

WAA is a population-based metaheuristic; in it, individuals update their positions according to a weighted average, guiding the search efficiently through the solution space [30]. The algorithm works through the following phases:

(a)

Initialization

A population matrix $X$ can be initialized with $N$ candidate solutions, each of dimensionality n, within the search boundaries using the following:

$$x_{i,j}=\mathrm{rand}·(U{B}_j-L{B}_j)+L{B}_j,i=1,\dots ,N,j=1,\dots ,n$$

(22)

where $L{B}_j$ and $U{B}_j$ are the lower and upper bounds for the $j$-th dimension, and $\mathrm{rand}$ is a random number in [0, 1].

(b)

Weighted Average Position Calculation

The population is ranked in accordance with the fitness function (either a “smaller-the-better” or “larger-the-better” criterion is used). The best $N_{\mathrm{Candidate}}$ solutions are selected and decrease adaptively with iterations according to Equation (23).

$$N_{Candidate}=\left(nP-4\right){\displaystyle \frac{it-1}{1-{Max}_{It}}}+nP$$

(23)

The weighted average position $X_{Miu}$ is then calculated. For a minimization (STB) problem, this is given by the following:

$$X_{Miu}={\displaystyle \frac{\sum _{i=1}^{N_{\mathrm{Candidate}}}{X}_i·({\mathrm{Sum}}_{Fitness}-\mathrm{Fitness}(X_i\left)\right)}{{\mathrm{Sum}}_{Fitness}·(N_{\mathrm{Candidate}}-1)}}$$

(24)

where ${\mathrm{Sum}}_{Fitness}$ is the sum of the fitness values for the selected candidates.

(c)

Search Phase Identification

At every iteration, a function $f\left(It\right)$ defines the search mode for each candidate:

$$f(It)=(\alpha ·\mathrm{rand}-1)·\mathrm{s}\mathrm{i}\mathrm{n}({\displaystyle \frac{\pi \times It}{{\mathrm{Max}}_{It}}})$$

(25)

Candidates with $f\left(It\right)\ge 0.5$ enter the exploitation phase, whereas others enter the exploration phase.

(d)

Position Update Strategies

The position update depends on the identified phase:

• Exploitation Phase: Refines solutions around promising areas by using three strategies:
  • Guidance from the global best ($X_{{\mathrm{Global}}_{Best}}$), personal best ($X_{{\mathrm{Personal}}_{Best}}$), and the weighted average ($X_{Miu}$) (Equation (26)).

    $$\begin{array}{c}{X}_i\left(It+1\right)=\hfill \\ {\omega }_{11}·\left(X_{Miu}\left(It\right)-X_{{Global}_{Best}}\left(It\right)\right)\hfill \\ +{\omega }_{12}·\left(X_{Miu}\left(It\right)-X_{{Personal}_{Best}}\left(It\right)\right)+{\omega }_{13}·X_{Miu}\left(It\right)\hfill \end{array}$$

    (26)
  • Movement between the personal best and the weighted average (Equation (27)).

    $$X_i\left(It+1\right)={\omega }_{21}·\left(X_{Miu}\left(It\right)-X_{{Personal}_{Best}}\left(It\right)\right)+{\omega }_{22}·X_{{Personal}_{Best}}\left(It\right)$$

    (27)
  • Movement between the global best and the weighted average (Equation (28)).

    $$X_i\left(it+1\right)={\omega }_{31}·\left(X_{Miu}\left(it\right)-X_{{Global}_{Best}}\left(it\right)\right)+{\omega }_{32}·X_{{Global}_{Best}}\left(it\right)$$

    (28)
• Exploration Phase: Broadens the search to avoid local optima using two strategies:
  • Lévy Flight: A random walk with intermittent long jumps (Equations (29)–(32)).

    $$S={\displaystyle \frac{U}{{\left|V\right|}^{\beta }}}$$

    (29)

    $$U=normal\left(0,{\sigma }_u^2\right), and V=normal(0,{\sigma }_v^2)$$

    (30)

    $${\sigma }_u={\left\{{\displaystyle \frac{\Gamma \left(1+\beta \right)sin(\pi \beta /2)}{\Gamma \left[\frac{\left(1+\beta \right)}{2}\right]\beta 2^{(\beta -1)2}}}\right\}}^{1/\beta }$$

    (31)

    $$X_{i,j}\left(it+1\right)=X_{{Global}_{Best,j}}\left(it\right)+S$$

    (32)
  • Random Reinitialization: The act of guiding search agents to new, random positions within the search space (Equation (33)).

    $$X_i\left(it+1\right)=rand·\left({{UB}_{min}-LB}_{min}\right)+{LB}_{min}$$

    (33)

2.5.2. Enhancement: The Elite Selection Mechanism (ESM)

Although effective, the classical WAA may suffer from premature convergence. In this respect, an ESM is incorporated to form the EWAA. This ESM guarantees that the best solutions are preserved over continuous generations, hence contributing to a more stable search and high convergence quality given in [31,32,33].

The initialization, fitness evaluation, and sorting of the EWAA are exactly like those in the conventional WAA. The application of the ESM is as follows:

• Elite Selection: After sorting the population, the top $E$ solutions (e.g., 10% of the population) are marked as the elite set $X_{\mathrm{elite}}$.

  $$X_{\mathrm{elite}}=\{X_1,X_2,\dots ,X_E\}$$

  (34)
  The individuals of this elite are preserved unchanged for the next generation.
• Update of Non-Elite Solutions: The rest of the $N-E$ non-elite solutions are updated according to the position update rules of the conventional WAA (presented in Section 2.5.1, d), which utilizes weighted average, global best, and personal best positions.

  $$X_i\left(it+1\right)=X_i\left(it\right)+{\omega }_1·\left(X_i\left(it\right)-X_{\mathrm{best}}\right)+{\omega }_2·\left(X_i\left(it\right)-X_{\mathrm{pbest}}\right)+{\omega }_3·\left(X_{\mathrm{avg}}-X_i\left(it\right)\right)$$

  (35)
• Merging of the populations: The revised non-elite population produced is combined with the elite set preserved to provide the new population for the next iteration.

$$X_{\mathrm{new}}=\{X_{\mathrm{elite}},X_{\mathrm{non}\text{-}\mathrm{elite}}\}$$

(36)

This mechanism provides a more robust search by consistently guiding the population with high-quality solutions, effectively balancing exploration and exploitation, and reducing the risk of converging to a local optimum. A flowchart of the complete WAA-ESM methodology is presented in Figure 1.

2.6. Stochastic Approach for Uncertainty Modeling

The two-point estimation method (2PEM) is used to model uncertainties in input variables, such as solar irradiance, wind speed, and load demand. The following steps outline the numerical procedure [34,35]:

• Identify Input Random Variables: Define the $m$ number of input random variables, $x_t$ for $t=\mathrm{1,2},\dots ,m$.
• Initialize Output Moments: Set the moments of the output variable $Y$ (e.g., power loss or cost) to zero: $E\left[Y^j\right]=0$ for $j=\mathrm{1,2},\dots$.
• For each random variable $t$:
  a. Determine Concentrated Locations: Calculate two standard locations $({\xi }_{t,1},{\xi }_{t,2})$ using the skewness (${\lambda }_{t,3}$) and kurtosis (${\lambda }_{t,4}$) of $x_t$:

  $${\xi }_{t,i}={\displaystyle \frac{{\lambda }_{t,3}}{2}}+(-1{)}^{3-i}\sqrt{{\lambda }_{t,4}-{\displaystyle \frac{3}{4}}{\lambda }_{t,3}^2},i=\mathrm{1,2}$$

  (37)

  b. Calculate Estimation Points: Determine the two estimation points $(x_{t,1},x_{t,2})$:

  $$x_{t,i}={\mu }_{x_t}+{\xi }_{t,i}{\sigma }_{x_t},i=\mathrm{1,2}$$

  (38)

  where ${\mu }_{x_t}$ and ${\sigma }_{x_t}$ are the mean and standard deviation of $x_t$.
  c. Form Input Vectors: Create two input vectors for the system model where all other variables are at their mean values:

  $$X_i=[{\mu }_{x_1},{\mu }_{x_2},\dots ,x_{t,i},\dots ,{\mu }_{x_m}],i=\mathrm{1,2}$$

  (39)

  d. Compute Weights: Calculate the weighting factors $(w_{t,1},w_{t,2})$ for the two points:

  $$w_{t,i}={\displaystyle \frac{(-1{)}^{3-i}}{{\xi }_{t,i}({\xi }_{t,1}-{\xi }_{t,2})}},i=\mathrm{1,2}$$

  (40)

  e. Update Output Moments: Run the system model $F\left(X\right)$ for each vector $X_i$ and update the moments of $Y$:

  $$E\left[Y^j\right]=E\left[Y^j\right]+{\sum }_{i=1}^2{w}_{t,i}·\left[F\right(X_i){]}^j$$

  (41)
• Central Point Evaluation (Optional for Hong’s 2PEM): Evaluate the system at the mean values of all inputs, $X_{\mu }=[{\mu }_{x_1},{\mu }_{x_2},\dots ,{\mu }_{x_m}]$. Calculate its weight $w_0$ and update the output moments accordingly.
• Final Statistics: After processing all variables, the mean ${\mu }_Y$ and standard deviation ${\sigma }_Y$ of the output are obtained as:

  $${\mu }_Y=E[Y],{\sigma }_Y=\sqrt{E[Y^2]-{\mu }_Y^2}$$

  (42)

This procedure efficiently propagates uncertainty from the inputs to the outputs, providing a full probabilistic characterization without the computational cost of extensive sampling.

3. Numerical Results and Discussion

This section addresses renewable resources and GES system location and capacity in a radial distribution network. The approach relies on the objective functions presented in Section 2.3, i.e., loss, emission, investment, and operation cost minimization, as well as constraints consideration. The provided method has been applied to a 33-bus distribution network [33]. The succeeding sections provide the data needed for equipment and systems studied together with simulation output under various circumstances.

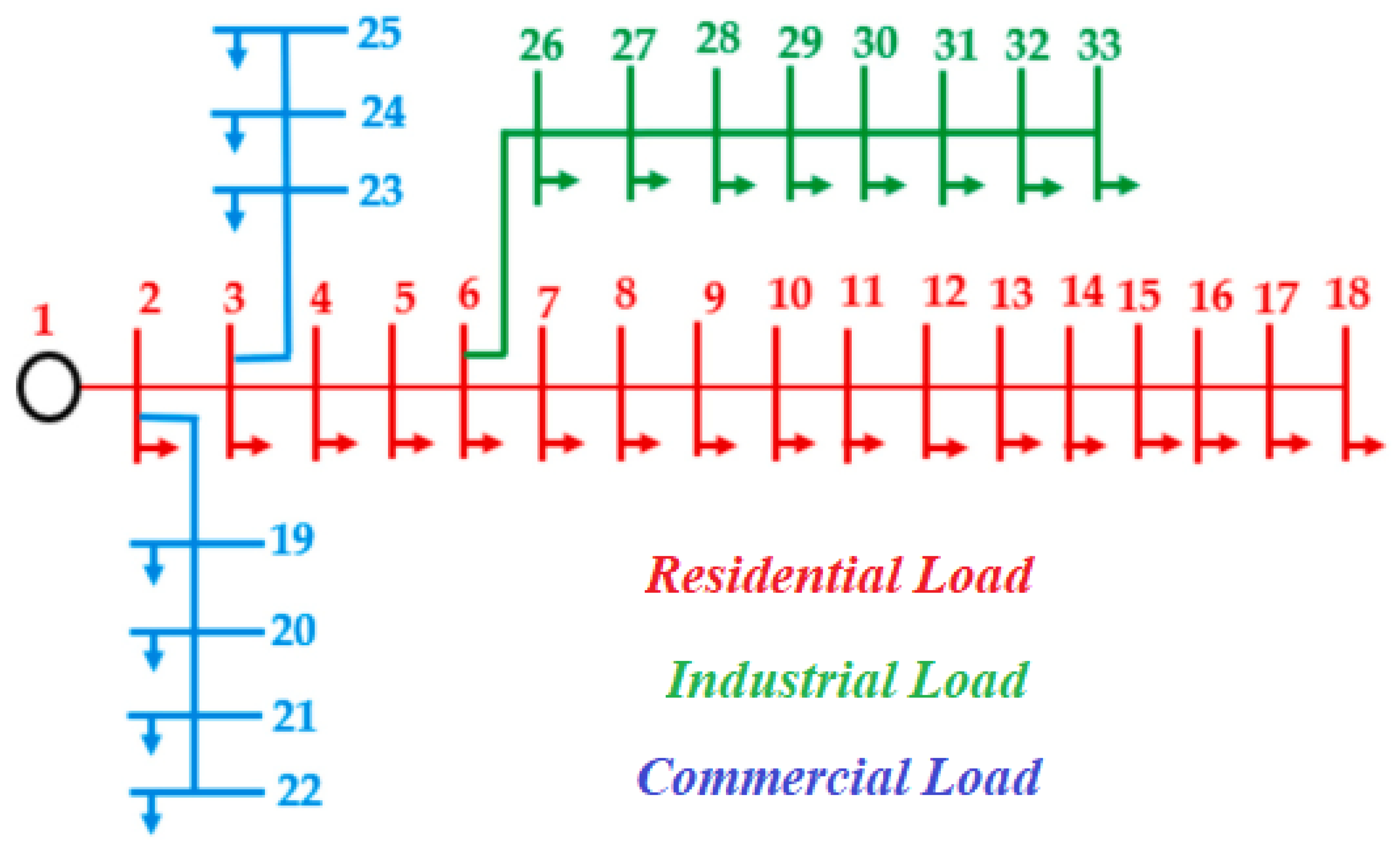
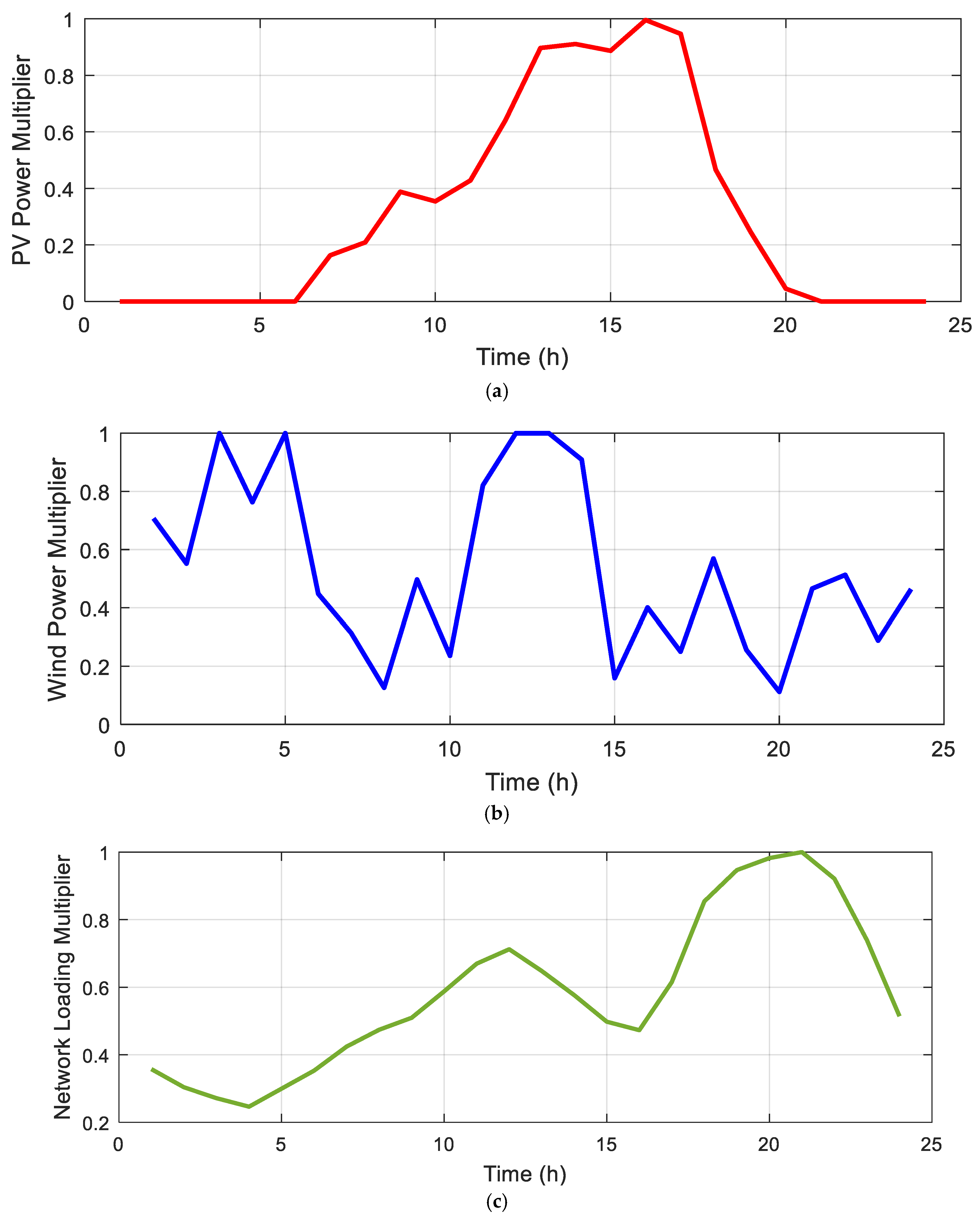
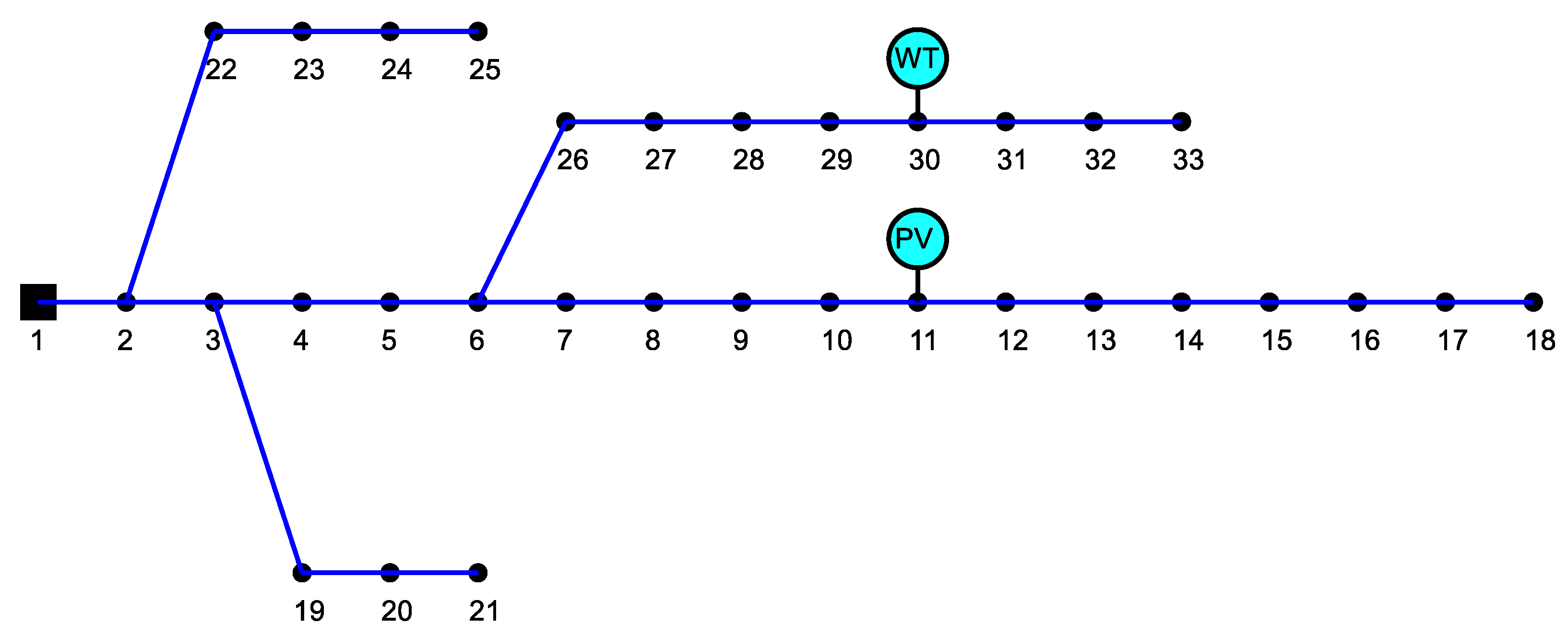
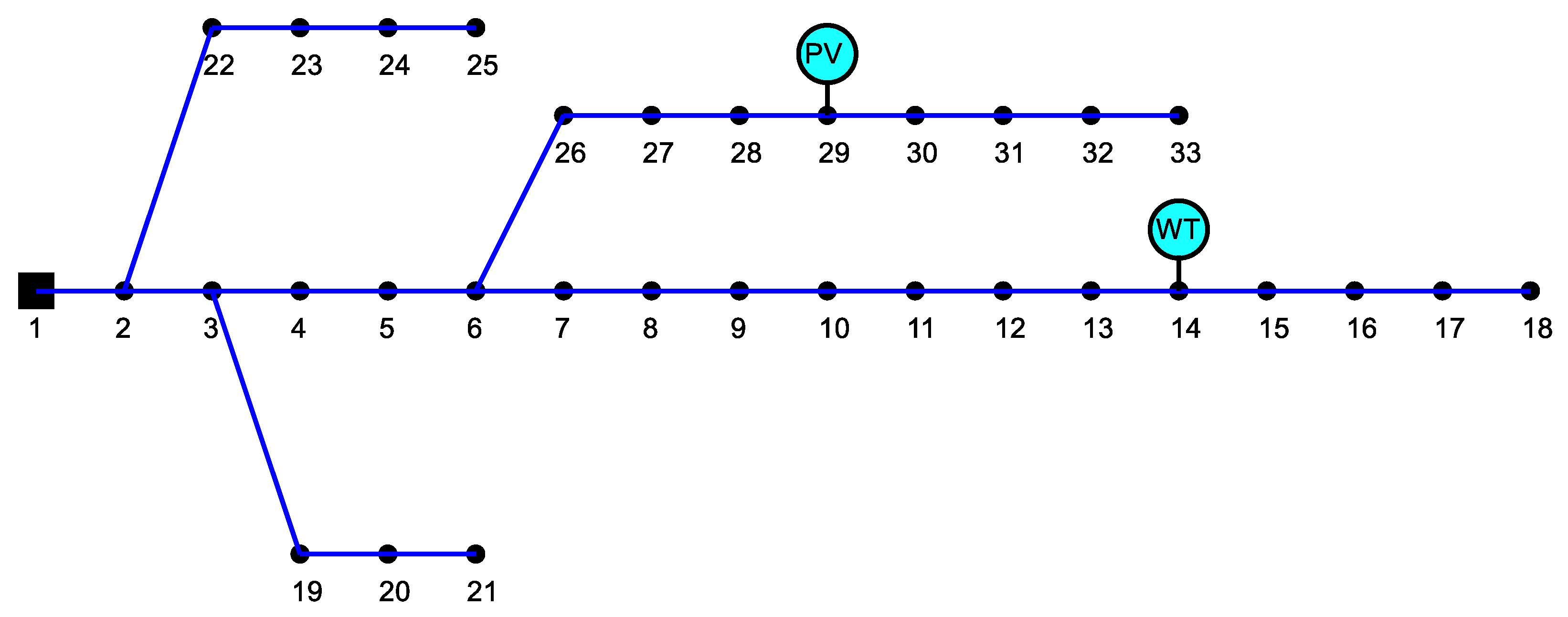
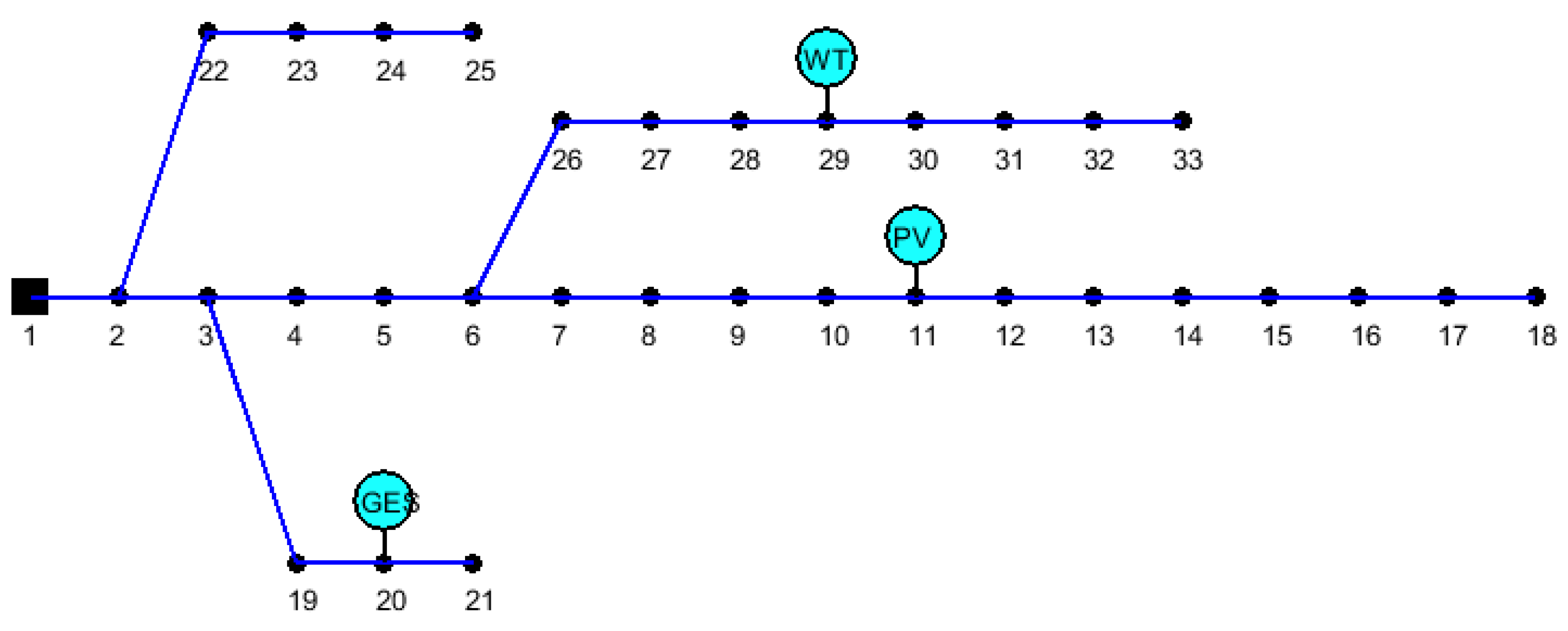
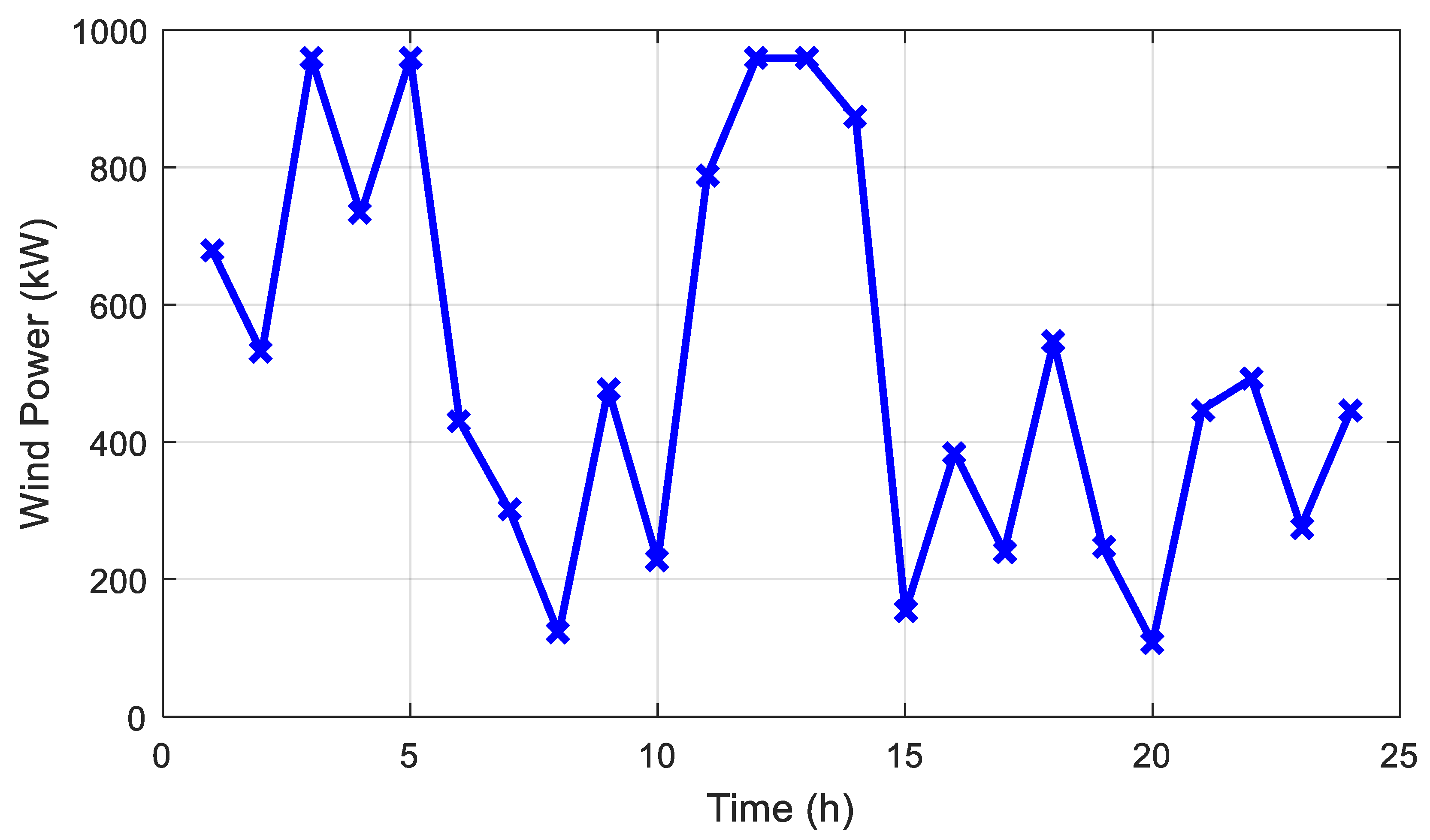
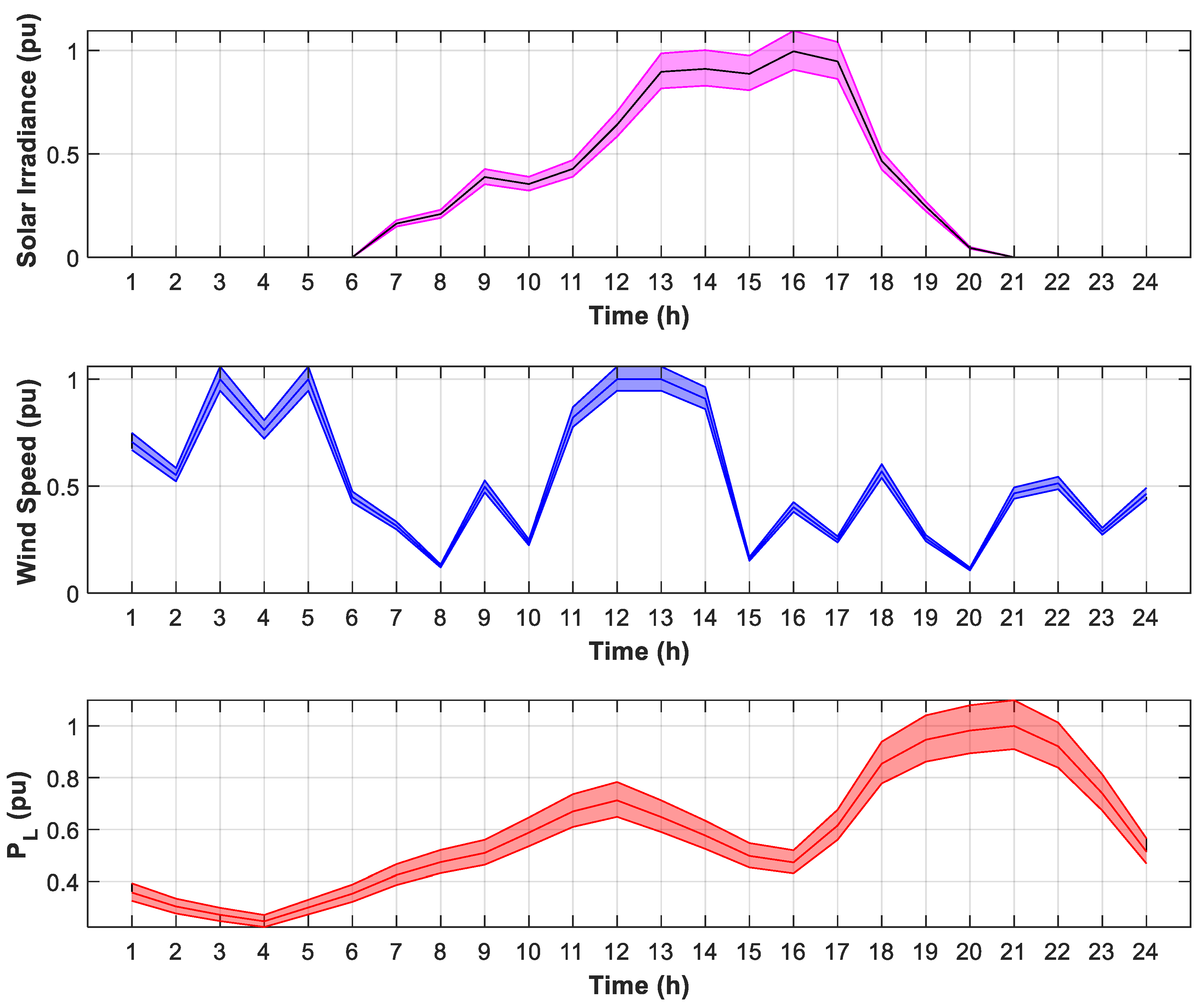
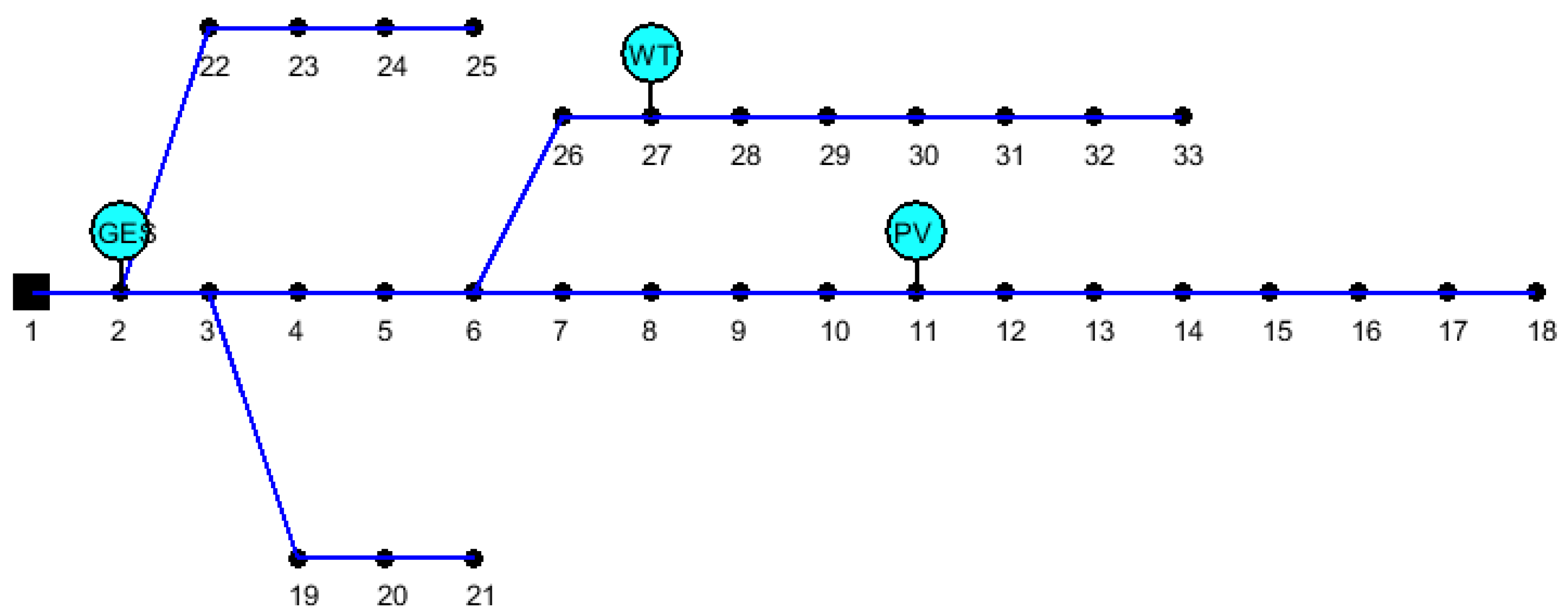
3.1. System Data Ans Simulation Scenarios

The system in question is the IEEE 33-bus network, which is shown in Figure 2 [36]. The network consists of 33 buses and 32 feeders, and the results of applying four scenarios on this system will be discussed below. Figure 3 shows the forecasted data for photovoltaic systems and wind turbines, as well as network loading. Apart from this,

Table 2. Cost parameters for WT, PV, and GES [27].

Parameter	Photovoltaic	Wind Turbine	GES
Investment cost (USD)	517	1200	1350
Operation and maintenance cost (USD/kWh)	5.17	12	13.5
Maximum capacity (kW)	2000	2000	400
Minimum capacity (kW)	0	0	0

and

Table 3. Cost parameters for main grid.

Parameter	Main Grid
Cost of energy loss (USD/kWh)	0.06
Grid cost (USD/kWh)	0.096
Emission cost (USD/kg/year)	57
NOx (kg/kWh)	0.0023
SO2 (kg/kWh)	0.0036
CO2 (kg/kWh)	0.9215

provide the cost-oriented factors of WT, PV, GES, and grid [27].

To evaluate the proposed methodology, four scenarios are considered for the case study:

• Scenario 1: Optimization of renewable energy sources (RES) without the GES system.
• Scenario 2: Optimization of RES with demand response and without GES using MO-EWAA.
• Scenario 3: Optimization of RES and GES using MO-EWAA.
• Scenario 4: Optimization of RES and GES considering a probabilistic model using MO-EWAA.

In this section, the simulation results for the proposed problem are presented and analyzed from both technical and economic perspectives, considering the four scenarios discussed earlier.

3.2. Results of Scenario One

The aim is to find the best location and size of the renewable energy resources without including the GES. The outcomes for the 33-bus network are shown in Figure 4. A WT of 676 kW is placed on bus 11 and a PV panel of 1232 kW on bus 30. In this situation, the use of GES is not considered. The results of this case provide suggestions for the potential placement and capacity of renewable sources without the added variable of energy storage options.

Table 4. Numerical optimization results for Scenario One.

Parameter	Base Network	Scenario One Values
WT Site and Capacity	--	@11/676 kW
PV Site and Capacity	--	@30/1232 kW
GES Site and Capacity	--	--
Active Power Losses (kW)	1709.597	1009.931
Reactive Power Losses (kVAR)	1159.583	684.857
Cost of Active Energy Loss (USD)	37,440.173	22,117.481
Pollution Cost (USD)	1,040,967,338	1,027,467,587
Investment and Operation Cost (USD)	--	1,021,216.180
HES Cost (USD)	--	--

displays the quantitative outcomes of the optimization process in Scenario One. For Scenario One, the location of wind turbines and photovoltaic panels, without the inclusion of GES, has resulted in the performance of the network being improved. In fact, the utilization of renewable sources of energy without energy storage has produced significant gains. Real and reactive losses have fallen by 40.93% and 40.94%, respectively. Also, the energy losses cost decreased by 40.94%. The pollution cost has also decreased, from USD 1,040,967,338 to USD 1,027,467,587, which is a decrease of USD 13,499,751, or 1.29%. The investment cost of the scenario amounts to USD 1,021,216.180, covering the investment cost in the photovoltaic panels (USD 395,429.179) and wind turbines (USD 625,787.001). The outcome shows the extent to which the effect of substituting renewable resources can contribute towards reducing operating costs, as well as environmental impact.

Figure 5 illustrates the real and reactive losses in the network for the same 24 h period for Scenario One, and this figure shows the reduction of the real and reactive losses in Scenario One against the base mode. In Scenario One, the use of renewable sources without storage has immensely cut down the network losses. It also reduced pollution-related costs. Reducing the system’s dissipation of energy and maximizing its efficiency reduced the total operation costs, creating economic as well as environmental savings. This shift not only increases the performance of the network but also enhances sustainability goals by minimizing the negative environmental impacts. The results underscore the need to utilize renewable resources in grid networks, particularly if storage units are not utilized.

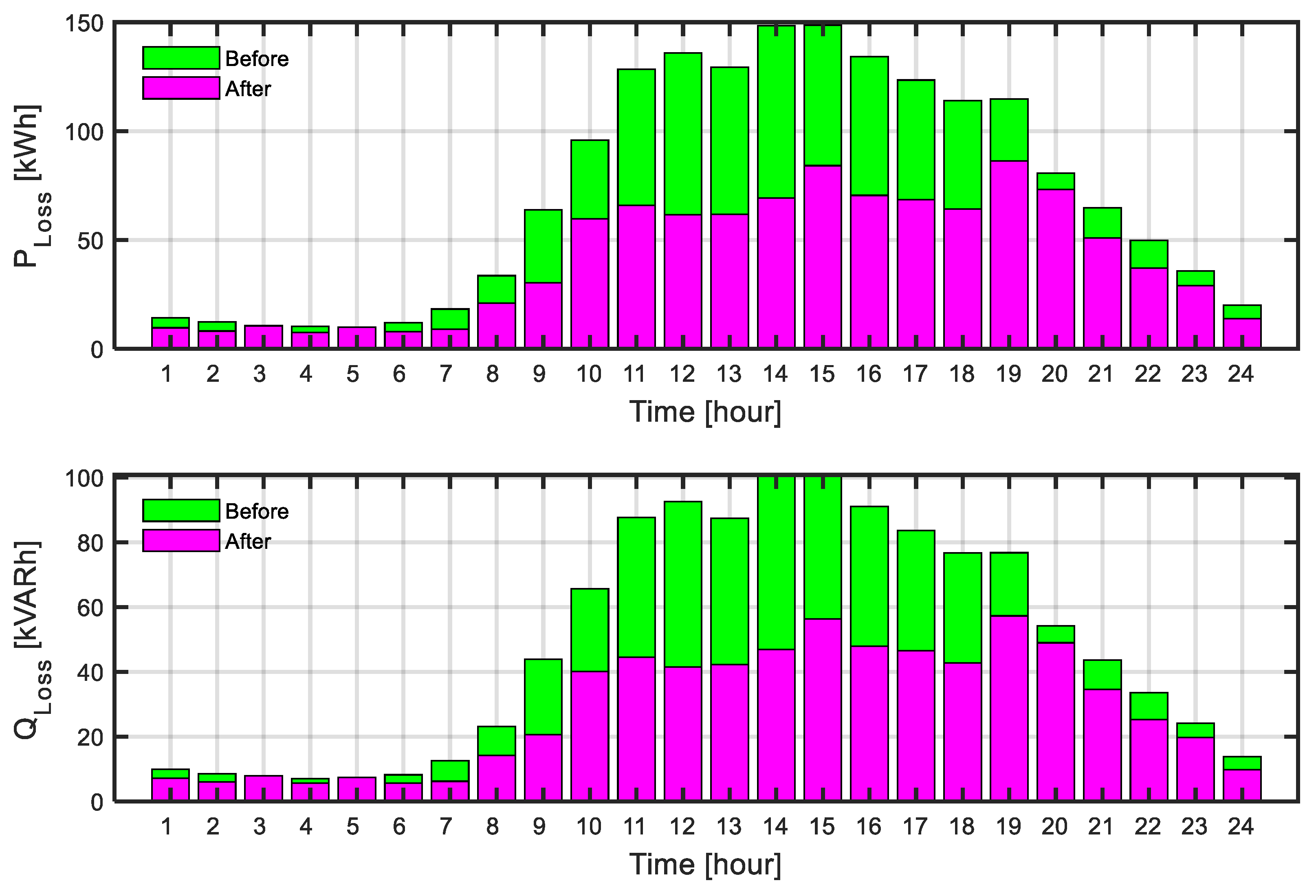
3.3. Results of Scenario Two

In the second scenario, the primary focus is on the deployment of load response strategies. This scenario investigates the impact of utilizing renewable resources in conjunction with demand response systems on the entire performance of the distribution system. The results of the 33-bus IEEE system optimization are presented in Figure 6, and the elaborate numerical optimization findings for Scenario Two are given in

Table 5. Numerical optimization results for Scenario Two.

Parameter	Base Network	Scenario Two Values
WT Site and Capacity	--	@14/459 kW
PV Site and Capacity	--	@29/1034 kW
GES Site and Capacity	--	--
Active Power Losses (kW)	1709.597	992.244
Reactive Power Losses (kVAR)	1159.583	678.560
Cost of Active Energy Loss (USD)	37,440.173	21,730.358
Pollution Cost (USD)	1,040,967,338	1,026,530,271
Investment and Operation Cost (USD)	--	757,111
DR Cost (USD)	--	43,901
HES Cost (USD)	--	--

. In these conditions, a 459 kW wind turbine is put at bus 14, while an installation of a 1034 kW PV is placed at bus 29. There is no hybrid energy storage system (HES) in this scenario, unlike the first case. The coupling of demand response with renewable sources aims to increase the efficiency of networks by changing the patterns of loads in relation to real-time network conditions. The approach demonstrates the potential for synergistic effects between renewable energy and demand-side management practices, where supply and demand are balanced, and the network is optimized.

In this case, the utilization of renewable energy sources and incentive-based demand response has resulted in active losses and their associated costs. The active losses decreased from 1709.597 kW to 992.244 kW, which is a reduction of 717.353 kW, or 41.96%. Similarly, the reactive losses have decreased from 1159.583 kVAR to 678.560 kVAR, which is a reduction of 481.023 kVAR, or 41.48%. The cost of energy due to active loss has also reduced significantly, from USD 37,440.173 to USD 21,730.358, a reduction of USD 15,709.815, or 41.96%. The cost of pollution has also reduced from USD 1,040,967,338 to USD 1,026,530,271, a reduction of USD 14,437,067, or 1.38%.

The total investment and operational expense of this situation amount to USD 757,111 in terms of expenses incurred on the installation of photovoltaic panels (USD 331,964) and wind turbines (USD 425,146). Furthermore, the expense of having the load response mechanism installed within this situation amounts to USD 43,901. These results clearly suggest the cost-effectiveness of using renewable resources and demand response mechanisms for reducing operating and environmental costs. By increasing the overall efficiency of the distribution grid, this approach not only leads to considerable cost savings but also serves to establish a more sustainable and efficient power grid. This process is a good example of how combining renewable energy with advanced demand-side management techniques can significantly enhance grid efficiency while decreasing the environmental impact.

Thus, in Scenario Two, the siting of renewable resources and demand response strategy has decreased the losses. The demand response strategy has also been used to achieve additional cost and loss reduction.

The findings indicate that renewable resources and DR integration can significantly improve the efficiency and overall performance of the distribution system. Not only do they yield substantial cost benefits, but they also help largely mitigate environmental pollution, thereby supporting environmental sustainability and long-term development goals. Figure 7 shows the losses over 24 h for Scenario Two, highlighting the reduction of both losses in Scenario One in comparison with the base mode. Further, Figure 8 displays the demand response power over the same 24 h time interval for Scenario Two, again illustrating the impact of demand-side management in grid performance optimization and energy loss reduction.

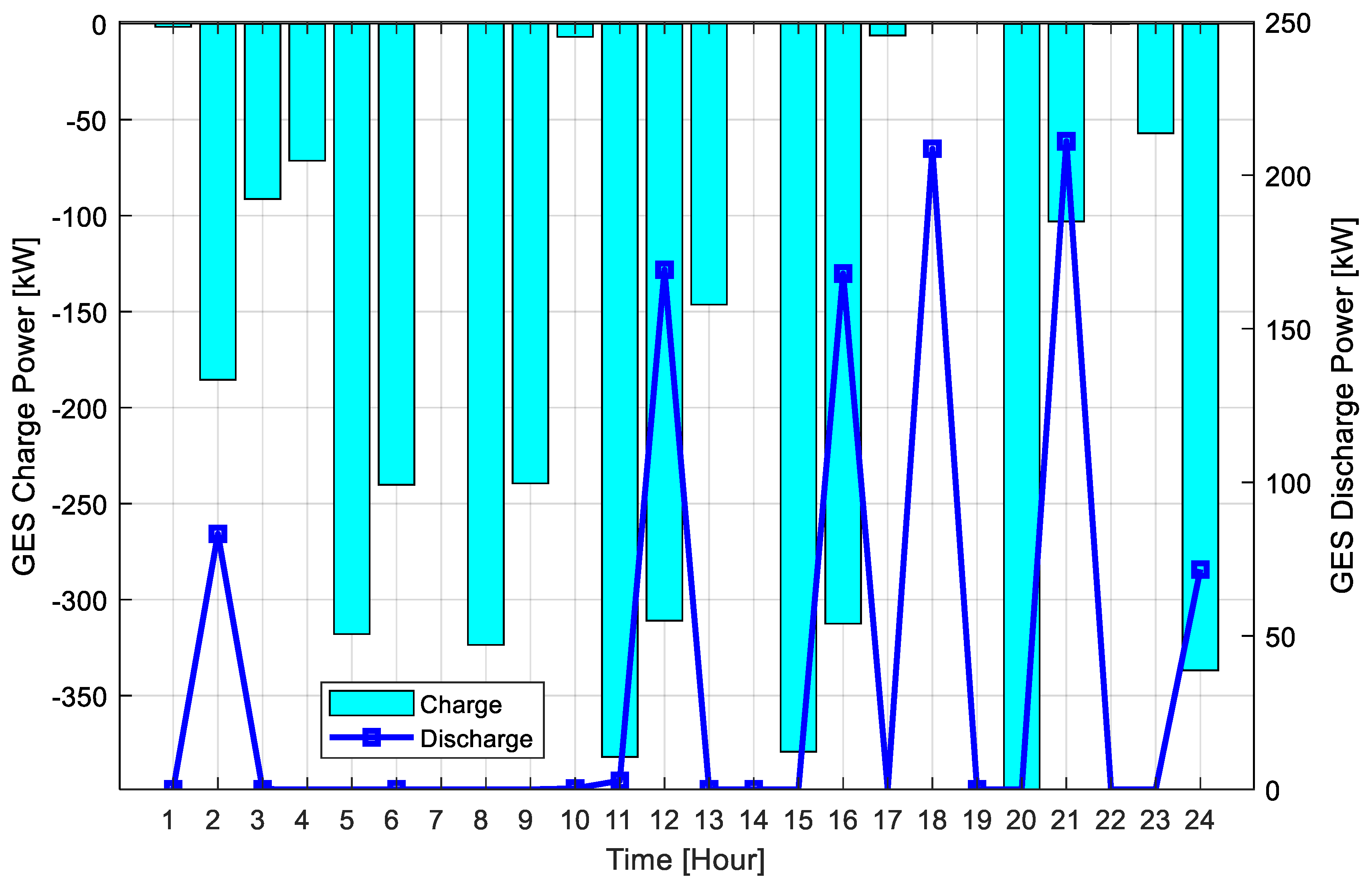
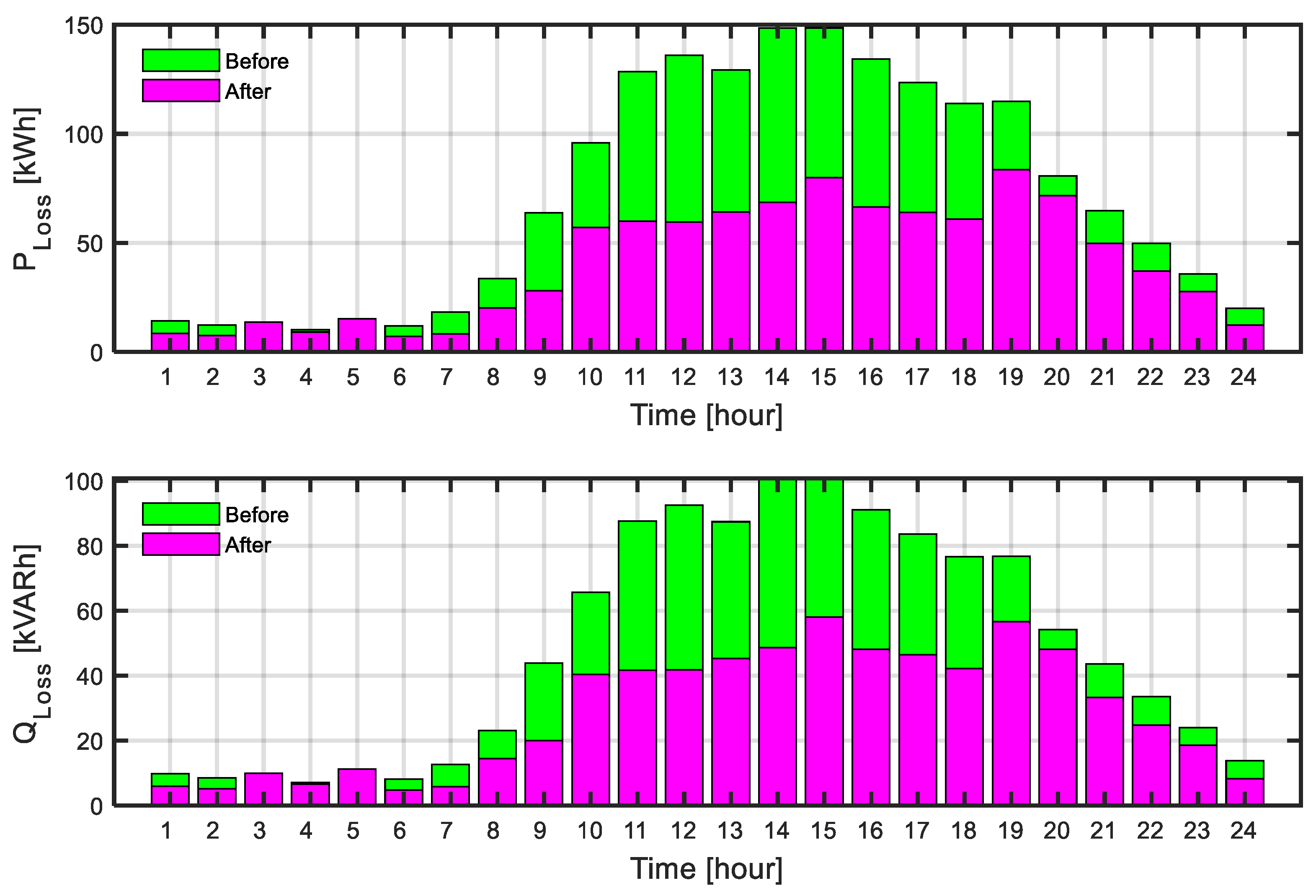
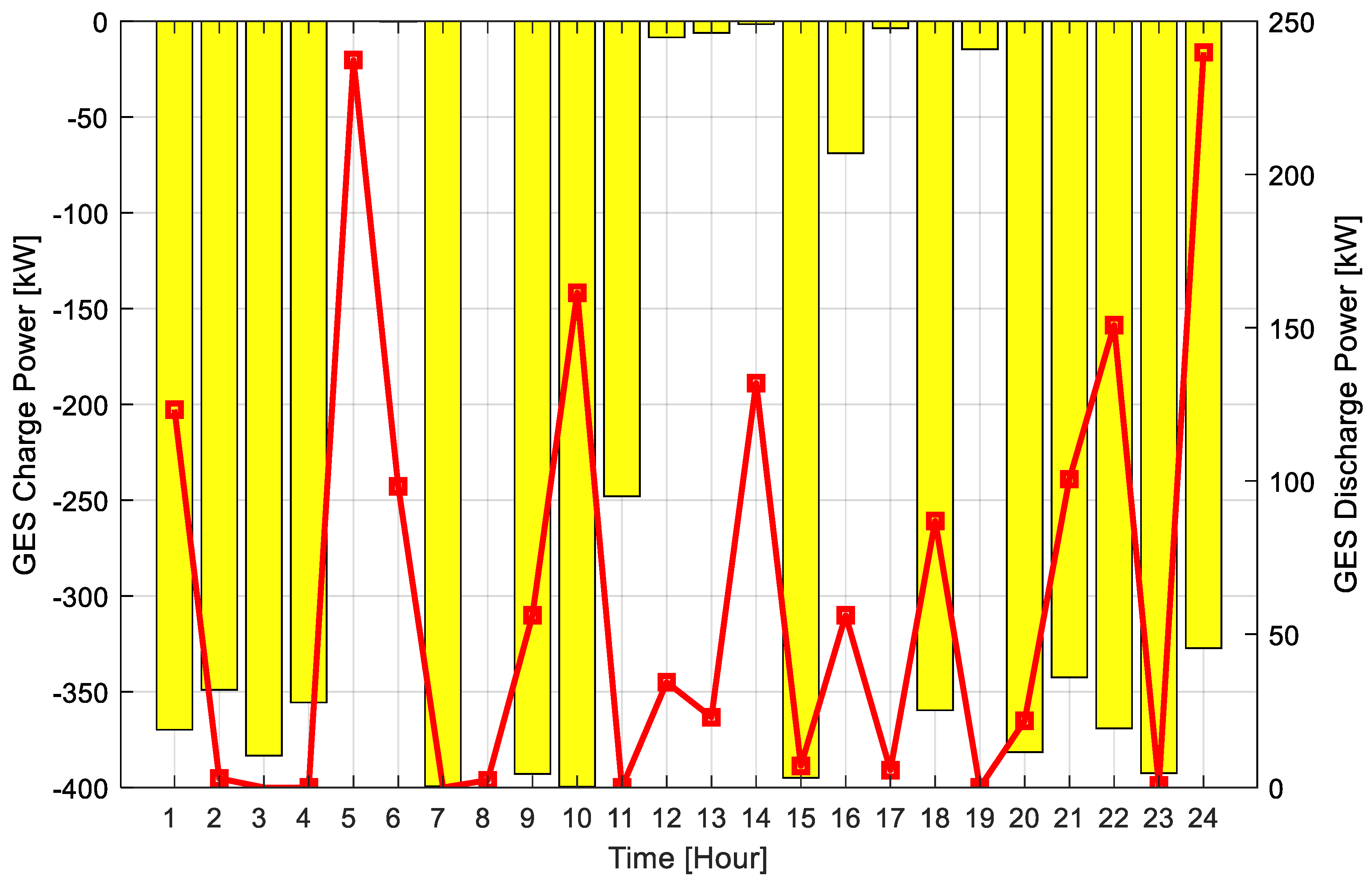
3.4. Results of Scenario Three

In the third scenario, load response is managed by applying GES instead of the incentive-based response program. This approach uses the GES to act as a source of energy in specific hours and as an energy consumer in other hours, so that more flexible management and optimization of the grid can be achieved. The 3D Pareto front solution set in Figure 9 illustrates the distribution of solutions generated by the proposed stochastic optimization framework with respect to three main performance criteria for Scenario Three. The red markers represent the trade-off surface among competing objectives, such as minimizing power losses, reducing overall costs, and improving operational reliability. The structured curve-like spread of points indicates that the MO-EWAA effectively balances exploration and exploitation during the optimization process. The coherent distribution of solutions suggests that the algorithm avoids premature convergence and instead captures a broad spectrum of Pareto-optimal solutions.

The results of the 33-bus system are illustrated in Figure 10, which illustrates the network performance under this scenario. Under this scenario, a wind power generation with a size of 959 kW is placed on bus 11, and a PV with 1268 kW capacity is installed at bus 29. A GES with 211.05 kW is also installed at bus 20, contributing to the capacity of the network to effectively balance demand and supply. This configuration represents the advantages of putting renewable resources together with energy storage in enhancing grid performance, particularly in managing variable energy consumption and system stability.

Numerical optimization results for Scenario Three are presented in

Table 6. Numerical optimization results for Scenario Three.

Parameter	Base Network	MO-EWAA	MO-WAA	MO-PSO	NSGA-II	MO-GWO
WT Site and Capacity	--	@29/959 kW	@26/973 kW	@29/971 kW	@29/978 kW	@29/968 kW
PV Site and Capacity	--	@11/1268 kW	@8/1305 kW	@13/1255 kW	@8/1311 kW	@13/1259 kW
GES Site and Capacity	--	@20/211.05 kW	@11/196.58 kW	@20/215.40 kW	@20/192.38 kW	@20/219.01 kW
Active Power Losses (kW)	1709.597	847.890	863.36	856.910	861.574	858.311
Reactive Power Losses (kVAR)	1159.583	578.146	610.20	589.372	607.033	591.248
Cost of Active Energy Loss (USD)	37,440.173	18,568.800	18,907.584	18,766.329	18,868.470	18,797.011
Pollution Cost (USD)	1,040,967,338	1,024,341,093	1,024,629,114	1,024,475,662	1,024,527,816	1,024,493,276
Investment and Operation Cost (USD)	--	1,295,191	1,318,403	1,303,227	1,322,791	1,302,425
DR Cost (USD)	--	--	--	--	--	--
HES Cost (USD)	--	11,542	12,092	11,859	12,165	11,923
Hypervolume		0.9263	0.8927	0.9058	0.9042	0.9046
Spacing		0.2029	0.2573	0.2210	0.2275	0.2234

. Simulation of Scenario Three reveals that the integration of renewable resources with GES has enhanced the performance of the distribution network significantly. Real and reactive losses are reduced by 50.40% and 50.14%, respectively, compared with the base network. These tremendous reductions in losses totaled the reduction in the cost of active loss energy, which fell from USD 37,440.173 to USD 18,568.800, a savings of USD 18,871.373, or 50.40%. This improvement highlights the importance of coupling renewable energy sources and energy storage devices in optimizing network efficiency, reducing operational cost, and improving overall grid stability. The results demonstrate the significant potential of these kinds of mechanisms in assisting towards more sustainable and economic energy management.

Even though the losses have drastically decreased, and the expenses are incurred, there is a marginal rise in the cost of emissions of 1.57%. The marginal increase in the pollution cost of 1.57% in Scenario 3, despite higher renewable penetration, is explained by the GES operational strategy. Charging the GES requires the system to draw more power from the main grid when the renewable generation is insufficient. If this charging falls within a time when the intensity of grid emissions is high, such as during peak evening hours, then the carbon footprint from this could offset some of the savings that renewables generate in terms of emissions. This indicates the need to optimize not just the sizing but also the temporal dispatch of storage in relation to the grid’s emission profile. While the overall performance of the system has improved, the marginal rise in pollution costs shows that the addition of storage systems and renewable sources may have secondary effects on environmental considerations, perhaps due to increased infrastructure or operational needs in certain areas. This necessitates further examination of the environmental effects of GES technology use in the grid. Further, the operational and investment costs in this instance increased to USD 1,295,191. This increase reflects the need for higher investment in renewable energy infrastructure. In Scenario Three, the active and reactive losses in the network have reduced significantly as a result of using renewable sources in conjunction with GES storage. The cost of investment is greater than in past scenarios where DR was given priority, yet this scenario still displays high economic efficiency. In general, the findings indicate that the integration of renewable resources, when combined with GES, can greatly enhance the efficiency and overall performance of the distribution system. These gains underscore the value of adding renewable energy and energy storage technologies in optimizing both the economic and operational aspects of the grid, with the ultimate goal of transitioning towards a more sustainable and affordable energy system.

The MO-EWAA superiority to solve Scenario Three is compared with MO-WAA, NSGA-II [37], MO-GWO [38], and MO-PSO algorithms. In terms of optimization performance based on Table 3, the MO-EWAA demonstrates superiority over MO-WAA, NSGA-II, MO-GWO, and MO-PSO when evaluated using the Hypervolume and Spacing indicators. Specifically, MO-EWAA achieves a Hypervolume value of 0.9263, which surpasses the 0.8927, 0.9058, 0.9042, and 0.9046 obtained by MO-WAA, NSGA-II, MO-GWO, and MO-PSO. In terms of optimization performance based on Table 6, the MO-EWAA demonstrates superiority over both MO-WAA and MO-PSO when evaluated using the Hypervolume and Spacing indicators. Specifically, MO-EWAA achieves a Hypervolume value of 0.9263, which surpasses the 0.8927 obtained by MO-WAA and the 0.9058 achieved by MO-PSO. A higher Hypervolume value reflects the algorithm’s ability to capture a wider portion of the objective space, thereby providing a broader spectrum of Pareto-optimal solutions and improving solution diversity. Furthermore, MO-EWAA also outperforms its counterparts in terms of the Spacing index, achieving the lowest value of 0.2029. In comparison, MO-WAA, NSGA-II, MO-GWO, and MO-PSO report values of 0.2573, 0.2210, 0.2275, and 0.2234, respectively. Since a smaller Spacing index indicates a more uniform distribution of solutions across the Pareto front, this result highlights that MO-EWAA ensures a more balanced and well-spread trade-off among objectives. Consequently, MO-EWAA, based on the Elite selection mechanism, not only enhances the diversity of solutions but also improves the quality of Pareto front representation, making it more effective for solving complex multi-objective optimization problems.

In network optimization, vast variations are shown between Scenario Three and Scenario Two, highlighting the effectiveness of GES combined with the renewable sources. Scenario Two from the demand response approach shows a decrease in active as well as reactive losses of 41.96% and 41.48%, respectively. Scenario Three from the utilization of GES reduces active as well as reactive losses of 50.40% and 50.14%, respectively. Active loss energy cost and emission cost are reduced by 41.96% and 1.38% for Scenario Two, but are reduced further in Scenario Three by 50.40% and 1.57%, respectively. Figure 11 illustrates active and reactive losses for the same 24 h period for Scenario Three.

Figure 12 and Figure 13 demonstrate the PV and WT power generation during 24 h for Scenario Three. Figure 14 indicates the 24 h charge and discharge power of the GES under Scenario Three. The reserve energy management of the GES has played a role in significantly improving the performance of the distribution network. By coordinating with the renewable energy sources, it has been successful in maintaining every one of the main objectives, such as raising energy efficiency, reducing losses, and maintaining grid stability. This integration of GES with renewable sources reflects a tremendous leap towards achieving an energy system that is more secure and sustainable.

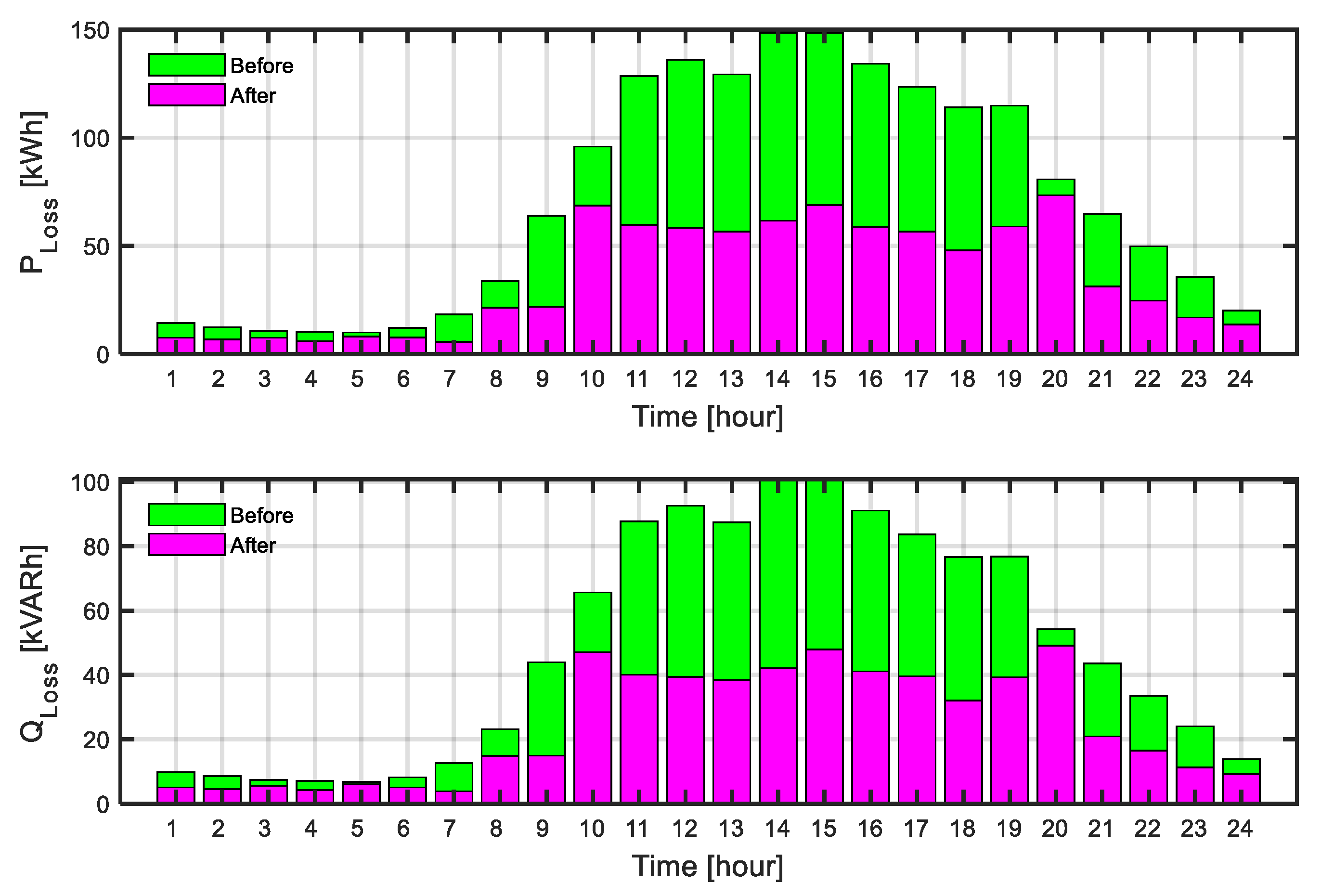
3.5. Results of Scenario Four

One important outcome from the stochastic model is that the optimal placement and sizing of units have changed when compared to the deterministic case-Scenario Three: For example, WT relocates to bus 27 from bus 29, and PV is sized at its maximum. This is because the 2PEM identifies locations and sizes that are less sensitive to worst-case scenarios of low wind or solar input, often favoring nodes with better access to the grid as a backup and maximizing the most cost-effective renewable source to mitigate risk.

In this scenario, a two-point estimation method is employed to deal with uncertainties concerning renewable resources and loads. The outcomes from the optimization algorithm indicate vast variations in key parameters, such as active loss, reactive loss, associated energy, and investment cost compared to Scenario Three. Scenario Four and Scenario Three share a common theme of maximizing renewable resource utilization in distribution systems but have different ways of dealing with uncertainty in load and resources. Scenario Three uses GES as a reaction to the load, whereas Scenario Four uses 2m + 1 PEM. This disparity highlights the flexibility of the two approaches in addressing the uncertainties of variable renewable generation and volatile load demand, ultimately affecting the network’s effectiveness and cost.

Probabilistic data of renewable resources and load via the 2m + 1 PEM for Scenario Four are presented in Figure 15.

The numerical optimization results for Scenario Four, based on the MO-EWAA and the two-point estimation method, are shown in

Table 7. Numerical optimization results for Scenario Four.

Parameter	MO-EWAA (Scenario Three)	MO-EWAA (Scenario Four)	MO-WAA (Scenario Four)	MO-PSO (Scenario Four)
WT Site and Capacity	@29/959 kW	@27/691 kW	@9/871	@6/1508 kW
PV Site and Capacity	@11/1268 kW	@11/2000 kW	@28/1697 kW	@15/786 kW
GES Site and Capacity	@20/211.05 kW	@2/239.83 kW	@3/43 kW	@2/41 kW
Active Power Losses (kW)	847.890	899.74	916.052	909.923
Reactive Power Losses (kVAR)	578.146	615.724	641.285	590.879
Cost of Active Energy Loss (USD)	18,568.800	19,704.306	20,061.538	19,927.314
Pollution Cost (USD)	1,024,341,093	1,045,406,492	1,045,626,527	1,045,573,112
Investment and Operation Cost (USD)	1,295,191	1,346,285	1,454,855	1,388,495
DR Cost (USD)	--	--	--	--
HES Cost (USD)	11,542	13,117	13,465	13,286
Computational Time (s)	--	279	317	305
Standard Deviation (%)	--	0.8571	1.2644	1.2193

. The approach employs a GES to act as a supply during some hours and a load during other hours to optimize the flexibility and efficiency of the system. The solution outcomes are shown in Figure 16. A WT of 691 kW capacity is placed at bus 27, and a photovoltaic system of 2000 kW capacity is mounted on bus 11. In addition to that, a GES system of 239.83 kW capacity is applied at bus 2. The above setup reflects the applicability of renewable sources and storage systems in enhancing network performance, evening out supply and demand, as well as reducing operational costs. Incorporation of GES enhances the management of energy swings and hence the general reliability and efficiency of the distribution system.

Based on the results that have been achieved and the comparison of Scenarios Three and Four (in Table 7), real and reactive losses and energy losses costs have increased by 6.11%, 6.50%, and 6.50%, respectively, due to uncertainty. The emissions cost and renewable investment cost have also increased by 2.056% and 3.94%, respectively, due to uncertainty in resource production and network load. In addition, the cost of GES has increased from USD 11,542 to USD 13,117 (13.64%) under the uncertainty model. The uncertainty of the renewable generation and load is modeled by 2m + 1 PEM, which makes the optimization adopt a more conservative and robust design. This robustness increases the loss, emission, and investment costs by 6.50%, 2.056%, and 3.94%, respectively. To hedge the risk of low solar/wind generation or high load, the model conducts the following:

• It invests in slightly larger WT/PV/GES units—increased investment cost—to make sure it is reliable in a wider range of conditions.
• It may be more reliable but possibly more expensive or pollute the grid power as a buffer, increasing operational costs and emissions.
• Optimal placement and sizing under uncertainty yield different power flow patterns that can lead to higher expected energy losses.

These increased ‘costs of uncertainty’ represent the premium required to ensure system reliability against variability. The cost augmentation in Scenario Four is for uncertainty consideration, and the system requires an increased consumption capability and greater investment. This approach helps to capture the uncertainty and variability of demand and supply, so that the network can better respond to potential change and uncertainty. As a result, although the cost is higher, the system is more resilient and better placed to maintain stability and efficiency during uncertainty. The use of probabilistic information and the two-point estimation technique helps managers to make more strategic choices in relation to renewable units, but at the expense of increased investment. Therefore, Scenario Four demonstrates how, with the use of probabilistic data and two-point estimation techniques, a great enhancement in network performance and reduction in related energy expenditure is achievable at the expense of having to be ready to respond to more complex conditions caused by uncertainty.

And the computational performance of the improved MO-EWAA in solving Scenario Four has been compared with traditional MO-WAA and MO-PSO algorithms through 25 independent runs of each algorithm with a population size of 50 and an iteration number of 200, based on the computational time metrics and percentage standard deviation from the final solution. As can be seen from Table 7, the proposed method reached the final result with fewer computation costs among other methods, and the final result percentage standard deviation of the proposed method was less than 1%, while the same for MO-WAA and MO-PSO methods was 1.2644% and 1.2193%, respectively, hence confirming the better performance of the proposed improved optimizer.

Figure 17 illustrates the active and reactive losses over the same 24 h period for Scenario Three. As shown in this figure, the active and reactive power loss decreases in comparison with the base network in Scenario Four.

In Figure 18, the 24 h discharge and charge powers of GES in Scenario Four highlight its effective coupling with renewable energy. Reserve energy management of GES maximizes grid operation through a balance between demand and supply, maximizing energy efficiency, and reducing operation costs. It also ensures grid stability through the counteraction of fluctuation in renewable energy output. By efficiently running energy storage, GES provides a reliable source of power during periods of low renewable generation, reducing reliance on conventional power sources. Through this integration, carbon emissions decrease, creating a cleaner, more robust supply network and, more significantly, helping to achieve the overall goal of shifting away from dirty sources of power towards cleaner options.

The reason for the large variation in optimal unit placement across scenarios includes the WT location between buses 11, 14, 29, and 27, which is driven by the complex interactions of objectives and constraints. Scenarios without GES (One and Two) use unit placements to minimize losses for a given load profile. Introducing GES (ScenarioThree) decouples energy delivery from generation, and resources can be placed for optimal grid support—e.g., loss reduction, voltage control-which may be at different nodes. Lastly, the stochastic model of Scenario Four prioritizes robustness over pure optimality in search of locations that perform well across a range of uncertain conditions, which resulted in the different final configuration.

4. Comparison with Previous Studies

Based on the results of Case III, the performance of the proposed MO-EWAA framework is compared with previous advanced studies, namely the multi-objective enhanced exponential distribution optimizer (MOEEDO) [39] and the multi-objective crested porcupine optimizer (MOCPO) [40], as detailed in

Table 8. The comparison results of Case III with previous studies (decreasing percentage versus base case).

Parameter	MO-EWAA	MOEEDO [39]	MOCPO [40]
Active Power Losses (kW)	50.40	41.96	44.03
Reactive Power Losses (kVAR)	50.14	41.48	43.05
Cost of Active Energy Loss (USD)	50.40	41.96	44.03
Pollution Cost (USD)	1.60	1.27	--

. The comparison confirms the superiority of the proposed MO-EWAA framework, which achieves the highest reduction percentages across key performance indicators. Specifically, MO-EWAA attains a 50.40% decrease in active power losses and a 50.14% reduction in reactive power losses, outperforming both MOEEDO (41.96% and 41.48%, respectively) and MOCPO (44.03% and 43.05%, respectively). Similarly, for the cost of active energy losses, MO-EWAA yields a 50.40% reduction, compared to 41.96% by MOEEDO and 44.03% by MOCPO. Furthermore, in terms of environmental impact, the proposed framework achieves a pollution cost reduction of 1.60%, surpassing the 1.27% reduction reported for MOEEDO in [37]. This demonstrates that the proposed MO-EWAA framework offers a more effective solution for minimizing power losses and associated costs, while also contributing to lower environmental pollution, thereby validating its enhanced performance in the optimal integration of renewable energy and storage systems within distribution networks.

5. Conclusions

This work presented the development and validation of a comprehensive stochastic multi-objective framework for the optimal integration of GES with renewable resources in distribution networks. The results, obtained from the detailed analysis of four different scenarios on a standard 33-bus test system, underpin the importance of advanced optimization and uncertainty modeling for the attainment of techno-economic-environmental objectives. The main conclusions are summarized as follows:

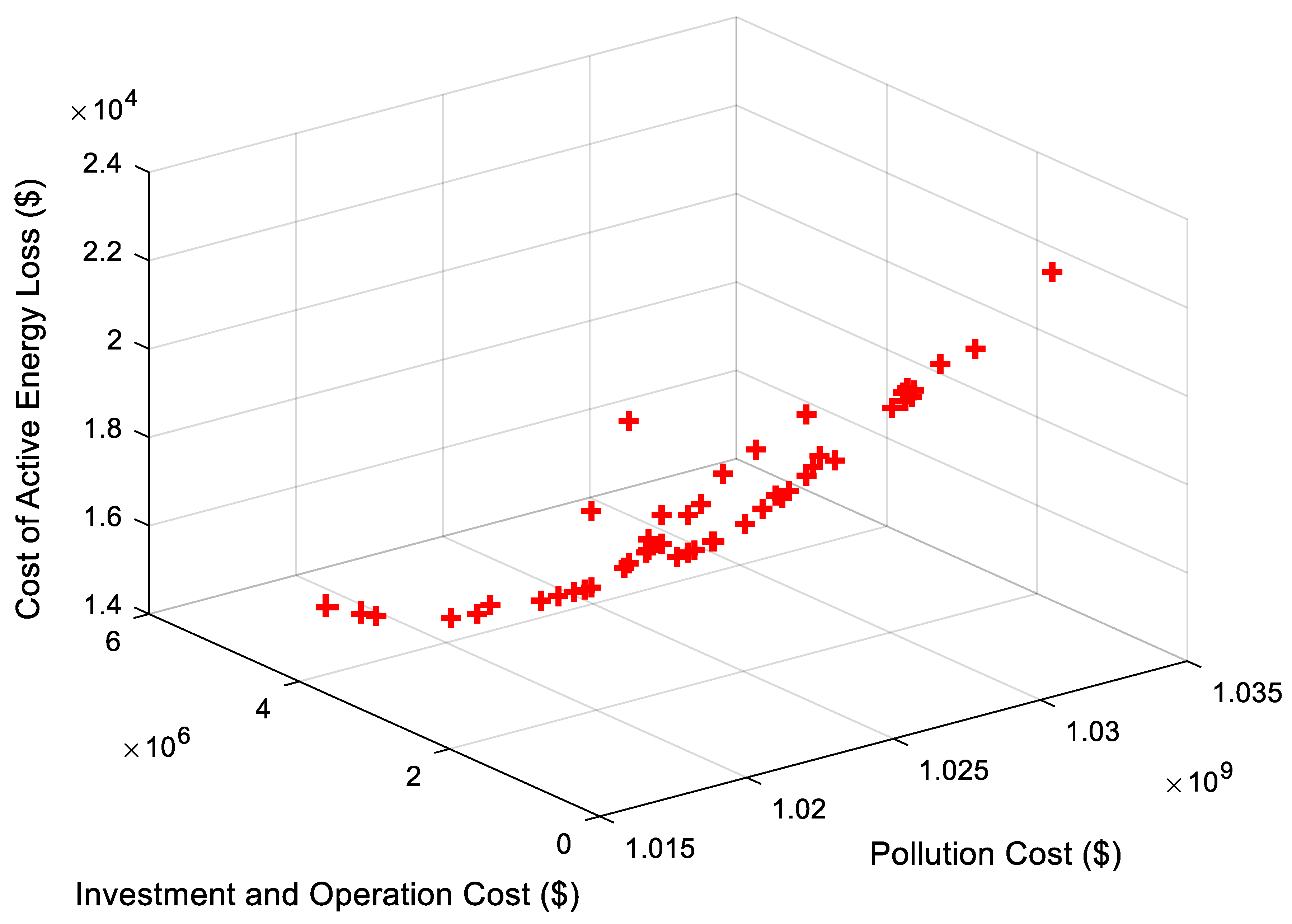
• The proposed MO-EWAA was rigorously tested against conventional MO-WAA, MO-PSO, NSGA-II, and MO-GWO. As evidenced by the results, MO-EWAA demonstrated superior performance by achieving the lowest active power losses (847.89 kW), the lowest investment and operational cost (USD 1,295,191), and the lowest pollution cost (USD 1,024,341,093). This practical superiority is complemented by its exceptional optimization metrics, where it achieved the highest Hypervolume (0.9263) and lowest Spacing (0.2029), confirming its superior ability to find a well-distributed and high-quality set of Pareto-optimal solutions. This combination of best-in-class practical results and robust multi-objective performance solidifies MO-EWAA as a highly effective and reliable optimizer for complex stochastic multi-objective problems in distribution networks.
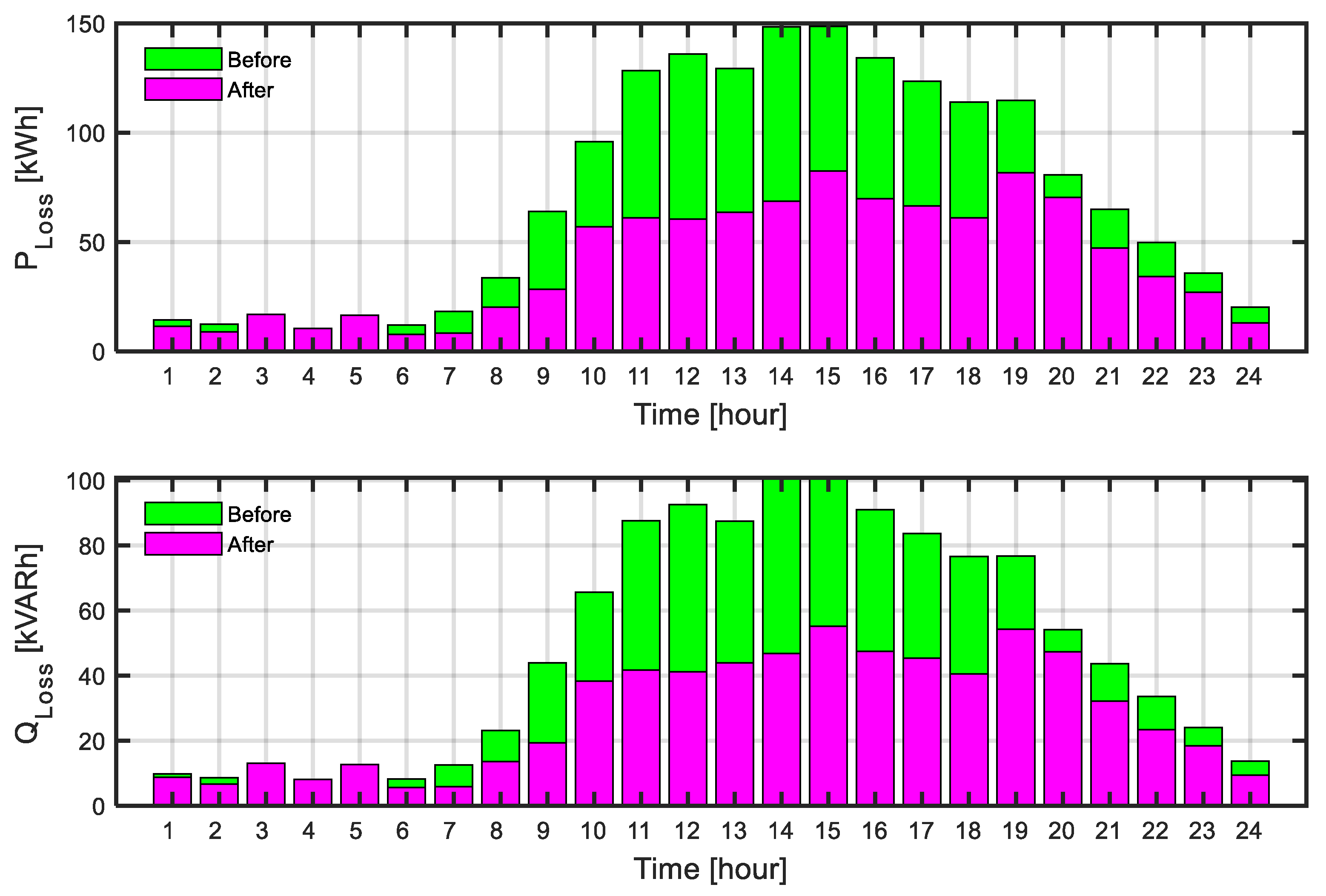
• GES integration with renewable resources proved to be a game-changing strategy. As can be viewed, Scenario Three, based entirely on operation via GES, has active and reactive power losses reduced by about 50.40% and 50.14%, respectively, demonstrating far superior performance compared to demand response-based scenarios—Scenario Two or renewable-alone-based Scenario One.
• The application of 2PEM in Scenario Four resulted in a power system where the uncertainties of renewable generation and load were quite pronounced. Although the stochastic model resulted in necessary increases in investment (3.94%) and operational costs—e.g., a 6.50% increase in energy loss cost—to ensure a robust system, it was a far more reliable and realistic result from the planning perspective, quantifying the cost of uncertainty and the value of risk-aware decisions.
• The MO-EWAA also showed the best computational performance by converging to the final solution much quicker compared to others, while having a standard deviation less than 1% over different runs; this confirms reliability and consistency against MO-WAA (1.2644%) and MO-PSO (1.2193%).

In brief, this research concludes that the synergistic integration of GES and renewables based on the proposed MO-EWAA with a stochastic framework can be an extremely efficient strategy for modernizing distribution networks and enhancing efficiency while minimizing environmental impacts; therefore, such approaches can help ensure operational resilience. Future work is recommended to conduct robust scheduling of multi-energy storage systems, including GES, batteries, and hydrogen with renewable sources in large-scale networks, which helps to further the advances in energy loss reduction and reliability improvement, together with emission control.