Determination of the Water Outflow Zone on the Ground Surface After a Pipe Failure Using Fractal Geometry

Abstract

Uncontrolled water outflows from water supply pipes can pose a serious threat to human safety and infrastructure due to the washing out of soil particles and the formation of subsurface voids, leading to soil subsidence (suffosion). One way to mitigate these hazards is by determining water outflow zones (WOZ) around underground pipes, within which water may emerge on the soil surface. This paper presents the final stage of a broader study on the use of fractal geometry for determining WOZ. Suffosion hole locations form point structures that exhibit features of probabilistic fractals, and their parameters depend on the number of points in the structure. The objectives of the study were: (1) to determine the minimum number of points required for a structure to be considered representative; (2) to establish a relationship for calculating the WOZ radius; and (3) to empirically verify the theoretical WOZ radius values. Representative structures were identified and used to calculate the R_fr parameter, which, after scaling to real conditions, enabled determination of the WOZ radius, ranging from 3.5 to 5.5 m. Empirical verification confirmed the method’s validity, as theoretical zones covered up to 100% of actual outflow points (96% overall). The developed method can be applied into decision-support systems for sustainable infrastructure planning, and more efficient use of water resources.

1. Introduction

The water distribution network (WDN) is a key component of urban infrastructure, responsible for ensuring a continuous supply of potable water to consumers in the required quantity, at the appropriate pressure, and in compliance with the quality standards defined by relevant legal regulations [1]. According to the water balance proposed by International Water Association (IWA), the difference between the water system input volume and the authorized water consumption is referred to as water losses, which are generally categorized into apparent losses and real losses [2]. The real losses occur primarily within the water supply network, as a result of failures, pipe bursts, and leaks from the underground infrastructure. On the other hand, the apparent losses refer to water that is consumed but not billed. It is lost due to the issues in meter inaccuracies, billing errors or data handling mistakes. Water utilities struggle to reduce both real and apparent losses in order to minimize the non-revenue water [3].

According to the requirements of the European Water Framework Directive [4] and the principles of sustainable water management [5], water utilities are obliged to monitor and report water losses. These data are not only a regulatory requirement but can also a support water system operation, regulation and planning [6,7]. Therefore, from both an environmental and economic standpoint, water utilities strive to reduce losses to the so-called economic level of leakage (ELL) [8]. This level represents the balance point at which the cost of leak detection and repair equals the economic value of the water saved, including the energy and treatment costs associated with its intake and distribution. In practice, achieving or maintaining the ELL requires a combination of preventive maintenance, hydraulic monitoring, and advanced leak detection techniques [9,10]. Recent policy developments emphasize the need for improving the efficiency and resilience of water supply networks [11]. Consequently, the detection, quantification, and mitigation of real water losses are becoming key components of integrated water resource management strategies. However, given the spatial complexity of water distribution systems, detecting and predicting water leakages remains a challenge. A wide range of leak detection approaches has been developed, including hardware-based methods, software-based methods, leakage localization methods, and smart water network approaches [12,13,14,15]. However, despite significant advances, the accurate localization of underground leaks and the prediction of potential water outflow zones on the surface remain difficult due to the complex interaction between hydraulic and geotechnical parameters [16,17].

The water supply systems are considered as components of the critical infrastructure, because their reliable operation is essential for public health, national security and economy [18,19]. Failures of water pipes can lead not only to interruptions in water delivery, but can also affect other infrastructure systems, such as transportation or energy. Although undesired, failures of water pipes are an inevitable aspect of system operation [20,21]. The nature and frequency of such failures, including their location, size, and the volume of water discharged—depends on a variety of factors such as pipe material and age, installation conditions, soil type, internal pressure, and local geological or hydrological conditions [22,23]. Additionally, cyclic pressure variations and temperature changes can accelerate material fatigue, further increasing the probability of leaks [24]. When a pipe failure occurs, the pressurized water flows into the surrounding soil matrix. The outflow of water into the soil can initiate suffosion processes—the washing out of fine particles from the soil structure [25], leading to local soil instability, subsidence, and even sinkhole formation. Such phenomena can endanger human safety, damage nearby underground utilities, and significantly increase the cost of emergency repairs [26].

One of the approaches to mitigating the negative effects of water pipe failures is the design of safety zones around the pipelines. These zones are defined as areas surrounding a water pipe where in the event of pipe failure, water is expected to reach the ground surface within a specific distance from the failure point. The identification of such zones are of great importance for spatial planning and urban engineering, as they allow for excluding sensitive areas from the construction of roads, pavements, or other underground installations. One way to determine the outflow zone is through a geometrical analysis of the distribution of water outflow points on the soil surface. These points create irregular sets that are difficult to be described on the concepts of classical Euclidean geometry but simultaneously meet the conditions for random fractals. The present paper is the third and final part of a research cycle devoted to the application of fractal geometry in identifying water outflow zones resulting from pipe failures. Building upon previous findings, the current study integrates theoretical and empirical approaches to propose a comprehensive methodology for determining the Water Outflow Zone (WOZ) on the ground surface after a pipe failure. The aim was to develop a mathematical formula that can be used by water utilities to predict the range of potential outflow areas under various operational and soil conditions.

2. Materials and Methods

The analyses presented in this article are the last part of a larger scope of research, the purpose of which is the WOZ determination in relation to the fractal characteristics of water outflows. The results of earlier analyses have already been published [27,28,29,30,31,32,33,34]. The full scope of research is presented in Figure 1.

The laboratory tests of an underground water pipeline failure scaled 1:10 were the basis of analyses. The tests were carried out for 5 different leak areas (2.83–18.84 cm²) and 7 values of pressure head in the tested pipe (3.0–6.0 m H₂O) [27,28,29]. The pipe was buried in the compacted sand (93–94% of the Proctor density). As a result of a physical leakage simulation, water flowed onto the surface, washing out the soil and forming suffosion holes [30,31,32]. These holes were assigned points in a coordinate system originating at the location of leak from the pipe. The points corresponding to the suffosion holes formed 12 real structures (RSs) embedded in a 2D space, exhibiting fractal characteristics. These structures were simplified to forms embedded in a one-dimensional space while preserving their fractal features, creating 12 so-called theoretical linear structures (TLSs). For each TLS, a parameter R_fr was determined, defined as the product of the fractal (box-counting) dimension (D_b) of the structure and the distance ${\left(R_w\right)}_{max}$ from the leakage point to the outermost point of the structure [29].

The analyses of the TLSs showed that the number of points forming each structure affects the value of R_fr. To assess the extent of this effect, it was necessary to repeat the analysis for larger number of different linear structures, especially those composed of a high number of points. This task was made possible through the use of the Monte Carlo method to generate hypothetical linear structures (HLSs) [33]. A total of 1920 pseudorandom number sequences were generated, composed of various numbers of points n_w (50, 100, 200, 300, …, 900, 1000, 1500, 2000, 3000, 4000, 5000). Each sequence constituted a single HLS, named depending on the corresponding TLS (

Table 1. Names of fractal structures depending on corresponding laboratory tests conditions.

Type of Struct.	Leak Area [cm2]					Pressure Height [m H2O]
	2.83	4.71	9.42	15.07	18.84	3.0	3.5	4.0	4.5	5.0	5.5	6.0
RS	F1	F2	F3	F4	F5	H1	H2	H3	H4	H5	H6	H7
TLS	F1″	F2″	F3″	F4″	F5″	H1″	H2″	H3″	H4″	H5″	H6″	H7″
HLS	HF1	HF2	HF3	HF4	HF5	HH1	HH2	HH3	HH4	HH5	HH6	HH7

). It should be emphasized that each HLS name (e.g., HF1) refers not to a single structure, but 160 structures—consisting of 50, 100, …, 5000 points (16 different numbers), each repeated 10 times.

For each HLS, the distance ${\left(R_w\right)}_{max}$, the fractal dimension D_b and parameter R_fr were determined. It was observed that for each HLS there is a certain threshold value n_w (denoted as $n_{wgr}$), starting from which it can be assumed that both the R_fr values cluster around the mean (condition I) and that the mean value of R_fr remains almost constant with increasing n_w (condition II). Therefore, it is necessary to determine $n_{wgr}$ as the sufficient number of points needed to construct a representative linear structure that could serve as the basis for dimensioning the water outflow zone on the surface after an underground pipe failure.

Since the R_fr parameter proved to be crucial in determining the WOZ radius,

Table 2. Mean values of the Rfr parameter for hypothetical linear structures [33].

nw	Rfr [cm] for HLSs:
	HF1s	HF2s	HF3s	HF4s	HF5s	HH1s	HH2s	HH3s	HH4s	HH5s	HH6s	HH7s
50	30.18	37.89	34.88	35.91	34.33	32.61	33.80	35.00	32.90	36.13	38.35	35.71
100	34.05	41.92	41.25	42.93	39.87	39.78	39.41	42.78	39.43	40.18	44.89	45.24
200	38.34	48.07	45.55	48.54	45.99	42.51	42.09	47.76	42.95	41.87	48.70	48.67
300	40.55	48.91	46.63	50.66	48.26	43.12	44.14	52.36	43.84	42.28	50.84	49.75
400	42.20	50.64	46.67	51.60	50.60	43.81	44.77	53.07	43.93	42.35	51.21	50.32
500	42.35	52.07	46.78	51.76	52.10	44.27	45.03	54.86	44.33	42.36	52.31	50.44
600	43.19	53.89	46.93	51.34	52.96	44.24	44.99	54.47	44.57	42.39	52.25	50.54
700	43.34	53.37	46.98	52.57	54.37	44.31	45.18	56.01	44.58	42.36	52.86	50.50
800	43.29	54.20	47.07	53.17	53.72	44.46	45.23	55.83	44.71	42.38	52.57	50.53
900	43.06	54.35	47.19	52.91	53.86	44.71	45.40	55.91	44.65	42.37	52.16	50.62
1000	43.38	54.37	47.23	53.48	54.75	44.65	45.38	57.03	44.75	42.37	52.87	50.66
1500	43.50	55.34	47.25	53.43	55.79	44.77	45.49	57.76	44.68	42.39	52.95	50.60
2000	43.73	55.67	47.15	53.66	56.81	44.79	45.54	57.65	44.75	42.40	53.14	50.67
3000	43.67	55.85	47.16	53.82	57.48	44.80	45.56	58.15	44.78	42.41	53.14	50.68
4000	43.66	55.88	47.12	53.95	57.60	44.81	45.53	58.13	44.80	42.40	53.15	50.71
5000	43.64	55.93	47.13	53.94	58.00	44.82	45.56	58.19	44.82	42.41	53.18	50.71

presents the mean R_fr values for all generated HLSs, as determined in previous studies [33]. The analyses preceding the research included in this article have been presented in detail in [27,28,29,30,31,32,33,34].

2.1. Determination of the Minimum Number of Points for Which the R_fr Values Are Concentrated Around the Mean (Condition I)

To assess the concentration of R_fr values around the mean, one of the descriptive statistics—the coefficient of variation (CV)—was used, defined as the ratio of the standard deviation to the mean. The CV of the R_fr parameter was calculated for 12 groups of HLSs for n_w = 50, 100, …, 5000. Based on the results, CV(n_w) plots were generated, and a trendline was fitted as the best match among exponential, linear, logarithmic, polynomial, and power functions.

Statistical textbooks do not provide a strict numerical threshold for the CV value that would indicate very low variability of the analyzed parameter. However, in literature examples, such values frequently do not exceed 5% (e.g., [35,36,37,38]). Therefore, we adopted the criterion that CV ≤ 5% indicates that the R_fr values are approximately equal to the mean. By substituting this threshold value into the trendline equations, the minimum number of points satisfying condition I was calculated (denoted as $n_{wI}$). In the final step of this stage, the resulting values of $n_{wI}$ were rounded to an accuracy of 50 if 25 < $n_{wI}$ < 100, and of 100 if $n_{wI}$ ≥ 100. If $n_{wI}$ ≤ 25, a value of 50 was adopted as the smallest analyzed number of structure points, even though rounding would yield zero.

2.2. Determination of the Minimum Number of Points for Which the Mean Values of R_fr Remain Almost Constant with Increasing n_w (Condition II)

To determine from which values of n_w the increase in R_fr (n_w) can be considered negligible, unit differences $r_{fri}$ were calculated according to Equation (1):

$$r_{fri}={\displaystyle \frac{R_{fr5000}-R_{fri}}{n_{w5000}-n_{wi}}},$$

(1)

where $R_{fr5000}$ and $R_{fri}$ denote mean R_fr values for structures consisting of 5000 and $n_{wi}$ points, respectively ($n_{wi}$ ∈ {$n_{wI}$, …, 4000}). Minimal value of $n_{wi}$ is $n_{wI}$, because conditions I and II must be met simultaneously.

These unit differences were then subjected to statistical evaluation. For this purpose, at a significance level of α = 0.05, a null hypothesis was tested—that starting from a certain value of n_w (denoted as $n_{wII}$) the unit differences $r_{fri}$ are equal to zero, against the alternative hypothesis—that $r_{fri}$ ≠ 0. The one-sample Student’s t-test was used to verify the hypothesis. The verification was carried out for all 12 groups of HLSs, and for each group, successive values of $n_{wII}$ ∈ {$n_{wI}$, …, 3000} were tested.

The hypothesis verification consisted in checking whether the critical interval $CI$ according to Formula (2) included the t-statistic according to Formula (3) at the adopted significance level.

$$CI=\left(-\infty ,-t_{cr}⟩\right.\cup \left.⟨t_{cr},+\infty \right),$$

(2)

$$t={\displaystyle \frac{\overline{r_{fri}}-\mu }{SD}}·\sqrt{n-1},$$

(3)

where $t_{cr}$ is the (1 − α/2) quantile of the t-distribution obtained from statistical tables for $n-1$ degrees of freedom, $\overline{r_{fri}}$—mean of $r_{fri}$ values for the analyzed $n_w$ range (from $n_{wII}$ to 5000) for a given group of structures, $\mu$—the expected value of the unit difference ($\mu$ = 0), SD and n—the standard deviation [cm] and the number of unit differences $r_{fri}$, respectively, for the analyzed $n_w$ range (from $n_{wII}$ to 5000). All calculations were performed in MS Excel 2019.

If $t\notin CI$, there were no reason to reject the null hypothesis at the significance level of α = 0.05. The smallest value of $n_{wII}$ (denoted as $n_{wgr}$) that satisfies condition $t\notin CI$ represents the minimum number of points required to create a representative structure, whose R_fr value is approximately equal to the R_fr values of structures composed of more than $n_{wgr}$ points. Since Student's t-tests were performed for structures consisting of $n_w\ge n_{wI}$ points (based on the results of the analysis described in Section 2.2), the value of $n_{wgr}$ can be considered the minimum number of points required to construct a representative structure.

2.3. WOZ Radius Determination

It was assumed that the WOZ is circular in shape, centered directly above the potential leak and covering the points of water outflow onto the ground surface. According to the conclusions presented in [33], if these points form a representative structure, i.e., composed of $n_{wgr}$ points, then it can be assumed that the WOZ radius (R_WOZ) corresponds to the R_fr parameter value of this structure. The R_fr values analyzed in this study were determined for HLSs developed based on laboratory tests conducted at a scale of 1:10 [29]. To use these R_fr values to determine the R_WOZ, they must be scaled to actual conditions. As previously published dimensional analysis results indicate, this requires multiplying the R_fr values of individual representative structure by 10 [27]. Furthermore, for practical reasons, it was proposed to round the obtained values to 0.5.

2.4. Field Tests

To verify the results obtained from laboratory tests and statistical analyses, field tests were carried out under real construction site conditions. The purpose of the field tests was to create a controlled water outflow from a pressure pipe, simulating an underground water pipe failure. The field test setups were constructed in two different locations (called A and B). In each location, four open excavations trenches were made, in which PE-HD water pipes were laid. The single excavation dimensions were as follows: 4.0 m × 0.7 m × 1.65 m (length × width × depth) in location A, and 5.0 m × 0.5 m × 1.90 m (length × width × depth) in location B. The scheme of the field study setup is presented in Figure 2. To achieve a physical simulation of water leakage from the pressure pipe into the ground, each PE-HD pipe (4) was cut along nearly its entire circumference at the midpoint of its length (5), leaving a 5 mm uncut segment to maintain the coaxial alignment of the separated parts. At the cut location, a knitted band made of thin, water-permeable fabric was placed over the pipe to protect the interior of the pipe from soil intrusion during the backfilling process. During the field test, the pipe was supplied with water from a fire hydrant. At the inlet end (1), the measuring set was installed, consisting of 2 ball valves (2) and a pressure gauge (3). Additionally, 1 ball valve (2) was installed at the outlet end (6).

The field tests were carried out in 3 measurement series. The first series was conducted at location A, while the second and third were conducted at Location B. All three series were performed at least 6 months after the construction of the field test setups—specifically after 7, 9, and 22 months, respectively. In both locations A and B, the natural soil was sandy with good permeability—the hydraulic conductivity averaged 3.34 × 10⁻⁴ m/s at location A and 1.52 × 10⁻⁴ m/s at location B. At location A, the same pipes diameters were used (PE-HD 63 × 3.8) and tests were conducted under pressure of 41 m H₂O for each trial (A1.1–A1.4). At Location A, the field test setup was differentiated by varying the pipe bedding. Two pipes were laid directly on the natural soil (series A1.1 and A1.2), while the other two (A1.3 and A1.4) were laid on a 10 cm sand bedding and backfilled with compacted 30 cm layers of sand. For series 2 and 3 conducted at location B, a uniform pressure was applied (36.5 m H₂O for series B2.1–B2.4 and 45 m H₂O for B3.1–B3.4), but the test setups differed in the pipe diameters used: PE-HD 110 × 4.2 mm for series B2.1, B2.2, B3.1, B3.2 and diameter 200 × 7.7 mm for B2.3, B2.4, B3.3, B3.4. Water pressure was measured using a digital hydrant logger (data recording interval: 0.1 s). No surges were recorded during the tests, Detailed information on the measurement series carried out is presented in

Table 3. Field tests setup details.

Field Tests Series	Bedding and Backfill Soil	Pipe		Excavation Trench			Tests Time in Months After Construction	Pressure
		Material	Diameter	Length	Width	Depth
			DN × g (mm)	(m)	(m)	(m)		(m H2O)
A1.1, A1.2 A1.3, A1.4	natural sand	PE-HD	63 × 3.8	4.0	0.7	1.65	7	41.0
B2.1, B2.2	natural	PE-HD	110 × 4.2	5.0	0.5	1.90	9	36.5
B2.3, B2.4			200 × 7.7
B3.1, B3.2	natural	PE-HD	110 × 4.2	5.0	0.5	1.90	22	45.0
B3.3, B3.4			200 × 7.7

. The data obtained during the physical simulations under real conditions included the location of water outflow at the ground surface and the time of water outflow, measured from the start of the experiment to the moment the water appeared on the surface. The location of the water outflow was determined using (x, y) coordinates relative to the outflow opening in the pipe (point 0,0). The measurements were carried out using a measuring tape with an accuracy of ±1 mm.

2.5. The Process of Empirical Verification

The proposed method for determining the radius of the water outflow zone on the soil surface after a failure of an underground water supply pipe was empirically verified based on the results of locating the outflow points during physical failure simulations conducted under real conditions at sites A and B (Section 2.4). The verification involved the radius values calculated from those laboratory data sets that corresponded to the conditions of the field experiments.

The leakage area of the pipe was strictly related to the pipe diameter, as the pipe had been damaged in such a way that water leakage occurred along the entire circumference. Therefore, when selecting the radius values calculated for HF1–HF5 to be used in empirical verification, the pipe diameter was taken into account. The internal pressure in the pipe during the laboratory tests served as the basis for selecting the radius values calculated for HH1–HF7. Based on this approach, the results of field tests A1.1–A1.4 were used to verify the WOZ radius determined for dataset HF1 (the 6 mm pipe diameter in the laboratory tests corresponded to a DN 63 × 3.8 mm pipe in the field tests), while the results of tests B2.1, B2.2, B3.1, and B3.2 were used to verify the WOZ radius determined for dataset HF2 (the 10 mm pipe diameter in the laboratory tests corresponded to a DN 110 × 4.2 mm pipe in the field tests). For tests B2.3, B2.4, B3.3, and B3.4, the verification concerned the outflow zones with radius determined for dataset HF3—a pipe diameter of 20 mm in the laboratory tests corresponded to a DN 200 × 7.7 mm pipe in the field tests (

Table 4. Representative structures (HLSs) selected for empirical verification according to pipe diameter.

HLS	Field Tests			Laboratory Tests
	Site	Series	Diameter (mm)	In. Diameter (mm)	Data Set (RS)
HF1	A	A1.1–A1.4	63 × 3.8	6.0	F1
HF2	B	B2.1, B2.2, B3.1, B3.2	110 × 4.2	10.0	F2
HF3	B	B2.3, B2.4, B3.3, B3.4	200 × 7.7	20.0	F3

). Analogously, the results of field tests A1.1–A1.4 (pipe pressure 41 m H₂O), B2.1–B2.4 (pipe pressure 36.5 m H₂O) and B3.1–B3.4 (pipe pressure 45 m H₂O) were used to verify the WOZ radius determined for dataset HH3, HH2 and HH4, which corresponded to laboratory conditions of 4.0, 3.5, and 4.5 m H₂O, respectively (

Table 5. Representative structures HLSs selected for empirical verification according to internal pressure in the pipe.

HLS	Field Tests			Laboratory Tests
	Site	Series	Pressure (m H2O)	Pressure (m H2O)	Data Set (RS)
HH2	B	B2.1, B2.2, B2.3, B2.4	36.5	3.5	H2
HH3	A	A1.1–A1.4	41.0	4.0	H3
HH4	B	B3.1, B3.2, B3.3, B3.4	45.0	4.5	H4

).

The empirical verification consisted in checking whether the actual water outflow points observed on the ground surface during field tests were located within the outflow zones whose size had been determined according to the methodology described in Section 2.1, Section 2.2, Section 2.3. The verification result was considered positive if at least 90% of the actual points were located within the theoretical zones.

3. Results and Discussion

3.1. The Minimum Number of Points for Which the R_fr Values Are Concentrated Around the Mean (Condition I)

The results of the CV calculations, which are the basis for assessing the clustering of R_fr values around the mean, are presented in

Table 6. CV of the R_fr parameter.

nw	CV [%] of Rfr for HLSs:
	HF1s	HF2s	HF3s	HF4s	HF5s	HH1s	HH2s	HH3s	HH4s	HH5s	HH6s	HH7s
50	8.98	5.34	3.87	5.46	11.80	8.14	6.96	14.39	9.20	2.23	7.95	6.98
100	8.20	8.87	3.45	5.28	7.05	4.86	4.13	7.31	3.13	3.62	6.98	2.23
200	3.60	5.97	1.72	4.11	4.31	3.27	3.84	4.06	1.80	0.75	4.62	1.59
300	2.47	4.50	1.10	2.67	6.60	2.09	1.52	6.55	1.81	0.22	1.79	1.52
400	2.08	4.31	1.24	1.75	3.34	1.57	1.47	3.39	0.95	0.12	2.79	0.69
500	2.09	4.84	1.05	3.53	3.79	0.89	0.82	2.56	0.63	0.17	1.48	0.67
600	1.22	3.14	0.78	1.86	2.99	0.61	0.76	3.39	0.84	0.05	1.43	0.51
700	1.11	2.36	0.73	1.03	2.21	0.62	0.60	1.31	0.39	0.12	0.50	0.46
800	0.77	1.80	0.43	0.57	3.39	0.42	0.61	1.92	0.39	0.06	1.63	0.51
900	1.50	1.30	0.35	0.65	3.72	0.46	0.42	1.62	0.42	0.10	1.65	0.41
1000	1.48	1.53	0.38	0.95	1.25	0.35	0.42	0.88	0.25	0.09	0.81	0.36
1500	0.59	1.14	0.38	0.88	1.98	0.15	0.16	0.88	0.27	0.09	0.66	0.44
2000	0.89	0.55	0.35	0.85	1.28	0.14	0.07	1.36	0.18	0.03	0.41	0.42
3000	0.46	0.33	0.36	0.60	1.26	0.07	0.04	0.39	0.11	0.01	0.38	0.35
4000	0.36	0.31	0.28	0.17	1.21	0.06	0.15	0.66	0.05	0.02	0.29	0.33
5000	0.38	0.31	0.31	0.20	0.43	0.04	0.05	0.59	0.04	0.01	0.35	0.32

. A clear decreasing trend in the CV values with increasing the number of points forming the structures was observed for all HLSs groups. The maximum CV value corresponded to n_w = 50 for nearly all HLSs, except HF2 and HH5, for which it was n_w = 100. The difference between the CV value at n_w = 50 and the maximum was 3.53% and 1.39% for HF2 and HH5, respectively. The minimum CV values for most HLSs corresponded to n_w = 5000. For HF1, HF4, and HH6, the minimum CV occurred at n_w = 4000, with the difference of only 0.02%, 0.03%, and 0.06%, respectively, compared to the CV value at nw = 5000. For HH2 and HH3, the minimum CV was observed at n_w = 3000, also with a very small difference compared to the CV at n_w = 5000 (0.11% and 0.27%, respectively). Considering all the values presented in Table 6, the highest CV = 14.39% occurred for the HH3 structure with n_w = 50, while the lowest CV = 0.01% was for the HH5 structure with n_w = 5000.

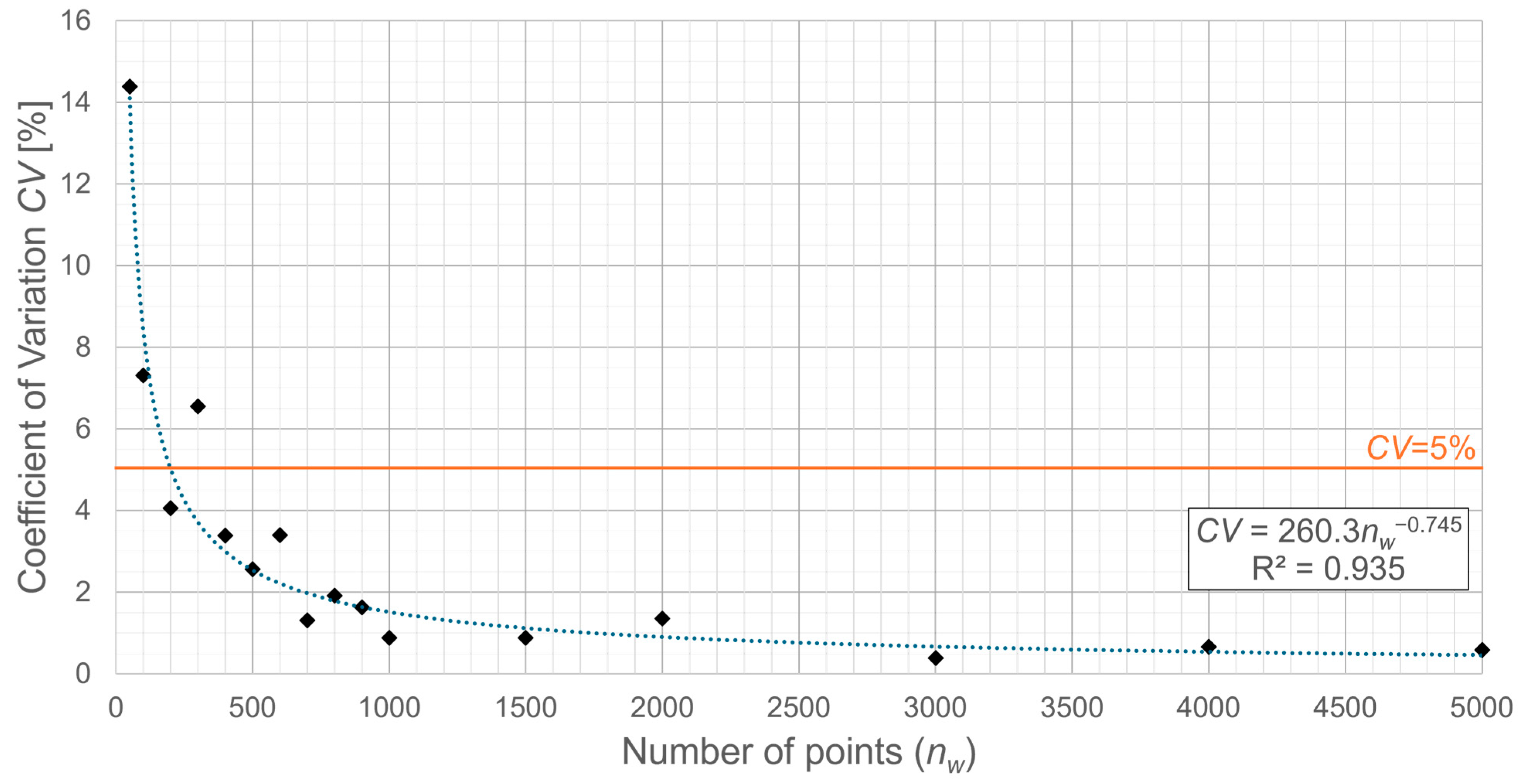
The CV(n_w) relationship proved to be a strictly decreasing function only for HF3. For the remaining structure groups, some deviations occurred, though the general decreasing trend was preserved. An example plot of the CV(n_w) relationship with the trend line for the HH3 structure group is shown in Figure 3.

Among the tested functions, the power trendline provided the best fit (

Table 7. Trend lines of the CV(n_w) relationships.

HLSs	Trendline Equation	R2	${\mathit{n}}_{\mathit{w}\mathit{I}}$
			Calculated	Rounded
HF1s	CV = 181.00nw−0.743	0.9331	125.27	100
HF2s	CV = 380.82nw−0.816	0.5147	202.33	200
HF2s *	CV = 492.19nw−0.884	0.8294	179.77	200
HF3s	CV = 44.298nw−0.63	0.9458	31.90	50
HF4s	CV = 180.43nw−0.765	0.7729	108.58	100
HF5s	CV = 134.21nw−0.600	0.9049	240.63	200
HH1s	CV = 1807.5nw−1.244	0.9331	113.86	100
HH2s	CV = 1210.0nw−1.183	0.8947	103.53	100
HH3s	CV = 260.3nw−0.745	0.9350	201.39	200
HH4s	CV = 763.04nw−1.125	0.9808	87.29	100
HH5s	CV = 382.51nw−1.242	0.5984	32.86	50
HH5s *	CV = 199.34nw−1.197	0.9408	21.74	50
HH6s	CV = 214.91nw−0.787	0.9007	118.94	100
HH7s	CV = 39.432nw−0.620	0.8845	27.96	50

* The HLS composed of 50 points was excluded from the analysis.

). The values of the coefficient of determination R² were large for the vast majority of structure groups: R² > 0.9 for 7 out of 12 structure groups, R² less than but close to 0.9 for 2 groups, and R² = 0.77 for one group. These large R² values confirmed at least a satisfactory fit (very good in most cases) of the power trendline to the CV(n_w) relationship. Unsatisfactory R² values (0.5 < R² < 0.6) were obtained for HF2 and HH5, where the maximum CV was reached at n_w = 100 (not at n_w = 50). After excluding the structures with n_w = 50 from the correlation analysis, a good and very good fit of the power trendline was achieved—R² > 0.8 for HF2 and R² > 0.9 for HH5.

Inserting CV = 5% into the trend line equation made it possible to calculate the minimum number of points $n_{wI}$ satisfying condition I. The calculation results of $n_{wI}$ are presented in the last two columns of Table 7. The highest rounded value of $n_{wI}$ was 200 (for 3 structure groups), and the lowest was 50 (also for 3 structure groups). For half of the analyzed HLSs (6 structure groups), $n_{wI}$ = 100. It is worth noting that regardless of whether the structure consisting of 50 points was excluded when determining the trend line equation or not, $n_{wI}$ = 200 and $n_{wI}$ = 50 were obtained for the HF2 and HH5 structures, respectively. In summary, $n_{wI}\in \left\{\mathrm{50,100,200}\right\}$ satisfies condition I.

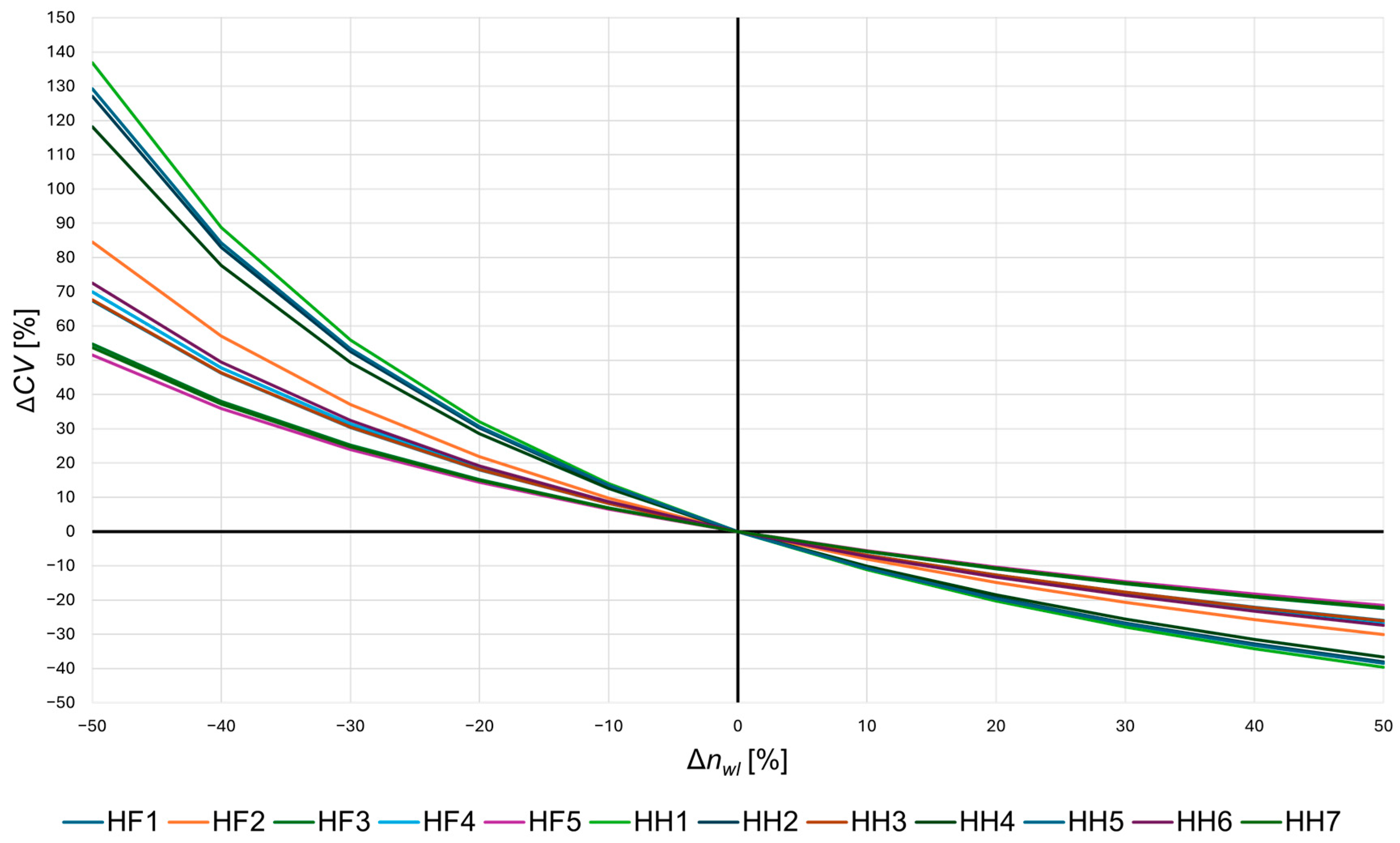
The correctness of the obtained $n_{wI}$ values was confirmed by the sensitivity analysis of the CV coefficient of the parameter R_fr to small variations in $n_{wI}$ (Figure 4). A decrease in $n_{wI}$ results in a clearly larger change in CV than an increase by the same percentage. For example, reducing $n_{wI}$ by 50% causes a 2.4–3.5 times greater change in the CV value than increasing $n_{wI}$ by 50%. Since the CV($n_{wI}$) relationship is a decreasing function, lowering $n_{wI}$ leads to an increase in CV, indicating a greater dispersion of the R_fr parameter values. The results of the analysis therefore confirm that the determined $n_{wI}$ values are indeed the smallest $n_w$ values satisfying condition I.

3.2. The Minimum Number of Points for Which the Mean Values of R_fr Remains Almost Constant with Increasing n_w (Condition II)

The values of unit differences $r_{fri}$, calculated according to Equation (1), are presented in

Table 8. Results of the relative difference $r_{fri}$ calculations.

nw	${\mathit{r}}_{\mathit{f}\mathit{r}\mathit{i}}\left({·10}^{-4}\right)$ for HLSs:
	HF1s	HF2s	HF3s	HF4s	HF5s	HH1s	HH2s	HH3s	HH4s	HH5s	HH6s	HH7s
50	–	–	24.75	–	–	–	–	–	–	12.67	–	30.30
100	19.57	–	12.00	22.47	–	10.28	12.55	–	11.00	4.54	16.92	11.16
200	11.04	16.36	3.29	11.24	25.03	4.80	7.23	21.74	3.89	1.13	9.33	4.25
300	6.56	14.94	1.05	6.97	20.73	3.63	3.01	14.26	2.08	0.27	4.98	2.04
400	3.13	11.50	0.99	5.09	16.08	2.19	1.72	11.13	1.93	0.12	4.28	0.86
500	2.86	8.57	0.77	4.85	13.12	1.22	1.18	7.41	1.09	0.11	1.93	0.60
600	1.03	4.64	0.44	5.90	11.46	1.31	1.30	8.46	0.57	0.04	2.10	0.39
700	0.69	5.96	0.33	3.19	8.45	1.20	0.88	5.08	0.57	0.12	0.75	0.49
800	0.83	4.11	0.15	1.83	10.20	0.86	0.77	5.61	0.27	0.05	1.45	0.42
900	1.40	3.85	−0.15	2.51	10.11	0.28	0.39	5.56	0.43	0.08	2.47	0.22
1000	0.64	3.91	−0.25	1.15	8.13	0.42	0.45	2.91	0.19	0.09	0.76	0.12
1500	0.41	1.69	−0.36	1.45	6.31	0.15	0.18	3.32	0.42	0.04	0.66	0.30
2000	−0.30	0.86	−0.09	0.92	3.97	0.09	0.07	1.81	0.23	0.03	0.14	0.28
3000	−0.16	0.41	−0.16	0.61	2.60	0.11	−0.03	0.20	0.21	0.00	0.18	0.14
4000	−0.25	0.45	0.06	−0.15	4.04	0.12	0.27	0.66	0.21	0.04	0.30	−0.02
5000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00

. The highest absolute values of $r_{fri}$ were observed for the HF5s structure group; however, these values remained close to zero, ranging from 2.6 × 10⁻⁴ for $n_w$ = 3000 (omitting 0 for $n_w$ = 5000) to 25.03 × 10⁻⁴ for $n_w{=n}_{wI}$. For the remaining HLSs, the absolute values of $r_{fri}$ were even lower: from the values of the order of 10⁻⁷ (HH5s), 10⁻⁶ (HF3s, HH1, HH2, HH7), or 10⁻⁵ (HF1, HF2s, HF4s, HH3s, HH4s, HH6s) for $n_w\ge 2000$, to the values of the order of 10⁻³ for $n_w{=n}_{wI}$.

Although all $r_{fri}$ values turned out to be close to zero, they were clearly higher (by 2–3 orders of magnitude) for lower n_w values compared to the highest n_w. Analyses using Student's t-test showed that for each HLSs group, there exists a structure of size $n_{wII}$ for which statistic $t\notin CI$, meaning there is no basis to reject the hypothesis that $r_{fri}$ = 0. An example illustrating the determination of the lowest $n_{wII}$ for which $t\notin CI$ ($n_{wgr}$) for the structures HF1s is presented in

Table 9. Determination of the $n_{wgr}$ value for the structures HF1s.

${\mathit{n}}_{\mathit{w}}$	Degrees of Freedom	t	${\mathit{t}}_{\mathit{c}\mathit{r}}$	$\mathit{t}\notin \mathit{C}\mathit{I}$?
100	13	2.1751	2.1604	no
200	12	2.2726	2.1788	no
300	11	2.3692	2.2010	no
400	10	2.5557	2.2281	no
500	9	2.2681	2.2622	no
600 *	8	2.2302	2.3060	yes
700	7	1.7760	2.3646	yes
800	6	1.3963	2.4469	yes
900	5	0.9695	2.5706	yes
1000	4	0.3104	2.7765	yes
1500	3	−0.4078	3.1824	yes
2000	2	−1.8532	4.3027	yes
3000	1	−3.2437	12.706	yes

* $n_w=n_{wgr}$ as the lowest $n_w$ for which $t\notin CI$.

, while the values of $n_{wgr}$ for all structures are provided in

Table 10. Results of the one-sample Student’s t-test for HLSs consisted of $n_{wgr}$ points.

HLS	${\mathit{n}}_{\mathit{w}\mathit{g}\mathit{r}}$	SD [cm]	t	${\mathit{t}}_{\mathit{c}\mathit{r}}$	$\mathit{t}\notin \mathit{C}\mathit{I}$?
HF1	600	0.000060	2.2302	2.3060	yes
HF2	1000	0.000146	2.0054	2.7765	yes
HF3	400	0.000043	2.1485	2.2281	yes
HF4	1000	0.000061	2.5870	2.7765	yes
HF5	1000	0.000219	2.5719	2.7765	yes
HH1	1000	0.000014	2.5951	2.7765	yes
HH2	1000	0.000018	2.0217	2.7765	yes
HH3	1000	0.000136	2.6128	2.7765	yes
HH4	100	0.000289	2.0569	2.1604	yes
HH5	50	0.000336	1.4368	2.1448	yes
HH6	900	0.000088	1.9085	2.5706	yes
HH7	50	0.000797	1.6134	2.1448	yes

. The highest value of $n_{wgr}$ was $n_{wgr}$ = 1000, obtained for half of the HLSs groups (6 out of 12). For three HLSs groups, the smallest possible values were obtained—$n_{wgr}$ = $n_{wI}$ (50 or 100). It can thus be stated that the values of $n_{wgr}$ vary considerably among the various HLS groups—therefore, one common value of $n_{wgr}$ cannot be assumed for all HLSs.

3.3. Determination of the Radius of the Water Outflow Zone

The $n_{wgr}$ values determine representative structures, based on which the radius of the water outflow zone following a failure of an underground water pipeline (R_WOZ) can be identified. According to the methodology (Section 2.3), the R_WOZ radius was adopted as the R_fr values determined for the representative structures, scaled to real-world conditions (R_RC) and rounded to the nearest 0.5 m (

Table 11. The R_fr values of representative structures and R_WOZ.

HLS	${\mathit{n}}_{\mathit{w}\mathit{g}\mathit{r}}$	Rfr [cm] (Table 1)	RRC [m]	RWOZ [m]
HF1	600	43.19	4.32	4.5
HF2	1000	54.37	5.44	5.5
HF3	400	46.67	4.67	4.5
HF4	1000	53.48	5.35	5.5
HF5	1000	54.75	5.48	5.5
HH1	1000	44.65	4.47	4.5
HH2	1000	45.38	4.54	4.5
HH3	1000	57.03	5.70	5.5
HH4	100	39.43	3.94	4.0
HH5	50	36.13	3.61	3.5
HH6	900	52.16	5.22	5.0
HH7	50	35.71	3.57	3.5

). Final values of R_WOZ ranged from 3.5 to 5.5 m.

The R_WOZ radius can be expressed mathematically as follows:

$$R_{WOZ}=\left\{\begin{array}{c}⌊R_{RC}⌋,if{R}_{RC}-⌊R_{RC}⌋<0.25\\ ⌊R_{RC}⌋+0.5,if0.25\le R_{RC}-⌊R_{RC}⌋<0.75\\ ⌊R_{RC}⌋+1.0,if{R}_{RC}-⌊R_{RC}⌋\ge 0.75\end{array}\right.,$$

(4)

where $⌊R_{RC}⌋$ denotes the entier (the foor function) of $R_{RC}$.

Taking into account that R_RC is the product of R_fr and the inverse of the scale at which the laboratory tests were conducted, and that R_fr is the product of the fractal dimension of the structure ($D_b\left(W_N\right)$) and the distance (in the laboratory scale) of the point forming the structure that is farthest from the origin of the coordinate system ((R_w)_max), the R_RC radius can be expressed as follows:

$$R_{RC}={\displaystyle \frac{1}{s}}·R_{fr}={\displaystyle \frac{1}{s}}·D_b\left(W_N\right)·{\left(R_w\right)}_{max},$$

(5)

where s denotes the scale of the laboratory model, R_fr [m], D_b, and (R_w)_max [m] are values of a representative structure.

Fractal (box-counting) dimension is defined as [39]:

$$D_b\left(W_N\right)=\underset{\delta \to 0}{\mathit{lim}}{\displaystyle \frac{\mathit{log}{N}_{\delta }\left(W_N\right)}{-\mathit{log}\delta }},$$

(6)

where $W_N$ is a non-empty, bounded subset of a finite-dimensional Euclidean space (in the presented investigations: $W_N$ = HF1, …, HF5, HH1, …, HH6 or HH7), $D_b\left(W_N\right)$ is the box-counting dimension of the set $W_N$, and $N_{\delta }\left(W_N\right)$ is the smallest number of sets of diameter δ (in the presented investigations: square of side δ) which can cover $W_N$.

The distance (R_w)_max can be expressed as:

$${\left(R_w\right)}_{max}=\underset{1\le i\le n_{\mathit{w gr}}}{\mathit{max}}\left\{{\left(R_w\right)}_i|i\in \mathbb{N}\right\},$$

(7)

where R_w [m] is the distance in the laboratory scale of any point creating the HLS from the origin and $\mathbb{N}$ is the set of natural numbers.

Substituting Equations (6) and (7) into Equation (5), the following expression is obtained:

$$R_{RC}={\displaystyle \frac{1}{s}}·\underset{\delta \to 0}{\mathit{lim}}{\displaystyle \frac{\mathit{log}{N}_{\delta }\left(W_N\right)}{-\mathit{log}\delta }}·\underset{1\le i\le n_{\mathit{w gr}}}{\mathit{max}}\left\{{\left(R_w\right)}_i|i\in \mathbb{N}\right\}.$$

(8)

Equations (4) and (8) form a system of equations that provides a mathematical description of the R_WOZ radius, based on fractal geometry.

3.4. Field Tests Results

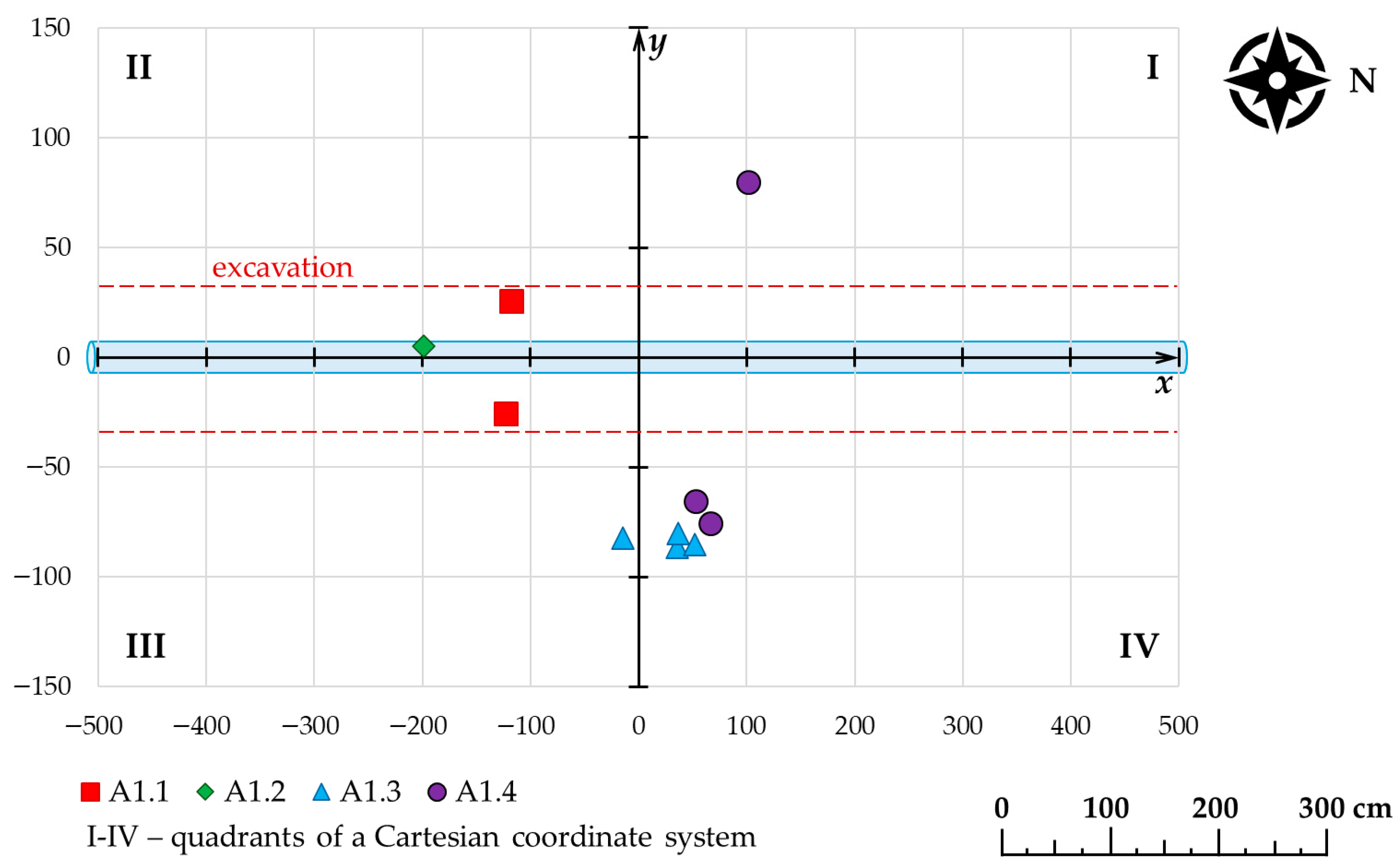
As a result of the controlled waterpipe failure in tests A1.1–A1.4, water outflowed at the ground surface through a total of 10 suffosion holes. As many as seven of these occurred during tests A1.3 and A1.4, where sand was used for backfilling the trench. Detailed results of field test experiments A1.1–A1.4 are presented in

Table 12. Field tests results—series A1.1–A1.4.

Field Tests Series	Type of Soil in the Excavation	Diameter	Pressure	Outflow Time t	Number of Outflows
		DN × g
		(mm)	(m H2O)	s
A1.1	natural	63 × 3.8	41.0	13.39	2
A1.2	natural	63 × 3.8	41.0	17.28	1
A1.3	sand	63 × 3.8	41.0	25.38	4
A1.4	sand	63 × 3.8	41.0	19.03	3

and Figure 5. One outflow hole was observed in the first quadrant of the coordinate system according to drawing 4 (at setup A1.4), two in the second quadrant (at stations A1.1 and A1.2), and two in the third quadrant (at stations A1.1 and A1.3), with by far the most—five—occurring in the fourth quadrant (at stations A1.3 and A1.4). At station A1.2, only one suffosion hole formed—right next to the vertical section of the test pipe. Most likely, the water found a so-called path of least resistance outflow along the pipe. At stations A1.1 and A1.2, the water outflow occurred only within the excavation area, whereas at the other two stations, it extended beyond the excavation boundaries. The average time for water to reach the surface at location A, measured from the start of the experiment, was 18.77 s across all test setups. For tests A1.1 and A1.2, the difference between the outflow times was 3.89 s, with an average of 15.33 s. For setups A1.3 and A1.4, the difference was 6.35 s, and the average time was 22.2 s. Significant differences were therefore observed in the number and location of outflow points, as well as in the time of outflow, when comparing tests with natural soil versus sand backfilling.

In the B2.1–B2.4 series at location B, a total of 9 outflow holes were recorded. Detailed results of field test experiments B2.1–B2.4 are presented in

Table 13. Field tests results—series B2.1–B2.4.

Field Tests Series	Type of Soil in the Excavation	Diameter	Pressure	Outflow Time t	Number of Outflows
		DN × g
		(mm)	(m H2O)	s
B2.1	natural	110 × 4.2	36.5	74.81	1
B2.2	natural	110 × 4.2	36.5	105.00	1
B2.3	natural	200 × 7.7	36.5	125.30	2
B2.4	natural	200 × 7.7	36.5	78.00	5

and Figure 6. Significantly fewer holes appeared at the stations where the leakage area was smaller (smaller pipe diameter). Only one hole formed in the first quadrant of the coordinate system (station B2.3), three holes in the second quadrant (one each at stations B2.1, B2.2, and B2.4), and five holes in the third quadrant (at stations B2.3 and B2.4). No water outflow hole was observed in the fourth quadrant. The average time for water to reach the ground surface in the B2.1–B2.4 test series was 95.78 s. At stations B2.1 and B2.4, the outflow times were comparable, the difference was only 3.19 s. The average times at stations B2.1 and B2.2, and B2.3 and B2.4, were 127.31 s and 101.65 s, respectively.

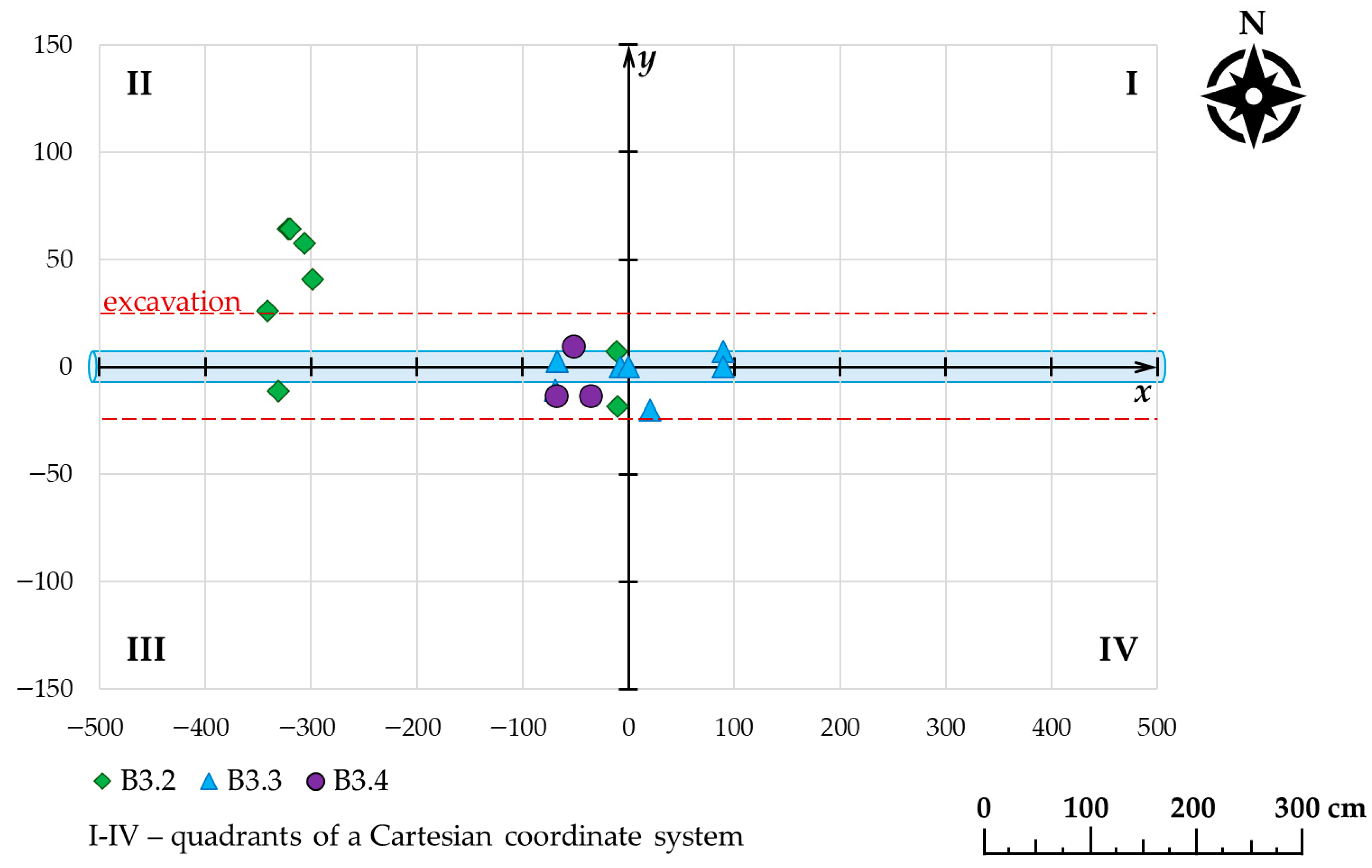
In the B3.1–B3.4 series of tests at location B, no water outflowed at station B3.1. The experiment was terminated after 660 s. The most likely reason for the lack of outflow was that the water found a so-called path of least resistance in the form of an underground corridor. At the remaining stations, water emerged in a total of 18 holes. Detailed results of field test experiments B3.1–B3.4 are presented in

Table 14. Field tests results—series B3.1–B3.4.

Field Tests Series	Type of Soil in the Excavation	Diameter	Pressure	Outflow Time t	Number of Outflows
		DN × g
		(mm)	(m H2O)	s
B3.1	natural	110 × 4.2	45.0	>660	0
B3.2	natural	110 × 4.2	45.0	147.98	8
B3.3	natural	200 × 7.7	45.0	37.19	7
B3.4	natural	200 × 7.7	45.0	47.10	3

and Figure 7. Station B3.3 was the only one where three water outflow holes were observed directly above the damaged water pipe. Among the other locations, one outflow point was found in both the first and fourth quadrants of the coordinate system (both at station B3.3), eight in the second quadrant (stations B3.2–B3.4), and five in the third quadrant (stations B3.2–B3.4). Excluding station B3.1, the water outflow times in the series B3.1–B3.4 were significantly more varied compared to series B2.1–B2.4. The difference between the longest outflow time (B3.4) and the shortest (B3.3) was 433.81 s, which was nearly twice the average outflow time for stations B3.2–B3.4, amounting to 217.72 s. Only at station B3.4 the outflow time in series B3.1–B3.4 was shorter than in series B2.1–B2.4.

3.5. Empirical Verification

In accordance with the adopted methodology, the results obtained for representative structures HF1–HF3 and HH2–HH4 (i.e., R_WOZ = 4.0, 4.5 and 5.0 m) were selected for empirical verification (

Table 15. R_WOZ results of representative structures (HLSs) selected for empirical verification with corresponding field test series.

HLS	HF1	HF2	HF3	HH2	HH3	HH4
RWOZ	4.5	5.5	4.5	4.5	5.5	4.0
Field Test Series	A1.1–A1.4	B2.1, B2.2, B3.1, B3.2	B2.3, B2.4, B3.3, B3.4	B2.1, B2.2, B2.3, B2.4	A1.1–A1.4	B3.1, B3.2, B3.3, B3.4

).

The verification results are shown in Figure 8a–c. The outflow zones with a radius R_WOZ of 4.0 m and 5.5 m fully covered all corresponding actual water outflow points observed on the soil surface during the field tests. In the case of the zone with R_WOZ = 4.0 m, 12 out of 18 points were situated no further than 1 m from the pipe leakage location, while the remaining six were no more than 1 m from the theoretical boundary of the zone. The point farthest from the leakage location was located 0.58 m from the zone boundary (Figure 8a). Among the points in the zone with 5.5 m, 8 out of 20 were no further than 1 m from the leakage location, and only one was located no further than 1 m (0.82 m) from the theoretical boundary of the zone (Figure 8c).

The only zone that did not cover all actual points was the one with R_WOZ = 4.5 m. All points outside this zone (3 out of 29) corresponded to suffosion holes that formed during the failure simulation at location B: one in series B2.1 (located 0.18 m beyond the theoretical zone boundary) and two in series B2.4 (located 0.37 m and 0.13 m beyond the boundary, respectively). One of the points (also from series B2.4) was located exactly on the zone boundary. Most of the points (18 out of 29) were no further than 1 m from the pipe leakage location (Figure 8b).

The summary of the verification results is presented in

Table 16. Summary of the empirical verification results.

RWOZ	Rw	Number of Actual Points			Percentage of Points Outside the Zone
		Total	Inside the Zone	Outside the Zone
4.0	0.00–3.42	18	18	0	0%
4.5	0.00–4.87	29	26	3	10%
5.5	0.13–4.68	20	20	0	0%
Total for zones		67	64	3	4%

. Two theoretically determined zones provided 100% coverage of the actual points corresponding to suffosion holes, and one provided 90% coverage. Taking into account all analyzed points, 3 out of 67 were located outside their respective zones, which represents only 4%. The overall result of the empirical verification of the proposed method for determining the WOZ radius was therefore considered positive.

4. Summary and Conclusions

This paper presents a method for determining the radius of the surface water outflow zone (R_WOZ) resulting from the failure of an underground water pipeline. The development of this method was made possible by previously demonstrating the fractal nature of HLS, obtained using the Monte Carlo method based on laboratory test results, and by showing that the parameter R_fr, which characterizes an HLS and depends on its fractal dimension, plays a key role in determining the dimensions of the water outflow zone (WOZ). In this study, the focus was placed on identifying a representative HLS, i.e., a structure with the smallest possible number of constituent points that simultaneously satisfies two conditions: (I) the values of the R_fr parameter determined for HLSs with the same number of points are clustered around the mean, and (II) the value of R_fr remains statistically constant with increasing number of points in the structure. Statistical analysis (coefficient of variation and Student’s t-test) enabled the determination of the minimum number of points required to satisfy both conditions I and II. The range of the resulting minimum point counts was wide—from 50 to 1000 points—depending on the conditions corresponding to each HLS under which the pipeline failure occurred (i.e., size of leakage and internal pipe pressure).

Based on this analysis, representative structures were identified, for which the R_fr parameter was calculated under laboratory conditions. Subsequently, after scaling to real-world conditions and rounding to 0.5 m, the radius of the WOZ was determined. The resulting R_WOZ values ranged from 3.5 to 5.5 m. Based on the performed analyses and the definition of the box-counting fractal dimension, a system of equations for determining the R_WOZ was proposed. The theoretical results were empirically validated using measurement data obtained during field investigations under real conditions. The empirical verification confirmed the validity of the proposed method for determining the R_WOZ. For zones with radii of 4.0 m and 5.5 m, 100% coverage of the actual outflow points was obtained, while the 4.5 m zone ensured 90% coverage. Considering all points recorded during the field tests, 96% were located within the boundaries of their corresponding theoretical zones.

Determining the WOZs sizes is only one of the issues related to inevitable water pipes failures. However, it is a highly important issue from the perspective of public safety and the protection of existing infrastructure. Therefore, research on water outflow from a pressurized pipe into the soil should be continued. This issue encompasses a wide spectrum of interrelated problems across various scientific disciplines—primarily fluid mechanics, hydrology, and soil rheology—thus a comprehensive understanding of these phenomena remains an open challenge. The determination of the WOZ using fractal geometry provides a novel framework for linking hydraulic processes with spatial risk assessment. The results obtained in this study can be incorporated into decision-support systems for sustainable infrastructure planning, promoting safer and more efficient use of water resources in urban environments. The developed method for determining the WOZ radius can find practical application by water utilities when routing new or renovating existing water pipelines. Including a buffer zone during GIS-based asset management or risk zoning, dependent on hydraulic flow parameters, can significantly reduce the impact of a potential water outflow and formation of suffosion holes on existing infrastructure, making it more resilient.

The research presented in this study focused on the geometric characterization of the set of points corresponding to suffosion holes. It therefore represents only one of the possible approaches to analysing water outflow from a leaking pressurized pipeline into the ground. Future research directions should also include the development of criteria for the location of proposed safety zones. This is a broad issue that requires, on the one hand, an analysis of the reliability of individual components of the water supply network, and on the other, consideration of the density and characteristics of the existing underground infrastructure and above-ground structures. The developed method for determining the WOZ radius can be further verified using CFD analyses and can also provide practical information for GIS and hydraulic modelling-supported spatial infrastructure management systems. It is worth noting that water supply networks are just one of many critical infrastructure systems, so appropriate planning and routing should also take into account interrelationships with other networks, such as transport, gas, and energy. The problem of the complex phenomenon of water flow in soil is currently analyzed not only in relation to water supply system failures [40,41,42,43,44,45], but is also widely examined in the context of other engineering structures [46,47,48,49,50,51,52,53]. The continuous interest of researchers in the water–soil interaction problem reflects the complexity of the phenomenon and highlights its importance in the broader context of safety.