A Sustainable Management-Oriented Model for Hydrodynamics and Pollutant Transport in Vegetated Seepage River Channels Using LBM-RDM

Abstract

This study investigates the hydrodynamic characteristics and pollutant transport in vegetated seepage channels, with a particular focus on the impacts of seepage and vegetation density on flow velocity and pollutant dispersion. The primary innovation of this research lies in the novel integration of the Lattice Boltzmann Method (LBM) and the Random Displacement Method (RDM) to establish a numerical model for simulating vertical flow velocity and pollutant transport in such channels. To enhance simulation accuracy, the sediment bed was treated as a porous medium. The findings reveal that higher seepage rates significantly increase pollutant infiltration, and denser vegetation further amplifies this effect by enhancing turbulent diffusion and mechanical dispersion within the vegetated zone. These insights are critical for sustainable groundwater protection and the design of vegetated buffer zones in river management. Furthermore, treating the sediment layer as a porous medium yielded more accurate flow velocity predictions. These results provide new insights into the complex interactions between seepage, vegetation, and pollutant transport, and offer a valuable theoretical basis for optimizing sustainable vegetation planting schemes and management practices in vegetated seepage rivers to protect groundwater quality.

1. Introduction

River water quality environments have always been a focus of attention, with river flow velocity and the transport of pollutants within them being the main factors affecting rivers [1,2]. Additionally, the difference in water levels between natural river channels and adjacent groundwater can cause seepage phenomena in the water flow [1,3]. Pollutants entering groundwater with the downward flow of water can lead to groundwater contamination. Therefore, it is essential to study the transport of pollutants during river seepage.

Flow velocity is an important criterion for measuring river hydrodynamics. In natural rivers, the distribution of flow velocity is mainly influenced by the bed slope and roughness [4]. Additionally, vegetation often exists in natural rivers, and it exerts a significant drag effect on the water flow, greatly influencing the velocity distribution within the river channel [5]. Wang and Liu [6] studied the canopy interaction mechanisms of rigid emergent aquatic vegetation, providing a more accurate understanding of the effects of lateral and longitudinal vegetation spacing on blockage and shading. Nosrati et al. [7] observed two effects caused by flexible vegetation patches: the shading effect and the blocking effect. In most vegetation patches, the shading effect dominates, leading to a reduction in the drag coefficient. Finally, a fitting formula based on the drag coefficient factor and Cauchy number was proposed.

The presence of vegetation significantly influences the transport of pollutants in river channels by enhancing both turbulent diffusion and mechanical dispersion of pollutants. Mechanical dispersion refers to the anomalous diffusion phenomenon of solute particles under the intense shear forces generated in vegetated areas. This phenomenon arises due to the reduction in advective transport rates, which is attributed to the resistance caused by vegetation [8]. Nepf et al. [9] proposed a model to simulate the random motion of fluid particles within vegetation. Their work emphasizes the complex and intimate relationship between mechanical dispersion and the resistance provided by vegetation, as well as its density. Lu and Dai [10] developed a large-eddy simulation model for flow and scalar transport in open channels with flexible vegetation, allowing for flexible simulation of vegetation deflection heights. Bai et al. [11] employed the Lattice Boltzmann method (LBM) and Random Displacement method (RDM) to establish a numerical model for flow velocity and pollutant transport in compound cross-sectional river channels, providing the lateral diffusion coefficients of pollutants in the main channel and floodplain under the influence of vegetation.

The condition of the riverbed also has a significant impact on water flow characteristics. In natural river channels, due to the porosity of granular materials and the water level difference between the riverbed and the groundwater table, water infiltrates through the boundaries of alluvial channels, rivers, and streams in the form of seepage. The presence of downward seepage leads to increased bed shear stress and sediment transport, thereby altering the hydrodynamic characteristics of the river channel [12]. Studies by Singha et al. [13] found that near-bed velocities increase due to suction effects, resulting in a more uniform velocity distribution. Ghysels et al. [14] proposed a concise and intuitive method based on existing building blocks in MODFLOW for simulating river–aquifer interactions in gaining rivers. Additionally, the presence of vegetation also influences the hydrodynamic distribution of the riverbed. Devi and Kumar [15] investigated the impact of submerged flexible vegetation on water flow in river channels with downward seepage, demonstrating that 10% seepage increases turbulence intensity by an average of 15%, and 15% seepage increases turbulence intensity by an average of 25%.

In earlier stages, the authors investigated the hydrodynamics and pollutant transport mechanisms in flexible vegetation-laden channels using models and achieved promising simulation results [16]. However, studies on pollutant transport in permeable channels are still scarce. This issue necessitates the simultaneous simulation of a multi-physics coupling problem encompassing hydrodynamics (velocity distribution), vegetation resistance, seepage effects, and pollutant diffusion. The presence of vegetation significantly alters the flow structure and pollutant dispersion patterns, while the coupling of seepage with flow through porous media enhances the nonlinear characteristics of the model. This study builds upon numerical models and establishes a module for simulating hydrodynamics and pollutant transport in vegetated river channels with seepage, utilizing the LBM and RDM. With experimental data from previous studies as validation, the research investigates the influence of seepage on flow velocity and pollutant transport in flexible vegetated river channels. The findings provide a theoretical basis for control strategies aimed at reducing groundwater contamination through vegetation arrangement.

2. Methods and Materials

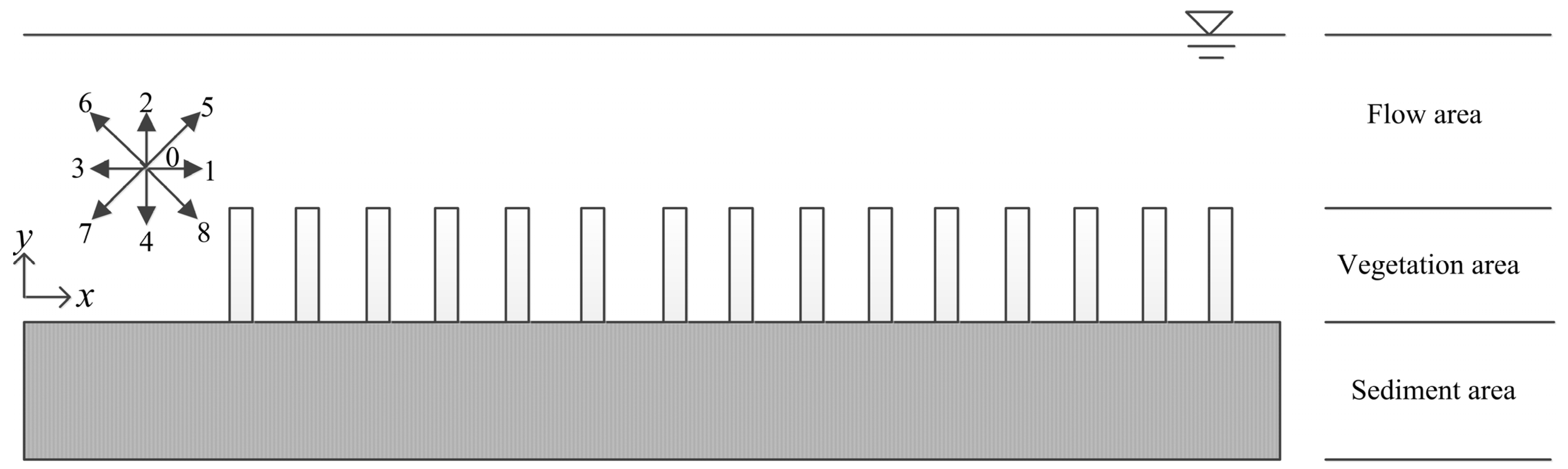
2.1. Numerical Model Framework

2.1.1. Hydraulic Model

For simulating the velocity distribution in a seepage channel, it is first necessary to solve the velocity layer by layer, which can be divided into three layers: the water flow layer, the vegetation layer, and the sediment layer. The sediment layer can be regarded as a saturated porous medium flow, and the volume force of the porosity coefficient should be added to the formula as Equation (1):

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial u_i}{\partial t}}+{\displaystyle \frac{\partial \left(u_i{u}_j\right)}{\partial t}}=\left(\nu +{\nu }_e\right){\displaystyle \frac{{\partial }^2{u}_i}{\partial x_j{x}_j}}-g{\displaystyle \frac{\partial z_b}{\partial x_i}}-S_{bi} Flow layer\\ {\displaystyle \frac{\partial u_i}{\partial t}}+{\displaystyle \frac{\partial \left(u_i{u}_j\right)}{\partial t}}=\left(\nu +{\nu }_e\right){\displaystyle \frac{{\partial }^2{u}_i}{\partial x_j{x}_j}}-g{\displaystyle \frac{\partial z_b}{\partial x_i}}-S_{bi}-F_v Vegetation Layer\\ {\displaystyle \frac{1}{ϵ}}{\displaystyle \frac{\partial \left(\rho u\right)}{\partial t}}+{\displaystyle \frac{1}{{ϵ}^2}}\nabla \left(\rho uu\right)=-\nabla p+\nabla \tau +\rho F_s Sediment Layer\end{array}\right.$$

(1)

where the Einstein summation convention over lattice indices is adopted; $t$ denotes the time; $u_i$ is the velocity; $\nu$ and ${\nu }_e$ represent kinematic and eddy viscosity, respectively; and $z_b$ is the bed elevation; $F_s$ is the volumetric force generated by porous materials; and $i$ represents the component in the Cartesian coordinate direction.

The model achieves hydrodynamic coupling between the water layer, vegetation layer, and sediment layer by enforcing continuity of velocity and shear stress, with the seepage velocity serving as a critical boundary condition at the top of the sediment layer.

$S_{bi}$ is the bed shear stress term in the $i$ direction and expressed as a Manning formula:

$$S_{bi}={\displaystyle \frac{g{n}^2}{h^{1/3}}}{u}_i\sqrt{u_j{u}_j}$$

(2)

where $n$ is Manning’s coefficient, and $h$ is the water depth.

Aberle et al. [17] proposed the following expression for the drag force of natural flexible vegetation ($F_v$):

$$F_v={\displaystyle \frac{1}{2}}{C}_{df}\rho \alpha A_f{u}_m^2$$

(3)

where $C_{df}$ is the coefficient of the flexible vegetation, $\alpha$ is the vegetation arranged density, $A_f$ is the project area of flexible vegetation, $u_m$ is the averaged velocity, and $\rho$ expresses the fluid density.

The drag coefficient of flexible vegetation is given by Järvelä [18] as

$$C_{df}=\left({\displaystyle \frac{U_m^{\chi }}{U_{\chi }^{\chi }}}\right)C_d$$

(4)

where $U_{\chi }$ is used to guarantee dimensional homogeneity of the relationship and is equal to the lowest velocity used in determining $\chi$, the value of $U_{\chi }$ is 0.1 m/s based on Järvelä [19], the reference value of $\chi$ is −1.11, and $C_d$ = 1 for cylindrical vegetation [20,21].

$F_s$ can be defined as follows [22]:

$$F_s={\displaystyle \frac{\nu }{K}}u+{\displaystyle \frac{\beta }{\sqrt{K}}}\left|u\right|u$$

(5)

$$K={\displaystyle \frac{{ϵ}^3{d}_p}{150\times {\left(1-ϵ\right)}^2}}$$

(6)

The application of the LBM in simulating water flow in river channels and in porous media has become relatively common. In this paper, the LBM is adopted to simulate the velocity distribution in permeable flows. The LBM is mainly divided into two processes: collision and streaming (or propagation). These two processes can be expressed by the following equations:

$$f_{\epsilon }\left(x+e_{\epsilon }∆t, t+∆t\right)=f_{\epsilon }\left(x, t\right)-{\displaystyle \frac{1}{{\tau }_t}}\left[f_{\epsilon }\left(x, t\right)-f_{\epsilon }^{eq}\left(x, t\right)\right]+{\displaystyle \frac{∆t}{N_{\epsilon }{e}^2}}{e}_{\epsilon i}{F}_i$$

(7)

where $f_{\epsilon }$ represents the distribution function of particles; $f^{eq}$ is the local equilibrium distribution function; $x$ is the space vector in Cartesian coordinates; $e=∆x/∆t$; $∆x$ is the lattice size, $∆x=1$ cm in this paper; $∆t$ is the time step, $∆t$ = 1 s in this paper; ${\tau }_t$ is the total relaxation time parameter; and $F_i$ denotes the external forces.

$N_{\epsilon }$ is a constant that can be defined as follows:

$$N_{\epsilon }={\displaystyle \frac{1}{e^2}}{\sum }_{\epsilon }{e}_{\epsilon i}{e}_{\epsilon i}$$

(8)

This paper adopts the commonly used Discrete Boltzmann Model D2Q9 (Figure 1) in simulating two-dimensional hydrodynamics [1]. The calculation of $e_{\epsilon }$ in the D2Q9 model is as follows:

$$e_{\epsilon }=\left\{\begin{array}{c}\left(0, 0\right), \epsilon =0\\ e\left[cos{\displaystyle \frac{\left(\alpha -1\right)\pi }{4}}, sin{\displaystyle \frac{\left(\alpha -1\right)\pi }{4}} \right], \epsilon =1, 2, 3, 4\\ \sqrt{2}e\left[cos{\displaystyle \frac{\left(\alpha -1\right)\pi }{4}}, sin{\displaystyle \frac{\left(\alpha -1\right)\pi }{4}} \right], \epsilon =5, 6 , 7, 8\end{array}\right.$$

(9)

The local equilibrium distribution function $f^{eq}$ can be expressed as

$$f_{\epsilon }^{eq}=\left\{\begin{array}{c}1-{\displaystyle \frac{5g}{6e^2}}-{\displaystyle \frac{2}{3e^2}}{u}_i{u}_i, \epsilon =0\\ {\displaystyle \frac{g}{6e^2}}+{\displaystyle \frac{1}{3e^2}}{e}_{\epsilon i}{u}_i+{\displaystyle \frac{1}{2e^4}}{e}_{\epsilon i}{e}_{\epsilon j}{u}_i{u}_j-{\displaystyle \frac{1}{6e^2}}{u}_i{u}_i, \epsilon =1, 2, 3, 4\\ {\displaystyle \frac{g}{24e^2}}+{\displaystyle \frac{1}{12e^2}}{e}_{\epsilon i}{u}_i+{\displaystyle \frac{1}{8e^4}}{e}_{\epsilon i}{e}_{\epsilon j}{u}_i{u}_j-{\displaystyle \frac{1}{24e^2}}{u}_i{u}_i, \epsilon =5, 6, 7, 8\end{array}\right.$$

(10)

The relaxation time parameter ${\tau }_t$ can be expressed as follows [23]:

$${\tau }_t={\displaystyle \frac{\tau +\sqrt{{\tau }^2+18C_s^2/\left(e^2\right)\sqrt{\prod ij\prod ij}}}{1}}$$

(11)

$$\prod ij={\sum }_{\epsilon }{e}_{\epsilon i}{e}_{\epsilon j}\left(f_{\alpha }-f_{\alpha }^{eq}\right)$$

(12)

where $\tau$ denotes the single-relaxation time and $C_s$ is the Smagorinsky constant, and $C_s=1/\sqrt{3}$ [24].

The external forces $F_{\epsilon i}$ can be expressed in the flow layer and vegetation layer as follows:

$$\left\{\begin{array}{c}{F}_{\epsilon i}=-g{\displaystyle \frac{\partial z_b}{\partial x_i}}-{\displaystyle \frac{g{n}^2}{h^{\frac{1}{3}}}}{u}_i\sqrt{u_j{u}_j} \mathrm{Flow} \mathrm{layer}\\ F_{\epsilon i}=-g{\displaystyle \frac{\partial z_b}{\partial x_i}}-{\displaystyle \frac{g{n}^2}{h^{\frac{1}{3}}}}{u}_i\sqrt{u_j{u}_j}-{\displaystyle \frac{1}{2}}{C}_{df}\rho \alpha A_f{U}_m^2 \mathrm{Vegetation} \mathrm{layer}\\ F_{\epsilon i}=-g{\displaystyle \frac{\partial z_b}{\partial x_i}}-{\displaystyle \frac{g{n}^2}{h^{\frac{1}{3}}}}{u}_i\sqrt{u_j{u}_j}-({\displaystyle \frac{u_j}{K}}{u}_i+{\displaystyle \frac{\beta }{\sqrt{K}}}\left|u_i\right|u_i) \mathrm{Sediment} \mathrm{Layer}\end{array}\right.$$

(13)

The external force term is assessed at the midpoint between the lattice point and its neighboring lattice point as

$$F_{\epsilon i}=F_{\epsilon i}\left(x_i+{\displaystyle \frac{1}{2}}{e}_{\epsilon i}∆t, t\right)$$

(14)

The effect of osmosis primarily influences $u_j$ at the bottom boundary of the sediment. Depending on the magnitude of the permeability, $u_j$ at the lower boundary of the sediment can be defined as follows:

$$u_j={\displaystyle \frac{Q_s}{A_s}}$$

(15)

2.1.2. Pollution Transport Model

This paper employs the RDM to simulate the transport of pollutants in vegetated seepage river flows. The RDM is a well-established approach for simulating pollutant transport and has been widely applied to numerous pollutant transport problems [25]. The pollutant transport model established in this study primarily focuses on the impact of hydrodynamic processes (advection, diffusion) on pollutant migration. To concentrate on the core mechanisms of these physical processes, the model simplifies the biogeochemical interactions between sediment and pollutants. Key assumptions include: (1) Sediment does not possess adsorption–desorption capacity for pollutants, meaning it is treated as a saturated inert porous medium; (2) The uptake and degradation of pollutants by vegetation and microorganisms are neglected. For pollutant transport, a piecewise continuous treatment of the diffusion coefficient is adopted, where specific diffusion coefficients are used within each layer, and coupling is achieved by ensuring the continuity of concentration and mass flux at the interfaces. The equation to simulate the particle position is expressed as [26]:

$$x_{i+1}=x_i+u\left(z_i\right)∆t$$

(16)

$$z_{i+1}=z_i+\left({\displaystyle \frac{d{D}_t}{dz}}\left(z_i\right)\right)∆t+R\sqrt{2D_t\left(z_i\right)∆t}$$

(17)

where $∆t$ denotes the time step, $R$ represents a random number showing a normal distribution with mean 0 and standard deviation 1, $C$ refers to the nutrient concentration in water (mg/L), and $D_t$ is the total diffusion coefficient of pollution (m²/s).

The diffusion process of pollutants in the water flow area is as follows: pollutants are mainly influenced by flow velocity, transverse effective diffusivity coefficient ($D_y$) and the longitude effective diffusivity coefficient ($D_x$) [27,28].

$${\displaystyle \frac{\partial C}{\partial t}}+u_x{\displaystyle \frac{\partial C}{\partial x}}+u_y{\displaystyle \frac{\partial C}{\partial y}}=D_x{\displaystyle \frac{{\partial }^{2}C}{\partial x^2}}+D_y{\displaystyle \frac{{\partial }^{2}C}{\partial y^2}}$$

(18)

The diffusion process in vegetated areas is as follows: the diffusion of pollutants is also influenced by the turbulent diffusion coefficient and the mechanical dispersion coefficient. Then the pollutant transport equation in the vegetation area will be changed as follows:

$${\displaystyle \frac{\partial C}{\partial t}}+u_x{\displaystyle \frac{\partial C}{\partial x}}+u_y{\displaystyle \frac{\partial C}{\partial y}}=D_t{\displaystyle \frac{{\partial }^{2}C}{\partial x^2}}+D_t{\displaystyle \frac{{\partial }^{2}C}{\partial y^2}}$$

(19)

The total dispersion in vegetation ($D_t$) can be described as follows [10]:

$$D_t=D_m+\epsilon {\left(C_{df}\alpha b^2\right)}^{1/3}{u}_{m}b+{\displaystyle \frac{{\beta }^2}{2}}\alpha u_m{b}^3$$

(20)

where $\epsilon =0.81$ and $\beta =\sqrt{2}$ are constants [29], $b$ is the stalk width, and $D_m$ is the molecular diffusion coefficient.

$${\displaystyle \frac{\partial C}{\partial t}}+u_x{\displaystyle \frac{\partial C}{\partial x}}+u_y{\displaystyle \frac{\partial C}{\partial y}}=D_{zs}{\displaystyle \frac{{\partial }^{2}C}{\partial x^2}}+D_{zs}{\displaystyle \frac{{\partial }^{2}C}{\partial y^2}}+R_p$$

(21)

In the sediment, the diffusion coefficient of pollutants varies and $D_{zs}$ can be expressed using the following formula:

$$D_{zs}={\phi }^{m-1}{D}_m$$

(22)

where $\phi$ is the porosity of sediment; m is empirical constant, and m = 3 is a constant [30].

Boundary conditions should be set at the free water surface to prevent the particles from swimming out of the channel boundary [31]:

$$z_i=2h-z_i, z_i>h$$

(23)

In the non-infiltration contaminant simulation group, contaminants are unable to penetrate deeper with the water flow. Therefore, when the contaminants reach the boundary of the sediment, they will rebound [31].

$$z_i=-z_i, z_i<-h_s$$

(24)

where $h_s$ is the height of sediment.

When there is infiltration flow, contaminants can reach deeper layers along with the downward-penetrating water flow. If $-h_s>z_i$, the particle is removed from the simulation domain indicates that it has seeped to the deeper layer. The contaminant leakage rate is defined as the percentage of contaminant particles that cross the bottom boundary of the sediment layer during the simulation period, relative to the initial total number of particles (10,000). After the simulation, the total number of leaked particles is counted, and the leakage rate is calculated by multiplying the ratio of this count to the initial total number of particles by 100%.

Error analysis was conducted to determine the difference between the predicted and measured data. The root mean square error $R^2$ was calculated by the following equations:

$$R^2=1-{\displaystyle \frac{SSE}{SST}},$$

(25)

$$SST={\sum }_{i=1}^N{(Y_i-meanY)}^2,$$

(26)

$$SSE={\sum }_{i=1}^N{(Y_i-X_i)}^2,$$

(27)

$$meanY={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{Y}_i,$$

(28)

where $N$ is the number of lateral measuring points; X and Y are the calculated and measured values.

The simulation flowchart is shown in Figure 2.

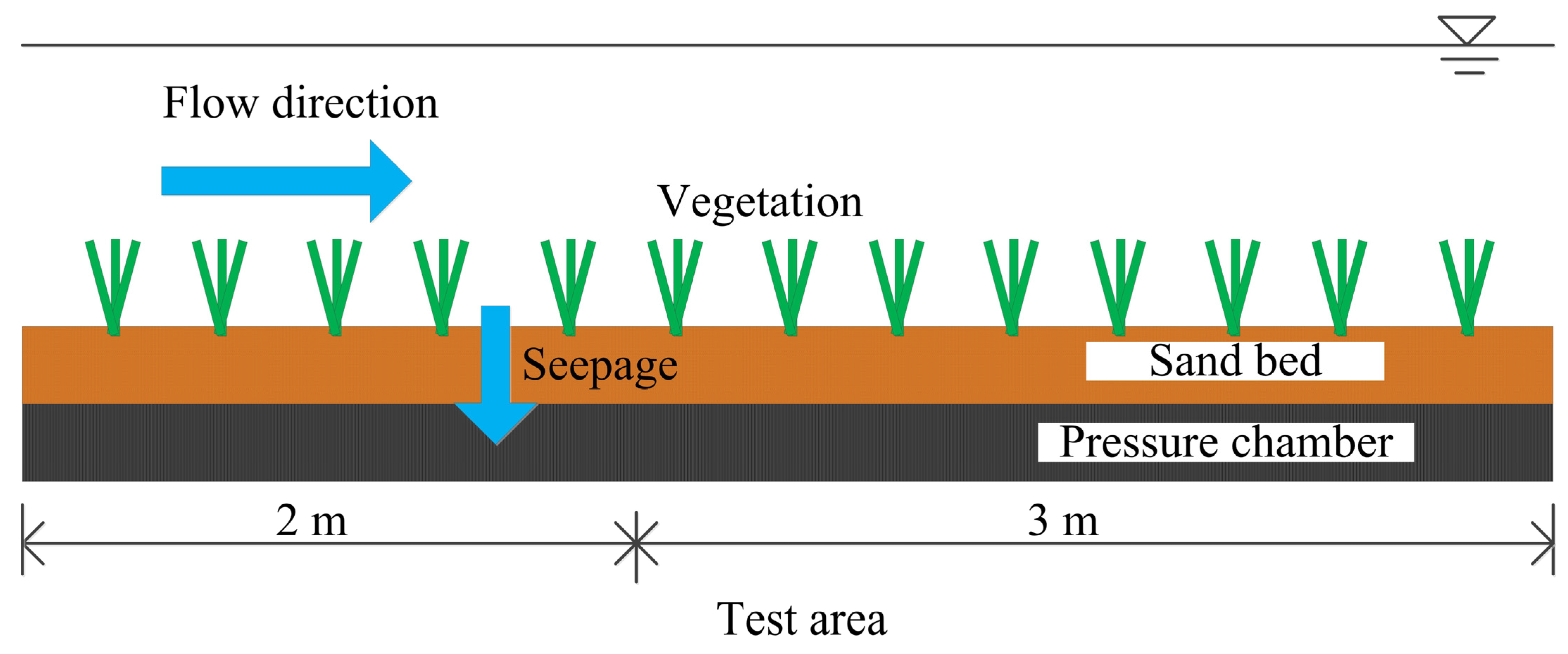
2.2. Validation Data

The velocity data for model validation were obtained from the experiments of Devi et al. [32]. The experiments were conducted in a 20 m-long, 1 m-wide, and 0.72 m-deep inclined flume. The test area had a length of 5 m, with water flowing through it. The test area was divided into three layers: the water flow layer, the sediment layer, and the seepage layer (Figure 3). An upstream reservoir introduced water into the flume, and a pressure chamber was arranged at the downstream end to regulate the desired percentage of seepage flow. The bed slope of the flume was fixed at 0.15%, which remained constant for all experiments. Instantaneous velocities were measured at a location 2 m from the test area inlet. A specific grain diameter ($d_{50}$ = 0.418 mm) was used. Flexible rubber cylinders with a diameter of 4 mm ($d_v$) and a height of 4 cm ($h_v$) were employed to simulate vegetation. Individual rubber cylinders were grouped into triplets to mimic vegetation patches, which were arranged in a staggered pattern. The deflection height of the vegetation ranged between 3 and 3.8 cm, with an average of 3.5 cm. Two different vegetation planting spacings ($S_v$) were adopted, namely 10 cm and 15 cm. Run1 for vegetation density of 44.4/m² with 0% seepage, Run2 for vegetation density of 44.4/m² with 10% seepage, Run3 for vegetation density of 44.4/m² with 15% seepage, Run4 for vegetation density of 100/m² with 0% seepage, Run5 for vegetation density of 100/m² with 10% seepage, Run6 for vegetation density of 100/m² with 15% seepage.

2.3. The Simulation Experiment of Pollution Retention

Simulation experiments were conducted using the same parameters shown in

Table 1. Pollutant seepage rates (%) for each experimental treatment under different seepage and vegetation density conditions.

Treatment	Run 1	Run 2	Run 3	Run 4	Run 5	Run 6
Pollution seepage rate (%)	0	4.85	7.79	0	13.53	15.23

. During simulation, the pollution source is set as a point instantaneous pollution source at z = 4 cm, and the simulation/experiment was configured with a pollutant retention time of 500 s and an initial pollutant count of 10,000 particles.

3. Results

The simulation results for flow velocity are shown in Figure 4, which presents a comparison between the simulated (lines) and measured (symbols) vertical velocity profiles for all six experimental runs detailed in Table 1. The left column (a, c, e) corresponds to a vegetation density of 44.4 plants/m², while the right column (b, d, f) corresponds to a higher density of 100 plants/m². Each row represents a different seepage rate: 0%, 10%, and 15%, from top to bottom. From the figure, it can be observed that the simulated flow velocity closely approximates the observed flow velocity, indicating a good simulation performance. In the absence of seepage, the flow velocity within the sediment tends to be more uniform. When seepage is present, the flow velocity in the sediment gradually increases, and the magnitude of this increase becomes larger as the seepage intensity increases. All simulation results indicate that a significant flow velocity has already developed at the interface between the water flow and the sediment. The increase in flow velocity is relatively small in the vegetation area, while it becomes significantly larger in the water flow area. By comparing experimental groups with and without seepage, it is found that seepage effectively enhances the average flow velocity in both the vegetation and water flow areas, and the improvement effect is more pronounced with greater seepage.

The simulation results for pollution transport are shown in Figure 5 and Figure 6. It can be observed that under non-seepage conditions, pollution spread significantly more within the water body, with less pronounced diffusion in the vegetation area and sediment zone. When seepage occurs, the diffusion of pollution in the vegetation area and sediment zone becomes more evident. The seepage rates of pollution are presented in Table 1. Due to the rebound of pollution at the lower boundary in the non-seepage group, the pollution seepage rate for this group is 0%. With the emergence of seepage, some pollution penetrate deeper into the soil along with the downward-flowing water. It can be seen that the pollution seepage rate for Run 2 is 4.85%, and for Run 3, it is 7.79%. As the amount of water seepage increases, the pollution seepage rate also increases significantly. The pollution seepage rate for Run 5 is 13.58%, and for Run 6, it is 15.23%. It can be noted that with an increase in vegetation density, the pollution seepage rate also increases significantly.

4. Discussion

4.1. Main Conclusions of This Study

This study establishes a numerical model for simulating hydrodynamics and contaminant transport in vegetation seepage channels by combining the LBM and RDM. Treating the sediment layer as a porous medium significantly enhances the accuracy of vertical velocity simulations. As the seepage rate increases, the velocity near the sediment-water interface notably rises, with larger increases observed at higher seepage intensities. Under no-infiltration conditions, contaminants primarily diffuse within the water flow layer; however, the presence of seepage enhances the penetration of contaminants into the sediment layer. Higher vegetation density leads to greater turbulent diffusion and mechanical dispersion coefficients within the vegetation zone, resulting in a significant increase in contaminant seepage rates (for example, when vegetation density increases from 44.4 plants/m² to 100 plants/m², the contaminant leakage rate rises from 7.79% to 15.23%). Seepage indirectly elevates the average velocities in both the vegetation zone and the water flow layer by enhancing bed shear stress and flow velocities within the sediment layer. High-density vegetation further exacerbates the risk of contaminant migration to groundwater by increasing the diffusion coefficient.

However, these phenomena are underpinned by critical physical mechanisms. Firstly, the enhancement of flow velocity by seepage originates from its fundamental alteration of the bed boundary condition. The downward seepage weakens the traditional no-slip boundary layer, effectively “thinning” the viscous sublayer near the bed. This allows the main flow momentum from the upper water layers to be transferred more efficiently to the near-bed region, leading to a significant increase in near-bed velocity and a more uniform velocity profile. Our treatment of the sediment layer as a porous medium accurately captures the continuity of velocity and shear stress at the water-sediment interface. It is precisely this coupling effect that dictates the higher flow velocity within the sediment pores, driven by the hydraulic gradient, must be accompanied by an accelerated flow at the bottom of the overlying water layer. This mechanism explains why a stronger seepage rate results in a more pronounced velocity increase at the interface.

Secondly, the positive correlation between vegetation density and the pollutant seepage rate reveals a “Stirring and Conveying” synergistic mechanism between vegetation and seepage. Dense vegetation generates substantial drag forces, which on one hand, convert the kinetic energy of the mean flow into turbulent kinetic energy, thereby enhancing the turbulent diffusion of pollutants. On the other hand, and more crucially, it creates highly heterogeneous flow paths, significantly amplifying the mechanical dispersion effect caused by spatial velocity variations. Here, the vegetation acts as an efficient “stirrer”, rapidly mixing pollutants from the main flow and delivering them to the sediment-water interface. Simultaneously, the downward seepage functions as an efficient “conveyor belt”, continuously removing pollutants that reach the interface and transporting them into deeper layers. Consequently, higher vegetation density intensifies the “stirring” action, supplying a greater flux of pollutants to the “conveyor belt”, which ultimately leads to the observed sharp increase in the seepage rate.

4.2. Comparison with Other Studies

Maclean and Willetts [33] experimentally found that seepage increases bed shear stress. This increase in bed shear force substantially elevates the flow velocity near the bed surface. Similarly, Chen and Chiew [34], Singha et al. [13], and Cao and Chiew [35] also observed a significant increase in bed surface velocities in seepage channels. Numerous studies have demonstrated the existence of substantial flow velocities within the soil [14]. In seepage channels, the water already possesses a certain velocity within the sediment, and according to the Navier–Stokes (N-S) equation, which states the continuity of velocity [1], the velocity in the water flow zone connects with that in the sediment zone, necessitating a higher velocity at the bed surface. Furthermore, the greater the seepage rate, the more significant the increase in flow velocity, aligning with previous research [15].

The higher velocities in the water flow zone transport pollutants to greater distances, aligning with previous research [16]. In the vegetated zone, pollutant diffusion is influenced by both turbulent diffusion and mechanical dispersion, resulting in a larger diffusion coefficient for pollutants [9]. Furthermore, as vegetation density increases, the diffusion coefficient of pollutants also increases [29]. The seepage water flow carries away the pollutants, and the greater the seepage water volume, the more pollutants are transported away with the flow [36,37]. This explains why, as shown in Table 1, a higher seepage rate corresponds to a higher pollutant seepage rate.

4.3. Advantages and Limitations

There are still some limitations in the research presented in this paper. The study assumes that the sediment is already in a state of pollutant saturation and does not consider the adsorption and desorption capacity of the sediment for pollutants. Traditional research recognizes sediment as both a source and a sink of pollutants, capable of absorbing pollutants from the river and releasing them back into the water [38]. If the research is to be applied in natural settings, the role of sediment as both a source and a sink must be taken into account. This would involve considering the equilibrium concentration of pollutants in the sediment and the concentration of pollutants in the water body, which can be represented by the following equation. The LBM-RDM coupled model adopted in this study performs excellently in simulating hydrodynamically driven contaminant transport, but it is essential to recognize the impact of several key simplifications on the interpretation of the results.

Firstly, the simplification regarding sediment–contaminant interactions is the primary limitation of this model. As described in the methodology section, the model does not account for the role of sediment as a ‘source’ and ‘sink’. Natural sediments significantly regulate contaminant concentrations in the overlying water through adsorption–desorption processes (as described by Equations (25) and (26)). Neglecting adsorption implies that the model simulates the transport of a ‘conservative’ contaminant (i.e., one that does not react with the medium) or a long-term scenario where the sediment has already reached adsorption saturation. This may lead the model to overestimate the initial leakage rate of the contaminant in the short term but underestimate the long-term accumulation and release risks of the contaminant in the sediment. For example, the rapid infiltration of contaminants observed in this study might be slowed by sediment adsorption in real environments; however, once the sediment becomes saturated, the risk of its continuous release as a secondary pollution source could be more severe than predicted by the model.

Secondly, treating the sediment layer as a homogeneous, saturated porous medium ignores its heterogeneity and anisotropy. Although this approach improves the accuracy of simulating vertical flow velocities, preferential flow paths (such as biopores and fractures) in natural riverbeds may become rapid conduits for contaminants, making actual leakage scenarios more spatially heterogeneous than the simulation results.

Finally, the model does not consider the biological uptake and degradation of contaminants by vegetation and microorganisms. This process is an important removal mechanism in natural systems, especially for nutrients and certain organic contaminants. Neglecting this process means that when evaluating the ecological function of vegetation, the model only considers its hydrodynamic effects (increasing diffusion) and overlooks its positive purification role.

Despite these limitations, the value of this study lies in clearly revealing the hydrodynamic mechanisms driven by the combined effects of seepage and vegetation that promote the downward migration of contaminants. Our results provide a solid benchmark of physical processes for more complex, integrated models that incorporate biogeochemical processes.

Additionally, vegetation in rivers can also absorb pollutants [39], and this aspect should also be incorporated into the model.

$${\displaystyle \frac{\partial C}{\partial t}}={\displaystyle \frac{\partial C_s}{\partial t}}+{\psi }_{1}C+{\psi }_{2}C,$$

(29)

where ${\displaystyle \frac{\partial C_s}{\partial t}}$ is the concentration of pollutants released from and absorbed by the sediment over time, ${\psi }_1$ is the rate constant for the vegetation absorb.

On the other hand, the pollutants in the sediment considered within this model are assumed to be in a saturated state. However, in reality, pollutants in sediment can exist in two distinct states: adsorption and desorption. The diffusion rate of these pollutants can be accurately measured using Fick’s first law, based on the nutrient concentration gradient within the pore water of the sediment. Furthermore, the processes of adsorption and desorption can be defined through the incorporation of a source term, as outlined by Higashino and Stefan [40]. The release of pollutants from the sediment can be mathematically represented by the equation proposed by Bai et al. [41].

$$\mathsf{\phi }{\displaystyle \frac{\partial C}{\partial t}}=\phi D_{zs}{\displaystyle \frac{{\partial }^{2}C}{\partial z^2}}-b(C-C_e)$$

(30)

where $b$ is the first-order rate constant (s⁻¹); $C_e$ is the equilibrium concentration of pollution in water under static hydrodynamic condition (mg/L).

The sedimentary layer is treated as a saturated porous medium in simulations, incorporating pore coefficient volume force. This approach improves accuracy in modeling vertical flow velocity under seepage conditions, as sedimentary layers consist of granular materials with porosity that permits water flow. However, it overlooks potential non-uniformity and anisotropy, which may affect local velocity distribution details. Under no-seepage conditions, pollutants are assumed to rebound at the sedimentary layer boundary, preventing further downward infiltration. This simplification focuses the model on seepage effects but ignores other mechanisms, like biological activity, that could allow pollutants to continue migrating downward in real environments.

This study has been thoroughly validated in terms of hydrodynamic simulation through comparison with measured velocity profiles, ensuring the reliability of the velocity field predictions. However, it must be explicitly stated that all results regarding contaminant transport and leakage rates (Figure 5 and Figure 6, Table 1) are numerical predictions based on the validated flow field and lack direct comparison with experimental data for validation. This constitutes a major limitation of this study. This limitation introduces uncertainties in the following aspects, which require careful consideration when interpreting the results: The total diffusivity $D_t$ of contaminants in the vegetated zone (Equation (20)) relies on a parameterization scheme determined through literature and empirical constants. Although this scheme has been used in previous studies, its universality under different seepage conditions and vegetation configurations is uncertain. If the actual diffusion coefficient is lower than the value used in the model, we may have overestimated the lateral mixing of contaminants in the vegetated zone and their delivery rate to the riverbed, consequently overestimating the leakage risk, and vice versa. The model neglects the adsorption of contaminants by sediments. This simplification almost certainly leads to an overestimation of the contaminant leakage rate, as the contaminants in the model can migrate freely with the water, whereas in natural environments, a portion would be retained by sediments. Therefore, the leakage rates presented in Table 1 (e.g., 15.23%) should be interpreted as the ‘potential maximum leakage risk’ under the most unfavorable hydrodynamic conditions, rather than values necessarily achieved in actual environments. Despite the aforementioned uncertainties, the core conclusion of this study—that the combined effect of seepage and vegetation density significantly increases the potential risk of contaminant migration towards groundwater—remains valid at a qualitative level. The model predictions clearly reveal the direction and relative magnitude of this physical mechanism: greater seepage and denser vegetation strengthen the driving force for downward contaminant migration. However, extreme caution must be exercised when applying the quantitatively predicted leakage rate values to actual management decisions.

4.4. Further Direction

Furthermore, the findings of this study require additional field test data for validation before they can be applied in natural conditions. Firstly, the distribution patterns and shapes of vegetation in nature are often irregular. This has a significant impact on flow velocity and pollutant transport. The influence of different vegetation layouts on vegetation drag force can be referenced from the research of Zhang et al. [42]. For the impact of irregular vegetation on flow velocity, the vertical stratification of vegetation can be considered based on its projected area to provide vertical drag force and diffusion coefficients [43]. The development and research of this model contribute to optimizing the management of vegetation planting schemes in vegetated seepage river channels, thereby contributing to the protection of groundwater quality.

5. Conclusions

This paper studies the distribution of flow velocity and the seepage pattern of pollutants in vegetated seepage channels through numerical modeling, yielding the following results:

(1) For simulating the flow velocity distribution in vegetated seepage channels, treating the sediment layer as a porous medium, a key refinement in this model, significantly improved the accuracy of vertical flow velocity predictions, particularly near the bed interface. Simulations confirmed that the vertical flow velocity increases correspondingly with higher seepage rates.

(2) Regarding pollutant transport, the presence of seepage is a key driver for pollutant migration into the sediment layer. The underlying mechanism is that high-density vegetation significantly increases the drag force, which enhances the turbulent diffusion and mechanical dispersion coefficients within the vegetated area. This, in turn, promotes the vertical mixing and transport of pollutants, making them more susceptible to being carried deeper into the sediment layer by the downward seepage flow. Consequently, under the same seepage rate, a higher vegetation density leads to an increased pollutant seepage rate.

(3) In future research, the impacts of sediment, vegetation, and microorganisms on pollutants should also be incorporated into our models. Additionally, the models should consider the effects of different vegetation layouts and irregular vegetation shapes on flow velocity distribution and pollutant transport. The uniform high-density planting model should be abandoned in favor of implementing “zonal management” based on groundwater vulnerability. In groundwater-sensitive areas, low-density vegetation or unvegetated buffer zones should be adopted to reduce contaminant infiltration risks, while high-density vegetation can be established in non-sensitive areas to enhance surface water purification.