Three-Phase Space Vector PWM Inverter for Induction Motor Drive with Leakage Current Reduction
Abstract
1. Introduction
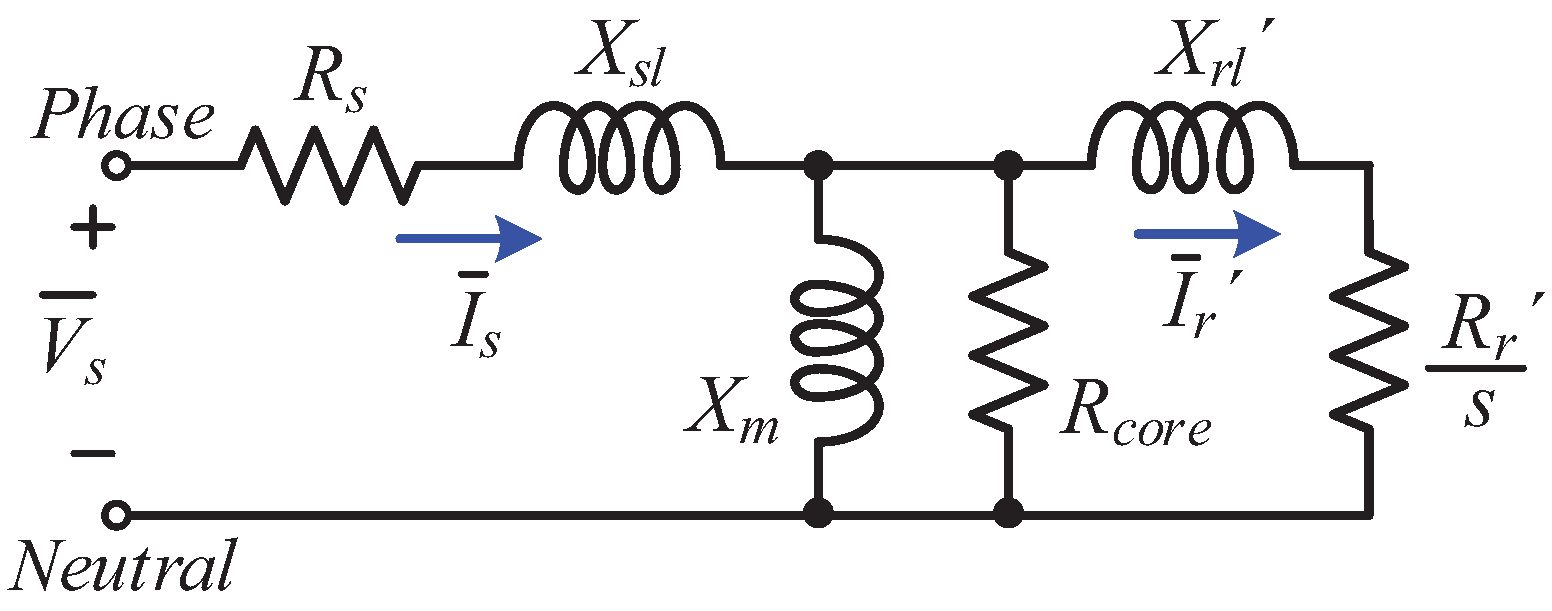
2. High-Frequency Induction Machine Modeling
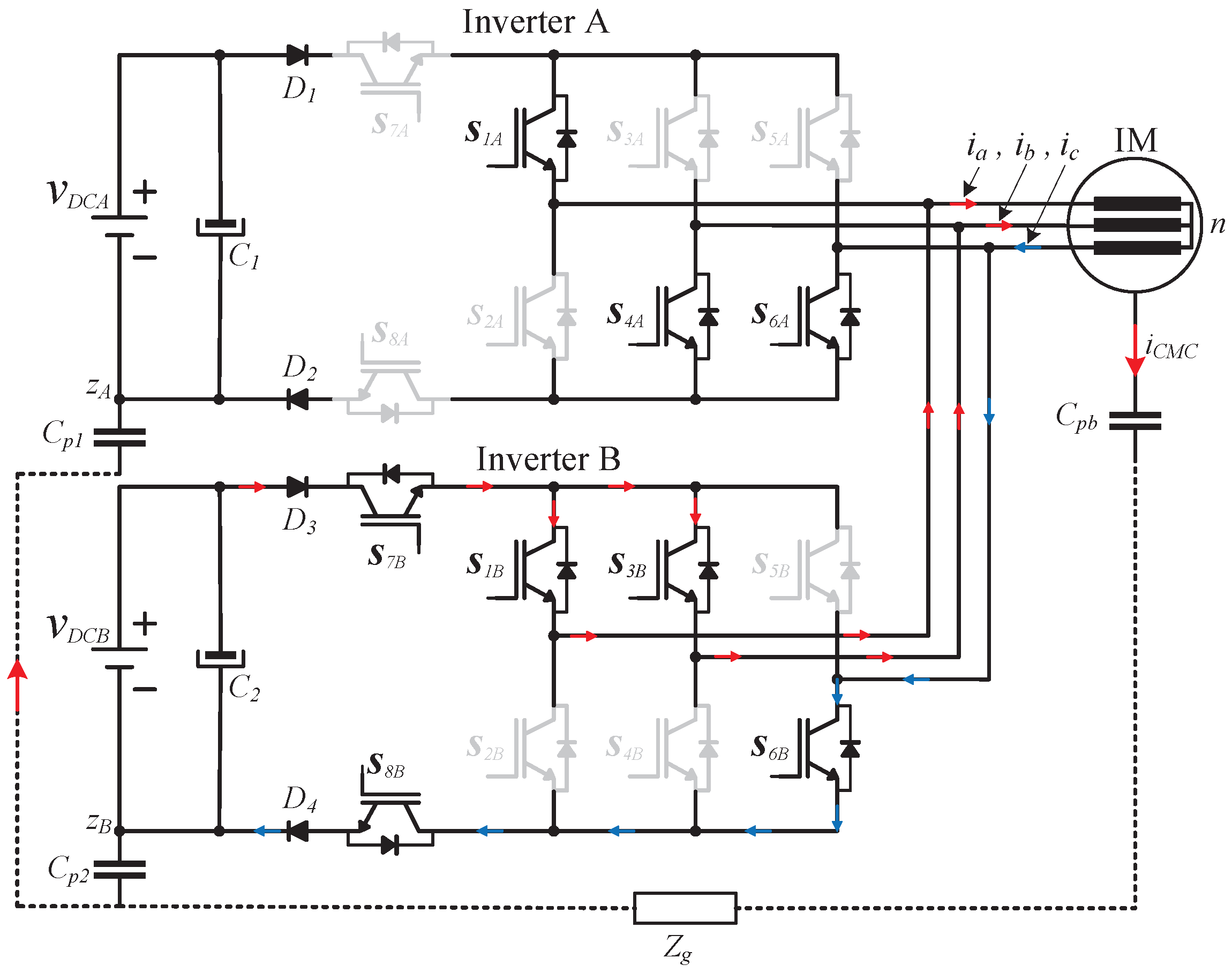
3. Proposed Induction Motor Drive
- The reference vector is located at the first sector, as it is shown in Figure 6;
- The load is predominantly inductive, as is the case of an induction motor;
- The space vector sequence is the one that is used for the conventional two-level three-phase inverter.
4. Proposed Modulation Strategy
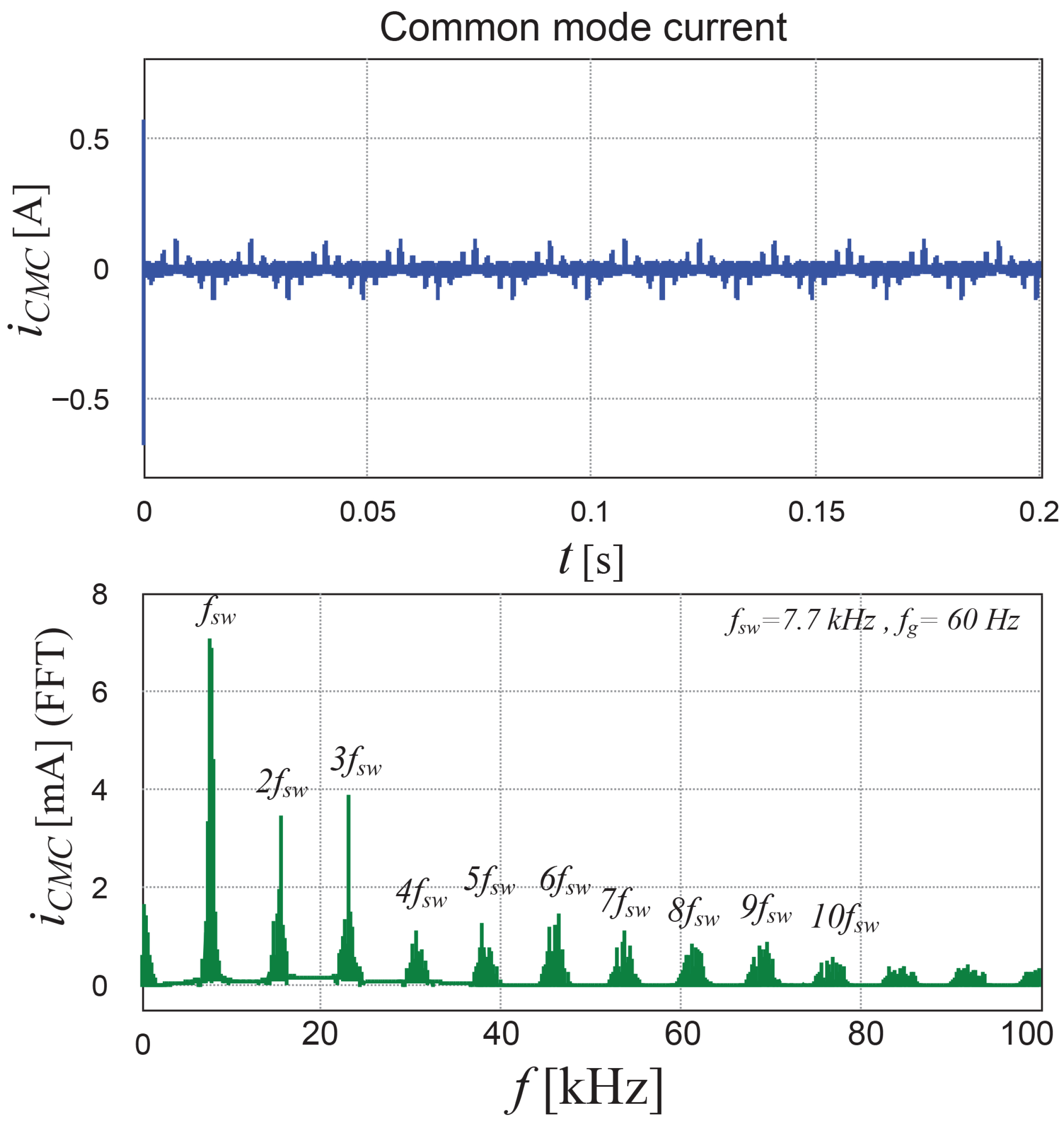
5. Numerical Results
6. Experimental Results
7. Comparative Study
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Altern current |
| DC | Direct current |
| PWM | Pulse width modulation |
| CMV | Common mode voltage |
| CMC | Common mode current |
| SVPWM | Space vector pulse width modulation |
| THD | Total harmonic distortion |
| IGBT | Isolated gate bipolar transistor |
| DSP | Digital signal processor |
| Common mode voltage | |
| Voltage between phase a and a common point | |
| Voltage between phase b and a common point | |
| Voltage between phase c and a common point | |
| Per-phase stator voltage | |
| Per-phase stator resistance | |
| Per-phase rotor resistance | |
| Per-phase stator leakage reactance | |
| Per-phase rotor leakage reactance | |
| Per-phase mutual reactance | |
| s | Mechanical slip of the induction motor |
| Stator current | |
| Rotor current | |
| Reference vector for the SVM | |
| Active vectors for the SVM | |
| Null vector for the SVM | |
| Times for active vectors | |
| Time for null vector | |
| Switching period |
References
- Saleh, S.A.; Jee, A.; Meng, J.; Thao, N.G.M.; Panetta, S. Effects of Multi-Level Converters on Common-Mode Voltages in Induction Motor Variable Frequency Drives. IEEE Trans. Ind. Appl. 2025. Early Access. [Google Scholar] [CrossRef]
- International Energy Agency. Global EV Outlook 2024, Moving Towards Increased Affordability; IEA Publications: Paris, France, 2024; Available online: https://www.iea.org/reports/global-ev-outlook-2024 (accessed on 28 September 2025).
- Yu, Y.; Pei, Y.; Chai, F.; Doppelbauer, M. Performance Comparison Between Permanent Magnet Synchronous Motor and Vernier Motor for In-Wheel Direct Drive. IEEE Trans. Ind. Electron. 2023, 70, 7761–7772. [Google Scholar] [CrossRef]
- Mishra, S.; Singh, B.; Varshney, A. Adaptive Flux Based Speed Estimation of Syn-Rel Motor Drive for Electric Vehicle with Solar-PV Assistance. IEEE Trans. Ind. Appl. 2024, 60, 6634–6644. [Google Scholar] [CrossRef]
- Monadi, M.; Nabipour, M.; Behbahani, F.A.; Pouresmaeil, E. Speed Control Techniques for Permanent Magnet Synchronous Motors in Electric Vehicle Applications Toward Sustainable Energy Mobility: A Review. IEEE Access 2024, 12, 119615–119632. [Google Scholar] [CrossRef]
- Ma, Y.; Jiang, D.; Liu, Z.; Yan, S.; Wang, Z.; Qu, R. Common-Mode Voltage Elimination of Dual Three-Phase Motor with Different Angular Displacements. IEEE Trans. Ind. Electron. 2024, 71, 5431–5442. [Google Scholar] [CrossRef]
- Zingariello, A.; Zhang, Z.; Griepentrog, G. Evaluation of the Common-Mode Current Propagation Paths in Motor Drive Systems. In Proceedings of the 2024 IEEE 9th Southern Power Electronics Conference (SPEC), Brisbane, Australia, 2–5 December 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Un, E.; Hava, A.M. A Near-State PWM Method with Reduced Switching Losses and Reduced Common-Mode Voltage for Three-Phase Voltage Source Inverters. IEEE Trans. Ind. Appl. 2009, 45, 782–793. [Google Scholar] [CrossRef]
- Cheng, H.; Yuan, W.; Wang, C.; Zhao, Z.; Hao, J. A Modified Carrier-Based PWM Strategy for Common Mode Voltage Elimination and Neutral Point Voltage Balance in a Unidirectional Three-Level Converter for AC Motor Drives. IEEE Trans. Ind. Electron. 2024, 71, 11876–11887. [Google Scholar] [CrossRef]
- Turzynski, M.; Musznicki, P. A Review of Reduction Methods of Impact of Common-Mode Voltage on Electric Drives. Energies 2021, 14, 4003. [Google Scholar] [CrossRef]
- Hota, A.; Agarwal, V. Novel Three-Phase H10 Inverter Topology with Zero or Constant Common-Mode Voltage for Three-Phase Induction Motor Drive Applications. IEEE Trans. Ind. Electron. 2022, 69, 7522–7525. [Google Scholar] [CrossRef]
- Lee, H.D.; Sul, S.K. A common mode voltage reduction in boost rectifier/inverter system by shifting active voltage vector in a control period. IEEE Trans. Power Electron. 2000, 15, 1094–1101. [Google Scholar] [CrossRef]
- Di Piazza, M.C.; Tine, G.; Vitale, G. An Improved Active Common-Mode Voltage Compensation Device for Induction Motor Drives. IEEE Trans. Ind. Electron. 2008, 55, 1823–1834. [Google Scholar] [CrossRef]
- Saleh, S.A. Wavelet Modulation with an Optimized Resolution-Level to Minimize Common-Mode Voltages in Variable Frequency Induction Motor Drives. IEEE Trans. Ind. Electron. 2025, 72, 3425–3437. [Google Scholar] [CrossRef]
- Wei, Y.; Diao, N.; Guo, X.; Hua, C.; Blaabjerg, F. A Novel Common-Mode Voltage Suppression Strategy for Current Source Converter. IEEE Trans. Ind. Electron. 2024, 71, 1104–1112. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Z.; Huang, W.; Shen, Y. Fault-Tolerant Control and Common-Mode Voltage Reduction for Dual Three-Phase CSIs Fed Motor Drives. IEEE Trans. Power Electron. 2025, 40, 4374–4385. [Google Scholar] [CrossRef]
- Jung, J.H.; Kim, J.M.; Liserre, M. Conducted EMI Reduction by Active Power Filter Embedded in Neutral-Point-Clamped Converters. IEEE Trans. Power Electron. 2023, 38, 15551–15565. [Google Scholar] [CrossRef]
- Han, D.; Peng, F.Z.; Dwari, S. A Multilevel Active CM Noise Power Filter for Multilevel Inverters. IEEE Trans. Ind. Electron. 2023, 70, 5454–5462. [Google Scholar] [CrossRef]
- Baranwal, R.; Basu, K.; Mohan, N. Carrier-Based Implementation of SVPWM for Dual Two-Level VSI and Dual Matrix Converter with Zero Common-Mode Voltage. IEEE Trans. Power Electron. 2015, 30, 1471–1487. [Google Scholar] [CrossRef]
- Long, B.; Chen, Z.; Hu, C.; Rodriguez, J.; Guerrero, J.M.; Zang, X. A Reduced Common-Mode Voltage Control Scheme for Three-Level H10 Converter Considering Dead-Time Effect. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 695–706. [Google Scholar] [CrossRef]
- Hota, A.; Agarwal, V. A Novel Leg-Integrated Switched Capacitor Inverter Topology for Three-Phase Induction Motor Drives. IEEE Trans. Ind. Electron. 2024, 71, 4353–4360. [Google Scholar] [CrossRef]
- Guo, X.; He, R.; Jian, J.; Lu, Z.; Sun, X.; Guerrero, J.M. Leakage Current Elimination of Four-Leg Inverter for Transformerless Three-Phase PV Systems. IEEE Trans. Power Electron. 2016, 31, 1841–1846. [Google Scholar] [CrossRef]
- Cacciato, M.; Consoli, A.; Scarcella, G.; Testa, A. Reduction of common-mode currents in PWM inverter motor drives. IEEE Trans. Ind. Appl. 1999, 35, 469–476. [Google Scholar] [CrossRef]
- Mirafzal, B.; Skibinski, G.L.; Tallam, R.M.; Schlegel, D.W.; Lukaszewski, R.A. Universal Induction Motor Model with Low-to-High Frequency-Response Characteristics. IEEE Trans. Ind. Appl. 2007, 43, 1233–1246. [Google Scholar] [CrossRef]
- IEEE 112-2017; IEEE Standard Test Procedure for Polyphase Induction Motors and Generators. IEEE: Piscataway, NJ, USA, 2017.
- Mirafzal, B.; Skibinski, G.L.; Tallam, R.M. Determination of Parameters in the Universal Induction Motor Model. IEEE Trans. Ind. Appl. 2009, 45, 142–151. [Google Scholar] [CrossRef]
- Suresh, G.; Toliyat, H.A.; Rendusara, D.A.; Enjeti, P.N. Predicting the transient effects of PWM voltage waveform on the stator windings of random wound induction motors. IEEE Trans. Power Electron. 1999, 14, 23–30. [Google Scholar] [CrossRef]
- Idir, N.; Weens, Y.; Moreau, M.; Franchaud, J.J. High-Frequency Behavior Models of AC Motors. IEEE Trans. Magn. 2009, 45, 133–138. [Google Scholar] [CrossRef]
- Mohammed, O.A.; Ganu, S.; Abed, N.; Liu, S.; Liu, Z. High frequency PM synchronous motor model determined by FE analysis. IEEE Trans. Magn. 2006, 42, 1291–1294. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Lazzari, M. Experimental High-Frequency Parameter Identification of AC Electrical Motors. IEEE Trans. Ind. Appl. 2007, 43, 23–29. [Google Scholar] [CrossRef]
- Hofmann, W.; Zitzelsberger, J. PWM-control methods for common mode voltage minimization—A survey. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, 2006, SPEEDAM 2006, Taormina, Italy, 23–26 May 2006; pp. 1162–1167. [Google Scholar]
- Ogasawara, S.; Akagi, H. Modeling and damping of high-frequency leakage currents in PWM inverter-fed AC motor drive systems. In Proceedings of the IAS ’95, Conference Record of the 1995 IEEE Industry Applications Conference Thirtieth IAS Annual Meeting, Orlando, FL, USA, 8–12 October 1995; pp. 29–36. [Google Scholar]
- Zare, F.; Adabi, J.; Nami, A.; Ghosh, A. Common mode voltage in a motor drive system with PFC. In Proceedings of the 14th International Power Electronics and Motion Control Conference EPE-PEMC 2010, Ohrid, Macedonia, 6–8 September 2010; pp. T4-57–T4-64. [Google Scholar]
- van der Broeck, H.W.; Skudelny, H.C.; Stanke, G.V. Analysis and realization of a pulsewidth modulator based on voltage space vectors. IEEE Trans. Ind. Appl. 1988, 24, 142–150. [Google Scholar] [CrossRef]
- Gubia, E.; Sanchis, P.; Ursua, A.; Lopez, J.; Marroyo, L. Ground currents in single-phase transformerless photovoltaic systems. Prog. Photovolt. Res. Appl. 2007, 15, 629–650. [Google Scholar] [CrossRef]
- Gupta, A.K.; Agrawal, H.; Agarwal, V. A Novel Three-Phase Transformerless H-8 Topology with Reduced Leakage Current for Grid-Tied Solar PV Applications. IEEE Trans. Ind. Appl. 2019, 55, 1765–1774. [Google Scholar] [CrossRef]
- Oriti, G.; Julian, A.L.; Lipo, T.A. A new space vector modulation strategy for common mode voltage reduction [in PWM invertors]. In Proceedings of the PESC97, Record 28th Annual IEEE Power Electronics Specialists Conference, Formerly Power Conditioning Specialists Conference 1970–71. Power Processing and Electronic Specialists Conference 1972, St. Louis, MO, USA, 27 June 1997; pp. 1541–1546. [Google Scholar]
- Freddy, T.S.; Rahim, N.A.; Hew, W.P.; Che, H.S. Modulation Techniques to Reduce Leakage Current in Three-Phase Transformerless H7 Photovoltaic Inverter. IEEE Trans. Ind. Electron. 2015, 62, 322–331. [Google Scholar] [CrossRef]
- Guo, X.; Xu, D.; Wu, B. Three-phase DC-bypass topologies with reduced leakage current for transformerless PV systems. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 43–46. [Google Scholar] [CrossRef]
- Rahimi, R.; Farhangi, S.; Farhangi, B.; Moradi, G.R.; Afshari, E.; Blaabjerg, F. H8 Inverter to Reduce Leakage Current in Transformerless Three-Phase Grid-Connected Photovoltaic systems. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 910–918. [Google Scholar] [CrossRef]




















| State | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 3 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 4 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| Parameter | Value | Parameter | Value/Part Number |
|---|---|---|---|
| 10 | |||
| , , | 25 | ||
| and | F | 7.7 kHz | |
| , , | 2 mH | 60 Hz | |
| 160 nF | DIODES/IGBTs | STTH200R04TV/SKM50GB12T4 |
| Topology | Num. of | Variation in | ||||
|---|---|---|---|---|---|---|
| S | D | CMV | % | |||
| 3- FB (NSPWM) [8] | 6 | 0 | to | 174.2 mA (Sim.) | 0–0.91 | |
| 3- FB (AZPWM) [37] | 6 | 0 | to | 185.0 mA (Sim.) | 0–0.91 | |
| H-7 topology [38] | 7 | 0 | to | 135.9 mA (Sim.) | 0–0.91 | |
| DC-bypass topology [39] | 8 | 2 | to | 109.9 mA (Sim.) | 0–0.91 | |
| H-8 topology [40] | 8 | 0 | to | 85.9 mA (Exp.) | 0–0.91 | |
| H-10 topology [20] | 10 | 0 | to | 81.73 mA (Exp.) | 0–0.91 | NA |
| Proposed | 16 | 2 | Constant | 86.5 mA | 0–0.91 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vazquez-Guzman, G.; Martinez-Rodriguez, P.R.; Rosas-Caro, J.C.; Rivera-Perez, E.; Verdin-Cruz, J.A.; Rodriguez-Cortes, C.J.; Langarica-Cordoba, D. Three-Phase Space Vector PWM Inverter for Induction Motor Drive with Leakage Current Reduction. Sustainability 2025, 17, 9317. https://doi.org/10.3390/su17209317
Vazquez-Guzman G, Martinez-Rodriguez PR, Rosas-Caro JC, Rivera-Perez E, Verdin-Cruz JA, Rodriguez-Cortes CJ, Langarica-Cordoba D. Three-Phase Space Vector PWM Inverter for Induction Motor Drive with Leakage Current Reduction. Sustainability. 2025; 17(20):9317. https://doi.org/10.3390/su17209317
Chicago/Turabian StyleVazquez-Guzman, Gerardo, Panfilo R. Martinez-Rodriguez, Julio C. Rosas-Caro, Emmanuel Rivera-Perez, Juan A. Verdin-Cruz, Christopher J. Rodriguez-Cortes, and Diego Langarica-Cordoba. 2025. "Three-Phase Space Vector PWM Inverter for Induction Motor Drive with Leakage Current Reduction" Sustainability 17, no. 20: 9317. https://doi.org/10.3390/su17209317
APA StyleVazquez-Guzman, G., Martinez-Rodriguez, P. R., Rosas-Caro, J. C., Rivera-Perez, E., Verdin-Cruz, J. A., Rodriguez-Cortes, C. J., & Langarica-Cordoba, D. (2025). Three-Phase Space Vector PWM Inverter for Induction Motor Drive with Leakage Current Reduction. Sustainability, 17(20), 9317. https://doi.org/10.3390/su17209317









