A System Dynamics-Based Simulation Study on Urban Traffic Congestion Mitigation and Emission Reduction Policies
Abstract
1. Introduction
2. Literature Review
3. Model Construction
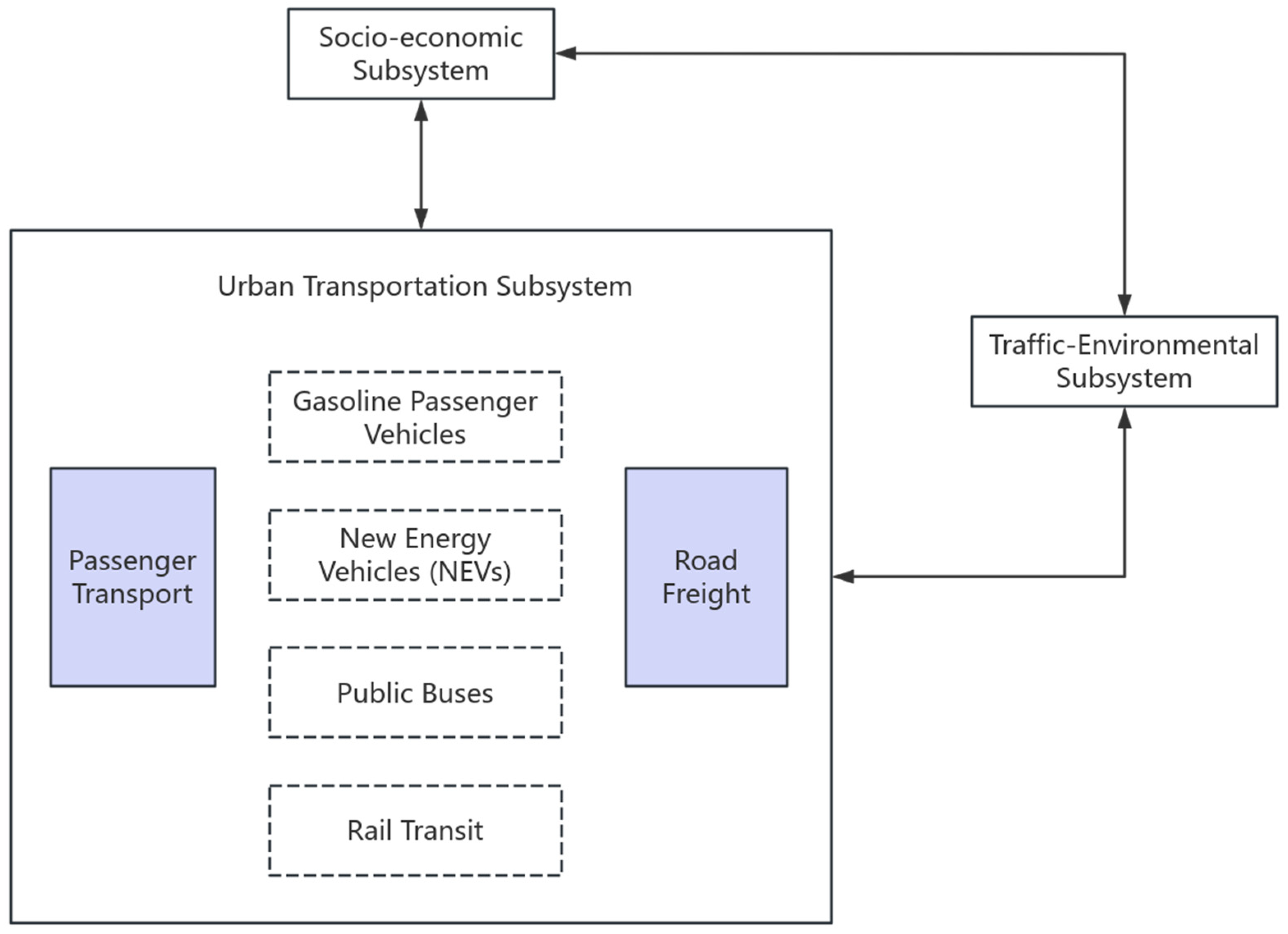
3.1. System Dynamics Model Construction
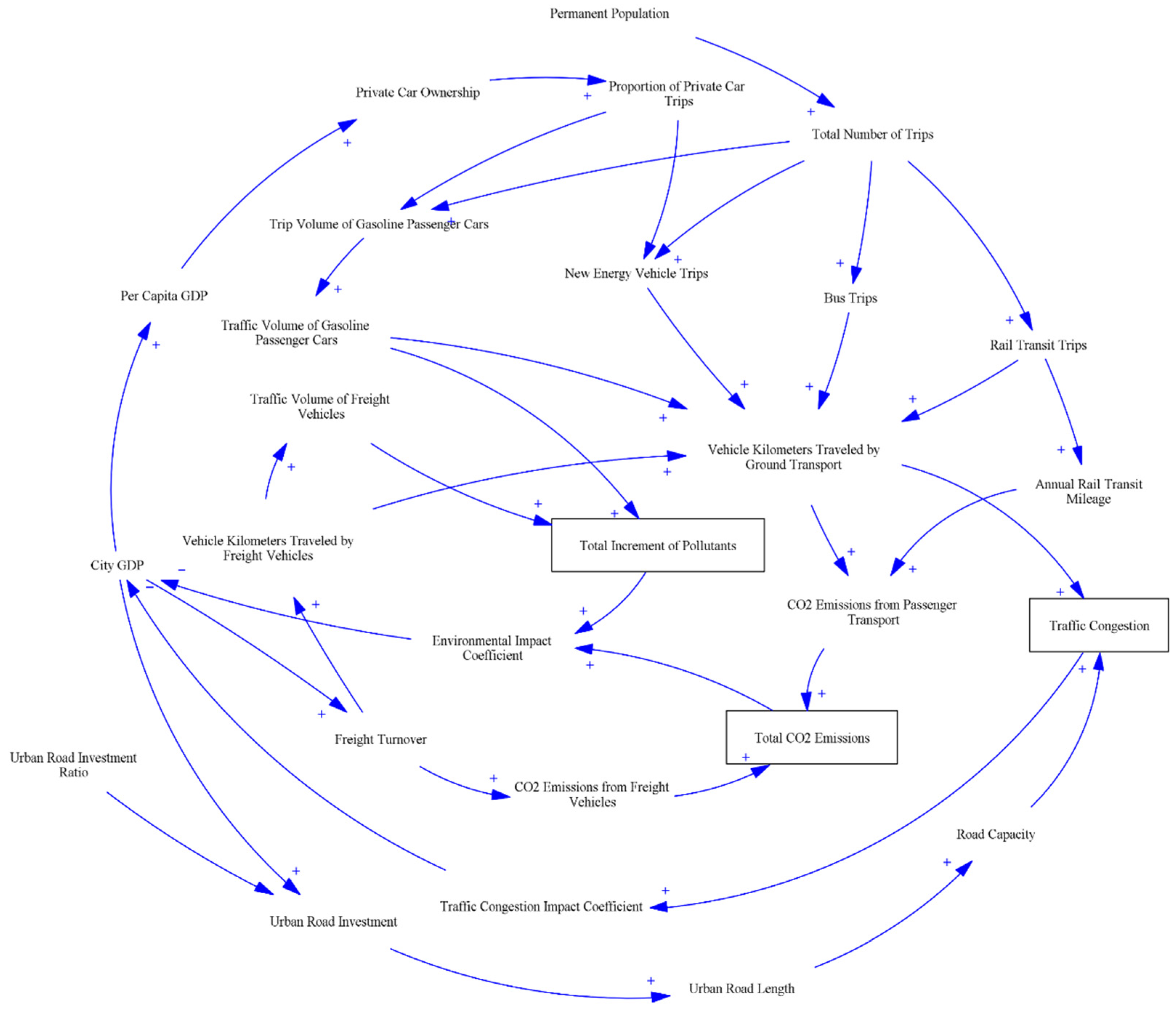
3.1.1. Causal Loop Diagram and Feedback Loops
- Urban GDP → +Urban Road Investment → +Road Capacity → −Traffic Congestion → +Traffic Congestion Impact Coefficient → −Urban GDP Increment → +Urban GDP
- 2.
- Urban GDP → +Per Capita GDP → +Private Car Ownership → +Private Car Modal Share → +Private Car Travel Volume → +Private Car Traffic Volume → +Total Increment of Pollutants → +Environmental Impact Coefficient → +Urban GDP Increment → −Urban GDP
- 3.
- Urban GDP → +Per Capita GDP → +Private Car Ownership → +Private Car Modal Share → +Private Car Travel Volume → +Private Car Traffic Volume → +Traffic Congestion → +Traffic Congestion Impact Coefficient → +Urban GDP Increment → −Urban GDP
- 4.
- Traffic Congestion → +Traffic Congestion Impact Coefficient → −Urban GDP Increment → +Urban GDP → +Urban Road Investment → +Road Capacity → −Traffic Congestion
- 5.
- Traffic Congestion → +Traffic Congestion Impact Coefficient → −Urban GDP Increment → +Urban GDP → +Per Capita GDP → +Private Car Ownership → +Private Car Modal Share → +Gasoline Car Travel Volume → +Gasoline Car Traffic Volume → +Vehicle Kilometers Traveled by Ground Transport → +Traffic Congestion
- 6.
- Traffic Congestion → +Traffic Congestion Impact Coefficient → −Urban GDP Increment → +Urban GDP → +Freight Turnover → +Vehicle Kilometers Traveled by Freight Vehicles → +Vehicle Kilometers Traveled by Ground Transport → +Traffic Congestion
- 7.
- Total Increment of Pollutants → +Environmental Impact Coefficient → −Urban GDP Increment → +Urban GDP → +Freight Turnover → +Vehicle Kilometers Traveled by Freight Vehicles → +CO2 Emissions from Freight Vehicles
- 8.
- Total Increment of Pollutants → +Environmental Impact Coefficient → −Urban GDP Increment → +Urban GDP → +Per Capita GDP → +Private Car Ownership → +Private Car Modal Share → +Gasoline Car Travel Volume → +Gasoline Car Traffic Volume → +Total Increment of Pollutants
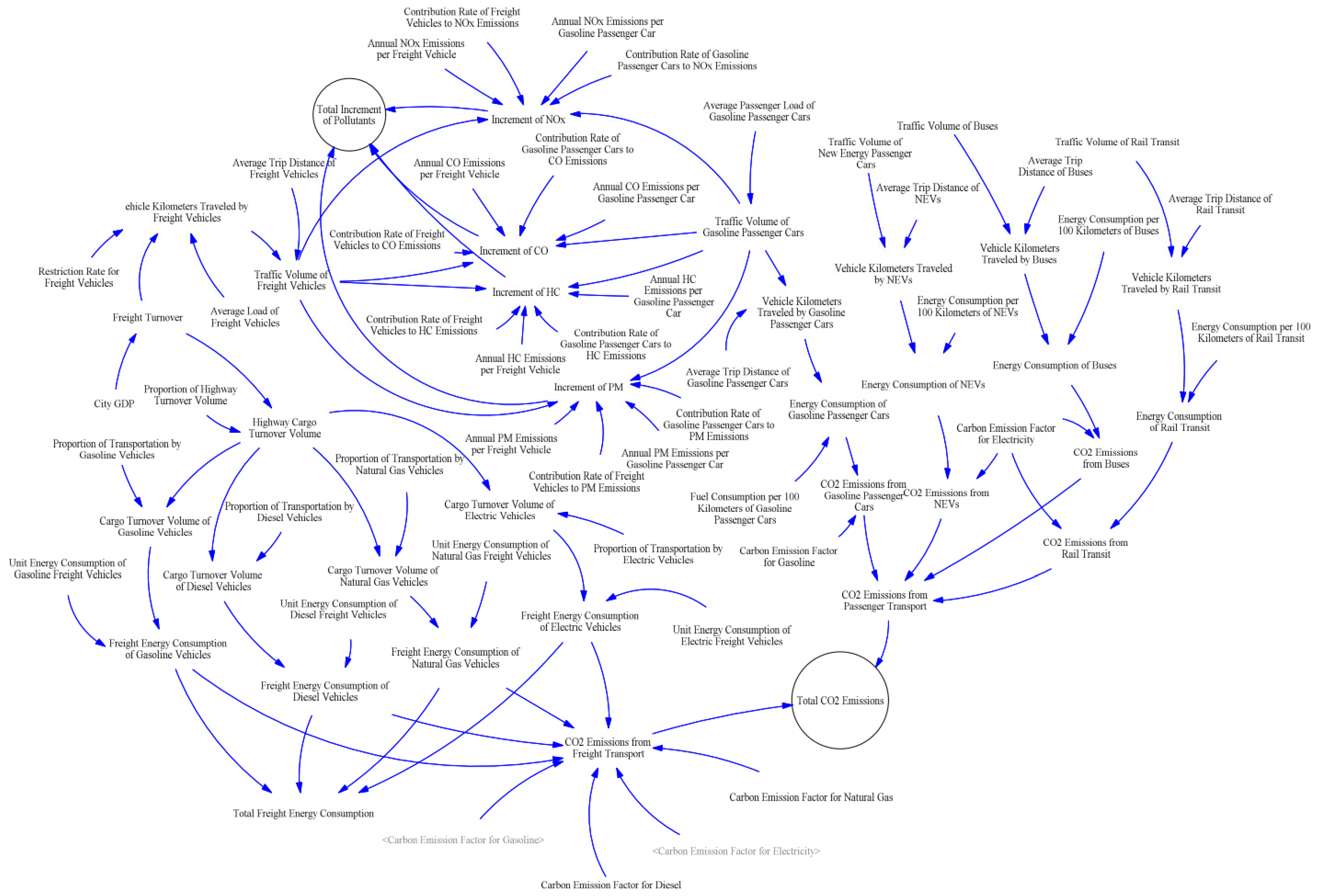
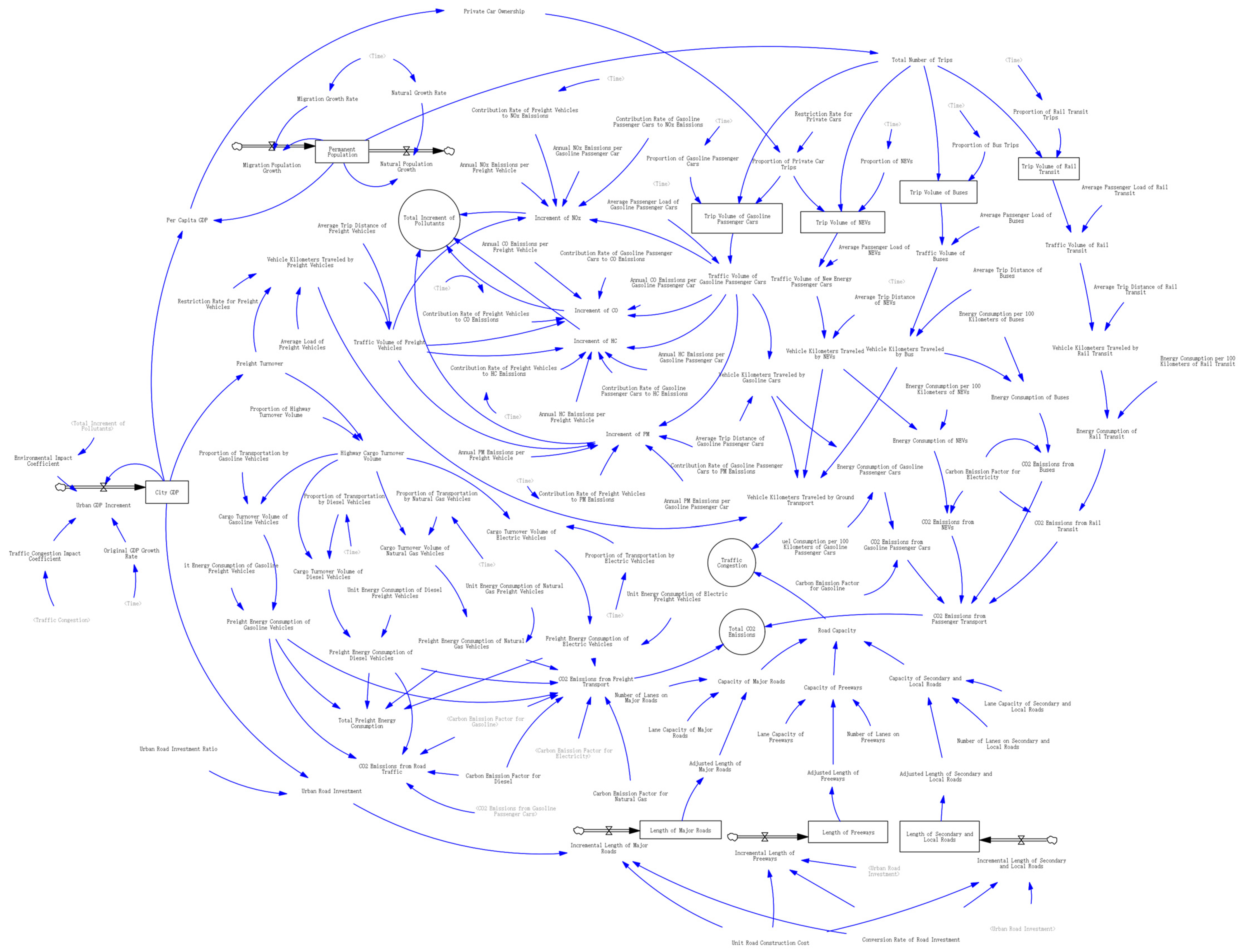
3.1.2. System Flow Diagram and Model Structural Equations
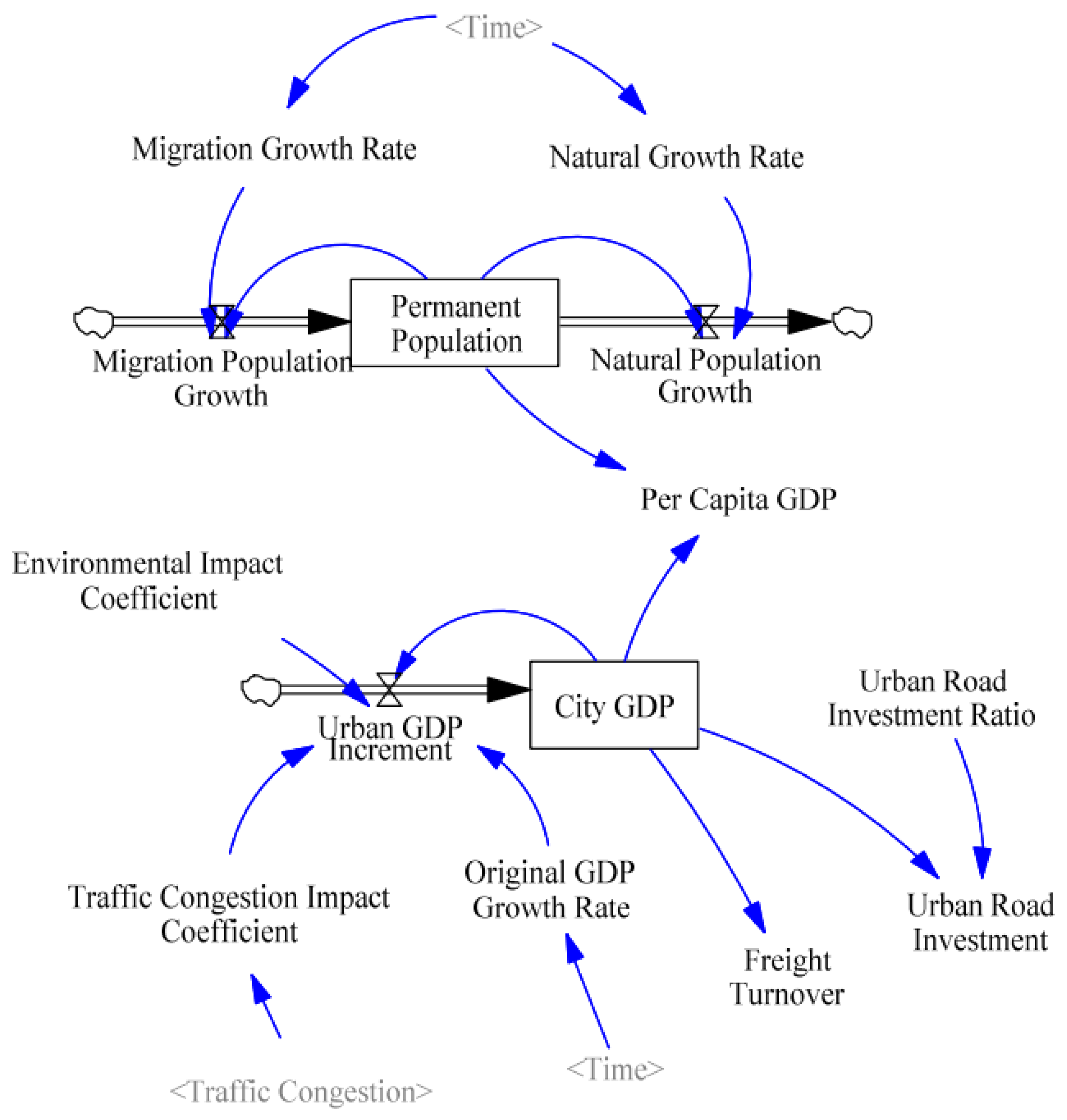
- Socio-Economic Subsystem
- —Total population at time t
- —Natural population increase at time t
- —Mechanical population increase at time t
- —Natural population growth rate at time t
- —Mechanical population growth rate at time t.
- —Gross Domestic Product at time t
- —Increment of GDP at time t
- —Original GDP growth rate at time t
- —Per capita GDP at time t
- —Traffic congestion impact coefficient, environmental pollution impact coefficient.
- 2.
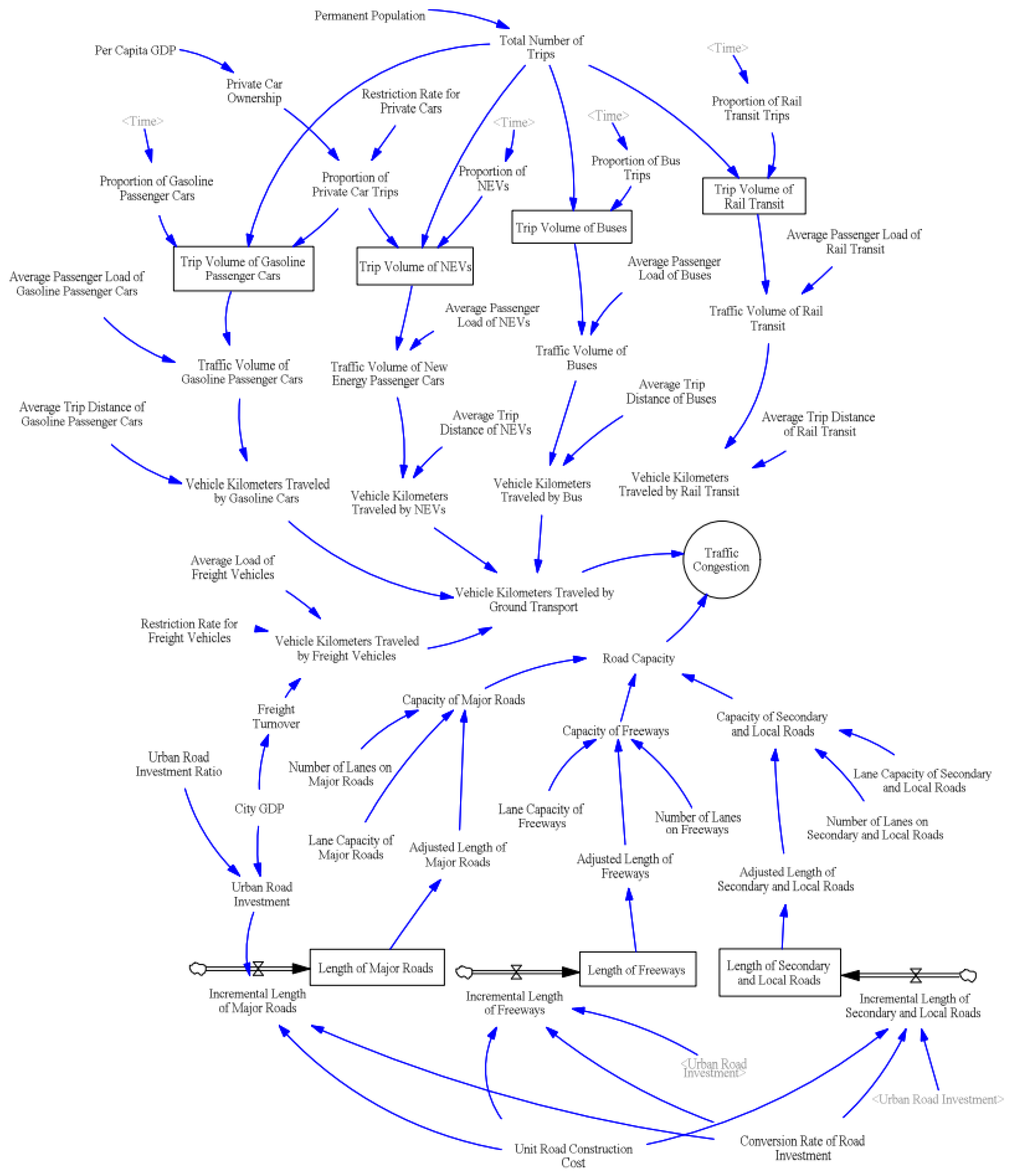
- Urban Transportation Subsystem
- Urban Transportation Subsystem
- —Total number of trips at time t
- , , , —Gasoline car trips at time t, new energy vehicle (NEV) trips at time t, Bus trips at time t, Rail transit trips at time t
- , —Proportion of gasoline cars and NEVs at time t
- , , , —Proportion of gasoline cars, NEVs, buses, and rail transit trips at time t
- , , , , —Gasoline car traffic volume at time t, NEV traffic volume at time t, bus traffic volume at time t, rail transit traffic volume at time t, and freight vehicles traffic volume at time t
- , , —Average passenger capacity of cars, buses, and rail transit
- —Restriction policy
- —Average travel distance for freight vehicles
- —Freight vehicle miles traveled (VMT) at time t
- , , , —Gasoline car, NEV, bus, and rail transit vehicle distance traveled at time t
- , , —Average travel distances for cars, buses, and rail transit
- 2.
- Urban Road Supply Subsystem
- , , —Freeway length at time t, major road length at time t, and secondary road and local road length at time t
- , , —Increment in the freeway, major road, secondary, and local road length
- —Road infrastructure investment at time t
- —Road investment conversion rate
- —Unit road construction cost
- —Road capacity
- —Lane capacity for road type i
- —Number of lanes for road type i
- —Length of road type i
- —Vehicle kilometers traveled by ground transport
- 3.
- Traffic Environment Subsystem
- (1)
- CO2 Emission
- , , , , —Energy consumption of gasoline cars, NEVs, buses, rail transit, and freight vehicles at time t
- , , , , —Energy consumption per 100 km for gasoline cars, NEVs, buses, rail transit, and freight vehicles
- , , , , —CO2 emissions of gasoline cars, NEVs, buses, rail transit, and freight vehicles at time t
- , , , N—Carbon emission factors for gasoline, diesel, electricity, and natural gas
- —Total CO2 emissions
- (2)
- Pollutant Emissions
- —Annual pollutant increment
- —Average annual emission of pollutant i per gasoline car
- —Contribution rate of pollutant i from gasoline cars
- —Average annual emission of pollutant i per freight vehicles
- —Contribution rate of pollutant i from freight vehicles
3.1.3. Parameter Design
3.1.4. Model Validation
- Actual Consistency Test
- 2.
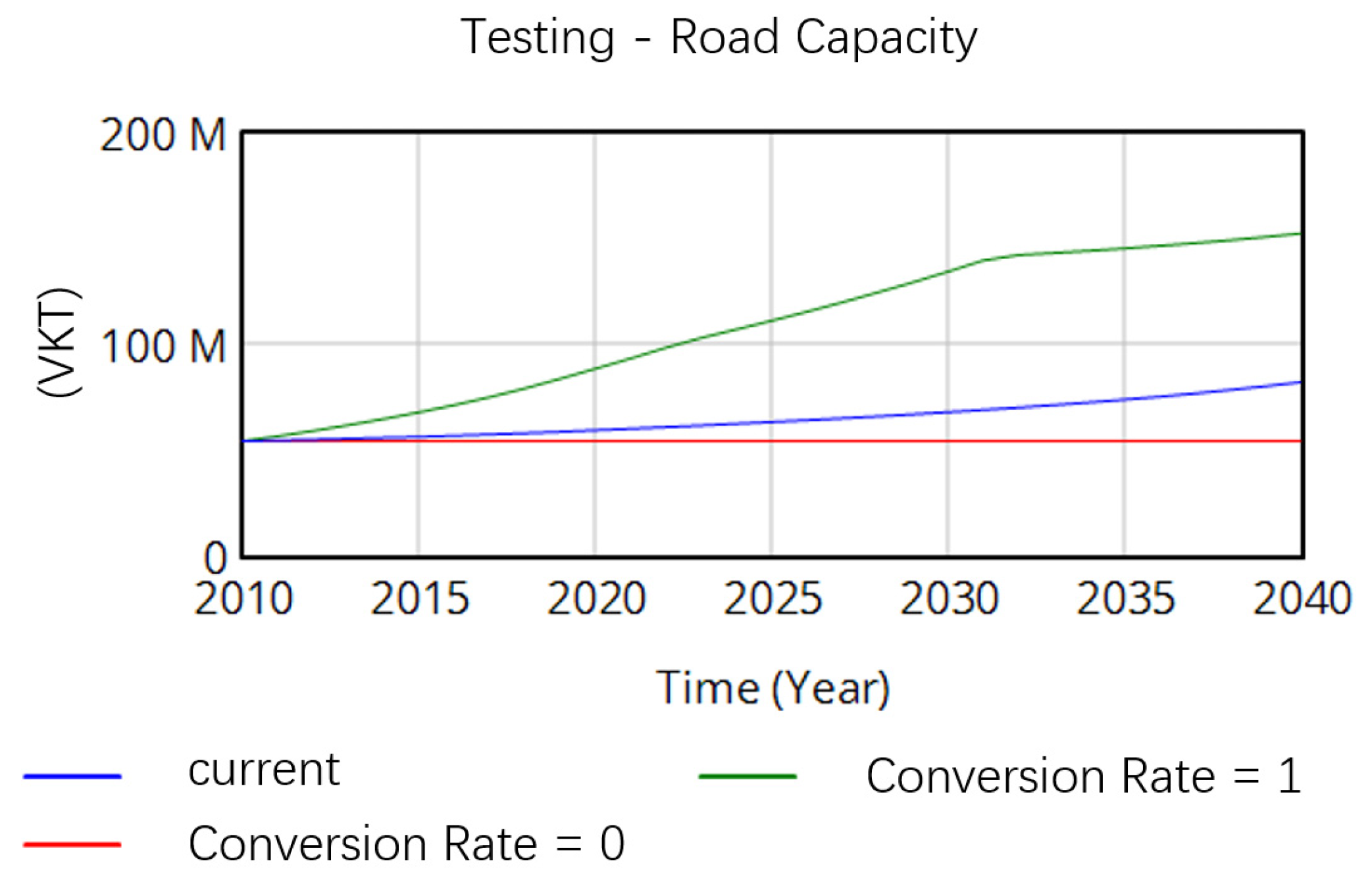
- Extreme Condition Test
- 3.
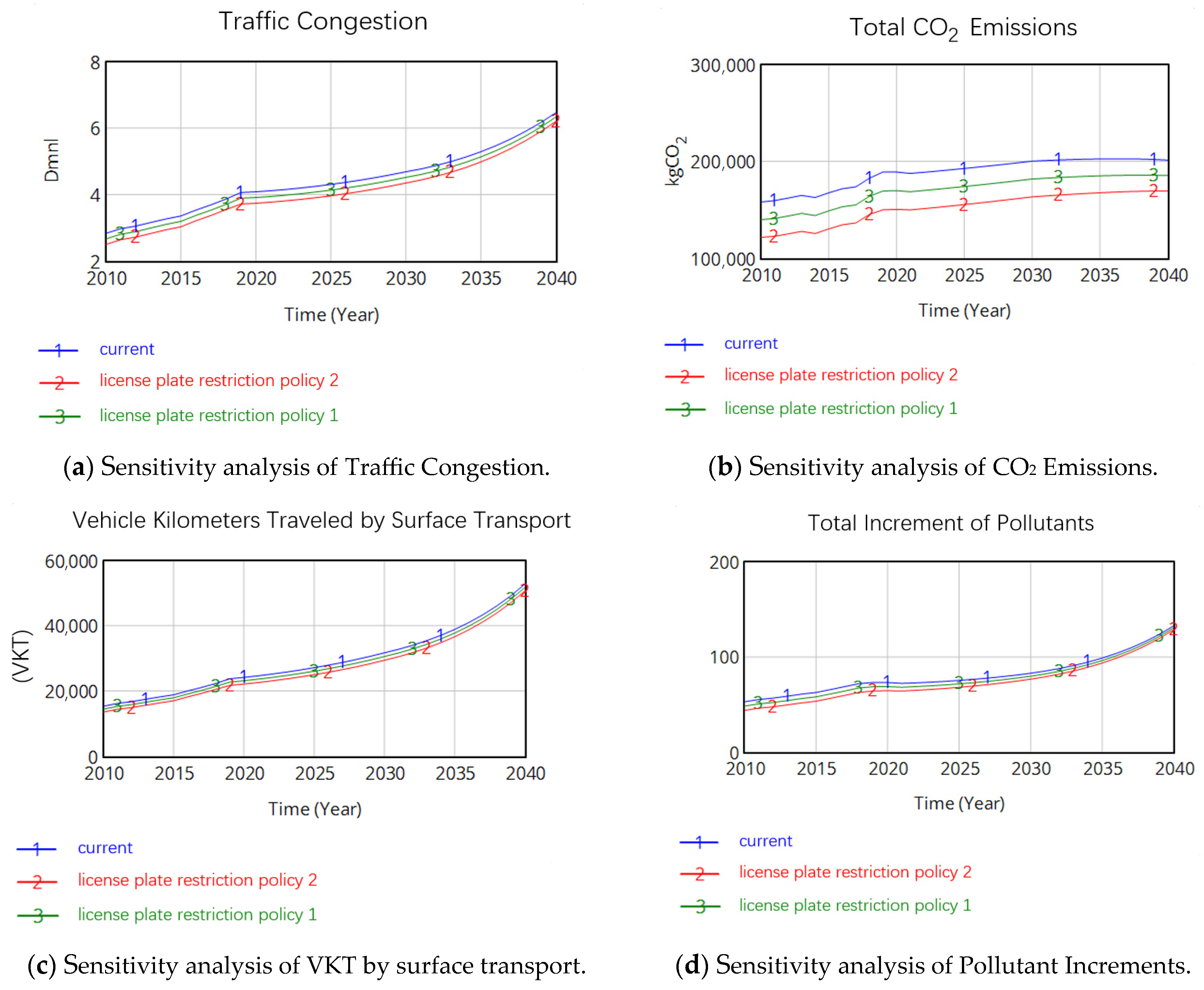
- Sensitivity testing
3.2. TOPSIS Model Construction
- Constructing the Decision Matrix
- 2.
- Standardizing the Decision Matrix
- 3.
- Calculating the Weighted Normalized Matrix
- 4.
- Identifying the Ideal and Negative Ideal Solutions
- 5.
- Calculating the Distances to the Ideal and Negative Ideal Solutions
- 6.
- Computing the Closeness Coefficient
4. Results and Discussion
4.1. Simulation and Optimization of Urban Traffic Congestion Mitigation and Emission Reduction Policies
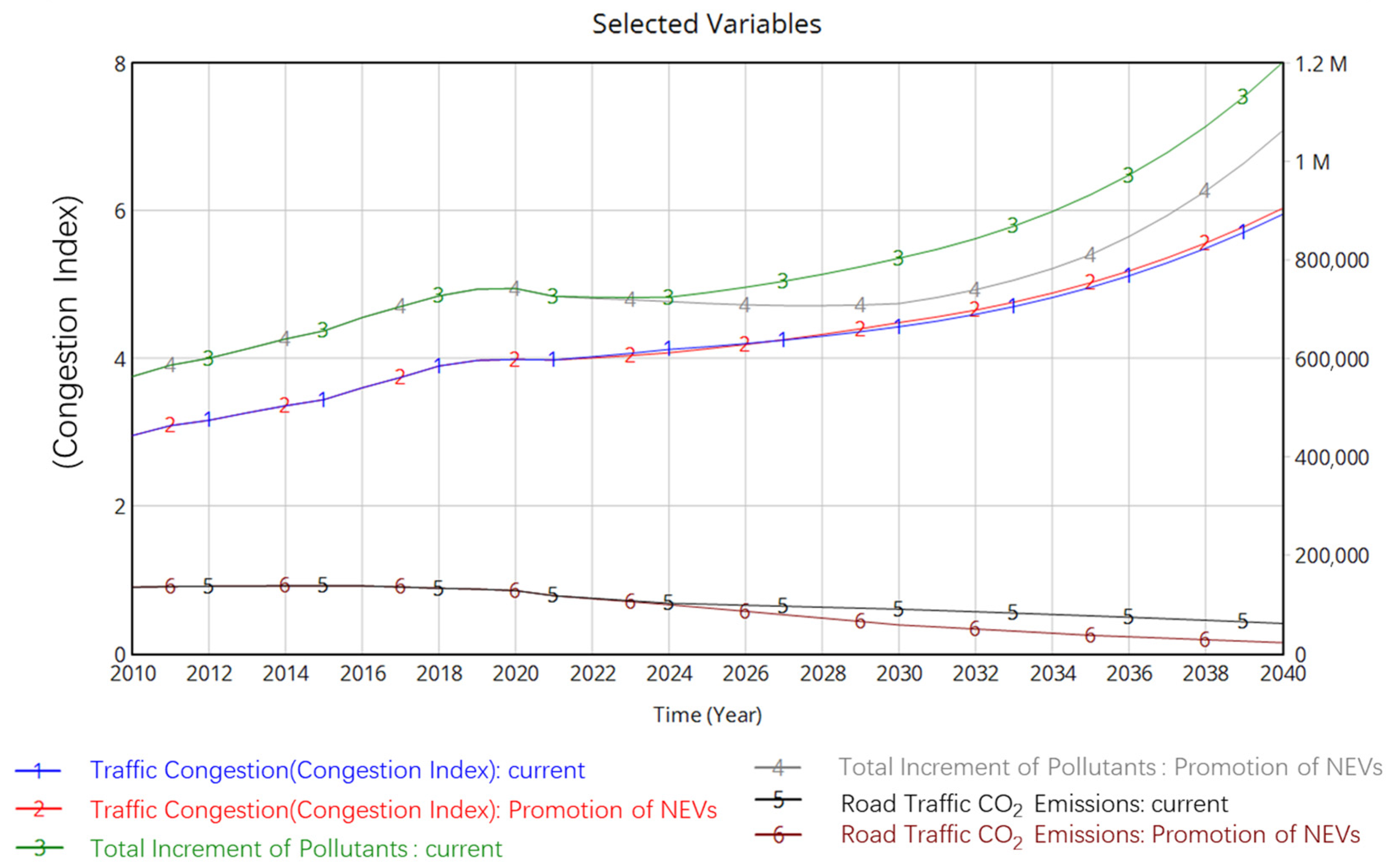
- Simulation Analysis of New Energy Vehicle Promotion Policy
- 2.
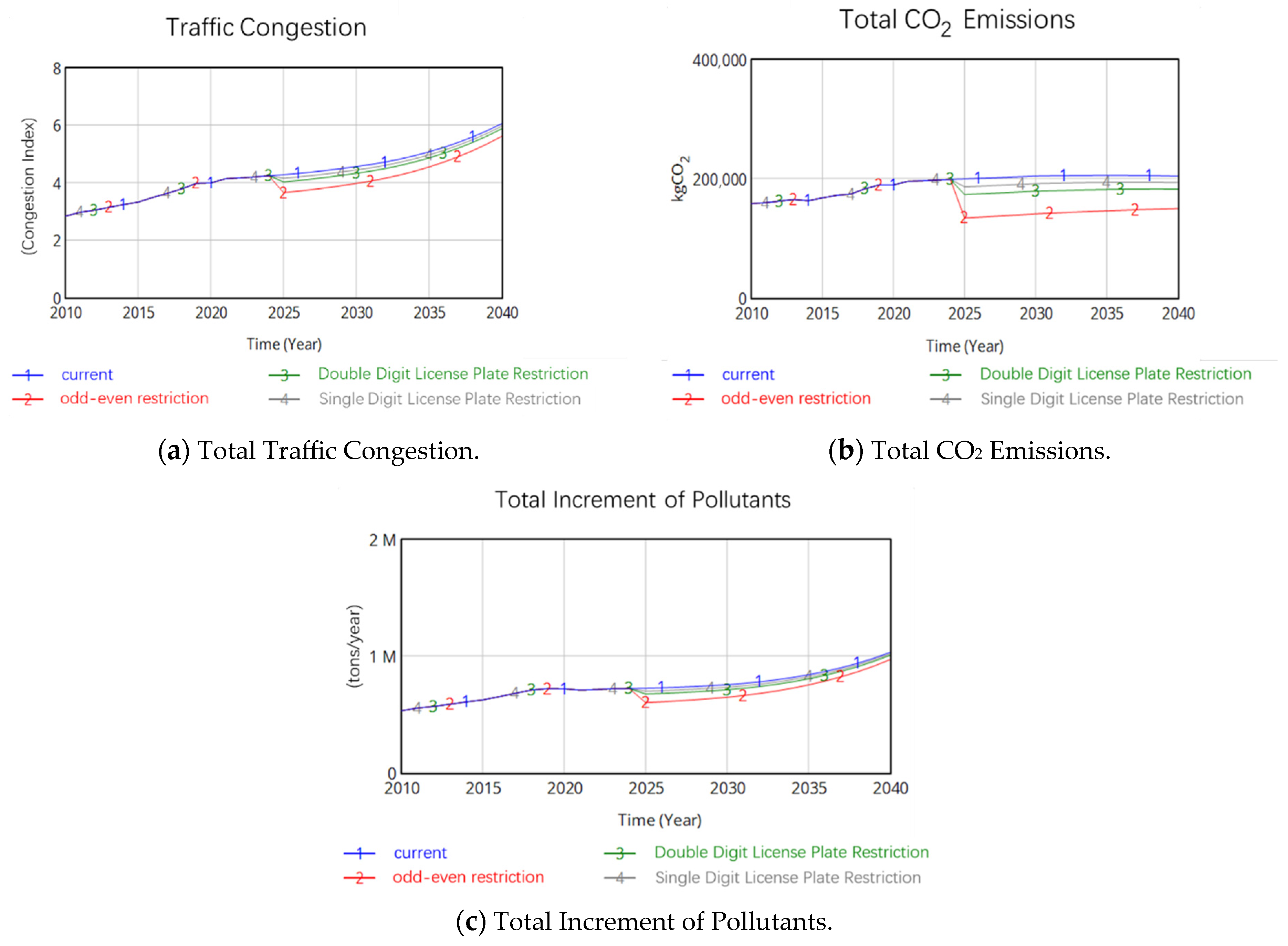
- Simulation Analysis of License Plate Restriction Policy
- 3.
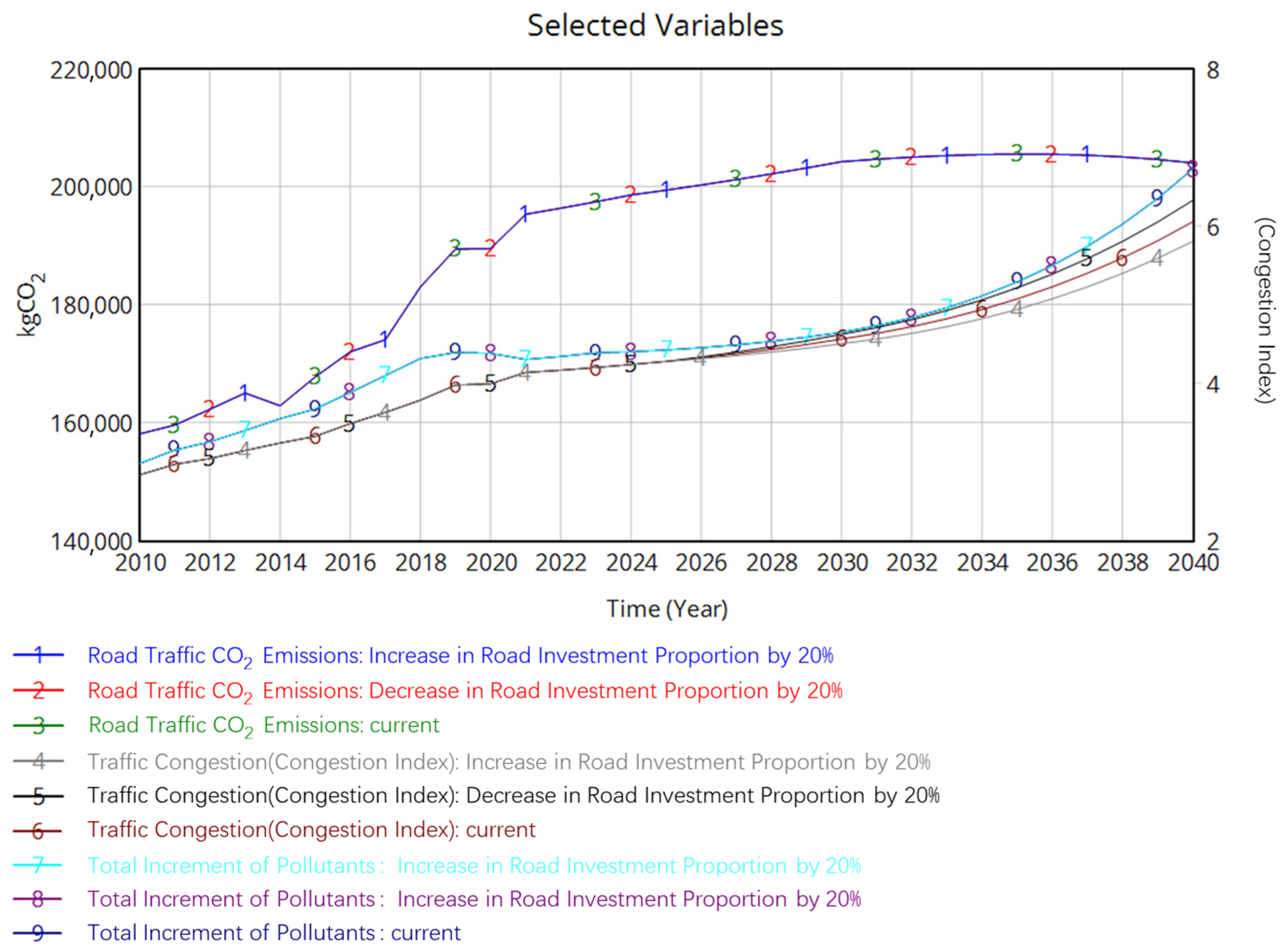
- Simulation Analysis of Road Investment Policy
- 4.
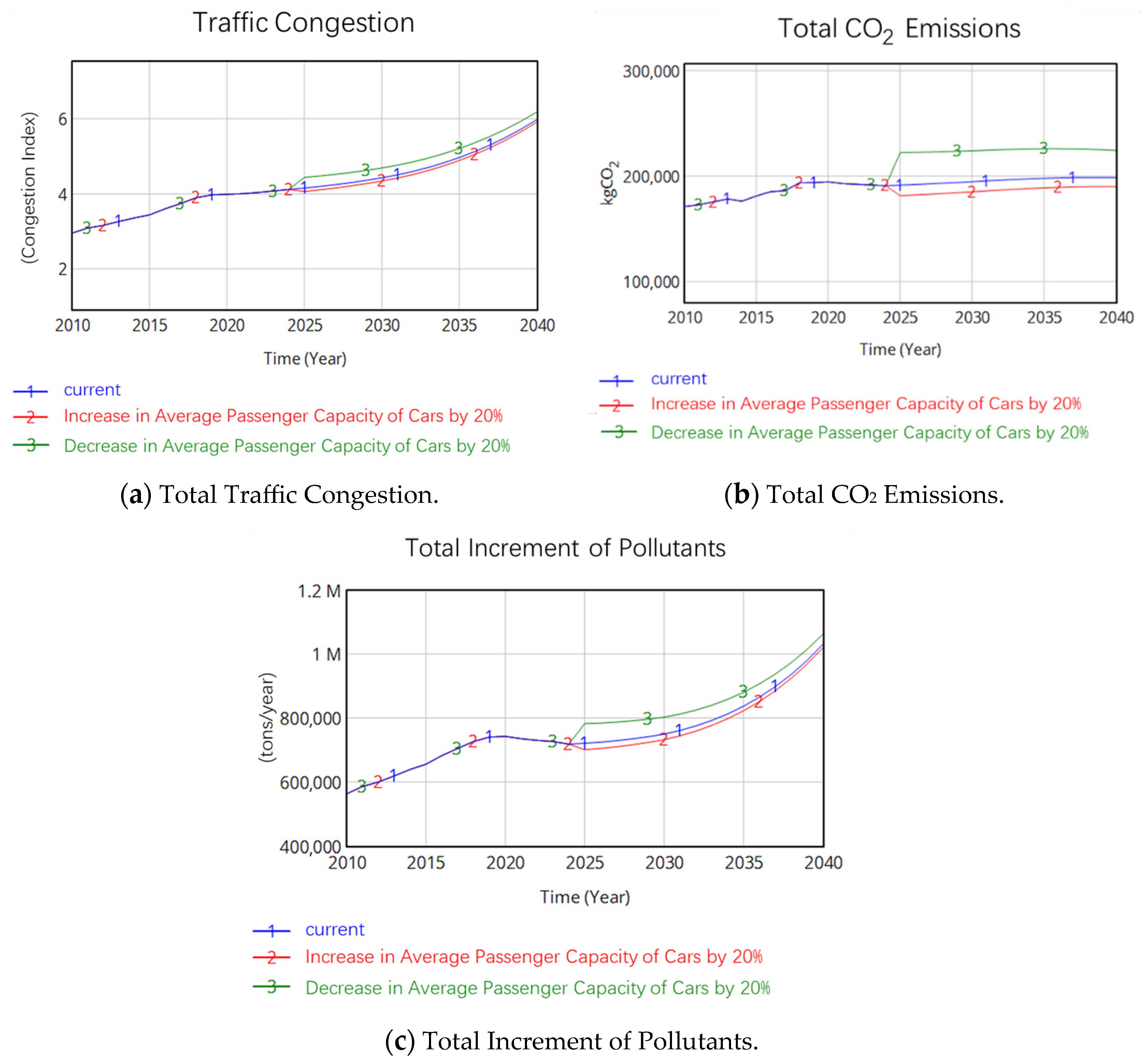
- Simulation Analysis of Ridesplitting Policy
- 5.
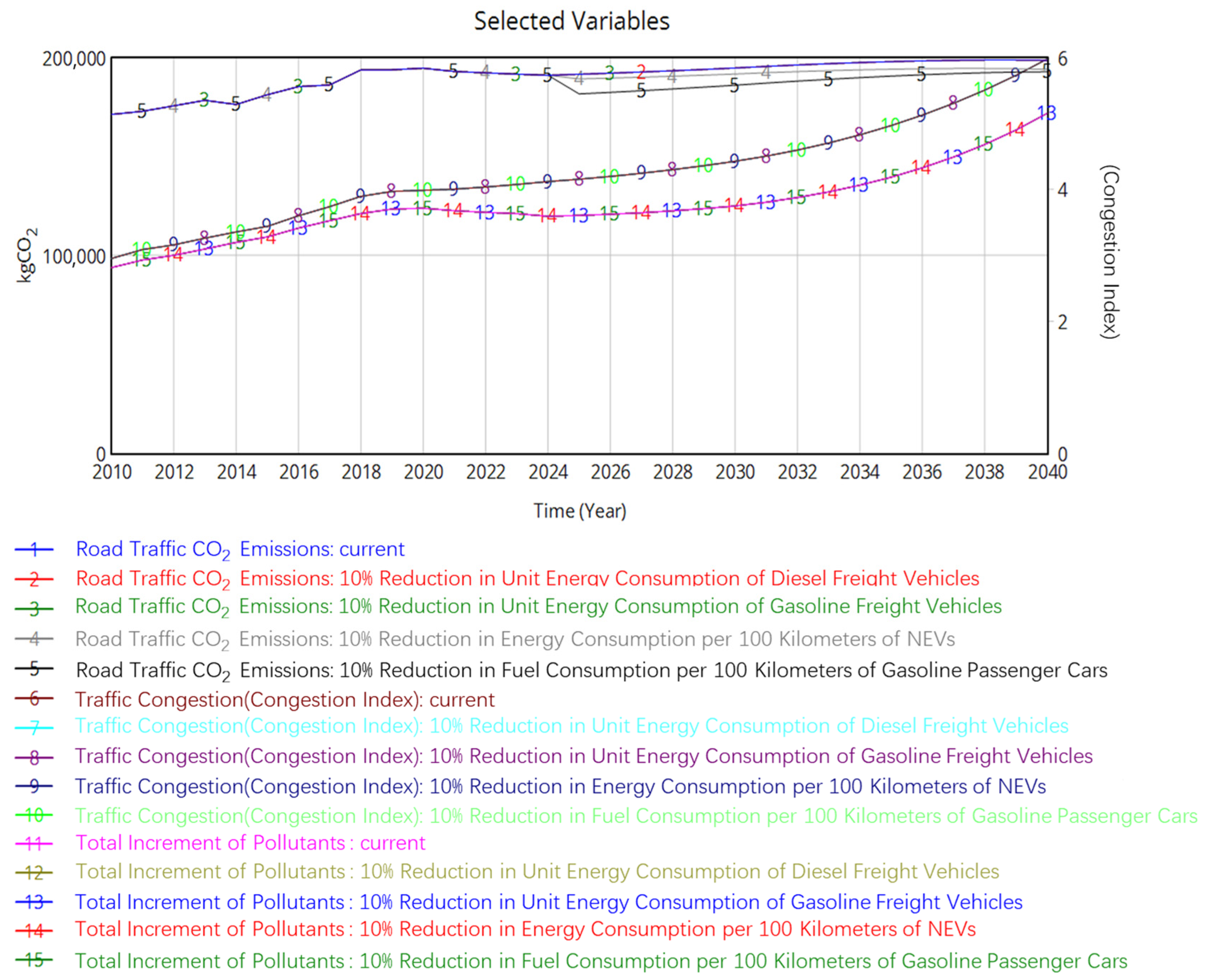
- Simulation Analysis of Technology Improvement Policy
4.2. Evaluation of Traffic Congestion Mitigation and Emission Reduction Policies Based on the TOPSIS Model
5. Conclusions and Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Creutzig, F.; Agoston, P.; Minx, J.C.; Canadell, J.G.; Andrew, R.M.; Le Quéré, C.; Peters, G.P.; Sharifi, A.; Yamagata, Y.; Dhakal, S. Urban infrastructure choices structure climate solutions. Nat. Clim. Chang. 2016, 6, 1054–1056. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, C. Decouple transport CO2 emissions from China’s economic expansion: A temporal-spatial analysis. Transp. Res. Part D Transp. Environ. 2020, 79, 102225. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, J. Characteristics, Impacts and trends of urban transportation. Encyclopedia 2022, 2, 1168–1182. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, Y.N.; Poon, J.; He, Z. China’s carbon dioxide emission and driving factors: A spatial analysis. J. Clean. Prod. 2019, 211, 640–651. [Google Scholar] [CrossRef]
- Bongaarts, J. IPCC, 2023: Climate Change 2023: Synthesis Report. Popul. Dev. Rev. 2024, 50, 577–580. [Google Scholar] [CrossRef]
- Rogelj, J.; Den Elzen, M.; Höhne, N.; Fransen, T.; Fekete, H.; Winkler, H.; Schaeffer, R.; Sha, F.; Riahi, K.; Meinshausen, M. Paris Agreement climate proposals need a boost to keep warming well below 2 C. Nature 2016, 534, 631–639. [Google Scholar] [CrossRef]
- Li, Z.; Bai, T.; Tang, C. How does the low-carbon city pilot policy affect the synergistic governance efficiency of carbon and smog? Quasi-experimental evidence from China. J. Clean. Prod. 2022, 373, 133809. [Google Scholar] [CrossRef]
- International Energy Agency. CO2 Emissions in 2023; International Energy Agency: Paris, France, 2024. [Google Scholar]
- Cai, J.; Deng, Z.; Li, L. High-resolution mapping of transport CO2 emission in Beijing–Tianjin–Hebei region: Spatial-temporal characteristics and decoupling effects. Int. J. Sustain. Transp. 2024, 18, 301–314. [Google Scholar] [CrossRef]
- Brand, C.; Dons, E.; Anaya-Boig, E.; Avila-Palencia, I.; Clark, A.; de Nazelle, A.; Gascon, M.; Gaupp-Berghausen, M.; Gerike, R.; Götschi, T. The climate change mitigation effects of daily active travel in cities. Transp. Res. Part D Transp. Environ. 2021, 93, 102764. [Google Scholar] [CrossRef]
- Liu, Z.; Deng, Z.; He, G.; Wang, H.L.; Zhang, X.; Lin, J.; Qi, Y.; Liang, X. Challenges and opportunities for carbon neutrality in China. Nat. Clim. Chang. 2022, 3, 141–155. [Google Scholar] [CrossRef]
- Sheldon, T.L.; Rubal, D. Consumer preferences for ride-hailing: Barriers to an autonomous, shared, and electric future. J. Clean. Prod. 2024, 434, 140251. [Google Scholar] [CrossRef]
- Hall, J.D.; Palsson, C.; Price, J. Is Uber a substitute or complement for public transit? J. Urban Econ. 2018, 108, 36–50. [Google Scholar] [CrossRef]
- Xu, S.; Sun, C.; Liu, N. Road congestion and air pollution-analysis of spatial and temporal congestion effects. Sci. Total Environ. 2024, 945, 173896. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Wu, Y.; Liu, H.; Huang, R.; Yang, L.; Li, Z.; Fu, L.; Hao, J. Real-world fuel consumption and CO2 emissions of urban public buses in Beijing. Appl. Energy 2014, 113, 1645–1655. [Google Scholar] [CrossRef]
- Jin, J.; Jin, J. Traffic congestion and air pollution: Empirical evidence before/after COVID-19 in Seoul, Korea. Int. J. Sustain. Transp. 2023, 17, 1356–1369. [Google Scholar] [CrossRef]
- Tafidis, P.; Gholamnia, M.; Sajadi, P.; Krishnan Vijayakrishnan, S.; Pilla, F. Evaluating the impact of urban traffic patterns on air pollution emissions in Dublin: A regression model using google project air view data and traffic data. Eur. Transp. Res. Rev. 2024, 16, 47. [Google Scholar] [CrossRef]
- Anjum, S.S.; Noor, R.M.; Aghamohammadi, N.; Ahmedy, I.; Kiah, L.M.; Hussin, N.; Anisi, M.H.; Qureshi, M.A. Modeling traffic congestion based on air quality for greener environment: An empirical study. IEEE Access 2019, 7, 57100–57119. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, L.; Lu, L.; Zhang, M.; Jiang, X.; Li, A. Modelling of congestion carbon emission measurement based on multiple regression analysis for traffic flow. In Proceedings of the 3rd International Conference on Internet of Things and Smart City (IoTSC 2023), Chongqing, China, 14 June 2023; SPIE: Washington, DC, USA, 2023; pp. 649–658. [Google Scholar]
- Zou, Y.; Hu, Q.; Han, W.; Zhang, S.; Chen, Y. Analyzing Travel and Emission Characteristics of Hazardous Material Transportation Trucks Using BeiDou Satellite Navigation System Data. Remote Sens. 2025, 17, 423. [Google Scholar] [CrossRef]
- Tommi, I.; Esa, H. Reviewing Truck Logistics: Solutions for Achieving Low Emission Road Freight Transport. Sustainability 2020, 12, 6714. [Google Scholar] [CrossRef]
- Liu, C.; Sun, K.; Zhang, Q. Study on the relationship between traffic volume and economy development in Nanjing City based on VAR model. J. Wuhan Univ. Technol. (Transp. Sci. Eng.) 2011, 35, 1058–1062. [Google Scholar]
- Jia, J. Interaction between urbanization and carbon emission in Guizhou Province. Energy Inform. 2024, 7, 43. [Google Scholar] [CrossRef]
- Chen, S.; Qin, P.; Tan-Soo, J.-S.; Xu, J.; Yang, J. An econometric approach toward identifying the relationship between vehicular traffic and air quality in Beijing. Land Econ. 2020, 96, 333–348. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, T.; Feiock, R.; Li, F. The impacts of China’s provincial energy policies on major air pollutants: A spatial econometric analysis. Energy Policy 2019, 132, 392–403. [Google Scholar] [CrossRef]
- Wen, L.; Bai, L. System dynamics modeling and policy simulation for urban traffic: A case study in Beijing. Environ. Model. Assess. 2017, 22, 363–378. [Google Scholar] [CrossRef]
- Wen, L.; Wang, A. System dynamics model of Beijing urban public transport carbon emissions based on carbon neutrality target. Environ. Dev. Sustain. 2023, 25, 12681–12706. [Google Scholar] [CrossRef]
- Jia, S.; Li, Y.; Fang, T. Can driving-restriction policies alleviate traffic congestion? A case study in Beijing, China. Clean Technol. Environ. Policy 2022, 24, 2931–2946. [Google Scholar] [CrossRef]
- Su, Y.; Liu, X.; Li, X. Research on traffic congestion based on system dynamics: The case of Chongqing, China. Complexity 2020, 2020, 6123896. [Google Scholar] [CrossRef]
- Chen, Z.; Zan, Z.; Jia, S. Effect of urban traffic-restriction policy on improving air quality based on system dynamics and a non-homogeneous discrete grey model. Clean Technol. Environ. Polic 2022, 24, 2365–2384. [Google Scholar] [CrossRef]
- Suryani, E.; Fadlillah, M.; Hendrawan, R.; Mudjahidin, M.; Pramundito, R.; Zahra, A.; Chou, S.; Dewabharata, A.; Rizqi, Z.; Rahmawati, R. Dynamic model to assess the impacts of government support for electric vehicles on the economy and environment sectors in Indonesia. Int. J. Sustain. Transp. 2025, 19, 35–54. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. 2006 IPCC Guidelines for National Greenhouse Gas Inventories; Institute for Global Environmental Strategies: Hayama, Japan, 2006. [Google Scholar]
- China SAE (Society of Automotive Engineers of China), National Strategy Institute of Automobile. Annual Evaluation Report of the Technology Roadmap for Energy-Saving and New Energy Vehicles 2023; China SAE: Beijing, China, 2023. (In Chinese) [Google Scholar]
| Subsystem | Key Factors |
|---|---|
| Socio-economic | GDP growth rate, GDP, per capita GDP, total permanent resident population |
| Urban transport | Road capacity, freight turnover, travel volume by mode of transport, modal split, total road length, vehicle kilometers traveled by ground transport, average occupancy rate of various transport modes |
| Traffic Environmental | Total CO2 emissions, annual vehicle emissions by pollutant type, total increment of pollutants, contribution rate of vehicles to various pollutants |
| Transport policy | License plate restriction policy, new energy vehicles promotion policy, road investment policy, technology improvement policy, carpooling promotion policy |
| Transport Policy | System Impact |
|---|---|
| License plate restriction | Directly restricts the entry and circulation of private cars, immediately reducing the total Vehicle Kilometers Traveled (VKT) and alleviating congestion. |
| New energy vehicles promotion | Accelerates the replacement of conventional fuel vehicles. This policy alters the vehicle stock composition and subsequently lowers the aggregate emission factor for CO2 and local air pollutants. |
| Road investment | Increases the physical capacity of the road network. This directly raises the overall Road Capacity, thereby improving the average travel speed and mitigating congestion. |
| Technology improvement | Simulates the continuous upgrading of conventional engine efficiency and emission standards, resulting in a gradual reduction in emissions per VKT over time. |
| Carpooling promotion | Aims to increase the average vehicle occupancy rate. This indirectly reduces the necessary VKT per trip for the same volume of passenger travel, resulting in both congestion and emission relief. |
| Energy Type | Gasoline | Diesel | Natural Gas | Electricity |
|---|---|---|---|---|
| Emission Factor | 2.2257 | 2.5479 | 1.9388 | 0.5703 |
| Unit | kgCO2/L | kgCO2/L | kgCO2/m3 | kgCO2/(kW·h) |
| Variable | Value | Unit |
|---|---|---|
| Urban GDP | 17,915.4 | CNY hundred million |
| Total Resident Population | 2302.66 | ten thousand people |
| Length of Major Roads | 300 | km |
| Length of Freeways | 200 | km |
| Length of Secondary and Local Roads | 4000 | km |
| Urban Road Investment | 0.002 | Dmnl |
| Average Passenger Capacity (Gasoline) | 1.8 | persons/vehicle |
| Average Travel Distance (Gasoline) | 14 | km |
| Gasoline Car Energy Consumption | 8.82 | L/100 km |
| Average Passenger Capacity (NEV) | 1.8 | persons/vehicle |
| Average Travel Distance (NEV) | 14 | km |
| NEV Energy Consumption | 15.17 | kWh/100 km |
| Average Passenger Capacity (Bus) | 21 | persons/vehicle |
| Average Travel Distance (Bus) | 12.5 | km |
| Bus Energy Consumption | 55.5 | kWh/100 km |
| Average Passenger Capacity (Rail) | 49 | persons/vehicle |
| Average Travel Distance (Rail) | 18.7 | km/person-trip |
| Rail Energy Consumption | 338.28 | kWh/100 km |
| NOx Emissions (Gasoline Cars) | 0.0043 | ton/year/vehicle |
| NOx Contribution Rate (Gasoline Cars) | 0.0897 | Dmnl |
| Number of Lanes (Major Roads) | 6 | - |
| Lane Capacity (Major Roads) | 8000 | vehicle-kilometers |
| Number of Lanes (Freeways) | 6 | - |
| Lane Capacity (Freeways) | 8000 | vehicle-kilometers |
| Number of Lanes (Secondary Roads) | 6 | - |
| Lane Capacity (Secondary Roads) | 8000 | vehicle-kilometers |
| Unit Road Construction Cost | 0.3 | CNY hundred million/km |
| Road Investment Conversion Rate | 0.15 | Dmnl |
| Year | Urban GDP (Actual Value) | Urban GDP (Simulated Value) | Urban GDP (Error Value) | Error |
|---|---|---|---|---|
| 2010 | 17,915.4 | 17,915.4 | 0 | 0.00% |
| 2011 | 20,009.7 | 19,880.2 | −129.5 | −0.65% |
| 2012 | 21,305.6 | 21,085.4 | −220.2 | −1.03% |
| 2013 | 23,204.1 | 22,840.3 | −363.8 | −1.57% |
| 2014 | 25,269.8 | 24,734.8 | −535 | −2.12% |
| 2015 | 26,887.0 | 26,206.6 | −680.4 | −2.53% |
| 2016 | 29,887.0 | 28,920.7 | −966.3 | −3.23% |
| 2017 | 32,925.0 | 31,638.8 | −1286.2 | −3.91% |
| 2018 | 36,011.8 | 34,376.6 | −1635.2 | −4.54% |
| 2019 | 37,987.6 | 36,113.1 | −1874.5 | −4.93% |
| 2020 | 38,963.3 | 36,965.7 | −1997.6 | −5.13% |
| Year | Resident Population (Actual Value) | Resident Population (Simulated Value) | Resident Population (Error Value) | Error |
|---|---|---|---|---|
| 2010 | 2302.66 | 2302.66 | 0 | 0.00% |
| 2011 | 2355.53 | 2321.33 | −34.2 | −1.45% |
| 2012 | 2398.5 | 2332.59 | −65.91 | −2.75% |
| 2013 | 2448.43 | 2342.46 | −105.97 | −4.33% |
| 2014 | 2467.06 | 2351.13 | −115.93 | −4.70% |
| 2015 | 2457.59 | 2361.35 | −96.24 | −3.92% |
| 2016 | 2467.37 | 2368.67 | −98.7 | −4.00% |
| 2017 | 2466.28 | 2380.68 | −85.6 | −3.47% |
| 2018 | 2475.39 | 2391.85 | −83.54 | −3.37% |
| 2019 | 2481.34 | 2403.43 | −77.91 | −3.14% |
| 2020 | 2488.36 | 2414.72 | −73.64 | −2.96% |
| Year | Total Travel Volume (Actual Value) | Total Travel Volume (Simulated Value) | Total Travel Volume (Error Value) | Error |
|---|---|---|---|---|
| 2013 | 3164 | 3161.75 | −2.25 | −0.07% |
| 2014 | 3168 | 3179.34 | 11.34 | 0.36% |
| 2015 | 3200 | 3200.09 | 0.09 | 0.00% |
| 2016 | 3221 | 3214.94 | −6.06 | −0.19% |
| 2017 | 3253 | 3239.31 | −13.69 | −0.42% |
| 2018 | 3268 | 3261.96 | −6.04 | −0.18% |
| 2019 | 3273 | 3285.45 | 12.45 | 0.38% |
| 2020 | 2612 | 3308.37 | 696.37 | 26.66% |
| C1 | C2 | C3 | |
|---|---|---|---|
| Y1 | 1 | 0.5816 | 0 |
| Y2 | 0.5240 | 0 | 0.3646 |
| Y3 | 0 | 1 | 1 |
| Y4 | 0.5951 | 0.1667 | 0.4690 |
| Y5 | 0.9506 | 0.7208 | 0.9919 |
| Y6 | 0.9506 | 0.7813 | 0.9919 |
| C1 | C2 | C3 | |
|---|---|---|---|
| Y1 | 0.3088 | 0.2070 | 0 |
| Y2 | 0.1618 | 0 | 0.1223 |
| Y3 | 0 | 0.3559 | 0.3353 |
| Y4 | 0.1837 | 0.0593 | 0.1572 |
| Y5 | 0.2935 | 0.2566 | 0.3326 |
| Y6 | 0.2935 | 0.2781 | 0.3326 |
| Policy | d+ | d− | Closeness Coefficient Cᵢ | Ranking |
|---|---|---|---|---|
| Y1 | 0.3717 | 0.3669 | 0.4967 | 3 |
| Y2 | 0.2028 | 0.4401 | 0.6845 | 1 |
| Y3 | 0.4890 | 0.3088 | 0.3871 | 4 |
| Y4 | 0.2490 | 0.3679 | 0.5963 | 2 |
| Y5 | 0.5124 | 0.1006 | 0.1641 | 5 |
| Y6 | 0.5235 | 0.0794 | 0.1317 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, G.; Zhu, Y.; Liu, W. A System Dynamics-Based Simulation Study on Urban Traffic Congestion Mitigation and Emission Reduction Policies. Sustainability 2025, 17, 9296. https://doi.org/10.3390/su17209296
Li X, Wang G, Zhu Y, Liu W. A System Dynamics-Based Simulation Study on Urban Traffic Congestion Mitigation and Emission Reduction Policies. Sustainability. 2025; 17(20):9296. https://doi.org/10.3390/su17209296
Chicago/Turabian StyleLi, Xiaomei, Guo Wang, Yangyang Zhu, and Weiwei Liu. 2025. "A System Dynamics-Based Simulation Study on Urban Traffic Congestion Mitigation and Emission Reduction Policies" Sustainability 17, no. 20: 9296. https://doi.org/10.3390/su17209296
APA StyleLi, X., Wang, G., Zhu, Y., & Liu, W. (2025). A System Dynamics-Based Simulation Study on Urban Traffic Congestion Mitigation and Emission Reduction Policies. Sustainability, 17(20), 9296. https://doi.org/10.3390/su17209296





