Predicting Soil Electrical Conductivity of Saturated Paste Extract Using Pedotransfer Functions in Northeastern Tunisia

Abstract

Soil electrical conductivity is a key indicator of soil salinity and sustainability, particularly in arid and semi-arid regions. Accurate estimation of EC is essential for managing soil salinity and ensuring crop productivity. Five pedotransfer functions (PTFs) were developed and evaluated for predicting electrical conductivity in a saturated paste extract using soil parameters, such as particle size analysis, pH, organic carbon, total nitrogen, cation exchange capacity, and electrical conductivity in a 1:5 soil-to-water extract, in agricultural soils of northern Tunisia. The accuracy of each PTF was systematically evaluated. PTF1 represented an R² value of 0.85, PTF2 showed an R² of 0.71 for the stepwise regression model, PTF3 achieved an R² of 0.84, PTF4, based on Lasso/Ridge regression, reached an R² of 0.89, and PTF5 reached an R² of 0.83. Our findings revealed regional variations in soil salinity, with certain areas showing elevated salinity levels that could affect agricultural sustainability. This research emphasizes the importance of developing ad hoc PTFs as a reliable tool for predicting soil salinity and, consequently, assuring sustainable soil management in northeastern Tunisia.

1. Introduction

Soil salinization is one of the most critical environmental challenges, affecting the suitability of soil for agriculture and crop production. It poses a particular threat to sustainable soil management in arid and semi-arid regions, where poor-quality water is commonly used for irrigation [1,2,3,4,5]. In semi-arid and arid regions, salinization is often exacerbated by climate change and the overuse of saline water for irrigation. High temperatures and insufficient rainfall alter the hydrological cycle, leading to water deficits that fail to meet the requirements of crops. Furthermore, frequent and intense evaporation events cause salt to accumulate in the soil horizons explored by roots, thereby reducing crop productivity even further [6,7]. Globally, soil salinity reduces the availability of essential nutrients (especially carbon and nitrogen) for plant uptake, interfering with microbial activity.

Many studies have shown that salinity can alter soil organic carbon (SOC) dynamics, influencing the release of greenhouse gases (GHGs), such as carbon dioxide (CO₂), methane (CH₄), and nitrous oxide (N₂O). The outcomes vary depending on soil conditions [8,9]. However, salinity is a major global issue that contributes to soil degradation, causing desertification and affecting approximately 350 million hectares around the world [10]. Inadequate agricultural systems, such as the use of saline water for irrigation and ineffective drainage systems, combined with climate change, have led to significant soil salinization over time [11,12]. These methods compromise environmental sustainability by reducing soil fertility, lowering crop yields, and decreasing biodiversity. They intensify desertification by disrupting plant growth cycles, biomass production, and nutrient cycling, thus threatening soil ecosystem services. Ultimately, salinity endangers food security by reducing crop productivity through land degradation, thereby compromising soil security. This highlights the urgent need to assess and predict soil salinity in order to prevent further soil salinization and ecological degradation and implement effective strategies to conserve soils and biodiversity [13]. Today, the growing global population and rising food demand are placing increasing pressure on land resources, while salinized areas are expanding at a rate of approximately 1 to 2 million hectares per year [14]. Climate change further intensifies the degradation of these valuable salt-affected soils. Additionally, salinity reduces crop yields by impairing plant growth through mechanisms such as ion toxicity, osmotic stress, and mineral deficiencies [15]. Salinity is a major environmental threat, with a significant socioeconomic impact, including reduced food security, increased poverty, and lower farmer profits [16]. Other studies have shown that salinity has affected approximately 1 billion hectares of land, equivalent to 7% of the Earth’s continental surface area. This widespread phenomenon poses a serious threat to environmental integrity and human well-being. Consequently, detecting and monitoring soil salinity has become a research priority in order to better understand its link with land degradation and to support the development of sustainable agricultural strategies and policies [5,17,18,19,20]. While recent studies have shown that overexploiting aquifers, particularly in arid and semi-arid regions, leads to soil and water resource salinization, the relationships between salinization, soil biogeochemistry, land use, and biodiversity have been neglected [21,22]. Soil salinization currently has a severe economic impact. It continues to challenge farmers and local economies, with annual global revenue losses estimated at around $27.3 billion [23]. Salt-affected areas currently cover an estimated 935 million hectares worldwide, around 70% of degraded land. These regions are located in areas of Africa, China, the Middle East, and various other Asian countries [10]. Furthermore, this degradation is intensified by secondary salinization processes related to water quality and soil type, especially in the context of climate change in Tunisia [24]. Specifically, salts in soil consist of electrically charged ions derived from natural resources, such as shallow groundwater, as well as from anthropogenic inputs, including fertilizers and low-quality irrigation water. Anthropic salinization is a form of secondary salinization resulting from the improper use of saline water for irrigation in agriculture. These practices reduce the soil’s capacity to support high-quality crop production, thereby disrupting the plant growth cycle.

The main causes of this type of salinization are as follows:

(i)

irrigation using brackish or saline water, which is often characterized by a moderate to high solute concentration.

(ii)

irrigation of soils containing naturally occurring fossil salts, especially in arid and semi-arid regions.

(iii)

rising saline water tables, which are often associated with deforestation and poor soil drainage.

Several studies [15,25] have also highlighted that secondary salinization results from the combined effect of low-quality water used for irrigation, inadequate drainage systems, and the excessive use of fertilizers. Globally, 20% of irrigated areas are affected by anthropogenic salinization [26]. It is also estimated that more than 50% of arable land will be salinized by 2050 [27]. Salinity can be measured using the electrical conductivity of either a saturated paste extract (ECe) or a 1:5 soil-to-water extract (EC_1:5). The saturated paste method (ECe) involves preparing a soil paste at the saturation point and extracting the solution for conductivity measurements. Although this method is more time-consuming and relatively expensive, it provides a reliable estimate of the concentration of soluble salts at field saturation, reflecting the real conditions in the field [28]. It is also the reference parameter used to classify soils and evaluate the grade of soil salinity for crop suitability. ECe is considered the most appropriate index for estimating the crop’s response to salinity, as it reflects the salinity stress experienced by plant roots in the field directly [29,30]. The 1:5 soil-to-water extract method is a widely used alternative for assessing soil salinity. It is simpler, less time-consuming, and more cost-effective than the saturated paste method. EC_1:5 involves mixing soil and deionized water in a fixed 1:5 ratio, allowing for standardized procedures and the development of conversion factors to estimate ECe [31]. However, this method may not be suitable for all soil types, particularly clay-rich soils, due to their high buffering capacity and water retention properties. ECe, typically expressed in dS m⁻¹, is a key parameter in agriculture for characterizing soil–water–plant interactions in saline conditions, reflecting the concentration of soluble ions in the soil solution: the higher the ion concentration, the greater the electrical conductivity. Consequently, ECe serves as a reliable indicator of soil salinity [31]. Over the past century, various methods have been developed to predict soil salinity, including statistical, remote sensing, and machine learning approaches. These methods have had a significant impact on the work of researchers around the world, helping them to develop environmental sustainability strategies [31,32]. Accurate prediction of soil salinity is essential for managing salt-affected lands and improving agricultural sustainability. Pedotransfer functions (PTFs) are defined as “equations or algorithms expressing relationships between soil properties different in difficulty of their measurement or their availability” [33]. They can be developed to estimate ECe from more accessible data like texture, bulk density, and organic matter content. Additionally, these PTFs are particularly useful for salinity prediction, as measuring ECe can be challenging and costly [31]. Statistical regression modeling is one of the most widely used tools for constructing PTFs and quantifying relationships between variables. Simple linear regression (SLR), involves one dependent (response) variable and one independent (predictor) variable, and uses the equation of a straight line [33]. Moreover, multiple linear regression (MLR) incorporates two or more predictors and one response variable, allows for more complex modeling of soil behavior. Regression models, whether simple or multiple have been a popular tool for PTF development for decades.

An advantage of these statistical approaches is the possibility of obtaining an accurate prediction of values and coefficients of the PTFs [34]. However, some researchers [35] have reported that the accuracy of these models was evaluated using various statistical metrics, such as R-squared (R²) and the mean absolute error (MAE), which quantify the difference between predicted and observed values. The development of PTFs requires many iterations steps: (i) the selection of soil properties to be used as predictors (i.e., feature selection); (ii) deciding the type of regression to use; and (iii) (the calibration and validation of model performance using metrics.

Those steps are not simple, as soil databases grow in complexity, involving many predictors; also, the relationships may be different across regions. Recently, innovations in PTF development have employed data mining and machine learning algorithms [31,33,36]. These tools can improve the flexibility and accuracy of models, particularly in heterogeneous landscapes like those found in Tunisia. Northern Tunisia, in particular, represents a typical semi-arid area characterized by high temperatures, moderate precipitation, and a high groundwater table, as well as elevated concentrations of soluble salts. The governorate of Manouba, which is the focus of this study, is one of the country’s most important agricultural zones, accounting for nearly 60% of national wheat production [37]. The region is characterized by moderate levels of soil organic carbon (SOC), high soil salinity, and considerable spatial variability in soil properties [24]. This heterogeneity highlights the need for accurate predictive models that can estimate ECe [11], as conventional methods of predicting soil salinity are often limited by insufficient data availability and their inability to capture the complex interactions between soil properties. Although many regional studies have been conducted to predict bulk density and soil hydraulic properties [36,38], no PTFs have yet been developed specifically for predicting soil ECe in northeastern Tunisia. In this context, this study addresses that gap by developing regression-based PTFs, offering not only an analytical tool to estimate ECe but also an operational instrument for managing salt-affected zones under climate change and poor-quality irrigation water. The predictive capability of the developed PTFs supports sustainable agriculture by providing farmers with management policies, such as scheduling irrigation based on ECe thresholds, informing soil amendment strategies (e.g., gypsum application), supporting crop selection and rotation, in line with salinity tolerance, and reducing field sampling costs while maintaining the precision of regional decisions.

This study aimed to develop robust PTFs for predicting ECe based on easily measurable soil properties, providing a practical and cost-effective prediction tool and supporting the control of soil degradation by salinization, with the aim of promoting sustainable soil management and monitoring to support the development of soil conservation policies.

2. Materials and Methods

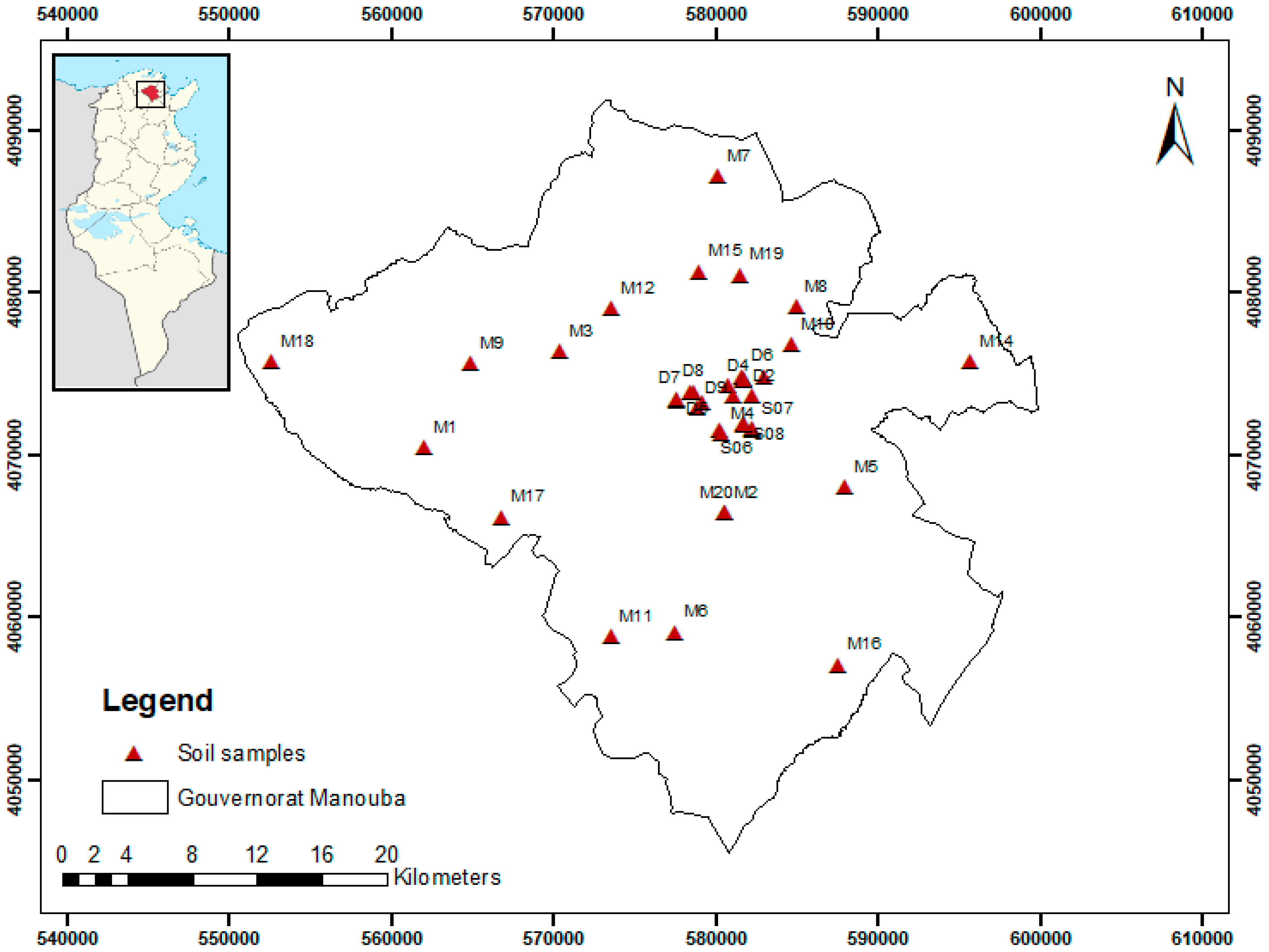
2.1. Study Sites

This study was conducted in Tunisia, a country in Northern Africa located between latitudes 32° and 38° North and longitudes 7° and 12° East. The region is known for its geographical diversity, with the northern areas being influenced by the Mediterranean Sea and the southern areas being bordered by the Sahara Desert. This variation gives rise to a range of different climate conditions, including dry summers and wet winters, which make the region susceptible to soil salinity degradation [38]. The research focused specifically on the Manouba governorate in northeastern Tunisia. The study area (Figure 1) covers approximately 1137 km², representing around 1.12% of Tunisia’s total surface area. It is located around 36°4′28″ N latitude and 10°6′4″ E longitude. The Manouba governorate has a Mediterranean climate, with an average annual rainfall of about 450 mm year⁻¹ and an annual average temperature of approximately 18.7 °C [39,40]. The region is known for its varied topography, which includes hills and fertile plains. The diversity makes it an ideal area in which to explore the impact of soil salinity on crop productivity and food security [40]. A significant expansion in water management infrastructure and drainage systems has been witnessed in the Manouba governorate, which has a significant number of irrigated zones, most of which were established after 1960 [41].

The area is characterized by alluvial formations and limestone series ranging from the continental Mio-Pliocene to the middle-upper Pleistocene [42].

The lithology of the region includes an alternation of clayey silt to clayey–sandy deposits, which varies based on topography [39,40,41]. Crops in the study area mainly consist of durum wheat. Apple, pear, and pomegranate groves, as well as vineyards, are also largely present.

Soil samples were collected over a two-year period (2022–2024), encompassing both dry and wet seasons, using a random sampling method stratified by soil types recognized in a preliminary soil survey of the study area to ensure representative soil characteristics throughout the governorate. A total of 46 soil samples were gathered from agricultural plots across the region (Figure 1). Sixteen samples were obtained from the southern part of the Medjerda River, specifically from the Jedaida district. A further ten samples were collected from the northern side of the river. The remaining 20 samples were collected across the governorate to enhance spatial representativeness. Furthermore, GPS coordinates were recorded for each sampling point. However, we collected a higher concentration of samples from agricultural zones alongside the Lower Medjerda Valley, without compromising the representation of less cultivated areas. Overall, our sampling strategy principally considered soil variability (physico-chemical properties and salinity) and variability in water irrigation sources, in order to obtain a robust dataset for modeling soil salinity across various soil types within the Manouba governorate. According to the WRB classification, most of the soils are classified as Calcisol, Vertisol, and Cambisol reference groups.

2.2. Soil Physical and Chemical Analyses

Laboratory analyses were conducted to characterize the physical and chemical properties of the soil samples. A standardized multi-step preparation process was followed to ensure reliable results and support the development of predictive models for soil electrical conductivity (ECe).

The soil samples were collected from the topsoil (0–20 cm depth) and then air-dried, manually ground, and sieved through a 2 mm mesh to remove coarse fragments and organic debris. The processed samples were then stored in labeled plastic bags prior to analysis.

The following methods were used to determine the soil properties:

−

The sedimentation method was used to determine soil texture [43].

−

The Walkley–Black method was used to measure soil organic carbon (SOC) [44].

−

The Kjeldahl digestion method was used to determine the total nitrogen content [45].

−

The BaCl₂-MgSO₄ complexometric titration method, using EDTA (Ethylene-diamine-tetra-acetic acid) as the titrant, was used to measure the cation exchange capacity (CEC) [46].

−

Soil pH was measured in a 1:2.5 soil-to-water suspension.

−

The Bernard calcimeter method was used to determine the calcium carbonate (CaCO₃) content [47].

Finally, two complementary methods were used to measure electrical conductivity: the EC_1:5 method and the ECe method:

(i)

EC_1:5 method: 20 g of soil was mixed with deionized water at a ratio of 1:5, shaken at 150 rpm for 120 min at 25 °C, and then filtered. The electrical conductivity of the supernatant was measured using a conductivity meter.

(ii)

Saturated paste extract (ECe) method: 200 g of soil was gradually moistened and mixed until a saturated paste consistency was achieved, as described by [28].

The paste was covered and left to equilibrate for 24 h at room temperature. The pore water was then extracted using suction filtration with Whatman no. 42 filter paper in a Buchner funnel, and its conductivity was measured using a calibrated conductivity meter.

2.3. Data Elaboration and Statistical Analysis

A descriptive statistical analysis was performed in Excel (Microsoft Office, 2019) to determine the data distribution. The R (version 4.4.1) and Tanagra (version 1.4) data mining software were used for advanced statistical analysis and the prediction of ECe distribution. Integrating these multi-tools, we developed robust pedotransfer functions (PTFs) for soil salinity prediction. Regression constitutes a data mining technique that models the relationship between variables by fitting an equation to a dataset.

Linear regression can be categorized into two distinct types: simple linear regression (SLR) and multiple linear regression (MLR). Both types were used in this study. The relationship between ECe and EC_1:5 has been described in models that predict salinity with SLR [48,49]. We tested PTFs from different studies in the literature to predict soil ECe from EC_1:5 [50]. In these PTFs, EC_1:5 is the input variable and ECe is the output. Two PTFs were examined in this study, particularly for clayey soils in arid and semi-arid regions, since they were developed for soils similar to those present in northern Tunisia.

The two PTFs are presented in Equations (I) and (II):

Model I: ECe = 6.53 × EC_1:5 − 0.108

(I)

Model II: ECe = 9.70 × EC_1:5

(II)

The PTFs developed in this study were calibrated and internally validated using a structured workflow involving covariate selection, regression modeling, and performance evaluation.

Following the initial descriptive analysis of soil properties and salinity indicators, which is presented in Table 1, principal component analysis (PCA) was applied to the full dataset of 46 soil samples to identify the most relevant predictors of ECe.

This multivariate technique reduced dimensionality and selected non-redundant soil covariates based on their contribution to explain the variance of the data (Table 2).

Following the PCA, MLR was applied to the entire dataset, with ECe as the dependent variable (target). The input variables, which include soil parameters selected by PCA, were used to predict ECe. The following regression equations were tested: MLR, stepwise MLR, Lasso, and Ridge MLR. Once the calibration phase had been completed and the regression equations had been developed, the next step was to validate the models in order to assess their predictive reliability and minimize overfitting. A K-fold cross-validation procedure (K = 5) was applied to the entire dataset. The data were randomly partitioned into five subsets, and each model was trained and tested iteratively across all combinations of these subsets. This process was guided by performance metrics, such as the root mean square error (RMSE) and the coefficient of determination (R²), which were recalculated after each iteration. This iterative calibration process ensured that the final equations were statistically robust in relation to the specific soil conditions of the study area. We evaluated the models by calculating additional metrics, such as the mean absolute error (MAE), the mean square error (MSE), and the R², indicating the proportion of variance in the observed values explained by the model.

Only the equations that produced high R² values, indicating a strong correlation between the predicted and measured ECe, were retained. It was the decisive factor in selecting the final PTFs [35].

3. Results

3.1. Descriptive Analysis

Table 1 shows the descriptive statistics of the soil properties determined as possible covariates for the modeling of PTFs.

Table 1. Descriptive statistics of soil physico-chemical parameters (n = 46).

Soil Parameters *	Unit	Mean	SD	Min	Max	Range	Skewness	Kurtosis	CV%
EC1:5	dS m−1	1.38	2.97	0.13	16.31	16.18	16.17	3.88	215.21
ECe	dS m−1	2.59	2.87	0.35	16.31	15.96	12.25	3.18	110.81
pH	---	7.39	0.33	6.44	8.04	1.60	0.78	−0.32	4.46
CaCO3	%	25.57	14.26	0.85	47.86	47.01	−1.39	−0.18	55.76
SOC	g·Kg−1	33.53	0.73	0.00	2.86	2.86	−0.46	0.21	2.18
TN	g·Kg−1	1.17	0.05	0.03	0.22	0.19	−0.10	0.73	4.27
CEC	Cmol(+).Kg−1	0.11	9.43	1.88	50.00	48.12	0.85	−0.10	8572
Clay	%	38.91	14.21	7.25	65.00	57.75	−0.14	−0.64	36.52
Silt	%	27.07	9.20	8.35	45.00	36.65	−0.59	−0.04	33.98
Sand	%	33.53	18.88	6.55	75.50	68.95	−0.28	0.62	56.30

* EC_1:5 = Soil electrical conductivity measured in soil: water extract at a 1:5 ratio; ECe = Soil electrical conductivity measured in a saturated paste; pH = Soil reaction; CaCO₃ = Calcium carbonate; SOC = Soil organic carbon; TN = Total nitrogen; CEC = Cation exchange capacity; Clay = Percentage of fine soil particles <0.002 mm in diameter; Silt = Percentage of intermediate soil particles between 0.002 and 0.05 mm in diameter; Sand = Percentage of coarse soil particles between 0.05 and 2 mm in diameter; SD = Standard deviation; and CV% = Coefficient of variation.

Table 1. Descriptive statistics of soil physico-chemical parameters (n = 46).

Soil Parameters *	Unit	Mean	SD	Min	Max	Range	Skewness	Kurtosis	CV%
EC1:5	dS m−1	1.38	2.97	0.13	16.31	16.18	16.17	3.88	215.21
ECe	dS m−1	2.59	2.87	0.35	16.31	15.96	12.25	3.18	110.81
pH	---	7.39	0.33	6.44	8.04	1.60	0.78	−0.32	4.46
CaCO3	%	25.57	14.26	0.85	47.86	47.01	−1.39	−0.18	55.76
SOC	g·Kg−1	33.53	0.73	0.00	2.86	2.86	−0.46	0.21	2.18
TN	g·Kg−1	1.17	0.05	0.03	0.22	0.19	−0.10	0.73	4.27
CEC	Cmol(+).Kg−1	0.11	9.43	1.88	50.00	48.12	0.85	−0.10	8572
Clay	%	38.91	14.21	7.25	65.00	57.75	−0.14	−0.64	36.52
Silt	%	27.07	9.20	8.35	45.00	36.65	−0.59	−0.04	33.98
Sand	%	33.53	18.88	6.55	75.50	68.95	−0.28	0.62	56.30

* EC_1:5 = Soil electrical conductivity measured in soil: water extract at a 1:5 ratio; ECe = Soil electrical conductivity measured in a saturated paste; pH = Soil reaction; CaCO₃ = Calcium carbonate; SOC = Soil organic carbon; TN = Total nitrogen; CEC = Cation exchange capacity; Clay = Percentage of fine soil particles <0.002 mm in diameter; Silt = Percentage of intermediate soil particles between 0.002 and 0.05 mm in diameter; Sand = Percentage of coarse soil particles between 0.05 and 2 mm in diameter; SD = Standard deviation; and CV% = Coefficient of variation.

The soil salinity indicators EC_1:5 and ECe show high coefficients of variation (CV%), at 215.21% and 110.81%, respectively. The pH shows a low CV (4.46%). Meanwhile, SOC (2.18%) and TN (4.27%) present very low CV% values. By contrast, CEC exhibits an exceptionally high CV% (8572%), driven by a very low mean value relative to the standard deviation. The high CV values of clay (36.52%), silt (33.98%), and sand (56.30%) reflect the wide range of textural classes in the topsoil dataset.

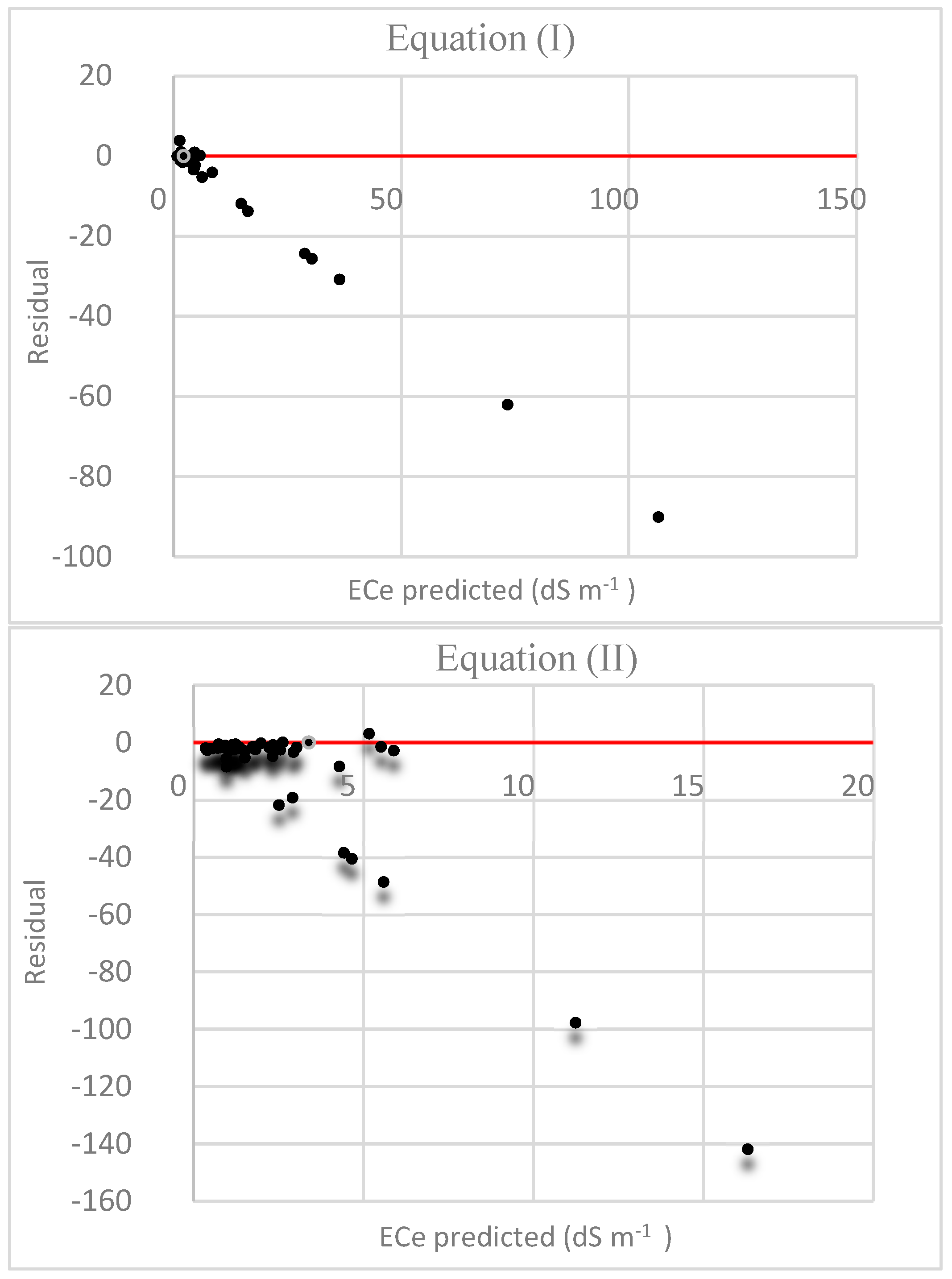
3.2. Validation of Literature-Based Pedotransfer Functions (PTFs)

Two PTFs (simple linear regression) from the literature were tested to estimate ECe from EC_1:5. Both models (Equations (I) and (II)) achieved an R² value of 0.87 when applied to the study area dataset. The accuracy of each tested SLR model was assessed visually. The residual plots from both tested models revealed predominantly negative residuals, ranging from −140 to +10 dS m⁻¹, with the largest errors being observed at predicted ECe values above 15 dS m⁻¹, indicating a tendency to overpredict ECe (Figure 2).

Figure 3 illustrates the bivariate relationship between ECe and EC_1:5, determined in the laboratory, highlighting the alignment between the two measured values, with an R² of 0.83.

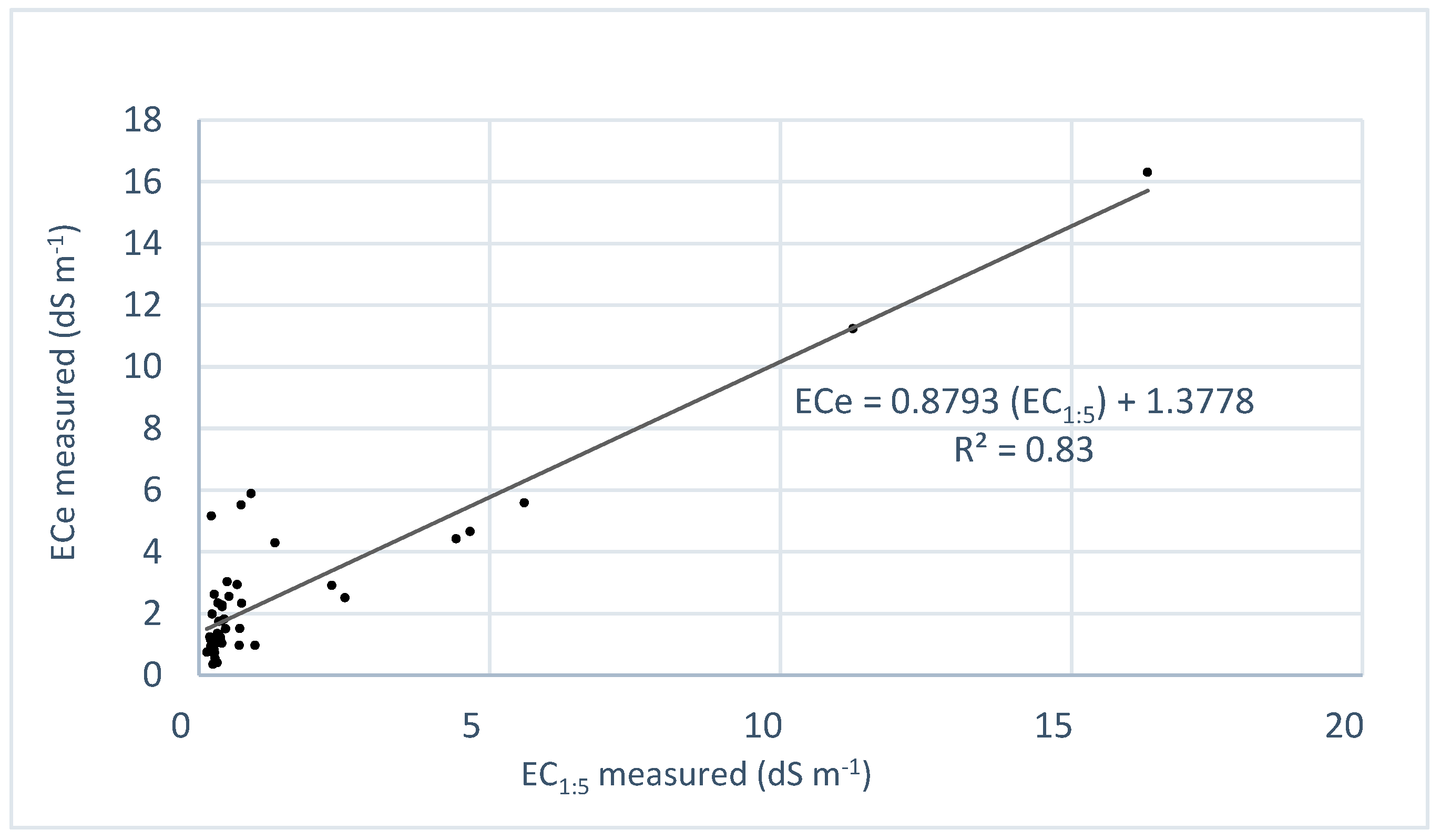
3.3. Development of New PTFs

Principal component analysis (PCA) was performed to explore the underlying structure of the soil dataset and to reduce dimensionality. Table 2 summarizes the correlation coefficients between soil attributes and the first ten principal components, alongside the percentage of variance explained by each axis. The first five components accounted for 86% of the total variance, suggesting that a small number of axes can effectively capture the dominant patterns in the data.

Table 2. Principal component analysis (PCA) of soil physico-chemical properties.

Soil Properties	PC1	PC2	PC3	PC4	PC5
EC 1:5	0.595	0.726	0.119	0.015	0.224
ECe	0.535	0.747	0.191	0.108	0.168
pH	−0.169	−0.323	−0.003	−0.216	0.885
CaCO3	0.451	−0.072	−0.434	−0.568	−0.237
Clay	0.643	−0.347	−0.108	0.634	0.039
Silt	0.637	−0.472	−0.134	−0.392	0.012
Sand	−0.786	0.504	0.128	−0.316	−0.028
SOC	−0.269	−0.573	0.595	0.200	−0.073
CEC	0.364	−0.349	0.497	−0.367	0.029
TN	0.337	0.113	0.762	−0.196	−0.157
Variance %	26	23	15	13	10
Cumulative Variance %	26	49	64	76	86

Table 2. Principal component analysis (PCA) of soil physico-chemical properties.

Soil Properties	PC1	PC2	PC3	PC4	PC5
EC 1:5	0.595	0.726	0.119	0.015	0.224
ECe	0.535	0.747	0.191	0.108	0.168
pH	−0.169	−0.323	−0.003	−0.216	0.885
CaCO3	0.451	−0.072	−0.434	−0.568	−0.237
Clay	0.643	−0.347	−0.108	0.634	0.039
Silt	0.637	−0.472	−0.134	−0.392	0.012
Sand	−0.786	0.504	0.128	−0.316	−0.028
SOC	−0.269	−0.573	0.595	0.200	−0.073
CEC	0.364	−0.349	0.497	−0.367	0.029
TN	0.337	0.113	0.762	−0.196	−0.157
Variance %	26	23	15	13	10
Cumulative Variance %	26	49	64	76	86

PCA was conducted on a set of key soil physico-chemical properties, including salinity indicators (EC_1:5 and ECe), pH, CaCO₃, texture components (percentages of clay, silt, and sand), SOC, CEC, and TN. The results show a high loading on the initial PC, suggesting salinity retention in finer soils (PC1), while the negative correlation in PC2 of SOC and silt reflects soil degradation or leaching effects in sandy soil. As for PC3, PC4, and PC5, texture, CaCO₃, and pH dominated the dataset structure as soil covariates.

In response to the consistent overprediction of the tested equations, new PTFs were developed using multiple linear regression (MLR), incorporating all the available soil parameters to evaluate the combined effects of soil properties on ECe.

The MLR provided the following PTF1:

$$\begin{gathered} \mathit{E}\mathit{C}\mathit{e}=\mathbf{8.58}+\left(\mathbf{0.90}\right)\times \mathit{E}\mathit{C} \mathbf{1}:\mathbf{5}+\left(\mathbf{0.0047}\right)\times \mathit{C}\mathit{E}\mathit{C}+\left(-\mathbf{0.916}\right)\times \mathit{p}\mathit{H}+ \\ \left(-\mathbf{0.002}\right)\times \mathit{C}\mathit{l}\mathit{a}\mathit{y}+\left(\mathbf{0.020}\right)\times \mathit{C}\mathit{a}\mathit{C}\mathit{O}\mathbf{3}+\left(\mathbf{0.14}\right)\times \mathit{S}\mathit{O}\mathit{C}+(-\mathbf{1.10})\times \mathit{T}\mathit{N} \end{gathered}$$

(PTF1)

The developed PTF1 demonstrates high predictive capability, with an R² of 0.85, showing that 85% of the variance in the observed ECe data is explained by the model. As for the prediction errors, an MAE of 0.80, an MSE of 1.23, and an RMSE of 1.11 were obtained. Additional MLR models were then performed, incorporating other textural parameters (silt and sand content). Initially, a stepwise linear regression model (PTF2) and an MLR model (PTF3), both containing all soil parameters, were used to predict ECe.

$$\mathit{E}\mathit{C}\mathit{e}=\mathbf{7.63}+\left(\mathbf{0.83}\right)\times \mathit{E}\mathit{C}\mathbf{1}:\mathbf{5}+(-\mathbf{0.85})\times \mathit{p}\mathit{H}$$

(PTF2)

The second PTF shows an MAE of 0.83, an MSE of 1.34, and an RMSE of 1.160, with an R² of 0.71

The following equation presents PTF3:

$$\begin{gathered} \mathit{E}\mathit{C}\mathit{e}=-\mathbf{0.34}+\left(\mathbf{0.860}\right)\times \mathit{E}\mathit{C} \mathbf{1}:\mathbf{5}+\left(\mathbf{0.003}\right)\times \mathit{C}\mathit{E}\mathit{C}+\left(-\mathbf{0.960}\right)\times \mathit{p}\mathit{H}+ \\ \left(-\mathbf{0.019}\right)\times \mathit{C}\mathit{a}\mathit{C}\mathit{O}\mathbf{3}+\left(\mathbf{0.089}\right)\times \mathit{C}\mathit{l}\mathit{a}\mathit{y}+\left(\mathbf{0.098}\right)\times \mathit{S}\mathit{i}\mathit{l}\mathit{t}+\left(\mathbf{0.091}\right)\times \mathit{S}\mathit{a}\mathit{n}\mathit{d}+ \\ \left(\mathbf{0.07}\right)\times \mathit{S}\mathit{O}\mathit{C}+\left(\mathbf{0.70}\right)\times \mathit{T}\mathit{N} \end{gathered}$$

(PTF3)

The resulting model achieved a high R² of 0.81, with the following corresponding error metrics: MAE = 0.81, MSE = 1.22, and RMSE = 1.10.

In order to improve the predictions, two linear regression models were conducted: Ridge regression and Lasso regression, presented in PTF4, as shown below.

$$\begin{gathered} \mathit{E}\mathit{C}\mathit{e}=\mathbf{15.39}+\left(\mathbf{0.760}\right)\times \mathit{E}\mathit{C}\mathbf{1}:\mathbf{5}+\left(\mathbf{0.002}\right)\times \mathit{C}\mathit{E}\mathit{C}+\left(-\mathbf{1.58}\right)\times \mathit{p}\mathit{H}+ \\ \left(-\mathbf{0.04}\right)\times \mathit{C}\mathit{a}\mathit{C}\mathit{O}\mathbf{3}+\left(-\mathbf{0.04}\right)\times \mathit{C}\mathit{l}\mathit{a}\mathit{y}+\left(-\mathbf{0.23}\right)\times \mathit{S}\mathit{O}\mathit{C}+\left(\mathbf{2.62}\right)\times \mathit{T}\mathit{N} \end{gathered}$$

(PTF4)

Both Lasso and Ridge regression (PTF4) achieved an R² value of 0.89.

However, Ridge regression showed slightly higher error values (MAE = 0.85, MSE = 1.29, and RMSE = 1.13). Lasso regression, however, demonstrated a more accurate model with similar predictor error values (MAE = 0.81, MSE = 1.25, and RMSE = 1.12).

Following the clustering process, another PTF was developed, with ECe as the dependent variable. The optimal predictor variables selected were SOC, TN, CEC, and EC_1:5. The developed PTF5 is shown below:

$$\begin{gathered} \mathit{E}\mathit{C}\mathit{e}=\mathbf{1.226}+\left(\mathbf{0.905}\right)\times \mathit{E}\mathit{C}\mathbf{1}:\mathbf{5}+\left(-\mathbf{0.005}\right)\times \mathit{C}\mathit{E}\mathit{C}+\left(\mathbf{0.220}\right)\times \mathit{S}\mathit{O}\mathit{C}+ \\ (-\mathbf{0.105})\times \mathit{T}\mathit{N} \end{gathered}$$

(PTF5)

PTF5 shows an R² value of 0.83, a low MAE of 0.82, an MSE of 1.33, and an RMSE of 1.157. Ultimately, the classification and regression tree (C-RT) model was also employed to estimate ECe based on EC_1:5 measurements. The optimal tree structure contained three terminal leaves, achieving the lowest minimum standard error (SE) of 1.6202. SE values were 1.1579 during the growing stage and 2.9832 during pruning.

The tree categorized the data as follows:

Tree Visualization:

• If EC_1:5 < 0.7100, then the average (ECe) = 1.5458 (std.dev = 1.0466 with 21 examples (70.00%))
• EC_1:5 >= 0.71000
• ├── If EC_1:5 < 8.4150, then the average (ECe) = 4.4012 (std.dev = 1.3537, with 8 examples (26.67%))
• └── If EC_1:5 > 8.4150, then the average (ECe) = 11.2400 (std.dev = −99999.0000, with 1 example (3.33%))

When EC_1:5 is <0.7100, the average ECe was 1.5458, representing 70% of the samples. For an EC_1:5 between 0.7100 and 8.4150, the average ECe was 4.4012. For EC_1:5 > 8.4150, the average ECe was 11.2400; however, this group contained only one sample, indicating an atypical result.

3.4. Model Performance Evaluation

Residual plots were examined for all developed pedotransfer functions (PTFs) in order to evaluate the fit of the model and detect the distribution of errors. The residuals were plotted against the predicted ECe values for all the developed PTFs and are shown in Figure 4 for comparative visualization. PTF1 and PTF2 show residuals ranging from −2 to +2 dS m⁻¹, while PTF3 shows localized anomalies near 10–15 dS m⁻¹. PTF4 and PTF5 show randomly distributed residuals across the full ECe scale (0–16 dS m⁻¹).

Table 3. Developed pedotransfer functions.

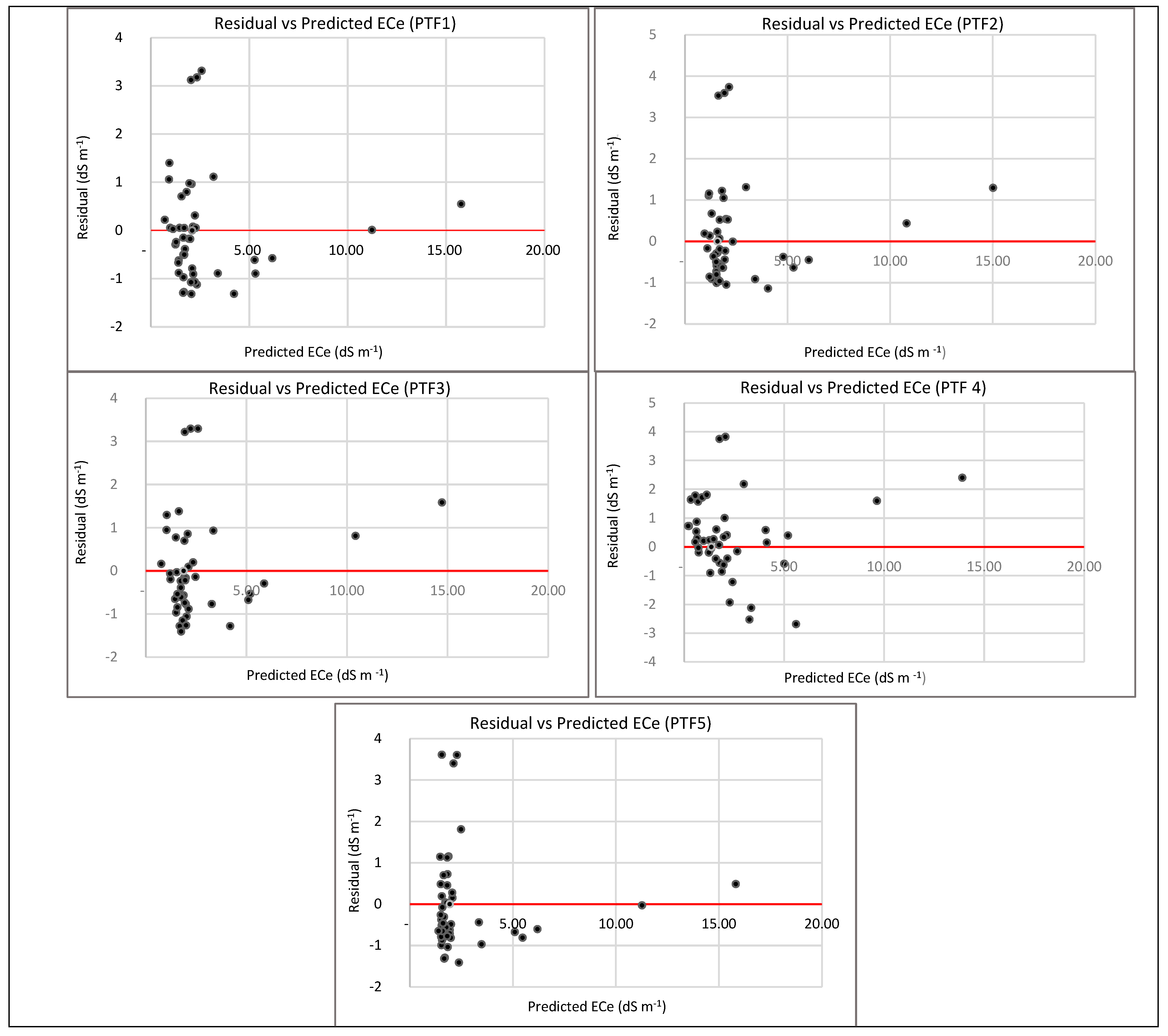
PTF	Soil Covariates	Equation	R2 Value
PTF1 Multiple linear regression	EC1:5−pH CEC−Clay CaCO3−SOC TN	ECe = 8.58 + (0.90) × EC1:5 + (0.0047) × CEC + (−0.916) × pH + (−0.002) × Clay + (0.020) × CaCO3 + (0.14) × SOC + (−1.10) × TN	0.85
PTF2 Stepwise linear regression	EC1:5−pH	ECe = 7.63 + (0.83) × EC1:5 + (−0.85) × pH	0.83
PTF3 Multiple linear regression	EC1:5−pH CEC−Clay–Silt–Sand CaCO3−SOC TN	ECe = −0.34 + (0.86) × EC1:5 + (0.003) × CEC + (−0.96) × pH + (−0.019) × CaCO3 + (0.089) × Clay + (0.098) × Silt + (0.091) × Sand + (0.07) × SOC + (−0.70) × TN	0.81
PTF4 Lasso and Ridge regression	EC1:5−pH CEC−Clay CaCO3−SOC TN	ECe = 15.39 + (0.76) × EC1:5 + (0.002) × CEC + (−1.58) × pH + (−0.04) × CaCO3 + (−0.04) × Clay + (−0.23) × SOC + (2.62) × TN	0.89
PTF5 Multiple linear regression	EC1:5−pH CEC−SOC TN	ECe = 1.226 + (0.905) × EC1:5 + (−0.005) × CEC + (0.220) × SOC + (−0.105) × TN	0.83

summarizes all the pedotransfer functions developed, predictive covariates used, and R² values.

4. Discussion

This research provides a comprehensive evaluation of topsoil salinity in northeastern Tunisia, where salinity is one of the major constraints to agricultural productivity. The descriptive statistics show significant variability across key soil parameters, reflecting the landscape heterogeneity of the study area. High EC_1:5 and ECe values were observed, indicating the presence of both slightly and highly saline soils (Table 1).

The wide range of salinity levels across the Manouba governorate reveals the diversity of soil types and conditions, which may require distinct management strategies to ensure soil health and agricultural sustainability. According to the results in Table 1, the dominance of calcareous and clayey soils can be confirmed. These soils are typical of the semi-arid regions of Tunisia due to their high concentration of CaCO₃ and clay [24]. Additionally, total nitrogen and soil organic carbon levels are quite consistent. This suggests that organic matter inputs are uniformly lower, which is a result of the effect of climate on organic matter accumulation and low biomass production due to poor water quality [24]. The CEC exhibits exceptionally high variability, driven by a very low mean value, as shown in Table 1. This extreme variability indicates moderate to high nutrient retention potential across the topsoils. It depends on the clay and organic matter contents and influences the soil’s ability to retain and exchange cations, thus affecting plant nutrition. The two simple linear regression equations from the literature [49,50], using EC_1:5 as the unique predictor of ECe, returned high R² values, which reached 0.87. These models confirm the strong correlation between ECe and EC_1:5, providing a practical and easy method for estimating salinity in clay-rich soils.

The bivariate relation between ECe and EC_1:5, both determined in soil samples collected, also confirmed the strong correlation between these two soil parameters. Residual plots for both SLR models adopted demonstrate that over 80% of residuals fell below zero, with outliers exceeding −100 dS m^–1 (Figure 2). The SLR models demonstrated limitations in terms of their predictive precision, despite their simplicity. The negative residuals show that ECe was systematically overpredicted. This prompted the development of more robust PTFs that integrate additional soil parameters. By accounting for the chemical and physical complexity of the soil matrix, these multivariate PTFs significantly improved the predictive accuracy, reduced error metrics, and produced more stable residual distributions. This allowed independent variables to be added or eliminated at each step of the regression, ultimately refining the model to include only the significant factors. The most influential soil covariates were identified, and multicollinearity among predictors for PTFs development was reduced using PCA following the descriptive analysis. The results of PCA (Table 2), which guided the selection of soil covariates by identifying the best predictors, such as EC_1:5 and fertility parameters (SOC, TN, and CEC), exhibited strong loadings on the first principal components. These traits capture the dominant gradients in soil behavior and are essential for predicting hydraulic and chemical properties. The high R² values (Table 3) confirm the robustness of these models in predicting ECe in semi-arid Mediterranean environments. These findings emphasize the significant influence of various soil parameters, such as pH, SOC, TN, CEC, and soil texture, on salt concentration. However, minimal differences in the predictive accuracy were observed (R² = 0.85 vs. 0.83), highlighting the effectiveness of incorporating soil parameters such as calcium carbonate (CaCO₃) as covariates in multiple linear regression (MLR). The first PTF showed slightly better performance, demonstrating the importance of incorporating all soil properties when predicting ECe. As an alternative, regression techniques such as multiple linear regression (MLR), stepwise linear regression (MLSR), and Lasso/Ridge regressions are more effective at predicting a dependent variable using one or more independent variables. However, Ridge and Lasso regression models generated better predictive performance, with R² = 0.89, demonstrating their ability to define multicollinearity with many variables, optimizing variable selection. Both stepwise linear regression and MLR confirmed the relationship between soil covariate selection and ECe prediction. To ensure accuracy and reduce the time consumption of procedures, it is essential to select the important covariates from all the measured soil parameters [51,52]. The stepwise linear regression model (PTF2 with R² = 0.84) combines the forward and backward elimination of inputs and is capable of handling data to generate the best model [53,54]. This regression technique provides access to complex analyses by eliminating the multicollinearity problem.

Some studies support our approach, emphasizing the importance of selecting predictors according to specific modeling and research goals. In fact, the results of research in southern Algeria [2], using stepwise regression to predict soil salinity by selecting soil covariates, align with our findings. Similarly, our findings based on identifying SOC, TN, and CEC as key predictors align with the results of research conducted in Morocco [55]. While linear models provided effective predictions, the C-Predictive Regression Tree (C-RT) model achieved optimal results, with R² = 0.77, by capturing nonlinear relationships between variables. This suggests that nonlinear approaches can enhance the predictive capability, particularly in areas where soils show high variability in properties. Another study [56] has shown that nonlinear models perform well in predicting salinity, especially in areas with heterogeneous soil types and poor water management strategies. The inclusion of additional soil parameters in MLR significantly improved models’ efficiency, as confirmed by Zhou et al. [56].

The three MLR pedotransfer functions provide the best estimation of soil electrical conductivity due to the optimization of variable selection. This outcome aligns with observations of the superior performance of regularization techniques in salinity prediction [57]. The conventional conversion factor between the electrical conductivity of saturated paste extracts (ECe) and total soluble salts (TSSs), as proposed by the US Salinity Laboratory Staff in 1954, assumes a linear relationship, typically expressed as TSS ≈ 640 × ECe. However, recent studies in arid regions, such as Abu Dhabi in the United Arab Emirates (UAE), have demonstrated that this relationship may not hold under local soil and climatic conditions. Al Qasmi et al. [58] used remote sensing and field data to model salinity variations, revealing significant discrepancies from standardized conversion factors and highlighting the requirement for region-specific calibration models. All these divergences highlight the need for the development and calibration of new local PTFs for salinity measurement. Studies conducted in Morocco demonstrated the importance of combining different statistical methods to estimate soil properties using covariates such as clay and silt content and soil organic carbon. They found that multiple linear regression models performed better than the Cubist algorithm regression tree and Random Forest, which aligns with the multi-tool approach used in this study [55]. Studies conducted by El Bahjaouy et al. [59] showed that the integration of Random Forest with spectral indices and physico-chemical properties in Morocco’s Tadla Plain achieved an R² value of 0.80. However, Ouzemou et al. [60] applied a polynomial regression to EC_1:5 ratios in semi-arid Moroccan soils, obtaining an R² value of 0.98. Zheng et al. [61] emphasized the advantages of nonlinear methods (N-MBL) in regions with heterogeneous soils, particularly where there are complex interactions between soil variables. This suggests that integrating nonlinear approaches can significantly enhance the predictive accuracy, particularly when soil properties interact in complex ways. More accurate predictions in areas at risk of high salinization can guide agricultural practices and policy decisions, thus preventing soil degradation. For example, regions with elevated ECe levels can be selected for specific management interventions, such as preventing leaching, optimizing drainage, or cultivating salt-tolerant crops [62].

In this study, the effectiveness of each predictive model was systematically assessed to identify the most suitable approach for ECe prediction. As part of the model evaluation process, the predictive performance of each PTF was assessed using residual plots and statistical indicators. This allowed a comparative analysis of their reliability at different salinity levels. The results of the tested SLR models (Figure 2) show that there is an overprediction of ECe. While the models perform adequately at low salinity levels (predicted ECe < 5 dS m⁻¹), their accuracy declines significantly in more saline conditions. This highlights the need for locally developed PTFs. The residual plots (Figure 4) generally concentrate near zero across all models, particularly within the lower ECe range. This indicates reliable performance under moderate salinity conditions. PTF1 and PTF2 demonstrate good accuracy up to 6 dS m⁻¹. However, occasional outliers suggest an underprediction in highly saline zones. PTF3 shows consistent performance up to 4 dS m⁻¹, although there are some isolated deviations near 10–15 dS m⁻¹. PTF4 and PTF5 show randomly distributed residuals, confirming homoscedasticity and model robustness. Beyond 12 dS m⁻¹, however, a slight trend of inaccuracy emerges, potentially due to nonlinear soil behavior or a limited representation of extreme values. Overall, the residual plots validate the predictive reliability of all models while also highlighting areas where further refinement could improve generalization, particularly at higher salinity levels. According to the predictive accuracy, PTF1 was the most appropriate, exhibiting the highest R² (0.85), despite having a large number of covariates. However, PTF5 offered a more practical solution for field applications, achieving an important R² (0.83) and p-value = 3.07 × 10⁻¹⁵ with fewer predictors that are less time-consuming and more cost-effective to measure. EC_1:5 appears to be the most influential predictor, demonstrating a very strong relationship with ECe.

The multiple computational tools, such as PCA-based covariate selection and the use of K-fold cross-validation (K = 5), provide a more detailed and accurate assessment of soil salinity than any single method alone. This study has significant practical implications for the sustainable management of soil in northeastern Tunisia, since the application of the models can provide useful and accurate predictions about soil salinity levels in order to adopt the optimal management of soils, including irrigation and drainage systems, thus avoiding soil degradation by salinization.

5. Conclusions

This research aimed to address the challenge of the accurate assessment of soil salinity using cost-effective and time-efficient methods. Although the electrical conductivity of saturated soil extracts remains the standard reference for salinity evaluation, its direct measurement is often limited by the complexity of sampling, laboratory costs, and time-consuming procedures. Since soil electrical conductivity prediction is highly sensitive to soil types and sampling period, our findings emphasize the importance of developing ad hoc pedotransfer functions that are both efficient and reliable, enabling a more accurate prediction of ECe. This study revealed that soil salinity levels, in this specific context, are influenced by key soil variables, such as pH, SOC, TN, and CEC. The predictive performance of the proposed models is significantly enhanced by these soil variables. PTFs provide a practical alternative for estimating ECe across diverse landscapes by leveraging easily measurable soil properties. Furthermore, they can serve as a reliable tool for monitoring soil salinization dynamics over time. Developed PTFs support soil scientists, farmers, and decision-makers in addressing sustainable soil management in the agricultural land of northeastern Tunisia, whereas the application of PTFs developed from a bigger dataset, and/or in different contexts, can show low accuracy. Finally, this approach supports sustainable soil management by facilitating early detection and informed decision-making in salt-affected regions, which is beneficial for long-term soil security.