Multi-Objective Optimization of Window Design for Energy and Thermal Comfort in School Buildings: A Sustainable Approach for Hot-Humid Climates
Abstract
1. Introduction
1.1. Background and Significance
1.2. Literature Review and Research Gap
1.3. Research Objectives and Significance
- To develop an integrated parametric modeling and optimization workflow by combining Rhino/Grasshopper with the NSGA-II algorithm to optimize window configurations for school buildings.
- To identify optimal window configurations that balance energy efficiency and thermal comfort, especially for schools in Guangzhou’s hot-humid climate, while considering crucial factors such as shading, glazing, and WWR.
- To analyze the trade-offs between energy efficiency and thermal comfort and provide actionable design insights for architects and engineers.
- To validate the optimization framework through a case study of a representative school building in Guangzhou, China, thereby demonstrating the framework’s real-world applicability.
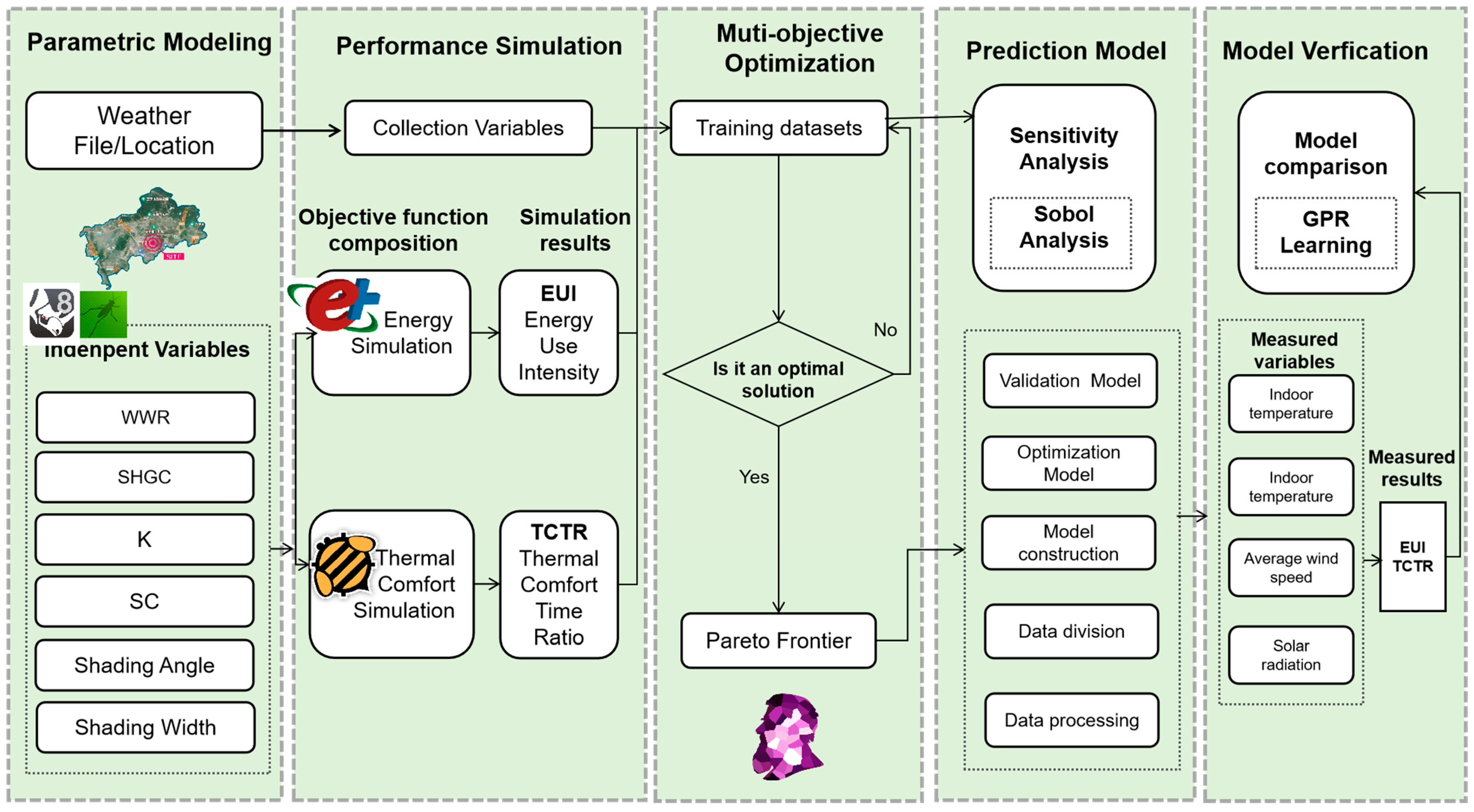
2. Methodology
- EnergyPlus: Version: 9.6, Manufacturer: U.S. Department of Energy, City: Washington, State: DC, Country: USA [38].
- Honeybee: Version: 1.5.0, Manufacturer: Ladybug Tools, City: London, State: N/A, Country: UK [39].
- Rhino 8: Version: 8.0, Manufacturer: Robert McNeel & Associates, City: Seattle, State: WA, Country: USA [40].
- Grasshopper: Version: 1.0, Manufacturer: Robert McNeel & Associates, City: Seattle, State: WA, Country: USA [41].
- Wallacei Plugin: Version: 1.2, Manufacturer: Ladybug Tools, City: London, State: N/A, Country: UK [42].
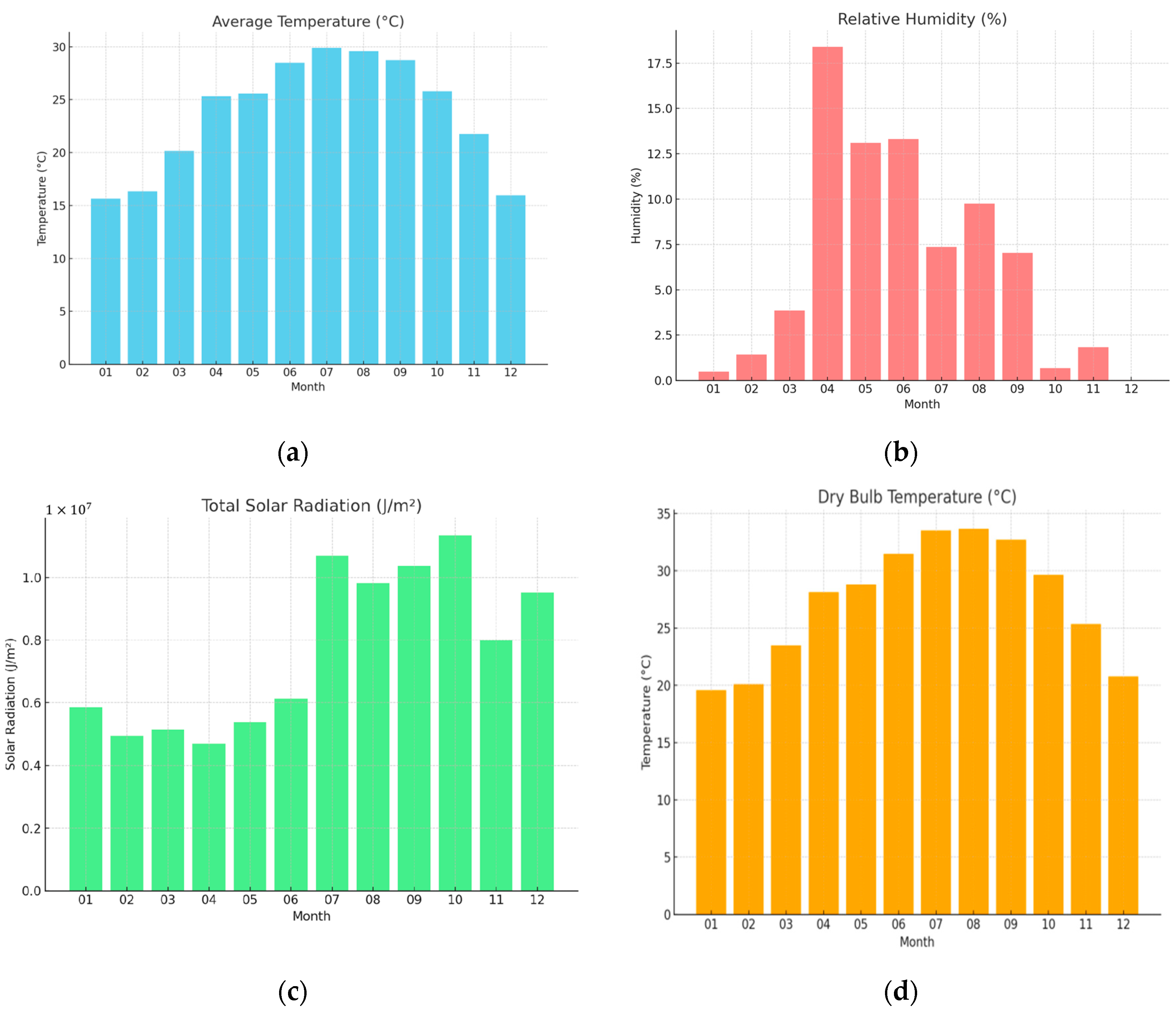
2.1. Climate Background
2.2. Performance Simulation Methods
- -
- is the total energy consumed by the building in kilowatt-hours per year (kWh/year).
- -
- is the total floor area of the building in square meters ().
- -
- represents the comfort index at time t, indicating whether the indoor environment meets thermal comfort standards. If = 1, the indoor environment meets the comfort standards, while if = 0, it does not.
- -
- is the total time period being considered, typically one year.
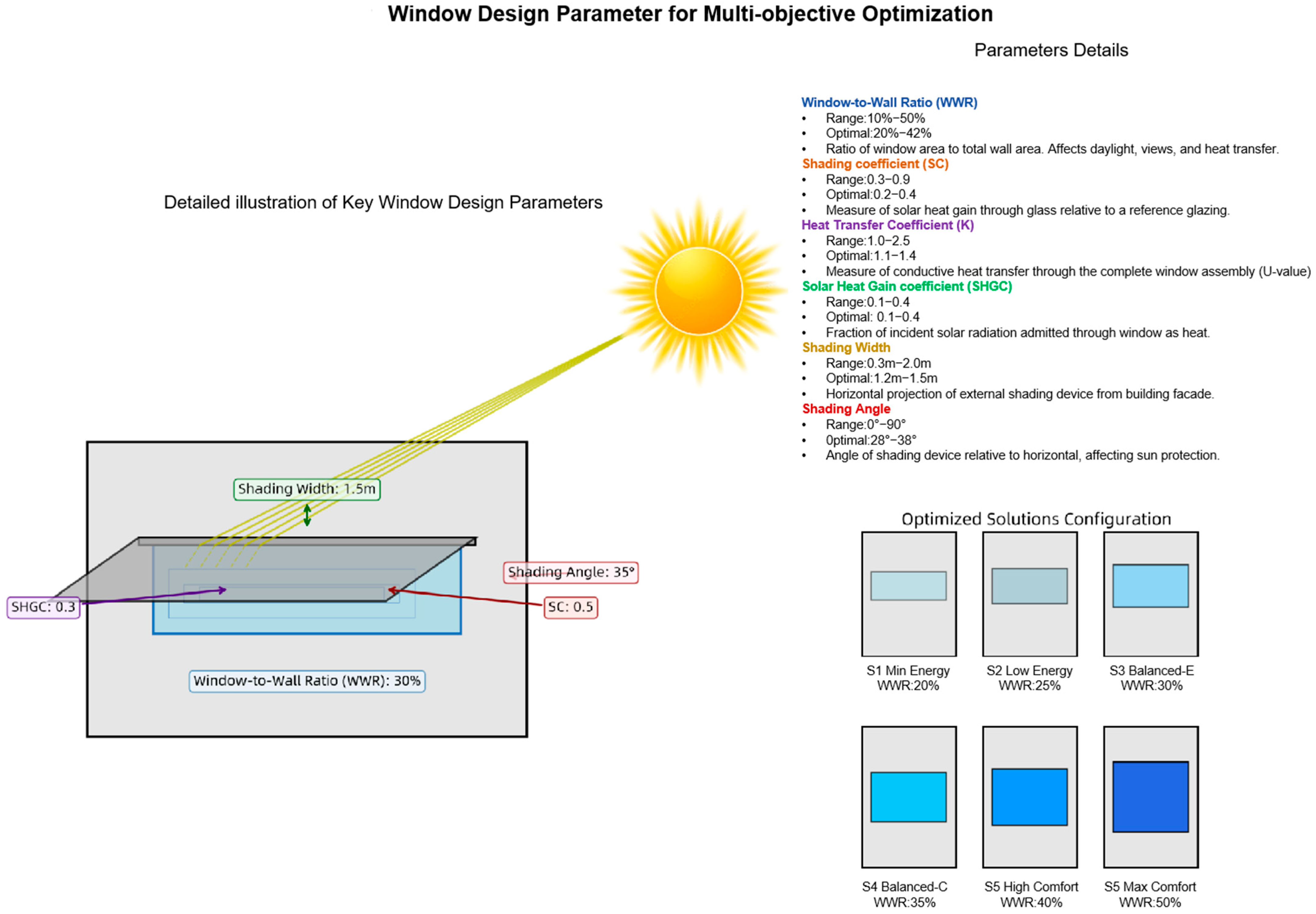
2.3. Selection of Design Parameters
- Window-to-Wall Ratio (WWR): This parameter regulates the equilibrium between daylight, ventilation, and cooling loads, essential for minimizing energy consumption while ensuring sufficient indoor lighting. This is particularly critical in hot-humid climates, where optimizing both cooling and natural ventilation is necessary [7,48].
- Solar Heat Gain Coefficient (SHGC): SHGC quantifies the fraction of incident solar heat enters the building through the window. In hot-humid climates, optimizing SHGC helps balance solar heat gain with the need for natural daylight, minimizing cooling energy consumption while maintaining occupant comfort [6,51].
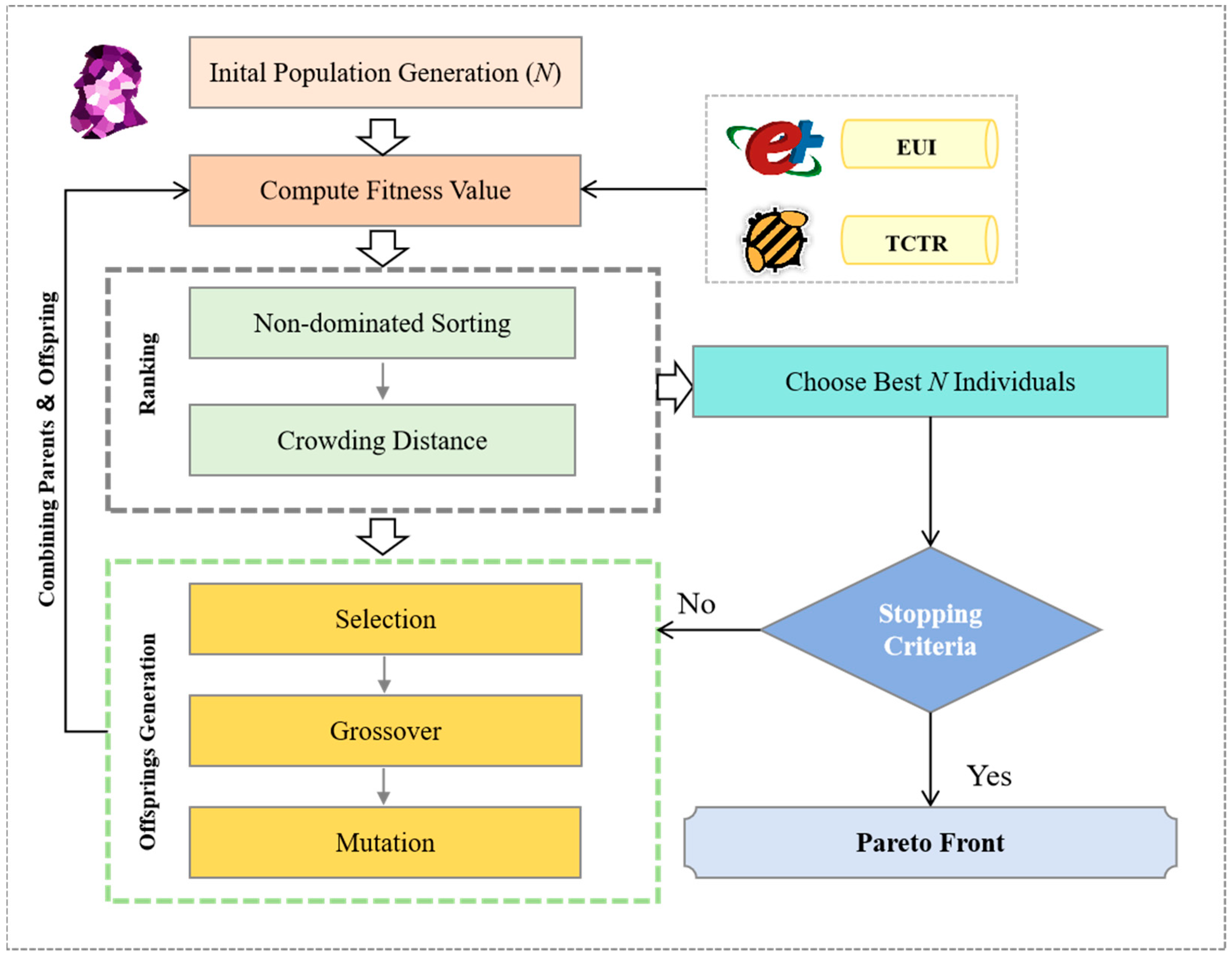
2.4. Multi-Objective Optimization
- -
- Energy Use Intensity function (EUI)
- -
- Thermal Comfort time percentage function (TC)
- -
- is the crowding distance of the -th solution,
- -
- and are the objective values of the neighboring solutions on the -th objective,
- -
- and are the maximum and minimum values of the -th objective.
2.5. Sensitivity Analysis and Machine Learning Models
- -
- is the conditional expectation of Y given the input parameter ,
- -
- is the variance of the output Y,
- -
- represents all input parameters except
3. Results
3.1. Model Simulation
3.1.1. Simulation
3.1.2. Multi-Objective Optimization Window Parameter Settings
| Parameter | Physical Meaning | Design Impact | Reference |
|---|---|---|---|
| Window-to-Wall Ratio (WWR) | Ratio of window area to total wall area. | Affects daylight, views, ventilation, and heat transfer. | Sharma et al., 2022 [74]; Wang et al., 2022 [75] |
| Shading Coefficient (SC) | Fraction of solar heat gain transmitted through shading device. | Controls solar gain, reduces cooling loads, and enhances shading efficiency. | Seyedzadeh et al., 2018 [76] |
| Solar Heat Gain Coefficient (SHGC) | The fraction of solar radiation admitted through the window as heat. | Influences cooling energy demand, impacts indoor temperature. | Kalmár, F. 2020 [77]; Alhuwayil et al., 2019 [78] |
| Heat Transfer Coefficient (K) | Measure of the total window system’s heat transmission performance. | Affects building energy efficiency and thermal insulation. | Alhuwayil et al., 2018 [78] |
| Shading Width | Horizontal projection length of the external shading device. | Provides sun protection, modifies daylight, and reduces solar heat gain. | Tan et al., 2024 [79] |
| Shading Angle | Angle between the shading device and the horizontal plane. | Optimizes sun protection seasonally, impacts view and daylight. | Mazzetto et al., 2025 [80] |
3.1.3. Constraints
0.20 ≤ SC ≤ 0.80
1.0 ≤ K ≤ 2.5 W/(m2·K)
0.1 ≤ SHGC ≤ 0.40
0.30 m ≤ Shading Width ≤ 2.0 m
0° ≤ Shading Angle ≤ 90°
TC ≥ 50%
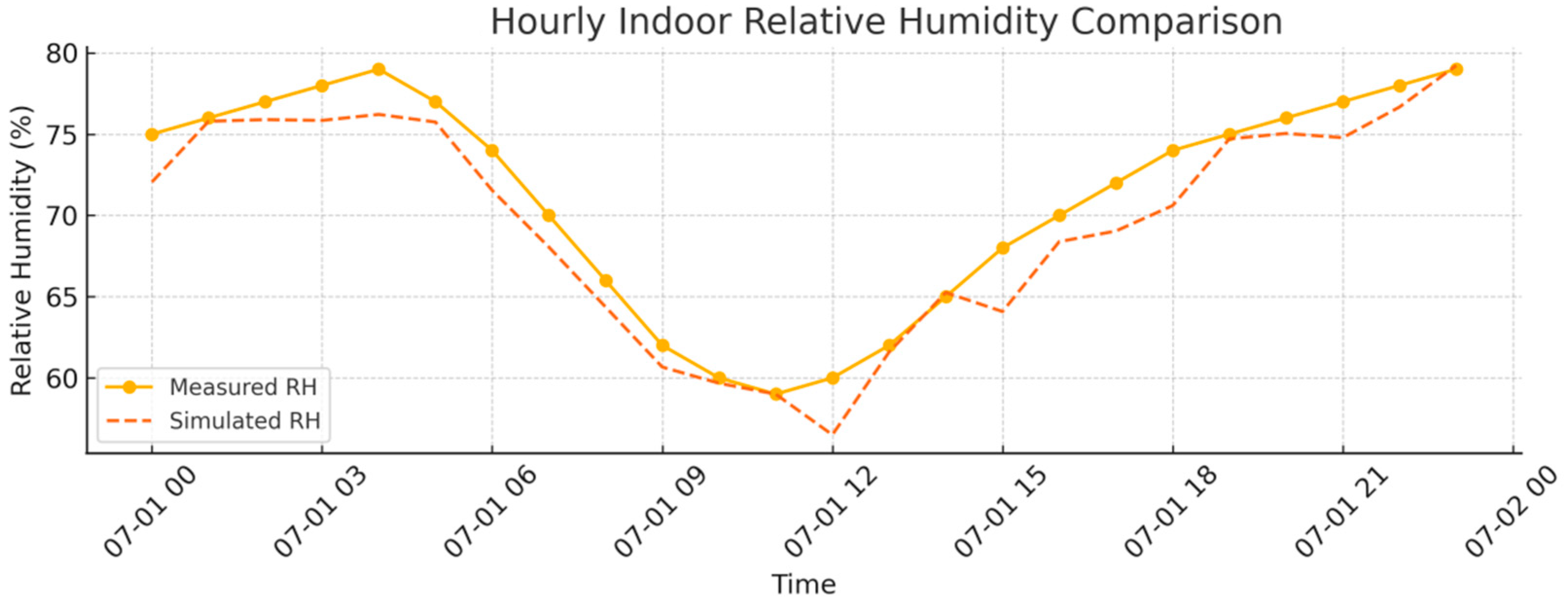
3.2. Simulation Results Verification and Case Analysis
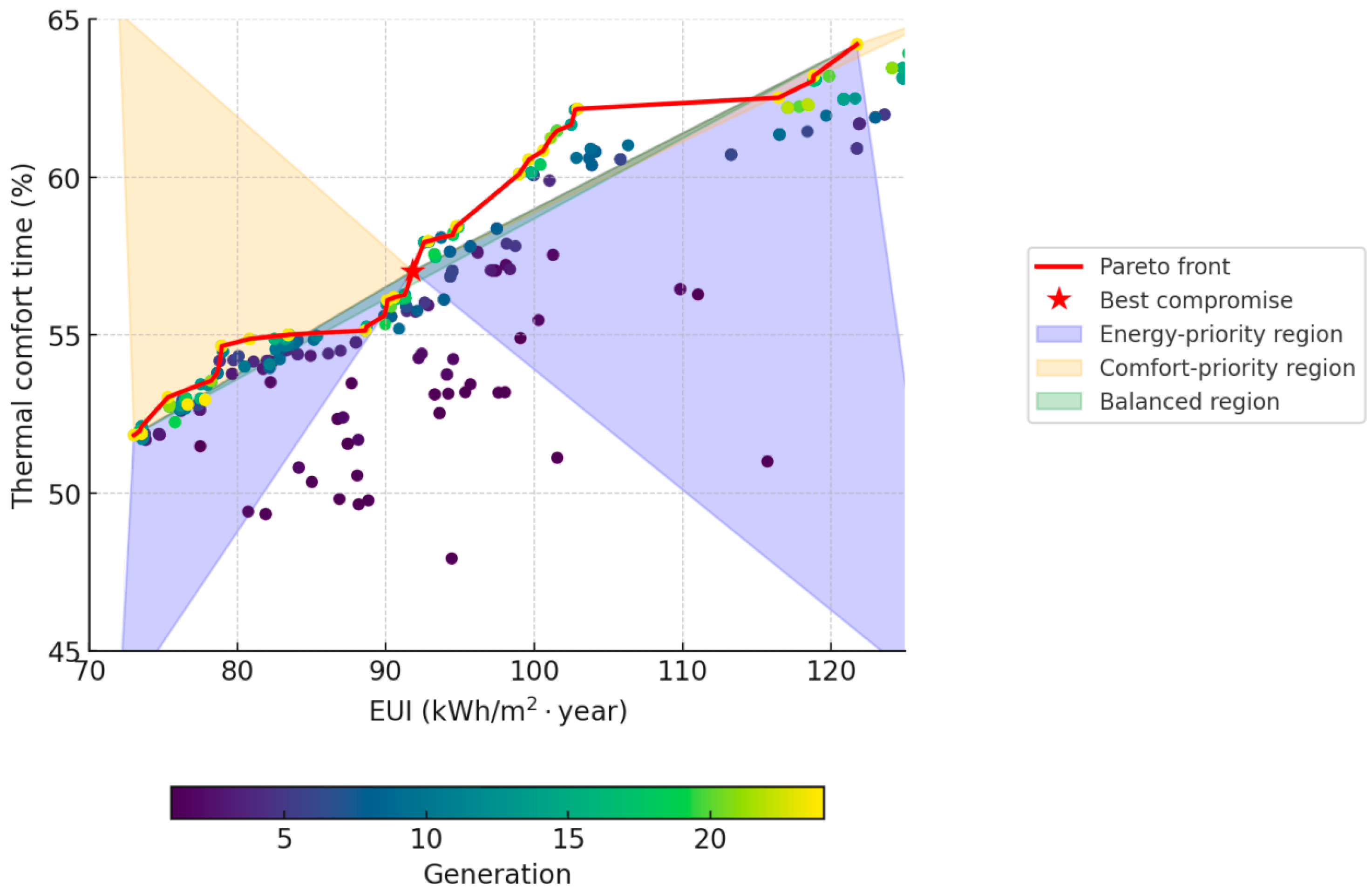
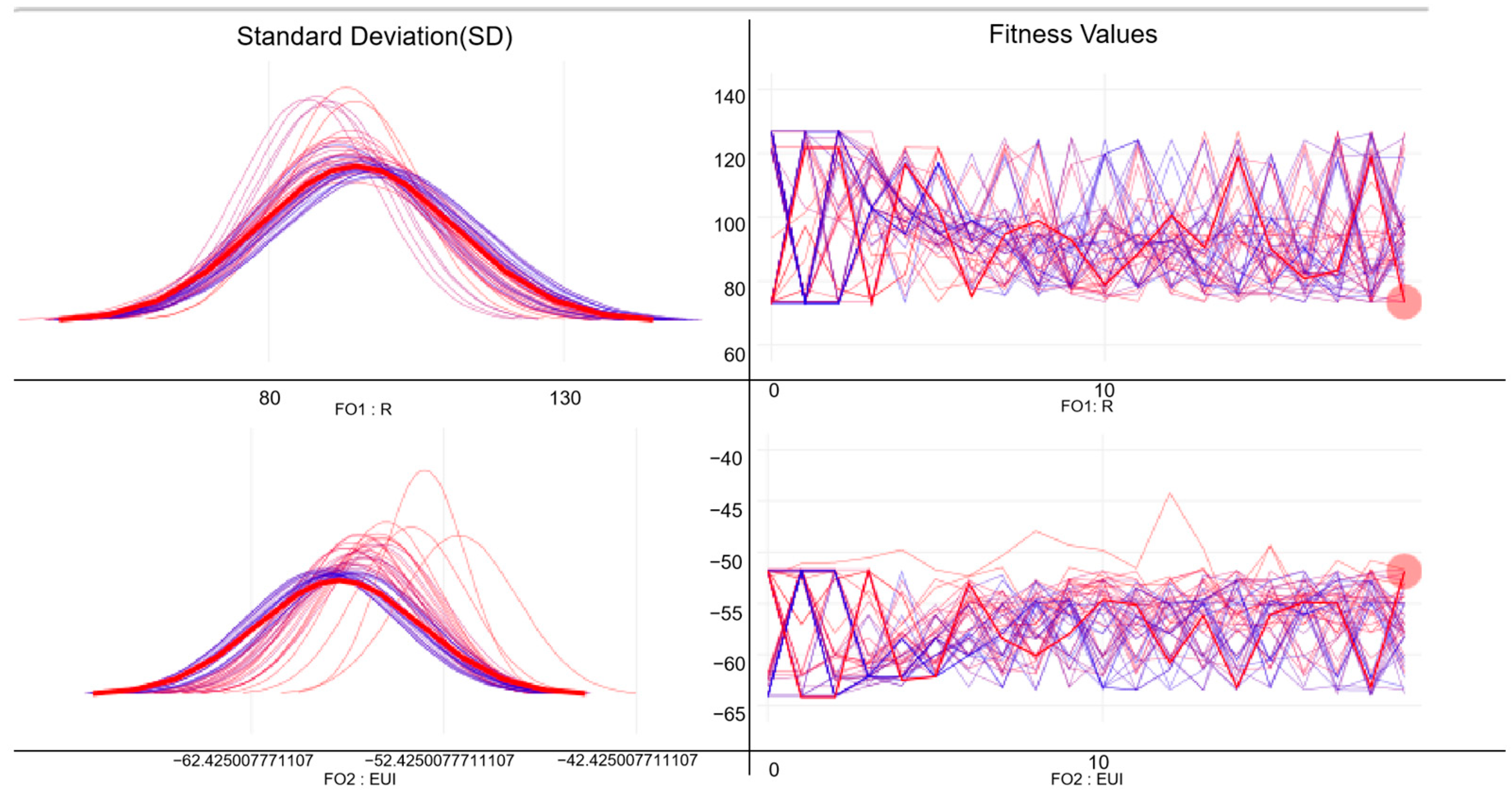
3.3. Multi-Objective Optimization Results
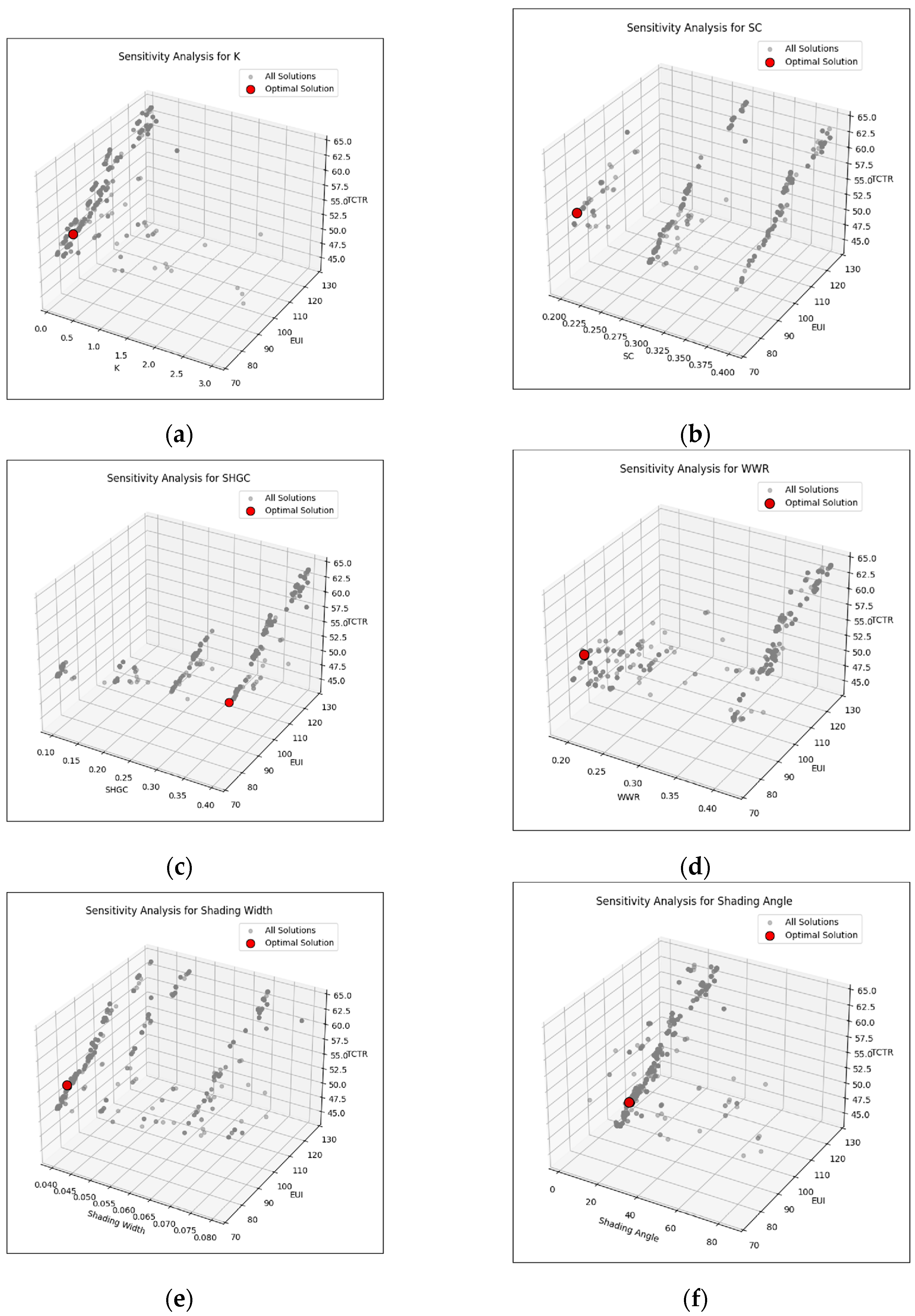
3.4. Sensitivity Analysis Results
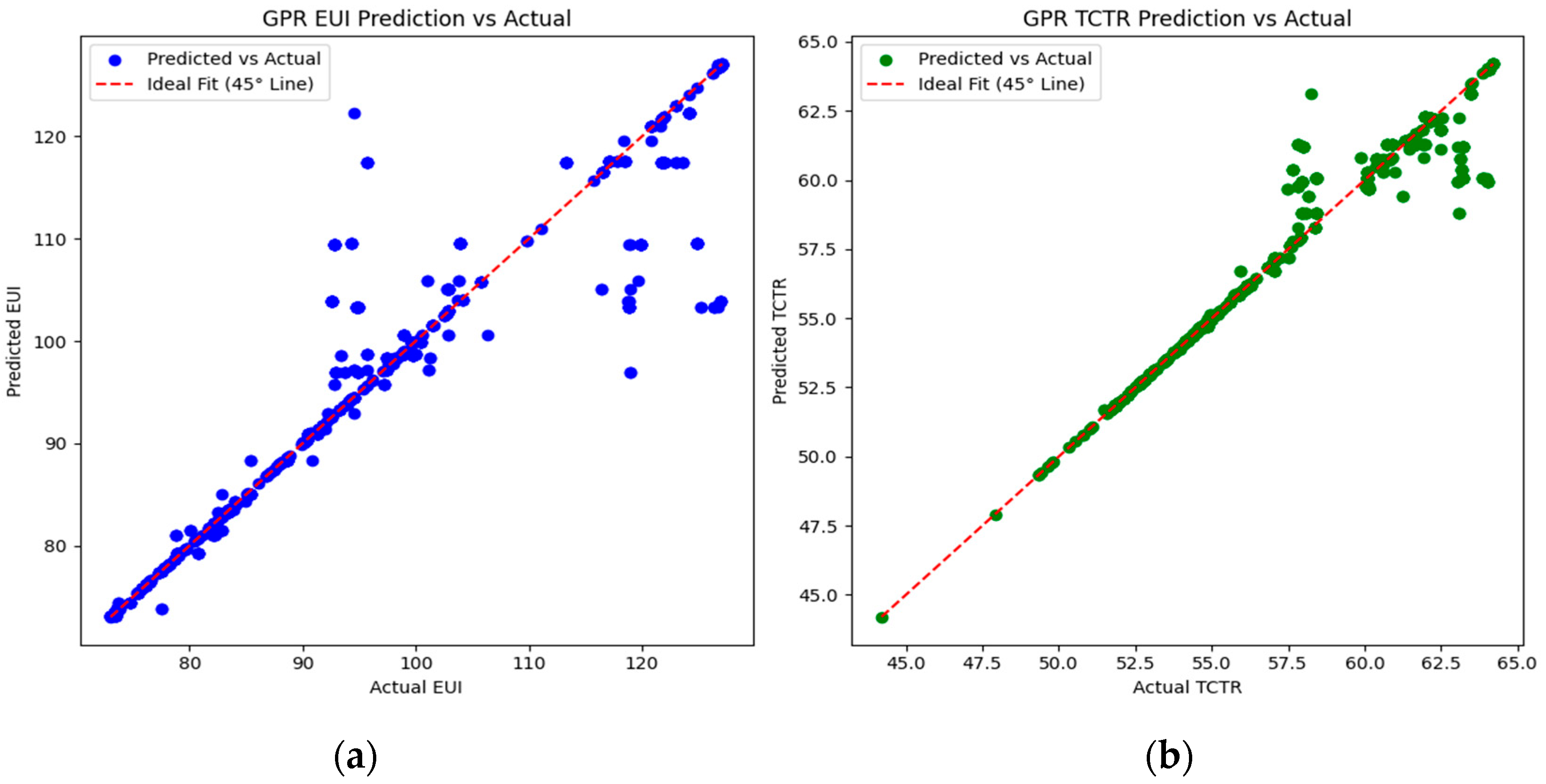
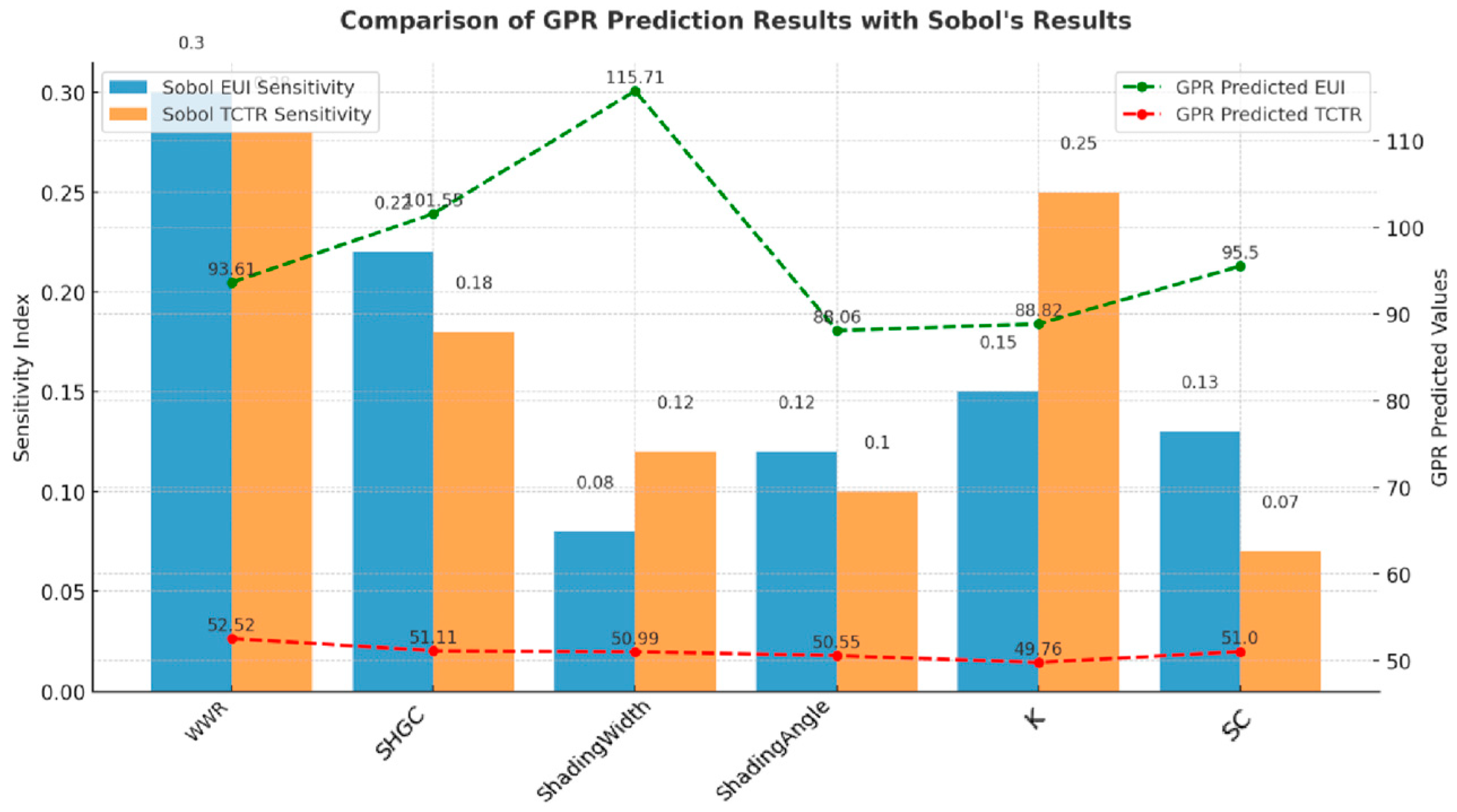
3.5. Machine Learning GPR Verification
4. Discussion
4.1. Optimization Results
4.1.1. Optimization of Window Design Parameters
4.1.2. Trade-Off EUI and TCTR
4.2. Sensitivity Index Analysis
4.3. GPR Learning Validation
4.4. Practical Implications and Physical Applications
4.5. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EUI | Energy Use Intensity |
| TCTR | Thermal Comfort Time Ratio |
| WWR | Window-to-Wall Ratio |
| SHGC | Solar Heat Gain Coefficient |
| SC | Shading Coefficient |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| GPR | Gaussian Process Regression |
| TMY | Typical Meteorological Year |
| LEED | Leadership in Energy and Environmental Design |
| BREEAM | Establishment Environmental Assessment Method |
| IAQ | Indoor Air Quality |
| HVAC | Heating, Ventilation, and Air Conditioning |
| PCMs | Phase Change Materials |
| GB | Green Building |
| FAR | Floor Area Ratio |
| SVF | Sky View Factor |
| BD | Building Density |
| R2 | Coefficient of Determination |
| RMSE | Root Mean Square Error |
| LHS | Latin Hypercube Sampling |
References
- International Energy Agency (IEA). CO2 Emissions in 2022. IEA. Available online: https://www.iea.org/reports/co2-emissions-in-2022 (accessed on 23 September 2025).
- You, K.; Ren, H.; Cai, W.; Huang, R.; Li, Y. Modeling carbon emission trend in China’s building sector to year 2060. Resour. Conserv. Recycl. 2023, 188, 106679. [Google Scholar] [CrossRef]
- Wang, Y. Report on Smart Education in China. In Smart Education in China and Central & Eastern European Countries; Springer: Berlin/Heidelberg, Germany, 2023; pp. 11–50. [Google Scholar] [CrossRef]
- China Statistical Yearbook 2023; China Statistics Press: Beijing, China, 2023; Available online: https://www.chinayearbooks.com/china-statistical-yearbook-2023.html (accessed on 23 September 2025).
- Global Sustainable Buildings Guide. Green Certification. Baker McKenzie. 2023. Available online: https://resourcehub.bakermckenzie.com/en/resources/global-sustainable-buildings/asia-pacific/china/topics/green-certification (accessed on 23 September 2025).
- GB/T 50378-2019; Assessment Standard for Green Building. Ministry of Housing and Urban-Rural Development of PRC. State Administration for Market Regulation: Beijing, China, 2019. Available online: https://www.chinesestandard.net/PDF.aspx/GBT50378-2019 (accessed on 23 September 2025).
- GB 50189-2015; Design Standard for Energy Efficiency of Public Buildings. Ministry of Housing and Urban-Rural Development of PRC. State Administration for Market Regulation: Beijing, China, 2015. Available online: http://www.jianbiaoku.com/webarbs/book/73810/1628137.shtml (accessed on 23 September 2025).
- U.S. Green Building Council (USGBC). LEED v5 Reference Guide for Operations and Maintenance: April 2025 Launch Edition. U.S. Green Building Council. 2025. Available online: https://www.usgbc.org/resources/leed-v5-reference-guide-operations-and-maintenance-april-2025-launch-edition (accessed on 23 September 2025).
- BRE Global. BREEAM in-Use International Technical Manual: Commercial Buildings (v6.0.0, Chinese Edition). Building Research Establishment. 2021. Available online: https://www.bregroup.cn/wp-content/uploads/2021/08/BIU-International-Commercial-Technical-Manual_V6.0_CN.pdf (accessed on 23 September 2025).
- Guo, T.; Lin, Z.; Zhao, Y.; Fang, Z.; Fan, Y.; Zhang, X.; Yang, J.; Li, Y. Investigation and optimization of outdoor thermal comfort in elementary school campuses: Example from a humid-hot area in China. Build. Environ. 2024, 248, 111055. [Google Scholar] [CrossRef]
- Yan, H.; Liu, Q.; Zhao, W.; Pang, C.; Dong, M.; Zhang, H.; Gao, J.; Wang, H.; Hu, B.; Yang, L.; et al. The coupled effect of temperature, humidity, and air movement on human thermal response in hot-humid and hot-arid climates in summer in China. Build. Environ. 2020, 177, 106898. [Google Scholar] [CrossRef]
- López-Pérez, L.A.; Flores-Prieto, J.J.; Ríos-Rojas, C. Adaptive thermal comfort model for educational buildings in a hot-humid climate. Build. Environ. 2019, 150, 181–194. [Google Scholar] [CrossRef]
- Tejero-González, A.; Andrés-Chicote, M.; García-Ibáñez, P.; Velasco-Gómez, E.; Rey-Martínez, F.J. Assessing the applicability of passive cooling and heating techniques through climate factors: An overview. Renew. Sustain. Energy Rev. 2016, 65, 727–742. [Google Scholar] [CrossRef]
- Hwang, R.-L.; Liao, W.-J.; Chen, W.-A. Optimization of energy use and academic performance for educational environments in hot-humid climates. Build. Environ. 2022, 222, 109434. [Google Scholar] [CrossRef]
- Orlik-Koźdón, B. Effect of indoor climatic conditions on the risk of water vapor condensation and mould growth. J. Build. Eng. 2024, 95, 110198. [Google Scholar] [CrossRef]
- Song, Y.; Liao, C. Structural materials, ventilation design and architectural art of traditional buildings in Guangdong, China. Buildings 2022, 12, 900. [Google Scholar] [CrossRef]
- Lakhdari, K.; Sriti, L.; Painter, B. Parametric optimization of daylight, thermal and energy performance of middle school classrooms, case of hot and dry regions. Build. Environ. 2021, 204, 108173. [Google Scholar] [CrossRef]
- Da’abis, M.S. Green school buildings and environmental holistic elements approach to cope with hot and humid climate challenges—Bahrain case study. J. Sustain. Cities Built Environ. 2024, 2, 1–40. [Google Scholar] [CrossRef]
- Al-Saadi, A.; Al-Saadi, S.; Khan, H.; Al-Hashim, A.; Al-Khatri, H. Judicious design solutions for zero energy school buildings in hot climates. Sol. Energy 2023, 264, 112050. [Google Scholar] [CrossRef]
- Alghamdi, S.; Tang, W.; Kanjanabootra, S.; Alterman, D. Effect of architectural building design parameters on thermal comfort and energy consumption in higher education buildings. Buildings 2022, 12, 329. [Google Scholar] [CrossRef]
- Franco, A.; Bartoli, C.; Conti, P.; Miserocchi, L.; Testi, D. Multi-objective optimization of HVAC operation for balancing energy use and occupant comfort in educational buildings. Energies 2021, 14, 2847. [Google Scholar] [CrossRef]
- Akopov, A.S.; Beklaryan, L.A.; Saghatelyan, A.K. Agent-based modelling of interactions between air pollutants and greenery using a case study of Yerevan, Armenia. Environ. Model. Sofware 2019, 116, 7–25. [Google Scholar] [CrossRef]
- Akopov, A.S. An lmproved Parallel Biobjective Hybrid Real-Coded Genetic Algorithm withClustering-Based Selection. Cybern. Inf. Technol. 2024, 24, 32–49. [Google Scholar] [CrossRef]
- Hwang, R.-L.; Chen, B.-L.; Chen, W.-A. Analysis of incorporating a phase change material in a roof for the thermal management of school buildings in hot-humid climates. Buildings 2021, 11, 248. [Google Scholar] [CrossRef]
- Mba, E.J.; Sam-amobi, C.G.; Okeke, F.O. An assessment of orientation on effective natural ventilation for thermal comfort in primary school classrooms in Enugu City, Nigeria. Eur. J. Sustain. Dev. 2022, 11, 114. [Google Scholar] [CrossRef]
- Cherier, M.K.; Hamdani, M.; Kamel, E.; Guermoui, M.; Bekkouche, S.M.E.A.; Al-Saadi, S.; Djeffal, R.; Bashir, M.O.; Elshekh, A.E.A.; Drozdova, L.; et al. Impact of glazing type, window-to-wall ratio, and orientation on building energy savings quality: A parametric analysis in Algerian climatic conditions. Case Stud. Therm. Eng. 2024, 61, 104902. [Google Scholar] [CrossRef]
- Yi, L.; Xie, Y.; Lin, C. Thermal environment and energy performance of a typical classroom building in a hot-humid region: A case study in Guangzhou, China. Geofluids 2022, 2022, 3226001. [Google Scholar] [CrossRef]
- Soroshnia, E.; Rahnamayizekavat, P.; Rashidi, M.; Sadeghi, M.; Samali, B. Passive intelligent kinetic external dynamic shade design for improving indoor comfort and minimizing energy consumption. Buildings 2023, 13, 1090. [Google Scholar] [CrossRef]
- Lala, B.; Murtyas, S.; Hagishima, A. Indoor thermal comfort and adaptive thermal behaviors of students in primary schools located in the humid subtropical climate of India. Sustainability 2022, 14, 7072. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Z.; Ma, X.; Lu, W.; Li, D.; Kojima, S. Optimization analysis of the residential window-to-wall ratio based on numerical calculation of energy consumption in the hot-summer and cold-winter zone of China. Sustainability 2020, 12, 6138. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, G.; Yan, C.; Wang, G.; Jiang, Y.; Zhao, K. A two-stage multi-objective optimization method for envelope and energy generation systems of primary and secondary school teaching buildings in China. Build. Environ. 2021, 204, 108142. [Google Scholar] [CrossRef]
- Li, L.; Qi, Z.; Ma, Q.; Gao, W.; Wei, X. Evolving multi-objective optimization framework for early-stage building design: Improving energy efficiency, daylighting, view quality, and thermal comfort. Build. Simul. 2024, 17, 2097–2123. [Google Scholar] [CrossRef]
- Song, B.; Bai, L.; Yang, L. Analysis of the long-term effects of solar radiation on the indoor thermal comfort in office buildings. Energy 2022, 247, 123499. [Google Scholar] [CrossRef]
- Li, Y.; He, J. Evaluating the improvement effect of low-energy strategies on the summer indoor thermal environment and cooling energy consumption in a library building: A case study in a hot-humid and less-windy city of China. Build. Simul. 2021, 14, 1423–1437. [Google Scholar] [CrossRef]
- Mba, E.J.; Okeke, F.O.; Okoye, U. Effects of wall openings on effective natural ventilation for thermal comfort in classrooms of primary schools in Enugu metropolis, Nigeria. JP J. Heat Mass Transf. 2021, 22, 269–304. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, L.; Zhang, L.; Wu, X. Optimizing energy efficiency and thermal comfort in building green retrofit. Energy 2021, 237, 121509. [Google Scholar] [CrossRef]
- Vijayan, D.S.; Sivasuriyan, A.; Patchamuthu, P.; Revathy, j. Thermal performance of energy-efficient buildings for sustainable development. Environ. Sci. Pollut. Res. 2021, 29, 51130–51142. [Google Scholar] [CrossRef] [PubMed]
- U.S. Department of Energy. EnergyPlus; Version 9.6; U.S. Department of Energy: Washington, DC, USA, 2021; Available online: https://energyplus.net (accessed on 21 September 2025).
- Ladybug Tools. Honeybee; Version 1.5.0; Ladybug Tools: London, UK, 2021; Available online: https://www.ladybug.tools/honeybee.html (accessed on 21 September 2025).
- Robert McNeel & Associates. Rhinoceros; Version 8.0; Robert McNeel & Associates: Seattle, WA, USA, 2023; Available online: https://www.rhino3d.com (accessed on 21 September 2025).
- Robert McNeel & Associates. Grasshopper; Version 1.0; Robert McNeel & Associates: Seattle, WA, USA, 2021; Available online: https://www.rhino3d.com/docs/grasshopper/Transform/Rotate-3D (accessed on 21 September 2025).
- Wallacei LLC. Wallacei; Version 1.2; Wallacei LLC: London, UK, 2021; Available online: https://www.wallacei.com (accessed on 21 September 2025).
- Jun, H.; Fei, H. Research on multi-objective optimization of building energy efficiency based on energy consumption and thermal comfort. Build. Serv. Eng. Res. Technol. 2024, 45, 1–15. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, T. Multi-objective optimization of energy, visual, and thermal performance for building envelopes in China’s hot summer and cold winter climate zone. J. Build. Eng. 2022, 59, 105034. [Google Scholar] [CrossRef]
- Zheng, S.; Huang, G.; Zhou, X.; Zhu, X. Climate-change impacts on electricity demands at a metropolitan scale: A case study of Guangzhou, China. Appl. Energy 2020, 261, 114295. [Google Scholar] [CrossRef]
- Cheung, P.K.; Jim, C.Y. Improved assessment of outdoor thermal comfort: 1-hour acceptable temperature range. Build. Environ. 2019, 151, 303–317. [Google Scholar] [CrossRef]
- Riaz, H.; Arif, S.; Yousuf, S.; Bashir, M.N.; Ali, M.M.; Badruddin, I.A. Thermal comfort model for classrooms using occupant-centered approach. Case Stud. Therm. Eng. 2025, 73, 106589. [Google Scholar] [CrossRef]
- Sayadi, S.; Hayati, A.; Salmanzadeh, M. Optimization of Window-to-Wall Ratio for Buildings Located in Different Climates: An IDA-Indoor Climate and Energy Simulation Study. Energies 2021, 14, 1974. [Google Scholar] [CrossRef]
- Merrin, M.J.; Meghana, C.; B, V. Evaluating the efficacy of external shading devices on building energy consumption: A case study in hot climate. Therm. Sci. 2025, 80. [Google Scholar] [CrossRef]
- Zakaria, N.M.; Omar, M.A.; Mukhtar, A. Numerical study on the thermal insulation of smart windows embedded with low thermal conductivity materials to improve the energy efficiency of buildings. CFD Lett. 2023, 15, 41–52. [Google Scholar] [CrossRef]
- Bhatia, A.; Sangireddy, S.A.R.; Garg, V. An approach to calculate the equivalent solar heat gain coefficient of glass windows with fixed and dynamic shading in tropical climates. J. Build. Eng. 2019, 22, 90–100. [Google Scholar] [CrossRef]
- DBJ 15-51-2020; Announcement on the release of the Guangdong Provincial Standard for Energy-Efficient Design of Public Buildings. Guangdong Provincial Department of Housing and Urban-Rural Development: Guangzhou, China, 2020. Available online: https://zfcxjst.gd.gov.cn/attachment/0/480/480712/3096758.pdf (accessed on 23 September 2025).
- Chai, J.; Fan, J. Advanced thermal regulating materials and systems for energy saving and thermal comfort in buildings. Mater. Today Energy 2022, 24, 100925. [Google Scholar] [CrossRef]
- Alotaibi, B.S.; Khalifa, K.R.M.; Abuhussain, M.A.; Yahua, M.S.; Maghrabi, A.; Abba, S.I. Integrating renewable-based solar energy into sustainable and resilient urban furniture coupled with a logical multi-comparison study of Cyprus and Saudi Arabia. Processes 2023, 11, 2887. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, X.; Lei, S.; Luo, M. Energy and comfort performance of occupant-centric air conditioning strategy in office buildings with personal comfort devices. Build. Simul. 2022, 15, 899–911. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Rajasekar, E.; Natarajan, S. Multi-objective building design optimization under operational uncertainties using the NSGA II algorithm. Buildings 2020, 10, 88. [Google Scholar] [CrossRef]
- Brownlee, A.E.I.; Wright, J.A. Constrained, mixed-integer and multi-objective optimisation of building designs by NSGA-II with fitness approximation. Appl. Soft Comput. 2015, 33, 114–126. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Reiter, S. A performance comparison of sensitivity analysis methods for building energy models. Build. Simul. 2015, 8, 651–664. [Google Scholar] [CrossRef]
- Nouri, A.; van Treeck, C.; Frisch, J. Sensitivity assessment of building energy performance simulations using MARS meta-modeling in combination with Sobol’ method. Energies 2024, 17, 695. [Google Scholar] [CrossRef]
- Kristensen, M.H.; Petersen, S. Choosing the appropriate sensitivity analysis method for building energy model-based investigations. Energy Build. 2016, 130, 166–176. [Google Scholar] [CrossRef]
- Shen, Y. Load estimation models for the heat demand of buildings: Application of optimized Gaussian process regression. J. Appl. Sci. Eng. 2024, 28, 1–10. [Google Scholar] [CrossRef]
- Maiworm, M.; Limon, D.; Findeisen, R. Online learning-based model predictive control with Gaussian process models and stability guarantees. Int. J. Robust Nonlinear Control 2021, 31, 8785–8812. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Zhai, Y.; Wang, Y.; Huang, Y.; Meng, X. A Multi-Objective Optimization Methodology for Window Design Considering Energy Consumption, Thermal Environment, and Visual Performance. Renew. Energy 2019, 134, 1190–1199. [Google Scholar] [CrossRef]
- Wu, S.; Zhou, P.; Xiong, Y.; Ma, C.; Wu, D.; Lu, W. Strategies for driving the future of educational building design in terms of indoor thermal environments: A comprehensive review of methods and optimization. Buildings 2025, 15, 816. [Google Scholar] [CrossRef]
- Gao, B.; Zhu, X.; Ren, J.; Ran, J.; Kim, M.K.; Liu, J. Multi-objective optimization of energy-saving measures and operation parameters for a newly retrofitted building in future climate conditions: A case study of an office building in Chengdu. Energy Rep. 2023, 9, 2269–2285. [Google Scholar] [CrossRef]
- Li, W.; Zhang, J.; Zhao, T. Indoor thermal environment optimal control for thermal comfort and energy saving based on online monitoring of thermal sensation. Energy Build. 2019, 197, 57–67. [Google Scholar] [CrossRef]
- Mahiwal, S.G.; Bhoi, M.K.; Bhatt, N. Evaluation of energy use intensity (EUI) and energy cost of commercial building in India using BIM technology. Asian J. Civ. Eng. 2021, 22, 877–894. [Google Scholar] [CrossRef]
- Li, S.; Li, Y.; Wang, M.; Peng, J.; He, Y. Optimization study of photovoltaic direct-driven air conditioning system based on occupants’ behavior and thermal comfort. Renew. Energy 2025, 251, 123389. [Google Scholar] [CrossRef]
- Troup, L.; Phillips, R.; Eckelman, M.J.; Fannon, D. Effect of window-to-wall ratio on measured energy consumption in US office buildings. Energy Build. 2019, 203, 109434. [Google Scholar] [CrossRef]
- Mohamed Nor Izam, N.S.; Itam, Z.; Sing, W.L.; Syamsir, A. Sustainable development perspectives of solar energy technologies with focus on solar photovoltaic—A review. Energies 2022, 15, 2790. [Google Scholar] [CrossRef]
- Ganji Kheybari, A.; Gutai, M.; Mok, B.; Cavana, G. Thermal comfort of standard and advanced glazed building envelopes. Energy Build. 2025, 329, 115211. [Google Scholar] [CrossRef]
- Wang, C.; Yang, H.; Ji, J. Performance analysis of a PV/T shading device for enhancing energy saving and human comfort. Appl. Energy 2024, 376, 124248. [Google Scholar] [CrossRef]
- Sharma, S.K.; Mohapatra, S.; Sharma, R.C.; Alturjman, S.; Altirjman, C.; Mostarda, L.; Stephan, T. Retrofitting Existing Buildings to Improve Energy Performance. Sustainability 2022, 14, 666. [Google Scholar] [CrossRef]
- Wang, X.; Li, W.; Luo, Z.; Wang, K.; Shah, S.P. A critical review on phase change materials (PCM) for sustainable and energy efficient building: Design, characteristics, performance and application. Energy Build. 2022, 260, 111923. [Google Scholar] [CrossRef]
- Seyedzadeh, S.; Pour Rahimian, F.; Glesk, I.; Roper, M. Machine learning for estimation of building energy consumption and performance: A review. Vis. Eng. 2018, 6, 5. [Google Scholar] [CrossRef]
- Kalmár, F.; Kalmár, T. Thermal Comfort Aspects of Solar Gains during the Heating Season. Energies 2020, 13, 1702. [Google Scholar] [CrossRef]
- Alhuwayil, W.K.; Mujeebu, M.A.; Algarny, A.M.M. Impact of external shading strategy on energy performance of multi-story hotel building in hot-humid climate. Energy 2019, 169, 1166–1174. [Google Scholar] [CrossRef]
- Tan, X.Y.; Mahyuddin, N.; Kamaruzzaman, S.N.; Mat Wajid, N.; Abidin, A.M.Z. Investigation into energy performance of a multi-building complex in a hot and humid climate: Efficacy of energy saving measures. Open House Int. 2024, 49, 489–513. [Google Scholar] [CrossRef]
- Mazzetto, S. Dynamic Integration of Shading and Ventilation: Novel Quantitative Insights into Building Performance Optimization. Buildings 2025, 15, 1123. [Google Scholar] [CrossRef]
- Chiesa, G.; Acquaviva, A.; Grosso, M.; Bottaccioli, L.; Floridia, M.; Pristeri, E.; Sanna, E.M. Parametric Optimization of Window-to-Wall Ratio for Passive Buildings Adopting a Scripting Methodology to Dynamic-Energy Simulation. Sustainability 2019, 11, 3078. [Google Scholar] [CrossRef]
- Chandrasekaran, C.; Sasidhar, K.; Madhumathi, A. Energy-efficient retrofitting with exterior shading device in hot and humid climate—Case studies from fully glazed multi-storied office buildings in Chennai, India. J. Asian Architect. Build. Eng. 2022, 22, 2209–2223. [Google Scholar] [CrossRef]
- GB 50033-2013; Standard for Daylighting Design of Buildings. China Architecture & Building Press: Beijing, China, 2013. Available online: http://www.jianbiaoku.com/webarbs/book/50/2440035.shtml (accessed on 23 September 2025).
- Enteria, N.; Yoshino, H. Energy-efficient and renewable energy-supported buildings in hot and humid regions. In Building in Hot and Humid Regions; Enteria, N., Awbi, H., Santamouris, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 185–203. [Google Scholar]
- Lee, Y.-J.; Kim, S.-H.; Ryu, J.-H.; Lee, K.-H. Optimizing window glass design for energy efficiency in South Korean office buildings: A hierarchical analysis using energy simulation. Buildings 2023, 13, 2850. [Google Scholar] [CrossRef]
- Lee, S.-J.; Song, S.-Y. Energy efficiency, visual comfort, and thermal comfort of suspended particle device smart windows in a residential building: A full-scale experimental study. Energy Build. 2023, 298, 113514. [Google Scholar] [CrossRef]
- Khalaf, M.; Ashrafian, T.; Demirci, C. Energy efficiency evaluation of different glazing and shading systems in a school building. E3S Web Conf. 2019, 111, 03052. [Google Scholar] [CrossRef]
- GB 50099-2011; Code for Design of School. China Architecture & Building Press: Beijing, China, 2012. Available online: http://www.jianbiaoku.com/webarbs/book/414/2559815.shtml (accessed on 21 September 2025).
- da Silva, F.; Veras, J.C.G. A design framework for a kinetic shading device system for building envelopes. Front. Archit. Res. 2023, 12, 837–854. [Google Scholar] [CrossRef]
- GB/T 50785-2012; Standardization Administration of the People’s Republic of China. Evaluation Standard for Indoor Thermal Environment in Civil Buildings. China National Standardization Management Committee: Beijing, China, 2012. Available online: https://www.chinesestandard.net/PDF.aspx/GBT50785-2012 (accessed on 23 September 2025).
- Yang, B.; Olofsson, T.; Wang, F.; Lu, W. Thermal Comfort in Primary School Classrooms: A Case Study under Subarctic Climate Area of Sweden. Build. Environ. 2018, 135, 237–245. [Google Scholar] [CrossRef]
- GB 50666-2011; Code for Construction of Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. China Architecture & Building Press: Beijing, China, 2011. Available online: https://www.chinesestandard.net/PDF.aspx/GB50666-2011 (accessed on 23 September 2025).
- Yue, N.; Li, L.; Morandi, A.; Zhao, Y. A metamodel-based multi-objective optimization method to balance thermal comfort and energy efficiency in a campus gymnasium. Energy Build. 2021, 253, 111513. [Google Scholar] [CrossRef]
- Heydari, A.; Sadati, S.E.; Gharib, M.R. Effects of different window configurations on energy consumption in building: Optimization and economic analysis. J. Build. Eng. 2021, 35, 102099. [Google Scholar] [CrossRef]
- Petersen, S.; Kristensen, M.H.; Knudsen, M.D. Prerequisites for Reliable Sensitivity Analysis of a High Fidelity Building Energy Model. Energy Build. 2019, 183, 1–16. [Google Scholar] [CrossRef]
- Liu, S.-Y.; How, J.P. Gaussian Processes for Learning and Control: A Tutorial with Examples. IEEE Control Syst. Mag. 2018, 38, 33–50. [Google Scholar] [CrossRef]
- Wang, H.; Liang, Q.; Hancock, J.T.; Khoshgoftaar, T.M. Feature selection strategies: A comparative analysis of SHAP-value and importance-based methods. J. Big Data 2024, 11, 44. [Google Scholar] [CrossRef]
- Triana, M.A.; De Vecchi, R.; Lamberts, R. Building Design for Hot and Humid Climate in a Changing World. In Building in Hot and Humid Regions: Historical Perspective and Technological Advances; Enteria, N., Awbi, H., Santamouris, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 59–73. [Google Scholar]
- Zeng, A.; Ho, H.; Yu, Y. Prediction of Building Electricity Usage Using Gaussian Process Regression. J. Build. Eng. 2020, 28, 101054. [Google Scholar] [CrossRef]
- Abdul Rahman, M.A.; Khalid, H.L.; Yusup, Y. Optimizing wind power for energy-efficient building design in tropical hot-humid climates of Malaysia. J. Sustain. Dev. 2011, 4, 217–230. [Google Scholar] [CrossRef]
- Kadi, B. Design Strategies for Energy-Efficient and Climate-Responsive Building: Case of Hot Humid Climate’s Library Building. In Proceedings of the Conference on Design Strategies for Energy Efficient and Climate Responsive Building, Istanbul, Turkey, August 2021; Available online: https://www.researchgate.net/publication/353760799 (accessed on 23 September 2025).
- Ye, Z.; Li, L.; Cao, W.; Wang, J.; Zhao, L.; Pang, Y.; Li, H.; Wan, F.; Huang, M. Hygrothermal response capacity prediction of traditional buildings in hot-humid regions of China under future climate change. J. Build. Eng. 2025, 107, 112733. [Google Scholar] [CrossRef]




| Constraint Name | Value Range/Requirement | Explanation | Reference |
|---|---|---|---|
| Window-to-Wall Ratio (WWR) | 0.10–0.50 | Ensure compliance with national and local building codes for educational buildings. | GB 50189-2015 [7]; Chiesa et al., 2019 [81] |
| Shading Coefficient (SC) | 0.20–0.80 | Range covers typical external shading devices suitable for hot-humid climates. | Chandrasekaran 2022 [82]; GB 50033-2013 [83] |
| Heat Transfer Coefficient (K) | 1.0–2.5 W/(m2·K) | Follows requirements of the “Design Standard for Energy Efficiency of Public Buildings.” | GB 50189-2015 [7]; Enteria et al., 2022 [84] |
| Solar Heat Gain Coefficient (SHGC) | 0.10–0.40 | Matches glazing options recommended for minimizing cooling loads in subtropical schools. | Lee, Y.-J et al., 2023 [85]; Lee, S.-J et al., 2019 [86] |
| Shading Width | 0.3–2.0 m | Conforms to feasible engineering practice and construction guidelines for sun shading elements. | Khalaf et al., 2019 [87]; GB 50096-2011 [88] |
| Shading Angle | 0°–90° | Reflects adjustable range for horizontal external shading based on climate-responsive design principles. | da Silva et al., 2023 [89]; GB 50033-2013 [83] |
| Thermal Comfort (TC) | ≥50% | Ensures compliance with recommended standards for indoor environmental quality in classrooms. | GB/T 50785-2012 [90]; Yang et al., 2018 [91] |
| Constructability | Must use standard materials/processes | Requires all window and shading systems to be easily constructed and maintainable in the local context. | GB 50666-2011 [92]; Enteria et al., 2019 [84] |
| Parameter | Instrument | Model | Measurement Range | Accuracy | Placement | Sampling Interval |
|---|---|---|---|---|---|---|
| Air Temperature | HOBO Data Logger | U12013 | −20 °C to 70 °C | ±0.35 °C (0–50 °C) | Near window, 1.1 m above floor | Every 5 min |
| Relative Humidity | HOBO Data Logger | U12013 | 5–95% RH | ±2.5% (10–90% RH typical) | Near window, 1.1 m above floor | Every 5 min |
| Outdoor Climate Data | China Meteorological Admin | TMY dataset | Regional typical values | — | Local weather station | Hourly |
| Parameter | Observed Pareto Range (Min–Max) | Recommended (IQR, 25–75%)—Practical Target | Short Note |
|---|---|---|---|
| WWR | 0.1–0.5 | 20–42% | Balance daylight and cooling load |
| SC | 0.20–0.90 | 0.20–0.40 | Lower SC reduces solar gain |
| K | 1.0–2.5 | 1.1–1.4 | Aim for improved glazing/frame assembly |
| SHGC | 0.10–0.40 | 0.10–0.40 | Use combined SHGC × shading factor when checking |
| Shading Width | 0.3–2.0 m | 1.2–1.5 m | Horizontal projection of external shade |
| Shading Angle | 0°–90° | 28°–38° | Angle relative to horizontal; optimizes seasonal protection |
| Solution | WWR | SC | SHGC | K (W·m−2·K−1) | Shading Width (m) | Shading Angle (°) |
|---|---|---|---|---|---|---|
| Lowest-EUI (energy-priority) | 0.2 | 0.40 | 0.10 | 1.1 | 1.04 | 27° |
| Highest-TCTR (comfort-priority) | 0.42 | 0.40 | 0.40 | 1.4 | 1.5 | 18° |
| Balanced (recommended compromise) | 0.40 | 0.30 | 0.40 | 1.2 | 1.22 | 28° |
| Metric | EUI (R2) | TCTR (R2) | EUI (RMSE) | TCTR (RMSE) |
|---|---|---|---|---|
| Training Set | 0.91 | 0.95 | 4.5 | 2.3 |
| Test Set | 0.89 | 0.94 | 5.1 | 2.7 |
| Solution Type | EUI (kWh/m2·year) | Thermal Comfort Time Ratio TCTR (%) | Energy Saving (%) | Comfort Improvement (%) |
|---|---|---|---|---|
| Lowest EUI Solution | 73.03 | 51.83 | 28.1 | 1.4 |
| Highest Comfort Solution | 118.84 | 63.21 | −17.0 | 23.7 |
| Balanced Solution | 94.75 | 58.44 | 6.7 | 14.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, T.; Ali, A.S.; Mahyuddin, N. Multi-Objective Optimization of Window Design for Energy and Thermal Comfort in School Buildings: A Sustainable Approach for Hot-Humid Climates. Sustainability 2025, 17, 8646. https://doi.org/10.3390/su17198646
Xia T, Ali AS, Mahyuddin N. Multi-Objective Optimization of Window Design for Energy and Thermal Comfort in School Buildings: A Sustainable Approach for Hot-Humid Climates. Sustainability. 2025; 17(19):8646. https://doi.org/10.3390/su17198646
Chicago/Turabian StyleXia, Tian, Azlan Shah Ali, and Norhayati Mahyuddin. 2025. "Multi-Objective Optimization of Window Design for Energy and Thermal Comfort in School Buildings: A Sustainable Approach for Hot-Humid Climates" Sustainability 17, no. 19: 8646. https://doi.org/10.3390/su17198646
APA StyleXia, T., Ali, A. S., & Mahyuddin, N. (2025). Multi-Objective Optimization of Window Design for Energy and Thermal Comfort in School Buildings: A Sustainable Approach for Hot-Humid Climates. Sustainability, 17(19), 8646. https://doi.org/10.3390/su17198646






