Drought Propagation and Risk Assessment in the Naoli River Basin Based on the SWAT-PLUS Model and Copula Functions
Abstract
1. Introduction
2. Study Area and Data Sources
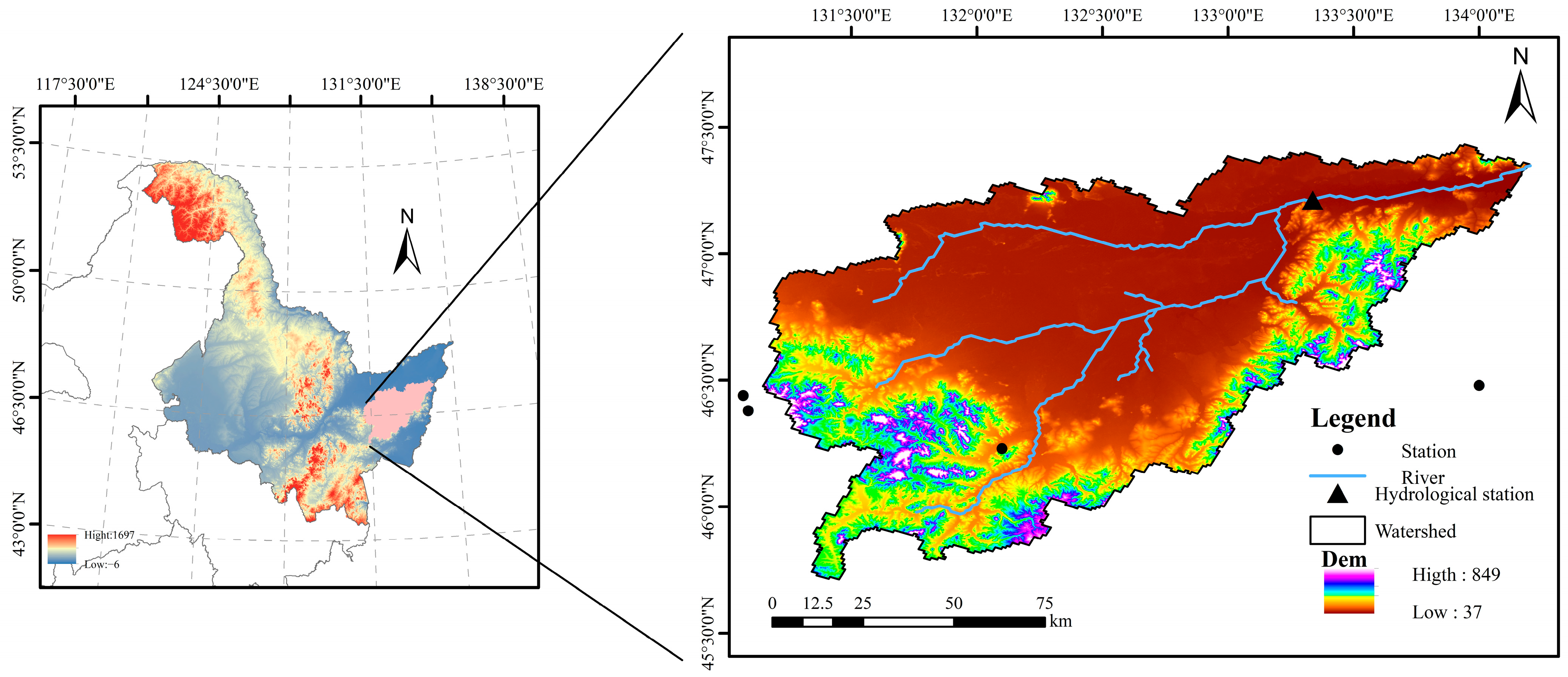
2.1. Overview of the Study Area
2.2. Data Source: Pre-Processing
3. Research Methods
3.1. SWAT Hydrological Model
3.2. Selection of CMIP6 Climate Models
3.3. PLUS Model
3.4. Multidimensional Drought and Travel Time Theory
3.4.1. Hydrological, Meteorological, and Agricultural Drought
3.4.2. Travel Time Theory
3.5. Copula Theory
3.5.1. Two-Dimensional Copula
3.5.2. C-Vine Copula Function
3.5.3. Evaluation Indicators and Joint Occurrence Probability
3.6. Lagged Correlation
3.7. Bayesian Network Probability Model
4. Results Analysis
4.1. SWAT Model Runoff Simulation and CMIP6 Global Climate Model Evaluation
4.1.1. SWAT Model Runoff Simulation Evaluation
4.1.2. CMIP6 Climate Model Assessment
4.2. Single-Variable Drought Characteristics of the Rao River Basin
4.3. Plus Land Use Simulation and Evaluation
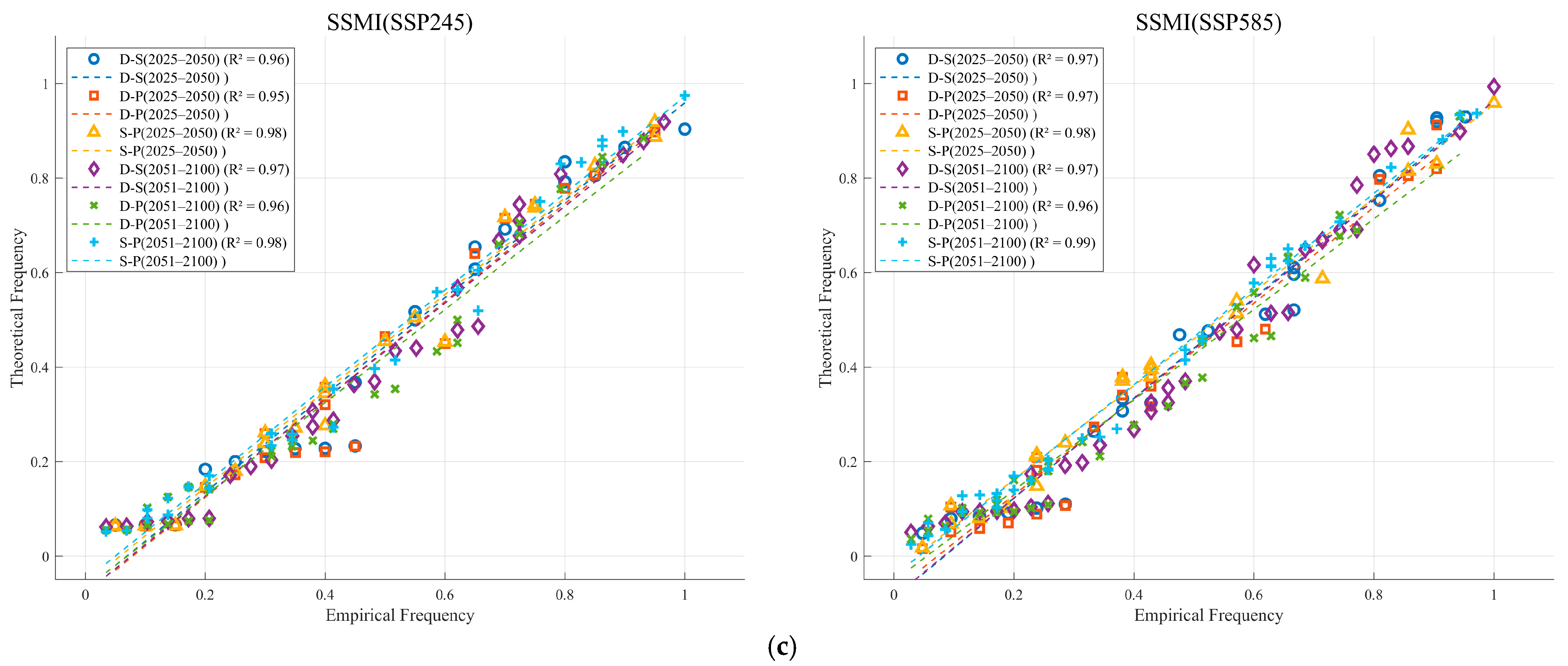
4.4. Marginal Distributions of Different Drought Characteristic Variables
4.5. Copula Functions for Multidimensional Drought Characteristic Variables
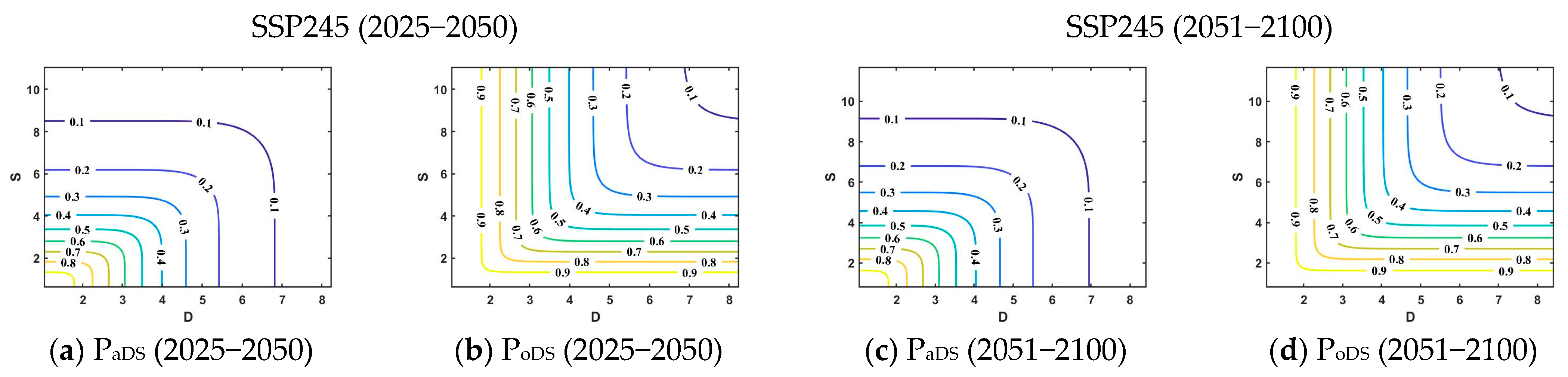
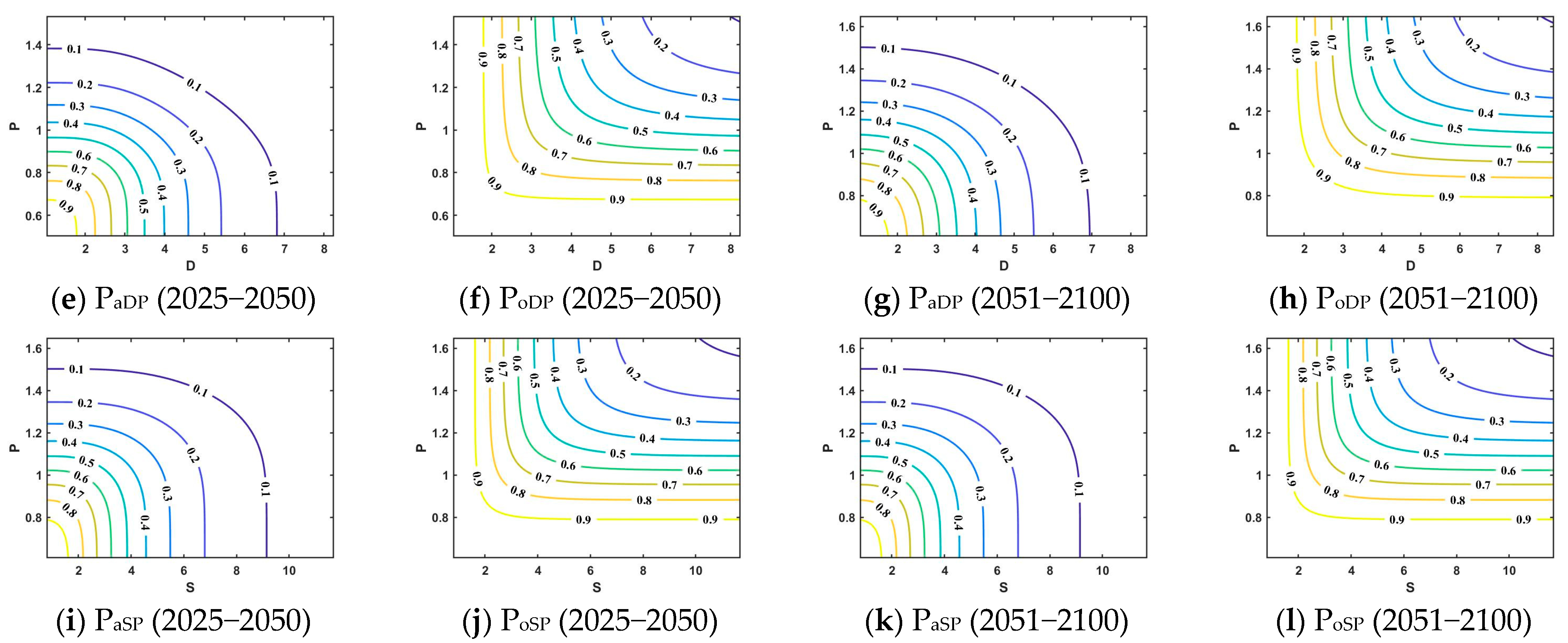
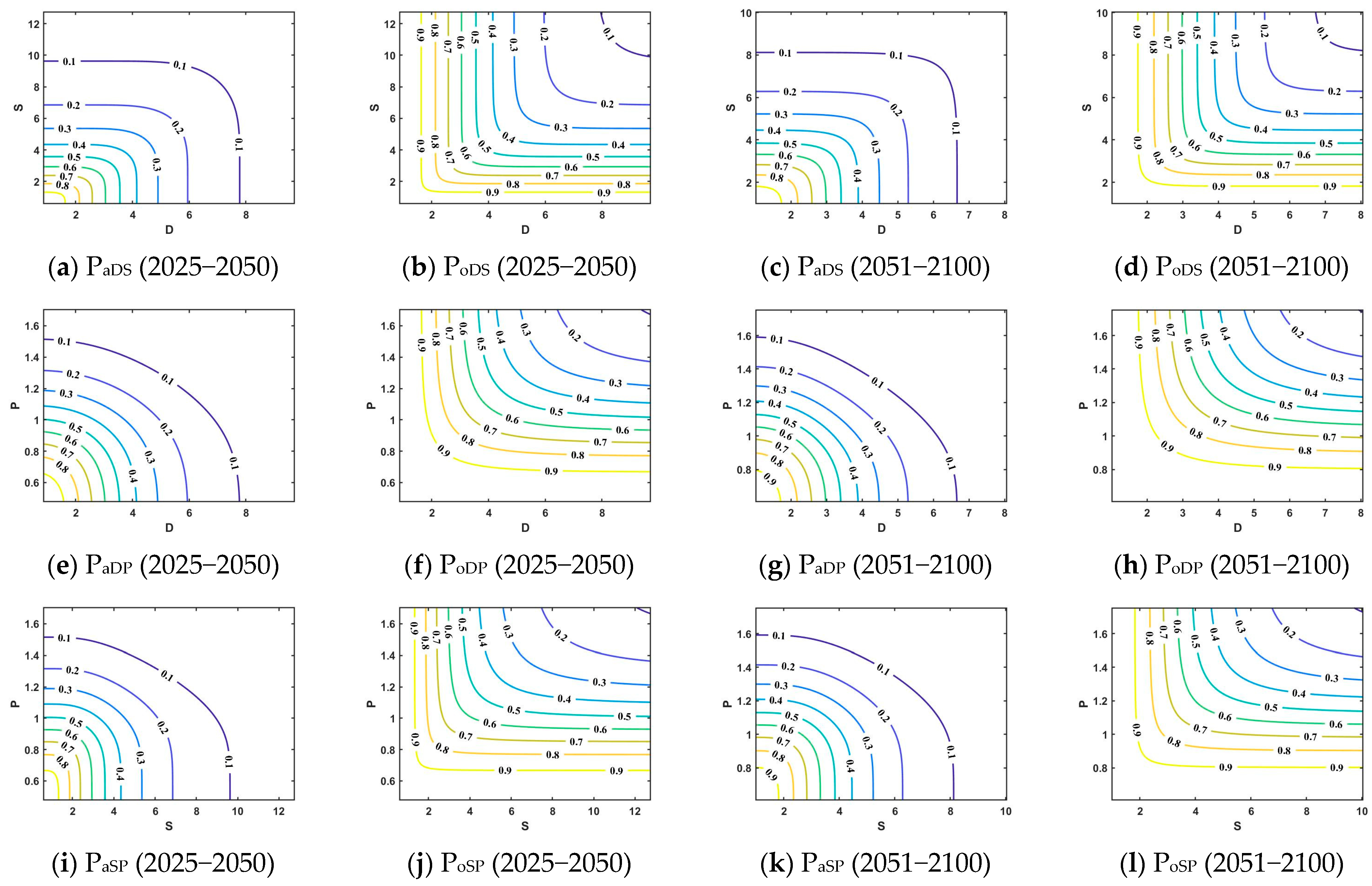
4.6. Probability of Joint Occurrence of Drought Under Different Combinations of Characteristic Variables
4.6.1. Two-Dimensional Probability of Joint Occurrence of Drought
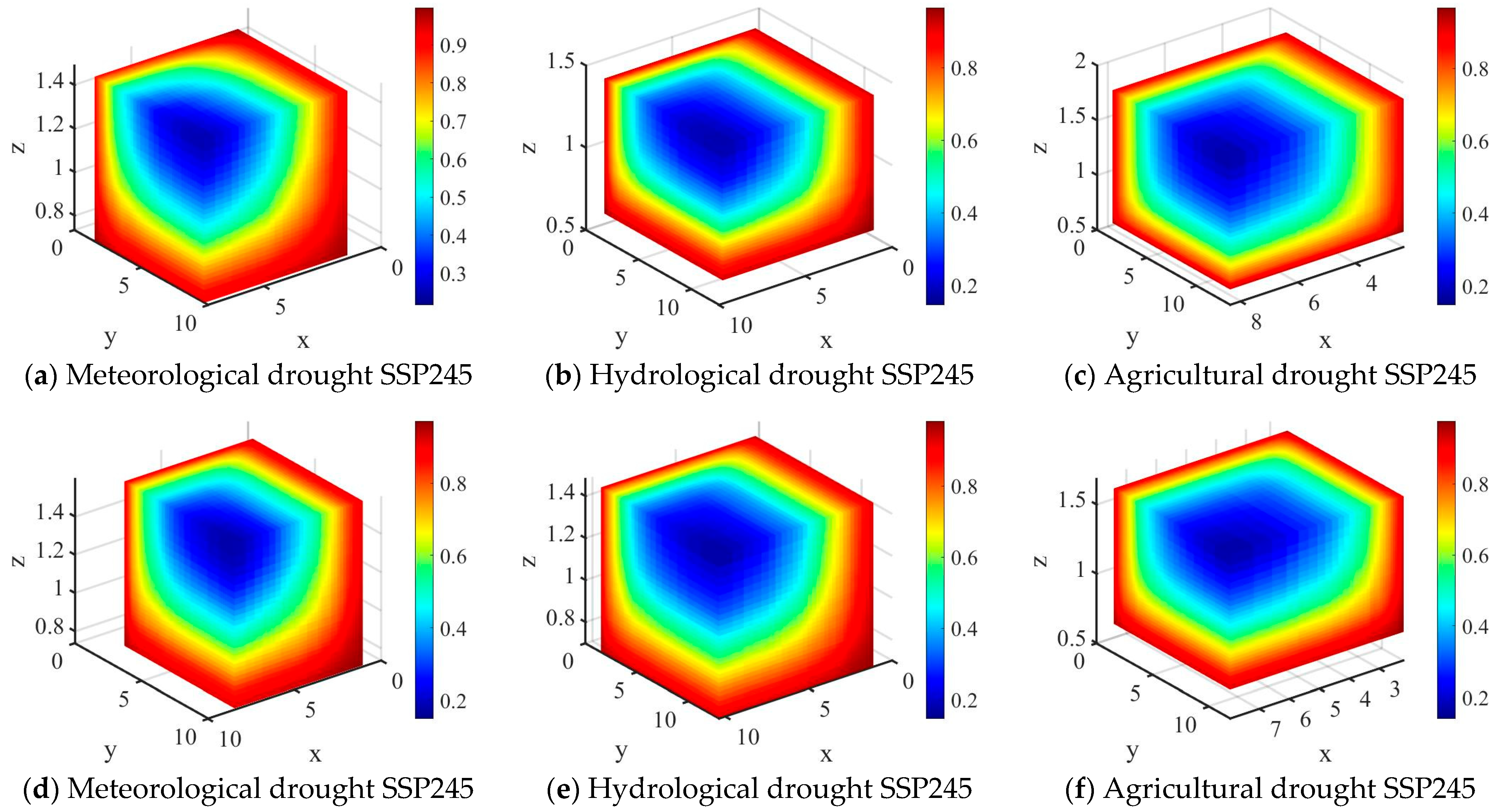
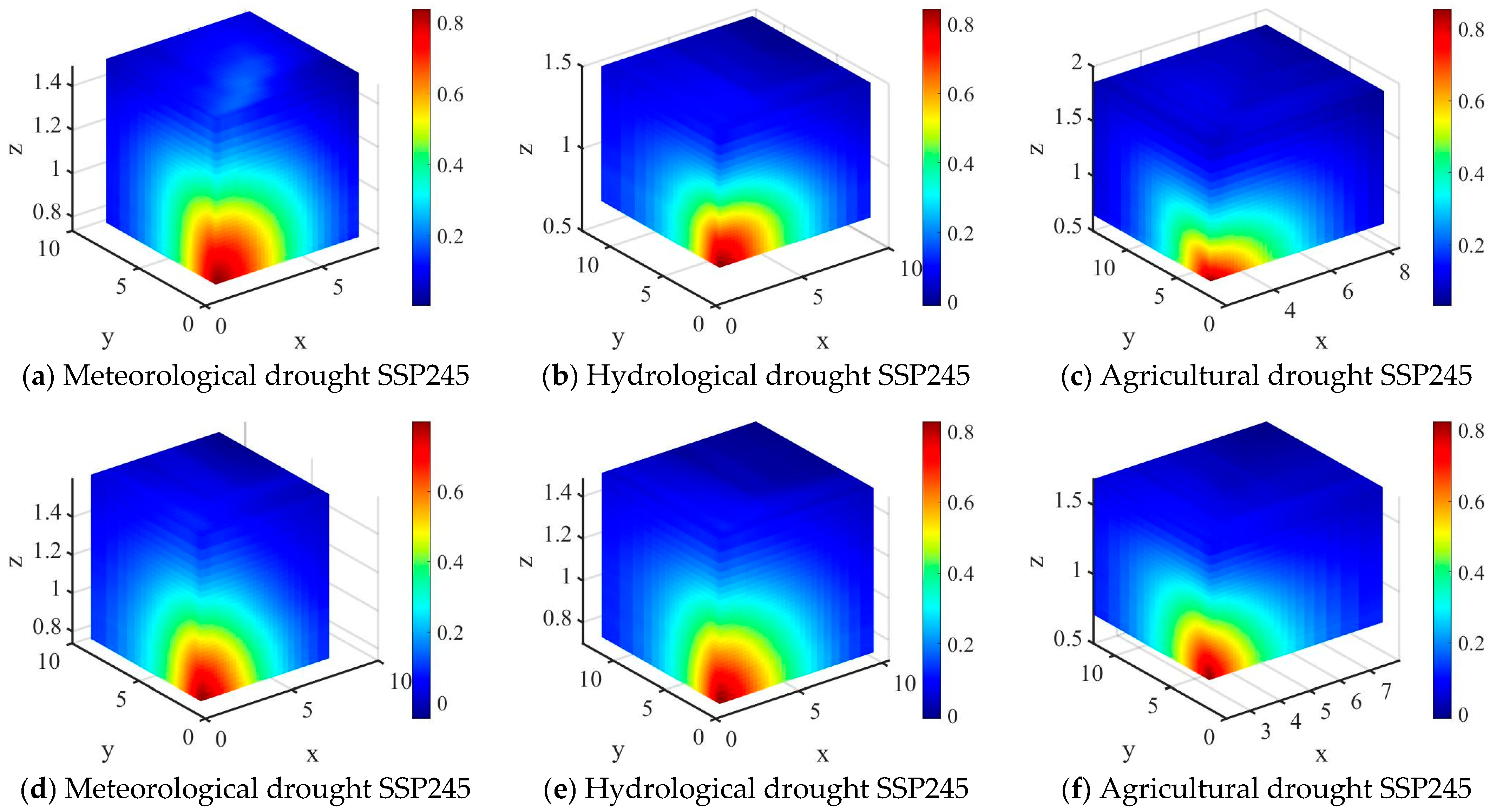
4.6.2. Probability of Simultaneous Occurrence of Three-Dimensional Drought
4.6.3. Time and Threshold for the Transition of Meteorological Drought to Hydrological and Agricultural Drought
4.6.4. Transmission Risks from Meteorological Drought to Hydrological Drought and Agricultural Drought
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, H.; Wang, L.; Zhang, J.; Chen, Y. A Global Drought-Aridity Index: The Spatiotemporal Standardized Precipitation Evapotranspiration Index. Ecol. Indic. 2023, 153, 110484. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, S.; Huang, Q.; Leng, G.; Fang, W.; Wang, L.; Wang, H. Propagation Thresholds of Meteorological Drought for Triggering Hydrological Drought at Various Levels. Sci. Total Environ. 2020, 712, 136502. [Google Scholar] [CrossRef]
- DeGuzman, K.; Knappenberger, T.; Brantley, E.; Olshansky, Y. Estimating Runoff Probability from Precipitation Data: A Binomial Regression Analysis. Hydrol. Process. 2023, 37, e15029. [Google Scholar] [CrossRef]
- Wu, Q.; Xie, T.; Liu, C.; Li, W.; Zhang, L.; Ran, G.; Xu, Y.; Tang, Y.; Han, Z.; Hu, C. Improving the Understanding of Rainfall-Runoff Processes: Temporal Dynamic of Event Runoff Response in Loess Plateau, China. J. Environ. Manag. 2025, 375, 123436. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, L.; Lv, X.; Yu, H.; Li, G. Changes in Stream Peak Flow and Regulation in Naoli River Watershed as a Result of Wetland Loss. Sci. World J. 2014, 2014, 209547. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, X.; Yonghe, S.; Zhike, C.; Wu, H.; Zhao, Y. Hydrological Evolution of Wetland in Naoli River Basin and its Driving Mechanism. Water Resour. Manag. 2012, 26, 1455–1475. [Google Scholar] [CrossRef]
- Xinqiang, D.; Kaiyang, C.; Xiangqin, L. Characteristics and Causes of Groundwater Dynamic Changes in Naoli River Plain, Northeast China. Water Supply 2020, 20, 2603–2615. [Google Scholar] [CrossRef]
- Bai, X.; Wang, B.; Qi, Y. The Effect of Returning Farmland to Grassland and Coniferous Forest on Watershed Runoff—A Case Study of the Naoli River Basin in Heilongjiang Province, China. Sustainability 2021, 13, 6264. [Google Scholar] [CrossRef]
- Possega, M.; García-Valdecasas Ojeda, M.; Gámiz-Fortis, S.R. Multi-Scale Analysis of Agricultural Drought Propagation on the Iberian Peninsula Using Non-Parametric Indices. Water 2023, 15, 2032. [Google Scholar] [CrossRef]
- Ojeda, M.G.-V.; Gámiz-Fortis, S.R.; Romero-Jiménez, E.; Rosa-Cánovas, J.J.; Yeste, P.; Castro-Díez, Y.; Esteban-Parra, M.J. Projected Changes in the Iberian Peninsula Drought Characteristics. Sci. Total Environ. 2021, 757, 143702. [Google Scholar] [CrossRef] [PubMed]
- Xiong, H.; Han, J.; Yang, Y. Propagation from Meteorological to Hydrological Drought: Characteristics and Influencing Factors. Water Resour. Res. 2025, 61, e2024WR037765. [Google Scholar] [CrossRef]
- Hanadé Houmma, I.; Hadri, A.; Boudhar, A.; El Khalki, E.M.; Oussaoui, S.; Karaoui, I.; El Midaoui, A.; Kinnard, C. Temporal Relationships Between Agricultural and Meteorological Drought over the Oum Er Rbia River, Morrocco. Big Earth Data 2025, 1–36. [Google Scholar] [CrossRef]
- Zhou, J.; Li, Q.; Wang, L.; Lei, L.; Huang, M.; Xiang, J.; Feng, W.; Zhao, Y.; Xue, D.; Liu, C. Impact of Climate Change and Land-use on the Propagation from Meteorological Drought to Hydrological Drought in the Eastern Qilian Mountains. Water 2019, 11, 1602. [Google Scholar] [CrossRef]
- Mello, C.R.; Guzman, J.A.; Vieira, N.P.; Viola, M.R.; Beskow, S.; Guo, L.; Alvarenga, L.A.; Rodrigues, A.F. Mitigating Severe Hydrological Droughts in the Brazilian Tropical High-Land Region: A Novel Land Use Strategy Under Climate Change. Int. Soil Water Conserv. Res. 2025, 13, 627–643. [Google Scholar] [CrossRef]
- Jiang, J.; Wang, Z.; Lai, C.; Wu, X.; Chen, X. Climate and Landuse Change Enhance Spatio-Temporal Variability of Dongjiang River Flow and Ammonia Nitrogen. Sci. Total Environ. 2023, 867, 161483. [Google Scholar] [CrossRef]
- Guédé, K.G.; Yu, Z.; Simonovic, S.P.; Gu, H.; Emani, G.F.; Badji, O.; Chen, X.; Sika, B.; Adiaffi, B. Combined Effect of Landuse/Landcover and Climate Change Projection on the Spatiotemporal Streamflow Response in Cryosphere Catchment in the Tibetan Plateau. J. Environ. Manag. 2025, 376, 124353. [Google Scholar] [CrossRef] [PubMed]
- Lv, K.; Si, Z.; Ren, W.; Zhao, Z. Exploring Ecosystem Services Dynamics and Interactions Under Future Climate Change: A Case Study of the City Cluster in the Middle Reaches of the Yangtze River. Ecol. Front. 2025, 45, 719–739. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, J.; Jiang, X. Spatial and Temporal Changes of Ecosystem Service Value and Its Influencing Mechanism in the Yangtze River Delta Urban Agglomeration. Sci. Rep. 2024, 14, 19476. [Google Scholar] [CrossRef]
- Zhou, H.; Tang, M.; Huang, J.; Mei, X.; Zhao, H. Driving Mechanisms and Multi-Scenario Simulation of Land Use Change Based on National Land Survey Data: A Case in Jianghan Plain, China. Front. Environ. Sci. 2024, 12, 1422987. [Google Scholar] [CrossRef]
- Liu, J.; Liu, B.; Wu, L.; Miao, H.; Liu, J.; Jiang, K.; Ding, H.; Gao, W.; Liu, T. Prediction of Land Use for the Next 30 Years Using the PLUS Model’s Multi-Scenario Simulation in Guizhou Province, China. Sci. Rep. 2024, 14, 13143. [Google Scholar] [CrossRef] [PubMed]
- Poonia, V.; Jha, S.; Goyal, M.K. Copula Based Analysis of Meteorological, Hydrological and Agricultural Drought Characteristics Across Indian River Basins. Int. J. Climatol. 2021, 41, 4637–4652. [Google Scholar] [CrossRef]
- Wei, H.; Liu, X.; Hua, W.; Zhang, W.; Ji, C.; Han, S. Copula-Based Joint Drought Index Using Precipitation, NDVI, and Runoff and Its Application in the Yangtze River Basin, China. Remote Sens. 2023, 15, 4484. [Google Scholar] [CrossRef]
- Tulungen, C.; Pradhanang, S.M. Assessment of Climate Change Effects of Drought Conditions Using the Soil and Water Assessment Tool. Agriculture 2024, 14, 233. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, B.; Li Liu, D.; Zhang, M.; Leslie, L.M.; Yu, Q. Using an Improved SWAT Model to Simulate Hydrological Responses to Land Use Change: A Case Study of a Catchment in Tropical Australia. J. Hydrol. 2020, 585, 124822. [Google Scholar] [CrossRef]
- Jin, L.; Xue, H.; Dong, G.; Han, Y.; Li, Z.; Lian, Y. Coupling the Remote Sensing Data-Enhanced SWAT Model with the Bidirectional Long Short-Term Memory Model to Improve Daily Streamflow Simulations. J. Hydrol. 2024, 634, 131117. [Google Scholar] [CrossRef]
- Golmohammadi, G.; Prasher, S.; Madani, A.; Rudra, R. Evaluating Three Hydrological Distributed Watershed Models: MIKE-SHE, APEX, SWAT. Hydrology 2014, 1, 20–39. [Google Scholar] [CrossRef]
- Tan, M.L.; Gassman, P.W.; Yang, X.; Haywood, J. A Review of SWAT Applications, Performance and Future Needs for Simulation of Hydro-Climatic Extremes. Adv. Water Resour. 2020, 143, 103662. [Google Scholar] [CrossRef]
- Keller, A.A.; Garner, K.; Rao, N.; Knipping, E.; Thomas, J. Hydrological Models for Climate-Based Assessments at the Watershed Scale: A Critical Review of Existing Hydrologic and Water Quality Models. Sci. Total Environ. 2023, 867, 161209. [Google Scholar] [CrossRef] [PubMed]
- Keleş Özgenç, E. Evaluation Using the SWAT Model of the Effects of Land Use Land Cover Changes on Hydrological Processes in the Gala Lake Basin, Turkey. Environ. Qual. Manag. 2024, 34, e22238. [Google Scholar] [CrossRef]
- Chi, G.; Zhu, B.; Huang, B.; Chen, X.; Shi, Y. Spatiotemporal Dynamics in Soil Iron Affected by Wetland Conversion on the Sanjiang Plain. Land Degrad. Dev. 2021, 32, 4669–4679. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, M.; Li, L.; Yin, R.; Huo, L. Holocene Terrestrialization Process on the Sanjiang Plain (China) and its Significance to the East Asian Summer Monsoon Circulation. Sci. Total Environ. 2022, 806, 150578. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Zhang, Z.; Fu, Z.; Xiong, S.; Chen, H.; Zhang, W.; Wang, S.; Zhang, D.; Lu, H.; Jiang, X. Impacts of Climatic Fluctuations and Vegetation Greening on Regional hydrological Processes: A Case Study in the Xiaoxinganling Mountains–Sanjiang Plain region, Northeastern China. Remote Sens. 2024, 16, 2709. [Google Scholar] [CrossRef]
- Luo, C.; Fu, X.; Zeng, X.; Cao, H.; Wang, J.; Ni, H.; Qu, Y.; Liu, Y. Responses of Remnant Wetlands in the Sanjiang Plain to Farming-Landscape Patterns. Ecol. Indic. 2022, 135, 108542. [Google Scholar] [CrossRef]
- Wu, Y.; Xu, N.; Wang, H.; Li, J.; Zhong, H.; Dong, H.; Zeng, Z.; Zong, C. Variations in the Diversity of the Soil Microbial Community and Structure Under Various Categories of Degraded Wetland in Sanjiang Plain, Northeastern China. Land Degrad. Dev. 2021, 32, 2143–2156. [Google Scholar] [CrossRef]
- Zhang, L.; Nan, Z.; Yu, W.; Ge, Y. Modeling Land-Use and Land-Cover Change and Hydrological Responses Under Consistent Climate Change Scenarios in the Heihe River Basin, China. Water Resour. Manag. 2015, 29, 4701–4717. [Google Scholar] [CrossRef]
- Liu, T.; Si, Z.; Liu, Y.; Wang, L.; Zhao, Y.; Wang, J. Runoff and Drought Responses to Land Use Change and CMIP6 Climate Projections. Water 2025, 17, 1696. [Google Scholar] [CrossRef]
- Long, S.; Gao, J.; Shao, H.; Wang, L.; Zhang, X.; Gao, Z. Developing SWAT-S to Strengthen the Soil Erosion Forecasting Performance of the SWAT Model. Land Degrad. Dev. 2024, 35, 280–295. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, Y.; Hou, J. Soil and Water Assessment Tool (SWAT)-Informed Deep Learning for Streamflow Forecasting with Remote Sensing and in Situ Precipitation and Discharge Observations. Remote Sens. 2024, 16, 3999. [Google Scholar] [CrossRef]
- Melaku, N.D.; Brown, C.W.; Tavakoly, A.A. Improving Process-Based Prediction of Stream Water Temperature in SWAT Using Semi-Lagrangian Formulation. J. Hydrol. 2025, 651, 132612. [Google Scholar] [CrossRef]
- Wang, Z.; He, Y.; Li, W.; Chen, X.; Yang, P.; Bai, X. A Generalized Reservoir Module for SWAT Applications in Watersheds Regulated by Reservoirs. J. Hydrol. 2023, 616, 128770. [Google Scholar] [CrossRef]
- Valencia, S.; Villegas, J.C.; Hoyos, N.; Duque-Villegas, M.; Salazar, J.F. Streamflow Response to Land Use/Land Cover Change in the Tropical Andes Using Multiple SWAT Model Variants. J. Hydrol. Reg. Stud. 2024, 54, 101888. [Google Scholar] [CrossRef]
- Cao, K.; Liu, X.; Fu, Q.; Wang, Y.; Liu, D.; Li, T.; Li, M. Dynamic and Harmonious Allocation of Irrigation Water Resources Under Climate Change: A SWAT-Based Multi-Objective Nonlinear Framework. Sci. Total Environ. 2023, 905, 167221. [Google Scholar] [CrossRef] [PubMed]
- Zabihi, O.; Ahmadi, A. Multi-Criteria Evaluation of CMIP6 Precipitation and Temperature Simulations over Iran. J. Hydrol. Reg. Stud. 2024, 52, 101707. [Google Scholar] [CrossRef]
- Mesgari, E.; Hosseini, S.A.; Hemmesy, M.S.; Houshyar, M.; Partoo, L.G. Assessment of CMIP6 Models’ Performances and Projection of Precipitation Based on SSP Scenarios over the MENAP Region. J. Water Clim. Change 2022, 13, 3607–3619. [Google Scholar] [CrossRef]
- Zhang, Z.; Duan, K.; Liu, H.; Meng, Y.; Chen, R. Spatio-Temporal Variation of Precipitation in the Qinling Mountains from 1970 to 2100 Based on CMIP6 Data. Sustainability 2022, 14, 8654. [Google Scholar] [CrossRef]
- Guo, W.; Yu, L.; Huang, L.; He, N.; Chen, W.; Hong, F.; Wang, B.; Wang, H. Ecohydrological Response to Multi-Model Land Use Change at Watershed Scale. J. Hydrol. Reg. Stud. 2023, 49, 101517. [Google Scholar] [CrossRef]
- Li, C.; Wu, Y.; Gao, B.; Zheng, K.; Wu, Y.; Li, C. Multi-Scenario Simulation of Ecosystem Service Value for Optimization of Land Use in the Sichuan-Yunnan Ecological Barrier, China. Ecol. Indic. 2021, 132, 108328. [Google Scholar] [CrossRef]
- Wang, R.; Zhao, J.; Chen, G.; Lin, Y.; Yang, A.; Cheng, J. Coupling PLUS–InVEST Model for Ecosystem Service Research in Yunnan Province, China. Sustainability 2022, 15, 271. [Google Scholar] [CrossRef]
- Lin, X.; Jiao, X.; Tian, Z.; Sun, Q.; Zhang, Y.; Zhang, P.; Ji, Z.; Chen, L.; Lun, F.; Chang, X. Projecting Diversity Conflicts of Future Land System Pathways in China Under Anthropogenic and Climate Forcing. Earth’s Future 2023, 11, e2022EF003406. [Google Scholar] [CrossRef]
- Van Vuuren, D.P.; Riahi, K.; Calvin, K.; Dellink, R.; Emmerling, J.; Fujimori, S.; Kc, S.; Kriegler, E.; O’Neill, B. The Shared Socio-Economic Pathways: Trajectories for Human Development and Global Environmental Change. Glob. Environ. Change 2017, 42, 148–152. [Google Scholar] [CrossRef]
- Kumari, P.; Rehana, S.; Singh, S.K.; Inayathulla, M. Development of a New Agro-Meteorological Drought Index (SPAEI-Agro) in a Data-Scarce Region. Hydrol. Sci. J. 2023, 68, 1301–1322. [Google Scholar] [CrossRef]
- Hua-zhu, X.; Yang-yang, L.; Guo-tao, D. Analysis of Spatial-Temporal Variation Characteristics of Meteorological Drought in the Hexi Corridor Based on SPEI Index. Chin. J. Agrometeorol. 2022, 43, 923. [Google Scholar]
- Zeng, J.; Li, J.; Lu, X.; Wei, Z.; Shangguan, W.; Zhang, S.; Dai, Y.; Zhang, S. Assessment of Global Meteorological, Hydrological and Agricultural Drought Under Future Warming Based on CMIP6. Atmos. Ocean. Sci. Lett. 2022, 15, 100143. [Google Scholar] [CrossRef]
- Rajwa-Kuligiewicz, A.; Bojarczuk, A. Streamflow Response to Catastrophic Windthrow and Forest Recovery in Subalpine Spruce Forest. J. Hydrol. 2024, 634, 131078. [Google Scholar] [CrossRef]
- Shuai, L.; Ling, Z.; Cun-Jie, Z.; Chan, X.; Qiang, Z.; Wen-Ting, G. Spatio-Temporal Variations and Propagation from Meteorological to Hydrological Drought in the Upper Yangtze River Basin over Last 120 Years. Adv. Clim. Change Res. 2023, 19, 263. [Google Scholar]
- Ding, Y.; Gong, X.; Xing, Z.; Cai, H.; Zhou, Z.; Zhang, D.; Sun, P.; Shi, H. Attribution of Meteorological, Hydrological and Agricultural Drought Propagation in Different Climatic Regions of China. Agric. Water Manag. 2021, 255, 106996. [Google Scholar] [CrossRef]
- Wang, F.; Lai, H.; Li, Y.; Feng, K.; Zhang, Z.; Tian, Q.; Zhu, X.; Yang, H. Dynamic Variation of Meteorological Drought and its Relationships with Agricultural Drought Across China. Agric. Water Manag. 2022, 261, 107301. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions de Repartition a N Dimensions et Leurs Marges; Université Paris: Paris, France, 1959. [Google Scholar]
- Zhao, T.; Zhang, Y.; Chen, X. Predictive Performance of NMME Seasonal Forecasts of Global Precipitation: A Spatial-Temporal Perspective. J. Hydrol. 2019, 570, 17–25. [Google Scholar] [CrossRef]
- Gamelin, B.L.; Feinstein, J.; Wang, J.; Bessac, J.; Yan, E.; Kotamarthi, V.R. Projected US Drought Extremes Through the Twenty-First Century with Vapor Pressure Deficit. Sci. Rep. 2022, 12, 8615. [Google Scholar] [CrossRef]
- Doble, R.; Walker, G.; Crosbie, R.; Guillaume, J.; Doody, T. An Overview of Groundwater Response to a Changing Climate in the Murray-Darling Basin, Australia: Potential Implications for the Basin System and Opportunities for Management. Hydrogeol. J. 2024, 32, 59–80. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, J.; Blanchette, M.; Rousseau, A.N.; Xu, Y.J.; Hu, B.; Zhang, G. Wetland Mitigation Functions on Hydrological Droughts: From Drought Characteristics to Propagation of Meteorological Droughts to Hydrological Droughts. J. Hydrol. 2023, 617, 128971. [Google Scholar] [CrossRef]
- Xu, D.; Bisht, G.; Tan, Z.; Sinha, E.; Di Vittorio, A.V.; Zhou, T.; Ivanov, V.Y.; Leung, L.R. Climate Change Will Reduce North American Inland Wetland Areas and Disrupt Their Seasonal Regimes. Nat. Commun. 2024, 15, 2438. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, J.; Offermann, F.; Ribeiro, A.F.; Finger, R. Drought Risk Management in Agriculture: A Copula Perspective on Crop Diversification. Agric. Econ. 2024, 55, 823–847. [Google Scholar] [CrossRef]

| Data Type | Data Name | Year | Data Source |
|---|---|---|---|
| Basic data | A dataset of multi-period remote sensing monitoring of land use in China CNLUCC | 2000, 2010, and 2020 | Chinese Academy of Sciences Center for Resources and Environmental Science and Data (https://www.resdc.cn/) |
| hydrological station data | 2020 | Earth Resources Data Cloud Platform (www.gis5g.com) | |
| Natural element | ASTER GDEM V3 (X1) | 2019 | Geospatial data cloud (https://www.gscloud.cn/) |
| slope (X2) | Calculated from DEM slope | ||
| Distance from water (X3) | 2019 | OpenStreetMap (https://www.openstreetmap.org) | |
| Temperature/forecast (X4) | 2040, 2060, and 2080 | Chinese Academy of Sciences Center for Resources and Environmental Science and Data (https://www.resdc.cn/) | |
| Precipitation/future precipitation (X5) | CMIP6 database (https://www.nccs.nasa.gov) | ||
| Socioeconomic factor | Population/future population (X6) | 2019, 2040, 2060, and 2080 | Chinese Academy of Sciences Center for Resources and Environmental Science and Data (https://www.resdc.cn/) |
| Scientific data bank (https://cstr.cn/31253.11.sciencedb.01683) | |||
| GDP/future GDP (X7) | Chinese Academy of Sciences Center for Resources and Environmental Science and Data (https://www.resdc.cn/) | ||
| Distance between government seat (city or county level) (X8 and X9) | 2019 | National Geographic Information Resources Catalog Service System (https://www.webmap.cn/) | |
| Nature reserve (X10) | 2019 | OpenStreetMap (https://www.openstreetmap.org) | |
| Distance to primary, secondary, and tertiary roads (X11, X12, and X13) | |||
| Night light (X14) |
| Pattern Name | Country | Spatial Resolution | Pattern Name | Country | Spatial Resolution |
|---|---|---|---|---|---|
| ACCESS-CM2 | Australia | 0.25° × 0.25° | EC-Earth3 | Europe | 0.25° × 0.25° |
| ACCESS-ESM1-5 | IPSL-CM6A-LR | ||||
| NorESM2-LM | Norway | MIROC6 | Japan | ||
| NorESM2-MM | MIROC-ES2L | ||||
| MPI-ESM1-2-HR | Germany | MRI-ESM2-0 | |||
| MPI-ESM1-2-LR | GFDL-CM4 GFDL-ESM4 | United States | |||
| INM-CM4-8 | Russia | CanESM5 | Canada |
| Land Use Type | Field Weight | SSP245 Scenario | SSP585 Scenario | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | F | G | W | B | U | C | F | G | W | B | U | ||
| C | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| F | 0.671 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| G | 0.008 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| W | 0.028 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| B | 0.001 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| U | 0.075 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| Scenario | Time | SPAEI | SRI | SSMI | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Event Count | Duration | Severity | Intensity | Event Count | Duration | Severity | Intensity | Event Count | Duration | Severity | Intensity | ||
| SSP245 | 2025–2050 | 22 | 3.91 | 4.27 | 1.01 | 17 | 5.00 | 6.78 | 1.18 | 20 | 5.40 | 6.90 | 1.10 |
| 2051–2100 | 41 | 4.15 | 4.93 | 1.12 | 36 | 4.72 | 5.20 | 0.99 | 29 | 4.34 | 5.60 | 1.15 | |
| SSP585 | 2025–2050 | 21 | 4.48 | 5.12 | 1.06 | 21 | 4.14 | 5.37 | 1.12 | 21 | 4.33 | 5.15 | 1.08 |
| 2051–2100 | 38 | 4.03 | 4.67 | 1.18 | 33 | 5.73 | 6.16 | 1.02 | 35 | 4.46 | 5.78 | 1.19 | |
| Scenario | Time Slot | Distribution Type | AIC Value | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Meteorological Drought | Hydrological Drought | Agricultural Drought | |||||||||
| D | S | P | D | S | P | D | S | P | |||
| SSP245 | 2025–2050 | Gamma | 89.67 | 102.51 | 8.49 | 83.46 | 102.00 | 27.18 | 100.04 | 119.83 | 24.66 |
| Weibull | 91.94 | 103.89 | 11.74 | 83.24 | 102.45 | 30.49 | 100.78 | 120.21 | 26.90 | ||
| Logistic | 96.79 | 113.35 | 11.58 | 87.21 | 112.62 | 31.64 | 106.11 | 132.10 | 29.22 | ||
| Normal | 96.81 | 114.22 | 11.19 | 85.50 | 115.33 | 33.71 | 104.59 | 132.03 | 28.54 | ||
| Exponential | 102.22 | 105.88 | 44.11 | 90.72 | 101.07 | 41.71 | 109.46 | 119.26 | 45.78 | ||
| 2051–2100 | Gamma | 179.90 | 207.78 | 13.83 | 176.44 | 191.65 | 9.04 | 121.80 | 157.15 | 39.55 | |
| Weibull | 185.74 | 211.34 | 19.94 | 181.76 | 194.07 | 18.18 | 123.61 | 158.53 | 44.80 | ||
| Logistic | 195.08 | 227.69 | 16.98 | 195.26 | 217.83 | 10.83 | 128.68 | 173.37 | 47.19 | ||
| Normal | 199.06 | 232.24 | 17.53 | 209.74 | 239.26 | 15.64 | 127.15 | 175.25 | 48.96 | ||
| Exponential | 204.43 | 218.94 | 95.78 | 185.76 | 192.71 | 73.54 | 145.20 | 159.87 | 68.04 | ||
| SSP585 | 2025–2050 | Gamma | 102.13 | 112.50 | 15.22 | 100.19 | 116.14 | 22.93 | 92.70 | 110.13 | 15.14 |
| Weibull | 105.53 | 113.93 | 16.64 | 103.11 | 116.60 | 24.97 | 94.26 | 111.37 | 18.58 | ||
| Logistic | 113.88 | 129.69 | 18.66 | 113.41 | 136.85 | 26.27 | 98.83 | 121.05 | 17.88 | ||
| Normal | 122.41 | 135.13 | 17.00 | 120.99 | 143.84 | 25.80 | 98.14 | 122.29 | 18.39 | ||
| Exponential | 106.95 | 112.58 | 46.25 | 103.70 | 114.60 | 48.74 | 105.59 | 112.83 | 47.25 | ||
| 2051–2100 | Gamma | 162.17 | 176.69 | 21.83 | 170.70 | 182.26 | −4.62 | 157.65 | 190.19 | 36.80 | |
| Weibull | 169.53 | 182.38 | 30.89 | 173.41 | 184.61 | −1.25 | 163.11 | 193.03 | 44.55 | ||
| Logistic | 175.64 | 187.59 | 24.76 | 184.60 | 199.52 | −1.52 | 169.34 | 209.05 | 42.57 | ||
| Normal | 187.33 | 200.95 | 28.61 | 184.79 | 203.13 | −3.07 | 176.45 | 220.25 | 45.85 | ||
| Exponential | 182.86 | 193.77 | 90.02 | 183.19 | 188.04 | 69.35 | 176.62 | 194.75 | 84.34 | ||
| Scenario | /Month | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 75% | 50% | 25% | 75% | 50% | 25% | 75% | 50% | 25% | |
| Meteorological drought | |||||||||
| SSP245 | 2 | 3 | 5 | 2.08 | 3.27 | 5.86 | 0.88 | 1.03 | 1.21 |
| SSP585 | 2 | 3 | 4 | 2.30 | 3.63 | 5.60 | 0.89 | 1.09 | 1.31 |
| Hydrological drought | |||||||||
| SSP245 | 2 | 4 | 6 | 1.90 | 3.87 | 6.21 | 0.81 | 0.97 | 1.17 |
| SSP585 | 3 | 3.5 | 6 | 2.32 | 3.32 | 6.08 | 0.84 | 1.00 | 1.21 |
| Agricultural drought | |||||||||
| SSP245 | 3 | 4 | 7 | 2.16 | 4.13 | 9.26 | 0.74 | 0.92 | 1.42 |
| SSP585 | 2 | 4 | 5.5 | 2.29 | 4.01 | 6.64 | 0.85 | 1.02 | 1.35 |
| Scenario | Meteorological Drought Level | Hydrological Drought Level: 2 | Hydrological Drought Level: 3 | Hydrological Drought Level: 4 | Hydrological Drought Level: 5 |
|---|---|---|---|---|---|
| SSP245 | 2 | 0.18 | 0.10 | 0.04 | 0.03 |
| 3 | 0.19 | 0.12 | 0.06 | 0.04 | |
| 4 | 0.19 | 0.14 | 0.09 | 0.08 | |
| 5 | 0.17 | 0.15 | 0.11 | 0.17 | |
| SSP585 | 2 | 0.19 | 0.12 | 0.06 | 0.03 |
| 3 | 0.20 | 0.15 | 0.08 | 0.05 | |
| 4 | 0.21 | 0.17 | 0.10 | 0.07 | |
| 5 | 0.21 | 0.19 | 0.14 | 0.12 |
| Scenario | Meteorological Drought Level | Agricultural Drought Level: 2 | Agricultural Drought Level: 3 | Agricultural Drought Level: 4 | Agricultural Drought Level: 5 |
|---|---|---|---|---|---|
| SSP245 | 2 | 0.19 | 0.12 | 0.06 | 0.03 |
| 3 | 0.20 | 0.15 | 0.08 | 0.05 | |
| 4 | 0.21 | 0.17 | 0.11 | 0.07 | |
| 5 | 0.21 | 0.19 | 0.14 | 0.12 | |
| SSP585 | 2 | 0.20 | 0.11 | 0.04 | 0.02 |
| 3 | 0.23 | 0.15 | 0.08 | 0.05 | |
| 4 | 0.22 | 0.18 | 0.12 | 0.10 | |
| 5 | 0.17 | 0.18 | 0.15 | 0.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Si, Z.; Zhao, Y.; Wang, J.; Liu, Y.; Wang, L. Drought Propagation and Risk Assessment in the Naoli River Basin Based on the SWAT-PLUS Model and Copula Functions. Sustainability 2025, 17, 8219. https://doi.org/10.3390/su17188219
Liu T, Si Z, Zhao Y, Wang J, Liu Y, Wang L. Drought Propagation and Risk Assessment in the Naoli River Basin Based on the SWAT-PLUS Model and Copula Functions. Sustainability. 2025; 17(18):8219. https://doi.org/10.3390/su17188219
Chicago/Turabian StyleLiu, Tao, Zhenjiang Si, Yusu Zhao, Jing Wang, Yan Liu, and Longfei Wang. 2025. "Drought Propagation and Risk Assessment in the Naoli River Basin Based on the SWAT-PLUS Model and Copula Functions" Sustainability 17, no. 18: 8219. https://doi.org/10.3390/su17188219
APA StyleLiu, T., Si, Z., Zhao, Y., Wang, J., Liu, Y., & Wang, L. (2025). Drought Propagation and Risk Assessment in the Naoli River Basin Based on the SWAT-PLUS Model and Copula Functions. Sustainability, 17(18), 8219. https://doi.org/10.3390/su17188219






