Evaluating Eutrophication and Water Clarity on Lake Victoria’s Ugandan Coast Using Landsat Data
Abstract
1. Introduction
2. Methodology
2.1. Study Area
2.2. Data Collection
In Situ Water Sampling and Satellite Data
2.3. Data Processing
2.3.1. Spectral Band Analysis and Modeling
2.3.2. Trophic State Index (TSI) Modeling
2.3.3. Algorithm Evaluation Metrics
3. Results and Discussion
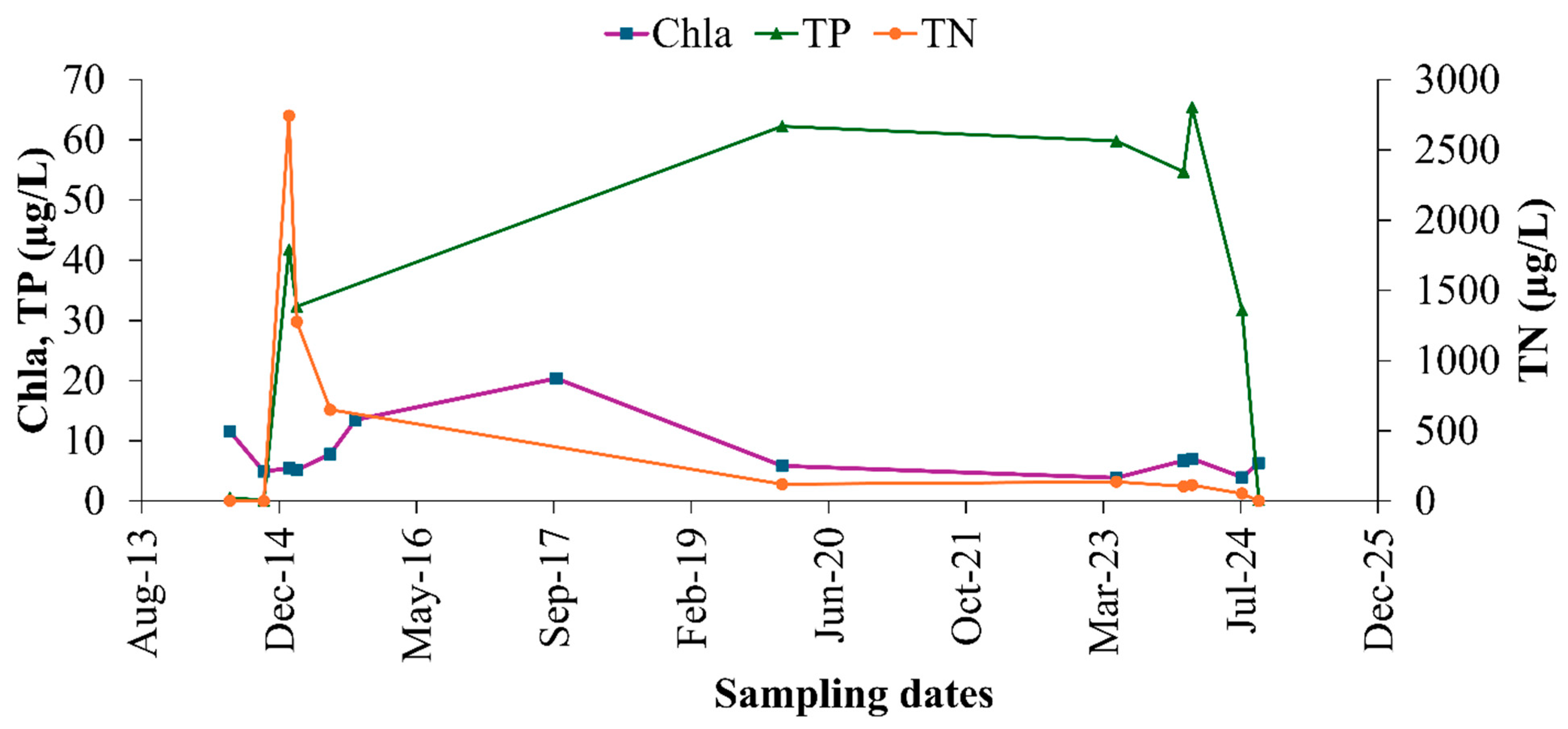
3.1. In Situ Water Quality Parameter Temporal Variation
3.2. Satellite Remote Sensing Correlation with in Situ Parameters
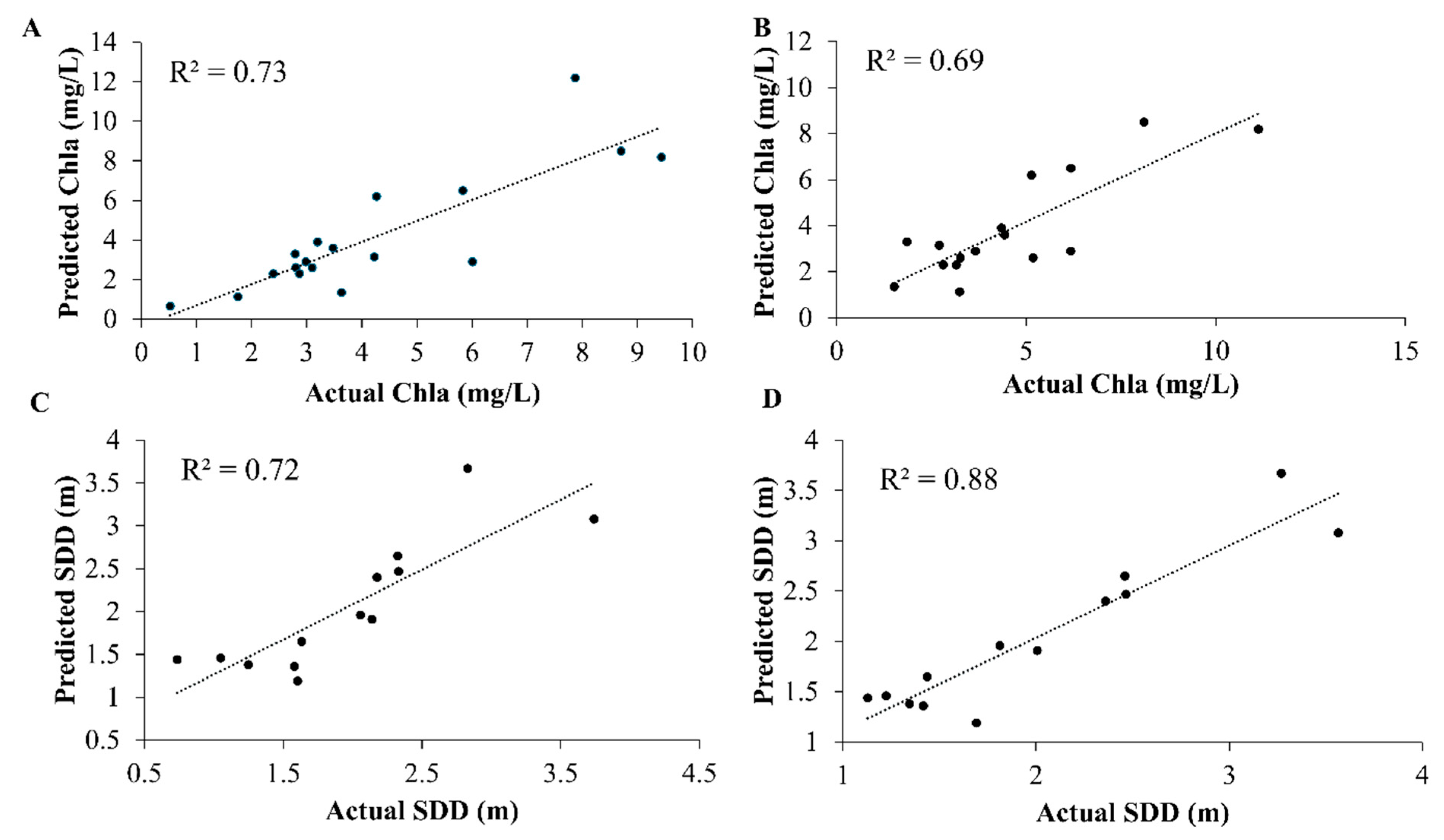
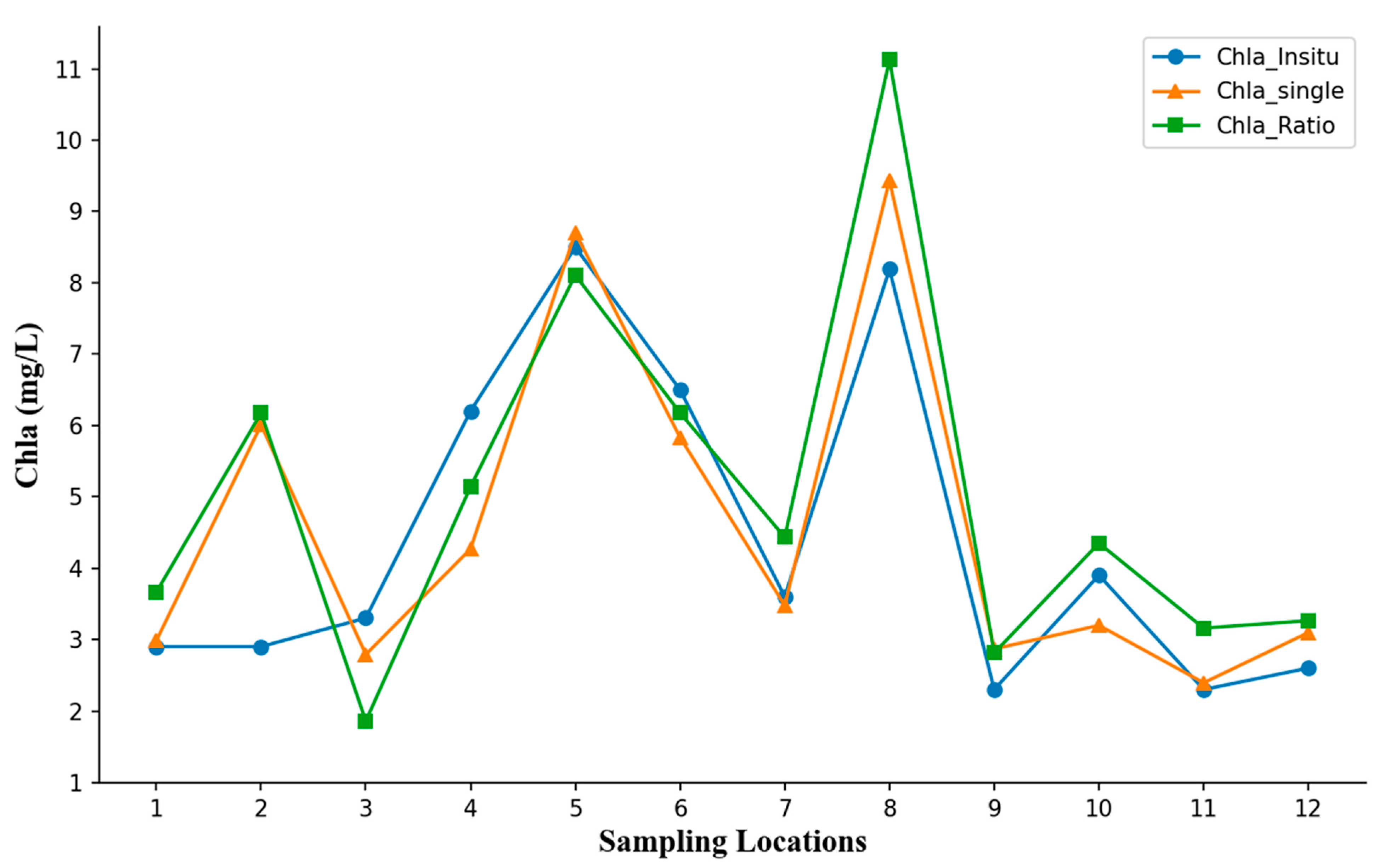
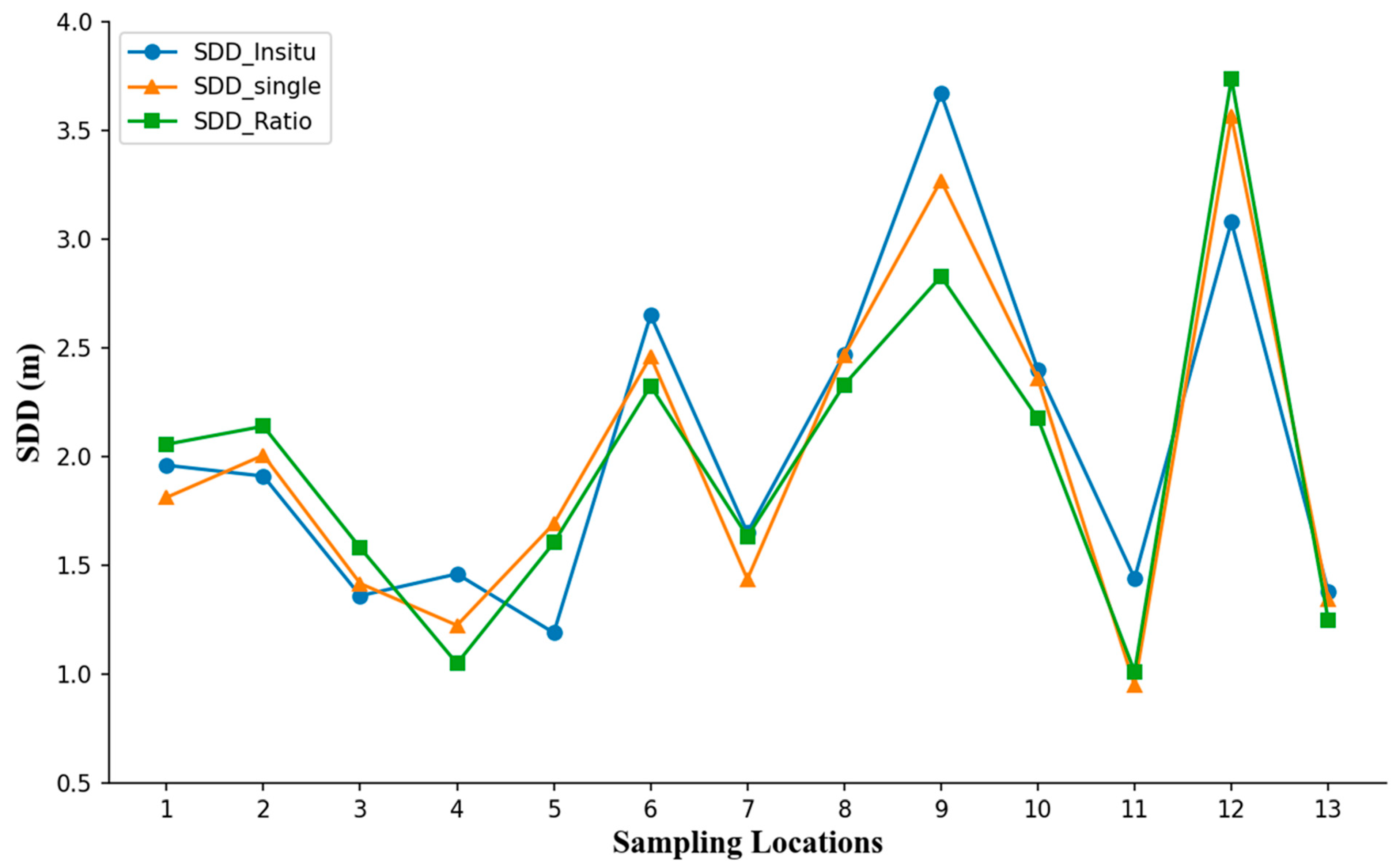
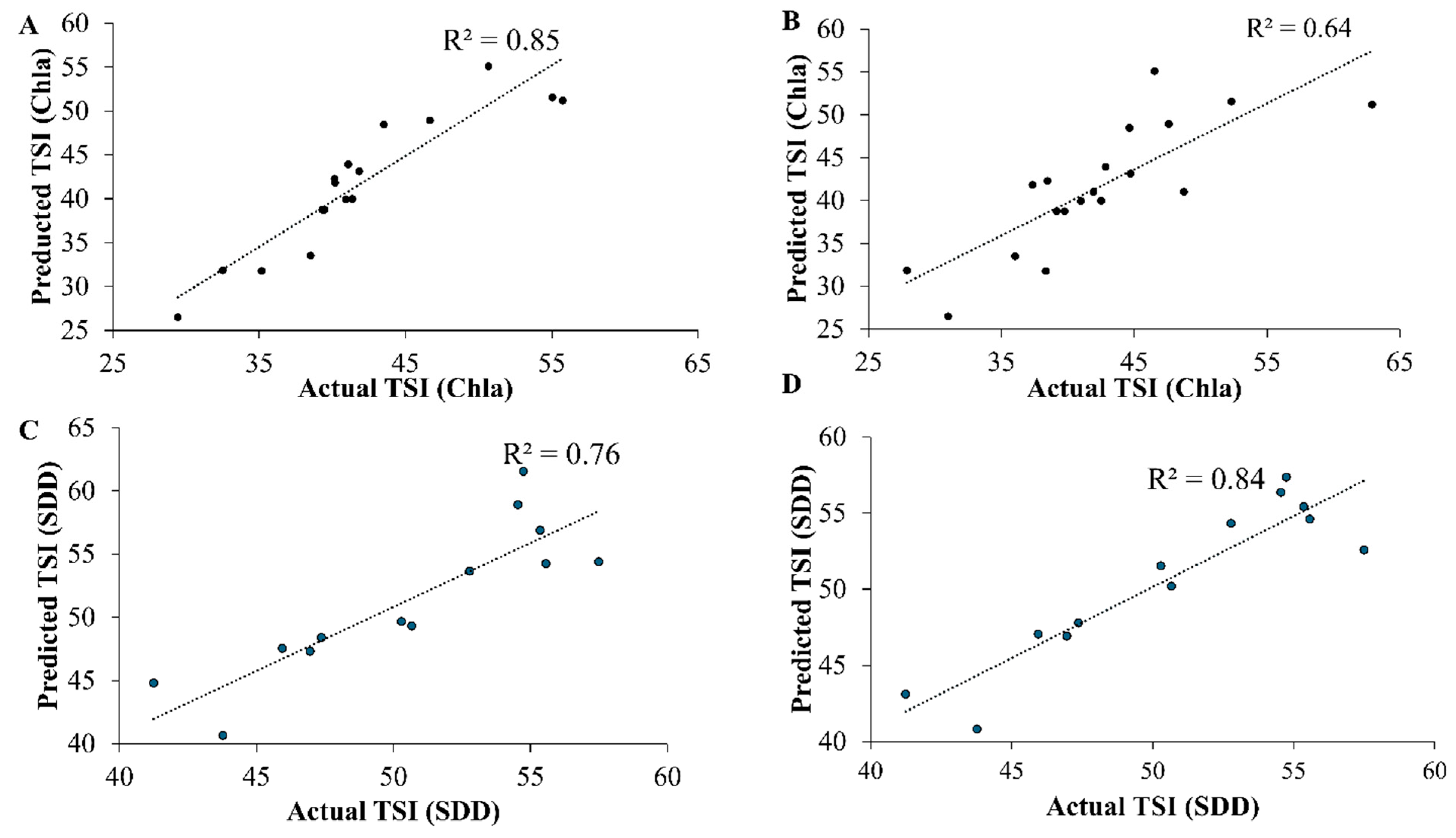
3.3. Application of Predictive Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nyamweya, C.; Lawrence, T.J.; Ajode, M.Z.; Smith, S.; Achieng, A.O.; Barasa, J.E.; Masese, F.O.; Taabu-Munyaho, A.; Mahongo, S.; Kayanda, R. Lake Victoria: Overview of research needs and the way forward. J. Great Lakes Res. 2023, 49, 102211. [Google Scholar] [CrossRef]
- Gidudu, A.; Letaru, L.; Kulabako, R.N. Empirical modeling of chlorophyll a from MODIS satellite imagery for trophic status monitoring of Lake Victoria in East Africa. J. Great Lakes Res. 2021, 47, 1209–1218. [Google Scholar] [CrossRef]
- Nyamweya, C.; Nyaboke, H.; Aura, C.; Momanyi, K.; Mlaponi, E.; Odoli, C.; Njiru, J. Lake Victoria’s bounty: A case for riparian countries’ blue economic investment. Front. Environ. Sci. 2022, 10, 952654. [Google Scholar] [CrossRef]
- Wu, G.; Chen, C.; Liu, Y.; Fan, X.; Niu, H.; Liu, Y. Developing a High-Resolution Seamless Surface Water Extent Time-Series over Lake Victoria by Integrating MODIS and Landsat Data. Remote Sens. 2023, 15, 3500. [Google Scholar] [CrossRef]
- Oyege, I.; Katwesigye, R.; Kiwanuka, M.; Mutanda, H.E.; Niyomukiza, J.B.; Kataraihya, D.J.; Kica, S.; Egor, M. Temporal trends of water quality parameters, heavy metals, microplastics, and emerging organic pollutants in Lake Victoria and its basin: Knowns, knowledge gaps, and future directions. Environ. Nanotechnol. Monit. Manag. 2024, 22, 100962. [Google Scholar] [CrossRef]
- Kiwanuka, M.; Mutanda, H.E.; Niyomukiza, J.B.; Nakasagga, E. Assessment of suitability of drinking water from the springs in Urban slums of Kampala. Environ. Chall. 2023, 10, 100667. [Google Scholar] [CrossRef]
- Nantaba, F.; Wasswa, J.; Kylin, H.; Palm, W.-U.; Bouwman, H.; Kümmerer, K. Occurrence, distribution, and ecotoxicological risk assessment of selected pharmaceutical compounds in water from Lake Victoria, Uganda. Chemosphere 2020, 239, 124642. [Google Scholar] [CrossRef]
- Obubu, J.P.; Mengistou, S.; Odong, R.; Fetahi, T.; Alamirew, T. Determination of the connectedness of land use, land cover change to water quality status of a shallow lake: A case of Lake Kyoga Basin, Uganda. Sustainability 2021, 14, 372. [Google Scholar] [CrossRef]
- Bugenyi, F.; Magumba, K. The present physicochemical ecology of Lake Victoria, Uganda. In Limnology, Climatology and Paleoclimatology of the East African Lakes; Routledge: London, UK, 2019; pp. 141–154. [Google Scholar]
- Mchau, G.J.; Makule, E.; Machunda, R.; Gong, Y.Y.; Kimanya, M. Harmful algal bloom and associated health risks among users of Lake Victoria freshwater: Ukerewe Island, Tanzania. J. Water Health 2019, 17, 826–836. [Google Scholar] [CrossRef]
- Nalumenya, B.; Rubinato, M.; Catterson, J.; Kennedy, M.; Bakamwesiga, H.; Wabwire, D. Assessing the Potential Impacts of Contaminants on the Water Quality of Lake Victoria: Two Case Studies in Uganda. Sustainability 2024, 16, 9128. [Google Scholar] [CrossRef]
- Zheng, G.; DiGiacomo, P.M. Uncertainties and applications of satellite-derived coastal water quality products. Prog. Oceanogr. 2017, 159, 45–72. [Google Scholar] [CrossRef]
- Schaeffer, B.A.; Schaeffer, K.G.; Keith, D.; Lunetta, R.S.; Conmy, R.; Gould, R.W. Barriers to adopting satellite remote sensing for water quality management. Int. J. Remote Sens. 2013, 34, 7534–7544. [Google Scholar] [CrossRef]
- Kintu, I.M.; Gidudu, A.; Letaru, L. Assessment of lake Victoria’s trophic status using satellite-derived Secchi disk depth. In Earth Observations and Geospatial Science in Service of Sustainable Development Goals, Proceedings of the 12th International Conference of the African Association of Remote Sensing and the Environment; Springer: Cham, Switzerland; pp. 79–87.
- Obubu, J.P.; Yoshihiko, I.; Rodgers, M.; Tatsuyuki, S.; Rebecca Walugembe, N. Application of Gon’s algorithm to monitor productivity using Sentinel-2 Multi-spectral Instrument in Lake Kyoga, Uganda. Phys. Chem. Earth Parts A/B/C 2025, 141, 104070. [Google Scholar] [CrossRef]
- Hoepffner, N.; Sathyendranath, S. Effect of pigment composition on absorption properties of phytoplankton. Mar. Ecol. Prog. Ser. 1991, 73, 11–23. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Maritorena, S.; Siegel, D.A.; O’Brien, M.C.; Toole, D.; Mitchell, B.G.; Kahru, M.; Chavez, F.P.; Strutton, P.; Cota, G.F. Ocean color chlorophyll a algorithms for SeaWiFS, OC2, and OC4: Version 4. SeaWiFS Postlaunch Calibration Valid. Anal. 2000, 3, 9–23. [Google Scholar]
- Gordon, H.R.; Brown, O.B.; Jacobs, M.M. Computed relationships between the inherent and apparent optical properties of a flat homogeneous ocean. Appl. Opt. 1975, 14, 417–427. [Google Scholar] [CrossRef]
- Sagan, V.; Peterson, K.T.; Maimaitijiang, M.; Sidike, P.; Sloan, J.; Greeling, B.A.; Maalouf, S.; Adams, C. Monitoring inland water quality using remote sensing: Potential and limitations of spectral indices, bio-optical simulations, machine learning, and cloud computing. Earth-Sci. Rev. 2020, 205, 103187. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L. Water quality retrieval from PRISMA hyperspectral images: First experience in a turbid lake and comparison with sentinel-2. Remote Sens. 2020, 12, 3984. [Google Scholar] [CrossRef]
- Ruddick, K.G.; Gons, H.J.; Rijkeboer, M.; Tilstone, G. Optical remote sensing of chlorophyll a in case 2 waters by use of an adaptive two-band algorithm with optimal error properties. Appl. Opt. 2001, 40, 3575–3585. [Google Scholar] [CrossRef]
- Hajigholizadeh, M.; Moncada, A.; Kent, S.; Melesse, A.M. Land–lake linkage and remote sensing application in water quality monitoring in lake okeechobee, Florida, USA. Land 2021, 10, 147. [Google Scholar] [CrossRef]
- Kutser, T.; Arst, H.; Miller, T.; Käärmann, L.; Milius, A. Telespectrometrical estimation of water transparency, chlorophyll-a and total phosphorus concentration of Lake Peipsi. Int. J. Remote Sens. 1995, 16, 3069–3085. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, H.; Fu, J.; Sheng, G. Water quality change in reservoirs of Shenzhen, China: Detection using LANDSAT/TM data. Sci. Total Environ. 2004, 328, 195–206. [Google Scholar] [CrossRef]
- Wu, C.; Wu, J.; Qi, J.; Zhang, L.; Huang, H.; Lou, L.; Chen, Y. Empirical estimation of total phosphorus concentration in the mainstream of the Qiantang River in China using Landsat TM data. Int. J. Remote Sens. 2010, 31, 2309–2324. [Google Scholar] [CrossRef]
- Li, J.; Wang, J.; Wu, Y.; Cui, Y.; Yan, S. Remote sensing monitoring of total nitrogen and total phosphorus concentrations in the water around Chaohu Lake based on geographical division. Front. Environ. Sci. 2022, 10, 1014155. [Google Scholar] [CrossRef]
- Xiong, J.; Lin, C.; Cao, Z.; Hu, M.; Xue, K.; Chen, X.; Ma, R. Development of remote sensing algorithm for total phosphorus concentration in eutrophic lakes: Conventional or machine learning? Water Res. 2022, 215, 118213. [Google Scholar] [CrossRef]
- Hood, R.R.; Subramaniam, A.; May, L.R.; Carpenter, E.J.; Capone, D.G. Remote estimation of nitrogen fixation by Trichodesmium. Deep Sea Res. Part II Top. Stud. Oceanogr. 2001, 49, 123–147. [Google Scholar] [CrossRef]
- Hanson, C.E.; Waite, A.M.; Thompson, P.A.; Pattiaratchi, C.B. Phytoplankton community structure and nitrogen nutrition in Leeuwin Current and coastal waters off the Gascoyne region of Western Australia. Deep Sea Res. Part II Top. Stud. Oceanogr. 2007, 54, 902–924. [Google Scholar] [CrossRef]
- Dörnhöfer, K.; Oppelt, N. Remote sensing for lake research and monitoring–Recent advances. Ecol. Indic. 2016, 64, 105–122. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Dall’Olmo, G.; Moses, W.; Rundquist, D.C.; Barrow, T.; Fisher, T.R.; Gurlin, D.; Holz, J. A simple semi-analytical model for remote estimation of chlorophyll-a in turbid waters: Validation. Remote Sens. Environ. 2008, 112, 3582–3593. [Google Scholar] [CrossRef]
- Kallio, K.; Kutser, T.; Hannonen, T.; Koponen, S.; Pulliainen, J.; Vepsäläinen, J.; Pyhälahti, T. Retrieval of water quality from airborne imaging spectrometry of various lake types in different seasons. Sci. Total Environ. 2001, 268, 59–77. [Google Scholar] [CrossRef]
- Lacaux, J.; Tourre, Y.; Vignolles, C.; Ndione, J.; Lafaye, M. Classification of ponds from high-spatial resolution remote sensing: Application to Rift Valley Fever epidemics in Senegal. Remote Sens. Environ. 2007, 106, 66–74. [Google Scholar] [CrossRef]
- Shafique, N.A.; Fulk, F.; Autrey, B.C.; Flotemersch, J. Hyperspectral remote sensing of water quality parameters for large rivers in the Ohio River basin. In Proceedings of the First Interagency Conference on Research in the Watershed, Benson, AZ, USA, 27–30 October 2003; pp. 216–221. [Google Scholar]
- Devi Prasad, A. Carlson’s trophic state index for the assessment of trophic status of two lakes in Mandya district. Adv. Appl. Sci. Res. 2012, 3, 2992–2996. [Google Scholar]
- Rocchini, R.; Swain, L. The British Columbia Water Quality Index; Water Quality Branch, EP Department, Ministry of Environment, Land and Park: Victoria, BC, Canada, 1995; p. 13. [Google Scholar]
- Carlson, R.E. A trophic state index for lakes 1. Limnol. Oceanogr. 1977, 22, 361–369. [Google Scholar] [CrossRef]
- Okungu, J.; Peterlis, O. Pollution Loads into Lake Victoria from the Kenyan Catchment; Ministry of Environment and Natural Resources: Kisumu, Kenya, 2002.
- Aroko, R.; Deus, D.; Ngereja, Z. Comparison of Multiple Linear Regression and Artificial Neural Network Models in retrieving Water Quality Parameters using Remotely Sensed Data: Lake Victoria (Tanzanian) Water. South Afr. J. Geomat. 2025, 14, 167–190. [Google Scholar] [CrossRef]
- Gholizadeh, M.; Melesse, A. Study on spatiotemporal variability of water quality parameters in Florida Bay using remote sensing. J. Remote Sens. GIS 2017, 6, 1000207. [Google Scholar] [CrossRef]
- Tang, Y.; Feng, Y.; Fung, S.; Xomchuk, V.R.; Jiang, M.; Moore, T.; Beckler, J. Spatiotemporal deep-learning-based algal bloom prediction for Lake Okeechobee using multisource data fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8318–8331. [Google Scholar] [CrossRef]
- Bhaskar, M.S.; Gidudu, A. Effect of landscape changes on the water quality of Murchison bay. Int. J. Adv. Remote Sens. GIS 2020, 9, 3350–3363. [Google Scholar] [CrossRef]
- Kiwanuka, M.; Oyege, I.; Balaji Bhaskar, M.S. Spatial and Temporal Dynamics of Water Quality in Lake Okeechobee Using Remote Sensing and Its Impact on Environmental Health. Remote Sens. 2025, 17, 3197. [Google Scholar] [CrossRef]
- Ssebiyonga, N.; Erga, S.R.; Hamre, B.; Stamnes, J.J.; Frette, Ø. Light conditions and photosynthetic efficiency of phytoplankton in Murchison Bay, Lake Victoria, Uganda. Limnologica 2013, 43, 185–193. [Google Scholar] [CrossRef]
- Vincent, O.; Gavin Akinyi, M. Spectral Reflectance and Algal Bloom Monitoring of Lake Victoria Using Remote Sensing Techniques, Winum Gulf of Kenya. Earth Sci. 2023, 12, 90–98. [Google Scholar] [CrossRef]
- Vincent, R.K.; Qin, X.; McKay, R.M.L.; Miner, J.; Czajkowski, K.; Savino, J.; Bridgeman, T. Phycocyanin detection from LANDSAT TM data for mapping cyanobacterial blooms in Lake Erie. Remote Sens. Environ. 2004, 89, 381–392. [Google Scholar] [CrossRef]
- Ali, M.; Ali, T.; Gawai, R.; Dronjak, L.; Elaksher, A. The Analysis of Land Use and Climate Change Impacts on Lake Victoria Basin Using Multi-Source Remote Sensing Data and Google Earth Engine (GEE). Remote Sens. 2024, 16, 4810. [Google Scholar] [CrossRef]
- Sani, I.S.; Manurung, P.; Fagge, A.U. NDWI–NDBI Overlay–Based Analysis of Coastal Fence Expansion and Hydrological Changes in Victoria Island, Lagos, Nigeria (2010–2015), with Machine Learning Validation. Remote Sens. Sustain. Ocean. 2024. [Google Scholar] [CrossRef]
- Olaka, L.A.; Ogutu, J.O.; Said, M.Y.; Oludhe, C. Projected climatic and hydrologic changes to Lake Victoria Basin Rivers under three RCP emission scenarios for 2015–2100 and impacts on the water sector. Water 2019, 11, 1449. [Google Scholar] [CrossRef]
- Vuai, S.; Ibembe, J.; Mungai, N. Spatial Variation of Nutrients in Sondu-Miriu and Simiyu-Duma Rivers: Implication on Sources and Factors Influencing their Transportation into the Lake Victoria. J. Earth Sci. Clim. Change 2012, 3, 1000119. [Google Scholar]
- UBOS. The National Population and Housing Census 2024—Final Report—Volume 1 (Main); Uganda Bureau of Statistics: Kampala, Uganda, 2024; p. 434.
- Kiggundu, N.; Abugri Anaba, L.; Banadda, N.; Wanyama, J.; Kabenge, I. Assessing land use and land cover changes in the Murchison Bay catchment of Lake Victoria basin in Uganda. J. Sustain. Dev. 2018, 11, 44–55. [Google Scholar] [CrossRef]
- Banadda, E.; Kansiime, F.; Kigobe, M.; Kizza, M.; Nhapi, I. Landuse-based nonpoint source pollution: A threat to water quality in Murchison Bay, Uganda. Water Policy 2009, 11, 94–105. [Google Scholar] [CrossRef]
- Anaba, L.A.; Banadda, N.; Kiggundu, N.; Wanyama, J.; Engel, B.; Moriasi, D. Application of SWAT to assess the effects of land use change in the Murchison Bay catchment in Uganda. Comput. Water Energy Environ. Eng. 2017, 6, 24–40. [Google Scholar] [CrossRef]
- Wasige, J.E.; Groen, T.A.; Smaling, E.; Jetten, V. Monitoring basin-scale land cover changes in Kagera Basin of Lake Victoria using ancillary data and remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 32–42. [Google Scholar] [CrossRef]
- Kahru, M.; Kudela, R.M.; Anderson, C.R.; Manzano-Sarabia, M.; Mitchell, B.G. Evaluation of satellite retrievals of ocean chlorophyll-a in the California Current. Remote Sens. 2014, 6, 8524–8540. [Google Scholar] [CrossRef]
- Galat, D.L.; Verdin, J.P. Patchiness, collapse and succession of a cyanobacterial bloom evaluated by synoptic sampling and remote sensing. J. Plankton Res. 1989, 11, 925–948. [Google Scholar] [CrossRef]
- Kutser, T. Passive optical remote sensing of cyanobacteria and other intense phytoplankton blooms in coastal and inland waters. Int. J. Remote Sens. 2009, 30, 4401–4425. [Google Scholar] [CrossRef]
- Matthews, M.W.; Bernard, S.; Robertson, L. An algorithm for detecting trophic status (chlorophyll-a), cyanobacterial-dominance, surface scums and floating vegetation in inland and coastal waters. Remote Sens. Environ. 2012, 124, 637–652. [Google Scholar] [CrossRef]
- Cao, Z.; Ma, R.; Liu, M.; Duan, H.; Xiao, Q.; Xue, K.; Shen, M. Harmonized chlorophyll-a retrievals in inland lakes from Landsat-8/9 and Sentinel 2A/B virtual constellation through machine learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4209916. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-year Landsat water clarity census of Minnesota’s 10,000 lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
- Kloiber, S.M.; Brezonik, P.L.; Olmanson, L.G.; Bauer, M.E. A procedure for regional lake water clarity assessment using Landsat multispectral data. Remote Sens. Environ. 2002, 82, 38–47. [Google Scholar] [CrossRef]
- Tan, W.; Liu, P.; Liu, Y.; Yang, S.; Feng, S. A 30-year assessment of phytoplankton blooms in Erhai Lake using Landsat imagery: 1987 to 2016. Remote Sens. 2017, 9, 1265. [Google Scholar] [CrossRef]
- Darryl, K.; Jennifer, R.; Jason, G.; Brian, Z.; Mike, C.; Glen, T.; Joseph Bishop, a. Monitoring algal blooms in drinking water reservoirs using the Landsat-8 Operational Land Imager. Int. J. Remote Sens. 2018, 39, 2818–2846. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Wang, L.; Wang, Y.; Zhang, X.; Zhu, Y.; Ma, G. Monitoring of low Chla concentration in Hulun Lake based on fusion of remote sensing satellite and ground observation data. Remote Sens. 2024, 16, 1811. [Google Scholar] [CrossRef]
- Nawaz, T.; Joshi, N.; Nelson, D.; Saud, S.; Abdelsalam, N.R.; Abdelhamid, M.M.; Jaremko, M.; Rahman, T.U.; Fahad, S. Harnessing the potential of nitrogen-fixing cyanobacteria: A rich bio-resource for sustainable soil fertility and enhanced crop productivity. Environ. Technol. Innov. 2024, 36, 103886. [Google Scholar] [CrossRef]
- Talling, J. The depletion of carbon dioxide from lake water by phytoplankton. J. Ecol. 1976, 64, 79–121. [Google Scholar] [CrossRef]
- Deirmendjian, L.; Descy, J.P.; Morana, C.; Okello, W.; Stoyneva-Gärtner, M.P.; Bouillon, S.; Borges, A.V. Limnological changes in Lake Victoria since the mid-20th century. Freshw. Biol. 2021, 66, 1630–1647. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Alikas, K.; Anstee, J.; Barbosa, C.; Binding, C.; Bresciani, M.; Cremella, B.; Giardino, C.; Gurlin, D. Simultaneous retrieval of selected optical water quality indicators from Landsat-8, Sentinel-2, and Sentinel-3. Remote Sens. Environ. 2022, 270, 112860. [Google Scholar] [CrossRef]
- Giardino, C.; Pepe, M.; Brivio, P.A.; Ghezzi, P.; Zilioli, E. Detecting chlorophyll, Secchi disk depth and surface temperature in a sub-alpine lake using Landsat imagery. Sci. Total Environ. 2001, 268, 19–29. [Google Scholar] [CrossRef] [PubMed]
- Gidudu, A.; Banura, C.; Namugga, A. Monitoring water quality on Lake Victoria using MODIS imagery. Int. J. Technoscience Dev. 2016, 3, 1–47. [Google Scholar]
- Duan, H.; Zhang, Y.; Zhang, B.; Song, K.; Wang, Z.; Liu, D.; Li, F. Estimation of chlorophyll-a concentration and trophic states for inland lakes in Northeast China from Landsat TM data and field spectral measurements. Int. J. Remote Sens. 2008, 29, 767–786. [Google Scholar] [CrossRef]
- Kiwanuka, M.; Balaji, B.M.S.; Leslie, R. Developing Satellite Remote Sensing Models for Water Quality Monitoring on Lake Victoria Region of Uganda. AGU Fall Meet. Abstr. 2024, 2024, H11K-0826. [Google Scholar]
- Nakkazi, M.T.; Nkwasa, A.; Martínez, A.B.; van Griensven, A. Linking land use and precipitation changes to water quality changes in Lake Victoria using earth observation data. Environ. Monit. Assess. 2024, 196, 1104. [Google Scholar] [CrossRef]
- Moradi, M.; Zoljoodi, M. Validation of standard ocean-color chlorophyll-a products in turbid coastal waters: A case study on statistical evaluation and quality control tests in the Persian Gulf. J. Mar. Syst. 2023, 240, 103875. [Google Scholar] [CrossRef]
- Li, L.; Sun, B.; Xue, C.; Zheng, Z.; Ma, Y. An Enhanced Transfer Learning Remote Sensing Inversion of Coastal Water Quality: A Case Study of Dissolved Oxygen. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 21065–21076. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O.; Seutloali, K.; Adelabu, S.; Shoko, C. Water quality monitoring in sub-Saharan African lakes: A review of remote sensing applications. Afr. J. Aquat. Sci. 2015, 40, 1–7. [Google Scholar] [CrossRef]




| Parameters | Mean | Std Dev | Min | Max | Range | Sample Size | Missing Data |
|---|---|---|---|---|---|---|---|
| Chla | 7.59 | 11.20 | 0.09 | 125.40 | 125.31 | 239 | 25 |
| TN | 414.42 | 609.56 | 0.18 | 4283.19 | 4283.01 | 124 | 140 |
| TP | 26.69 | 26.20 | 0.02 | 100.73 | 100.71 | 104 | 160 |
| SDD | 2.59 | 0.89 | 0.80 | 4.60 | 3.80 | 206 | 58 |
| Turb | 1.52 | 1.72 | 0 | 10.50 | 10.50 | 83 | 181 |
| Bands | Wavelength (Micrometers) |
|---|---|
| Band 1—Aerosols | 0.43–0.45 |
| Band 2—Blue | 0.45–0.51 |
| Band 3—Green | 0.53–0.59 |
| Band 4—Red | 0.64–0.67 |
| Band 5—Near-Infrared (NIR) | 0.85–0.88 |
| Band 6—Shortwave Infrared (SWIR) 1 | 1.57–1.65 |
| Band 7—Shortwave Infrared (SWIR) 2 | 2.11–2.29 |
| Parameters | Chla (µg/L) | TN (µg/L) | TP (µg/L) | SDD (m) | Turb (NTU) |
|---|---|---|---|---|---|
| Chla (µg/L) | 1.00 | 0.50 | 0.24 | −0.39 | 0.27 |
| TN (µg/L) | 0.50 | 1.00 | 0.33 | −0.32 | 0.56 |
| TP (µg/L) | 0.24 | 0.33 | 1.00 | 0.33 | −0.23 |
| SDD (m) | −0.39 | −0.32 | 0.33 | 1.00 | 0.25 |
| Turb (NTU) | 0.27 | 0.56 | −0.23 | 0.25 | 1.00 |
| Metric | Chla (Single) µg/L | Chla (Ratio) µg/L | TSI_Chla (Single) | TSI_Chla (Ratio) | SDD (Single) (m) | SDD (Ratio) (m) | TSI_SDD (Single) | TSI_SDD (Ratio) |
|---|---|---|---|---|---|---|---|---|
| RMSE | 1.50 | 2.81 | 3.26 | 4.70 | 0.42 | 0.27 | 2.89 | 2.02 |
| MAE | 0.99 | 1.72 | 1.59 | 1.85 | 0.34 | 0.21 | 2.28 | 1.54 |
| MAPE (%) | 32.09 | 44.42 | 6.20 | 8.82 | 13.53 | 11.38 | 4.52 | 3.04 |
| Model | Significant Predictors (p < 0.05) | VIF Range | Notes |
|---|---|---|---|
| SDD (R42,R43,R61,R62) | R42, R43, R61, R62 | 1.66–3.00 | All predictors are significant, and acceptable VIFs |
| Chla (R21,R52,R43,R54) | R21, R52 (R43 and R54 borderline) | 3.86–12.83 | R43 and R54 borderline, collinearity observed (VIF > 10) |
| TSI(Chla) (R52,R54,R61) | R52, R54, R61 | 1.09–2.38 | All predictors are significant, low VIFs |
| TSI(SDD) (R42,R43,R71,R72) | R42, R43, R71, R72 | 1.49–5.06 | All predictors are significant, and acceptable VIFs |
| TSI(Chla) (B1,B2,B4,B7) | B1, B2, B4, B7 | 3.91–30.62 | All predictors significant, but DOSB2–B7 show high collinearity |
| TSI(SDD) (B1,B2,B3,B5) | B1, B2, B3, B5 | 8.74–40.49 | Significant, high collinearity across predictors |
| Chla (B1, B2, B4, B6) | B1, B2, B4, B6 | 5.80–40 | All predictors significant; however, high VIF values (>30 for B4, B6). Residuals suggest mild heteroscedasticity. |
| SDD (B1,B2,B3) | B1, B2, B3 | 15.45–50.6 | High collinearity, interpret cautiously |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiwanuka, M.; Leslie, R.; Gidudu, A.; Obubu, J.P.; Melesse, A.; Balaji Bhaskar, M.S. Evaluating Eutrophication and Water Clarity on Lake Victoria’s Ugandan Coast Using Landsat Data. Sustainability 2025, 17, 9056. https://doi.org/10.3390/su17209056
Kiwanuka M, Leslie R, Gidudu A, Obubu JP, Melesse A, Balaji Bhaskar MS. Evaluating Eutrophication and Water Clarity on Lake Victoria’s Ugandan Coast Using Landsat Data. Sustainability. 2025; 17(20):9056. https://doi.org/10.3390/su17209056
Chicago/Turabian StyleKiwanuka, Moses, Randy Leslie, Anthony Gidudu, John Peter Obubu, Assefa Melesse, and Maruthi Sridhar Balaji Bhaskar. 2025. "Evaluating Eutrophication and Water Clarity on Lake Victoria’s Ugandan Coast Using Landsat Data" Sustainability 17, no. 20: 9056. https://doi.org/10.3390/su17209056
APA StyleKiwanuka, M., Leslie, R., Gidudu, A., Obubu, J. P., Melesse, A., & Balaji Bhaskar, M. S. (2025). Evaluating Eutrophication and Water Clarity on Lake Victoria’s Ugandan Coast Using Landsat Data. Sustainability, 17(20), 9056. https://doi.org/10.3390/su17209056








