Heuristic Optimization Rules Applied for the Sustainable Design of Lightweight Engineering Structures Under Loads Subject to Random Changes
Abstract
1. Introduction
2. Methods
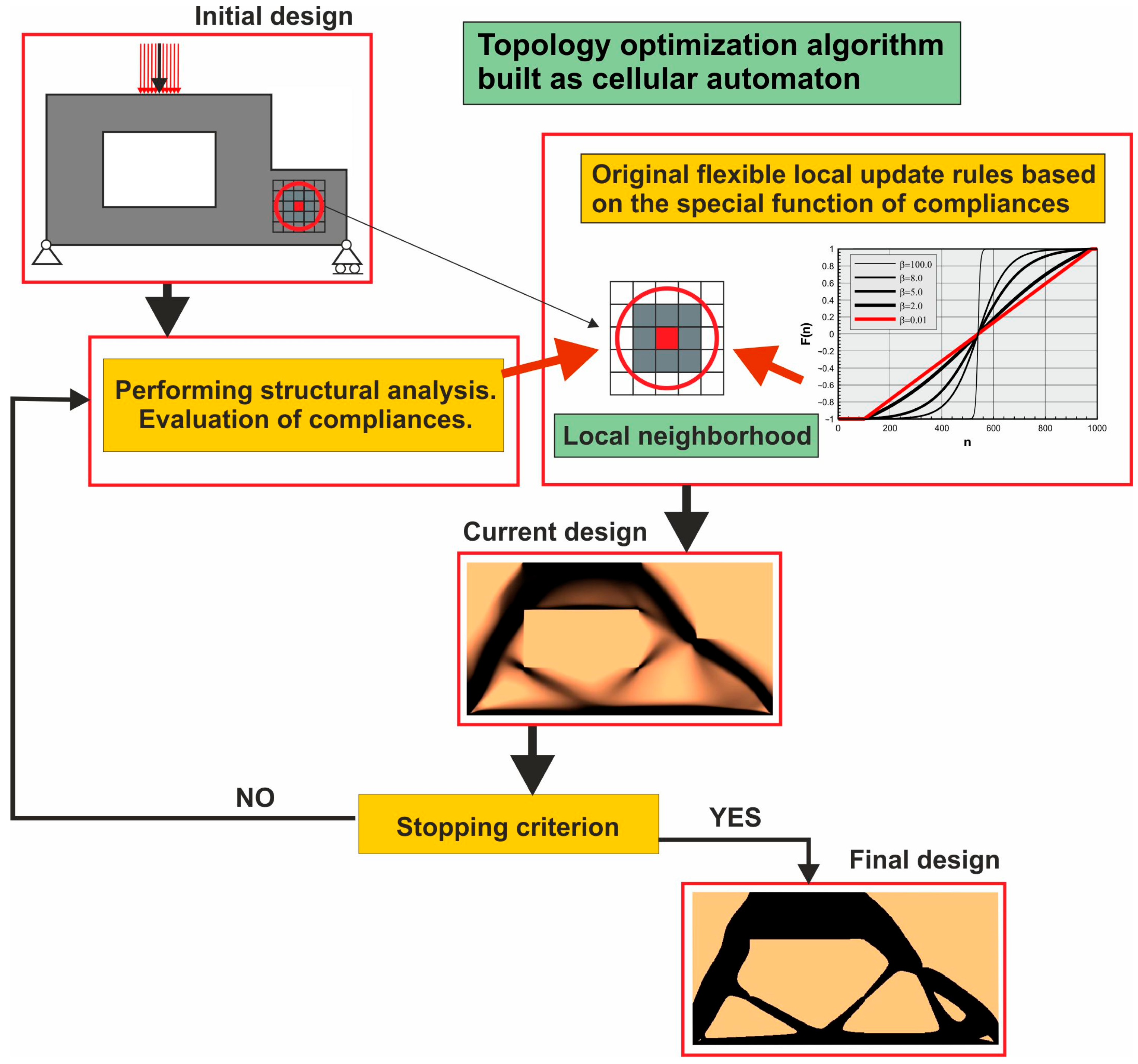
2.1. Lightweight Design Through the Utilization of Topology Optimization
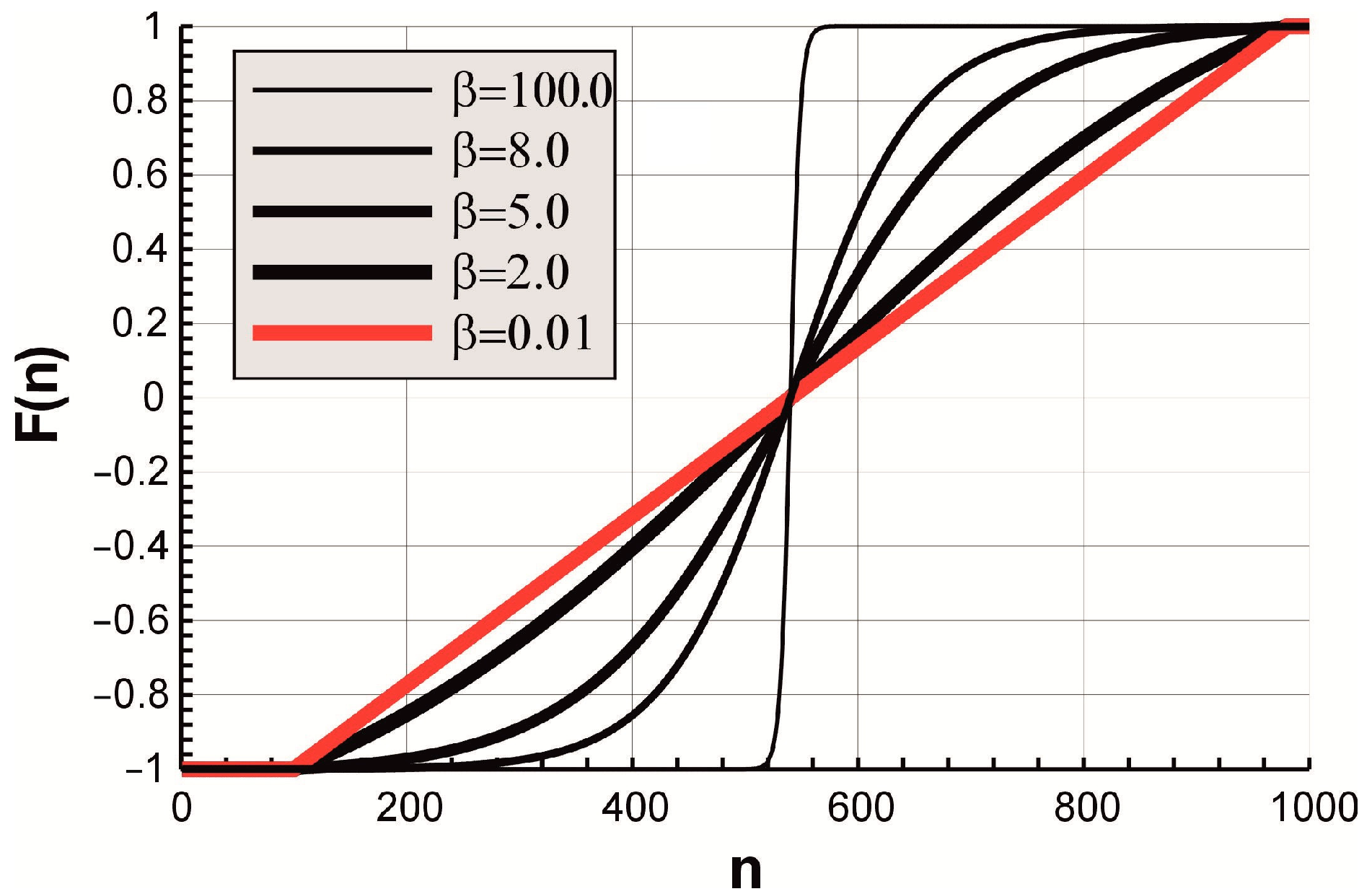
2.2. Heuristic Optimization Tool for Use in Sustainable Design
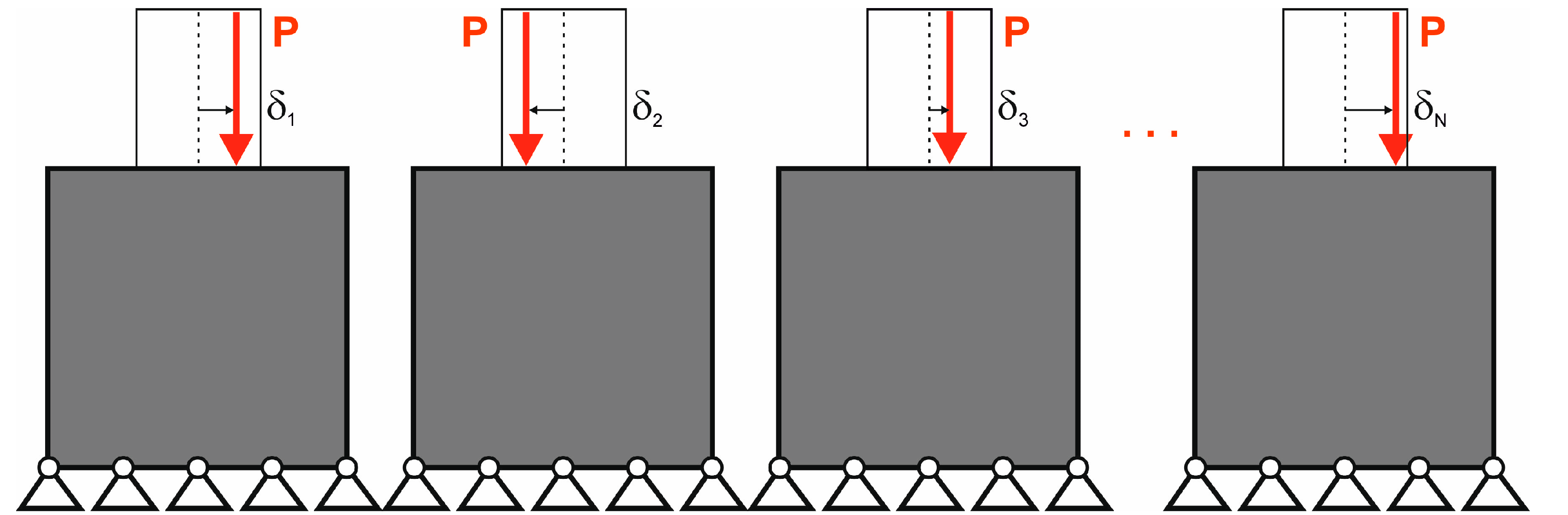
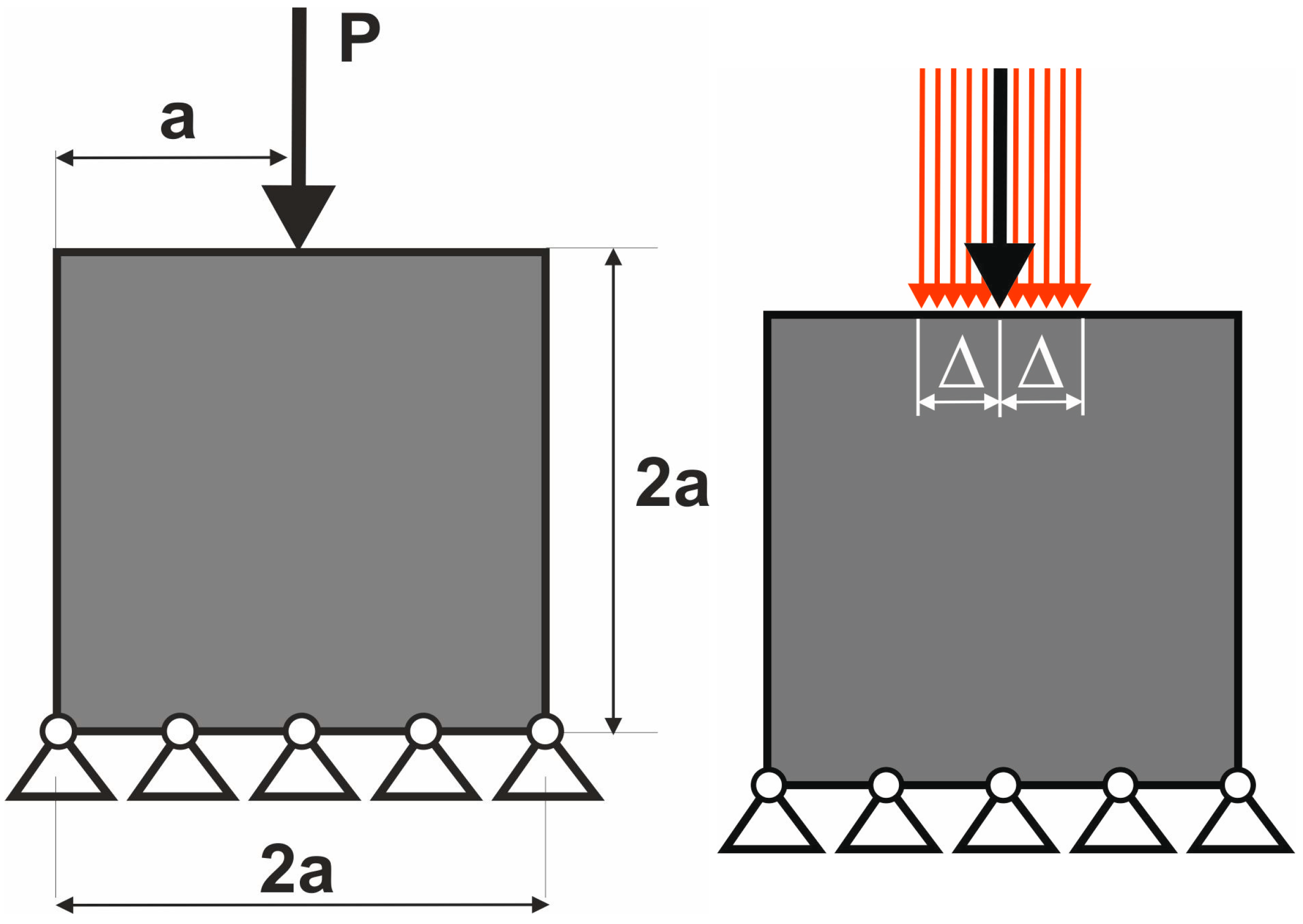
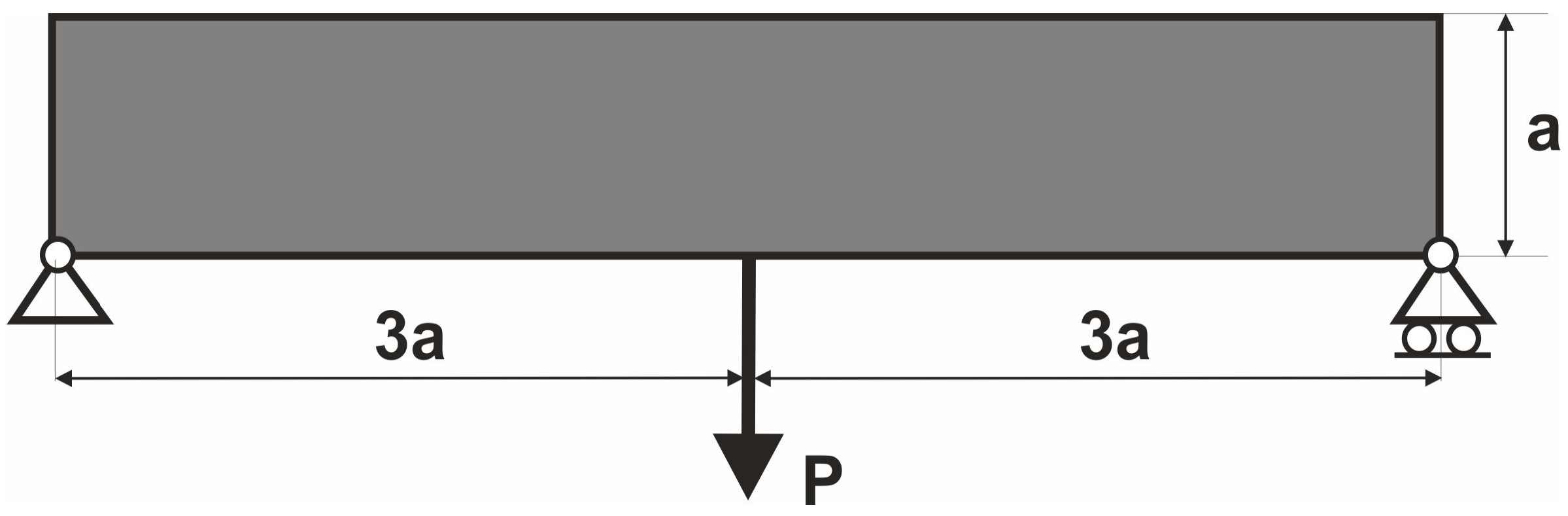
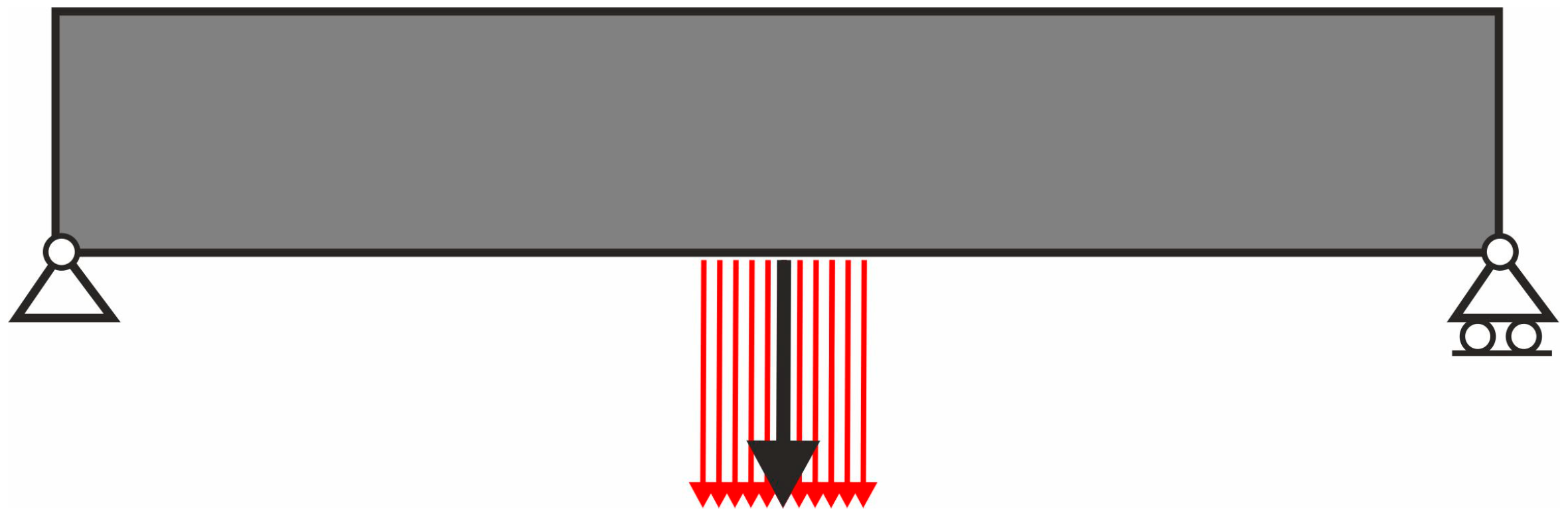
2.3. Simulation of Loads Applied at Randomly Selected Positions
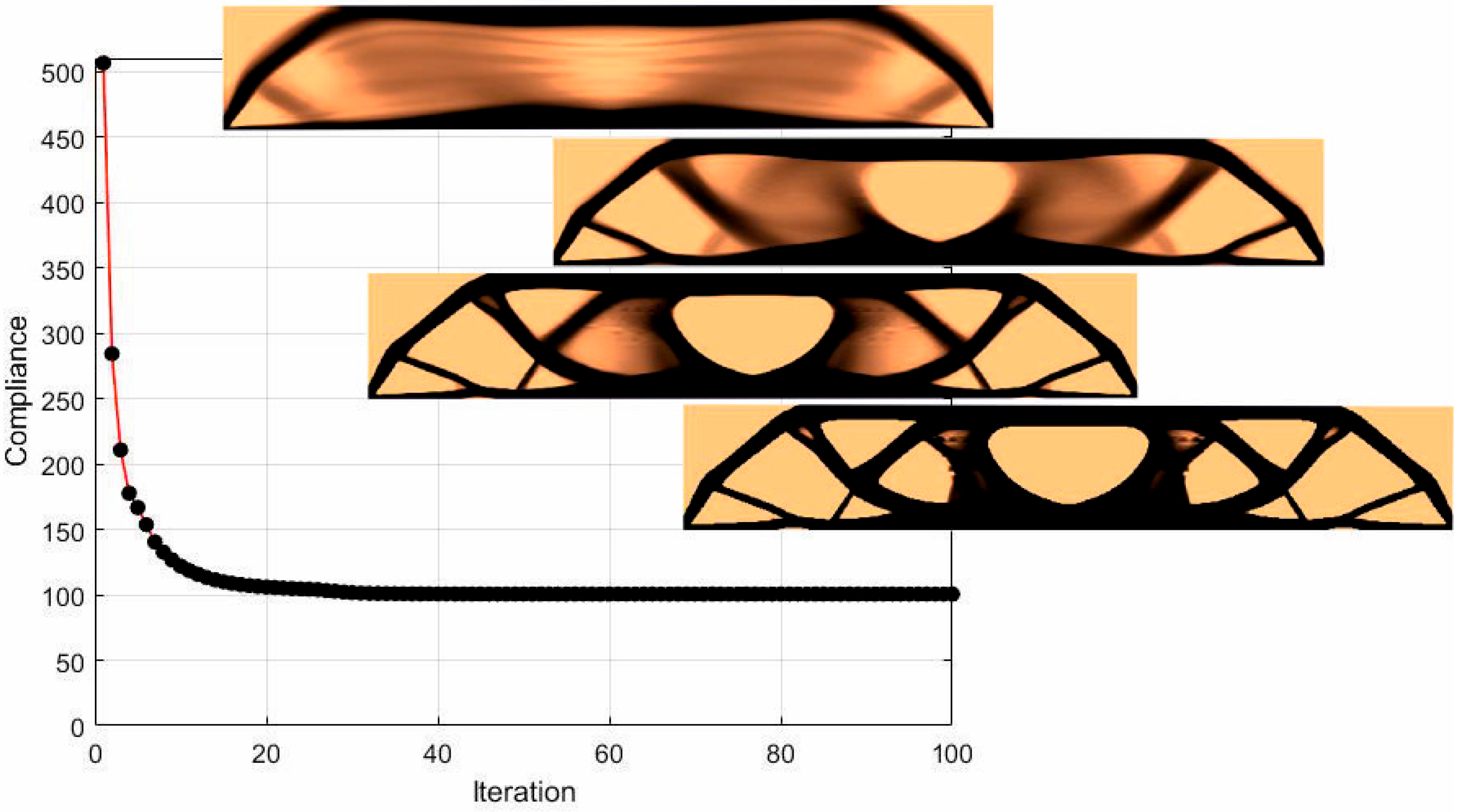
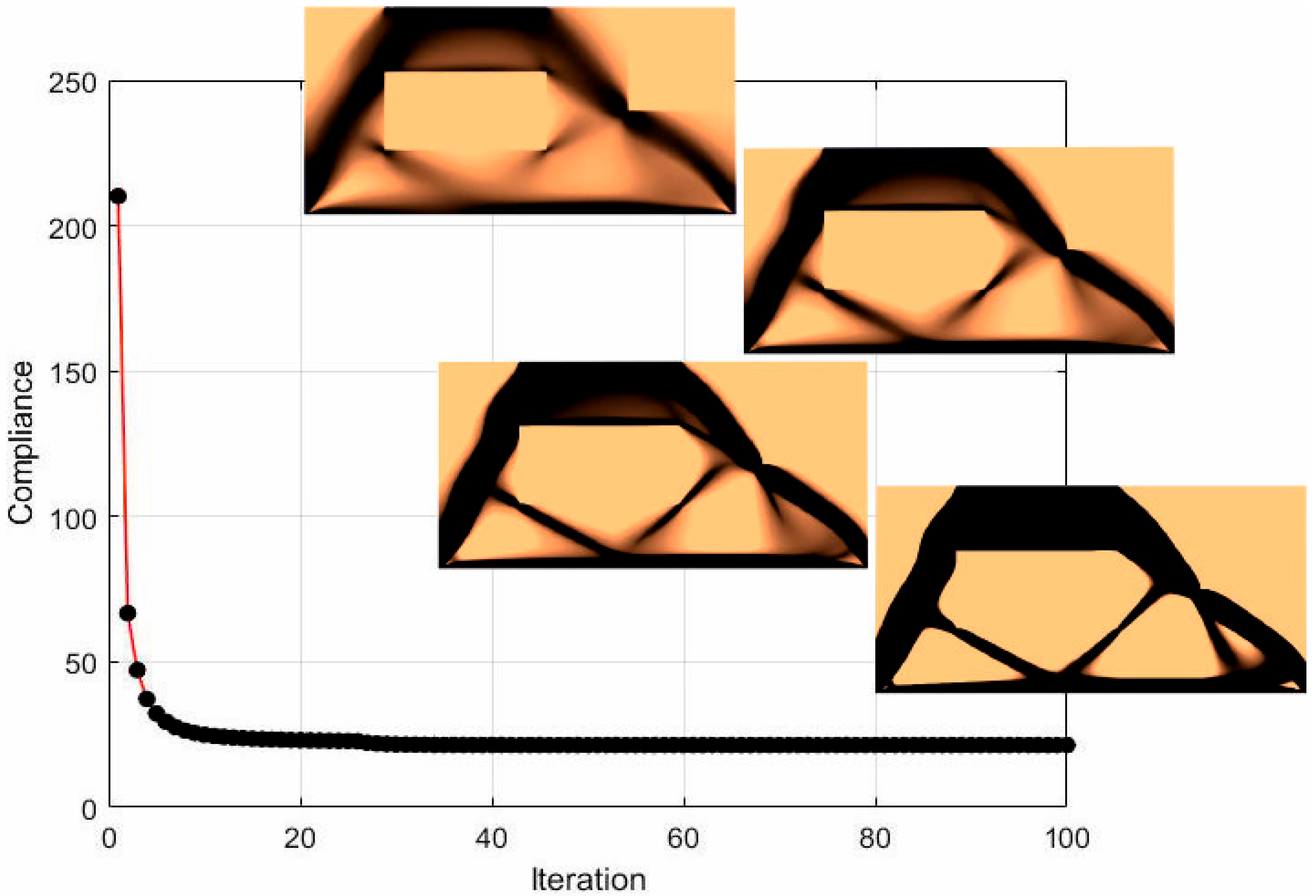
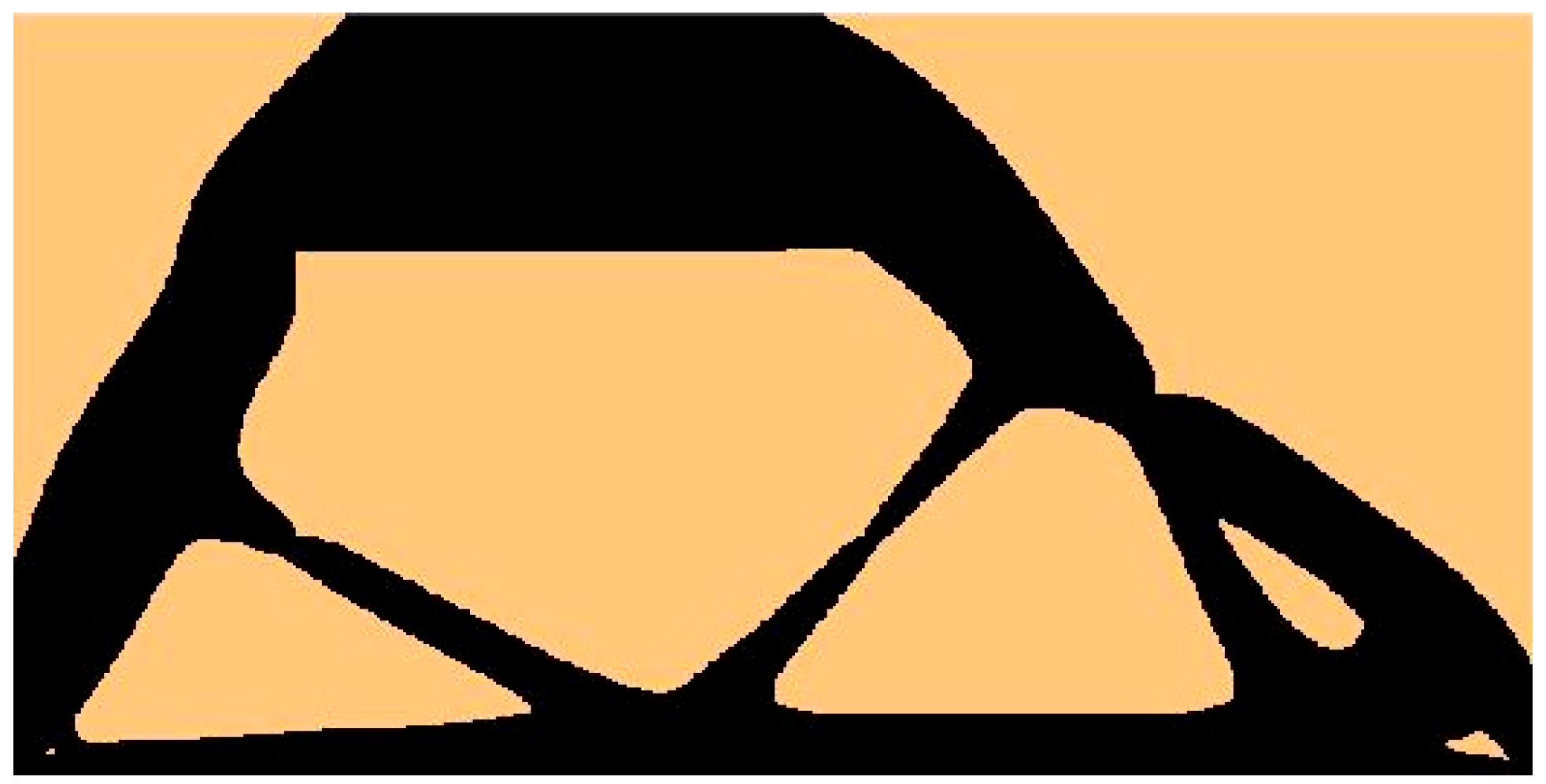
3. Results
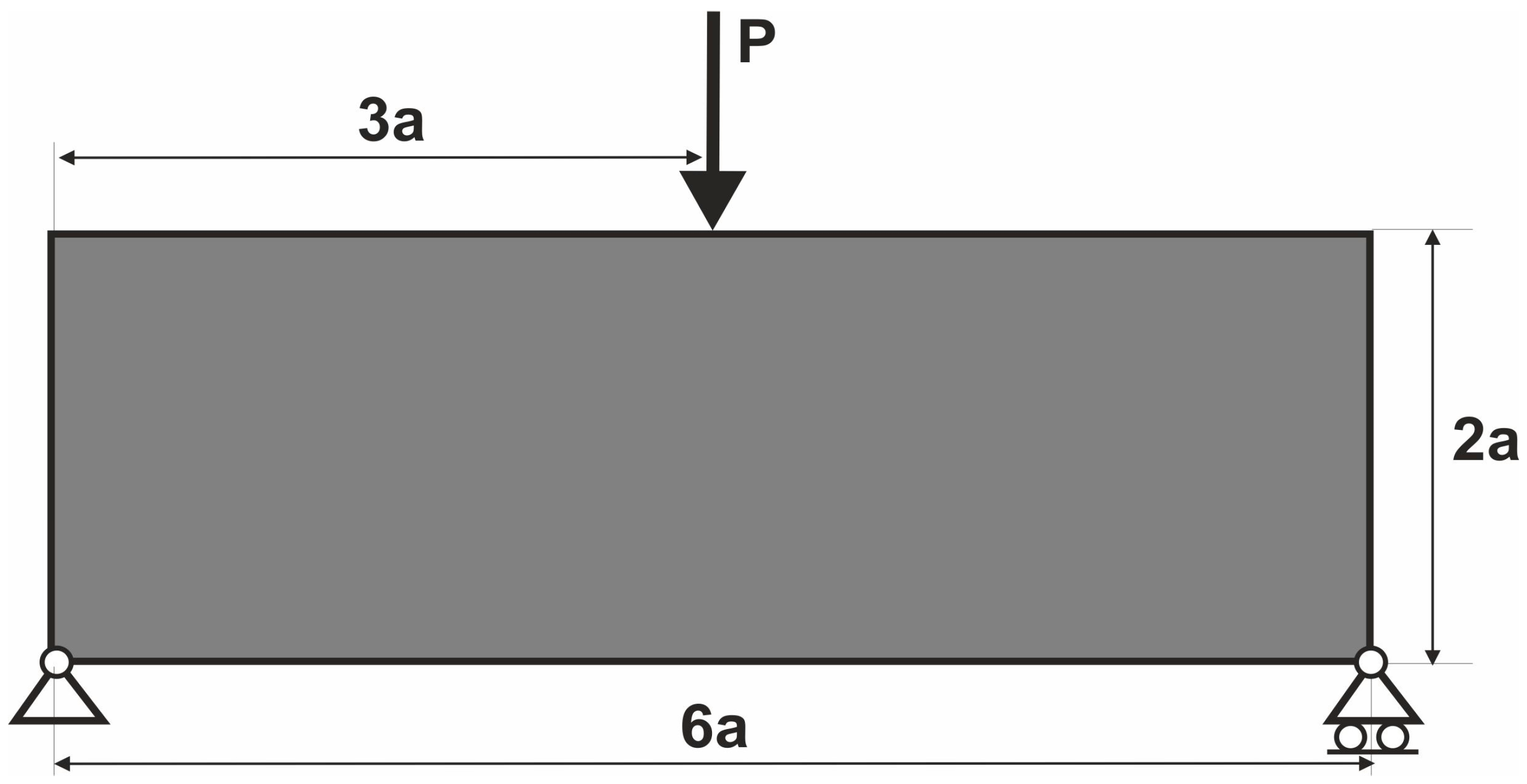
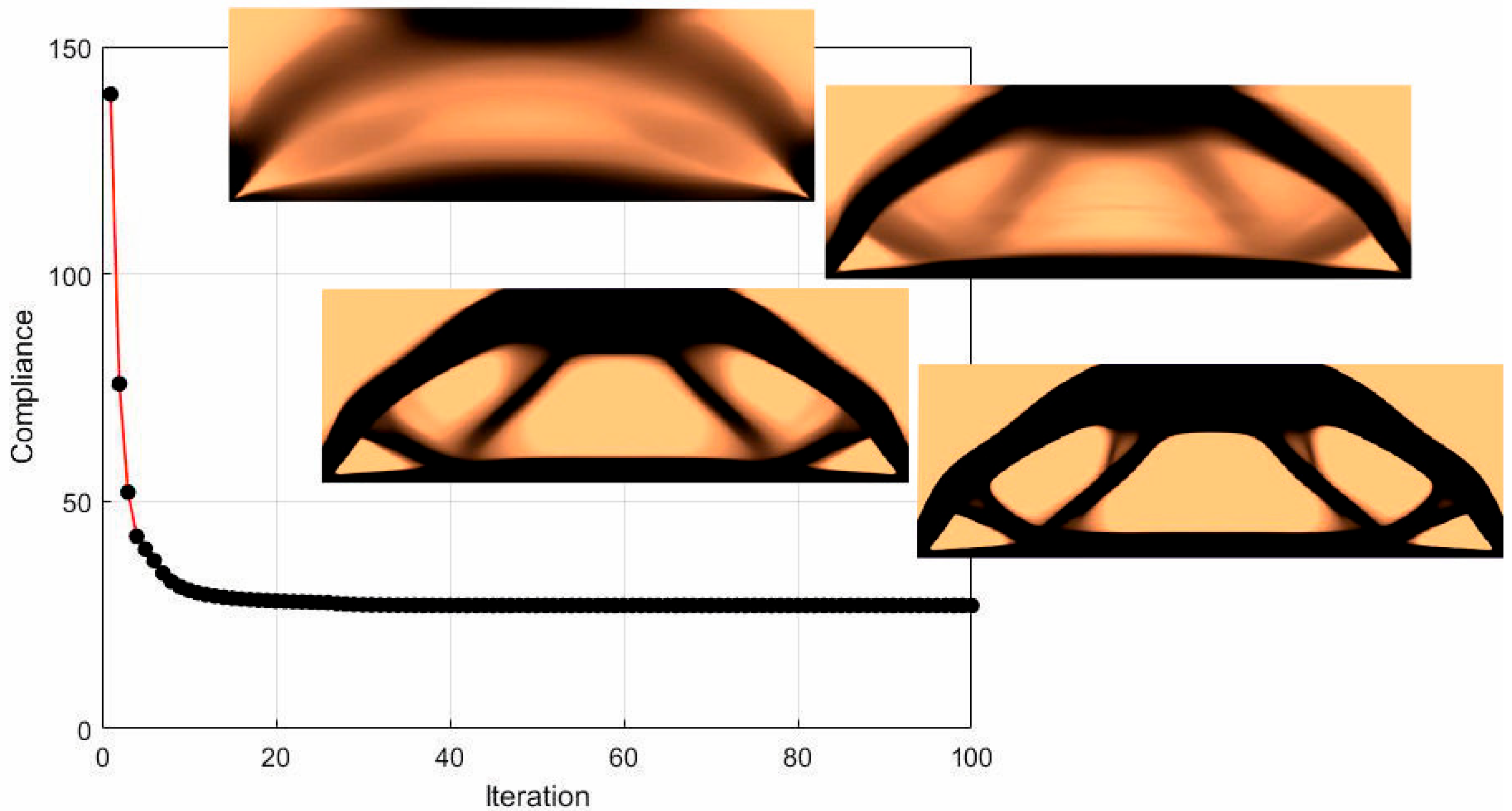
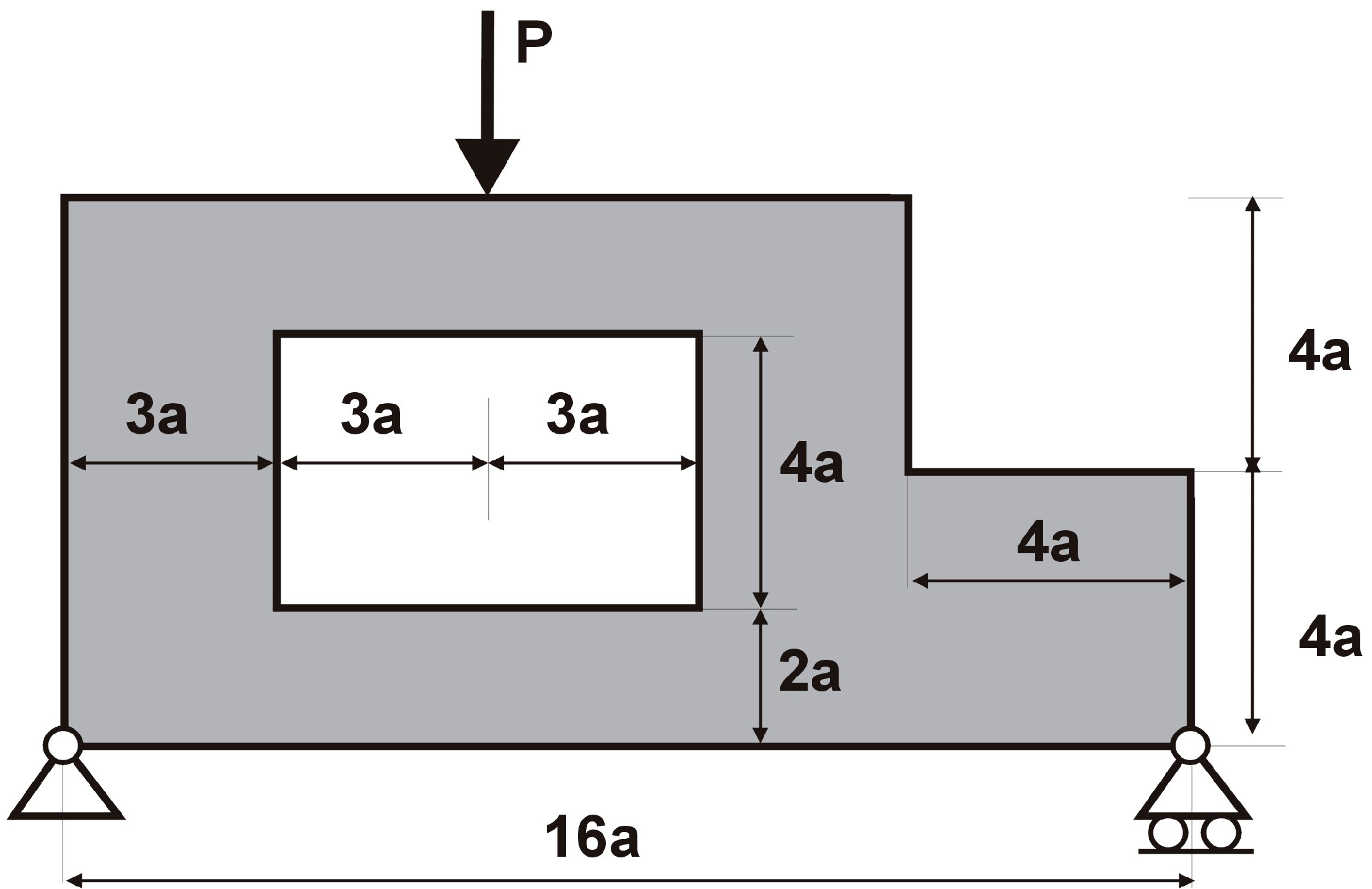
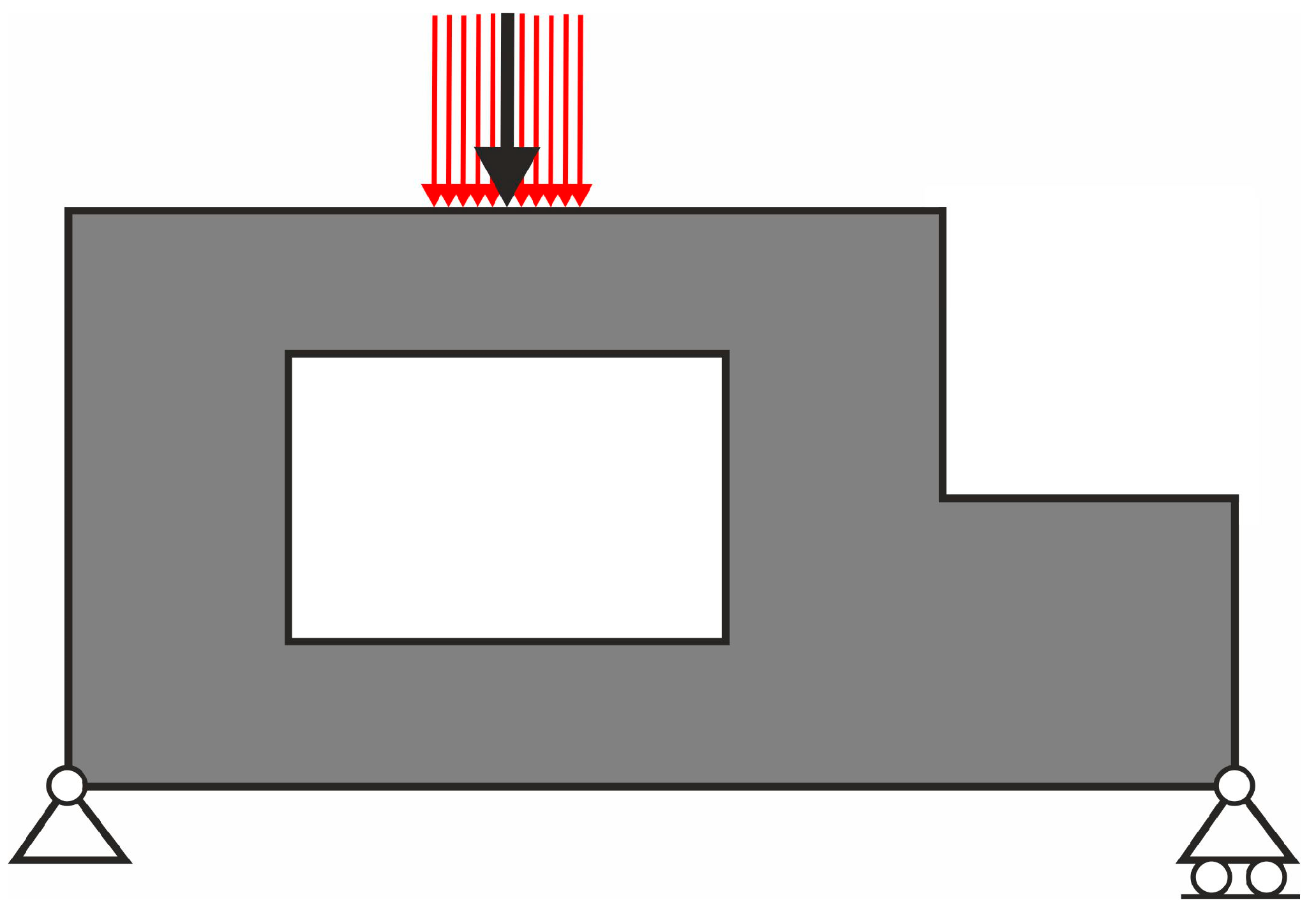
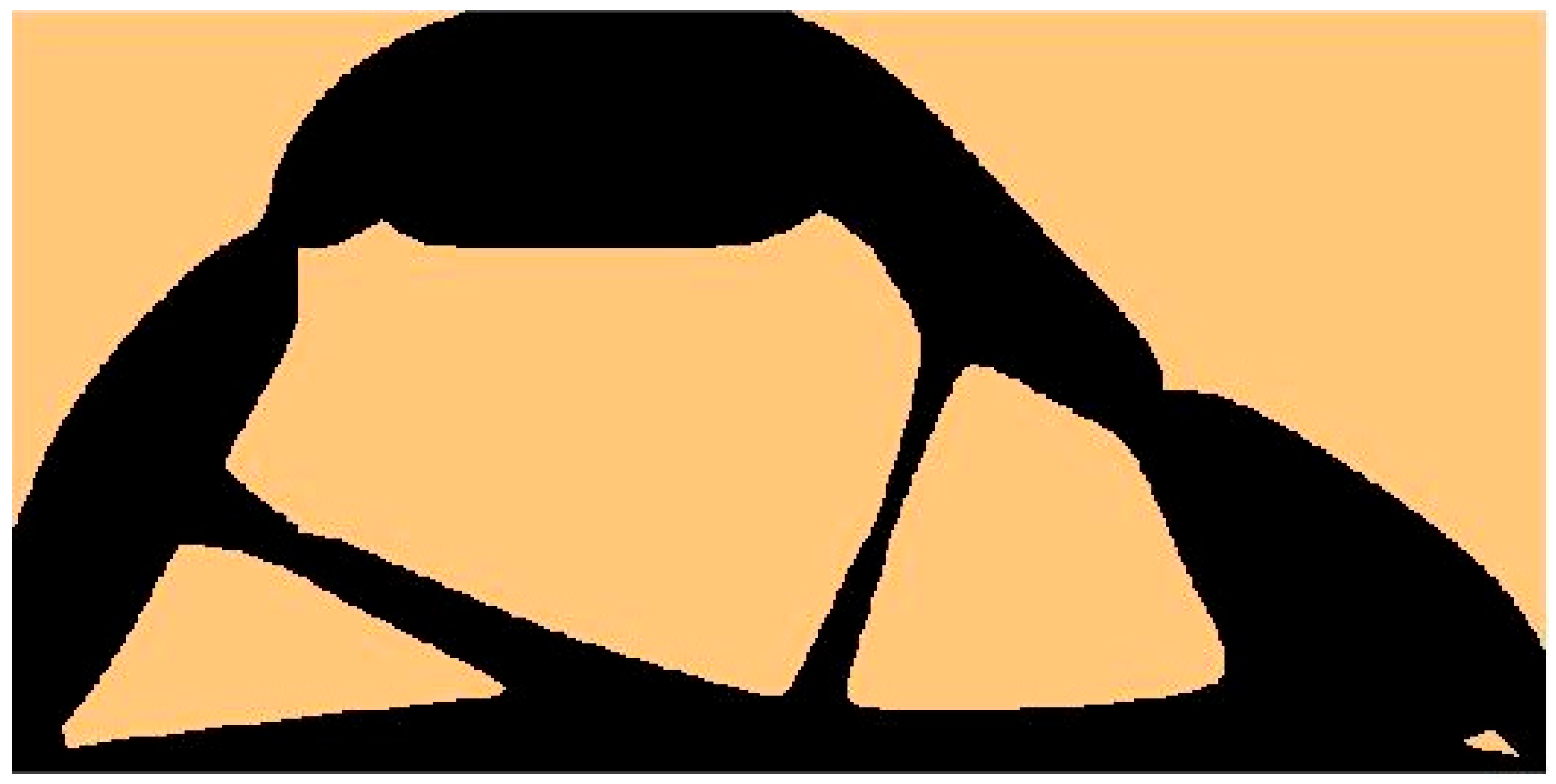
3.1. The Test Structure 1
3.2. The Test Structure 2
3.3. The Test Structure 3
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mathur, V.; Farouq, M.M.; Labaran, Y.H. The carbon footprint of construction industry: A review of direct and indirect emission. J. Sustain. Constr. Mater. Technol. 2021, 6, 101–115. [Google Scholar] [CrossRef]
- Hanifa, M.; Agarwal, R.; Sharma, U.; Thapliyal, P.C.; Singh, L.P. A review on CO2 capture and sequestration in the construction industry: Emerging approaches and commercialised technologies. J. CO2 Util. 2023, 67, 102292. [Google Scholar] [CrossRef]
- Kim, H.C.; Wallington, T.J. Life Cycle Assessment of Vehicle Lightweighting: A Physics-Based Model To Estimate Use-Phase Fuel Consumption of Electrified Vehicles. Environ. Sci. Technol. 2016, 50, 11226–11233. [Google Scholar] [CrossRef]
- Lu, Q.; Zhou, G.H.; Xiao, Z.D.; Chang, F.T.; Tian, C.L. A selection methodology of key parts based on the characteristic of carbon emissions for low-carbon design. Int. J. Adv. Manuf. Technol. 2017, 94, 3359–3373. [Google Scholar] [CrossRef]
- Duriez, E.; Morlier, J.; Charlotte, M.; Azzaro-Pantel, C. Ecodesign with topology optimization. Procedia CRIP 2022, 109, 454–459. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, H.; Zhang, L.; Bao, H.H.; Liu, Z.F. Low-carbon design of structural components by integrating material and structural optimization. Int. J. Adv. Manuf. Technol. 2018, 95, 4547–4560. [Google Scholar] [CrossRef]
- Lee, A.W.; Chung, S.Y.; Low, J.S.C.; Lu, W.F. Beyond light weighting, adapting topology optimisation to support ecodesign. Procedia CRIP 2023, 116, 366–371. [Google Scholar] [CrossRef]
- He, B.; Tang, W.; Wang, J.; Huang, S.; Deng, Z.; Wang, Y. Low-carbon conceptual design based on product life cycle assessment. Int. J. Adv. Manuf. Technol. 2015, 81, 863–874. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X. Sustainable design of reinforced concrete structural members using embodied carbon emission and cost optimization. J. Build. Eng. 2021, 44, 102940. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology optimization. In Theory, Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Y.; Nguyen-Thanh, N.; Li, W.; Li, S.; Zhou, K. Adaptive topology optimization for enhancing resistance to brittle fracture using the phase field model. Comput. Methods Appl. Mech. Eng. 2024, 431, 117237. [Google Scholar] [CrossRef]
- Fairclough, H.E.; He, L.; Asfaha, T.B.; Rigby, S. Adaptive topology optimization of fail-safe truss structures. Struct. Multidisc. Optim. 2023, 66, 148. [Google Scholar] [CrossRef]
- Senatore, G.; Wang, Y. Topology Optimization of Adaptive Structures: New Limits of Material Economy. Comput. Methods Appl. Mech. Eng. 2024, 422, 116710. [Google Scholar] [CrossRef]
- Rong, Y.; Zhao, Z.L.; Feng, X.Q.; Xie, Y.M. Structural topology optimization with an adaptive design domain. Comput. Methods Appl. Mech. Eng. 2022, 389, 114382. [Google Scholar] [CrossRef]
- Herrero-Pérez, D.; Picó-Vicente, S.G.; Martínez-Barberá, H. Adaptive density-based robust topology optimization under uncertain loads using parallel computing. Eng. Comput. 2024, 40, 21–43. [Google Scholar] [CrossRef]
- Vadillo Morillas, A.; Meneses Alonso, J.; Bustos Caballero, A.; Castejón Sisamón, C.; Ceruti, A. Adaptive Variable Design Algorithm for Improving Topology Optimization in Additive Manufacturing Guided Design. Inventions 2024, 9, 70. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, X.; Zhu, B.; Wang, R.; Cui, C.; Zhang, H. Topology Optimization of Geometrically Nonlinear Structures Based on a Self-Adaptive Material Interpolation Scheme. Machines 2023, 11, 1047. [Google Scholar] [CrossRef]
- Wang, Y.; Sigmund, O. Topology optimization of multi-material active structures to reduce energy consumption and carbon footprint. Struct. Multidisc. Optim. 2024, 67, 5. [Google Scholar] [CrossRef]
- Ryan-Johnson, W.P.; Wolfe, L.C.; Byron, C.R.; Nagel, J.K.; Zhang, H. A Systems Approach of Topology Optimization for Bioinspired Material Structures Design Using Additive Manufacturing. Sustainability 2021, 13, 8013. [Google Scholar] [CrossRef]
- Borda, F.; La Rosa, A.D.; Filice, L.; Gagliardi, F. Environmental impact of process constrained topology optimization design on automotive component’ life. Int. J. Mater. Form. 2023, 16, 48. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, W.; Li, R.; Zhou, J.; Luo, Z. Study on Sustainable Lightweight Design of Airport Waiting Chair Frame Structure Based on ANSYS Workbench. Sustainability 2024, 16, 5350. [Google Scholar] [CrossRef]
- Habeeb, H.A.; Wahab, D.A.; Azman, A.H.; Alkahari, M.R. Design Optimization Method Based on Artificial Intelligence (Hybrid Method) for Repair and Restoration Using Additive Manufacturing Technology. Metals 2023, 13, 490. [Google Scholar] [CrossRef]
- Tajs-Zielińska, K.; Bochenek, B. Novel topology optimization techniques adapted to strengthening of civil structures suffering from the effects of material degradation. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 052010. [Google Scholar] [CrossRef]
- Alkhatib, F.H.; Kasim, N.; Goh, W.I.; Al-masudi, A.A.H. Multidisciplinary Computational Optimization: An Integrated Approach to Achieve Sustainability in Tall Building Design at Early Stage—Review. In Proceedings of the Third International Sustainability and Resilience Conference, Climate Change, Sakheer, Bahrain, 15–16 November 2021. [Google Scholar]
- Kundu, R.D.; Zhang, X.S. Sustainability-oriented multimaterial topology optimization: Designing efficient structures incorporating environmental effects. Struct. Multidisc. Optim. 2025, 68, 17. [Google Scholar] [CrossRef]
- Zhao, B.; Yi, J.; Jiang, C.; Lu, X. Experimental study on seismic performance of super highrise building with topology optimized diagonal mega frame. J. Build. Eng. 2023, 76, 107003. [Google Scholar] [CrossRef]
- Stoiber, N.; Kromoser, B. Topology optimization in concrete construction: A systematic review on numerical and experimental investigations. Struct. Multidisc. Optim. 2021, 64, 1725–1749. [Google Scholar] [CrossRef]
- Amir, O. A topology optimization procedure for reinforced concrete structures. Comput. Struct. 2013, 114, 46–58. [Google Scholar] [CrossRef]
- Cui, H.; Xie, L.; Xiao, M.; Deng, M. Conceptual design of reinforced concrete structures using truss-like topology optimization. Arch. Civ. Eng. 2022, 68, 523–537. [Google Scholar] [CrossRef]
- Tajs-Zielińska, K. Topology Optimization of Periodic Structures Subject to Self-Weight Loading Using a Heuristic Method. Materials 2024, 17, 5652. [Google Scholar] [CrossRef]
- Bochenek, B.; Tajs-Zielińska, K. On predicting optimal structural topologies in the presence of random loads. Materials 2025, 18, 2819. [Google Scholar] [CrossRef]
- Zhan, D.; Tian, A.Q.; Ni, S.Q. Optimizing PID control for multi-model adaptive high-speed rail platform door systems with an improved metaheuristic approach. Int. J. Electr. Power Energy Syst. 2025, 169, 110738. [Google Scholar] [CrossRef]
- Houssein, E.H.; Saeed, M.K.; Hu, G.; Al-Sayed, M.A. Metaheuristics for Solving Global and Engineering Optimization Problems: Review, Applications, Open Issues and Challenges. Arch. Comput. Methods Eng. 2024, 31, 4485–4519. [Google Scholar] [CrossRef]
- Akan, T.; Anter, A.M.; Etaner-Uyar, A.Ş.; Oliva, D. Engineering Applications of Modern Metaheuristics. In Studies in Computational Intelligence; Springer International Publishing: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Gresia, J.; Senhora, F.V.; Paulino, G.H. Topology optimization with continuously varying load magnitude and direction for compliance minimization. Struct. Multidisc. Optim. 2024, 67, 179. [Google Scholar] [CrossRef]
- Wang, D.; Gao, W. Robust topology optimization under multiple independent uncertainties of loading positions. Int. J. Numer. Meth. Eng. 2020, 121, 4944–4970. [Google Scholar] [CrossRef]
- Kumar, A.; Chhabra, D. Parametric topology optimization approach for sustainable development of customized orthotic appliances using additive manufacturing. Mech. Adv. Mat. Struct. 2023, 31, 5276–5289. [Google Scholar] [CrossRef]
- Mantawy, I.M.; Migliorino, J.; Mackin, A.; Ahmed, A.; Hanoun, Z.; Donovan, T.; Dustal, M.; Felixbrod, A.; Ruhl, R.; Sibor, D.; et al. Topology-Optimization-Based Additive Construction for Sustainability. In Proceedings of the IABSE Symposium: Construction’s Role for a World in Emergency, Manchester, UK, 10–14 April 2024. [Google Scholar]
- Liu, J.; Ma, Y. Sustainable Design-Oriented Level Set Topology Optimization. J. Mech. Des. 2017, 139, 011403. [Google Scholar] [CrossRef]
- Fassi, H.F.; Aniyou, H. Towards an Optimal Motor Mounting Bracket Using Topology Optimization Combined with Sustainability and Manufacturing Cost Analysis. MPER 2023, 14, 109–116. [Google Scholar] [CrossRef]
- Hoschke, K.; Pfaff, A.; Kappe, K.; Hahn, P.; May, M. Topology Optimization and Additive Manufacturing of a Cargo Door Latch Fitting. In Proceedings of the Towards More Sustainable Aviation, AIAA Aviation Forum and Ascend, Las Vegas, NV, USA, 29 July–2 August 2024. [Google Scholar] [CrossRef]
- Azad, M.M.; Kim, D.; Khalid, S.; Kim, H.S. Topology Optimization and Fatigue Life Estimation of Sustainable Medical Waste Shredder Blade. Mathematics 2022, 10, 1863. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, Y.; Feng, J. From Material Selection to Structural Topology Optimization: Sustainable Product Design Based on Carbon Footprint Allocation. J. Mech. Des. 2024, 146, 122001. [Google Scholar] [CrossRef]
- Shobeiri, V. Structural topology optimization and application to sustainability. In Proceedings of the ACAM10: 10th Australasian Congress on Applied Mechanics, Melbourne, Australia, 1 January 2021. [Google Scholar]
- Ogunnowo, E.O.; Ogu, E.; Egbumokei, P.I.; Dienagha, I.I.; Digitemie, W.N. Conceptual Model for Topology Optimization in Mechanical Engineering to Enhance Structural Efficiency and Material Utilization. IRE 2024, 7, 1705977. [Google Scholar]
- Logo, J.; Ismail, H. Milestones in the 150-Year History of Topology Optimization: A Review. Eng. Opt. 2020, 27, 97–132. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology optimization approaches: A comparative review. Struct. Multidisc. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Tang, T.; Wang, L.; Zhu, M.; Zhang, H.; Dong, J.; Yue, W.; Xia, H. Topology Optimization: A Review for Structural Designs Under Statics Problems. Materials 2024, 17, 5970. [Google Scholar] [CrossRef]
- O’Shaughnessy, C.; Masoero, E.; Gosling, D. Topology optimization using the discrete element method. Part 1: Methodology, validation, and geometric nonlinearity. Meccanica 2022, 57, 1213–1231. [Google Scholar] [CrossRef]
- Oliviera, H.L.; Leonel, E.D. Boundary element method applied to topology optimization using the level set method and an alternative velocity regularization. Meccanica 2019, 54, 549–563. [Google Scholar] [CrossRef]
- Bendsøe, M.P. Optimal shape design as a material distribution problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Zhou, M.; Rozvany, G. The COC algorithm, Part II: Topological, geometrical and generalized shape optimization. Comput. Methods Appl. Mech. Eng. 1991, 89, 309–336. [Google Scholar] [CrossRef]
- Inou, N.; Shimotai, N.; Uesugi, T. A cellular automaton generating topological structures. In Proceedings of the 2nd European Conference on Smart Structures and Materials, Glasgow, Scotland, 12–14 October 1994. [Google Scholar] [CrossRef]
- Inou, N.; Uesugi, T.; Iwasaki, A.; Ujihashi, S. Self-organization of mechanical structure by cellular automata. Key Eng. Mater. 1998, 145, 1115–1120. [Google Scholar] [CrossRef]
- Tajs-Zielińska, K.; Bochenek, B. Topology algorithm built as an automaton with flexible rules. Bull. Pol. Acad. Sci. Tech. Sci. 2021, 69, e138813. [Google Scholar] [CrossRef]
- Tajs-Zielińska, K.; Bochenek, B. Cellular Automata Approach to Topology Optimization of Graded Multi-Material Structures. Appl. Sci. 2023, 13, 2929. [Google Scholar] [CrossRef]
- Zaitsev, D.A. A generalized neighborhood for cellular automata. Theor. Comput. Sci. 2017, 666, 21–35. [Google Scholar] [CrossRef]
- Tovar, A.; Patel, N.; Kaushik, A.K.; Letona, G.A.; Renaud, J.E.; Sanders, B. Hybrid Cellular Automata: A biologically-inspired structural optimization technique. In Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Albany, NY, USA, 30 August–1 September 2004. [Google Scholar] [CrossRef]
- Bochenek, B. An easy way for the generation of structural topologies under random loads using cellular automata. Acta Polytech. Hung. 2023, 20, 9–28. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, C. Robust structural topology optimization under random field loading uncertainty. Struct. Multidisc. Optim. 2024, 50, 517–522. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tajs-Zielińska, K.; Bochenek, B. Heuristic Optimization Rules Applied for the Sustainable Design of Lightweight Engineering Structures Under Loads Subject to Random Changes. Sustainability 2025, 17, 7011. https://doi.org/10.3390/su17157011
Tajs-Zielińska K, Bochenek B. Heuristic Optimization Rules Applied for the Sustainable Design of Lightweight Engineering Structures Under Loads Subject to Random Changes. Sustainability. 2025; 17(15):7011. https://doi.org/10.3390/su17157011
Chicago/Turabian StyleTajs-Zielińska, Katarzyna, and Bogdan Bochenek. 2025. "Heuristic Optimization Rules Applied for the Sustainable Design of Lightweight Engineering Structures Under Loads Subject to Random Changes" Sustainability 17, no. 15: 7011. https://doi.org/10.3390/su17157011
APA StyleTajs-Zielińska, K., & Bochenek, B. (2025). Heuristic Optimization Rules Applied for the Sustainable Design of Lightweight Engineering Structures Under Loads Subject to Random Changes. Sustainability, 17(15), 7011. https://doi.org/10.3390/su17157011






