The Effect of Generator-Side Charges on Investment in Power Generation and Transmission Under Demand Uncertainty
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.3. Research Objectives and Contributions
2. Model
2.1. Settings
2.2. Optimal Investment Timing and Capacity in the TL Framework
2.3. Optimal Investment Timing and Capacity in the GL Framework
3. Numerical Analysis
3.1. Parameters
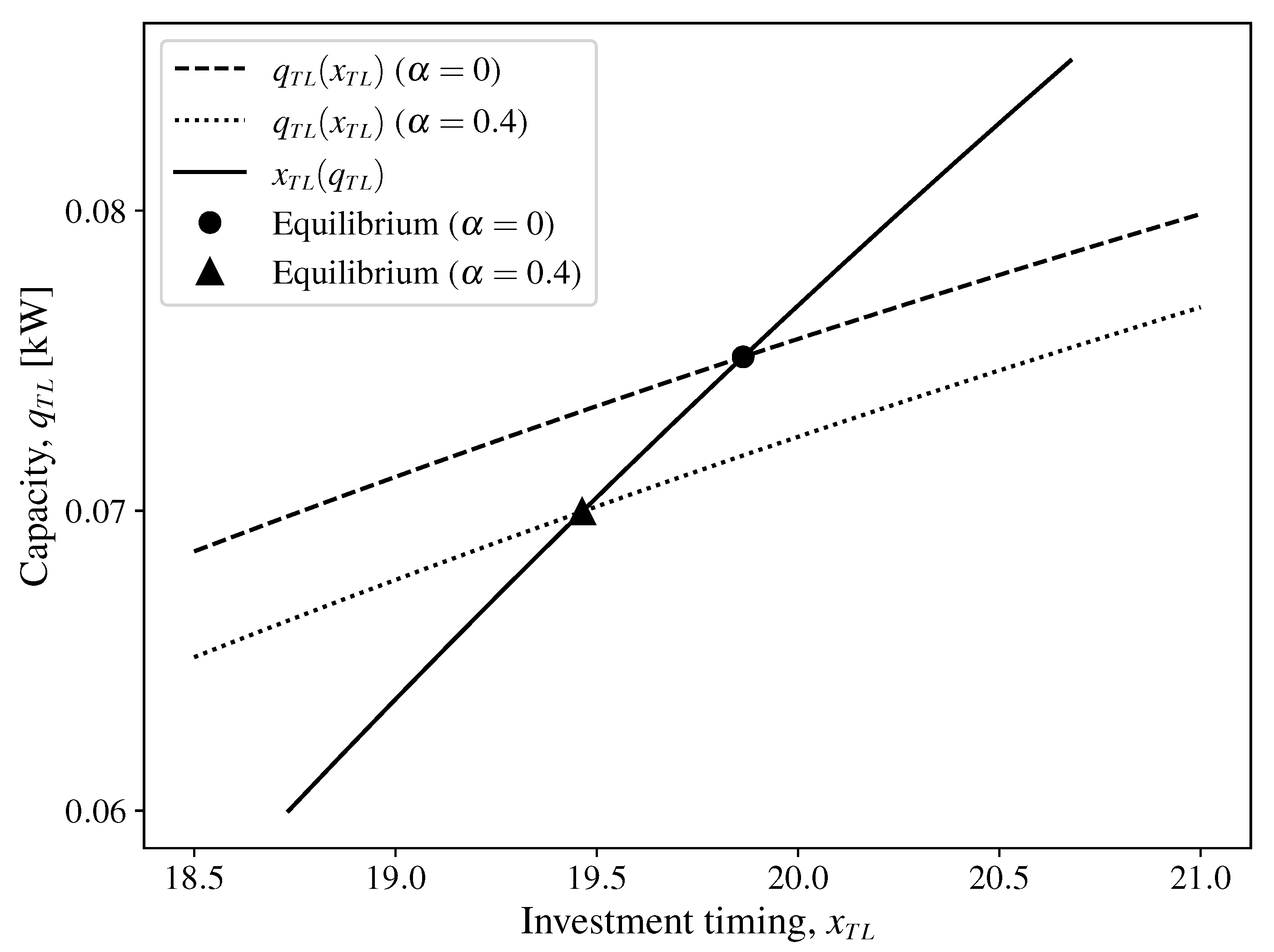
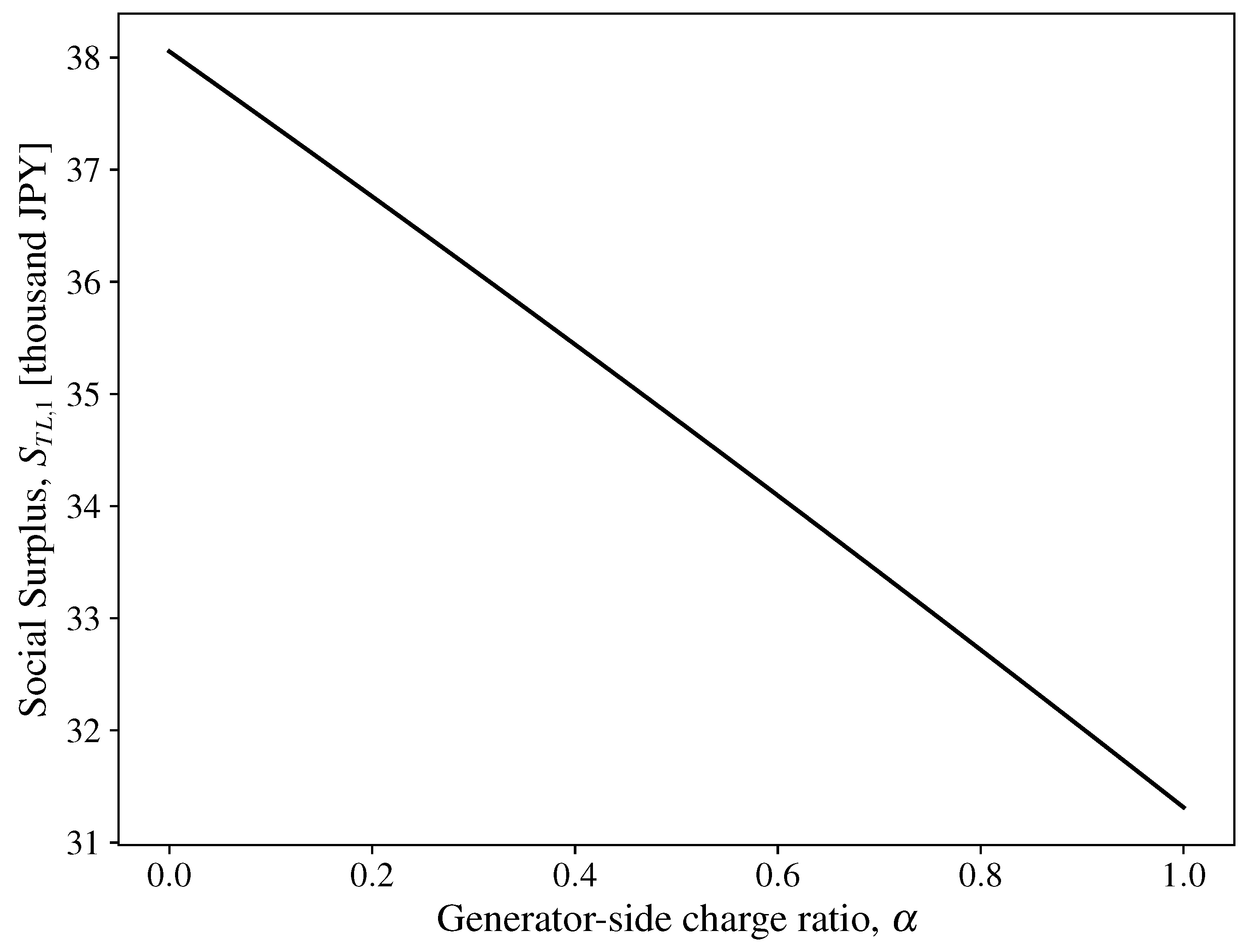
3.2. Analysis of Investment Timing, Capacity, and Social Surplus in the TL Framework
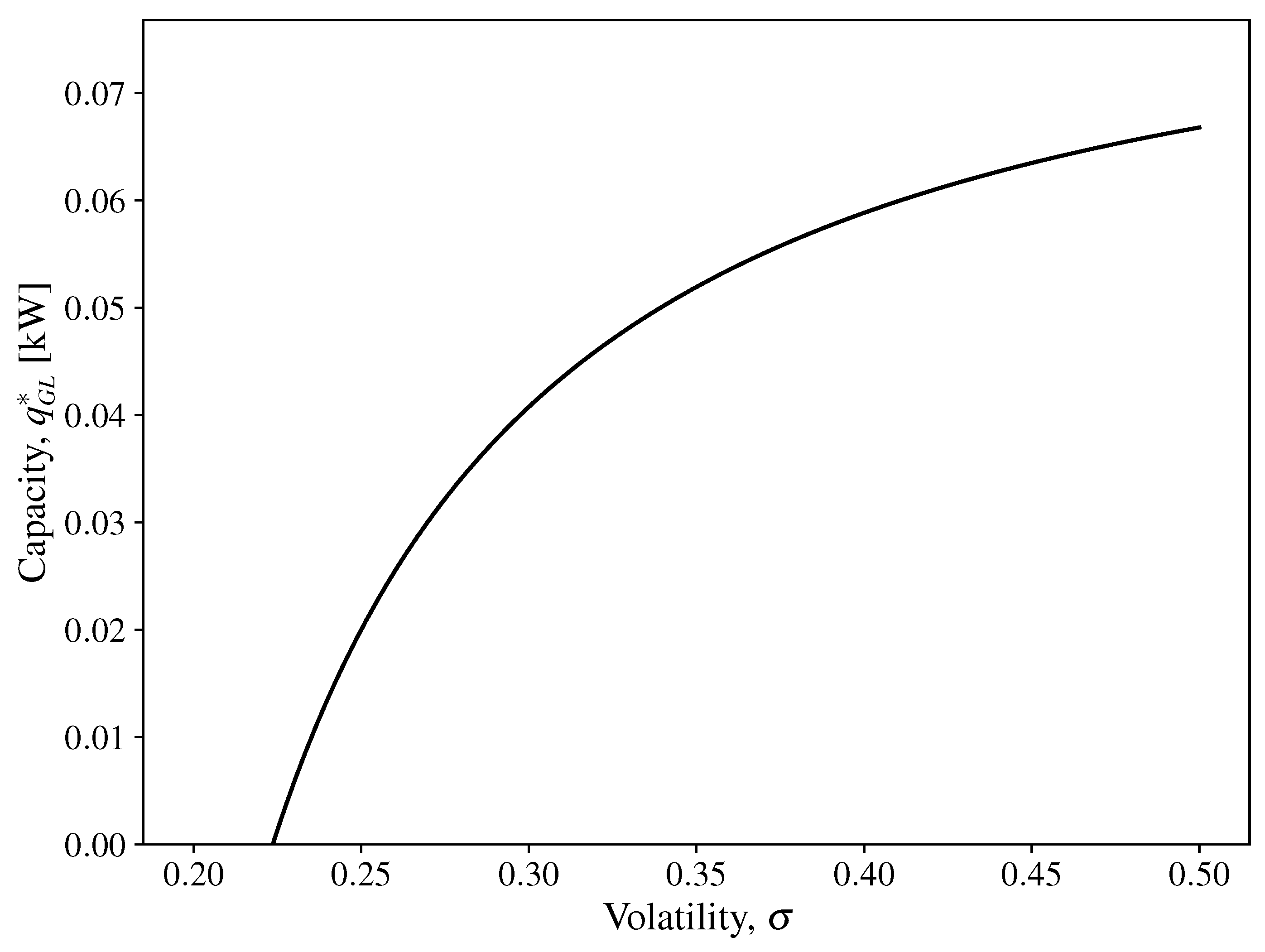
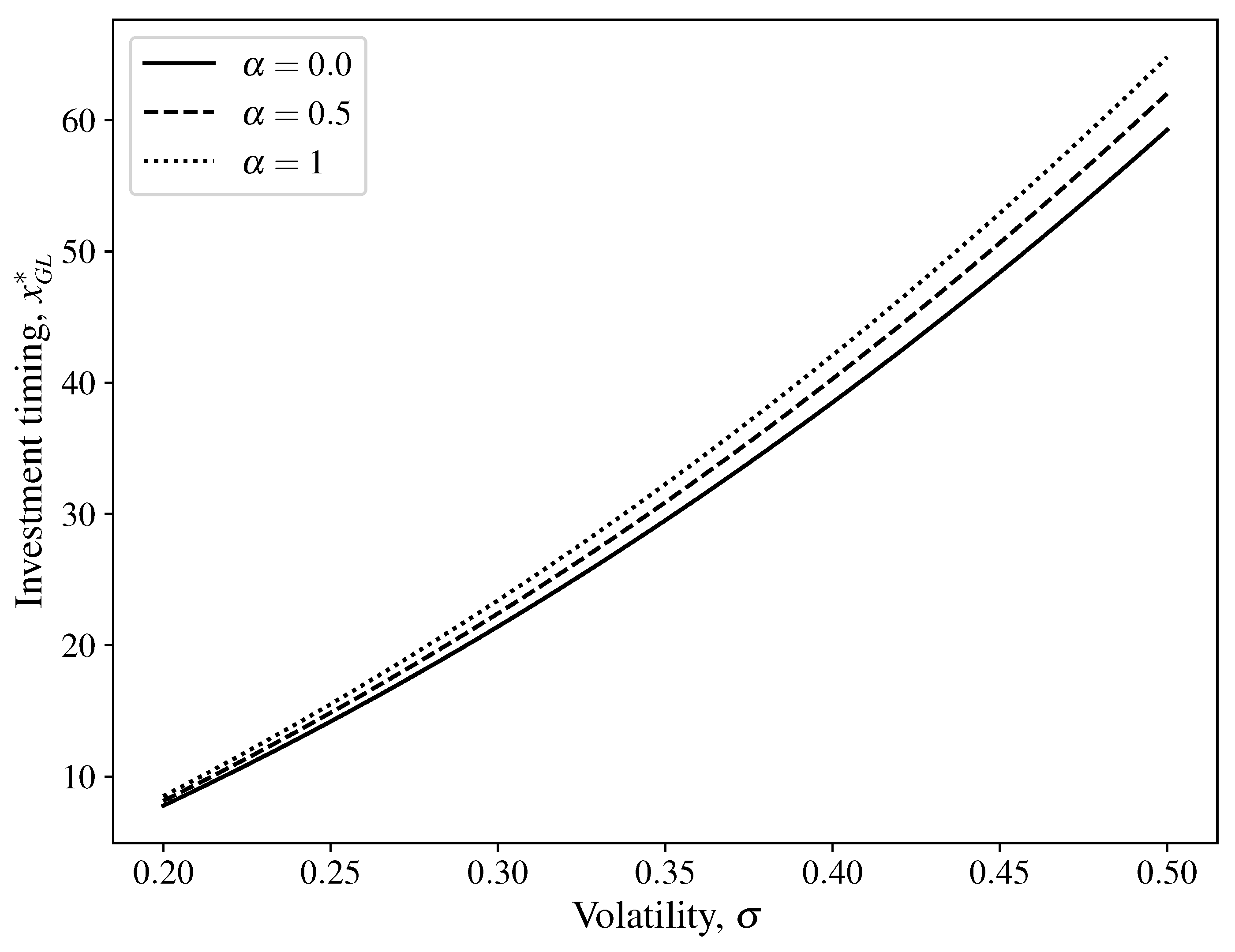
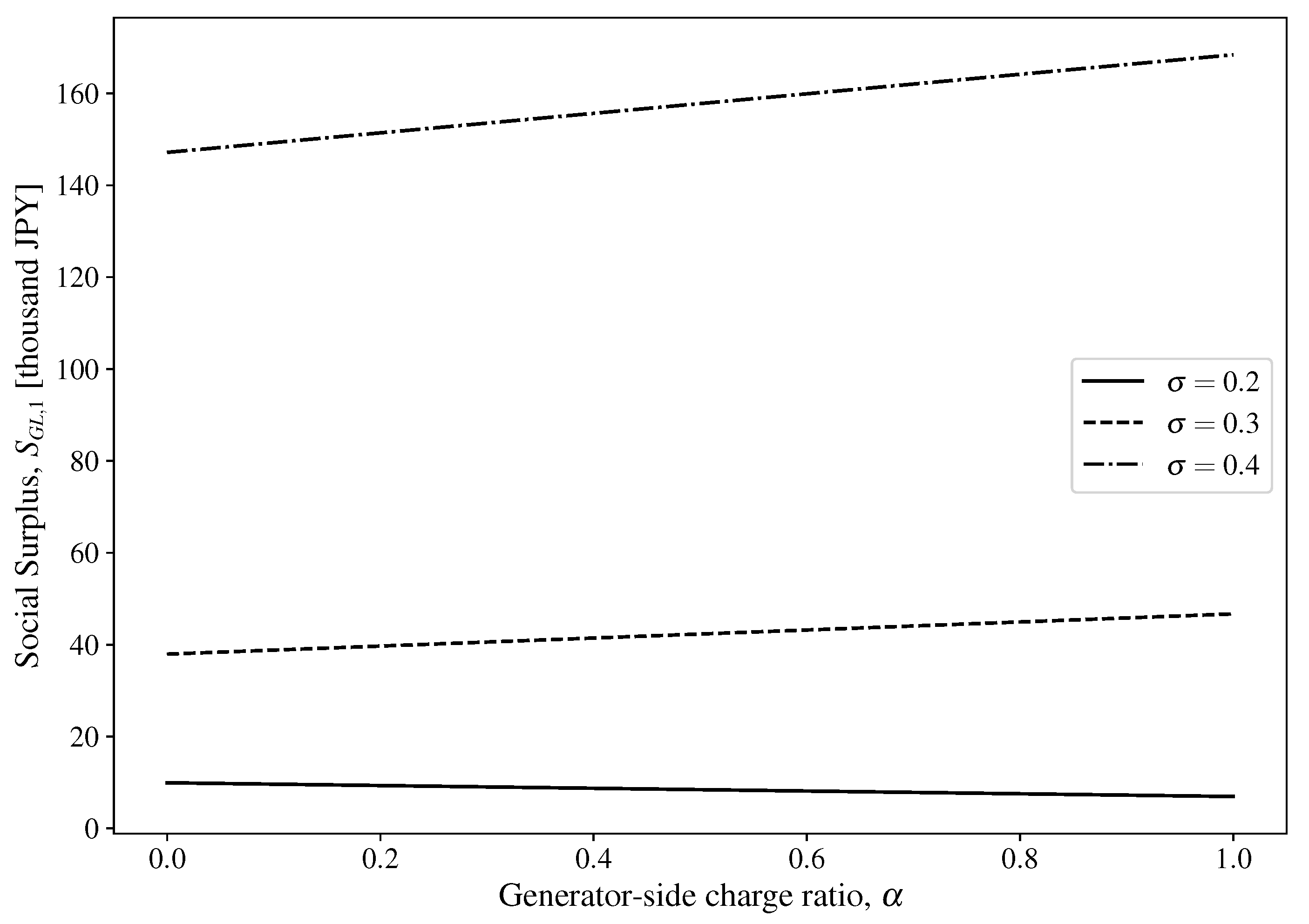
3.3. Analysis of Investment Timing, Capacity, and Social Surplus in the GL Framework
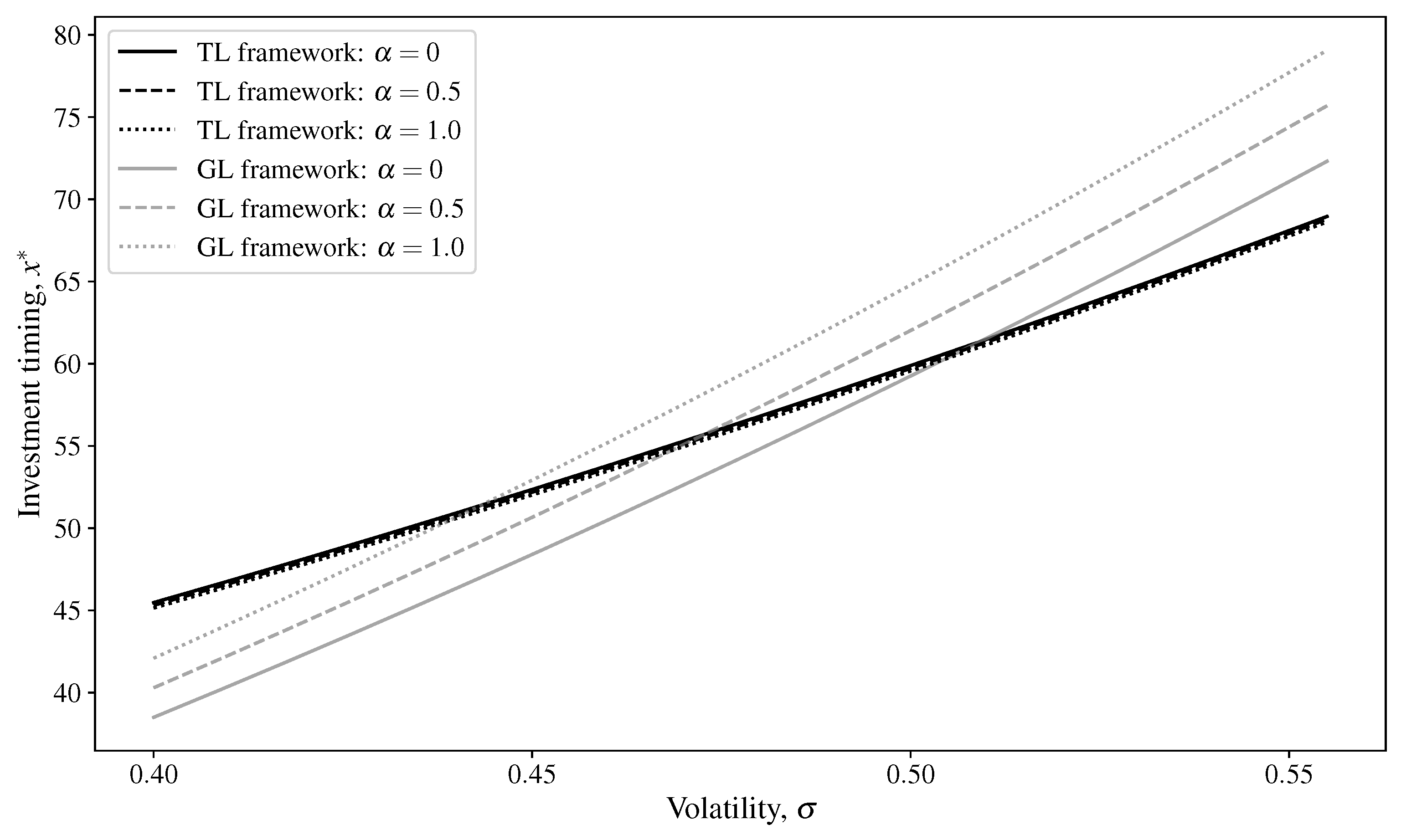
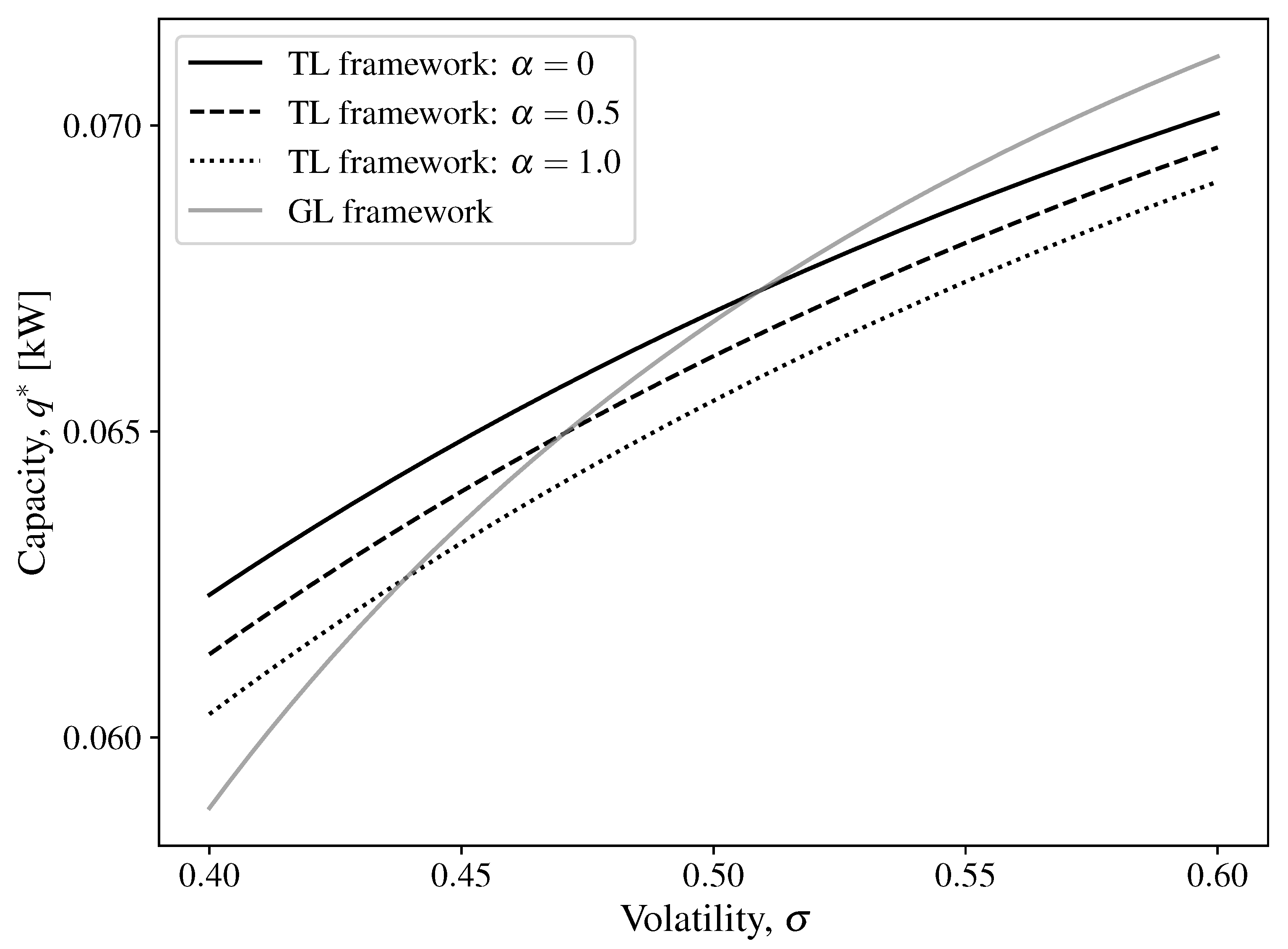
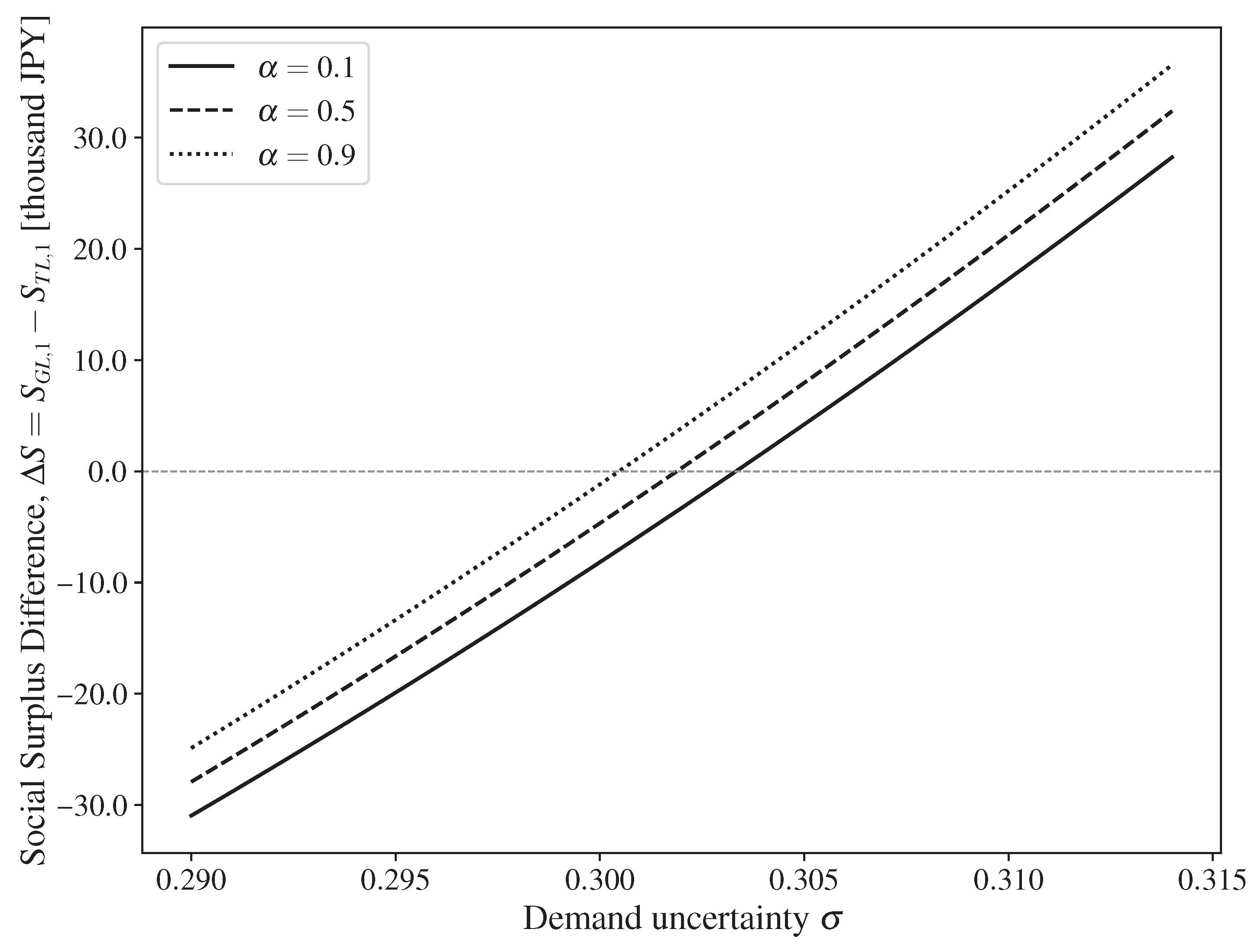
3.4. Comparative Analysis of Investment Timing, Capacity, and Social Surplus
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Chen, Y.; Goldfarb, L.; Gomis, M.I.; Matthews, J.B.R.; Berger, S.; et al. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. In Climate Change 2021: The Physical Science Basis; Technical report, Intergovernmental Panel on Climate Change (IPCC); IPCC: Paris, France, 2021. [Google Scholar]
- IEA. World Energy Outlook 2023; IEA: Paris, France, 2023. [Google Scholar]
- IREA. Renewable Power Generation Costs in 2022; IRENA: Bonn, Germany, 2023. [Google Scholar]
- IEA. Renewables 2023: Analysis and forecast to 2028; IEA: Paris, France, 2023. [Google Scholar]
- Notton, G.; Nivet, M.L.; Voyant, C.; Paoli, C.; Darras, C.; Motte, F.; Fouilloy, A. Intermittent and stochastic character of renewable energy sources: Consequences, cost of intermittence and benefit of forecasting. Renew. Sustain. Energy Rev. 2018, 87, 96–105. [Google Scholar] [CrossRef]
- Herding, L.; Cossent, R.; Rivier, M.; Bañales, S. Assessing the impact of renewable energy penetration and geographical allocation on transmission expansion cost: A comparative analysis of two large-scale systems. Sustain. Energy Grids Netw. 2024, 38, 101349. [Google Scholar] [CrossRef]
- IEA. Net Zero by 2050: A Roadmap for the Global Energy Sector; IEA: Paris, France, 2021. [Google Scholar]
- Newbery, D. Efficient Renewable Electricity Support: Designing an Incentive-compatible Support Scheme. Energy J. 2023, 44, 1–22. [Google Scholar] [CrossRef]
- Avar, A.; El-Eslami, M.K.S. A new benefit-based transmission cost allocation scheme based on capacity usage differentiation. Electr. Power Syst. Res. 2022, 208, 107880. [Google Scholar] [CrossRef]
- Agency for Natural Resources and Energy. Toward the Implementation of Generator-Side Transmission Charges; Agency for Natural Resources and Energy: Tokyo, Japan, 2023.
- Office of Gas and Electricity Markets (Ofgem). Assessment of Locational Pricing in the GB Electricity Market; Technical report; Office of Gas and Electricity Markets (Ofgem): London, UK, 2023.
- Ministry of Economy and Industry. Study on Transmission Tariff Systems in Foreign Countries; Ministry of Economy and Industry: New Delhi, India, 2024.
- Orfanos, G.A.; Tziasiou, G.T.; Georgilakis, P.S.; Hatziargyriou, N.D. Evaluation of transmission pricing methodologies for pool based electricity markets. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011; pp. 1–8. [Google Scholar]
- Kumar, N.; Reddy, Y.; Das, D.; Padhy, N. Allocation of transmission charge by using MVA-Mile approaches for restructured Indian power utility. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–29 July 2011; pp. 1–6. [Google Scholar]
- Xiao, Y.; Wang, X.; Wang, X.; Du, C. Transmission cost allocation by power tracing based equivalent bilateral exchanges. CSEE J. Power Energy Syst. 2016, 2, 1–10. [Google Scholar] [CrossRef]
- Rao, M.S.S.; Soman, S.A.; Chitkara, P.; Gajbhiye, R.K.; Hemachandra, N.; Menezes, B.L. Min-Max Fair Power Flow Tracing for Transmission System Usage Cost Allocation: A Large System Perspective. IEEE Trans. Power Syst. 2010, 25, 1457–1468. [Google Scholar] [CrossRef]
- Torres.; Lívi.; Ramos, F.S. Allocating Benefits Due to Shared Resources Using Shapley Value and Nucleolus in Dynamic Network Data Envelopment Analysis. Mathematics 2024, 12, 698. [Google Scholar] [CrossRef]
- Mehta, R.P.; Soman, S.A.; Rao, M.S.S. A novel method for transmission system cost allocation with better accuracy and fairness. Sådhanå 2022, 47, 62. [Google Scholar] [CrossRef]
- Grimm, V.; Martin, A.; Schmidt, M.; Weibelzahl, M.; Zöttl, G. Transmission and generation investment in electricity markets: The effects of market splitting and network fee regimes. Eur. J. Oper. Res. 2016, 254, 493–509. [Google Scholar] [CrossRef]
- Agaton, C.B.; Karl, H. A real options approach to renewable electricity generation in the Philippines. Energy Sustain. Soc. 2018, 8, 1. [Google Scholar] [CrossRef]
- Shahab Bahrami, M.H.A. A decentralized trading algorithm for an electricity market with generation uncertainty. Appl. Energy 2018, 218, 520–532. [Google Scholar] [CrossRef]
- Yang, J.; Fuss, S.; Johansson, D.J.; Azar, C. Investment dynamics in the energy sector under carbon price uncertainty and risk aversion. Energy Clim. Chang. 2023, 4, 100110. [Google Scholar] [CrossRef]
- Lavrutich, M.; Hagspiel, V.; Siddiqui, A.S. Transmission investment under uncertainty: Reconciling private and public incentives. Eur. J. Oper. Res. 2023, 304, 1167–1188. [Google Scholar] [CrossRef]
- Ito, K.; Tanaka, M.; Takashima, R. Strategic investment in power generation and transmission under a feed-in premium scheme: A game theoretic real options analysis. Ann. Oper. Res. 2024, 343, 349–372. [Google Scholar] [CrossRef]
- Newbery, D.M. European deregulation problems of liberalising the electricity industry. Eur. Econ. Rev. 2002, 46, 919–927. [Google Scholar] [CrossRef]
- Tohidi, Y.; Hesamzadeh, M.R.; Regairaz, F. Sequential coordination of transmission expansion planning with strategic generation investments. IEEE Trans. Power Syst. 2016, 32, 2521–2534. [Google Scholar] [CrossRef]
- Sauma, E.E.; Oren, S.S. Proactive planning and valuation of transmission investments in restructured electricity markets. J. Regul. Econ. 2006, 30, 358–387. [Google Scholar] [CrossRef]
- United States of America Federal Energy Regulatory Commission, U.S. Order Accepting Tariff Revisions Subject to Condition. 2022. Available online: https://www.ferc.gov/media/e-4-er22-2844-000 (accessed on 14 July 2025).
- Department of Energy & Climate Change Government Response to the Technical Consultation on the Model for Improving Grid Acces. 2010. Available online: https://www.gov.uk/government/organisations/department-of-energy-climate-change (accessed on 14 July 2025).
- NREL. Renewable Energy Zone (REZ) Transmission Planning Process: A Guidebook for Practitioners. 2017. Available online: https://docs.nrel.gov/docs/fy17osti/69043.pdf (accessed on 14 July 2025).
- Schwartz, E. Valuing Long-term Commodity Assets. J. Energy Financ. Dev. 1998, 3, 85–99. [Google Scholar] [CrossRef]
- Dixit, A.K.; Pindyck, R.S. Investment Under Uncertainty; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Agency for Natural Resources and Energy. On the Verification of Power Generation Costs: Document 4 from the 1st Meeting of the Working Group on Power Generation Cost Verification, Advisory Committee for Natural Resources and Energy. 2024. Available online: https://www.enecho.meti.go.jp/committee/council/basic_policy_subcommittee/mitoshi/cost_wg/2024/04.html (accessed on 16 May 2025).
- Agency for Natural Resources and Energy. Specifications of Each Power Source: Document 3 from the 8th Meeting of the Working Group on Power Generation Cost Verification, Advisory Committee for Natural Resources and Energy. 2021. Available online: https://www.enecho.meti.go.jp/committee/council/basic_policy_subcommittee/mitoshi/cost_wg/2021/008.html (accessed on 16 May 2025).
- Organization for Cross-Regional Coordination of Transmission Operators. On the Publication of Standard Unit Costs for Transmission Facilities. 2016. Available online: https://www.occto.or.jp/access/oshirase/2015/files/20160329_tanka_kouhyou.pdf (accessed on 16 May 2025).
- Electricity and Gas Market Surveillance Commission. On the Notification of Changes to the Specified Retail Supply Provisions Following Approval of Amendments to the Transmission Service Agreement: Document 3 from the 54th Meeting of the Tariff System Expert Committee. 2024. Available online: https://www.egc.meti.go.jp/english/committee/pdf/annualreport2024.pdf (accessed on 16 May 2025).


| Parameter | Symbol | Value |
|---|---|---|
| Annual operating time | h | 8760 [h] |
| Capacity factor | k | 0.7 |
| Expected growth rate of demand shock | 0.0 | |
| Volatility of demand shock | 0.1 | |
| Discount rate | 0.05 | |
| Slope of inverse demand function () | 0.001 | |
| Transmission tariff | 1.0 [JPY/kWh] | |
| Generation cost | C | 9.4 [JPY/kWh] |
| Installation cost of power generation | 161,000 [JPY/kW] | |
| Installation cost of transmission line | 54,600 [JPY/kW] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hiraiwa, H.; Ito, K.; Takashima, R. The Effect of Generator-Side Charges on Investment in Power Generation and Transmission Under Demand Uncertainty. Sustainability 2025, 17, 6824. https://doi.org/10.3390/su17156824
Hiraiwa H, Ito K, Takashima R. The Effect of Generator-Side Charges on Investment in Power Generation and Transmission Under Demand Uncertainty. Sustainability. 2025; 17(15):6824. https://doi.org/10.3390/su17156824
Chicago/Turabian StyleHiraiwa, Hirotaka, Kazuya Ito, and Ryuta Takashima. 2025. "The Effect of Generator-Side Charges on Investment in Power Generation and Transmission Under Demand Uncertainty" Sustainability 17, no. 15: 6824. https://doi.org/10.3390/su17156824
APA StyleHiraiwa, H., Ito, K., & Takashima, R. (2025). The Effect of Generator-Side Charges on Investment in Power Generation and Transmission Under Demand Uncertainty. Sustainability, 17(15), 6824. https://doi.org/10.3390/su17156824






