Abstract
As China commits to reaching peak carbon emissions and achieving carbon neutrality, accurately predicting the provincial carbon peak year is vital for designing effective, region-specific policies. This study proposes an integrated approach based on extended STIRPAT and GA-BiLSTM models to predict China’s provincial carbon peak year. First, based on panel data across 30 provinces in China from 2000 to 2023, we construct a multidimensional indicator system that encompasses socioeconomic factors, energy consumption dynamics, and technological innovation using the extended STIRPAT model, which explains 87.42% of the variation in carbon emissions. Second, to improve prediction accuracy, a hybrid model combining GA-optimized BiLSTM networks is proposed, capturing temporal dynamics and optimizing parameters to address issues like overfitting. The GA-BiLSTM model achieves an R2 of 0.9415, significantly outperforming benchmark models with lower error metrics. Third, based on the model constructed above, the peak years are projected for baseline, low-carbon, and high-carbon scenarios. In the low-carbon scenario, 19 provinces are projected to peak before 2030, which is 8 more than in the baseline scenario. Meanwhile, under the high-carbon scenario, some provinces such as Jiangsu and Hebei may fail to peak by 2040. Finally, based on the predicted carbon peak year, provinces are categorized into four pathways—early, recent, later, and non-peaking—to provide targeted policy recommendations. This integrated framework significantly enhances prediction precision and captures regional disparities, enabling tailored decarbonization strategies that support China’s dual carbon goals of balancing economic growth with environmental protection. The approach provides critical insights for region-specific low-carbon transitions and advances sustainable climate policy modeling.
1. Introduction
The increasing frequency and intensity of extreme weather events, driven by global warming, pose substantial threats to sustainable human development, ecological stability, and economic prosperity. Scientific consensus affirms that carbon dioxide (CO2) emissions are the primary driver of the climate crisis [1]. In response to this pressing challenge, the international community has mobilized a range of strategies, including binding multilateral agreements like the Paris Agreement, diversified policy instruments, accelerated technological innovation in clean energy, and enhanced climate finance mechanisms.
China, as the world’s largest emitter and pivotal climate actor [2], announced its ambitious “Dual Carbon” goals in 2020, committing to peak carbon emissions by 2030 and achieve carbon neutrality by 2060. This pledge has catalyzed rapid advancements in China’s climate policy framework, evolving from macro-level targets to detailed micro-level management measures. However, pronounced regional disparities in economic development stages, industrial structures, resource endowments, and energy consumption patterns create critical challenges for achieving these national goals.
Since the proposal of the “dual-carbon” target, research on provincial carbon peaking in China has expanded significantly, focusing on three key areas: influencing factors of carbon emission, carbon emission forecasting methods, and carbon peak prediction methods. Identifying emission drivers provides the theoretical foundation for forecasting models, while accurate emission forecasts serve as essential inputs for predicting provincial peaking timelines. Studies have evolved from single-model approaches to hybrid models, progressing from macro-level predictions to micro-level deconstructions.
In assessing carbon emission drivers, researchers emphasize the need for robust indicator systems to analyze emission-related challenges. Early studies relied on basic dimensions such as energy consumption and economic development, but recent work has incorporated more comprehensive socioeconomic and environmental variables. Yang et al. [3] developed a carbon peaking evaluation system based on climate ambition, low-carbon status, and emission trends, categorizing China’s 30 provinces into six groups to inform policy recommendations. Similarly, Zhang et al. [4] proposed an innovative peak carbon maturity index evaluation system for buildings, which quantified the peak carbon capacity of the building sector in different provinces and classified the types of development in each province. Jiao et al. [5] introduced a multidimensional system with 21 sub-indicators, employing advanced techniques like gray correlation analysis to address data complexity. Zhu et al. [6] identified construction EC drivers via a stochastic population-affluence-technology model, using six indexes in three extended models to explore direct/indirect factors, while recent studies like Bashir et al. [7] added sustainable development perspectives, assessing G20 carbon drivers and policy/technology-based reduction to support global management.
The prediction methods for carbon emission and carbon peak have also diversified, spanning the EKC curve [8], the LEAP model [9] and the STIRPAT model [10,11,12], the Kaya model [13], the LMDI decomposition method [14,15], the gray prediction method [16], and the neural network model [17], which have been widely used in different regions and under various conditions, showing their respective strengths and limitations. Recent innovations includ[14,15e hybrid approaches. Ding et al. [18] develop an integrated model combining graph representation learning, factor analysis, and random forests to assess and predict carbon emission patterns in the Pearl River Delta. Yu et al. [19] utilize a LASSO regression model to forecast carbon trajectories, validating regression coefficients with confidence intervals and cross-validation. Shen et al. [20] innovatively proposed a multi-objective Markal–Macro model to explore China’s optimal carbon peaking pathway. Wang et al. [21] enhance sector-specific carbon estimates in Henan using an electricity–energy–carbon model, emphasizing the importance of sectoral electricity data. Zhou et al. [22] achieved high-frequency municipal carbon tracking in Guangxi using electricity big data, offering real-time policy insights for localized peak management. Li et al. [23] pioneered an enterprise-scale application of the Electric Carbon Model in Qinghai Province, demonstrating how electricity–consumption data enables precise carbon accounting at microeconomic levels. Zhan et al. [24] develop an event-resilient CO2 forecasting model for aviation, outperforming existing methods and supporting industry deployment for sustainable fuel use.
In recent years, machine learning and deep learning methods have been more and more widely used in carbon emission prediction, showing their powerful ability in dealing with complex, nonlinear relational data. In the field of transportation, machine learning algorithms are widely used to predict the CO2 emissions of vehicles. Li et al. [25] used artificial neural network (ANN) and vehicle dynamics methods to predict the instantaneous CO2 emissions of a small diesel vehicle, achieving high prediction accuracy. Sundaram et al. [26] studied the use of multiple machine learning algorithms such as random forest, support vector machine, gradient boosting, multilayer perceptron classifier, K-nearest neighbor, and decision tree to predict carbon dioxide emissions from various countries across the globe, and the results showed that the prediction accuracy of random forest and gradient boosting models reached a high prediction-accuracy level. To improve prediction accuracy, researchers have also proposed hybrid models that combine machine learning with nature-inspired optimization algorithms to improve prediction accuracy. Zhang et al. [27] combined the environmental Kuznets curve theory and proposed an integrated SSA-FAGM-SVR model for predicting carbon emissions using the Sparrow Search Algorithm to optimize the Fractional Accumulation Gray Model and support vector regression. Lu et al. [28] used a Monte Carlo simulation and LSTM neural networks to predict the evolutionary trend of industrial carbon emissions in China. Mussa et al. [29] used particle swarm optimization-augmented ANN to optimize energy demand forecasts. These hybrid machine learning models effectively address the limitations of conventional approaches, significantly enhancing prediction accuracy and reliability. By analyzing emission patterns and their key drivers, policymakers and stakeholders can develop data-driven strategies for more effective carbon mitigation.
Parallel to these advancements, research specifically targeting carbon peaking predictions has proliferated, evolving from national-scale projections to provincial-level trajectory mapping. Meng et al. [30] analyzed multi-scenario projections for the provinces and cities involved in the South-to-North Water Diversion Project through the STIRPAT model and found that the provincial governments responded positively to the central government’s carbon peaking target by adopting measures, including financial subsidies and policy support, to promote low-carbon development. Zhang et al. [31] applied the LEAP model to predict carbon peaking pathways for China’s public buildings, demonstrating that coordinated energy efficiency improvements and grid decarbonization could enable peak emissions by 2030. Rao et al. [32] proposed a new STIRPAT extended model based on the generalized Divisia index method and ridge regression, combined with scenario analysis methods, predicted that the peak of carbon emissions in Hubei Province would occur in 2025, and provided emission reduction recommendations in terms of industrial structure, energy structure, and urbanization. Similarly, Deng et al. [33] used the PSO-XGBoost-RF model to predict the carbon peaks of the cities in the Yellow River Basin under different pathways, and the results showed that the peak of carbon emissions is expected to be reached in 2033. These studies not only provide a scientific basis for local governments but also support the development of more effective carbon peaking policies.
Despite these advances, limitations persist in the existing body of research on China’s provincial carbon peak prediction: (1) Regional or industry-specific data constraints hinder comprehensive cross-provincial comparisons and fail to adequately account for interregional differences and policy implementation realities. (2) Insufficient consideration of provincial disparities in economic development levels, industrial structures, and energy mixes limits the applicability and generalizability of findings. (3) Methodological gaps, including limitations in data processing techniques and prediction methods, as well as incomplete incorporation of key carbon emission drivers within indicator systems, lead to suboptimal prediction accuracy.
To tackle these challenges, this study proposes an integrated framework based on extended STIRPAT and GA-BiLSTM models to predict China’s provincial carbon peak year. The predictions facilitate the development of more accurate and differentiated carbon management strategies, which are crucial for promoting a sustainable low-carbon transition across different regions. The contributions of our work are highlighted as follows:
- Utilizing panel data across 30 provinces in China from 2000 to 2023, we construct a multidimensional driver indicator system based on the extended STIRPAT model, explicitly incorporating resource endowments and policy differences for systematic cross-provincial comparison. This system systematically accounts for socioeconomic, energy-related, and structural disparities across provinces, embedding sustainable development dimensions into emission estimation.
- To overcome limitations in prediction accuracy inherent in traditional models, we develop a hybrid GA-BiLSTM algorithm. This approach synergizes the deep temporal feature extraction of BiLSTM networks with the global optimization power of genetic algorithms (GAs), significantly enhancing the precision of carbon emission forecasts.
- Leveraging this advanced prediction framework, we forecast the carbon peak timelines by constructing three distinct, policy-relevant scenarios that reflect varying levels of ambition and intervention. Based on these timelines, we categorize the 30 Chinese provinces into four distinct peaking pathways, which form the basis for proposing targeted, region-specific policy recommendations. This provides actionable insights into the unique risks and sustainable development opportunities associated with different provincial trajectories.
The remainder of this paper is structured as follows: Section 2 characterizes the spatiotemporal evolution of carbon emissions across Chinese provinces and analyzes key influencing factors using the extended STIRPAT model. Section 3 details the development and application of the GA-BiLSTM hybrid model for predicting provincial carbon emissions and peaks under different scenarios, presenting results and pathway classification. Section 4 discusses policy implications and methodological contributions, while Section 5 concludes with key findings and future research directions.
2. Analysis of Factors Affecting Carbon Emissions
2.1. Measurement of Carbon Emissions
According to the Intergovernmental Panel on Climate Change (IPCC) Guidelines for National Greenhouse Gas Emission Inventories issued by the IPCC, this paper adopts the carbon emission factor method to calculate emissions:
where Activity Data refers to energy consumption quantities, while Emission Factor represents carbon dioxide emissions per unit of energy consumed.
Energy consumption encompasses production and consumption activities that generate greenhouse gas emissions, including fossil fuel combustion, limestone raw material processing, and net purchases of electricity and steam. Emission factors vary by fuel type, reflecting differences in carbon content per energy unit. For accurate carbon emission measurements, physical consumption data must be converted to standard units. Following the China Energy Statistical Yearbook classification system (http://www.stats.gov.cn/, accessed on 15 July 2025), we categorize final energy consumption into nine types. Table 1 presents the corresponding conversion factors and carbon emission factors for these energy sources.

Table 1.
Energy conversion factors and carbon emission factors.
Figure 1a shows the trend of China’s carbon emissions from 2000 to 2023. Emissions increased steadily over this period, with distinct growth phases. The rate of increase was higher in the earlier years and slowed down in later years. Figure 1b illustrates the carbon emissions from 30 Chinese provinces between 2000 and 2023, displaying the average, maximum, and minimum values. From 2000 to 2012, both the average and maximum emissions show a rapid upward trend, while the minimum value remains relatively stable. After 2012, the growth rates of average and maximum emissions slow down, and by 2020, the minimum value exhibits a slight upward trend. This pattern indicates a shift in China’s emission growth dynamics over the analyzed period.
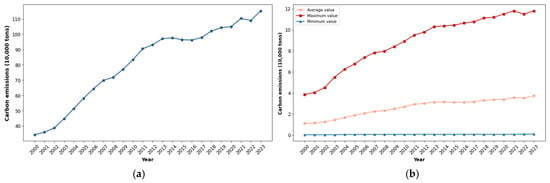
Figure 1.
Temporal characterization of carbon emissions in China from 2000 to 2023. (a) China’s total carbon emissions from 2000 to 2023; (b) maximum, minimum, and average carbon emissions of Chinese provinces from 2000 to 2023.
Figure 2 illustrates the spatiotemporal distribution of China’s provincial carbon emissions from 2000 to 2023. Spatially, emissions exhibit a distinct geographical pattern, with higher levels in eastern versus western regions and greater outputs in northern compared to southern areas. The Bohai Rim region, including Liaoning, Hebei, and Shandong, consistently represents the highest emission zone, contributing over 20% of national emissions annually.
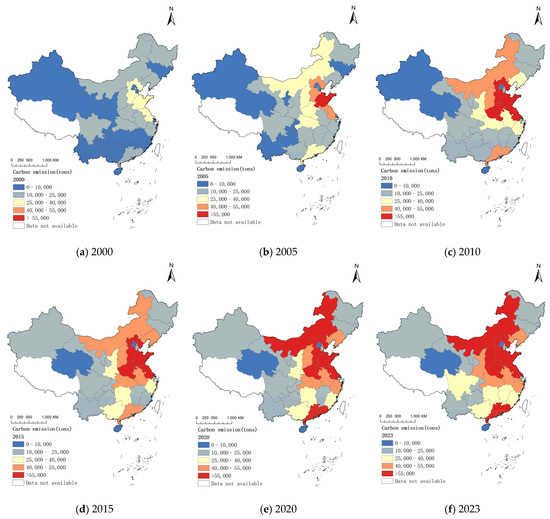
Figure 2.
Carbon emissions in 30 Chinese provinces from 2000 to 2023.
Temporally, all provinces show a continued upward trend in emissions. In 2000, most provinces emitted either less than 10 million tons or between 10 and 25 million tons, with central and western regions mainly in the lowest emission category. By 2005, emissions increased noticeably, especially in northeastern and coastal provinces, transitioning into higher emission categories. This upward trend persisted through 2010, with multiple northeastern and central provinces reaching 40–55 million tons, followed by further intensification in eastern and central regions by 2015. In 2020, most eastern coastal and northeastern provinces exhibited emissions exceeding 40 million tons, with several regions crossing into the higher categories. By 2023, this pattern continued, with many regions in eastern China and the northeastern areas showing emissions at or above the 55,000 tons category, reflecting persistent growth in provincial emissions.
2.2. Extended STIRPAT Model
The STIRPAT model, proposed by Dietz and Rosa in 1994 [34], aims to explore the effects of population, affluence, and technology on environmental impacts through regression analyses, and its flexibility and quantitative characteristics make it suitable for coping with diverse societal economic environments. The basic form of the model is
where I denotes environmental impacts, P is the total population, A is the level of affluence, T is the level of technology, which is measured using an indicator such as the intensity of energy consumption, a is a constant term, b, c, and d are regression coefficients, and e is an error term.
In order to analyze the influencing factors of carbon emissions more comprehensively, the error term e is usually explained specifically by adding the influencing factors of industrial structure, energy structure, and policy intervention [35,36,37] to construct the extended STIRPAT model as follows:
where is a constant term representing the base intercept value of the model, , , , , , are the elasticity coefficients of population size, GDP per capita, energy intensity, industrial structure, energy structure, and urbanization level, respectively. is the unobservable individual fixed effect, and is a random error term containing other influences or measurement errors not included in the model. The specific definitions, clarifications, and data sources of these variables are presented in Table 2.

Table 2.
Factors affecting carbon emissions.
2.3. Empirical Results and Analysis
This study analyzes six key indicators: year-end resident population, per capita GDP, energy intensity, secondary industry GDP index, coal consumption share, and urbanization rate. After careful data preprocessing to address missing values, Table 3 shows the results of descriptive statistics for the logarithmic transformation of these variables. The analysis reveals distinct patterns across indicators. Transformed carbon emissions, population size, and GDP per capita show relatively high central tendency values, while energy intensity and energy structure exhibit lower mean values. Dispersion analysis indicates similar volatility between carbon emissions and population size, followed by industrial structure and energy structure. The urbanization rate demonstrates the least variability with the most concentrated distribution.

Table 3.
Data descriptive statistics.
Notably, carbon emissions show the widest logarithmic range, while industrial structure displays significant negative skewness. Energy structure exhibits pronounced heterogeneity, with substantial differences between extreme values. These statistically robust variations in central tendency, dispersion, and distribution ranges provide a reliable foundation for subsequent modeling and enhance the validity of our empirical results.
To address potential multicollinearity among the STIRPAT variables, Variance Inflation Factor analysis was conducted, and the results are presented in Table 4. All VIF values are below the threshold of 10, with the highest being 3.028 for GDP per capita and an average VIF of 2.055. This indicates that severe multicollinearity is absent, thereby confirming the reliability of the regression analysis. Although urbanization and GDP per capita are theoretically correlated, they exhibit low pairwise collinearity, with VIF values less than 3.028. This validates their independent inclusion in the model.

Table 4.
Multicollinearity test.
To assess the model’s robustness, this study performed a heteroskedasticity test. The Breusch–Pagan test yielded a p-value of 0.000, significantly below the 0.05 significance threshold, confirming the presence of heteroskedasticity. Consequently, heteroskedasticity-robust standard errors were employed in the regression analysis. Table 5 demonstrates that both the significance levels and coefficient estimates of the variables remain substantially consistent after implementing heteroskedasticity-robust standard errors, thereby confirming the robustness of the model results.

Table 5.
Heteroscedasticity test.
Table 6 shows the Pearson’s correlation coefficients of the main variables, which indicate that there is not a high degree of correlation between the variables selected in this study, providing a good basis for the subsequent analysis.

Table 6.
Pearson correlation coefficient.
Table 7 shows that the overall fit of the model is high, with an of 0.8767 and an adjusted of 0.8742, indicating that the model is able to explain about 87.42% of the variation in carbon emissions. Specifically, as shown in Table 4, the coefficient of population size is 0.9878, with a significance level of 1%; the coefficient of GDP per capita is 1.0000, with a significance level of 1%; the coefficient of energy intensity is 1.1833, with a significance level of 1%; the coefficient of industrial structure is −0.1002, with a significance level of 1%; and the energy structure coefficient is 0.1809, with a significance level of 1%.

Table 7.
Overall fit of the model.
The analysis reveals three key positive relationships with carbon emissions: population size, GDP per capita, and energy intensity all show statistically significant positive effects. This suggests that carbon emissions increase substantially with population growth, economic expansion, and declining energy use efficiency. In contrast, industrial structure demonstrates a significant negative effect, implying that industrial structure optimization can effectively reduce carbon emissions. Interestingly, the energy structure coefficient shows a positive relationship, indicating that current patterns of energy structure optimization may paradoxically lead to increased carbon emissions.
This study analyzes the differential impacts of population size, industrial structure, energy intensity, energy structure, and urbanization level on carbon emissions based on provincial regression analyses [38,39], as presented in Table 8. The findings reveal significant regional heterogeneity in carbon emission driving mechanisms across Chinese provinces.

Table 8.
Regression results of factors influencing provincial domains.
Population effects exhibit polarization. Resource-endowed provinces like Yunnan and Qinghai show high elasticity, with lnP coefficients of 398.636 and 25.655, respectively, reflecting their resource-dependent economies and ecological fragility. In contrast, labor-exporting regions such as Sichuan and Inner Mongolia demonstrate weaker impacts, with lnP coefficients of −34.044 (significant at 10%) and −23.14, respectively, due to structural imbalances in labor forces and constrained energy demand growth.
Industrial structure and energy intensity impacts vary by development stage. Industrializing regions like Chongqing and Xinjiang are highly sensitive to secondary sector expansion, with lnIS coefficients of 0.052 and 0.046, which are significant at 10%, respectively, whereas service-dominated Shanghai shows minimal effects, with an lnIS coefficient of 0.04. Traditional industrial provinces like Shanxi face short-term emission reduction constraints from structural inertia, with an lnT coefficient of 0.142, indicating energy intensity remains a key driver.
Energy structure and urbanization effects further highlight regional disparities. Shandong and Tianjin exhibit high coal-dependency elasticity, with lnES coefficients of 0.156 (significant at 10%) and 0.420 (significant at 10%), respectively, signaling substantial clean energy substitution potential. Urbanization drives divergent outcomes. Beijing’s lnUR coefficient of 12.024 indicates that a 1% increase in urbanization raises emissions by 12.02% through infrastructure and service-sector expansion, while Hainan’s tourism-driven economy shows decoupling between urbanization and industrial energy use with a negative lnUR coefficient of −0.669.
The model fit also reveals the boundaries of the effectiveness of policy interventions. Provinces such as Xinjiang and Ningxia have strong model explanatory power, with carbon emission changes mainly originating from observed variables, and policy design can be accurately aligned; whereas Guizhou and Guangxi have a lower fit, implying that other unobserved variables, such as ecological compensation policies and cross-border population flows, may interfere with the emission reduction effect.
In summary, these findings underscore the critical need for tailored provincial strategies aligned with sustainable development objectives. Resource-rich regions must implement stringent controls on energy-intensive industry expansion to prevent ecological degradation while maintaining economic viability. Transitioning provinces should prioritize industrial upgrading and clean energy substitution to decouple economic growth from emissions trajectories. Structurally locked-in areas require targeted technological innovation to overcome path dependencies and advance systemic reforms that simultaneously address emission reduction and sustainable resource management. This approach enables balanced progress toward both economic development and environmental goals across China’s diverse regional contexts.
3. Prediction of Carbon Peak Based on GA-BiLSTM Model
3.1. GA-BiLSTM Model
The GA-BiLSTM model is a bidirectional Long Short-Term Memory (BiLSTM) model optimized based on the genetic algorithm (GA) [40,41,42], which combines the deep mining ability of BiLSTM on time series features with the global parameter optimization advantage of the GA, effectively solving the overfitting and local optimization problems of traditional deep learning models under small sample data and improving the prediction accuracy of carbon emission time series data through the integrated learning approach.
3.1.1. BiLSTM Algorithm
BiLSTM consists of forward LSTM and reverse LSTM, and its core structure contains input gates, oblivion gates, output gates, and cellular units, as shown in Figure 3. In this Figure, main connection lines represent the forward propagating path of forward LSTM, and the reverse propagating path of reverse LSTM is also shown. These two way paths form BiLSTM’s bidirectional information processing logic: forward LSTM extracts forward order features by processing the sequence in positive order, while reverse LSTM extracts reverse order features via reverse order processing. Their combination enables comprehensive use of bidirectional sequence information. The specific formulas are as follows:
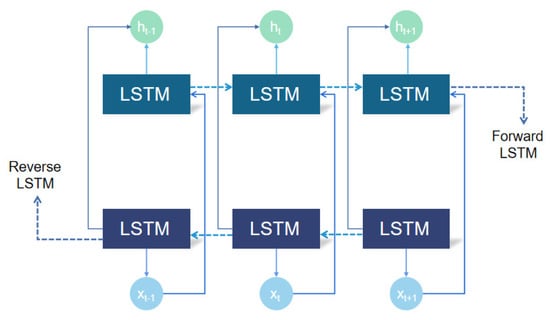
Figure 3.
Bidirectional structure diagram of BiLSTM algorithm.
- (1)
- The forgetting gate controls the information to be kept or discarded in the cell state:
- (2)
- The input gate determines the probability of new information entering the cellular unit:
- (3)
- Cell state renewal determines the information flow in the cell state by combining the forgetting gate and input gate outputs to update the cell state:
- (4)
- The output gate controls the output of the hidden layer at the current moment:
BiLSTM learns both forward and backward features of the time series through a bidirectional structure and eventually splices the outputs from both directions as the final result.
3.1.2. GA Algorithm
The genetic algorithm (GA) is a heuristic search algorithm inspired by the process of natural selection and biological evolution. It operates by iteratively transforming a population of candidate solutions into a new population, using mechanisms such as selection, crossover, and mutation to guide the search towards optimal solutions. In this study, the GA was employed to optimize the hyperparameters of the BiLSTM algorithm, including the learning rate, number of hidden layer neurons, batch size, and dropout rate. The steps are as follows:
- (1)
- Encoding: Each hyperparameter combination is encoded as a chromosome using binary representation.
- (2)
- Initialization population: This randomly generates the initial parameter combination as the parent population.
- (3)
- Fitness calculation: The fitness function is defined based on the optimization objective, which is used to determine the individual fitness values within the population.
- (4)
- Evolutionary operation: Highly adapted individuals are selected for reproduction. Crossover involves randomly pairing individuals and exchanging genes, while mutation randomly alters gene values to increase diversity. The process continues until reaching the maximum number of iterations or convergence of fitness, identifying the optimal parameter combination.
- (5)
- Decoding: This interprets the most fit individual in the final generation as the optimal solution to the problem.
The GA’s global search capability mitigates BiLSTM’s sensitivity to manual hyperparameter tuning. By dynamically balancing exploration and exploitation, the GA efficiently navigates high-dimensional hyperparameters, ensuring robust model performance even under small-sample constraints. This integration is critical for enhancing prediction accuracy while minimizing overfitting risks.
3.1.3. Combining Models
To further improve the robustness, this paper adopts the Bagging algorithm to integrate multiple GA-BiLSTM weak learners, as shown in Figure 4. The figure illustrates the integrated process of GA-BiLSTM models. It begins with random sampling to create multiple diverse sub-training sets. Each set is used to train a GA-optimized BiLSTM model in parallel. The BiLSTM, with its bidirectional structure and gates for dynamic feature adjustment, learns temporal features. Finally, the predictions from each model are combined with weights based on their validation performance to achieve the integrated output. The specific process is as follows:
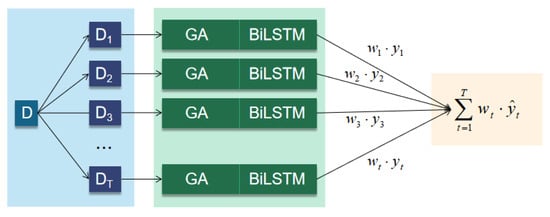
Figure 4.
The framework integrating GA and BiLSTM models.
- (1)
- Random sampling: The original training set is input first, and then, T sub-training sets are generated by performing put-back sampling, with the purpose of increasing the diversity among base learners and avoiding overfitting a single data distribution:
- (2)
- Parallelized model training: The base learner structure trains a GA-BiLSTM model for each subset . GA optimization parameters include learning rate , number of hidden layer neurons , batch size , etc. The BiLSTM structure consists of a bidirectional LSTM network with input gates, forgetting gates, and output gates that dynamically adjust timing features:
- (3)
- Weighted fusion: Input the prediction result of each base learner and dynamically assign weights according to the validation set performance, with higher weights for high-performance models:
3.2. Data Sources and Preprocessing
To ensure data consistency across provinces, this study utilized urban carbon emission data (2000–2023) from the China Carbon Accounting Database (CEADs) [43,44,45,46,47] (https://www.ceads.net/, accessed on 15 July 2025), which provides uniform and continuous measurements that better suit our research objectives. Socioeconomic data were primarily sourced from the China Urban Statistical Yearbook (2000–2023), China Energy Statistical Yearbook (2000–2023), and relevant provincial statistical yearbooks.
To ensure the reliability of the empirical analysis, systematic data preprocessing was performed, including missing value imputation and data normalization. The dataset comprises panel data from 30 Chinese provinces between 2000 and 2023, obtained from the National Bureau of Statistics and provincial energy yearbooks. Preprocessing involved imputing missing values using the K-nearest neighbors method with three neighbors and Euclidean distance, and standardizing the data with RobustScaler to enhance robustness against outliers. The imputation accuracy was validated using metrics such as Mean Absolute Bias (MAB) and root mean square error (RMSE), indicating high precision. Unlike Z-score normalization, RobustScaler employs median and interquartile range, reducing the influence of outliers. These steps harmonize measurement scales across indicators while preserving data integrity for subsequent analysis.
3.3. Prediction of Carbon Emission Based on GA-BiLSTM Model
3.3.1. Model Evaluation Indicators
In order to verify the prediction performance of the GA-BiLSTM model, the coefficient of determination, mean square error, mean absolute error, and root mean square error were used in this study as the evaluation metrics, calculated as follows:
where is the true value of the th sample, is the predicted value of the th sample, is the average of the true value, and is the total number of samples. measures the model’s ability to explain the data changes, the closer to 1, indicating that the model fits the data better; if it is a negative number, then the model predicts poorer than the simple mean prediction. MSE reflects the average squared error between the predicted value and the real value; the smaller the value, the higher the model prediction accuracy. MAE indicates the average absolute deviation between the predicted value and the real value; the smaller the value, the more accurate the model prediction. RMSE is the square root of the MSE, whose scale is consistent with the original data, which is easier to interpret intuitively, and the smaller the value, the better the model performance.
3.3.2. Experiments and Analysis of Results
The model uses a two-layer, bidirectional LSTM architecture to enhance temporal feature extraction. Input sequences consist of 12 time steps to capture short-term dependencies. Each LSTM layer has 64 hidden units, with a dropout rate of 0.3 to prevent overfitting. Layer normalization is applied after the LSTM output to improve training stability. The final hidden state is passed through a ReLU-activated fully connected layer, followed by another fully connected layer that produces the output. This setup balances complexity and generalization for robust performance. Additionally, a genetic algorithm optimizes key hyperparameters, including learning rate, batch size, and number of neurons. The GA parameters, listed in Table 9, are based on extensive testing and aim to balance search thoroughness with computational efficiency. This approach helps identify optimal hyperparameter combinations, enhancing the model’s performance and robustness.

Table 9.
Model parameters.
To assess the GA-BiLSTM model’s performance, we conducted a comprehensive validation before applying it for projections. The dataset was divided into training (80%) and testing (20%) subsets to compare actual carbon emissions with model-predicted values. As shown in Figure 5, the results reveal strong agreement between observed and predicted values of emission trajectories. The model accurately captures key emission trends, including the rapid growth during 2006–2010 associated with industrial expansion and the subsequent slowdown after 2013 due to industrial restructuring. Throughout the evaluation period, the model maintains minimal deviation from actual values, with predicted value curves closely following observed trends. These validation results demonstrate the model’s excellent historical fitting capability and predictive reliability, providing a robust basis for scenario analysis.
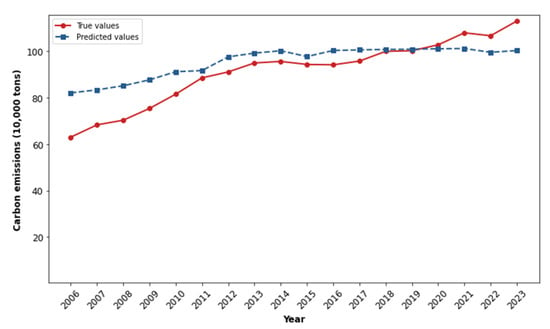
Figure 5.
Comparison of the predicted values with the true values.
In this study, several commonly used prediction algorithms were selected for comparison in predicting carbon emissions from various provinces and regions, including linear regression (LR), support vector machine (SVM), random forest (RF), gradient boosted regression (GBR), the feed-forward neural network (FNN), and Long short-term memory (LSTM). LR is a basic statistical model that predicts the target variable by fitting a linear relationship and is suitable for simple linear data relationships. SVM uses a Radial Basis Function kernel to deal with nonlinear data and is suitable for classification and regression problems in high-dimensional spaces. RF is an integrated learning method that improves prediction accuracy and robustness by constructing multiple decision trees and averaging their results. GBR constructs strong predictive models by progressively optimizing the residuals and is suitable for complex nonlinear data. FNN simulates complex nonlinear relationships through multi-layer neurons and is suitable for handling large-scale and high-dimensional data. LSTM specializes in capturing temporal dependencies in sequential data through gated memory cells, offering distinct advantages for time-series forecasting. The study adopts the above models to forecast the carbon emissions of each province and region, respectively.
Comparative analysis of evaluation metrics in Table 10 demonstrates that the GA-BiLSTM model exhibits significant advantages. Regarding explanatory power, its R2 reaches 0.9415, substantially exceeding all other models, indicating an exceptional ability to explain 94.15% of data variance. For error metrics, LSTM achieves the best performance in both MSE at 0.1837 and RMSE at 0.4286, surpassing all other models. GA-BiLSTM records MSE of 0.2299, comparable to RF at 0.2251, while its RMSE of 0.4795 ranks second only to LSTM. In terms of MAE, GA-BiLSTM achieves 0.3544, slightly higher than RF at 0.3476 but notably lower than LSTM at 0.3874, reflecting greater prediction stability and reduced error dispersion. Traditional machine learning models all show R2 below 0.6819, with generally inferior error metrics compared to GA-BiLSTM, revealing limitations in capturing temporal features.

Table 10.
Indices for the evaluation of models.
In summary, GA-BiLSTM delivers near-optimal overall performance with its near-perfect R2 combined with competitively low error metrics across all categories. While LSTM demonstrates specialized advantages in minimizing prediction deviation, its explanatory capability remains comparatively limited. These results validate the effectiveness of integrating genetic algorithm parameter optimization with bidirectional LSTM networks for temporal modeling, establishing GA-BiLSTM as the superior choice for comprehensive carbon emission prediction tasks.
3.4. Prediction of Carbon Peak Year and Analysis of Carbon Peak Pathways Under Different Scenarios
3.4.1. Scenario Setting
In this study, a total of three carbon emission scenarios, namely, baseline, low carbon, and high carbon, were set to forecast China’s carbon emissions from 2024 to 2040, and the specific parameter settings are shown in Table 11.

Table 11.
Rate of change of factors influencing carbon emissions in different scenarios.
The parameters in Table 11 integrate established research and policy-driven settings [48], aligning assumptions with China’s 14th Five-Year Plan targets. The 3% annual reduction under the low-carbon scenario (2024–2030) reflects the plan’s binding goal for cutting energy intensity and is validated by historical trends of consistent efficiency gains, technological progress, and reinforced decarbonization policies. This ensures the scenarios remain policy-relevant and empirically grounded.
Figure 6 reveals distinct carbon emission trajectories for China under baseline, low-carbon, and high-carbon scenarios, all showing declining trends but with varying reduction rates and pathways. The baseline scenario indicates an 11% reduction from 15 million tons to 13.5 million tons, while the low-carbon scenario demonstrates more significant reductions from its 14.6 million-ton peak. This superior performance results from comprehensive energy structure optimization, improved energy intensity, and accelerated industrial restructuring that effectively reduces high-carbon sector consumption. In contrast, the high-carbon scenario shows limited progress due to persistent conventional development patterns, slow energy intensity improvements, and continued fossil fuel dependence, leading to minimal carbon intensity reductions. Additional constraints include slowing population growth and delayed industrial restructuring, which collectively diminish the emission reduction potential. This analysis confirms that the low-carbon approach effectively combines policy, technological, and structural interventions, while the high-carbon scenario underscores the climate risks of conventional development. These findings suggest policymakers should prioritize the low-carbon pathway through coordinated energy system transformation and industrial upgrading policies, while remaining vigilant against potential mitigation stagnation in baseline conditions.
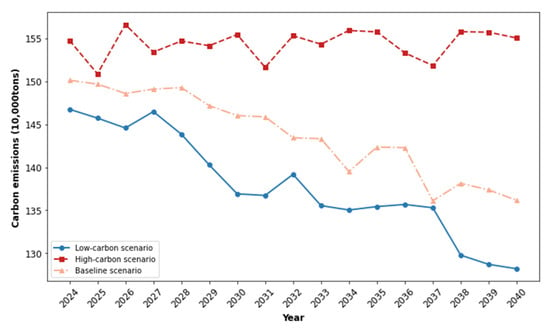
Figure 6.
Total provincial carbon emissions in China under three scenarios.
3.4.2. Prediction of Carbon Peak Year Under Three Scenarios
Based on the level of economic development, industrial structure characteristics, and the progress of emission reduction policies in each province, this paper employed the GA-BiLSTM model to predict the carbon emissions of 30 provinces in China. The carbon peak year for each province was then determined according to the following two principles: (1) If the emissions in year t are the highest during 2024–2040 and continue to decline steadily from t + 1 to 2040 (referring to a stable rate of decline after reaching the peak, with no significant rebound before 2040), year t is considered the carbon peak year. (2) Provinces with emissions that continue to rise or do not show a sustained decline by 2040 are classified as “no peak before 2040”. Ultimately, the carbon peak years for each province under the baseline, low-carbon, and high-carbon scenarios were obtained, as shown in Table 12, Table 13 and Table 14. A carbon peak year marked as “\” indicates that the province has not achieved carbon peaking before 2040.

Table 12.
Carbon peak year in 30 Chinese provinces under the baseline scenario.

Table 13.
Carbon peak year in 30 Chinese provinces under the low-carbon scenario.

Table 14.
Carbon peak year in 30 Chinese provinces under the high-carbon scenario.
According to provincial carbon peaking forecasts under different scenarios, China’s regions demonstrate significant variations in their carbon peaking processes, reflecting disparities in economic development levels, industrial structure characteristics, and policy implementation effectiveness. Major eastern municipalities and developed regions, particularly Beijing, Tianjin, and Shanghai, have emerged as national low-carbon transition leaders by achieving early carbon peaks through industrial structure optimization and rigorous emission control measures. Coastal economic powerhouses like Guangdong, Zhejiang, and Jiangsu attained concentrated carbon peak years through technological innovation and efficient policy execution, though they require enhanced regional cooperation to sustain their emission reduction achievements.
The industrial transformation challenges appear more pronounced in energy-dependent central and western regions. While central provinces such as Henan and Hunan achieved relatively early peaks through industrial decarbonization, Hubei and Anhui’s transition delays resulted in later peaking. Traditional energy bases like Shaanxi, Shanxi, and Inner Mongolia exhibit significantly delayed carbon peak years compared to the national average due to heavy coal dependence and insufficient clean energy substitution, underscoring the pressing need for energy structure transformation. Conversely, provinces, including Chongqing, Guizhou, and Qinghai, attained earlier peaks through renewable energy utilization and low-carbon industrial development, demonstrating the compatibility of ecological preservation and economic growth.
Energy-exporting and industrial-based provinces show distinct peaking patterns. Regions like Guangxi, Ningxia, and Xinjiang experience considerable peaking time fluctuations due to uneven industrial restructuring, while traditional industrial provinces such as Liaoning and Heilongjiang show early peaking in certain areas but remain vulnerable to emission rebound risks from regional development imbalances.
The comparative scenario analysis reveals that provinces generally achieve earlier peaks under low-carbon conditions, validating the synergistic benefits of policy and technological interventions. Conversely, the high-carbon scenario prolongs the transition for energy-intensive central and western regions due to persistent path dependency. Future strategies should emphasize tailored policy interventions addressing regional specificities, including accelerated clean energy investment in traditional energy bases and enhanced carbon market mechanisms for industrial transformation laggards, to ensure coordinated progress toward national carbon peaking objectives.
3.4.3. Analysis of Carbon Peak Pathways Under Three Scenarios
Based on the temporal patterns and economic structures observed across provinces under the baseline, low-carbon, and high-carbon scenarios, Table 15 presents China’s regional carbon peaking process, classified into four distinct pathways: early peaking, recent peaking (achieving peak by 2030), later peaking (reaching peak by 2040), and non-peaking (not peaking before 2040). By systematically analyzing emission characteristics and carbon peak years across these provincial categories, this classification provides policymakers with more precise reference points for decision-making.

Table 15.
Provinces’ carbon peak pathways under three scenarios.
Early peaking provinces demonstrate stable peaking across baseline, low-carbon, and high-carbon scenarios. These regions achieve carbon peaking ahead of others due to advanced industrial restructuring and rigorous policy implementation. However, they must remain vigilant against potential carbon emission rebounds that may result from post-peak economic expansion or growth in high-value-added industries. Strategic priorities should focus on leading zero-carbon technology exports, establishing international standards, and fostering green technology innovation hubs.
Recent peaking provinces predominantly feature traditional energy-dependent economies. Their fundamental challenge lies in the disproportionate dominance of high-carbon industries like coal and metallurgy. For instance, Shanxi’s integrated coal-power development model creates significant energy intensity effects, delaying its low-carbon scenario peak until 2030. These regions should accelerate renewable energy-based development by leveraging national wind power initiatives and interregional transmission infrastructure to overcome entrenched high-carbon industrial dependencies.
Later peaking provinces typically reach baseline scenario peaks before 2040, with timing significantly influenced by policy scenarios. Zhejiang exemplifies this variability, achieving earlier peaking through industrial upgrading under low-carbon scenarios while facing persistent transition pressures under baseline conditions. These provinces require enhanced policy coordination and technological investment, including exploration of GDP carbon-intensity-based horizontal ecological compensation mechanisms to reconcile economic growth with emission reduction objectives. Specific cases like Hebei and Guangxi necessitate cross-provincial green power transmission and capacity replacement solutions.
Non-peaking provinces demand comprehensive industrial chain decarbonization. Jiangsu, as a major industrial province, requires strict carbon quota constraints. Hainan can pioneer comprehensive clean energy electrification in transport and buildings, potentially developing a Bohai Forum-based zero-carbon demonstration zone. Henan needs tailored emission reduction plans for its aluminum industry.
The substantial provincial variations in carbon peak years and pathways vividly reflect structural contradictions in regional development models and resource endowments. Early peaking provinces should concentrate on zero-carbon technology leadership while preventing post-peak emission rebounds. Recent peaking provinces must prioritize renewable energy infrastructure to break high-carbon path dependencies. Later peaking provinces need coordinated policy mechanisms and regional compensation systems. Non-peaking provinces require deep industrial restructuring, with Hainan potentially modeling comprehensive clean energy transitions. This differentiated approach enables the progressive, spatially balanced achievement of national carbon peaking objectives, ultimately establishing structural foundations for carbon neutrality.
4. Discussion
This study uncovers complex spatial and temporal patterns in China’s provincial carbon emissions, with significant policy implications. Notably, regional disparities—particularly east–west and north–south divides—highlight the need for tailored strategies that consider local economic structures and resources. Early-peaking regions like Beijing and Shanghai demonstrate the success of strict emission controls and industrial restructuring, though they face ongoing challenges of rebound as their economies develop. Conversely, resource-dependent provinces struggle with coal-reliant industries that slow their transition efforts. This tension between regional growth models and decarbonization underscores the urgency for policies that balance emission reduction with economic transformation.
Lagging provinces reliant on coal and heavy industry need targeted measures to accelerate peaking. Financial incentives could include energy conservation and emission reduction funding tied to emission cuts, with part of local fiscal revenue allocated as matching funds for renewables in provinces making notable annual coal reduction progress. Industrial support may involve tax rebates for carbon capture adoption in energy-intensive sectors, like steel, cement, and chemicals, plus preferential loans for coal boiler replacements. For resource-dependent regions like Xinjiang and Gansu, ecological compensation mechanisms can guide support for wind and solar bases. Subsidies for grid infrastructure will reduce renewable curtailment, while funded green skills training will reskill coal workers for renewable maintenance roles. Meanwhile, renewable energy power market trading mechanisms will help regions with abundant renewable resources better integrate into the national power market, enhancing clean energy consumption capacity to accelerate fossil energy replacement.
The superior performance of the GA-BiLSTM model in capturing these complex dynamics suggests that hybrid approaches combining econometric analysis with machine learning optimization offer promising tools for policymakers. By more accurately predicting the provincial carbon peak year, such models enable targeted interventions that account for local conditions. For instance, the identification of four distinct peaking pathways provides a valuable typology for designing differentiated support mechanisms, from technology transfer programs for early achievers to structural transition funds for lagging regions. The scenario analysis further reinforces how policy choices can significantly alter emission trajectories, with the low-carbon pathway demonstrating the potential of coordinated technology and structure interventions.
In addition to tailoring policies based on regional development stages and resource endowments, strengthening inter-provincial collaboration is crucial for addressing spatial disparities and promoting low-carbon transitions. Early-peaking provinces, such as Beijing, Tianjin, Shanghai, and other developed areas in China, can play a pivotal role by supporting high-emission regions through technology transfer, demonstration projects, and capacity building. This cooperation could include technological support, financial investments, and the facilitation of information and talent flows, forming a collaborative regional low-carbon development network. For example, establishing regional green finance mechanisms can provide necessary funding for clean energy and energy efficiency upgrades in high-emission areas. Facilitating inter-provincial energy grid connectivity can optimize resource allocation, while cross-regional carbon trading platforms and information-sharing systems can enhance transparency and cooperation. Such mechanisms will enable high-emission regions to adopt cleaner energy technologies—such as wind and solar power—thus reducing regional disparities and contributing to national emission reduction targets.
Several limitations point to important directions for future research. The reliance on provincial-level data necessarily masks important sectoral and sub-regional variations that could refine policy targeting. Incorporating more granular industry-specific data could yield insights into the micro-level dynamics of emission reduction. Additionally, while the current model captures key socioeconomic drivers, expanding the framework to include real-time policy feedback mechanisms could enhance its utility for dynamic policy assessment. The methodology developed here, though focused on China, may also offer valuable insights for other large economies confronting similar regional disparities in their decarbonization efforts.
The broader implications of these findings extend to the fundamental tension between economic development and environmental sustainability. The study demonstrates that while carbon peaking is achievable across diverse regional contexts, its timing and pathway depend heavily on the ability to align structural economic transformation with emission reduction goals. This suggests that China’s dual-carbon targets will require not just technological solutions but deep institutional innovations that can reconcile these sometimes competing priorities. The provincial variations revealed in this analysis offer both cautionary tales and promising models for how this balance might be struck in different development contexts.
5. Conclusions
This study establishes an integrated framework for predicting China’s provincial carbon peak trajectories by synthesizing extended STIRPAT modeling, GA-BiLSTM hybrid algorithms, and scenario-based pathway analysis. The hybrid model achieves a high prediction accuracy, with an R-squared of 0.9415 and significantly lower RMSE and MAE compared to other methods, effectively capturing complex emission dynamics. The analysis identifies key regional disparities, with 19 provinces expected to peak before 2030 under ambitious pathways, 8 more than in baseline scenarios, while some energy-dependent provinces face delayed peaking beyond 2040. These quantitative findings provide crucial insights for targeted policy formulation.
First, by employing an extended STIRPAT model that incorporated socioeconomic, energy-related, and technological factors, we quantified carbon emission drivers across 30 provinces from 2000 to 2023. The analysis reveals pronounced spatial disparities characterized by an “east-high, west-low; north-high, south-low” pattern, with the Bohai Rim region contributing over 20% of national emissions. Key drivers included population growth, economic affluence, and energy intensity, exhibiting significant positive effects, while industrial structure optimization demonstrated notable emission reduction potential, particularly in heavily industrialized provinces. Crucially, the results expose substantial regional heterogeneities. Resource-dependent provinces showed 3.2 times higher population elasticity than industrial hubs, underscoring the need for differentiated policy approaches.
Second, to address prediction limitations, we developed a GA-BiLSTM hybrid model that synergized BiLSTM’s bidirectional temporal feature extraction with genetic algorithm hyperparameter optimization. This integration resolves critical challenges in time-series prediction, including overfitting and local optima traps, by dynamically optimizing hyperparameters and employing Bagging-based ensemble learning to enhance generalization under small-sample constraints. When validated against conventional models, including LR, SVM, RF, GBR, FNN, and LSTM, this approach demonstrated superior performance, achieving an R2 of 0.9415, along with lower RMSE and MAE. This confirms its enhanced capability to capture complex nonlinear emission dynamics while mitigating overfitting.
Third, leveraging this optimized model, we projected provincial carbon peak timelines under three policy scenarios during 2024–2040. Scenario analysis shows that under ambitious low-carbon pathways, synergistic policy–technology interventions enabled 19 provinces to peak before 2030, 8 more than under baseline conditions. Conversely, energy-intensive provinces like Jiangsu and Hebei risked non-peaking before 2040 in high-carbon scenarios due to industrial path dependence. The model’s theoretical advances directly translate to actionable policy insights: precise peak-year predictions empower region-specific decarbonization strategies, such as accelerating clean energy transitions in coal-dependent provinces and preventing carbon rebound in early-peaking regions like Beijing through green innovation hubs.
Finally, based on the scenario analysis results, we summarize four distinct pathways. Early-peaking regions achieved success through industrial restructuring, recent-peaking provinces leveraged structural optimization, later-peaking areas showed scenario-dependent outcomes, while non-peaking provinces required fundamental industrial transformation. This research advances both policy design and predictive methodology for regional decarbonization. By demonstrating how province-specific interventions, particularly accelerated clean energy transitions in coal-dependent regions, can simultaneously achieve emission reduction and economic growth objectives, it provides actionable strategies for harmonizing development and sustainability. Methodologically, the GA-BiLSTM framework enables dynamic policy assessment aligned with the Sustainable Development Goals. In the future, we will incorporate granular sectoral data to refine pathway design, develop real-time policy feedback mechanisms, and extend comparative studies to economies facing similar decarbonization challenges.
Author Contributions
Conceptualization, L.C. and H.C.; methodology, L.C. and H.C.; software, L.C.; validation, L.C., H.C. and Y.G.; formal analysis, L.C., H.C. and Y.G.; writing—original draft preparation, L.C.; writing—review and editing H.C. and Y.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support the findings of this paper are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kumar, S.; Chatterjee, U.; David Raj, A.; Sooryamol, K.R. Global Warming and Climate Crisis/Extreme Events. In Climate Crisis: Adaptive Approaches and Sustainability; Springer Nature Switzerland: Cham, Switzerland, 2023. [Google Scholar]
- Chen, J.; Feng, Y.; Zhang, Z.; Wang, Q.; Ma, F. Exploring the patterns of China’s carbon neutrality policies. J. Environ. Manag. 2024, 371, 123092. [Google Scholar] [CrossRef]
- Pingjian, Y.; Shuan, P.; Nihed, B.; Linyan, D.; Xiaomin, L.; Runpu, L.; Guozhu, M. An integrated evaluation on China’s provincial carbon peak and carbon neutrality. J. Clean. Prod. 2022, 377, 134497. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, M.; Jiang, H.; Guan, D. Deep learning-based stepwise peaking roadmap of carbon emissions in Chinese provincial building sector. Build. Environ. 2025, 270, 112505. [Google Scholar] [CrossRef]
- Jiao, X.; Wu, J.; Mao, Y.; Yan, M. Carbon efficiency evaluation method for urban energy system with multiple energy complementary. Glob. Energy Interconnect. 2024, 7, 142–154. [Google Scholar] [CrossRef]
- Zhu, C.; Chang, Y.; Li, X.; Shan, M. Factors influencing embodied carbon emissions of China’s building sector: An analysis based on extended STIRPAT modeling. Energy Build. 2022, 255, 111607. [Google Scholar] [CrossRef]
- Bashir, M.A.; Qing, L.; Manzoor, S.; Durrani, S.K.; Jingting, L.; Sultan, N. Quest for environmental management and sustainability: Evaluating the drivers of territorial and consumption-based carbon emissions in G-20 economies. J. Environ. Manag. 2025, 377, 124721. [Google Scholar] [CrossRef]
- Jiang, Q.; Khattak, S.I.; Rahman, Z.U. Measuring the simultaneous effects of electricity consumption and production on carbon dioxide emissions (CO2e) in China: New evidence from an EKC-based assessment. Energy 2021, 229, 120616. [Google Scholar] [CrossRef]
- Shi, C.; Qin, G.; Tan, Q.; Yang, J.; Chen, X.; Liu, Q.; Zhang, T.; Kammen, D.M. Simulation of hydrogen transportation development path and carbon emission reduction path based on LEAP model—A case study of Beijing-Tianjin-Hebei Region. Energy Policy 2024, 194, 114337. [Google Scholar] [CrossRef]
- Abdullah Abbas Amer, E.A.; Ali Meyad, E.M.; Meyad, A.M.; Mohsin, A.K.M. Impacts of renewable and disaggregated non-renewable energy consumption on CO2 emissions in GCC countries: A STIRPAT model analysis. Heliyon 2024, 10, e30154. [Google Scholar] [CrossRef]
- Cong, X.; Zhao, M.; Li, L. Analysis of Carbon Dioxide Emissions of Buildings in Different Regions of China Based on STIRPAT Model. Procedia Eng. 2015, 121, 645–652. [Google Scholar] [CrossRef]
- Yu, S.; Zhang, Q.; Hao, J.L.; Ma, W.; Sun, Y.; Wang, X.; Song, Y. Development of an extended STIRPAT model to assess the driving factors of household carbon dioxide emissions in China. J. Environ. Manag. 2023, 325, 116502. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, X. Tracking China’s CO2 emissions using Kaya-LMDI for the period 1991–2022. Gondwana Res. 2024, 133, 60–71. [Google Scholar] [CrossRef]
- He, Y.; Xing, Y.; Zeng, X.; Ji, Y.; Hou, H.; Zhang, Y.; Zhu, Z. Factors influencing carbon emissions from China’s electricity industry: Analysis using the combination of LMDI and K-means clustering. Environ. Impact Assess. Rev. 2022, 93, 106724. [Google Scholar] [CrossRef]
- Quan, C.; Cheng, X.; Yu, S.; Ye, X. Analysis on the influencing factors of carbon emission in China’s logistics industry based on LMDI method. Sci. Total Environ. 2020, 734, 138473. [Google Scholar] [CrossRef]
- Cai, K.; Wu, L. Grey prediction of carbon emission and carbon peak in several developing countries. Eng. Applicat. Artif. Intell. 2024, 133, 108210. [Google Scholar] [CrossRef]
- Wen, T.; Liu, Y.; Bai, Y.H.; Liu, H. Modeling and forecasting CO2 emissions in China and its regions using a novel ARIMA-LSTM model. Heliyon 2023, 9, e21241. [Google Scholar] [CrossRef]
- Ding, Y.; Li, Y.; Zheng, H.; Mei, M.; Liu, N. A graph-factor-based random forest model for assessing and predicting carbon emission patterns—Pearl River Delta urban agglomeration. J. Clean. Prod. 2024, 469, 143220. [Google Scholar] [CrossRef]
- Yu, F.-W.; Ho, W.-T.; Wong, C.-F.J. Predicting and decarbonizing carbon emissions from building energy use in Hong Kong: A LASSO regression approach. Energy Sustain. Dev. 2024, 78, 101374. [Google Scholar] [CrossRef]
- Shen, L.; Yuan, Q.; He, Q.; Jiang, P.; Ji, H.; Shi, J. Simulation and Pathway Selection for China’s Carbon Peak: A Multi-Objective Nonlinear Dynamic Optimization Approach. Sustainability 2024, 17, 154. [Google Scholar] [CrossRef]
- Wang, Y.; Ji, H.; Wang, S.; Wang, H.; Shi, J. Research on Carbon Emissions Estimation in Key Industries Based on the Electricity–Energy–Carbon Model: A Case Study of Henan Province. Energies 2024, 17, 2933. [Google Scholar] [CrossRef]
- Zhou, C.; Ji, H.; Liu, B.; Tang, H.; Zhang, H.; Shi, J. High-Frequency Estimation and Prediction of Carbon Emissions in Chinese Municipalities: A Case Study of 14 Municipalities in Guangxi Province. Energies 2025, 18, 1382. [Google Scholar] [CrossRef]
- Li, Z.; Pan, Q.; Shi, J.; Ji, H. Construction and Application of Enterprise Electric Carbon Model: A Study Based on Key Enterprises in Qinghai Province. Sustainability 2025, 17, 2243. [Google Scholar] [CrossRef]
- Zhan, J.; He, W.; Gasparri, E.; Grace, K.; Yin, D.; Shen, S.; Wang, Y.; Li, J. Carbon emission assessment and interpretability improvement empowered by machine learning: A case study in four cities, China. Energy Build. 2025, 334, 115530. [Google Scholar] [CrossRef]
- Li, S.; Tong, Z.; Haroon, M. Estimation of transport CO2 emissions using machine learning algorithm. Transport. Res. Part D 2024, 133, 104276. [Google Scholar] [CrossRef]
- Sundaram, A.; Varghese, I.K.; RejiKumar, G. Machine Learning Approaches for Real-time Carbon Emission Prediction and Mitigation. In Proceedings of the 2023 IEEE Technology & Engineering Management Conference—Asia Pacific (TEMSCON-ASPAC), Singapore, 14–16 December 2023. [Google Scholar]
- Zhang, Y.; Li, X.; Zhang, Y. A novel integrated optimization model for carbon emission prediction: A case study on the group of 20. J. Environ. Manag. 2023, 344, 118422. [Google Scholar] [CrossRef]
- Peng, L.; Liu, S.; Liu, R.; Wang, L. Effective long short-term memory with differential evolution algorithm for electricity price prediction. Energy 2018, 162, 1301–1314. [Google Scholar] [CrossRef]
- Mussa, A.A.Y.; Khalifa, W.M.S. MLP Enhanced CO2 Emission Prediction Model with LWSSA Nature Inspired Optimization. Sci. Rep. 2025, 15, 1891. [Google Scholar] [CrossRef]
- Meng, Q.; Li, B.; Zheng, Y.; Zhu, H.; Xiong, Z.; Li, Y.; Li, Q. Multi-Scenario Prediction Analysis of Carbon Peak Based on STIRPAT Model-Take South-to-North Water Diversion Central Route Provinces and Cities as an Example. Land 2023, 12, 2035. [Google Scholar] [CrossRef]
- Zhang, C.; Luo, H. Research on carbon emission peak prediction and path of China’s public buildings: Scenario analysis based on LEAP model. Energy Build. 2023, 289, 113053. [Google Scholar] [CrossRef]
- Rao, C.; Huang, Q.; Chen, L.; Goh, M.; Hu, Z. Forecasting the carbon emissions in Hubei Province under the background of carbon neutrality: A novel STIRPAT extended model with ridge regression and scenario analysis. Environ. Sci. Pollut. 2023, 30, 57460–57480. [Google Scholar] [CrossRef]
- Deng, G.; Zhu, Q.; Shen, Y. Research on the prediction and realization path of urban carbon peak along the Yellow River Basin. Heliyon 2024, 10, e38883. [Google Scholar] [CrossRef]
- Dietz, T.; Rosa, E.A. Rethinking the Environmental Impacts of Population, Affluence and Technology. Hum. Ecol. Rev. 1994, 1, 277–300. [Google Scholar]
- Wang, N.; Qu, Z.; Li, J.; Zhang, Y.; Wang, H.; Xi, H.; Gu, Z. Spatial-temporal patterns and influencing factors of carbon emissions in different regions of China. Environ. Res. 2025, 276, 121447. [Google Scholar] [CrossRef]
- Zhi-Wen, H.; Qian-Bin, D.; Xiao-Long, C. Forecasting carbon emissions in Chinese coastal cities based on a gated recurrent unit model. Energy Rep. 2024, 12, 5747–5756. [Google Scholar] [CrossRef]
- Wu, H.; Yang, Y.; Li, W. Analysis of spatiotemporal evolution characteristics and peak forecast of provincial carbon emissions under the dual carbon goal: Considering nine provinces in the Yellow River basin of China as an example. Atmos. Pollut. Res. 2023, 14, 101828. [Google Scholar] [CrossRef]
- Yu, Z.; Khan, S.A.R.; Ponce, P.; Lopes de Sousa Jabbour, A.B.; Chiappetta Jabbour, C.J. Factors affecting carbon emissions in emerging economies in the context of a green recovery: Implications for sustainable development goals. Technol. Forecast. Soc. Change 2022, 176, 121417. [Google Scholar] [CrossRef]
- Li, S.; Yao, L.; Zhang, Y.; Zhao, Y.; Sun, L. China’s provincial carbon emission driving factors analysis and scenario forecasting. Environ. Sustain. Indic. 2024, 22, 100390. [Google Scholar]
- Simarjit, K.; Anju, B.; Anshu, P. GA-BiLSTM: An intelligent energy prediction and optimization approach for individual home appliances. Evol. Syst. 2023, 15, 413–427. [Google Scholar]
- Jujie, W.; Zhenzhen, Z.; Dongming, G. An enhanced hybrid model based on multiple influencing factors and divide-conquer strategy for carbon price prediction. Omega 2023, 120, 102922. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, Q.; Zhi, J.; Yao, X.; Li, L.; Shi, C. Carbon peak prediction in China based on Bagging-integrated GA-BiLSTM model under provincial perspective. Energy 2024, 313, 133519. [Google Scholar] [CrossRef]
- Shan, Y.; Liu, J.; Liu, Z.; Xu, X.; Shao, S.; Wang, P.; Guan, D. New provincial CO2 emission inventories in China based on apparent energy consumption data and updated emission factors. Appl. Energy 2016, 184, 742–750. [Google Scholar] [CrossRef]
- Shan, Y.; Huang, Q.; Guan, D.; Hubacek, K. China CO2 emission accounts 2016–2017. Sci. Data 2020, 7, 54. [Google Scholar] [CrossRef]
- Shan, Y.; Guan, D.; Zheng, H.; Ou, J.; Li, Y.; Meng, J.; Mi, Z.; Liu, Z.; Zhang, Q. China CO2 emission accounts 1997–2015. Sci. Data 2018, 5, 170201. [Google Scholar] [CrossRef]
- Xu, J.; Guan, Y.; Oldfield, J.; Guan, D.; Shan, Y. China carbon emission accounts 2020–2021. Appl. Energy 2024, 360, 122837. [Google Scholar] [CrossRef]
- Guan, Y.; Shan, Y.; Huang, Q.; Chen, H.; Wang, D.; Hubacek, K. Assessment to China’s Recent Emission Pattern Shifts. Earth’s Future 2021, 9, e2021EF002241. [Google Scholar] [CrossRef]
- Cai, L.; Luo, J.; Wang, M.; Guo, J.; Duan, J.; Li, J.; Li, S.; Liu, L.; Ren, D. Pathways for municipalities to achieve carbon emission peak and carbon neutrality: A study based on the LEAP model. Energy 2023, 262, 125435. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).