Abstract
Production scheduling and machine tool intermittent state control separately influence a workshop’s machining and intermittent energy consumption. Effective scheduling decisions and intermittent state control are crucial for optimizing the overall energy consumption in the workshop. However, the scheduling scheme determines the machine tool intermittent durations, which imposes strong constraints on the decision-making process for intermittent state control. This makes it difficult for intermittent state control to be used in providing feedback and optimizing scheduling decisions, significantly limiting the overall energy-saving potential of the workshop. To this end, a workshop energy-saving scheduling method is proposed integrating machine tool intermittent state control. Firstly, the variation characteristics of workshop machining energy consumption, machine tool intermittent durations, and intermittent energy consumption are analyzed, and an energy-saving optimization strategy is designed. Secondly, by incorporating variables such as intermittent durations, intermittent energy consumption, and variable operation start time, a multi-objective integrated optimization model is established. Thirdly, the energy-saving optimization strategy is integrated into chromosome encoding, and multiple crossover and mutation genetic operator strategies, along with a low-level selection strategy, are introduced to improve the NSGA-II algorithm. Finally, the effectiveness of the proposed method is verified through a machining case. Results show that the generated Gantt chart reflects both production scheduling and intermittent state control decision outcomes, resulting in a 1.51% reduction in makespan, and 3.90% reduction in total energy consumption.
1. Introduction
The high energy consumption in machining workshops poses significant challenges to sustainable energy development [1]. Statistical data reveal that machine tools exhibit low effective energy efficiency ratios during the machining process, with actual operational efficiency typically below 30% [2]. Approximately 20% of the total energy is dissipated during machine intermittent phases [3]. These findings demonstrate substantial energy waste during machine tool operation, indicating considerable potential for energy conservation [4]. Currently, production scheduling and machine tool intermittent state control have become critical measures for improving workshop energy efficiency. Production scheduling reduces machining energy consumption and shortens machine intermittent durations by optimizing operation sequencing and machine tool selection [5]. Meanwhile, machine tool intermittent state control minimizes non-machining energy losses by transitioning idling machines to standby or stop modes [6]. Consequently, integrated research on production scheduling and intermittent state control holds significant importance for advancing green transformation in manufacturing workshops.
However, current production scheduling and machine tool intermittent state control are typically optimized independently. Production scheduling schemes usually determine the intermittent durations, thereby imposing strong constraints on the decision-making process of intermittent state control. This strong constraint makes it difficult for intermittent state control to provide feedback for optimizing scheduling decisions, resulting in significant energy losses during both machining and intermittent phases, which consequently reduces overall energy efficiency. In existing studies, scholars have primarily investigated workshop energy-saving scheduling from two perspectives: production scheduling and machine tool intermittent state control. This section now reviews the state-of-the-art research progress in both production scheduling and intermittent state energy-saving control, followed by a critical summary of their limitations.
In the domain of production scheduling research, Xiao et al. employed an improved non-dominated sorting genetic algorithm to optimize workshop scheduling [7]. Lu et al. proposed an adaptive genetic algorithm to address energy-saving scheduling in hybrid flow shops [8]. Li et al. reduced workshop energy consumption through optimized job sequencing and machine tool selection [9]. Jiang et al. developed a discrete animal migration optimization algorithm to minimize total energy consumption [10]. Jesus et al. utilized metaheuristic algorithms to solve the combined optimization problem of production scheduling and machine allocation [11]. He et al. considered the impact of scheduling optimization on workshop production efficiency and energy consumption, proposing an adaptive multi-objective differential evolution algorithm [12]. Li et al. proposed a dual deep Q-network co-evolutionary algorithm for energy-saving scheduling optimization [13]. Luo et al. investigated energy-saving scheduling in flexible workshops by implementing chromosome encoding for three subproblem vectors: machine allocation, speed selection, and operation sequencing [14]. Mehdi et al. presented a multi-population multi-objective memetic algorithm with periodic local search, which optimizes the operation sequence and adjusts the machine tool operating speed [15]. Zhao et al. studied energy-saving scheduling in no-wait flow shops, proposing a two-stage co-evolutionary algorithm combining job sequencing and machine tool speed [16]. Wang et al. examined job allocation and parallel machine configuration in distributed heterogeneous flow shops, formulating a multi-objective energy optimization model to simultaneously minimize makespan and total energy consumption [17]. Marsetiya et al. designed a hybrid Aquila optimizer to determine optimal processing sequences for minimal energy expenditure [18]. Zhang et al. considered the job allocation and sequencing problem between factories, proposing a multi-objective particle swarm optimization algorithm based on Q-learning to solve energy-saving scheduling problem in flow shops [19]. Hao et al. developed a preference-based multi-objective PSO algorithm. It optimizes energy efficiency in workshop batch scheduling [20]. Liu et al. developed an improved quantum-behaved particle swarm optimization algorithm for solving workshop energy-saving optimization models [21]. However, these studies primarily focus on energy optimization during machining phases, neglecting intermittent state energy losses during non-machining periods.
In the field of machine tool intermittent state energy-saving control, Thulasingam et al. proposed an energy-saving control system that reduces intermittent state energy consumption [22]. Duan et al. introduced an intermittent energy-saving strategy, and developed a mathematical model to minimize total machine tool energy consumption [23]. Yin et al. analyzed energy losses under different working conditions and proposed a multi-state alternating energy-saving strategy [24]. Xu et al. implemented a state transition strategy to optimize workshop energy efficiency during intermittent phases [25]. Duan et al. incorporated on/off strategies during machine intermittent phases, adjusting power on/off timing to reduce workshop energy consumption [26]. Renna et al. developed an adaptive machine on/off control strategy based on production buffer information and customer order fulfillment, effectively lowering energy waste during non-machining phases [27]. Liu et al. optimized the production mode of machine tool on/off switching, reducing unnecessary energy losses [28]. Tan et al. introduced an on/off scheduling method that accounts for intermittent durations to minimize total workshop energy usage [29]. Wang et al. formulated a Markov decision process-based intermittent state control strategy, significantly reducing intermittent energy waste [30]. However, most proposed energy-saving strategies rely on predetermined production schedules and fixed time thresholds, failing to adequately account for the coupling relationship between production scheduling and machine tool intermittent state control. This undermines the effectiveness of implementing the workshop’s energy-saving strategies.
Several scholars have investigated energy-saving workshop scheduling incorporating intermittent state control. Tian et al. analyzed the impact of production scheduling on workshop energy consumption, establishing a flexible workshop energy-saving scheduling model that considers machine on/off strategies [31]. Wei et al. examined the energy-saving effect of adjusting machine tool intermittent states on workshop energy consumption, proposing a hybrid energy-saving scheduling strategy [32]. Ham et al. studied energy-saving flexible workshop scheduling with on/off strategies, developing a mixed-integer linear programming model for solutions [33]. Gong et al. employed a two-stage memetic algorithm to optimize production scheduling by adjusting machine startup times [34]. Guo et al. introduced a hybrid genetic algorithm achieving energy conservation through controlled ultra-low-speed machine operation [35]. Wei et al. combined the multi-objective genetic algorithm U-NSGA-III with the heuristic MME method, aiming to optimize both non-machining energy consumption and total weighted delay [36]. Ali et al. applied multi-objective gray wolf optimization (MOGWO). The algorithm solves green scheduling problems for high-energy machine tools; it specifically addresses unrelated parallel batch processes [37]. Caldeira et al. proposed an energy-saving flexible workshop scheduling model incorporating machine tool on/off strategies, with the objective of minimizing energy consumption during workshop production processes [38]. Sagar et al. developed an energy-aware production planning model for flexible manufacturing systems, demonstrating that the introduction of machine on/off strategies effectively reduces workshop energy costs associated with just-in-time delivery [39]. Wang et al. established a multi-objective optimization model for energy-efficient flexible workshop scheduling based on job operation sequences and machine allocation, further proposing a limited-restart energy-saving strategy to optimize workshop energy utilization efficiency [40]. However, these studies typically implement energy-saving control of machine intermittent states only after completing production scheduling. This post-scheduling approach fixes both intermittent durations and available intermittent states of the machine tool beforehand, consequently constraining the overall energy-saving potential of the workshop.
In summary, this paper proposes a workshop energy-saving scheduling method integrating production scheduling with machine tool intermittent state control, effectively reducing makespan and lowering both machining and intermittent energy consumption. The innovations of this paper are as follows:
(1) The interaction relationship between production scheduling and machine tool intermittent state control is studied. The variation characteristics in workshop machining energy consumption, machine tool intermittent durations, and intermittent energy consumption under the interaction of production scheduling and intermittent state control are analyzed, highlighting the necessity of their integration. An integrated energy-saving optimization strategy for the workshop, incorporating intermittent state control, is designed.
(2) A multi-objective integrated optimization scheduling model for workshop energy-saving is established. Variables such as machine tool intermittent durations, intermittent energy consumption, the set of optional intermittent states, and variable operation start times are introduced. The model incorporates constraints such as intermittent state determination and variable operation identification. The optimization objectives are to minimize makespan, machining energy consumption, and intermittent energy consumption, leading to the development of a multi-objective integrated optimization model.
(3) An improved multi-objective integrated optimization algorithm is proposed. The energy-saving optimization strategy is integrated into the encoding, and a four-layer chromosome encoding mechanism, which considers operation sequencing, machine tool selection, and intermittent state control, is designed. Additionally, multiple crossover, mutation genetic operators, and low-level selection strategies are introduced to improve the NSGA-II algorithm, addressing the issue of reduced algorithm search efficiency caused by the expansion of the solution space after integration.
The chapter arrangement of this paper is as follows: Section 2 introduces the workshop energy-saving scheduling problem integrated with intermittent state control, and proposes an integrated energy-saving optimization strategy for the workshop. Section 3 establishes a multi-objective integrated optimization model. Section 4 presents an improved NSGA-II algorithm. Section 5 evaluates and compares the proposed method through experiments. Finally, Section 6 provides conclusions and discusses future research directions. The overall framework is illustrated in Figure 1.
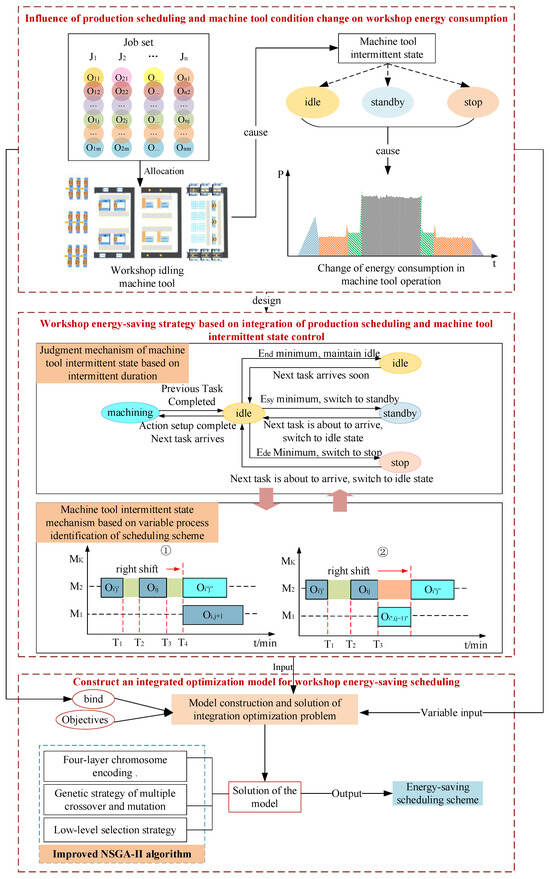
Figure 1.
The overall framework.
2. Design of Integrated Workshop Energy-Saving Optimization Strategy
The energy-saving scheduling problem in workshops with integrated machine tool intermittent state control is described as follows: At the initial time, the workshop contains jobs, denoted as the set , where each job consists of operations represented by set . These operations can be processed on available machine tools in set , with each operation executable on any machine that satisfies its machining capability requirements.
Production scheduling and machine tool intermittent state control constitute two tightly coupled decision-making processes in workshop energy systems. Production scheduling, through operation sequencing and machine tool selection, directly governs job allocation patterns, thereby determining intermittent durations and consequently influencing both machining and intermittent energy consumption. The intermittent state control optimizes scheduling decisions by transitioning machines to standby or stop modes, which similarly affects machining and intermittent energy consumption. These interdependent mechanisms collectively determine the overall energy consumption performance of manufacturing workshops.
The scheduling scheme typically determines the intermittent durations of machine tools, imposing strong constraints on the decision-making process of intermittent state control, and consequently increasing intermittent energy consumption. Therefore, to reduce unnecessary machine intermittent duration and associated energy waste, it is essential to rationally arrange production scheduling through optimized operation sequencing and machine selection, thereby enhancing overall production efficiency. The strong constraining effect of production scheduling on intermittent state control is illustrated in Figure 2.
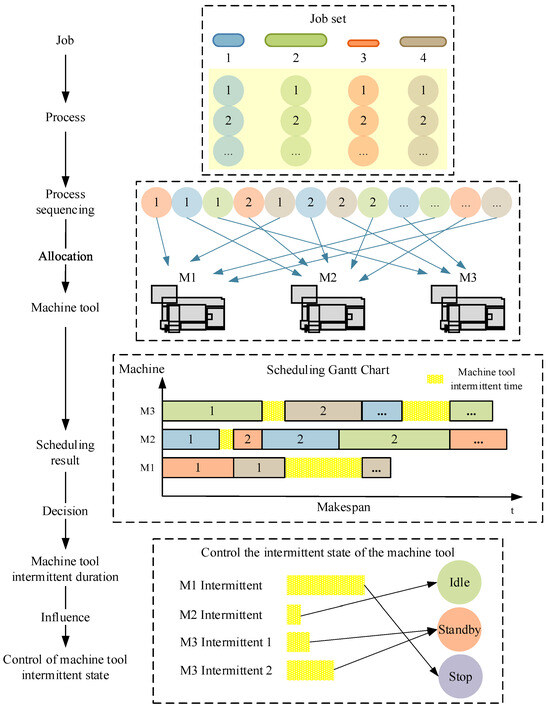
Figure 2.
The strong constraints of production scheduling on intermittent state control of machine tools.
Among the three intermittent states of machine tools—idle, standby, and stop—each state transition requires different switching durations. Consequently, intermittent state control directly influences intermittent durations. Proper intermittent state control can provide feedback to optimize scheduling decisions, thereby reducing unnecessary machine intermittent durations, shortening job completion cycles, decreasing workshop energy consumption, and ultimately enhancing overall production efficiency. The impact of machine tool intermittent state control on workshop production scheduling is demonstrated in Figure 3.
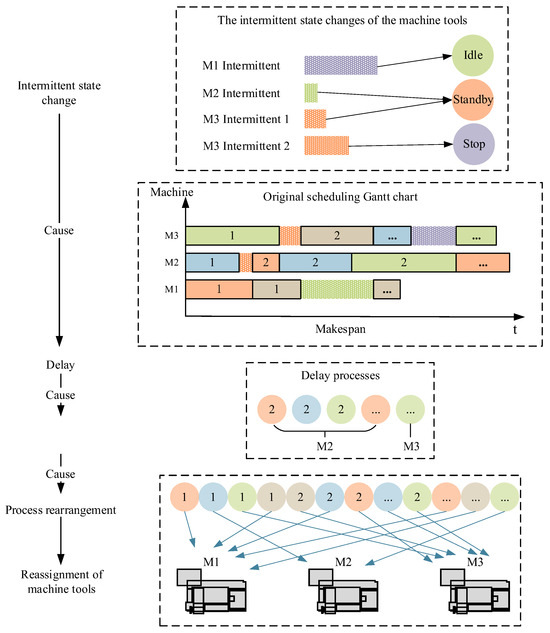
Figure 3.
Strong constraint effect of production scheduling on machine tool intermittent state control.
In production scheduling, operation sequencing and machine selection typically determine machine intermittent durations, imposing strong constraints on intermittent state control decisions. This makes it difficult for intermittent state control to feedback optimization scheduling decisions, further limiting a workshop’s overall energy-saving potential. Furthermore, human factors such as operational errors may alter intermittent state control (e.g., transitioning from idle to standby or stop states), prolonging intermittent durations and causing subsequent production delays that invalidate predetermined schedules, necessitating the rescheduling of operations and machine reassignment. Consequently, to maximize energy-saving potential and optimize overall workshop performance, the integrated co-optimization of production scheduling and intermittent state control is essential. This integrated approach enhances production efficiency, reduces energy waste, and ultimately improves energy-saving scheduling effectiveness.
To simultaneously minimize machining energy consumption, intermittent energy consumption, and maximize production efficiency in workshop production, an integrated energy-saving optimization strategy is proposed that combines production scheduling with intermittent state control. Firstly, the strategy identifies feasible intermittent state sets based on intermittent durations, and calculates their corresponding energy consumption, selecting the state with minimal energy demand. Subsequently, it recognizes variable operations in the scheduling scheme, and adjusts their machining start times to provide feedback for scheduling optimization. Using these updated start times, the strategy recalculates intermittent durations and corresponding state sets, reevaluates energy consumption for each state, and ultimately implements the most energy-saving intermittent configuration. The detailed energy-saving optimization strategy is structured as follows:
(1) Judgment mechanism of machine tool intermittent state based on intermittent durations.
The three intermittent states of machine tools—idle, standby, and stop—exhibit significant differences in energy consumption. The effective reduction in workshop intermittent energy consumption can be achieved by accurately determining machine states and controlling their low-energy operation. Upon completion of production scheduling decisions, the feasible intermittent state set for each intermittent period is obtained based on machine intermittent duration. The energy consumption of each state in the set is then calculated, and the state with minimal energy demand is selected for operation: (1) idle mode is maintained when it demonstrates the lowest energy consumption, (2) standby mode is activated when it proves most energy-saving, or (3) stop is implemented when it yields minimal energy waste. This optimal state selection ensures the most energy-saving intermittent performance, thereby eliminating unnecessary energy dissipation. Concurrently, machines are controlled to transition back to machining states before subsequent operations arrive. As illustrated in Figure 4, this determination mechanism significantly reduces machine intermittent energy consumption, and enhances overall workshop energy utilization efficiency.
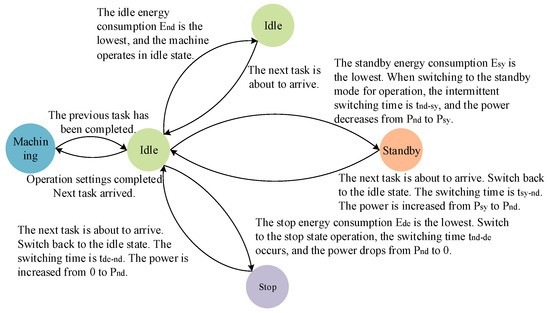
Figure 4.
Judgment mechanism of machine tool intermittent state based on intermittent durations.
(2) Machine tool intermittent state adjustment mechanism based on variable operation identification of scheduling scheme.
Building upon this foundation, the intermittent state adjustment mechanism based on the variable operation identification of scheduling schemes is employed to optimize the scheduling scheme. Under the constraints of maintaining the original makespan, avoiding interference with other operations, and meeting job delivery deadlines, this mechanism identifies variable operations capable of start-time adjustments, and rationally reschedules their machining sequences. Subsequently, it updates the revised intermittent durations and corresponding feasible intermittent state sets, reapplies the judgment mechanism of intermittent state based on intermittent durations to recalculate energy consumption for each state, and implements the most energy-saving intermittent mode. Through this adaptive control loop, intermittent state control effectively feeds back into scheduling optimization, further refining the production scheduling to reduce both machining and intermittent energy consumption simultaneously, thereby enhancing overall workshop energy utilization efficiency and production productivity.
An example of a machine tool intermittent state adjustment mechanism based on variable operation identification in scheduling schemes is shown in Figure 5, where operation denotes the preceding operation of on machine , operation represents the succeeding operation of on machine , and operation indicates the subsequent operation within the same job . In the actual workshop production, it is essential to consider temporal constraints between each operation and its machine-specific predecessor/successor operations, and its job-inherent subsequent operation. Therefore, the variable operations that can adjust their start time of machining can be identified, providing the foundation for intermittent state control to feedback-optimize scheduling decisions through two scenarios.
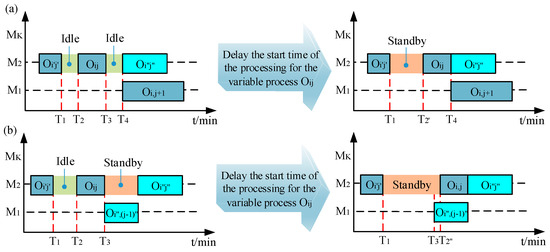
Figure 5.
An example of machine tool intermittent state adjustment mechanism based on the variable operation identification of scheduling schemes: (a) when operation is not the last operation of job , is temporal constraint of variable operation; (b) when operation is the last operation of job , is temporal constraint of variable operation.
- (1)
- When operation is not the last operation of job , is the temporal constraint of variable operation as shown in Equation (1).
- (2)
- When operation is the last operation to be performed on job , is the temporal constraint of variable operation as shown in Equation (2):where is the start time of operation , is the completion time of operation , is the completion time of operation , is the start time of operation , and is the start time of operation .
3. The Multi-Objective Integrated Optimization Model
3.1. Notations
In this paper, time-related quantities are measured in minutes while power-related quantities are in watts. The definitions of all variables are summarized in Table 1.

Table 1.
Notations.
3.2. Assumptions
(1) All machines have four fundamental operating states: machining, idle, standby, and stop, with the capability to transition between these states.
(2) A number of machine tools are available in the workshop. Several jobs are to be processed, each containing at least one operation.
(3) Each machine can process only one operation at a time.
(4) Each operation is assigned to only one machine.
(5) No precedence constraints exist between operations of different jobs, except for the emergency parts.
(6) Operations of the same job have predefined machining sequences.
(7) Once started, an operation cannot be interrupted.
(8) Both operation machining times and machine state transition times are known.
(9) Job transportation times between machines are negligible.
3.3. The Integrated Optimization Model
In order to improve workshop efficiency, reduce energy consumption in the production process, ensure timely completion of jobs, and minimize the makespan and total energy consumption of the workshop, an integrated optimization model for workshop energy-saving scheduling considering intermittent state control is established as follows:
where Equation (3) defines a general objective function. Equation (4) integrates two optimization objectives: minimizing the makespan and total energy consumption of the workshop. Equation (5) is the total machining energy consumption. Equation (6) represents the total intermittent energy consumption. Equation (7) represents the total energy consumption of the idle state. Equation (8) represents the total energy consumption of the standby state. Equation (9) represents the total energy consumption of the stop state. Equation (10) represents the machine tool restart energy consumption. Equation (11) represents the energy consumption for state-switching between the machine tool idle and standby states.
3.4. The Constraint Condition of Integrated Optimization Model
To ensure the feasibility and rationality of scheduling solutions, achieve energy-saving objectives, and maintain practical validity in workshop production, the integrated optimization model for workshop energy-saving scheduling must satisfy the following constraints:
where Equation (12) defines intermittent durations between consecutive operations on the same machine. Equations (13) and (14) specify the control conditions for idle state during intermittent periods, while Equation (15) quantifies the corresponding energy consumption. Equations (16) and (17) establish standby state control criteria, with Equation (18) modeling the standby energy consumption. Equations (19) and (20) govern stop state transitions, complemented by Equation (21) for reboot energy consumption. Equation (22) ensures no job exceeds its deadline. Equation (23) prioritizes jobs with shorter deadlines. Equation (24) enforces machine state exclusivity ( permits only one intermittent state among idle/standby/stop, whereas disables intermittent state control). Equation (25) states that the start time of the next operation for any job must not be earlier than the completion time of the previous operation. Equation (26) states that any operation can be processed only once on a machine tool. Equation (27) states that only one operation can be processed on any machine tool at the same time. Equation (28) states that once an operation has started, it cannot be interrupted. Equation (29) states that the machining time of any operation does not exceed its delivery date. Equation (30) ensures non-negative time variables.
4. An Improved NSGA-II Algorithm for Integrated Optimization
The NSGA-II algorithm proposed by Deb et al. has demonstrated excellent performance in solving multi-objective optimization problems [41]. However, when applied to integrated workshop energy-saving scheduling with intermittent state control, it fails to achieve the co-optimization of production scheduling and intermittent state control, often suffering from premature convergence or local optima. To this end, a four-layer chromosome encoding method, which considers operation sequencing, machine tool selection, and machine tool intermittent state control, is designed by integrating the energy-saving optimization strategy into the chromosome encoding mechanism. Furthermore, multiple crossover and mutation genetic operators are introduced, and, combined with a lower-level selection strategy, the algorithm is improved. The framework of the improved NSGA-II algorithm is shown in Figure 6.
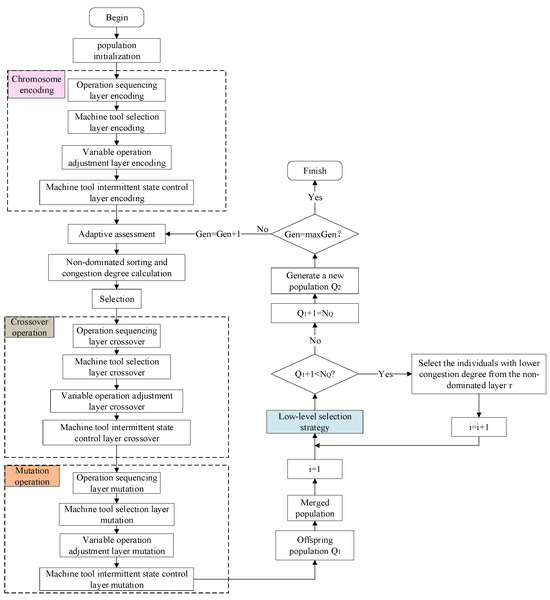
Figure 6.
The framework of the improved NSGA-II algorithm.
4.1. A Four-Layer Chromosome Encoding Mechanism
Algorithmic performance is significantly influenced by encoding methods, where an effective encoding approach can efficiently and accurately solve complex optimization problems, through enhanced information transfer and solution space exploration. In light of the characteristics of multi-objective integrated optimization problems, a four-layer chromosome encoding method is proposed. This approach directly employs sequence numbers to represent operation sequencing, machine tool selection, and intermittent state control, transforming key process information into a computer-processable format. Each gene locus corresponds to a specific manufacturing operation, explicitly mapping actual production processes. By implementing this structured encoding, information transmission efficiency is improved and redundant solutions in the search space are reduced, thereby accelerating algorithm convergence while enhancing solution quality and stability.
Figure 7 illustrates a four-layer chromosome encoding sequence. The first layer, Operation Sequencing (OS), encodes with job operation numbers (e.g., ‘21’ in sequence (21,11,22,31,12,32,23,33,13) represents the first operation of job 2). The second layer, Machine Selection (MS), uses indices to designate machines from the available set (, ,) for each operation (e.g., ‘1’ in sequence (1,3,2,3,2,1,3,2,1) assigns operation to machine ). The third layer, Variable Operation Adjustment (OD), employs logic values (0/1) to flag whether allows start-time adjustments (1 = adjustable, 0 = fixed). The fourth layer, Intermittent State Control (IC), selects energy-optimal states from the set (0,, , ) (e.g., ‘2’ in sequence (3,0,2,0,0,0) indicates standby mode for machine during its first intermittent period, while ‘0’ denotes no intermittent state activation for in the second intermittent). Notably, the OS, MS, and OD layers share equal length as they follow the operation order, whereas the IC layer sequentially processes each machine’s inter-operation intermittent durations derived from the preceding layers.
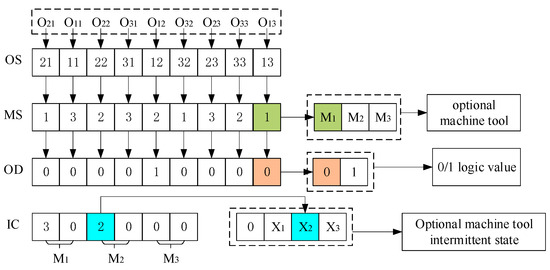
Figure 7.
An example of a four-layer chromosome encoding is provided.
The pseudocode for encoding the variable operation adjustment layer and the machine tool intermittent state control layer is presented in Algorithms 1 and 2.
| Algorithm 1: encoding of variable operation adjustment layer |
| Input: encoding information from operation sequencing layer and machine tool selection layer |
| Output: encoding information for variable operation adjustment layer |
| 1: Connect to encoding information from operation sequencing layer and machine tool selection layer |
| 2: Traverse through all operations to retrieve the current operation and its machining machine |
| 3: If there exists preceding operation and succeeding operation on machine |
| 4: If there exists operation |
| 5: Intermittent duration = calculate intermittent duration (between operation and operation , between operation and operation , between operation and operation ) |
| 6: If the start time of operation
can be adjusted, set the adjustment encoding of operation
to the logic value 1 Otherwise, set the adjustment encoding of operation to the logic value 0 |
| 7: For operation , if it is the last operation in the list, print the encoding information for the variable operation adjustment layer Otherwise, continue to the next operation and its machine information |
| Algorithm 2: encoding of machine tool intermittent state control layer |
| Input: Encoding information from operation sequencing layer, machine tool selection layer, and variable operation adjustment layer |
| Output: Encoding information for machine tool intermittent state control layer |
| 1: Connect to the encoding information from operation sequencing layer, machine tool selection layer, and variable operation adjustment layer |
| 2: Traverse through all operations; calculate intermittent durations between current operation on machine and the succeeding operation |
| 3: If the intermittent duration is greater than 0 |
| 4: If the intermittent duration is less than the minimum standby intermittent duration of the machine |
| 5: If the intermittent duration is less than the minimum stop intermittent duration of the machine |
| 6: Obtain the set of executable machine tool intermittent state |
| 7: Energy consumption = calculate energy consumption (intermittent duration, power) |
| 8: Select the state with the lowest energy consumption from |
| 9: Encode |
| 9: For operation , if it is the last operation in the list, print the encoding information for the machine tool intermittent state control layer |
| Otherwise, continue calculating intermittent durations between the next operation of machine in the operation list and its subsequent operation |
4.2. The Crossover and Mutation of Multiple Strategies
Crossover and mutation are two crucial genetic operators in the NSGA-II algorithm, directly influencing its search capability and global optimization performance. The crossover operator generates new offspring by recombining parental genes, facilitating information exchange, maintaining population diversity, and exploring potential high-quality solutions across a broad search space. The mutation operator enhances solution diversity by randomly altering individual genes, helping escape local optima, and improving global search performance. By employing multiple crossover and mutation operators, the algorithm effectively increases search efficiency and population diversity, thereby promoting the discovery of globally optimal solutions. Notably, these genetic operations must adhere to specific constraints, such as job priorities, machine machining capabilities, and adjustable operation identification. When executing these operations under such constraints, certain infeasible individuals may be generated. In such cases, constraint-handling methods are applied to ensure all solutions remain within the feasible domain, guaranteeing the practical operability of the final solutions.
Figure 8 illustrates the crossover operation process, which consists of the following four steps: (1) OS crossover. Two crossover points are randomly selected in parent 1. The gene sequence to the left of crossover point 1 is copied to the left side of child 1, while the sequence to the right of crossover point 2 is copied to the right side of child 1. Subsequently, the remaining positions in child 1 are filled with distinct gene sequences selected from parent 2. (2) MS crossover. The OS portion of parent 1 is directly copied to child 1. Then, a set of randomly selected operations are chosen, and their corresponding MS portions from parent 1 are copied to child 1, with these operations being marked. For the unmarked operations, the corresponding MS portions from parent 2 are used to fill the remaining positions in child 1. (3) OD crossover. A number of gene sequences are randomly selected from parent 1 and copied to child 1. The remaining positions in child 1 are then sequentially filled with distinct gene sequences from parent 2. (4) IC crossover. A set of crossable IC sequences are randomly selected from parent 2 and copied to the corresponding positions in child 1. The remaining positions are filled with the corresponding IC sequences from parent 1 in sequence.
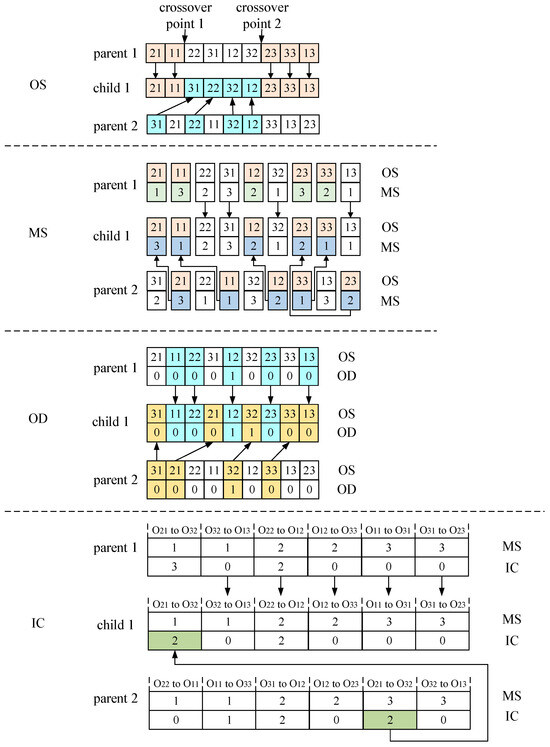
Figure 8.
Indication of crossover operation.
Figure 9 illustrates the mutation operation process, which consists of the following four steps: (1) OS mutation. Two subsequences are randomly selected, and the first gene of each subsequence is swapped with the last gene, the second gene with the penultimate gene, and so on until all genes are exchanged, thereby generating a new sequence. (2) MS mutation. Two positions are randomly chosen, and operation numbers and machine sequence numbers at these positions are swapped to produce a new MS sequence. (3) OD mutation. Several positions are randomly selected, and their current logic values are replaced with different logic sequence numbers to generate a new OD sequence. The mutated sequence is then checked for compliance with operational constraints. If it violates the constraints, adjustments are made accordingly. (4) IC mutation. Among all intermittent periods, the machine intermittent state with the highest energy consumption is selected and mutated with equal probability. The chosen intermittent state, denoted as , is replaced with another distinct intermittent state from the set of executable machine intermittent state associated with the corresponding operation.
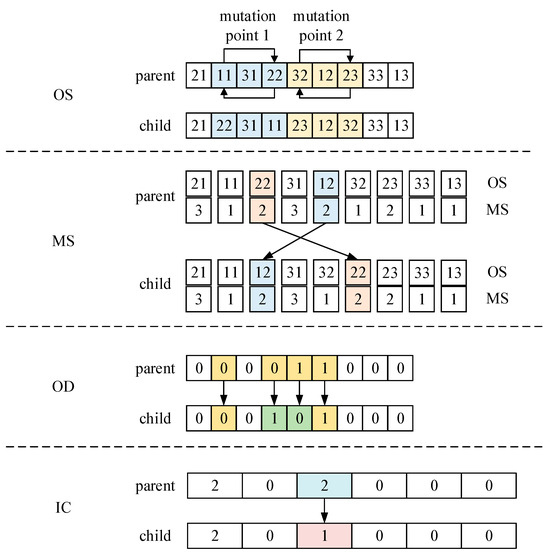
Figure 9.
Indication of mutation operation.
4.3. A Low-Level Selection Strategy
When solving multi-objective integrated optimization problems using the NSGA-II algorithm, insufficient population diversity often emerges as a critical issue. Typically, NSGA-II algorithm employs non-dominated sorting and crowding distance computation to select parent individuals, preferentially retaining those with larger crowding distances for subsequent generations. While this selection mechanism effectively preserves elite individuals and accelerates convergence in most scenarios, it may inadvertently reduce population diversity when addressing complex problems. This preferential strategy can exacerbate uneven population distribution, potentially leading to premature convergence or entrapment in local optima. Consequently, the algorithm’s search space breadth and solution diversity become constrained, limiting its overall optimization performance.
To address this issue, a low-level selection strategy (LS) is proposed, which reasonably determines the number of superior and inferior individuals based on different non-dominated levels and population size, thereby achieving balanced population distribution. Specifically, in addition to preferentially selecting parents with higher crowding distances from the top non-dominated layers for the next generation, the strategy retains a certain proportion of inferior individuals from various non-dominated levels, as formulated in Equation (31). This approach effectively enhances population size and diversity while significantly mitigating uneven population distribution.
where represents the number of selected individuals from the -th non-dominant level, denotes the highest non-dominant level of population, signifies the selected level index, and indicates the population size.
4.4. Benchmark Testing
To validate the effectiveness of the improved algorithm in solving integrated optimization problems of different scales, this study employs standard test cases MK01 (small-scale) and MK06 (large-scale) from Reference [42], combined with machine tool power consumption data from Reference [43]. The parameters of the standard test cases are presented in Table 2, while the machine tool power parameters are detailed in Table 3. We compare the performance of the NSGA-II algorithm with and without the low-level selection strategy when solving cases MK01 and MK06, with the results illustrated in Figure 10 and Figure 11.

Table 2.
Parameter value ranges of the benchmark instances.

Table 3.
Operating power parameter ranges of machine tools.
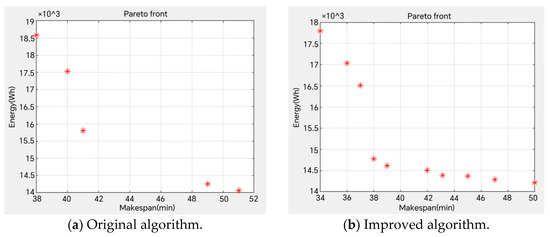
Figure 10.
Pareto front distribution plots with small-scale case MK01.
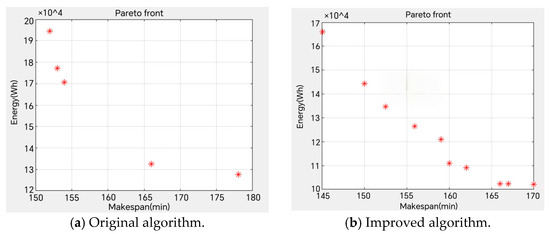
Figure 11.
Pareto front distribution plots with large-scale case MK06.
The results demonstrate that the improved algorithm with the low-level selection strategy obtains superior solutions for multi-objective integrated optimization problems. Particularly for large-scale case MK06, it shows outstanding performance in both total energy consumption and makespan, achieving significant energy and time savings.
5. Case Study
To verify the effectiveness and feasibility of the proposed methodology for solving multi-objective integrated optimization problems in workshop scheduling, an improved NSGA-II algorithm is employed for simulation in the MATLAB R2023a environment. Section 5.1 introduces the case background and initial scenario data. In Section 5.2, the integrated optimization model and improved algorithm are employed to solve the case studies, with the results systematically compared against those obtained from the asynchronous optimization model. This comparative analysis validates both the effectiveness and feasibility of the integrated optimization approach. Subsequently, Section 5.3 compares the proposed energy-saving optimization strategy with hypothetical strategies where machine tools persistently maintain always idle, standby, or stop states during intermittent periods, thereby validating the effectiveness of the proposed energy-saving strategy. Furthermore, comparative experiments between the improved NSGA-II algorithm and its original version, validating both the effectiveness and superiority of the proposed algorithmic improvements, are conducted. Finally, in Section 5.4, we conducted comparative experiments between the improved NSGA-II algorithm and other multi-objective optimization algorithms. Through rigorous evaluation across multiple dimensions including solution quality and distribution uniformity, the results demonstrate the superior performance of improved NSGA-II algorithm in addressing the multi-objective integrated optimization problem.
5.1. Experimental Background
The experimental data are obtained from an engine component factory in a discrete manufacturing environment. This case study represents a 9 × 6 scheduling problem, where 9 denotes the number of jobs to be processed, and 6 indicates the quantity of available machine tools in the workshop. The NSGA-II algorithm parameters are configured as follows: population size is = 200, maximum generations = 100, crossover rate = 0.8, and mutation rate = 0.1. Table 4 details the average operational power and state-switching time for each machine tool under different intermittent states. Table 5 provides the complete machining information for all nine jobs, including operation sequences and machining requirements.

Table 4.
The average operational power and average state-switching time of each machine tool intermittent state.

Table 5.
The machining information of the jobs.
5.2. Comparison Analysis with Asynchronous Optimization
To validate the energy-saving effects of the proposed integrated optimization method, the information in Table 6 and Table 7 is used. The proposed integrated optimization model, combined with the improved genetic algorithm, is applied to solve and verify the case. A comparative analysis is conducted with the asynchronous optimization method. In the asynchronous optimization method, encoding is first performed for the operation sequencing layer, machine selection layer, and variable operation adjustment layer, with optimization focusing on minimizing total workshop energy consumption and makespan while maintaining unchanged machine intermittent states. After obtaining pareto front solutions, the workshop energy-saving optimization strategy is applied to adjust the machine intermittent states. The integrated optimization results presented in Figure 12a demonstrate a makespan of 32.6 and total workshop energy consumption of 5376.875 , while the asynchronous optimization results shown in Figure 12b exhibit a makespan of 33.1 and energy consumption of 5594.846 . Upon completion of each machining process, all machines enter idle, standby, or stop state. Consequently, the scheduling decisions in the figures only display changes in machine intermittent states, with detailed state-switching processes omitted for enhanced visualization clarity.

Table 6.
Comparison of results between integrated optimization and asynchronous optimization.

Table 7.
Analysis of the effects of different energy-saving strategies.
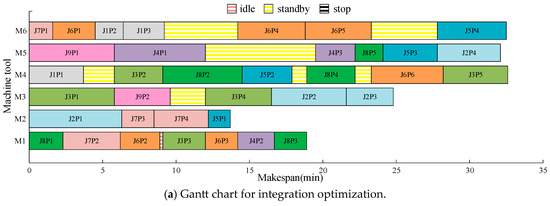
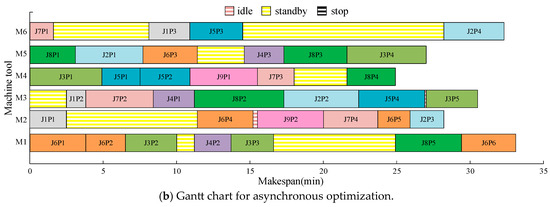
Figure 12.
Gantt chart for integrated optimization and asynchronous optimization.
Table 6 compares the energy-saving effects between integrated and asynchronous optimization methods when solving the same case study. The comparison covers three key metrics: makespan, total energy consumption, and machine tool utilization (MTU). Results show the integrated method outperforms asynchronous optimization. It reduces makespan by 1.51%, shortening production cycles significantly. Total energy consumption decreases by 3.83%, demonstrating improved energy efficiency. Detailed energy savings are achieved across all operational states: (1) Machining energy consumption: 0.37% reduction. (2) Intermittent energy consumption: 47.54% reduction. (3) Idle state energy consumption: 55.06% reduction. (4) Standby state energy consumption: 56.17% reduction. (5) Switching energy consumption (idle-standby): 28.03% reduction. Additionally, the integrated method increases MTU by 11.72%. This reduction in machine intermittent durations enhances overall production efficiency.
Figure 13 presents a comparative histogram of energy consumption distribution between integrated and asynchronous optimization approaches. The integrated method demonstrates clear energy savings, reducing machining energy by 19.279 and intermittent energy by 198.692 compared to asynchronous optimization. The superior performance stems from the integrated method’s holistic approach. It simultaneously optimizes production scheduling and machine intermittent state control. This coordinated strategy effectively minimizes unnecessary energy waste. This highlights the benefits of integrated optimization in energy management and production efficiency, providing reliable support for improving enterprise productivity and reducing costs.
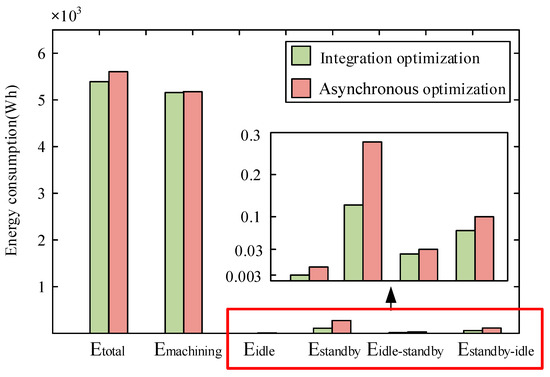
Figure 13.
The energy consumption of integrated optimization is compared with that of asynchronous optimization.
The energy consumption difference between integrated and asynchronous optimization methods primarily results from machine intermittent state control. The asynchronous approach generates longer intermittent duration. This increases intermittent energy consumption. Consequently, total workshop energy usage and production costs rise. In contrast, the integrated method adopts a global optimization perspective. It combines production scheduling with intermittent state control. This dual approach achieves higher energy efficiency during both machining and intermittent phases. Significant reductions in overall workshop energy consumption are realized.
5.3. Analysis of Energy-Saving Optimization Strategy and Algorithm Improvement
To verify the effectiveness of the proposed workshop energy-saving optimization strategy in reducing machine intermittent energy consumption, comparisons are made with three hypothetical strategies: maintaining in always idle, standby, or stop states during intermittent periods. The energy-saving performance comparison, based on integrated optimization results of operation sequencing and machine selection, is presented in Table 7. Results demonstrate that the energy-saving optimization strategy successfully completes production as scheduled while significantly reducing intermittent energy consumption. Compared to the three alternative strategies, it achieves energy consumption reductions of 40.53%, 6.30%, and 78.64%, respectively. Additionally, the energy-saving optimization strategy did not cause any machining delays, while the always standby and always stop strategies resulted in varying degrees of machining delays, with the always stop strategy causing the most significant delays.
Furthermore, to further validate the superiority of the improved NSGA-II algorithm with the low-level selection strategy, comparative experiments are conducted against the original algorithm. The resulting pareto front solutions are shown in Figure 14. The results demonstrate two key advantages of the improved algorithm: (1) It obtains higher-quality solutions for the integrated optimization problem. (2) It achieves better performance in both workshop energy consumption and makespan. These enhancements translate to significant reductions in production cycle times and overall energy usage, and the low-level selection strategy proves particularly effective.
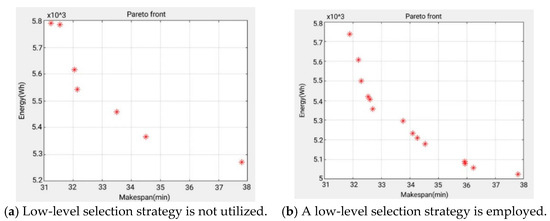
Figure 14.
Pareto front distribution plots with and without low-level selection strategy are shown.
5.4. Comparative Analysis with Other Algorithms
To further validate the effectiveness of the improved NSGA-II algorithm in solving the multi-objective integrated optimization problem, a comparative analysis is conducted with the Multi-Objective Particle Swarm Optimization (MOPSO) algorithm [44]. The parameter settings for the MOPSO algorithm are as follows: population size = 200, maximum generations = 100, inertia weight ω dynamically adjusted within the range [0.1, 0.8], learning factors = = 0.8, mutation probability 0.1.
With total workshop energy consumption and makespan as the optimization objectives, the case study is solved using the two aforementioned algorithms, and the distribution of their obtained pareto front solutions is illustrated in Figure 15. The solution results represent the mean of multiple independent runs. A comprehensive comparison of solution performance between the NSGA-II and MOPSO algorithms in this practical application demonstrates that the improved NSGA-II algorithm exhibits superior optimization capability. Specifically, the improved NSGA-II algorithm yields a greater number of pareto front solutions with more uniform distribution, and demonstrates better ability to capture a potential solution set in the optimization space.
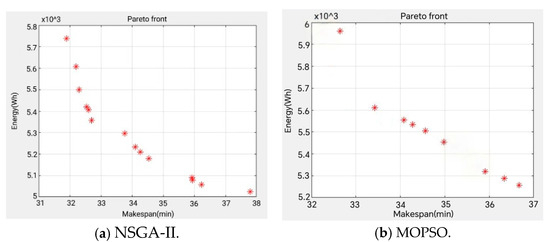
Figure 15.
Comparative analysis of pareto front solutions obtained by two optimization algorithms.
In summary, this study achieves certain energy-saving effects through the integrated optimization of production scheduling and machine tool intermittent state control. In the experimental case, compared to the traditional asynchronous optimization model, the proposed integrated optimization model demonstrates significant improvements, reducing total workshop energy consumption by 3.90% and intermittent energy consumption by 47.54%. The improved NSGA-II algorithm, through optimized genetic operations, outperforms the MOPSO algorithm in terms of both solution quality and distribution uniformity, demonstrating its superior capability in solving multi-objective integrated optimization problems in workshop environments.
However, it should be noted that the current research conclusions are primarily derived from standard cases and specific-scale scheduling scenarios (9 jobs × 6 machines). The applicability of the method to large-scale production systems requires further validation. Moreover, the model’s effectiveness is constrained by the following assumptions:
(1) Machine state-switching times and operational power are treated as fixed values;
(2) Job transportation time and possible machining interruptions are neglected.
Therefore, future research should focus on relaxing these simplifying assumptions by incorporating more practical production variables, including machine breakdowns and transportation delays, to enhance the method’s generalizability and applicability in real-world industrial settings.
6. Conclusions
To achieve comprehensive energy-saving scheduling in the workshop, an integrated machine tool intermittent state control method for workshop energy-saving scheduling is proposed. Firstly, the variation characteristics of workshop machining energy consumption, machine tool intermittent duration, and intermittent energy consumption are investigated, and an integrated workshop energy-saving optimization strategy is designed. Secondly, variables such as intermittent duration, intermittent energy consumption, and variable operation start times are introduced. By incorporating constraints like intermittent state determination and variable operation identification, a multi-objective integrated optimization model is developed. Thirdly, the energy-saving optimization strategy is integrated into the chromosome encoding, and a four-layer chromosome encoding method is designed. Additionally, the NSGA-II algorithm is improved by integrating multiple crossover, mutation genetic operators, and low-level selection strategies to address the issue of reduced search efficiency caused by the expanded solution space after integration. Finally, the method’s effectiveness is validated through machining examples. The results show that the proposed method significantly reduces overall workshop energy consumption and makespan. The generated scheduling Gantt chart reflects both production scheduling and intermittent state control decision results, effectively guiding workers in production.
Compared with existing methods, the integrated machine tool intermittent state control energy-saving scheduling method not only shortens the makespan of jobs, but also achieves overall energy savings in workshop machining and intermittent energy consumption. Future research will further consider the impact of disturbance factors on workshop production and focus on applying energy-saving optimization strategy in dynamic workshops.
Author Contributions
Conceptualization, H.C., S.Z. and H.L.; methodology, H.C. and S.Z.; software, H.C.; validation, H.C., S.Z. and Z.J.; formal analysis, H.C.; investigation, H.C.; resources, S.Z. and Z.J.; data curation, H.C.; writing—original draft preparation, H.C.; writing—review and editing, H.C.; visualization, H.C.; supervision, S.Z., Z.J. and H.L.; project administration, S.Z.; funding acquisition, H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant number 52375508).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Lu, Y.K.; Sheng, B.Y.; Fu, G.C.; Luo, R.P.; Chen, G.; Huang, Y.Z. Prophet-EEMD-LSTM based method for predicting energy consumption in the paint workshop. Appl. Soft Comput. 2023, 143, 110447. [Google Scholar] [CrossRef]
- Sihag, N.; Sangwan, K.S. A systematic literature review on machine tool energy consumption. J. Clean. Prod. 2020, 275, 123125. [Google Scholar] [CrossRef]
- Pawanr, S.; Gupta, K. A review on recent advances in the energy efficiency of machining processes for sustainability. J. Energies 2024, 17, 3659. [Google Scholar] [CrossRef]
- Yu, H.; Fang, X.F.; Feng, L.H. Research on the method of machine tool running state management based on digital twin. In Proceedings of the ICEM 2023, Amsterdam, The Netherland, 13–16 June 2023; pp. 231–243. [Google Scholar]
- Li, R.; Gong, W.Y.; Lu, C.; Wang, L. A learning-based memetic algorithm for energy-efficient flexible job-shop scheduling with type-2 fuzzy processing time. IEEE Trans. Evol. Comput. 2022, 27, 610–620. [Google Scholar] [CrossRef]
- Fernandes, J.M.R.C.; Homayouni, S.M.; Fontes, D.B.M.M. Energy-efficient scheduling in job shop manufacturing systems: A literature review. Sustainability 2022, 14, 6264. [Google Scholar] [CrossRef]
- Xiao, Y.J.; Yin, S.S.; Ren, G.Q.; Liu, W.L. Study on flexible job shop scheduling problem considering energy saving. J. Intell. Fuzzy. Syst. 2024, 46, 5493–5520. [Google Scholar] [CrossRef]
- Lu, H.; Qiao, F. An efficient adaptive genetic algorithm for energy saving in the hybrid flow shop scheduling with batch production at last stage. Expert Syst. 2022, 39, e12678. [Google Scholar] [CrossRef]
- Li, C.S.; Zhang, B.; Han, Y.Y.; Wang, Y.T.; Li, J.Q.; Gao, K.Z. Energy-efficient hybrid flowshop scheduling with consistent sublots using an improved cooperative coevolutionary algorithm. Mathematics 2022, 11, 77. [Google Scholar] [CrossRef]
- Jiang, T.H.; Zhu, H.Q.; Gu, J.C.; Liu, L.; Song, H.C. A discrete animal migration algorithm for dual-resource constrained energy-saving flexible job shop scheduling problem. J. Intell. Fuzzy Syst. 2022, 42, 3431–3444. [Google Scholar] [CrossRef]
- Para, J.; Del Ser, J.; Nebro, A.J. Energy-aware multi-objective job shop scheduling optimization with metaheuristics in manufacturing industries: A critical survey, results, and perspectives. Appl. Sci. 2022, 12, 1491. [Google Scholar] [CrossRef]
- He, L.J.; Cao, Y.L.; Li, W.F.; Cao, J.J.; Zhong, L.C. Optimization of energy-efficient open shop scheduling with an adaptive multi-objective differential evolution algorithm. Appl. Soft Comput. 2022, 118, 108459. [Google Scholar] [CrossRef]
- Li, R.; Gong, W.Y.; Wang, L.; Lu, C.; Pan, Z.X.; Zhuang, X.Y. Double DQN-based coevolution for green distributed heterogeneous hybrid flowshop scheduling with multiple priorities of jobs. IEEE Trans. Autom. Sci. Eng. 2023, 21, 6550–6562. [Google Scholar] [CrossRef]
- Luo, S.; Zhang, L.X.; Fan, Y.S. Energy-efficient scheduling for multi-objective flexible job shops with variable processing speeds by grey wolf optimization. J. Clean. Prod. 2019, 234, 1365–1384. [Google Scholar] [CrossRef]
- Abedi, M.; Chiong, R.; Noman, N.; Zhang, R. A multi-population, multi-objective memetic algorithm for energy-efficient job-shop scheduling with deteriorating machines. Expert Syst. Appl. 2020, 157, 113348. [Google Scholar] [CrossRef]
- Zhao, F.Q.; He, X.; Wang, L. A two-stage cooperative evolutionary algorithm with problem-specific knowledge for energy-efficient scheduling of no-wait flow-shop problem. JIEEE Trans. Cybern. 2020, 51, 5291–5303. [Google Scholar] [CrossRef]
- Wang, G.C.; Li, X.Y.; Gao, L.; Li, P.G. Energy-efficient distributed heterogeneous welding flow shop scheduling problem using a modified MOEA/D. Swarm Evol. Comput. 2021, 62, 100858. [Google Scholar] [CrossRef]
- Utama, D.M.; Ibrahim, M.F.; Wijaya, D.S.; Widodo, D.S.; Primayesti, M.D. A novel hybrid Aquila optimizer for energy-efficient hybrid flow shop scheduling. Results Control. Optim. 2022, 9, 100177. [Google Scholar] [CrossRef]
- Zhang, W.Q.; Geng, H.L.; Li, C.; Gen, M.; Zhang, G.H.; Deng, M.L. Q-learning-based multi-objective particle swarm optimization with local search within factories for energy-efficient distributed flow-shop scheduling problem. J. Intell. Manuf. 2023, 36, 185–208. [Google Scholar] [CrossRef]
- Hao, H.Q.; Zhu, H.P.; Luo, Y.B. Preference learning based multiobjective particle swarm optimization for lot streaming in hybrid flowshop scheduling with flexible assembly and time windows. Expert Syst. Appl. 2025, 290, 128345. [Google Scholar] [CrossRef]
- Liu, W.L.; Xu, J.L.; Ren, G.Q.; Xiao, Y.J. An improved quantum particle swarm algorithm for solving multi-objective fuzzy flexible job shop scheduling problem. J. Intell. Fuzzy Syst. 2023, 45, 4885–4905. [Google Scholar] [CrossRef]
- Thulasingam, M.K.; Periyanayagam, A.D.V.R. Techno economic (TE) analysis of ENCON measures and energy efficient opportunities for the machinery in the engineering workshop. Energy Syst. 2024, 1–30. Available online: https://link.springer.com/article/10.1007/s12667-024-00683-7#citeas (accessed on 30 June 2025).
- Duan, J.G.; Wang, J.H. Energy-efficient scheduling for a flexible job shop with machine breakdowns considering machine idle time arrangement and machine speed level selection. Comput. Ind. Eng. 2021, 161, 107677. [Google Scholar] [CrossRef]
- Yin, R.X.; Li, C.W.; Feng, X.Q.; Yang, Q.B. Flexible flow shop scheduling and energy saving optimization strategy under low carbon target. J. Phys. Conf. Ser. 2021, 1939, 012095. [Google Scholar] [CrossRef]
- Xu, E.B.; Li, Y.; Liu, Y.; Du, J.Y.; Gao, X.Q. Energy saving scheduling strategy for job shop under TOU and tiered electricity price. Alex. Eng. J. 2022, 61, 459–467. [Google Scholar] [CrossRef]
- Duan, J.G.; Feng, M.Y.; Zhang, Q.L. Energy-efficient collaborative scheduling of heterogeneous multi-stage hybrid flowshop for large metallic component manufacturing. J. Clean. Prod. 2022, 375, 134148. [Google Scholar] [CrossRef]
- Renna, P. Energy saving by switch-off policy in a pull-controlled production line. Sustain. Prod. Consum. 2018, 16, 25–32. [Google Scholar] [CrossRef]
- Liu, Z.F.; Yan, J.; Cheng, Q.; Yang, C.B.; Sun, S.W.; Xue, D.Y. The mixed production mode considering continuous and intermittent processing for an energy-efficient hybrid flow shop scheduling. J. Clean. Prod. 2020, 246, 119071. [Google Scholar] [CrossRef]
- Tan, B.; Oktay, K.; Siamak, K. Energy-efficient production control of a make-to-stock system with buffer-and time-based policies. Int. J. Prod. Res. 2024, 62, 5809–5827. [Google Scholar] [CrossRef]
- Wang, X.H.; Dai, Y.P.; Jia, Z.Y. Energy-efficient on/off control in serial production lines with Bernoulli machines. Flex. Serv. Manuf. J. 2022, 36, 103–128. [Google Scholar] [CrossRef]
- Tian, Y.; Gao, Z.X.; Zhang, L.; Chen, Y.J.; Wang, T.Y. A Multi-objective optimization method for flexible job shop scheduling considering cutting-tool degradation with energy-saving measures. Mathematics 2023, 11, 324. [Google Scholar] [CrossRef]
- Wei, Z.Z.; Liao, W.Z.; Zhang, L.Y. Hybrid energy-efficient scheduling measures for flexible job-shop problem with variable machining speeds. Expert Syst. Appl. 2022, 197, 116785. [Google Scholar] [CrossRef]
- Ham, A.; Park, M.J.; Kim, K.M. Energy-aware flexible job shop scheduling using mixed integer programming and constraint programming. Math. Probl. Eng. 2021, 2021, 8035806. [Google Scholar] [CrossRef]
- Gong, G.L.; Chiong, R.; Deng, Q.W.; Gong, X.R.; Lin, W.H.; Han, W.W.; Zhang, L. A two-stage memetic algorithm for energy-efficient flexible job shop scheduling by means of decreasing the total number of machine restarts. Swarm Evol. Comput. 2022, 75, 101131. [Google Scholar] [CrossRef]
- Guo, J.; Wang, L.M.; Kong, L.; Lv, X.T. Energy-efficient flow-shop scheduling with the strategy of switching the power statuses of machines. Sustain. Energy Technol. Assess. 2022, 53, 102649. [Google Scholar] [CrossRef]
- Wei, H.J.; Li, S.B.; Quan, H.F.; Liu, D.C.; Rao, S.; Li, C.J.; Hu, J.J. Unified multi-objective genetic algorithm for energy efficient job shop scheduling. IEEE Access 2021, 9, 954542–954557. [Google Scholar] [CrossRef]
- Ali, F.; Bahareh, S.Z.; Akhavan, N.S.T. Unrelated parallel batch processing machine scheduling for production systems under carbon reduction policies: NSGA-II and MOGWO metaheuristics. Soft Comput. 2023, 27, 17063–17091. [Google Scholar]
- Caldeira, R.H.; Gnanavelbabu, A.; Vaidyanathan, T. An effective backtracking search algorithm for multi-objective flexible job shop scheduling considering new job arrivals and energy consumption. Comput. Ind. Eng. 2020, 149, 106863. [Google Scholar] [CrossRef]
- Sagar, K.V.; Jerald, J.; Khan, M.A. An energy-aware optimisation model to minimise energy consumption and carbon footprint in a flexible manufacturing system. Int. J. Interact. Des. Manuf. (IJIDeM) 2023, 18, 2869–2880. [Google Scholar] [CrossRef]
- Wang, Z.X.; He, M.W.; Wu, J.; Chen, H.N.; Cao, Y. An improved MOEA/D for low-carbon many-objective flexible job shop scheduling problem. Comput. Ind. Eng. 2024, 188, 109926. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Pratap, A.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Brandimarte, P. Routing and scheduling in a flexible job shop by tabu search. Ann. Oper. Res. 1993, 41, 157–183. [Google Scholar] [CrossRef]
- Meng, L.L.; Zhang, C.Y.; Shao, X.Y.; Ren, Y.P. MILP models for energy-aware flexible job shop scheduling problem. J. Clean. Prod. 2019, 210, 710–723. [Google Scholar] [CrossRef]
- Halder, T.; Debnath, B.K. Multi-objective closed-loop supply chain inventory model with learning and forgetting under carbon emission policies using NSGA-II, MOPSO, and TOPSIS. Appl. Soft Comput. 2025, 180, 113291. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).