Sustainable Risk Management in Construction Through a Hybrid Fuzzy WINGS-ANP Method for Assessing Negative Impacts During Open Caisson Sinking
Abstract
1. Introduction
2. Methodology
2.1. Concept of the Proposed Hybrid Method
- Ability to solve complex, multi-dimensional decision-making problems;
- Capacity to handle problems involving difficult-to-measure factors;
- Integration of the evaluation model with expert-based approaches;
- Implementation of a simplified evaluation model using linguistic expressions to define preferences;
- Inclusion of group evaluation and aggregation of expert judgments;
- Incorporation of uncertainty into the decision-making environment;
- Capability for a comprehensive assessment of negative impacts occurring during open caisson sinking, including identification of cause-and-effect relationships and their intensity;
- Applicability to other areas requiring the analysis of cause-and-effect relationships and the assessment of their intensity.
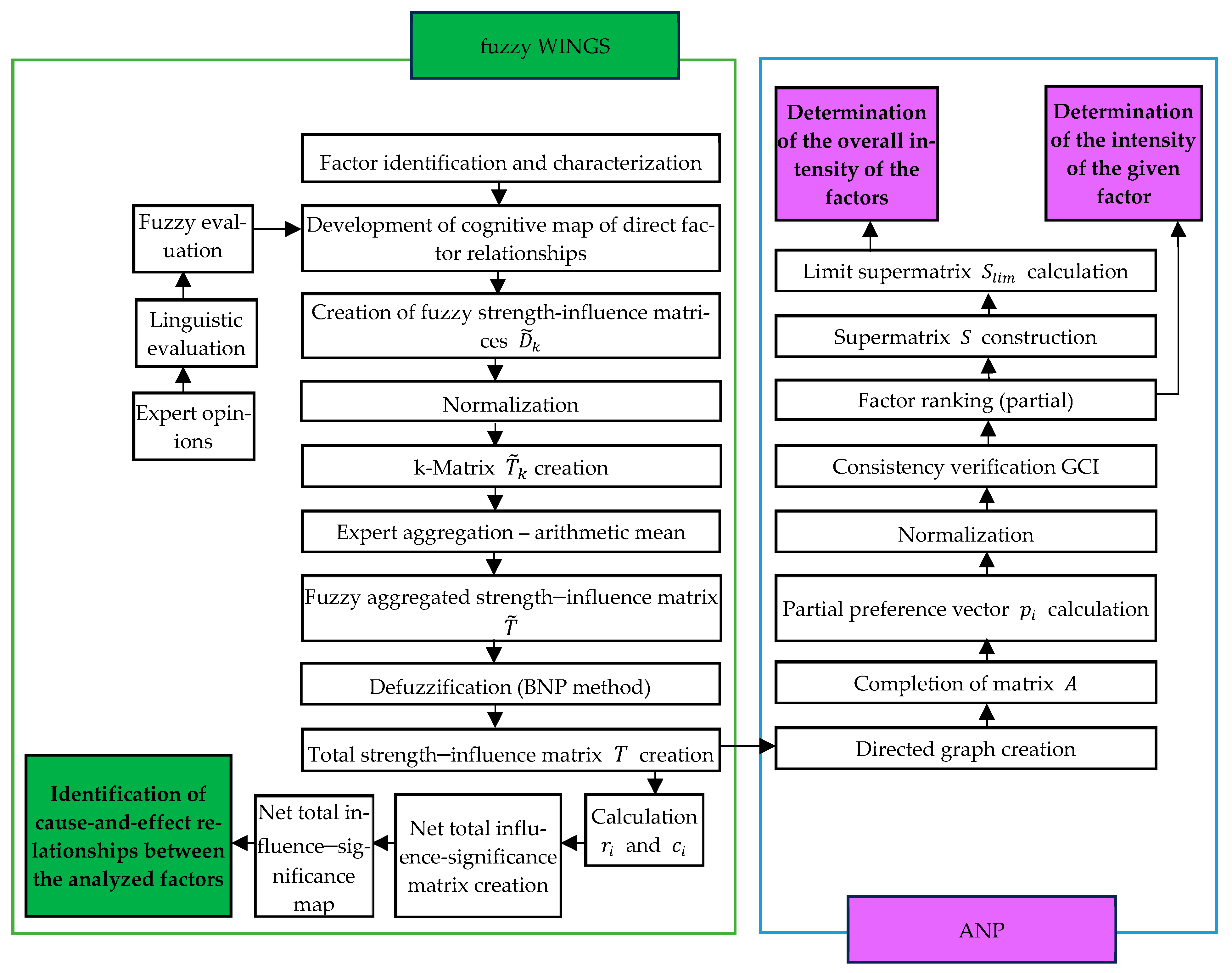
2.2. Stage One—Fuzzy WINGS Method
2.3. Stage Two—ANP Method
3. Implementation of the Fuzzy WINGS–ANP Hybrid Method for Assessing Negative Impacts Occurring During Open Caisson Sinking
3.1. Set of Analyzed Factors
- Ground settlement outside the open caisson (GS);
- Damage or destruction of adjacent structures (DD);
- Tilting of the open caisson from the vertical (TS);
- Lateral displacement of the open caisson (LD);
- Uncontrolled sinking of the open caisson (US);
- Structural damage to the open caisson (e.g., cracking or spalling) (SD);
- Damage to the base of the open caisson (including cutting edge failure) (DB);
- Detachment of the bottom ring of the open caisson (DR);
- Flotation or uplift of the open caisson (FU);
- Freezing of the open caisson to surrounding soil (FS);
- Hanging of the open caisson due to high side friction (HC);
- Complete failure or collapse of the open caisson (CF).
3.2. Expert Analysis
3.3. Results and Discussion of the Hybrid Fuzzy WINGS–ANP Method
- ∘
- —dotted line;
- ∘
- —dense dotted line;
- ∘
- —dashed line;
- ∘
- —thin solid line;
- ∘
- —thick solid line.
4. Conclusions
- ∘
- Hard-to-measure factors can be addressed through pairwise comparisons.
- ∘
- Utility-based methods are suitable for evaluating complex decision-making problems involving such factors.
- ∘
- Existing methods do not simultaneously support the identification of cause-and-effect relationships and the assessment of factor intensity.
- ∘
- Under uncertain conditions and diverging expert opinions, fuzzy logic proves effective.
- ∘
- The combination of fuzzy WINGS and ANP is suitable for analyzing both causal relationships and the intensity of impacts.
- ∘
- A comprehensive decision-making approach was developed to process imprecise and incomplete data specific to the evaluated task;
- ∘
- A universal analytical tool was created, which can also be applied to other complex decision problems involving the need to determine causal relationships and factor intensities.
- ∘
- The hybrid method supports engineering teams in making informed decisions about preventive and corrective measures during construction execution.
- ∘
- The method can be adapted to other geotechnical and construction technologies (e.g., microtunneling or deep foundations) where uncertainty and complex interdependencies are present.
- ∘
- The findings provide a strong foundation for developing risk management scenarios, contingency plans, and monitoring procedures.
- ∘
- The method contributes to sustainable construction practices by improving process quality, reducing execution errors, and enhancing safety and material efficiency.
- ∘
- Due to its structure, the method may be integrated into digital monitoring systems (e.g., BIM or IoT platforms) to enable real-time impact analysis and decision support.
- ∘
- In future studies, the author plans to explore fuzzy ANP structures that preserve uncertainty throughout the entire decision-making process, eliminating the need for defuzzification and, consequently, the simplification of data. This approach will allow for a more accurate representation of complex relationships between factors and enhance the reliability of results under conditions of uncertainty.
- ∘
- In future research, consistency indices tailored to fuzzy data will be considered, or a stability analysis of expert assessments will be conducted prior to defuzzification, in order to account for the uncertainty level that is not captured by traditional ANP consistency verification.
- ∘
- In future work, the proposed method may be expanded to include an additional step aimed at directly assigning risk levels to the identified negative impacts. This enhancement would support more comprehensive risk management in construction projects conducted under uncertainty.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Safiullah, A.M.M. Geotechnical Problems of Bridge Construction in Bangladesh. In Proceedings of the Japan-Bangladesh Joint Seminar on Advances in Bridge Engineering, Dhaka, Bangladesh, 10 August 2005; pp. 135–146. [Google Scholar]
- Allenby, D.; Waley, G.; Kilburn, D. Examples of Open Caisson Sinking in Scotland. Proc. Inst. Civ. Eng. Geotech. Eng. 2009, 162, 59–70. [Google Scholar] [CrossRef]
- Abdrabbo, F.; Gaaver, K. Challenges and Uncertainties Relating to Open Caissons. DFI J.—J. Deep Found. Inst. 2012, 6, 21–32. [Google Scholar] [CrossRef]
- Royston, R.; Sheil, B.B.; Byrne, B.W. Monitoring the Construction of a Large-Diameter Caisson in Sand. Proc. Inst. Civ. Eng. Geotech. Eng. 2022, 175, 323–339. [Google Scholar] [CrossRef]
- Abdrabbo, F.M.; Gaaver, K.E. Applications of the Observational Method in Deep Foundations. Alex. Eng. J. 2012, 51, 269–279. [Google Scholar] [CrossRef]
- Dachowski, R.; Gałek-Bracha, K. Determination of the Occurrence of Negative Impacts during Lowering of Sinking Wells Using the Fuzzy TOPSIS Method. Sustainability 2024, 16, 899. [Google Scholar] [CrossRef]
- Chen, W.; Ma, J.; Wang, Q.; Jiang, B. Experimental Study on the Lateral Distribution of the Sidewall Friction of Large and Deep-Water Caissons. Mar. Georesour. Geotechnol. 2022, 40, 392–403. [Google Scholar] [CrossRef]
- Jiang, B.N.; Wang, M.T.; Chen, T.; Zhang, L.L.; Ma, J.L. Experimental Study on the Migration Regularity of Sand Outside a Large, Deep-Water, Open Caisson during Sinking. Ocean Eng. 2019, 193, 106601. [Google Scholar] [CrossRef]
- Kudella, P. Senkkästen. In Grundbau-Taschenbuch; Witt, K.J., Ed.; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar] [CrossRef]
- Lai, F.; Zhang, N.; Liu, S.; Sun, Y.; Li, Y. Ground Movements Induced by Installation of Twin Large Diameter Deeply-Buried Caissons: 3D Numerical Modeling. Acta Geotech. 2021, 16, 2933–2961. [Google Scholar] [CrossRef]
- Saha, G.P. The Sinking of Well Foundations in Difficult Situations. J. Indian Road Congr. 2007, 68, 123–131. [Google Scholar]
- Li, P.; Song, E.; Zheng, T. Initial Sinking Method for Large Open Caisson in a Highway Bridge Project; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; Volume 2, ISBN 9783319971148. [Google Scholar]
- Nonveiller, E. Open Caissons for Deep Foundations. J. Geotech. Eng. 1987, 113, 424–439. [Google Scholar] [CrossRef]
- Mordovets, E.E.; Permyakov, Y.V.; Shkol’nikov, D.B.; Geukharov, L.M. Sinking a Prefabricated Reinforced-Concrete Well in a Thixotropic Jacket. Soil Mech. Found. Eng. 1970, 7, 185–187. [Google Scholar] [CrossRef]
- Zhang, J. Numerical Simulation on the Whole Sinking Process of Open Caisson with an Improved SPH Method. Math. Probl. Eng. 2021, 2021, 6699880. [Google Scholar] [CrossRef]
- Lenzi, M.; Halsegger, W.; Semprich, S. Experimental and Numerical Investigations of the Guided Caisson Method Recherches Expérimentales et Numériques Sur La Méthode Du Caisson Guidé; IOS Press: Amsterdam, The Netherlands, 2006; pp. 1625–1628. [Google Scholar] [CrossRef]
- Chavda, J.T.; Mishra, S.; Dodagoudar, G.R. Experimental Evaluation of Ultimate Bearing Capacity of the Cutting Edge of an Open Caisson. Int. J. Phys. Model. Geotech. 2020, 20, 281–294. [Google Scholar] [CrossRef]
- Alampalli, S.; Venkatanarayana, P. Laboratory Investigation on Caissons-Deformations and Vertical Load Distributions. Soils Found. 1997, 37, 61–69. [Google Scholar] [CrossRef]
- Ter-Galustov, S.A.; Ponomarenko, A.I.; Opershtein, V.L.; Ivanov, V.D. Experience in Sinking an Open Caisson in a Thixotropic Lining. Soil Mech. Found. Eng. 1966, 3, 128–131. [Google Scholar] [CrossRef]
- Zhu, S.; Nan, H.; Zheng, Y. Research and Application of BIM Cloud Monitoring System for Open Caisson Construction of Super Large Bridge. IOP Conf. Ser. Earth Environ. Sci. 2020, 510, 2–6. [Google Scholar] [CrossRef]
- Jiang, B.; Ma, J.; Chu, J. The Influence of Soil Surrounding the Caisson Cutting Edge to Excavation and Sinking. In Proceedings of the International Conference on Geotechnical and Earthquake Engineering, Chongqing, China, 20–21 October 2018; pp. 435–448. [Google Scholar]
- Sun, Y.; Su, J.B.; Xia, X.; Xu, Z. Numerical Analysis of Soil Deformation behind the Reaction Wall of an Open Caisson Induced by Horizontal Parallel Pipe-Jacking Construction. Can. Geotech. J. 2015, 52, 2008–2016. [Google Scholar] [CrossRef]
- Lai, F.; Liu, S.; Deng, Y.; Sun, Y.; Wu, K.; Liu, H. Numerical Investigations of the Installation Process of Giant Deep-Buried Circular Open Caissons in Undrained Clay. Comput. Geotech. 2020, 118, 103322. [Google Scholar] [CrossRef]
- Royston, R.; Phillips, B.; Sheil, B.; Byrne, B. Bearing Capacity beneath Tapered Blades of Open Dug Caissons in Sand. Civ. Eng. Res. Irel. 2016, 2016, 473–478. [Google Scholar]
- Sheil, B.; Royston, R.; Byrne, B. Real-Time Monitoring of Large-Diameter Caissons; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; Volume 1, ISBN 9783319971124. [Google Scholar]
- Dachowski, R.; Gałek, K. Risk of Emergency Situations of Underground Objects in the Perspective of Multi-Criteria Decision Making. Arch. Civ. Eng. 2019, 65, 149–162. [Google Scholar] [CrossRef]
- Ginda, G. Metody Porównywania Parami w Budownictwie i Dziedzinach Pokrewnych; Dolnośląskie Wydawnictwo Edukacyjne: Wrocław, Poland, 2015. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill International Book Company: New York, NY, USA, 1980. [Google Scholar]
- Sun, C.; Chen, L.; Xiao, J.; Liu, Q.; Zuo, J. Low-Carbon and Fundamental Properties of Eco-Efficient Mortar with Recycled Powders. Materials 2021, 14, 7503. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Zhang, W.; Han, J.; Liu, Z.; Liu, J.; Huang, Y. Experimental Research on Crack Resistance of Steel–Polyvinyl Alcohol Hybrid Fiber-Reinforced Concrete. Materials 2024, 17, 3097. [Google Scholar] [CrossRef]
- Skrzek, K.; Mazgajczyk, E.; Dybała, B. Application of Fuzzy Logic-Based Expert Advisory Systems in Optimizing the Decision-Making Process for Material Selection in Additive Manufacturing. Materials 2025, 18, 324. [Google Scholar] [CrossRef]
- Gabus, A.; Fontela, E. World Problems, an Invitation to Further Thought Within the Framework of DEMATEL; Battelle Geneva Res. Center: Geneva, Switzerland, 1972. [Google Scholar]
- Michnik, J. Weighted Influence Non-Linear Gauge System (WINGS)-An Analysis Method for the Systems of Interrelated Components. Eur. J. Oper. Res. 2013, 228, 536–544. [Google Scholar] [CrossRef]
- Sagan, J.; Sobotka, A. Analysis of Factors Affecting the Circularity of Building Materials. Materials 2021, 14, 7296. [Google Scholar] [CrossRef] [PubMed]
- Pacana, A.; Siwiec, D. Method of Determining Sequence Actions of Products Improvement. Materials 2022, 15, 6321. [Google Scholar] [CrossRef]
- Radziszewska-Zielina, E.; Śladowski, G. Supporting the Selection of a Variant of the Adaptation of a Historical Building with the Use of Fuzzy Modelling and Structural Analysis. J. Cult. Herit. 2017, 26, 53–63. [Google Scholar] [CrossRef]
- Śladowski, G. Selected Cases of Modeling and Structural Analysis of Decision Problems in the Construction Sector. Przegląd Bud. 2023, 94, 98–102. [Google Scholar] [CrossRef]
- Singh, T.; Goswami, C.; Patnaik, A.; Lendvai, L. Optimal Design of Ceramic Based Hip Implant Composites Using Hybrid AHP-MOORA Approach. Materials 2022, 15, 3800. [Google Scholar] [CrossRef]
- Fuse, K.; Dalsaniya, A.; Modi, D.; Vora, J.; Pimenov, D.Y.; Giasin, K.; Prajapati, P.; Chaudhari, R.; Wojciechowski, S. Integration of Fuzzy AHP and Fuzzy TOPSIS Methods for Wire Electric Discharge Machining of Titanium (Ti6Al4V) Alloy Using RSM. Materials 2021, 14, 7408. [Google Scholar] [CrossRef]
- Janowska-Renkas, E.; Jakiel, P.; Fabianowski, D.; Matyjaszczyk, D. Optimal Selection of High-Performance Concrete for Post-Tensioned Girder Bridge Using Advanced Hybrid MCDA Method. Materials 2021, 14, 6553. [Google Scholar] [CrossRef] [PubMed]
- Balsara, S.; Jain, P.K.; Ramesh, A. An Integrated Approach Using AHP and DEMATEL for Evaluating Climate Change Mitigation Strategies of the Indian Cement Manufacturing Industry. Environ. Pollut. 2019, 252, 863–878. [Google Scholar] [CrossRef] [PubMed]
- Tseng, M.L. Application of ANP and DEMATEL to Evaluate the Decision-Making of Municipal Solid Waste Management in Metro Manila. Environ. Monit. Assess. 2009, 156, 181–197. [Google Scholar] [CrossRef] [PubMed]
- Azizi, A.; Malekmohammadi, B.; Jafari, H.R.; Nasiri, H.; Amini Parsa, V. Land Suitability Assessment for Wind Power Plant Site Selection Using ANP-DEMATEL in a GIS Environment: Case Study of Ardabil Province, Iran. Environ. Monit. Assess. 2014, 186, 6695–6709. [Google Scholar] [CrossRef]
- Michnik, J. Wielokryterialne Metody Wspomagania Decyzji w Procesie Innowacji; Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach: Katowice, Poland, 2013. [Google Scholar]
- Śladowski, G. Wielokryterialny Model Decyzyjny Wyboru Funkcji Użytkowej w Adaptacji Budynków Zabytkowych. 2017. Available online: https://repozytorium.biblos.pk.edu.pl/resources/26164 (accessed on 23 June 2025).
- Li, R.J. Fuzzy Method in Group Decision Making. Comput. Math. Appl. 1999, 38, 91–101. [Google Scholar] [CrossRef]
- Prusak, A.; Stefanów, P. AHP-Analityczny Proces Hierarchiczny. Budowa i Analiza Modeli Decyzyjnych Krok Po Kroku; Ekonomia Zarządzanie C.H.Beck: Warszawa, Poland, 2014; ISBN 978-83-255-6072-0. [Google Scholar]
- Lin, C.J.; Wu, W.W. A Causal Analytical Method for Group Decision-Making under Fuzzy Environment. Expert Syst. Appl. 2008, 34, 205–213. [Google Scholar] [CrossRef]
- Muhammad, M.N.; Cavus, N. Fuzzy DEMATEL Method for Identifying LMS Evaluation Criteria. Procedia Comput. Sci. 2017, 120, 742–749. [Google Scholar] [CrossRef]
- Tzeng, G.; Huang, J. Multiaple Atribute Decision Making. Methods and Applications; Chapman and Hall/CRC: New York, NY, USA, 2011; ISBN 9781439861578. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process (AHP) for Decision Making and the Analytic Network Process (ANP) for Decision Making with Dependence and Feedback; Creative Decisions Foundation: Pittsburgh, PA, USA, 2003. [Google Scholar]
- Stoltmann, A. Zastosowanie Metody AHP Do Porównania Kryteriów Wyboru Lokalizacji Budowy Farmy Wiatrowej. Zesz. Nauk. Wydz. Elektroetchniki Autom. Politech. Gdańskiej 2015, 42, 187–190. [Google Scholar]
- Aguarón, J.; Moreno-Jiménez, J.M. The Geometric Consistency Index: Approximated Thresholds. Eur. J. Oper. Res. 2003, 147, 137–145. [Google Scholar] [CrossRef]
- Crawford, G.; Williams, C. A Note on the Analysis of Subjective Judgment Matrices. J. Math. Psychol. 1985, 29, 387–405. [Google Scholar] [CrossRef]


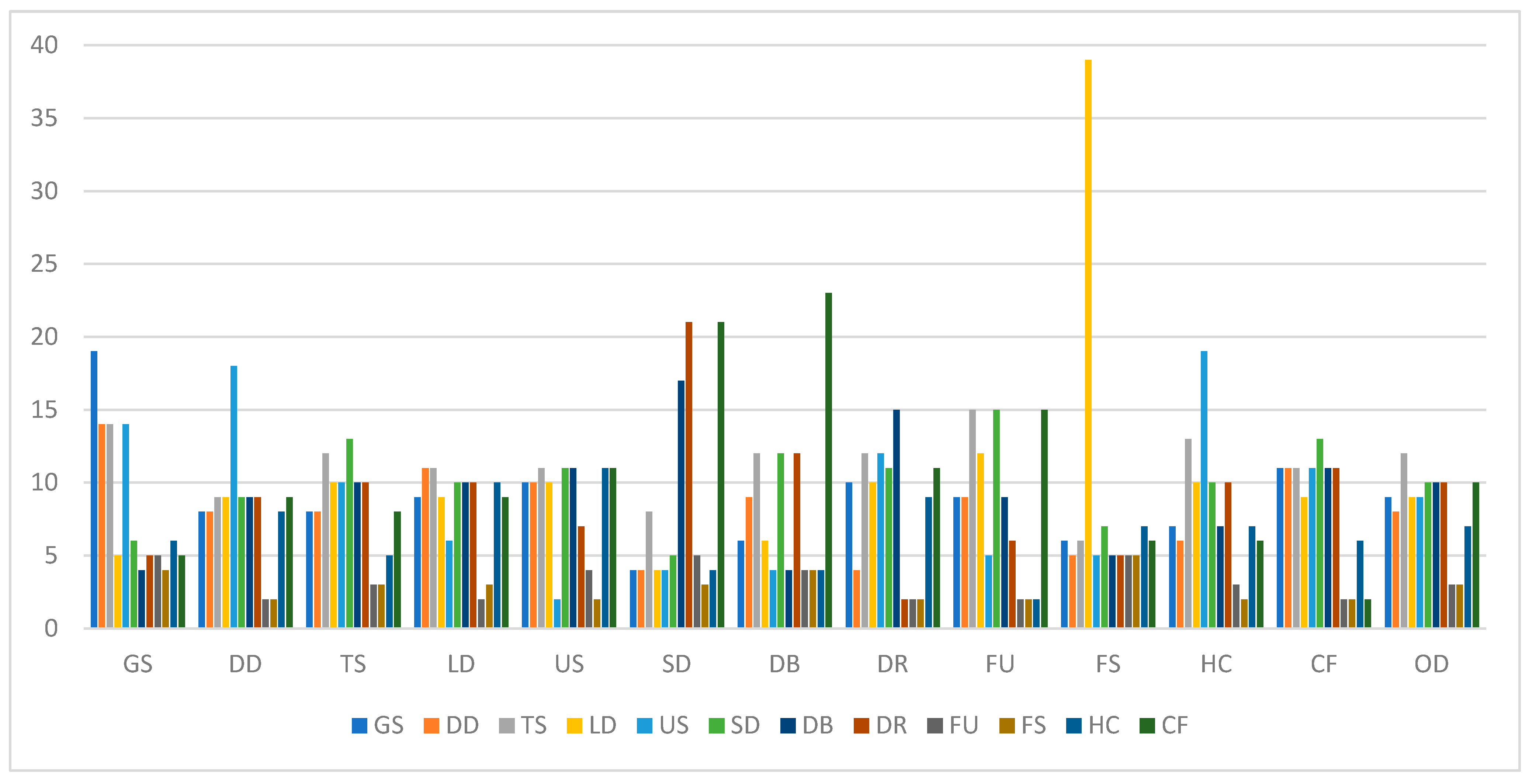
| Article | Negative Impacts | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GS | DD | TS | LD | US | SD | DB | DR | FU | FS | HC | CF | |
| Abdrabbo, Gaaver, 2014 [3] | + | + | + | |||||||||
| Royston, Byrne, Sheil, 2022 [4] | + | + | + | + | + | |||||||
| Allenby, Waley, Kilburn, 2009 [2] | + | + | + | + | + | |||||||
| Chen, Ma, Wang, Jiang, 2021 [7] | + | + | ||||||||||
| Jiang, Wang, Chen, Zhang, Ma, 2019 [8] | + | + | ||||||||||
| Kudella, 2018 [9] | + | + | + | + | + | |||||||
| Lai, Zhang, Liu et al., 2021 [10] | + | |||||||||||
| Saha, 2005 [11] | + | + | + | + | ||||||||
| Peng, Song, 2018 [12] | + | + | ||||||||||
| Nonveiller, 1987 [13] | + | + | + | + | ||||||||
| Mordovets, Permyakov et al., 1970 [14] | + | + | ||||||||||
| Zhang, 2021 [15] | + | + | ||||||||||
| Lenzi, Halsegger, Semprich, 2005 [16] | + | |||||||||||
| Chavda, Mishra Dodagoudar, 2019 [17] | + | + | + | + | + | + | ||||||
| Alampalli, Peddibotla, 1997 [18] | + | |||||||||||
| Ter-Galustov, et al., 1966 [19] | + | + | ||||||||||
| Zhu, Nan, Zheng, 2020 [20] | + | + | ||||||||||
| Jiang, Ma, Chu, 2018 [21] | + | + | + | |||||||||
| Abdrabbo, Gaaver, 2012 [3] | + | + | ||||||||||
| Susn, Su, Xia, Xu, 2015 [22] | + | |||||||||||
| Lai, Liu, Deng et al. [23] | + | |||||||||||
| Royston, Phillips, Sheil, Byrne, 2016 [24] | + | |||||||||||
| Sheil, Royston, Byrne, 2018 [25] | + | + | + | + | ||||||||
| Dachowski, Gałek, 2019 [26] | + | + | + | + | + | + | ||||||
| Dachowski, Gałek-Bracha, 2024 [6] | + | + | + | + | + | + | + | + | + | + | + | + |
| Symbol | Negative Impacts |
|---|---|
| GS | Ground settlement outside the open caisson |
| DD | Damage or destruction of adjacent structures |
| TS | Tilting of the open caisson from the vertical |
| LD | Lateral displacement of the open caisson |
| US | Uncontrolled sinking of the open caisson |
| SD | Structural damage to the open caisson (e.g., cracking or spalling) |
| DB | Damage to the base of the open caisson (including cutting edge failure) |
| DR | Detachment of the bottom ring of the open caisson |
| FU | Flotation or uplift of the open caisson |
| FS | Freezing of the open caisson to surrounding soil |
| HC | Hanging of the open caisson due to high side friction |
| CF | Complete failure or collapse of the open caisson |
| Method | Expanded Method Name | Description | Advantages | Limitations |
|---|---|---|---|---|
| AHP | Analytic Hierarchy Process | Analytic Hierarchy Process for pairwise comparisons and hierarchy structuring. | Simple, structured decision support; intuitive pairwise comparisons. | Does not handle feedback loops; subjective input. |
| Fuzzy AHP | Fuzzy Analytic Hierarchy Process | Fuzzy extension of AHP for uncertain and qualitative judgments. | Handles vagueness and imprecision in expert input. | Defuzzification may reduce information richness. |
| DEMATEL | Decision Making Trial and Evaluation Laboratory | Determines interdependencies among factors using pairwise comparisons. | Reveals cause–effect relationships; visual representation. | Limited to influence structure; may oversimplify relationships. |
| WINGS | Weighted Influence Non-linear Gauge System | Enhancement of DEMATEL with intensity measurement of influences. | Captures strength of influence; useful in systems with feedback. | Complex interpretation; requires intensity calibration. |
| Fuzzy WINGS | Fuzzy Weighted Influence Non-linear Gauge System | Fuzzy version of WINGS allowing uncertainty in influence intensity. | Accounts for uncertainty and interrelations with fuzziness. | Sensitive to fuzzy set definitions and thresholds. |
| MOORA | Multi-Objective Optimization by Ratio Analysis | Multi-Objective Optimization method for ratio analysis. | Efficient ranking in multi-criteria decisions. | Ignores factor interdependencies. |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution | Ranks alternatives based on their proximity to an ideal best and distance from an ideal worst solution. | Effective in ranking and selection problems. | May oversimplify in presence of complex dependencies. |
| Fuzzy TOPSIS | Fuzzy Technique for Order of Preference by Similarity to Ideal Solution | Fuzzy extension of TOPSIS for decision-making under uncertainty. | Improves decision accuracy under uncertainty. | Depends on fuzzy set definitions; computationally intensive. |
| EA FAHP | Extent Analysis Fuzzy Analytic Hierarchy Process | Enhanced Fuzzy AHP integrating fuzzy logic in high-strength concrete mix design. | Customizable for specific concrete design optimization. | Requires detailed fuzzy modeling and validation. |
| ANP | Analytic Network Process | Analytic Network Process allowing for interdependent network structures. | Considers feedback and complex interdependencies. | Needs careful structure definition; complex for large systems. |
| Hybrid AHP-DEMATEL | Hybrid Analytic Hierarchy Process–Decision Making Trial and Evaluation Laboratory | Combines AHP and DEMATEL to evaluate complex strategies. | Allows integrated causal and hierarchical analysis. | Integration complexity; needs clear interface definition. |
| Hybrid ANP-DEMATEL | Hybrid Analytic Network Process–Decision Making Trial and Evaluation Laboratory | Integrates ANP and DEMATEL within GIS or decision systems. | Supports layered interdependent analysis in spatial contexts. | High data and processing requirements. |
| Fuzzy WINGS + ANP | Fuzzy Weighted Influence Non-linear Gauge System + Analytic Network Process | Hybrid approach combining fuzzy WINGS and ANP for causal and intensity analysis. | Combines causal mapping and intensity evaluation under uncertainty. | Still under validation. |
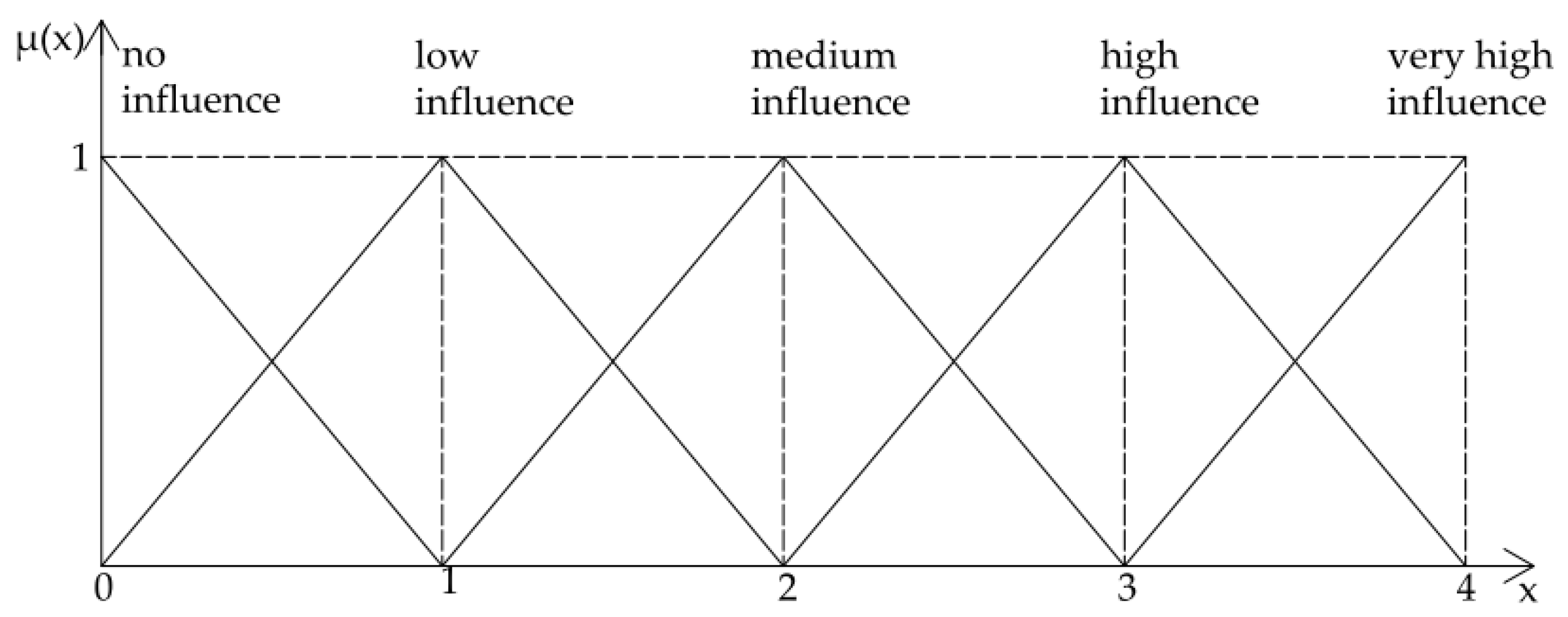
| Influence Intensity Rating | |
|---|---|
| Linguistic term | Triangular fuzzy number |
| No influence | (0, 0, 1) |
| Low influence | (0, 1, 2) |
| Medium influence | (1, 2, 3) |
| High influence | (2, 3, 4) |
| Very high influence | (3, 4, 4) |
| n | 3 | 4 | >4 |
|---|---|---|---|
| 0.3147 | 0.3526 | 0.370 |
| GS | DD | TS | LD | US | SD | DB | DR | FU | FS | HC | CF | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GS | 0.0064 | 0.0060 | 0.0050 | 0.0025 | 0.0060 | 0.0035 | 0.0018 | 0.0029 | 0.0023 | 0.0013 | 0.0033 | 0.0023 |
| DD | 0.0054 | 0.0042 | 0.0054 | 0.0050 | 0.0074 | 0.0059 | 0.0051 | 0.0050 | 0.0014 | 0.0014 | 0.0041 | 0.0055 |
| TS | 0.0042 | 0.0046 | 0.0064 | 0.0052 | 0.0058 | 0.0065 | 0.0057 | 0.0052 | 0.0023 | 0.0024 | 0.0040 | 0.0047 |
| LD | 0.0051 | 0.0061 | 0.0062 | 0.0052 | 0.0042 | 0.0067 | 0.0062 | 0.0062 | 0.0018 | 0.0024 | 0.0061 | 0.0056 |
| US | 0.0075 | 0.0079 | 0.0086 | 0.0075 | 0.0037 | 0.0080 | 0.0089 | 0.0062 | 0.0046 | 0.0014 | 0.0086 | 0.0089 |
| SD | 0.0027 | 0.0027 | 0.0049 | 0.0028 | 0.0028 | 0.0030 | 0.0068 | 0.0074 | 0.0038 | 0.0014 | 0.0021 | 0.0073 |
| DB | 0.0045 | 0.0050 | 0.0061 | 0.0044 | 0.0036 | 0.0070 | 0.0038 | 0.0068 | 0.0033 | 0.0027 | 0.0033 | 0.0083 |
| DR | 0.0075 | 0.0052 | 0.0083 | 0.0072 | 0.0089 | 0.0090 | 0.0095 | 0.0032 | 0.0036 | 0.0027 | 0.0080 | 0.0089 |
| FU | 0.0072 | 0.0080 | 0.0096 | 0.0085 | 0.0057 | 0.0099 | 0.0070 | 0.0069 | 0.0024 | 0.0011 | 0.0037 | 0.0098 |
| FS | 0.0021 | 0.0018 | 0.0029 | 0.0096 | 0.0024 | 0.0031 | 0.0018 | 0.0024 | 0.0014 | 0.0013 | 0.0039 | 0.0027 |
| HC | 0.0053 | 0.0048 | 0.0077 | 0.0068 | 0.0081 | 0.0062 | 0.0057 | 0.0068 | 0.0030 | 0.0018 | 0.0059 | 0.0047 |
| CF | 0.0090 | 0.0090 | 0.0097 | 0.0086 | 0.0095 | 0.0103 | 0.0099 | 0.0099 | 0.0049 | 0.0024 | 0.0071 | 0.0022 |
| Negative Impacts | Ranking (Factor Importance) | Total Involvement and Total Role | Number of Causes | Number of Effects | Factor Type | ||
|---|---|---|---|---|---|---|---|
| GS | Ground settlement outside the open caisson | 4 | 0.02804 | −0.02381 | 3 | 8 | Effect |
| DD | Damage or destruction of adjacent structures | 11 | 0.01766 | −0.00951 | 3 | 8 | Effect |
| TS | Tilting of the open caisson from the vertical | 6 | 0.02731 | −0.02407 | 1 | 10 | Effect |
| LD | Lateral displacement of the open caisson | 3 | 0.02834 | −0.01522 | 4 | 6 | Effect |
| US | Uncontrolled sinking of the open caisson | 7 | 0.02468 | 0.01381 | 7 | 4 | Cause |
| SD | Structural damage to the open caisson (e.g., cracking or spalling) | 5 | 0.0275 | −0.02750 | 0 | 10 | Effect |
| DB | Damage to the base of the open caisson (including cutting edge failure) | 9 | 0.02161 | −0.01333 | 4 | 7 | Effect |
| DR | Detachment of the bottom ring of the open caisson | 8 | 0.02181 | 0.01326 | 9 | 2 | Cause |
| FU | Flotation or uplift of the open caisson | 1 | 0.04575 | 0.04511 | 11 | 0 | Cause |
| FS | Freezing of the open caisson to surrounding soil | 12 | 0.01581 | 0.01325 | 9 | 2 | Cause |
| HC | Hanging of the open caisson due to high side friction | 10 | 0.02043 | 0.00671 | 6 | 5 | Cause |
| CF | Complete failure or collapse of the open caisson | 2 | 0.03188 | 0.02131 | 9 | 2 | Cause |
| GS | DD | TS | LD | US | SD | DB | DR | FU | FS | HC | CF | OD | Stage II Total | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GS | 0.1760 | 0.0870 | 0.0770 | 0.0920 | 0.0992 | 0.0421 | 0.0557 | 0.0995 | 0.0858 | 0.0548 | 0.0752 | 0.1109 | 0.0900 | 1.0554 |
| DD | 0.1440 | 0.0810 | 0.0770 | 0.1020 | 0.0992 | 0.0421 | 0.0883 | 0.0439 | 0.0858 | 0.0484 | 0.0563 | 0.1109 | 0.0839 | 0.9792 |
| TS | 0.1440 | 0.0870 | 0.1270 | 0.1020 | 0.1111 | 0.0751 | 0.1204 | 0.1149 | 0.1536 | 0.0548 | 0.1347 | 0.1109 | 0.1122 | 1.3356 |
| LD | 0.0480 | 0.0870 | 0.0980 | 0.0920 | 0.0992 | 0.0421 | 0.0557 | 0.0995 | 0.1172 | 0.3921 | 0.0966 | 0.0945 | 0.0906 | 1.3219 |
| US | 0.1440 | 0.1780 | 0.0980 | 0.0620 | 0.0242 | 0.0421 | 0.0439 | 0.1149 | 0.0457 | 0.0548 | 0.1912 | 0.1109 | 0.0942 | 1.1098 |
| SD | 0.0610 | 0.0870 | 0.1270 | 0.1020 | 0.1111 | 0.0502 | 0.1204 | 0.1149 | 0.1536 | 0.0699 | 0.0966 | 0.1262 | 0.1016 | 1.2198 |
| DB | 0.0390 | 0.0870 | 0.0980 | 0.1020 | 0.1111 | 0.1696 | 0.0439 | 0.1462 | 0.0858 | 0.0484 | 0.0752 | 0.1109 | 0.0981 | 1.1172 |
| DR | 0.0480 | 0.0870 | 0.0980 | 0.1020 | 0.0691 | 0.2051 | 0.1204 | 0.0231 | 0.0651 | 0.0548 | 0.0966 | 0.1109 | 0.0952 | 1.0802 |
| FU | 0.0480 | 0.0230 | 0.0360 | 0.0220 | 0.0385 | 0.0502 | 0.0439 | 0.0231 | 0.0184 | 0.0484 | 0.0255 | 0.0232 | 0.0336 | 0.4002 |
| FS | 0.0390 | 0.0230 | 0.0360 | 0.0270 | 0.0145 | 0.0342 | 0.0346 | 0.0194 | 0.0148 | 0.0484 | 0.0207 | 0.0147 | 0.0268 | 0.3266 |
| HC | 0.0610 | 0.0810 | 0.0510 | 0.1020 | 0.1111 | 0.0421 | 0.0439 | 0.0854 | 0.0205 | 0.0699 | 0.0752 | 0.0612 | 0.0686 | 0.8043 |
| CF | 0.0480 | 0.0870 | 0.0770 | 0.0920 | 0.1111 | 0.2051 | 0.2288 | 0.1149 | 0.1536 | 0.0548 | 0.0563 | 0.0147 | 0.1054 | 1.2435 |
| Stage I—Fuzzy WINGS | Stage II—ANP | Total of Both Stages | Final Ranking | |||||
|---|---|---|---|---|---|---|---|---|
| Stage I Total | Stage I Rank | Stage II Total | Stage II Rank | |||||
| GS | 0.0280 | 0.0238 | 0.0519 | 4 | 1.0554 | 8 | 1.1972 | 8 |
| DD | 0.0177 | 0.0095 | 0.0272 | 11 | 0.9792 | 9 | 1.0902 | 9 |
| TS | 0.0273 | 0.0240 | 0.0514 | 5 | 1.3356 | 1 | 1.4992 | 1 |
| LD | 0.0283 | 0.0152 | 0.0436 | 6 | 1.3219 | 2 | 1.4561 | 2 |
| US | 0.0247 | 0.0138 | 0.0385 | 7 | 1.1098 | 6 | 1.2426 | 6 |
| SD | 0.0275 | 0.0275 | 0.0550 | 2 | 1.2198 | 4 | 1.3764 | 4 |
| DB | 0.0216 | 0.0133 | 0.0349 | 9 | 1.1172 | 5 | 1.2502 | 5 |
| DR | 0.0218 | 0.0132 | 0.0351 | 8 | 1.0802 | 7 | 1.2105 | 7 |
| FU | 0.0457 | 0.0451 | 0.0909 | 1 | 0.4002 | 11 | 0.5247 | 11 |
| FS | 0.0158 | 0.0132 | 0.0291 | 10 | 0.3266 | 12 | 0.3824 | 12 |
| HC | 0.0204 | 0.0067 | 0.0271 | 12 | 0.8043 | 10 | 0.9000 | 10 |
| CF | 0.0319 | 0.0213 | 0.0532 | 3 | 1.2435 | 3 | 1.4021 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gałek-Bracha, K. Sustainable Risk Management in Construction Through a Hybrid Fuzzy WINGS-ANP Method for Assessing Negative Impacts During Open Caisson Sinking. Sustainability 2025, 17, 5848. https://doi.org/10.3390/su17135848
Gałek-Bracha K. Sustainable Risk Management in Construction Through a Hybrid Fuzzy WINGS-ANP Method for Assessing Negative Impacts During Open Caisson Sinking. Sustainability. 2025; 17(13):5848. https://doi.org/10.3390/su17135848
Chicago/Turabian StyleGałek-Bracha, Katarzyna. 2025. "Sustainable Risk Management in Construction Through a Hybrid Fuzzy WINGS-ANP Method for Assessing Negative Impacts During Open Caisson Sinking" Sustainability 17, no. 13: 5848. https://doi.org/10.3390/su17135848
APA StyleGałek-Bracha, K. (2025). Sustainable Risk Management in Construction Through a Hybrid Fuzzy WINGS-ANP Method for Assessing Negative Impacts During Open Caisson Sinking. Sustainability, 17(13), 5848. https://doi.org/10.3390/su17135848






