Optimal Incremental Conductance-Based MPPT Control Methodology for a 100 KW Grid-Connected PV System Employing the RUNge Kutta Optimizer
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Literature Review and Research Gaps
1.3. Key Contributions of the Paper
- High tuning accuracy, enabling better controller performance;
- Efficient convergence, with a good balance between exploration and exploitation;
- Robustness under diverse environmental conditions, such as step, ramp, and realistic irradiance profiles;
- Superior performance compared to other recent algorithms such as the GTO and AVO, as demonstrated through comparative simulations.
- The proposal of an innovative control strategy for MPPT in PV systems, named the IC-MPPT-(FOPI-PI) controller, which has been assessed and validated through MATLAB/Simulink simulations using a 100 kW benchmark PV system integrated into the grid;
- The first reported application of a new algorithm known as the RUNge Kutta Optimizer (RUN) to fine-tune the FOPI-PI controller parameters, comparing its performance with other recent metaheuristic optimization strategies like GTO and AVO to demonstrate the control scheme’s efficacy;
- The designed RUN-based IC-MPPT-(FOPI-PI) control strategy surpasses existing competitors in the MPPT research domain (PI [15] and FOPI [16] controllers) by precisely and efficiently tracking maximum power across diverse atmospheric conditions, including step, ramp, and realistic irradiance, considering constant and ramping temperature.
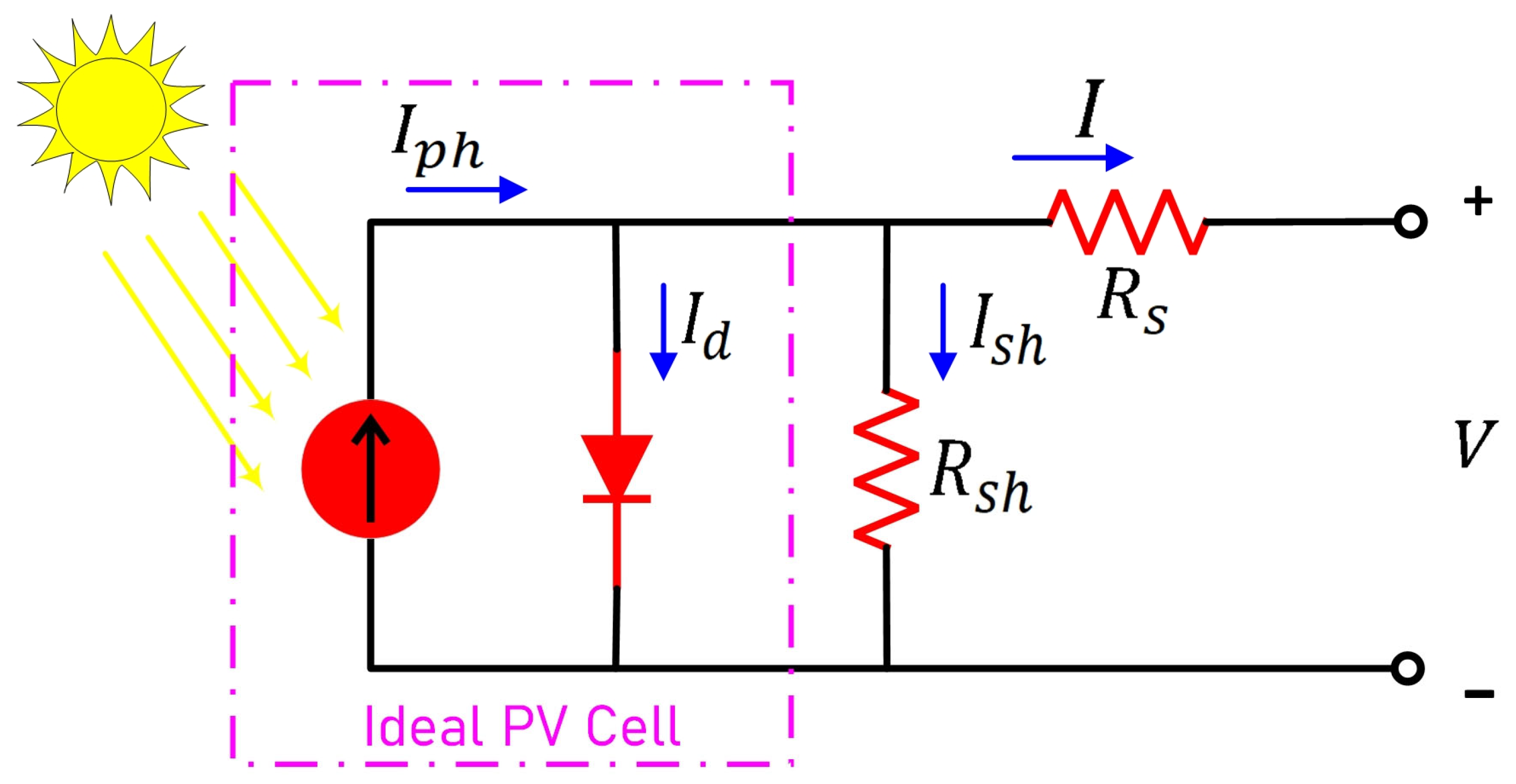
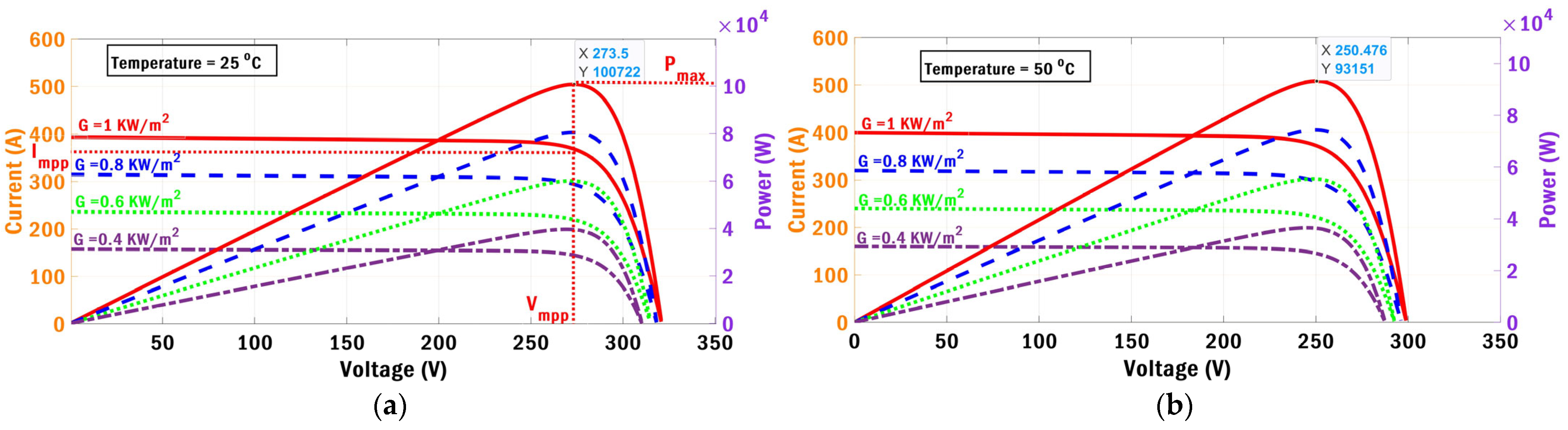
2. PV Modeling and System Setup
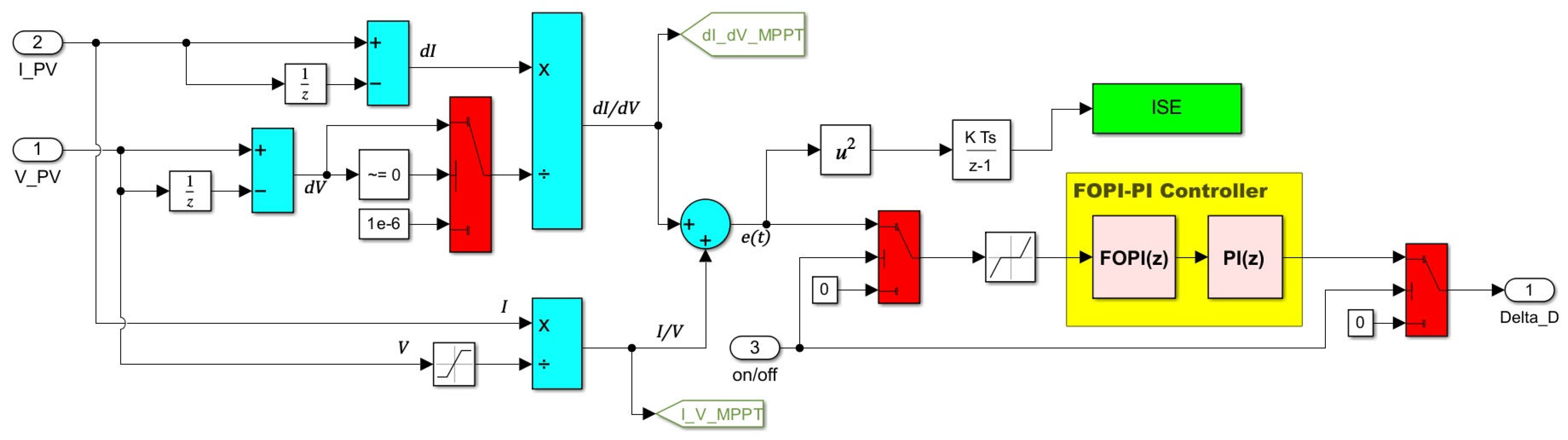
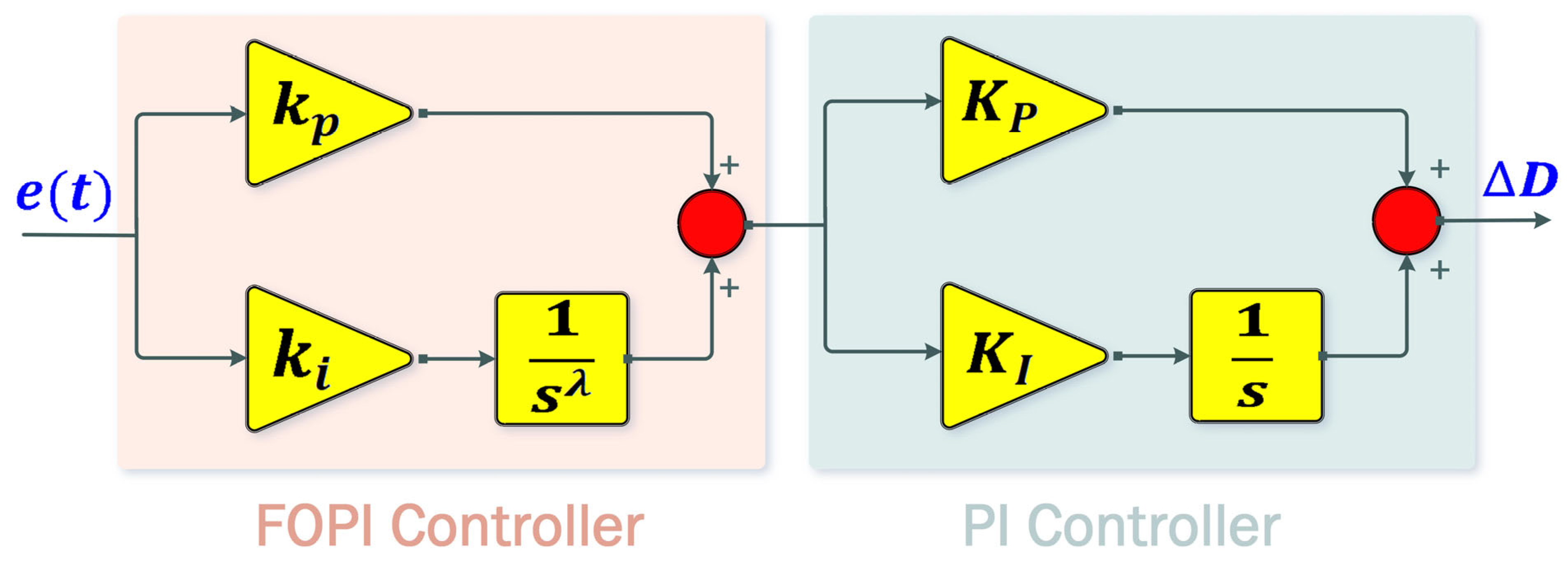
3. IC-MPPT-(FOPI-PI) Control Approach
4. RUN Optimization Description
4.1. Population Initialization
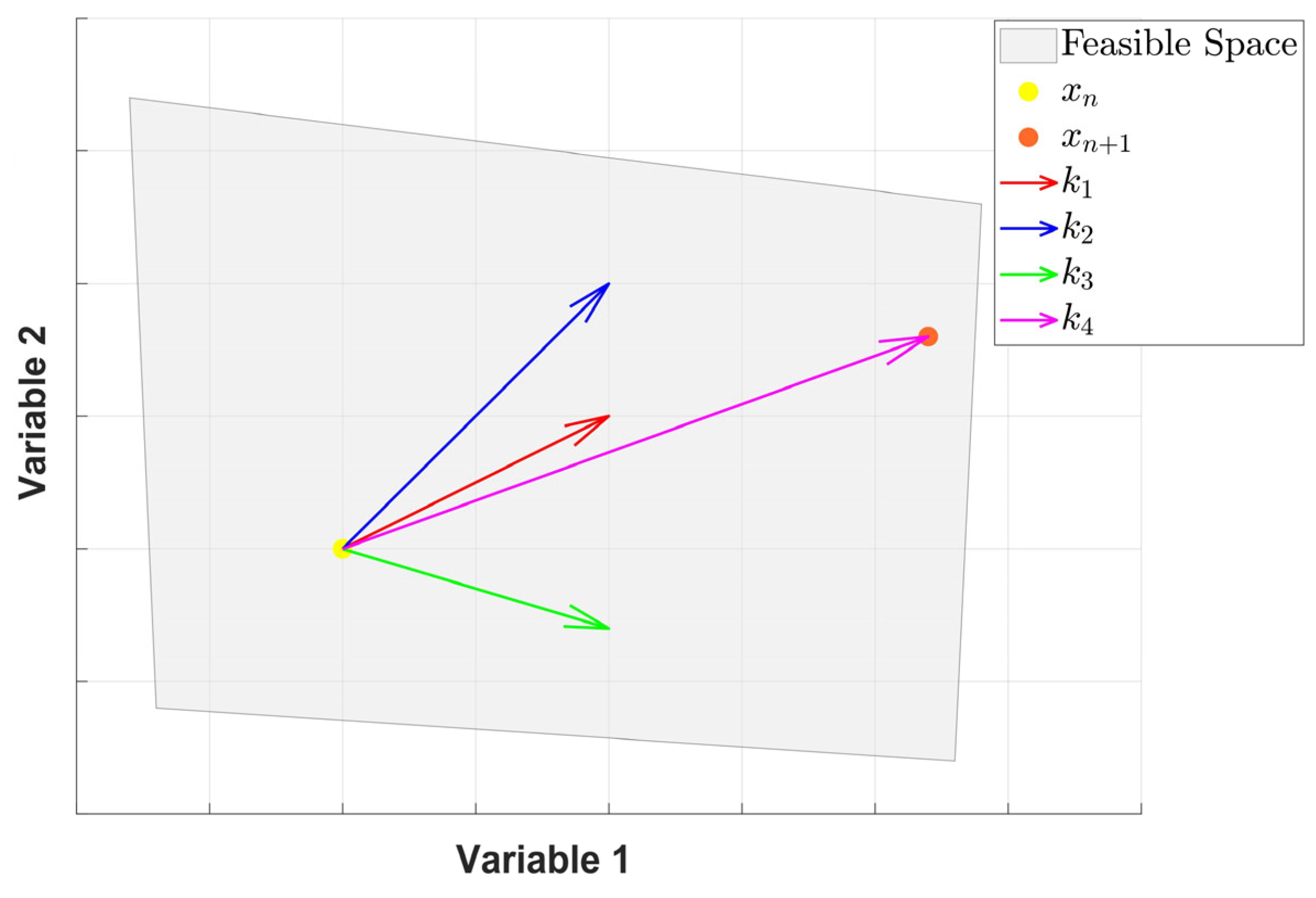
4.2. The Mathematical Description of Searching Methodology
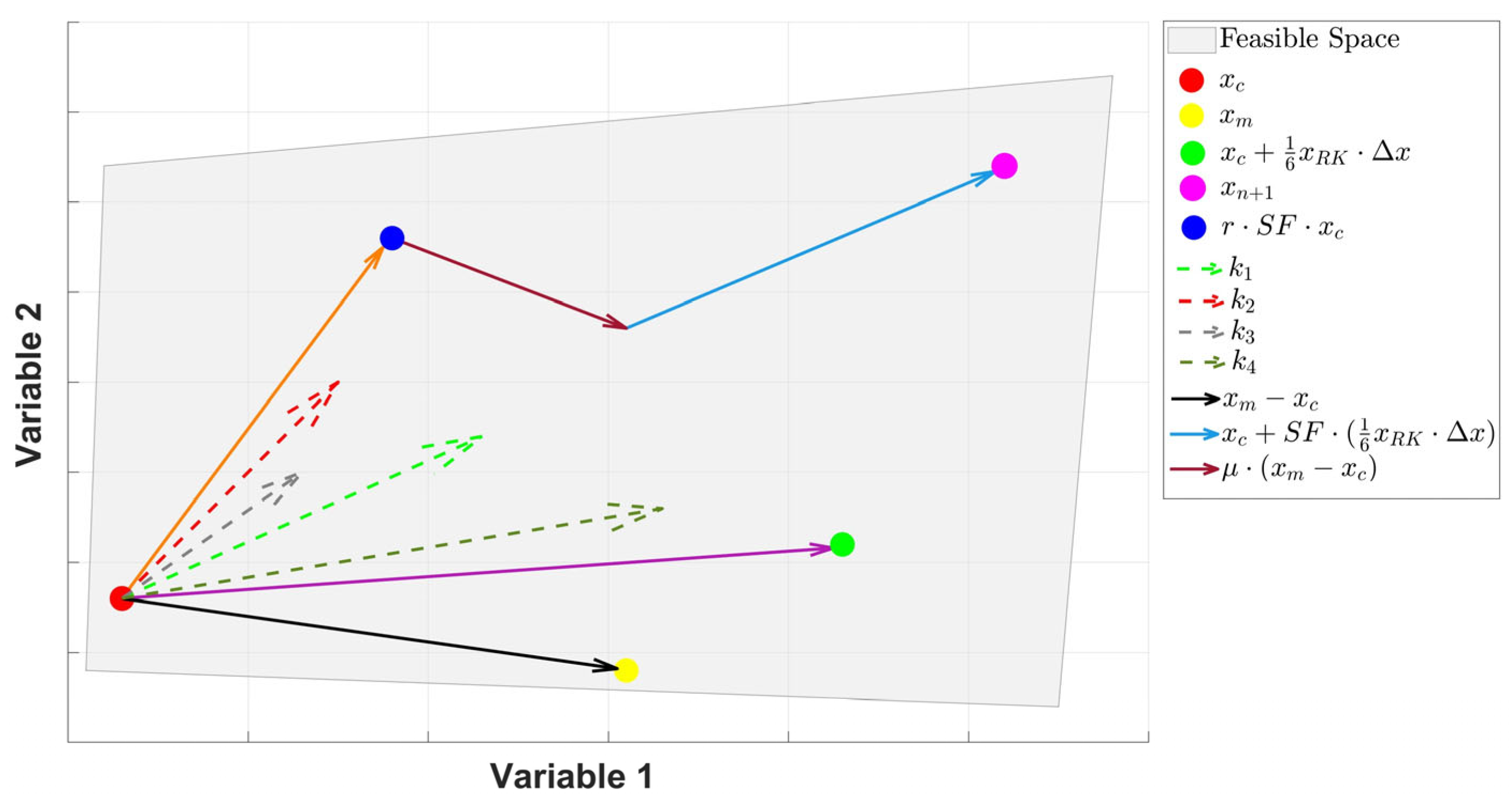
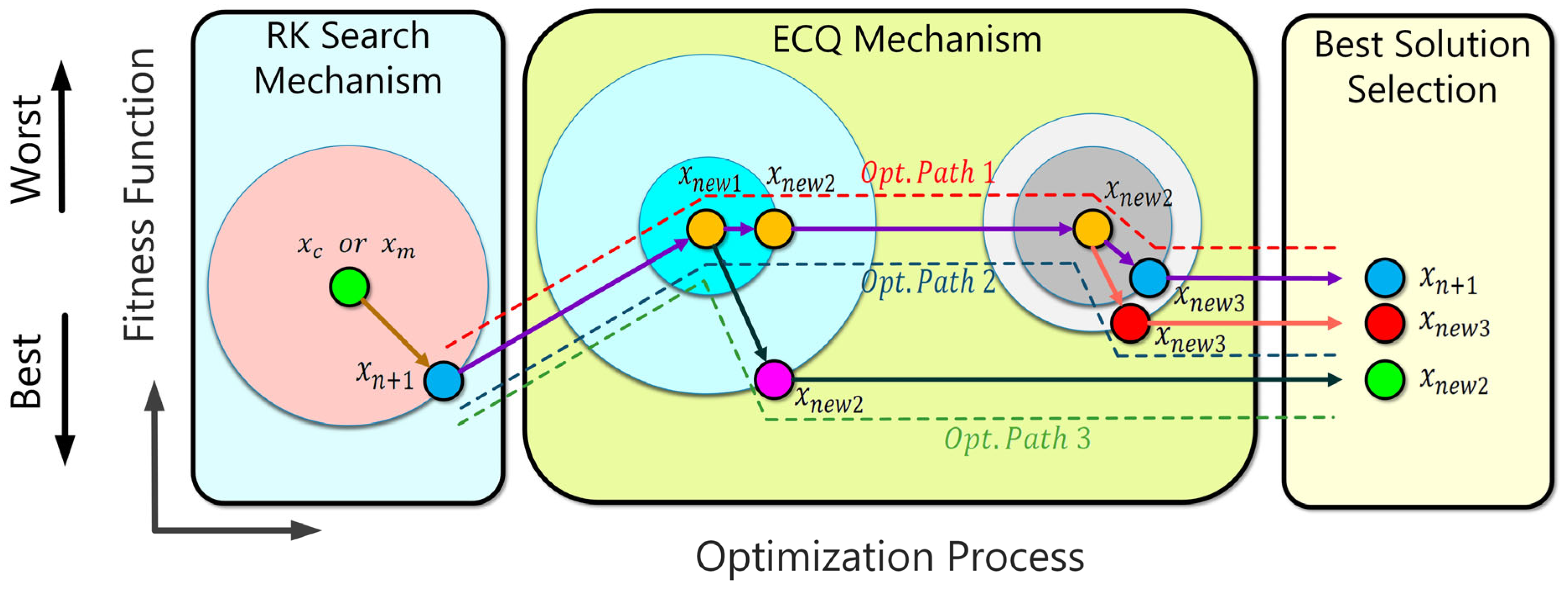
4.3. Updating Solutions
4.4. Enriched Candidate Quality (ECQ)
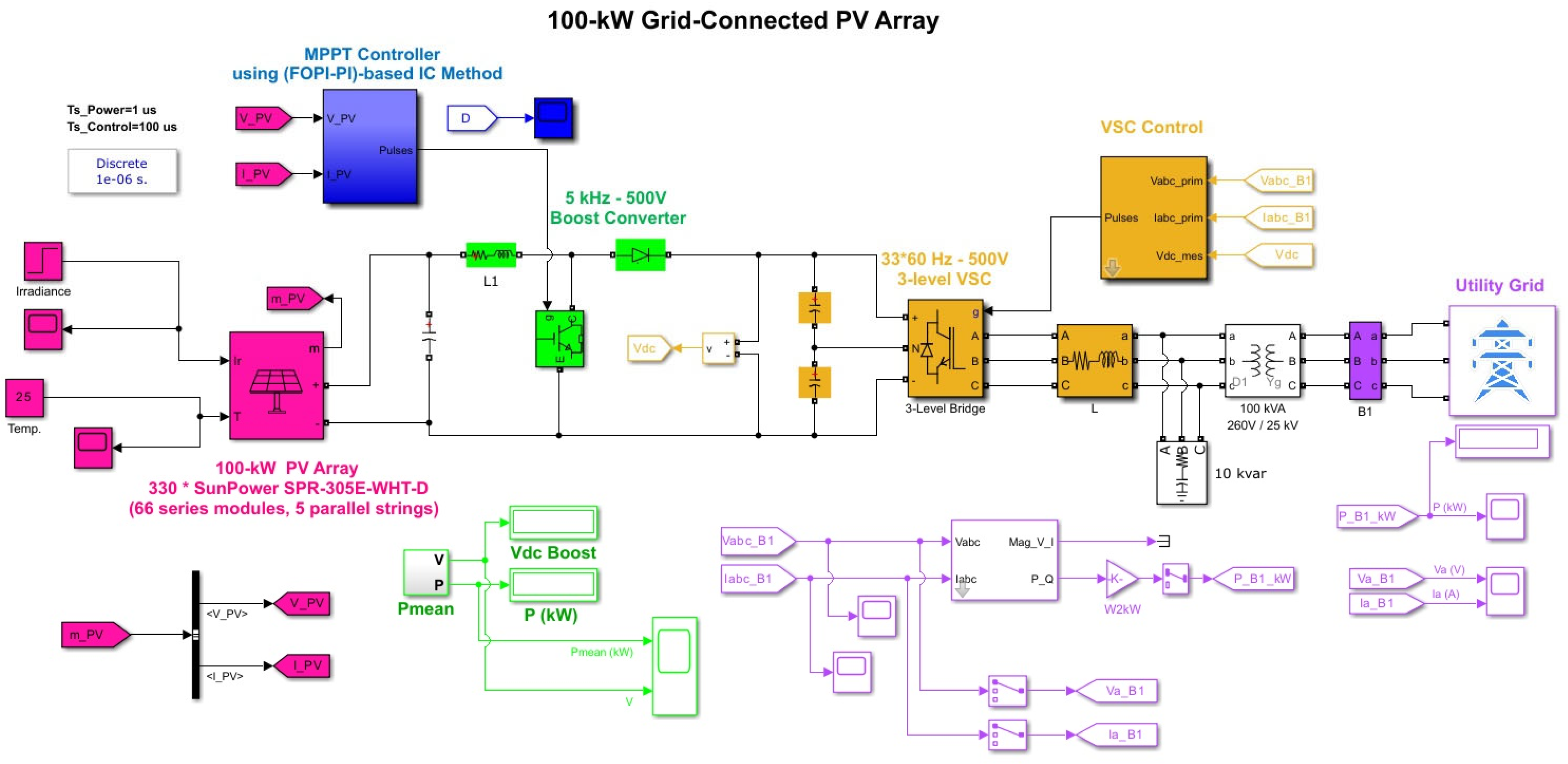
5. Simulation Framework
- ➢
- Step 1. Choose the suitable number of search agents and maximum iterations for all three compared optimization methods (AVO, GTO and RUN);
- ➢
- Step 2. Determine the appropriate upper and lower limits for the proposed FOPI-PI controller parameters (, , , , ) to ensure precise and rapid performance;
- ➢
- Step 3. Designate ISE as a fitness function derived from Simulink;
- ➢
- Step 4. Execute AVO, GTO and RUN on the PV simulation model within the aforementioned constraints;
- ➢
- Step 5. Update the best-found controllers’ parameters, which score the lowest ISE, during the iterative process of the optimization;
- ➢
- Step 6. Following the last iteration of the optimization, we can derive the most optimal settings of the three compared controllers for the efficient extraction of photovoltaic output power.
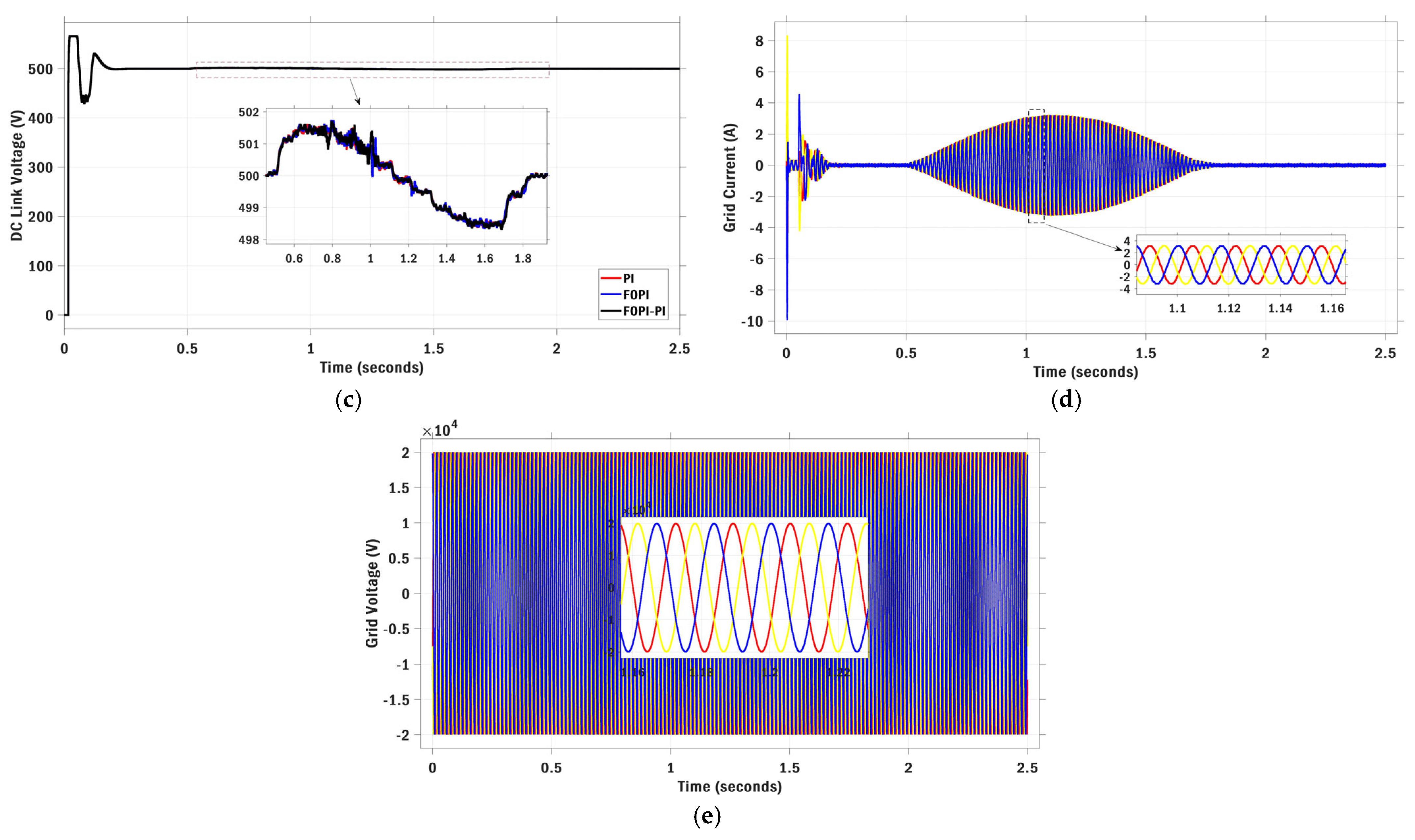
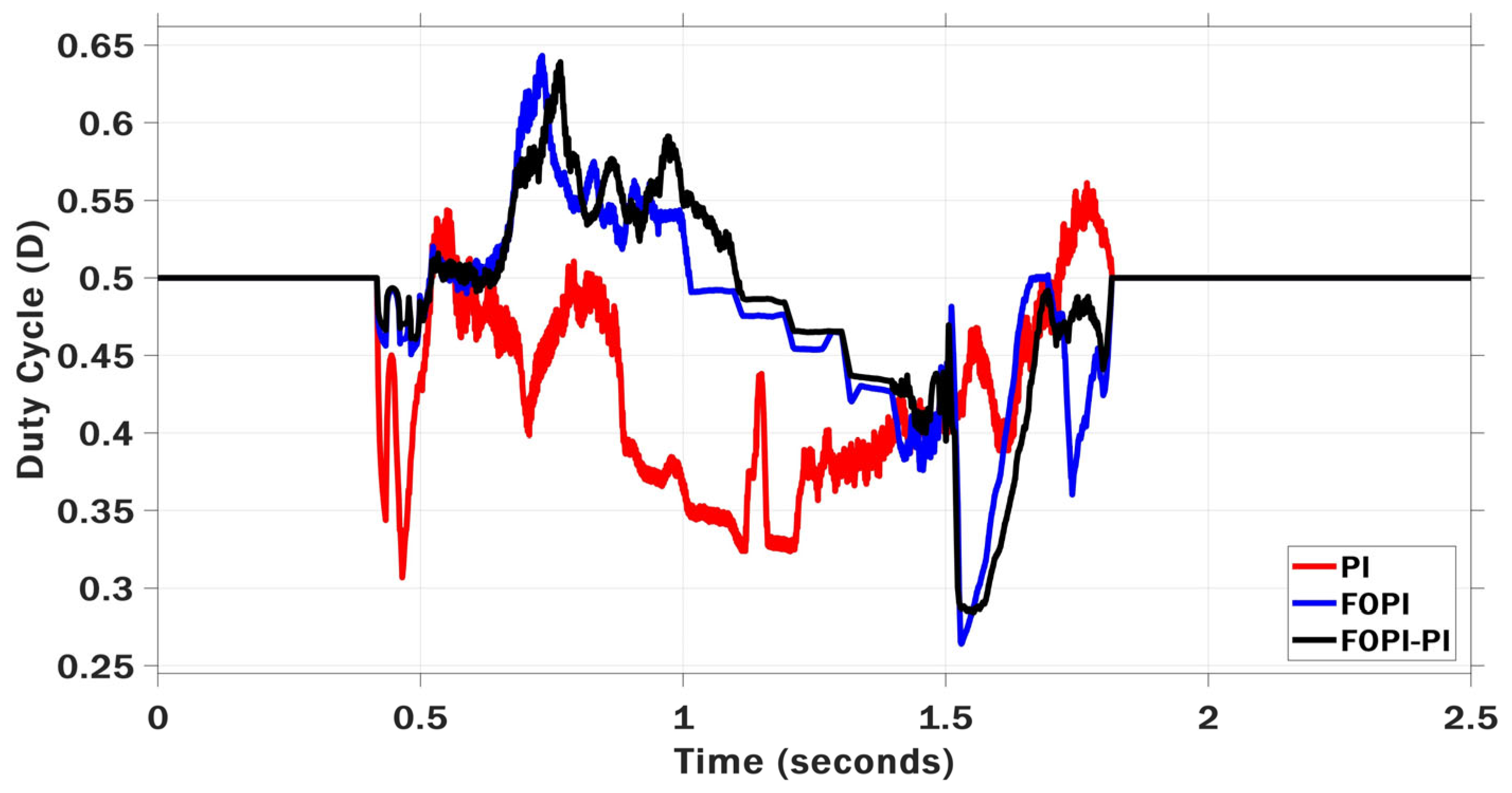
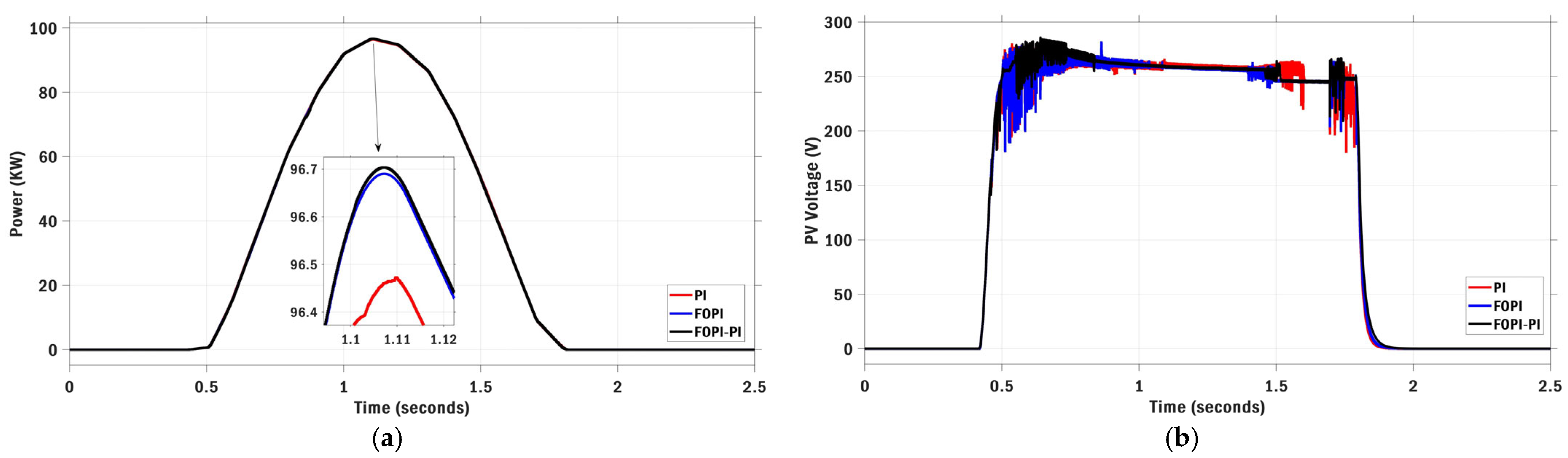
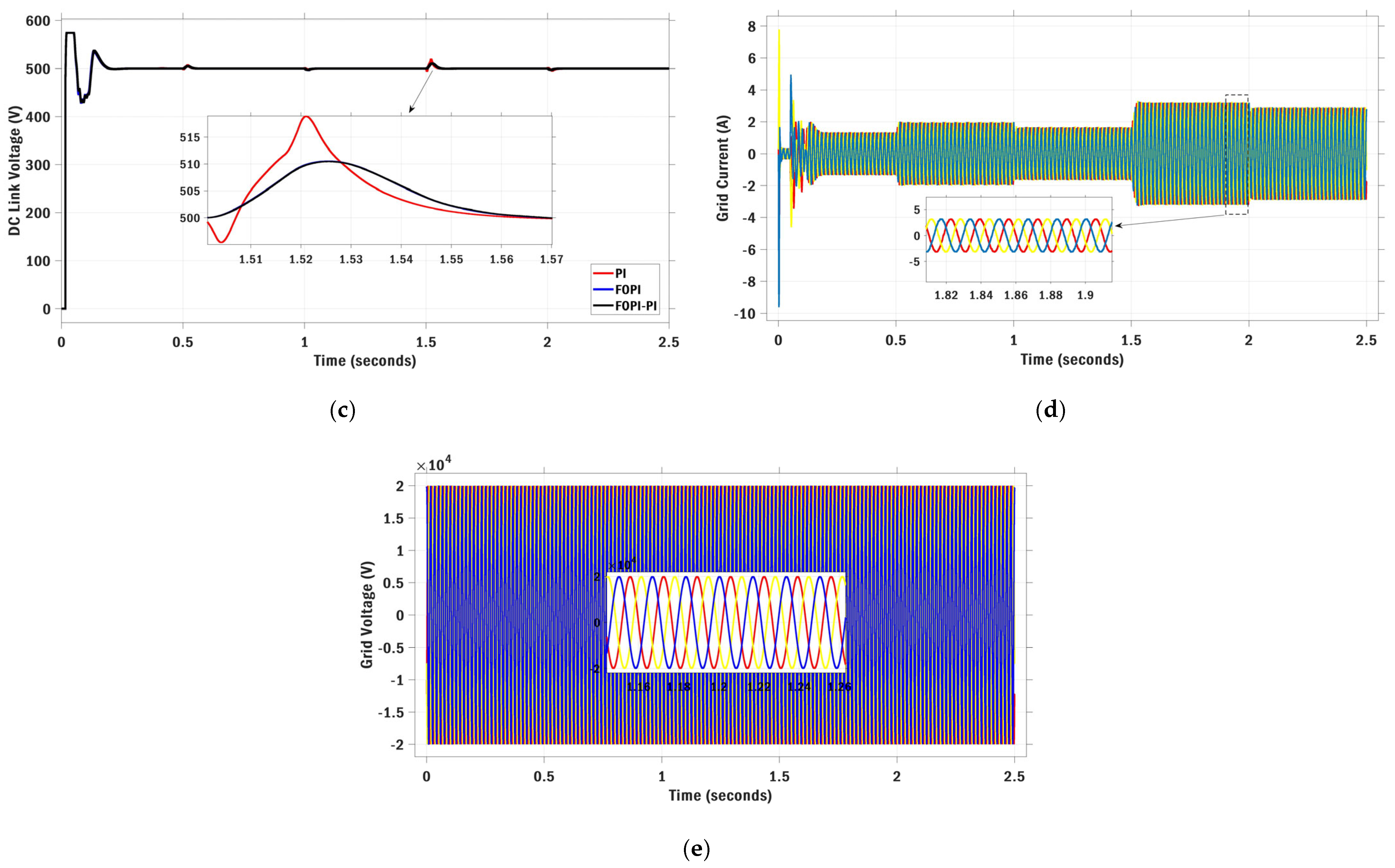
6. Results and Discussion
- Scenario I: Stepwise irradiance variation with constant temperature.
- Scenario II: Ramp irradiance and temperature variations.
- Scenario III: Realistic irradiance variation with constant temperature.
- Scenario IV: Realistic irradiance and temperature variations.
- Scenario V: Multi-stepwise irradiance and temperature variations.
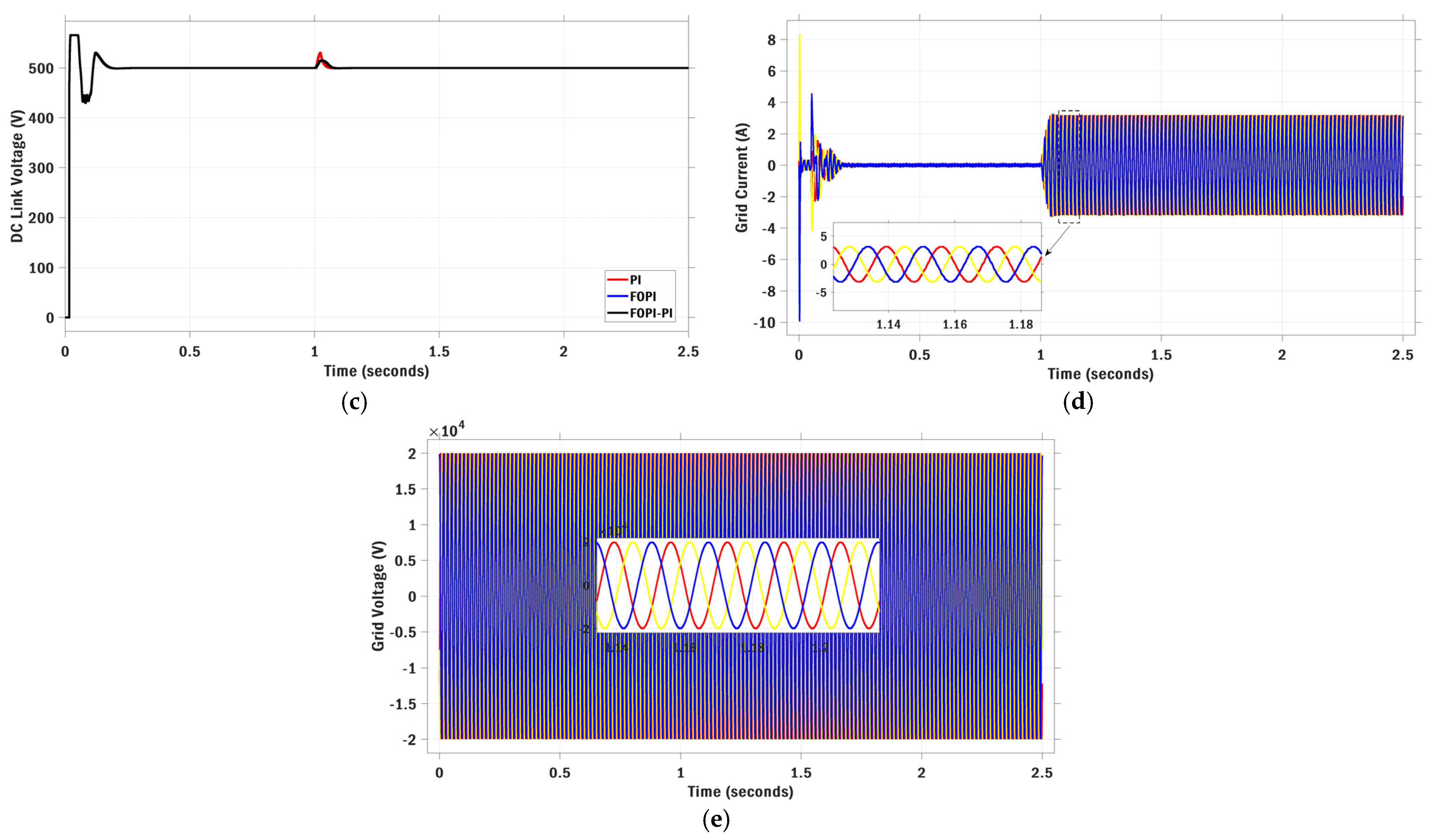
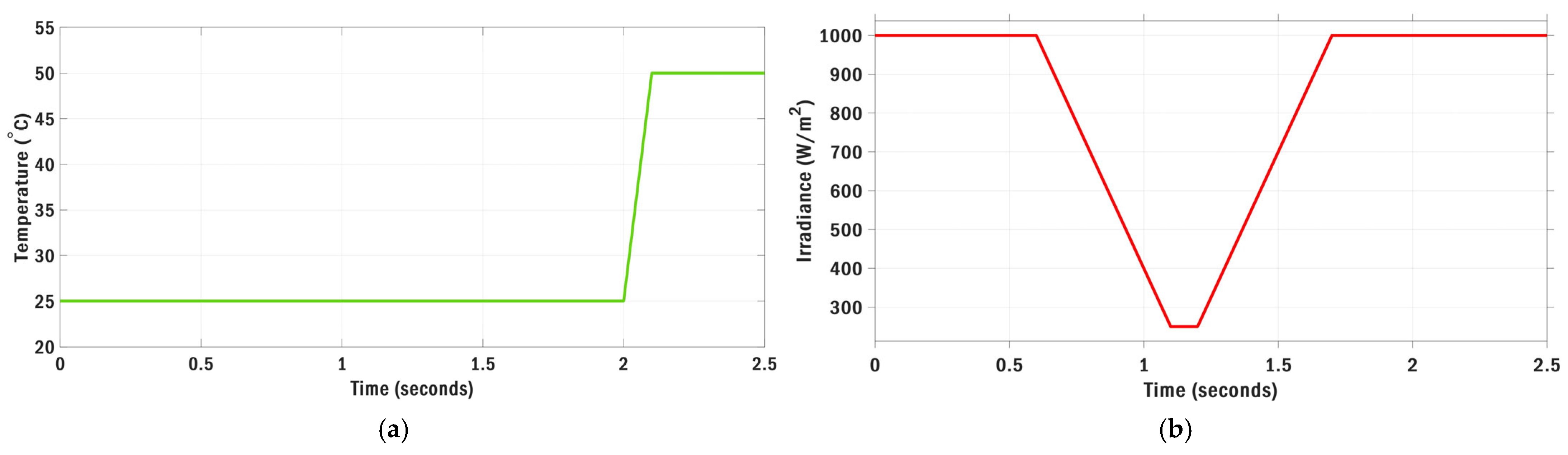
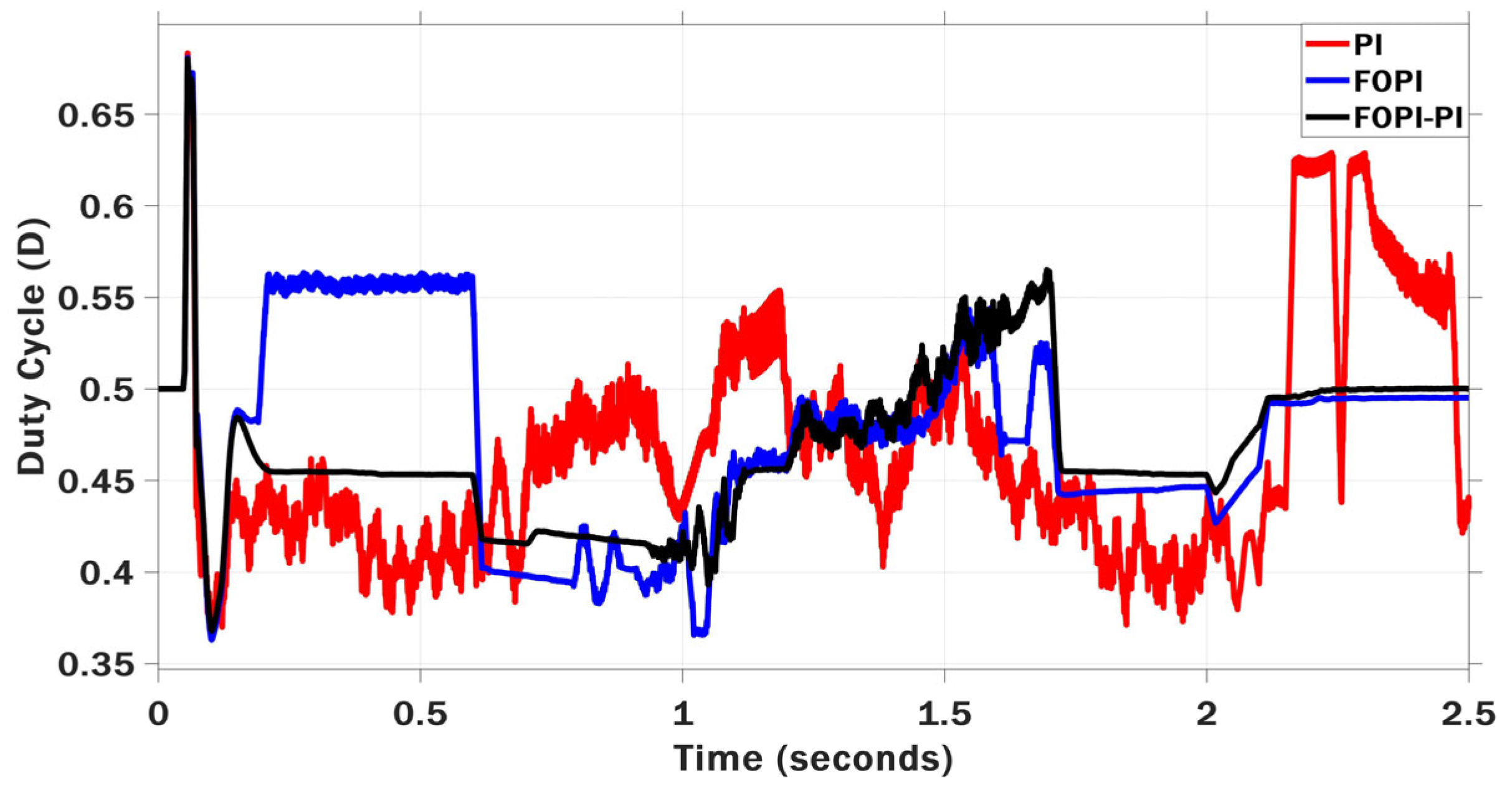
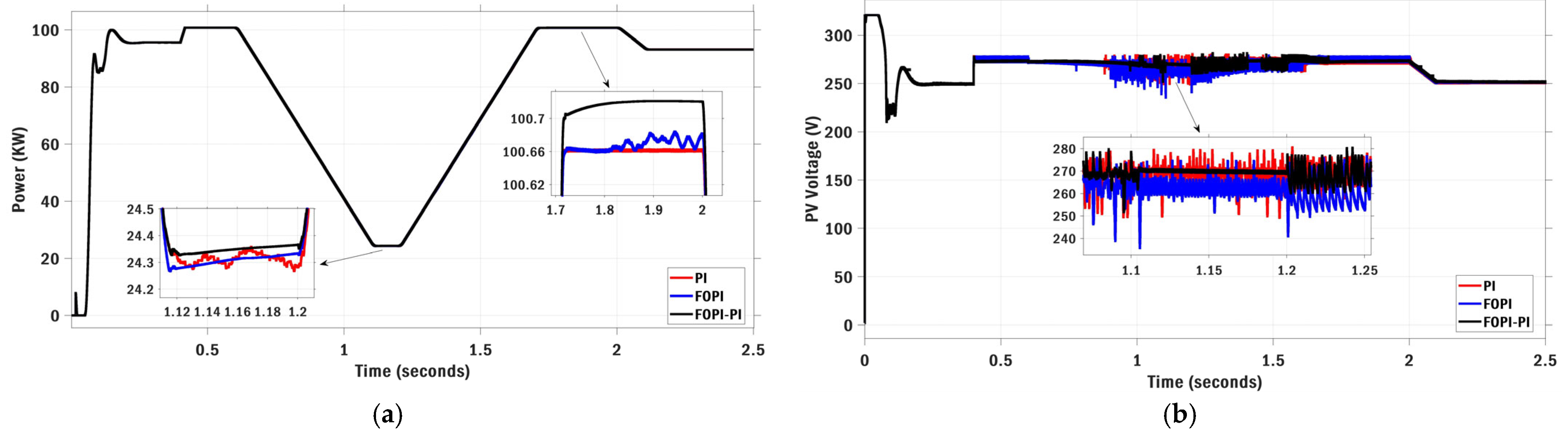
6.1. Scenario I: Stepwise Irradiance Variation with Constant Temperature
6.2. Scenario II: Ramp Irradiance and Temperature Variations
6.3. Scenario III: Realistic Irradiance Variation with Constant Temperature
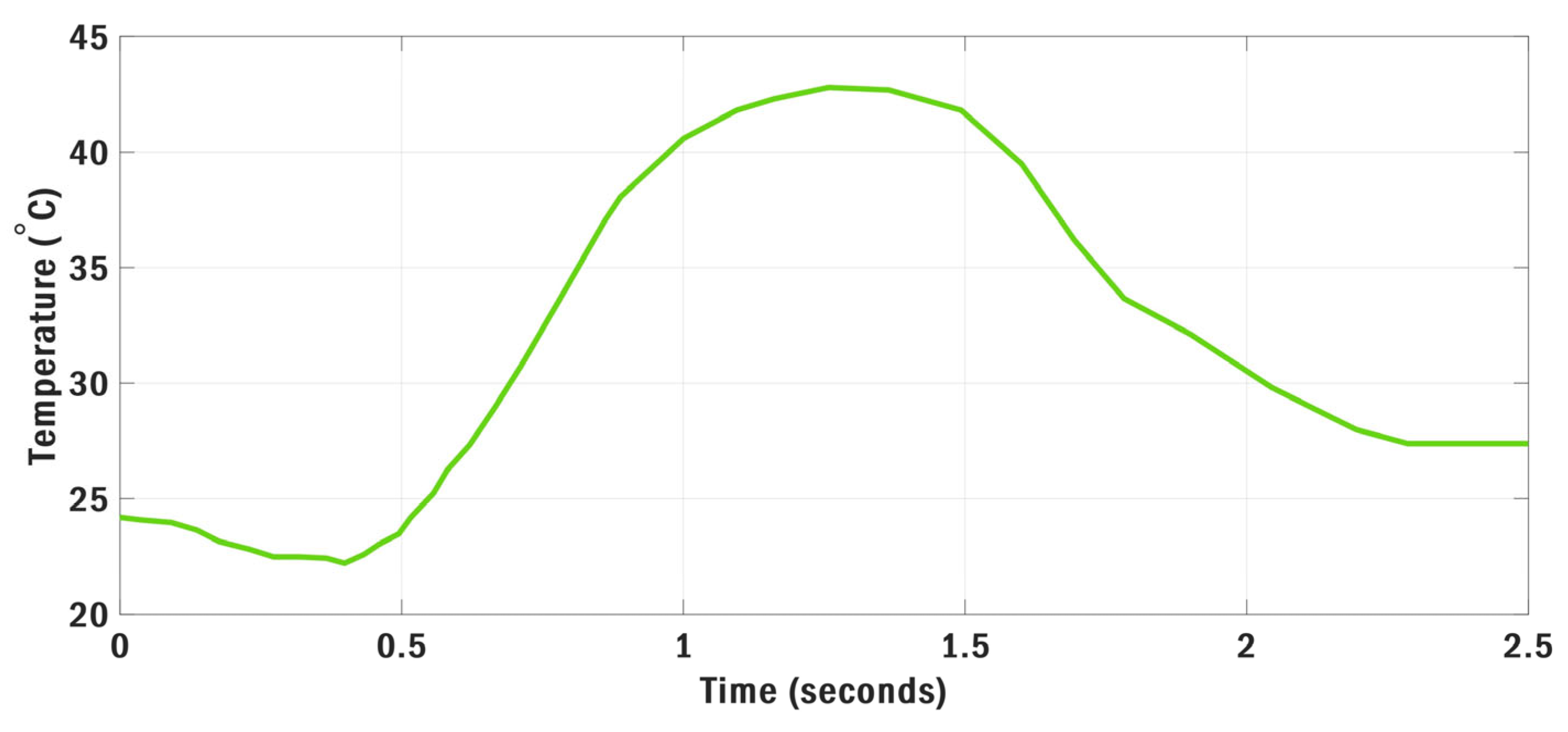
6.4. Scenario IV: Realistic Irradiance and Temperature Variations
6.5. Scenario V: Multi-Stepwise Irradiance and Temperature Variations
7. Conclusions
8. Limitations and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| IC | Incremental Conductance |
| GTO | Gorilla Troops Optimizer |
| AVO | African Vultures Optimizer |
| RUN | Runge–Kutta Optimizer |
| FOPI | Fractional Order Proportional Integral |
| PV | Photovoltaic |
| IRENA | International Renewable Energy Agency |
| RES | Renewable Energy Source |
| HC | Hill Climbing |
| FOCV | Fractional Open-Circuit Voltage |
| DDM | Double Diode Model |
| SaBO | Self-Adaptive Bonobo Optimizer |
| GOA | Grasshopper Optimization Algorithm |
| UL | Upper Limit |
| ISE | Integral of Squared Error |
| FLCs | Fuzzy Logic Controllers |
| ANNs | Artificial Neural Networks |
| EAs | Evolutionary Algorithms |
| MPPT | Maximum Power Point Tracking |
| GSC | Generation Side Converter |
| SDM | Single Diode Model |
| DO | Dandelion Optimizer |
| P&O | Perturb and Observe |
| STCs | Standard Test Conditions |
| e(t) | Error Signal |
| LL | Lower Limit |
| TDM | Triple Diode Model |
| FSCC | Fractional Short-Circuit Current |
References
- Ahmad, R.; Murtaza, A.F.; Sher, H.A. Power tracking techniques for efficient operation of photovoltaic array in solar applications—A review. Renew. Sustain. Energy Rev. 2019, 101, 82–102. [Google Scholar] [CrossRef]
- International Renewable Energy Agency (IRENA). Renewable Capacity Highlights; 11 April 2022; IRENA: Abu Dhabi, United Arab Emirates, 2022. [Google Scholar]
- Yang, B.; Yu, T.; Zhang, X.; Li, H.; Shu, H.; Sang, Y.; Jiang, L. Dynamic leader-based collective intelligence for maximum power point tracking of PV systems affected by partial shading condition. Energy Convers. Manag. 2019, 179, 286–303. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Diab, A.A.; Rezk, H. Partial shading mitigation of PV systems via different meta-heuristic techniques. Renew. Energy 2019, 130, 1159–1175. [Google Scholar] [CrossRef]
- Raiker, G.A.; Loganathan, U. Current control of boost converter for PV interface with momentum-based perturb and observe MPPT. IEEE Trans. Ind. Appl. 2021, 57, 4071–4079. [Google Scholar] [CrossRef]
- Jately, V.; Azzopardi, B.; Joshi, J.; Sharma, A.; Arora, S. Experimental analysis of hill-climbing MPPT algorithms under low irradiance levels. Renew. Sustain. Energy Rev. 2021, 150, 111467. [Google Scholar] [CrossRef]
- Ali, M.N.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M. An efficient fuzzy-logic-based variable-step incremental conductance MPPT method for grid-connected PV systems. IEEE Access 2021, 9, 26420–26430. [Google Scholar] [CrossRef]
- Nadeem, A.; Sher, H.A.; Murtaza, A.F. Online fractional open-circuit voltage maximum output power algorithm for photovoltaic modules. IET Renew. Power Gener. 2020, 14, 188–198. [Google Scholar] [CrossRef]
- Nadeem, A.; Sher, H.A.; Murtaza, A.F.; Ahmed, N. Online current-sensorless estimator for PV open-circuit voltage and short-circuit current. Sol. Energy 2021, 213, 198–210. [Google Scholar] [CrossRef]
- Fathi, M.; Parian, J.A. Intelligent MPPT for photovoltaic panels using a novel fuzzy logic and artificial neural networks based on evolutionary algorithms. Energy Rep. 2021, 7, 1338–1348. [Google Scholar] [CrossRef]
- Dehghani, M.; Taghipour, M.; Gharehpetian, G.B.; Abedi, M. Optimized fuzzy controller for MPPT of grid-connected PV systems in rapidly changing atmospheric conditions. J. Mod. Power Syst. Clean Energy 2020, 9, 376–383. [Google Scholar] [CrossRef]
- Chellakhi, A.; El Beid, S.; El Marghichi, M.; Bouabdalli, E.M. An amended low-cost indirect MPPT strategy with a PID controller for boosting PV system efficiency. Results Eng. 2024, 24, 103526. [Google Scholar] [CrossRef]
- Chellakhi, A.; El Beid, S.; Abouelmahjoub, Y.; Doubabi, H. An Enhanced Incremental Conductance MPPT Approach for PV Power Optimization: A Simulation and Experimental Study. Arab. J. Sci. Eng. 2024, 49, 16045–16064. [Google Scholar] [CrossRef]
- Chellakhi, A.; El Beid, S.; El Marghichi, M.; Bouabdalli, E.M.; Harrison, A.; Abouobaida, H. Implementation of a Low-Cost Current Perturbation-Based Improved P&O MPPT Approach Using Arduino Board for Photovoltaic Systems. e-Prime—Adv. Electr. Eng. Electron. Energy 2024, 10, 100807. [Google Scholar]
- Mohamed Ahmed Ebrahim Mohamed, S.N.A.; Metwally, M.E. Arithmetic Optimization Algorithm Based Maximum Power Point Tracking for Grid-Connected Photovoltaic System. Sci. Rep. 2023, 13, 5961. [Google Scholar]
- Tadj, M.; Chaib, L.; Choucha, A.; Aldaoudeyeh, A.-M.; Fathy, A.; Rezk, H.; Louzazni, M.; El-Fergany, A. Enhanced MPPT-Based Fractional-Order PID for PV Systems Using Aquila Optimizer. Math. Comput. Appl. 2023, 28, 99. [Google Scholar] [CrossRef]
- Mansoor, M.; Mirza, A.F.; Ling, Q. Harris hawk optimization-based MPPT control for PV systems under partial shading conditions. J. Clean. Prod. 2020, 274, 122857. [Google Scholar] [CrossRef]
- Pilakkat, D.; Kanthalakshmi, S. An improved P&O algorithm integrated with artificial bee colony for photovoltaic systems under partial shading conditions. Sol. Energy 2019, 178, 37–47. [Google Scholar]
- Guo, K.; Cui, L.; Mao, M.; Zhou, L.; Zhang, Q. An improved gray wolf optimizer MPPT algorithm for PV system with BFBIC converter under partial shading. IEEE Access 2020, 8, 103476–103490. [Google Scholar] [CrossRef]
- Huang, Y.P.; Huang, M.Y.; Ye, C.E. A fusion firefly algorithm with simplified propagation for photovoltaic MPPT under partial shading conditions. IEEE Trans. Sustain. Energy 2020, 11, 2641–2652. [Google Scholar] [CrossRef]
- Fares, D.; Fathi, M.; Shams, I.; Mekhilef, S. A novel global MPPT technique based on squirrel search algorithm for PV module under partial shading conditions. Energy Convers. Manag. 2021, 230, 113773. [Google Scholar] [CrossRef]
- Phanden, R.K.; Sharma, L.; Chhabra, J.; Demir, H.İ. A novel modified ant colony optimization-based maximum power point tracking controller for photovoltaic systems. Mater. Today Proc. 2021, 38, 89–93. [Google Scholar] [CrossRef]
- Mosaad, M.I.; Abed El-Raouf, M.O.; Al-Ahmar, M.A.; Banakher, F.A. Maximum power point tracking of PV system based on cuckoo search algorithm—Review and comparison. Energy Procedia 2019, 162, 117–126. [Google Scholar] [CrossRef]
- Charin, C.; Ishak, D.; Zainuri, M.A.A.M.; Ismail, B.; Jamil, M.K.M. A hybrid of bio-inspired algorithm based on Levy flight and particle swarm optimizations for photovoltaic system under partial shading conditions. Sol. Energy 2021, 217, 1–14. [Google Scholar] [CrossRef]
- Kumar, K.K.; Bhaskar, R.; Koti, H. Implementation of MPPT algorithm for solar photovoltaic cell by comparing short-circuit method and incremental conductance method. Procedia Technol. 2014, 12, 705–715. [Google Scholar] [CrossRef]
- Zakzouk, N.E.; Elsaharty, M.A.; Abdelsalam, A.K.; Helal, A.A.; Williams, B.W. Improved performance low-cost incremental conductance PV MPPT technique. IET Renew. Power Gener. 2016, 10, 561–568. [Google Scholar] [CrossRef]
- Başoğlu, M.E.; Çakır, B. An improved incremental conductance-based MPPT approach for PV modules. Turk. J. Electr. Eng. Comput. Sci. 2015, 23, 1687–1697. [Google Scholar] [CrossRef]
- Alrajoubi, H.; Oncu, S. A golden section search assisted incremental conductance MPPT control for PV-fed water pump. Int. J. Renew. Energy Res. 2022, 12, 1628–1636. [Google Scholar]
- Stephen, A.A.; Musasa, K.; Davidson, I.E. Modelling of solar PV under varying condition with an improved incremental conductance and integral regulator. Energies 2022, 15, 2405. [Google Scholar] [CrossRef]
- Banu, I.V.; Beniuga, R.; Istrate, M. Comparative analysis of the perturb-and-observe and incremental conductance MPPT methods. In Proceedings of the 2013 8th International Symposium on Advanced Topics in Electrical Engineering (ATEE), București, Romania, 23–26 May 2013; pp. 1–6. [Google Scholar]
- Singh, P.; Shukla, N.; Gaur, P. Modified variable step incremental-conductance MPPT technique for photovoltaic system. Int. J. Inf. Technol. 2021, 13, 2483–2490. [Google Scholar] [CrossRef]
- Liu, F.; Duan, S.; Liu, F.; Liu, B.; Kang, Y. A variable step size INC MPPT method for PV systems. IEEE Trans. Ind. Electron. 2008, 55, 2622–2628. [Google Scholar]
- Gupta, A.K.; Pachauri, R.K.; Maity, T.; Chauhan, Y.K.; Mahela, O.P.; Khan, B.; Gupta, P.K. Effect of various incremental conductance MPPT methods on the charging of battery load fed by solar panel. IEEE Access 2021, 9, 90977–90988. [Google Scholar] [CrossRef]
- Loukriz, A.; Haddadi, M.; Messalti, S. Simulation and experimental design of a new advanced variable step size incremental conductance MPPT algorithm for PV systems. ISA Trans. 2016, 62, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Oshaba, A.S.; Ali, E.S.; Abd Elazim, S.M. PI controller design for MPPT of photovoltaic system supplying SRM via BAT search algorithm. Neural Comput. Appl. 2017, 28, 651–667. [Google Scholar] [CrossRef]
- Mirza, A.F.; Mansoor, M.; Ling, Q.; Khan, M.I.; Aldossary, O.M. Advanced variable step size incremental conductance MPPT for a standalone PV system utilizing a GA-tuned PID controller. Energies 2020, 13, 4153. [Google Scholar] [CrossRef]
- Youssef, A.; Telbany, M.E.; Zekry, A. Reconfigurable generic FPGA implementation of fuzzy logic controller for MPPT of PV systems. Renew. Sustain. Energy Rev. 2018, 82, 1313–1319. [Google Scholar] [CrossRef]
- Maissa, F.; Barambones, O.; Lassad, S.; Fleh, A. A robust MPP tracker based on sliding mode control for a photovoltaic-based pumping system. Int. J. Autom. Comput. 2017, 14, 489–500. [Google Scholar] [CrossRef]
- Mao, M.; Guo, K.; Cui, L.; Zhou, L.; Zhang, Q. Classification and summarization of solar photovoltaic MPPT techniques: A review based on traditional and intelligent control strategies. Energy Rep. 2020, 6, 1312–1327. [Google Scholar] [CrossRef]
- Kiran, S.R.; Basha, C.H.H.; Singh, V.P.; Dhanamjayulu, C.; Prusty, B.R.; Khan, B. Reduced simulative performance analysis of variable step size ANN-based MPPT techniques for partially shaded solar PV systems. IEEE Access 2022, 10, 48875–48889. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. A grey wolf optimizer for optimum parameters of multiple PI controllers of a grid-connected PMSG driven by variable speed wind turbine. IEEE Access 2018, 6, 44120–44128. [Google Scholar] [CrossRef]
- Aguilar, M.E.B.; Coury, D.V.; Machado, F.R.; Reginatto, R.T. Tuning of DFIG wind turbine controllers with voltage regulation subjected to electrical faults using a PSO algorithm. J. Control Autom. Electr. Syst. 2021, 32, 1417–1428. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Augmented grey wolf optimizer for grid-connected PMSG-based wind energy conversion systems. Appl. Soft Comput. 2018, 69, 504–515. [Google Scholar] [CrossRef]
- Ebrahim, M.A.; Fattah, R.M.A.; Saied, E.M.; Maksoud, S.M.A.; Khashab, H.E. An islanded microgrid droop control using Henry gas solubility optimization. Int. J. Innov. Technol. Explor. Eng. 2021, 10, 43–48. [Google Scholar] [CrossRef]
- Amin, M.N.; Soliman, M.A.; Hasanien, H.M.; Abdelaziz, A.Y. Grasshopper optimization algorithm-based PI controller scheme for performance enhancement of a grid-connected wind generator. J. Control Autom. Electr. Syst. 2020, 31, 393–401. [Google Scholar] [CrossRef]
- Lotfy Haridy, A.; Ali Mohamed Abdelbasset, A.A.; Mohamed Hemeida, A.; Mohamed Ali Mohamed, Z. Optimum controller design using the ant lion optimizer for PMSG driven by wind energy. J. Electr. Eng. Technol. 2021, 16, 367–380. [Google Scholar] [CrossRef]
- El-Banna, M.H.; Hammad, M.R.; Megahed, A.I.; AboRas, K.M.; Alkuhayli, A.; Gowtham, N. On-grid optimal MPPT for fine-tuned inverter-based PV system using golf optimizer considering partial shading effect. Alex. Eng. J. 2024, 103, 180–196. [Google Scholar] [CrossRef]
- Mosaad, M.I. Application of DPC to improve the integration of DFIG into wind energy conversion systems using FOPI controller. Wind Eng. 2025, 49, 123–138. [Google Scholar] [CrossRef]
- Khairalla, A.G.; Kotb, H.; AboRas, K.M.; Ragab, M.; ElRefaie, H.B.; Ghadi, Y.Y.; Yousef, A. Enhanced control strategy and energy management for a photovoltaic system with hybrid energy storage based on self-adaptive bonobo optimization. Front. Energy Res. 2023, 11, 1283348. [Google Scholar] [CrossRef]
- Alharbi, M.; Ragab, M.; AboRas, K.M.; Kotb, H.; Dashtdar, M.; Shouran, M.; Elgamli, E. Innovative AVR-LFC design for a multi-area power system using hybrid fractional-order PI and PIDD2 controllers based on dandelion optimizer. Mathematics 2023, 11, 1387. [Google Scholar] [CrossRef]
- Okba, S.; Saadi, R.; Hammoudi, M.Y.; Himeur, Y.; Betka, A.; Atalla, S.; Mansoor, W. Dual loop FOPI controller-based Equilibrium Optimizer tuning approach for three-phase interleaved boost converter; PEMFC HEVs. IEEE Access 2024, 12, 56789–56805. [Google Scholar] [CrossRef]
- Shaban, H.; Houssein, E.H.; Pérez-Cisneros, M.; Oliva, D.; Hassan, A.Y.; Ismaeel, A.A.; AbdElminaam, D.S.; Deb, S.; Said, M. Identification of parameters in photovoltaic models through a Runge–Kutta optimizer. Mathematics 2021, 9, 2313. [Google Scholar] [CrossRef]
- Ekinci, S.; Rizk-Allah, R.M.; Izci, D.; Çelik, E. Multi-strategy improved Runge–Kutta optimizer and its promise to estimate the model parameters of solar photovoltaic modules. Heliyon 2024, 10, e15332. [Google Scholar] [CrossRef] [PubMed]
- Sajid, I.; Sarwar, A.; Tariq, M.; Bakhsh, F.I.; Hussan, M.R.; Ahmad, S.; Mohamed, A.S.N.; Ahmad, A. Runge–Kutta optimization-based selective harmonic elimination in an H-bridge multilevel inverter. IET Power Electron. 2023, 16, 1849–1865. [Google Scholar] [CrossRef]
- Selim, A.; Kamel, S.; Houssein, E.H.; Jurado, F.; Hashim, F.A. A modified Runge–Kutta optimization for optimal photovoltaic and battery storage allocation under uncertainty and load variation. Soft Comput. 2024, 28, 10369–10389. [Google Scholar] [CrossRef]
- Nyandieka, O.M.; Segera, D.R. A Chaotic Multi-Objective Runge–Kutta Optimization Algorithm for Optimized Circuit Design. Math. Probl. Eng. 2023, 2023, 6691214. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Halder, B.; Heddam, S.; Goliatt, L.; Tan, M.L.; Sa’adi, Z.; Al-Khafaji, Z.; Homod, R.Z.; Rashid, T.A.; Yaseen, Z.M. An enhanced multi-operator Runge–Kutta algorithm for optimizing complex water engineering problems. Sustainability 2023, 15, 1825. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Gandomi, A.H.; Chu, X.; Chen, H. RUN beyond the metaphor: An efficient optimization algorithm based on Runge–Kutta method. Expert Syst. Appl. 2021, 181, 115079. [Google Scholar] [CrossRef]
- Bataineh, K. Improved hybrid algorithms-based MPPT algorithm for PV system operating under severe weather conditions. IET Power Electron. 2019, 12, 703–711. [Google Scholar] [CrossRef]
- Elgendy, M.A.; Zahawi, B.; Atkinson, D.J. Assessment of the incremental conductance maximum power point tracking algorithm. IEEE Trans. Sustain. Energy 2013, 4, 108–117. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Soleimanian Gharehchopogh, F.; Mirjalili, S. Artificial gorilla troops optimizer: A new nature-inspired meta-heuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Ismaeel, A.A.K.; Houssein, E.H.; Oliva, D.; Said, M. Gradient-based optimizer for parameter extraction in photovoltaic models. IEEE Access 2021, 9, 13403–13416. [Google Scholar] [CrossRef]
- Mehta, H.K.; Warke, H.; Kukadiya, K.; Panchal, A.K. Accurate expressions for single-diode-model solar cell parameterization. IEEE J. Photovolt. 2019, 9, 803–810. [Google Scholar] [CrossRef]
- Ali, A.I.M.; Sayed, M.A.; Mohamed, E.E.M. Modified efficient perturb and observe maximum power point tracking technique for grid-tied PV system. Int. J. Electr. Power Energy Syst. 2018, 99, 192–202. [Google Scholar] [CrossRef]
- MathWorks. Detailed Model of a 100 kW Grid-Connected PV Array. Available online: https://www.mathworks.com/help/sps/ug/detailed-model-of-a-100-kw-grid-connected-pv-array.html (accessed on 16 April 2025).

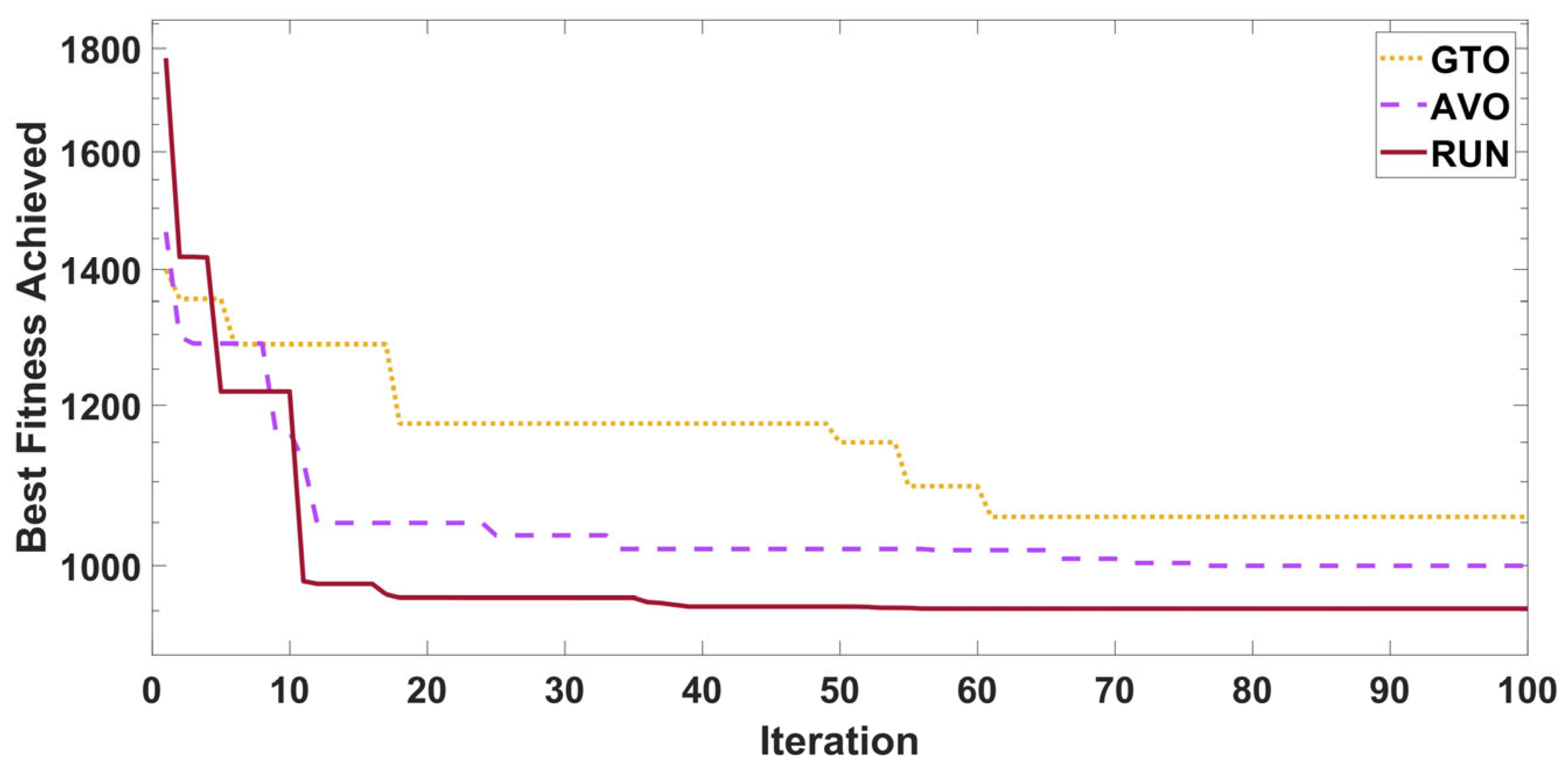
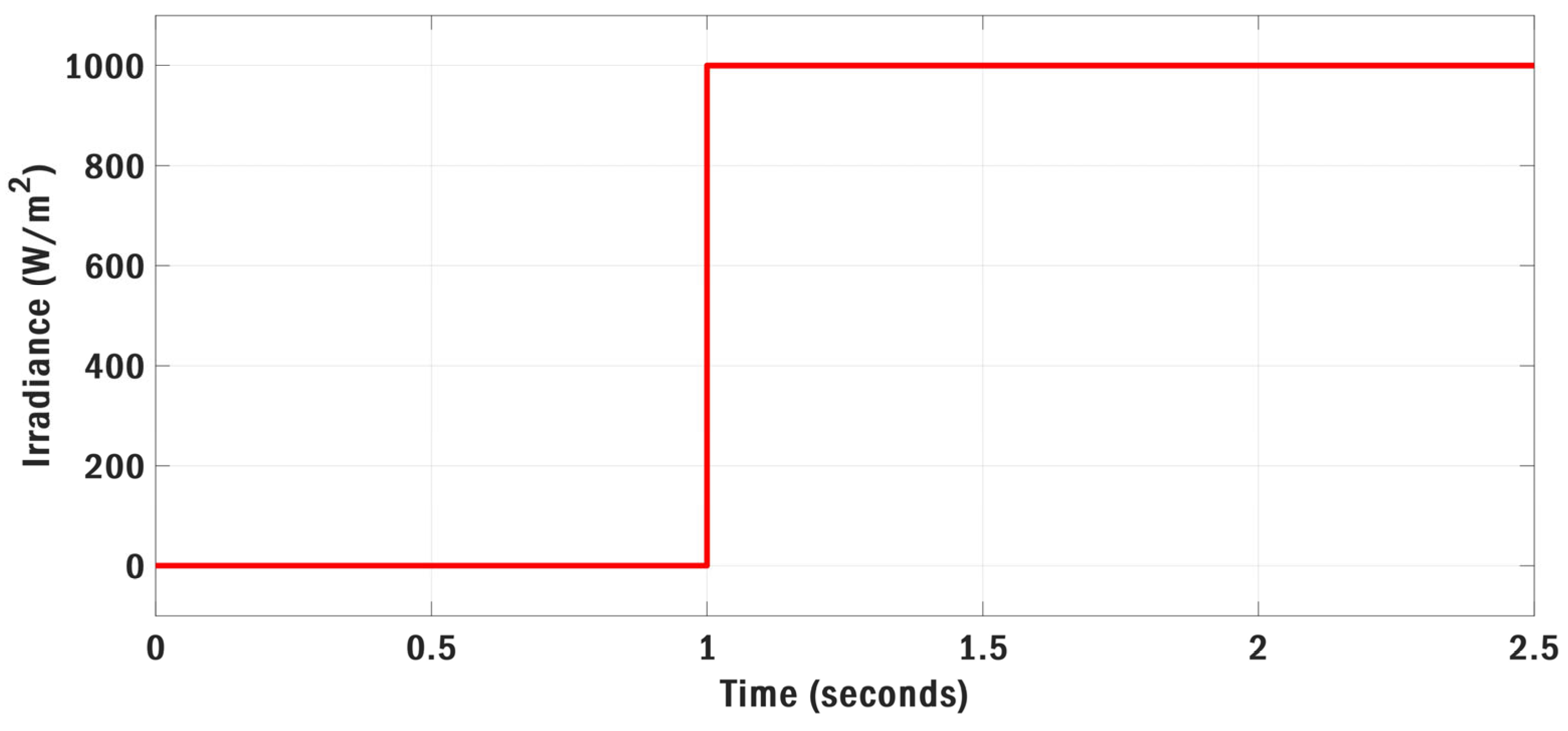
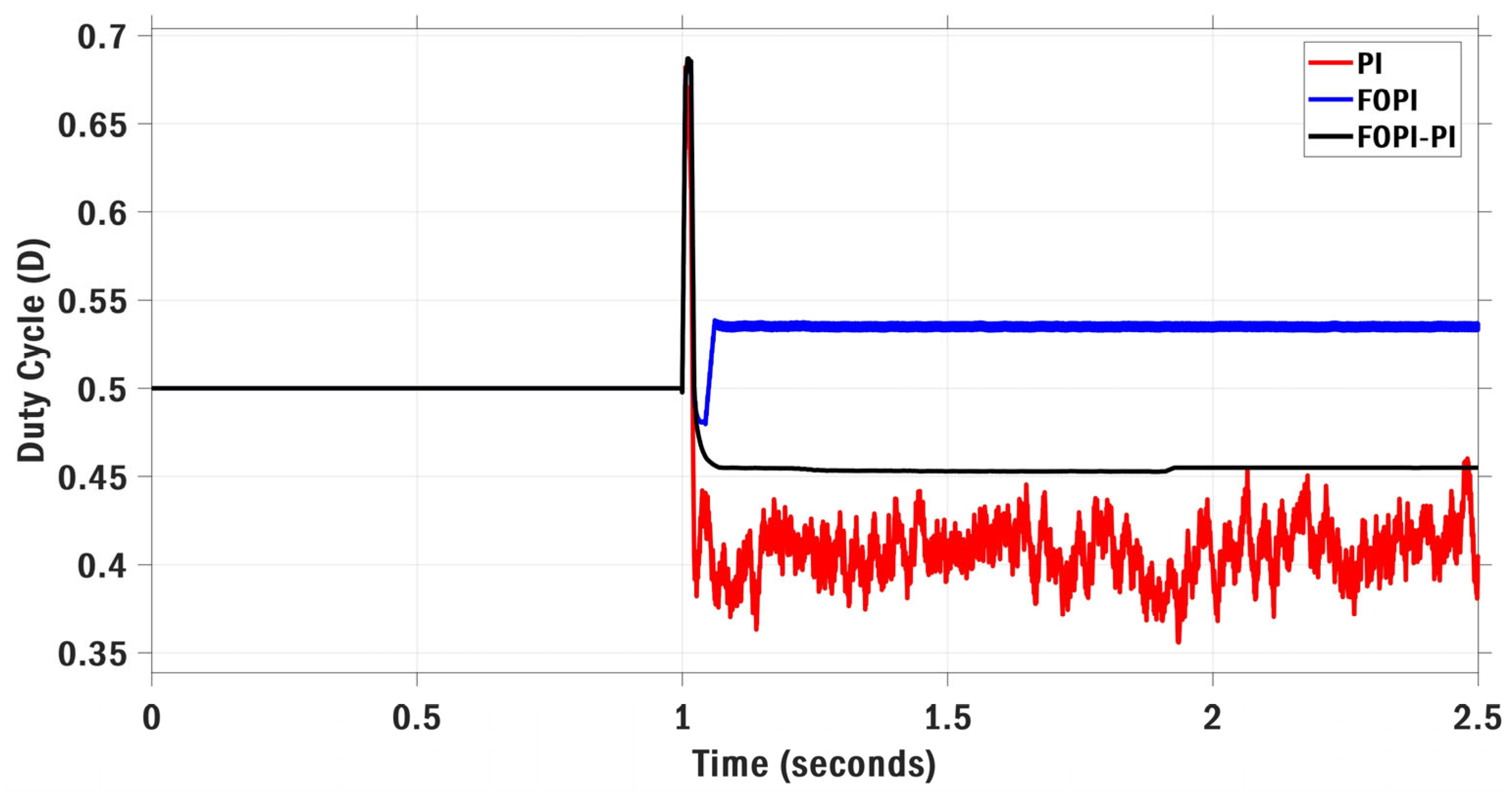
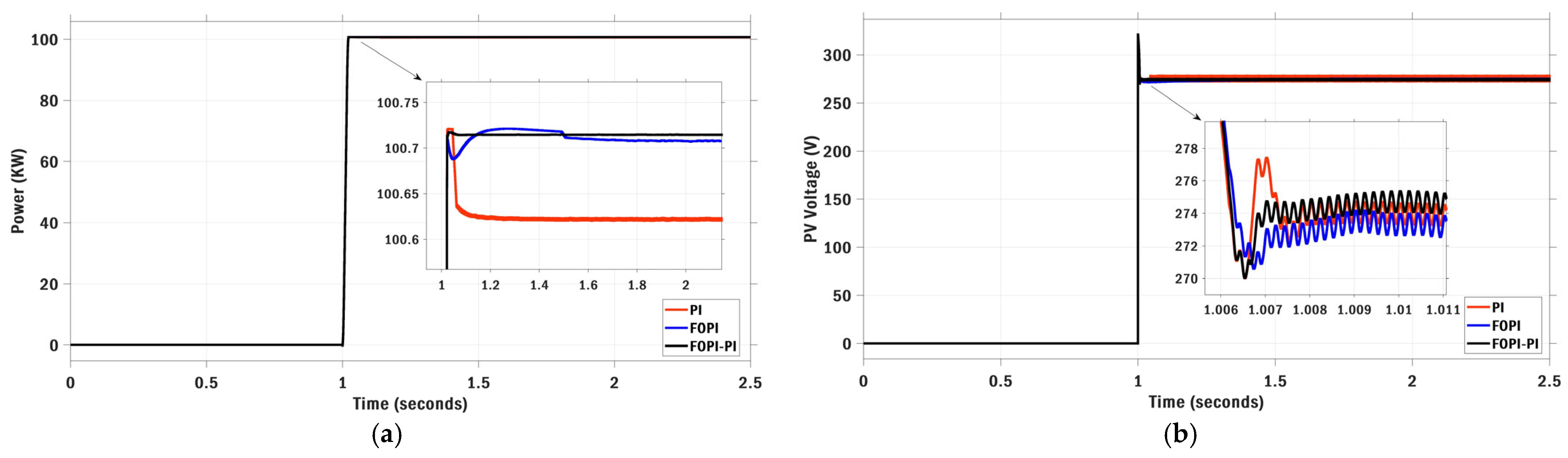
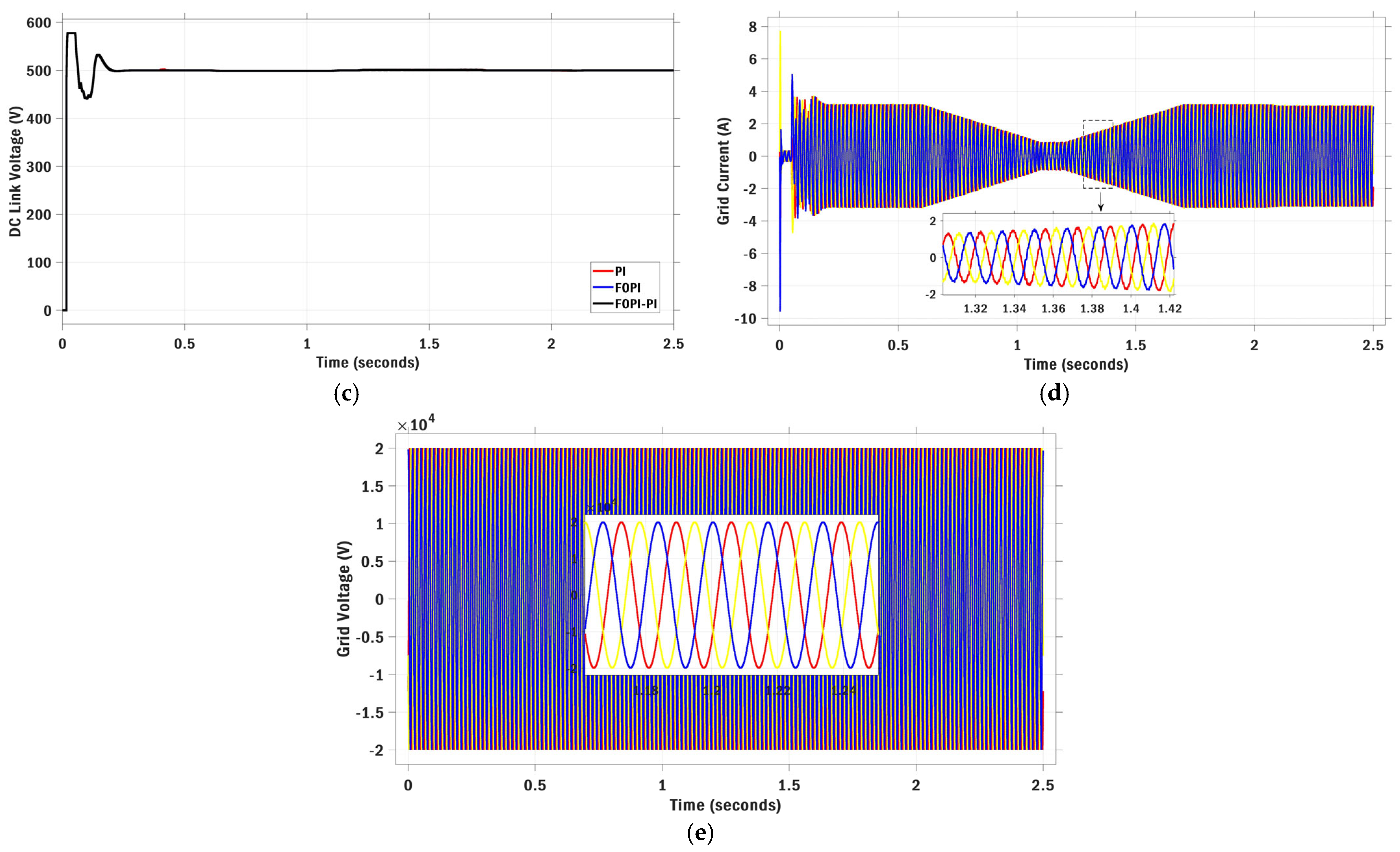
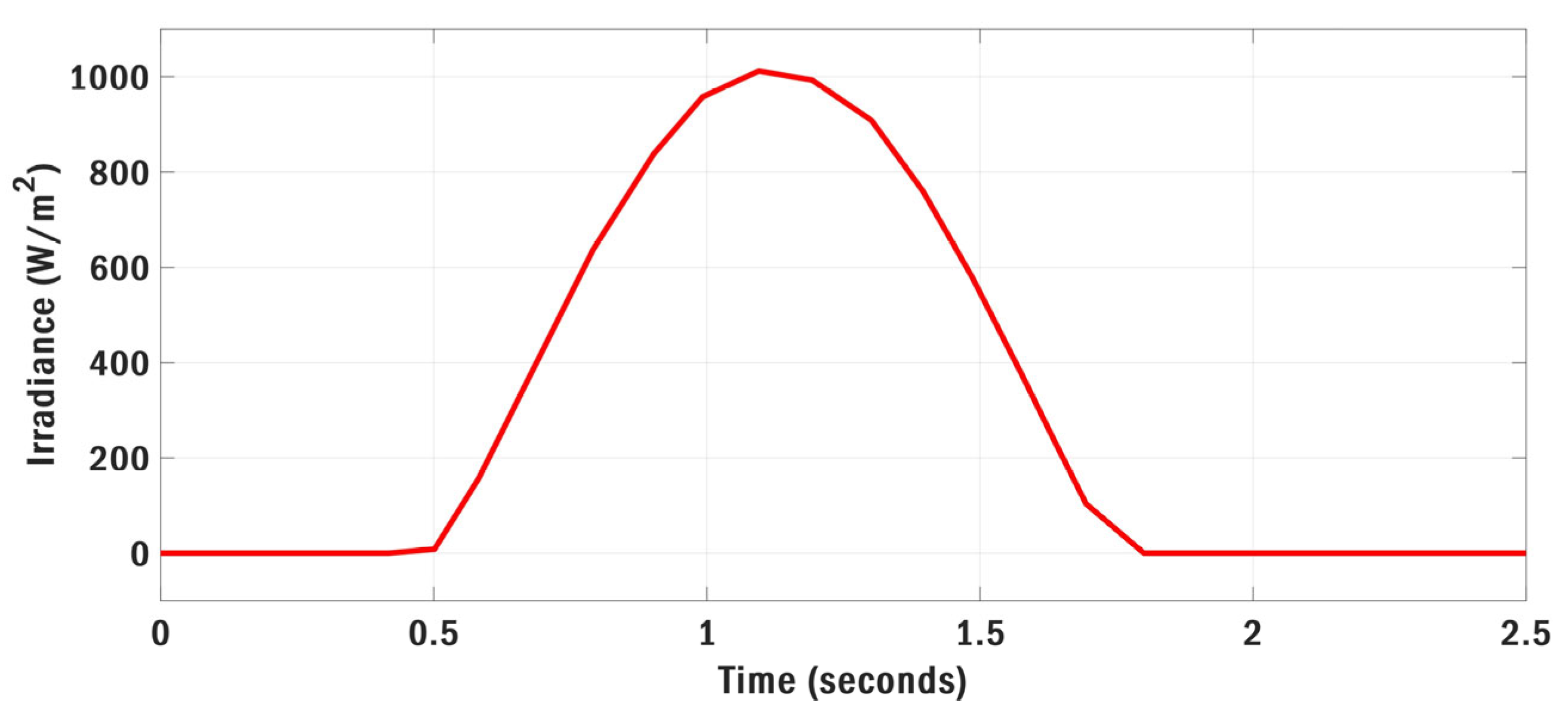
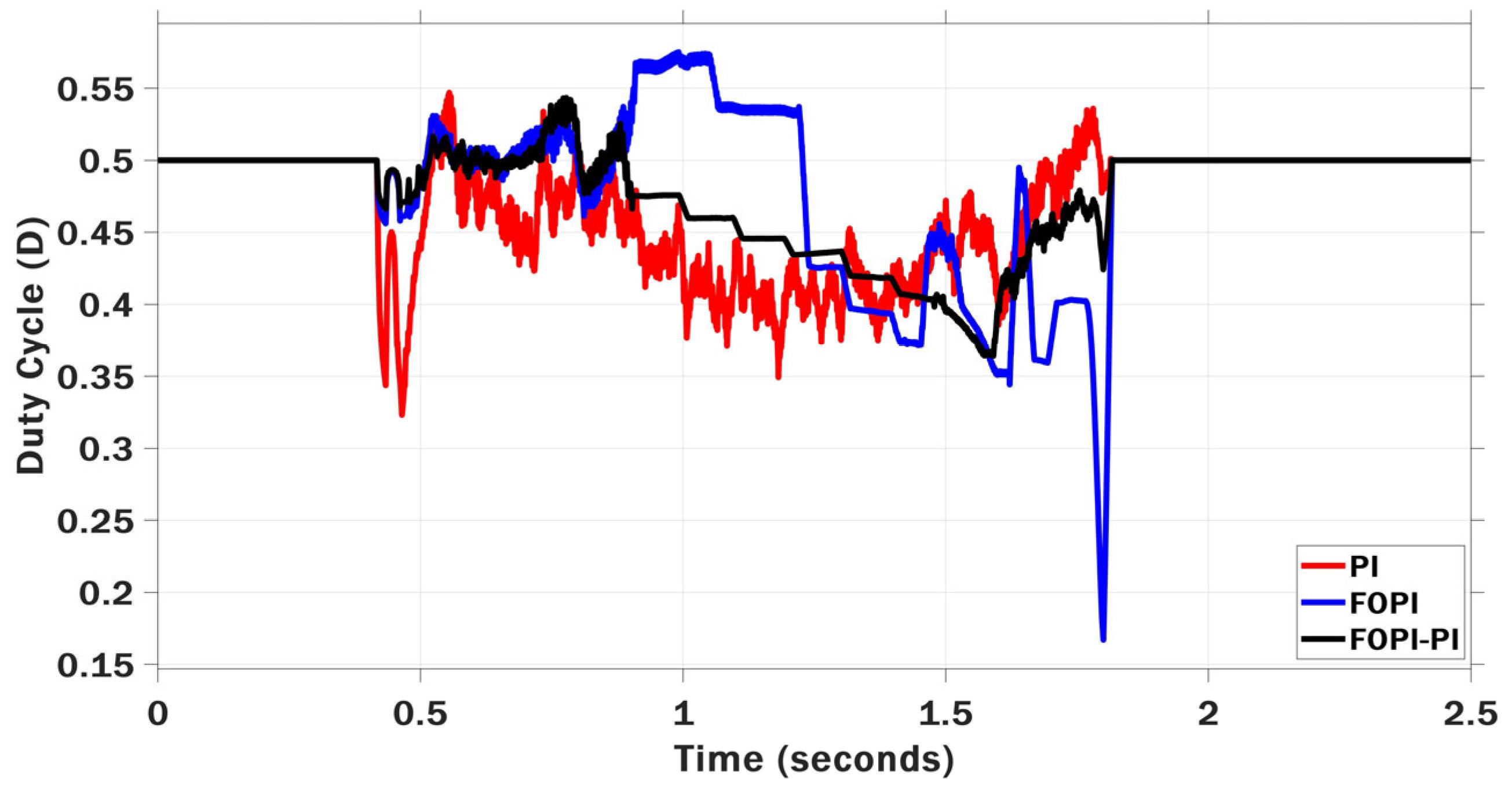
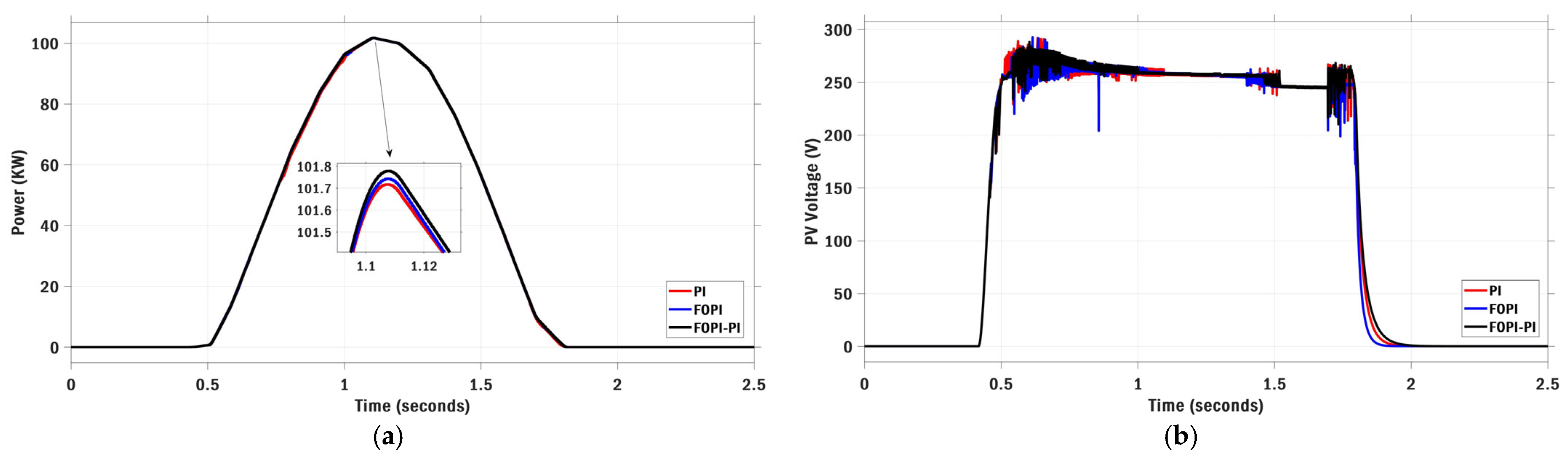
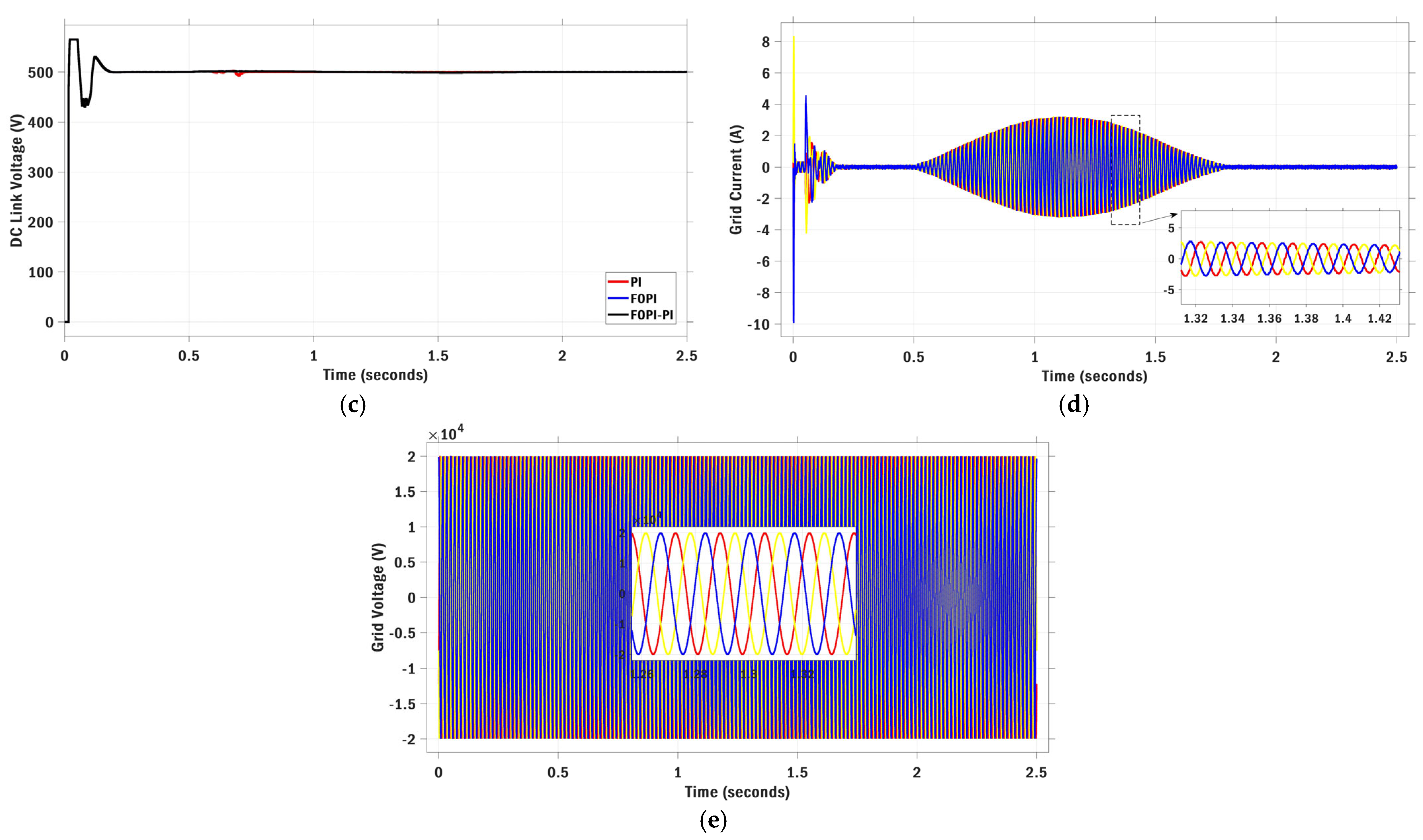
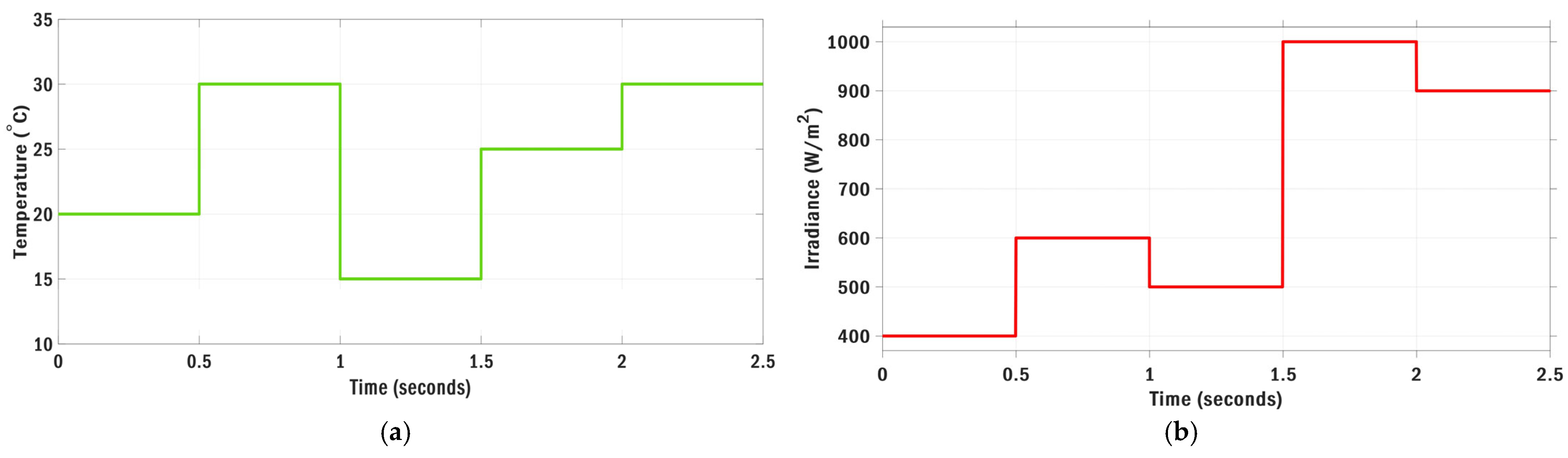
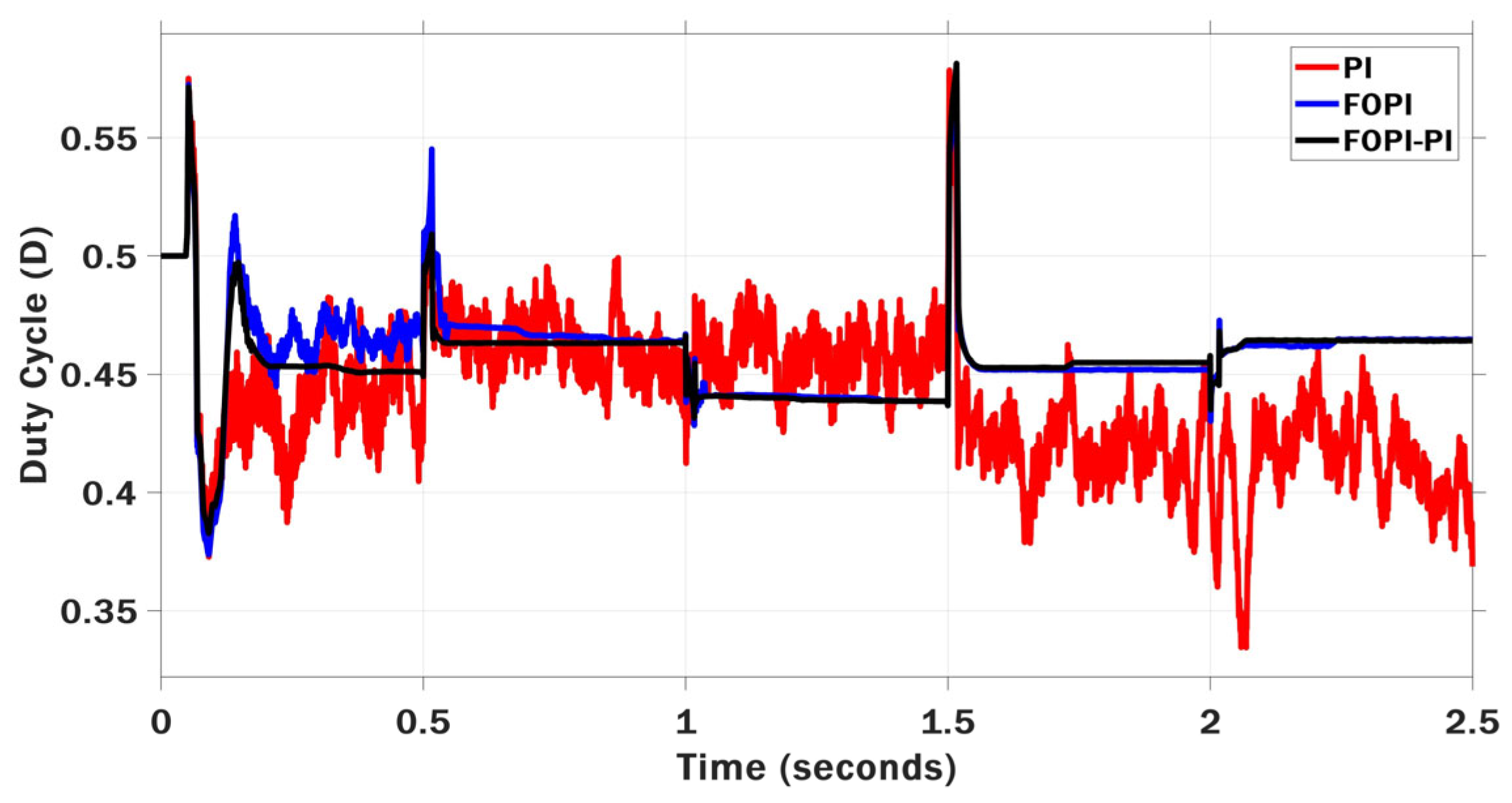
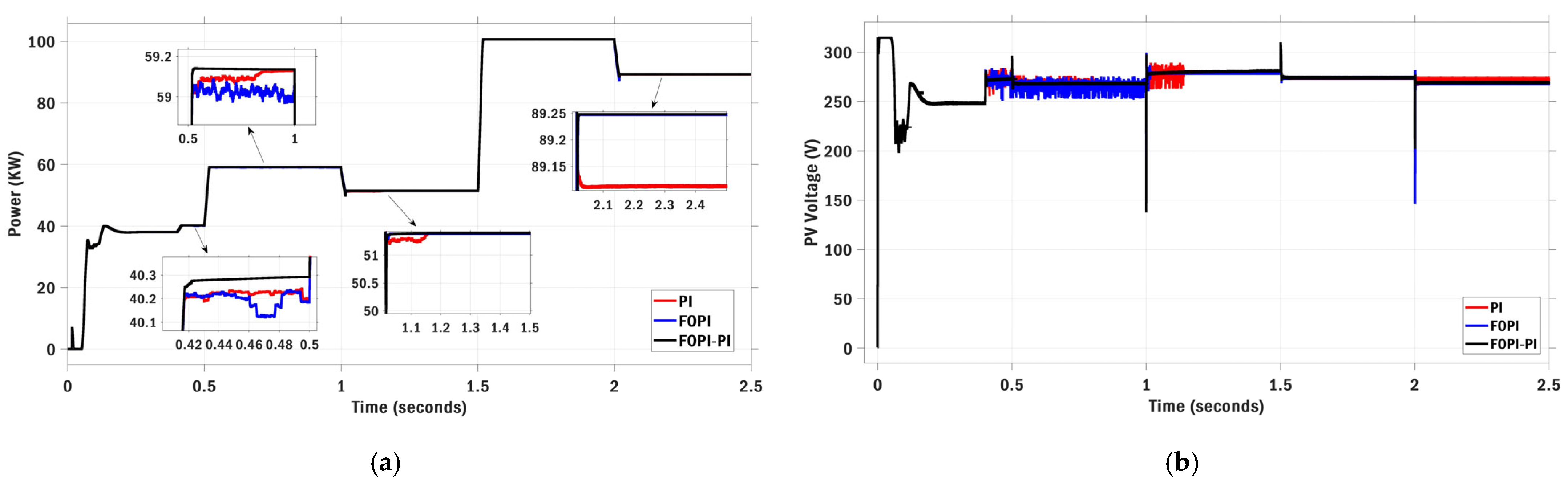
| Optimization | Parameters | Value | Max Iteration | Search Agents | Boundary Limits |
|---|---|---|---|---|---|
| RUN | H | 0.9 | 100 | 30 | |
| k1 | 0.2 | ||||
| k2 | 0.5 | ||||
| k3 | 0.7 | ||||
| k4 | 0.3 | ||||
| r1, r2, μ, β | [0:1] | ||||
| AVO | A | 1.9 | 100 | 30 | |
| b | 1.1 | ||||
| r1, r2, r3 | [0:1] | ||||
| GTO | p | 0.25 | 100 | 30 | |
| c | 1.2 | ||||
| r1, r2 | [0:1] |
| Feature | MATLAB/SIMULINK R2024b |
| Sampling control step | s |
| Solver type | Discrete-fixed step (auto) |
| Powergui | Discrete with s sampling time |
| Processor | AMD Ryzen 7 3700U with Radeon, 2.30 GHz |
| Optimization | PI | FOPI | |||
|---|---|---|---|---|---|
| RUN | 0.081 | 0.423 | 3.992 | 3.439 | 0.837 |
| AVO | 0.057 | 0.893 | 3.148 | 2.826 | 0.258 |
| GTO | 0.035 | 0.367 | 3.739 | 3.952 | 0.355 |
| Controller | PI | FOPI | |||
|---|---|---|---|---|---|
| FOPI-PI (Proposed) | 0.081 | 0.423 | 3.992 | 3.439 | 0.837 |
| FOPI | -- | -- | 0.476 | 0.071 | 0.543 |
| PI | 0.511 | 1.411 | -- | -- | -- |
| Controller | Fitness Value (ISE) | T-Rising (Seconds) | T-Settling (Seconds) | P-Maximum (KW) | Overshoot Percentage | Efficiency % |
|---|---|---|---|---|---|---|
| FOPI-PI (Proposed) | 16.781 | 0.0012 | 0.015 | 100.714 | 0.0109 | 99.984 |
| FOPI | 16.829 | 0.0013 | 0.094 | 100.708 | 0.0198 | 99.978 |
| PI | 17.442 | 0.0013 | 0.084 | 100.622 | 0.0158 | 99.893 |
| Controller | Fitness Value (ISE) | T-Rising (seconds) | T-Settling (seconds) | P-Maximum (KW) | Overshoot Percentage | Efficiency % |
|---|---|---|---|---|---|---|
| FOPI-PI (Proposed) | 27.905 | 0.0017 | 0.02 | 100.721 | 0.0094 | 99.999 |
| FOPI | 53.471 | 0.0022 | 0.025 | 100.633 | 0.0496 | 99.905 |
| PI | 51.246 | 0.0019 | 0.03 | 100.715 | 0.0148 | 99.995 |
| Controller | Fitness Value (ISE) | T-Rising (Seconds) | T-Settling (Seconds) | P-Maximum (KW) | Overshoot Percentage | Efficiency % |
|---|---|---|---|---|---|---|
| FOPI-PI (Proposed) | 326 | 0.0023 | 0.042 | 101.79 | 0.0124 | 99.993 |
| FOPI | 617 | 0.0027 | 0.055 | 101.75 | 0.0298 | 99.962 |
| PI | 694 | 0.0029 | 0.063 | 101.71 | 0.0243 | 99.947 |
| Controller | Fitness Value (ISE) | T-Rising (Seconds) | T-Settling (Seconds) | P-Maximum (KW) | Overshoot Percentage | Efficiency % |
|---|---|---|---|---|---|---|
| FOPI-PI (Proposed) | 353 | 0.0024 | 0.042 | 96.72 | 0.0131 | 95.385 |
| FOPI | 667 | 0.0029 | 0.055 | 96.68 | 0.0303 | 95.285 |
| PI | 1023 | 0.0031 | 0.063 | 96.46 | 0.0324 | 95.128 |
| Controller | Fitness Value (ISE) | T-Rising (Seconds) | T-Settling (Seconds) | P-Maximum (KW) | Overshoot Percentage | Efficiency % |
|---|---|---|---|---|---|---|
| FOPI-PI (Proposed) | 35.361 | 0.0054 | 0.02 | 100.714 | 0.0117 | 99.984 |
| FOPI | 62.149 | 0.0061 | 0.029 | 100.708 | 0.0139 | 99.978 |
| PI | 57.504 | 0.0063 | 0.024 | 100.622 | 0.0148 | 99.893 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AboRas, K.M.; Alhazmi, A.H.; Megahed, A.I. Optimal Incremental Conductance-Based MPPT Control Methodology for a 100 KW Grid-Connected PV System Employing the RUNge Kutta Optimizer. Sustainability 2025, 17, 5841. https://doi.org/10.3390/su17135841
AboRas KM, Alhazmi AH, Megahed AI. Optimal Incremental Conductance-Based MPPT Control Methodology for a 100 KW Grid-Connected PV System Employing the RUNge Kutta Optimizer. Sustainability. 2025; 17(13):5841. https://doi.org/10.3390/su17135841
Chicago/Turabian StyleAboRas, Kareem M., Abdullah Hameed Alhazmi, and Ashraf Ibrahim Megahed. 2025. "Optimal Incremental Conductance-Based MPPT Control Methodology for a 100 KW Grid-Connected PV System Employing the RUNge Kutta Optimizer" Sustainability 17, no. 13: 5841. https://doi.org/10.3390/su17135841
APA StyleAboRas, K. M., Alhazmi, A. H., & Megahed, A. I. (2025). Optimal Incremental Conductance-Based MPPT Control Methodology for a 100 KW Grid-Connected PV System Employing the RUNge Kutta Optimizer. Sustainability, 17(13), 5841. https://doi.org/10.3390/su17135841





