Photovoltaic System Performance Under Partial Shading Conditions: Insight into the Roles of Bypass Diode Numbers and Inverter Efficiency Curve
Abstract
1. Introduction
- -
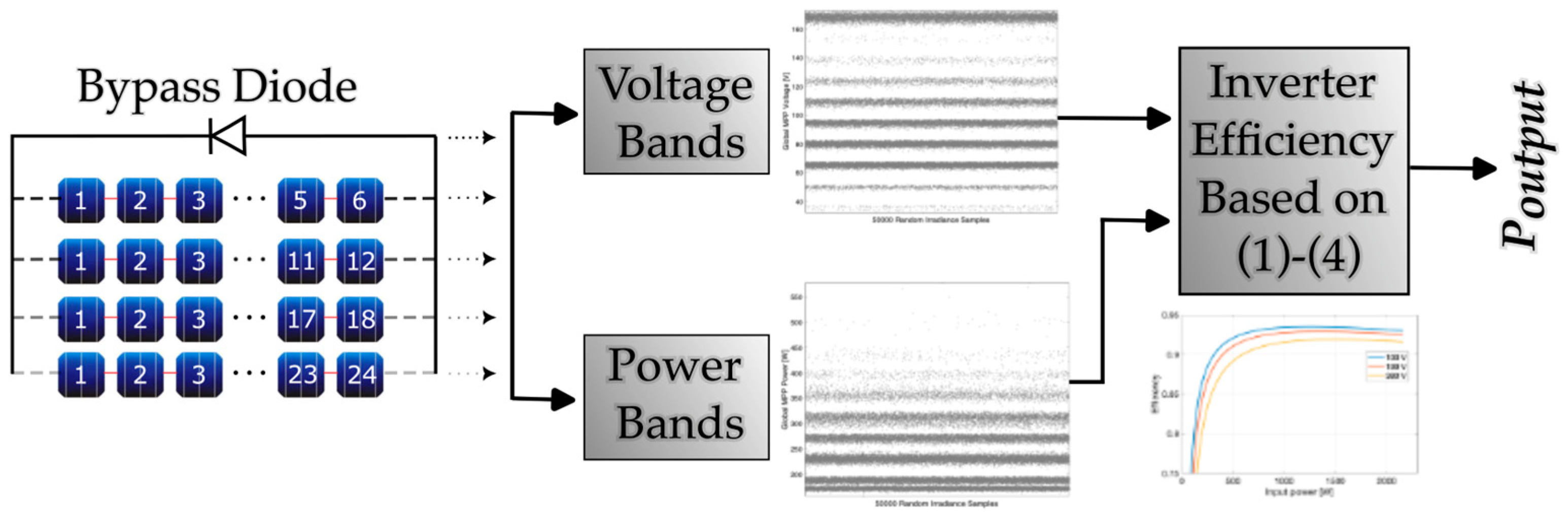
- Bypass diode configuration is systematically analyzed not only for its influence on global MPP power but also for how it shifts operating voltage into different regions of the inverter efficiency curve.
- -
- Three commercial inverters with distinct voltage-dependent efficiency characteristics are modeled to reflect real-world behavior beyond idealized efficiency assumptions.
- -
- A probabilistic framework is used to simulate partial shading scenarios and voltage-band formation, which provides more detailed and comprehensive insight into global MPP distributions.
- -
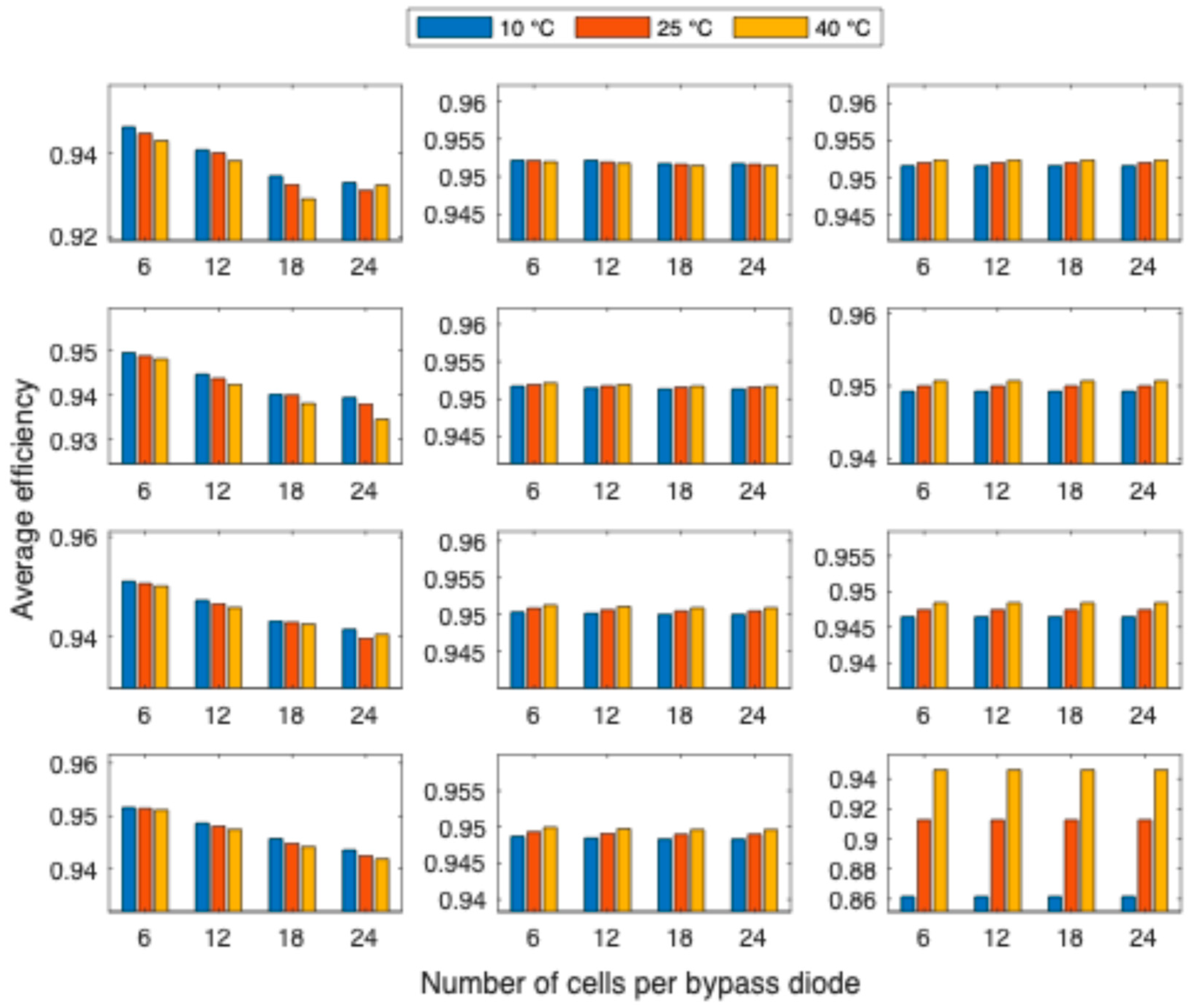
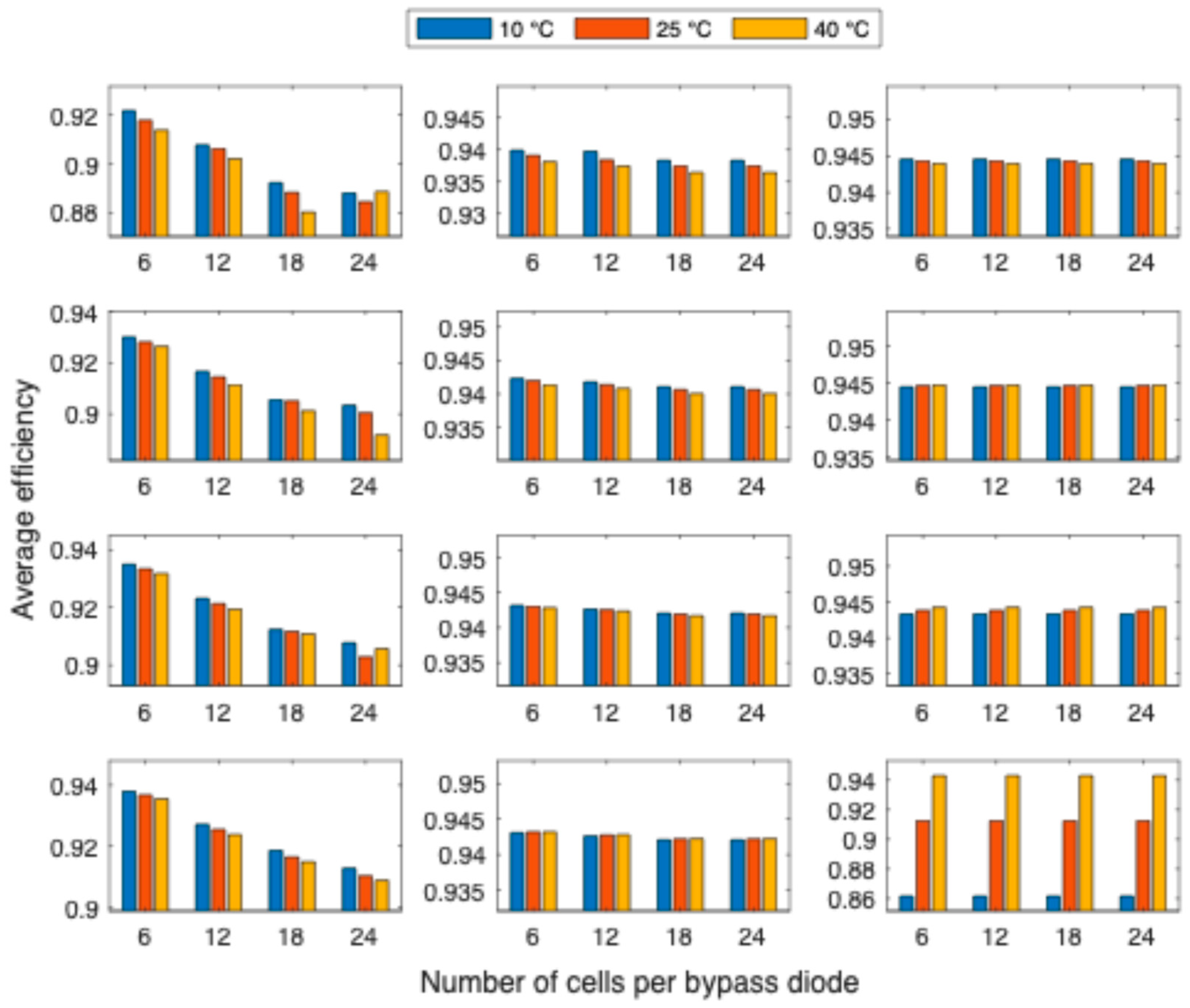
- The interaction between inverter loading ratio (ILR), ambient temperature, and bypass diode number is jointly considered to evaluate how these parameters influence average DC/AC efficiency.
- -
- Voltage-band formation is linked directly to inverter efficiency performance, highlighting the critical importance of considering voltage-dependent efficiency curves in shading-prone environments.
2. Inverter Efficiency Curve in Terms of Input Voltage and Input Power
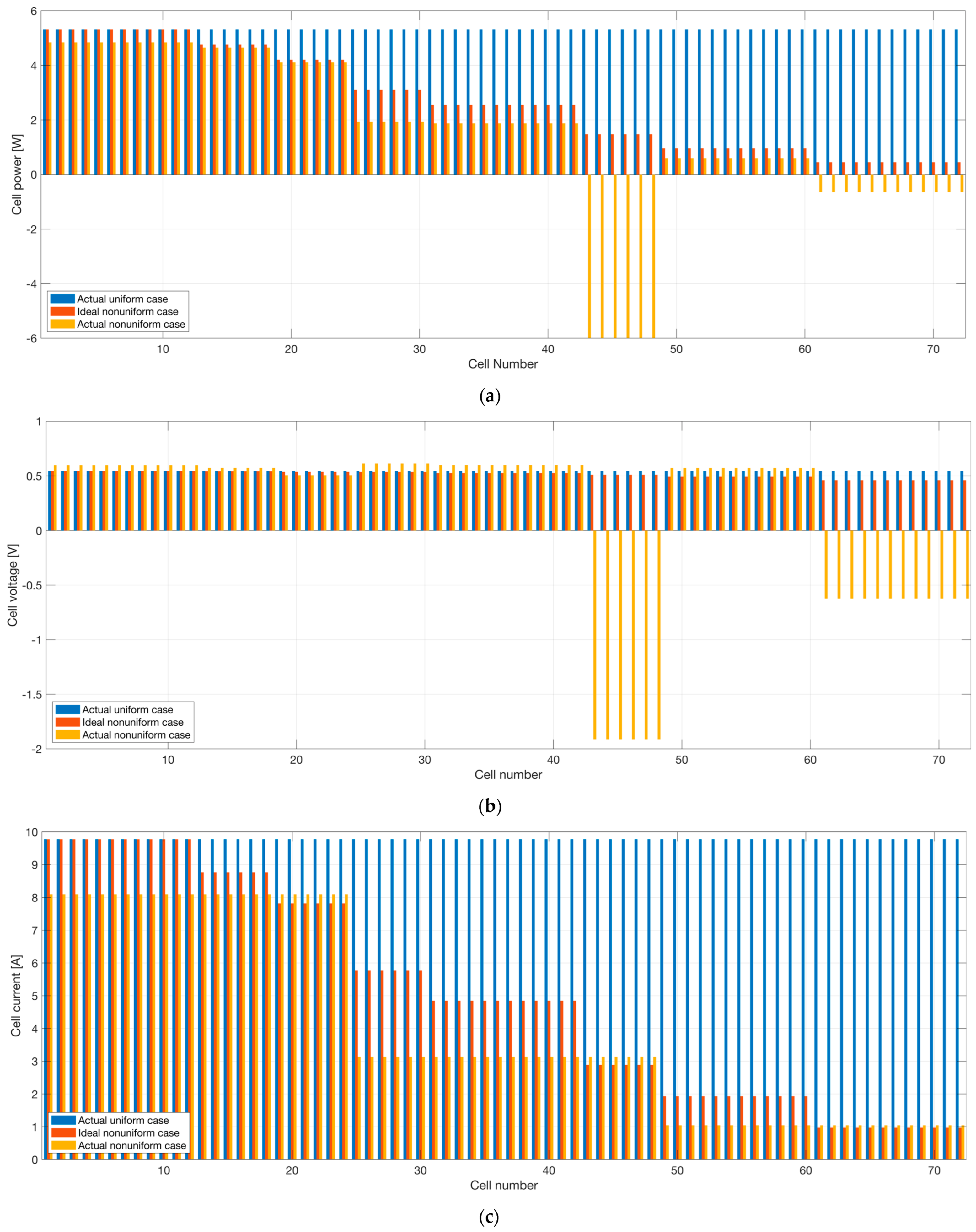
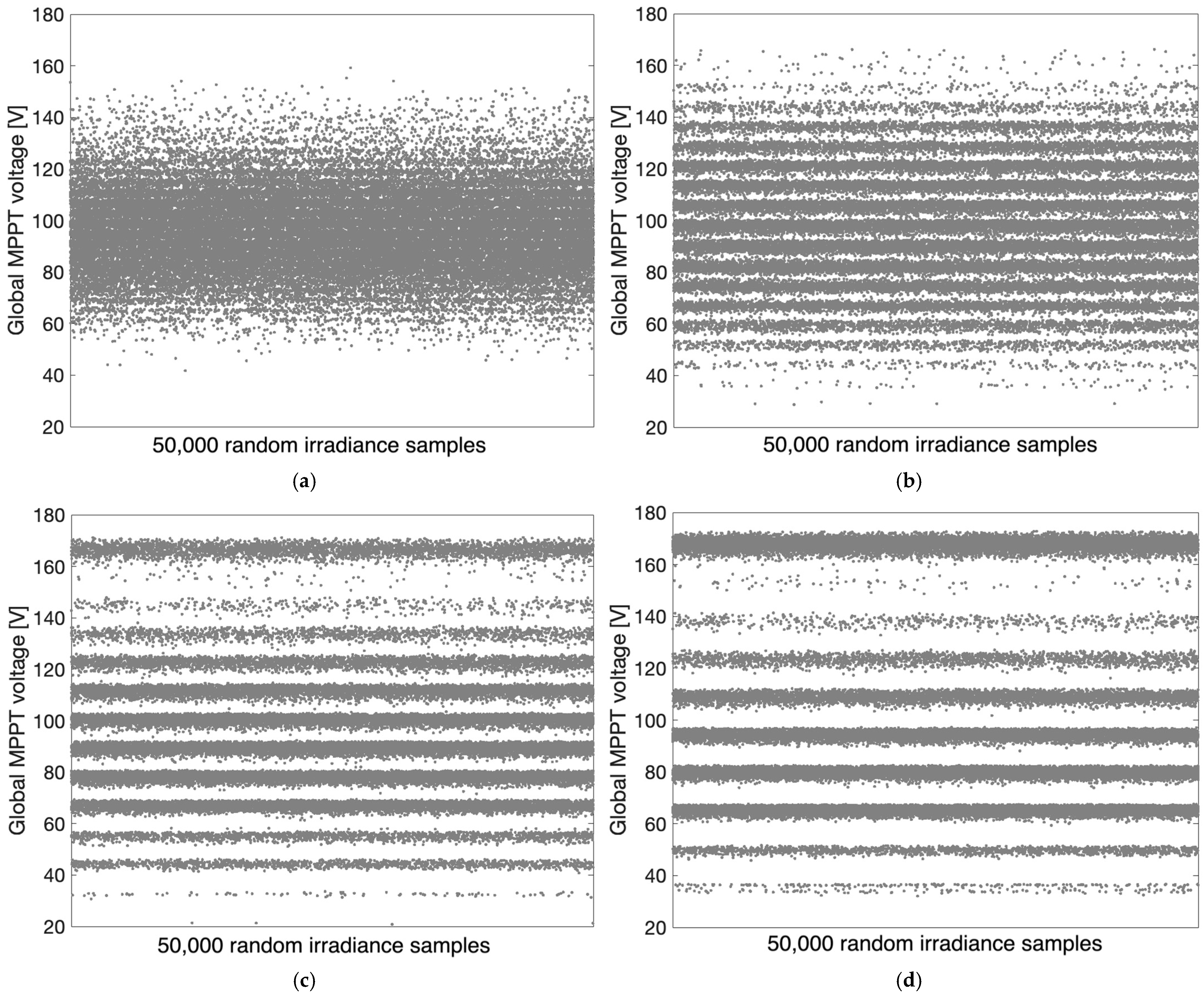
3. Global MPP Voltage and Power with Different Number of Bypass Diodes
- Six cells per bypass diode.
- Twelve cells per bypass diode.
- Eighteen cells per bypass diode.
- Twenty-four cells per bypass diode.
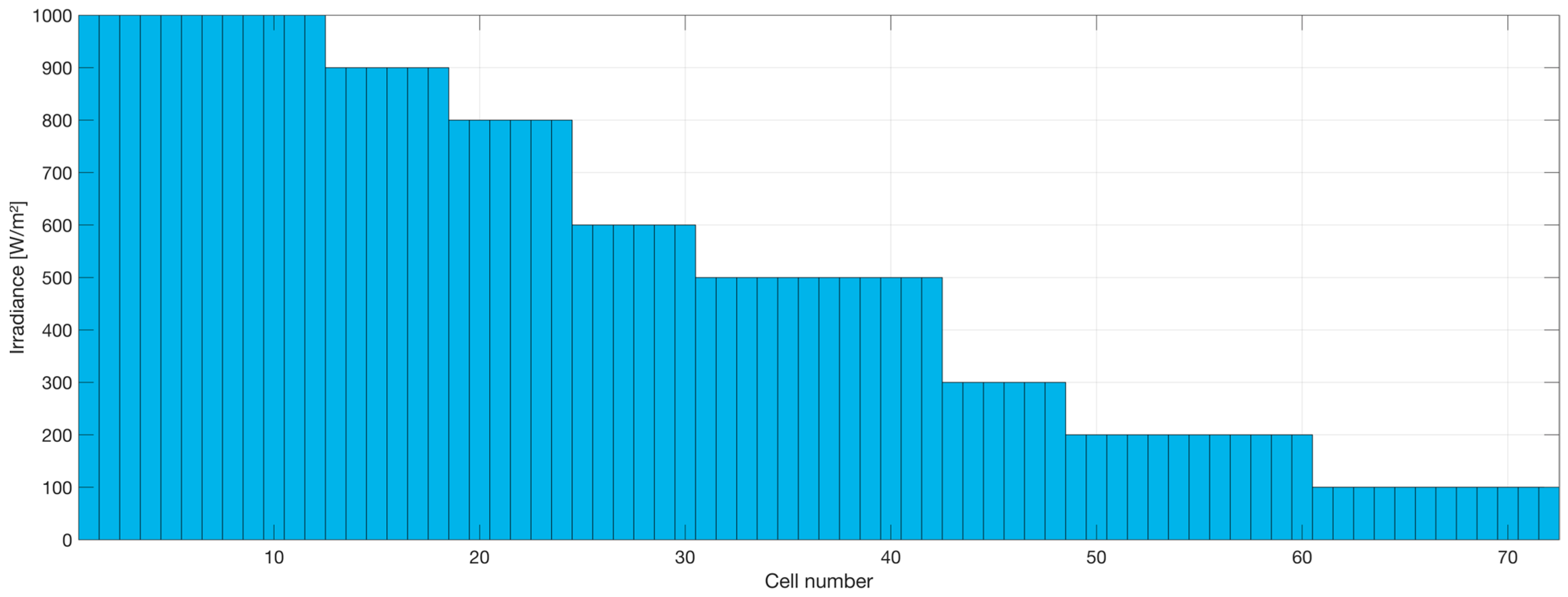
4. Results and Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- IEA. Clean Energy Market Monitor 2024. Available online: https://www.iea.org/reports/clean-energy-market-monitor-march-2024 (accessed on 12 April 2025).
- Hwang, I. Application of photovoltaic systems for rural electrification at remote islands. Sol. Energy Mater. Sol. Cells 1997, 47, 295–302. [Google Scholar] [CrossRef]
- Razmjoo, A.; Ghazanfari, A.; Østergaard, P.A.; Abedi, S. Design and analysis of grid-connected solar photovoltaic systems for sustainable development of remote areas. Energies 2023, 16, 3181. [Google Scholar] [CrossRef]
- Rana, M.M.; Uddin, M.; Sarkar, M.R.; Shafiullah, G.M.; Mo, H.; Atef, M. A review on hybrid photovoltaic–battery energy storage system: Current status, challenges, and future directions. J. Energy Storage 2022, 51, 104597. [Google Scholar] [CrossRef]
- Sinha, S.; Chandel, S.S. Review of recent trends in optimization techniques for solar photovoltaic–wind based hybrid energy systems. Renew. Sustain. Energy Rev. 2015, 50, 755–769. [Google Scholar] [CrossRef]
- Chen, S.; Li, P.; Brady, D.; Lehman, B. Determining the optimum grid-connected photovoltaic inverter size. Sol. Energy 2013, 87, 96–116. [Google Scholar] [CrossRef]
- Aribia, H.B.; El-Rifaie, A.M.; Tolba, M.A.; Shaheen, A.; Moustafa, G.; Elsayed, F.; Elshahed, M. Growth optimizer for parameter identification of solar photovoltaic cells and modules. Sustainability 2023, 15, 7896. [Google Scholar] [CrossRef]
- Peippo, K.; Lund, P.D. Optimal sizing of solar array and inverter in grid-connected photovoltaic systems. Sol. Energy Mater. Sol. Cells 1994, 32, 95–114. [Google Scholar] [CrossRef]
- Rodrigo, P.M.; Velázquez, R.; Fernández, E.F. DC/AC conversion efficiency of grid-connected photovoltaic inverters in central Mexico. Sol. Energy 2016, 139, 650–665. [Google Scholar] [CrossRef]
- Vaicys, J.; Norkevicius, P.; Baronas, A.; Gudzius, S.; Jonaitis, A.; Peftitsis, D. Efficiency evaluation of the dual system power inverter for on-grid photovoltaic system. Energies 2022, 15, 161. [Google Scholar] [CrossRef]
- Munoz, J.; Martinez-Moreno, F.; Lorenzo, E. On-site characterisation and energy efficiency of grid-connected PV inverters. Prog. Photovolt. Res. Appl. 2011, 19, 192–201. [Google Scholar] [CrossRef]
- Krauter, S.; Bendfeld, J. Efficiency ranking of photovoltaic microinverters and energy yield estimations for photovoltaic balcony power plants. Energies 2024, 17, 5551. [Google Scholar] [CrossRef]
- Fernandes, P.; Reis, A.; Velasco, L.N.; Francisco, T.M.; Resende, E.C.; Freitas, L.C.G. Evaluation of a grid-connected photovoltaic system at the university of Brasília based on Brazilian Standard for performance monitoring and analysis. Sustainability 2024, 16, 11212. [Google Scholar] [CrossRef]
- Ketjoy, N.; Chamsa-ard, W.; Mensin, P. Analysis of factors affecting efficiency of inverters: Case study grid-connected PV systems in lower northern region of Thailand. Energy Rep. 2021, 7, 3857–3868. [Google Scholar] [CrossRef]
- Notton, G.; Lazarov, V.; Stoyanov, L. Optimal sizing of a grid-connected PV system for various PV module technologies and inclinations, inverter efficiency characteristics and locations. Renew. Energy 2010, 35, 541–554. [Google Scholar] [CrossRef]
- Sarniak, M.T. Researches of the impact of the nominal power ratio and environmental conditions on the efficiency of the photovoltaic system: A case study for Poland in Central Europe. Sustainability 2020, 12, 6162. [Google Scholar] [CrossRef]
- Mondol, J.D.; Yohanisa, Y.G.; Norton, B. Optimal sizing of array and inverter for grid-connected photovoltaic systems. Sol. Energy 2006, 80, 1517–1539. [Google Scholar] [CrossRef]
- Wang, H.X.; Munoz-García, M.A.; Moreda, G.P.; Alonso-García, M.C. Optimum inverter sizing of grid-connected photovoltaic systems based on energetic and economic considerations. Renew. Energy 2018, 118, 709–717. [Google Scholar] [CrossRef]
- Burger, B.; Rüther, R. Inverter sizing of grid-connected photovoltaic systems in the light of local solar resource distribution characteristics and temperature. Sol. Energy 2006, 80, 32–45. [Google Scholar] [CrossRef]
- Väisänen, J.; Kosonen, A.; Ahola, J.; Sallinen, T.; Hannula, T. Optimal sizing ratio of a solar PV inverter for minimizing the levelized cost of electricity in Finnish irradiation conditions. Sol. Energy 2019, 185, 350–362. [Google Scholar] [CrossRef]
- Deschamps, E.M.; Rüther, R. Optimization of inverter loading ratio for grid-connected photovoltaic systems. Sol. Energy 2019, 179, 106–118. [Google Scholar] [CrossRef]
- Balfour, J.; Hill, R.; Walker, A.; Robinson, G.; Gunda, T.; Desai, J. Masking of photovoltaic system performance problems by inverter clipping and other design and operational practices. Renew. Sustain. Energy Rev. 2021, 145, 111067. [Google Scholar] [CrossRef]
- Good, J.; Johnson, J.X. Impact of inverter loading ratio on solar photovoltaic system performance. Appl. Energy 2016, 177, 475–486. [Google Scholar] [CrossRef]
- Fairbrother, A.; Quest, H.; Özkalay, E.; Wälchli, P.; Friesen, G.; Ballif, C.; Virtuani, A. Long-term performance and shade detection in building integrated photovoltaic systems. Sol. RRL 2022, 6, 2100583. [Google Scholar] [CrossRef]
- Kaushika, N.D.; Mishra, A.; Rai, A.K. Solar Photovoltaics Technology, System Design, Reliability and Viability; Springer: New Delhi, India, 2018. [Google Scholar]
- Strache, S.; Wunderlich, R.; Heinen, S. A comprehensive, quantitative comparison of inverter architectures for various PV systems, PV cells, and irradiance profiles. IEEE Trans. Sustain. Energy 2014, 5, 813–822. [Google Scholar] [CrossRef]
- Matter, K.; El-Khozondar, H.J.; El-Khozondar, R.J.; Suntio, T. Matlab/Simulink modeling to study the effect of partially shaded condition on photovoltaic array’s maximum power point. Int. Res. J. Eng. Technol. 2015, 2, 697–703. [Google Scholar]
- El-Khozondar, H.J.; El-Khozondar, R.J.; Matter, K. Parameters influence on MPP value of the photovoltaic cell. Energy Procedia 2015, 74, 1142–1149. [Google Scholar] [CrossRef]
- Reyes-Suárez, L.I.; Guerrero-Ramírez, G.V.; Mares-Gardea, A.E.; Cervantes-Bobadilla, M.; Adam-Medina, M.; García-Morales, J. Solar energy harvesting under partial shading conditions through a reconfiguration strategy using a multi-port DC–DC converter. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 495. [Google Scholar] [CrossRef]
- Kotti, R.; Shireen, W. Efficient MPPT control for PV systems adaptive to fast changing irradiation and partial shading conditions. Sol. Energy 2015, 114, 397–407. [Google Scholar] [CrossRef]
- Craciunescu, D.; Fara, L. Investigation of the partial shading effect of photovoltaic panels and optimization of their performance based on high-efficiency FLC algorithm. Energies 2023, 16, 1169. [Google Scholar] [CrossRef]
- International Energy Agency Photovoltaics Power System Programme, Task 13. Performance of Partially Shaded PV Generators Operated by Optimized Power Electronics; Report IEA-PVPS T13-27:2024. 2024. Available online: https://iea-pvps.org/wp-content/uploads/2024/11/IEA-PVPS-T13-27-2024.pdf (accessed on 10 May 2025).
- Silvestre, S.; Boronat, A.; Chouder, A. Study of bypass diodes configuration on PV modules. Appl. Energy 2009, 86, 1632–1640. [Google Scholar] [CrossRef]
- Yadav, A.S.; Mukherjee, V. Comprehensive investigation of various bypass diode associations for killer-SuDoKu PV array under several shading conditions. Energy 2022, 239, 122014. [Google Scholar] [CrossRef]
- Daliento, S.; Di Napoli, F.; Guerriero, P.; d’Alessandro, V. A modified bypass circuit for improved hot spot reliability of solar panels subject to partial shading. Sol. Energy 2016, 134, 211–218. [Google Scholar] [CrossRef]
- Bauwens, P.; Doutreloigne, J. NMOS-based integrated modular bypass for use in solar systems (NIMBUS): Intelligent bypass for reducing partial shading power loss in solar panel applications. Energies 2016, 9, 450. [Google Scholar] [CrossRef]
- Zheng, H.; Li, S.; Challoo, R.; Proano, J. Shading and bypass diode impacts to energy extraction of PV arrays under different converter configurations. Renew. Energy 2014, 68, 58–66. [Google Scholar] [CrossRef]
- Fauzan, L.; Sim, Y.H.; Yun, M.J.; Choi, H.; Lee, D.Y.; Cha, S.I. Power from shaded photovoltaic modules through bypass-diode-assisted small-area high-voltage structures. Renew. Sustain. Energy Rev. 2025, 208, 115047. [Google Scholar] [CrossRef]
- Azad, M.A.; Tariq, M.; Sarwar, A.; Sajid, I.; Ahmad, S.; Bakhsh, F.I.; Sayed, A.E. A particle swarm optimization–adaptive weighted delay velocity-based fast-converging maximum power point tracking algorithm for solar PV generation system. Sustainability 2023, 15, 15335. [Google Scholar] [CrossRef]
- Demoulias, C. A new simple analytical method for calculating the optimum inverter size in grid-connected PV plants. Electr. Power Syst. Res. 2010, 80, 1197–1204. [Google Scholar] [CrossRef]
- Chouder, A.; Silvestre, S.; Sadaoui, N.; Rahmani, L. Modeling and simulation of a grid connected PV system based on the evaluation of main PV module parameters. Simul. Model. Pract. Theory 2012, 20, 46–58. [Google Scholar] [CrossRef]
- Scarabelot, L.T.; Rambo, C.R.; Rampinelli, G.A. A relative power-based adaptive hybrid model for DC/AC average inverter efficiency of photovoltaics systems. Renew. Sustain. Energy Rev. 2018, 92, 470–477. [Google Scholar] [CrossRef]
- Rampinelli, G.A.; Krenzinger, A.; Romero, F.C. Mathematical models for efficiency of inverters used in grid connected photovoltaic systems. Renew. Sustain. Energy Rev. 2014, 34, 578–587. [Google Scholar] [CrossRef]
- King, D.L.; Gonzalez, S.; Galbraith, G.M.; Boyson, W.E. Performance Model for Grid-Connected Photovoltaic Inverters; Sandia Report SAND2007-5036; Sandia National Laboratories (SNL): Albuquerque, NM, USA, 2007. [Google Scholar]
- MathWorks. Solar Cell, MATLAB Documentation. Available online: https://www.mathworks.com/help/sps/ref/solarcell.html (accessed on 3 February 2025).
- Pannebakker, B.B.; de Waal, A.C.; van Sark, W.G.J.H.M. Photovoltaics in the shade: One bypass diode per solar cell revisited. Prog. Photovolt. Res. Appl. 2017, 25, 836–849. [Google Scholar] [CrossRef]
- El-Khozondar, H.J.; El-Khozondar, R.J.; Matter, K.; Suntio, T. A review study of photovoltaic array maximum power tracking algorithms. Renewables 2016, 3, 3. [Google Scholar] [CrossRef]
- Lefevre, B.; Herteleer, B.; De Breucker, S.; Driesen, J. Bayesian inference based MPPT for dynamic irradiance conditions. Sol. Energy 2018, 174, 1153–1162. [Google Scholar] [CrossRef]
- Kumar, M.; Panda, K.P.; Rosas-Caro, J.C.; Valderrabano-Gonzalez, A.; Panda, G. Comprehensive review of conventional and emerging maximum power point tracking algorithms for uniformly and partially shaded solar photovoltaic systems. IEEE Access 2023, 11, 31778–31798. [Google Scholar] [CrossRef]
- Wang, N.; Guo, Y.; Liu, L.; Shao, S. Numerical assessment and optimization of photovoltaic-based 4 hydrogen-oxygen co-production energy system: A machine learning and multi-objective strategy. Renew. Energy 2024, 227, 120483. [Google Scholar] [CrossRef]
- MathWorks. Creating Custom Components, MATLAB Documentation. Available online: https://www.mathworks.com/help/simscape/lang/creating-custom-components.html (accessed on 3 February 2025).
- da Silva, R.M.; Fernandes, J.L.M. Hybrid photovoltaic/thermal (PV/T) solar systems simulation with Simulink/Matlab. Sol. Energy 2010, 84, 1985–1996. [Google Scholar] [CrossRef]
- Alonso Garcia, M.C.; Balenzategui, J.L. Estimation of photovoltaic module yearly temperature and performance based on Nominal Operation Cell Temperature calculations. Renew. Energy 2004, 29, 1997–2010. [Google Scholar] [CrossRef]
- Zeb, K.; Uddin, W.; Khan, M.A.; Ali, Z.; Ali, M.U.; Christofides, N.; Kim, H.J. A comprehensive review on inverter topologies and control strategies for grid connected photovoltaic system. Renew. Sustain. Energy Rev. 2018, 94, 1120–1141. [Google Scholar] [CrossRef]
- Lu, F.; Guo, S.; Walsh, T.M.; Aberle, A.G. Improved PV module performance under partial shading conditions. Energy Procedia 2013, 33, 248–255. [Google Scholar] [CrossRef]
- IEA. Snapshot of Global PV Market 2024. Available online: https://iea-pvps.org/snapshot-reports/snapshot-2024/ (accessed on 3 February 2025).
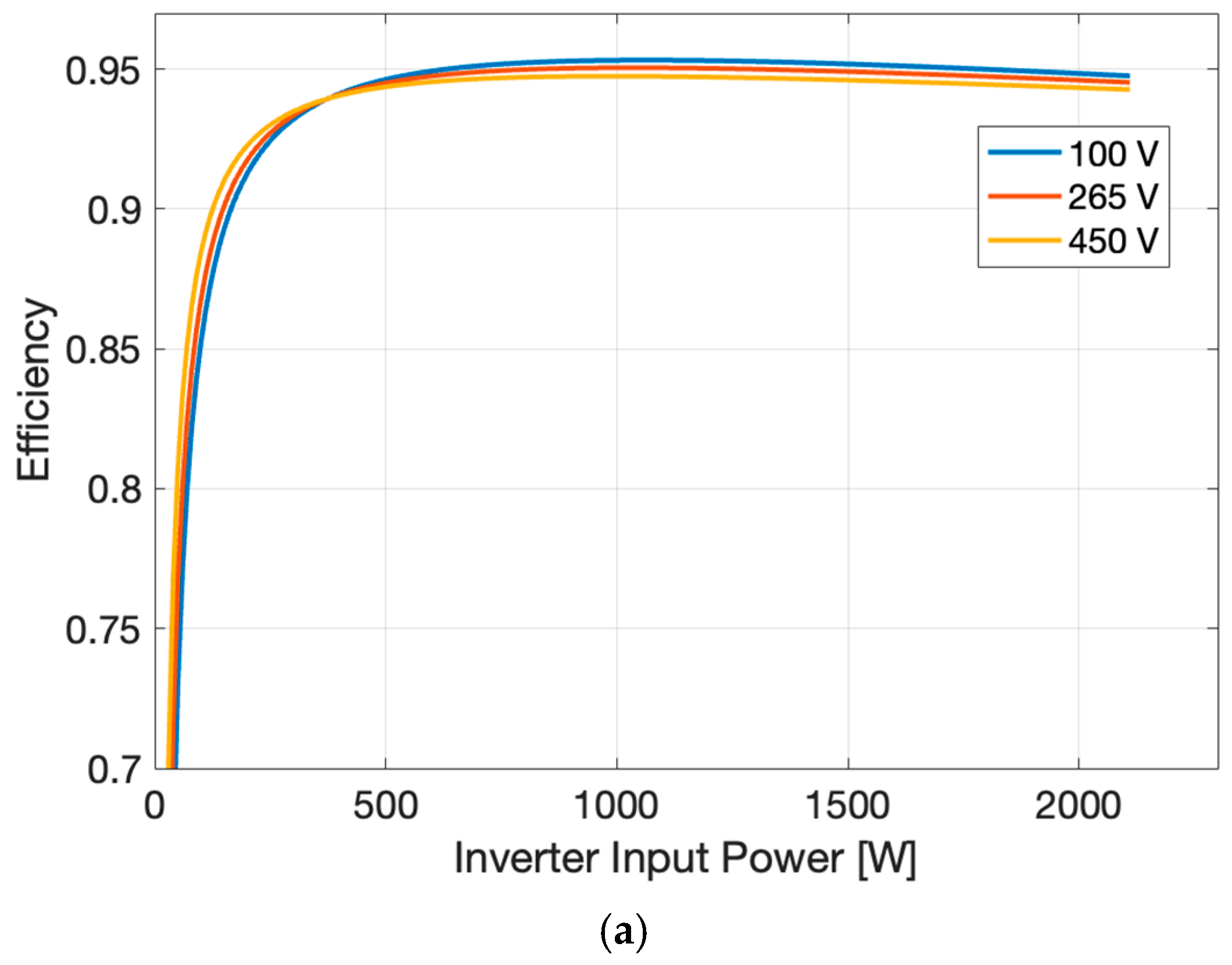
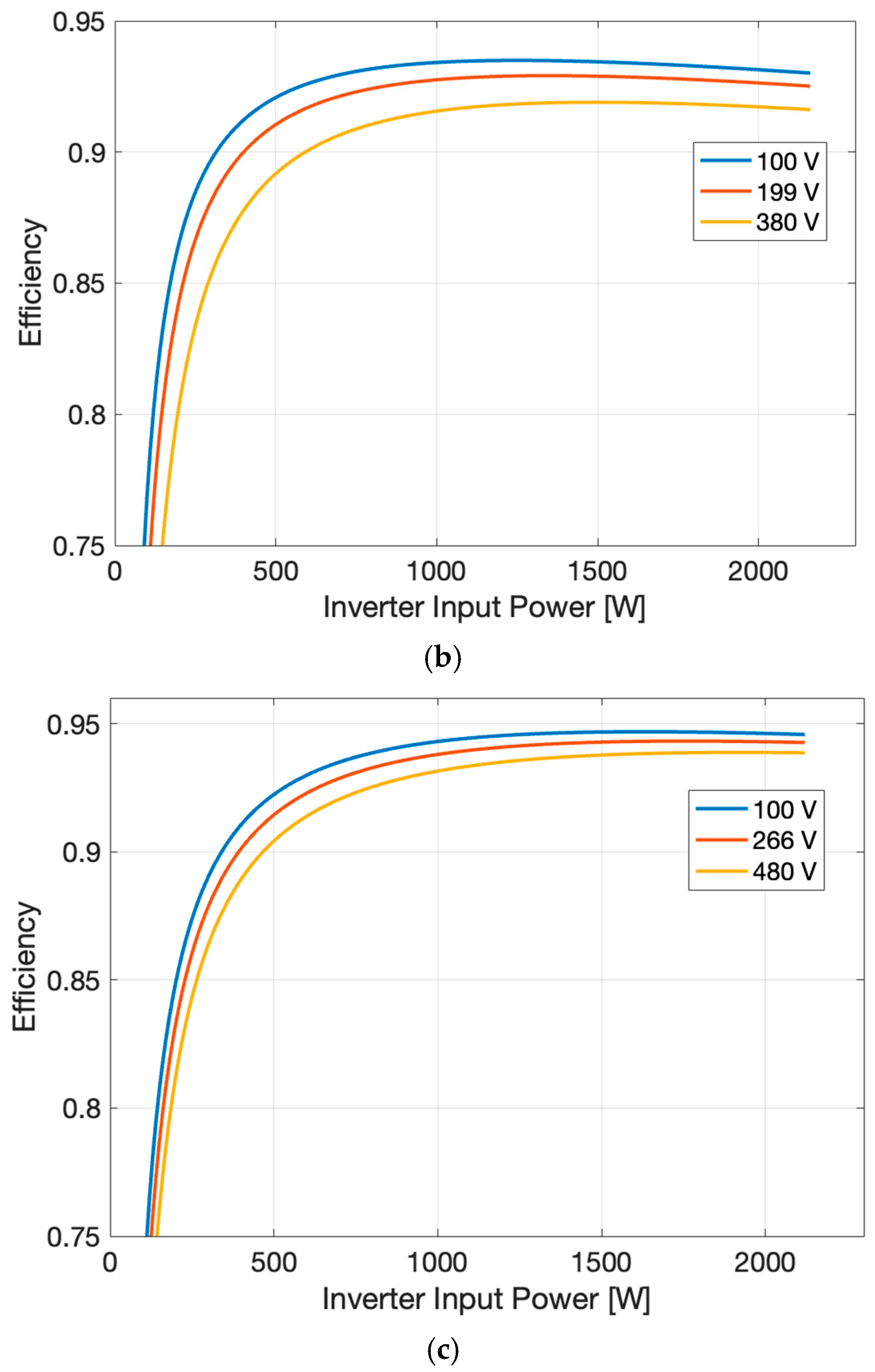

| Parameters | Inverters | ||
|---|---|---|---|
| A | B | C | |
| [W] | 2000 | 2000 | 2000 |
| [W] | 2116 | 2161 | 2122 |
| [1/V] | 0.000015 | 0.000055 | 0.000020 |
| [1/V] | −0.001225 | 0.001703 | 0.000583 |
| [1/V] | −0.000857 | 0.000315 | −0.000317 |
| [W] | 10.484756 | 24.465775 | 28.845461 |
| [V] | 265 | 199 | 266 |
| [1/W] | −9.53044 × 10−6 | −0.000013 | −9.12500 × 10−6 |
| [V] | 100 | 100 | 100 |
| [V] | 450 | 380 | 480 |
| Characteristic | Value |
|---|---|
| 405 | |
| 50.32 | |
| 10.35 | |
| 41.70 | |
| 9.72 | |
| 72 | |
| −0.30 | |
| 0.06 | |
| 45 |
| Number of Modules | Heavily Shaded Condition | Moderately Shaded Condition | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 4 | 0.10 (105, 498) 0.10 (101, 485) 0.09 (97, 478) 0.09 (109, 513) 0.08 (93, 477) 0.08 (114, 529) 0.07 (89, 477) 0.06 (118, 546) 0.06 (85, 482) 0.05 (122, 560) | 0.04 (81, 485) 0.04 (78, 477) 0.03 (126, 564) 0.02 (74, 465) 0.02 (130, 564) 0.02 (144, 478) 0.02 (70, 444) 0.02 (63, 411) 0.01 (135, 548) | 0.10 (99, 470) 0.10 (95, 457) 0.10 (91, 451) 0.10 (103, 485) 0.09 (87, 445) 0.08 (107, 501) 0.07 (111, 516) 0.06 (80, 448) 0.06 (83, 445) 0.05 (115, 530) | 0.04 (76, 453) 0.03 (73, 446) 0.03 (119, 533) 0.02 (69, 431) 0.02 (123, 527) 0.02 (136, 448) 0.01 (59, 384) 0.01 (65, 417) 0.01 (127, 515) | 0.11 (92, 442) 0.11 (89, 430) 0.10 (85, 420) 0.09 (96, 456) 0.09 (100, 471) 0.08 (81, 413) 0.07 (78, 416) 0.07 (104, 486) 0.05 (74, 415) 0.05 (108, 498) | 0.03 (111, 500) 0.03 (71, 418) 0.03 (67, 412) 0.02 (128, 418) 0.02 (115, 493) 0.02 (64, 403) 0.01 (119, 472) 0.01 (60, 386) 0.01 (55, 356) | 0.80 (172, 880) 0.08 (149, 914) 0.05 (146, 898) 0.04 (153, 939) 0.02 (157, 964) 0.01 (132, 939) | 0.82 (162, 835) 0.07 (141, 867) 0.04 (144, 890) 0.04 (138, 854) 0.02 (148, 913) 0.01 (124, 892) | 0.84 (152, 790) 0.09 (131, 815) 0.04 (135, 838) 0.02 (139, 861) 0.01 (118, 839) |
| 5 | 0.09 (132, 618) 0.09 (128, 604) 0.08 (136, 636) 0.08 (123, 592) 0.08 (140, 653) 0.07 (119, 586) 0.07 (115, 584) 0.06 (144, 672) 0.05 (111, 591) 0.05 (107, 602) 0.05 (148, 689) | 0.04 (103, 608) 0.03 (152, 703) 0.03 (99, 605) 0.03 (172, 636) 0.02 (84, 539) 0.02 (157, 712) 0.02 (95, 596) 0.02 (91, 576) 0.02 (161, 713) | 0.10 (120, 570) 0.09 (128, 601) 0.09 (124, 583) 0.08 (116, 557) 0.08 (132, 619) 0.07 (112, 550) 0.07 (108, 548) 0.06 (136, 636) 0.05 (104, 551) 0.05 (139, 651) 0.04 (100, 561) | 0.03 (143, 665) 0.03 (97, 566) 0.03 (93, 564) 0.02 (147, 673) 0.02 (89, 555) 0.02 (78, 503) 0.02 (166, 562) 0.02 (151, 668) 0.01 (85, 540) 0.01 (155, 651) | 0.10 (116, 548) 0.10 (112, 534) 0.09 (119, 565) 0.09 (123, 583) 0.08 (108, 522) 0.08 (104, 514) 0.07 (127, 599) 0.06 (97, 511) 0.05 (101, 507) 0.05 (131, 615) 0.04 (93, 518) | 0.04 (77, 492) 0.04 (89, 524) 0.03 (135, 626) 0.02 (154, 530) 0.02 (139, 631) 0.02 (85, 520) 0.02 (143, 624) | 0.84 (215, 1101) 0.07 (183, 1125) 0.05 (188, 1148) 0.03 (192, 1176) 0.01 (163, 1161) | 0.85 (203, 1044) 0.06 (173, 1070) 0.05 (177, 1090) 0.03 (181, 1114) 0.02 (185, 1144) | 0.87 (190, 988) 0.05 (166, 1028) 0.04 (162, 1012) 0.03 (171, 1058) 0.01 (145, 1038) |
| 6 | 0.09 (162, 758) 0.08 (154, 723) 0.08 (150, 709) 0.08 (158, 739) 0.07 (166, 778) 0.06 (146, 696) 0.06 (171, 796) 0.06 (141, 693) 0.05 (107, 684) 0.05 (137, 692) | 0.05 (175, 815) 0.04 (133, 707) 0.04 (179, 833) 0.03 (129, 720) 0.03 (125, 729) 0.03 (199, 810) 0.03 (121, 735) 0.03 (183, 850) 0.02 (117, 727) 0.02 (187, 861) | 0.09 (145, 682) 0.09 (149, 699) 0.08 (153, 717) 0.08 (141, 669) 0.07 (156, 735) 0.07 (137, 656) 0.06 (161, 754) 0.06 (133, 652) 0.05 (129, 645) 0.05 (165, 772) | 0.05 (184, 773) 0.04 (125, 661) 0.04 (169, 789) 0.04 (100, 637) 0.03 (121, 672) 0.03 (117, 676) 0.03 (173, 804) 0.02 (113, 685) 0.02 (109, 677) | 0.09 (137, 649) 0.09 (141, 667) 0.09 (133, 633) 0.08 (145, 686) 0.08 (129, 620) 0.07 (149, 703) 0.07 (125, 610) 0.07 (99, 615) 0.06 (153, 721) 0.06 (121, 603) | 0.04 (117, 608) 0.04 (157, 738) 0.04 (177, 697) 0.04 (113, 616) 0.03 (161, 756) 0.03 (109, 626) 0.02 (165, 762) | 0.85 (258, 1320) 0.07 (220, 1351) 0.05 (226, 1384) 0.02 (233, 1428) 0.01 (195, 1393) | 0.87 (244, 1253) 0.07 (208, 1286) 0.05 (215, 1328) 0.01 (185, 1323) | 0.89 (229, 1185) 0.07 (196, 1221) 0.03 (203, 1260) 0.01 (174, 1253) |
| 7 | 0.08 (189, 881) 0.08 (180, 844) 0.08 (185, 862) 0.07 (176, 828) 0.07 (193, 900) 0.06 (197, 920) 0.06 (172, 812) 0.05 (168, 804) 0.05 (164, 799) 0.05 (201, 939) 0.04 (206, 958) 0.04 (156, 816) | 0.03 (160, 804) 0.03 (151, 837) 0.03 (210, 976) 0.03 (121, 782) 0.03 (147, 854) 0.02 (230, 954) 0.02 (143, 863) 0.02 (214, 993) 0.02 (139, 864) 0.02 (135, 859) 0.01 (131, 837) 0.01 (218, 1009) | 0.08 (173, 816) 0.08 (169, 798) 0.08 (177, 834) 0.08 (166, 781) 0.07 (181, 852) 0.06 (162, 768) 0.06 (185, 871) 0.06 (158, 757) 0.05 (189, 889) 0.05 (154, 750) 0.04 (119, 764) 0.04 (150, 756) | 0.04 (193, 908) 0.04 (213, 909) 0.03 (146, 763) 0.03 (197, 926) 0.03 (142, 774) 0.02 (138, 793) 0.02 (134, 804) 0.02 (201, 941) 0.02 (130, 802) | 0.09 (162, 766) 0.09 (166, 785) 0.08 (158, 748) 0.08 (154, 732) 0.08 (170, 803) 0.07 (150, 716) 0.06 (174, 821) 0.06 (146, 707) 0.05 (178, 840) 0.05 (142, 699) 0.04 (182, 858) 0.04 (138, 704) | 0.03 (134, 708) 0.03 (186, 875) 0.03 (130, 723) 0.02 (109, 703) 0.02 (207, 805) 0.02 (126, 737) 0.02 (190, 891) 0.02 (122, 746) 0.01 (194, 892) 0.01 (118, 740) | 0.87 (302, 1540) 0.08 (258, 1580) 0.04 (267, 1633) 0.01 (226, 1609) | 0.89 (284, 1463) 0.08 (244, 1504) 0.03 (252, 1555) | 0.91 (267, 1383) 0.07 (229, 1425) 0.02 (238, 1474) |
| Number of Modules | Heavily Shaded Condition | Moderately Shaded Condition | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 4 | 0.12 (104, 350) 0.11 (87, 370) 0.11 (95, 366) 0.11 (120, 352) 0.10 (112, 345) 0.10 (79, 352) 0.09 (128, 368) 0.07 (71, 330) | 0.06 (136, 388) 0.04 (63, 313) 0.04 (144, 410) 0.02 (55, 290) 0.01 (152, 431) 0.01 (45, 259) 0.01 (163, 420) | 0.12 (98, 330) 0.11 (82, 348) 0.11 (113, 333) 0.11 (106, 327) 0.10 (90, 345) 0.10 (74, 332) 0.09 (121, 350) 0.07 (67, 311) | 0.06 (128, 368) 0.04 (136, 390) 0.04 (59, 294) 0.02 (52, 271) 0.01 (144, 410) 0.01 (154, 398) 0.01 (42, 240) | 0.12 (92, 311) 0.11 (99, 308) 0.11 (106, 315) 0.11 (77, 324) 0.10 (84, 325) 0.10 (114, 330) 0.09 (70, 311) 0.07 (62, 291) | 0.06 (121, 348) 0.04 (128, 368) 0.03 (55, 275) 0.02 (135, 388) 0.01 (48, 252) 0.01 (39, 222) 0.01 (142, 409) 0.01 (151, 297) | 0.98 (173, 882) 0.01 (154, 943) 0.01 (148, 910) | 0.99 (163, 838) 0.01 (143, 884) | 0.99 (153, 792) 0.01 (135, 838) |
| 5 | 0.10 (140, 418) 0.10 (149, 428) 0.09 (107, 464) 0.09 (99, 446) 0.09 (124, 439) 0.08 (132, 420) 0.08 (115, 464) 0.08 (156, 447) 0.07 (164, 468) | 0.06 (91, 423) 0.04 (172, 489) 0.04 (83, 396) 0.02 (180, 512) 0.02 (75, 374) 0.01 (188, 534) 0.01 (67, 354) 0.01 (200, 534) 0.01 (57, 327) | 0.10 (132, 396) 0.10 (140, 405) 0.09 (101, 436) 0.09 (125, 397) 0.09 (117, 415) 0.08 (148, 425) 0.08 (108, 438) 0.08 (93, 421) 0.07 (155, 444) | 0.06 (85, 399) 0.05 (163, 465) 0.04 (78, 372) 0.02 (170, 487) 0.02 (70, 350) 0.01 (60, 324) 0.01 (178, 508) 0.01 (189, 507) | 0.10 (131, 383) 0.10 (124, 372) 0.09 (117, 373) 0.09 (94, 409) 0.09 (109, 391) 0.09 (139, 401) 0.08 (101, 410) 0.08 (87, 396) 0.07 (146, 420) | 0.06 (80, 373) 0.05 (153, 440) 0.03 (73, 348) 0.02 (160, 461) 0.02 (66, 327) 0.02 (170, 479) 0.01 (56, 306) | 0.99 (216, 1102) 0.01 (190, 1163) | 0.99 (203, 1047) 0.01 (178, 1100) | 0.99 (191, 990) 0.01 (168, 1041) |
| 6 | 0.09 (169, 491) 0.08 (177, 506) 0.08 (185, 526) 0.08 (161, 485) 0.07 (127, 565) 0.07 (119, 541) 0.07 (135, 567) 0.07 (193, 547) 0.07 (144, 540) 0.06 (153, 500) | 0.06 (111, 514) 0.05 (200, 570) 0.04 (103, 485) 0.03 (208, 593) 0.02 (95, 455) 0.02 (83, 436) 0.02 (217, 615) 0.01 (224, 637) 0.01 (235, 657) | 0.09 (167, 480) 0.09 (174, 499) 0.09 (159, 464) 0.08 (152, 458) 0.07 (119, 532) 0.07 (182, 521) 0.07 (111, 511) 0.07 (127, 534) 0.07 (135, 512) 0.06 (144, 472) | 0.06 (104, 485) 0.05 (189, 542) 0.04 (97, 457) 0.03 (197, 564) 0.02 (89, 429) 0.02 (205, 586) 0.01 (78, 409) 0.01 (216, 612) | 0.09 (156, 454) 0.09 (149, 439) 0.09 (164, 472) 0.08 (142, 434) 0.07 (171, 492) 0.07 (111, 499) 0.07 (119, 502) 0.07 (135, 441) 0.07 (104, 480) 0.07 (127, 480) | 0.06 (97, 455) 0.05 (178, 512) 0.03 (90, 428) 0.03 (185, 533) 0.02 (83, 402) 0.02 (192, 554) 0.01 (73, 384) 0.01 (203, 580) | 0.99 (259, 1323) 0.01 (226, 1384) | 0.99 (244, 1256) 0.01 (213, 1316) | 0.99 (229, 1188) 0.01 (201, 1247) |
| 7 | 0.08 (205, 585) 0.08 (213, 606) 0.07 (197, 567) 0.07 (189, 555) 0.07 (221, 628) 0.07 (139, 639) 0.06 (146, 665) 0.06 (154, 668) 0.06 (131, 609) 0.06 (164, 647) | 0.05 (181, 560) 0.05 (229, 650) 0.05 (173, 591) 0.04 (123, 575) 0.04 (237, 673) 0.03 (115, 544) 0.02 (102, 514) 0.02 (245, 695) 0.02 (257, 729) | 0.08 (193, 555) 0.08 (201, 575) 0.08 (186, 537) 0.07 (178, 527) 0.07 (208, 596) 0.07 (154, 605) 0.06 (130, 604) 0.06 (137, 626) 0.06 (123, 575) 0.06 (216, 618) | 0.05 (171, 526) 0.05 (145, 644) 0.05 (163, 557) 0.04 (115, 542) 0.04 (224, 640) 0.02 (108, 513) 0.02 (231, 661) 0.02 (242, 692) 0.01 (101, 489) 0.01 (90, 475) | 0.09 (181, 525) 0.09 (189, 544) 0.08 (174, 508) 0.07 (196, 564) 0.07 (167, 494) 0.06 (128, 588) 0.06 (144, 567) 0.06 (160, 498) 0.06 (121, 568) 0.05 (152, 531) | 0.05 (203, 585) 0.05 (135, 600) 0.05 (115, 540) 0.04 (210, 606) 0.04 (108, 508) 0.02 (217, 626) 0.02 (228, 656) 0.02 (101, 480) 0.02 (90, 452) | 0.99 (302, 1543) 0.01 (263, 1611) | 0.99 (285, 1466) 0.01 (249, 1536) | 0.99 (267, 1386) 0.01 (235, 1459) |
| Number of Modules | Heavily Shaded Condition | Moderately Shaded Condition | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 4 | 0.18 (95, 284) 0.17 (83, 266) 0.15 (106, 309) 0.13 (71, 250) 0.12 (118, 338) 0.07 (176, 184) | 0.06 (130, 370) 0.04 (59, 280) 0.03 (141, 403) 0.03 (47, 231) 0.01 (153, 436) 0.01 (34, 226) | 0.18 (89, 269) 0.17 (78, 252) 0.15 (100, 293) 0.13 (67, 236) 0.12 (112, 322) 0.07 (166, 175) | 0.06 (123, 352) 0.04 (55, 265) 0.03 (134, 383) 0.03 (44, 218) 0.01 (145, 415) 0.01 (32, 211) | 0.18 (84, 254) 0.17 (73, 237) 0.15 (94, 277) 0.13 (62, 221) 0.12 (105, 304) 0.07 (156, 166) | 0.06 (115, 333) 0.04 (51, 249) 0.03 (126, 362) 0.03 (41, 204) 0.01 (136, 393) 0.01 (30, 197) | 1.00 (172, 882) | 1.00 (163, 838) | 1.00 (153, 792) |
| 5 | 0.16 (116, 342) 0.15 (127, 367) 0.14 (104, 325) 0.12 (139, 397) 0.11 (92, 310) 0.09 (151, 430) 0.07 (80, 299) | 0.06 (162, 462) 0.04 (219, 239) 0.03 (68, 320) 0.02 (174, 495) 0.01 (56, 280) 0.01 (186, 529) 0.01 (43, 283) | 0.16 (109, 324) 0.15 (120, 349) 0.14 (98, 307) 0.12 (131, 377) 0.11 (87, 292) 0.09 (142, 408) 0.07 (75, 282) | 0.05 (153, 440) 0.04 (207, 227) 0.03 (63, 302) 0.02 (164, 471) 0.01 (51, 264) 0.01 (175, 503) | 0.16 (113, 330) 0.16 (102, 306) 0.14 (92, 288) 0.13 (123, 357) 0.11 (81, 274) 0.09 (134, 386) 0.07 (71, 266) | 0.05 (144, 416) 0.04 (195, 214) 0.03 (59, 284) 0.02 (154, 446) 0.01 (48, 246) 0.01 (165, 477) | 1.00 (216, 1103) | 1.00 (203, 1047) | 1.00 (191, 990) |
| 6 | 0.15 (148, 427) 0.14 (137, 400) 0.13 (160, 457) 0.12 (125, 381) 0.10 (172, 489) 0.09 (113, 371) 0.07 (184, 522) | 0.06 (101, 361) 0.04 (257, 331) 0.03 (195, 555) 0.03 (88, 414) 0.02 (207, 589) 0.01 (77, 364) 0.01 (64, 318) | 0.15 (140, 405) 0.14 (129, 380) 0.13 (151, 434) 0.12 (118, 360) 0.10 (162, 465) 0.09 (106, 351) 0.07 (173, 496) | 0.06 (95, 338) 0.04 (242, 317) 0.04 (184, 528) 0.02 (83, 391) 0.02 (68, 326) 0.02 (195, 559) | 0.15 (131, 383) 0.14 (121, 358) 0.13 (142, 410) 0.12 (110, 339) 0.10 (152, 439) 0.09 (99, 330) 0.07 (163, 470) | 0.06 (89, 315) 0.04 (228, 300) 0.04 (173, 500) 0.02 (77, 367) 0.02 (63, 307) 0.02 (183, 530) | 1.00 (259, 1323) | 1.00 (244, 1256) | 1.00 (229, 1188) |
| 7 | 0.14 (169, 485) 0.13 (181, 516) 0.13 (158, 458) 0.11 (193, 549) 0.10 (146, 440) 0.09 (204, 582) 0.08 (134, 430) 0.06 (122, 427) | 0.05 (216, 615) 0.03 (110, 436) 0.02 (228, 648) 0.02 (297, 399) 0.02 (97, 459) 0.01 (83, 396) 0.01 (239, 681) | 0.14 (160, 460) 0.13 (171, 490) 0.13 (149, 434) 0.11 (182, 521) 0.10 (137, 417) 0.09 (193, 553) 0.08 (126, 406) 0.06 (115, 401) | 0.05 (204, 585) 0.03 (103, 418) 0.03 (282, 372) 0.02 (215, 616) 0.01 (91, 433) 0.01 (78, 372) 0.01 (226, 648) | 0.14 (150, 435) 0.13 (160, 463) 0.13 (139, 409) 0.11 (171, 493) 0.10 (129, 391) 0.09 (118, 382) 0.08 (181, 523) 0.06 (107, 375) | 0.05 (192, 553) 0.03 (265, 348) 0.03 (96, 398) 0.02 (202, 583) 0.01 (85, 405) 0.01 (212, 614) 0.01 (72, 347) | 1.00 (302, 1543) | 1.00 (285, 1466) | 1.00 (267, 1386) |
| Number of Modules | Heavily Shaded Condition | Moderately Shaded Condition | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 4 | 0.22 (177, 182) 0.21 (85, 249) 0.21 (69, 212) 0.16 (100, 287) 0.10 (115, 330) | 0.04 (131, 372) 0.04 (53, 252) 0.01 (146, 416) 0.01 (38, 199) | 0.22 (168, 173) 0.21 (80, 236) 0.21 (65, 201) 0.16 (94, 273) 0.10 (109, 313) | 0.04 (123, 354) 0.04 (50, 237) 0.01 (138, 395) 0.01 (35, 192) | 0.23 (158, 164) 0.22 (75, 223) 0.21 (61, 190) 0.16 (88, 258) 0.10 (102, 296) | 0.04 (116, 335) 0.03 (45, 218) 0.01 (130, 374) | 1.00 (172, 882) | 1.00 (163, 838) | 1.00 (153, 792) |
| 5 | 0.19 (98, 287) 0.18 (221, 229) 0.18 (114, 326) 0.17 (83, 252) 0.13 (129, 368) | 0.07 (144, 411) 0.03 (160, 455) 0.03 (66, 310) 0.01 (51, 245) 0.01 (175, 498) | 0.19 (209, 218) 0.18 (92, 272) 0.18 (107, 310) 0.17 (78, 238) 0.13 (122, 350) | 0.07 (136, 390) 0.03 (151, 432) 0.03 (62, 292) 0.01 (48, 231) 0.01 (165, 474) | 0.20 (197, 206) 0.19 (87, 257) 0.17 (100, 293) 0.16 (73, 225) 0.13 (114, 331) | 0.07 (128, 369) 0.03 (142, 409) 0.03 (58, 275) 0.01 (44, 218) 0.01 (155, 448) | 1.00 (216, 1102) | 1.00 (203, 1047) | 1.00 (191, 990) |
| 6 | 0.20 (264, 286) 0.18 (127, 365) 0.17 (112, 326) 0.15 (142, 406) 0.10 (158, 450) 0.09 (97, 300) | 0.05 (173, 493) 0.02 (188, 537) 0.02 (79, 372) 0.02 (64, 302) | 0.20 (252, 261) 0.18 (120, 347) 0.17 (105, 308) 0.15 (134, 386) 0.10 (149, 427) 0.08 (91, 288) | 0.05 (163, 469) 0.02 (178, 510) 0.02 (60, 285) 0.02 (74, 352) 0.01 (192, 552) | 0.21 (237, 248) 0.18 (112, 328) 0.17 (99, 291) 0.15 (126, 365) 0.10 (140, 404) 0.07 (85, 276) | 0.06 (154, 444) 0.02 (167, 483) 0.02 (56, 267) 0.01 (69, 330) 0.01 (181, 523) | 1.00 (259, 1323) | 1.00 (244, 1256) | 1.00 (229, 1188) |
| 7 | 0.22 (309, 328) 0.16 (141, 404) 0.15 (125, 364) 0.15 (156, 445) 0.12 (171, 488) 0.08 (187, 532) | 0.04 (202, 575) 0.04 (110, 371) 0.02 (217, 619) 0.01 (92, 432) 0.01 (77, 365) | 0.22 (292, 312) 0.16 (132, 383) 0.16 (118, 345) 0.15 (147, 423) 0.12 (162, 464) 0.08 (176, 505) | 0.04 (191, 547) 0.03 (104, 359) 0.02 (205, 588) 0.01 (87, 408) 0.01 (72, 344) | 0.22 (275, 296) 0.16 (124, 361) 0.16 (111, 326) 0.15 (138, 400) 0.12 (152, 439) 0.08 (165, 478) | 0.04 (179, 517) 0.03 (97, 345) 0.02 (193, 557) 0.01 (81, 383) 0.01 (67, 322) | 1.00 (302, 1543) | 1.00 (285, 1465) | 1.00 (267, 1385) |
| Number of Modules | |||
|---|---|---|---|
| 4 | 1.00 (163, 1327) | 1.00 (153, 1253) | 1.00 (143, 1176) |
| 5 | 1.00 (203, 1658) | 1.00 (191, 1566) | 1.00 (179, 1470) |
| 6 | 1.00 (244, 1990) | 1.00 (229, 1879) | 1.00 (214, 1764) |
| 7 | 1.00 (285, 2321) | 1.00 (267, 2192) | 1.00 (250, 2058) |
| Inverter | Number of Cells per Bypass Diode | Mean (%) | Min (%) | Max (%) |
|---|---|---|---|---|
| A | 6 | 0.3948 | −0.0032 | 1.4654 |
| 12 | 0.2314 | −0.0065 | 0.9659 | |
| 18 | 0.0579 | −0.3520 | 0.3822 | |
| B | 6 | 0.9385 | −0.0032 | 3.2582 |
| 12 | 0.5230 | −0.0065 | 2.0590 | |
| 18 | 0.1307 | −0.8802 | 0.9457 | |
| C | 6 | 1.1066 | −0.0032 | 3.8950 |
| 12 | 0.6262 | −0.0065 | 2.4731 | |
| 18 | 0.1618 | −0.9492 | 1.0628 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sezgin-Ugranlı, H.G. Photovoltaic System Performance Under Partial Shading Conditions: Insight into the Roles of Bypass Diode Numbers and Inverter Efficiency Curve. Sustainability 2025, 17, 4626. https://doi.org/10.3390/su17104626
Sezgin-Ugranlı HG. Photovoltaic System Performance Under Partial Shading Conditions: Insight into the Roles of Bypass Diode Numbers and Inverter Efficiency Curve. Sustainability. 2025; 17(10):4626. https://doi.org/10.3390/su17104626
Chicago/Turabian StyleSezgin-Ugranlı, Hatice Gül. 2025. "Photovoltaic System Performance Under Partial Shading Conditions: Insight into the Roles of Bypass Diode Numbers and Inverter Efficiency Curve" Sustainability 17, no. 10: 4626. https://doi.org/10.3390/su17104626
APA StyleSezgin-Ugranlı, H. G. (2025). Photovoltaic System Performance Under Partial Shading Conditions: Insight into the Roles of Bypass Diode Numbers and Inverter Efficiency Curve. Sustainability, 17(10), 4626. https://doi.org/10.3390/su17104626






