Next Article in Journal
A Hybrid MRA-BN-NN Approach for Analyzing Airport Service Based on User-Generated Contents
Next Article in Special Issue
Effects of PLA-Type and Reinforcement Content on the Mechanical Behavior of Additively Manufactured Continuous Ramie Fiber-Filled Biocomposites
Previous Article in Journal
Enhancing Work Productivity through Generative Artificial Intelligence: A Comprehensive Literature Review
Previous Article in Special Issue
Sustainable Powder-Based Additive Manufacturing Technology
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sustainability
Volume 16
Issue 3
10.3390/su16031167
sustainability-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Incorporation of Defects in Finite Elements to Model Effective Mechanical Properties of Metamaterial Cells Printed by Selective Laser Melting

by
Gonzalo Vera-Rodríguez
1,
Laura Moreno-Corrales
1,
Iván Marín-González
1,
Daniel Barba
1,
Francisco J. Montáns
1,2 and
Miguel Ángel Sanz-Gómez
1,*
1
E.T.S. de Ingeniería Aeronáutica y del Espacio, Universidad Politécnica de Madrid, Pza. Cardenal Cisneros 3, 28040 Madrid, Spain
2
Department of Mechanical and Aerospace Engineering, Herbert Wertheim College of Engineering, University of Florida, Gainesville, FL 32611, USA
*
Author to whom correspondence should be addressed.
Sustainability 2024, 16(3), 1167; https://doi.org/10.3390/su16031167
Submission received: 28 November 2023 / Revised: 22 January 2024 / Accepted: 25 January 2024 / Published: 30 January 2024
(This article belongs to the Special Issue Additive Manufacturing and Sustainable Material Design)
Browse Figures
Versions Notes

Abstract

:
Additively printed mechanical metamaterial structures optimize material, energy and waste, producing more sustainable products. Their introduction in the production workflow depends on having proper tools for accurately predicting their performance. However, the additive manufacturing process incorporates significant defects which result in an important change of the effective properties of the metamaterial cell. Finite element predictions using perfect geometries and nominal base material properties result in important errors which may require excessive uncertainty-related safety design margins. This work presents a methodology to introduce the effect of the most common defects in finite element models to compute the effective mechanical response of different metamaterials printed by Selective Laser Melting. It is shown that even at elastic infinitesimal strains, the defects produce an important change in the effective mechanical capabilities of the metamaterial, which also depend on the type of the metamaterial cell studied and on the type and magnitude of defects. With the proposed methodology, which incorporates the distribution of defects in the finite element model, the predicted mechanical properties of the metamaterial better match the experimental ones. It is shown that the initial discrepancies in the order of 100 % are reduced to an order of 5 % .

1. Introduction

Additive manufacturing (AM) eliminates manufacturing constraints [1] and brings flexibility and new design opportunities with relevant improvements in sustainability [2,3]. For example, it involves substantially less material, may use recyclable AM-grade powder, and it reduces weight in transport with subsequent energy savings. Furthermore, it suits consumer needs, avoiding large batches and storage space while facilitating locally manufactured, on-demand, spare parts [2]. Main features of AM in different fields, including sustainability aspects, may be found in [4,5]. AM is increasingly being used also in more complex fields like biomedicine, tissue engineering or regenerative medicine, allowing the creation of synthetic structures that are motivated in, and are geometrically similar to, existing natural structures in the human body [6,7,8]. Regarding the mechanical properties, we often seek mechanical equivalence more than geometrical equivalence, so a proper quantification of the influence of manufacturing defects in mechanical properties is also crucial in these cases. Mechanical metamaterials are usually 3D printed and play an inherent role not only in the optimal design of components for performance and sustainability, but also in applications like intelligent metamaterials [9,10] and energy harvesting [11,12], among others. Mechanical metamaterials are commonly structured in lattices, which are small repetitive structures (the unit cell) at a smaller scale than the main component. In this work, we focus on metamaterials for mechanical and structural applications [13] manufactured by Selective Laser Melting (SLM).
Though there is no universally accepted definition of metamaterial, metamaterials are considered artificial or engineered “materials” with properties that are rarely present in conventional materials [14,15,16,17]. There are applications of metamaterials for electronics, electromagnetism, sensor devices, optics or heat transmission [18,19,20,21,22,23]. Mechanical metamaterials are usually designed from the geometric repetition of a unit cell in the different directions of the space, creating more complex structures [24,25,26], such as honeycomb sandwiches and plates or other hierarchical structures [27,28,29,30]. Mechanical metamaterials present new or extreme mechanical properties [31,32], like extreme stiffness/density ratios [33,34,35,36], customizable and tunable auxetic behavior [37,38,39], high specific plastic dissipation or fracture propagation improvements [40,41,42,43]. These are also dependent on the different metamaterial scales addressed (macro-/micro-/nano-structures) [44,45,46,47].
Computational methods like computed-aided design and engineering have long been used in the production industry [48]. Mechanical metamaterial structures are typically manufactured by 3D printing, departing from 3D computational virtual models using computer-aided design (CAD) programs and generating printing files [49,50,51] (typically STL). Much more than in other manufacturing methods [52], various studies have shown that the manufacturing process of a mechanical metamaterial influences its final mechanical properties, deviating from the pretended ones [53]. If the structure of the manufactured material is analyzed at both the micro and macro scales, the formation of a series of defects can be observed, such as, for example, porosity or incomplete fusion holes, defects of the microstructure that affect its mechanical properties [54,55,56,57], and geometric deviations from the intended topology [58,59]. These defects depend on factors such as the selected base printing material, the chosen additive manufacturing technique, or the selected parameters in the printing process [60,61].
The origin of defects affecting the effective mechanical properties of a 3D printed metamaterial are classified into four categories [62,63,64,65]:
  • Three-dimensional printing equipment. In a typical Selective Laser Melting (SLM) or powder bed fusion (PBF) procedure, the main elements of the equipment are the laser, the base plate, the powder deposition mechanism and the printing chamber. Defects can be associated with any of them. Regarding the laser, poor calibration can induce several types of defects in the piece such as, for example, unmelted parts, porosity, or low precision [66]. Regarding the relevance of the base plate, defects usually appear due to insufficient thickness in that plate, causing poor heat dissipation between the component and the base plate. In this case, apart from geometric defects, the defects can also consist of cracks of delaminations [67]. The SLM process operates in an inert gas atmosphere, such as argon and nitrogen, needing a chamber. Factors such as the rate of gas filling or even its trajectory may contribute to the appearance of defects that also affect the geometric precision of the piece or the porosity of the printed material [68]. The powder deposition mechanism also contributes to the defects. For example, an uneven deposition of the powder layers causes a bad physical interaction between the laser beam and the material, resulting again in defects, such as porosity [69].
  • Manufacturing sequence interactions. The interaction between the newly deposited powder, the molten powder and the laser beam affects the creation of defects that influence the finish of the piece. These interactions determine the energy density transferred to the material, defined as the applied energy per unit volume to a material during a PBF process. For an SLM process, the energy density E is defined by the following equation [70]:
    E = P V h t J mm 3
    where P is the laser power (W), V is the scan speed ( mm / s ), h is the span spacing ( mm ), and t is the layer thickness ( mm ). There is a relationship between the energy density and the final density of the piece. For this reason, combinations between them, allowing final pieces with an adequate density and qualities, are considered [56,71].
  • Deposition materials. The quality of the powders during the manufacturing process is an important factor for the final result of the obtained solid part, affecting both its precision and its quality. The flowability of powder and its apparent density (volumetric density) are two of the characteristics that have a major influence in the final quality. Fewer defects are obtained when spherical and smooth particles are used in the process, with an approximate size of 10–45 μ m in SLM [72].
  • Orientation and preparation of specimen. Two aspects have a crucial impact on the quality and performance of the resulting pieces [73,74]: the printing direction, the specimen orientation, and the auxiliary supports. Orientation has importance in the final properties and in the anisotropy of these properties. Orientation also affects how heat flows towards the base plate. Supports have also this function, along with reducing residual stresses that are created in some parts of the piece.

2. Types of Defects Modeled

Defects can be classified according to their type as shown in [59,62,75,76,77,78]: (1) geometric and dimensional deviations, (2) superficial quality defects as balling or surface oxidation, (3) microstructural porosity or heterogeneity, and (4) mesoscopic mechanical alterations, such as holes, porosity or low strength [76].
In this work geometrical and dimensional deviations, as well as porosity are addressed. Defects are modeled by statistically altering the positions of nodes and performing alterations of thickness (conicity defects). Porosity and micromechanical defects are introduced through equivalent moduli and a related phenomenological law. The proposed procedure to introduce these defects follows.

2.1. Undulations

This type of defect causes a geometric inaccuracy between the CAD model and the final printed model. This inaccuracy is due to the fact that there is a shrinkage and a deformation in the axes of the printed material, which normally can take place in the X Y plane (bed plane), or in the building direction, the Z direction [79,80]. The shrinkage is usually greater in the Z direction than in the X Y plane, and there is also relatively less shrinkage when the nominal dimensions of the piece are larger [81,82,83]. In SLM processes, two types of shrinkage are distinguished: the thermal shrinkage, that is due to the cyclical heating that the part undergoes during the manufacturing process, and the sintering shrinkage due to material densification [84,85,86,87]. Some of the parameters that control this type of defect are the laser power, the scan speed, and the temperature of the bed between the part and the base plate, among others [76,81,88].

2.2. Conicity in the Edges of the Lattice

When a sample is printed, the deposition of the material substrate on it is non-homogeneous, where a greater amount of material at the corners of the edges with respect to their central areas is observed [89]. Imperfections appear in the material due to its non-homogeneity and the impurities affecting the microstructure of the printed material [59,90]. Non-homogeneity may be associated with impurities during the process, the different characteristics of the size of the powder, and the crystallographic textures [65]. Among the many parameters that can contribute to the appearance of this defect is the high-temperature gradient between the laser beam and the deposited powder in relatively short times, causing significant effects in the printed part [70]. Other parameters to consider are the deposition of the powder or its solidification [62,76,91].

2.3. Porosity

This defect consists of voids that appear in some areas of the molten material: on the surface of the piece, between the adjacent layers, or inside a layer. The most frequent location is within layers. Pores may have different sizes, spatial distributions and shapes. Porosity is a critical defect to study because it affects both the performance of the piece (fatigue) and the appearance of cracks in the component [62,65,92]. Many parameters influence porosity during manufacturing, such as the energy density or powder size: the higher the energy density and the smaller the powder size, the lower the resulting porosity. This happens because both factors favor a better sintering and adhesion of the metal powder [76,93].

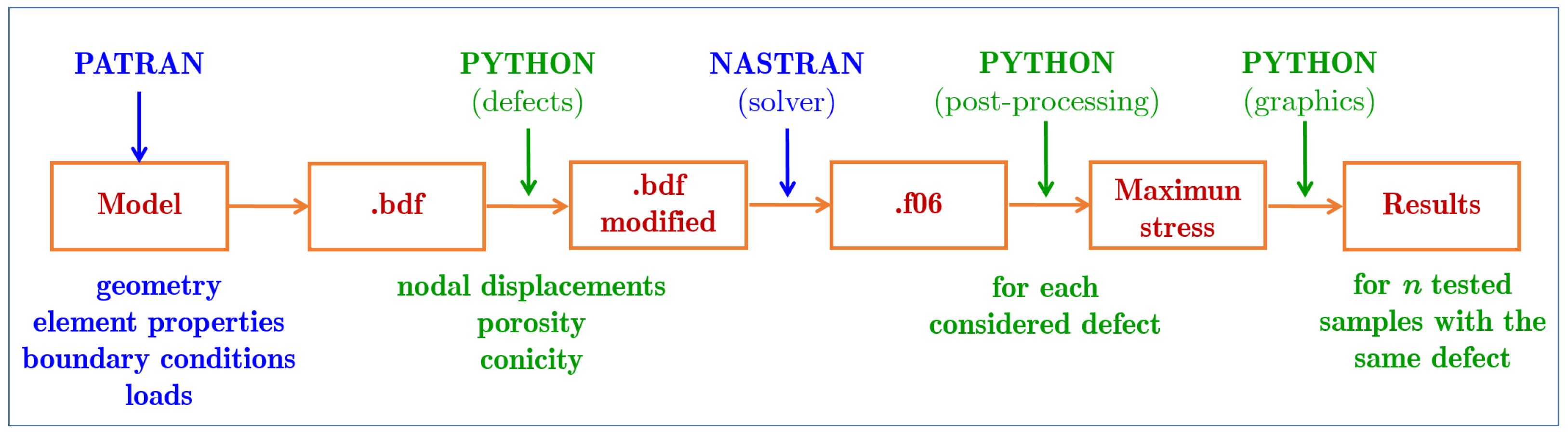
3. Methodology to Model Defects in the Lattice

Defects may be experimentally analyzed and statistically quantified using different techniques [94,95,96,97,98,99]. This section describes a proposal to incorporate them into finite element modeling.
In particular, as just study examples, the methodology to incorporate defects in the model using three different cell types is described here, see Figure 1. The characteristics of each cell type are given in Table 1. These cells, repeated in space, constitute the metamaterial of which testing beams are made. These beams are subjected to a three-point bending test and a four-point bending test, using the Standard Test Method for Flexural Properties of Sandwich Constructions (C393), which follows the ASTM rules [100,101].
The side of the confining cube for each cell shown in Figure 1 is approximately 7 mm and equal for the three. The dimensions of the metamaterial core of the composite beams are 28 × 28 × 300 mm , which means that each core has 4 cells in width, 4 cells in height and 42 cells in length.
For the tests, the beams are simply supported with a span of 300 mm . The loads are applied at the center of the span for the three-point bending test (3Pb). For the four-point bending test (4Pb), two equal loads are located at a quarter of the span from each support, see Figure 2. The testing layout follows the ASTM C393 requirements [100]. This standard provides requirements about the section and the span/height ratio of the beam, which needs specific consideration, considering that the beam is composed of metamaterial cells.
Table 1. Characteristics of the unit cells chosen.
Table 1. Characteristics of the unit cells chosen.
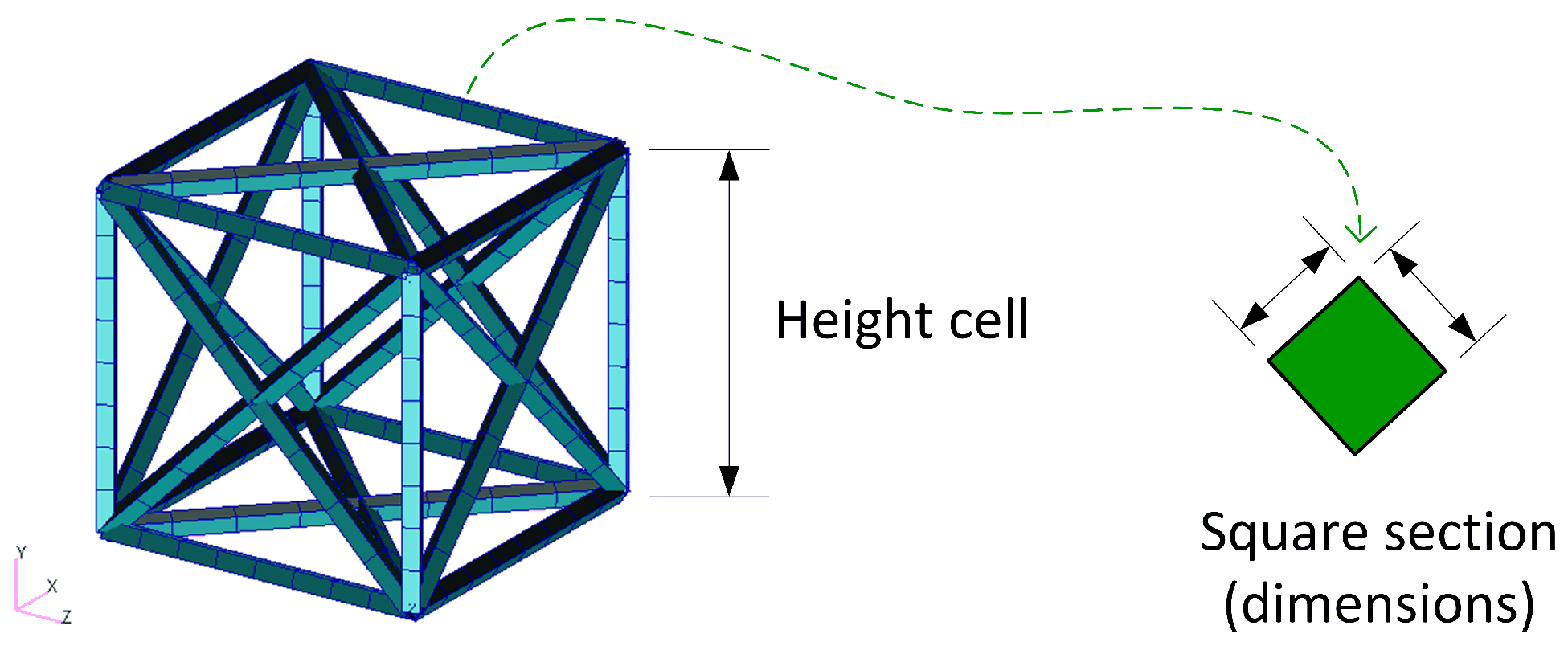
Cell (See Figure 3)Subelement
Section Type		Section
(mm2)		Cell Height
(mm)		E
(GPa)		 ν
Face center cubic (FCC)Square 0.7 × 0.7 7700.33
Octet truss (OT)Square 0.7 × 0.7 7700.33
Truncated octahedron (TO)Square 0.7 × 0.7 7700.33
The final design of the finite element model with the commercial code Patran/Nastran [102,103,104] is performed pursuing a behavior of the composite sandwich beam balanced between the stiffness contribution of the cladding skins (where the bending axial forces dominate) and the stiffness contribution of the core (where the bending shear forces dominate). To this end, compliance with the standard described in the test method ASTMC393 is preserved. An example of the models with 28 × 28 × 300 mm dimensions (i.e., 4 × 4 × 42 cells) is shown in Figure 4, in this case with truncated octahedrons.
At the top and bottom of the beam, a shell with a thickness of 5 mm is placed to ensure a proper transmission of the point loads throughout the composite beam and to the metamaterial core. The thickness of the shell is determined to avoid punching and to allow the distribution of the supporting loads. Furthermore, the resulting final displacement field does not present localized deformations in any part of the model, but at the same time, the mechanical role of the shell in the global bending stiffness is also marginal. In the finite element model, the shell is modeled with a Nastran CQUAD4 element, and it is linked to the metamaterial beams through the “glued contact” of Nastran [102,103,104] by means of a set of permanent multipoint constraints which avoid the separation between skins and core during the deformation (Figure 5).
The metamaterial subelements (bar elements) are modeled as 3D beams. To determine the equivalent section of such elements, the approach is to consider beams resulting in the same relative density ρ for the three metamaterial types. This relative density is the ratio between the solid volume and the total volume of the sample. Following this approach, the width and height of the square cross section of the beams used to reproduce each cell are 0.4 mm for the FCC, 0.35 mm for the OT and 0.5 mm for the TO. Those values give the same relative density of ρ = 0.1 for the beams composed of any of the three cells studied. Another case studied is ρ = 0.5 , for which beam dimensions are 1.0 mm for the FCC, 0.65 mm for the OT and 0.9 mm for the TO. All the tests were performed with the two relative densities (0.1 and 0.5), and no special sensibility was found regarding the increment of stresses due to the defects introduced. Thus, in other to avoid repetition of the results, the plots shown for the theoretical cases are the ones with ρ = 0.1 . The mechanical properties used for the lattice beams without defects are E = 70 GPa and υ = 0.33 [105,106].
In the 3Pb bending test, the total load applied is 2800 N (P), which is shared between the cells along the width of the top middle section. For the 4Pb bending test, two loading points of 1400 N are located at a quarter from each support, see Figure 6. The supports are restricted, ensuring an isostatic configuration of the loaded beam.

3.1. Defects Considered and Their Simulation

Figure 6 shows a sketch of the defects considered in the lattice bars. The effect of the imperfections in the metamaterial is characterized by the change in the stress tensor at a similar loading state. For this analysis, the material is considered linear elastic, neglecting microplasticity effects. Specific details of the modeling for each defect case follow.

3.1.1. Lattice Bar Undulations

For characterizing these non-homogeneities in a simple manner, each edge is divided into six macro elements, obtaining a symmetrical distribution of the material for each edge of the unit cells, see Figure 6. Each macroelement has 4 regular equal beam elements with the purpose of uncoupling the finite element mesh size from the refining in the defect description for general purposes. To model these edges, 24 elements reproduce the bending and shear of a beam with sufficient accuracy regardless of the length-to-thickness ratio. Note that Nastran’s “CBEAM” elements are of the Timoshenko type, including residual bending flexibility [107,108,109,110]. The choice of this type of element for the simulations is due to the facility of modeling with this finite element and the lower computational cost required in its numerical solutions, instead of the more common models, where the material is discretized with volumetric tetrahedral or hexahedral finite elements [111,112,113], which requires a complex and arduous elaboration and with a higher computational cost as well. On the other hand, because we aim at conclusions for a practical procedure, the choice of 6 macroelements is to balance between the proper description of defects, and a reasonable computational cost for possible complex structures. Fewer macroelements will be clearly insufficient for a proper description of the effects, and more macroelements will unnecessarily increase the computational cost in large complex structures, where the use of one finite element per macroelement is advisable to avoid large computational costs. Of course, a very fine and detailed description of the defects is possible for the cases in this paper, but the conclusions then may not be applicable to the gross descriptions needed in typical complex structures.
For the case of modeling bar undulations, each designed model in CAD has small variations of the position of its nodes to simulate the conditions when it is 3D printed, differing from the canonical model, see Figure 6. To model the defect in the algorithm, any node of the mesh, initially located in a spatial direction ( x , y , z ) in the original CAD design can modify its position in the three directions. To this end, a distribution to increase or decrease for each direction a maximum allowed magnitude ( x ± Δ x , y ± Δ y , z ± Δ z ) is defined. Additionally, the parameter ρ indicates the density of nodes with the position altered. If ρ = 1 , the nodes of the mesh have suffered statistically random variations in the position of their nodes with respect to their initial position. If ρ = 0.5 , then it would indicate that only half of the nodes have changed their initial positions. Modified nodes are randomly selected.

3.1.2. Conicity in the Edges of the Lattice

For this case, similar meshes as for the previous case are used. Following experimental observations over the geometry of the printed cells [7,114], where bars exhibit a nonconstant section area, the elements located in the corners of the edge are assigned the greatest amount of material, the macro elements in the central area have half the amount of that material, and the connection elements between the corner and the central area are modeled with 75% of the material assigned to the corner. This defect in the algorithm is implemented as a variation in the section of all edges of the unit cells that constitute the testing beam, as shown in Figure 7.

3.1.3. Porosity Gradient

To implement this defect, two hypotheses are considered. In the first one, the pores are uniformly distributed within each edge, which causes a decrease in the Young’s modulus on the original base material. In the second one, there is an additional variation in the Young modulus along the edge. This modulus is randomly distributed along some metamaterial edges [114,115].

3.1.4. Computational Modeling Sequence

The computational modeling scheme for introducing defects is given in Figure 8. First, we use Patran to build the initial canonical model, including the geometry, properties, boundary conditions and loads. The program generates an output file (.bdf). This file is modified using a Python script that inserts the mentioned defects (separately or all together depending on the purpose of the analysis). Subsequently, the modified file (.bdf modified) is executed on Nastran [102,103], generating the solution file (.f06). This file is introduced in another Python script for post-processing, selecting the average and the maximum stresses. Finally, the results for the n tested samples are compiled, allowing for the representation of the stresses for each type of unit cell used in the beam.

4. Sensitivity Analysis

In this section, the results of the three-point and four-point virtual bending tests are presented to analyze the sensitivity through the maximum stress variation in the three metamaterial cell types: FCC (face-centered cubic), OT (octet truss) and TO (truncated octahedron). Tests are performed for both geometrically linear and non-linear cases, but since the results for the non-linear cases differ little from the linear ones, only the results of the linear cases are shown.

4.1. Position of the Nodes

Figure 9a shows the results obtained when modeling this type of defect from the amount of nodal deviation. It is observed that, whereas the TO unit cell is the cell that sustains larger stress due to its geometric configuration, it is also the least affected by this imperfection since the maximum stress obtained is almost insensitive to it, with only a slight deviation between the 3Pb and the 4Pb bending tests.
In Figure 9b, the amount of elements affected from the defect is considered, i.e., it considers the effect when the number of elements with imperfections increases for a fixed nodal displacement distribution. It is seen that the curves for the FCC and OT unit cells have, for elements with low concentrations of defects, a slight slope. Both cell curves have an asymptotic value. For the case of the TO unit cell, the value of the maximum stress is almost unaffected by the increase in the defect density.

4.2. Porosity

This defect is modeled by changing the effective elastic modulus of some elements according to the porosity, see Figure 9c. In the three tested samples (OT, FCC, and TO), the stresses caused by this defect are almost constant for the two types of bending tests (3Pb and 4Pb). Whereas an increase in porosity should, in general, increase the maximum stress, the overall structure is under isostatic loading conditions, and the internal stresses in the metamaterial bars re-equilibrate, maintaining the overall equivalent stress distribution in the beams; hence, the maximum stress in the bars near the skins at the most bending-demanded sections and the maximum stresses in the metamaterial cell bars, due to shear in the sections near the support, are constant. This defect maintains, almost unaltered, the stress distributions.

4.3. Conicity

In Figure 9d, we show the obtained results for the samples when we apply the conicity defect (changes in section). We observe that the results are independent of whether the samples are tested at 3Pb or 4Pb tests for the FCC and OT unit cells, with slight deviation in the stress when the same samples are built with TO unit cells. For the three cases studied, the results show a parabolic-type curve, the parabola being more pronounced in the case of the OT unit cell where the cell could reach a stress of 900 MPa . This stress exceeds the elastic limit of the base material, so plastic effects should be introduced and studied at that point. This increase in stress is associated with the fact that the TO unit cell has a lower shear stiffness than the rest of the unit cells (OT and FCC), so near the sections with concentrated loads, the metamaterial cell deformations are larger, so the cell bars suffer relevant shear and bending, resulting in a higher concentration of stress in the corners of the cell bars. On the other hand, due to their larger shear stiffness, the TO and FCC cells present more or less the same behavior for the conicity defect without appreciating great differences in the stress when the section is reduced. This is attributed to the better shear behavior of the cells, avoiding bar bending and stress concentrations, allowing better redistribution. Cell topologies with better shear stiffness are less sensitive to conicity defects because they force the cell bars to work as truss structures rather than as beams, see Figure 10.

5. Experimental Validation

In this section, a comparison of the proposed model with the obtained experimental data is performed. Experimental data were obtained from [116], a compression test of the metamaterial cells, whose properties are shown in Table 2. The experimental sample is a specimen of metamaterial containing the previously described defects, and whose imperfections are characterized through the tomographic technique [116,117,118,119], using the same experimental procedure and similar specimen layout as already described in reference [116,120]. The data herein are for cells consisting of an hexahedron with circular section bars, where the diameter is varied, reported in [116]. The choice of the cell type for this section follows from the conclusions of the previous section. The properties of the base material E and ν (Young modulus and Poisson ratio) correspond to the Ti-6Al-4V base material used as a substrate material in its powder form. This alloy and its variants are widely used in a wide range of aerospace, industrial and biomedical applications, among others, for their numerous features, such as high corrosion resistance, light weight and high strength [121,122,123].
Each cell is characterized by an ideal fraction solid denoted with the symbol s. The metamaterial unit cells are used to build the model of dimensions 7 × 7 × 10 mm shown in Figure 11. A constant displacement in the Z (vertical) direction is imposed at the top, while the bottom is simply supported. Each edge of the cell is divided into six macroelements of a nonconstant-sized area, each of them containing four Timoshenko-type beam elements. All types of defects as described in the previous section are introduced in the model. These defects and their real statistical distribution were previously characterized through tomography geometrical measurements in [116] and the segmentation of the pore fraction in different parts of the printed metamaterial as described in [120].

5.1. Methods: Experimental Determination of Defects

The procedure for the experimental determination of the defects follows.
  • Diameter and node deviations: Digital scans of the latticed structures [116] are used to measure the diameter distribution of the beams. Diameters are measured along the different beams randomly at 50 different locations to extract the statistical distributions. The same optical images are used to identify the centroids of different sections and calculate the geometrical deviation from the ideal central beam line. X , Y and Z direction deviations are calculated using both X Z and Y Z plane photographs. In total, 483 sections are analyzed for the s = 15 % solid fraction case, 496 sections for s = 25 % , and 535 sections for s = 35 % along 30 different beams for each case as shown in Table 3 (Nodal deviation) and Table 4 (Conicity).
  • Porosity: X-ray tomographies of the lattice structures are performed in [116] to identify internal defects. Thirty random beams are reconstructed and analyzed to extract the porosity fraction of each beam. The homogenized results of each beam are used to produce the statistical distribution of the percentage of porosity within the beams, see Table 5.

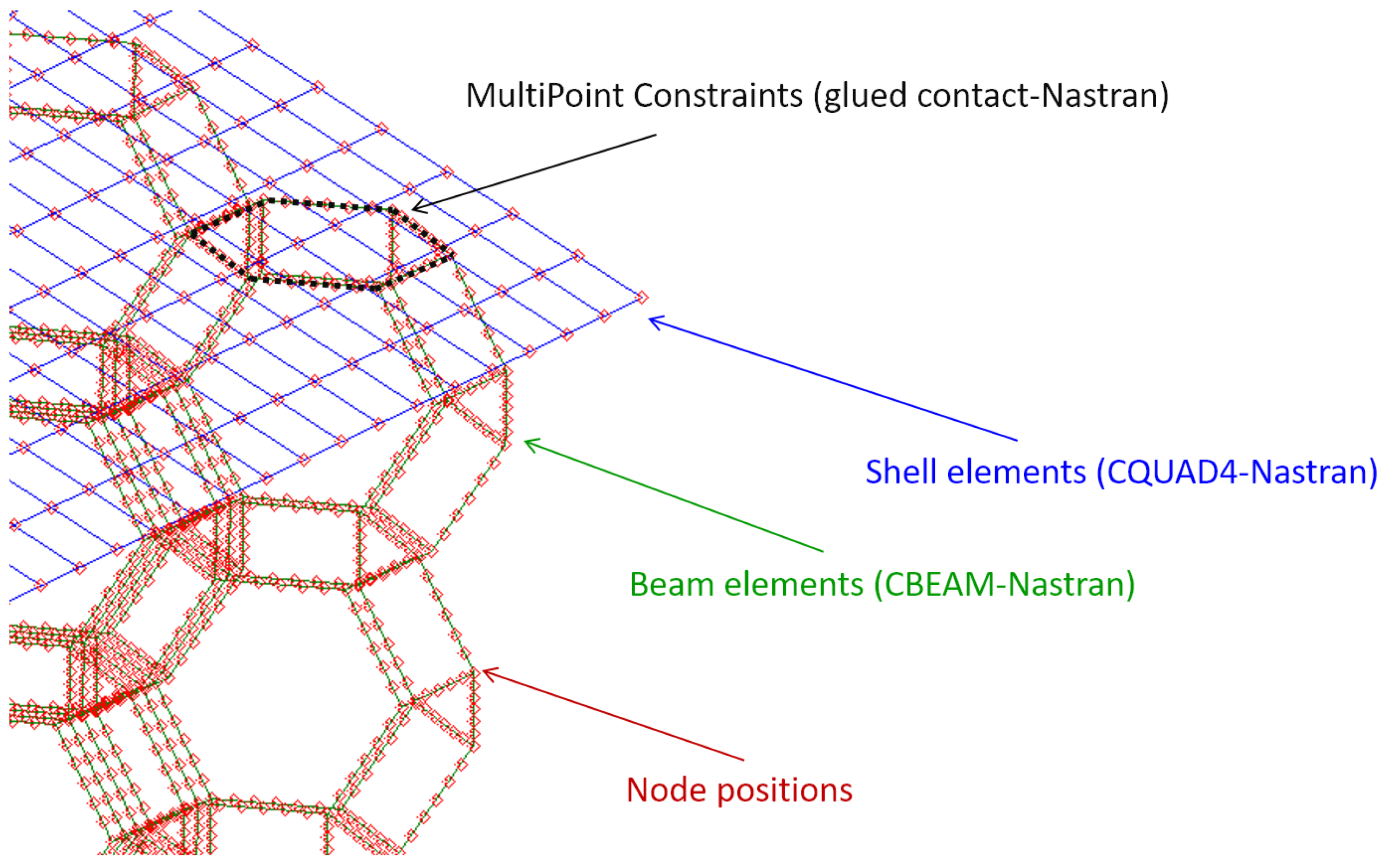
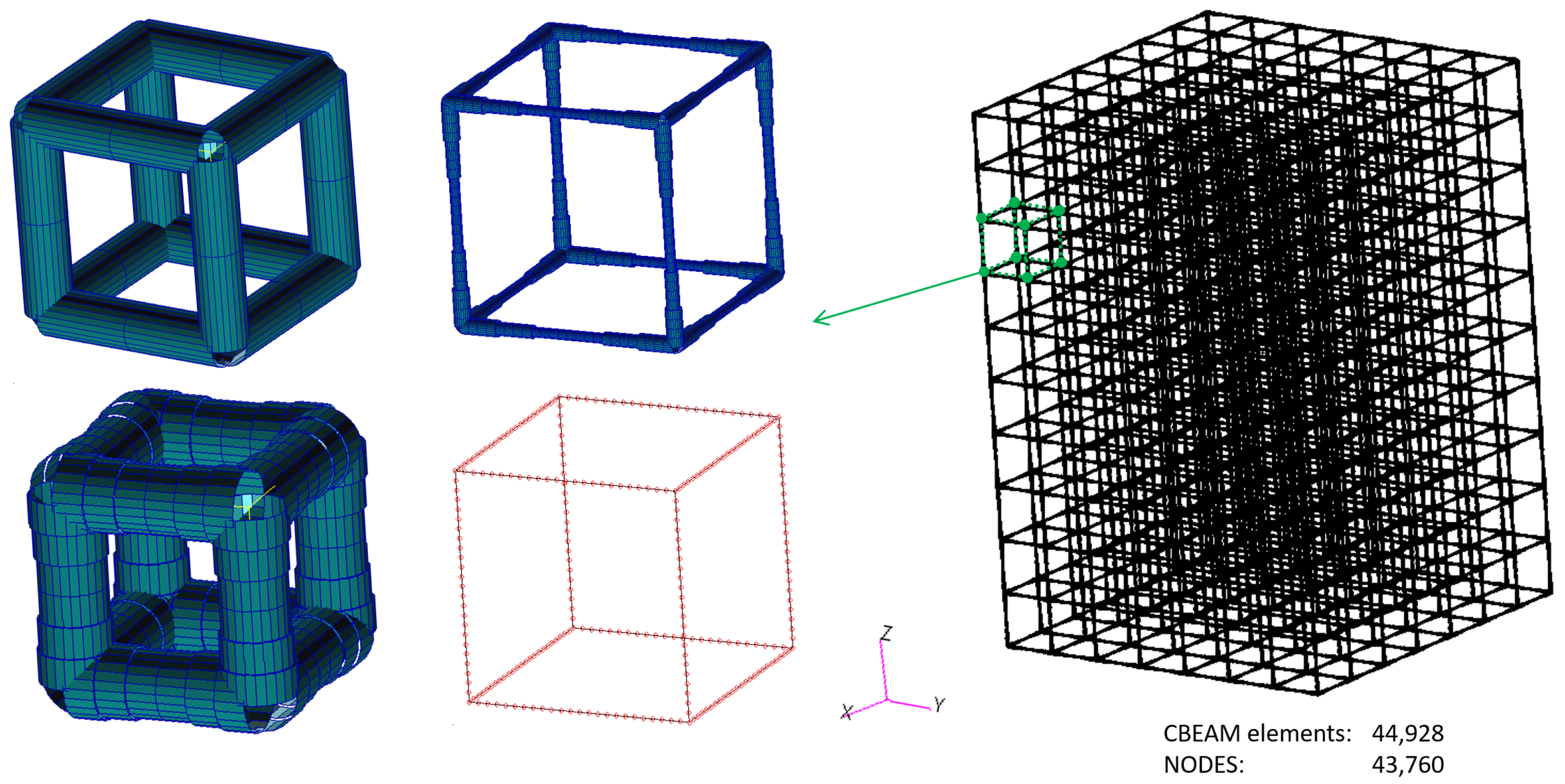
5.2. Methods: Finite Element Modeling

The finite element modeling techniques for reproducing the experimental test follow:
  • Error in the position of the nodes: For all the ideal solid fractions s, the parameter ρ is set to ρ = 1 because the experimental data indicate that it can be considered that all the nodes have changed with respect to their original position in the CAD model, see Table 3. Therefore, all mesh nodes have been altered.
  • Conicity in the edges of the lattice: For each ideal solid fraction s, the distribution of measured diameters is translated to edges of the finite element mesh, see Table 4. This distribution results in a corresponding distribution of the Young modulus for the 12 elements of each edge, given in Table 6.
  • Porosity gradient: This defect results in a variation of Young’s modulus E with respect to the reference value E 0 . Given the large variety of pore types, the physical relationship that exists between porosity and moduli is not evident. However, the following expression is used in this work because of the good correlation obtained [124]:
    E = E 0 1 − p 1 + p / f
    where p is the fraction of pores in the solid, and f is a shape factor for the pores. In addition, motivated by the experimental observations, additional assumptions are made. (1) It is considered that the distribution of pores is uniform within the material, and (2) it is assumed that the shape of the pores is spherical, so we set f = 1 [124]. However, since only the linear region is being considered, f does not significantly affect the results [124]. When addressing the nonlinear behavior, f must consider plastic evolution and pore shape changes in the material. Table 5 shows the final distribution of pores that we applied for each ideal solid fraction of material s.

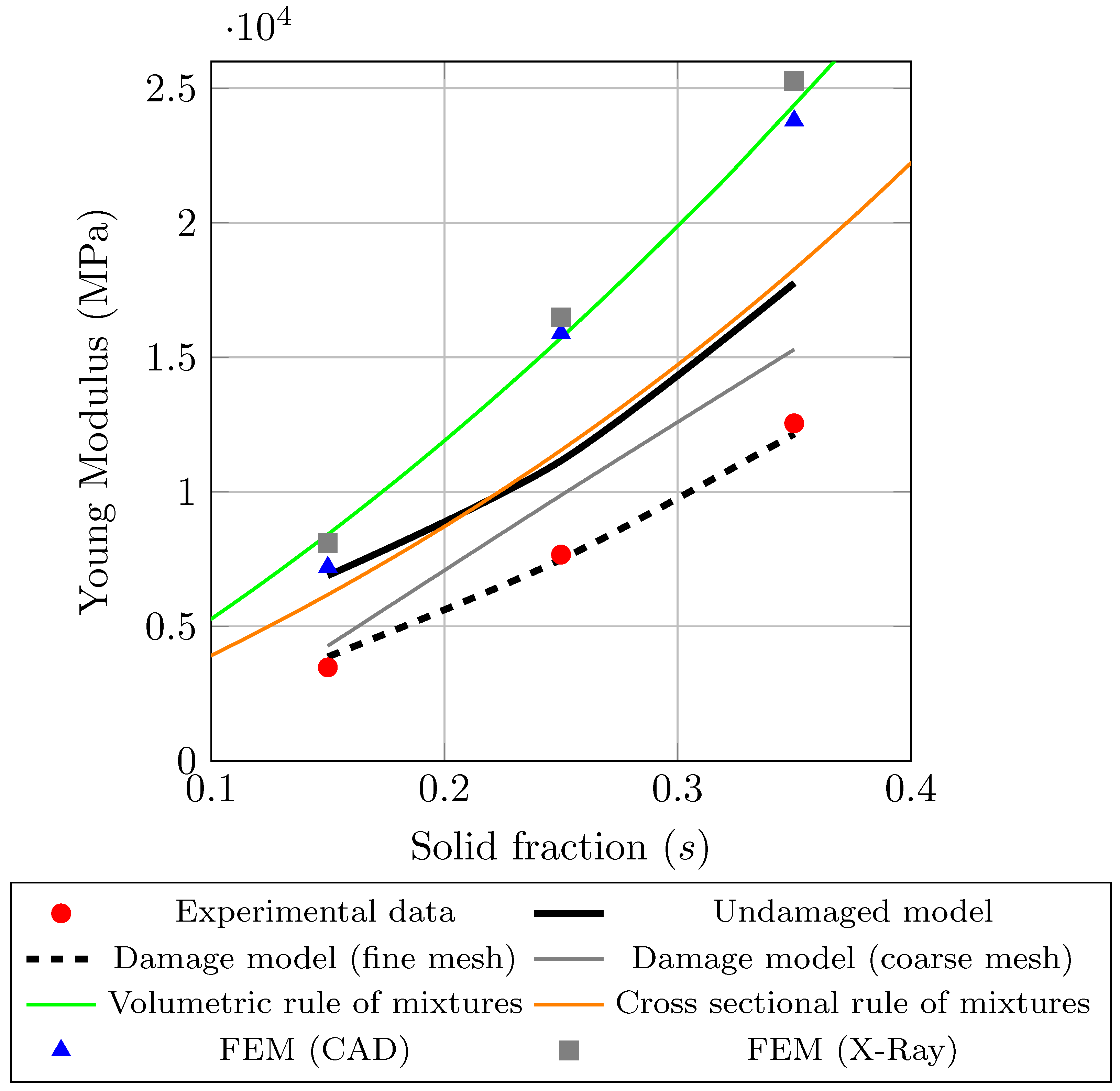
5.3. Results

Two types of finite element models were analyzed. The topology (cell vertex positions) of one of them was obtained directly from the canonical (design) CAD file. For the other one, the position of the cell vertices was obtained from X-ray images of a real 3D-printed specimen (hence including already geometrical position errors and overall shrinkage). To any of these models, the above-mentioned defects may also be incorporated. The resulting values for the modulus of elasticity for each ideal solid fraction are collected in Table 6 and Table 7. Table 6 compares the experimental values against the simulation values from both the initial nominal CAD model, where the defects were incorporated, and the finite element model with the overall geometry obtained from the X-rays. It can be observed that there are important differences between the experimental modulus of elasticity and those obtained from the CAD model with the nominal designed structure and with the structure topology from X-ray (the actual printed structure).
Table 7 shows the predicted Young moduli when the distributions of defects are incorporated in the finite element model, departing from the nominal CAD model. It is observed that the results of the corrected CAD models incorporating the distributions of defects are much more in agreement with the experimental results than those obtained from nominal, unmodified CAD models, see Table 7. The remaining differences may be due to other types of defects not incorporated in this work, or from statistical errors.
Figure 12 shows the modulus of elasticity versus the ideal solid fraction s. The red dots represent the experimental data of the printed model, incorporating the defects. The blue triangles represent the finite element model results (FEM) with the geometry obtained from the CAD model (Patran), while the gray squares represent the finite element model results, where the geometry applied on the finite elements is obtained using the data of X-ray tomography [116]. In both these meshes, the edge defects are not explicitly incorporated. The black line corresponds to the model without porosity, while the dashed black line and the gray line correspond to the models with porosity defects introduced. The difference between the latter lines corresponds to the mesh used, where the finer mesh has 12 elements per edge, whereas the coarser mesh has 6 elements per edge. Finally, the green and orange lines correspond to the rule of mixtures for the modulus of elasticity and the density of the model. The green line corresponds to the solid modulus of elasticity and the total density, whereas for the orange line, the same modulus is used, but the density is modified, being in this case that of the sectional area.

6. Conclusions

Additive manufacturing (AM) eliminates manufacturing constraints, brings flexibility, usually involves less and recycable material, reduces weight, and facilitates the local, on-demand manufacturing of parts. Hence, AM is an important technology in industrial sustainability, and is key in producing optimal components. Mechanical metamaterials are optimal cell-based designs tailored for specific mechanical demands. However, CAD metamaterial designs and subsequent finite element models give metamaterial property predictions that are in large error compared to actually experimental ones. This is due to the important presence of defects due to the 3D printing of the component. It is of paramount importance to develop procedures that automatically incorporate those defects in the finite element models so that the predicted “design” mechanical properties are in agreement with those of the final printed component.
In this work, a procedure to introduce the distributions of defects in an initial CAD undamaged model is presented. First, the influence of each type of defect was studied. Thereafter, three defect distributions were introduced simultaneously in the CAD model and compared with the experimental results. The results are promising since, when typical defect distributions were incorporated in the finite element models, the predicted moduli were in much smaller error compared to the experimental values.
Much research is still needed to verify that the methodology extends to a large variety of component types and loading conditions, as well as to other important mechanical properties, like ductility and life under fatigue loads.

Author Contributions

G.V.-R.: investigation, software, data curation, formal analysis, visualization, writing—original draft, writing—review and editing. L.M.-C.: investigation, validation-numerical data, visualization, writing—original draft. I.M.-G. investigation, software, data curation, visualization. D.B.: conceptualization, investigation, validation-experimental data. F.J.M.: supervision, project administration, funding acquisition, writing—review and editing. M.Á.S.-G.: conceptualization, investigation, methodology, supervision, resources, writing—review and editing. All authors have read and agreed to the published version of the manuscript.

Funding

The authors acknowledge on the computational part of this work: this project has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie Grant Agreement No. 101007815. The authors are grateful to Prof. Roger Reed for his support on the experimental results of this work. Sustainability 16 01167 i001

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

For the data supporting, please contact the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Uribe-Lam, E.; Treviño-Quintanilla, C.D.; Cuan-Urquizo, E.; Olvera-Silva, O. Use of additive manufacturing for the fabrication of cellular and lattice materials: A review. Mater. Manuf. Process. 2020, 36, 257–280. [Google Scholar] [CrossRef]
  2. Niaki, M.K.; Torabi, S.A.; Nonino, F. Why manufacturers adopt additive manufacturing technologies: The role of sustainability. J. Clean. Prod. 2019, 222, 381–392. [Google Scholar] [CrossRef]
  3. Godina, R.; Ribeiro, I.; Matos, F.; T. Ferreira, B.; Carvalho, H.; Peças, P. Impact assessment of additive manufacturing on sustainable business models in industry 4.0 context. Sustainability 2020, 12, 7066. [Google Scholar] [CrossRef]
  4. Pou, J.; Riveiro, A.; Paulo, D.J. Additive Manufacturing; Elsevier: Horth-Holland, The Netherlands, 2021. [Google Scholar] [CrossRef]
  5. Andreas, G.; Jan-Steffen, H. Additive Manufacturing; Hanser Verlag: Munich, Germany, 2016. [Google Scholar]
  6. Bertol, L.S.; Júnior, W.K.; Silva, F.P.d.; Aumund-Kopp, C. Medical design: Direct metal laser sintering of Ti–6Al–4V. Mater. Des. 2010, 31, 3982–3988. [Google Scholar] [CrossRef]
  7. Barba, D.; Alabort, E.; Reed, R. Synthetic bone: Design by additive manufacturing. Acta Biomater. 2019, 97, 637–656. [Google Scholar] [CrossRef]
  8. Gander, M.J. Optimized Schwarz Methods. SIAM J. Numer. Anal. 2006, 44, 699–731. [Google Scholar] [CrossRef]
  9. Liaskos, C.; Tsioliaridou, A.; Ioannidis, S. Towards a circular economy via intelligent metamaterials. In Proceedings of the 2018 IEEE 23rd International Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD), Barcelona, Spain, 17–19 September 2018; pp. 1–6. [Google Scholar]
  10. Schwarz, A.; Lichti, T.; Wenz, F.; Scheuring, B.M.; Hübner, C.; Eberl, C.; Elsner, P. Development of a Scalable Fabrication Concept for Sustainable, Programmable Shape-Morphing Metamaterials. Adv. Eng. Mater. 2022, 24, 2200386. [Google Scholar] [CrossRef]
  11. Tan, T.; Yan, Z.; Zou, H.; Ma, K.; Liu, F.; Zhao, L.; Peng, Z.; Zhang, W. Renewable energy harvesting and absorbing via multi-scale metamaterial systems for Internet of things. Appl. Energy 2019, 254, 113717. [Google Scholar] [CrossRef]
  12. Chen, Z.; Guo, B.; Yang, Y.; Cheng, C. Metamaterials-based enhanced energy harvesting: A review. Phys. Condens. Matter 2014, 438, 1–8. [Google Scholar] [CrossRef]
  13. Zadpoor, A.A. Mechanical meta-materials. Mater. Horiz. 2016, 3, 371–381. [Google Scholar] [CrossRef]
  14. Liu, Y.; Zhang, X. Metamaterials: A new frontier of science and technology. Chem. Soc. Rev. 2011, 40, 2494–2507. [Google Scholar] [CrossRef]
  15. Cui, T.J.; Smith, D.R.; Liu, R. Metamaterials; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
  16. Kadic, M.; Milton, G.W.; van Hecke, M.; Wegener, M. 3D metamaterials. Nat. Rev. Phys. 2019, 1, 198–210. [Google Scholar] [CrossRef]
  17. Zheludev, N.I.; Kivshar, Y.S. From metamaterials to metadevices. Nat. Mater. 2012, 11, 917–924. [Google Scholar] [CrossRef]
  18. Phenomena of Optical Metamaterials; Elsevier: Amsterdam, The Netherlands, 2019. [CrossRef]
  19. Dielectric Metamaterials; Elsevier: Amsterdam, The Netherlands, 2020. [CrossRef]
  20. Zahra, S.; Ma, L.; Wang, W.; Li, J.; Chen, D.; Liu, Y.; Zhou, Y.; Li, N.; Huang, Y.; Wen, G. Electromagnetic Metasurfaces and Reconfigurable Metasurfaces: A Review. Front. Phys. 2021, 8, 593411. [Google Scholar] [CrossRef]
  21. Gao, S.; Wei, K.; Yang, H.; Tang, Y.; Yi, Z.; Tang, C.; Tang, B.; Yi, Y.; Wu, P. Design of Surface Plasmon Resonance-Based D-Type Double Open-Loop Channels PCF for Temperature Sensing. Sensors 2023, 23, 7569. [Google Scholar] [CrossRef]
  22. Wang, J.; Dai, G.; Huang, J. Thermal Metamaterial: Fundamental, Application, and Outlook. iScience 2020, 23, 101637. [Google Scholar] [CrossRef]
  23. Huang, Z.; Zheng, Y.; Li, J.; Cheng, Y.; Wang, J.; Zhou, Z.K.; Chen, L. High-Resolution Metalens Imaging Polarimetry. Nano Lett. 2023, 23, 10991–10997. [Google Scholar] [CrossRef]
  24. Jia, Z.; Liu, F.; Jiang, X.; Wang, L. Engineering lattice metamaterials for extreme property, programmability, and multifunctionality. J. Appl. Phys. 2020, 127, 150901. [Google Scholar] [CrossRef]
  25. Jiao, P.; Mueller, J.; Raney, J.R.; Zheng, X.; Alavi, A.H. Mechanical metamaterials and beyond. Nat. Commun. 2023, 14, 6004. [Google Scholar] [CrossRef]
  26. Feng, J.; Fu, J.; Yao, X.; He, Y. Triply periodic minimal surface (TPMS) porous structures: From multi-scale design, precise additive manufacturing to multidisciplinary applications. Int. J. Extrem. Manuf. 2022, 4, 022001. [Google Scholar] [CrossRef]
  27. Zhang, Q.; Yang, X.; Li, P.; Huang, G.; Feng, S.; Shen, C.; Han, B.; Zhang, X.; Jin, F.; Xu, F.; et al. Bioinspired engineering of honeycomb structure—Using nature to inspire human innovation. Prog. Mater. Sci. 2015, 74, 332–400. [Google Scholar] [CrossRef]
  28. Ashby, M.F.; Evans, T.; Fleck, N.; Hutchinson, J.W.; Wadley, H.N.G.; Gibson, L.J. Metal Foams; Butterworth-Heinemann: Woburn, MA, USA, 2014. [Google Scholar]
  29. Miranda, E.; Nobrega, E.; Ferreira, A.; Dos Santos, J. Flexural wave band gaps in a multi-resonator elastic metamaterial plate using Kirchhoff-Love theory. Mech. Syst. Signal Process. 2019, 116, 480–504. [Google Scholar] [CrossRef]
  30. Miranda, E., Jr.; Nobrega, E.; Rodrigues, S.; Aranas, C., Jr.; Dos Santos, J. Wave attenuation in elastic metamaterial thick plates: Analytical, numerical and experimental investigations. Int. J. Solids Struct. 2020, 204–205, 138–152. [Google Scholar] [CrossRef]
  31. Berger, J.B.; Wadley, H.N.G.; McMeeking, R.M. Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness. Nature 2017, 543, 533–537. [Google Scholar] [CrossRef]
  32. Bertoldi, K.; Vitelli, V.; Christensen, J.; van Hecke, M. Flexible mechanical metamaterials. Nat. Rev. Mater. 2017, 2, 17066. [Google Scholar] [CrossRef]
  33. Li, X.; Peng, W.; Wu, W.; Xiong, J.; Lu, Y. Auxetic mechanical metamaterials: From soft to stiff. Int. J. Extrem. Manuf. 2023, 5, 042003. [Google Scholar] [CrossRef]
  34. Seetoh, I.P.; Leong, B.; Yi, E.L.; Markandan, K.; Kanaujia, P.K.; Lai, C.Q. Extremely stiff and lightweight auxetic metamaterial designs enabled by asymmetric strut cross-sections. Extrem. Mech. Lett. 2022, 52, 101677. [Google Scholar] [CrossRef]
  35. Kundu, D.; Ghuku, S.; Naskar, S.; Mukhopadhyay, T. Extreme Specific Stiffness Through Interactive Cellular Networks in Bi-Level Micro-Topology Architected Metamaterials. Adv. Eng. Mater. 2022, 25, 2201407. [Google Scholar] [CrossRef]
  36. Wang, Y.; Sigmund, O. Quasiperiodic mechanical metamaterials with extreme isotropic stiffness. Extrem. Mech. Lett. 2020, 34, 100596. [Google Scholar] [CrossRef]
  37. Ben-Yelun, I.; Gómez-Carano, G.; San Millán, F.J.; Sanz, M.; Montáns, F.J.; Saucedo-Mora, L. GAM: General Auxetic Metamaterial with Tunable 3D Auxetic Behavior Using the Same Unit Cell Boundary Connectivity. Materials 2023, 16, 3473. [Google Scholar] [CrossRef]
  38. Jin, Y.; Xie, C.; Gao, Q.; Zhou, X.; Li, G.; Du, J.; He, Y. Fabrication of multi-scale and tunable auxetic scaffolds for tissue engineering. Mater. Des. 2021, 197, 109277. [Google Scholar] [CrossRef]
  39. Zhao, Z.; Yuan, C.; Lei, M.; Yang, L.; Zhang, Q.; Chen, H.; Qi, H.J.; Fang, D. Three-Dimensionally Printed Mechanical Metamaterials With Thermally Tunable Auxetic Behavior. Phys. Rev. Appl. 2019, 11, 044074. [Google Scholar] [CrossRef]
  40. Karapiperis, K.; Radi, K.; Wang, Z.; Kochmann, D.M. A Variational Beam Model for Failure of Cellular and Truss-Based Architected Materials. Adv. Eng. Mater. 2023, 2300947. [Google Scholar] [CrossRef]
  41. Jiang, W.Z.; Teng, X.C.; Ni, X.H.; Zhang, X.G.; Cheng, X.; Jiang, W.; Han, D.; Zhang, Y.; Ren, X. An improved re-entrant honeycomb with programmable densification and multistage energy-absorbing performance. Eng. Struct. 2024, 301, 117318. [Google Scholar] [CrossRef]
  42. Bauer, J.; Kraus, J.A.; Crook, C.; Rimoli, J.J.; Valdevit, L. Tensegrity Metamaterials: Toward Failure-Resistant Engineering Systems through Delocalized Deformation. Adv. Mater. 2021, 33, 2005647. [Google Scholar] [CrossRef] [PubMed]
  43. Benedetti, M.; du Plessis, A.; Ritchie, R.; Dallago, M.; Razavi, N.; Berto, F. Architected cellular materials: A review on their mechanical properties towards fatigue-tolerant design and fabrication. Mater. Sci. Eng. R Rep. 2021, 144, 100606. [Google Scholar] [CrossRef]
  44. Lee, J.; Singer, J.P.; Thomas, E.L. Micro/Nanostructured Mechanical Metamaterials. Adv. Mater. 2012, 24, 4782–4810. [Google Scholar] [CrossRef] [PubMed]
  45. Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
  46. Zheludev, N.I. The Road Ahead for Metamaterials. Science 2010, 328, 582–583. [Google Scholar] [CrossRef]
  47. Fischer, S.C.L.; Hillen, L.; Eberl, C. Mechanical Metamaterials on the Way from Laboratory Scale to Industrial Applications: Challenges for Characterization and Scalability. Materials 2020, 13, 3605. [Google Scholar] [CrossRef]
  48. Paulo, D.J. Computational Methods and Production Engineering; Elsevier-Woodhead: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
  49. Kocovic, P. History of additive manufacturing. In 3D Printing and Its Impact on the Production of Fully Functional Components; IGI Global: Hershey, PA, USA, 2017; pp. 1–24. [Google Scholar] [CrossRef]
  50. Guo, N.; Leu, M.C. Additive manufacturing: Technology, applications and research needs. Front. Mech. Eng. 2013, 8, 215–243. [Google Scholar] [CrossRef]
  51. Ligon, S.C.; Liska, R.; Stampfl, J.; Gurr, M.; Mülhaupt, R. Polymers for 3D Printing and Customized Additive Manufacturing. Chem. Rev. 2017, 117, 10212–10290. [Google Scholar] [CrossRef]
  52. Davim, J. Paulo. Statistical and Computational Techniques in Manufacturing; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
  53. Zhang, M.; Yang, Z.; Lu, Z.; Liao, B.; He, X. Effective elastic properties and initial yield surfaces of two 3D lattice structures. Int. J. Mech. Sci. 2018, 138, 146–158. [Google Scholar] [CrossRef]
  54. Moreno-Cabezali, B.M.; Fernandez-Crehuet, J.M. Application of a fuzzy-logic based model for risk assessment in additive manufacturing R&D projects. Comput. Ind. Eng. 2020, 145, 106529. [Google Scholar] [CrossRef]
  55. Yazdani Sarvestani, H.; Akbarzadeh, A.; Mirbolghasemi, A.; Hermenean, K. 3D printed meta-sandwich structures: Failure mechanism, energy absorption and multi-hit capability. Mater. Des. 2018, 160, 179–193. [Google Scholar] [CrossRef]
  56. Gong, H.; Rafi, K.; Gu, H.; Starr, T.; Stucker, B. Analysis of defect generation in Ti–6Al–4V parts made using powder bed fusion additive manufacturing processes. Addit. Manuf. 2014, 1–4, 87–98. [Google Scholar] [CrossRef]
  57. Simchi, A.; Petzoldt, F.; Pohl, H. On the development of direct metal laser sintering for rapid tooling. J. Mater. Process. Technol. 2003, 141, 319–328. [Google Scholar] [CrossRef]
  58. Campoli, G.; Borleffs, M.; Amin Yavari, S.; Wauthle, R.; Weinans, H.; Zadpoor, A. Mechanical properties of open-cell metallic biomaterials manufactured using additive manufacturing. Mater. Des. 2013, 49, 957–965. [Google Scholar] [CrossRef]
  59. Liu, L.; Kamm, P.; García-Moreno, F.; Banhart, J.; Pasini, D. Elastic and failure response of imperfect three-dimensional metallic lattices: The role of geometric defects induced by Selective Laser Melting. J. Mech. Phys. Solids 2017, 107, 160–184. [Google Scholar] [CrossRef]
  60. Khaing, M.; Fuh, J.; Lu, L. Direct metal laser sintering for rapid tooling: Processing and characterisation of EOS parts. J. Mater. Process. Technol. 2001, 113, 269–272. [Google Scholar] [CrossRef]
  61. Zhang, B.; Li, Y.; Bai, Q. Defect Formation Mechanisms in Selective Laser Melting: A Review. Chin. J. Mech. Eng. 2017, 30, 515–527. [Google Scholar] [CrossRef]
  62. Grasso, M.; Colosimo, B.M. Process defects andin situmonitoring methods in metal powder bed fusion: A review. Meas. Sci. Technol. 2017, 28, 044005. [Google Scholar] [CrossRef]
  63. Thampy, V.; Fong, A.Y.; Calta, N.P.; Wang, J.; Martin, A.A.; Depond, P.J.; Kiss, A.M.; Guss, G.; Xing, Q.; Ott, R.T.; et al. Subsurface Cooling Rates and Microstructural Response during Laser Based Metal Additive Manufacturing. Sci. Rep. 2020, 10, 1981. [Google Scholar] [CrossRef] [PubMed]
  64. Vevers, A.; Kromanis, A.; Gerins, E. Co2 Laser Powered Metal 3D Printer Parameter Influence on Part Quality. In DAAAM Proceedings; DAAAM International: Vienna, Austria, 2018; pp. 0955–0960. [Google Scholar] [CrossRef]
  65. Toma, A.; Condruz, R.; Carlanescu, R.; Daniel, I. A mini-review on non-destructive techniques for additive manufactured metal parts. AIP Conf. Proc. 2020, 2302, 060017. [Google Scholar] [CrossRef]
  66. Moylan, S.; Drescher, J.; Donmez, M. Powder Bed Fusion Machine Performance Testing. In Proceedings of the Dimensional Accuracy and Surface Finish in Additive Manufacturing, 2014 ASPE, ASPE Spring Topical Meeting–D, Berkley, CA, USA, 16 April 2014. Number 57. [Google Scholar]
  67. Prabhakar, P.; Sames, W.; Dehoff, R.; Babu, S. Computational modeling of residual stress formation during the electron beam melting process for Inconel 718. Addit. Manuf. 2015, 7, 83–91. [Google Scholar] [CrossRef]
  68. Ferrar, B.; Mullen, L.; Jones, E.; Stamp, R.; Sutcliffe, C. Gas flow effects on selective laser melting (SLM) manufacturing performance. J. Mater. Process. Technol. 2012, 212, 355–364. [Google Scholar] [CrossRef]
  69. Foster, B.K.; Reutzel, E.W.; Nassar, A.R.; Hall, B.; Brown, S.W.J.; Dickman, C.J. Optical, Layerwise Monitoring of Powder Bed Fusion; University of Texas at Austin: Austin, TX, USA, 2015. [Google Scholar]
  70. Thijs, L.; Verhaeghe, F.; Craeghs, T.; Humbeeck, J.V.; Kruth, J.P. A study of the microstructural evolution during selective laser melting of Ti–6Al–4V. Acta Mater. 2010, 58, 3303–3312. [Google Scholar] [CrossRef]
  71. Gong, H. Generation and Detection of Defects in Metallic Parts Fabricated by Selective Laser Melting and Electron Beam Melting and Their Effects on Mechanical Properties. Ph.D. Thesis, University of Louisville, Louisville, KY, USA, 2013. [Google Scholar] [CrossRef]
  72. Sames, W.J.; List, F.A.; Pannala, S.; Dehoff, R.R.; Babu, S.S. The metallurgy and processing science of metal additive manufacturing. Int. Mater. Rev. 2016, 61, 315–360. [Google Scholar] [CrossRef]
  73. Gibson, I.; Rosen, D.; Stucker, B.; Khorasani, M. Direct Write Technologies. In Additive Manufacturing Technologies; Springer International Publishing: Cham, Swtizerland, 2021; pp. 319–345. [Google Scholar]
  74. Delgado, J.; Ciurana, J.; Rodríguez, C.A. Influence of process parameters on part quality and mechanical properties for DMLS and SLM with iron-based materials. Int. J. Adv. Manuf. Technol. 2011, 60, 601–610. [Google Scholar] [CrossRef]
  75. Pasini, D.; Guest, J.K. Imperfect architected materials: Mechanics and topology optimization. MRS Bull. 2019, 44, 766–772. [Google Scholar] [CrossRef]
  76. Malekipour, E.; El-Mounayri, H. Common defects and contributing parameters in powder bed fusion AM process and their classification for online monitoring and control: A review. Int. J. Adv. Manuf. Technol. 2017, 95, 527–550. [Google Scholar] [CrossRef]
  77. Gordon, J.V.; Narra, S.P.; Cunningham, R.W.; Liu, H.; Chen, H.; Suter, R.M.; Beuth, J.L.; Rollett, A.D. Defect structure process maps for laser powder bed fusion additive manufacturing. Addit. Manuf. 2020, 36, 101552. [Google Scholar] [CrossRef]
  78. Singla, A.K.; Banerjee, M.; Sharma, A.; Singh, J.; Bansal, A.; Gupta, M.K.; Khanna, N.; Shahi, A.; Goyal, D.K. Selective laser melting of Ti6Al4V alloy: Process parameters, defects and post-treatments. J. Manuf. Process. 2021, 64, 161–187. [Google Scholar] [CrossRef]
  79. Liu, Y.; Yang, Y.; Wang, D. Investigation into the shrinkage in Z-direction of components manufactured by selective laser melting (SLM). Int. J. Adv. Manuf. Technol. 2016, 90, 2913–2923. [Google Scholar] [CrossRef]
  80. Paul, R.; Anand, S.; Gerner, F. Effect of Thermal Deformation on Part Errors in Metal Powder Based Additive Manufacturing Processes. J. Manuf. Sci. Eng. 2014, 136, 031009. [Google Scholar] [CrossRef]
  81. Zhu, H.H.; Lu, L.; Fuh, J.Y.H. Study on Shrinkage Behaviour of Direct Laser Sintering Metallic Powder. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2006, 220, 183–190. [Google Scholar] [CrossRef]
  82. Hopkinson, N.; Sercombe, T. Process repeatability and sources of error in indirect SLS of aluminium. Rapid Prototyp. J. 2008, 14, 108–113. [Google Scholar] [CrossRef]
  83. Zago, M.; Lecis, N.F.M.; Vedani, M.; Cristofolini, I. Dimensional and geometrical precision of parts produced by binder jetting process as affected by the anisotropic shrinkage on sintering. Addit. Manuf. 2021, 43, 102007. [Google Scholar] [CrossRef]
  84. Cui, X.; Zhang, S.; Zhang, C.; Chen, J.; Zhang, J.; Dong, S. Additive manufacturing of 24CrNiMo low alloy steel by selective laser melting: Influence of volumetric energy density on densification, microstructure and hardness. Mater. Sci. Eng. A 2021, 809, 140957. [Google Scholar] [CrossRef]
  85. Seede, R.; Shoukr, D.; Zhang, B.; Whitt, A.; Gibbons, S.; Flater, P.; Elwany, A.; Arroyave, R.; Karaman, I. An ultra-high strength martensitic steel fabricated using selective laser melting additive manufacturing: Densification, microstructure, and mechanical properties. Acta Mater. 2020, 186, 199–214. [Google Scholar] [CrossRef]
  86. Larimian, T.; Kannan, M.; Grzesiak, D.; AlMangour, B.; Borkar, T. Effect of energy density and scanning strategy on densification, microstructure and mechanical properties of 316L stainless steel processed via selective laser melting. Mater. Sci. Eng. A 2020, 770, 138455. [Google Scholar] [CrossRef]
  87. Guo, M.; Gu, D.; Xi, L.; Zhang, H.; Zhang, J.; Yang, J.; Wang, R. Selective laser melting additive manufacturing of pure tungsten: Role of volumetric energy density on densification, microstructure and mechanical properties. Int. J. Refract. Met. Hard Mater. 2019, 84, 105025. [Google Scholar] [CrossRef]
  88. Ning, Y.; Wong, Y.; Fuh, J.; Loh, H. An approach to minimize build errors in direct metal laser sintering. IEEE Trans. Autom. Sci. Eng. 2006, 3, 73–80. [Google Scholar] [CrossRef]
  89. Sercombe, T.B.; Xu, X.; Challis, V.; Green, R.; Yue, S.; Zhang, Z.; Lee, P.D. Failure modes in high strength and stiffness to weight scaffolds produced by Selective Laser Melting. Mater. Des. 2015, 67, 501–508. [Google Scholar] [CrossRef]
  90. Song, B.; Zhao, X.; Li, S.; Han, C.; Wei, Q.; Wen, S.; Liu, J.; Shi, Y. Differences in microstructure and properties between selective laser melting and traditional manufacturing for fabrication of metal parts: A review. Front. Mech. Eng. 2015, 10, 111–125. [Google Scholar] [CrossRef]
  91. Du Plessis, A.; Kouprianoff, D.P.; Yadroitsava, I.; Yadroitsev, I. Mechanical Properties and In Situ Deformation Imaging of Microlattices Manufactured by Laser Based Powder Bed Fusion. Materials 2018, 11, 1663. [Google Scholar] [CrossRef]
  92. Edwards, P.; O’Conner, A.; Ramulu, M. Electron Beam Additive Manufacturing of Titanium Components: Properties and Performance. J. Manuf. Sci. Eng. 2013, 135, 061016. [Google Scholar] [CrossRef]
  93. Gu, D.; Shen, Y. Processing conditions and microstructural features of porous 316L stainless steel components by DMLS. Appl. Surf. Sci. 2008, 255, 1880–1887. [Google Scholar] [CrossRef]
  94. Wilbig, J.; de Oliveira, F.B.; Obaton, A.F.; Schwentenwein, M.; Rübner, K.; Günster, J. Defect detection in additively manufactured lattices. Open Ceram. 2020, 3, 100020. [Google Scholar] [CrossRef]
  95. Chen, Y.; Peng, X.; Kong, L.; Dong, G.; Remani, A.; Leach, R. Defect inspection technologies for additive manufacturing. Int. J. Extrem. Manuf. 2021, 3, 022002. [Google Scholar] [CrossRef]
  96. Yeganeh, M.; Shahryari, Z.; Talib Khanjar, A.; Hajizadeh, Z.; Shabani, F. Inclusions and Segregations in the Selective Laser-Melted Alloys: A Review. Coatings 2023, 13, 1295. [Google Scholar] [CrossRef]
  97. Jiao, Z.; Wu, X.; Yu, H.; Xu, R.; Wu, L. High cycle fatigue behavior of a selective laser melted Ti6Al4V alloy: Anisotropy, defects effect and life prediction. Int. J. Fatigue 2023, 167, 107252. [Google Scholar] [CrossRef]
  98. Zhang, Y.; Gao, Q. A Generalized Method for Dispersion Analysis of Guided Waves in Multilayered Anisotropic Magneto-Electro-Elastic Structures. Shock Vib. 2022, 2022, 1346719. [Google Scholar] [CrossRef]
  99. Miranda, E.; Aranas, C.; Rodrigues, S.; Silva, H.; Reis, G.; Paiva, A.; Dos Santos, J. Dispersion Diagram of Trigonal Piezoelectric Phononic Structures with Langasite Inclusions. Crystals 2021, 11, 491. [Google Scholar] [CrossRef]
  100. ASTM C393; Flexural Properties of Flat Sandwich Constructions. American Society for Testing and Materials: West Conshohocken, PA, USA, 2020. [CrossRef]
  101. ASTM C297; Standard Test Method for Flatwise Tensile Strength of Sandwich Constructions. American Society for Testing and Materials: West Conshohocken, PA, USA, 2017. [CrossRef]
  102. MSC Nastran 2022. 1 Linear Static Analysis User’s Guide; Hexagon AB: Irvine, CA, USA, 2022. [Google Scholar]
  103. MSC Nastran 2022. 1—Nonlinear (SOL 400) User’s Guide; Hexagon AB: Irvine, CA, USA, 2023. [Google Scholar]
  104. Raghu, S. Finite Element Modelling Techniques in MSC NASTRAN; Createspace Independent Publishing Platform: North Charleston, SC, USA, 2010. [Google Scholar]
  105. Martin, J.H.; Barnes, J.E.; Rogers, K.A.; Hundley, J.; LaPlant, D.L.; Ghanbari, S.; Tsai, J.T.; Bahr, D.F. Additive manufacturing of a high-performance aluminum alloy from cold mechanically derived non-spherical powder. Commun. Mater. 2023, 4, 39. [Google Scholar] [CrossRef]
  106. Rometsch, P.A.; Zhu, Y.; Wu, X.; Huang, A. Review of high-strength aluminium alloys for additive manufacturing by laser powder bed fusion. Mater. Des. 2022, 219, 110779. [Google Scholar] [CrossRef]
  107. Macneal, R.H. A simple quadrilateral shell element. Comput. Struct. 1978, 8, 175–183. [Google Scholar] [CrossRef]
  108. NASA. The NASTRAN Theoretical Manual, Level 17.5; NASA: Washington, DC, USA, 1981. [Google Scholar]
  109. Macneal, R.H. Finite Elements: Their Design and Performance (Mechanical Engineering); Mechanical Engineering; CRC Press: Boca Raton, FL, USA, 1993; Volume 89. [Google Scholar]
  110. Hughes. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Civil and Mechanical Engineering; Dover Publications: Mineola, NY, USA, 2000. [Google Scholar]
  111. Karamooz Ravari, M.; Kadkhodaei, M.; Badrossamay, M.; Rezaei, R. Numerical investigation on mechanical properties of cellular lattice structures fabricated by fused deposition modeling. Int. J. Mech. Sci. 2014, 88, 154–161. [Google Scholar] [CrossRef]
  112. Cui, S.; Gong, B.; Ding, Q.; Sun, Y.; Ren, F.; Liu, X.; Yan, Q.; Yang, H.; Wang, X.; Song, B. Mechanical Metamaterials Foams with Tunable Negative Poisson’s Ratio for Enhanced Energy Absorption and Damage Resistance. Materials 2018, 11, 1869. [Google Scholar] [CrossRef]
  113. Chen, X.; Tan, H. An effective length model for octet lattice. Int. J. Mech. Sci. 2018, 140, 279–287. [Google Scholar] [CrossRef]
  114. Melancon, D.; Bagheri, Z.; Johnston, R.; Liu, L.; Tanzer, M.; Pasini, D. Mechanical characterization of structurally porous biomaterials built via additive manufacturing: Experiments, predictive models, and design maps for load-bearing bone replacement implants. Acta Biomater. 2017, 63, 350–368. [Google Scholar] [CrossRef] [PubMed]
  115. Cheng, X.; Li, S.; Murr, L.; Zhang, Z.; Hao, Y.; Yang, R.; Medina, F.; Wicker, R. Compression deformation behavior of Ti–6Al–4V alloy with cellular structures fabricated by electron beam melting. J. Mech. Behav. Biomed. Mater. 2012, 16, 153–162. [Google Scholar] [CrossRef] [PubMed]
  116. Garrido, C.; Orbell, J.; Alabort, E.; Barba, D.; Reed, R. On the effect of processing defects on the performance of additively manufactured cellular materials. Unpublished manuscript. 2023. [Google Scholar]
  117. Buzug, T.M. Computed Tomography. In Springer Handbook of Medical Technology; Springer: Berlin/Heidelberg, Germany, 2011; pp. 311–342. [Google Scholar] [CrossRef]
  118. Barber, D.C.; Brown, B.H. Applied potential tomography. J. Phys. E Sci. Instrum. 1984, 17, 723–733. [Google Scholar] [CrossRef]
  119. Woodward, M.J.; Nichols, D.; Zdraveva, O.; Whitfield, P.; Johns, T. A decade of tomography. Geophysics 2008, 73, VE5–VE11. [Google Scholar] [CrossRef]
  120. Dastani, K.; Movahhedy, M.R.; Yu, H.; Khodaygan, S.; Zhang, L.; Wang, M.Y. Effect of geometric deviations on the strength of additively manufactured ultralight periodic shell-based lattices. Eng. Fail. Anal. 2023, 150, 107328. [Google Scholar] [CrossRef]
  121. Murr, L.; Quinones, S.; Gaytan, S.; Lopez, M.; Rodela, A.; Martinez, E.; Hernandez, D.; Martinez, E.; Medina, F.; Wicker, R. Microstructure and mechanical behavior of Ti–6Al–4V produced by rapid-layer manufacturing, for biomedical applications. J. Mech. Behav. Biomed. Mater. 2009, 2, 20–32. [Google Scholar] [CrossRef] [PubMed]
  122. Peters, M.; Kumpfert, J.; Ward, C.; Leyens, C. Titanium Alloys for Aerospace Applications. Adv. Eng. Mater. 2003, 5, 419–427. [Google Scholar] [CrossRef]
  123. Li, X.; Wang, C.; Zhang, W.; Li, Y. Fabrication and characterization of porous Ti6Al4V parts for biomedical applications using electron beam melting process. Mater. Lett. 2009, 63, 403–405. [Google Scholar] [CrossRef]
  124. Nielsen, L.F. Elasticity and Damping of Porous Materials and Impregnated Materials. J. Am. Ceram. Soc. 1984, 67, 93–98. [Google Scholar] [CrossRef]
Sustainability 16 01167 g001
Figure 1. Unit cells of the metamaterials used in this study and finite element models for sandwich beam cores. From left to right: face-center cubic (FCC), octet truss (OT) and truncated octahedron (TO) cells and their respective beams.
Figure 1. Unit cells of the metamaterials used in this study and finite element models for sandwich beam cores. From left to right: face-center cubic (FCC), octet truss (OT) and truncated octahedron (TO) cells and their respective beams.
Sustainability 16 01167 g001
Sustainability 16 01167 g002
Figure 2. Considered load cases for the composite metamaterial beams: 3Pb (left) and 4Pb (right) bending tests in the y z plane.
Figure 2. Considered load cases for the composite metamaterial beams: 3Pb (left) and 4Pb (right) bending tests in the y z plane.
Sustainability 16 01167 g002
Sustainability 16 01167 g003
Figure 3. Dimensions of a typical metamaterial unit cell: face-center cubic (FCC) cell.
Figure 3. Dimensions of a typical metamaterial unit cell: face-center cubic (FCC) cell.
Sustainability 16 01167 g003
Sustainability 16 01167 g004
Figure 4. The 3D finite element model for composed beam and octahedron lattice in Patran–Nastran.
Figure 4. The 3D finite element model for composed beam and octahedron lattice in Patran–Nastran.
Sustainability 16 01167 g004
Sustainability 16 01167 g005
Figure 5. The 3D finite element model of the metamaterial composite beam using TO cells, including details of the multipoint constraints interface (named glued contact in Patran–Nastran) and element types.
Figure 5. The 3D finite element model of the metamaterial composite beam using TO cells, including details of the multipoint constraints interface (named glued contact in Patran–Nastran) and element types.
Sustainability 16 01167 g005
Sustainability 16 01167 g006
Figure 6. Idealized drawing showing the three imperfections implemented in the finite element models: undulations (left), conicity in the edges of the lattice (middle), and porosity gradient (right).
Figure 6. Idealized drawing showing the three imperfections implemented in the finite element models: undulations (left), conicity in the edges of the lattice (middle), and porosity gradient (right).
Sustainability 16 01167 g006
Sustainability 16 01167 g007
Figure 7. Discretized beam elements showing a depiction of the conicity imperfection implemented (nonconstant section area).
Figure 7. Discretized beam elements showing a depiction of the conicity imperfection implemented (nonconstant section area).
Sustainability 16 01167 g007
Sustainability 16 01167 g008
Figure 8. Scheme of the computational modeling sequence.
Figure 8. Scheme of the computational modeling sequence.
Sustainability 16 01167 g008
Sustainability 16 01167 g009
Figure 9. Relation of the computed maximum stresses with the type and amount of defect for the two types of tests. (a) Undulation defects: correlation of the nodal displacement with the stress for each cell type. (b) Undulation defects: relation of the maximum stress with the percentage of elements suffering a nodal displacement. (c) Porosity defects: relation of the porosity (i.e., Young modulus) with the maximum stress. (d) Conicity defects: relation of the maximum stress with the percentage of reduction of the middle section of the edges (% conicity).
Figure 9. Relation of the computed maximum stresses with the type and amount of defect for the two types of tests. (a) Undulation defects: correlation of the nodal displacement with the stress for each cell type. (b) Undulation defects: relation of the maximum stress with the percentage of elements suffering a nodal displacement. (c) Porosity defects: relation of the porosity (i.e., Young modulus) with the maximum stress. (d) Conicity defects: relation of the maximum stress with the percentage of reduction of the middle section of the edges (% conicity).
Sustainability 16 01167 g009
Sustainability 16 01167 g010
Figure 10. Comparison of the deformation and distortion suffered by two metamaterial cores in the composite beam: FCC and TO (4Pb test). The depicted displacement is scaled at a maximum of 30% of the beam span.
Figure 10. Comparison of the deformation and distortion suffered by two metamaterial cores in the composite beam: FCC and TO (4Pb test). The depicted displacement is scaled at a maximum of 30% of the beam span.
Sustainability 16 01167 g010
Sustainability 16 01167 g011
Figure 11. Metamaterial unit cell and tested sample during the virtual compression test.
Figure 11. Metamaterial unit cell and tested sample during the virtual compression test.
Sustainability 16 01167 g011
Sustainability 16 01167 g012
Figure 12. The modulus of elasticity versus each solid ideal fraction s. The figure shows a comparison of different models with defects (damaged models) and without defects (original model), where the initial geometry for the finite element model is created with Patran (FEM CAD), and finally the model with the geometry for the finite elements obtained from X-ray data (FEM X-ray). Also, the results of the rule of mixtures (cross sectional and volumetric) are represented.
Figure 12. The modulus of elasticity versus each solid ideal fraction s. The figure shows a comparison of different models with defects (damaged models) and without defects (original model), where the initial geometry for the finite element model is created with Patran (FEM CAD), and finally the model with the geometry for the finite elements obtained from X-ray data (FEM X-ray). Also, the results of the rule of mixtures (cross sectional and volumetric) are represented.
Sustainability 16 01167 g012
Table 2. Characteristics of the Ti6Al4V unit cells for different solid fractions s = 15 , s = 25 and s = 35 and different the nominal diameters (NDs). Note that the nominal Young modulus E = 114 GPa , the Poisson ratio ν = 0.33 and the height h = 1.36 mm are the same for the three cases.
Table 2. Characteristics of the Ti6Al4V unit cells for different solid fractions s = 15 , s = 25 and s = 35 and different the nominal diameters (NDs). Note that the nominal Young modulus E = 114 GPa , the Poisson ratio ν = 0.33 and the height h = 1.36 mm are the same for the three cases.
CellSection TypeND (mm)E (GPa) ν Height (mm)
Cubic edge (s = 15)Circular0.331140.331.36
Cubic edge (s = 25)Circular0.421140.331.36
Cubic edge (s = 35)Circular0.531140.331.36
Table 3. Nodal deviation extracted from the data study in [116]. The smaller the deviation range ( μ m), the greater the density distribution per range (%) for the three s fractions studied. Each column adds to the total of 100% for each axis.
Table 3. Nodal deviation extracted from the data study in [116]. The smaller the deviation range ( μ m), the greater the density distribution per range (%) for the three s fractions studied. Each column adds to the total of 100% for each axis.
Density Distribution per Range (%)
Deviation Range ( μ m) s = 0.15 s = 0.25 s = 0.35
xyzxyzxyz
0–15818676868879918980
15–30759444226
30–45435326213
45–60324224214
60–75222222133
75–90222222222
90–105102103022
Table 4. Conicity for 12 elements in each edge of the beam extracted from data study in [116]. Each row is the % of material within the fraction s that has the minimum diameter, for example, 200, and the maximum, for example, 225. Each column adds the total of the possible for each fraction s (100%).
Table 4. Conicity for 12 elements in each edge of the beam extracted from data study in [116]. Each row is the % of material within the fraction s that has the minimum diameter, for example, 200, and the maximum, for example, 225. Each column adds the total of the possible for each fraction s (100%).
Diameter Range (μm)Density Distribution per Range (%)
s = 0.15 s = 0.25 s = 0.35
200–225300
225–250600
250–2751100
275–3001800
300–325301.40
325–350182.60
350–37574.20
375–40049.20
400–425223.40.2
425–450128.32
450–475018.24
475–50006.36.4
500–52504.322
525–55001.829
550–57500.324
575–600008
600–625002.3
625–650002.1
Table 5. Pore distribution in the elements extracted from data study in [116]. Each row is the % of material within the fraction s that has the minimum number of pores, for example, 0, and the maximum, for example, 1.
Table 5. Pore distribution in the elements extracted from data study in [116]. Each row is the % of material within the fraction s that has the minimum number of pores, for example, 0, and the maximum, for example, 1.
Porosity Range (%)Density Distribution per Range (%)
s = 0.15 s = 0.25 s = 0.35
0–15.412.37.9
1–28.918.614.2
2–322.925.629.6
3–416.518.618.6
4–514.614.610.4
5–68.23.23.2
6–79.21.95.8
7–85.11.54.5
8–92.10.82.1
9–100.90.90.9
10–111.20.81.3
11–122.11.21.4
12–132.90.00.1
13–140.00.00.0
14–150.00.00.0
15–160.00.00.0
Table 6. Comparison of the experimental Young modulus E ( MPa ) [116] and the nominal moduli obtained by the two simulation approaches. The CAD approach refers to the nominal cell, whereas the X-ray approach corresponds to a cell with the actual topology of the cell obtained from X-rays. Note the important difference between the design values and the actual experimental values. Additional defects are still not incorporated.
Table 6. Comparison of the experimental Young modulus E ( MPa ) [116] and the nominal moduli obtained by the two simulation approaches. The CAD approach refers to the nominal cell, whereas the X-ray approach corresponds to a cell with the actual topology of the cell obtained from X-rays. Note the important difference between the design values and the actual experimental values. Additional defects are still not incorporated.
CellExperimentSimulation (CAD)Simulation (X-ray)
Cubic edge (s = 15)3471 ± 577193 ± 318095 ± 36
Cubic edge (s = 25)7665 ± 69115,894 ± 8216,488 ± 80
Cubic edge (s = 35)12,546 ± 91223,798 ± 15225,471 ± 137
Table 7. Young’s moduli E (MPa) for the simulation when defects have been incorporated. Twelve elements per edge of the cell cube for the tested samples during the compression test.
Table 7. Young’s moduli E (MPa) for the simulation when defects have been incorporated. Twelve elements per edge of the cell cube for the tested samples during the compression test.
CellExperimental
Modulus (MPa)		Simulation (CAD) with Defects (Maximum)Simulation (CAD) with Defects (Minimum)
Cubic edge (s = 15)3471 ± 573863.703785.29
Cubic edge (s = 25)7665 ± 6917483.227305.15
Cubic edge (s = 35)12,546 ± 91212,152.5011,873.99
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Vera-Rodríguez, G.; Moreno-Corrales, L.; Marín-González, I.; Barba, D.; Montáns, F.J.; Sanz-Gómez, M.Á. Incorporation of Defects in Finite Elements to Model Effective Mechanical Properties of Metamaterial Cells Printed by Selective Laser Melting. Sustainability 2024, 16, 1167. https://doi.org/10.3390/su16031167

AMA Style

Vera-Rodríguez G, Moreno-Corrales L, Marín-González I, Barba D, Montáns FJ, Sanz-Gómez MÁ. Incorporation of Defects in Finite Elements to Model Effective Mechanical Properties of Metamaterial Cells Printed by Selective Laser Melting. Sustainability. 2024; 16(3):1167. https://doi.org/10.3390/su16031167

Chicago/Turabian Style

Vera-Rodríguez, Gonzalo, Laura Moreno-Corrales, Iván Marín-González, Daniel Barba, Francisco J. Montáns, and Miguel Ángel Sanz-Gómez. 2024. "Incorporation of Defects in Finite Elements to Model Effective Mechanical Properties of Metamaterial Cells Printed by Selective Laser Melting" Sustainability 16, no. 3: 1167. https://doi.org/10.3390/su16031167

APA Style

Vera-Rodríguez, G., Moreno-Corrales, L., Marín-González, I., Barba, D., Montáns, F. J., & Sanz-Gómez, M. Á. (2024). Incorporation of Defects in Finite Elements to Model Effective Mechanical Properties of Metamaterial Cells Printed by Selective Laser Melting. Sustainability, 16(3), 1167. https://doi.org/10.3390/su16031167

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop