Multi-Criteria Model for Identifying and Ranking Risky Types of Maritime Accidents Using Integrated Ordinal Priority Approach and Grey Relational Analysis Approach

Abstract

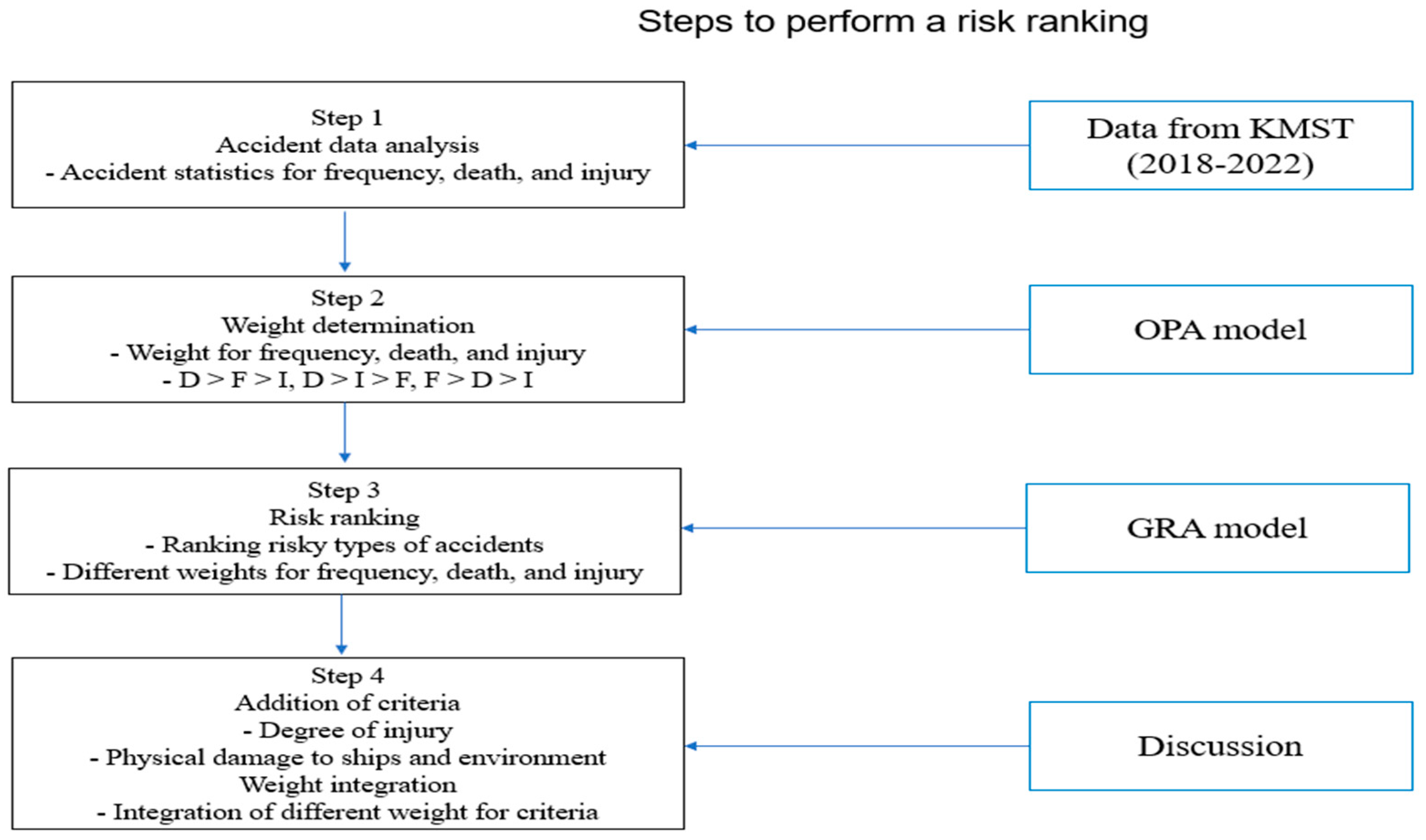
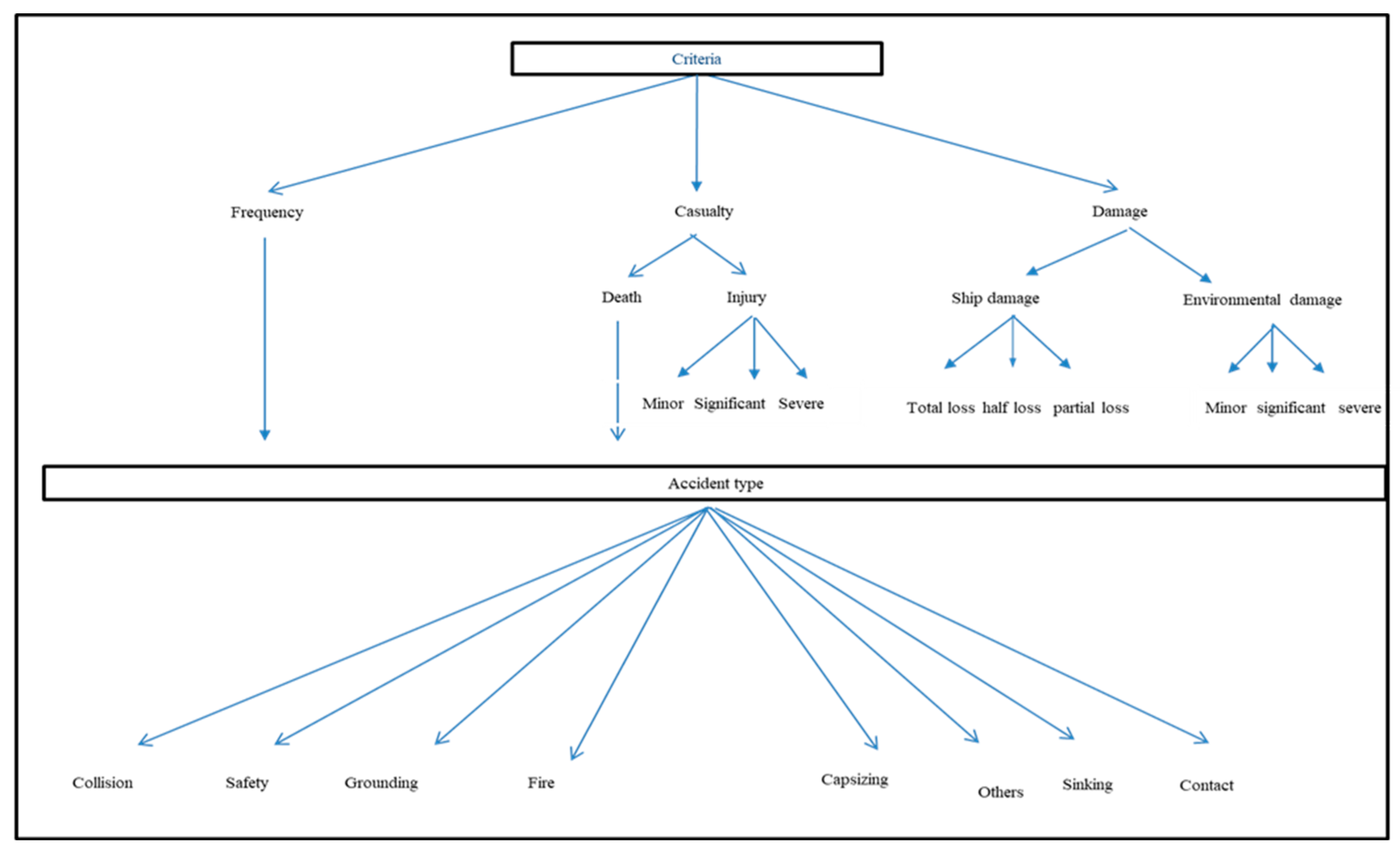
Accidents in marine operations are occurring consistently despite government safety initiatives and efforts to lower the number of accidents and the ensuing human casualties. Since each accident type has a different frequency and casualty rate, identifying risky accident types is important to determine the priority for taking necessary risk reduction actions. Usually, a risk is calculated using two criteria, i.e., the frequency and fatality of an accident. However, the accident statistics show that for the last 5 years from 2018 to 2022, the injury rate is more than three times the death rate in maritime accidents in Korean waters. Considering the importance of injury, unlike other previous studies, we perform a risk analysis with three criteria, i.e., frequency, death, and injury to complement the conventional risk calculation methods, which can help decision-makers allocate the limited resources to the riskiest types of accidents in order of priority. In doing so, we employed an integrated ordinal priority approach (OPA) and grey relational analysis (GRA) method to assign proper weight to each criterion and rank eight accident types. We categorized the accidents types into three different groups where safety accidents and collisions were ranked as the most dangerous types. The combined OPA and GRA technique has been effectively applied to other risky industries, as well as the maritime industry. Additionally, the proposed method is suitable for multi-criteria models when each criterion has a different importance. Finally, the method can be integrated into the framework of the risk ranking process to enhance the analysis results.

1. Introduction

The IMO (International Maritime Organization) provides guidelines to evaluate the accident risk in the maritime industry, and the purpose of a risk analysis is to enhance maritime safety, including the protection of life, the marine environment, and property [1]. The term risk is generally defined as a function of two factors: the frequency and consequence of an unwanted event. The consequence of an event includes fatality, economic loss, or damage to physical structures such as ships, port facilities, operating systems, etc. Usually, the risk of an accident is computed by the product of frequency and consequence, and the overall risk score is obtained. The calculated risk values are then compared for ranking and prioritizing risks among different accidents. The purpose of ranking the events is to assign limited resources to the most serious risk items [2], and for maritime accidents, decision-makers choose risk mitigation measures in order of priority so that resources can be assigned to the riskiest accident types. However, often in practice, the risk score alone is not sufficient to identify and rank accidents.

Among the various methodologies currently in use, the risk matrix method is one of the most widely used methods due to its simplicity and availability for risk ranking in marine activities [3]. A risk matrix is an (n × n) matrix consisting of two axes (column and row) representing the consequence and frequency of an accident. With this method, risk assessors can rank accidents and take risk mitigation actions in priority order.

However, various sets of frequencies and consequences may come up with the same risk value (consequently the same risk ranking), even though the implications of the same risk value may be significantly different (

Table 1. A risk matrix for the risk calculation.

Risk Index
		Severity (Consequence)
		CI 1	2	3	4
FI	Frequency	Minor (0.01)	Significant (0.1)	Severe (1)	Catastrophic (10)
7	Frequent	8	9	10	11
6		7	8	9	10
5	Reasonably Probable	6	7	8	9
4		5	6	7	8
3	Remote	4	5	6	7
2		3	4	5	6
1	Extremely Remote	2	3	4	5

Source: IMO guideline (2018) [1].

). Therefore, this may result in wrong or inefficient decision-making, wasting time and resources available.

Another disadvantage of existing risk ranking methods, including the risk matrix, is that they do not consider the relative importance between frequency and consequence. In many real-life applications, these two factors may have different weights.

For the risk calculation of maritime accidents, the IMO suggests that injuries be converted into equivalent fatalities, depending on the degree of severity. With a single fatality set to one, injuries are assigned corresponding numbers and the resulting fatalities are calculated by adding these numbered injuries. However, over the last five years from 2018–2022, the total number of injuries in maritime accidents was 1934, which is more than 3.5 times the fatalities at 545. Especially, for aquatic leisure equipment accidents, the injury was shown to be eight times higher than death.

For the land transportation system, road accident injuries are one of the major causes leading to death, and the Montenegro government adopted an action plan to reduce fatalities by 50% and injuries by 30% by 2019 [4]. Additionally, according to casualty statistics for industrial accidents [5], the number of injured workers in 2022 was 106,038, which is 47.7% higher than the fatalities at 2223. Among the injured workers, 29,635 were treated for more than 6 months, followed by 39,487 workers treated between 3 months and 6 months. More than 80% of injuries needed at least 1 month of medical treatment. The accident frequency and severity rates vary from industry to industry [2], and injury accounts for the major human casualty in many risky industries. However, there are few studies dealing with injury as an independent factor in the risk analysis process.

In this study to address the above-mentioned problems inherent in traditional risk calculation, we propose a multi-criteria (factors) risk ranking approach where the ordinal priority approach (OPA) and grey relational analysis (GRA) are employed to weight each criterion and rank risky types of maritime accidents, respectively. Considering the adverse effects of injury on human lives and economic activities, unlike other previous studies, we extend the scope of analysis to three criteria, i.e., frequency, death (fatality), and injury.

The purpose of the study is to propose an integrated OPA and GRA approach to rank risky maritime accident types in an effort to complement existing risk ranking methods within the risk assessment framework. The remainder of the study is as follows. In Section 2, the literature on risk analysis methods commonly used for maritime accidents is reviewed and the combined OPA and GRA approach is described. In Section 3, a multi-criteria decision-making model is constructed where the combined OPA and GRA method is employed to rank risky types of maritime accidents. For empirical illustration, accident data over the 2018 to 2022 period from the Korean Maritime Safety Tribunal (KMST) are used. Moreover, some issues concerning additional criteria and weight adjustment methods are briefly expressed. Additionally, in Section 4, conclusions and limitations, including future studies, are discussed.

2. Literature Review

The literature review consists of two parts: risk analysis tools and multi-criteria decision-making techniques. A risk analysis of maritime accidents basically focuses either on estimating the frequency (probability) and consequence of accidents or determining the risk level in terms of a numerical value for the improvement of maritime safety if the risk level is unacceptable.

For estimation, there exist many useful analysis tools, quantitative or qualitative, depending on the availability and reliability of accident data. For example, expert judgment is employed when data are not reliable or limited, and the decisions on frequency and consequence are determined by the expertise. Fault Tree Analysis (FTA) and Event Tree Analysis (ETA) are systematic and analytical methods that are widely used for the estimation of frequency and consequence probabilistically, where FTA is effectively used to predict frequency (probability) and ETA is to estimate the consequences of accidents. An FTA represents causal relationships among different events organized in a top-down hierarchical order with AND or OR logic gates, and the probabilities of events at all levels from bottom to top are calculated.

The top event probability is interpreted as the probability of system failure, equipment malfunction, maritime vessel accident, etc. As an application of FTA to maritime vessel accidents, Köse et al. (1998) [6] and Kim et al. (2017) [7] considered various factors and computed corresponding probabilities. On the other hand, an ETA is used when one is interested in the effects of a failure, malfunction, or an accident. After an initiating event occurs, which may be the top event of FTA, ensuing events are bifurcated with YES (success) or NO (failure) logic. These events usually involve mitigation measures to prevent the accident from propagating further and, depending on YES or NO for each ensuing event, there exist several paths leading to different consequences, i.e., different fatalities or physical damages to the system. Cho and Kim (2017) [8] estimated human casualties and environmental damage in hazardous material transportation accidents with ETA.

Other useful probabilistic techniques applied in accident risk analysis include a Bayesian Network (BN), which uses conditional probabilities among influencing variables related to accidents. Some of the recent studies applied to maritime accidents are briefly presented. Antão and Soares (2019) [9] constructed a BN to investigate the influence of human factors contributing to ship accidents. Ung (2021) [10], using a BN, created a navigation risk estimation model to investigate the characteristics of maritime accidents and showed that the accident types of collision, grounding, and fire required more attention. Hänninen et al. (2014) [11], for the improvement of maritime safety, applied a BN method and suggested that IT systems are strongly advised for safety management on vessel navigation. Wu et al. (2021) [12] constructed a decision-making BN for consequence reduction in collision accidents, which can be utilized as a useful emergency response model. Recently. Kim et al. (2024) [13] identified and analyzed the risk factors in marine leisure activities with a BN and calculated corresponding probabilities leading to accidents. They suggested that more legal and institutional studies need to be performed to improve marine safety.

On the other hand, fuzzy set theory can be a useful tool to be applied in many risk-related applications when linguistic expressions are required due to the lack and/or uncertainty of accident data. For the use of the method, basically, the frequency (probability) and consequence of an accident are expressed by corresponding membership functions with different shapes. Sur and Kim (2020) [14] calculated the risk value for each accident type with fuzzy set theory using maritime accident data.

Some of the other applications with fuzzy theory are Massami (2014) [15] and Liu et al. (2017) [16] for road traffic accidents, Lu (2016) [17] for the chemical industry, and Yang et al. (2018) [18] and Wang et al. (2019) [19] for the impact of climate change.

For a risk-level determination, as one of the universally accepted risk ranking methods, risk matrices are effectively used in decision-making for risk improvement [20] because of their simple structure for calculating the risk value. The Frequency Index (FI) and Consequence Index (CI) of a risk matrix described in the IMO guidelines are shown in Table 1, where, for example, if an accident’s severity (consequence) is minor and the frequency is frequent, the resulting risk value is calculated by summing two numbers: one and seven. The risk level is then classified as one of three categories: acceptable, ALARP (as low as reasonably practicable), or unacceptable. If the risk level is unacceptable, risk mitigation measures should be implemented at all costs to lower the risk to the level of ALARP. For the application of the ALARP principle, see MSC-MEPC.2/Circ.12/Rev.2 (2018) [1]. For the application of the risk matrix in the maritime industry, Pallis (2017) [21] calculated the risk of fatality in container ports and Akyildiz (2015) [22] evaluated the risk level of fishing vessel accidents based on the step-by-step procedure described by the IMO. A combined approach for the risk level determination was performed by Asuelimen et al. (2020) [23] in seismic vessel accidents using the risk matrix and FTA method.

The traditional risk matrix uses predefined frequency and consequence categories. However, if they are poorly or wrongly defined, the resulting risk values may be of little help for risk management [24]. For the weaknesses and strengths of the risk matrix, see Alp (2006) [25]. To sum up, despite its simplicity, use of the risk matrix has difficulty in both determining the frequency and consequence categories objectively in the design stage and allocating the frequency and consequence of an accident properly, which often leads to wrong or incorrect conclusions on the decision of the risk level.

Additionally, as shown in Table 1, one disadvantage of the risk matrix in risk ranking is that there are four different possible (frequency and consequence) choices having the same risk value of eight, diagonally from upper left to lower right. Other risk values also have multiple frequency and consequence pairs with the same risk ranking.

In the risk matrix, injury is converted into a fatality equivalent. The numerical values in parentheses following qualitative descriptions for severity represent equivalent numbers to those linguistic terms where the expression ‘severe’ is a single fatality (or multiple severe injuries) and 10 represents multiple fatalities. The numbers 0.01 and 0.1 for minor and significant represent single or minor injuries and multiple or severe injuries, respectively. The conversion coefficients for minor and significant injuries were used by Chlomoudis et al. (2016) [26] to calculate human casualties in container terminals, whereas Kim et al. (2023) [27], in their study, converted missing and injury to fatality equivalents by assigning 0.996 and 0.043, respectively. Another application was found by Cho and Kim (2017) [8] for the risk evaluation of human casualties in a maritime accident, where six levels of severity (minor, moderate, serious, severe, critical, and fatal) from the VSL (Value of Statistical Life) guideline was used for road traffic accidents with fatal set to one and other injuries converted according to their relative importance against fatality. Xu et al. (2023) [28], in an extensive review of maritime transportation safety management, introduced various risk analysis methodologies and future potential issues for the safe sustainability of the maritime industry.

A multi-criteria decision-making (MCDM) problem deals with conflicting criteria for selecting the best alternative from among a feasible set of alternatives. Wang et al. (2009) [29] reviewed crucial criteria and MCDM methods in a sustainable energy decision-making problem. Janackovic et al. (2011) [30] presented safety-related factors and MCDM methods in occupational safety management systems. A variety of MCDM techniques were introduced by Alinezhad and Khalili (2019) [31].

Among others grey relational analysis (GRA) has been applied to a variety of MCDM problems, where the rankings of alternatives are determined in the order of competitiveness by measuring the performance of each criterion [32]. GRA can analyze factors effectively with less data, which overcomes the disadvantages of traditional statistical techniques [33]. For the studies associated with marine accidents, Liu and Wu (2004) [33] ranked major human factors causing ship collisions using GRA and selected improper lookout and ship handling as the most unsafe factors, whereas improper routing plans and failure to fix were shown to be the least unsafe. Su et al. (2019) [34] performed GRA to rank the types of oil spill accidents from oil tankers. Among seven major different types, the ‘other’ factor (unlisted reasons, such as illegal discharge of wasted oil) was ranked first for a smaller oil spill less than 7 tons in quantity, and collision was the main factor for a larger oil spill more than 7 tons. Pillay and Wang (2003) [2] applied GRA to FMEA (Failure Mode and Effect Analysis) to rank the risks of three components, failure probability, failure severity, and the probability of not detecting failure, for an ocean-going fishing vessel. Wang and Lee (2010) [35], in their study on the risk analysis of Keelung harbor, applied GRA to investigate the relationship between maritime casualties and accident sites, where coastal and in-port areas were the risky accident sites and the main casualties were fire/explosion and machinery damage.

As a diverse application of GRA, Nayakappa et al. (2019) [36] expressed the methodology of GRA as one of the good options for decision-making in complex problems and reviewed its application in various fields, such as manufacturing/production and service operations, which involve multiple selection attributes. Some of the applications are described by Hsiao et al. (2017) [37] in the study of selecting the best product design, and they applied the GRA technique with five criteria in the production planning problem. Lo and Liou (2018) [38] integrated GRA with the FMEA method to determine the risk priority for a production system. Xu and Xu (2018) [39] considered GRA with safety criteria to rank mine enterprises for safe mine production in an effort to prevent accidents leading to human deaths. Stanujkic et al. (2013) [40], in ranking Serbian banks, compared well-known MCDM methods, including GRA, and expressed the advantages and disadvantages of the techniques. Yu and Wu (2016) [41] selected nine influencing factors for the development of the tourism industry.

From a logistics point of view, Cai (2017) [42] chose the best mode of freight transportation to enhance the economy of the region, and Malek et al. (2017) [43] ranked suppliers in a supply chain system with various factors. Sur and Kim (2020) [32] used GRA and ranked beneficial countries by opening the Northern Sea Route between Asia and Europe. However, few studies consider GRA in the marine industry to rank maritime accidents.

Recently, studies on further development of calculation tools and main causes for accidents have been performed. Rakonjac et al. (2021) [44] structured hierarchical indicators for road safety management and introduced the GRA methodology to assign weights to multi-layered decision-making problems with criteria and sub-criteria in a hierarchical order. Dominguez-Péry et al. (2021) [45] provided a review on maritime accidents related to human errors and identified the main causes for accidents. To overcome the uncertainty inherent in the traditional risk matrix, Kim et al. (2023) [27] proposed a probabilistic risk matrix using the Markov chain method with which a long-term expected risk value was estimated.

In this study, we construct a multi-criteria model for ranking risky types of maritime accidents. For multi-criteria problems, it is required to assign a proper weight to each criterion, depending on the degree of importance in ranking alternatives to be considered. Subjective weighting methods, such as pairwise comparisons among criteria, are the most widely used in decision-making [30]. However, in many real-world applications, expert opinion or judgment on criteria may be inaccurate or unreliable, resulting in the wrong assignment of weights. To handle this uncertainty, Ataei et al. (2020) [46] proposed a method of ordinal priority approach (OPA) that simply ranks the criteria. We employ OPA to compute the weights by prioritizing criteria in order of importance and the overall ranking of risky maritime accident types is determined by GRA.

Based on the above literature review on risk analysis tools, the differences between existing methods and the proposed technique are summarized as follows. First, criteria weights are objectively determined through OPA, whereas criteria are not weighted for conventional methods. Second, the GRA is used to rank risky accident types, and efficient risk mitigation strategies to reduce the frequency and/or human casualties can be planned and implemented. However, the conventional methods usually require risk criteria to determine the degree of resulting risk. Third, the combined method can be extended to risk ranking problems with more criteria. Moreover, the OPA–GRA method can be integrated with other risk methods to improve the accuracy of the results. In

Table 2. Comparison of risk calculation methods.

	FTA-ETA	Risk Matrix	Fuzzy Set	OPA-GRA
Tool	Probability	Numerical value or linguistic expression	Membership functions	Mathematical formula
Criteria	Frequency Fatality	Frequency Fatality	Frequency fatality	Frequency Fatality Injury
Extension to multiple criteria	No	No	Possible	Yes
Weight	No	No	No	Yes (OPA)
Risk result	Numerical value	Numerical value	Numerical value or linguistic expression	Risk ranking (GRA)
Risk assessment criteria	ALARP principle	ALARP principle	ALARP principle	Not required
Risk reduction measures	Hard to identify the priority	Hard to identify the priority	Hard to identify the priority	Easy to identify the priority

below, major risk calculation techniques are compared.

3. Ranking Risky Types of Maritime Accidents

The stepwise procedure for the risk ranking analysis is stated below [Figure 1]. The first step is to analyze the maritime accident data from KMST focusing on frequency (F), death (D), and injury (I). In step 2, using the OPA method, we assign corresponding weights to three criteria based on the analysis results from step 1. Since existing risk ranking methods perform a risk analysis by assuming equal importance between the frequency and consequence, in this study, we consider three possible cases for weight assignment, i.e., (1) D > F > I, (2) D > I > F, and (3) F > D > I. In step 3, the risk ranking of accident types is performed using the GRA method with weights for the criteria obtained in step 2. The ranking results are then compared and checked for the effect of weight changes on the ranking order. Step 4 discusses topics on additional criteria such as physical loss/damage and weight adjustment when each criterion has different weights.

Based on the diagram depicted in Figure 1, we proceed as follows.

3.1. Accident Data Analysis

The maritime accidents and casualty rates are briefly described as follows. For the last five years, from 2018–2022, the total number of maritime accidents that occurred was 14,381 and fishing vessel accidents accounted for 9401 (65.4%) among all ship types.

The total number of human casualties was 545 fatalities, including missing and 439 (80.6%) due to fishing vessel accidents. Injuries were 1943, more than three times the fatalities.

As shown in the above statistics, the fishing vessel has the highest accident frequency and human casualties. In this study, we confine ourselves to fishing vessel accidents leading to casualties for the risk ranking. In general, the maritime accident frequency is not necessarily proportional to human casualties and they vary from one accident type to another, as seen in

Table 3. Accident statistics for frequency, death, and injury among accident types.

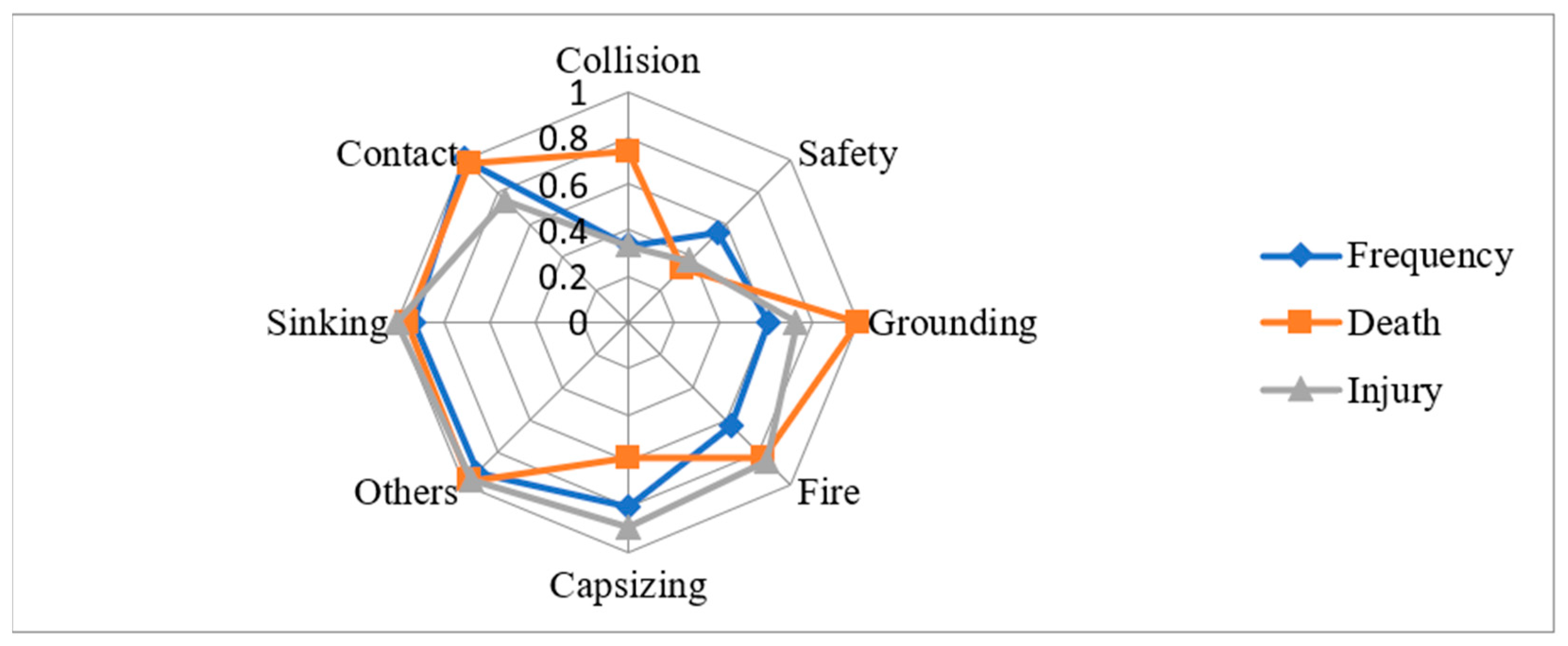
	Frequency (Ranking)	Death (Ranking)	Injury (Ranking)
Collision	1684 (1)	46 (3)	605 (1)
Safety	731 (2)	255 (1)	498 (2)
Grounding	586 (3)	2 (8)	119 (3)
Fire	537 (4)	28 (4)	62 (5)
Capsizing	282 (5)	90 (2)	48 (6)
Others	141 (6)	6 (6)	20 (7)
Sinking	137 (7)	7 (5)	9 (8)
Contact	77 (8)	5 (7)	108 (4)

Others: Life preserver damage, facility damage, propeller damage, steering gear damage, etc. Source: https://www.kmst.go.kr/web/index.do (accessed on 10 May 2024).

below, where the ranking of accident types is presented in parentheses under each criterion in decreasing order of occurrence. Safety is ranked 1st for death but 2nd in both frequency and injury. For contact accidents, frequency is ranked 8th, death is 7^th, and injury is 4th. Other accident types also differ in rankings under different criteria. The frequency is the number of ships, and death and injury are the number of people.

3.2. Weight Determination for Three Criteria by an Ordinal Priority Approach (OPA)

In practice, for a multi-criteria decision-making problem, even the best alternative hardly reflects the ideal level of all the criteria because the criteria usually conflict with each other. Since the criteria have varying importance, they need to be weighted [47,48] and it is crucial to assign proper weights to the criteria, considering the relative importance among death, frequency, and injury in our case. Common criteria are arranged in hierarchical order and compared in a pairwise manner for the weight calculation. However, experts may not have enough expertise or knowledge of the criteria, and it is difficult to assign proper weights to criteria with a pairwise comparison.

Therefore, to avoid uncertainty in the weight determination, instead of applying existing weighting methods, we employ the ordinal priority approach [46,49], which only requires the selection of criteria in order of importance. Since there are few previous studies concerning weight assignments to frequency and consequence in risk analyses, we consider three possible cases for the preference of one criterion over another: (1) death (D) > frequency (F) > injury (I), (2) death (D) > injury (I) > frequency (F), and (3) frequency (F) > death (D) > injury (I). As death is a more critical casualty than injury, we exclude the case of frequency (F) > injury (I) > death (D). The weights for criteria are obtained by the following linear programming model [46]:

MaximizeZ

(1)

Subject to

Z ≤ j(r(Wjk(r) − Wjk(r + 1)))   for all j, k, r

(2)

Z ≤ jm(Wjk(m)  for all j, m

(3)

$${\sum }_j^n{\sum }_k^m\mathrm{W}\mathrm{j}\mathrm{k}=1$$

(4)

Wjk ≥ 0  for all j, k

(5)

where Z is an objective function; j is the index of preference of criteria, j = 1, 2,…, n; k is the index of maritime accident types, k = 1, …, m; and Wjk(r) is a weight of accident type k having rth rank under criterion j. Equation (4) represents the sum of all weights as one. The weight of criterion j is obtained from Equation (6) as follows:

$$\mathrm{Wj}={\sum }_k^m\mathrm{W}\mathrm{j}\mathrm{k} \mathrm{\text{for}} \mathrm{\text{all}} \mathrm{\text{j}}$$

(6)

Using Equations (1)–(6), computed weights for criteria for the three cases are shown in

Table 4. Weights for criteria with different orders of importance.

Order of Importance	Death	Frequency	Injury
D > F > I	0.567208	0.243722	0.189068
D > I > F	0.558142	0.162791	0.279069
F > D > I	0.272934	0.545109	0.181956

.

3.3. Risk Ranking of Accident Types by the Grey Relational Analysis (GRA)

GRA was first proposed by Ju-Long (1982) [50] and is suitable for making decisions in ranking accidents with incomplete information [2]. Unlike other statistical analysis methods that deal with a large amount of sampling data, grey relational analysis requires less data [33]. Using the weights for criteria presented in Table 4, we employ GRA to rank accident types. The GRA requires comparative series, criteria, and standard series with which the risk ranking of alternatives is calculated by the following steps.

3.3.1. Normalization of Original Data, if Required

If criteria are measured in different units, the original data need to be normalized based on the benefit or cost type to make them unitless.

3.3.2. Construction of a Comparative Series

Construct a matrix with criteria and alternatives.

$$x=\left(\begin{array}{ccccc}{x}_1\left(1\right)& x_1\left(2\right)& x_1\left(3\right)& \cdots & x_1\left(m\right)\\ x_2\left(1\right)& x_2\left(2\right)& x_2\left(3\right)& \cdots & x_2\left(m\right)\\ x_3\left(1\right)& x_3\left(2\right)& x_3\left(3\right)& \cdots & x_3\left(m\right)\\ ⋮& ⋮& ⋮& & ⋮\\ x_n\left(1\right)& x_n\left(2\right)& x_n\left(3\right)& \cdots & x_n\left(m\right)\end{array}\right)$$

(7)

where

• x_i(j) = the value of alternative i under criterion j,
• m = the number of criteria, and
• n = the number of alternatives.

3.3.3. Determination of a Standard Series

A standard series represents the desired level of all the criteria and is denoted by

$$x_0=(x_0\left(1\right), x_0\left(2\right), x_0\left(3\right)\dots x_0(m\left)\right)$$

(8)

3.3.4. Calculation of the Grey Relational Coefficient (GRC: $\mathsf{\gamma }({\mathrm{x}}_0\left(\mathrm{j}\right),{\mathrm{x}}_{\mathrm{i}}\left(\mathrm{j}\right))$

The GRC is calculated using the following equation:

$$\mathsf{\gamma }(x_0\left(j\right), x_i\left(j\right))=\frac{{{\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{i}}\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{j}}\left|x_0\left(j\right)-x_i\left(j\right)\right|+\mathsf{\zeta }{{\mathrm{m}\mathrm{a}\mathrm{x}}_{\mathrm{i}}\mathrm{m}\mathrm{a}\mathrm{x}}_{\mathrm{j}}|x_0\left(j\right)-x_i\left(j\right)|}{\left|x_0\left(j\right)-x_i\left(j\right)\right|+\mathsf{\zeta }{{\mathrm{m}\mathrm{a}\mathrm{x}}_{\mathrm{i}}\mathrm{m}\mathrm{a}\mathrm{x}}_{\mathrm{j}}|x_0\left(j\right)-x_i\left(j\right)|}$$

(9)

where

• ζ is the distinguishing coefficient with ζ ∈ [0, 1], and usually ζ = 0.5 is used.

3.3.5. Assignment of Weights to Criteria

The weights for criteria are determined depending on the relative importance and the sum equals one.

$${\sum }_{\mathrm{j}}{\mathrm{w}}_{\mathrm{j}}=1$$

(10)

3.3.6. Calculation of the Grey Relational Grade (GRG)

Finally, the grey relational grade (GRG: $\mathrm{\Gamma }\left(x_0,x_i\right)),$ representing the degree of relation, is computed using the following equation:

$$\mathrm{\Gamma }\left(x_0,x_i\right)={\sum }_{\mathrm{j}}{\mathrm{w}}_{\mathrm{j}}\mathsf{\gamma }(x_0\left(j\right), x_i\left(j\right))$$

(11)

3.3.7. Determination of the Rank of Alternatives

The higher the value produced from GRG, the higher the rank of alternatives.

Following the procedure for GRA summarized above, we calculate the rank of accident types. Since all the criteria are cost typed, i.e., the smaller the better, we apply Equation (12) for the normalization of the original data as follows:

$${\mathrm{x}}_{{\mathrm{i}}^{\mathrm{*}}}\left(\mathrm{j}\right)=\frac{\mathrm{m}\mathrm{a}\mathrm{x}{\mathrm{X}}_{\mathrm{i}}\left(\mathrm{j}\right){-\mathrm{X}}_{\mathrm{i}}\left(\mathrm{j}\right)}{\max {\mathrm{X}}_{\mathrm{i}}\left(\mathrm{j}\right)-\mathrm{m}\mathrm{i}\mathrm{n}{\mathrm{X}}_{\mathrm{i}}\left(\mathrm{j}\right)}$$

(12)

where ${\mathrm{X}}_{\mathrm{i}}\left(\mathrm{j}\right)$ and ${\mathrm{x}}_{{\mathrm{i}}^{\mathrm{*}}}\left(\mathrm{j}\right)$ are original and normalized values of alternative i under criterion j, and $\min {\mathrm{X}}_{\mathrm{i}}\left(\mathrm{j}\right)$ and $\max {\mathrm{X}}_{\mathrm{i}}\left(\mathrm{j}\right)$ are the original lowest and highest values under criterion j. Using Equation (12), the converted normalized data and the standard series of one for each criterion are shown in

Table 5. Normalized data and standard series.

Accident Type	Frequency	Death	Injury
Standard series	1	1	1
Collision	0	0.826087	0
Safety	0.59303	0	0.17953
Grounding	0.683261	1	0.815436
Fire	0.713752	0.897233	0.911074
Capsizing	0.872433	0.652174	0.934564
Others	0.960174	0.98419	0.981544
Sinking	0.962663	0.980237	1
Contact	1	0.988142	0.833893

.

The GRCs Are T

The GRCs are computed using Equation (9) and are shown in Table 5, which presents the relationship between the goal (standard series) and actual accident data. The GRC ranges for accident types are roughly (0.33, 0.74) for safety and collision; (0.59, 0.88) for grounding, fire, and capsizing; and (0.75, 0.97) for others, sinking, and contact, respectively.

Figure 2 below shows the overall distribution of GRCs for the criteria, where safety has the lowest GRC in death among other accident types, while collision has the lowest GRC in frequency and injury. On the other hand, the GRCs for the accident types of others, sinking, and contact are closer to the level of standard series in all three criteria than other types of accidents.

The next step is to calculate GRG of each accident type by summing the weighted GRCs using Table 4,

Table 6. The GRCs for accident types.

Accident Type	Frequency	Death	Injury
Collision	0.333333	0.741935	0.333333
Safety	0.551286	0.333333	0.378653
Grounding	0.61219	1	0.730392
Fire	0.635932	0.829508	0.849003
Capsizing	0.796728	0.589744	0.884273
Others	0.926225	0.969349	0.964401
Sinking	0.930515	0.961977	1
Contact	1	0.976834	0.75063

, and Equation (11). The following

Table 7. Ranking of accident types for Case 1.

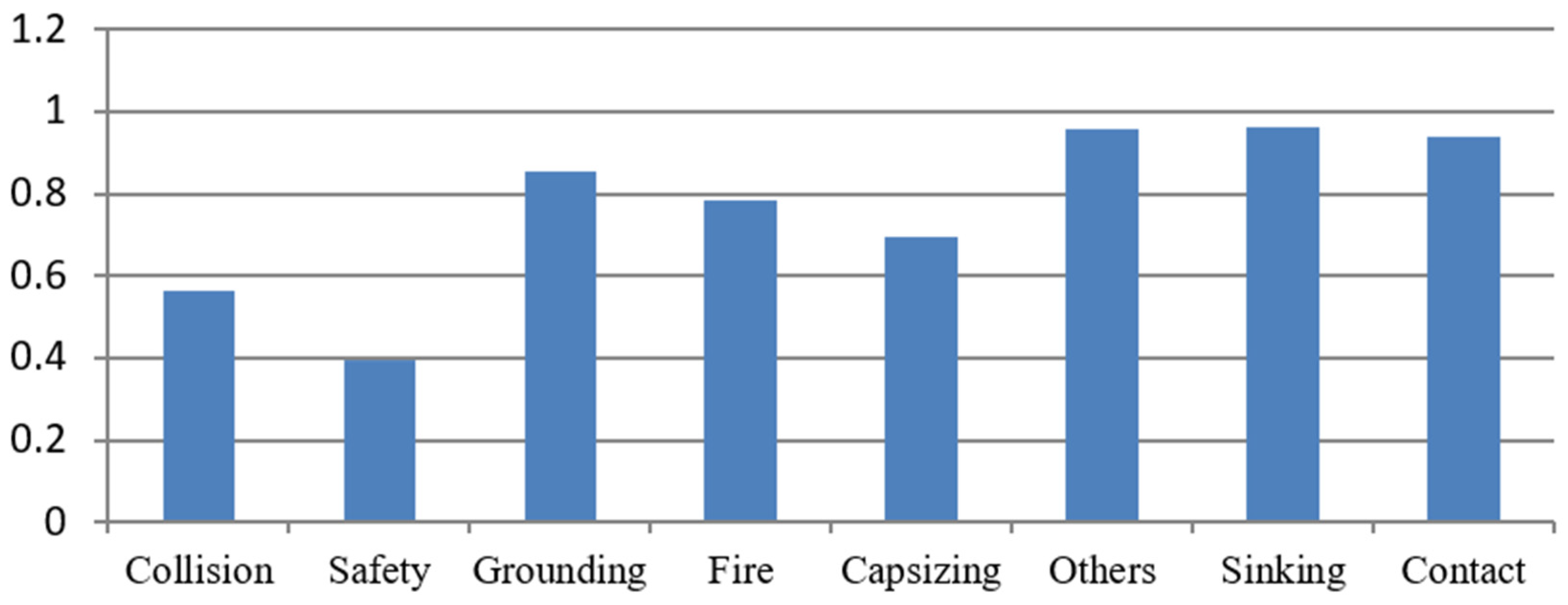
Accident Type	GRG	Ranking	Weights for Criteria
Collision	0.565095	2	Death 0.567208 Frequency 0.243722 Injury 0.189068
Safety	0.395021	1
Grounding	0.854506	5
Fire	0.786014	4
Capsizing	0.695875	3
Others	0.957901	7
Sinking	0.961496	8
Contact	0.93971	6

,

Table 8. Ranking of accident types for Case 2.

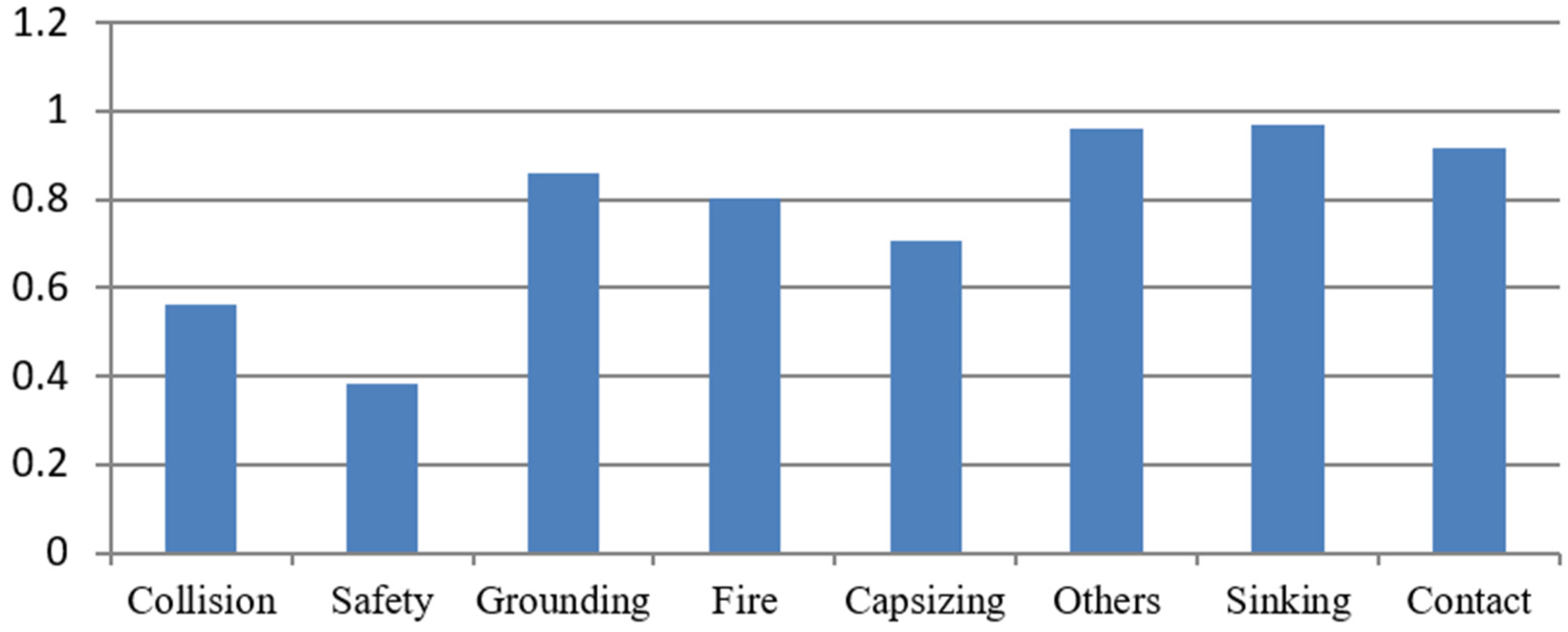
Accident Type	GRG	Ranking	Weights for Criteria
Collision	0.561391	2	Death 0.567208 Frequency 0.162791 Injury 0.279069
Safety	0.381461	1
Grounding	0.861629	5
Fire	0.803436	4
Capsizing	0.705633	3
Others	0.960948	7
Sinking	0.967467	8
Contact	0.917473	6

and

Table 9. Ranking of accident types for Case 3.

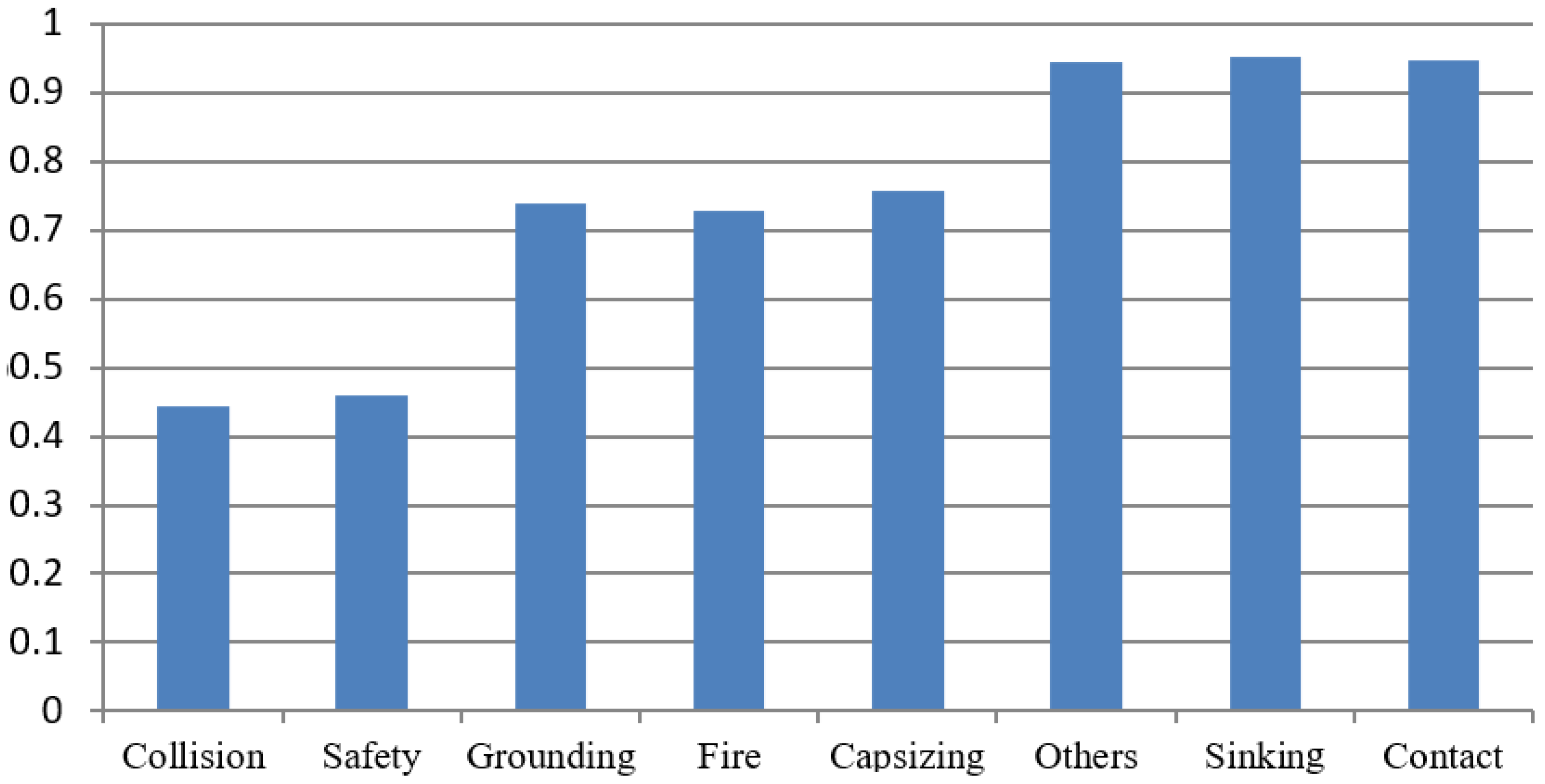
Accident Type	GRG	Ranking	Weight for Criteria
Collision	0.444854	1	Death 0.272934 Frequency 0.545109 Injury 0.181956
Safety	0.460387	2
Grounding	0.739544	4
Fire	0.727534	3
Capsizing	0.756163	5
Others	0.944940	6
Sinking	0.951744	8
Contact	0.948301	7

and Figure 3, Figure 4 and Figure 5 show the resulting GRGs and ranks of accident types for the three different cases.

(A) Case 1: D > F > I

The GRG for each accident type and overall ranking with the criteria order of death (D) > frequency (F) > injury (I) is presented in Table 7. The accident types are ranked in accordance with the increasing order of GRGs because the smallest GRG represents the riskiest one. The safety type requires the highest attention in establishing risk mitigation polices. The range of GRGs for safety and collision is (0.39, 0.56), whereas for grounding, fire, and capsizing, the range is (0.69, 0.85), and for others, sinking, and contact, the range is (0.93, 0.96).

Figure 3 shows the ranking where safety is followed by collision (group 1), the group of three accident types, grounding, fire, and capsizing (group 2), and the remaining three accident types, others, sinking, and contact (group 3).

(B) Case 2: D > I > F

Table 8 shows GRGs for each accident type and overall rankings, with injury and frequency being interchanged in order of importance.

As shown in Figure 4, the ranking of accident types remains the same as Case 1; however, collision, safety, and contact are decreased, whereas the other five accident types are increased in GRG values compared to Case 1.

(C) F > D > I

For case (C), frequency has the highest priority in importance over death and injury. Table 9 shows GRGs for each accident type and overall rankings with frequency > death > injury.

Unlike the above two cases, collision is located at the top of the ranking list followed by safety, exchanging the ranking order with each other. The main reason is because the safety type has a higher GRC in frequency than collision, which results in a higher GRG. Figure 5 shows the changes in the ranking of accident types.

The ranking changes among accident types for the three cases are summarized in

Table 10. Risk rankings with different criteria weights.

Weight	Collision	Safety	Grounding	Fire	Capsizing	Others	Sinking	Contact
D > F > I	2	1	5	4	3	7	8	6
D > I > F	2	1	5	4	3	7	8	6
F > D > I	1	2	4	3	5	6	8	7

, the results of which show the influence of weights on the risk ranking. The decision maker can have flexibility in prioritizing risky accident types and distributing limited resources among them.

From the above analysis results, we classify accident types into three categories:

Risk category 1—the 1st risky type of accident is safety and collision;

Risk category 2—the 2nd risky type of accident is grounding, fire, and capsizing;

Risk category 3— the 3rd risky type of accident is others, sinking, and contact.

Some suggestions for implementing risk reduction measures.

Table 11. Main cause of each accident type.

Accident Type	Main Cause	Number of Accidents	Number of Total Accidents	Ratio of Accidents
Collision	Negligence of look out forward	425	469	0.906183
Safety	Violation of safety regulations	139	159	0.874214
Grounding	Negligence of confirming position	44	51	0.862745
Fire	Defect in ship or engine system	28	67	0.41791
Capsizing	Unsafe loading of cargo	7	17	0.411765
Others	Unsafe operation of engine system	17	53	0.320755
Sinking	Improper management of ship operation	11	76	0.144737
Contact	Improper ship design and building	29	102	0.284314

below shows the most influential cause of each accident type (across all ship types), and its ratio to the frequency is presented in the last column. For category 1, 90% of the accidents leading to collision were caused by “Negligence of look out forward”, and 87% of safety accident types were due to “Violation of safety regulations”.

Since most of the main causes for accidents are human factors rather than mechanical or equipment failures, measures to eliminate or reduce these causes can significantly decrease the frequency of accidents.

3.4. Discussion

3.4.1. Addition of Criteria

Due to the increase in maritime traffic and operational frequency of ships, the catastrophic nature of maritime accidents has posed a serious threat to life, property, and the environment [51]. Since injury is classified into several classes depending on its degree of severity, the criterion on injury needs to be further categorized into minor, significant, severe, and catastrophic, as suggested by the IMO.

Other possible criteria to be included are damages to ships and the surrounding marine environment. According to accident statistics from KMST, the degree of ship loss (total loss, severe loss, and partial loss) varies from accident type to type. For collision, contact, grounding, and others, the damage to ships mainly ranges from no to partial loss; for the capsizing type, the range is between partial and severe losses; and for accident types of fire and sinking, a wider range of damage from partial to total losses is reported. Additionally, damage to the marine environment is inevitable to some degree when an accident in waters occurs, and linguistic terms, i.e., minor, significant, severe, and catastrophic, should be included when calculating the risk ranking. Figure 6 below presents the overall criteria organized in a hierarchical order for a more detailed analysis.

3.4.2. Weight Integration

Different weight values lead to different evaluation results, and there are also subjective and objective weighting methods [30]. As seen in Table 10, the ranking of accident types can be changed with different weights assigned to criteria. Since there exists no superior weighting method over others, one way to deal with this inconsistency is to integrate weights into a single weight for each criterion. Two methods (traditional and revised) are introduced by Xu and Xu (2018) [39]. The traditional way to combine weights is

$${\mathrm{W}}_{\mathrm{j}}=\frac{{\alpha }_{\mathrm{j}}{\mathsf{\beta }}_{\mathrm{j}}}{\sum {\alpha }_{\mathrm{j}}{\mathsf{\beta }}_{\mathrm{j}}},$$

(13)

where ${\alpha }_{\mathrm{j}}$, ${\mathsf{\beta }}_{\mathrm{j},} {\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{W}}_{\mathrm{j}}$ are subjective, objective, and integrated weights, respectively, of criterion j, and ${\alpha }_{\mathrm{j}}$ can be obtained from expert opinion/judgement or AHP method.

The reasonable integrated weight should be between the two weights, but there is a case when the newly adjusted weight is located outside the range produced by these two original weights [39]. To deal with this problem, they proposed another method

$${\mathrm{W}}_{\mathrm{j}}=\mathsf{\lambda }{\alpha }_{\mathrm{j}}+(1-\mathsf{\lambda }){\mathsf{\beta }}_{\mathrm{j}},$$

(14)

where $\mathsf{\lambda }$ is a preference coefficient between 0 and 1 $\left(0\le \mathsf{\lambda }\le 1\right)$. With this linear combination of ${\alpha }_{\mathrm{j}}$ and ${\mathsf{\beta }}_{\mathrm{j}}$, the resulting weight $({\mathrm{W}}_{\mathrm{j}}$) is located between the two weights. As the coefficient $\mathsf{\lambda }$ becomes closer to one, ${\mathrm{W}}_{\mathrm{j}}$ becomes ${\alpha }_{\mathrm{j}}$, and as $\mathsf{\lambda }$ approaches zero, ${\mathrm{W}}_{\mathrm{j}}$ approaches ${\mathsf{\beta }}_{\mathrm{j}}$. In the study extending the above Equations (13) and (14), we have the following methods for integrating weights:

$${\mathrm{W}}_{\mathrm{j}}=\frac{{\alpha }_{\mathrm{j}}{\mathsf{\beta }}_{\mathrm{j}}{\mathsf{\delta }}_{\mathrm{j}}}{\sum {\alpha }_{\mathrm{j}}{\mathsf{\beta }}_{\mathrm{j}}{\mathsf{\delta }}_{\mathrm{j}}}$$

(15)

and

$$W_j={A_1\alpha }_{\mathrm{j}}+A_2{\mathsf{\beta }}_{\mathrm{j}}{+A}_3{\mathsf{\delta }}_{\mathrm{j}}$$

(16)

$${\sum }_i{A}_i=1$$

(17)

Applying the above formulas, we present the combined weight for each criterion in

Table 12. Weight integration for the criteria.

	Equation (15)	Equation (16)	Weight Range
Death	0.751637	0.472677	(0.272934, 0.567208)
Frequency	0.164849	0.306236	(0.162791, 0.545109)
Injury	0.083514	0.221086	(0.181956, 0.279069)

, where the adjusted weights for death and injury are outside the weight range when production Formula (15) is used. Applying addition Formula (16), the newly adjusted weights for death, frequency, and injury are all inside the corresponding weight ranges, with $A_i$ = 1/3.

4. Conclusions

A risk analysis approach is effectively applied to compute the current risk level and helps reduce the frequency and fatality by employing risk mitigation measures. However, in real-life situations, one may need multiple criteria, and an objective assignment of weights is required in the risk calculation process.

For the two-criteria problem, various risk computational tools have been extensively developed and utilized in diverse risky industries. Previous studies mainly used two criteria applying equal weights, and for some research, injury was converted into fatality equivalents. However, the maritime accident statistics shows that the number of injuries is several times higher than deaths.

Therefore, considering the growing concern on injury, unlike existing conventional risk ranking methods, we modelled a multi-criteria decision problem with frequency, death, and injury and ranked risky types of maritime accidents. To determine the corresponding importance of each criterion, an OPA method was applied to provide decision makers with flexible alternatives to assign weights by simply deciding which criterion is more important than others. With the weights obtained from OPA, the GRA is applied to rank the risky types of accidents, which is useful when the accident data are not enough or are incomplete.

With the combined approach, we have the following findings. The accident types are classified into three different risk groups: collision and safety are the most risky ones, followed by a group of grounding, fire, and capsizing classified as the 2nd risky category, and finally sinking, contact, and others are ranked 3rd. The ranking order of accidents was changed when different weights were assigned, which implies that ignoring the relative importance among criteria may lead to wrong or impractical ranking decisions. Additionally, as shown in the Discussion section, the proposed method can be extended to different models having more criteria, and other weighting methods (quantitative or qualitative) can be effectively integrated with OPA into single objective weight.

Based on the above results, we made some contributions. First, the combined OPA and GRA approach has diverse applications in the maritime industry, i.e., ranking the ship types (oil tanker, container ship, passenger ship, and other types of ships), ranking dangerous ports or waterways, etc. Additionally, it can cover other risky areas, i.e., chemical, nuclear, and hazardous materials causing serious consequences when an accident occurs. Second, while traditional risk analysis methods deal with two factors, frequency and consequence, the proposed method can be applied to multi-criteria problems having different criteria units, such as fatality, economic loss, damage to system (equipment and facility), and other adverse effect. Third, the risk ranking approach can be integrated with other risk analysis techniques into a framework of a risk assessment process that would improve the accuracy of the results. Finally, since each accident type has the most influential factors leading to disastrous maritime accidents, the ranking results obtained from the study can provide priority in the selection of risk mitigation policies for more effective maritime operations.

However, there exist some limitations in the study, despite the flexibility of the approach towards a decision-making system. As human factors are the main causes of accidents, a more detailed classification and selection of main factors for each accident type need to be further investigated. The grey relational grade (GRG) obtained from GRA is used to describe the relationships between factors and to determine the factors that significantly influence the given system’s performance [51]. In general, multiple factors are responsible for maritime accidents, which occur at the same time or in the order of occurrence of ensuing factors after an initiating factor. Therefore, identifying the most and least influencing factors causing accidents is another issue to be addressed. The selection of criteria affecting the risk ranking also needs to be considered in the design phase of model construction to reflect accident-related environments. For successful applications of the proposed approach, accidents leading to various types of injury, i.e., road traffic accidents, accidents in the workplace, etc., should also be included in future research.