Exploring the Spatio-Temporally Heterogeneous Impact of Traffic Network Structure on Ride-Hailing Emissions Using Shenzhen, China, as a Case Study
Abstract
1. Introduction
- (1)
- The important role of traffic network structure in traffic analysis has been recognized, yet its impact mechanism on ride-hailing emissions remains unclear. Previous studies on the factor analysis of travel emissions have primarily focused on lines and stations density, which may not fully characterize the complexity of road network structures. Therefore, a more comprehensive perspective is needed to understand this influence.
- (2)
- In studies focusing on the factor analysis of travel emissions, consideration of spatial non-stationarity is prevalent. Although some scholars have attempted to explain the spatio-temporal non-stationarity effects of variables using the GTWR model, they mainly employ a fixed kernel function approach. This approach lacks exploration into adaptive bandwidths, failing to fully consider the spatio-temporal heterogeneity of urban transportation systems.
- (3)
- In addition, despite the fact that many scholars have recognized the importance of analyzing key factors influencing ride-hailing emissions, translating these research results into practice and deriving specific policy measures to promote low-carbon travel remains a rather difficult challenge.
- (1)
- Unlike previous studies that primarily focused on line and station density, this study incorporates critical features of public transportation network structure, such as accessibility and centrality, into the analysis. This novel approach provides a more comprehensive understanding of the complex interplay between travel demand and network structure across different transportation modes. Our framework facilitates the development of precise transportation management strategies, thereby enhancing the overall efficiency and sustainability of public transportation systems.
- (2)
- To address the limitations of traditional GTWR models in terms of spatio-temporal scale, this study introduces a novel approach: the unilateral temporal weighting scheme GTWR (U-GTWR) model. By utilizing an adaptive kernel function to estimate the spatio-temporal weighting matrix, the model dynamically adjusts weights based on the characteristics of samples from various regions at previous time points. It offers a more nuanced understanding of spatio-temporal heterogeneity within urban transportation systems, thereby providing researchers and policymakers with valuable insights for effective emissions reduction strategies.
- (3)
- This study explores practical policy for low-carbon travel by examining the complex relationship between influencing factors and ride-hailing emissions. Special insights into spatio-temporal bandwidth selection and coefficients of independent variables are provided, offering targeted policy recommendations to optimize urban spatial structure and promote low-emission modes. This work aims to bridge the gap between scholarly insights and actionable strategies for emission reduction in urban and transportation systems.
2. Literature Review
2.1. Factors Affecting Travel Emissions
2.2. Methods Applied in Existing Research
3. Methodology
3.1. Geographically and Temporally Weighted Regression Model
3.2. Determination of Weight Matrix and Bandwidth Parameters
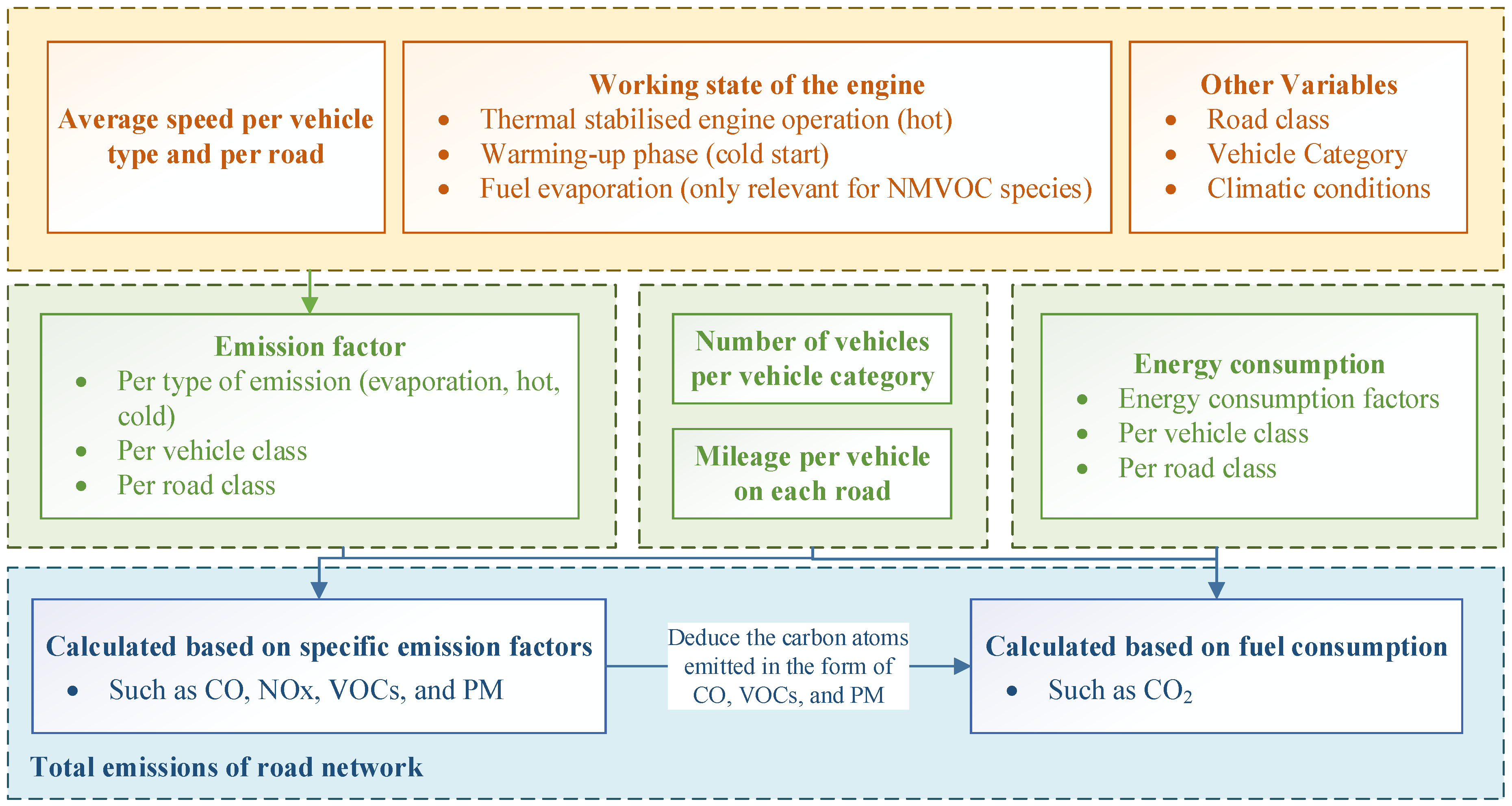
3.3. Travel Emission Calculation Model
4. Data Description and Processing
4.1. Study Area
4.2. Dependent Variables
4.3. Independent Variables
4.4. Variable Statistics and Screening
5. Results Analysis
5.1. Model Performance Comparison
5.2. Spatio-Temporal Bandwidth Analysis
5.3. Analysis of Spatio-Temporally Heterogeneous Effects
6. Conclusions
- (1)
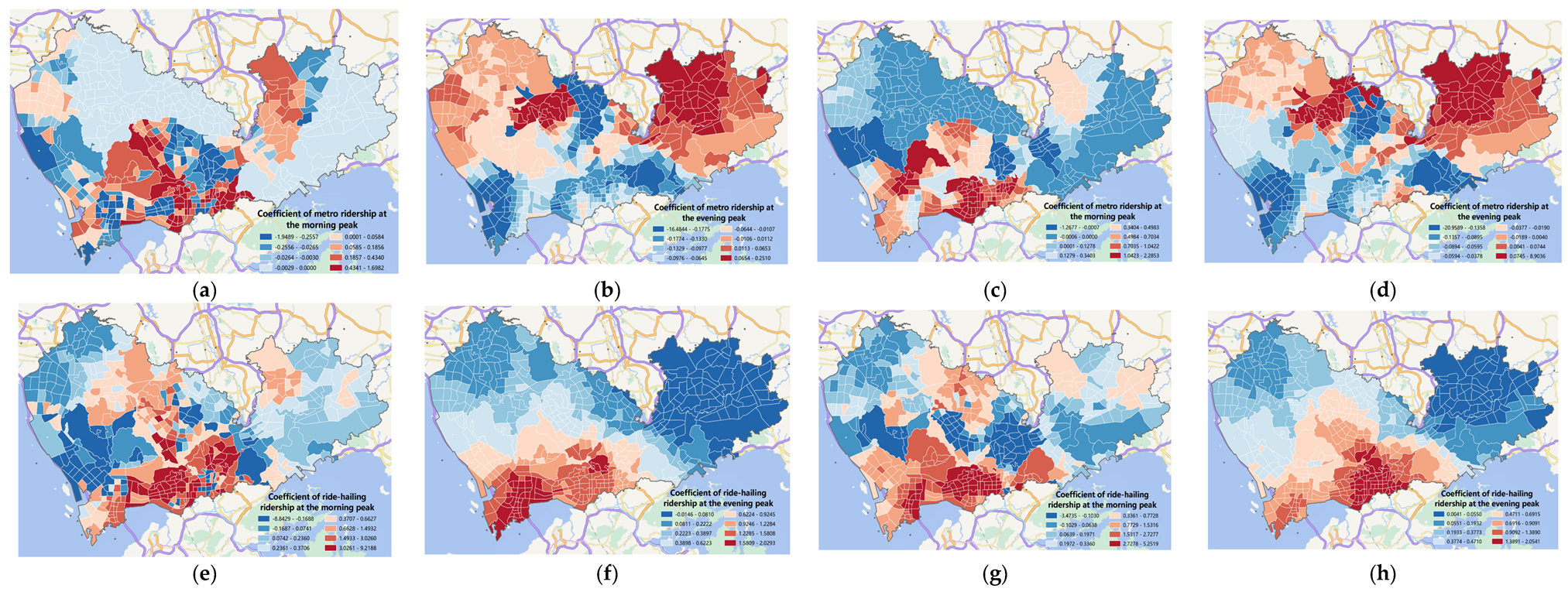
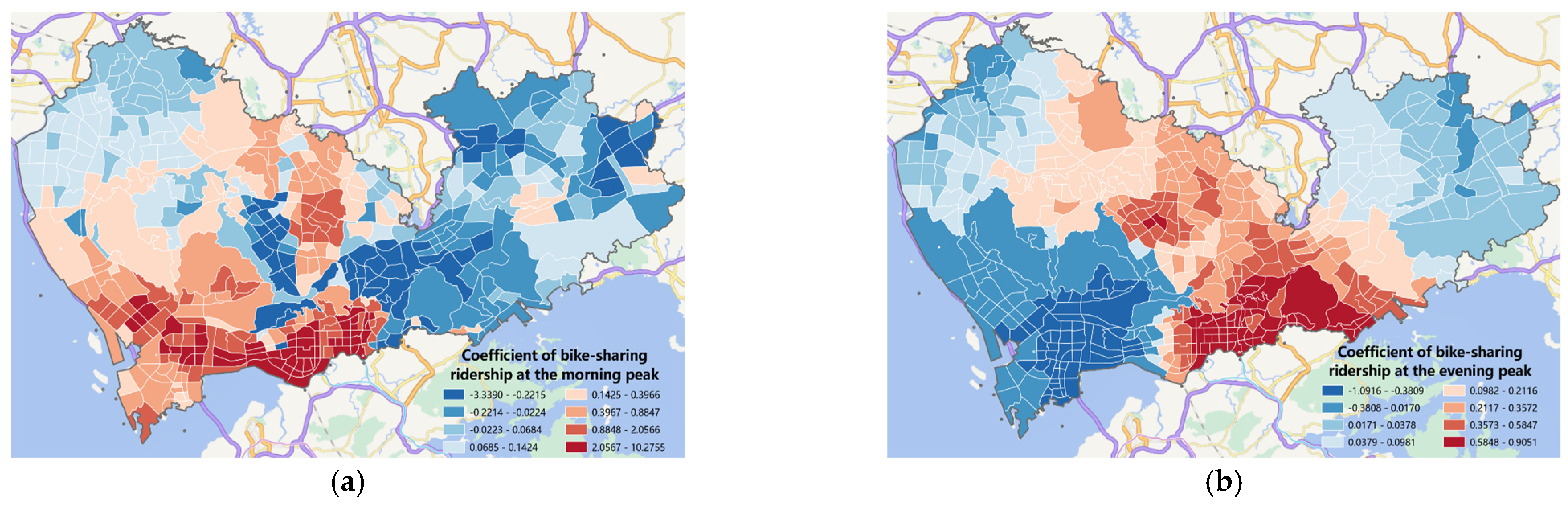
- In terms of travel demand, the study found that metro travel demand in downtown areas has a positive impact on ride-hailing travel emissions during the morning peak and a negative impact during the evening peak. Therefore, urban managers can encourage more commuters to choose metro travel by improving the quality and efficiency of metro services. Additionally, it is important to consider the layout of metro lines and the surrounding areas’ demand to optimize the coverage of metro lines, better meeting the travel demand during weekend morning peaks. Moreover, considering the differences in the impact of bike-sharing and ride-hailing travel demand across different regions, region-specific policies should be adopted. For areas where bike-sharing demand has a negative impact, promoting the use of bike-sharing for short-distance commuting can reduce reliance on ride-hailing services. Conversely, for areas where bike-sharing demand has a positive impact, enhancing the quality of bike-sharing services can increase their competitiveness.
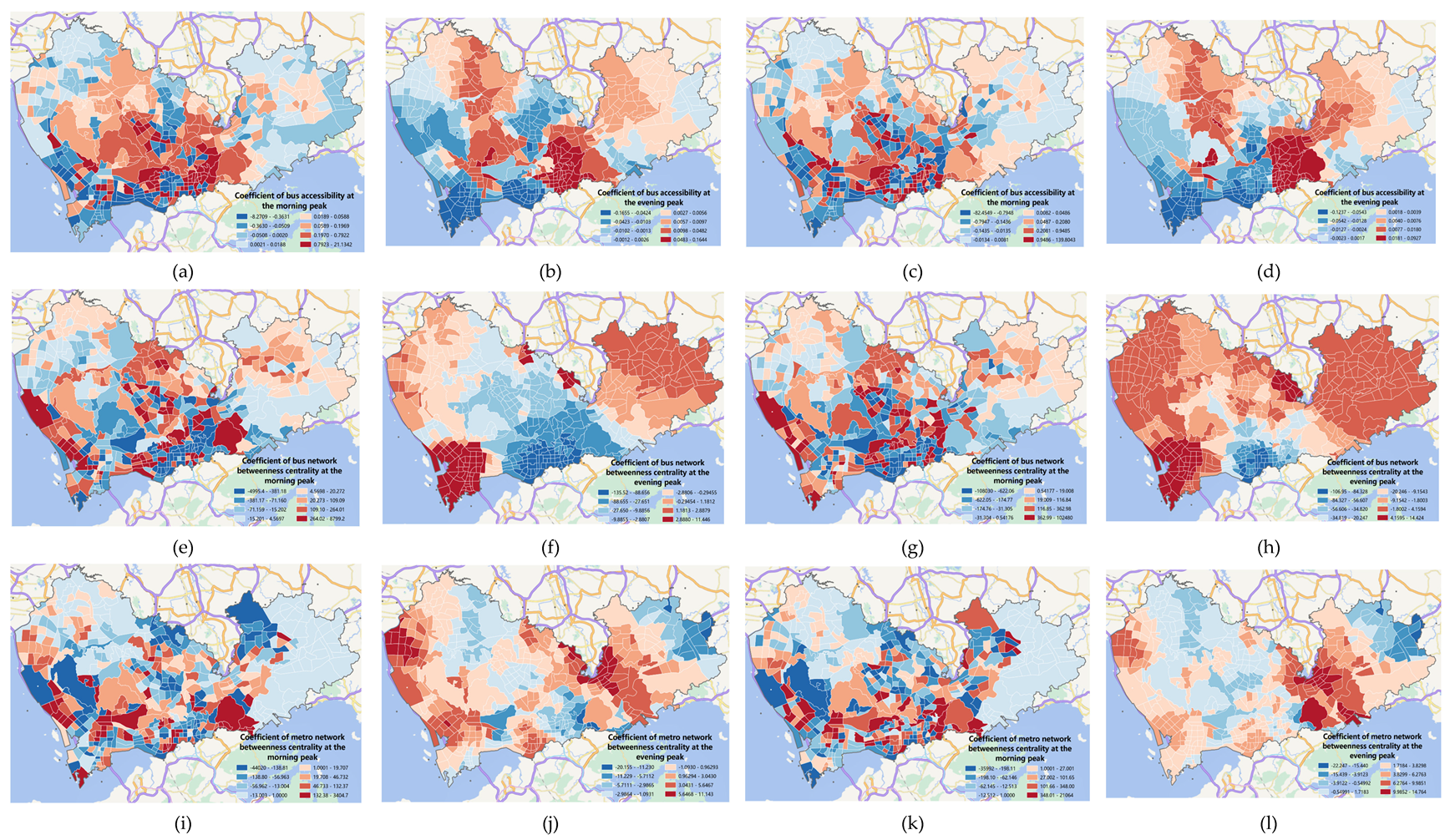
- (2)
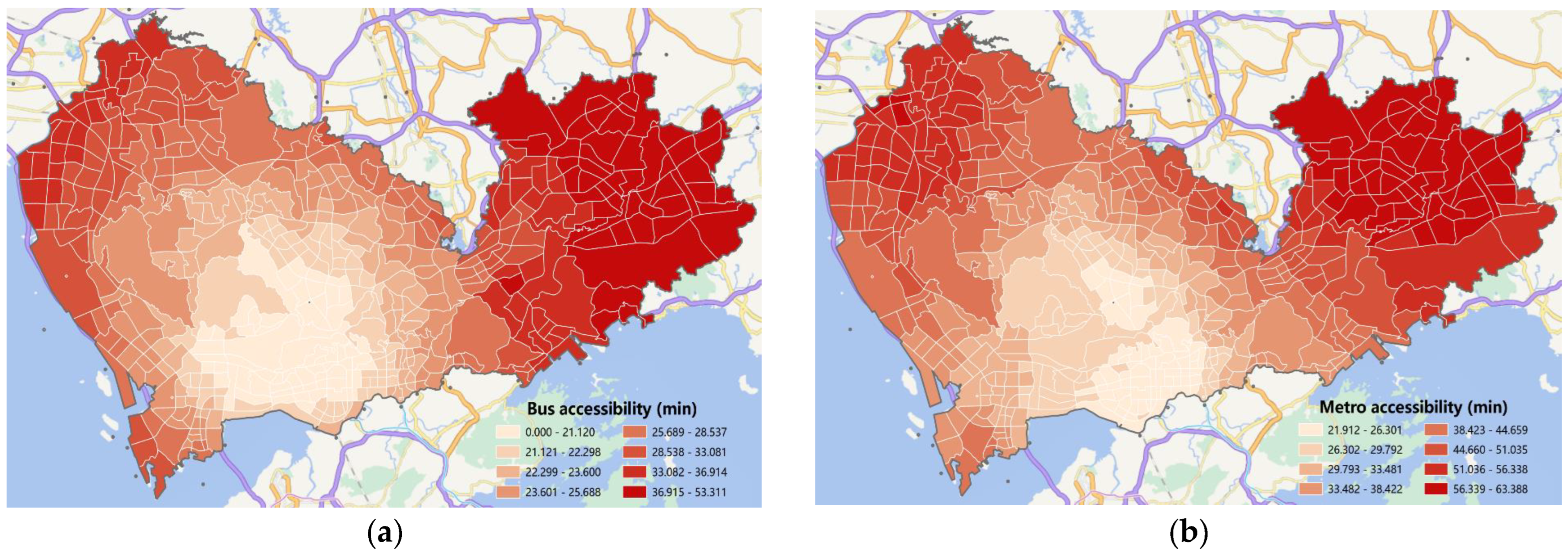
- In terms of public transportation services, the study revealed that the impact of bus accessibility on ride-hailing travel emissions is primarily concentrated in the central areas of Shenzhen, with particularly significant negative effects observed in the Nanshan and Futian districts during the evening peak period. To address this phenomenon, urban managers can enhance the quality of bus services in central areas by increasing routes, improving frequency, and introducing intelligent systems to reduce the reliance of citizens on ride-hailing services. Additionally, measures such as installing traffic signs and providing transfer facilities at key areas such as transportation hubs and intersections can also encourage residents to choose public transportation. Furthermore, the impact of network node betweenness centrality on ride-hailing travel emissions appears to be more scattered during the morning peak period but more concentrated during the evening peak period. Therefore, urban managers should develop differentiated transportation planning and management policies based on the characteristics of each region to promote sustainable and low-carbon travel modes. For example, to address the negative impact of bus network node betweenness centrality in the Futian district, policy recommendations may include increasing bus route density and optimizing planning to cover important commercial, residential, and office areas.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pant, P.; Harrison, R.M. Estimation of the contribution of road traffic emissions to particulate matter concentrations from field measurements: A review. Atmos. Environ. 2013, 77, 78–97. [Google Scholar] [CrossRef]
- Birol, F. CO2 Emissions from Fuel Combustion Highlights, 2020th ed.; OECD/IEA: Paris, France, 2020. [Google Scholar]
- Sui, Y.; Zhang, H.; Song, X.; Shao, F.; Yu, X.; Shibasaki, R.; Sun, R.; Yuan, M.; Wang, C.; Li, S.; et al. GPS data in urban online ride-hailing: A comparative analysis on fuel consumption and emissions. J. Clean. Prod. 2019, 227, 495–505. [Google Scholar] [CrossRef]
- Zhao, P.; Kwan, M.-P.; Qin, K. Uncovering the spatiotemporal patterns of CO2 emissions by taxis based on Individuals’ daily travel. J. Transp. Geogr. 2017, 62, 122–135. [Google Scholar] [CrossRef]
- Rodier, C. The Effects of Ride Hailing Services on Travel and Associated Greenhouse Gas Emissions. 2018. Available online: https://escholarship.org/uc/item/2rv570tt (accessed on 20 March 2024).
- Rodier, C.; Michaels, J. The Effects of Ride-Hailing Services on Greenhouse Gas Emissions. 2019. Available online: https://escholarship.org/uc/item/4vz52416#main (accessed on 20 March 2024).
- Tikoudis, I.; Martinez, L.; Farrow, K.; Bouyssou, C.G.; Petrik, O.; Oueslati, W. Ridesharing services and urban transport CO2 emissions: Simulation-based evidence from 247 cities. Transp. Res. Part D Transp. Environ. 2021, 97, 102923. [Google Scholar] [CrossRef]
- Tirachini, A. Ride-hailing, travel behaviour and sustainable mobility: An international review. Transportation 2020, 47, 2011–2047. [Google Scholar] [CrossRef]
- Wei, K.; Vaze, V.; Jacquillat, A. Transit planning optimization under ride-hailing competition and traffic congestion. Transp. Sci. 2022, 56, 725–749. [Google Scholar] [CrossRef]
- Babar, Y.; Burtch, G. Examining the heterogeneous impact of ride-hailing services on public transit use. Inf. Syst. Res. 2020, 31, 820–834. [Google Scholar] [CrossRef]
- Lv, Y.; He, L.; Sun, H.; Xu, G. Substituted Relationship between Ride-hailing and Public Transit and Emission Reduction Potential. J. Transp. Syst. Eng. Inf. Technol. 2023, 23, 11. [Google Scholar]
- Luo, H.; Chahine, R.; Gkritza, K.; Cai, H. What motivates the use of shared mobility systems and their integration with public transit? Evidence from a choice experiment study. Transp. Res. Part C Emerg. Technol. 2023, 155, 104286. [Google Scholar] [CrossRef]
- Li, X.; Du, M.; Zhang, Y.; Yang, J. Identifying the factors influencing the choice of different ride-hailing services in Shenzhen, China. Travel Behav. Soc. 2022, 29, 53–64. [Google Scholar] [CrossRef]
- Loa, P.; Habib, K.N. Examining the influence of attitudinal factors on the use of ride-hailing services in Toronto. Transp. Res. Part A Policy Pract. 2021, 146, 13–28. [Google Scholar] [CrossRef]
- Chen, J.; Li, W.; Zhang, H.; Cai, Z.; Sui, Y.; Long, Y.; Song, X.; Shibasaki, R. GPS data in urban online ride-hailing: A simulation method to evaluate impact of user scale on emission performance of system. J. Clean. Prod. 2021, 287, 125567. [Google Scholar] [CrossRef]
- Ao, Y.; Yang, D.; Chen, C.; Wang, Y. Effects of rural built environment on travel-related CO2 emissions considering travel attitudes. Transp. Res. Part D Transp. Environ. 2019, 73, 187–204. [Google Scholar] [CrossRef]
- Wu, X.; Tao, T.; Cao, J.; Fan, Y.; Ramaswami, A. Examining threshold effects of built environment elements on travel-related carbon-dioxide emissions. Transp. Res. Part D Transp. Environ. 2019, 75, 1–12. [Google Scholar] [CrossRef]
- Shao, Q.; Zhang, W.; Cao, X.; Yang, J. Built environment interventions for emission mitigation: A machine learning analysis of travel-related CO2 in a developing city. J. Transp. Geogr. 2023, 110, 103632. [Google Scholar] [CrossRef]
- Saberi, M.; Mahmassani, H.S.; Brockmann, D.; Hosseini, A. A complex network perspective for characterizing urban travel demand patterns: Graph theoretical analysis of large-scale origin–destination demand networks. Transportation 2017, 44, 1383–1402. [Google Scholar] [CrossRef]
- Saberi, M.; Rashidi, T.H.; Ghasri, M.; Ewe, K. A complex network methodology for travel demand model evaluation and validation. Netw. Spat. Econ. 2018, 18, 1051–1073. [Google Scholar] [CrossRef]
- Jenelius, E. Network structure and travel patterns: Explaining the geographical disparities of road network vulnerability. J. Transp. Geogr. 2009, 17, 234–244. [Google Scholar] [CrossRef]
- Badia, H.; Argote-Cabanero, J.; Daganzo, C.F. How network structure can boost and shape the demand for bus transit. Transp. Res. Part A Policy Pract. 2017, 103, 83–94. [Google Scholar] [CrossRef]
- Zheng, J.; Xu, M.; Li, R.; Yu, L. Research on group choice behavior in green travel based on planned behavior theory and complex network. Sustainability 2019, 11, 3765. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, C.; Liu, W. Urban daily travel carbon emissions accounting and mitigation potential analysis using surveyed individual data. J. Clean. Prod. 2018, 192, 821–834. [Google Scholar] [CrossRef]
- Xu, B.; Lin, B. Factors affecting carbon dioxide (CO2) emissions in China’s transport sector: A dynamic nonparametric additive regression model. J. Clean. Prod. 2015, 101, 311–322. [Google Scholar] [CrossRef]
- Gan, M.; Liu, X.; Chen, S.; Yan, Y.; Li, D. The identification of truck-related greenhouse gas emissions and critical impact factors in an urban logistics network. J. Clean. Prod. 2018, 178, 561–571. [Google Scholar] [CrossRef]
- Xue, Y. Empirical research on household carbon emissions characteristics and key impact factors in mining areas. J. Clean. Prod. 2020, 256, 120470. [Google Scholar] [CrossRef]
- Choi, K.; Zhang, M. The impact of metropolitan, county, and local land use on driving emissions in US metropolitan areas: Mediator effects of vehicle travel characteristics. J. Transp. Geogr. 2017, 64, 195–202. [Google Scholar] [CrossRef]
- Ma, J.; Liu, Z.; Chai, Y. The impact of urban form on CO2 emission from work and non-work trips: The case of Beijing, China. Habitat Int. 2015, 47, 1–10. [Google Scholar] [CrossRef]
- Qin, H.; Huang, Q.; Zhang, Z.; Lu, Y.; Li, M.; Xu, L.; Chen, Z. Carbon dioxide emission driving factors analysis and policy implications of Chinese cities: Combining geographically weighted regression with two-step cluster. Sci. Total Environ. 2019, 684, 413–424. [Google Scholar] [CrossRef] [PubMed]
- Yuan, W.; Sun, H.; Chen, Y.; Xia, X. Spatio-Temporal evolution and spatial heterogeneity of influencing factors of SO2 Emissions in Chinese cities: Fresh evidence from MGWR. Sustainability 2021, 13, 12059. [Google Scholar] [CrossRef]
- Cheng, R.; Zeng, W.; Zheng, Y. Exploring the Influence of Built Environment on Demand of Online Car-Hailing Travel Using Multi-Scale Geographically Temporal Weighted Regression Model. 2023. Available online: https://www.researchsquare.com/article/rs-3014459/v1 (accessed on 20 March 2024).
- Kuonen, S. Estimating greenhouse gas emissions from travel–a GIS-based study. Geogr. Helv. 2015, 70, 185–192. [Google Scholar] [CrossRef]
- Cao, X.; Yang, W. Examining the effects of the built environment and residential self-selection on commuting trips and the related CO2 emissions: An empirical study in Guangzhou, China. Transp. Res. Part D Transp. Environ. 2017, 52, 480–494. [Google Scholar] [CrossRef]
- Christensen, L. Environmental impact of long distance travel. Transp. Res. Procedia 2016, 14, 850–859. [Google Scholar] [CrossRef]
- Czepkiewicz, M.; Heinonen, J.; Ottelin, J. Why do urbanites travel more than do others? A review of associations between urban form and long-distance leisure travel. Environ. Res. Lett. 2018, 13, 073001. [Google Scholar] [CrossRef]
- Akopov, A.S.; Beklaryan, L.A. Traffic Improvement in Manhattan Road Networks With the Use of Parallel Hybrid Biobjective Genetic Algorithm. IEEE Access 2024, 12, 19532–19552. [Google Scholar] [CrossRef]
- Santos, O.; Ribeiro, F.; Metrôlho, J.; Dionísio, R. Using Smart Traffic Lights to Reduce CO2 Emissions and Improve Traffic Flow at Intersections: Simulation of an Intersection in a Small Portuguese City. Appl. Syst. Innov. 2023, 7, 3. [Google Scholar] [CrossRef]
- Li, P.; Zhao, P.; Brand, C. Future energy use and CO2 emissions of urban passenger transport in China: A travel behavior and urban form based approach. Appl. Energy 2018, 211, 820–842. [Google Scholar] [CrossRef]
- Xia, C.; Xiang, M.; Fang, K.; Li, Y.; Ye, Y.; Shi, Z.; Liu, J. Spatial-temporal distribution of carbon emissions by daily travel and its response to urban form: A case study of Hangzhou, China. J. Clean. Prod. 2020, 257, 120797. [Google Scholar] [CrossRef]
- Hong, J.; Goodchild, A. Land use policies and transport emissions: Modeling the impact of trip speed, vehicle characteristics and residential location. Transp. Res. Part D Transp. Environ. 2014, 26, 47–51. [Google Scholar] [CrossRef]
- Ding, C.; Wang, Y.; Xie, B.; Liu, C. Understanding the role of built environment in reducing vehicle miles traveled accounting for spatial heterogeneity. Sustainability 2014, 6, 589–601. [Google Scholar] [CrossRef]
- Song, S.; Diao, M.; Feng, C.C. Individual transport emissions and the built environment: A structural equation modelling approach. Transp. Res. Part A Policy Pract. 2016, 92, 206–219. [Google Scholar] [CrossRef]
- Yang, W.; Wang, S.; Zhao, X. Measuring the direct and indirect effects of neighborhood-built environments on travel-related CO2 emissions: A structural equation modeling approach. Sustainability 2018, 10, 1372. [Google Scholar] [CrossRef]
- Barla, P.; Miranda-Moreno, L.F.; Lee-Gosselin, M. Urban travel CO2 emissions and land use: A case study for Quebec City. Transp. Res. Part D Transp. Environ. 2011, 16, 423–428. [Google Scholar] [CrossRef]
- Zhu, X.; Li, R. An analysis of decoupling and influencing factors of carbon emissions from the transportation sector in the Beijing-Tianjin-Hebei Area, China. Sustainability 2017, 9, 722. [Google Scholar] [CrossRef]
- Chow Alice, S.Y. Spatial-modal scenarios of greenhouse gas emissions from commuting in Hong Kong. J. Transp. Geogr. 2016, 54, 205–213. [Google Scholar] [CrossRef]
- Ma, J.; Zhou, S.; Mitchell, G.; Zhang, J. CO2 emission from passenger travel in Guangzhou, China: A small area simulation. Appl. Geogr. 2018, 98, 121–132. [Google Scholar] [CrossRef]
- Reichert, A.; Holz-Rau, C.; Scheiner, J. GHG emissions in daily travel and long-distance travel in Germany–Social and spatial correlates. Transp. Res. Part D Transp. Environ. 2016, 49, 25–43. [Google Scholar] [CrossRef]
- Modarres, A. Commuting and energy consumption: Toward an equitable transportation policy. J. Transp. Geogr. 2013, 33, 240–249. [Google Scholar] [CrossRef]
- Shim, G.E.; Rhee, S.M.; Ahn, K.H.; Chung, S.B. The relationship between the characteristics of transportation energy consumption and urban form. Ann. Reg. Sci. 2006, 40, 351–367. [Google Scholar] [CrossRef]
- Qin, B.; Han, S.S. Planning parameters and household carbon emission: Evidence from high-and low-carbon neighborhoods in Beijing. Habitat Int. 2013, 37, 52–60. [Google Scholar] [CrossRef]
- Zahabi, S.A.H.; Miranda-Moreno, L.; Patterson, Z.; Barla, P.; Harding, C. Transportation greenhouse gas emissions and its relationship with urban form, transit accessibility and emerging green technologies: A Montreal case study. Procedia-Soc. Behav. Sci. 2012, 54, 966–978. [Google Scholar] [CrossRef]
- Sohrab, S.; Csikós, N.; Szilassi, P. Connection between the spatial characteristics of the road and railway networks and the air pollution (PM10) in urban–rural fringe zones. Sustainability 2022, 14, 10103. [Google Scholar] [CrossRef]
- Zhou, S.; Lin, R. Spatial-temporal heterogeneity of air pollution: The relationship between built environment and on-road PM2.5 at micro scale. Transp. Res. Part D Transp. Environ. 2019, 76, 305–322. [Google Scholar] [CrossRef]
- Yu, C.; Deng, Y.; Qin, Z.; Yang, C.; Yuan, Q. Traffic volume and road network structure: Revealing transportation-related factors on PM2.5 concentrations. Transp. Res. Part D Transp. Environ. 2023, 124, 103935. [Google Scholar] [CrossRef]
- Çetin, M.; Sevik, H. Change of air quality in Kastamonu city in terms of particulate matter and CO2 amount. Oxid. Commun. 2016, 39, 3394–3401. [Google Scholar]
- Glaeser, E.L.; Kahn, M.E. The greenness of cities: Carbon dioxide emissions and urban development. J. Urban Econ. 2010, 67, 404–418. [Google Scholar] [CrossRef]
- Song, Y.; Miller, H.J.; Stempihar, J.; Zhou, X. Green accessibility: Estimating the environmental costs of network-time prisms for sustainable transportation planning. J. Transp. Geogr. 2017, 64, 109–119. [Google Scholar] [CrossRef]
- De Coensel, B.; Can, A.; Degraeuwe, B.; De Vlieger, I.; Botteldooren, D. Effects of traffic signal coordination on noise and air pollutant emissions. Environ. Model. Softw. 2012, 35, 74–83. [Google Scholar] [CrossRef]
- Brand, C.; Preston, J.M. ‘60–20 emission’—The unequal distribution of greenhouse gas emissions from personal, non-business travel in the UK. Transp. Policy 2010, 17, 9–19. [Google Scholar] [CrossRef]
- Brand, C.; Goodman, A.; Rutter, H.; Song, Y.; Ogilvie, D. Associations of individual, household and environmental characteristics with carbon dioxide emissions from motorised passenger travel. Appl. Energy 2013, 104, 158–169. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Ota, K.; Dong, M.; Yu, C.; Jin, H. Predicting transportation carbon emission with urban big data. IEEE Trans. Sustain. Comput. 2017, 2, 333–344. [Google Scholar] [CrossRef]
- Jermsittiparsert, K.; Chankoson, T. Behavior of tourism industry under the situation of environmental threats and carbon emission: Time series analysis from Thailand. Int. J. Energy Econ. Policy 2019, 9, 366–372. [Google Scholar] [CrossRef]
- Shu, Y.; Lam Nina, S.N. Spatial disaggregation of carbon dioxide emissions from road traffic based on multiple linear regression model. Atmos. Environ. 2011, 45, 634–640. [Google Scholar] [CrossRef]
- Yang, W.; Li, T.; Cao, X. Examining the impacts of socio-economic factors, urban form and transportation development on CO2 emissions from transportation in China: A panel data analysis of China’s provinces. Habitat Int. 2015, 49, 212–220. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, J.; Liu, P. A geographically weighted regression approach to investigate the effects of traffic conditions and road characteristics on air pollutant emissions. J. Clean. Prod. 2019, 239, 118084. [Google Scholar] [CrossRef]
- Wu, J.; Jia, P.; Feng, T.; Li, H.; Kuang, H.; Zhang, J. Uncovering the spatiotemporal impacts of built environment on traffic carbon emissions using multi-source big data. Land Use Policy 2023, 129, 106621. [Google Scholar] [CrossRef]
- Liu, J.; Li, S.; Ji, Q. Regional differences and driving factors analysis of carbon emission intensity from transport sector in China. Energy 2021, 224, 120178. [Google Scholar] [CrossRef]
- Wang, S.; Shi, C.; Fang, C.; Feng, K. Examining the spatial variations of determinants of energy-related CO2 emissions in China at the city level using Geographically Weighted Regression Model. Appl. Energy 2019, 235, 95–105. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, Q.; Huang, F.; Qiu, R.; Lin, Y.; Zhang, L.; Hu, X. Understanding spatial variation in the driving pattern of carbon dioxide emissions from taxi sector in great Eastern China: Evidence from an analysis of geographically weighted regression. Clean Technol. Environ. Policy 2020, 22, 979–991. [Google Scholar] [CrossRef]
- Lian, W.; Sun, X.; Xing, W.; Gao, T.; Duan, H. Coordinated development and driving factor heterogeneity of different types of urban agglomeration carbon emissions in China. Environ. Sci. Pollut. Res. 2023, 30, 35034–35053. [Google Scholar] [CrossRef] [PubMed]
- Lyu, T.; Wang, Y.; Ji, S.; Feng, T.; Wu, Z. A multiscale spatial analysis of taxi ridership. J. Transp. Geogr. 2023, 113, 103718. [Google Scholar] [CrossRef]
- Leung, Y.; Mei, C.L.; Zhang, W.X. Testing for spatial autocorrelation among the residuals of the geographically weighted regression. Environ. Plan. A 2000, 32, 871–890. [Google Scholar] [CrossRef]
- Huang, B.; Wu, B.; Barry, M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Crespo, R.; Yao, J. Geographical and temporal weighted regression (GTWR). Geogr. Anal. 2015, 47, 431–452. [Google Scholar] [CrossRef]
- Dubé, J.; Legros, D. Spatial econometrics and the hedonic pricing model: What about the temporal dimension? J. Prop. Res. 2014, 31, 333–359. [Google Scholar] [CrossRef]
- Hong, Z.; Wang, J.; Wang, H. Introducing bootstrap test technique to identify spatial heterogeneity in geographically and temporally weighted regression models. Spat. Stat. 2022, 51, 100683. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, J.; Fung, T.; Yu, H.; Mei, C.; Leung, Y.; Zhou, Y. Multiscale geographically and temporally weighted regression with a unilateral temporal weighting scheme and its application in the analysis of spatiotemporal characteristics of house prices in Beijing. Int. J. Geogr. Inf. Sci. 2021, 35, 2262–2286. [Google Scholar] [CrossRef]
- Tu, W.; Cao, R.; Yue, Y.; Zhou, B.; Li, Q.; Li, Q. Spatial variations in urban public ridership derived from GPS trajectories and smart card data. J. Transp. Geogr. 2018, 69, 45–57. [Google Scholar] [CrossRef]
- Allen, W.B.; Liu, D.; Singer, S. Accesibility measures of US metropolitan areas. Transp. Res. Part B Methodol. 1993, 27, 439–449. [Google Scholar] [CrossRef]
- Gaglione, F.; Gargiulo, C.; Zucaro, F.; Cottrill, C. Urban accessibility in a 15-minute city: A measure in the city of Naples, Italy. Transp. Res. Procedia 2022, 60, 378–385. [Google Scholar] [CrossRef]
- Capasso Da Silva, D.; King, D.A.; Lemar, S. Accessibility in practice: 20-minute city as a sustainability planning goal. Sustainability 2019, 12, 129. [Google Scholar] [CrossRef]
- Moreno, C.; Allam, Z.; Chabaud, D.; Gall, C.; Pratlong, F. Introducing the “15-Minute City”: Sustainability, resilience and place identity in future post-pandemic cities. Smart Cities 2021, 4, 93–111. [Google Scholar] [CrossRef]
- Chakour, V.; Eluru, N. Examining the influence of stop level infrastructure and built environment on bus ridership in Montreal. J. Transp. Geogr. 2016, 51, 205–217. [Google Scholar] [CrossRef]
- Leung Ian, X.Y.; Chan, S.Y.; Hui, P.; Lio, P. Intra-city urban network and traffic flow analysis from GPS mobility trace. arXiv 2011, arXiv:11055839. [Google Scholar]
- Henry, E.; Bonnetain, L.; Furno, A.; El Faouzi, N.E.; Zimeo, E. Spatio-temporal correlations of betweenness centrality and traffic metrics. In Proceedings of the 2019 6th International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Cracow, Poland, 5–7 June 2019. [Google Scholar]
- Dai, T.; Ding, T.; Liu, Q.; Liu, B. Node centrality comparison between bus line and passenger flow networks in Beijing. Sustainability 2022, 14, 15454. [Google Scholar] [CrossRef]
- Tang, J.; Gao, F.; Han, C.; Cen, X.; Li, Z. Uncovering the spatially heterogeneous effects of shared mobility on public transit and taxi. J. Transp. Geogr. 2021, 95, 103134. [Google Scholar] [CrossRef]
- Lee, Y.; Chen, G.Y.H.; Circella, G.; Mokhtarian, P.L. Substitution or complementarity? A latent-class cluster analysis of ridehailing impacts on the use of other travel modes in three southern US cities. Transp. Res. Part D Transp. Environ. 2022, 104, 103167. [Google Scholar] [CrossRef]
- Thorhauge, M.; Vij, A.; Cherchi, E. Heterogeneity in departure time preferences, flexibility and schedule constraints. Transportation 2021, 48, 1865–1893. [Google Scholar] [CrossRef]
- Ma, X.; Yang, J.; Ding, C.; Liu, J.; Zhu, Q. Joint analysis of the commuting departure time and travel mode choice: Role of the built environment. J. Adv. Transp. 2018, 2018, 4540832. [Google Scholar] [CrossRef]
- Ha, J.; Lee, S.; Ko, J. Unraveling the impact of travel time, cost, and transit burdens on commute mode choice for different income and age groups. Transp. Res. Part A Policy Pract. 2020, 141, 147–166. [Google Scholar] [CrossRef]
- Rahman, M.; Akther, M.S.; Recker, W. The first-and-last-mile of public transportation: A study of access and egress travel characteristics of Dhaka’s suburban commuters. J. Public Transp. 2022, 24, 100025. [Google Scholar] [CrossRef]
- Meng, M.; Koh, P.P.; Wong, Y.D. Influence of socio-demography and operating streetscape on last-mile mode choice. J. Public Transp. 2016, 19, 38–54. [Google Scholar] [CrossRef]
- Li, X.; Xu, J.; Du, M.; Liu, D.; Kwan, M.P. Understanding the spatiotemporal variation of ride-hailing orders under different travel distances. Travel Behav. Soc. 2023, 32, 100581. [Google Scholar] [CrossRef]
- Dias, F.F.; Lavieri, P.S.; Kim, T.; Bhat, C.R.; Pendyala, R.M. Fusing multiple sources of data to understand ride-hailing use. Transp. Res. Rec. 2019, 2673, 214–224. [Google Scholar] [CrossRef]
- Pan, R.; Yang, H.; Xie, K.; Wen, Y. Exploring the equity of traditional and ride-hailing taxi services during peak hours. Transp. Res. Rec. 2020, 2674, 266–278. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, T.; Fukuda, H.; Ma, M. Evidence of Multi-Source Data Fusion on the Relationship between the Specific Urban Built Environment and Urban Vitality in Shenzhen. Sustainability 2023, 15, 6869. [Google Scholar] [CrossRef]
- Bi, H.; Ye, Z.; Zhang, Y. Analysis of the integration usage patterns of multiple shared mobility modes and metro system. Transp. Res. Rec. 2021, 2675, 876–894. [Google Scholar] [CrossRef]
- Liu, F.; Gao, F.; Yang, L.; Han, C.; Hao, W.; Tang, J. Exploring the spatially heterogeneous effect of the built environment on ride-hailing travel demand: A geographically weighted quantile regression model. Travel Behav. Soc. 2022, 29, 22–33. [Google Scholar] [CrossRef]
- Tao, Z.; Zhou, J.; Lin, X.; Chao, H.; Li, G. Investigating the impacts of public transport on job accessibility in Shenzhen, China: A multi-modal approach. Land Use Policy 2020, 99, 105025. [Google Scholar] [CrossRef]
- Ou, X.; Li, C. The Analysis of Bus Route Optimization Based on Taxi GPS Data. In Proceedings of the CICTP 2020, Xi’an, China, 14–16 August 2020; pp. 3282–3294. [Google Scholar]
- Bi, H.; Ye, Z.; Hu, L.; Zhu, H. Why they don’t choose bus service? Understanding special online car-hailing behavior near bus stops. Transp. Policy 2021, 114, 280–297. [Google Scholar] [CrossRef]
- Munch, E.; Proulhac, L. Is work hours’ flexibility really a solution to morning peak period congestion? Comparative analysis between Paris and San Francisco. J. Transp. Geogr. 2023, 113, 103712. [Google Scholar] [CrossRef]
- Liu, W.; Li, X.; Liu, T.; Liu, B. Approximating betweenness centrality to identify key nodes in a weighted urban complex transportation network. J. Adv. Transp. 2019, 2019, 9024745. [Google Scholar] [CrossRef]






| Variable | Average | Standard Deviation | Description | ||
|---|---|---|---|---|---|
| Dependent variable | |||||
| Ride-hailing emissions (Weekdays) | y | 5.8110 | 12.2199 | Emissions generated by ride-hailing travel per kilometer per hour on weekdays (kg/km) | |
| Ride-hailing emissions (Weekend) | 5.6494 | 12.4222 | Emissions generated by ride-hailing travel per kilometer per hour on weekend (kg/km) | ||
| Independent variable | |||||
| Travel demand (4) | Bus ridership (Weekdays) | x1 | 2.8636 | 2.4140 | Natural logarithm of bus ridership per hour on weekdays |
| Bus ridership (Weekend) | 2.8300 | 2.3120 | Natural logarithm of bus ridership per hour on weekend | ||
| Metro ridership (Weekdays) | x2 | 1.0108 | 2.2659 | Natural logarithm of metro ridership per hour on weekdays | |
| Metro ridership (Weekend) | 0.9992 | 2.2293 | Natural logarithm of metro ridership per hour on weekend | ||
| Ride-hailing ridership (Weekdays) | x3 | 2.2241 | 2.1606 | Natural logarithm of ride-hailing ridership per hour on weekdays | |
| Ride-hailing ridership (Weekend) | 2.3599 | 2.0628 | Natural logarithm of ride-hailing ridership per hour on weekend | ||
| Bike-sharing ridership (Weekdays) | x4 | 1.9100 | 2.2343 | Natural logarithm of bike-sharing ridership per hour on weekdays | |
| Bike-sharing ridership (Weekend) | 3.7078 | 1.7060 | Natural logarithm of bike-sharing ridership per hour on weekend | ||
| Land use (7) | Commercial land density | x5 | 155.4727 | 184.6213 | The number of commercial lands per square kilometer |
| Residential land density | x6 | 43.1141 | 50.6933 | The number of residential lands per square kilometer | |
| Leisure land density | x7 | 53.1142 | 62.0186 | The number of leisure lands per square kilometer | |
| Catering land density | x8 | 83.5013 | 96.3907 | The number of catering lands per square kilometer | |
| Public service land density | x9 | 88.2451 | 101.3098 | The number of public service lands per square kilometer | |
| Transportation facility land density | x10 | 47.7839 | 66.0291 | The number of transportation facilities lands per square kilometer | |
| Land-use entropy index | x11 | 1.0718 | 0.2685 | The index to evaluate the diversity of land use | |
| Demographics (2) | Population density | x12 | 14.4973 | 14.4888 | The number of people per square kilometer |
| Employed population density | x13 | 1.8321 | 1.9911 | The number of employed people per square kilometer | |
| Traffic network structure (10) | Bus lines density | x14 | 91.7586 | 230.2714 | The length of bus lines per square kilometer (km−1) |
| Bus stations density | x15 | 45.1554 | 42.0940 | The number of bus stations per square kilometer | |
| Bus accessibility | x16 | 27.7111 | 7.3157 | The accessibility of bus stations (min) | |
| Bus network betweenness centrality | x17 | 0.0138 | 0.0182 | The average values of betweenness centrality of nodes in the bus network | |
| Metro lines density | x18 | 1.8434 | 3.0026 | The length of metro lines per square kilometer (km−1) | |
| Metro stations density | x19 | 0.3129 | 1.6045 | The number of metro stations per square kilometer | |
| Metro accessibility | x20 | 39.6499 | 11.5565 | The accessibility of metro stations (min) | |
| Metro network betweenness centrality | x21 | 0.0157 | 0.0384 | The average values of node betweenness centrality in the metro network | |
| Road network density | x22 | 12.0990 | 7.6207 | The length of road segments per square kilometer (km−1) | |
| Road network betweenness centrality | x23 | 0.0016 | 0.0023 | The average values of node betweenness centrality in the road network | |
| Variable | Weekdays (17) | Weekend (16) | |||||
|---|---|---|---|---|---|---|---|
| VIF | Coff. | VIF | Coff. | ||||
| Bus ridership | x1 | 4.2756 | 0.0131 | 3.7600 | −0.0143 | ||
| Metro ridership | x2 | 1.8377 | 0.1401 *** | √ | 1.8401 | 0.1252 *** | √ |
| Ride-hailing ridership | x3 | 7.3728 | 0.3482 *** | √ | 6.3744 | 0.3312 *** | √ |
| Bike-sharing ridership | x4 | 5.2137 | 0.2664 *** | √ | 0.1702 *** | ||
| Commercial land density | x5 | 4.4186 | 0.2376 *** | √ | 4.4333 | 0.2041 *** | √ |
| Residential land density | x6 | 0.3818 *** | 0.3606 *** | ||||
| Leisure land density | x7 | 0.3521 *** | 0.3310 *** | ||||
| Catering land density | x8 | 5.0998 | 0.2958 *** | √ | 5.1317 | 0.2805 *** | √ |
| Public service land density | x9 | 0.3547 *** | 0.3394 *** | ||||
| Transportation facility land density | x10 | 6.6903 | 0.3993 *** | √ | 6.6972 | 0.3701 *** | √ |
| Land-use entropy index | x11 | −0.0634 *** | −0.0688 *** | ||||
| Population density | x12 | 4.0244 | 0.3409 *** | √ | 4.0228 | 0.3243 *** | √ |
| Employed population density | x13 | 3.3981 | 0.2784 *** | √ | 3.3857 | 0.2546 *** | √ |
| Bus lines density | x14 | 1.3132 | 0.5893 *** | √ | 1.3135 | 0.6040 *** | √ |
| Bus stations density | x15 | 5.4143 | 0.3075 *** | √ | 5.4157 | 0.2910 *** | √ |
| Bus accessibility | x16 | 4.4289 | −0.3185 *** | √ | 4.0165 | −0.3053 *** | √ |
| Bus network betweenness centrality | x17 | 1.7452 | −0.0784 *** | √ | 1.7345 | −0.0834 *** | √ |
| Metro lines density | x18 | 1.8143 | 0.1614 *** | √ | 1.8158 | 0.1574 *** | √ |
| Metro stations density | x19 | 1.6124 | 0.1467 *** | √ | 1.6140 | 0.1566 *** | √ |
| Metro accessibility | x20 | −0.4026 *** | −0.3863 *** | ||||
| Metro network betweenness centrality | x21 | 1.3848 | 0.1242 *** | √ | 1.3778 | 0.1208 *** | √ |
| Road network density | x22 | 6.6089 | 0.2769 *** | √ | 6.4430 | 0.2592 *** | √ |
| Road network betweenness centrality | x23 | 1.4457 | −0.0490 *** | √ | 1.4470 | −0.0506 *** | √ |
| Time | Weekdays | Weekend | Time | Weekdays | Weekend | ||||
|---|---|---|---|---|---|---|---|---|---|
| bs | bt (Unit: Hour) | bs | bt (Unit: Hour) | bs | bt (Unit: Hour) | bs | bt (Unit: Hour) | ||
| T1 | 0.2321 | 0 | 0.2319 | 0 | T13 | 0.2181 | 1 | 0.2184 | 1 |
| T2 | 0.2127 | 1 | 0.1296 | 1 | T14 | 0.2307 | 6 | 0.2292 | 1 |
| T3 | 0.1874 | 1 | 0.1980 | 2 | T15 | 0.9966 | 1 | 0.9969 | 1 |
| T4 | 0.1097 | 3 | 0.0422 | 3 | T16 | 0.9996 | 1 | 0.9996 | 1 |
| T5 | 0.0368 | 2 | 0.0296 | 3 | T17 | 0.9993 | 1 | 0.9966 | 1 |
| T6 | 0.0299 | 2 | 0.1291 | 1 | T18 | 0.0341 | 17 | 0.0277 | 17 |
| T7 | 0.1288 | 1 | 0.1300 | 1 | T19 | 0.0287 | 2 | 0.0299 | 2 |
| T8 | 0.1300 | 1 | 0.1303 | 1 | T20 | 0.1966 | 1 | 0.2399 | 1 |
| T9 | 0.1288 | 1 | 0.1322 | 1 | T21 | 0.1417 | 1 | 0.1307 | 1 |
| T10 | 0.1809 | 1 | 0.1300 | 1 | T22 | 0.0311 | 2 | 0.0280 | 3 |
| T11 | 0.1663 | 1 | 0.1641 | 1 | T23 | 0.0299 | 3 | 0.0280 | 4 |
| T12 | 0.2442 | 1 | 0.2342 | 1 | T24 | 0.0322 | 2 | 0.0284 | 5 |
| Variable | Mean | Std. | 1st Qu. | Median | 3st Qu. | |
|---|---|---|---|---|---|---|
| Weekdays | ||||||
| Metro ridership | −0.326 | 2.298 | −0.161 | 0.000 | 0.008 | |
| Ride-hailing ridership | 0.778 | 1.513 | 0.037 | 0.326 | 1.342 | |
| Bike-sharing ridership | 0.076 | 1.367 | −0.080 | 0.028 | 0.370 | |
| Commercial land density | −0.005 | 0.544 | −0.003 | 0.000 | 0.001 | |
| Catering land density | 0.010 | 0.736 | −0.003 | 0.000 | 0.013 | |
| Transportation facility land density | 0.021 | 1.283 | −0.002 | 0.004 | 0.033 | |
| Population density | 0.015 | 3.935 | −0.008 | 0.011 | 0.095 | |
| Employed population density | −0.275 | 53.937 | −0.157 | 0.011 | 0.214 | |
| Bus lines density | 0.097 | 7.853 | 0.001 | 0.007 | 0.030 | |
| Bus stations density | −0.059 | 6.996 | −0.020 | −0.002 | 0.003 | |
| Bus accessibility | −0.124 | 12.096 | −0.002 | 0.004 | 0.040 | |
| Bus network betweenness centrality | 600.883 | 62,502.976 | −27.493 | −1.228 | 2.058 | |
| Metro lines density | −1.896 | 265.719 | −0.037 | 0.004 | 0.481 | |
| Metro stations density | 5.843 | 791.567 | −1.325 | −0.040 | 0.313 | |
| Metro network betweenness centrality | −139.247 | 12,625.103 | −5.726 | −0.012 | 3.502 | |
| Road network density | −0.039 | 15.063 | −0.187 | −0.034 | −0.002 | |
| Road network betweenness centrality | −795.522 | 222,774.734 | 12.203 | 96.892 | 320.894 | |
| Weekend | ||||||
| Metro ridership | −0.115 | 5.666 | −0.089 | 0.000 | 0.008 | |
| Ride-hailing ridership | 0.713 | 1.642 | 0.047 | 0.324 | 1.346 | |
| Commercial land density | −0.004 | 0.376 | −0.004 | 0.000 | 0.001 | |
| Catering land density | 0.002 | 0.573 | −0.002 | 0.001 | 0.014 | |
| Transportation facility land density | 0.042 | 1.576 | −0.002 | 0.003 | 0.032 | |
| Population density | 0.016 | 3.239 | −0.012 | 0.006 | 0.090 | |
| Employed population density | −0.316 | 59.457 | −0.094 | 0.010 | 0.194 | |
| Bus lines density | 0.050 | 2.021 | 0.000 | 0.006 | 0.030 | |
| Bus stations density | −0.021 | 3.192 | −0.022 | −0.001 | 0.004 | |
| Bus accessibility | −0.074 | 10.763 | −0.011 | 0.001 | 0.021 | |
| Bus network betweenness centrality | 208.598 | 14,034.037 | −23.521 | −0.827 | 2.350 | |
| Metro lines density | −6.893 | 288.524 | −0.025 | 0.002 | 0.436 | |
| Metro stations density | 18.155 | 735.058 | −0.983 | −0.011 | 0.263 | |
| Metro network betweenness centrality | −44.587 | 2960.608 | −3.061 | 0.233 | 5.470 | |
| Road network density | −0.034 | 20.334 | −0.172 | −0.023 | 0.001 | |
| Road network betweenness centrality | 1044.160 | 148,441.500 | 8.592 | 91.820 | 332.229 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Zhao, C.; Zeng, Y.; Tang, J. Exploring the Spatio-Temporally Heterogeneous Impact of Traffic Network Structure on Ride-Hailing Emissions Using Shenzhen, China, as a Case Study. Sustainability 2024, 16, 4539. https://doi.org/10.3390/su16114539
Gao W, Zhao C, Zeng Y, Tang J. Exploring the Spatio-Temporally Heterogeneous Impact of Traffic Network Structure on Ride-Hailing Emissions Using Shenzhen, China, as a Case Study. Sustainability. 2024; 16(11):4539. https://doi.org/10.3390/su16114539
Chicago/Turabian StyleGao, Wenyuan, Chuyun Zhao, Yu Zeng, and Jinjun Tang. 2024. "Exploring the Spatio-Temporally Heterogeneous Impact of Traffic Network Structure on Ride-Hailing Emissions Using Shenzhen, China, as a Case Study" Sustainability 16, no. 11: 4539. https://doi.org/10.3390/su16114539
APA StyleGao, W., Zhao, C., Zeng, Y., & Tang, J. (2024). Exploring the Spatio-Temporally Heterogeneous Impact of Traffic Network Structure on Ride-Hailing Emissions Using Shenzhen, China, as a Case Study. Sustainability, 16(11), 4539. https://doi.org/10.3390/su16114539







