In the first part of this section, the values of the optimum tilt angles will be presented, and after that, their use efficiency will be analyzed.
3.1. Optimum Tilt Angles for Europe
Considering the models presented in the previous section of the paper, several algorithms were developed to calculate the optimum tilt angles. The obtained results are further presented.
- a.
Yearly optimum tilt angles (βy)
Four models have been considered for the
βy estimation: the empirical model proposed by Patko (PTK) [
23], the regression model proposed by C. Martin (CM) [
24], the regression model proposed by Modarresi (MOD) [
25] and the radiation search-based method (SBM). The yearly optimum tilt angles obtained are presented in
Table 2.
As the model proposed by Patko assumes that the optimum tilt angle is equal to the latitude, it will provide the highest values of βy, of all four models. A quite good correlation can be observed in values provided by the model proposed by C. Martin and the search-based method.
- b.
Bi-annual optimum tilt angles (βb)
The bi-annual optimum tilt angles have been determined using only the radiation search-based method (SBM), considering two distinct seasons along the year, namely the warm season and the cold season. However, these two seasons have been delimited on the following assumptions:
Calendar-based: the warm season extends from 1 March to 30 September, while the cold season extends from 1 October to 28 February.
Astronomical definition: the warm season extends between the spring and autumn equinox (from 20 March to 22 September), while the cold season extends from 23 September to 19 March.
Thus, the SBM algorithm was tuned according to the mentioned assumptions, and the values obtained considering the calendar delimited seasons were noted as cSBM (calendar search-based method), while the other ones as aSBM (astronomical search-based method). The values of the bi-annual optimal tilt angles are presented in
Table 3.
As expected, the optimum tilt angles for the warm season are lower than those for the cold season. However, one can notice that when astronomical seasons are considered, the optimum tilt angles are slightly higher than those determined for the calendar-based seasons, for both warm and cold seasons.
- c.
Seasonal optimum tilt angles (βs)
A seasonal adjustment of the PV panel’s tilt angle assumes that the year is split into four seasons, typically spring, summer, autumn, and winter, and the optimum tilt angle (βs) is determined for each season.
In our analysis, we determined the value of
βs for each season using the mathematical expressions previously presented in
Table 1.
Similar to the bi-annual tilt angles, previously determined, when using the SBM algorithm, the seasons were delimited on a calendar-based assumption and according to the astronomical definition, as follows:
Calendar-based: Spring—1 March to 30 May; Summer—1 June to 31 August; Autumn—1 September to 30 November; Winter—1 December to 28 February;
Astronomical definition: Spring—20 March to 20 June, Summer—21 June to 22 September; Autumn—23 September to 20 December; Winter—21 December to 19 March.
The calculated values of
βs are presented in
Table 4 for the considered latitudes.
Of all models, the one proposed by Patko will provide the highest values for the
βs in spring, and the lowest values in autumn. Changing how seasons are delimited has a significant impact on the optimum tilt values. As one can notice in
Table 4, when using the astronomical definition
βs, there will be lower values in winter and spring, and higher values in summer and autumn, compared to those obtained under the calendar-based scenario.
- d.
Monthly optimum tilt angles (βm)
The monthly optimum tilt angles have also been determined according to the three models presented in
Table 1, and the obtained values of
βm are presented in
Table 5 for latitudes between 35° and 45°, and in
Table 6 for the other latitudes.
The model proposed by El-Kassaby (KSB) and the search-based model (SBM) provides the closest results as their mean bias error (MBE) is −1.34°, while MBE between SBM and MOD is 1.45°, and between KSB and MOD, it is 2.79°. The model proposed by El-Kassabi tends to provide higher optimum tilt angles from January to April and from August to December for most of the latitudes; the maximum difference being under 7° for 60° latitude, and smaller values at latitudes over 40° for the summer months.
3.2. Efficiency of Using Bi-Annual, Seasonal, and Monthly Optimum Tilt Angles
While some comparisons between the angles determined according to various models have been presented in the previous section, the main objective of this study is to evaluate the efficiency of several adjustments (two, four, and twelve) of a surface tilt angle throughout the year. This analysis was conducted by determining the annual total solar irradiation received by a surface that is tilted according to the bi-annual, seasonal, and monthly optimum tilt angles (previously presented in
Table 3,
Table 4,
Table 5 and
Table 6) and comparing it with the annual total irradiation provided by the yearly optimum tilt angle (from
Table 2).
For the determination of solar irradiation, a new algorithm was developed, considering the Liu and Jordan mathematical model. The results obtained when using the yearly optimum tilt angles and the bi-annual tilt angles are presented in
Table 7, and the results obtained when seasonal and monthly optimum tilt angles have been considered are presented in
Table 8.
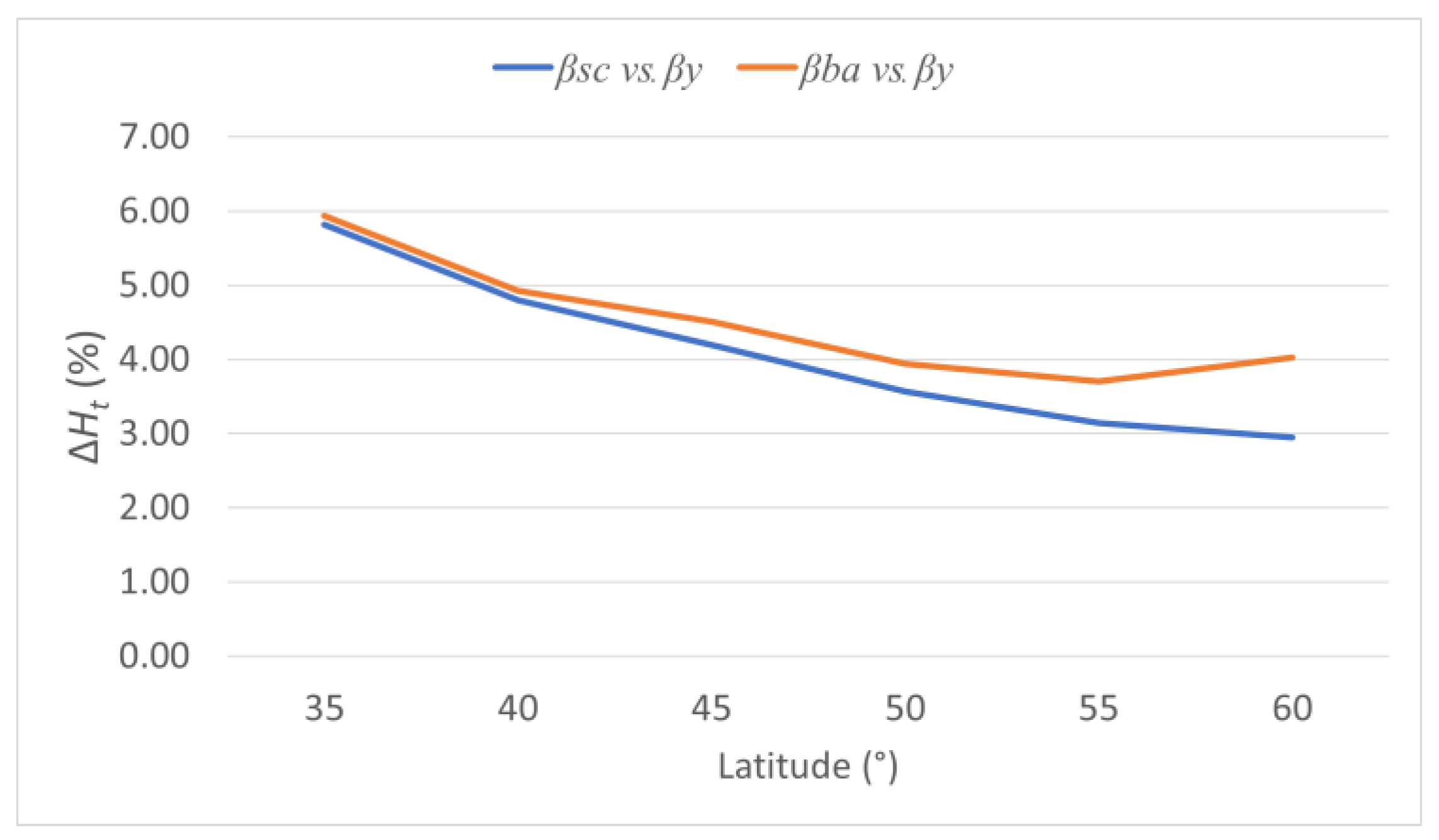
When the yearly optimum tilt angles are compared, it can be observed that those provided by the SBM algorithm are ensuring the highest values of the total incident irradiation, and the absolute differences between the use of SBM angles and those predicted by the other three models are presented in
Figure 1.
As one can notice, the differences between using the angles proposed by the considered methods are under 10 kWh/m2, apart from the model proposed by Patko, which underperforms at latitudes higher than 40°, as the differences in terms of incident irradiation grow to over 15 kWh/m2, the maximum difference being over 32 kWh/m2 at 55° latitude. A very good correlation can be observed between the results obtained using the angle determined by SBM and the regression model proposed by C. Martin.
Similar conclusions can be drawn when considering the data in
Table 8, as the model proposed by Patko ensures, once again, the smallest values of the incident radiation (as it was the case when the yearly optimum tilt angles have been analyzed—see
Figure 1). However, the differences between the results provided by the other two models are rather insignificant. Hence, one can conclude that these simple models, based on empirical equations, could be successfully used to determine the optimum tilt angles for any time interval wanted and any location, thus avoiding the complexity of the radiation search-based methods.
The impact of multiple changes of tilt angle across the year has been analyzed considering the optimum tilt angles determined according to the SBM algorithm. The annual total irradiation of the yearly optimum tilt angle was considered as a reference, and the increase in incident irradiation on the surface, when using bi-annual, seasonal and monthly tilt angles has been determined, both in absolute and relative values. Thus, in
Table 9, the absolute gains of incident radiation by all latitudes are presented, while
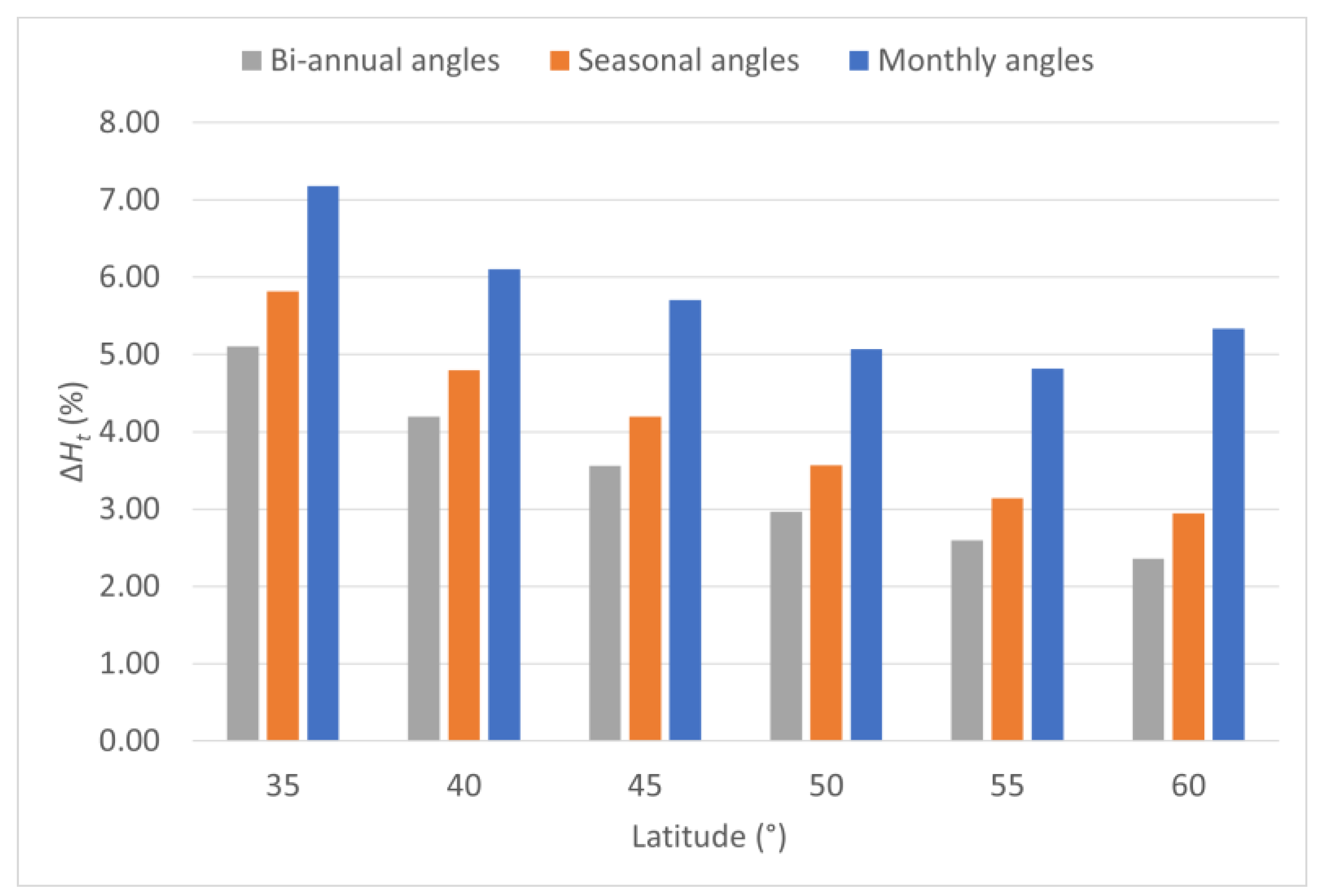
Figure 2 depicts these gains in relative values.
One can notice that the monthly optimization of the tilt angles ensures the best performances, as expected, but its efficiency is not the same for all latitudes across Europe, as the highest increases of total incident radiation (over 100 kWh/m2) are reported at 35° and 40° latitude, with a maximum of 157.2 kWh/m2 at 35°, while at lower and higher latitudes, the gains of incident radiation are less important.
A similar pattern can be observed for the bi-annual and seasonal angles as well, as such an optimization of the surface’s tilt angle will boost the incident irradiation, especially at lower latitudes (35° and 40°). In relative values, the increase in the incident solar irradiation due to the monthly optimization of the tilt angle is slightly over 7% at 35° latitude, with values lower than 6% at the other analyzed latitudes.
At the same time the efficiency of seasonal optimum angles is rather marginal when compared to that of the bi-annual angles, the gains of solar irradiation being under 20 kWh/m2, at 35° latitude and even smaller in the rest.