Abstract
The internal components of a smart building interact through a compatible fabric and logic. A smart building integrates systems, structure, services, management, and their interrelationships to create a dynamic and cost-efficient environment. Smart buildings reduce the amount of cooling and heating load required to cool and heat spaces, thereby lowering operating costs and energy consumption without sacrificing occupant comfort. Smart structures are an Internet of Things (IoT) concern. The Internet of Things is a global network that virtualizes commonplace objects. The Internet of Things infuses non-technical objects with technology. IoT development has led to the creation of new protocols based on architectures for wireless sensor networks. Energy conservation extends the life and improves the performance of these networks, while overcoming the limitations of IoT node batteries. This research seeks to develop a data transmission model for routing IoT data in smart buildings. Utilization of intelligent object clustering and particle swarm optimization (PSO), chaotic particle swarm optimization (CPSO), and fractional chaotic order particle swarm optimization (FCPSO) optimization methods. Using the proposed algorithm to minimize energy consumption in the IoT is possible due to the algorithm’s ability to mitigate the problem by considering the number of parameters that can have a significant impact on performance, which is the goal of many optimization approaches.
1. Introduction
The term Internet of Things (IoT) refers to a vast network of actual physical objects such as machines, buildings, and other things that have sensors, network connections, and software integrated into them as a tiny system []. These embedded systems share information with one another as well as gathering data from the environment around the physical items. The integration of the physical world based on computer systems through the IoT improves efficiency, accuracy, and the economy. Cyber-physical systems are a broad term for sensors and actuators used in the IoT [,].
These kinds of systems can be said to contain various forms of smart cities, residences, and transportation. The IoT is made up of several components, including sensors, software, and hardware, which communicate with one another using radio waves []. Each of these systems communicates with the others over wired and wireless networks if the grouping of these components is employed as an embedded system [,]. Establishing communication between things in the physical world enables real-time awareness of the physical world and an emergency response based on the data collected. The ever-increasing development of smart buildings and the rate of innovation in this field have prompted numerous researchers to implement a wide range of applications [,]. A smart building is one that is equipped with a robust communication infrastructure that can continuously react to and adapt to changing environmental circumstances, and that enables the building’s occupants to use the available resources more efficiently and boost their security and comfort []. In order to lower the expenses of the construction industry and make optimal use of technology and the application of communication and computer technologies, the energy efficiency of building management and automation systems will increase. The savings coming from the employment of these solutions can therefore quickly offset the associated expenses []. Intelligent control systems will have a high degree of adaptability, allowing them to be quickly adapted to the diverse optimization strategies for energy usage in smart buildings. During operation, it is also simple to adjust and optimize operations for improved management, energy cost reduction, and maintenance cost reduction. In an intelligent building, many of the behaviors that occupants display habitually and unconsciously are performed by intelligent systems, saving time and money on labor.
In many of the proposed methods, the authors have addressed only one of these weaknesses, and the simultaneous elimination of these two weaknesses has received less attention. Various algorithms and models, such as greedy routing, opportunistic routing, data transmission methods, and clustering, have been developed in order to reduce energy consumption and extend the lifetime of wireless nodes in the IoT.
In this study, two tools are employed concurrently to mitigate the deficiencies of the standard particle swarm optimization algorithm. We wish to determine which of chaotic particle swarm optimization (CPSO) and fractional chaotic order particle swarm optimization (FCPSO) improves the overall convergence of the particle swarm optimization (PSO) algorithm and protects it from local optima. Additionally, fractional order derivatives are employed to accelerate the convergence rate of the particles toward the optimal general response. Taking into account the significance of optimizing energy consumption in organizations and smart buildings, the proposed method is based on the clustering of intelligent objects and fuzzy systems. The proposed method aims to optimize energy consumption in smart buildings via the IoT.
2. Related Works
Numerous studies have been undertaken to develop answers for the effective application of IoT-related building energy consumption. Even though great advancements have been made, the methodologies are quite diverse, and the challenges are still extremely difficult, posing an ongoing problem for the research community.
In reality, equipment and appliances in a smart home can be monitored and managed in the form of objects by employing IoT technology and web-based or mobile applications based on this technology [,]. In general, an IoT node has limited resources, including processing power and energy supply. If an IoT node must operate in an environment without a direct power connection, it requires a battery. To solve this issue, a significant amount of research has been undertaken on how to reduce energy consumption in wireless sensor networks (WSNs) as a battery-constrained sensing technology, and a number of techniques and approaches have been created to boost battery usage in an effective manner [,]. A WSN may be utilized as a component of IoT technology to build a variety of IoT platforms. The development of various routing algorithms, such as opportunistic routing and greedy algorithms, can reduce sensor network energy usage. In addition to the development of routing protocols, clustering techniques in sensor networks are an extra method for lowering sensor energy consumption and extending network lifetime. The clustering-of-objects approach is one of the efficient ways to lower energy usage during the information transfer phase in the IoT. Each cluster in clustering has a node designated as the cluster head, which is in charge of organizing network activities and gathering data from sensor nodes. Additionally, the cluster head eliminates unnecessary and redundant data packets, reducing overheads and interference. By decreasing the size and quantity of nodes in the routing, it also lowers routing complexity [,]. Additionally, the clustering approach makes sensor networks more scalable and stable. Load balancing, which divides network responsibilities between member nodes according to energy and battery memory, is another benefit of the clustering process. The primary objective of this study is to reduce energy consumption during the data transmission cycle. IoT applications are extremely time-sensitive and crucial; therefore, the majority of communication and processing operations must be accomplished in a restricted amount of time to avoid negative outcomes. Consequently, ensuring real-time support in large-scale IoT networks is one of the most significant and demanding research topics. This allows the communication center to enhance the monitoring of agents. Cloud services can provide applications such as social networks for agent monitoring, environmental data analysis, and network analysis, etc., to advanced users. Cloud computing plays a crucial role in delivering high-performance computing and supporting several operating system platforms [].
A genetic algorithm is offered by Ahmed et al. [] as a solution for enhancing the energy efficiency of existing Cloud of Things energy plans. The ETCORA algorithm is contrasted with the proposed strategy, which is then subjected to extensive numerical simulations to demonstrate its utility. The results of the analysis indicate that the proposed strategy for optimizing energy use results in enhanced overall performance. A fuzzy algorithm-based method for modeling energy loss optimization scheduling with many targets is proposed by Ding and Wu []. In the IoT context, the multi-objective equipment scheduling optimization equation is created, and the fuzzy algorithm is introduced into the single-target energy loss problem. In order to reduce the overall energy consumption of device scheduling in an IoT context, the algorithm searches for idle device time and optimizes the device scheduling energy consumption model. Fanian et al. [] use the shuffling frog leaping algorithm (SFLA) to present a method for picking fuzzy input parameters in a fuzzy multi-hop clustering protocol called PS-SFLA. This technique consists of three primary phases, each of which is introduced in three variants for the purpose of step-by-step evaluation. In the initial iteration, the most common and diverse parameters were extracted from the literature review and formulated. Kadri and Koudil [] provide a technique for mapping tasks with reliability in mind. It utilizes a combination of multi-objective optimization and reinforcement learning (RL). It enables the recovery of persistent faults in processing elements that may occur in a homogenous 2D-Mesh NoC, while pursuing the optimal performance-reliability tradeoff. A multi-objective biogeography-based optimization method (MOBBO) is proposed for the development of optimal species distributions.
The data center has changed into a virtualized server network supported by hardware-assisted virtualization with the introduction of the new cloud-based approach. To fulfill the increased expectations of users, a new algorithm for resource management and real-time scheduling is required. In wireless networks, cluster-based routing algorithms offer an efficient means of enhancing network performance by separating sensor nodes into distinct groups [].
Given the significance of optimizing energy consumption in organizations and smart buildings in this study, a data transmission model for routing data among IoT nodes in smart buildings is proposed. The proposed method is based on smart object clustering and a particle swarm optimization (PSO). The proposed method’s goal is to optimize energy consumption in smart buildings powered by the IoT [,]. To improve the energy efficiency of the networks and prevent the early failure of the network, the potential choice of the cluster head with the remaining energy of the sensor node was addressed. A joint method based on communication cost and residual energy was utilized to choose cluster heads in a hybrid energy-efficient distributed clustering protocol (HEED). Due to the fact that the clustering process was terminated after an arbitrary number of iterations, there were insufficient cluster heads to cover the entire sensor region []. Consequently, some sensor nodes may have evaded the coverage of the cluster heads and are now referred to as isolated nodes. Constantly searching for cluster heads or communicating directly with the base station causes these nodes to consume a great deal of energy. Due to their additional task of transmitting data to the base station, cluster heads consume significantly more battery power than other nodes [,].
3. Optimization Model
In this section, first the PSO algorithm is stated, then the CPSO and FCPSO algorithms are presented, and finally, using the theory of fractional order derivatives, the FCPSO algorithm is formulated.
3.1. Particle Swarm Optimization Algorithm
Initially, the implementation-relevant characteristics of the system model are introduced in depth. For the proposed protocol, we assume a large, dense network and a database that is predominantly static. When deployed within the network, all items are identical in terms of their physical properties, energy capacity, and transmission range. Each network object is aware of its geographical position and home base. The operation is carried through via a PSO algorithm [,].
The standard particle swarm optimization starts with a set of random solutions and searches for the optimal solution by updating the generations. There are two learning processes in particle swarm optimization: the cognitive learning process, which is based on the history and past of each particle. The process of social learning is based on the history and past of all particles and is obtained from the exchange of information between all particles in the population. Particles move in the multidimensional search space. While moving, each particle updates its position according to its experience and the experience of neighboring particles, and after receiving information about its best position and the best position of its neighbors, it updates its position based on a mathematical function. Each particle searches for its coordinates in the problem-solving space, which takes the best solution obtained so far (pbest) as the best particle location (gbest). Meanwhile, all particles move toward the best particles. In each iteration, the optimization includes gbest and pbest changes in the velocity of each particle toward the locations. The mathematical model of particle movement is in the form of Equation (1):
where the parameters , and are real and positive weights that show the effect of inertia. The best cognitive component (the best location of the particles) and the best social component (the best location of the particles) are known when determining the new speed for a particle. A coefficient “and” a |R-dimensional random vector in which each component is a random variable with a uniform distribution between zero and one, the natural number r represents the dimension of the problem search space. The variables and are respectively the velocity and position vectors of the particle in the tth iteration. The and are the components of the best cognitive position and the best social position, respectively [].
3.2. Chaotic Particle Swarm Optimization Algorithm
The chaotic particle swarm algorithm is a combination of the standard particle swarm optimization algorithm and a chaotic mapping in which, this mapping, in the initialization process as well as the evolution process of the particle swarm optimization algorithm. Chaos is a phenomenon in non-linear systems that includes numerous unstable round motions. In other words, chaos is a random behavior in a certain nonlinear system []. A chaotic mapping is a time-discrete dynamical system as follows:
Chaotic mapping can be used to generate sequences of numbers. These sequences, which are known as chaotic sequences, have characteristics of chaotic mapping such as being random, independent of time, and being regular, and accordingly, no state is repeated in them. Chaotic sequences are considered as random sequences and are used as a random parameter in the optimization algorithm of chaotic particle swarms. In this way, chaotic sequences are a suitable tool to control the particle swarm optimization algorithm and prevent the algorithm from being placed in a local optimal point during the search process, as well as the early convergence phenomenon, which is one of the problems of the standard algorithm. So far, many chaotic maps have been introduced to improve the particle swarm optimization algorithm. For the algorithm proposed in this article, logistic chaos mapping is used to produce uniform particles in order to improve the quality of the initial population generation and avoid local optimal points [,].
3.3. Fractional Chaotic Particle Swarm Optimization Algorithm
After generating the initial population in the algorithm, the position and speed of the particles should be updated. In this article, the method of fractional order derivatives is used to model the movement of particles []. In general, the equations of particle swarm optimization algorithms in discrete form are as follows:
and the continuous form of the above equations is as follows:
Because the particles move in a zigzag pattern, due to the complexity of the particle movement and the dependence of their movement on the previous position, fractional order derivatives are used which have a better description of the long-term past of the particle movement [,]. The above equations were written using Caputo’s fractional derivative model as follows:
By discretizing Caputo’s fractional Mortier derivative for v and x, the velocity and location of the particles based on the fractional Mortier derivative () are as follows:
The stability of the particle swarm optimization algorithm has been proven by applying fractional order derivatives [].
The important point in determining the optimal value of the order of the fractional derivative is that this value depends on the optimization problem and has a specific value for each problem.
3.4. Interface Node to Send Data Selection
Taking into account the two criteria of energy and distance difference, the proposed technique selects the intermediate node from among all live nodes in the network that have optimal conditions. As an intermediate node, it is optimal to choose a node that does not deplete the energy of the entire network. The energy utilized to convey data to the interface node is determined by calculating the relationship between the energy reduction of the sending nodes and Equation (7).
where EijBS shows the energy used to send data from the i node through the j interface node to reach the base station. d(si,sj) shows the distance from node i to node j and d(si,BS) represents the distance of node i to the base station. The energy used to send information to the base station is obtained directly from Equation (8).
The difference between these two quantities of energy consumption (Equation (9)) must be more than zero in order that the network’s total energy does not drop when the interface node is chosen.
The intricacy of these two-stage procedures is intimidating for engineers who seek to integrate search algorithms in production goods. Although some techniques’ source codes are available, they may not be immediately implementable in a company’s actual products. The complexity analysis comparison for optimization methods is presented in Table 1.

Table 1.
Complexity comparison of the optimization method.
4. Evaluation of the Proposed Method
MATLAB has been used to simulate and evaluate IoT and PSO, CPSO, and FCPSO information security in smart buildings. In addition, the results of the proposed method were compared to those of similar methods. Numerous parameters are affected; the values of these parameters are highly dependent on convergence improvement. In this study, the following parameters are considered when transferring data to the center or between objects:
- -
- Etx, Erx: the energy used to transmit and receive data in nodes, respectively.
- -
- Dij: distance between node i and j.
- -
- Eelec: the available energy in each node.
- -
- Fij: data transmission rate between two nodes.
- -
- CS, CR, CB: base station node cost, sensor node cost, and amplifier node cost, respectively.
All simulations are performed in a Windows 10 operating system using 2.5 GHz quad-core processors, a working frequency 2 and with a memory capacity of 8 GB. Simulation is done in MATLAB 2020 software. To check the efficiency of the proposed algorithm, 10 testbench functions were used (Table 2) [,]. In all functions, the target point is zero, the optimal point is zero, and the dimensions of all functions are r = 50.

Table 2.
Testbench functions and interval.
The simulation results of initial population generation with the help of chaos with objective functions are shown in Table 3. As can be seen Table 1, in some cases, the results of the improved algorithm with CPSO are weaker than the standard algorithm. The presentation of the FCPSO shows a better performance than the PSO and CPSO for higher fractional order derivative values. According to the obtained results, the proposed FCPSO algorithm shows better performance than the other two algorithms for each, which is one of the most important achievements of this proposed algorithm.

Table 3.
The result of PSO, CPSO and FCPSO algorithms in testbench functions for different orders of derivatives.
In Table 4, the results of running simulations with three different optimization methods (PSO, CPSO, and FCPSO) are compared in order to draw conclusions about energy usage in the IoT. Comparisons are made between the algorithms’ computation times as well as the average positioning errors they produce.

Table 4.
The simulation results of energy consumption in IoT using three optimization algorithms.
It can be seen that the amount of error in the CPSO optimization algorithm is higher than in the other two algorithms. It can be further easily seen that the mean error using the proposed algorithm is significantly lower than the other two algorithms; therefore, the error has been significantly reduced.
The implemented algorithm has been evaluated in two modes of information transfer of all nodes (objects) to the information center and information transfer from one node to another, as well as their respective energy consumptions. There is a random placement of objects in the implementation space. Figure 1 depicts an example of object placement in coordinate space.
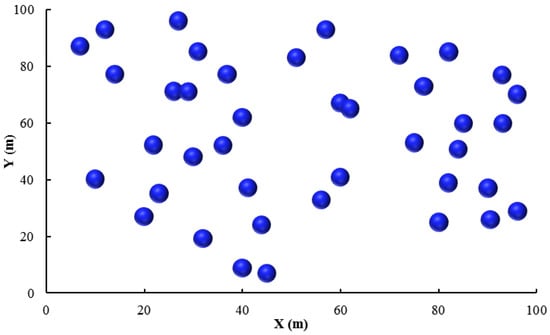
Figure 1.
Object placement in coordinate space.
Figure 2 depicts the energy consumption in two normal states and the optimal state chosen by the FCPSO algorithm for information transmission. As shown in Figure 2, when the FCPSO is used to transfer information between the objects and to the center, the energy of the objects is drastically reduced.
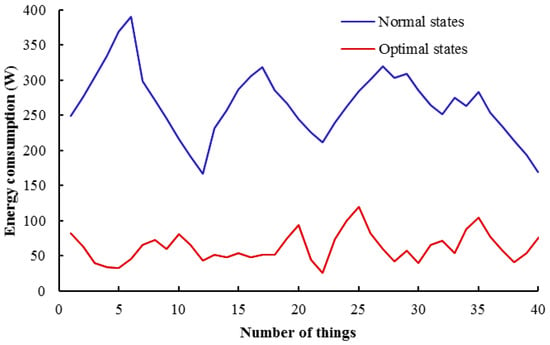
Figure 2.
Energy consumption in objects.
Additionally, Figure 3 displays the volume of data generated by the objects.
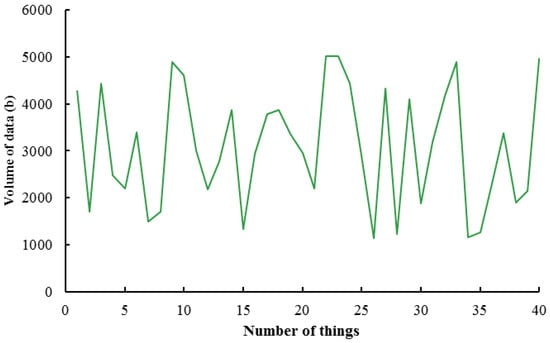
Figure 3.
The amount of data created per object.
Each object’s data for transmission to the center is generated at random at the start of the simulation (Figure 3). Nodes can be viewed in two states, normal nodes 1 and amplifier nodes 2, as a second method for evaluating the proposed energy-saving strategy. In this instance, amplifier nodes refer to a sensor node with excess energy; in fact, the amplifier node is a positive operator when executing the algorithm on the cost function of the FCPSO algorithm, thereby increasing the energy of the amplifier object. In addition, random is the selection of the sensor node (normal) and amplifier. Similar to the previous investigation, the total number of objects in this one is 40, and the center’s characteristics are unchanged. Figure 4a illustrates the energy improvement relative to the initial state. In a scenario where the FCPSO method is used for information transmission, energy consumption can be reduced by employing the FCPSO method for optimization. A second testing method employs the same method described for evaluating the parameters Etx and Erx. These two parameters can be viewed as a single parameter whose value can be arbitrarily determined for each object. The FCPSO method outperforms the standard transfer mode in this test mode. Figure 4b illustrates a comparison between these two processes.
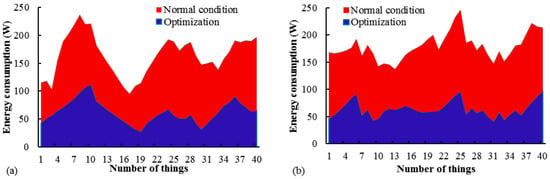
Figure 4.
Comparison of (a) energy consumption reduction, and (b) the energy required for data transmission and reception of two normal methods and FCPSO optimization.
The execution time criterion is subjected to further testing as well. When compared to the amount of time needed to complete authentication requests in IoT-based smart buildings, this metric appears to be significantly faster. A comparison has been made between three methods. The first option is to use the FCPSO algorithm to optimize the method. The second approach involves performing an analysis of ZigBee. ZigBee is a type of wireless network that accomplishes its tasks through the transmission of a signal from one piece of hardware to another. This contributes to the network becoming more robust and extensive. ZigBee can be utilized in a wide variety of applications, including door locks, thermostats, dimmer switches, and many others []. KNX is the third approach, and is an open-source protocol that is typically utilized for automation. Because each KNX system is intelligent and operates on more than one physical layer, the functionality of other devices connected to the network is unaffected if one of the systems fails. KNX is a building control system []. As can be seen in Figure 5, the packet sizes have become significantly bigger across the board.
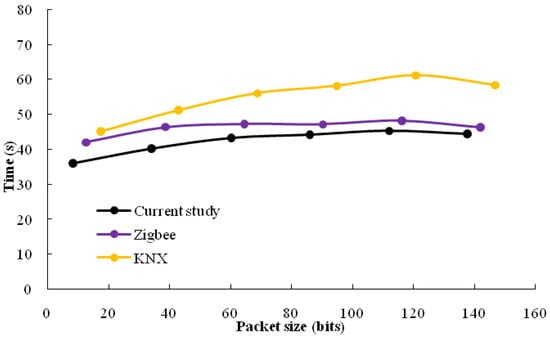
Figure 5.
Execution time with different methods.
In Figure 6, in this measure, the amount of memory consumed (in megabytes) to complete authentication requests in smart buildings based on the IoT has been examined and compared based on the number of packets sent; the results indicate that the third method has the lowest amount of memory consumption for more packages, whereas the proposed method was not able to reduce memory consumption for high package counts.
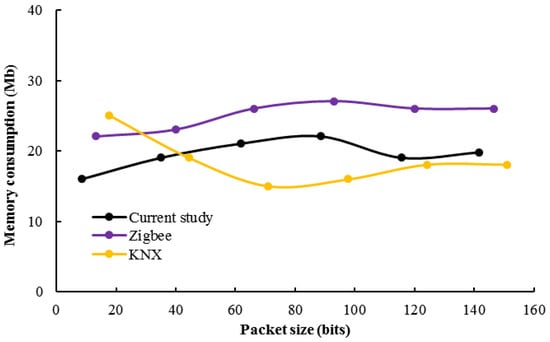
Figure 6.
Memory required with different methods.
In a second test, the amount of energy required to transmit data from the source to the destination is assessed. The quantity of data packets has increased at each successive stage. Figure 7 demonstrates that the proposed method utilizes less energy than comparable methods.
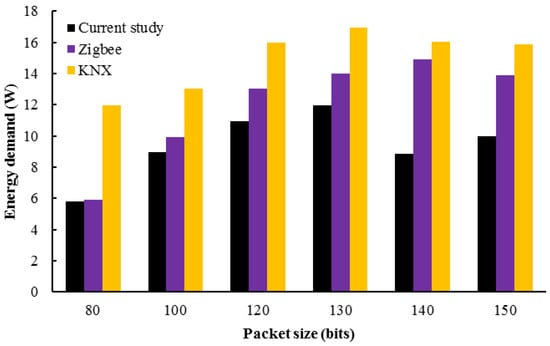
Figure 7.
The energy demand to transmit the request with different methods.
The accuracy criterion indicates how effectively the suggested technique can accurately display the identify in IoT-based smart buildings. In Figure 8, the accuracy of the suggested technique for 188 unique identity effects is compared to the accuracy of the second and third methods (described previously) for various packages.
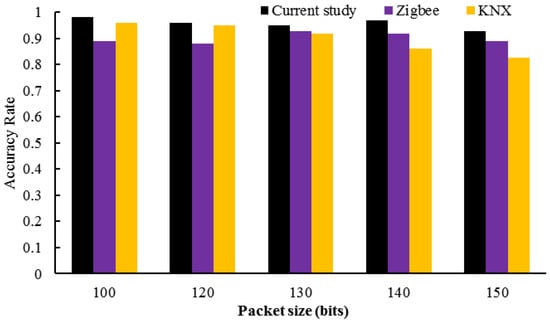
Figure 8.
Comparison of accuracy criteria with different methods.
The simulation results indicate that the proposed method is more accurate than the second and third methods for identifying distinct packages in IoT-based smart buildings.
5. Conclusions and Suggestions for Future Work
The energy consumption model in IoT networks is dependent on the hardware, data processing, and communication interface. In this study, the cycle-based model and information transfer to the base station and between items were utilized for energy consumption and the IoT network. The most significant challenges in IoT routing are each node’s power consumption, comparability, fault tolerance, and network dynamics. For effective communication and information transfer, it is necessary to evaluate a node’s quality using the appropriate criteria. In this study, the energy used to transmit and receive data in the nodes, the energy available in each node, the distance between two nodes, and the data transmission rate between two nodes were evaluated. In accordance with the goal of this study, which is to optimize energy consumption in the IoT, an FCPSO algorithm was used to reduce energy consumption during information transmission. Using the FCPSO algorithm to reduce energy consumption in the IoT is possible due to the algorithm’s ability to optimize the problem by considering the number of parameters that can have a significant impact on the performance of the problem, which is the goal of many optimization problems. The simulation results demonstrated that employing an FCPSO method improves and decreases energy consumption during program execution and the information transfer cycle. The most significant limitation of this study is that there are not enough data that can be relied on to construct an optimal model. Because of this, there is a greater possibility that the model will not converge. Another topic that deserves attention in this area is the degree of computational difficulty that new models of data transmission require.
According to the outcomes of implementation and ongoing study in this subject, the following recommendations can be made for future work:
- -
- Practical implementation of the proposed method in a smart environment that uses the IoT, such as smart buildings.
- -
- Using the proposed method for multicast routing, additional research can be conducted in this area, such as how to select routes.
- -
- Utilizing alternative evolutionary algorithms and evaluating their outcomes to increase the reduction of current overheads and reach more ideal results.
- -
- Combining the proposed method with other algorithms, such as tree-based algorithms, and presenting it within the IoT domain.
Author Contributions
Conceptualization, N.K.A.D.; Methodology, W.-C.W. and B.T.S.; Software, B.T.S. and Y.C.-E.; Validation, J.R.N.A.; Formal analysis, W.-C.W. and J.R.N.A.; Investigation, N.K.A.D., J.R.N.A., M.A.-B., A.A.-M. and Y.C.-E.; Resources, M.A.-B. and A.A.-M.; Data curation, M.A.-B. and A.A.-M.; Writing—original draft, N.K.A.D.; Writing—review and editing J.R.N.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ray, P.P. A Survey on Internet of Things Architectures. J. King Saud Univ. Comput. Inf. Sci. 2018, 30, 291–319. [Google Scholar]
- Motlagh, N.H.; Mohammadrezaei, M.; Hunt, J.; Zakeri, B. Internet of Things (IoT) and the Energy Sector. Energies 2020, 13, 494. [Google Scholar] [CrossRef]
- Lee, J.; Ruy, W.S. Multi-Objective Parametric Optimization of FPSO Hull Dimensions. Int. J. Nav. Archit. Ocean Eng. 2021, 13, 734–745. [Google Scholar] [CrossRef]
- Shaheen, M.A.M.; Hasanien, H.M.; Alkuhayli, A. A Novel Hybrid GWO-PSO Optimization Technique for Optimal Reactive Power Dispatch Problem Solution. Ain Shams Eng. J. 2021, 12, 621–630. [Google Scholar] [CrossRef]
- Alayi, R.; Mohkam, M.; Seyednouri, S.R.; Ahmadi, M.H.; Sharifpur, M. Energy/Economic Analysis and Optimization of on-Grid Photovoltaic System Using CPSO Algorithm. Sustainability 2021, 13, 12420. [Google Scholar] [CrossRef]
- Humayun, M.; Jhanjhi, N.Z.; Alsayat, A.; Ponnusamy, V. Internet of Things and Ransomware: Evolution, Mitigation and Prevention. Egypt. Inform. J. 2021, 22, 105–117. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Al-Rizzo, H. Task Scheduling in Internet of Things Cloud Environment Using a Robust Particle Swarm Optimization. Concurr. Comput. Pract. Exp. 2020, 32, e5442. [Google Scholar] [CrossRef]
- Kabalci, Y.; Kabalci, E.; Padmanaban, S.; Holm-Nielsen, J.B.; Blaabjerg, F. Internet of Things Applications as Energy Internet in Smart Grids and Smart Environments. Electronics 2019, 8, 972. [Google Scholar] [CrossRef]
- Lee, J.; Kim, B.C.; Ruy, W.S.; Han, I.S. Parametric Optimization of FPSO Hull Dimensions for Brazil Field Using Sophisticated Stability and Hydrodynamic Calculations. Int. J. Nav. Archit. Ocean Eng. 2021, 13, 478–492. [Google Scholar] [CrossRef]
- Li, F.; Zhang, Z.; Armaou, A.; Xue, Y.; Zhou, S.; Zhou, Y. Study on ADRC Parameter Optimization Using CPSO for Clamping Force Control System. Math. Probl. Eng. 2018, 2018, 1–8. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Al-Rizzo, H. Beamforming Optimization in Internet of Things Applications Using Robust Swarm Algorithm in Conjunction with Connectable and Collaborative Sensors. Sensors 2020, 20, 2048. [Google Scholar] [CrossRef] [PubMed]
- Wadood, A.; Kim, C.H.; Khurshiad, T.; Farkoush, S.G.; Rhee, S.B. Application of a Continuous Particle Swarm Optimization (CPSO) for the Optimal Coordination of Overcurrent Relays Considering a Penalty Method. Energies 2018, 11, 869. [Google Scholar] [CrossRef]
- Elsisi, M.; Tran, M.Q.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Deep Learning-Based Industry 4.0 and Internet of Things towards Effective Energy Management for Smart Buildings. Sensors 2021, 21, 1038. [Google Scholar] [CrossRef] [PubMed]
- Al-Turjman, F.; Hasan, M.Z.; Al-Rizzo, H. Task Scheduling in Cloud-Based Survivability Applications Using Swarm Optimization in IoT. Trans. Emerg. Telecommun. Technol. 2019, 30, e3539. [Google Scholar] [CrossRef]
- Li, Y.; Miao, S.; Luo, X.; Wang, J. Optimization Scheduling Model Based on Source-Load-Energy Storage Coordination in Power Systems. In Proceedings of the 2016 22nd International Conference on Automation and Computing, ICAC 2016: Tackling the New Challenges in Automation and Computing, Colchester, UK, 7–8 September 2016; pp. 120–125. [Google Scholar]
- Rana, B.; Singh, Y.; Singh, P.K. A Systematic Survey on Internet of Things: Energy Efficiency and Interoperability Perspective. Trans. Emerg. Telecommun. Technol. 2021, 32, e4166. [Google Scholar] [CrossRef]
- Wu, Z.; Nie, Y.; Chen, S.; Zhang, H.; Wang, L. Double Layers Clustering Algorithm Based on CPSO for Wireless Sensor Networks. Inf. Technol. J. 2012, 11, 1737–1743. [Google Scholar] [CrossRef]
- Ahmed, Z.E.; Hasan, M.K.; Saeed, R.A.; Hassan, R.; Islam, S.; Mokhtar, R.A.; Khan, S.; Akhtaruzzaman, M. Optimizing Energy Consumption for Cloud Internet of Things. Front. Phys. 2020, 8, 358. [Google Scholar] [CrossRef]
- Ding, X.; Wu, J. Study on Energy Consumption Optimization Scheduling for Internet of Things. IEEE Access 2019, 7, 70574–70583. [Google Scholar] [CrossRef]
- Fanian, F.; Kuchaki Rafsanjani, M.; Borumand Saeid, A. Fuzzy Multi-Hop Clustering Protocol: Selection Fuzzy Input Parameters and Rule Tuning for WSNs. Appl. Soft Comput. 2021, 99, 106923. [Google Scholar] [CrossRef]
- Kadri, N.; Koudil, M. Multi-Objective Biogeography-Based Optimization and Reinforcement Learning Hybridization for Network-on Chip Reliability Improvement. J. Parallel Distrib. Comput. 2022, 161, 20–36. [Google Scholar] [CrossRef]
- Lalitha, K.; Kamalam, G.K.; Priyan, R.; Rithanya, A.S.; Shanmugapriya, P. Optimizing the Sensor Deployment Strategy for Large-Scale Internet of Things (IoT) Using Artificial Bee Colony. AIP Conf. Proc. 2021, 2387, 140032. [Google Scholar]
- Lan, K.; Fong, S.; Song, W.; Vasilakos, A.V.; Millham, R.C. Self-Adaptive Pre-Processing Methodology for Big Data Stream Mining in Internet of Things Environmental Sensor Monitoring. Symmetry 2017, 9, 244. [Google Scholar] [CrossRef]
- Sani, A.S.; Yuan, D.; Jin, J.; Gao, L.; Yu, S.; Dong, Z.Y. Cyber Security Framework for Internet of Things-Based Energy Internet. Future Gener. Comput. Syst. 2019, 93, 849–859. [Google Scholar] [CrossRef]
- Khare, V.; Nema, S.; Baredar, P. Optimisation of the Hybrid Renewable Energy System by HOMER, PSO and CPSO for the Study Area. Int. J. Sustain. Energy 2017, 36, 326–343. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Al-Rizzo, H.; Al-Turjman, F.; Rodriguez, J.; Radwan, A. Internet of Things Task Scheduling in Cloud Environment Using Particle Swarm Optimization. In Proceedings of the 2018 IEEE Global Communications Conference, GLOBECOM 2018—Proceedings, Abu Dhabi, United Arab Emirates, 9–13 December 2018. [Google Scholar]
- Rasheed, M.; Omar, R.; Sulaiman, M.; Halim, W.A. Particle Swarm Optimisation (PSO) Algorithm with Reduced Numberof Switches in Multilevel Inverter (MLI). Indones. J. Electr. Eng. Comput. Sci. 2019, 14, 1114–1124. [Google Scholar] [CrossRef]
- Vadivel, R.; Sudalaimuthu, T. Cauchy Particle Swarm Optimization (CPSO) Based Migrations of Tasks in a Virtual Machine. Wirel. Pers. Commun. 2021, 127, 2229–2246. [Google Scholar] [CrossRef]
- Li, J.; Kang, L.; Li, X.; Chen, Z.; Zhang, Y. Characterizing Cluster Formation in Wireless Sensor Networks: A Chaos Particle Swarm Optimization Approach. J. Comput. Inf. Syst. 2015, 11, 957–966. [Google Scholar] [CrossRef]
- Peraza-Vázquez, H.; Peña-Delgado, A.F.; Echavarría-Castillo, G.; Morales-Cepeda, A.B.; Velasco-Álvarez, J.; Ruiz-Perez, F. A Bio-Inspired Method for Engineering Design Optimization Inspired by Dingoes Hunting Strategies. Math. Probl. Eng. 2021, 2021, 1–19. [Google Scholar] [CrossRef]
- Peraza-Vázquez, H.; Peña-Delgado, A.; Ranjan, P.; Barde, C.; Choubey, A.; Morales-Cepeda, A.B. A Bio-Inspired Method for Mathematical Optimization Inspired by Arachnida Salticidade. Mathematics 2021, 10, 102. [Google Scholar] [CrossRef]
- Osipov, M. Home Automation with Zigbee. In Lecture Notes in Computer Science; Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5174 LNCS, pp. 263–270. [Google Scholar]
- Gopalsamy, B.N. Communication Trends in Internet of Things; IGI Global: Hershey, PA, USA, 2017; pp. 284–305. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).