Research on Acquisition Performance of FFT Algorithm for Low-Frequency Spread-Spectrum Signals Using Acoustic Sensors
Abstract
1. Introduction
2. Improved FFT Acquisition Algorithm
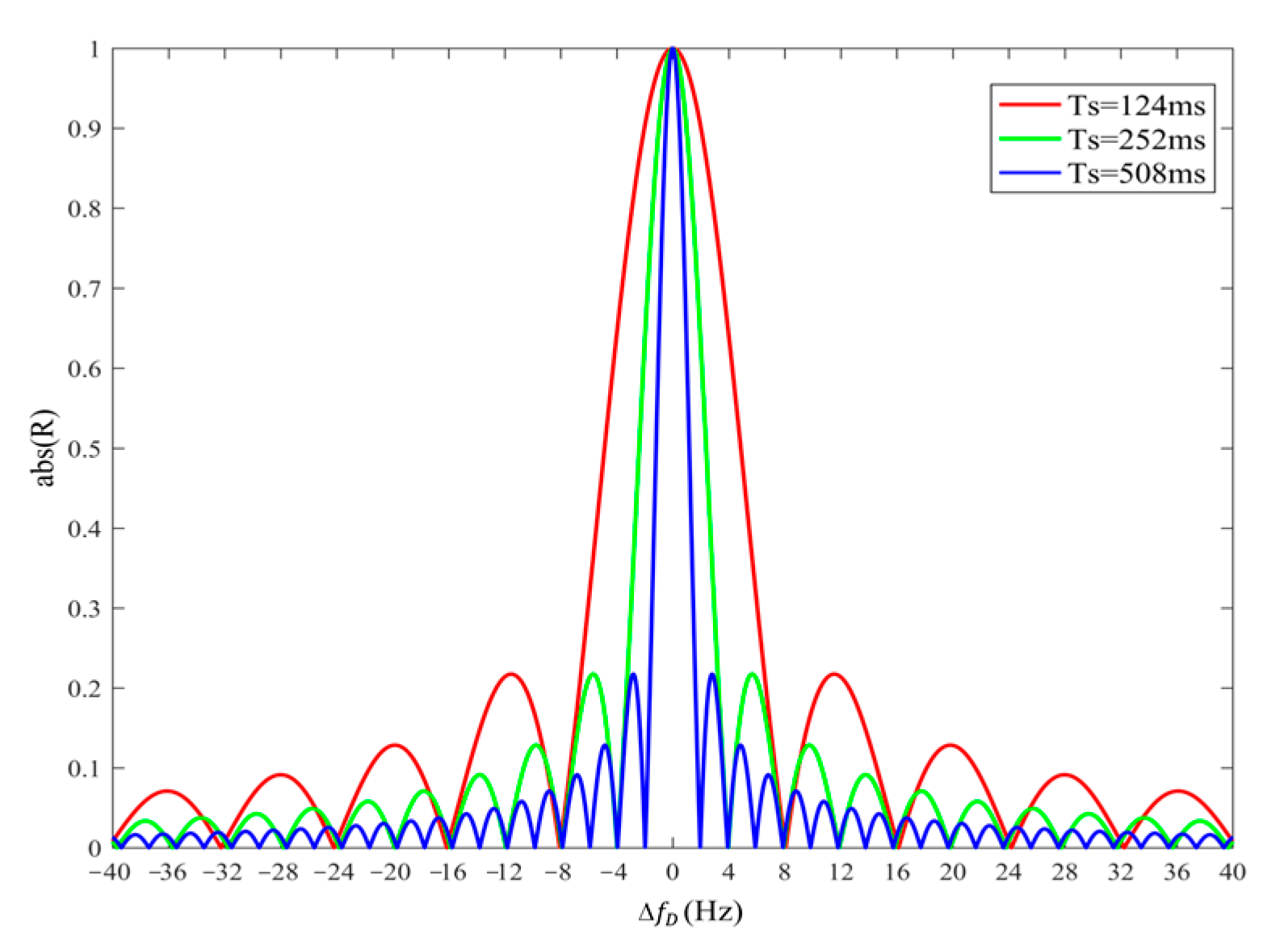
2.1. Fuzzy Function and 2D Search Step Size
2.2. Conventional FFT Acquisition Methods
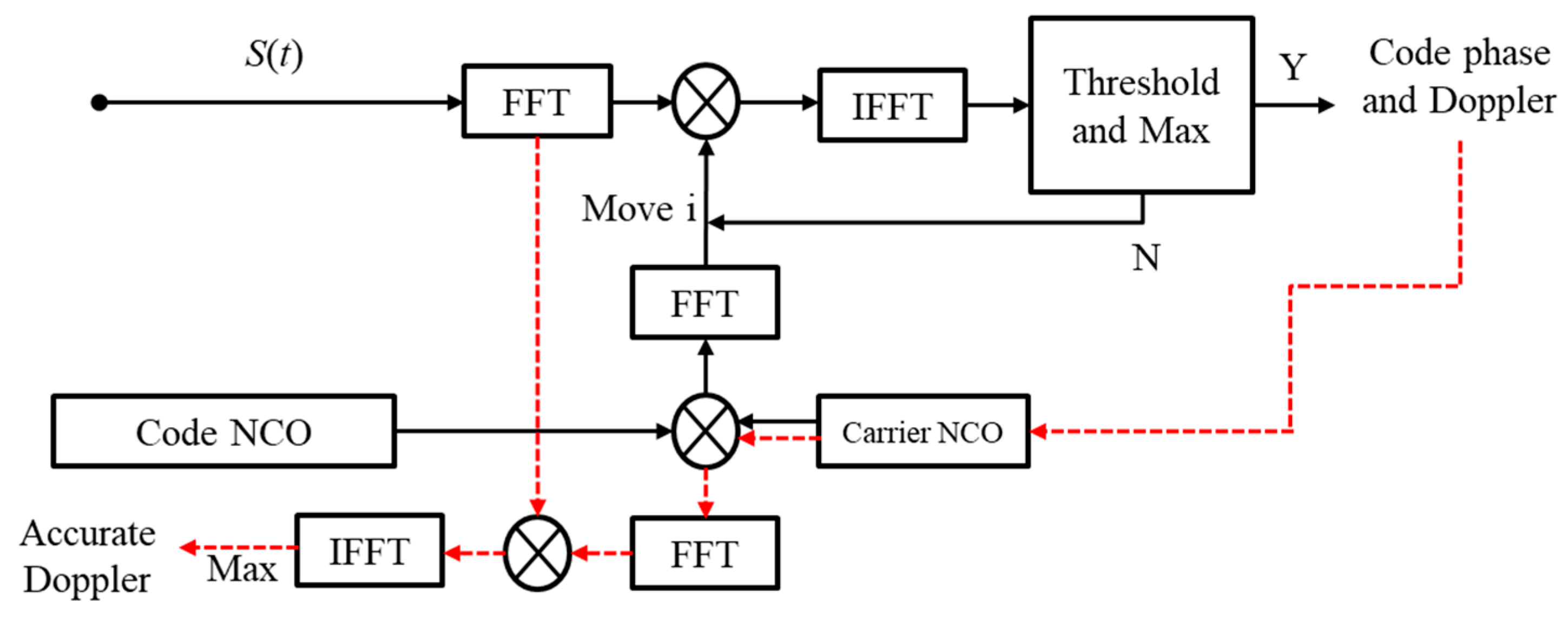
2.3. FFT-Based Circular Shift Fast Acquisition Algorithm Combining Maximum Correlation and Threshold Discrimination
3. Simulation Analysis of Factors Affecting Algorithm Performance
3.1. Effect of Spread-Spectrum Signal Waveform Parameters
3.2. Effect of Sampling Frequency
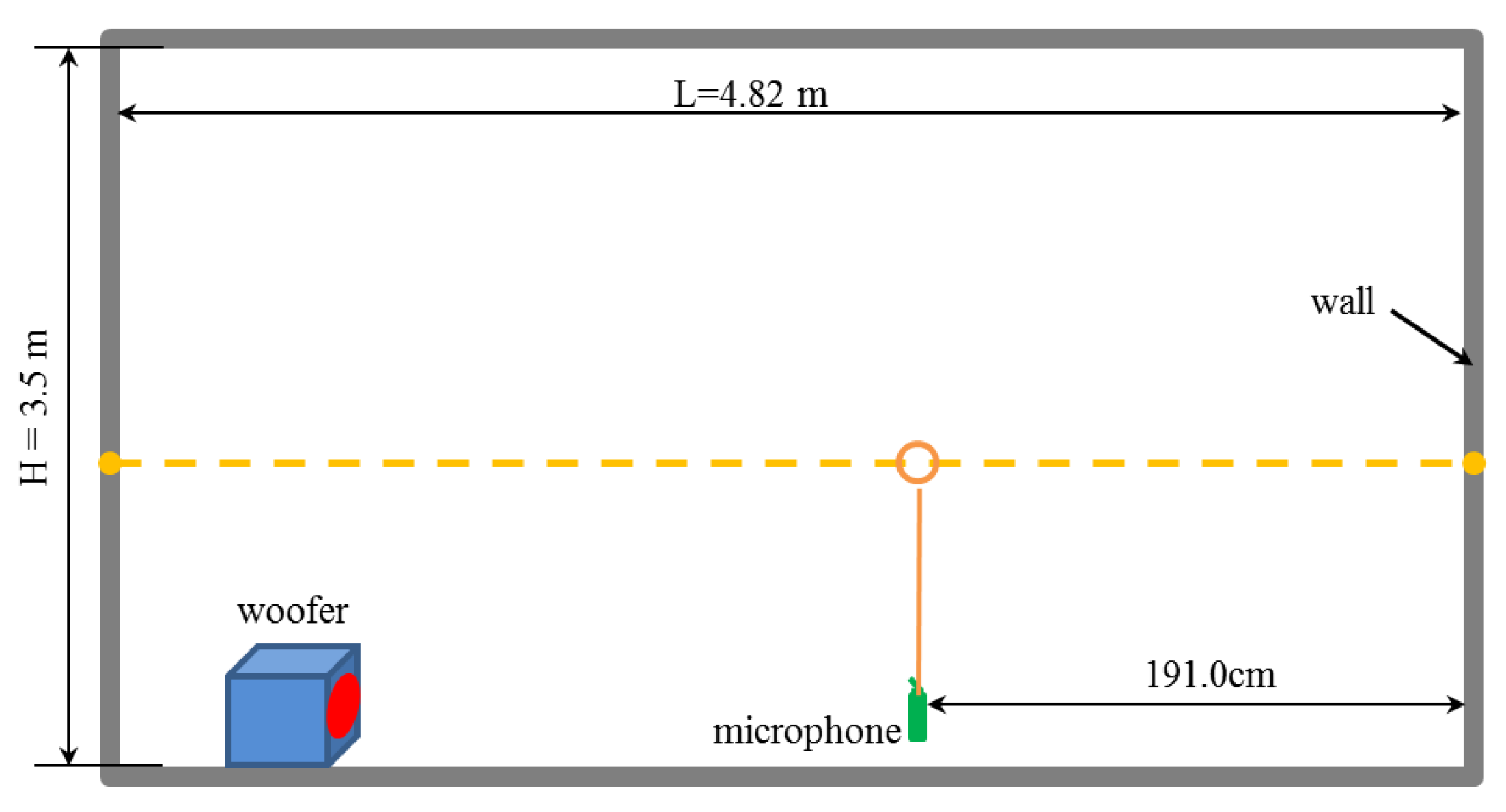
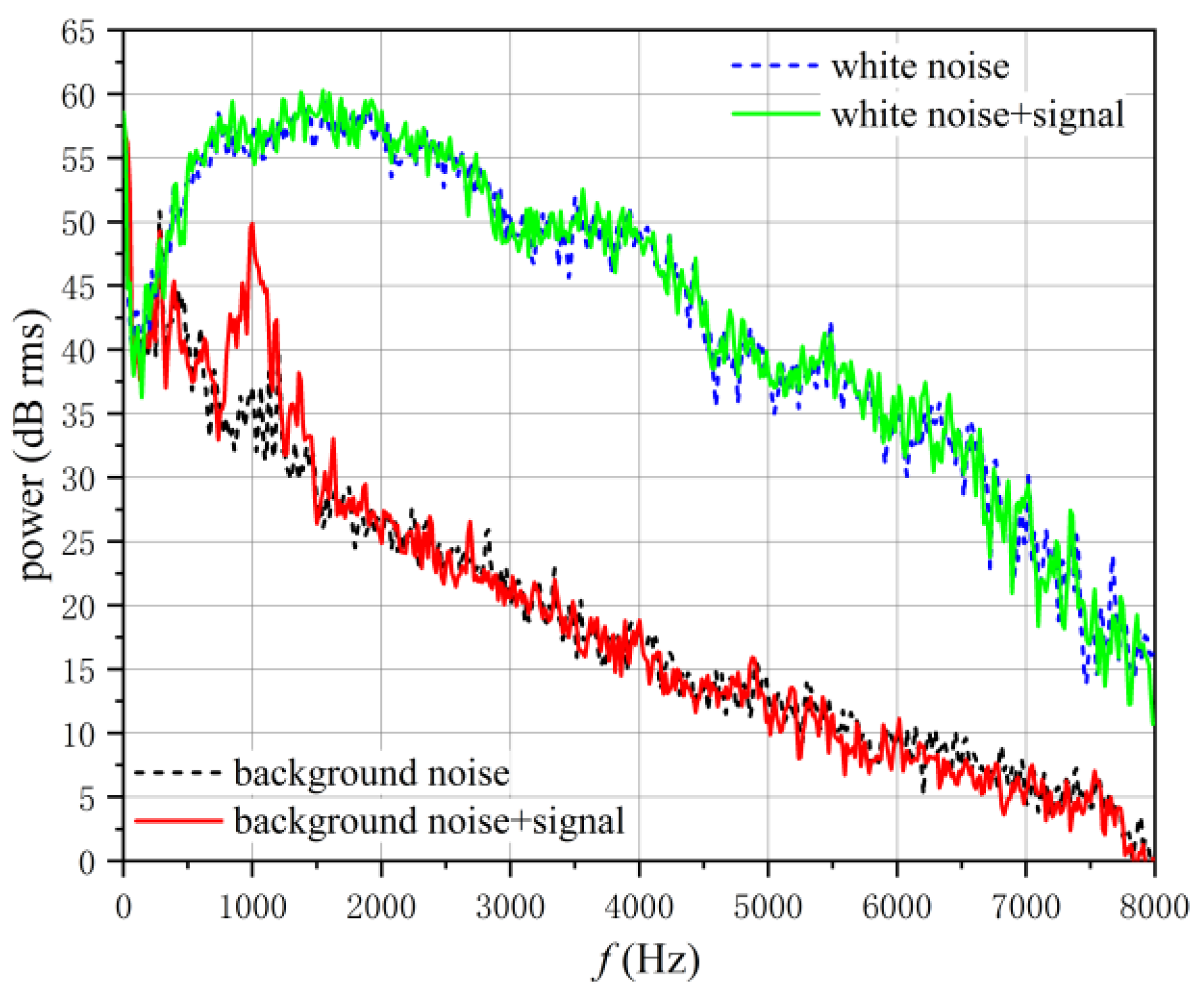
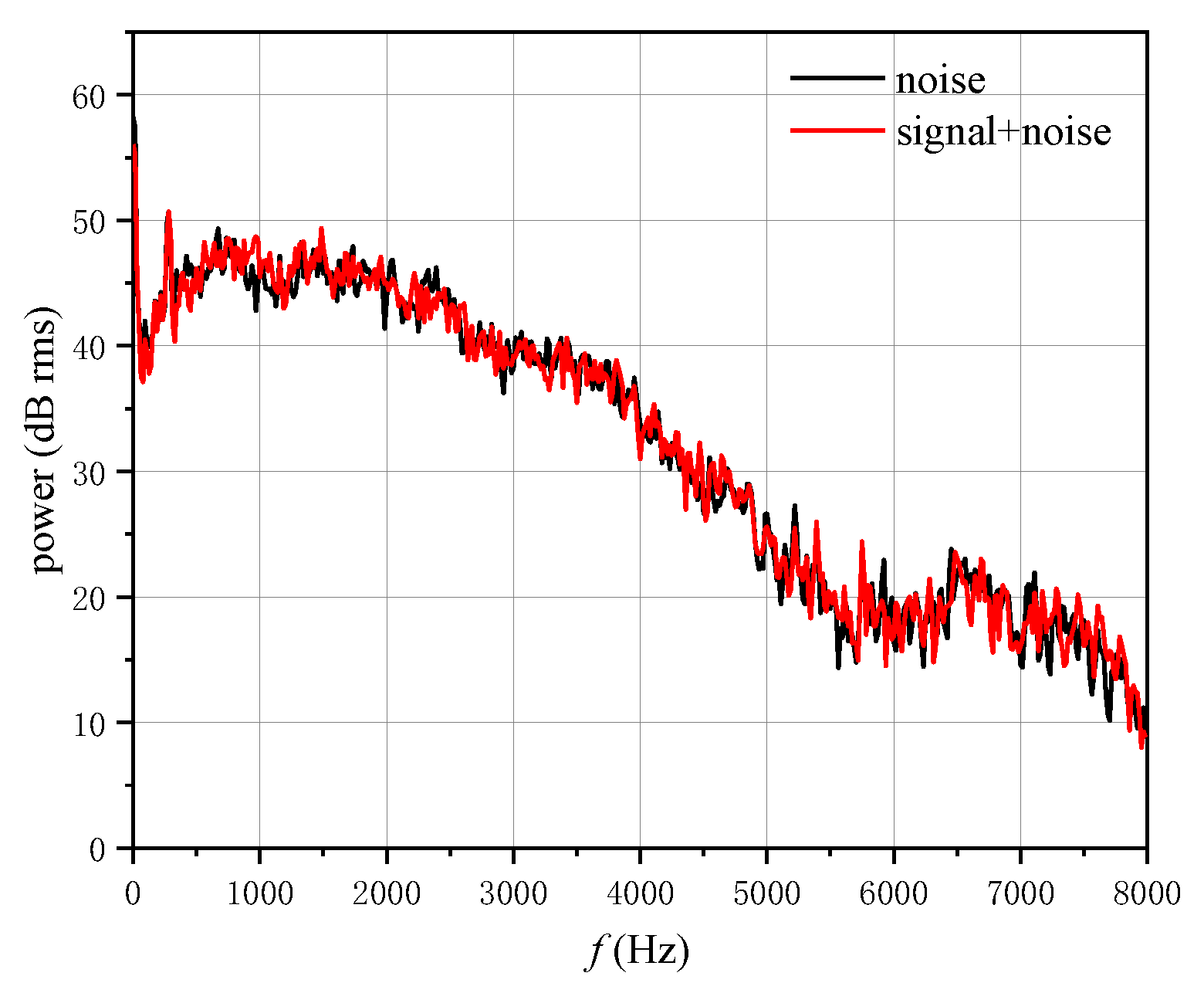
4. Experimental Verifications
4.1. Accuracy Verification of Improved FFT Acquisition Algorithm
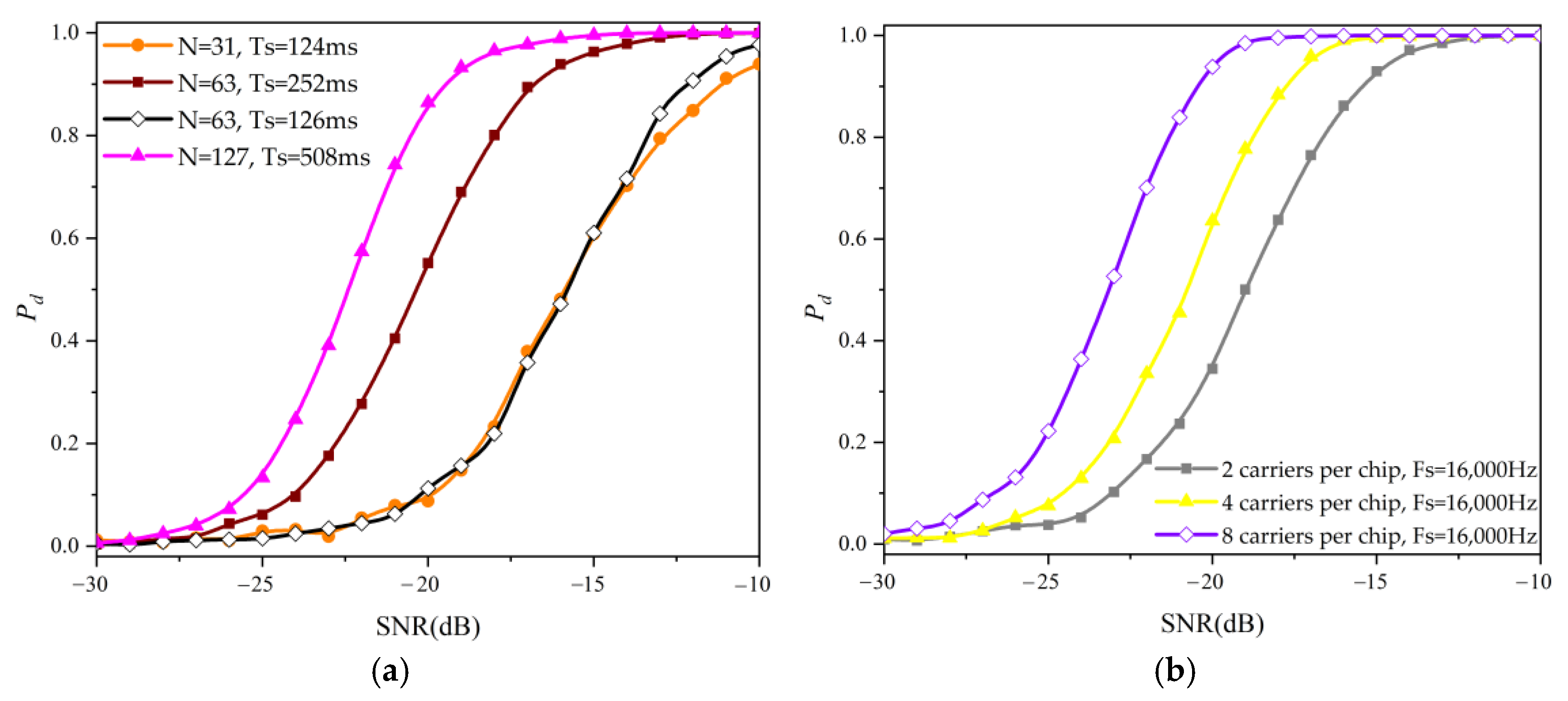
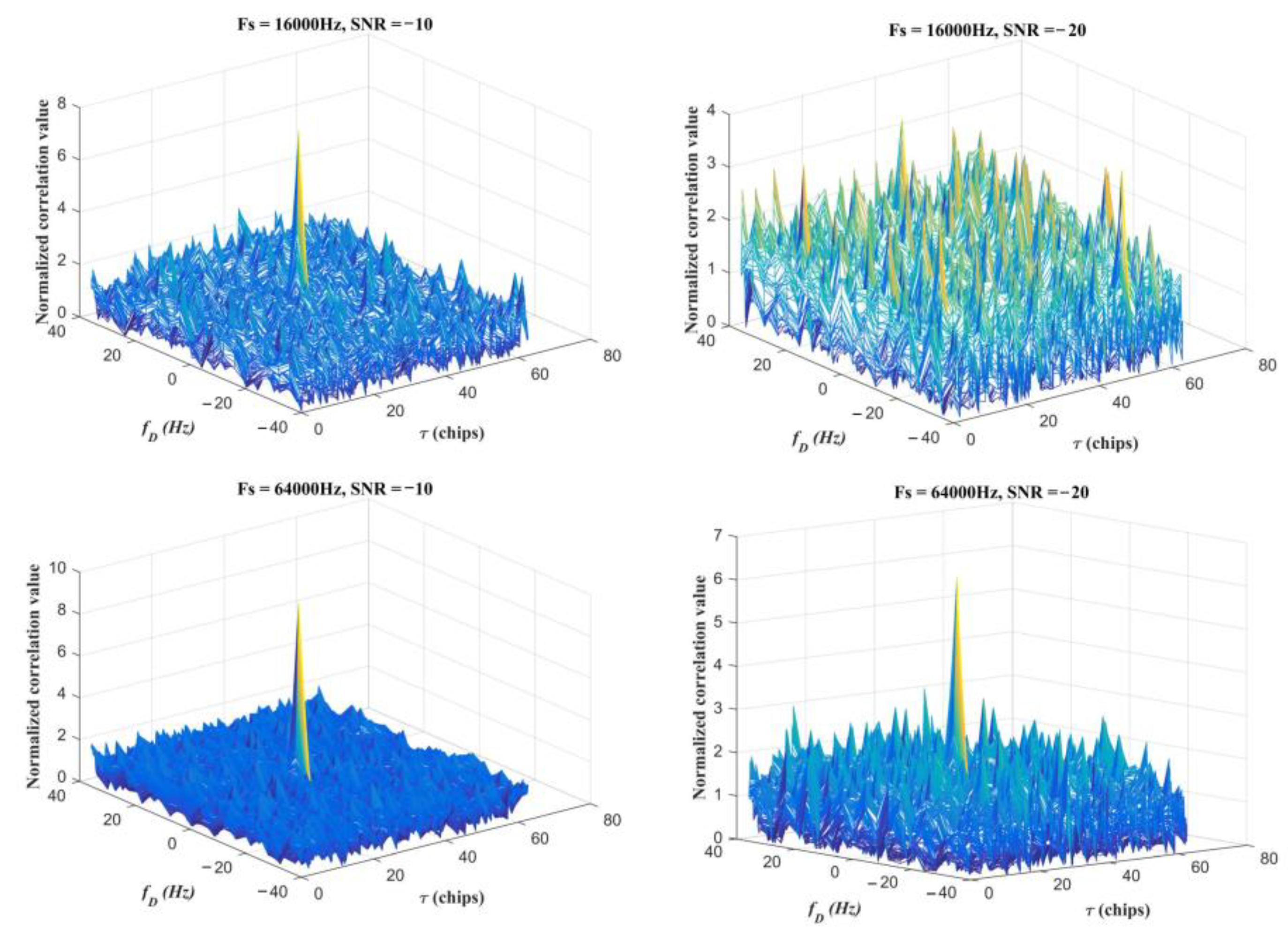
4.2. Verification of the Effects of Spread-Spectrum Signal Waveform Parameters and Sampling Frequency on Acquisition Performance
4.2.1. Spread-Spectrum Signal Waveform Parameters
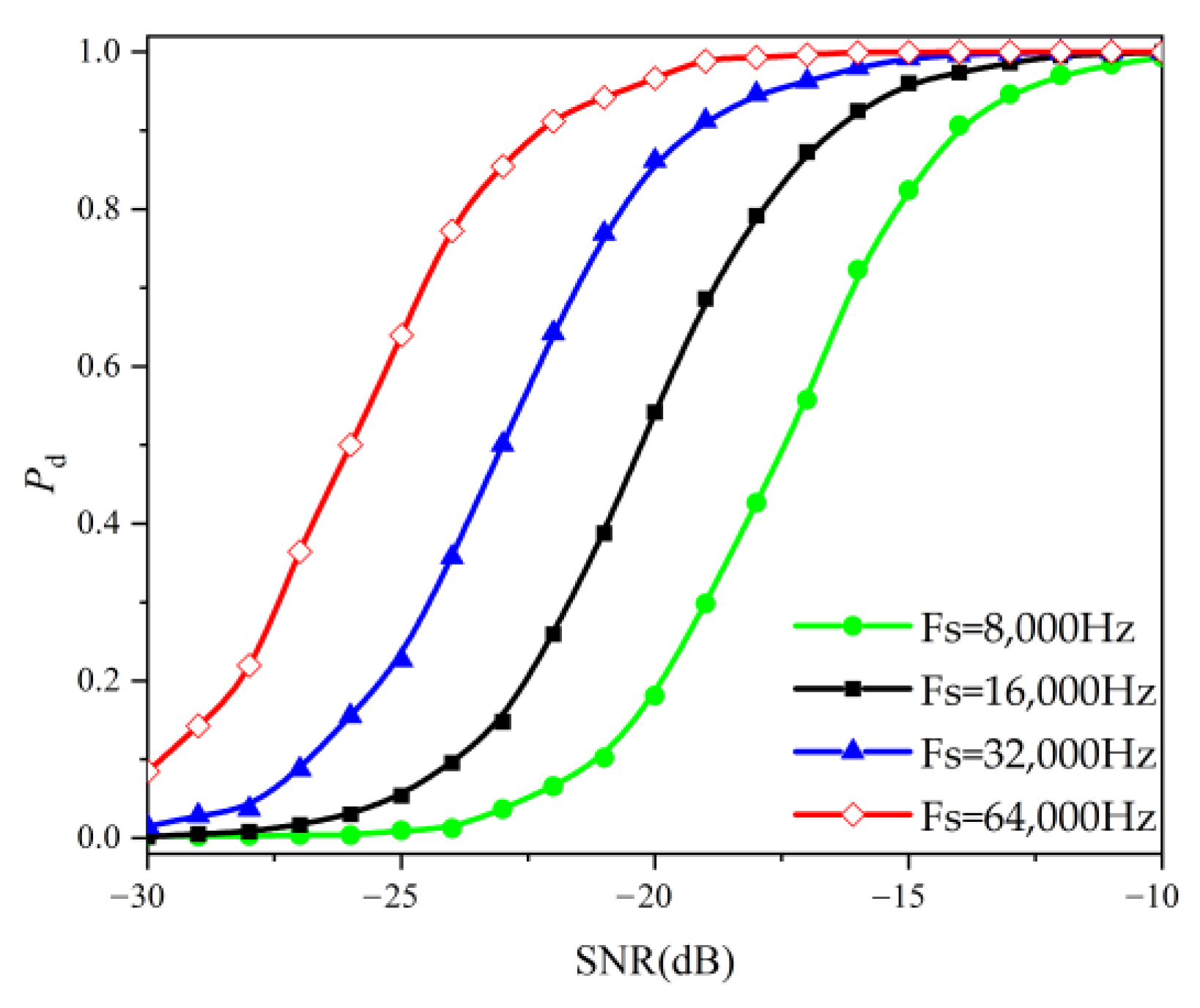
4.2.2. Sampling Frequency
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tian, R.; Chi, Y. Spread Spectrum Communication, 2nd ed.; Qinghua University Publishing House: Beijing, China, 2014; pp. 21–29. [Google Scholar]
- Peterson, R.L.; Borth, D.E.; Ziemer, R.E. Introduction to Spread Spectrum Communications, 1st ed.; Person Education: London, UK, 1995; pp. 1–32. [Google Scholar]
- Bullock, S.R. Global Navigation Satellite System. In Transceiver and System Design for Digital Communications, 5th ed.; The Institution of Engineering and Technology: London, UK, 2017; Volume 13, pp. 310–325. [Google Scholar]
- Heinrichs, G.; Rohmer, G.; Henkel, F. A fully digital direct-sequence spread-spectrum receiver architecture for GNSS applications. In Proceedings of the 2000 IEEE 6th International Symposium on Spread Spectrum Techniques and Applications, Parsippany, NJ, USA, 6–8 September 2000; Volume 512, pp. 510–514. [Google Scholar] [CrossRef]
- Tamang, N.D.; Sur, S.N.; Bera, S.; Bera, R. A Review on Spread Spectrum Radar. Adv. Electron. Commun. Comput. 2018, 1, 653–664. [Google Scholar] [CrossRef]
- Toru, I.; Yoshikawa, Y.; Izumi, S.; Kawaguchi, H. Subcentimeter Precision Ranging System for Moving Targets with a Doppler-Effect- Compensated Ultrasonic Direct Sequence Spread Spectrum. IEEE Trans. Instrum. Meas. 2020, 70, 1–8. [Google Scholar] [CrossRef]
- Kumakura, K.; Suzuki, A.; Iyota, T. Code division positioning by continuous signals using spread spectrum ultrasonic waves. Int. Conf. Indoor Position. Indoor Navig. 2013, 1–8. [Google Scholar] [CrossRef]
- Paredes, J.A.; Álvarez, F.J.; Aguilera, T.; Villadangos, J.M. 3D Indoor Positioning of UAVs with Spread Spectrum Ultrasound and Time-of-Flight Cameras. Sensors 2017, 18, 89. [Google Scholar] [CrossRef]
- Stojanovic, M.; Proarkis, J.; Rice, J.; Green, M. Spread spectrum underwater acoustic telemetry. IEEE Ocean. Eng. Soc. 1998, 652, 650–654. [Google Scholar] [CrossRef]
- Freitag, L.; Ball, K.; Partan, J.; Koski, P.; Singh, S. Long range acoustic communications and navigation in the Arctic. Ocean. 2015 MTS/IEEE Wash. 2015, 1–5. [Google Scholar] [CrossRef]
- Zhu, M.; Wu, Y. Development of underwater acoustic communication technology. J. Chin. Acad. Sci. 2019, 34, 289–296. [Google Scholar] [CrossRef]
- Brusin, E. Direct Sequence Spread Spectrum Signal’s Demodulator Acquisition Implementation Based on Fast Fourier Transform. Part 1. Problem Statement and Solution Approach. Proc. Telecommun. Univ. 2022. [Google Scholar] [CrossRef]
- Grant, P.; Spangenberg, S.; Scott, I.; McLaughlin, S.; Povey, G.; Cruickshank, D. Doppler estimation for fast acquisition in spread spectrum communication systems. IEEE 5th Int. Symp. Spread Spectr. Technol. Appl. 1998, 101, 106–110. [Google Scholar] [CrossRef]
- Spangenberg, S.M.; Scott, I.; McLaughlin, S.; Povey, G.J.; Cruickshank, D.G.; Grant, P.M. An FFT-Based Approach for Fast Acquisition in Spread Spectrum Communication Systems. Wirel. Pers. Commun. 2000, 13, 27–55. [Google Scholar] [CrossRef]
- Huang, R.; Li, C.; Zhang, H.; Xie, Q. An Improved PMF-FFT Acquisition Algorithm Based on Trigonometric Polynomial Interpolation. In Proceedings of the 2022 6th International Conference on Electronic Information Technology and Computer Engineering, Xiamen, China, 21–23 October 2022. [Google Scholar] [CrossRef]
- Ren, C. Acquisition and Tracking of GPS C/A Code in High Dynamic. Master’s Thesis, Xi’an University of Science and Technology, Xi’an, China, 2020. [Google Scholar]
- Shi, X.; Shen, Y.; Wang, Y. Fuzzy Logic Control for Doppler Search in DSSS Systems. IEEE Trans. Fuzzy Syst. 2019, 28, 2232–2243. [Google Scholar] [CrossRef]
- Ma, X. Design and Performance Evaluation of Spread Spectrum Code for Satellite Navigation Signal. Master’s Thesis, University of Chinese Academy of Sciences, Shenzhen, China, 2020. [Google Scholar] [CrossRef]
- Mina, T.Y.; Gao, G.X. Designing Low-Correlation GPS Spreading Codes with a Natural Evolution Strategy Machine-Learning Algorithm. J. Inst. Navig. 2022, 69, 1–23. [Google Scholar] [CrossRef]
- Sun, B.; Zheng, Z.; Zhou, Y.; Zhang, R. Research on fast acquisition algorithm of spread spectrum signal based on PMF-FFT. In Proceedings of the 2022 7th International Conference on Communication, Chengdu, China, 18–20 November 2022; pp. 291–296. [Google Scholar] [CrossRef]
- Hussain, A.; Ahmed, A.; Magsi, H.; Soomro, J.; Bukhari, S.; Ro, J.-S. Adaptive Data Length Method for GPS Signal Acquisition in Weak to Strong Fading Conditions. Electronics 2021, 10, 1735. [Google Scholar] [CrossRef]


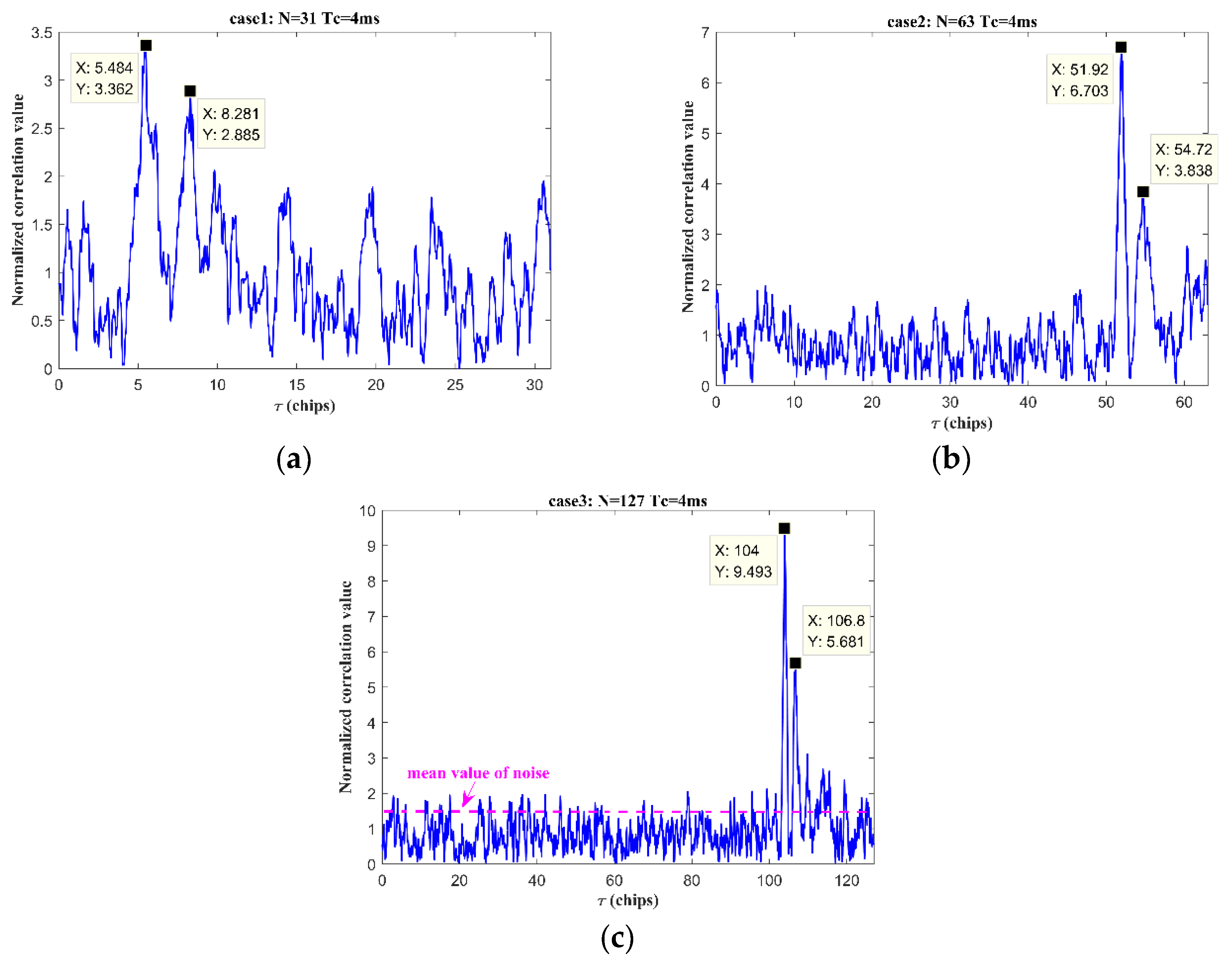
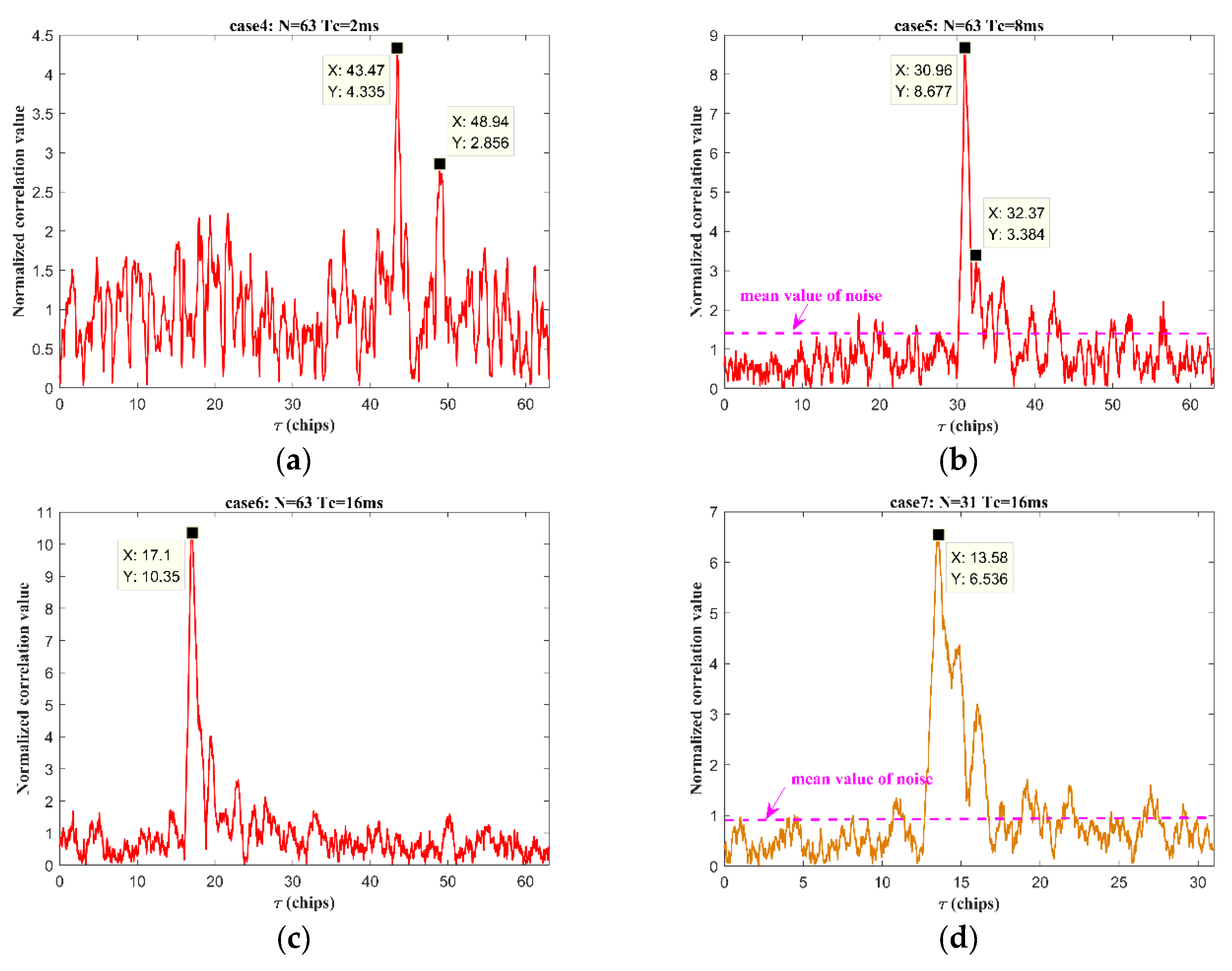
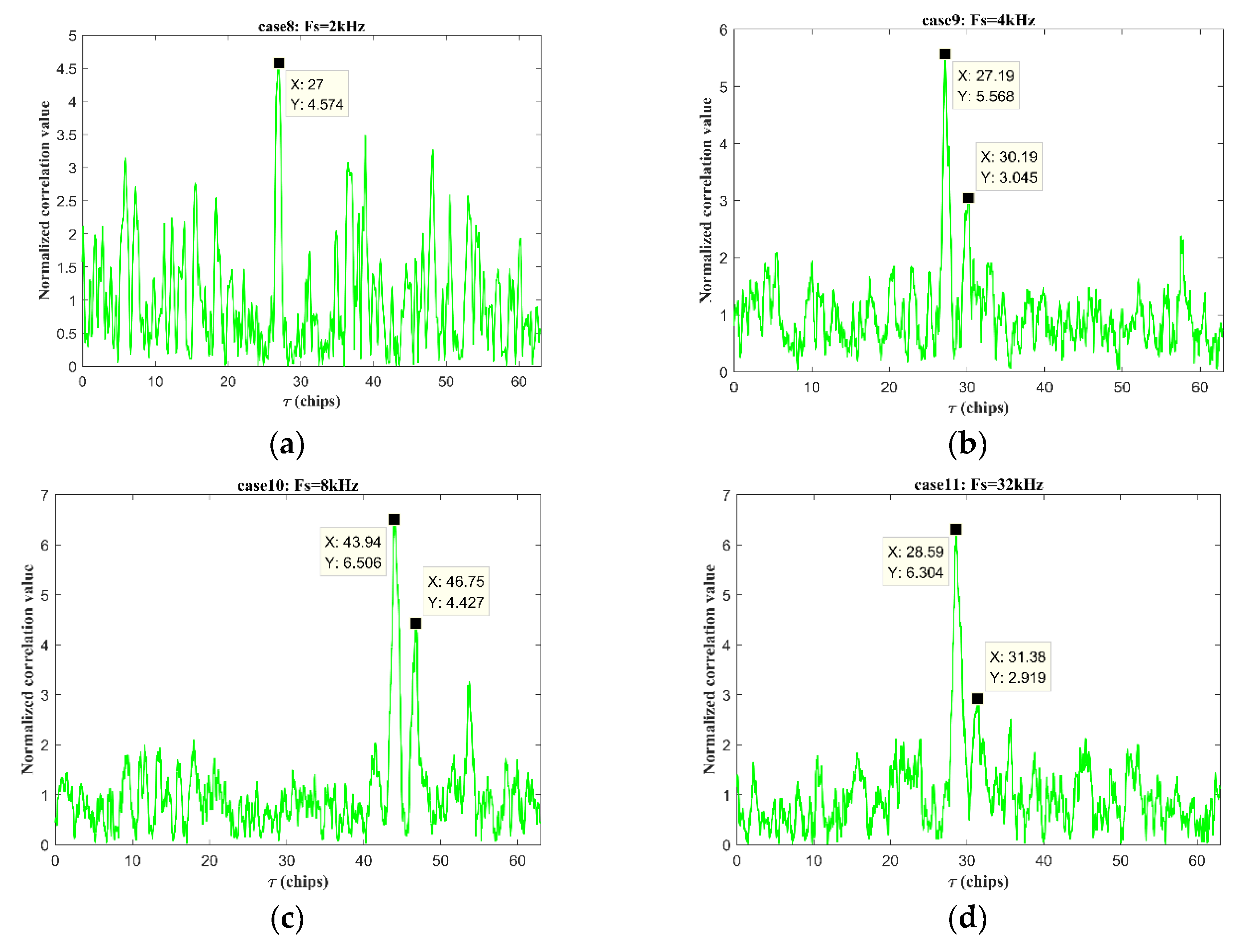
| Case | Code Length N | No. of Intra-Chip Carriers | Tc | Ts | Sampling Frequency Fs |
|---|---|---|---|---|---|
| 1 | 31 | 4 | 4 ms | 124 ms | 16 kHz |
| 2 | 63 | 4 | 4 ms | 252 ms | 16 kHz |
| 3 | 127 | 4 | 4 ms | 508 ms | 16 kHz |
| 4 | 63 | 2 | 2 ms | 126 ms | 16 kHz |
| 5 | 63 | 8 | 8 ms | 504 ms | 16 kHz |
| 6 | 63 | 16 | 16 ms | 1008 ms | 16 kHz |
| 7 | 31 | 16 | 16 ms | 496 ms | 16 kHz |
| 8 | 63 | 4 | 4 ms | 252 ms | 2 kHz |
| 9 | 63 | 4 | 4 ms | 252 ms | 4 kHz |
| 10 | 63 | 4 | 4 ms | 252 ms | 8 kHz |
| 11 | 63 | 4 | 4 ms | 252 ms | 32 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Zhou, Q.; Xie, Z.; Liu, W.; Lü, X. Research on Acquisition Performance of FFT Algorithm for Low-Frequency Spread-Spectrum Signals Using Acoustic Sensors. Sustainability 2023, 15, 6405. https://doi.org/10.3390/su15086405
Tang Y, Zhou Q, Xie Z, Liu W, Lü X. Research on Acquisition Performance of FFT Algorithm for Low-Frequency Spread-Spectrum Signals Using Acoustic Sensors. Sustainability. 2023; 15(8):6405. https://doi.org/10.3390/su15086405
Chicago/Turabian StyleTang, Yongzhuang, Qidou Zhou, Zhiyong Xie, Wenxi Liu, and Xiaojun Lü. 2023. "Research on Acquisition Performance of FFT Algorithm for Low-Frequency Spread-Spectrum Signals Using Acoustic Sensors" Sustainability 15, no. 8: 6405. https://doi.org/10.3390/su15086405
APA StyleTang, Y., Zhou, Q., Xie, Z., Liu, W., & Lü, X. (2023). Research on Acquisition Performance of FFT Algorithm for Low-Frequency Spread-Spectrum Signals Using Acoustic Sensors. Sustainability, 15(8), 6405. https://doi.org/10.3390/su15086405







