A Short-Term Prediction Model of Wind Power with Outliers: An Integration of Long Short-Term Memory, Ensemble Empirical Mode Decomposition, and Sample Entropy
Abstract
1. Introduction
2. Theory of Method
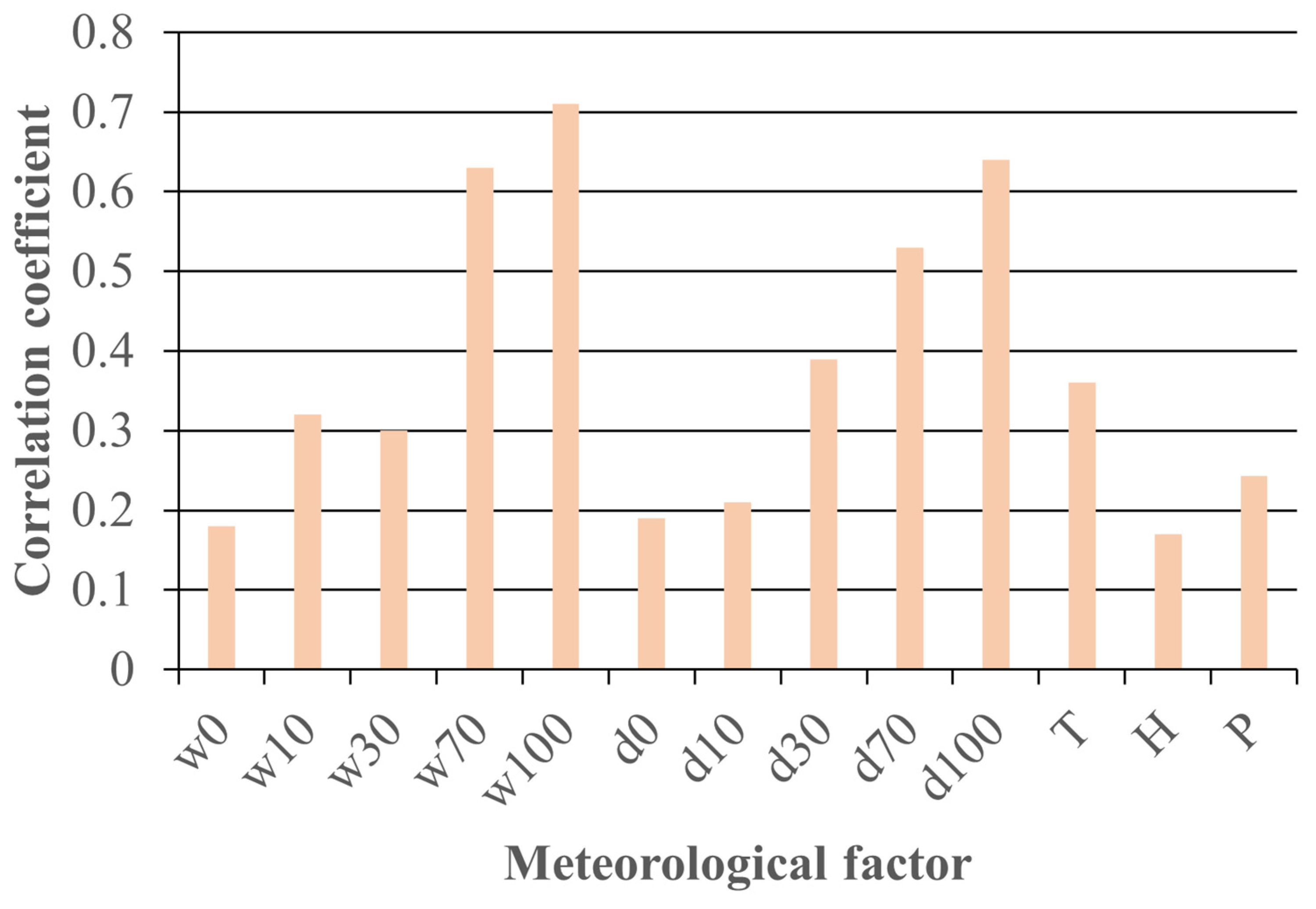
2.1. Pearson Correlation Coefficient
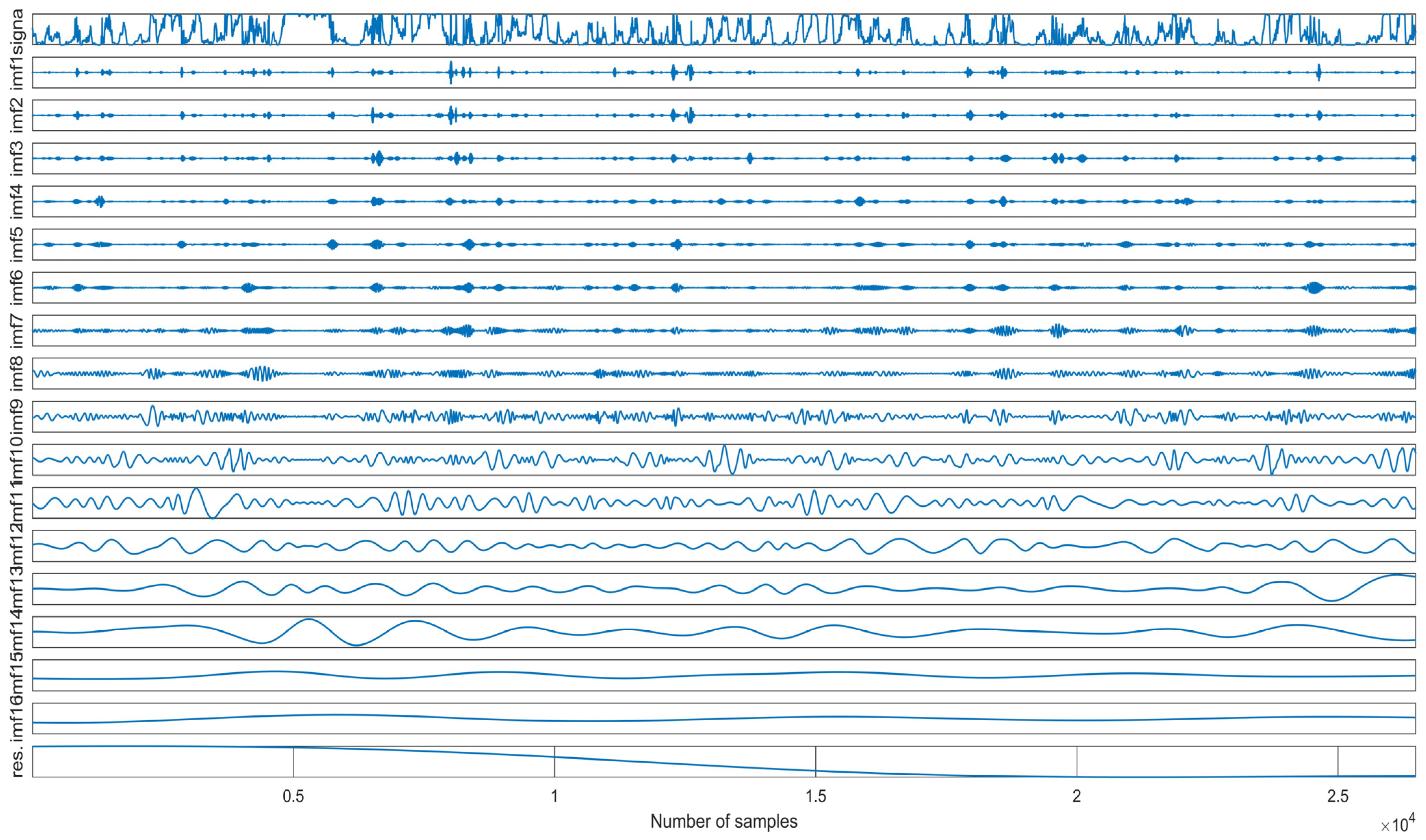
2.2. EEMD of Wind Power
2.3. Sample Entropy
2.4. Asymmetric Error Loss Function
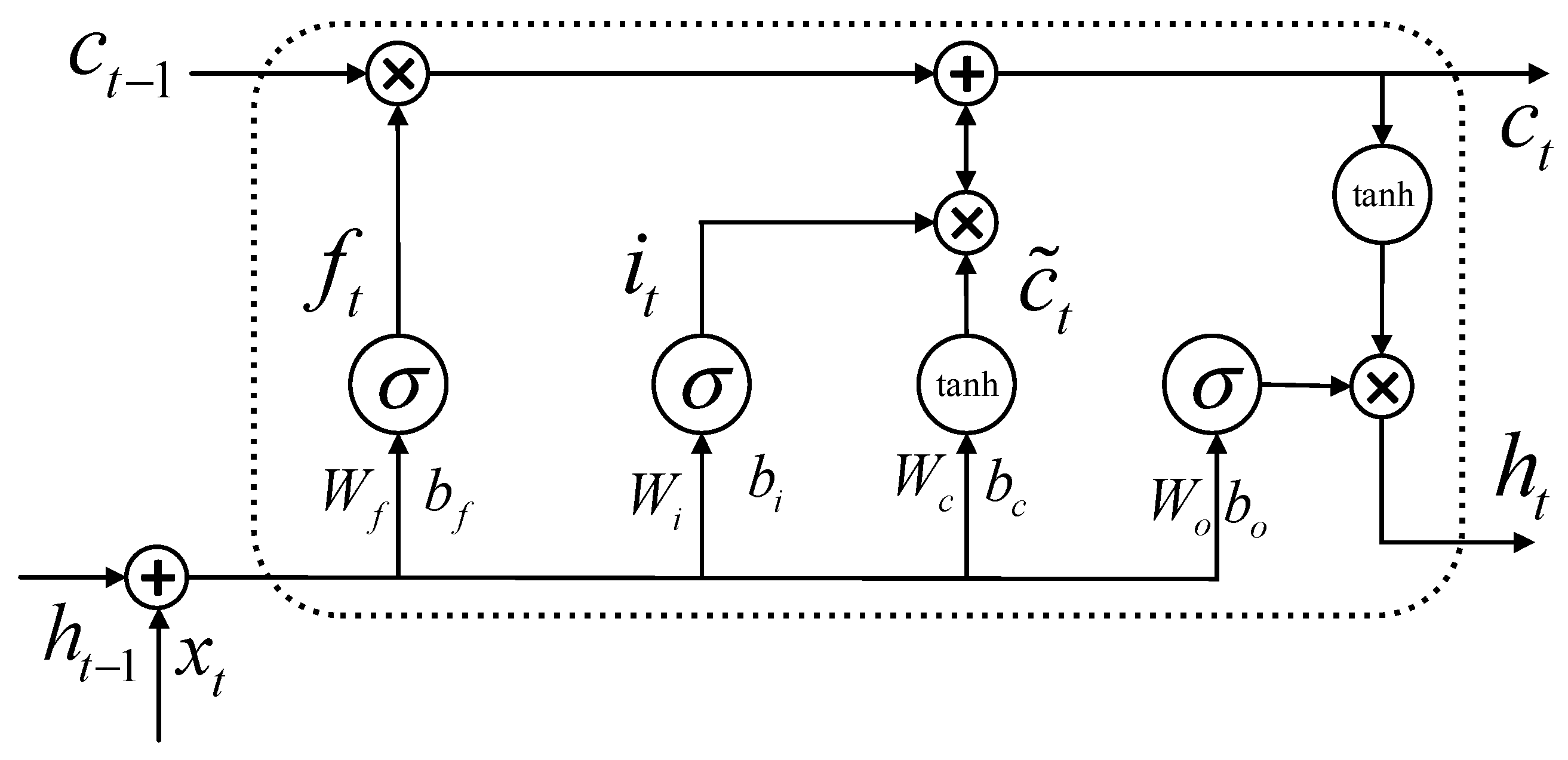
2.5. Long Short-Term Memory
2.6. Particle Swarm Optimization
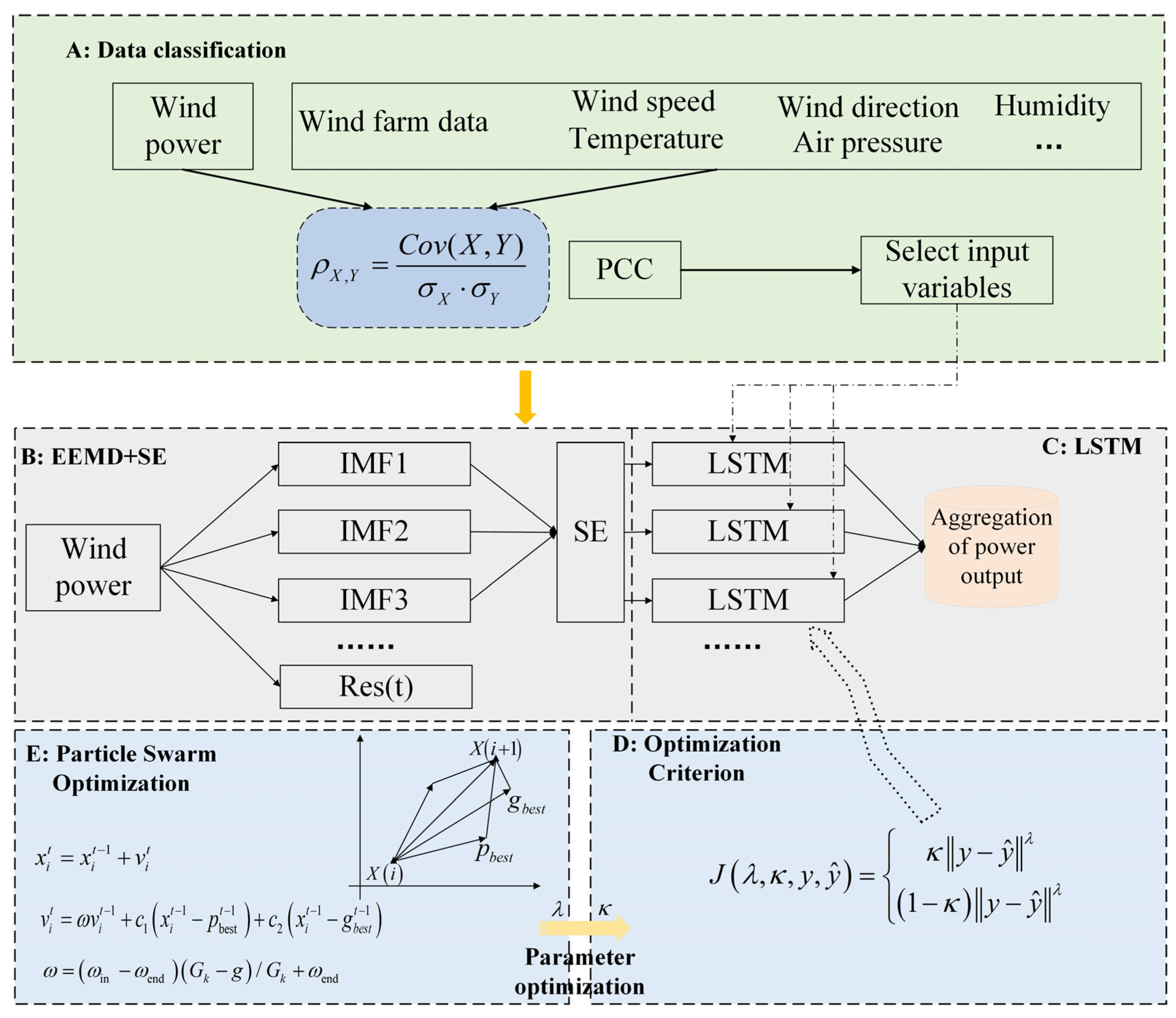
2.7. Prediction Model
3. Discussion
3.1. Data Description
3.2. Model Evaluation
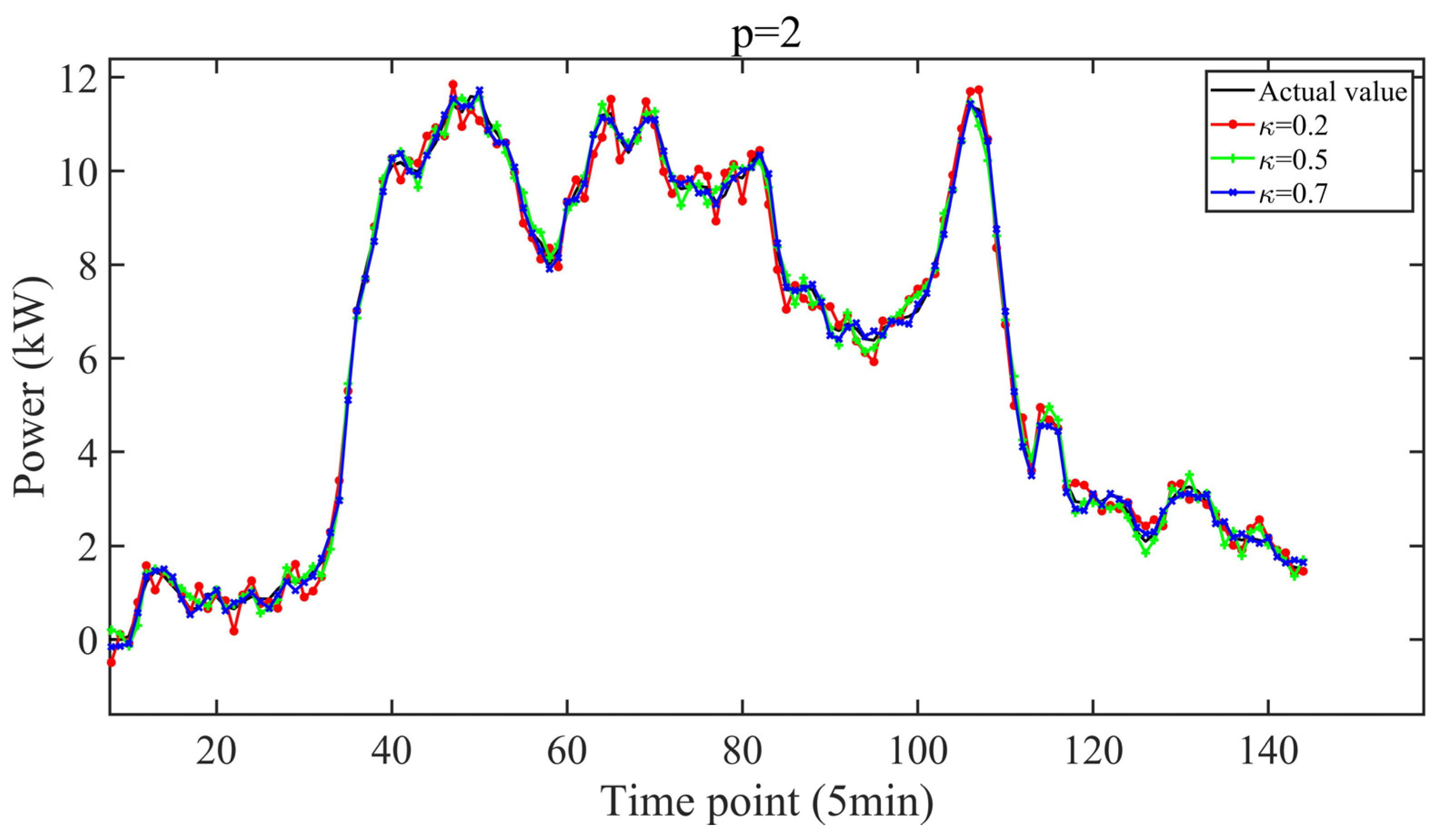
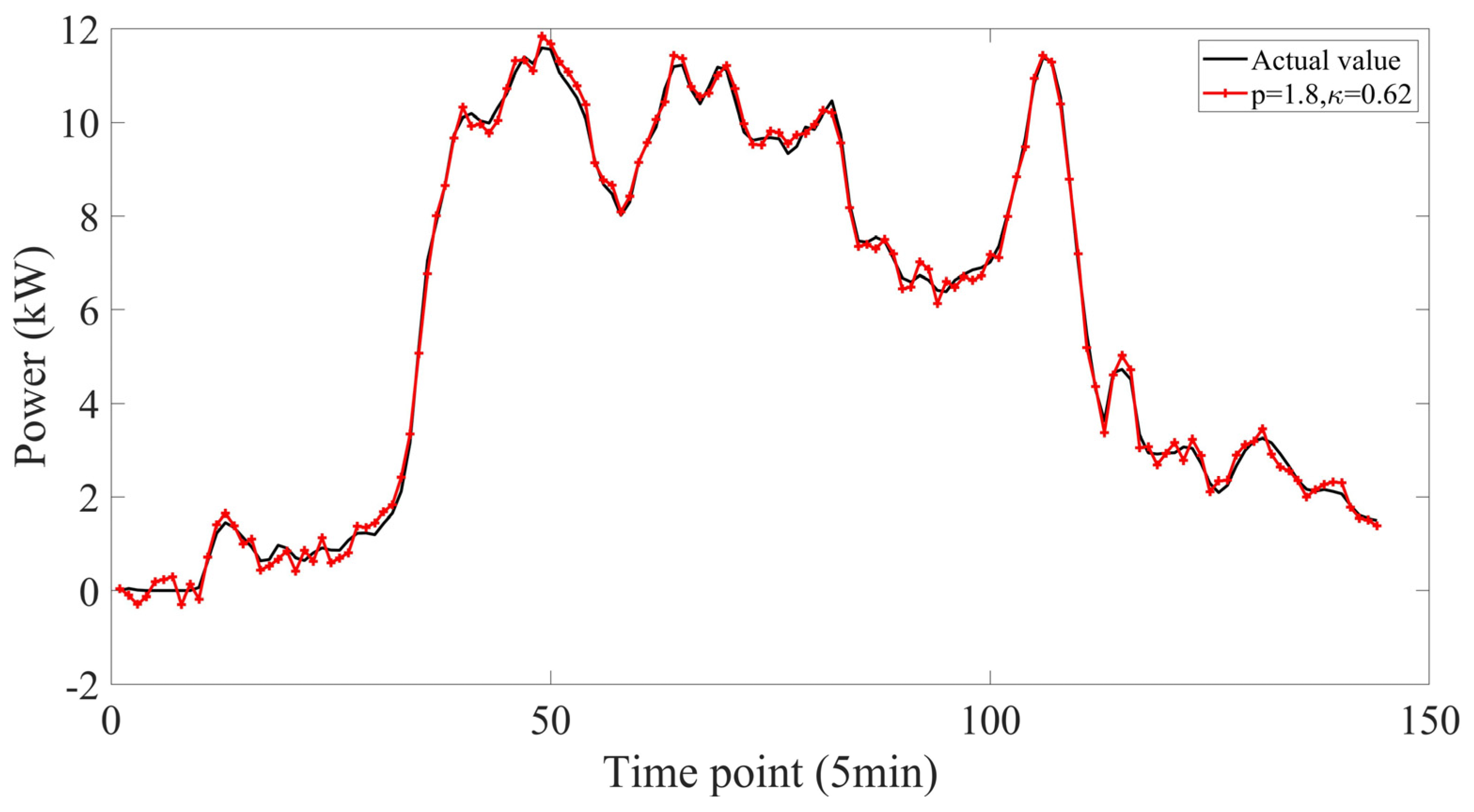
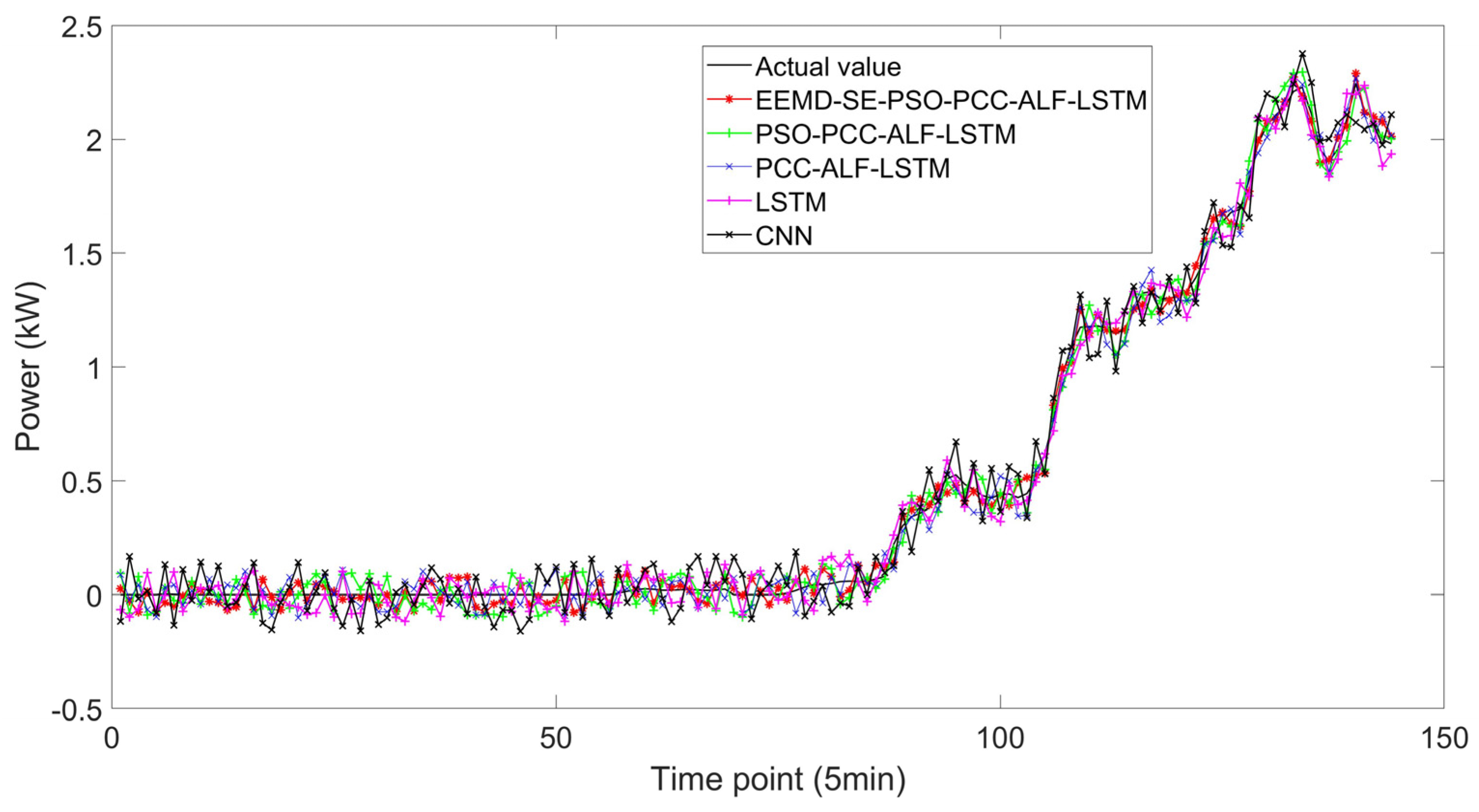
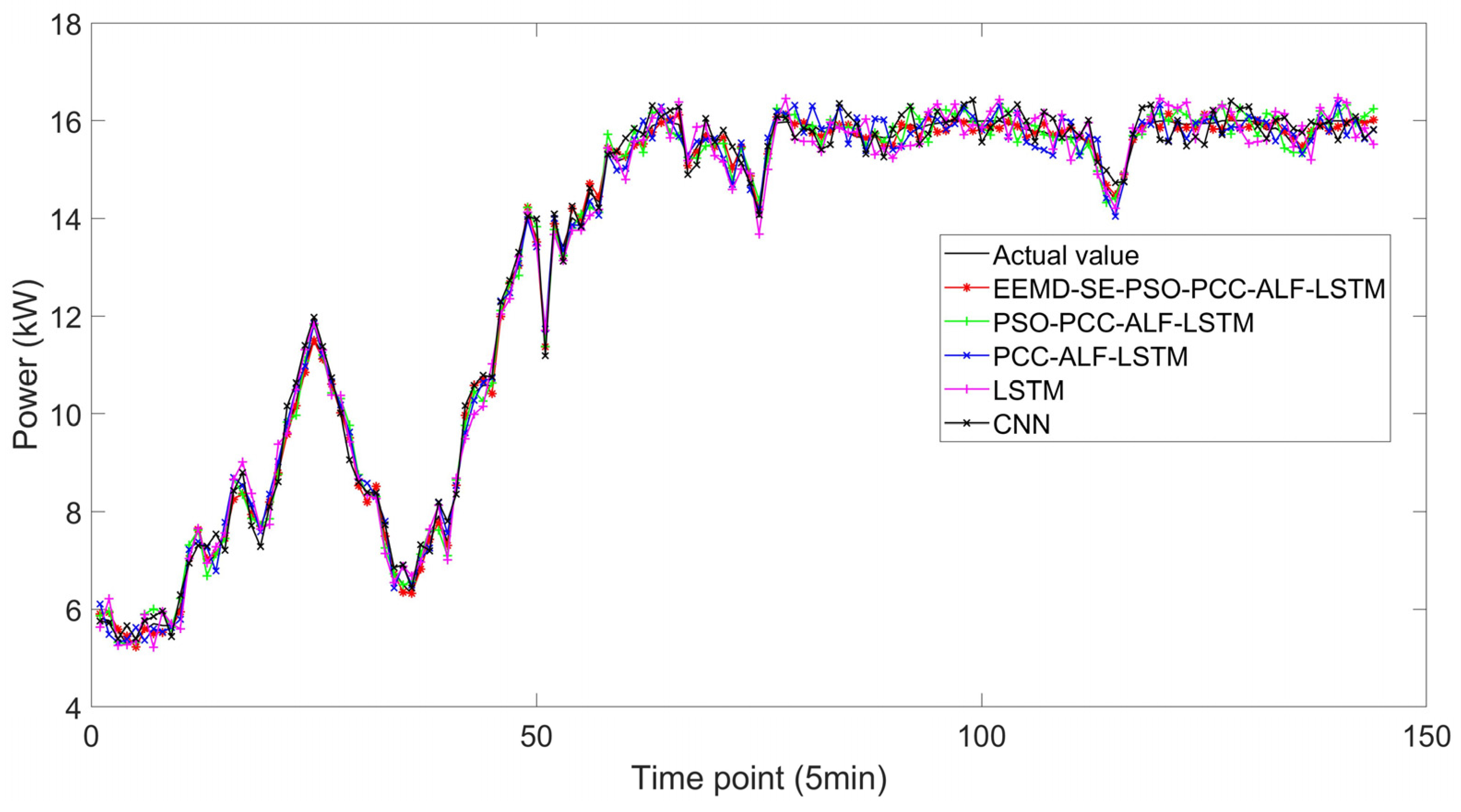
3.3. Discussion of PCC-ALF-LSTM and PSO-PCC-ALF-LSTM
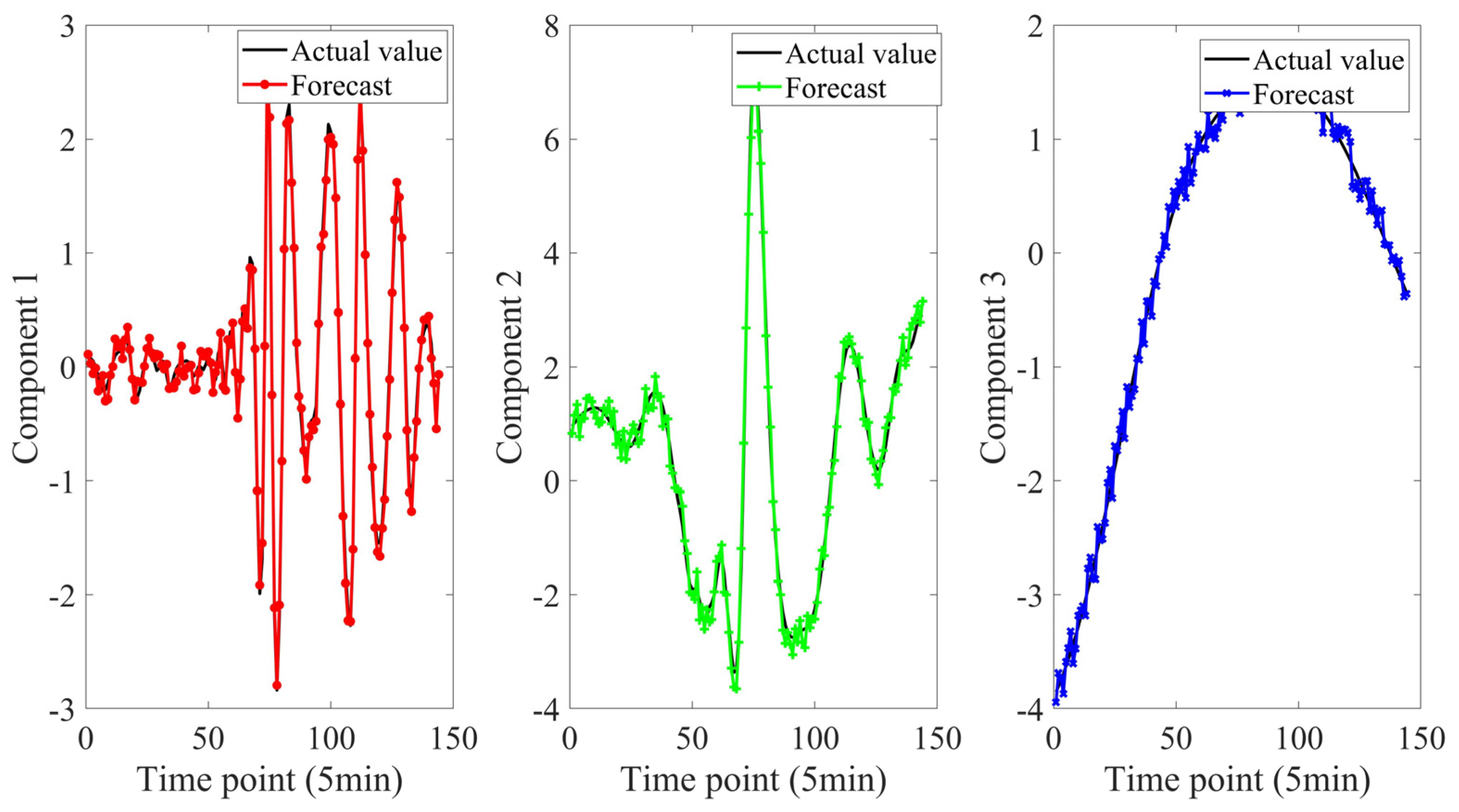
3.4. Discussion of EEMD-SE-PSO-PCC-ALF-LSTM
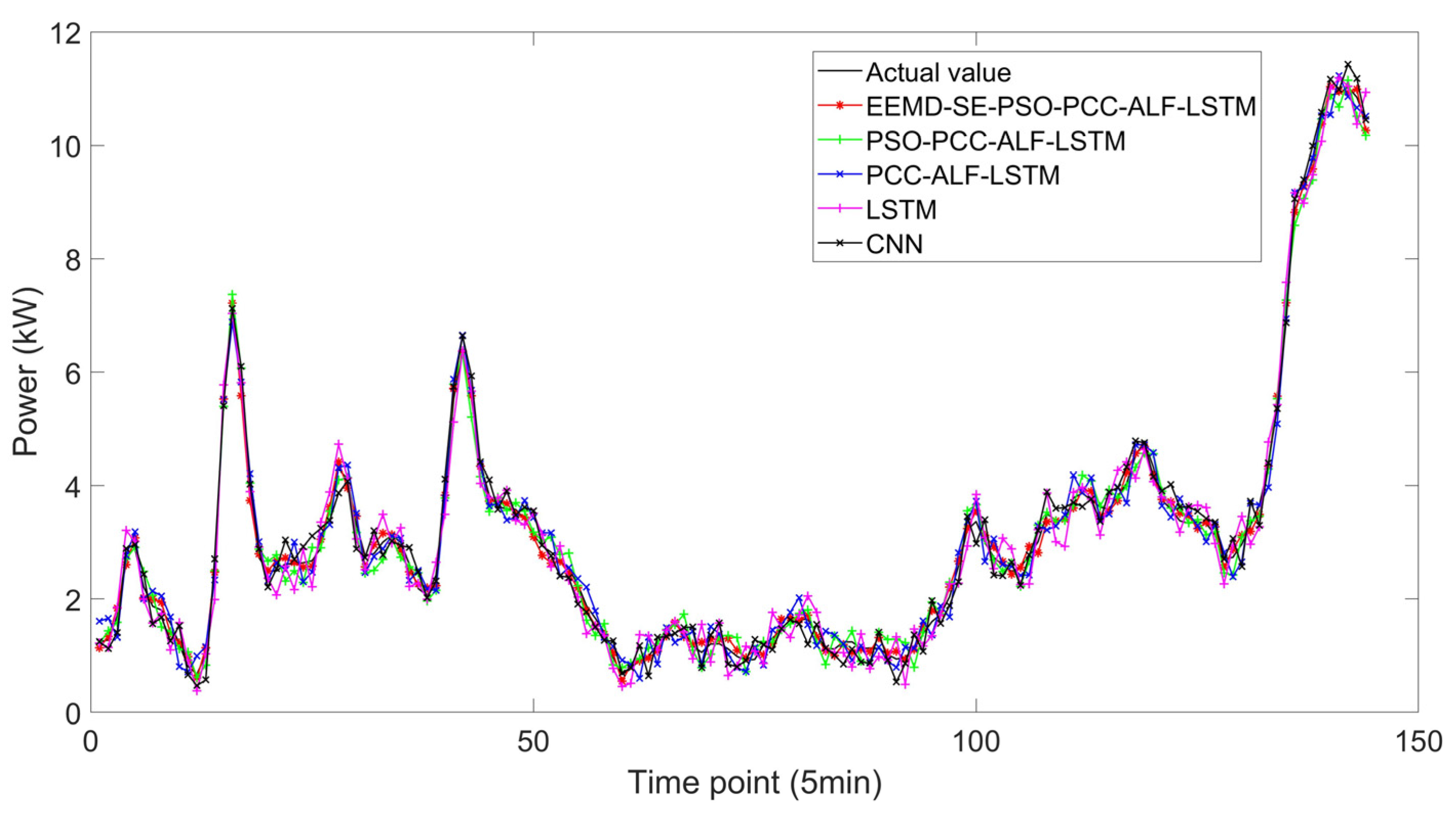
3.5. Discussion of the Comparison of Different Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bludszuweit, H.; Dominuez-Navarro, J.A.; Llombart, A. Statistical analysis of wind power forecast error. IEEE Trans. Power Syst. 2002, 23, 983–991. [Google Scholar] [CrossRef]
- Amjady, N.; Abedinia, O. Short term wind power prediction based on improved kriging interpolation, empirical mode decomposition, and closed-loop forecasting engine. Sustainability 2017, 9, 2104. [Google Scholar] [CrossRef]
- Landberg, L. A mathematical look at a physical power prediction model. Wind. Energy Inter-Natl. J. Prog. Appl. Wind. Power Convers. Technol. 1998, 1, 23–28. [Google Scholar] [CrossRef]
- Lange, M. Analysis of the Uncertainty of Wind Power Predictions; Universitat Oidenburg: Oldenburg, Germany, 2003. [Google Scholar]
- An, G.; Jiang, Z.; Chen, L.; Cao, X.; Li, Z.; Zhao, Y. Ultra short-term wind power forecasting based on sparrow search algorithm optimization deep extreme learning machine. Sustainability 2021, 13, 10453. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J. Transfer learning based multi-layer extreme learning machine for probabilistic wind power forecasting. Appl. Energy 2022, 312, 118729. [Google Scholar] [CrossRef]
- Zhang, C.; Hua, L.; Ji, C.; Shahzad Nazir, M.; Peng, T. An evolutionary robust solar radiation prediction model based on WT-CEEMDAN and IASO-optimized outlier robust extreme learning machine. Appl. Energy 2022, 32, 119518. [Google Scholar] [CrossRef]
- Liu, Z.; Mahdi, H.; Amirhosein, T. Novel forecasting model based on improved wavelet transform, informative feature selection, and hybrid support vector machine on wind power forecasting. J. Ambient. Intell. Humaniz. Comput. 2018, 9, 1919–1931. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Y. Short-term wind speed forecasting based on fast ensemble empirical mode decomposition, phase space reconstruction, sample entropy and improved back-propagation neural network. Energy Convers. Manag. 2018, 157, 1–12. [Google Scholar] [CrossRef]
- Zhang, S.H. Wind power prediction based on genetic neural network. AIP Conf. Proc. 2017, 1834, 020012. [Google Scholar]
- Ma, T.; Wang, C.; Wang, J. Particle-swarm optimization of ensemble neural networks with negative correlation learning for forecasting short-term wind speed of wind farms in western China. Inf. Sci. 2019, 505, 157–182. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Farh, H.; Saud, M. Impact of PSO reinitialization on the accuracy of dynamic global maximum power detection of variant partially shaded PV systems. Sustainability 2019, 11, 2091. [Google Scholar] [CrossRef]
- Wu, Q.; Lin, H. Short-term wind speed forecasting based on hybrid variational mode decomposition and least squares support vector machine optimized by bat algorithm model. Sustainability 2019, 11, 652. [Google Scholar] [CrossRef]
- Liao, C.W.; Wang, I.; Lin, K.P. A fuzzy seasonal long short-term memory network for wind power forecasting. Mathematics 2021, 9, 1178. [Google Scholar] [CrossRef]
- Zheng, W.; Bo, W.; Liu, C. Improved BP neural network algorithm to wind power forecast. J. Eng. 2017, 13, 940–943. [Google Scholar]
- Jiang, Y.; Zhang, B.; Xing, F. Super-short-term multi-step prediction of wind power based on GA-VNN model of chaotic time series. Power Syst. Technol. 2015, 39, 2160–2166. [Google Scholar]
- Bourakadi, D.E.; Yahyaouy, A.; Boumhidi, J. Improved extreme learning machine with autoencoder and particle swarm optimization for short-term wind power prediction. Neural Comput. Appl. 2021, 34, 4643–4659. [Google Scholar] [CrossRef]
- Zhou, B.; Ma, X.; Luo, Y. Wind power prediction based on LSTM networks and nonparametric kernel density estimation. IEEE Access 2019, 7, 165279–165292. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, R.; Ma, Y.; Ma, M.; Zhou, Q.; Lu, Q.; Zhang, J. Research on ultra-short term forecasting technology of wind power output based on wake model. J. Phys. Conf. Ser. 2022, 2166, 012041. [Google Scholar] [CrossRef]
- Jaihuni, M.; Basak, J.K.; Khan, F.; Okyere, F.G.; Sihalath, T.; Bhujel, A.; Park, J.; Lee, D.H.; Kim, H.T. A novel recurrent neural network approach in forecasting short term solar irradiance. ISA Trans. 2022, 121, 63–74. [Google Scholar] [CrossRef]
- Wang, W.; Tian, G.; Yuan, G.; Pham, D.T. Energy-time tradeoffs for remanufacturing system scheduling using an invasive weed optimization algorithm. J. Intell. Manuf. 2021, 34, 1065–1083. [Google Scholar] [CrossRef]
- Lu, P.; Ye, L.; Pei, M. Short-term wind power forecasting based on meteorological feature extraction and optimization strategy. Renew. Energy 2022, 184, 198–216. [Google Scholar] [CrossRef]
- Yin, H.; Ou, Z.; Huang, S.; Meng, A. A cascaded deep learning wind power prediction approach based on a two-layer of mode decomposition. Energy 2019, 189, 301–316. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, T.; Zhang, D. A data-driven deep sequence-to-sequence long-short memory method along with a gated recurrent neural network for wind power forecasting. Energy 2022, 239, 369–397. [Google Scholar] [CrossRef]
- Song, Z.; Jiang, Y.; Zhang, Z. Short-term wind speed forecasting with markov-switching model. Appl. Energy 2014, 130, 103–112. [Google Scholar] [CrossRef]
- Li, G.; Shi, J. On comparing three artificial neural networks for wind speed forecasting. Appl. Energy 2010, 87, 2313–2320. [Google Scholar] [CrossRef]


| Meteorological Factor | Abbreviation | Unit |
|---|---|---|
| wind speed at 0 m | ||
| wind speed at 10 m | w10 | m/s |
| wind speed at 30 m | w30 | m/s |
| wind speed at 70 m | w70 | m/s |
| wind speed at 100 m | w100 | m/s |
| wind direction at 0 m | ||
| wind direction at 10 m | d10 | ° |
| wind direction at 30 m | d30 | ° |
| wind direction at 70 m | d70 | ° |
| wind direction at 100 m | d100 | ° |
| temperature | T | ℃ |
| humidity | H | %rh |
| pressure | P | Pa |
| Parameters | MAE | RMSE | |
|---|---|---|---|
| 8.13 | 11.31 | ||
| 9.67 | 12.18 | ||
| 8.07 | 11.24 | ||
| 7.62 | 10.36 | ||
| 9.67 | 12.18 | ||
| 8.69 | 11.74 | ||
| PSO optimization | 7.51 | 9.36 | |
| Reconstruction Component | Sub-Model |
|---|---|
| Component 1 | IMF1, IMF5, IMF7, IMF12-15 |
| Component 2 | IMF2, IMF10, IMF11, IMF12-16 |
| Component 3 | IMF3, IMF4, IMF6, IMF8, IMF9 |
| Model | Parameters | |||
|---|---|---|---|---|
| ALF | PSO | SE | LSTM | |
| PCC-ALF-LSTM | / | / | Maximum epoch: 300. Learning rate: 0.01. Number of neurons: 32 | |
| PSO-PCC-ALF-LSTM | / | |||
| EEMD-SE-PSO-PCC-ALF-LSTM | ||||
| Model | MAE | RMSE |
|---|---|---|
| PCC-ALF-LSTM | 8.34 | 14.27 |
| PSO-PCC-ALF-LSTM | 7.36 | 9.91 |
| EEMD-SE-PSO-PCC-ALF-LSTM | 6.78 | 8.63 |
| Season | Reconstruction Component | Sub-Model |
|---|---|---|
| Spring | Component 1 | IMF1, IMF5, IMF7, IMF12-15 |
| Component 2 | IMF2, IMF10, IMF11, IMF12-14 | |
| Component 3 | IMF3, IMF6, IMF8, IMF9 | |
| Component 4 | IMF4, IMF15-17 | |
| Autumn | Component 1 | IMF1, IMF6, IMF10, IMF13 |
| Component 2 | IMF2, IMF7, IMF9, IMF14 | |
| Component 3 | IMF3, IMF8, IMF11 | |
| Component 4 | IMF4, IMF5, IMF9, IMF15-17 | |
| Winter | Component 1 | IMF1, IMF7, IMF9, IMF11 |
| Component 2 | IMF2, IMF4, IMF10, IMF12 | |
| Component 3 | IMF3, IMF5, IMF6, IMF13-14 |
| Model | Parameters | ||||
|---|---|---|---|---|---|
| ALF | PSO | SE | LSTM | ||
| PCC-ALF-LSTM | / | / | Maximum epoch: 300. Learning rate: 0.01. Number of neurons: 32. Hidden layer: 3. | / | |
| PSO-PCC-ALF-LSTM | / | / | |||
| EEMD-SE-PSO-PCC-ALF-LSTM | / | ||||
| LSTM (MSE) | / | / | / | / | |
| CNN | Convolutional layers: 5, Kernel number: 5, Kernel size: 2 * 2, Number of full connection layers: 8, Output layer: 1 | ||||
| Model | EEMD-SE-PSO-PCC-ALF-LSTM | ||||||
|---|---|---|---|---|---|---|---|
| Season | Autumn | Winter | |||||
| Parameters | |||||||
| Season | Model | MAE | RMSE | Training Time (s) |
|---|---|---|---|---|
| Spring | PCC-ALF-LSTM | 9.63 | 13.69 | 46.78 |
| PSO-PCC-ALF-LSTM | 7.97 | 10.32 | 57.59 | |
| EEMD-SE-PSO-PCC-ALF-LSTM | 6.32 | 9.12 | 103.37 | |
| LSTM | 9.57 | 12.97 | 45.37 | |
| CNN | 9.36 | 11.77 | 39.87 | |
| Autumn | PCC-ALF-LSTM | 8.47 | 11.36 | 45.97 |
| PSO-PCC-ALF-LSTM | 7.48 | 9.57 | 59.34 | |
| EEMD-SE-PSO-PCC-ALF-LSTM | 7.06 | 8.32 | 112.01 | |
| LSTM | 9.12 | 12.35 | 43.62 | |
| CNN | 8.97 | 11.89 | 37.39 | |
| Winter | PCC-ALF-LSTM | 11.36 | 14.36 | 48.35 |
| PSO-PCC-ALF-LSTM | 10.58 | 13.85 | 55.19 | |
| EEMD-SE-PSO-PCC-ALF-LSTM | 8.96 | 12.31 | 117.38 | |
| LSTM | 13.74 | 15.97 | 46.37 | |
| CNN | 12.35 | 14.86 | 40.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Y.; Zhang, K.; Shao, Q.; Chen, Z. A Short-Term Prediction Model of Wind Power with Outliers: An Integration of Long Short-Term Memory, Ensemble Empirical Mode Decomposition, and Sample Entropy. Sustainability 2023, 15, 6285. https://doi.org/10.3390/su15076285
Du Y, Zhang K, Shao Q, Chen Z. A Short-Term Prediction Model of Wind Power with Outliers: An Integration of Long Short-Term Memory, Ensemble Empirical Mode Decomposition, and Sample Entropy. Sustainability. 2023; 15(7):6285. https://doi.org/10.3390/su15076285
Chicago/Turabian StyleDu, Yuanzhuo, Kun Zhang, Qianzhi Shao, and Zhe Chen. 2023. "A Short-Term Prediction Model of Wind Power with Outliers: An Integration of Long Short-Term Memory, Ensemble Empirical Mode Decomposition, and Sample Entropy" Sustainability 15, no. 7: 6285. https://doi.org/10.3390/su15076285
APA StyleDu, Y., Zhang, K., Shao, Q., & Chen, Z. (2023). A Short-Term Prediction Model of Wind Power with Outliers: An Integration of Long Short-Term Memory, Ensemble Empirical Mode Decomposition, and Sample Entropy. Sustainability, 15(7), 6285. https://doi.org/10.3390/su15076285








