Alternating Iterative Power-Flow Algorithm for Hybrid AC–DC Power Grids Incorporating LCCs and VSCs

Abstract

AC–DC power-flow calculation is the basis for studying HVDC systems. Since traditional iterative methods need many alternative iterations and have convergence problems, this paper proposes an alternating iterative power-flow algorithm for hybrid AC–DC power grids incorporating line-commutated converters (LCCs) and voltage source converters (VSCs). Firstly, the algorithm incorporates the converter interface model into the AC side, considering the influence of the DC side on the AC side, and establishes an AC-augmented Jacobian matrix model with LCC/VSC interface equation variables. Then, according to the type of converter, control mode, and DC grid control strategy, a DC grid power-flow calculation model under various control modes is established for realizing the power-flow decoupling calculation of AC–DC power grids incorporating LCCs and VSCs. The accuracy and effectiveness of the improved algorithm are evaluated using modified IEEE 57 bus AC–DC networks and the CIGRE B4 DC grid test system. The improved algorithm is applicable to various DC grid control modes and considers the reasonable adjustment of the DC grid variable constraints and operating modes.

1. Introduction

A hybrid AC–DC transmission system consisting of a line-commutated converter (LCC)/voltage source converter (VSC) and AC grid is likely to become an important transmission method in the future [1,2,3]. With the increasing scale of the DC grid, the non-linear discrete control process of the DC grid changes the dynamic characteristics of the AC grid, and the difficulty of operation control increases sharply [4,5]. At the same time, the vulnerability of the DC grid to faults has also changed the scope of fault impact and put forward new requirements for relevant stability and recovery-control technology [6,7]. In addition, power-flow analysis is an important premise and foundation when analyzing the steady and transient operation of AC–DC power grids, while designing the corresponding control modes [8,9,10]. To meet this need, in our paper, by incorporating the converter interface model into the AC side, we propose an alternating iterative power-flow algorithm for hybrid AC–DC power grids incorporating LCCs and VSCs, consider the interaction between the DC side and the AC side, and establish an augmented-exchange Jacobian matrix model with LCC/VSC interface equation variables.

In recent years, extensive research efforts have been carried out on AC–DC power-flow calculation methods to support the increasing scale of DC grids [11,12,13]. Hybrid AC–DC power-flow calculation methods can be divided into two categories: unified solution methods and alternating solution methods [14,15]. Unified solution methods have satisfactory convergence, and the number of iterations is small. However, the program inheritance is poor [16,17]. As the size of the DC grid increases, so does the computational complexity, resulting in a decrease in iteration speed [18]. The alternating iteration method has the advantages of fast calculation speed, strong program inheritance, and convenient control-mode switching [19,20,21]. However, it has high requirements for the initial value of the AC grid and poor convergence. In response to these problems, scholars have conducted research [22,23,24,25,26]. An alternative solution approach is proposed to solve the multi-terminal VSC-HVDC power-flow problem [22,23]. This is a full VSC-HVDC power-flow solution, but the strong convergence characteristics of the Newton–Raphson method are sacrificed due to the sequential iterative solution adopted. Authors of [24] present a new model of VSC-HVDC aimed at power-flow solutions using the Newton–Raphson method. Due to its pure AC–DC grid decomposition, the simplification of elements within the converter stations is not required. In [25], based on typical three- and five-terminal DC grids, the nodal admittance matrix-based Gauss–Seidel method and the nodal impedance matrix-based Gauss–Seidel method were investigated and compared for a DC grid power-flow calculation. Authors of [26] analyzed the reasons for repeated alternating and proposed an AC–DC decoupled hybrid power-flow algorithm for a hybrid power system with VSC.

The open-source program MatACDC is based on VSC-HVDC for a power-flow calculation of an AC–DC hybrid system [27]. This program is based on the Matpower program for AC power-flow calculation and is used to calculate the conventional power flow of the hybrid system. MatACDC uses a sequential AC–DC power-flow routine to solve the network. The traditional sequential methods need many alternative iterations and have convergence problems. In order to overcome the shortcomings of these two types of method, researchers have also achieved some results in this area. In [28], a general alternating iterative AC–DC power-flow method is proposed, which is based on the decoupled equivalence of different control methods of a VSC on the AC and the DC sides. It avoids the repeated alternation process and reduces the total calculation amount by adjusting the control parameter of a VSC and the dividing line between AC and DC subsystems. When the AC side is a radial distribution network, the convergence of the calculation becomes poor when using the forward backpropagation method for the AC-side power-flow calculation; this is the next problem to be investigated and solved by this AC–DC decoupling power-flow algorithm.

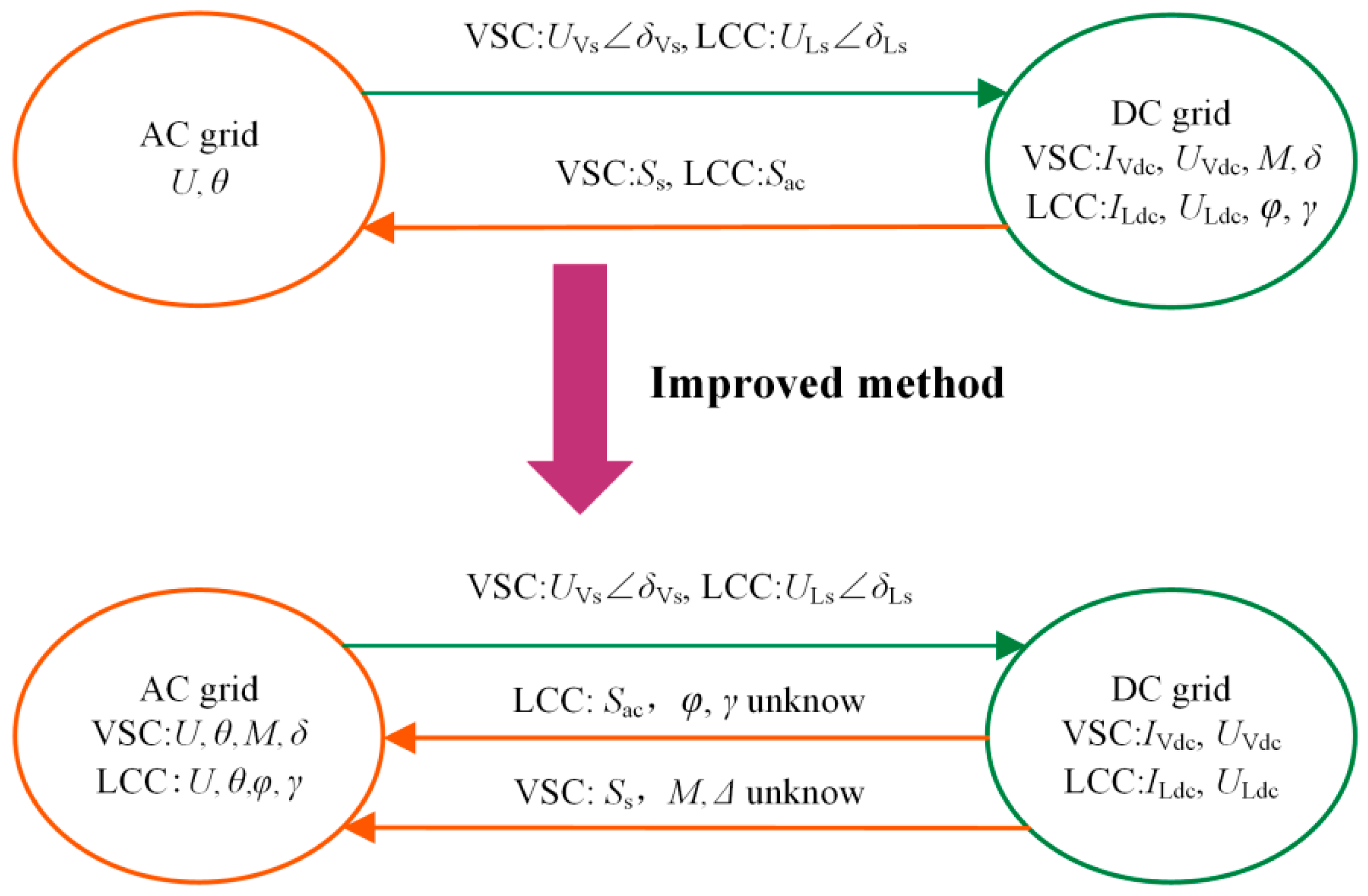
Table 1 includes the main features of the literature on AC–DC power-flow calculations. Nevertheless, the latest research still has limitations in two aspects: (1) In traditional alternating iterations, due to the poor coupling between AC and DC, multiple iterations are required to realize the convergence of the power-flow calculation results. With the increasing scale of the DC grid, this problem will be more prominent. (2) VSC and LCC differ significantly in terms of control modes. The two power-flow calculation models and their algorithms are not universal. In AC–DC power-flow calculations with a VSC, the characteristics of the loss of the VSC, various control strategies of the DC grid, and efficient calculation methods under various control modes must be considered. In addition, in the calculation of AC–DC power flow with an LCC, the coupling relationship between the DC state variable and the AC side must be considered. The main aims of this paper are follows: based on the traditional alternating iterative method, this paper incorporates the converter interface model into the AC side, considers the interaction between the DC side and AC side, and establishes an augmented-exchange Jacobian matrix model with LCC/VSC interface equation variables. According to the type of converter, the control mode, and the DC grid strategy, a DC grid power-flow calculation model under various control modes is established for realizing the AC–DC power-flow decoupling calculation with LCC/VSC. The improved algorithm is applicable to various types of converter, various converter control modes, various DC grid control modes, and reasonable adjustments of the DC grid variable constraints and operation modes. The algorithm reduces the calculational burden for the DC power flow, especially for the calculation of AC–DC power flow with many DC nodes, which can effectively reduce the number of iterations. Therefore, the main contributions of this work can be summarized as follows:

• The proposed algorithm considers the characteristics of the loss of a VSC, various control strategies of a DC grid, efficient calculation methods under various control modes, and the coupling relationship between the DC state variable and the AC side.
• The proposed power-flow calculation algorithm for AC and DC grids with LCC and VSC is applicable to various DC grid control modes and considers the reasonable adjustment of DC grid variable constraints and operating modes.
• The proposed DC grid power-flow calculation model under various control modes is established to realize an AC/DC power-flow decoupling calculation with LCC/VSC.
• The augmented Jacobian matrix model with LCC/VSC interface equation variables can reduce the dimension of the DC Jacobian matrix, and the number of iterations is significantly reduced.

Table 1. The main features of the literature on AC–DC power-flow calculation.

Literature	Methods	Interaction Effects	Converter Types	Control Modes	Computational Efficiency
Ref. [12]	Holomorphic embedding	Not considered	VSC AC/DC systems	Can accommodate various control modes	Can save both time and storage
Ref. [13]	Alternating iterative	Not considered	VSC AC/DC systems	Not considered	Ensures the convergence of NR algorithm
Ref. [16]	Unified iterative	Not considered	VSC AC/DC systems	Different control modes are set for the converter	Greatly shortens the calculation time
Ref. [21]	Alternating iterative	Not considered	VSC AC/DC systems	Not considered	Improves the power-flow calculation speed
Ref. [22]	Alternating iterative	Not considered	LCC AC/DC systems	Not considered	Integrates with existing AC power-flow algorithms
Ref. [23]	Alternating iterative	Not considered	LCC AC/DC systems	Not considered	Provides accurate and reliable results for practical applications
Ref. [24]	Alternating iterative	Not considered	VSC AC/DC systems	Not considered	Can reduce the number of iterations
Ref. [26]	Alternating iterative	Not considered	VSC AC/DC systems	Considers converter control methods	Reduces the total calculation amount
Ref. [27]	Alternating iterative	Considers the constraints between the AC and DC grid	VSC AC/DC systems	Considers variety of converter control strategies	Provides a user flexibility to define the AC and HVDC
Ref. [28]	Alternating iterative	Not considered	VSC AC/DC systems	The control mode of VSC is analyzed	Avoids the repeated alternation process and reduces the total calculation amount
This paper	Alternating iterative	Considers the interaction between the DC side and AC side	VSC-LCC AC/DC systems	The DC power-flow calculation under various control modes is established	Especially with many DC nodes, which can effectively reduce the number of iterations

Table 1. The main features of the literature on AC–DC power-flow calculation.

Literature	Methods	Interaction Effects	Converter Types	Control Modes	Computational Efficiency
Ref. [12]	Holomorphic embedding	Not considered	VSC AC/DC systems	Can accommodate various control modes	Can save both time and storage
Ref. [13]	Alternating iterative	Not considered	VSC AC/DC systems	Not considered	Ensures the convergence of NR algorithm
Ref. [16]	Unified iterative	Not considered	VSC AC/DC systems	Different control modes are set for the converter	Greatly shortens the calculation time
Ref. [21]	Alternating iterative	Not considered	VSC AC/DC systems	Not considered	Improves the power-flow calculation speed
Ref. [22]	Alternating iterative	Not considered	LCC AC/DC systems	Not considered	Integrates with existing AC power-flow algorithms
Ref. [23]	Alternating iterative	Not considered	LCC AC/DC systems	Not considered	Provides accurate and reliable results for practical applications
Ref. [24]	Alternating iterative	Not considered	VSC AC/DC systems	Not considered	Can reduce the number of iterations
Ref. [26]	Alternating iterative	Not considered	VSC AC/DC systems	Considers converter control methods	Reduces the total calculation amount
Ref. [27]	Alternating iterative	Considers the constraints between the AC and DC grid	VSC AC/DC systems	Considers variety of converter control strategies	Provides a user flexibility to define the AC and HVDC
Ref. [28]	Alternating iterative	Not considered	VSC AC/DC systems	The control mode of VSC is analyzed	Avoids the repeated alternation process and reduces the total calculation amount
This paper	Alternating iterative	Considers the interaction between the DC side and AC side	VSC-LCC AC/DC systems	The DC power-flow calculation under various control modes is established	Especially with many DC nodes, which can effectively reduce the number of iterations

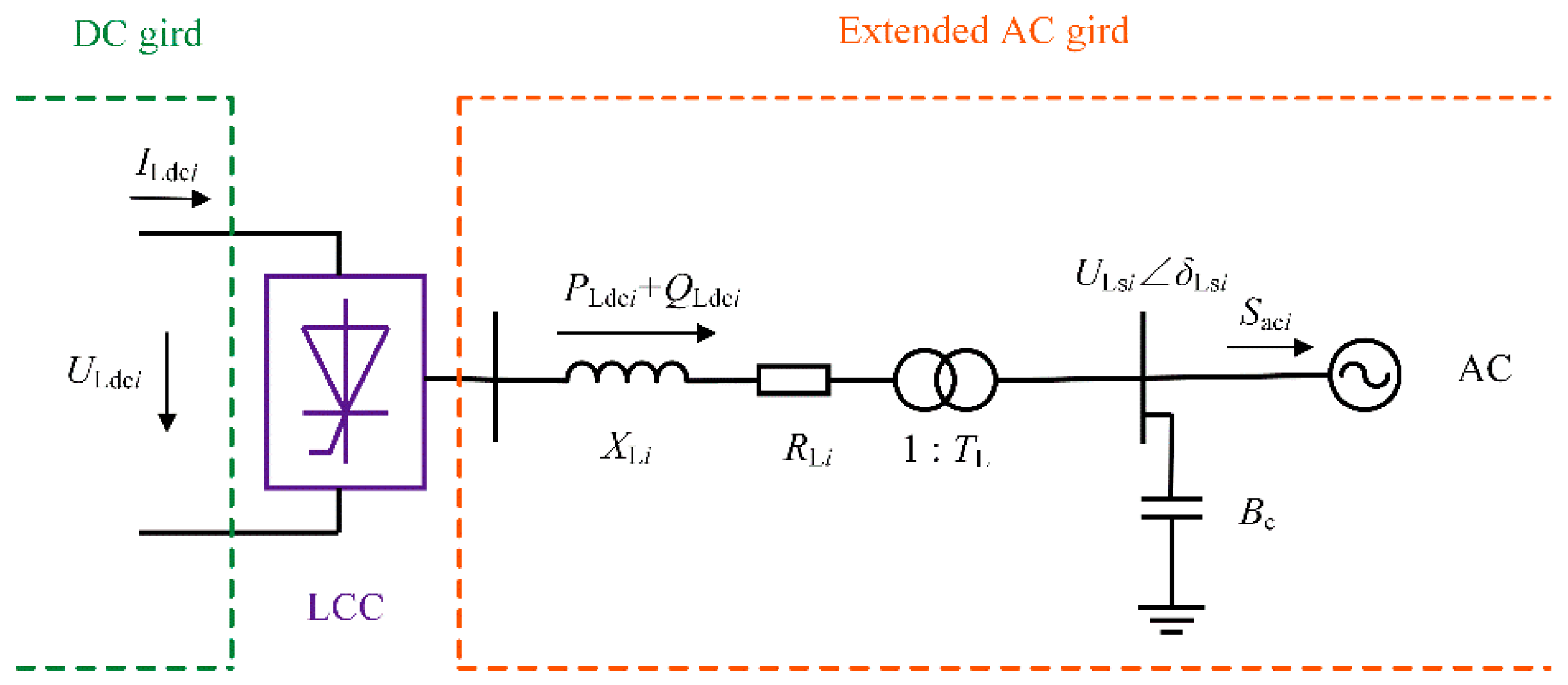
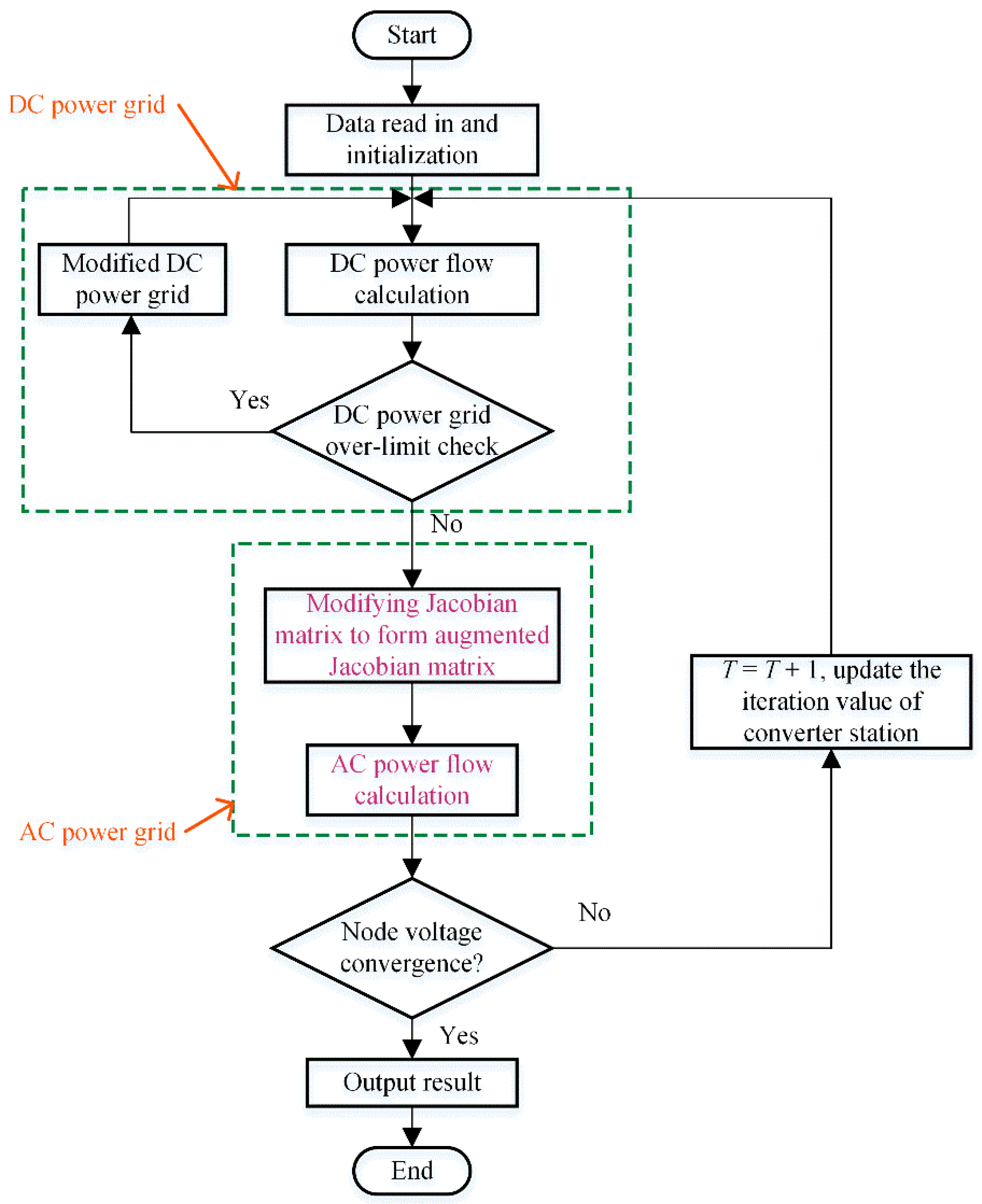
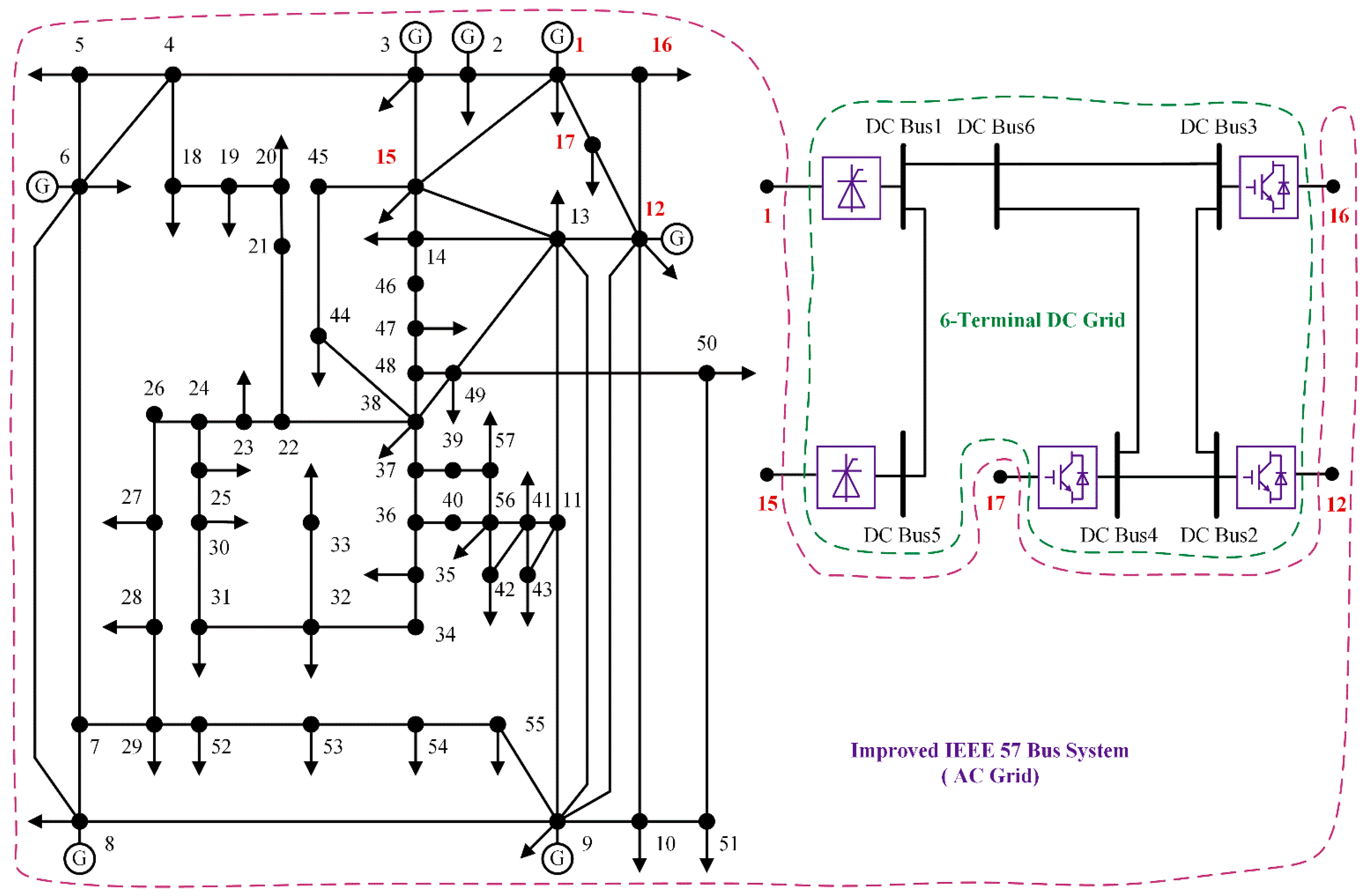
The remainder of this paper is organized as follows: Section 2.1 introduces the converter station model. Section 2.2 introduces the improvement of the alternating iteration method for AC–DC power-flow calculation. Section 3 provides the solution methodology of our model. In Section 4, a modified IEEE 57 bus system with six terminals of DC power grids and the CIGRE B4 bus system are simulated in MATLAB, and the numerical results are discussed. Section 5 concludes this study.

2. Proposed Method

2.1. Converter Station Model

2.1.1. Converter Station Model of a VSC

The simplified model of a VSC station is illustrated in Figure 1. The interface equation of the converter station is connected to the AC side. All the losses of the converter station are borne by the AC grid. The AC power grid is replaced by the voltage source at the common connection point of the AC bus, which is connected to the VSC through a transformer, filter, and commutation reactor.

In Figure 1, T_V is the converter transformer ratio of the VSC; B_f is the converter station filter susceptance of the VSC; R_Vi is the converter station equivalent resistance of the VSC; X_Vi is the converter station equivalent reactance of the VSC, which satisfies Z_Vi = R_Vi + jX_Vi; S_si = P_si + jQ_si is the apparent power of the common connection point of the VSC; S_ci = P_ci + jQ_ci is the apparent power of the AC side of the VSC; U_ci∠δ_ci is the voltage of the AC side of the VSC; U_Vsi∠δ_Vsi is the common connection point node voltage of the VSC; and I_Vdci and U_Vdci are the DC current and the DC voltage, respectively, of the VSC. The following are derived:

$$P_{\mathrm{s}i}=U_{\mathrm{V}\mathrm{s}i}^2{G}_i-\frac{{\mu }_i{M}_i}{\sqrt{2}}{U}_{\mathrm{V}\mathrm{d}\mathrm{c}i}{U}_{\mathrm{V}\mathrm{s}i}^{}[G_i\cos ({\delta }_{\mathrm{V}\mathrm{s}i}-{\delta }_{\mathrm{c}i})+B_i\sin ({\delta }_{\mathrm{V}\mathrm{s}i}-{\delta }_{\mathrm{c}i})]$$

(1)

$$Q_{\mathrm{s}i}=-U_{\mathrm{V}\mathrm{s}i}^2{B}_i+\frac{{\mu }_i{M}_i}{\sqrt{2}}{U}_{\mathrm{V}\mathrm{d}\mathrm{c}i}{U}_{\mathrm{V}\mathrm{s}i}^{}[B_i\cos ({\delta }_{\mathrm{V}\mathrm{s}i}-{\delta }_{\mathrm{c}i})-G_i\sin ({\delta }_{\mathrm{V}\mathrm{s}i}-{\delta }_{\mathrm{c}i})]+U_{\mathrm{V}\mathrm{s}i}^2{B}_{\mathrm{f}}$$

(2)

$$U_{\mathrm{c}i}=\frac{{\mu }_i{M}_i}{\sqrt{2}}{U}_{\mathrm{V}\mathrm{d}\mathrm{c}i}$$

(3)

where P_si and Q_si are the active power and the reactive power, respectively, by the AC system; G_i and B_i are the conductance and susceptance, respectively, of the AC side of the VSC to the common node, including the converter station and converter transformer; μ_i is the DC voltage utilization rate; and M_i is the modulation ratio.

2.1.2. Converter Station Model of an LCC

The basic unit of an LCC is a six-pulse converter, and the interface equation of the converter station is connected to the AC side. All the losses of converter station are borne by the AC grid. Figure 2 illustrates a simplified model of an LCC station.

In Figure 2, I_Ldci and U_Ldci are the DC current and the DC voltage of the LCC, respectively; X_Li is the equivalent reactance of the LCC; R_Li is the equivalent resistance of the LCC; T_L is the transformer ratio of the LCC; U_Lsi∠δ_Lsi is the AC bus voltage of the LCC; B_c is the filter susceptance of the LCC; and S_aci = P_aci + jQ_aci is the apparent power of the common connection point of the LCC. The converter station model of the LCC can be expressed as follows:

$$U_{\mathrm{L}\mathrm{d}\mathrm{c}i}=\frac{3\sqrt{2}{T}_{\mathrm{L}}{U}_{\mathrm{L}\mathrm{s}i}{n}_t}{\pi }\cos {\gamma }_i-\frac{3}{\pi }{X}_{\mathrm{L}i}{I}_{\mathrm{L}\mathrm{d}\mathrm{c}i}{n}_t$$

(4)

$$U_{\mathrm{L}\mathrm{d}\mathrm{c}i}=\frac{3\sqrt{2}{T}_{\mathrm{L}}{U}_{\mathrm{L}\mathrm{s}i}{n}_t{k}_s}{\pi }\cos \phi$$

(5)

$$I_{\mathrm{L}\mathrm{s}i}=T_{\mathrm{L}}{n}_t{k}_s\frac{\sqrt{6}}{\pi }{I}_{\mathrm{L}\mathrm{d}\mathrm{c}i}$$

(6)

$$P_{\mathrm{L}\mathrm{d}\mathrm{c}i}=U_{\mathrm{L}\mathrm{d}\mathrm{c}i}{I}_{\mathrm{L}\mathrm{d}\mathrm{c}i}$$

(7)

$$Q_{\mathrm{L}\mathrm{d}\mathrm{c}i}=U_{\mathrm{L}\mathrm{d}\mathrm{c}i}{I}_{\mathrm{L}\mathrm{d}\mathrm{c}i}\tan \phi$$

(8)

$$P_{\mathrm{a}\mathrm{c}i}=P_{\mathrm{L}\mathrm{d}\mathrm{c}i}+P_{\mathrm{Lloss}i}$$

(9)

$$Q_{\mathrm{a}\mathrm{c}i}=Q_{\mathrm{L}\mathrm{d}\mathrm{c}i}+Q_{\mathrm{c}}^{}$$

(10)

where γ_i is the control angle of the LCC; n_t is the number of converter bridges; k_s is a constant, which is typically equal to 0.995; φ is the power factor angle; I_Lsi is the current of the converter transformer; P_Ldci + jQ_Ldci denotes power injections to inverter i; P_Llossi is the converter loss, for which the calculation method will be specified below; Q_c represents the generated reactive power of the filter susceptance B_c.

2.1.3. Converter Losses

The EC62751 standard recommends the use of electromagnetic transient simulation for calculation, followed by curve fitting to obtain an accurate model, which can be expressed as a quadratic function of the converter current. To explain the parameters of VSCs and LCCs in a unified way, if the subscript x in all equations in this paper is 0, the DC node is the converter-free access node; if x is L, the DC node is connected to an LCC; and if x is V, the DC node is connected to a VSC. The converter loss is expressed in the following equation.

$$P_{x\mathrm{loss}i}==c_i+b_i{I}_{xi}+a_i{I}_{xi}^2$$

(11)

In the equation, a_i, b_i, and c_i are the loss characteristic coefficients. The converter that is connected to the DC node is an LCC, at this time I_xi = I_Lsi. The inverter that is connected to the DC node is a VSC, and I_xi = I_Vci, which can be calculated via the following equation:

$$I_{\mathrm{V}\mathrm{c}i}=\left|\frac{U_{{}_{\mathrm{V}\mathrm{s}i}}-U_{\mathrm{c}i}}{Z_{\mathrm{V}i}}\right|$$

(12)

2.2. Improvement of the Alternating Iteration Method for AC–DC Power-Flow Calculation

2.2.1. Steady-State Model Adjustment of the DC Converter Station

In the iterative process, the traditional alternating iterative method solves the AC grid equation and the DC grid equation separately [29,30]. As the proportion of the DC load increases, the dimension of the DC grid equation increases, and the number of iterations increases.

Based on the scenario that is described above, the traditional alternating iterative method model is modified as follows:

• The interface equation of the converter is connected to the AC side, and all the losses of the converter stations will be on the AC grid.
• The AC grid equation variables increase the interface equation variables of the converter. According to the converter type, for a VSC, the state variables δ and M of the DC system are merged into the AC flow equation for solving. For an LCC, the state variables φ and γ of the DC system are merged into the AC flow equation for solving.

The modified alternating iteration method for AC–DC power-flow calculation considers the coupling relationship between the power flows, as illustrated in Figure 3. After modification, the control variables of the DC power grid are only related to DC parameters, which further enhances the flexibility of the DC control mode.

2.2.2. DC Grid Power-Flow Model

A DC power network is a pure resistance linear network, which can be described by the corresponding conductance matrix. In the above division of AC and DC systems, the DC power, DC loads, and LCC/VSC stations are treated as nonlinear components and are not included in the linear network, as illustrated in the following Figure 4.

For a DC grid with n DC nodes, the relationship between the node current and the node voltage can be expressed by the nodal equation:

$$I_{x\mathrm{d}\mathrm{c}i}=Y_{\mathrm{dc}}{U}_{x\mathrm{d}\mathrm{c}i}$$

(13)

In the equation, I_xdci = [I_xdc1, I_xdc2,…, I_xdcn]^T is the node current vector; U_xdci = [U_xdc1, U_xdc2,…, U_xdcn]^T is the node voltage vector; and Y_dc is the DC network node conductance matrix.

In addition, the expressions of the injected power (P_xdci), current (I_xdci), and voltage (U_xdci) of the DC node are as follows:

$$P_{x\mathrm{d}\mathrm{c}i}=I_{x\mathrm{d}\mathrm{c}i}{U}_{x\mathrm{d}\mathrm{c}i}$$

(14)

If the DC node contains DC power or a DC load, they must be added to perform the above calculation. Substituting Equation (13) into Equation (14):

$$P_{x\mathrm{d}\mathrm{c}i}={\displaystyle \sum _{j=1}^n{Y}_{ij}{U}_{x\mathrm{d}\mathrm{c}j}{U}_{x\mathrm{d}\mathrm{c}i}}$$

(15)

In the equation, Y_ij is an element of matrix Y_dc.

Due to the use of self-commutated semiconductors and direct current vector control strategies, a VSC station has the flexibility to control the active and reactive variables. Active power control includes constant DC active power control, constant DC voltage control, constant DC current control, and droop control. Reactive power control includes constant AC reactive power control and constant AC voltage control [31,32].

The most common operation control method of an LCC is constant DC current control and extinction angle control [33]. In addition, constant DC active power control and constant DC voltage control can be applied, among other control modes [34].

From the above derivation, it is concluded that the converter imbalance equation that corresponds to the active power control is:

$$\Delta P_{x\mathrm{d}\mathrm{c}i}=P_{x\mathrm{d}\mathrm{c}is}-{\displaystyle \sum _{j=1}^n{Y}_{ij}{U}_{x\mathrm{d}\mathrm{c}j}{U}_{x\mathrm{d}\mathrm{c}i}}$$

(16)

In the equation, P_xdcis is the specified active power.

In addition, the DC imbalance equations that correspond to the constant DC voltage control, constant DC current control, droop control, and extinction angle (trigger angle) control are:

$$\Delta U_{x\mathrm{d}\mathrm{c}i}=U_{x\mathrm{d}\mathrm{c}is}-U_{x\mathrm{d}\mathrm{c}i}$$

(17)

$$\Delta I_{x\mathrm{d}\mathrm{c}i}=I_{x\mathrm{d}\mathrm{c}is}-{\displaystyle \sum _{j=1}^n{Y}_{ij}{U}_{x\mathrm{d}\mathrm{c}j}}$$

(18)

$$\Delta d_{1xi}=U_{x\mathrm{d}\mathrm{c}i}-U_{x\mathrm{d}\mathrm{c}is}+k_{droopxi}({\displaystyle \sum _{j=1}^n{Y}_{ij}{U}_{x\mathrm{d}\mathrm{c}j}{U}_{x\mathrm{d}\mathrm{c}i}}-P_{x\mathrm{d}\mathrm{c}is})$$

(19)

$$\Delta d_{\mathrm{L}i}=\frac{\sqrt{2}{T}_{\mathrm{L}}{U}_{\mathrm{L}\mathrm{s}i}}{X_{\mathrm{L}i}sign}\cos {\gamma }_i^s-\frac{\pi }{3X_{\mathrm{L}i}{n}_{t}sign}{U}_{\mathrm{L}\mathrm{d}\mathrm{c}i}-{\displaystyle \sum _{j=1}^n{Y}_{ij}{U}_{\mathrm{L}\mathrm{d}\mathrm{c}j}}$$

(20)

In the equations, I_xdcis and U_xdcis are the specified direct current and the specified direct voltage, and ${\gamma }_i^s$ is the specified control angle for the LCC.

The above equations are developed based on the Taylor equation, and the matrix form of Newton’s power-flow correction equation is obtained by ignoring the high-order terms as follows:

$$\Delta X=J_{DC}^{}\Delta U$$

(21)

In the equation, ΔX = [⋯, ΔP_xdc, ΔI_xdc, Δd_1x, Δd_Li, ⋯]^T, ΔU is DC voltage vector for each node other than the constant DC voltage control, and J_DC is the DC Jacobian matrix. If there is only one constant DC voltage control converter in the above equation, the matrix dimension is n−1, which is effectively reduced compared with the traditional alternating iterative matrix dimension.

2.2.3. AC Grid Power-Flow Model

For an AC node (without a converter), the power mismatch equation is:

$$\left\{\begin{array}{l}\Delta P_{ai}=P_{ai}-U_{ai}{\displaystyle \sum _{}^{j\in i}{U}_j(G_{ij}\cos {\theta }_{ij}+B_{ij}\sin {\theta }_{ij})}\\ \Delta Q_{ai}=Q_{ai}-U_{ai}{\displaystyle \sum _{}^{j\in i}{U}_j(G_{ij}\sin {\theta }_{ij}-B_{ij}\cos {\theta }_{ij})}\end{array}\right.$$

(22)

where subscript a denotes that the node is a pure AC node; P_ai and Q_ai are the specified active power and reactive power for the node; j is connected to AC node i with a common connection node; U_ai and U_j are the voltages of nodes i and j, respectively; G_ij and B_ij are the conductance and susceptance, respectively, of the AC node; and θ_ij is the phase angle difference between nodes i and j, which is expressed as θ_ij = θ_i − θ_j.

For a node with the converter, according to the division of the AC system and the DC system that is specified above, the power mismatch equations are as follows:

$$\left\{\begin{array}{l}\Delta P_{ti}=P_{ti}-U_{ti}{\displaystyle \sum _{}^{j\in i}{U}_j(G_{ij}\cos {\theta }_{ij}+B_{ij}\sin {\theta }_{ij})}-P_{\mathrm{a}\mathrm{c}i}\\ \Delta Q_{ti}=Q_{ti}-U_{ti}{\displaystyle \sum _{}^{j\in i}{U}_j(G_{ij}\sin {\theta }_{ij}-B_{ij}\cos {\theta }_{ij})-Q_{\mathrm{a}\mathrm{c}i}}\end{array}\right.$$

(23)

In the equations, subscript t denotes the DC node.

For VSCs:

$$\left\{\begin{array}{l}{P}_{\mathrm{a}\mathrm{c}i}=P_{si}({\delta }_{\mathrm{c}i},M_i)\\ Q_{\mathrm{a}\mathrm{c}i}=Q_{si}({\delta }_{\mathrm{c}i},M_i)\end{array}\right.$$

(24)

The state variables δ and M of the DC system are merged into the AC flow equation for solving. Since there are two more variables to solve, new equations must be added. Assuming that the number of VSCs is n_v, it is necessary to add 2n_v equations. The original AC Jacobian matrix must be augmented to extend the 2n_v dimensions. The supplementary equations are as follows:

$$\Delta P_{\mathrm{V}i}=P_{\mathrm{V}\mathrm{d}\mathrm{c}i}-P_{si}({\delta }_{\mathrm{c}i},M_i)+P_{\mathrm{V}\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}i}$$

(25)

$$\Delta Q_{\mathrm{V}i}=Q_{\mathrm{V}\mathrm{r}\mathrm{e}\mathrm{f}i}-Q_{si}({\delta }_{\mathrm{c}i},M_i)$$

(26)

Combining the above four equations yields:

$$\left[\begin{array}{c}\Delta P\\ \Delta Q\\ \Delta P_{\mathrm{V}}\\ \Delta Q_{\mathrm{V}}\end{array}\right]=\left[\begin{array}{cccc}{H}^{*} & N^{*}& A_{PM}& A_{P\delta }\\ J^{*}& L^{*} & A_{QM} & A_{Q\delta }\\ F_{P_{\mathrm{V}}{\delta }_{\mathrm{s}}}& F_{P_{\mathrm{V}}U}& S_{P_{\mathrm{V}}M}& S_{P_{\mathrm{V}}\delta }\\ F_{Q_{\mathrm{V}}{\delta }_{\mathrm{s}}}& F_{Q_{\mathrm{V}}U}& S_{Q_{\mathrm{V}}M}& S_{Q_{\mathrm{V}}\delta }\end{array}\right]\left[\begin{array}{c}\Delta \delta \\ \Delta U\\ \Delta M\\ \Delta {\delta }_{\mathrm{c}}\end{array}\right]$$

(27)

where H^*, N^*, J^*, and L^* are the augmented Jacobian matrices after the addition of the state variables δ and M to the original AC Jacobian matrix; A_PM, A_Pδ, A_QM, A_Qδ are the augmented Jacobian matrices of the AC active and reactive powers to state variables δ and M; $F_{P_{\mathrm{V}}{\delta }_{\mathrm{s}}},F_{P_{\mathrm{V}}U},F_{Q_{\mathrm{V}}{\delta }_{\mathrm{s}}},F_{Q_{\mathrm{V}}U}$ are the augmented Jacobian matrices of the active and reactive powers to the AC voltage phase angle and amplitude at common connection points of the VSC; and $S_{P_{\mathrm{V}}M},S_{P_{\mathrm{V}}\delta },$$S_{Q_{\mathrm{V}}M},S_{Q_{\mathrm{V}}\delta }$ are the augmented Jacobian matrices of the active and reactive powers to the state variables δ and M at common connection points of the VSC. The expression is as follows:

$$\begin{array}{l}{H}^{*} =H+\frac{\partial P_{\mathrm{s}}}{\partial \delta },N^{*}=N+\frac{\partial P_{\mathrm{s}}}{\partial U}\\ J^{*} =J+\frac{\partial Q_{\mathrm{s}}}{\partial \delta },L^{*}=L+\frac{\partial Q_{\mathrm{s}}}{\partial U}\end{array}$$

(28)

$$A_{PM}=-U_{\mathrm{V}\mathrm{s}i}^{}\frac{{\mu }_i}{\sqrt{2}}{U}_{\mathrm{V}\mathrm{d}\mathrm{c}i}[G\cos ({\delta }_{\mathrm{V}\mathrm{s}i}-{\delta }_{\mathrm{c}i})+B\sin ({\delta }_{\mathrm{V}\mathrm{s}i}-{\delta }_{\mathrm{c}i})]$$

(29)

$$A_{P{\delta }_{\mathrm{c}}}=F_{P_{\mathrm{V}}\delta }=-S_{P_{\mathrm{V}}\delta }=U_{\mathrm{V}\mathrm{s}i}^{}\frac{{\mu }_{i}M}{\sqrt{2}}{U}_{\mathrm{V}\mathrm{d}\mathrm{c}i}[B\cos ({\delta }_{\mathrm{V}\mathrm{s}i}-{\delta }_{\mathrm{c}i})-G\sin ({\delta }_{\mathrm{V}\mathrm{s}i}-{\delta }_{\mathrm{c}i})]$$

(30)

$$A_{QM}=-S_{Q_{\mathrm{V}}M}=U_{\mathrm{V}\mathrm{s}i}^{}\frac{{\mu }_i}{\sqrt{2}}{U}_{\mathrm{V}\mathrm{d}\mathrm{c}i}[B\cos ({\delta }_{\mathrm{V}\mathrm{s}i}-{\delta }_{\mathrm{c}i})-G\sin ({\delta }_{\mathrm{V}\mathrm{s}i}-{\delta }_{\mathrm{c}i})]$$

(31)

$$A_{Q{\delta }_{\mathrm{c}}}=F_{Q_{\mathrm{V}}{\delta }_{\mathrm{s}}}=-S_{Q_{\mathrm{V}}\delta }=U_{\mathrm{V}\mathrm{s}i}^{}\frac{{\mu }_{i}M}{\sqrt{2}}{U}_{\mathrm{V}\mathrm{d}\mathrm{c}i}[G\cos ({\delta }_{\mathrm{V}\mathrm{s}i}-{\delta }_{\mathrm{c}i})+B\sin ({\delta }_{\mathrm{V}\mathrm{s}i}-{\delta }_{\mathrm{c}i})]$$

(32)

$$F_{P_{\mathrm{V}}U}=-2U_{\mathrm{V}\mathrm{s}}^{}G+\frac{2a(U_{\mathrm{V}\mathrm{s}}^{}-\frac{\mu M}{\sqrt{2}}{U}_{\mathrm{V}\mathrm{d}\mathrm{c}i})}{{\left|Z\right|}^2}+\frac{b}{\left|Z\right|}-\frac{\mu M}{\sqrt{2}}{U}_{\mathrm{V}\mathrm{d}\mathrm{c}}[G\cos ({\delta }_{\mathrm{V}\mathrm{s}}-{\delta }_c)+B\sin ({\delta }_{\mathrm{V}\mathrm{s}}-{\delta }_c)]$$

(33)

$$F_{Q_{\mathrm{V}}U}=2U_{\mathrm{V}\mathrm{s}}^{}B-\frac{\mu M}{\sqrt{2}}{U}_{\mathrm{V}\mathrm{d}\mathrm{c}}[B\cos ({\delta }_{\mathrm{V}\mathrm{s}}-{\delta }_c)-G\sin ({\delta }_{\mathrm{V}\mathrm{s}}-{\delta }_c)]-2U_{\mathrm{V}\mathrm{s}}^{}{B}_{\mathrm{f}}$$

(34)

$$S_{P_{\mathrm{V}}M}=U_{\mathrm{V}\mathrm{s}i}^{}\frac{{\mu }_i}{\sqrt{2}}{U}_{\mathrm{V}\mathrm{d}\mathrm{c}i}[G\cos ({\delta }_{\mathrm{V}\mathrm{s}i}-{\delta }_{\mathrm{c}i})+B\sin ({\delta }_{\mathrm{V}\mathrm{s}i}-{\delta }_{\mathrm{c}i})]-\frac{2a(U_{\mathrm{V}\mathrm{s}}^{}-\frac{\mu M}{\sqrt{2}}{U}_{\mathrm{V}\mathrm{d}\mathrm{c}i})}{{\left|Z\right|}^2}\frac{\mu }{\sqrt{2}}{U}_{\mathrm{V}\mathrm{d}\mathrm{c}i}-\frac{b}{\left|Z\right|}\frac{\mu }{\sqrt{2}}{U}_{\mathrm{V}\mathrm{d}\mathrm{c}i}$$

(35)

For LCCs:

$$\left\{\begin{array}{l}{P}_{\mathrm{a}\mathrm{c}i}=P_{\mathrm{a}\mathrm{c}i}(I_{\mathrm{L}\mathrm{d}\mathrm{c}i},U_{\mathrm{L}\mathrm{d}\mathrm{c}i})\\ Q_{\mathrm{a}\mathrm{c}i}=Q_{\mathrm{a}\mathrm{c}i}(I_{\mathrm{L}\mathrm{d}\mathrm{c}i},U_{\mathrm{L}\mathrm{d}\mathrm{c}i},\phi )\end{array}\right.$$

(36)

In the equations, the state variable φ of the DC grid is merged into the AC flow equation for solving. To make the equations solvable, a new equation must be added. The corresponding augmentation terms must be added to the original AC Jacobian matrix. In addition, to obtain the control variable γ, according to Equations (4) and (5), the supplementary equations are as follows:

$$\Delta d_{1i}=U_{\mathrm{L}\mathrm{d}\mathrm{c}i}-\frac{3\sqrt{2}{T}_{\mathrm{L}}{U}_{\mathrm{L}\mathrm{s}i}{n}_t}{\pi }\cos {\gamma }_i+\frac{3}{\pi }{X}_{\mathrm{L}i}{I}_{\mathrm{L}\mathrm{d}\mathrm{c}i}{n}_t$$

(37)

$$\Delta d_{2i}=U_{\mathrm{L}\mathrm{d}\mathrm{c}i}-\frac{3\sqrt{2}{T}_{\mathrm{L}}{U}_{\mathrm{L}\mathrm{s}i}{n}_t{k}_s}{\pi }\cos \phi$$

(38)

If the tap of the converter transformer is determined, from Equations (36)–(38), the following can be obtained:

$$\left[\begin{array}{c}\Delta P\\ \Delta Q\\ \Delta d_1\\ \Delta d_2\end{array}\right]=\left[\begin{array}{cccc}{H}_L^{*} & N_L^{*} & A_{P\gamma }& A_{P\phi }\\ J_L^{*} & L_L^{*} & A_{Q\gamma } & A_{Q\phi }\\ F_{d_1\delta }& F_{d_{1}U}& S_{d_1\gamma }& S_{d_1\phi }\\ F_{d_2\delta }& F_{d_{2}U}& S_{d_2\gamma }& S_{d_2\phi }\end{array}\right]\left[\begin{array}{c}\Delta \delta \\ \Delta U\\ \Delta \gamma \\ \Delta \phi \end{array}\right]$$

(39)

In the equations,$A_{P\gamma },A_{P\phi },A_{Q\gamma },A_{Q\phi }$ are the augmented Jacobian matrices of the AC active and reactive powers to state variables φ and γ; $F_{d_1\delta },F_{d_{1}U},F_{d_2\delta },F_{d_{2}U}$ are the augmented Jacobian matrices of the supplementary equation of an LCC to the AC voltage phase angle and amplitude; and $S_{d_1\gamma },S_{d_1\phi },S_{d_2\gamma },S_{d_2\phi }$ are the augmented Jacobian matrices of the supplementary equation of an LCC to state variables φ and γ. The expression is as follows:

$$A_{Q\phi }=-U_{\mathrm{L}\mathrm{d}\mathrm{c}i}{I}_{\mathrm{L}\mathrm{d}\mathrm{c}i}{\sec }^2\phi$$

(40)

$$F_{d_{1}U}=-\frac{3\sqrt{2}{T}_{\mathrm{L}}{n}_t}{\pi }\cos {\gamma }_i$$

(41)

$$S_{d_1\gamma }=-\frac{3\sqrt{2}{T}_{\mathrm{L}}{U}_{\mathrm{L}\mathrm{s}i}{n}_t}{\pi }$$

(42)

$$F_{d_{2}U}=-\frac{3\sqrt{2}{T}_{\mathrm{L}}{n}_t{k}_s}{\pi }\cos \phi$$

(43)

$$S_{d_2\phi }=\frac{\partial \Delta d_2}{\partial \phi }=\frac{3\sqrt{2}{T}_{\mathrm{L}}{U}_{\mathrm{L}\mathrm{s}i}{n}_t{k}_s}{\pi }\sin \phi$$

(44)

According to the above analysis, for LCCs, assuming that the number of LCCs is n_l, it is necessary to increase the 2n_l dimensions on the basis of the original AC Jacobian matrix. Although the Jacobian matrix dimensionality is increased, the corresponding extended Jacobian matrix is simple to calculate, easy to implement, and has fewer nonzero elements.

2.2.4. Dimensions of the Jacobian Matrix of the Improved Alternating Iteration Method

• AC Jacobian Matrix

According to the above analysis, assuming that the number of VSCs is n_v, the original AC Jacobian matrix must be augmented by 2n_v dimensions. For LCCs, assuming that the number of LCCs is n_l, it is necessary to increase the 2n_l dimensions on the basis of the original AC Jacobian matrix.

2.

DC Jacobian Matrix

In the traditional alternating iteration method, for VSCs, the number of VSCs is assumed to be n_v, and the DC grid contains four variables to solve, thereby requiring 4n_v equations. Similarly, for LCCs, the number of LCCs is assumed to be n_l, and the DC grid contains four variables to solve, thereby requiring 4n_l equations. Assuming that single-point voltage control is adopted in the DC power grid, the dimension of the DC Jacobian matrix is 4(n_v + n_l) − 1 in the traditional alternating iteration method. In the improved method, the dimension of the DC Jacobian matrix is only (n_v + n_l) − 1, which is 3(n_v + n_l) less than the traditional method. The main reason is that in the process of solving for VSCs, the state variables δ and M of the DC system are merged into the AC power-flow equation for solution; and for LCCs, the state variables γ and φ of the DC power grid are merged into the AC power-flow equation for solution.

3. Algorithm Flow and Date

If the system does not contain an LCC of extinction angle (trigger angle) control, the DC state variables are not related to the AC side. In contrast, if an LCC contains extinction angle (trigger angle) control, the DC state variables are related to the AC bus voltage of the LCC of extinction angle (trigger angle) control, regardless of the other AC state quantities. When calculating the power flow of the DC subsystem, the AC bus voltage of the LCC is regarded as a constant value.

3.1. Iterative Initial Value of the DC Grid

In DC power-flow calculation, the parameters that characterize the operation status of each DC node are the DC voltage, DC current, DC power, and control angle (the converter is an LCC) [35,36,37]. Depending on whether the variables are known, the initial value of the DC node iteration is selected, as presented in

Table 2. Variables and initial iteration values of DC nodes with various control modes.

Converter Station Control Mode	Known Variable	Unknown Variable	Iterative Initial Value
Constant DC power control	Pxdcis	Uxdci	Uxdci(0) = 1.0
Constant DC current control	Ixdcis	Uxdci	Uxdci(0) = 1.0
Constant DC voltage control	Uxdcis	Pxdci	Pxdci(0) = −ΣPxdcj
Voltage droop control	-	Uxdci, Pxdci	Uxdci(0) = Uxdcis, Pxdci(0) = Pxdcis
Extinction angle (trigger angle) control	cos${\gamma }_i^s$	Uxdci	Uxdci(0) = 1.0

.

3.2. Control Mode of the DC Power Grid

It is assumed that there are n DC nodes in the DC grid and that the control mode is single-point voltage control. Only one DC node uses constant DC voltage control to control the voltage, to ensure that the DC voltage tracks the reference value of the voltage [38].

In an n-node network with multipoint voltage droop control, there are m DC nodes with DC voltage droop control. Their control characteristics are expressed as:

$$f_i=U_{x\mathrm{d}\mathrm{c}i}-U_{x\mathrm{d}\mathrm{c}is}+k_{droopxi}(P_{x\mathrm{d}\mathrm{c}i}-P_{x\mathrm{d}\mathrm{c}is})=0$$

(45)

In the equation, i = 1, 3,…, m and k_droopxi is the droop coefficient.

If a power shortage in the network causes the DC voltage to droop, the m-voltage droop control stations increase the power that is injected into the network according to their own operating curves. The power unit operates on a drooping curve with various coefficient values, and the output power differs at the same DC bus voltage [39].

Suppose Figure 5 shows the drooping curves of three moments of the same unit in the system, which initially runs at point B. If the unit must output more power, the coefficient must be reduced; if the unit must reduce its power output, the coefficient must be increased. During the operation of the system, the transmission power of the unit can be adjusted by dynamically adjusting the coefficient of the drooping curve.

3.3. Operation Analysis of the DC Power Grid

For DC power-flow calculation, it is necessary to check whether the DC power grid variables exceed the limit. At the same time, during normal operation, in order to ensure the safe operation of a VSC converter station, the VSC converter station needs to adjust its control mode in time so that it can operate in a safe area [40].

3.3.1. Over-Limit Verification of the DC Power Grid

If the node voltage exceeds the limit, it is necessary to modify the voltages of all constant voltage control or droop control stations because the resistance of the DC network is low and the DC voltage of the whole network is approximately the same.

$$U_{x\mathrm{d}\mathrm{c}is}=U_{x\mathrm{d}\mathrm{c}is}-\alpha \max (\Delta U_{\mathrm{d}\mathrm{c}\lim j})$$

(46)

In the equation, α is the margin coefficient, which is greater than 1.0, and ∆U_dclimj is the overlimit voltage of the jth node in the DC network.

If the node power of a droop control station exceeds the limit and multipoint voltage droop control is adopted, there are voltage station nodes whose node power does not exceed the limit. According to the following equations, the powers of overlimit and within-limit voltage stations are modified:

$$P_{x\mathrm{d}\mathrm{c}is}=P_{x\mathrm{d}\mathrm{c}is}-\alpha \Delta P_{\mathrm{d}\mathrm{c}\lim i}\hspace{1em}i\in V_1$$

(47)

$$P_{x\mathrm{d}\mathrm{c}is}=P_{x\mathrm{d}\mathrm{c}is}-\frac{\alpha {\displaystyle \sum _{i\in V_1}\Delta P_{\mathrm{d}\mathrm{c}\lim i}}}{n_{V_2}}\hspace{1em}j\in V_2$$

(48)

In the equations, i ∈ V₁ is the droop control station node with a power that exceeds the limit, j ∈ V₂ is the droop control station node with a power that does not exceed the limit, $n_{V_2}$ is the number of elements in V₂, and ∆P_dclimi denotes the DC power that exceeds the limit of the ith droop control station node.

3.3.2. Analysis of VSC Operation Characteristics

Figure 6 shows the safe operation area of an VSC converter station considering the voltage constraints and transmission capacity constraints of converter stations. The upper and lower arcs in the figure are the corresponding reactive power boundaries when the converter bus voltage operates at the upper and lower limits. The circular area is the transmission capacity constraint of the converter, the rectifier operation area is on the left, the inverter operation area is on the right, and the shaded part is the actual operation area of the VSC converter station.

As shown in Figure 6, if the reactive power control mode of the converter station is set to constant reactive power control, it is at point A in the figure during normal operation. If the load of the AC PCC node or adjacent nodes increases, the amplitude of the PCC voltage will be reduced due to insufficient reactive power, which will lead to the voltage of converter bus being lower than its lower limit, as shown at point B. At this time, it is necessary to change the constant reactive power control into constant AC voltage control to provide a reactive power support capacity for the system to improve the AC node voltage. The system operation point will be moved to point C to maintain the voltage of the VSC converter station within a reasonable range. If the reactive power control mode of the converter station is set to constant AC voltage control, it is at point X during normal operation. If the load of the PCC node continues to increase significantly, the reactive power injected into the AC system PCC by the VSC converter station will also increase, resulting in the converter bus voltage being higher than its upper limit, as shown at point Y. At this time, the control mode of the VSC converter station shall be changed from constant AC voltage control to constant reactive power control. The set value of reactive power is the maximum reactive power injection value under the constraint of converter transmission capacity. The system operates at point Z to avoid out-of-limit power flow.

3.4. Algorithm Flow

The key to solving an AC–DC power flow via alternating iteration is the coupling relationship between the AC and DC power flows. In the traditional alternating iteration method for AC–DC power-flow calculation, the influence of the AC system on the DC system is generated by the voltage of the AC bus. If the voltage is known, the power flow of the DC system can be solved independently. The influence of the DC system on the AC system is generated by the AC injection power of the converter station. If the power is known, the power flow of the AC system can also be solved independently. In this paper, the traditional alternating current and power-flow calculation alternating iterative method model is modified. After modification, the influence of the AC system on the DC system is still generated by the AC bus voltage, but the effect of the DC system on the AC system is generated by the DC injection power of the converter station. At this time, the state variables of the DC power grid only include the DC current and the DC voltage. The calculation process of the improved alternating iterative method is illustrated in Figure 7. First, the data are read for DC grid power-flow calculations, and if the DC grid does not exceed the limit, the AC-side augmented Jacobian matrix is subsequently obtained for AC-side power-flow calculations.

3.5. Test System

To evaluate the accuracy and effectiveness of the improved alternating iteration power-flow algorithm for AC–DC power grids, a modified IEEE 57 bus system with six terminals of DC power grids and a CIGRE B4 bus system are simulated in MATLAB. It is compared with the method proposed in the literature [28,41]. The case-study settings are listed in

Table 3. Case-study settings.

Case	Study Setting	Study Objective
Case 1	Single-point voltage control (improved 57-bus, 6-terminal DC grid)	Evaluate the accuracy of the improved algorithm and compare it with the original algorithm in terms of the number of iterations
Case 2	Voltage droop control (improved 57-bus, 6-terminal DC grid)	Evaluate the performance of the improved algorithm in the droop control mode
Case 3	Voltage droop control (improved CIGRE B4 bus, with 14 DC grid nodes and 11 AC grid nodes)	Evaluate the performance of the improved algorithm in terms of the number of iterations with an increase in the number of DC converter stations

.

3.5.1. Case 1

In Case 1, a modified IEEE 57 bus system is considered. A six-terminal DC power grid with a voltage level of ±200 kV was added to the system. The topological structure is illustrated in Figure 8. The reference capacity of the AC–DC network is 100 MVA. The reference voltage of the DC power grid is 200 kV. Converter stations 1 and 5 are LCCs, DC bus 6 consists of pure DC nodes without a converter, and the remaining are VSCs. The AC-side parameters (which include the loss characteristics) and the DC-grid-line parameters of the five converter stations are listed in

Table 4. AC-side parameters and loss characteristics of VSCs in a six-terminal DC grid.

Converter Station	Transformer	Filter	Loss Characteristic
1	0.001 + j0.083	0.2	0.5, 2, 8
2	0.0015 + j0.2	0	1, 4, 8
3	0.003 + j0.25	0.1	6, 12, 12
4	0.003 + j0.25	0	2, 4, 4
5	0.003 + j0.175	0.2	0.5, 2, 8

and

Table 5. DC branch parameters in a six-terminal DC grid.

Numbering	1	2	3	4	5	6
Scheme 1	1	1	2	2	3	4
Termination bus	5	7	3	4	7	7
Line resistance	0.025	0.005	0.015	0.015	0.01	0.015

. The DC grid adopts a single-point voltage control. The control methods and reference values are specified in

Table 6. Control methods and reference values of the converter stations in case 1.

Converter Station	Active Control	Reactive Power Control
1	ULdcis= 0.97	-
2	PVdcis = 0.5	QVref = 0
3	PVdcis = 0.4	QVref = 0.1
4	PVdcis = 0.6	QVref = 0
5	PLdcis = 0.5	-

.

3.5.2. Case 2

In an AC–DC hybrid power grid, VSC control strategies are flexible and diverse, so the power-flow calculation of AC–DC hybrid power grids considering control strategies becomes an important problem that needs to be studied urgently. Reference [42] proposed a power-flow model of an AC–DC hybrid power grid considering VSC control strategy, and flexibly realized a power-flow calculation of the hybrid power grid under different control strategies. However, the unified iterative method was used to solve the model, and the program inheritance was poor. With the expansion of DC network nodes, the calculation amount will increase accordingly, resulting in a decrease in the iterative speed. In this paper, the improved alternating iteration method is used to establish the DC power-flow calculation model under various control modes, and an AC–DC power-flow decoupling calculation with LCC/VSC hybrid DC is realized. In case 2, the DC grid uses multipoint voltage droop control, in which converter stations 1 and 2 are voltage stations, to realize voltage droop control, as presented in

Table 7. Parameters of the converter stations with droop control in case 2.

Converter Station	Udcs	Pdcs	Qs	Droop Coefficient
1	0.995	0.30	-	0.04
2	1.005	0.95	0	0.04

. The remaining stations are power stations, and the control method is the same as in case 1.

3.5.3. Case 3

Case 3 uses the CIGRE B4 bus system [43], which was proposed by the B4 Working Group of the International Large Power Grid Conference. The parameters of the system are specified in the literature [44]. The system has 11 AC buses and 15 DC buses, as illustrated in Figure 9. To test the converter models and control methods that are proposed in this paper, the converter control methods in the original example are modified as follows: (1) Cm-A1 is set to an LCC using droop control; (2) Cm-B2 is set to an LCC with fixed angle control; (3) Cm-B3 is set to an LCC using droop control.

The converter drooping coefficient is assumed to be 0.1, and the converter loss parameters are assumed to be a = 0.01, b = 0.04, and c = 0. Partial results are listed in

Table 8. Partial results of the power-flow calculation.

DC Bus	Inverter Type	Pdc	Udc
Cm-A1	LCC	−0.3878	1.0142
Cm-B3	LCC	−0.7337	0.9318
Cb-A1	VSC	1.5902	1.0019
Cm-E1	VSC	−0.1000	0.9714

. The calculation results are approximately consistent with the results of the original example, and the accuracy of the method is demonstrated again.

4. Results and Discussion

The traditional alternating iteration method and the method in this paper are applied to case 1. The results of the two algorithms are compared in

Table 9. Comparison of the improved algorithm and the traditional algorithm.

Variable	Number of Nodes	Traditional Method Results	Improved Method Results	Error
ULdc	1 (LCC1)	1.04041	1.04038	2.7 × 10−5
UVdc	12 (VSC2)	0.95123	0.95118	4.8 × 10−5
UVdc	16 (VSC3)	0.95712	0.95712	1.3 × 10−6
ULdc	17 (LCC4)	1.05872	1.05869	3.1 × 10−5
UVdc	15 (VSC5)	0.98124	0.98121	3.5 × 10−5
U0dc	DC Bus 6	0.96543	0.96535	7.9 × 10−5

. The maximum error of all state variables in the AC–DC power grid is 7.9 × 10⁻⁵; the improved alternating iteration algorithm in this paper is accurate.

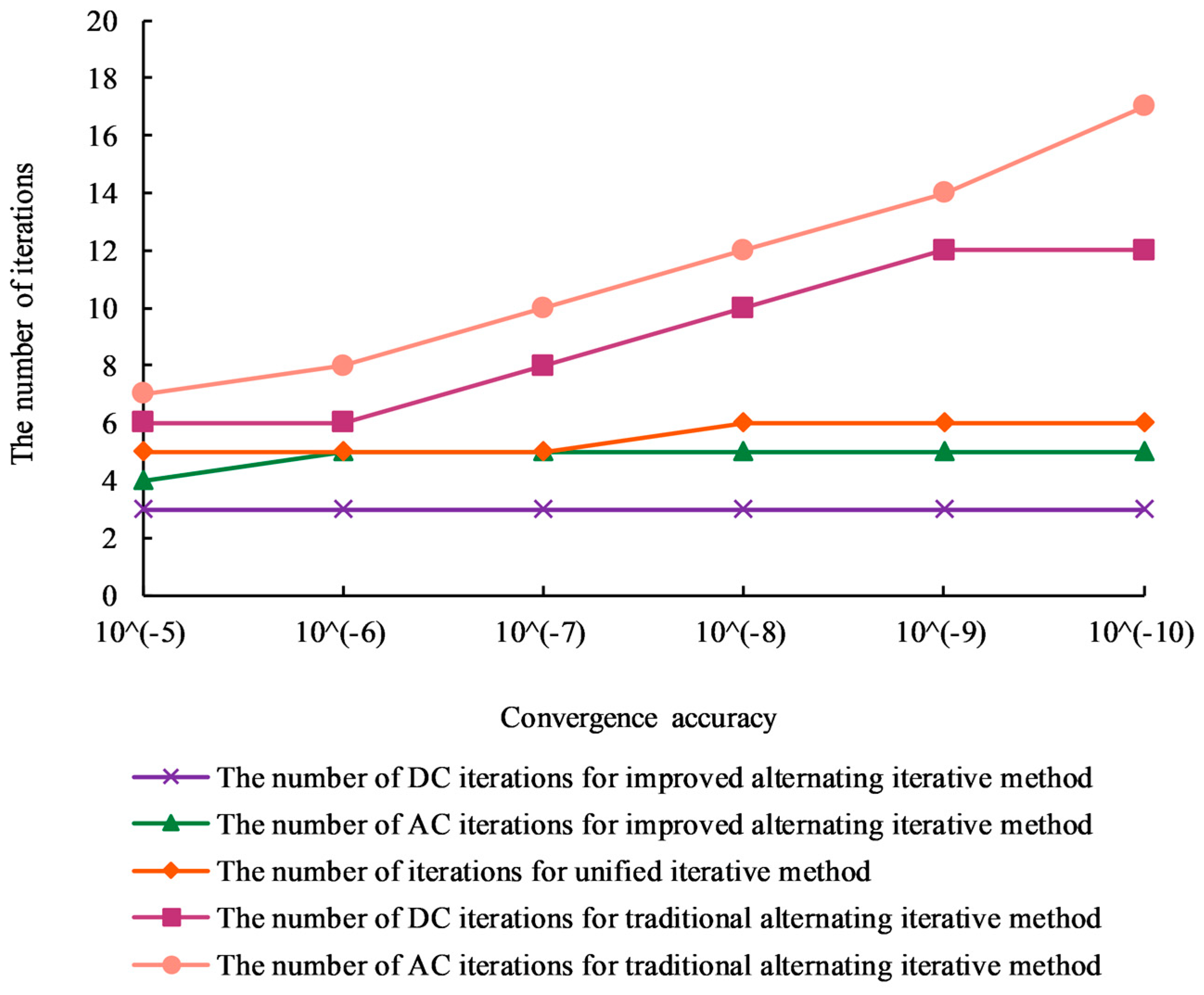
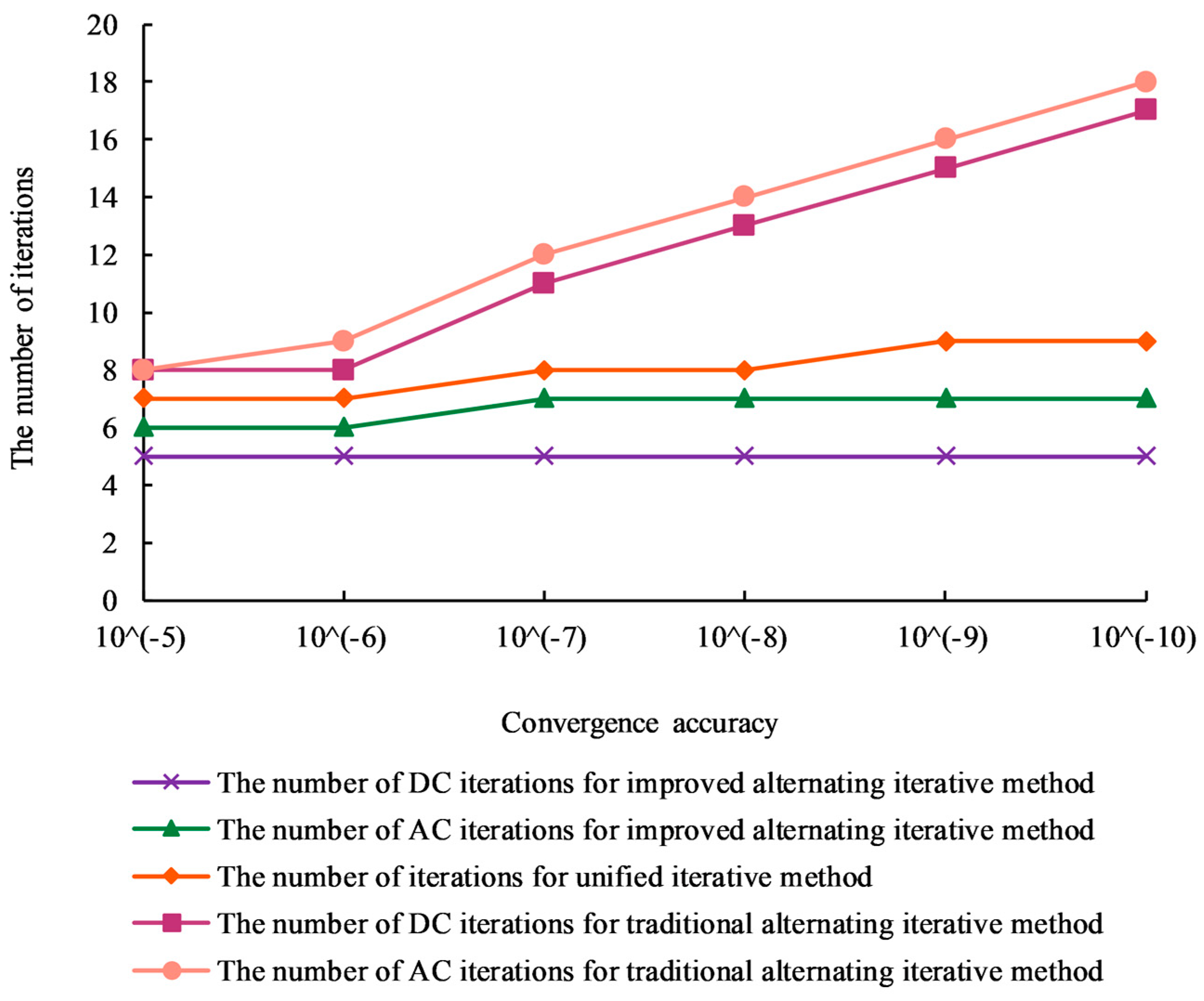
In reference [45], a hybrid AC–DC power-flow alternative iterative algorithm is proposed to solve the current difficulties in the power-flow calculation of LCC–VSC hybrid DC transmission systems. However, the initial value should be reasonably selected to ensure power-flow convergence and accurate results. Figure 10 compares three methods: the method that is proposed in this paper, the traditional alternating iteration method, and the unified iteration method. The number of DC power-flow iterations, the number of AC power-flow iterations, and number of iterations of the improved alternating iterative method are all less than those of the traditional alternating iterative method. Moreover, the improved method is not sensitive to an increase in the convergence precision: the number of iterations remains approximately unchanged. The number of iterations increases linearly with the convergence precision. Compared with the unified iterative method, the method has similar convergence, and the number of iterations does not increase linearly with the accuracy.

Considering the convergence accuracy of 10⁻⁷ as an example, the differences in the Jacobian matrix dimension, the number of iterations, and the calculation time between the traditional AC–DC power-flow algorithm and the proposed algorithm are examined. The results are presented in

Table 10. Comparison results with the conventional algorithms for case 2.

Item		Unified Iteration Method	Alternating Iteration Method	Proposed Algorithm
Convergence accuracy		10−7	10−7	10−7
DC Jacobian Matrix dimension		-	23	5
Number of iterations	AC	5	10	5
	DC		8	3
Calculation time		1.57 s	2.16 s	1.02 s

. According to the table, for case 1, the dimension of the DC Jacobian matrix is reduced by 18 compared with the traditional alternating iteration method. All three methods can converge. Under the same convergence accuracy, the difference in the number of iterations is substantial. The method that is proposed in this paper has the advantages of the unified iteration method in terms of the number of iterations and the convergence speed.

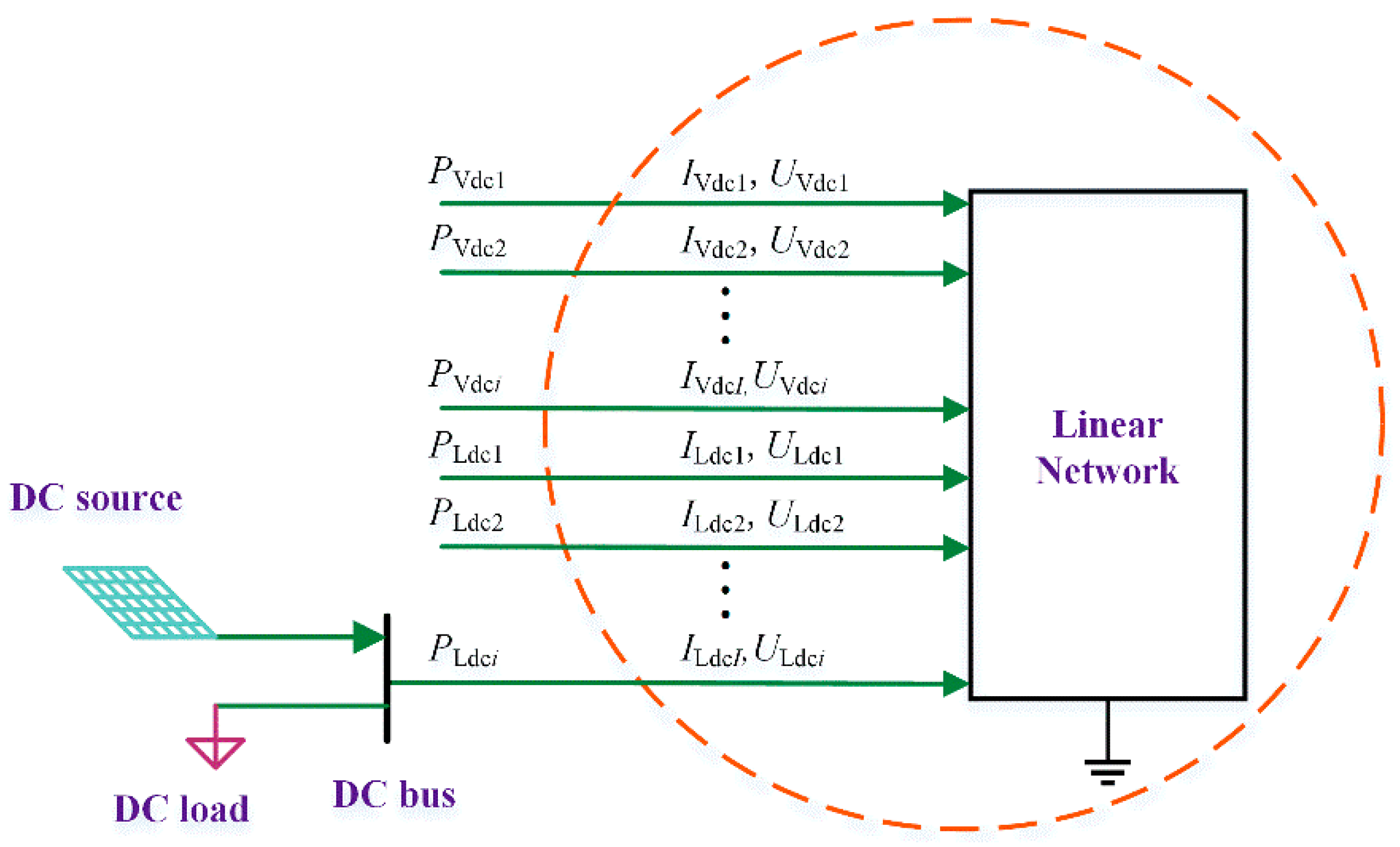
In the power-flow calculation results, the voltage, current, and power of the AC grid are within reasonable ranges. The power flow of the converter station accurately tracks the reference value. The power-flow calculation results of the DC power grid are presented in detail in

Table 11. Power-flow calculation results of the DC power grid (droop control).

Situation	DC Node	1	2
Before the power of DC bus 3 is increased	Uxdc	0.9893	0.9984
	Pxdc	0.4416	1.1142
After the power of DC bus 3 is increased	Uxdc	0.9903	0.9933
	Pxdc	0.7013	0.9573
After changing the droop coefficient	Uxdc	0.9909	0.9989
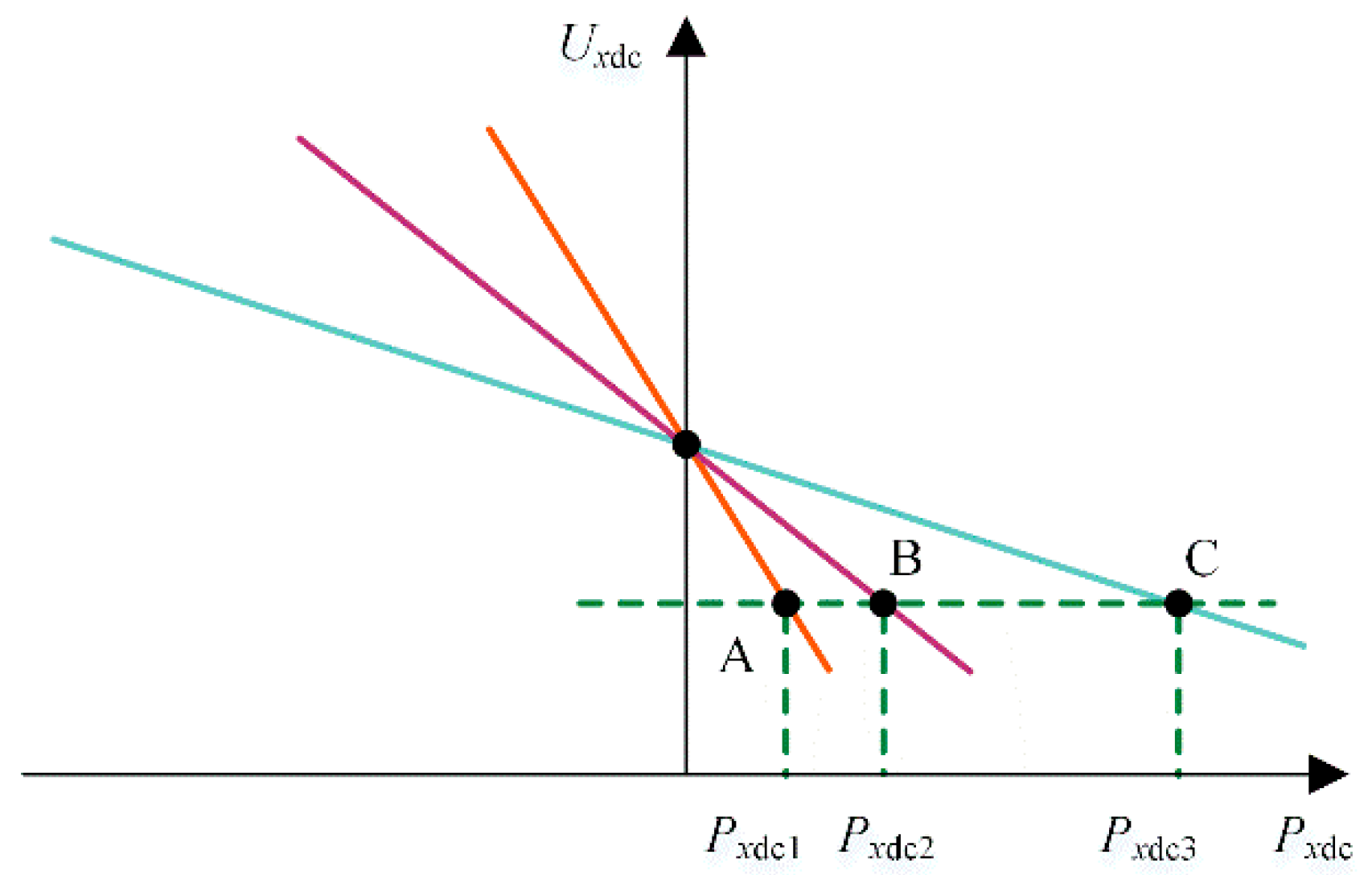
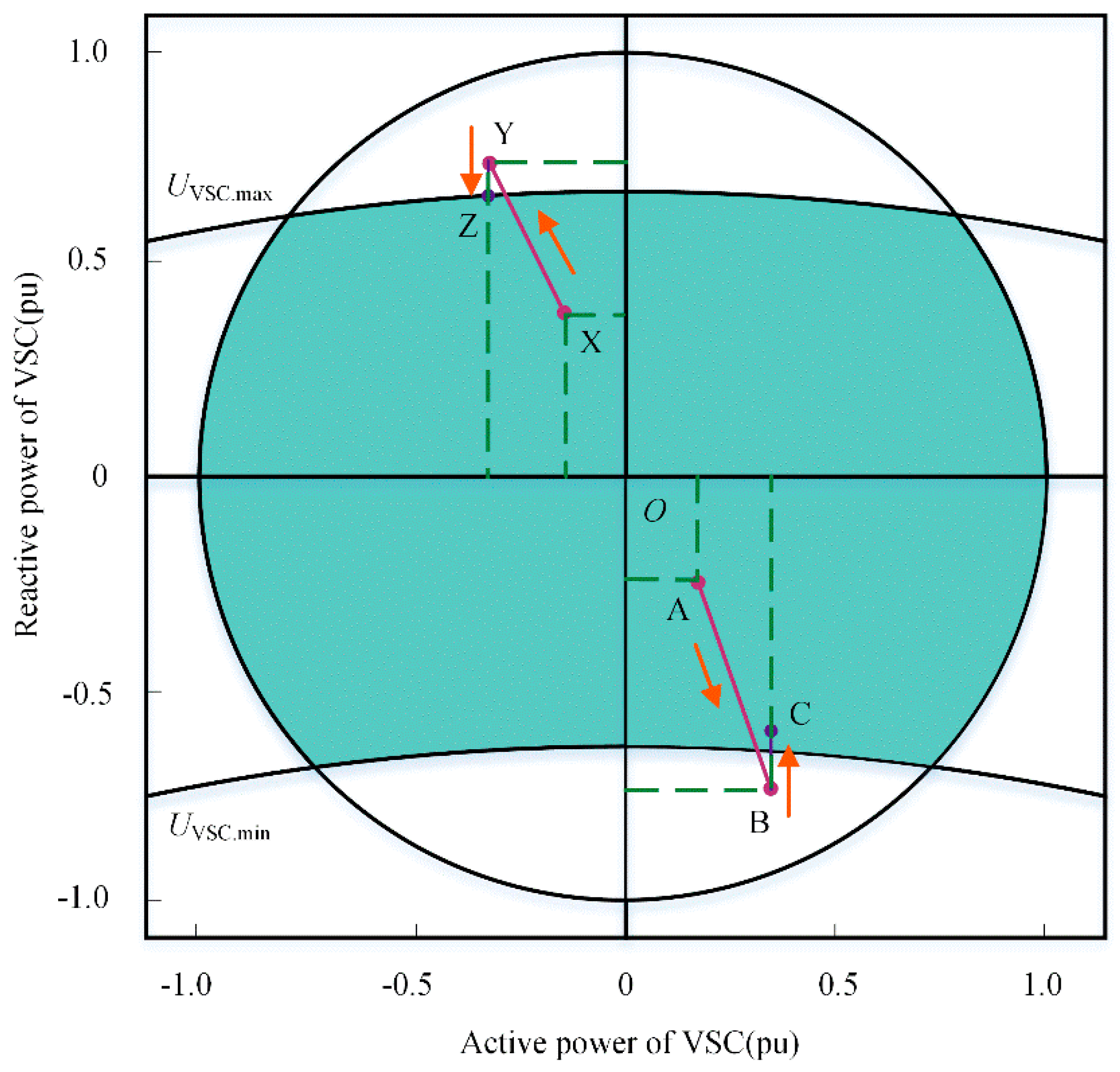
	Pxdc	0.5027	1.0520

, in which the DC voltage and the DC power of DC node 1 and DC node 2 satisfy the droop control characteristics.

If the DC power of DC bus 3 is increased to 0.7, the DC powers of DC bus 1 and DC bus 2 are 0.7013 and 0.9573, respectively, while the original drooping coefficient of the converter station is unchanged. At this time, the voltages of DC bus 1 and DC bus 2 are 0.9903 and 0.9933, respectively. By changing the drooping coefficient, the original drooping coefficients of DC bus 1 and DC bus 2 are reduced by 0.02 and increased by 0.02, respectively. The powers of the DC buses are 0.5027 and 1.0520, and the DC voltages are 0.9909 and 0.9989. The above conditions all satisfy the droop control requirements.

The calculation results demonstrate that the improved alternating iterative method is suitable for single-point voltage control and multipoint voltage droop control and can accurately calculate AC–DC power flow. For the control methods of multipoint voltage control and voltage droop control with a dead zone, the improved method of this paper is still suitable.

The CIGRE B4 node system has 11 AC buses and 14 DC buses. Compared with other DC bus systems, it has more DC buses; hence, it is more suitable for analyzing the improved AC–DC calculation method. Figure 11 compares the proposed method, the traditional alternating iteration method, and the unified iteration method in terms of the number of iterations. With an increase in the number of DC buses, the number of iterations of the improved alternating iterative method does not increase significantly. In contrast, the number of iterations of the traditional alternating iteration method and the unified iteration method increases substantially. Moreover, under the proposed method, with an increase in the convergence precision, the number of iterations remains approximately unchanged. Under the traditional iteration method, with an increase in convergence accuracy, the number of iterations increases more substantially.

Similarly, the convergence accuracy of 10⁻⁷ is considered as an example to illustrate the differences between the traditional AC–DC power-flow algorithm and the proposed algorithm in terms of the Jacobian matrix dimension, the number of iterations, and the calculation time. The results are presented in

Table 12. Comparison results with conventional algorithms for case 3.

Items		Unified Iteration Method	Alternating Iteration Method	Proposed Algorithm
Convergence accuracy		10−7	10−7	10−7
DC Jacobian matrix dimension		-	59	14
Number of iterations	AC	8	12	7
	DC		11	5

. Compared with the traditional alternating iteration method, the dimensions of the DC Jacobian matrix in case 3 are reduced by 45 and the number of iterations is significantly reduced.

5. Conclusions

In traditional alternating iterations, due to the poor coupling between AC and DC, multiple iterations are required to achieve convergence of the power-flow calculation results. With the increasing scale of the DC grid, this problem will become more critical. In light of this situation, based on the traditional alternating iterative method, this paper proposes an improved power-flow calculation algorithm for AC and DC grids with LCCs and VSCs. The main conclusions are as follows:

• In the actual operation of the grid, the method is applicable to various types of converter, various converter control modes, various DC grid control methods, and reasonable adjustments of the DC grid variable constraints and operation modes.
• The converter interface model is divided into the AC side and the DC side, the influence of the DC side on the AC side is considered, and an augmented Jacobian matrix model with LCC/VSC interface equation variables is established. According to the type of converter, control mode, and DC grid strategy, a DC grid power-flow calculation model under various control modes is established to realize an AC–DC power-flow decoupling calculation with LCC/VSC.
• The computation burden of the power-flow calculation of the DC grid is reduced, especially for the calculation of the actual AC and DC power flow with many DC buses, which can reduce the number of iterations, improve the calculation speed, and realize the convergence of unified iteration.